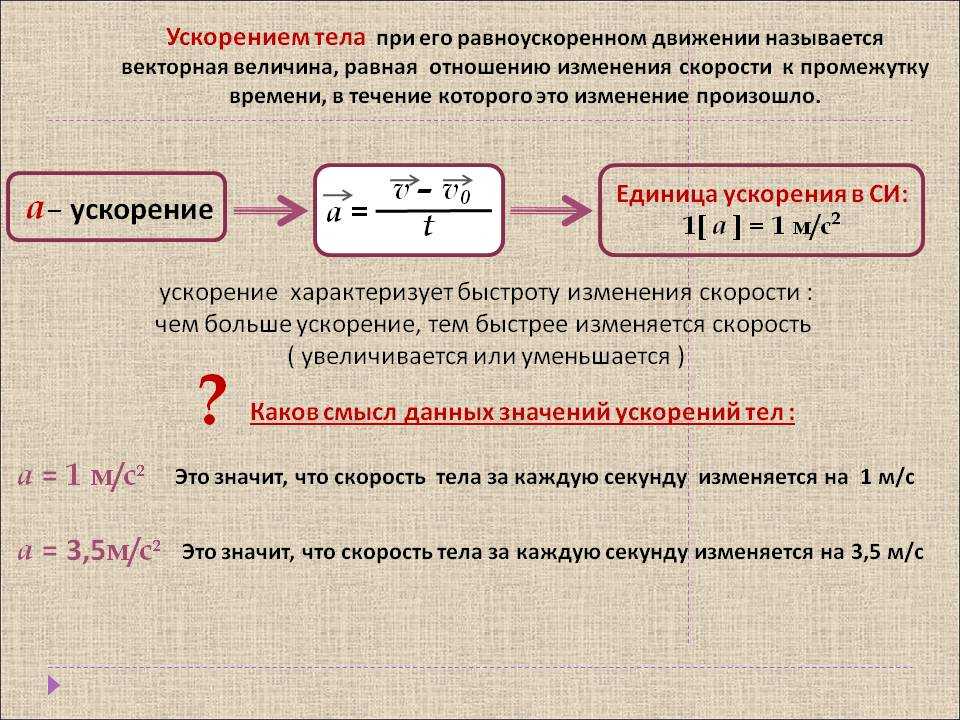
Когда автомобиль тормозит его ускорение направлено: Когда автомобиль тормозит, его ускорение направлено …

Содержание

Автомобиль тормозит на прямолинейном участке дороги. Какое направление имеет вектор ускорения?

Автомобиль тормозит на прямолинейном участке дороги. Какое направление имеет вектор ускорения? Против направления движения автомобиля.

спросил от Вопросы и ответы в категории Естественные науки

Ваш ответ

Отображаемое имя (по желанию):

Отправить мне письмо на это адрес если мой ответ выбран или прокомментирован:Отправить мне письмо если мой ответ выбран или прокомментирован

Конфиденциальность: Ваш электронный адрес будет использоваться только для отправки уведомлений.

Анти-спам проверка:

Чтобы избежать проверки в будущем, пожалуйста войдите или зарегистрируйтесь.

1 Ответ

0 голосов

Против направления движения автомобиля.
Против направления движения автомобиля.
Против направления движения автомобиля.

ответил от reed

Куда направлено ускорение

☰

Ускорение — это быстрота изменения скорости.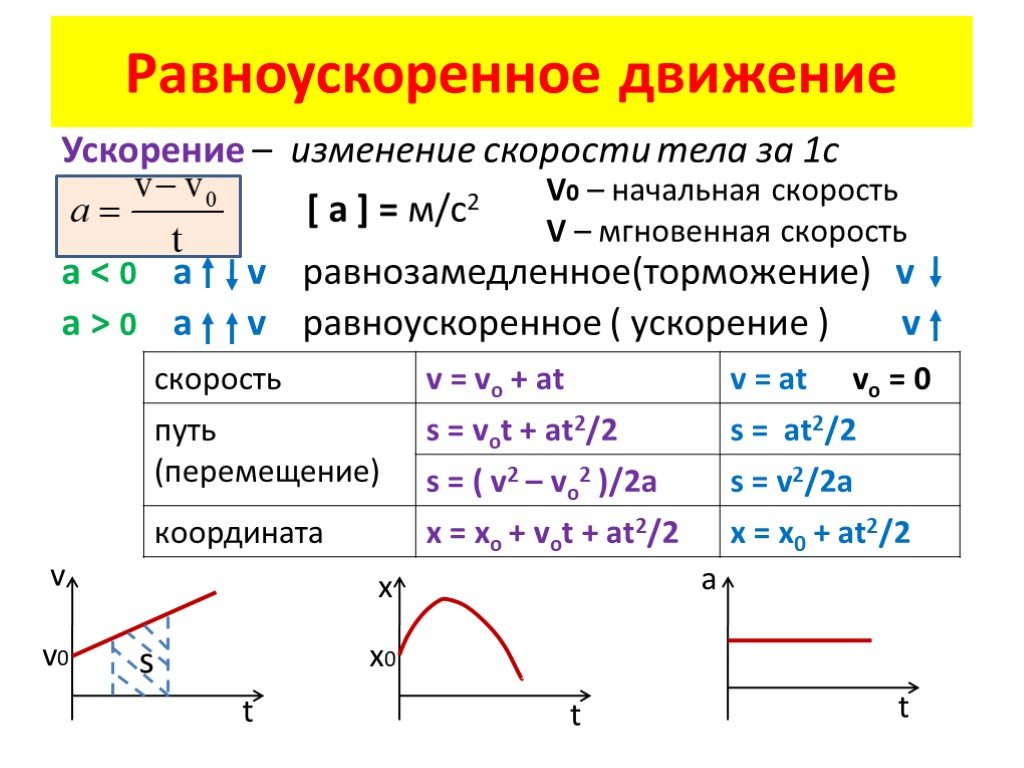 В системе СИ ускорение измеряется в метрах за секунду в квадрате (м/с²), то есть показывает, на сколько изменяется скорость тела за одну секунду.

Если, например, ускорение тела равно 10 м/с², то это значит, что за каждую секунду скорость тела увеличивается на 10 м/с. Так, если до начала ускорения тело двигалось с постоянной скоростью 100 м/с, то после первой секунды движения с ускорением его скорость составит 110 м/с, после второй — 120 м/с и т. д. В данном случае скорость тела постепенно увеличивалась.

Но скорость тела может постепенно и уменьшаться. Обычно так происходит при торможении. Если то же тело, двигавшееся с постоянной скоростью 100 м/с, начинает уменьшать свою скорость на 10 м/с в каждую секунду, то через две секунды его скорость будет равна 80 м/с. А через 10 с тело вообще остановится.

Во втором случае (при торможении) мы можем сказать, что ускорение является отрицательной величиной. Действительно, чтобы найти текущую скорость после начала торможения, надо из начальной скорости вычесть ускорение умноженное на время. Например, какова скорость тела через 6 секунд после торможения? 100 м/с — 10 м/с² · 6 с = 40 м/с.

Поскольку ускорение может принимать как положительные, так и отрицательные значения, то это значит, что ускорение является векторной величиной.

Из рассмотренных примеров мы могли бы сказать, что при разгоне (увеличении скорости) ускорение положительная величина, а при торможении — отрицательная. Однако не так все просто, когда мы имеем дело с системой координат. Здесь скорость тоже оказывается величиной векторной, способной быть как положительной, так и отрицательной. Поэтому то, куда направлено ускорение, зависит от направления скорости, а не от того, уменьшается скорость или увеличивается под действием ускорения.

Если скорость тела направлена в положительном направлении оси координат (скажем, X), то тело за каждую секунду времени увеличивает свою координату. Так, если в момент начала измерения тело находилось в точке с координатой 25 м и начало двигаться с постоянной скоростью 5 м/с в положительном направлении оси X, то через одну секунду тело будет находиться в координате 30 м, через 2 с — 35 м.

Вообще, чтобы найти координату тела в определенный момент времени, надо к начальной координате прибавить скорость умноженную на количество прошедшего времени. Например, 25 м + 5 м/с · 7 с = 60 м. В данном случае тело через 7 секунд окажется в точке с координатой 60. Здесь скорость — положительная величина, так как координата увеличивается.

Скорость отрицательна, когда ее вектор направлен в отрицательном направлении оси координат. Пусть тело из предыдущего примера начало двигаться не в положительном, а в отрицательном направлении оси X с постоянной скоростью. Через 1 с тело будет в точке с координатой 20 м, через 2 с — 15 м и т. д. Теперь чтобы найти координату, надо из начальной вычесть скорость умноженную на время. Например, где будет тело через 8 с? 25 м — 5 м/с · 8 с = -15 м. То есть тело окажется в точке с координатой x, равной -15. В формуле перед скоростью мы ставим знак минус (-5 м/с), значит скорость – отрицательная величина.

Назовем первый случай (когда тело двигается в положительном направлении оси X) A, а второй случай B. Рассмотрим, куда будет направлено ускорение при торможении и разгоне в обоих случаях.

В случае A при разгоне ускорение будет направлено в ту же сторону, что и скорость. Поскольку скорость положительна, то и ускорение будет положительно.

В случае A при торможении ускорение направлено в противоположном скорости направлении. Так как скорость положительная величина, то ускорение — будет отрицательной, то есть вектор ускорения будет направлен в отрицательном направлении оси X.

В случае B при разгоне направление ускорения будет совпадать с направлением скорости, а значит ускорение будет направлено в отрицательном направлении оси X (ведь туда же направлена и скорость). Обратите внимание, несмотря на то, что ускорение отрицательно, оно все же увеличивает модуль скорости.

В случае B при торможении ускорение направлено противоположно скорости. Так как скорость имеет отрицательное направление, то ускорение окажется положительной величиной. Но при этом будет уменьшать модуль скорости. Например, начальная скорость была -20 м/с, ускорение равно 2 м/с². Скорость тела через 3 с, окажется равной -20 м/с + 2 м/с² · 3 с = -14 м/с.

Таким образом, ответ на вопрос «куда направлено ускорение» зависит от того, по отношению к чему оно рассматривается. По отношению к скорости ускорение может быть направлено в ту же сторону, что и скорость (при разгоне), или в противоположную сторону (при торможении).

В системе координат положительное и отрицательное ускорение само по себе ничего не говорит от том, тормозило ли тело (уменьшало свою скорость) или разгонялось (увеличивало скорость). Надо смотреть на то, куда направлена скорость.

Ускорение | Физика

Цели обучения

К концу этого раздела вы сможете:

Определять и различать мгновенное ускорение, среднее ускорение и замедление.
Вычислить ускорение, зная начальное время, начальную скорость, конечное время и конечную скорость.

Рис. 1. Самолет снижает скорость или замедляется перед посадкой на Сен-Мартене. Его ускорение противоположно направлению его скорости. (кредит: Стив Конри, Flickr)

В повседневном разговоре ускорить означает ускорить. Ускоритель в автомобиле фактически может заставить его ускориться. Чем больше ускорение , тем больше изменение скорости за заданное время. Формальное определение ускорения соответствует этим понятиям, но более широкое.

Среднее ускорение

Среднее ускорение равно скорости изменения скорости ,

[латекс]\bar{a}=\frac{\Delta v}{\Delta t}=\frac{{ v}_{f}-{v}_{0}}{{t}_{f}-{t}_{0}}[/latex]

, где [латекс]\бар{а}[/латекс] — среднее ускорение, v — скорость, а t — время. (Полоса над и означает среднее ускорение .)

Поскольку ускорение представляет собой скорость в м/с, деленную на время в с, единицами СИ для ускорения являются м/с ² , метры в секунду в квадрате или метры в секунду в секунду, что буквально означает, на сколько метров в секунду скорость изменяется каждую секунду.

Вспомните, что скорость — это вектор, у него есть и величина, и направление. Это означает, что изменение скорости может быть изменением величины (или скорости), но оно также может быть изменением направления . Например, если автомобиль поворачивает с постоянной скоростью, он ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение происходит, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по тому и другому.

Ускорение как вектор

Ускорение является вектором в том же направлении, что и изменение скорости, Δ v . Поскольку скорость является вектором, она может изменяться как по величине, так и по направлению. Таким образом, ускорение — это изменение либо скорости, либо направления, либо того и другого.

Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда совпадает с направлением движения . Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление .

Рис. 2. Поезд метро в Сан-Паулу, Бразилия, замедляет скорость перед въездом на станцию. Он ускоряется в направлении, противоположном направлению его движения. (кредит: Юсуке Кавасаки, Flickr)

Предупреждение о неправильном понимании: замедление против отрицательного ускорения

Замедление всегда относится к ускорению в направлении, противоположном направлению скорости. Замедление всегда снижает скорость. Однако отрицательное ускорение равно ускорению в отрицательном направлении в выбранной системе координат . Отрицательное ускорение может быть, а может и не быть замедлением, а замедление может считаться или не считаться отрицательным ускорением. Например, рассмотрим рисунок 3.

Рисунок 3. (a) Этот автомобиль ускоряется, двигаясь вправо. Поэтому он имеет положительное ускорение в нашей системе координат. (b) Этот автомобиль замедляется, когда он движется вправо. Следовательно, в нашей системе координат он имеет отрицательное ускорение, потому что его ускорение направлено влево. Автомобиль тоже тормозит: направление его ускорения противоположно направлению его движения. (c) Этот автомобиль движется влево, но со временем замедляется. Следовательно, его ускорение положительно в нашей системе координат, потому что оно направлено вправо. Однако автомобиль замедляется, потому что его ускорение противоположно его движению. (d) Этот автомобиль ускоряется, когда он движется влево. Он имеет отрицательное ускорение, потому что он ускоряется влево. Однако, поскольку его ускорение направлено в том же направлении, что и его движение, оно ускоряется (а не замедляется).

Пример 1. Расчет ускорения: скаковая лошадь выезжает из ворот

Рис. 4. (кредит: Джон Салливан, PD Photo.org)

Скаковая лошадь, выйдя из ворот, разгоняется из состояния покоя до скорости 15,0 м/ с на запад через 1,80 с. Каково его среднее ускорение?

Стратегия

Сначала мы рисуем эскиз и назначаем проблеме систему координат. Это простая задача, но ее всегда полезно визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.

Рисунок 5.

Мы можем решить эту задачу, определив Δ v и Δ t по имеющейся информации, а затем рассчитав среднее ускорение непосредственно из уравнения [латекс]\bar{a}=\frac{\ Delta v}{\Delta t}=\frac{{v}_{f}-{v}_{0}}{{t}_{f}-{t}_{0}}[/latex].

Решение

1. Определите известные. v ₀ = 0, v _f = −15,0 м/с (знак минус указывает направление на запад), Δ 9{2}[/latex]

Обсуждение

Отрицательный знак ускорения означает, что ускорение направлено на запад. Ускорение 8,33 м/с ² строго на запад означает, что лошадь увеличивает свою скорость на 8,33 м/с строго на запад каждую секунду, то есть на 8,33 метра в секунду в секунду, что мы записываем как 8,33 м/с ². . Это действительно среднее ускорение, потому что езда не плавная. Позже мы увидим, что ускорение такой величины потребовало бы, чтобы всадник удерживался с силой, почти равной его весу.

Мгновенное ускорение

Мгновенное ускорение a , или ускорение в определенный момент времени , получается тем же процессом, который обсуждался для мгновенной скорости во времени, скорости и скорости, т. е. рассматривая бесконечно малый отрезок времени. Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рис. 6 показаны графики зависимости мгновенного ускорения от времени для двух очень разных движений. На рис. 6(а) ускорение немного меняется, и среднее значение по всему интервалу почти такое же, как мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение так, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около 1,8 м/с ²). На рисунке 6(b) ускорение резко меняется со временем. В таких ситуациях лучше рассматривать меньшие временные интервалы и выбирать для каждого среднее ускорение. Например, движение на интервалах времени от 0 до 1,0 с и от 1,0 до 3,0 с можно рассматривать как отдельные движения с ускорениями +3,0 м/с ² и –2,0 м/с ² соответственно.

Рис. 6. Графики зависимости мгновенного ускорения от времени для двух различных одномерных движений. а) Здесь ускорение меняется незначительно и всегда в одном и том же направлении, так как оно положительно. Среднее значение по интервалу почти такое же, как ускорение в любой момент времени. (b) Здесь ускорение сильно различается, возможно, представляя посылку на ленточном конвейере почтового отделения, которая ускоряется вперед и назад, когда она толкается. В такой ситуации необходимо рассматривать небольшие промежутки времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.

В следующих нескольких примерах рассматривается движение поезда метро, показанного на рис. 7. В (а) шаттл движется вправо, а в (б) — влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые рассуждения, которые используются при решении задач.

Рис. 7. Одномерное движение поезда метро, рассмотренное в примере 2, примере 3, примере 4, примере 5, примере 6 и примере 7. Здесь мы выбрали ось x так, что + означает вправо, а − означает влево для перемещений, скоростей и ускорений. (a) Поезд метро движется вправо из x0 в xf. Его водоизмещение Δx равно +2,0 км. (b) Поезд движется влево от x′0 до x′f. Его смещение Δx′ равно −1,5 км. (Обратите внимание, что штриховой символ (′) используется просто для того, чтобы различить перемещение в двух разных ситуациях. Для того, чтобы все отображалось на диаграмме, расстояния и размеры автомобилей представлены в разных масштабах.)

Пример 2. Расчет перемещения: поезд метро

Каковы величина и знак перемещений поезда метро, показанного в частях (а) и (б) на рис. 7?

Стратегия

Чертеж с системой координат уже предоставлен, поэтому нам не нужно делать эскиз, но мы должны проанализировать его, чтобы убедиться, что мы понимаем, что он показывает. Обратите особое внимание на систему координат. Для нахождения смещения воспользуемся уравнением ∆ x = x _f − x ₀ . Это просто, поскольку заданы начальная и конечная позиции.

Решение

1. Определите известные. In the figure we see that x _f = 6.70 km and x ₀ = 4.70 km for part (a), and x ′ _f = 3.75 km and x ′ ₀ = 5,25 км для участка (b).

2. Найдите смещение в части (a).

[латекс]\Delta x={x}_{f}-{x}_{0}=6,70\text{км}-4,70\text{км} = \text{+}2,00\text{км} [/latex]

3. Решите для смещения в части (b).

[латекс]\Delta x′ ={x′}_{f}-{x′}_{0}=\text{3,75 км}-\text{5,25 км} = -\text{1,50 км}[ /латекс]

Обсуждение

Направление движения в (а) — вправо, и поэтому его смещение имеет положительный знак, тогда как движение в (б) — влево и, следовательно, имеет отрицательный знак.

Пример 3. Сравнение пройденного расстояния с перемещением: поезд метро

Каковы расстояния, пройденные при движениях, показанных в частях (а) и (б) поезда метро на рисунке 7?

Стратегия

Чтобы ответить на этот вопрос, подумайте об определениях расстояния и пройденного расстояния и о том, как они связаны с перемещением. Расстояние между двумя положениями определяется как величина смещения, которое было найдено в примере 1. Пройденное расстояние — это общая длина пути, пройденного между двумя положениями. (См. Перемещение.) В случае поезда метро, показанного на рисунке 7, пройденное расстояние равно расстоянию между начальным и конечным положениями поезда.

Решение

1. Перемещение по части (а) составило +2,00 км. Следовательно, расстояние между начальным и конечным положениями составило 2,00 км, а пройденное расстояние составило 2,00 км.

2. Перемещение по части (b) составило −1,5 км. Следовательно, расстояние между начальным и конечным положениями составило 1,50 км, а пройденное расстояние — 1,50 км.

Обсуждение

Расстояние является скаляром. У него есть величина, но нет знака, указывающего направление.

Пример 4. Расчет ускорения: поезд метро разгоняется

Предположим, что поезд на рис. 7(а) разгоняется из состояния покоя до 30,0 км/ч за первые 20,0 с своего движения. Каково его среднее ускорение за этот промежуток времени?

Стратегия

Сейчас стоит сделать простой набросок:

Рисунок 8. Эта задача состоит из трех шагов. Сначала мы должны определить изменение скорости, затем мы должны определить изменение времени и, наконец, мы используем эти значения для расчета ускорения.

Решение

1. Найдите известные. v ₀ = 0 (поезда отправляются из состояния покоя), v _f = 30,0 км/ч, Δ t = 20,0 с.

2. Вычислить Δ v . Поскольку поезд стартует из состояния покоя, его скорость изменится на [latex]\Delta v\text{=}\text{+}\text{30,0 км/ч}[/latex], где плюс означает скорость вправо .

3. Подставьте известные значения и найдите неизвестное, [латекс]\бар{а}[/латекс]. 9{2}[/latex]

Обсуждение

Знак плюс означает, что ускорение направлено вправо. Это разумно, потому что поезд стартует из состояния покоя и заканчивается со скоростью вправо (тоже положительной). Таким образом, ускорение происходит в том же направлении, что и изменение скорости, как это всегда и бывает.

Пример 5. Расчет ускорения: поезд метро замедляется

Теперь предположим, что в конце пути поезд на рис. 7(а) замедляется до полной остановки со скорости 30,0 км/ч за 8,00 с. Каково его среднее ускорение при остановке?

Стратегия

Рис. 9. В этом случае поезд замедляется, и его ускорение отрицательно, потому что он движется влево. Как и в предыдущем примере, мы должны найти изменение скорости и изменение времени, а затем найти ускорение.

Решение

1. Определите известные. v ₀ = 30,0 км/ч, v _f = 0 км/ч (поезд стоит, поэтому его скорость равна 0), а Δ t = 8,00 с.

2. Решите изменение скорости, Δ v .

Δ V = V _F — V ₀ = 0 — 30,0 км/ч = — 30,0 км/ч

3. Подключа и найдите [латекс]\бар{а}[/латекс].

[латекс]\bar{a}=\frac{\Delta v}{\Delta t}=\frac{-\text{30}\text{.}\text{0 км/ч}}{8\ text{.}\text{00 s}}[/latex]

4. Преобразуйте единицы измерения в метры и секунды. 9{2}\text{.}[/latex]

Обсуждение

Знак минус указывает, что ускорение направлено влево. Этот знак разумен, поскольку в этой задаче поезд изначально имеет положительную скорость, а отрицательное ускорение будет препятствовать движению. Опять же, ускорение происходит в том же направлении, что и изменение скорости, которая здесь отрицательная. Это ускорение можно назвать замедлением, потому что оно имеет направление, противоположное скорости.

Графики зависимости положения, скорости и ускорения от времени для поездов в Примере 4 и Примере 5 показаны на рисунке 10. (Мы приняли, что скорость остается постоянной от 20 до 40 с, после чего поезд замедляется. )

Рис. 10. (а) Положение поезда во времени. Обратите внимание, что положение поезда меняется медленно в начале пути, а затем все быстрее и быстрее по мере того, как он набирает скорость. Затем его положение меняется медленнее, так как он замедляется в конце пути. В середине пути, пока скорость остается постоянной, положение изменяется с постоянной скоростью. (b) Скорость поезда во времени. Скорость поезда увеличивается по мере того, как он ускоряется в начале пути. Он остается таким же в середине пути (где нет ускорения). Она уменьшается по мере торможения поезда в конце пути. в) ускорение поезда во времени. Поезд имеет положительное ускорение, так как в начале пути он ускоряется. Он не имеет ускорения, так как в середине пути движется с постоянной скоростью. Его ускорение отрицательно, так как в конце пути оно замедляется.

Пример 6. Вычисление средней скорости поезда метро

Какова средняя скорость поезда в части b примера 2, показанном еще раз ниже, если путь до места занимает 5,00 мин?

Рисунок 11.

Стратегия

Средняя скорость равна смещению, деленному на время. Здесь оно будет отрицательным, так как поезд движется влево и имеет отрицательное смещение.

Решение

1. Определите известные. x ′ _f = 3,75 км, x ′ ₀ = 5,25 км, Δ t = 5,00 мин.

2. Определить перемещение, Δ x ′. В Примере 2 мы нашли, что Δ x ′ равно −1,5 км.

3. Найдите среднюю скорость.

[латекс]\bar{v}=\frac{\Delta x′}{\Delta t}=\frac{-\text{1,50 км}}{\text{5,00 мин}}[/latex]

4. Преобразование единиц.

[латекс]\bar{v}=\frac{\Delta x′}{\Delta t}=\left(\frac{-1\text{. }\text{50 км}}{5\text{ .}\text{00 мин}}\right)\left(\frac{\text{60 мин}}{1 ч}\right)=-\text{18}\text{0,0 км/ч}[/ латекс]

Обсуждение

Отрицательная скорость указывает на движение влево.

Пример 7. Расчет замедления: поезд метро

Наконец, предположим, что поезд на рисунке 2 замедляется до полной остановки со скорости 20,0 км/ч за 10,0 с. Каково его среднее ускорение?

Стратегия

Еще раз нарисуем набросок:

Рис. 12.

Как и прежде, мы должны найти изменение скорости и изменение времени для расчета среднего ускорения.

Решение

1. Найдите известные. v ₀ = −20 км/ч, v _f = 0 км/ч, Δ t = 10,0 с.

2. Вычислить Δ v . Изменение скорости здесь действительно положительное, так как

[латекс]\Delta v={v}_{f}-{v}_{0}=0-\left(-\text{20 км/ч}\ right)\text{=}\phantom{\rule{0.25}{0ex}}\text{+}\text{20 км/ч}[/latex]

3. Найдите [латекс]\bar{a} [/латекс].

[латекс]\bar{a}=\frac{\Delta v}{\Delta t}=\frac{+\text{20}\text{0,0 км/ч}}{\text{10}\ текст{.}0 с}[/латекс] 9{2}[/latex]

Обсуждение

Знак плюс означает, что ускорение направлено вправо. Это разумно, потому что поезд изначально имеет отрицательную скорость (влево) в этой задаче, а положительное ускорение противодействует движению (и, следовательно, вправо). Опять же, ускорение происходит в том же направлении, что и изменение скорости, которая здесь положительна. Как и в примере 5, это ускорение можно назвать замедлением, поскольку оно происходит в направлении, противоположном скорости.

Знак и направление

Пожалуй, самое важное, что следует отметить в этих примерах, — это знаки ответов. В выбранной нами системе координат плюс означает, что величина находится справа, а минус означает, что она находится слева. Это легко представить для смещения и скорости. Но это немного менее очевидно для ускорения. Большинство людей интерпретируют отрицательное ускорение как замедление объекта. Этого не было в примере 2, где положительное ускорение замедляло отрицательную скорость. Решающим отличием было то, что ускорение было в направлении, противоположном скорости. В самом деле, отрицательное ускорение будет увеличить отрицательную скорость. Например, поезд, движущийся влево на рисунке 11, ускоряется за счет ускорения влево. В этом случае как v , так и a отрицательны. Знаки плюс и минус указывают направления ускорений. Если ускорение имеет тот же знак, что и изменение скорости, то тело ускоряется. Если ускорение имеет знак, противоположный изменению скорости, то тело замедляется.

Проверьте свое понимание

Самолет приземляется на взлетно-посадочную полосу, летящую на восток. Опишите его ускорение.

Решение

Если мы возьмем восток за положительное значение, то ускорение самолета будет отрицательным, поскольку он движется на запад. Он также замедляется: его ускорение противоположно направлению его скорости.

Исследования PhET: Моделирование движущегося человека

Узнайте о графиках положения, скорости и ускорения. Перемещайте человечка вперед-назад с помощью мыши и зарисовывайте его движение. Установите положение, скорость или ускорение, и пусть симуляция переместит человека за вас.

Нажмите, чтобы загрузить симуляцию. Запуск с использованием Java.

Резюме раздела

Концептуальные вопросы

1. Возможно ли, чтобы скорость была постоянной, а ускорение не равно нулю? Приведите пример такой ситуации.

2. Может ли скорость быть постоянной, а ускорение не равным нулю? Объяснять.

3. Приведите пример, в котором скорость равна нулю, а ускорение – нет.

4. Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, то как направлено его ускорение? Ускорение положительное или отрицательное?

5. Знаки плюс и минус используются в одномерном движении для указания направления. Каков знак ускорения, уменьшающего модуль отрицательной скорости? положительной скорости?

Задачи и упражнения

1. Гепард может разогнаться из состояния покоя до скорости 30,0 м/с за 7,00 с. Каково его ускорение?

2. Профессиональное приложение. Доктор Джон Пол Стэпп был офицером ВВС США, изучавшим влияние экстремального замедления на организм человека. 10 декабря 1954, Стапп ехал на ракетных салазках, разгоняясь из состояния покоя до максимальной скорости 282 м/с (1015 км/ч) за 5,00 с, и резко возвращался в состояние покоя всего за 1,40 с! Вычислите его ускорение (а) и замедление (б). Выразите каждое число кратным г (9,80 м/с ² ), взяв его отношение к ускорению свободного падения.

3. Пассажирка выезжает из гаража задним ходом с ускорением 1,40 м/с ² .(a) Сколько времени потребуется ей, чтобы достичь скорости 2,00 м/с? (b) Если она затем затормозится до полной остановки через 0,800 с, каково ее замедление?

4. Предположим, что межконтинентальная баллистическая ракета выходит из состояния покоя до суборбитальной скорости 6,50 км/с за 60,0 с (фактическая скорость и время засекречены). Каково его среднее ускорение в м/с ² и в кратных g (9,80 м/с ² ).

Глоссарий

ускорение:: скорость изменения скорости; изменение скорости во времени

среднее ускорение:: изменение скорости, деленное на время, за которое она изменяется

мгновенное ускорение:: ускорение в определенный момент времени

замедление:: ускорение в направлении, противоположном скорости; ускорение, приводящее к уменьшению скорости

Избранные решения задач и упражнений

1. 4,29 м/с ²

3. (a) 1,43 с (b) -2,50 м/с ²

Примеры

Ускорение — важное понятие в физике, используемое для описания движения и решения задач. В этой статье мы определим ускорение, формулу ускорения и его единицы. Мы рассмотрим примеры того, как найти ускорение, включая положительное ускорение и отрицательное ускорение.

Заинтересованы в лицензии школы Альберта?

Что мы рассматриваем

Обзор: кинематические термины

Есть несколько кинематических терминов, которые вам необходимо знать, чтобы понимать ускорение. Первый кинематический термин — скорость. Скорость — это скорость изменения положения или перемещения во времени. Смещение — другое название изменения положения. Помните, что объект, движущийся с постоянной скоростью, постоянно меняет свое положение каждую секунду. Карта движения ниже показывает объект, движущийся с постоянной скоростью.

Также важно помнить определение векторных величин. Векторы — это величины, которые имеют как величину, или размер, так и направление. Например, скорость является векторной величиной, потому что она описывает как скорость движения объекта (величина), так и направление, в котором движется объект. Подробный обзор векторов, скаляров, смещения и скорости можно найти в нашем блоге Альберта. сообщение введение кинематики.

Исследуйте скалярную и векторную практику на Альберте

Что такое ускорение?

Ускорение определяется как скорость изменения скорости. Это означает, что если скорость объекта увеличивается или уменьшается, то объект ускоряется. В отличие от объекта, движущегося с постоянной скоростью, ускоряющийся объект не будет иметь постоянного изменения положения каждую секунду. Ускоряющийся объект может преодолевать все большее и большее расстояние с каждой секундой или все меньше и меньше расстояния с каждой секундой. Первая карта движения ниже показывает ускоряющийся объект, который ускоряется, а вторая карта движения показывает ускоряющийся объект, который замедляется. 92. Эти единицы происходят от единиц скорости, метров в секунду, и единиц времени, секунд. Поскольку ускорение — это изменение скорости во времени, его единицами измерения являются единицы скорости (метры в секунду), деленные на единицы времени (секунды).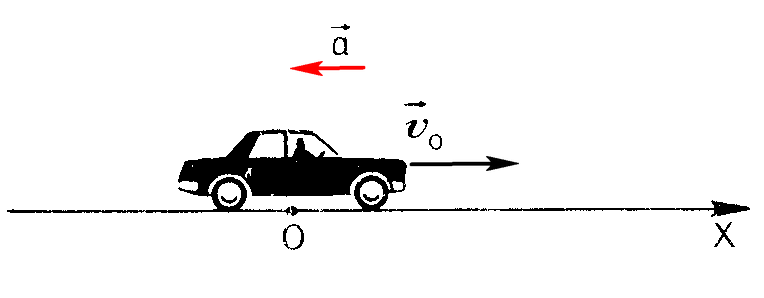

Для получения дополнительной информации об ускорении и некоторых примеров просмотрите это короткое видео.

Формула ускорения

Используя наше определение ускорения, мы можем составить формулу для расчета ускорения.

Формула ускорения
a=\dfrac{\Delta v}{t}

Здесь a — ускорение, \Delta v — изменение скорости, t — время.

Прежде чем вычислять ускорение, вам часто нужно сначала вычислить изменение скорости. Это разница между конечной скоростью объекта, v_f, и его начальной скоростью, v_i.

Формула изменения скорости
\Delta v = v_f — v_i

Как найти ускорение

В следующем разделе мы рассмотрим несколько примеров расчета ускорения. Сначала мы увидим пример положительного ускорения, затем пример отрицательного ускорения.

Пример 1: Как найти ускорение автомобиля, ускоряющегося

Автомобиль трогается с места и движется вперед, разогнавшись до 26\text{ м/с} за 8\text{ с}. Вычислите ускорение автомобиля.

Первым шагом в решении этой задачи является определение изменения скорости. Поскольку автомобиль стартовал из состояния покоя, его начальная скорость v_i равна 0\text{ м/с}. Его конечная скорость 26\text{ м/с}. Следовательно, изменение скорости автомобиля равно: 92

Пример 2. Как найти ускорение замедляющегося автомобиля

Теперь давайте рассмотрим ситуацию, когда объект замедляется.

Автомобиль, первоначально двигавшийся вперед со скоростью 26\text{ м/с}, приближается к школе и замедляется до скорости 11\text{ м/с} за 3\text{ с}. Вычислите ускорение автомобиля.

Первый шаг — найти изменение скорости. Начальная скорость автомобиля 26\text{ м/с}, а конечная скорость 11\text{ м/с}.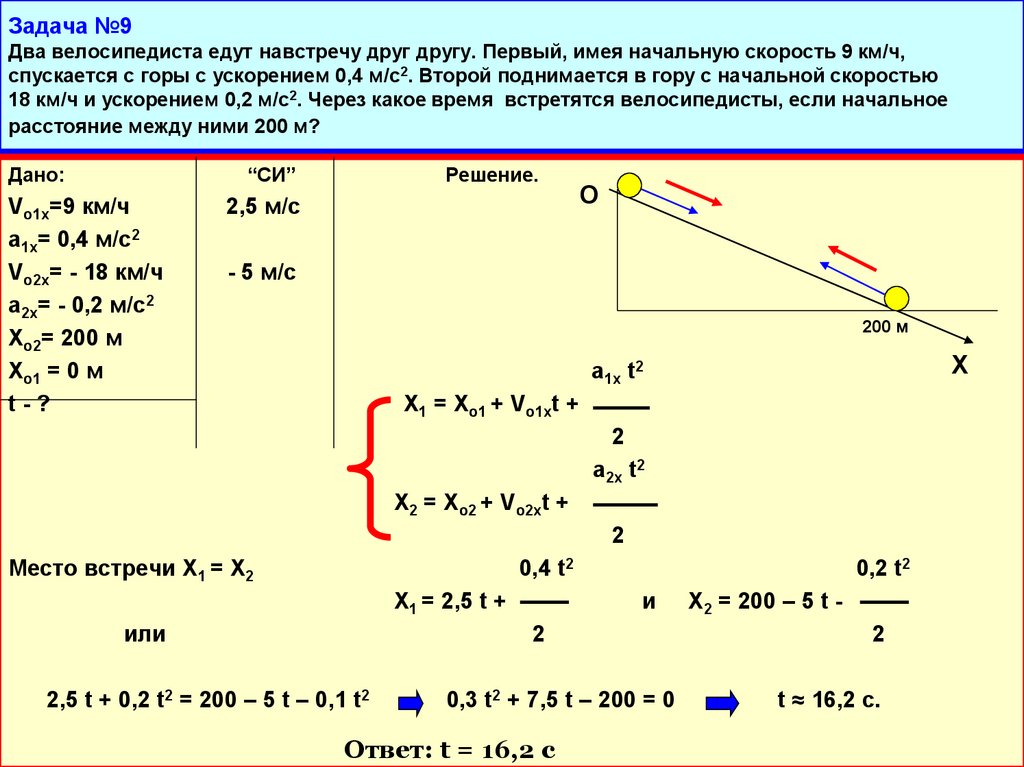 Следовательно, изменение скорости автомобиля равно: 92

В следующем разделе мы более подробно объясним, что означает отрицательное ускорение.

Изучение практики ускорения на Альберте

Определение направления ускорения

Как векторная величина, ускорение имеет как величину, так и направление. Направление ускорения зависит от того, ускоряется или замедляется объект, а также от направления движения объекта. В общем, если объект ускоряется, его ускорение будет в том же направлении, что и его движение. Если объект замедляется, его ускорение происходит в направлении, противоположном его движению.

Примеры положительного ускорения

Существует два типа ситуаций, когда объект может иметь положительное ускорение. Если объект ускоряется и движется в положительном направлении, он имеет положительное ускорение. Автомобиль, ускоряющийся в первом примере, был примером положительного ускорения. Автомобиль движется вперед в положительном направлении и ускоряется, поэтому ускорение совпадает с направлением движения автомобиля.

Объект также может иметь положительное ускорение, если он замедляется при движении в отрицательном направлении. Поскольку объект замедляется, ускорение направлено в сторону, противоположную его движению.

Примеры отрицательного ускорения

Как мы видели во втором примере, объект может иметь отрицательное ускорение, когда объект замедляется при движении в положительном направлении. Автомобиль в школьной зоне двигался вперед в положительном направлении и замедлялся, поэтому ускорение было в направлении, противоположном движению автомобиля.

Объект также может иметь отрицательное ускорение, если он ускоряется при движении в отрицательном направлении. Поскольку объект ускоряется, его ускорение совпадает с направлением его движения.

Заинтересованы в лицензии школы Альберта?

Использование формулы ускорения

Теперь, когда мы рассмотрели ускорение и то, как найти его величину и направление, мы можем применить эти знания для решения более сложных задач по физике.

Пример 1. Как найти ускорение падающего мяча

Мяч, брошенный из состояния покоя, достигает скорости падения 24,5\text{ м/с} после падения в течение 2,5\text{ с}. Какова величина и направление ускорения мяча? 92)(1,5\текст{с})=9\текст{м/с}

Изменение скорости — это разница между конечной и начальной скоростями объекта. Используя наше изменение скорости и начальную скорость скейтбордиста, получаем:

\Delta v = v_f — v_i

9\текст{м/с}=v_f-(2\текст{м/с})

Последним шагом для определения конечной скорости является добавление начальной скорости к изменению скорости:

v_f=9\text{ м/с}+2\text{ м/с}=11\text{ м /с}

Следовательно, конечная скорость скейтбордиста 11\text{ м/с} направлена вниз по рампе.

Дополнительные примеры кинематики на Альберте

Уравнения кинематики

Теперь, когда вы знаете все четыре кинематических термина (время, перемещение, скорость и ускорение), вы сможете более полно описать движение объектов.

Когда автомобиль тормозит его ускорение направлено: Когда автомобиль тормозит, его ускорение направлено …

Автомобиль тормозит на прямолинейном участке дороги. Какое направление имеет вектор ускорения?

Ваш ответ

1 Ответ

Похожие вопросы

Куда направлено ускорение

Ускорение | Физика

Цели обучения

Пример 1. Расчет ускорения: скаковая лошадь выезжает из ворот

Мгновенное ускорение

Пример 2. Расчет перемещения: поезд метро

Пример 3. Сравнение пройденного расстояния с перемещением: поезд метро

Пример 4. Расчет ускорения: поезд метро разгоняется

Пример 5. Расчет ускорения: поезд метро замедляется

Пример 6. Вычисление средней скорости поезда метро

Пример 7. Расчет замедления: поезд метро

Знак и направление

Проверьте свое понимание

Исследования PhET: Моделирование движущегося человека

Резюме раздела

Концептуальные вопросы

Задачи и упражнения

Глоссарий

Избранные решения задач и упражнений

Примеры

Пример 1: Как найти ускорение автомобиля, ускоряющегося

Пример 2. Как найти ускорение замедляющегося автомобиля

Примеры положительного ускорения

Примеры отрицательного ускорения

Использование формулы ускорения

Пример 1. Как найти ускорение падающего мяча

Добавить комментарий Отменить ответ