Движение по окружности — задачи
Задача 1. За промежуток времени  с тело прошло половину окружности радиусом 100 см. Найти среднюю путевую скорость
с тело прошло половину окружности радиусом 100 см. Найти среднюю путевую скорость  и модуль средней скорости
и модуль средней скорости  .
.
Решение: средней путевой скоростью называется средняя скорость прохождения пути, которую мы с вами вычисляем, деля весь путь (длину траектории) на все время. Модуль средней скорости еще называют средней скоростью по перемещению. Ее можно определить, разделив перемещение на время. Тогда длина пути – это длина половины окружности, а перемещение – длина диаметра.


Ответ: средняя путевая скорость – 0,314 м/с, средняя скорость по перемещению – 0,2 м/с
Задача 2. Однородный диск радиусом 0,5 м катится без проскальзывания со скоростью 2 м/с. Найти скорость точек диска  . Найти геометрическое место всех точек диска, скорость которых 2 м/с. Угол
. Найти геометрическое место всех точек диска, скорость которых 2 м/с. Угол 

Скорость точек окружности
Решение:
Точка A – центр вращения. Поэтому ее скорость относительно поверхности, по которой катится диск, равна 0. Поскольку в условии сказано, что диск катится со скоростью 2 м/с, то это означает, что с такой скоростью относительно поверхности будет передвигаться его центр:  м/с. Поэтому точка А относительно центра будет передвигаться с точно такой же скоростью – со скоростью 2 м/с, и это и будет линейная скорость вращения диска, то есть скорость всех точек, лежащих на его краю, относительно центра
м/с. Поэтому точка А относительно центра будет передвигаться с точно такой же скоростью – со скоростью 2 м/с, и это и будет линейная скорость вращения диска, то есть скорость всех точек, лежащих на его краю, относительно центра м/с. Линейные скорости показаны для точек
м/с. Линейные скорости показаны для точек  оранжевыми стрелками. Эти стрелки показывают, какой была бы скорость данной точки, если бы диск не катился, а вращался бы, например, на оси, проходящей через его центр. Но наш диск катится. Поэтому к линейной скорости вращения каждой точки необходимо еще прибавить скорость движения диска относительно опоры. То есть к каждой рыжей стрелке прибавим (векторно) скорость точки О – центра диска – черную стрелку. Тогда-то и становится понятным, почему у точки
оранжевыми стрелками. Эти стрелки показывают, какой была бы скорость данной точки, если бы диск не катился, а вращался бы, например, на оси, проходящей через его центр. Но наш диск катится. Поэтому к линейной скорости вращения каждой точки необходимо еще прибавить скорость движения диска относительно опоры. То есть к каждой рыжей стрелке прибавим (векторно) скорость точки О – центра диска – черную стрелку. Тогда-то и становится понятным, почему у точки  скорость равна 0 – линейная скорость вращения направлена влево, а скорость качения – вправо, и поскольку они равны, то гасят друг друга:
скорость равна 0 – линейная скорость вращения направлена влево, а скорость качения – вправо, и поскольку они равны, то гасят друг друга:  . В точке C скорости, напротив, сложатся, поскольку они сонаправлены:
. В точке C скорости, напротив, сложатся, поскольку они сонаправлены:  м/с.
м/с.
Определим теперь скорости точек  и
и  . Понятно, что они будут равны численно, но направлены в разные стороны.
. Понятно, что они будут равны численно, но направлены в разные стороны.


Осталось разобраться с точкой  . Сделаем еще один рисунок. Линейная скорость вращения всегда направлена по касательной, то есть перпендикулярно радиусу
. Сделаем еще один рисунок. Линейная скорость вращения всегда направлена по касательной, то есть перпендикулярно радиусу  . Углы, которые образуются между векторами, показаны на рисунке, в том числе угол
. Углы, которые образуются между векторами, показаны на рисунке, в том числе угол  . Тогда в параллелограмме
. Тогда в параллелограмме  угол
угол  , а так как
, а так как
 , то все углы в треугольнике равны
, то все углы в треугольнике равны  и он равносторонний, то есть
и он равносторонний, то есть  м/с. Также можно было найти длину этого вектора скорости по теореме косинусов или складывая проекции векторов. Можно догадаться, что точка, симметричная точке E относительно A также имеет скорость, равную 2 м/с. Вообще точки, лежащие на одном и том же расстоянии от центра вращения A будут иметь равные скорости, линии равных скоростей (геометрические места точек с равными скоростями) показаны на рисунке различного цвета дугами: единственная точка (точка C) будет иметь скорость 4 м/с, точки, лежащие на рыжей дуне, будут иметь скорости, равные
м/с. Также можно было найти длину этого вектора скорости по теореме косинусов или складывая проекции векторов. Можно догадаться, что точка, симметричная точке E относительно A также имеет скорость, равную 2 м/с. Вообще точки, лежащие на одном и том же расстоянии от центра вращения A будут иметь равные скорости, линии равных скоростей (геометрические места точек с равными скоростями) показаны на рисунке различного цвета дугами: единственная точка (точка C) будет иметь скорость 4 м/с, точки, лежащие на рыжей дуне, будут иметь скорости, равные  , точки, лежащие на синей дуге, будут иметь скорости, равные 2 м/с, как у точки E.
, точки, лежащие на синей дуге, будут иметь скорости, равные 2 м/с, как у точки E.

Пробуксовывание
Задача 3. Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса  , если известно, что скорость нижней точки
, если известно, что скорость нижней точки  м/c, а верхней –
м/c, а верхней –  м/c.
м/c.
Решение:
Если колесо пробуксовывает, то это означает, что скорость его нижней точки не равна нулю, то есть его центр вращения – не точка касания поверхности, центр вращения будет расположен выше. Но центр вращения находится и не в центре колеса. Найти его можно, если провести вертикальный диаметр, построить вектора скоростей в масштабе, а затем, соединив концы векторов скоростей прямой линией, отметить точку пересечения этой линии с диаметром. У нас на рисунке это точка О. Точка К – центр колеса, его скорость нам и нужно найти. Из подобия треугольников  и
и  запишем отношения сходственных сторон:
запишем отношения сходственных сторон:

Тогда




Тогда 

Теперь обратимся к подобным треугольникам  и
и  . Для них отношение сходственных сторон равно:
. Для них отношение сходственных сторон равно:



Откуда  м/с.
м/с.
Ну а более простым решение было бы, если бы мы просто нашли среднее арифметическое скоростей, ведь точка, про которую нас спрашивают, лежит по центру между точками приложения векторов скоростей  и
и 
 со знаком «минус»:
со знаком «минус»: 
м/с.
Ответ: 4 м/с.

Проскальзывание
Задача 4. Обруч, проскальзывая, катится по горизонтальной ровной поверхности. В некоторый момент скорость верхней точки А 
 м/с. Определить скорость концов диаметра
м/с. Определить скорость концов диаметра  , перпендикулярного к
, перпендикулярного к  , для того же момента времени. Под какими углами они направлены к горизонту?
, для того же момента времени. Под какими углами они направлены к горизонту?Решение:
Проскальзывание – это ситуация, когда скорость нижней точки (точки касания обручем земли) не нулевая, но направлена она в сторону качения. В этом случае центр вращения, так же, как и в случае пробуксовки, не совпадает с центром колеса. Более того, центр вращения даже не внутри колеса – он снаружи (точка О). Как и в предыдущей задаче, можно найти его таким же способом – проведя линию через концы скоростей и найдя ее пересечение с продолжением вертикального диаметра. И, точно так же, как в предыдущей задаче, можно определить скорость центра колеса как среднее арифметическое, только обе скорости направлены у нас теперь в одну сторону, поэтому ставим знак «плюс» перед обеими:

м/с.
Так как скорость точки  есть результат векторного сложения линейной скорости вращения колеса
есть результат векторного сложения линейной скорости вращения колеса 
 , то можем из этого сделать вывод, что линейная скорость вращения равна 2 м/с – ровно на столько скорость центра колеса, найденная нами, отличается от скорости точки
, то можем из этого сделать вывод, что линейная скорость вращения равна 2 м/с – ровно на столько скорость центра колеса, найденная нами, отличается от скорости точки  , данной в условии задачи. Линейную скорость на рисунке не показывала, или показывала не везде. Скорости точек
, данной в условии задачи. Линейную скорость на рисунке не показывала, или показывала не везде. Скорости точек  и
и  равны численно, но направлены по-разному. Их скорости – также результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра, а, так как эти две скорости перпендикулярны друг другу, то результат их сложения может быть найден по Пифагору:
равны численно, но направлены по-разному. Их скорости – также результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра, а, так как эти две скорости перпендикулярны друг другу, то результат их сложения может быть найден по Пифагору: 
Понятно, что раз скорости перпендикулярны друг другу, то являются катетами некоторого прямоугольного треугольника, и связывает их между собой функция тангенса, поэтому угол наклона к горизонту скорости точки  можно найти как
можно найти как

Ответ:  ,
, 

Шарик катится по двум линейкам
Задача 5. Шарик радиусом  см катится равномерно и без проскальзывания по двум параллельным линейкам, расстояние между которыми равно
см катится равномерно и без проскальзывания по двум параллельным линейкам, расстояние между которыми равно  см, и за время
см, и за время  с проходит
с проходит  см. С какими скоростями движутся верхняя и нижняя точки шарика?
см. С какими скоростями движутся верхняя и нижняя точки шарика?
На рисунке изображено, как двигается шарик, при этом для удобства показан как вид спереди, так и вид сбоку. Поскольку скорость шарика равна  м/с, то эта скорость – скорость поступательного движения его центра масс – точки А. Центр вращения шарика находится в точке О – на уровне края линеек. Определим положение точки О – определим длину отрезка
м/с, то эта скорость – скорость поступательного движения его центра масс – точки А. Центр вращения шарика находится в точке О – на уровне края линеек. Определим положение точки О – определим длину отрезка  . Это легко сделать, зная радиус шарика и рассмотрев рисунок, из треугольника
. Это легко сделать, зная радиус шарика и рассмотрев рисунок, из треугольника  . Центр вращения в данный момент неподвижен, а точка А двигается относительно него со скоростью 0,6 м/с. Поэтому скорость нижней точки
. Центр вращения в данный момент неподвижен, а точка А двигается относительно него со скоростью 0,6 м/с. Поэтому скорость нижней точки  будет
будет


Таким же способом определяем скорость верхней точки  :
:


Ответ: скорость нижней точки 0,15 м/c, скорость верхней 1,35 м/c.
Задача 6. Автомобиль движется по закругленному шоссе, имеющему радиус кривизны  м. Закон движения автомобиля имеет вид:
м. Закон движения автомобиля имеет вид:  , где
, где  м,
м,  м/с,
м/с,  м/с
м/с . Найти скорость автомобиля
. Найти скорость автомобиля  , его тангенциальное
, его тангенциальное  , нормальное
, нормальное  и полное
и полное  ускорения в момент времени
ускорения в момент времени  с.
с.
Решение.
Путь:

Производная пути – линейная скорость:

Вторая производная – тангенциальное ускорение:

Нормальное ускорение:

Полное ускорение:

Задача7. Угол поворота диска радиусом  см изменяется со временем по закону
см изменяется со временем по закону  . Определить зависимости от времени угловой скорости, углового ускорения и линейной скорости точек диска.
. Определить зависимости от времени угловой скорости, углового ускорения и линейной скорости точек диска.
Решение: угловая скорость – производная угла:

Угловое ускорение – производная угловой скорости:

Линейная скорость:

Задача 8. Точка движется по окружности с постоянным угловым ускорением  рад/
рад/ . Найти угол между скоростью и ускорением через 1 с после начала движения. Начальная скорость точки равна 0.
. Найти угол между скоростью и ускорением через 1 с после начала движения. Начальная скорость точки равна 0.
Решение: так как тангенциальное ускорение и линейная скорость совпадают по направлению, то определим обе составляющие ускорения: как нормальную, так и тангенциальную. Угол между полным ускорением и его тангенциальной составляющей можно тогда будет найти через функцию тангенса.
Известно, что нормальное ускорение  , тангенциальное ускорение
, тангенциальное ускорение  . При этом
. При этом  , или
, или  . Тогда
. Тогда 
Искомый угол:

Ответ: 

Два концентрических колеса
Задача 9. Два концентрических колеса радиусами  см и
см и  см вращаются с угловыми скоростями
см вращаются с угловыми скоростями  рад/c и
рад/c и  рад/с соответственно. Между ними зажато третье колесо так, как показано на рисунке. Какова угловая скорость этого колеса вокруг собственной оси? Проскальзывания нет.
рад/с соответственно. Между ними зажато третье колесо так, как показано на рисунке. Какова угловая скорость этого колеса вокруг собственной оси? Проскальзывания нет.
Решение: определим радиус маленького (третьего) колеса, м:

Определим линейную скорость точек первого колеса:

Определим линейную скорость точек второго колеса:

Найдем угловую скорость маленького колеса, зная, что линейная скорость его точек равна линейной скорости больших колес, так как проскальзывания нет:

Ответ: 20 рад/с
Задача 10. Гайку закручивают на болт за время  . Длина болта
. Длина болта  , резьба составляет угол
, резьба составляет угол  с плоскостью гайки. Найдите угловую скорость гайки, если радиус болта равен
с плоскостью гайки. Найдите угловую скорость гайки, если радиус болта равен  .
.

Скорость вращения гайки по ходу завинчивания на болт
Решение: при закручивании гайка не только вращается, но и движется вдоль болта поступательно, например, спускается вниз. Поэтому точка, взятая на ребре гайки, будет обладать двумя составляющими скорости: скорость, с которой она будет двигаться вниз вдоль болта (назовем ее  ) и скорость, с которой эта точка вращается – это уже знакомая нам линейная скорость (
) и скорость, с которой эта точка вращается – это уже знакомая нам линейная скорость ( ). Тогда
). Тогда  .
.
Из рисунка видно, что


С другой стороны, так как длина болта  , а гайка спускается по нему за время
, а гайка спускается по нему за время  , то
, то

Тогда

И можно определить  :
:

Тогда

Ответ: 
easy-physic.ru
§7. Движение по окружности. Плоское движение
7.1. За промежуток времени t = 10 с материальная точка прошла одну треть окружности радиуса R = 1 м. Определить среднюю путевую скорость и модуль средней скорости.
7.2. Две точки равномерно движутся по окружности, причем первая точка движется по часовой стрелке, вторая — против часовой стрелки. Период обращения первой точки Т1 = 5 с, период второй точки Т2 = 2 с. Найти время между двумя последовательными встречами точек.
7.3. Определить линейную скорость Земли v при ее орбитальном движении. Средний радиус земной орбиты R = 1,5108 км.
7.4. Пропеллер самолета радиусом R = 1,5 м вращается при посадке с частотой n = 2000 мин–1, посадочная скорость самолета относительно Земли v = 162 км/ч. Определить скорость точки на конце пропеллера u относительно Земли. Какова траектория движения этой точки?
7 .5.Две точки
М и К движутся равномерно по окружности
(см. рисунок) с угловыми скоростями
м = 0,2
рад/с и к = 0,3 рад/с. В начальный момент времени
угол между радиусами этих точек 0 = /3.
В какой момент времени эти точки
встретятся?
.5.Две точки
М и К движутся равномерно по окружности
(см. рисунок) с угловыми скоростями
м = 0,2
рад/с и к = 0,3 рад/с. В начальный момент времени
угол между радиусами этих точек 0 = /3.
В какой момент времени эти точки
встретятся?
7.6. Механические часы показывают время t = 4 ч. Через какой промежуток времени t1 минутная стрелка догонит часовую?
7.7. Сколько разNв сутки встречаются часовая и секундная стрелки часов?
7.8. Тяжелый шарик на нити вращается в горизонтальной плоскости так, что нить описывает коническую поверхность. Определить длину нити L, если частота вращения шарика n = 0,5 с–1, его центростремительное ускорение aц = 8 м/с2 и угол отклонения нити от вертикали = 45.
7.9. Мальчик вращает камень, привязанный к веревке длинной L = 0,8 м, в вертикальной плоскости с частотой n = 4 с–1. В тот момент, когда веревка была расположена горизонтально, она оборвалась. На какую высоту h взлетит камень?
7.10. Пуля, летевшая горизонтально, пробила один за другим два диска, насаженных на один вал и вращающихся с частотой n = 10 с–1. Расстояние между дисками S = 30 см. Найти скорость пули v между дисками, если угловое смещение пробоин φ = 9 и пробоины оказались расположенными на одинаковом расстоянии от оси вращения.
7.11. Стержень вращается вокруг оси, походящей перпендикулярно стержню через некоторую его точку. Скорости концов стрежня при этом равны v1 = 1м/с и v2 = 5 м/с. Угловая скорость стержня ω = 1 с–1. Найти длину стрежня.
7.12. Найти радиус вращающегося колеса, если известно, что линейная скорость точек обода колеса в n = 2,5 раза больше линейной скорости точки, лежащей на расстоянии d = 5 см ближе к оси колеса.
7 .13.Диск
радиуса R катится без
проскальзывания с постоянной скоростью v по
горизонтальной дороге
(см. рисунок). Найти ускорения
точек A
и B
и
скорости точек С
и D
относительно
дороги.
.13.Диск
радиуса R катится без
проскальзывания с постоянной скоростью v по
горизонтальной дороге
(см. рисунок). Найти ускорения
точек A
и B
и
скорости точек С
и D
относительно
дороги.
7.14. Катушка с нитью катится по горизонтальному столу без проскальзывания. Внутренний радиус катушки r, внешний R. С какой скоростью vО перемещается ось катушки O относительно стола, если конец нити тянут в горизонтальном направлении со скоростью v? Рассмотреть два случая (см. на рисунке пункты а и б).
7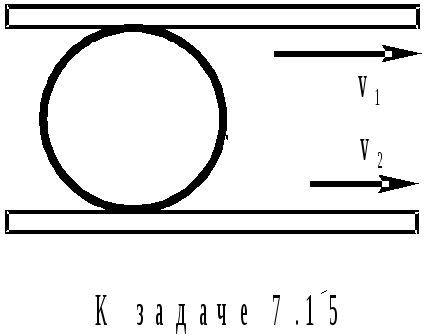 .15.Цилиндрический
каток радиусом R
помещен между двумя параллельными
рейками. Рейки движутся в одну сторону
со скоростями v1 и v2 (см. рисунок). Определить угловую скорость
вращения катка и скорость его центра,
если проскальзывание отсутствует.
.15.Цилиндрический
каток радиусом R
помещен между двумя параллельными
рейками. Рейки движутся в одну сторону
со скоростями v1 и v2 (см. рисунок). Определить угловую скорость
вращения катка и скорость его центра,
если проскальзывание отсутствует.
7.16. Диск, радиус которого R, катится без скольжения с постоянной скоростью v. Найти геометрическое место точек на диске, которые в данный момент имеют скорости относительно Земли, модуль которых равен 1,5v.
7.17. Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса vО, если модуль скорости его нижней точки v1 = 2 м/с, а верхней — v2 = 10 м/с, причем скорости этих точек направлены в противоположные стороны.
7.18. Шарик, радиус которого R = 5 см, катится равномерно и без проскальзывания по двум параллельным брускам квадратного сечения. Расстояние между брусками d = 6 см. За время t = 2 с шарик проходит путь S = 1,2 м. С какими скоростями движутся верхняя и нижняя точки шарика?
7.19. По горизонтальной плоскости катится без скольжения с постоянной скоростью v обруч радиусом R. Выразить модуль скорости различных точек обруча относительно плоскости как функцию угла между вертикалью и прямой, проведенной между точкой прикосновения обруча с плоскостью и данной точкой обруча. Определить скорость vР точки Р обруча при = 30.
7 .20.Автомобиль
движется со скоростью v
= 60 км/ч. С какой частотой n
вращаются его колеса, если они катятся
по шоссе без скольжения, а внешний
диаметр покрышек колес равен d
= 60 см? Найти центростремительное
ускорение ацс внешнего слоя резины на покрышках его
колес.
.20.Автомобиль
движется со скоростью v
= 60 км/ч. С какой частотой n
вращаются его колеса, если они катятся
по шоссе без скольжения, а внешний
диаметр покрышек колес равен d
= 60 см? Найти центростремительное
ускорение ацс внешнего слоя резины на покрышках его
колес.
7.21. Два одинаковых диска расположены так, как показано на рисунке. Диск 1 неподвижен. На какой угол повернется диск 2, обойдя без проскальзывания один раз диск 1?
7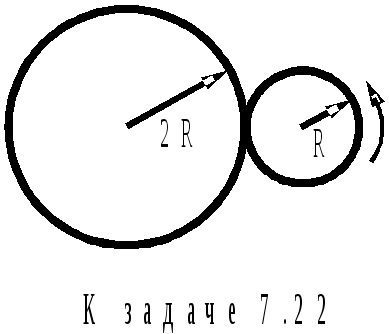 .22.У диска 1
радиус R,
у диска 2 радиус в два раза больше (см.
рисунок). Диск 2 неподвижен. Сколько
оборотов N
сделает диск 1, обойдя без проскальзывания
один раз диск 2?
.22.У диска 1
радиус R,
у диска 2 радиус в два раза больше (см.
рисунок). Диск 2 неподвижен. Сколько
оборотов N
сделает диск 1, обойдя без проскальзывания
один раз диск 2?
7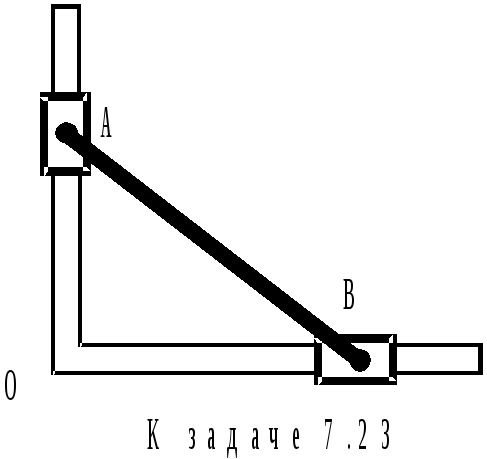 .23.Стержень
шарнирно соединен с муфтами А и В, которые
перемещаются по двум взаимно
перпендикулярным рейкам (см. рисунок).
Муфта А движется с постоянной скоростью
vA = 30 см/с. Найти скорость vB муфты В в момент, когда угол ОАВ = 60.
.23.Стержень
шарнирно соединен с муфтами А и В, которые
перемещаются по двум взаимно
перпендикулярным рейкам (см. рисунок).
Муфта А движется с постоянной скоростью
vA = 30 см/с. Найти скорость vB муфты В в момент, когда угол ОАВ = 60.
7.24. Стержень АС движется так, что в данный момент времени скорость т.А направлена под углом к АС, а скорость т.В, лежащей между точками А и С, направлена вдоль стержня. Определить скорость точки С, если vА = 6 м/c, vВ = 5 м/c, АВ = 10,5 м, ВС = 5 м.
studfile.net
Тестовые задания по физике 10 класс
А)2.2 c
Б)4.2 с
В)3.2 с
Г)2.2 с
29. Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса v, если известно, что скорость его нижней точки v1 = 2 м/с, а верхней — v2 = 10 м/с.
А)6
Б)4
В)3
Г)5
30. Материальная точка массой 0,1 кг движется под действием трех сил, модули которых равны 10 Н. Векторы сил лежат в одной плоскости и образуют два угла по 60°. С каким ускорением движется точка?
А)100 м/с2
Б)200 м/с2
В)300 м/с2
Г)150 м/с2
31. На горизонтальной гладкой поверхности вплотную лежат два одинаковых кубика. К первому кубику приложена горизонтальная сила 6 Н в направлении второго кубика. Чему равна результирующая сила, действующая на второй кубик? Трением пренебречь.
А) 6 Н
Б)3 Н
В)1 Н
Г)4 Н
32. Постоянная вертикальная сила поднимает груз массой 1 кг за 1 c на высоту 2 м из состояния покоя. Чему равна эта сила?
А)4 Н
Б)10 Н
В)14 Н
Г)8 Н
33. Тело массой 1 кг брошено под углом к горизонту. В наивысшей точке траектории ускорение тела было 12 м/с2. Какая сила сопротивления действовала на тело в этот момент?
А)10 Н
Б)12 Н
В)7 Н
Г)8 Н
34. Шар массой 0,5 кг, падая с высоты 10 м, попадает в снег и пробивает в нем яму глубиной 0,8 м. Считая движение в воздухе и в снегу равноускоренным и силу сопротивления воздуха равной 0,6 Н, найдите силу сопротивления при движении в снегу.
А)50 Н
Б)130 Н
В)80 Н
Г)60 Н
35. На тело массой 2 кг, находящееся на гладком горизонтальном столе, действует сила 30 Н, направленная вверх под углом 30° к горизонту. С какой силой тело давит на стол?
А)20 Н
Б) 5 Н
В)10 Н
Г)15 Н
36. Небольшой груз массой 5 кг подвешен к потолку лифта с помощью двух нитей, одна длиной 30 см, другая длиной 40 см. Расстояние между точками крепления нитей к потолку 50 см. Лифт поднимается с ускорением 2 м/с2. Найдите силу натяжения короткой нити.
А)18 Н
Б)48 Н
В)60 Н
Г)50 Н
37. Свободно летящее тело попадает в среду, где на него действует сила сопротивления, пропорциональная скорости. К моменту, когда его скорость уменьшилась вдвое, тело прошло путь 60 м. Какое расстояние пройдет оно с этого момента до остановки? Силу тяжести не учитывать.
А)20 м
Б)40 м
В)60 м
Г)80 м
38. Автоинспектор установил, что след от торможения автомобиля на асфальтовой дороге равен 40 м. С какой скоростью ехал автомобиль, если коэффициент трения колес об асфальт 0,5?
А)72 м/с
Б)36 км/ч
В)15 м/с
Г)5 км/ч
39. Небольшой груз массой 0,5 кг может перемещаться без трения по горизонтальному стержню, прикрепленному к вертикальной оси. Груз связан с осью пружиной. Какова жесткость пружины, если при вращении стержня вокруг вертикальной оси с угловой скоростью 3 рад/с пружина растягивается в 2 раза?
А)5 Н/м
Б)9 Н/м
В)6 Н/м
Г)2 Н/м
40. В кабине, укрепленной на конце штанги, находится человек. Штанга с кабиной вращается в вертикальной плоскости с угловой скоростью 0,7 рад/с. Какова должна быть длина штанги, чтобы человек в верхней точке траектории испытывал состояние невесомости?
А)5 м
Б)7 м
В)49 м
Г)20 м
41. Невесомый стержень вращается в горизонтальной плоскости с угловой скоростью 30 рад/с. На расстояниях 0,4 м и 0,3 м от оси вращения закреплены грузы, имеющие массы 0,2 кг и 0,1 кг соответственно. Какая горизонтальная сила действует на ось вращения, если ось находится между грузами?
А)72 Н
Б)45 Н
В)95 Н
Г99 Н
42. С какой скоростью едет автомобиль по выпуклому мосту, радиус кривизны которого 63 м, если давление автомобиля на мост в верхней точке моста в два раза больше, чем в точке, направление на которую из центра кривизны моста составляет 30° с вертикалью?
А)72 км/ч
Б)36 м/с
В)21 км/ч
Г)15 м/с
43. Тело массой 0,1 кг вращается в вертикальной плоскости на нити длиной 1 м. Ось вращения расположена над полом на высоте 2 м. При прохождении нижнего положения нить обрывается, и тело падает на пол на расстоянии 4 м (по горизонтали) от точки обрыва нити. Определите силу натяжения нити в момент ее обрыва.
А)2 Н
Б)6 Н
В)9 Н
Г)5 Н
44. На горизонтальной вращающейся платформе на расстоянии 10 см от оси вращения лежит груз. Коэффициент трения между грузом и платформой 0,01. При какой угловой скорости вращения платформы груз начнет скользить?
А)0.1 рад/с
Б)1 рад/с
В)10 рад/с
Г)0.001 рад/с
45. Гоночный автомобиль массой 2500 кг едет по шоссе со скоростью 360 км/ч вдоль экватора. На сколько отличаются силы давления автомобиля на полотно дороги при его движении с запада на восток и с востока на запад? Угловая скорость вращения Земли 7,3×10–5 рад/с.
А)73 Н
Б)45 Н
В)82 Н
Г)54 Н
46. Резиновый шнур длиной 0,8 м и массой 300 г имеет форму круглого кольца. Его положили на гладкую горизонтальную поверхность и раскрутили вокруг вертикальной оси так, что скорость каждого элемента кольца равна 3 м/с. Найдите удлинение шнура, если его жесткость 30 Н/м.
А)3 см
Б)30 см
В)10 см
Г)8 см
47. Самолет, летящий со скоростью 540 км/ч, наклоняется при повороте на угол, тангенс которого 0,3. Чему равен радиус поворота?
А)5400 м
Б)6.5 км
В)7500 м
Г)10 км
48. На внутренней поверхности сферы радиусом 12,5 см находится маленькая шайба. До какой минимальной угловой скорости нужно раскрутить сферу вокруг вертикальной оси, чтобы шайба не проскальзывала, находясь на 7,5 см ниже ее центра? Коэффициент трения 0,5.
А)5 рад/с
Б)7 рад/с
В)6 рад/с
Г)4 рад/с
49. Санки массой 18 кг равномерно передвигают по горизонтальному участку дороги с помощью веревки, наклоненной под углом 30° к горизонту. Коэффициент трения 0,08. Найдите работу силы натяжения на пути 100 м.
А)1800 Дж
Б)1376 Дж
В)2572 Дж
Г)1763 Дж
50. Нефть откачивают из скважины глубиной 500 м с помощью насоса, потребляющего мощность 10 кВт. Какой КПД (в процентах) насоса, если за 1 минуту его работы на поверхность земли подается 96 кг нефти?
А)96
Б)92
В)84
Г)80
infourok.ru
§6. Движение под углом к горизонту — Механика 9 кл 2009 в2
Подборка по базе: ситуац задачи 5.doc, курс лекций по ТУТК для ЗО (1).doc, Земельное задачи.docx, ден. масса задачи.docx, Сборник лекций по неврологии.doc, Ответы на экзаменационные задачи.doc, № 1 Задачи.doc, 2. Задачи оперативно-розыскной деятельности..docx, Курс лекций Инф 1 курс.doc, СРС ситуативные задачи 1.docx.
6.1. Тело брошено с поверхности земли с начальной скоростью v0 = 20 м/с под углом α = 60 к горизонту. Определите: а) скорость тела vмакс в верхней точке траектории; б) время полета тела tпол; в) максимальную высоту подъема тела Hмакс; г) дальность полета тела Lмакс; д) модуль перемещения тела от начальной точки до наивысшей точки траектории; е) время Δt1, прошедшее от броска до того момента, когда модуль вертикальной составляющей скорости уменьшился в 2 раза.
6.2. С вышки бросили камень в горизонтальном направлении. Через время t1 = 10 с он упал на расстоянии L = 50 м по горизонтали от вышки. Определите начальную скорость камня и высоту вышки.
6.3. Тело брошено горизонтально с башни высотой H. Какова должна быть начальная скорость тела, чтобы расстояние по горизонтали от башни до места падения тела на землю равно высоте башни?
6.4. Тело брошено с поверхности Земли с некоторой скоростью под углом = 600 к горизонту. Чему равно отношение максимальной высоты подъема к дальности горизонтального полета?
6.5. Камень бросают под углом α = 60 к горизонту. Если начальную скорость камня уменьшить, то дальность полета уменьшается на ΔL = 30 м. На сколько при этом уменьшается максимальная высота подъема камня?
6.6. Тело брошено с поверхности Земли под углом к горизонту. Какую наибольшую высоту H достигает тело, если оно упало на поверхность Земли через время t1 = 4 с?
6.7. С крыши здания, высота которого H = 40 м, брошено тело со скоростью v0 = 20 м/с под углом = 60 к горизонту. На каком расстоянии L от здания (по горизонтали) упадет тело на поверхность Земли?
6 .8. Цель, находящаяся на холме, видна с места расположения орудия под углом к горизонту. Дистанция (расстояние по горизонтали от орудия до цели) равна L. Стрельба по цели производится при угле возвышения (см. рисунок). Определить начальную скорость v0 снаряда, попадающего в цель.
.8. Цель, находящаяся на холме, видна с места расположения орудия под углом к горизонту. Дистанция (расстояние по горизонтали от орудия до цели) равна L. Стрельба по цели производится при угле возвышения (см. рисунок). Определить начальную скорость v0 снаряда, попадающего в цель.
6 .9. Упругое тело падает с высоты h на наклонную плоскость. Определить, через сколько времени t1 после отражения тело упадет на наклонную плоскость. Как это время зависит от угла наклонной плоскости?
.9. Упругое тело падает с высоты h на наклонную плоскость. Определить, через сколько времени t1 после отражения тело упадет на наклонную плоскость. Как это время зависит от угла наклонной плоскости?
6.10. Камень бросают горизонтально с вершины горы, имеющей уклон (см. рисунок). С какой скоростью v0должен быть брошен камень, чтобы он упал на гору на расстоянии L от вершины?
6.11. Тело бросают горизонтально со скоростью v0 с плоскости, уклон которой равен . Каким будет наибольшее удаление тела от плоскости H? Чему будет равна скорость тела v в момент наибольшего удаления от плоскости?
6.12. Тело брошено под углом = 60 к горизонту со скоростью v0 = 20 м/с. Определить скорости v1 и v2 этого тела на высоте h = 3 м.
6.13. Под углом = 60к горизонту брошено тело с начальной скоростью v0 = 20 м/с. Через сколько времени скорость тела будет направлена под углом = 30 к горизонту?
6.14. Начальная скорость брошенного камня v0 = 10 м/с, а спустя промежуток времени t1 = 0,5 с скорость камня v1 = 7 м/с. На какую максимальную высоту H над начальным уровнем поднимется камень?
6.15. Из гондолы дирижабля, движущегося горизонтально, на высоте H = 400 м выпал предмет. С какой скоростью двигался дирижабль, если груз в момент падения на землю имел скорость v = 90 м/с?
6.16. Из точки, находящейся на достаточно большой высоте над землей, одновременно бросили два камня: первый вертикально вверх с начальной скоростью v0 = 10 м/с, а второй – вниз под углом α = 30 к горизонту с начальной скоростью 2v0. Определите расстояние между камнями в тот момент времени, когда скорость первого камня уменьшилась в два раза?
6.17. Из точки, находящейся на некоторой высоте над землей, с одинаковыми по модулю начальной скоростью v0 = 10 м/с бросили два тела: одно вертикально вверх, второе горизонтально. Чему равно расстояние между телами в тот момент времени, когда первое тело поднялось до верхней точки, а второе тело в этот момент ещё не успело упасть на землю?
6.18. На некоторой высоте одновременно из одной точки брошены два тела под углом = 45 к вертикали со скоростью v = 20 м/с: одно вниз, другое вверх. Определить разность высот h на которых будут тела через время t1 = 2 с.
6.19. Доказать, что при свободном движении тел вблизи поверхности Земли их относительная скорость постоянна.
6 .20. Из т.А свободно падает тело. Одновременно из т.В под углом к горизонту бросают другое тело (см. рисунок) так, чтобы оба тела столкнулись в воздухе. Показать, что угол не зависит от модуля начальной скорости v0 тела, брошенного из точки В. Определить угол , если H = 6,5 м, L = 10 м. Чему равна высота, на которой произойдет столкновение тел, если v0 = 12 м/с?
.20. Из т.А свободно падает тело. Одновременно из т.В под углом к горизонту бросают другое тело (см. рисунок) так, чтобы оба тела столкнулись в воздухе. Показать, что угол не зависит от модуля начальной скорости v0 тела, брошенного из точки В. Определить угол , если H = 6,5 м, L = 10 м. Чему равна высота, на которой произойдет столкновение тел, если v0 = 12 м/с?
6.21. Два тела падают с одной и той же высоты H = 20 м.. На пути одного тела на высоте h = 10 м находится расположенная под углом = 45 к горизонту площадка, от которой это тело упруго отражается. Как различаются времена и модули скоростей падения этих тел?
§7. Движение по окружности. Плоское движение
7.1. За промежуток времени t = 10 с материальная точка прошла одну треть окружности радиуса R = 1 м. Определить среднюю путевую скорость и модуль средней скорости.
7.2. Две точки равномерно движутся по окружности, причем первая точка движется по часовой стрелке, вторая — против часовой стрелки. Период обращения первой точки Т1 = 5 с, период второй точки Т2 = 2 с. Найти время между двумя последовательными встречами точек.
7.3. Определить линейную скорость Земли v при ее орбитальном движении. Средний радиус земной орбиты R = 1,5108 км.
7.4. Пропеллер самолета радиусом R = 1,5 м вращается при посадке с частотой n = 2000 мин–1, посадочная скорость самолета относительно Земли v = 162 км/ч. Определить скорость точки на конце пропеллера u относительно Земли. Какова траектория движения этой точки?
7 .5. Две точки М и К движутся равномерно по окружности (см. рисунок) с угловыми скоростями м = 0,2 рад/с и к = 0,3 рад/с. В начальный момент времени угол между радиусами этих точек 0 = /3. В какой момент времени эти точки встретятся?
.5. Две точки М и К движутся равномерно по окружности (см. рисунок) с угловыми скоростями м = 0,2 рад/с и к = 0,3 рад/с. В начальный момент времени угол между радиусами этих точек 0 = /3. В какой момент времени эти точки встретятся?
7.6. Механические часы показывают время t = 4 ч. Через какой промежуток времени t1 минутная стрелка догонит часовую?
7.7. Сколько раз N в сутки встречаются часовая и секундная стрелки часов?
7.8. Тяжелый шарик на нити вращается в горизонтальной плоскости так, что нить описывает коническую поверхность. Определить длину нити L, если частота вращения шарика n = 0,5 с–1, его центростремительное ускорение aц = 8 м/с2 и угол отклонения нити от вертикали = 45.
7.9. Мальчик вращает камень, привязанный к веревке длинной L = 0,8 м, в вертикальной плоскости с частотой n = 4 с–1. В тот момент, когда веревка была расположена горизонтально, она оборвалась. На какую высоту h взлетит камень?
7.10. Пуля, летевшая горизонтально, пробила один за другим два диска, насаженных на один вал и вращающихся с частотой n = 10 с–1. Расстояние между дисками S = 30 см. Найти скорость пули v между дисками, если угловое смещение пробоин φ = 9 и пробоины оказались расположенными на одинаковом расстоянии от оси вращения.
7.11. Стержень вращается вокруг оси, походящей перпендикулярно стержню через некоторую его точку. Скорости концов стрежня при этом равны v1 = 1м/с и v2 = 5 м/с. Угловая скорость стержня ω = 1 с–1. Найти длину стрежня.
7.12. Найти радиус вращающегося колеса, если известно, что линейная скорость точек обода колеса в n = 2,5 раза больше линейной скорости точки, лежащей на расстоянии d = 5 см ближе к оси колеса.
7 .13. Диск радиуса Rкатится без проскальзывания с постоянной скоростью vпо горизонтальной дороге (см. рисунок). Найти ускорения точек A и B и скорости точек С и D относительно дороги.
.13. Диск радиуса Rкатится без проскальзывания с постоянной скоростью vпо горизонтальной дороге (см. рисунок). Найти ускорения точек A и B и скорости точек С и D относительно дороги.
7.14. Катушка с нитью катится по горизонтальному столу без проскальзывания. Внутренний радиус катушки r, внешний R. С какой скоростью vО перемещается ось катушки O относительно стола, если конец нити тянут в горизонтальном направлении со скоростью v? Рассмотреть два случая (см. на рисунке пункты а и б).
7 .15. Цилиндрический каток радиусом R помещен между двумя параллельными рейками. Рейки движутся в одну сторону со скоростями v1 и v2 (см. рисунок). Определить угловую скорость вращения катка и скорость его центра, если проскальзывание отсутствует.
.15. Цилиндрический каток радиусом R помещен между двумя параллельными рейками. Рейки движутся в одну сторону со скоростями v1 и v2 (см. рисунок). Определить угловую скорость вращения катка и скорость его центра, если проскальзывание отсутствует.
7.16. Диск, радиус которого R, катится без скольжения с постоянной скоростью v. Найти геометрическое место точек на диске, которые в данный момент имеют скорости относительно Земли, модуль которых равен 1,5v.
7.17. Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса vО, если модуль скорости его нижней точки v1 = 2 м/с, а верхней — v2 = 10 м/с, причем скорости этих точек направлены в противоположные стороны.
7.18. Шарик, радиус которого R = 5 см, катится равномерно и без проскальзывания по двум параллельным брускам квадратного сечения. Расстояние между брусками d = 6 см. За время t = 2 с шарик проходит путь S = 1,2 м. С какими скоростями движутся верхняя и нижняя точки шарика?
7.19. По горизонтальной плоскости катится без скольжения с постоянной скоростью v обруч радиусом R. Выразить модуль скорости различных точек обруча относительно плоскости как функцию угла между вертикалью и прямой, проведенной между точкой прикосновения обруча с плоскостью и данной точкой обруча. Определить скорость vР точки Р обруча при = 30.
7 .20. Автомобиль движется со скоростью v = 60 км/ч. С какой частотой n вращаются его колеса, если они катятся по шоссе без скольжения, а внешний диаметр покрышек колес равен d = 60 см? Найти центростремительное ускорение ацс внешнего слоя резины на покрышках его колес.
.20. Автомобиль движется со скоростью v = 60 км/ч. С какой частотой n вращаются его колеса, если они катятся по шоссе без скольжения, а внешний диаметр покрышек колес равен d = 60 см? Найти центростремительное ускорение ацс внешнего слоя резины на покрышках его колес.
7.21. Два одинаковых диска расположены так, как показано на рисунке. Диск 1 неподвижен. На какой угол повернется диск 2, обойдя без проскальзывания один раз диск 1?
7 .22. У диска 1 радиус R, у диска 2 радиус в два раза больше (см. рисунок). Диск 2 неподвижен. Сколько оборотов N сделает диск 1, обойдя без проскальзывания один раз диск 2?
.22. У диска 1 радиус R, у диска 2 радиус в два раза больше (см. рисунок). Диск 2 неподвижен. Сколько оборотов N сделает диск 1, обойдя без проскальзывания один раз диск 2?
7 .23. Стержень шарнирно соединен с муфтами А и В, которые перемещаются по двум взаимно перпендикулярным рейкам (см. рисунок). Муфта А движется с постоянной скоростью vA = 30 см/с. Найти скорость vBмуфты В в момент, когда угол ОАВ = 60.
.23. Стержень шарнирно соединен с муфтами А и В, которые перемещаются по двум взаимно перпендикулярным рейкам (см. рисунок). Муфта А движется с постоянной скоростью vA = 30 см/с. Найти скорость vBмуфты В в момент, когда угол ОАВ = 60.
7.24. Стержень АС движется так, что в данный момент времени скорость т.А направлена под углом к АС, а скорость т.В, лежащей между точками А и С, направлена вдоль стержня. Определить скорость точки С, если vА = 6 м/c, vВ = 5 м/c, АВ = 10,5 м, ВС = 5 м.
topuch.ru
Толкаем автомобиль | Колесо
Все современные колесные экипажи, и прежде всего автомобили, имеют колеса на шарикоподшипниках. Какой выигрыш это дает?
Нагруженный легковой автомобиль «Волга» весит около двух тонн. Каждый шофер знает, что, если на ровном асфальтовом шоссе у него отказал двигатель, один человек в состоянии сдвинуть «Волгу» с проезжей части на обочину. Шофер знает и другое: самое трудное столкнуть машину с места. А уж после того как она пришла в движение, поддерживать ее можно даже одной рукой.
Но на что же затрачивается сила давления руки на машину, если, по нашему собственному утверждению, используя колесо с шарикоподшипником, мы полностью избавились от трения скольжения?
Настала пора рассмотреть еще один вид трения — трение качения.
Начнем с того, что, когда идеальная окружность катится по идеальной плоскости, никакого трения, в том числе и трения качения, нет. Но беда в том, что на свете не бывает ни идеальных плоскостей, ни идеальных окружностей.
Мы уже много раз говорили, что любая реальная поверхность содержит неровности: бугорки и впадины. Поэтому, если даже колесо представляет собой идеальную окружность, точнее, идеальный цилиндр, все равно, катясь по реальной поверхности, колесо то взбирается на бугорки, то проваливается во впадины.
Подъем на бугорки сопровождается подъемом и колеса, и телеги, и положенного на телегу груза. Ну, а на подъем груза, конечно же, нужно затрачивать силу. Эта сила и проявляется как сопротивление движению, получившее в технике название трения качения. Чем больший груз давит на колеса, тем больше сила сопротивления. Поэтому, как и в случае с трением скольжения, сила трения качения пропорциональна весу груза.
Можно ли избавиться от трения качения или хотя бы сделать его меньше? Самый верный способ вы уже знаете. Надо изготовлять колеса в виде идеальных цилиндров и катить их по дороге, представляющей собой абсолютно гладкую горизонтальную поверхность. Примерно так и поступают при изготовлении шарикоподшипников.
В шарикоподшипнике единственным видом трения остается трение качения. Чтобы сделать его меньше, поверхности, по которым катятся шарики, и сами шарики полируют. Используют также смазку, которая заполняет микроскопические впадины между бугорками. Благодаря этому в шарикоподшипниках силу трения качения удается почти свести к нулю. Каждый велосипедист знает, как долго продолжает вращаться по инерции колесо велосипеда, если хорошенько его раскрутить. Причина здесь именно в том, что во втулке велосипедного колеса установлены шарикоподшипники.
Ну, а как быть с трением качения внешней поверхности колеса о дорогу? Снова нам приходит на ум все тот же рецепт: отполировать дорогу, и снова приходится с сожалением от него отказаться. Правда, не до конца. Конечно, при езде по гладкой дороге трение качения меньше, поэтому современные автострады, как правило, покрывают асфальтом.
Но гладкость хороша лишь до определенного предела. На абсолютно гладкой дороге автомобиль нельзя столкнуть с места — ноги станут скользить по дороге. Конечно, исправный автомобиль не надо толкать, упираясь ногами в дорогу. Автомобиль движется, отталкиваясь от дороги теми же колесами, — у нас еще будет случай поговорить об этом. Но и колесами тоже не оттолкнешься от абсолютно гладкой поверхности.
Пожалуй, самые ровные дороги на свете — железнодорожные рельсы. Поверхность их делается гладкой еще на заводе. Затем она дополнительно полируется, когда по рельсам движутся локомотивы и вагоны. Недаром рельсы всегда блестят. Гладкая поверхность рельсов делается именно для того, чтобы свести к минимуму трение качения. Железнодорожный вагон с грузом в шестьдесят тонн, если его предварительно как следует разогнать, могут толкать по горизонтальному пути всего человек пять. Состав из ста таких вагонов легко тянет один локомотив.
Но хуже обстоит дело, когда железнодорожный состав нужно стронуть с места. Бывает так, что колеса локомотива вращаются, а сам локомотив стоит на месте. В этом случае говорят, что колеса пробуксовывают. Благодаря гладкости рельсов мы получаем малое трение качения, но и сила трения скольжения, которая в данном случае помогает локомотиву оттолкнуться от рельсов, оказывается недостаточной, чтобы сдвинуть состав с места.
В таких случаях под колеса локомотива посыпают песок. Песок увеличивает неровности на поверхности рельсов и, соответственно, увеличивает силу трения скольжения. И все же количество вагонов, которые можно подцепить к одному локомотиву, ограничивается в первую очередь величиной силы трения скольжения, или, как говорят железнодорожники, сцеплением колес локомотива с рельсами.
По тем же соображениям в состав асфальтовой массы, покрывающей автострады, обычно добавляют все тот же песок. Поэтому сила трения скольжения между колесами автомобиля и покрытием дороги оказывается достаточно большой. В сухую погоду автомобиль легко разогнать с места и легко остановить. Но совсем иначе ведет себя автомобиль на мокром после дождя шоссе. А вот если водяная пленка на шоссе к тому же еще подмерзнет. Нет у шоферов большего врага, чем гололед на дорогах.
Есть еще один способ уменьшить величину силы трения качения. Способ этот очень прост и состоит в том, чтобы увеличивать внешний диаметр колеса. Что при этом получается, достаточно хорошо видно из рисунка.
Художник изобразил два соседних бугорка на дороге и два колеса — маленькое и большое. Маленькое колесо почти целиком помещается между выступами. Чтобы двигаться вперед, ему надо подняться на всю высоту бугорка. Большое колесо просто перекатывается с вершины одного бугорка на вершину другого.
Ясно, что сопротивление движению во втором случае будет меньше. Именно по этой причине, если вы разгонитесь до одной и той же скорости по одной и той же дороге на велосипеде и на роликовых коньках, а потом станете двигаться но инерции, то на велосипеде вы продвинетесь на значительно большее расстояние. По этой же причине диаметр колес у велосипеда больше, чем у легкового автомобиля. Велосипед мы приводим в движение собственной силой, и конструкторы стремятся как только можно облегчить наш труд. Автомобиль двигают «лошадиные силы> мотора, и можно позволить какую-то небольшую их часть затратить на преодоление силы трения качения.
Но почему бы и у автомобиля не делать колеса большого диаметра? Хотя бы для того, чтобы экономить горючее?
Кстати говоря, у самых первых моделей автомобиля колеса были больше, чем у их нынешних потомков.
Оказывается, делать слишком большие колеса тоже нельзя. Во-первых, большое колесо больше весит. Вспомним, что в общем случае объем, а следовательно, масса и вес цилиндра увеличиваются как куб его радиуса. Поэтому если сделать слишком большое колесо, то выигрыш за счет увеличения радиуса компенсируется проигрышем за счет увеличения веса. Особенно у экипажей, предназначенных для перевозки малых грузов.
Вы, конечно, обращали внимание, что у грузовых автомобилей внешний радиус колес тем больше, чем на больший груз они рассчитаны. Для того чтобы большие колеса велосипеда весили поменьше, их делают не сплошными, а на очень тонких спицах (колеса со спицами были и у старых моделей автомобилей).
Есть еще одно соображение, по которому и диаметр и массу колеса нельзя делать очень большими. Это все та же инерция. Тяжелое колесо большого диаметра труднее разогнать и, соответственно, труднее остановить. Последнее особенно страшно, когда надо затормозить внезапно. Кроме того, чем быстрее вращается колесо, тем в большей степени сказывается его инерция. В частности, поэтому с увеличением максимальной скорости автомобилей стали уменьшать радиус их колес.
И, наконец, последнее замечание. Даже на совершенно гладкой дороге не так просто получить небольшую величину силы трения качения. Многое зависит и от материала дороги. Что происходит, например, когда автомобиль движется по песку? Поверхность песка можно разровнять и сделать достаточно гладкой. Но под действием веса экипажа колеса проваливаются в песок. Получается то же самое, как если бы колесо оказалось между двумя бугорками на неровной дороге.
Колеса локомотива или железнодорожного вагона давят на рельсы, и рельсы слегка прогибаются. Правда, в отличие от песка рельсы испытывают упругую деформацию и расправляются после того, как вагон проезжает. Но все равно получается так, что, даже двигаясь по горизонтальному рельсовому пути, колеса вагонов все время как бы взбираются в гору.
Основной вывод, который мы можем сделать из всего сказанного, таков: полностью избавиться от силы трения качения нельзя. Именно поэтому, чтобы поддерживать постоянной скорость прямолинейного равномерного движения железнодорожного вагона по горизонтальному гладкому рельсовому пути, все же требуется усилие пяти, а то и более человек.
Чтобы читатель не разочаровался в колесах, попросим его подсчитать в уме, сколько человек понадобилось бы, чтобы груз в шестьдесят тонн нести на плечах.
www.stroitelstvo-new.ru
