Что сила сопротивления воздуха. Величина силы сопротивления воздуха
Коэффициент сопротивления дает возможность учитывать потери энергии при движении тела. Чаще всего рассматривают два типа движения: движение по поверхности и движение в веществе (жидкости или газе). Если рассматривают движение по опоре, то обычно говорят о коэффициенте трения. В том случае, если рассматривают движение тела в жидкости или газе, то имеют в виду коэффициент сопротивления формы.
Определение коэффициента сопротивления (трения) скольжения
ОПРЕДЕЛЕНИЕ
Коэффициентом сопротивления (трения) называют коэффициент пропорциональности, связывающий силу трения () и силу нормального давления (N) тела на опору. Обычно данный коэффициент обозначают греческой буквой . В таком случае коэффициент трения определим как:
Речь идет о коэффициенте трения скольжения, который зависит от совокупных свойств трущихся поверхностей и является безразмерной величиной. Коэффициент трения зависит от: качества обработки поверхностей, трущихся тел, присутствия на них грязи, скорости движения тел друг относительно друга и т.д. Коэффициент трения определяют эмпирически (опытным путем).
Определение коэффициент сопротивления (трения) качения
ОПРЕДЕЛЕНИЕ
Коэффициент сопротивления (трения) качения обозначают чаще буквой . Его можно определить с помощью отношения момента силы трения качения () к силе с которой тело прижимается к опоре (N):
Данный коэффициент, имеет размерность длины. Основной его единицей в системе СИ будет метр.
Определение коэффициента сопротивления формы
ОПРЕДЕЛЕНИЕ
Коэффициент сопротивления формы — физическая величина, которая определяет реакцию вещества на перемещение тела внутри нее. Можно сказать иначе: это физическая величина, которая определяет реакцию тела на движение в веществе. Данный коэффициент определяется эмпирически, его определением служит формула:
где — сила сопротивления, — плотность вещества, — скорость течения вещества (или скорость движения тела в веществе), площадь проекции тела на плоскость перпендикулярную к направлению движения (перпендикулярная потоку).
Иногда, если рассматривают движение вытянутого тела, то считают:
где V — объем тела.
Рассматриваемый коэффициент сопротивления является безразмерной величиной. Он не учитывает эффектов на поверхности тел, поэтому формула (3) может стать не пригодна, если рассматривается вещество, которое имеет большую вязкость. Коэффициент сопротивления (C) является постоянной величиной пока число Рейнольдса (Re) является неизменным. В общем случае .
Если тело имеет острые ребра, то эмпирически получено, что для таких тел коэффициент сопротивления остается постоянным в широкой области чисел Рейнольдса. Так опытным путем получено, что для круглых пластинок поставленных поперек воздушного потока, при значения коэффициента сопротивления находятся в пределах от 1,1 до 1,12. При уменьшении числа Рейнольдса () закон сопротивления переходит в закон Стокса, который для круглых пластинок имеет вид:
Сопротивление шаров было исследовано для широкой области чисел Рейнольдса до Для получили:
В справочниках представлены коэффициенты сопротивления для круглых цилиндров, шаров и круглых пластинок в зависимости от числа Рейнольдса.
В авиационной технике задача о нахождении формы тела с минимальным сопротивлением имеет особое значение.
Примеры решения задач
ПРИМЕР 1
| Задание | Максимальная скорость автомобиля на горизонтальном участке дороги равна при максимальной мощности его равной P. Коэффициент лобового сопротивления автомобиля C, а наибольшая площадь сечения в направлении, перпендикулярном скорости S. Автомобиль подвергся реконструкции, наибольшую площадь сечения в направлении, перпендикулярном скорости уменьшили до величины , оставив коэффициент сопротивления без изменения. Считайте силу трения о поверхность дороги неизменной, найдите какова максимальная мощность автомобиля, если его скорость на горизонтальном участке дороги стала равна . Плотность воздуха равна . |
| Решение | Сделаем рисунок. Мощность автомобиля определим как: где — сила тяги автомобиля. Считая, что автомобиль на горизонтальном участке дороги движется с постоянной скоростью, запишем второй закон Ньютона в виде: В проекции на ось X (рис.1), имеем: Силу сопротивления, которую испытывает автомобиль, двигаясь в воздухе, выразим как: Тогда мощность автомобиля можно записать: Выразим из (1.5) силу трения автомобиля о дорогу: Запишем выражение для мощности, но с изменёнными по условию задачи параметрами автомобиля: Учтем, что сила трения автомобиля о дорогу не изменилась, и примем во внимание выражение (1.6): |
| Ответ |
ПРИМЕР 2
| Задание | Какова максимальная скорость шарика, который свободно падает в воздухе, если известны: плотность шарика (), плотность воздуха (), масса шарика (), коэффициент сопротивления C? |
| Решение | Сделаем рисунок. Запишем второй закон Ньютона для |
owix.ru
Сила сопротивления подъему
Вес автомобиля, который движется на подъеме, можно разложить на две составляющие (см. рис. 3.12): параллельную и перпендикулярную поверхности дороги. Составляющая силы тяжести, параллельная поверхности дороги, представляет собой силу сопротивления подъему, Н:
Рп = G sin α,
где G — вес автомобиля, Н; α — угол подъема, °.
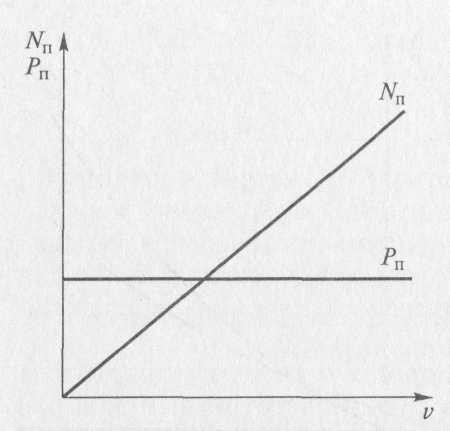
Рис. 3.16. Зависимости силы сопротивления подъему Рп и мощности Nп, необходимой для его преодоления, от скорости автомобиля
В качестве характеристики крутизны подъема наряду с углом α используют величину i, называемую уклоном и равную i = Нп/Bп , где Нп — высота подъема; Вп — длина его проекции на горизонтальную плоскость. Сила сопротивления подъему может быть направлена как в сторону движения, так и против него. В процессе подъема она действует в направлении, противоположном движению, и является силой сопротивления движению. При спуске эта сила, направленная в сторону движения, становится движущей.
Зная силу сопротивления подъему, можно определить мощность, кВт, необходимую для преодоления этого сопротивления:
,
где v — скорость автомобиля, м/с.
Зависимости силы сопротивления подъему Рп
Сила сопротивления дороги
Сила сопротивления дороги представляет собой сумму сил сопротивления качению и сопротивления подъему:
Рд = Рк + Рп
ИЛИ
Рд = f G cos α + G sin α = G (f cos α + sin α).
Выражение в скобках, характеризующее дорогу в общем случае, называется коэффициентом сопротивления дороги:
ψ = f cos α + sin α.
При малых углах подъема (не превышающих 5°), характерных для большинства автомобильных дорог с твердым покрытием, коэффициент сопротивления дороги
ψ = f + i.
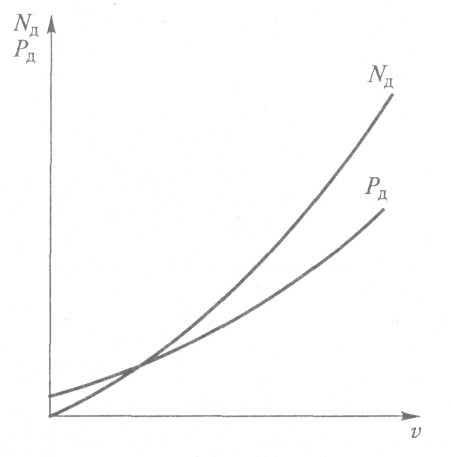
Рис. 3.17. Зависимости силы сопротивления дороги Рд и мощности Nд , затрачиваемой на его преодоление, от скорости автомобиля
Сила сопротивления дороги в этом случае
Рд = ψ G.
Зная силу сопротивления дороги, можно определить мощность, кВт, необходимую для его преодоления:
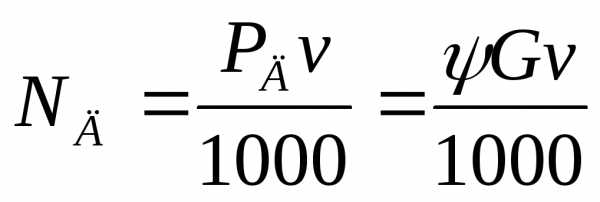 ,
,
где скорость автомобиля v выражена в м/с, вес G – в Н, мощность Nд — в кВт.
Зависимости силы сопротивления дороги Рд и мощности Nд, затрачиваемой на его преодоление, от скорости автомобиля v представлены на рис. 3.17.
Сила сопротивления воздуха
При движении действие силы сопротивления воздуха обусловлено перемещением частиц воздуха и их трением о поверхность автомобиля. Если он движется при отсутствии ветра, то сила сопротивления воздуха, Н:
Рв = kвFаv2,
тогда как при наличии ветра
Рв = kвFа(v± vв)2,
где kв — коэффициент сопротивления воздуха (коэффициент обтекаемости), Н·с2/м4; Fa — лобовая площадь автомобиля, м2; v — скорость автомобиля, м/с; vв — скорость ветра, м/с (знак «+» соответствует встречному ветру, знак «–» — попутному).
Коэффициент сопротивления воздуха, зависящий от формы и качества поверхности автомобиля, определяется экспериментально при продувке в аэродинамической трубе.
Коэффициент сопротивления воздуха, Н·с2/м4, составляет 0,2…0,35 для легковых автомобилей, 0,35…0,4 — для автобусов и 0,6…0,7 — для грузовых автомобилей. При наличии прицепов сопротивление воздуха увеличивается, так как возрастает наружная поверхность трения и возникают завихрения воздуха между тяга-
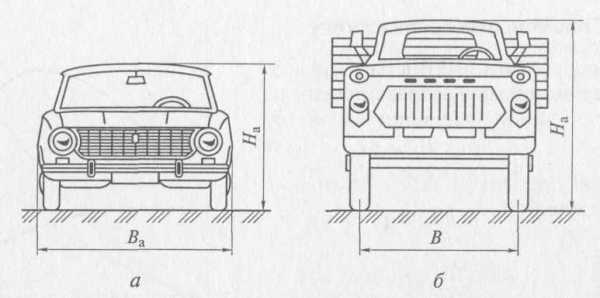
Рис. 3.18. Площади лобового сопротивления легкового (а) и грузового
(б) автомобилей
чом и прицепами. При этом каждый прицеп вызывает увеличение коэффициента kв в среднем на 15…25 %.
Лобовая площадь автомобиля зависит от его типа (рис. 3.18). Ее приближенное значение, м2, можно вычислить по следующим формулам:
Fa = BHa — для грузовых автомобилей и автобусов;
Fa = 0,78BaHa — для легковых автомобилей,
где В — колея колес автомобиля, м; На — наибольшая высота автомобиля, м; Ва — наибольшая ширина автомобиля, м.
Мощность, кВт, затрачиваемая на преодоление сопротивления воздуха:
– при отсутствии ветра;
– при отсутствии ветра.

Зависимости силы сопротивления воздуха Рв и мощности Nв , необходимой для преодоления этого сопротивления, от скорости автомобиля v приведены на рис. 3.19.
Рис. 3.19. Зависимости силы сопротивления воздуха Рв и мощности Nв , необходимой для преодоления этого сопротивления, от скорости автомобиля
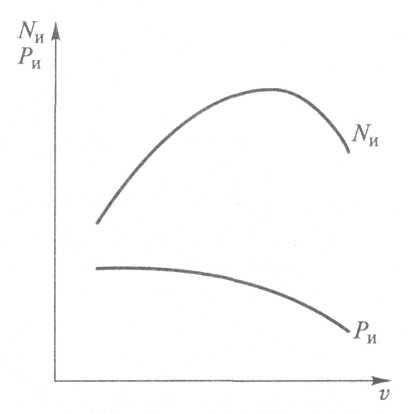
Сила сопротивления разгону возникает вследствие затрат энергии на раскручивание вращающихся частей двигателя и трансмиссии, а также колес при движении автомобиля с ускорением.
Сила сопротивления разгону, Н:
 ,
,
Рис. 3.20. Зависимости силы сопротивления разгону Ри и мощности Nи , необходимой для преодоления этого сопротивления, от скорости автомобиля
где G — вес автомобиля, Н; g — ускорение силы тяжести, м/с2; δвр — коэффициент учета вращающихся масс автомобиля; j — ускорение автомобиля, м/с2.
Мощность, кВт, затрачиваемая на разгон:
Зависимости силы сопротивления разгону Ри и мощности Nи, необходимой для преодоления этого сопротивления, от скорости автомобиля v представлены на рис. 3.20.
studfile.net
Силы действующие на автомобиль при движении
На движущийся автомобиль действует ряд сил, часть из которых направлена по оси движения автомобиля, а часть — под углом к этой оси. Условимся называть первые из этих сил продольными, а вторые боковыми.
Продольные силы могут быть направлены как по ходу, так и против хода движения автомобиля. Силы, направленные по ходу движения, являются движущимися и стремятся продолжить движение. Силы, направленные против хода движения, являются силами сопротивления и стремятся остановить автомобиль.
На автомобиль, движущийся по горизонтальному и прямому участку дороги, действуют следующие продольные силы:
При движении автомобиля в гору возникает сила сопротивления подъему, а при разгоне автомобиля—сила сопротивления разгону (сила инерции).
Тяговая сила
Развиваемый двигателем автомобиля крутящий момент передается на ведущие колеса. В передаче крутящего момента от двигателя к ведущим колесам участвуют механизмы трансмиссии. Крутящий момент на ведущих колесах зависит от крутящего момента двигателя и передаточных чисел коробки передач и главной передачи. В точке касания колес с поверхностью дороги крутящий момент вызывает окружную силу. Противодействие дороги этой окружной силе выражается реактивной силой, передаваемой от дороги на ведущее колесо. Эта сила направлена в сторону движения автомобиля и называется толкающей или тяговой силой. Тяговая сила от колес передается на ведущий мост и далее на раму, заставляя автомобиль двигаться. Величина тяговой силы тем больше, чем больше крутящий момент двигателя и передаточные числа коробки передач и главной передачи. Тяговая сила на ведущих колесах достигает наибольшей величины при движении автомобиля на низшей передаче, поэтому низшую передачу используют при трогании с места автомобиля с грузом, при движении автомобиля по бездорожью. Величина тяговой силы на ведущих колесах автомобиля ограничивается сцеплением шин с поверхностью дороги.
Сила сцепления колес с дорогой
Трение, возникающее между ведущими колесами автомобиля и дорогой, называется силой сцепления. Сила сцепления равна произведению коэффициента сцепления на сцепной вес, т. е. вес, приходящийся на ведущие колеса автомобиля. Величина коэффициента сцепления шин с дорогой зависит от качества и состояния дорожного покрытия, формы и состояния рисунка протектора шины, давления воздуха в шине.
У легковых автомобилей полный вес распределяется по осям примерно поровну. Поэтому сцепной вес его можно принять равным 50% полного веса. У грузовых автомобилей при полной их нагрузке сцепной вес (вес, приходящийся на заднюю ось) составляет примерно 60—70% полного веса.
Величина коэффициента сцепления имеет большое значение для эксплуатации автомобиля и безопасности движения, так как от него зависят проходимость автомобиля, тормозные качества, возможность, пробуксовки и заноса ведущих колес. При незначительном коэффициенте сцепления трогание автомобиля с места сопровождается пробуксовкой, а торможение — скольжением колес. В результате автомобиль иногда не удается тронуть с места, а при торможении происходит резкое увеличение тормозного пути и возникновение заноса.
На асфальтобетонных покрытиях в жаркую погоду на поверхность выступает битум, делая дорогу маслянистой и более скользкой, что снижает коэффициент сцепления. Особенно сильно снижается коэффициент сцепления при смачивании дороги первым дождем, когда образуется еще не смытая пленка жидкой грязи. Заснежённая или обледенелая дорога особенно опасна в теплую погоду, когда поверхность подтаивает.
При увеличении скорости движения коэффициент сцепления снижается, в особенности на мокрой дороге, так как выступы рисунка протектора шины не успевают продавливать пленку влаги.
Исправное состояние рисунка протектора шины имеет большое значение при движении по грунтовым дорогам, снегу, песку, а также по дорогам с твердым покрытием, по покрытым пленкой грязи или воды. Благодаря наличию выступов рисунка опорная площадь шины уменьшается и, следовательно, возрастает удельное давление на поверхность дороги. При этом легче продавливается грязевая пленка и восстанавливается контакт с дорожным покрытием, а на легком грунте происходит непосредственное зацепление выступов рисунка за грунт.
Повышенное давление воздуха в шине уменьшает ее опорную поверхность, вследствие чего удельное давление возрастает настолько, что при трогании с места и при торможении может произойти разрушение резины и сцепление колес с дорогой уменьшается.
Таким образом, величина коэффициента сцепления зависит от многих условий и может изменяться в довольно значительных пределах. Так как много дорожно-транспортных происшествий происходит из-за плохого сцепления, то водители должны уметь приблизительно оценивать величину коэффициента сцепления и выбирать скорость движения и приемы управления в соответствии с ним.
Сила сопротивления воздуха
При движении автомобиль преодолевает сопротивление воздуха, которое складывается из нескольких сопротивлений:
- лобового сопротивления (около 55—60% всего сопротивления воздуха)
- создаваемого выступающими частями—подножками автобуса или автомобиля, крыльями (12—18%)
- возникающего при прохождении воздуха через радиатор и подкапотное пространство (10—15%) и др.
Передней частью автомобиля воздух сжимается и раздвигается, в то время как в задней части автомобиля создается разрежение, которое вызывает образование завихрений.
Сила сопротивления воздуха зависит от величины лобовой, поверхности автомобиля, его формы, а также от скорости движения. Лобовую площадь грузового автомобиля определяют как произведение колеи (расстояние между шинами) на высоту автомобиля. Сила сопротивления воздуха возрастает пропорционально квадрату скорости движения автомобиля (если скорость возрастает в 2 раза, то сопротивление воздуха увеличивается в 4 раза).
Для улучшения обтекаемости и уменьшения сопротивления воздуха ветровое стекло автомобиля располагают наклонно, а выступающие детали (фары, крылья, ручки дверей) устанавливают заподлицо с внешними очертаниями кузова. У грузовых автомобилей можно уменьшить силу сопротивления воздуха, закрыв грузовую платформу брезентом, натянутым между крышей кабины и задним бортом.
Сила сопротивления качению
На каждое колесо автомобиля постоянно действует вертикальная нагрузка, которая вызывает вертикальную реакцию дороги. При движении автомобиля на него действует сила сопротивления качению, которая возникает вследствие деформации шин и дороги и трения шин о дорогу.
Сила сопротивления качению равна произведению полного веса автомобиля на коэффициент сопротивления качению шин, который зависит от давления воздуха в шинах и качества дорожного покрытия. Вот- некоторые значения коэффициента сопротивления качению шин:
- для асфальтобетонного покрытия— 0,014—0,020
- для гравийного покрытия—0,02—0,025
- для песка—0,1—0,3
Сила сопротивления подъему
Автомобильная дорога состоит из чередующихся между собой подъемов и спусков и редко имеет горизонтальные участки большой длины.
При движении на подъем автомобиль испытывает дополнительное сопротивление, которое зависит от угла наклона дороги к горизонту. Сопротивление подъему тем больше, чем больше вес автомобиля и угол наклона дороги. При подъезде к подъему необходимо правильно оценить возможности преодоления подъема. Если подъем непродолжительный, его преодолевают с разгоном автомобиля перед подъемом. Если подъем продолжительный, его преодолевают на пониженной передаче, переключившись на нее у начала подъема.
При движении автомобиля на спуске сила сопротивления подъему направлена в сторону движения и является движущей силой.
Сила сопротивления разгону
Часть тяговой силы при разгоне затрачивается на ускорение вращающихся масс, главным образом маховика коленчатого вала двигателя и колес автомобиля. Для того чтобы автомобиль начал двигаться с определенной скоростью, ему необходимо преодолеть силу сопротивления разгону, равную произведению массы автомобиля на ускорение. При разгоне автомобиля сила сопротивления разгону направлена в сторону, обратную движению. При торможении автомобиля и замедлении его движения эта сила направлена в сторону движения автомобиля. Бывают случаи, когда при резком разгоне груз или пассажиры падают из открытого кузова, с сидений мотоцикла, а при резком торможении пассажиры ударяются о лобовое стекло или о передний борт автомобиля. Для того чтобы таких случаев не было, необходимо, плавно увеличивая частоту вращения коленчатого вала двигателя, преодолевать силу сопротивления разгону и плавно осуществлять торможение автомобиля.
Центр тяжести
На автомобиль, как и на любое другое тело, действует сила тяжести, направленная вертикально вниз. Центром тяжести автомобиля называют такую точку автомобиля, от которой вес автомобиля распределяется равномерно во всех направлениях. У автомобиля центр тяжести располагается между передней и задней осью на высоте около 0,6 м для легковых и 0,7—1,0 м для грузовых. Чем ниже расположен центр тяжести, тем устойчивее автомобиль против опрокидывания. При загрузке автомобиля грузом центр тяжести поднимается у легковых автомобилей примерно на 0,3—0,4 м, а у грузовых на 0,5 м и более в зависимости от рода груза. При неравномерном укладывании груза центр тяжести может также сместиться вперед, назад или в сторону, при этом будут нарушаться устойчивость автомобиля и легкость управления.
ustroistvo-avtomobilya.ru
Сила тяжести, трения, реакции опоры, упругости, Архимеда, сопротивления, вес. Направление, точка приложения, природа возникновения
Тестирование онлайн
Что надо знать о силе
Сила — векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле
Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:
Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.
Закон Гука
Сила упругости направлена противоположно деформации.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле
При параллельном соединении жесткость
Жесткость образца. Модуль Юнга.
Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел здесь.
Вес тела
Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!
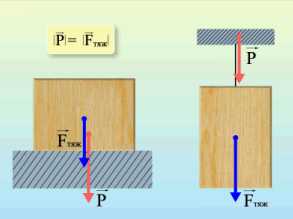
Формулы определения веса нет. Обозначается эта силы буквой .
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.
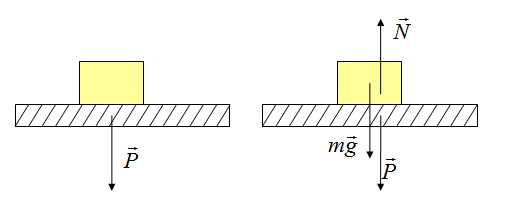
Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!
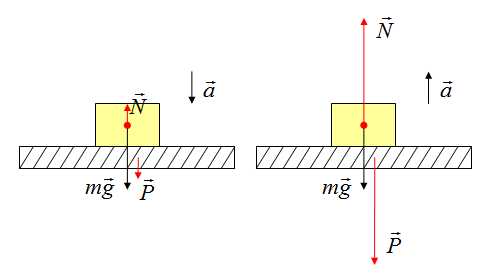
Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка — отношение веса к силе тяжести
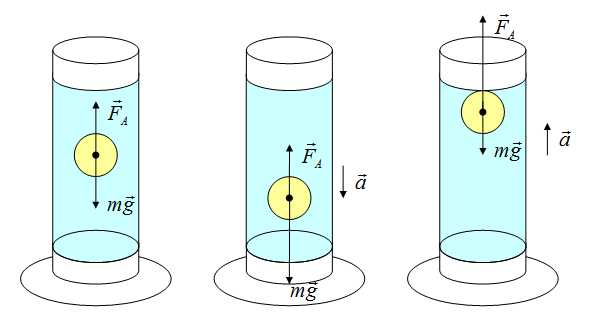
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
Рассмотрим взаимное притяжение предмета и Земли. Между ними, согласно закону гравитации возникает сила
А сейчас сравним закон гравитации и силу тяжести
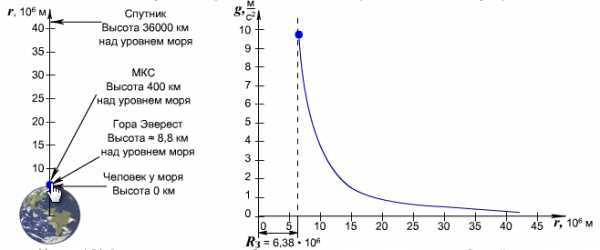
Величина ускорения свободного падения зависит от массы Земли и ее радиуса! Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты.
Расстояние от центра Земли до полюсов меньше, чем до экватора. Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.
При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли.
fizmat.by
Как зависит сила сопротивления воздуха от формы предмета и его массы
Одним из проявлений силы взаимного тяготения является сила тяжести, т.е. сила притяжения тел к Земле. Если на тело действует только сила тяжести, то оно совершает свободное падение. Следовательно, свободное падение – это падение тел в безвоздушном пространстве под действием притяжения к Земле, начинающееся из состояния покоя.
Впервые это явление изучил Галилей, но из-за отсутствия воздушных насосов он не мог провести опыт в безвоздушном пространстве, поэтому Галилей производил опыты в воздухе. Отбрасывая все второстепенные явления, встречающиеся при движении тел в воздухе, Галилей открыл законы свободного падения тел. (1590г.)
- 1-й закон. Свободное падение является прямолинейным равномерноускоренным движением.
- 2-й закон. Ускорение свободного падения в данном месте Земли для всех тел одинаково; среднее его значение равно 9,8 м/с.
Зависимости между кинематическими характеристиками свободного падения получаются из формул для равноускоренного движения, если в этих формулах положить а = g. При v0 = 0 V = gt, H = gt2 \2, v = √2gH .
Практически воздух всегда оказывает сопротивление движению падающего тела, причем для данного тела сопротивление воздуха тем больше, чем больше скорость падения. Следовательно, по мере увеличения скорости падения сопротивление воздуха увеличивается, ускорение тела уменьшается и, когда сопротивление воздуха сделается равным силе тяжести, ускорение свободно падающего тела станет равным нулю. В дальнейшем движение тела будет равномерным движением.
Реальное движение тел в земной атмосфере происходит по баллистической траектории, существенно отличающейся от параболической из-за сопротивления воздуха. Например, если выпустить из винтовки пулю со скоростью 830 м/с под углом α = 45о к горизонту и зафиксировать с помощью кинокамеры фактическую траекторию трассирующей пули и место ее падения, то дальность полета окажется равной примерно 3,5 км. А если рассчитать по формуле, то оно окажется 68, 9 км. Разница огромная!
Сопротивление воздуха зависит от четырех факторов: 1) РАЗМЕР движущегося предмета. Большой объект, очевидно, получит большее сопротивление, чем маленький. 2) ФОРМА движущегося тела. Плоская пластина определенной площади будет оказывать гораздо большее сопротивление ветру, чем обтекаемое тело (форма капли), имеющее ту же площадь сечения для такого же ветра, реально в 25 раз большее! Круглый предмет находится где-то посередине. (Это и есть причина, по которой корпуса всех автомобилей, самолетов и парапланов имеют по возможности скругленную или каплевидную форму: она уменьшает сопротивление воздуха и позволяет двигаться быстрее при меньших усилиях на двигатель, а значит, при меньших затратах топлива). 3) ПЛОТНОСТЬ ВОЗДУХА. Нам уже известно, что один кубический метр весит около 1,3 кг на уровне моря, и, чем выше вы поднимаетесь, тем менее плотным становится воздух. Эта разница может играть некоторую практическую роль при взлете только очень с большой высоты. 4) СКОРОСТЬ. Каждый из трех рассмотренных до сих пор факторов дает пропорциональный вклад в воздушное сопротивление: если вы увеличиваете один из них вдвое, сопротивление также удваивается; если вы уменьшаете любой из них в два раза, сопротивление падает наполовину.
СОПРОТИВЛЕНИЕ ВОЗДУХА равно ПОЛОВИНЕ ПЛОТНОСТИ ВОЗДУХА, умноженной на КОЭФФИЦИЕНТ СОПРОТИВЛЕНИЯ, умноженной на ПЛОЩАДЬ СЕЧЕНИЯ и умноженной на КВАДРАТ СКОРОСТИ.
Введем следующие символы: D — сопротивление воздуха; р — плотность воздуха; А — площадь сечения; cd — коэффициент сопротивления; υ — скорость воздуха.
Теперь имеем: D = 1/2 х р х cd x A x υ 2
При падении тела в реальных условиях ускорение тела не будет равно ускорению свободного падения. В этом случае 2 закон Ньютона примет вид ma = mg – Fсопр –Fарх
Fарх. =ρqV , так как плотность воздуха мала, можно пренебречь, тогда ma = mg – ηυПроанализируем это выражение. Известно, что на тело, движущееся в воздухе, действует сила сопротивления . Почти очевидно, что эта сила зависит от скорости движения и размеров тела, например площади поперечного сечения S, причем эта зависимость типа «чем больше υ и S, тем больше F». Можно еще уточнить вид этой зависимости, исходя из соображений размерностей (единиц измерения). Действительно, сила измеряется в ньютонах ([F] = Н), а Н = кг·м/с2. Видно, что секунда в квадрате входит в знаменатель. Отсюда сразу ясно, что сила должна быть пропорциональна квадрату скорости тела ([υ2] = м2/с2) и плотности ([ρ] = кг/м3) — конечно, той среды, в которой движется тело. Итак,
А чтобы подчеркнуть, что эта сила направлена против вектора скорости.
Мы узнали уже очень много, но это еще не все. Наверняка сила сопротивления (аэродинамическая сила) зависит и от формы тела — не случайно ведь летательные аппараты делаются «хорошо обтекаемыми». Чтобы учесть и эту предполагаемую зависимость, можно в полученное выше соотношение (пропорциональность) ввести безразмерный множитель, который не нарушит равенства размерностей в обеих частях этого соотношения, но превратит его в равенство:
Представим себе шарик, движущийся в воздухе, например, дробинку, горизонтально вылетевшую с начальной скоростью — Если бы не было сопротивления воздуха, то на расстоянии х за время дробинка сместилась бы по вертикали вниз на. Но из-за действия силы сопротивления (направленной против вектора скорости) время полета дробинки до вертикальной плоскости х будет больше t0. Следовательно, сила тяжести дольше будет действовать на дробинку, так что она опустится ниже y0.
И вообще, дробинка будет двигаться по другой кривой , уже не являющейся параболой (ее называют баллистической траекторией).
При наличии атмосферы падающие тела помимо силы тяжести испытывают воздействие сил вязкого трения о воздух. В грубом приближении при малых скоростях силу вязкого трения можно считать пропорциональной скорости движения. В этом случае уравнение движения тела (второй закон Ньютона) имеет вид ma = mg – η υ
Сила вязкого трения, действующая на движущиеся с небольшими скоростями тела сферической формы примерно пропорциональна площади их поперечного сечения, т.е. квадрату радиуса тел: F = -η υ= — const R2 υ
Масса же сферического тела постоянной плотности пропорциональна его объему, т.е. кубу радиуса m = ρ V = ρ 4/3π R3
Уравнение написано с учетом направления оси OY вниз, где η –коэффициент сопротивления воздуха. Эта величина зависит от состояния среды и параметров тела (массы тела, размеров и формы). Для тела шаровидной формы, по формуле Стокса η =6(m(r где m – масса тела, r – радиус тела, ( — коэффициент вязкости воздуха.
Рассмотрим для примера падение шариков из разного материала. Возьмем два шарика одинакового диаметра, пластмассовый и железный. Примем для наглядности, что плотность железа в 10 раз больше плотности пластмассы, поэтому железный шар будет иметь массу в 10 раз больше, соответственно его инертность будет в 10 раз выше, т.е. под воздействием той же силы он будет ускоряться в 10 раз медленнее.
В вакууме на шарики действует только сила тяжести, на железный в 10 раз больше чем на пластмассовый, соответственно разгоняться они будут с одним и тем же ускорением (в 10 раз большая сила тяжести компенсирует в 10 раз большую инертность железного шарика). При одинаковом ускорении одно и то же расстояние оба шарика пройдут за одно и то же время, т.е. другими словами упадут одновременно.
В воздухе: к действию силы тяжести добавляются сила аэродинамического сопротивления и Архимедова сила. Обе эти силы направлены вверх, против действия силы тяжести, и обе зависят только от размера и скорости движения шариков ( не зависят от их массы) и при равных скоростях движения равны для обоих шариков.
T.о. результирующая трех сил действующих на железный шарик будет уже не в 10 раз превышать аналогичную результирующую деревянного, а в больше чем 10, инертность же железного шарика остается больше инертности деревянного все в те же 10 раз.. Соответственно ускорение железного шарика будет больше, чем пластмассового, и упадет он раньше.
www.microarticles.ru
