Механические свойства жидкостей: 1.3. Механические характеристики и основные свойства жидкостей

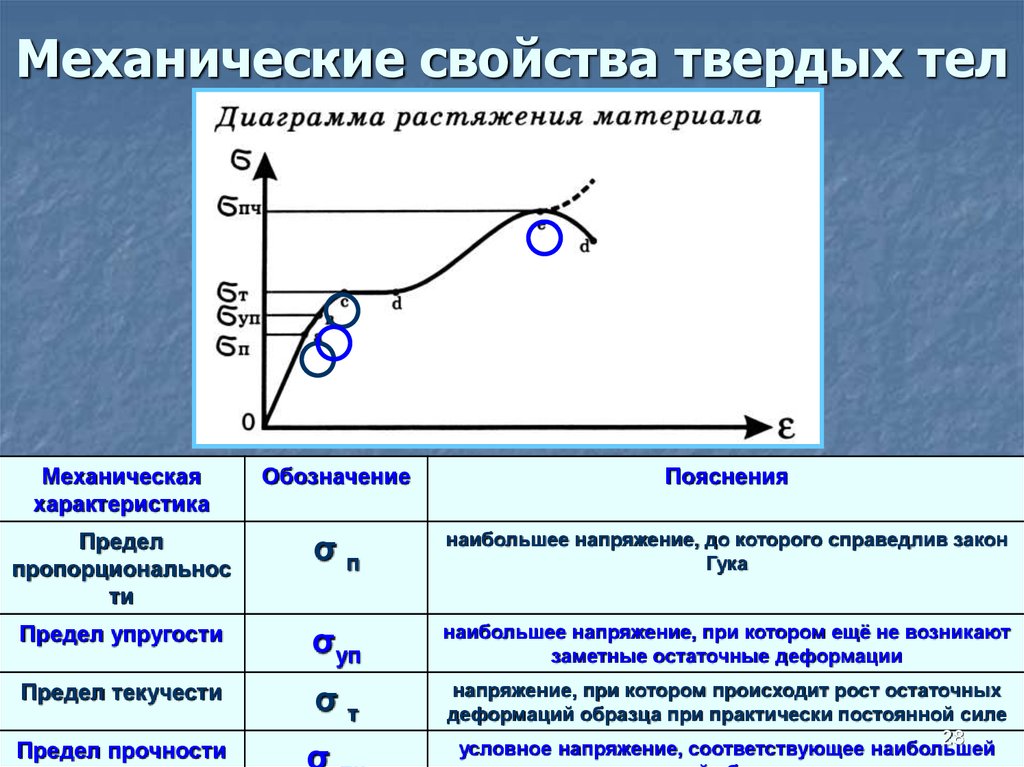
1.3. Механические характеристики и основные свойства жидкостей

Основные механические характеристики

Одной из основных механических характеристик жидкости является ее плотность. Плотностью жидкости называют массу жидкости заключенную в единице объема.

Удельным весомназывают вес единицы объема жидкости, который определяется по формуле:

С увеличением температуры удельный вес жидкости уменьшается.

Основные физические свойства

1. Сжимаемость — свойство жидкости изменять свой объем под действием давления. Сжимаемость жидкости характеризуется коэффициентом объемного сжатия, который определяется по формуле

где V — первоначальный объем жидкости, dV — изменение этого объема, при увеличении давления на величину dP.

Величина обратная βV называется модулем объемной упругости жидкости:

Модуль объемной упругости не постоянен и зависит от давления и температуры.

При гидравлических расчетах сжимаемостью жидкости обычно пренебрегают и считают жидкости практически несжимаемыми. Сжатие жидкостей в основном обусловлено сжатием растворенного в них газа.

Сжимаемость понижает жесткость гидропривода, т.к., на сжатие затрачивается энергия. Сжимаемость может явиться причиной возникновения автоколебаний в гидросистеме, создает запаздывание в срабатывании гидроаппаратуры и исполнительных механизмах.

Иногда сжимаемость жидкостей полезна — ее используют в гидравлических амортизаторах и пружинах.

2. Температурное расширение — относительное изменение объема жидкости при увеличении температуры на 1°С при Р = const. Характеризуется коэффициентом температурного расширения

Поскольку для капельных жидкостей коэффициент температурного расширения ничтожно мал, то при практических расчетах его не учитывают.

3. Сопротивление растяжению

. Особыми физическими опытами было показано, что покоящаяся жидкость (в частности вода, ртуть) иногда способна сопротивляться очень большим растягивающим усилиям. Но в обычных условиях такого не происходит, и поэтому считают, что жидкость не способна сопротивляться растягивающим усилиям.

Рис. 1.6. Силы поверхностного натяжения

4. Силы поверхностного натяжения — эти силы стремятся придать сферическую форму жидкости. Силы поверхностного натяжения обусловлены поверхностными силами и направлены всегда внутрь рассматриваемого объема перпендикулярно свободной поверхности жидкости. Рассмотрим бесконечно малый объем жидкости на свободной поверхности. На него будут действовать силы со стороны соседних объемов. В результате, если сложить вектора всех сил действующих на рассматриваемый объем, то суммарная составляющая сила будет направлена перпендикулярно внутрь рассматриваемого объема.

5. Вязкость жидкости — свойство жидкости сопротивляться скольжению или сдвигу ее слоев. Суть ее заключается в возникновении внутренней силы трения между движущимися слоями жидкости, которая определяется по формуле Ньютона

где S — площадь слоев жидкости или стенки, соприкасающейся с жидкостью, м², μ- динамический коэффициент вязкости, или сила вязкостного трения, dυ /dy — градиент скорости, перпендикулярный к поверхности сдвига.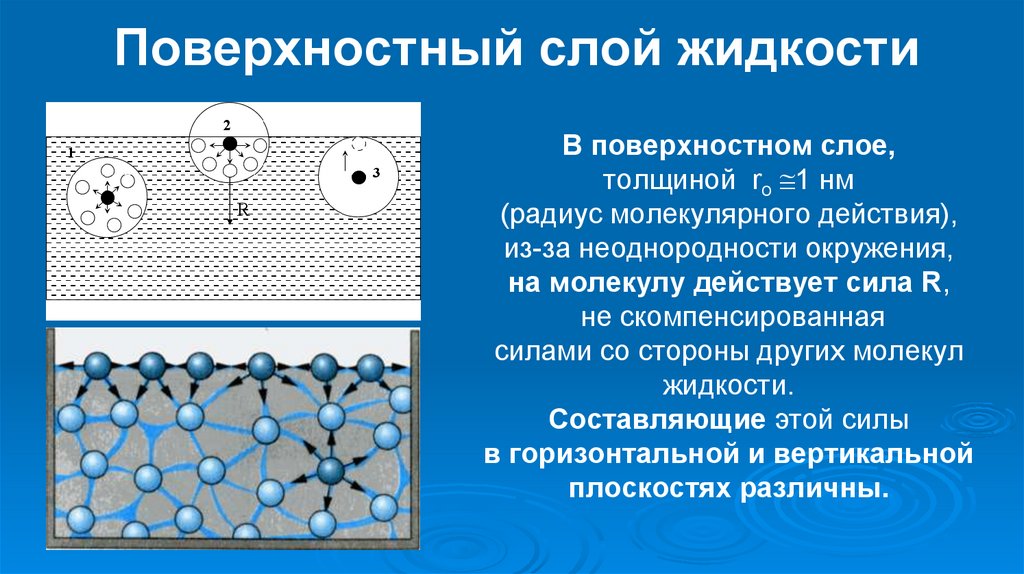

Отсюда динамическая вязкость равна

где τ — касательные напряжения жидкости, τ = T/S.

При течении вязкой жидкости вдоль твердой стенки происходит торможение потока, обусловленное вязкостью (рис.1.7). Скорость уменьшается по мере уменьшения расстояния y от стенки. При этом при y = 0, скорость падает до нуля, а между слоями происходит проскальзывание, сопровождающееся возникновением касательных напряжений τ.

Рис. 1.7. Профиль скоростей при течении вязкой жидкости вдоль стенки

Величина обратная динамическому коэффициенту вязкости (1/μ) называется текучестью жидкости.

Отношение динамического коэффициента вязкости к плотности жидкости называется кинематическим коэффициентом вязкости:

Величина ν (произносится «ню») равная 1см²/с называется стоксом (Ст), а 0,01 Ст — 1 сантистоксом (сСт).

Процесс определения вязкости называется вискозиметрией, а приборы, которыми она определяется вискозиметрами. Помимо оценки вязкости с помощью динамического и кинематического коэффициентов пользуются условной вязкостью — градусы Энглера ( Е). Вязкостью, выраженной в градусах Энглера, называется отношение времени истечения 200 см³ испытуемой жидкости через капилляр

d = 2,8 мм к времени истечения такого же объема воды при t = 20 С

Такой прибор называется вискозиметром Энглера. Для пересчета градусов Энглера в стоксы для минеральных масел применяется формула

Таким образом, для оценки вязкости жидкости можно использовать три величины, которые связаны межу собой

Рис. 1.8. Способы оценки вязкости жидкости

Вязкость жидкости зависит от температуры и от давления. При повышении температуры вязкость жидкости уменьшается и наоборот. У газов наблюдается обратное явление: с повышением температуры вязкость увеличивается, с понижением температуры — уменьшается.

6. Пенообразование.

Выделение воздуха из рабочей жидкости при падении давления может вызвать пенообразование. На интенсивность пенообразования оказывает влияние содержащаяся в рабочей жидкости вода: даже при ничтожном количестве воды (менее 0,1% по массе рабочей жидкости) возникает устойчивая пена. Образование и стойкость пены зависят от типа рабочей жидкости, от ее температуры и размеров пузырьков, от материалов и покрытий гидроаппаратуры. Особенно пенообразование происходит интенсивно в загрязненных жидкостях и бывших в эксплуатации. При температуре жидкости свыше 70 С происходит быстрый спад пены.

7. Химическая и механическая стойкость. Характеризует способность жидкости сохранять свои первоначальные физические свойства при эксплуатации и хранении.

Окисление жидкости сопровождается выпадением из нее смол и шлаков, которые откладываются на поверхности элементов гидропривода в виде твердого налета. Снижается вязкость и изменяется цвет жидкости. Продукты окисления вызывают коррозию металлов и уменьшают надежность работы гидроаппаратуры.

Налет вызывает заклинивание подвижных соединений, плунжерных пар, дросселирующих отверстий, разрушение уплотнений и разгерметизацию гидросистемы.

8. Совместимость. Совместимость рабочих жидкостей с конструкционными материалами и особенно с материалами уплотнений имеет очень большое значение. Рабочие жидкости на нефтяной основе совместимы со всеми металлами, применяемыми в гидромашиностроении, и плохо совместимы с уплотнениями, изготовленными из синтетической резины и из кожи. Синтетические рабочие жидкости плохо совмещаются с некоторыми конструкционными материалами и не совместимы с уплотнениями из маслостойкой резины.

9. Испаряемость жидкости. Испаряемость свойственна всем капельным жидкостям, однако интенсивность испарения неодинакова у различных жидкостей и зависит от условий в которых она находится: от температуры, от площади испарения, от давления, и от скорости движения газообразной среды над свободной поверхностью жидкости (от ветра).

10. Растворимость газов в жидкостях характеризуется объемом растворенного газа в единице объема жидкости и определяется по закону Генри:

где V_Г — объем растворенного газа; V_Ж — объем жидкости; k — коэффициент растворимости; Р — давление; Р_а — атмосферное давление.

Коэффициент k имеет следующие значения при 20 С: для воды 0,016, керосина 0,13, минеральных масел 0,08, жидкости АМГ-10 — 0,1. При понижении давления выделяется растворимый в жидкости газ. Это явление может отрицательно сказываться на работе гидросистем.

Механика и свойства жидкостей. (Лекция 3)

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

1. Лекция 3

Механика и свойства
жидкостей
Содержание:
1) Условие неразрывности струи
2) Вязкость жидкостью Закон Ньютона
3) Течение вязкой жидкости по трубе
4) Измерение вязкости
5) Ламинарное и турбулентное течение
6) Поверхностное натяжение
7) Смачивание и несмачивание

2.

Условие неразрывности струи•S1, S2 – площади сечений
трубы
•h2, h3 – высота над уровнем
земли
•ν1, ν2 – скорости жидкости
•в сечениях S1 и S2
•l1, l2 – пути, проходимые
•жидкостью за одно и то же
время
•Δh=h2-h3 – перепад высот
Разветвление крупного
сосуда на множество
капилляров равносильно
увеличению площади его
сечения, т.к. суммарная
площадь сечения
капилляров больше
площади сечения до
разветвления

4. Вязкость жидкости

• С
Закон Ньютона для вязкой жидкости:
Способность реальных
жидкостей оказывать сопротивление
движению в них тел или собственному
течению за счет сил межмолекулярного
взаимодействия называется
внутренним трением или вязкостью

5. Зависимость вязкости жидкости от температуры

Зависимость коэффициента вязкости от температуры для жидкостей описывается
следующим уравнением:
Где — коэффициент вязкости, W – энергия активации, T – абсолютная температура, k –
постоянная Больцмана, A – коэффициент, который зависит от температуры.

6. Вязкости некоторых жидкостей

7. Течение вязкой жидкости по трубе

• об
P1›P2 ΔP=P1-P2
жидкость течет за счет
разности давлений
R- радиус трубы
l – длина трубы
— Распределение скорости жидкости по трубе круглого
сечения
— Объем жидкости, протекающий по трубе за время t

8. Измерение вязкости

Ротационный вискозиметр
Капиллярный вискозиметр Гесса

9. Метод падающего шарика

Закон Стокса:
Ламинарное течение — течение, при
котором
жидкость
или
газ
перемещается
слоями
без
перемешивания и пульсаций (то есть
беспорядочных быстрых изменений
скорости и давления).
Увеличение скорости течения вязкой
жидкости вследствие неоднородности
давления создает завихрения и
движение становится вихревым, или
турбулентным. При турбулентном
течении скорость частиц в каждом
месте беспорядочно и хаотически
изменяется,
движение
является
нестационарным
Поверхностное натяжение
Коэффициент
поверхностного
натяжения — величина, численно
равная
работе,
совершенной
молекулярными
силами
при
изменении
площади
свободной
поверхности жидкости на 1 м2 при
постоянной температуре .
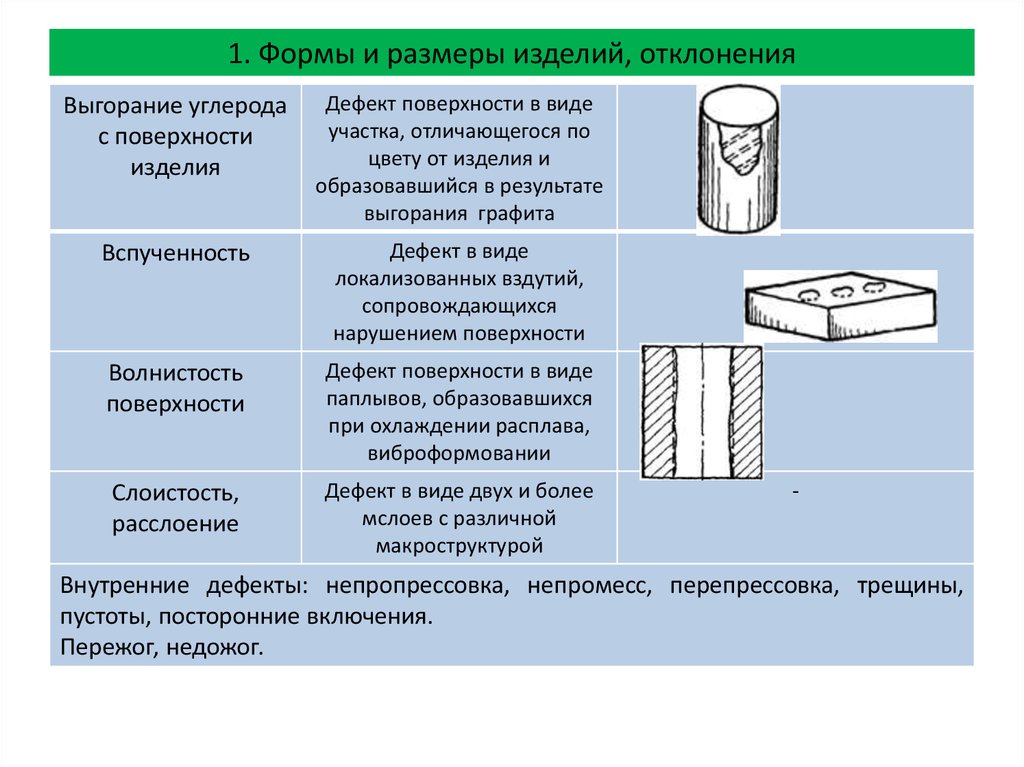
Коэффициент поверхностного натяжения σ
численно равен силе поверхностного натяжения,
действующей на единицу длины границы
свободной поверхности жидкости. Коэффициент
поверхностного натяжения зависит от природы
жидкости, от температуры и от наличия примесей.
При увеличении температуры он уменьшается.
При критической температуре, когда исчезает
различие между жидкостью и паром, σ = 0.
Смачивание и несмачивание
Смачивание
—
это
поверхностное
явление,
заключающееся
во
взаимодействии жидкости с
поверхностью твердого тела
или другой жидкости.
Отмеченный
на
рисунке угол θ называют краевым углом.
Краевой угол
образуется плоской
поверхностью
твердого
тела
и
плоскостью, касательной к свободной
поверхности жидкости, где граничат
твердое тело, жидкость и газ; внутри
краевого
угла
всегда
находится
жидкость.
Для
смачивающих
жидкостей краевой угол острый, а для не
смачивающих — тупой. Чтобы действие
силы тяжести не искажало краевой угол,
каплю надо брать как можно меньше.

English     Русский Правила

Механические свойства жидкостей Класс 11 Примечания Физика Глава 10

• Жидкости — это субстанции, которые могут течь, например, жидкости и газы. Он не имеет определенной формы.
• Когда объект погружен в покоящуюся жидкость, жидкость обычно воздействует на его поверхность. Это называется тягой жидкости.
• Давление
Тяга, приходящаяся на единицу площади поверхности покоящейся жидкости, называется давлением.

• Когда жидкость находится в равновесии, сила, действующая на ее поверхность, везде перпендикулярна. Давление одинаково на том же горизонтальном уровне.
• Давление в любой точке жидкости зависит от глубины (h) под поверхностью, плотности жидкости и ускорения свободного падения.
• Закон Паскаля
Согласно закону Паскаля, давление, прикладываемое к замкнутой жидкости, без уменьшения передается каждой порции жидкости и стенкам сосуда.
• Гидравлическая система работает по закону Паскаля. Сила, приложенная к площади, отношение будет одинаковым во всех поперечных сечениях.

Примечание: В большем поперечном сечении действует большая сила, а в меньшем по соотношению сечении действует меньшая сила 4cross.
• Столб высотой h жидкости с плотностью p оказывает давление P, заданное

• Если P _a  быть атмосферным давлением, то давление в жидкости на глубине h от ее свободной поверхности определяется выражением P = P _а + л.с.г. Соотношение верно только для несжимаемых жидкостей.
• Манометрическое давление (P _g ) представляет собой разницу абсолютного давления (P) и атмосферного давления (P _a ).
Абсолютное давление (P) = Манометрическое давление (P _g ) + Атмосферное давление (P _a )
P _g =PP _a
• Закон Архимеда
Когда тело частично или полностью погружено в жидкость, оно теряет часть своего веса. Потеря
веса тела в жидкости равна весу жидкости, вытесненной погруженной
частью тела.
• Подъемная сила, действующая на жидкость, вытесняемую при погружении тела, называется выталкивающей силой. Из-за этого наблюдается очевидная потеря веса тела.
• Закон плавучести
«Тело плавает в жидкости, если вес жидкости, вытесненной погруженной частью тела, равен весу тела».
. Когда тело полностью или частично погружено в жидкость, то на тело действуют различные силы:
(i) восходящая тяга (T), действующая в центре плавучести и величина которой равна
весу вытесненной жидкости и
• (ii) вес тела (W), действующего вертикально вниз через его центр тяжести.
(а) Когда W > T, тело утонет в жидкости;
(б) Когда W = T, то тело останется в равновесии внутри жидкости;
(c) Когда W < T, то тело всплывет на поверхность жидкости так, что вес жидкости, вытесненной за счет ее погруженной части, будет равен весу тела. Таким образом, тело будет плавать, только часть его будет погружена в жидкость.
• Поток жидкости называется стационарным или прямолинейным, если такая частица жидкости проходит через
через данную точку движется по тому же пути и с той же скоростью, что и предыдущая частица, проходящая через эту же точку.
• Если жидкость течет по горизонтальной поверхности в виде слоев с разной скоростью, то течение жидкости называется ламинарным течением.
• Течение жидкости, при котором скорости всех частиц, пересекающих данную точку, неодинаковы, а движение жидкости становится неравномерным или беспорядочным, называется турбулентным течением.
• Уравнение непрерывности
Согласно уравнению неразрывности, если по длине трубы нет источника или стока жидкости, то масса жидкости, пересекающей любое сечение трубы в единицу времени, остается постоянной. т.е. „A ₁ V ₁ ρ ₁ = A ₂ V ₂ ρ ₂
для неспреждаемых жидкостей (то есть жидкости) ρ ₁ = ρ ₂ и LEWIDS).
a ₁ v ₁ =a ₂ v ₂
– Это означает, что скорость потока жидкости больше там, где труба уже, а скорость потока меньше
где сечение трубы больше.
• Энергия жидкости
Жидкость может обладать тремя видами энергии: (i) кинетической энергией, (ii) потенциальной энергией и (iii) энергией давления
Энергия, которой обладает жидкость вследствие ее движения, называется кинетической энергией. т. е. 1/2мв ² .
Потенциальная энергия жидкости массы m на высоте h определяется формулой Ф.Е. = mgh
Энергия, которой обладает жидкость благодаря своему давлению, называется энергией давления. Энергия давления жидкости в объеме dV = PdV
Энергия давления на единицу массы жидкости

• Теорема Бернулли
Для несжимаемой, невязкой, безвихревой жидкости с обтекаемым потоком сумма энергии давления, кинетической энергии и потенциальной энергии на единицу массы является константой, т. е. ,

• Для стационарного течения невязкой жидкости по горизонтальной трубе уравнение Бернулли упрощается как вступает в игру, когда жидкость находится в движении в виде слоев, имеющих относительное движение. Он противостоит относительному движению различных слоев. Вязкость также называют трением жидкости.
• Вязкая сила напрямую зависит от площади слоя и градиента скорости.

• Коэффициент вязкости
Коэффициент вязкости жидкости равен касательной силе, необходимой для поддержания единичного градиента скорости между двумя параллельными слоями жидкости, площадь каждого из которых равна единице.

Единицей коэффициента вязкости в СИ является пуазейль (Pl) или Па-с или Нм ^-2  с или кг·м ^-1  с ^-1 . Размерная формула q [ML ^-1 Т ^-1 ].
• Закон Стокса
Согласно закону Стокса сила обратного сопротивления, действующая на небольшое сферическое тело радиуса r, движущееся со скоростью v через вязкую среду с коэффициентом вязкости ή, определяется выражением
F = 6πήr
• Терминал Скорость
Максимальная постоянная скорость, которую приобретает тело при свободном падении в вязкой среде. Это достигается, когда кажущийся вес компенсируется силой вязкости.
Дано

где p — плотность материала тела радиуса r, o — плотность среды.
• Уравнение Пуазейля
Согласно Пуазейлю, если поддерживается разность давлений (P) на двух концах капиллярной трубки длиной l и радиусом r, то объем жидкости, выходящей из трубки в расчете на второй прямо пропорционален перепаду давления (P).
(ii) прямо пропорциональна четвертой степени радиуса (r) капиллярной трубки.
(iii) обратно пропорциональна коэффициенту вязкости (ή) жидкости.
(iv) обратно пропорциональна длине (i) капиллярной трубки.
Задается как

• Число Рейнольдса
Число Рейнольдса Re — безразмерное число, значение которого дает приблизительное представление о том, будет ли течение жидкости обтекаемым или турбулентным. Он определяется как

, где p = плотность жидкости, текущей со скоростью u, d — диаметр трубы, а q — вязкость жидкости. Величина Re остается неизменной в любой системе единиц.
• Наблюдается, что поток является обтекаемым или ламинарным для R _e  <= 1000, а поток является турбулентным для R _e  >= 2000. Поток становится нестационарным для R _e  между 1000 и 2000. Критическое значение R _e , при котором устанавливается турбулентность, одинакова для геометрически подобных течений.
• R _e  также может быть выражено как отношение силы инерции (силы инерции, т. е. массы движущейся жидкости или силы инерции препятствия на ее пути) к силе вязкости, т. е.

• Критическая скорость
Критическая скорость – это скорость течения жидкости, до которой ее течение является прямолинейным, а выше – турбулентным.
Определяется как

, где K — безразмерная константа, q — коэффициент вязкости жидкости, p — плотность жидкости, r — радиус трубы.
• Поверхностное натяжение
Это свойство жидкости, благодаря которому свободная поверхность покоящейся жидкости стремится иметь минимальную площадь и поэтому ведет себя как растянутая эластичная мембрана.
• Сила, действующая на единицу длины линии, проведенной на поверхности жидкости и перпендикулярной к ней параллельно поверхности, называется силой поверхностного натяжения.
Задается как
Единицей поверхностного натяжения в системе СИ является Нм ^-1  , а его размерная формула [MT ^-2 ],
• Поверхностная энергия
Энергия, которой обладает поверхность жидкости, называется поверхностной энергией. . Изменение поверхностной энергии является произведением поверхностного натяжения и изменения площади поверхности при постоянной температуре.
• Высота, на которую поднимается вода в капиллярной трубке радиуса r, равна

, где T — поверхностное натяжение жидкости, а 0 — угол контакта.
За счет поверхностного натяжения возникает избыточное давление на вогнутой стороне поверхностной пленки жидкости над
выпуклой стороной и равно 2T/r . Для мыльного пузыря избыточное давление равно 4T/r, где r обозначает радиус поверхности.
• Угол контакта
Угол, который касательная к поверхности жидкости в точке контакта образует с твердой поверхностью внутри жидкости, называется углом контакта.
• Межмолекулярная сила между молекулами одного и того же материала называется силой сцепления. Однако сила между молекулами различных материалов называется силой сцепления.
• Теорема Торричелли
Согласно этой теореме скорость истечения, т. е. скорость, с которой жидкость вытекает из отверстия (т. е. узкого отверстия), равна той, которую приобрело бы свободно падающее тело, падая через расстояние по вертикали, равное глубине отверстия ниже свободной поверхности жидкости.
Скорость определяется выражением
V = √2gh
• Эффект Магнуса
Когда мячу придается вращение, когда он находится в потоке молекул воздуха, он будет следовать по кривой траектории, выпуклой к стороне большего давления. Эта идея лежит в основе того, что мяч от спин-боулеров получает подъемную силу и ареодинамику.

Класс 11 Примечания по физике

Механические свойства жидкостей: закон Паскаля, принцип Архимеда

Механические свойства жидкостей изучаются, чтобы понять пригодность жидкостей для различных целей. Примером важности механических свойств жидкостей может быть использование горючей и летучей жидкости внутри автомобильного двигателя, что позволяет ему легко гореть и сжиматься.

В этой теме мы собираемся обсудить свойство жидкости, такие материалы, как жидкие и газообразные, могут свободно течь в пространстве, и поэтому такой материал известен как жидкость. Но давайте сначала разберемся, в чем разница между жидкостью и твердым телом? В отличие от твердых тел, жидкости не имеют определенной формы. Это означает, что сила взаимодействия между атомами и молекулами жидкостей не так сильна, как в твердых телах, поэтому жидкости не имеют собственной формы.

С точки зрения физических различий между свойствами твердых и жидких тел твердые и жидкие вещества менее сжимаемы по сравнению с газами.

Кроме того, ключевым свойством жидкостей является то, что они оказывают очень малое сопротивление касательному напряжению, а их форма изменяется при приложении очень небольшого напряжения сдвига. Сдвиг стресс жидкостей примерно в миллион раз меньше, чем у твердых веществ

to‌get‌ ‌ ‌ ‌ ‌details‌ ‌on‌ ‌‌kekeTic‌ ‌theory‌ ‌ ‌gases‌, ‌ ‌candidates‌ ‌can‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌candidates‌ ‌can‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌candidates‌ ‌can‌ ‌ ‌ ‌ ‌ ‌candidates‌ ‌can‌ ‌ ‌ ‌ ‌ ‌candidates‌ ‌can‌ ‌ ‌ ‌ ‌ ‌candidates‌ ‌can‌ ‌ ‌ ‌ ‌ ‌candidates‌.

• Жидкости в состоянии покоя
• Давление и плотность
• Закон Паскаля
• Hydraulic Machine Lift
• Variation of Pressure with Height
• Archimedes’ Principle
• Laws of Floatation
• Equation of Continuity 
• Energy of a Fluid
• Bernoulli’s Theorem
• Applications of Bernoulli’s Theorem
• Coefficient of Viscosity
• Закон Стокса
• Закон Торричелли
• Уравнение Пуазейля
• Число Рейнольдса
• Типы течения жидкости
• Трубка потока
• Поверхностное натяжение и вязкость
• Давление жидкости и его применения
• Часто задаваемые вопросы о механических свойствах жидкостей

Жидкости в состоянии покоя

В физике есть специальный термин, известный как гидростатика, который касается характеристик жидкостей в состоянии покоя. {-2}\), как и у давления 93\). Теперь, если смешать одну и ту же жидкость с различной плотностью d1 и d2 соответственно, то плотность смеси будет

\(d= {d_1 + d_2 \over 2}\)

Аналогично, если две жидкости одинакового объема и массы m1 и m2 для плотности d1 и d2 соответственно смешиваются вместе, тогда средняя плотность смеси равна

\(d= {\text{общая масса} \over \text{общий объем}}= {{m_1+m_2 } \over {{m_1\over {d_1}}+{m_2 \over{d_2}}}}}\)

Вы‌ ‌можете‌ ‌также‌ ‌проверить‌ ‌подробности‌ ‌о‌‌‌Vector‌.‌  93 \)

Закон Паскаля

Согласно Блезу Паскалю, французский ученый заметил, что давление в покоящейся жидкости одинаково во всех точках, если они находятся на одной высоте.

т. е. давление, оказываемое жидкостью на объект на определенной высоте, будет одинаковым во всех направлениях и, следовательно, его можно выразить как

\(p_a=p_b=p_c \Longrightarrow {F_a \over{A_a}} ={F_b \over{A_b}}={F_c \over{A_c}}\)

Из приведенного выше рисунка видно, что сила, действующая на площадь в покоящейся жидкости, всегда будет испытывать давление, перпендикулярное площади их поверхности. , и объект будет испытывать одинаковое давление по всей поверхности.

Проверить‌ ‌‌Равномерный‌ ‌Круговой‌ ‌Движение‌‌ ‌статью‌ здесь‌ 

Гидравлический машинный подъемник

Существует ряд законов, таких как гидравлические подъемники и тормоза. Эти устройства использовали жидкости для передачи давления.

В гидравлическом подъемнике, как показано на рисунке ниже, два поршня разделены пространством, заполненным жидкостью.

Теперь, как предположил Паскаль, обе платформы будут иметь одинаковое давление, хотя платформа имеет разные поверхности, поэтому сила, действующая на поверхность 2, будет намного больше, чем на силу 1. 9{-2}}} \ times 2000 = 666.67n \)

Check‌ ‌‌power‌ ‌in‌ ‌ac‌ ‌circuit‌‌ ‌for‌ ‌details‌ ‌here.‌

. одинаковая высота будет равна. Но что будет, если мы измерим давление на другой высоте?

Рассмотрим жидкость в состоянии покоя в сосуде, как показано ниже.

Для заданного цилиндра мы можем рассмотреть две поверхности, поверхности 1 и 2, как показано на рисунке.

Теперь, когда данная жидкость находится в состоянии покоя, результирующая горизонтальная сила должна быть равна нулю, а вес цилиндра будет уравновешен вертикальной силой, создаваемой жидкостью.

Отсюда мы можем сказать, что сила на поверхности 2 будет уравновешивать вес цилиндра mg и силу, действующую на поверхность 1.

Что выражается как +P_1A \\\)

\(\следовательно, A(P_2-P_1)=mg \\\)

Где масса жидкости m может быть выражена через плотность и объем,

M = ρv = ρgha

\ (\, следовательно, \ delta p = p_2-p_1 = \ rho gh \)

read‌ ‌about‌ ‌the‌ ‌‌atom‌ ‌ & ‌ ‌nuclei‌‌ ‌ ‌ ‌ ‌ ‌ ‌‌atom‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌ ‌. жидкости, давление на верхней поверхности (P1) будет равно атмосферному давлению Pa, приведенное выше уравнение можно изменить следующим образом: Здесь p — давление на объект на любой высоте, Pa — атмосферное давление, ρ — плотность жидкости, а h — глубина тела, тогда как избыточное давление, т. е. P-Pa, известно как манометрическое давление. 95 \) PA

to‌ ‌get‌ ‌ ‌ ‌details‌ ‌on‌ ‌‌nuclear‌ ‌physics‌, ‌ ‌candidates‌ ‌can‌ ‌visit‌ ‌ ‌ ‌linked‌ ‌article.‌

Archimeddes ‘Принцип 92222222. aRemders aRembers aRembers aRembers aRembers aRembers aR. , равная весу вытесненной жидкости, действует на него». Таким образом, когда твердое тело полностью погружено в жидкость, оно теряет вес, равный весу вытесненной им жидкости.

То есть кажущийся вес = фактический вес — выталкивающая сила = мг+gV

где m — масса объекта, ρ — плотность жидкости

1. Следовательно, если нет гравитации, нет и направленного вверх толчка. Восходящая сила, приложенная к объекту, называется выталкивающей силой.
2. Если масса объекта равна m, то mg — это вес объекта. Вес любого объекта всегда направлен вниз. Вот почему объекты могут плавать в жидкости; поэтому его также называют законами плавания.

Для‌‌подробной‌‌‌о‌‌‌Колебания‌‌‌‌см‌‌‌‌‌в‌ ‌связанной‌ ‌статье. ‌ 

Законы плавания

Итак, если на объект, плавающий в жидкости, действует восходящая сила, величина которой равна весу вытесненной жидкости. Таким образом,

 

Уравнение неразрывности

Теперь рассмотрим несжимаемую невязкую жидкость, протекающую через полую трубу с площадями поперечного сечения A1 и A2 в любой точке.

Будем считать, что поток жидкости прямолинейный, следовательно, согласно уравнению неразрывности

\(A_1\rho_1v_1=A_2\rho_2v_2\)

Здесь ρ1 и ρ2 — соответствующие плотности жидкости, а v1 и v2 — скорости на площадях поперечного сечения A1 и A2.

Теперь, если жидкость несжимаема, ρ1 = ρ2

\(v_1A_1=v_2A_2\)

Это известно как уравнение неразрывности

Энергия жидкости

Жидкость обладает тремя видами энергии. Они следующие:

• Кинетическая энергия: Энергия, которой обладает жидкость вследствие ее движения 92+\rho gh=constant\)

  Это уравнение известно как уравнение Бернулли, и оно очень полезно при изучении течения жидкости.

  Применение теоремы Бернулли

  Распылитель – Это инструмент, используемый для распыления духов и воды. Работа атомайзера основана на принципе Бернулли. При нажатии на резиновый баллон воздух устремлялся из горизонтальной трубки, снижая давление до Р2. Давление Р2 меньше давления Р1 в сосуде. Поэтому жидкость поднимается вверх и с помощью высокоскоростного воздуха распадается на мелкие брызги.

  Горелка Бунзена – Горелка Бунзена является одним из наиболее часто используемых приборов, основанных на принципе Бернулли. Когда газ выходит из сопла, скорость газа увеличивается. В результате вокруг сопла создается область пониженного давления. Атмосферный воздух поступает к горелке, а воздух, необходимый для горения, всасывается через имеющиеся на горелке отверстия.

  Коэффициент вязкости

  Вязкость – это свойство жидкости, которое объясняет противодействие жидкости вследствие ее относительного движения.

  Обычно возникает из-за трения между двумя слоями жидкости и прямо пропорционально градиенту скорости

  , т. е. может быть выражено как сила вязкости между двумя слоями жидкости:

  [\(F= -{\ eta Adv \over{dt}}\)

  Здесь η = коэффициент вязкости

  A = площадь поперечного сечения

  Здесь отрицательный знак показывает, что сила вязкости действует в направлении, противоположном направлению потока жидкости.

  Закон Стокса

  Когда тело падает в жидкость, оно увлекает контактирующий с ним слой жидкости.

  Между разными слоями жидкости устанавливается относительное движение, в результате чего на тело действует тормозящая сила. И эта сила определяется как

  \(F=6\pi{\eta}r\nu\)

  Где

  v = скорость тела

  r = радиус тела

  η = коэффициент вязкости жидкости

  Закон Торричелли

  Слово «отток» означает отток жидкости. Торричелли обнаружил, что скорость истечения из открытого резервуара определяется формулой, идентичной скорости свободно падающего тела

  . Рассмотрим резервуар с жидкостью плотностью ρ с небольшим отверстием в боку на высоте y1 от дна как мы можем видеть на рис. ниже воздуха над жидкостью, поверхность которой находится на высоте y2, находится под давлением P.2_1+\rho gy_1=P+\rho gy_2\) …….(\(\следовательно, P_1=P_a \text{ и } P_2=P\)) 

  Теперь, взяв y1 -y2 = h, мы получим

  \(v_1 =\sqrt{2gh+{2(PP_a) \over {\rho}}}\)

  • Случай 1: Если P ≫ Pa, 2gh можно игнорировать
  • Случай 2: Если P = Pa ,

  Это уравнение также используется для описания свободно падающих предметов и также представляет собой уравнение Торричелли

  Уравнение Пуазейля

  Пуазейль дал уравнение для объема жидкости, выходящей из капиллярной трубки. Мы предполагаем, что перепад давления (P) поддерживается на двух концах капиллярной трубки, имеющей длину «l» и радиус «r». Объем жидкости, выходящей из трубки в секунду, равен 94\over{8l\eta}}\)

  Число Рейнольдса

  Число Рейнольдса R — безразмерное число, используемое для определения того, будет ли течение жидкости обтекаемым или турбулентным. Он определяется как

  \(R={\rho\nu{d}\over{\eta}}\)

  , где \(\rho\)= плотность жидкости, текущей со скоростью 

  d обозначает диаметр трубы

  \(\эта\) — вязкость жидкости.

  Значение R остается неизменным в любой системе единиц.

  • для re <= 1000: стриглизированный или ламинарный поток
  • для re> = 2000: турбулентный поток
  • для R между 1000 и 2000: Поток становится нестабильным
  Типов потока флюида 9000 2

можно разделить на три типа:

Стабильный и нестационарный поток.

Установившийся поток относится к состоянию, при котором свойства жидкости в точке системы не меняются с течением времени. Нестационарный поток относится к потоку, при котором количество жидкости, протекающей в секунду, непостоянно.

Равномерный и неравномерный поток.

Равномерный поток означает одинаковую скорость потока на единицу площади. Неравномерный поток означает, что скорость не является постоянной в данный момент времени.

Обтекаемый или ламинарный и турбулентный поток.

Ламинарный поток или обтекаемый поток – это когда жидкость течет параллельными слоями. Разрыва между слоями нет. Турбулентный поток – это поток, при котором жидкость подвергается нерегулярным колебаниям или перемешиванию.

Проточная трубка

Трубка потока представляет собой трубчатую область жидкости, окруженную границей, состоящей из линий тока. Трубка потока ведет себя как труба той же формы. Ни один слой жидкости не пересекает границы трубки потока.

Поверхностное натяжение и вязкость

• Это свойство жидкости, благодаря которому свободная поверхность жидкости в состоянии покоя действует как растянутая мембрана, стремящаяся сжаться, чтобы уменьшить площадь своей поверхности.
• Поверхностное натяжение — сила на единицу длины (или поверхностная энергия на единицу площади), действующая в плоскости раздела между жидкостью и ограничивающей поверхностью.
• Это дополнительная энергия, которой обладают молекулы на границе раздела по сравнению с внутренней частью.
• Поверхностное натяжение представляет собой силу, действующую перпендикулярно единице длины воображаемой линии, проведенной на поверхности жидкости, и может быть выражена как

\(T=\frac{F}{l}\)

Здесь T — поверхностное натяжение, F — сила, действующая на поверхность (сила сцепления), а l — единица длины.

Давление жидкости и его применение

Давление жидкости представляет собой вес жидкости, разделенный на площадь.

• Гидростатическое давление в жидкости используется в автомобильных тормозах.
• Игла шприца работает от давления жидкости.
• Гидростатический пресс работает на давлении жидкости.

Надеюсь, приведенное выше руководство по физике помогло вам получить краткое представление о механических свойствах жидкостей. Если вам нужно больше практики, загрузите приложение Testbook и получите доступ к бесплатным пробным тестам и практическим наборам!

Часто задаваемые вопросы о механических свойствах жидкостей

Q.1 Что подразумевается под относительной плотностью?

Ans.1 Относительная плотность также называется удельным весом. Относительная плотность вещества определяется как отношение плотности вещества к плотности воды при 4°C

Q.2 Что такое закон Паскаля?

Ответ 2 Согласно Блезу Паскалю, французский ученый заметил, что давление в покоящейся жидкости одинаково во всех точках, если они находятся на одной высоте.

Q.3 Что такое поверхностное натяжение жидкостей?

Ответ 3 Поверхностное натяжение – это сила на единицу длины (или поверхностная энергия на единицу площади), действующая в плоскости раздела между жидкостью и ограничивающей поверхностью.