Мост уитстона принцип: схема, принцип действия и т.д.

Измерительный мост Уинстона (Уитстона)

Измерительный мост, позволяющий определять величину неизвестного электрического сопротивления, был изобретён британским учёным Самуэлом Кристи в 1833 году, и позже модернизирован и популяризирован другим британским учёным, Чарьзом Витстоном в 1843 году.

Схема измерительного моста Уинстона.
P1 — P3 — диагональ питания; P2 — P4 — измерительная диагональ моста;
R1, R2 — левое плечо, R3, R_x — правое плечо моста.

Принцип работы

Принцип измерения неизвестного сопротивления основан на уравнивании отношений сопротивлений в обоих плечах моста, при этом гальванометр, включённый между этими плечами, будет показывать нулевое напряжение. На рисунке R_x — это неизвестное сопротивление, которое требуется измерить. R1, R2 и R3 — резисторы с известными значениями сопротивлений, причём резистор R2 переменный. Если отношение двух известных сопротивлений в плече R2/R1 равно отношению сопротивлений в плече R_x/R3, то в этом случае напряжение между точками схемы P2 и P4 будет равно нулю, и через гальванометр V ток не будет течь. Если же мост разбалансирован, то отклонение гальванометра будут указывать на то, что сопротивление резистора R2 слишком большое или слишком маленькое. Переменный резистор R2 регулируют до тех пор, пока гальванометр не укажет на ноль.

По гальванометру можно определять отсутствие тока в цепи с очень большой точностью. Следовательно, если резисторы R1, R2 и R3 — высокоточные, то неизвестное сопротивление R_x может быть измерено с большой точностью. Небольшие изменения сопротивления R_x разбалансируют измерительный мост, что обнаруживается по показанию гальванометра.

При сбалансированном мосте выполняется равенство R2/R1 = R_x/R3.

Отсюда R_x = R3*R2 / R1

В случае если сопротивления R1, R2 и R3 известны, а резистор R2 — постоянный, то неизвестное сопротивление R_x может быть рассчитано с помощью законов Кирхгофа. Этот метод измерения часто используется при применении измерительного моста в тензометрии, совместно с тензодатчиком, так как считать показания с гальванометра получится гораздо быстрее, чем балансировать мост переменным резистором.

Расчёт

Используя первый закон Кирхгофа, найдём токи, протекающие в узлах P2 и P4:

I₃ — I_x + I_G = 0
I₁ — I₂ — I_G = 0

Далее с помощью второго закона Кирхгофа найдём напряжения в контурах P1-P2-P4 и P2-P3-P4:

(I₃ * R3) — (I_G * R_G) — (I₁ * R1) = 0
(I_x * R_x) — (I₂ * R₂) + (I_G * R_G) = 0

Мост сбалансирован, следовательно I_G = 0, так что вторая система уравнений сократится:

I₃ * R3 = I₁ * R1
I_x * R_x = I₂ * R₂

Решая эту систему уравнений, получим:

R_x = R2 * I₂ * I₃ * R3 / (R1 * I₁ * I_x)

Из первого закона Кирхгофа следует, что I₃ = I_x и I₁ = I₂. Следовательно величина неизвестного сопротивления R_x будет определятся по формуле:

R_x = R3*R2/R1

Если известны сопротивления всех четырёх резисторов и величина питающего напряжения U_пит, а сопротивление гальванометра достаточно высокое, так что током I_G, протекающим через него можно пренебречь, то напряжение U между точками моста P2 и P4 может быть найдено путём расчёта каждого из делителей напряжения, вычтя затем напряжение на одном делителе из напряжения на другом делителе. В этом случае получится следующее уравнение:

U = R_x * U_пит / (R3 + R_x) — R2 * U_пит / (R1 + R2)

Напряжение питания U_пит можно вынести за скобки, в этом случае получится выражение:

U = (R_x / (R3 + R_x) — R2 / (R1 + R2)) * U_пит

Где U — напряжение в точке P2 относительно точки P4.

Измерительный мост Уинстона иллюстрирует концепцию дифференциальных измерений, результаты которых могут быть очень точными. Различные разновидности моста Уинстона используются для измерения ёмкости, индуктивности, импеданса и других величин. Одной из разновидностей моста является мост Кельвина, специально предназначенный для измерения малых сопротивлений. Во многих случаях измерение величины неизвестного сопротивления связано с измерением некоторых физических параметров, таких как сила, температура, давление и т.д., здесь в качестве измеряемого сопротивления используется соответствующий резистивный датчик.

В 1865 году Джеймс Максвелл применил измерительный мост Уинстона, питаемый переменным током, для измерения индуктивности, и в 1926 году Алан Блюмлейн подверг этот мост усовершенствованию.

Модификации основной схемы измерительного моста

Мост Уинстона является основной схемой измерительных мостов, но так же существуют различные его модификации, с помощью которых можно проводить измерения различных типов сопротивлений, когда основная схема моста для этого не подходит. Вот несколько разновидностей основной схемы измерительного моста:

• Мост Кери Фостера, предназначенный для измерения малых сопротивлений;
• Делитель Кельвина-Варлея
• Мост Кельвина
• Мост Максвелла

BACK

Измерительные мосты постоянного и переменного тока. Принципы измерений: мост Уитстона

Выберите страну

Выберите регион

Выберите город

При обслуживании металлических кабельных линий наиболее часто пользуются измерительными мостами, хотя для поиска мест повреждения кабеля существуют и другие приборы.

Во-первых, они обеспечивают высокую точность в широком диапазоне измеряемых величин. Во-вторых, их применение позволяет организовать измерения таким образом, чтобы компенсировать посторонние влияния, что незаменимо для локализации неисправности. В-третьих, они недороги.

Учитывая сказанное, полезно ознакомиться не только с устройством измерительных мостов, но и с принципами их применения для локализации неисправностей. Впрочем, говоря языком математики, для построения оптимальных схем измерения такие знания необходимы, но недостаточны. Диагностика — это всегда и опыт, и искусство.

Принцип работы мостовой схемы измерения продемонстрировано на Рисунке 1 (RM1a), а способ ее применения на практике — на Рисунке 2 (RM2a). Сопротивление R1 вычисляется исходя из полученного при балансировке моста соотношения R4/R3, в качестве R2 используется резистор с известным значением. Конечно, сказанное дает только самое общее представление об измерительной схеме моста. На самом деле он устроен гораздо сложнее — современные мосты создаются на основе цифровых процессоров.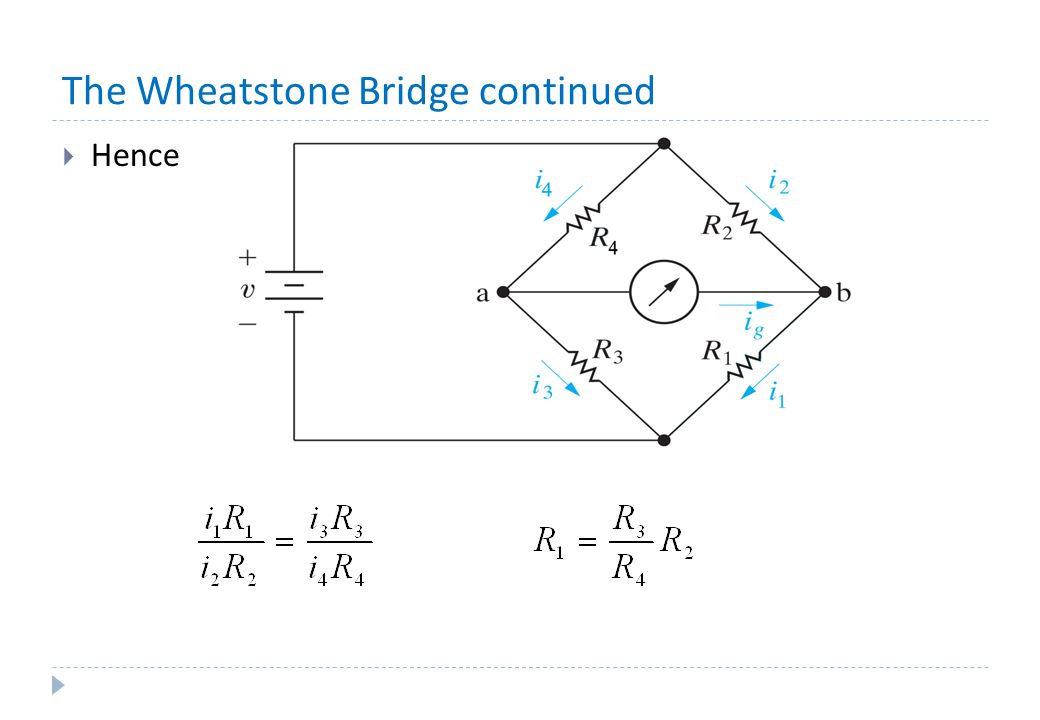

Микропроцессорное ядро позволяет автоматизировать процедуру измерения (в первых моделях оператор должен был пользоваться калькулятором, сегодня же все расчеты выполняются аппаратурой), обеспечить многофункциональность устройства (многие мосты интегрированы с другими измерительными приборами — мультиметрами, рефлектометрами и т. п.), устранить помехи (посторонние постоянные и переменные напряжения почти всегда присутствуют на жилах кабелей), организовать дальнейшую обработку накопленных результатов измерений (хранение, обмен с компьютером, печать протоколов) и др.

Рассмотренный выше мост, используемый для измерения сопротивления, носит имя Уитстона (Wheatstone). Для подключения измеряемых цепей в нем применяются всего две клеммы (B и C). Более сложные схемы реализованы в двух других мостах — Муррея (Murray) и Купфмюллера (Kupfmuller) (RM2в). Здесь измеряемые цепи подключаются с помощью трех клемм (A, B и C). В более сложных схемах Хиборна/Графа (Hilborn/Graf) задействуются четыре клеммы (A, B, B’ и C) (RM3).

Смысл увеличения числа точек подключения станет понятен при рассмотрении схем измерения с применением мостов.

Еще один момент. Все упомянутые мостовые схемы используются для измерений при постоянном токе (определяются величины активных сопротивлений, подключенных к клеммам). Кроме того, мостовые схемы Уитстона и Муррея используются для измерений при переменном токе (определяются величины емкостей, подключенных к клеммам). В таких мостах источником напряжения служит генератор синусоидального напряжения.

Теперь остановимся на схемах измерений. С помощью моста Уитстона при постоянном токе измеряют сопротивление витой пары (шлейфа), сопротивление изоляции жил пары, сопротивление изоляции между жилами и экраном (RM3, RM4, RM5).

Значения упомянутых параметров используются для диагностики кабельных линий. Локализация же неисправностей требует определения места повреждения на кабельной линии. При помощи моста постоянного тока несложно вычислить расстояние до места повреждения. Зная сопротивление шлейфа Rшл и погонное сопротивление жил кабеля Rпог, можно воспользоваться формулой: Lпары = Rшл / 2Rпог, и рассчитать длину витой пары.

Погонное сопротивление медных жил определяется табличным способом по их сечению. Оно зависит не только от сечения жил, но и от их температуры. Чтобы избежать ошибки, нужно использовать значение погонного сопротивления для соответствующей температуры (особенно важно это для воздушных кабельных линий, где температура меняется в широких пределах). В простых мостах значения вводятся оператором вручную из таблиц. В более сложных приборах при помощи автоматической или полуавтоматической калибровочной процедуры определяется поправочный коэффициент по измеренному значению температуры (для чего в комплекте прибора присутствует щуп-датчик).

Длина витой пары может быть установлена также мостовым методом при переменном токе. В таком случае измеряемым параметром является емкость витой пары. Разделив емкость витой пары на ее погонную емкость, получим длину витой пары.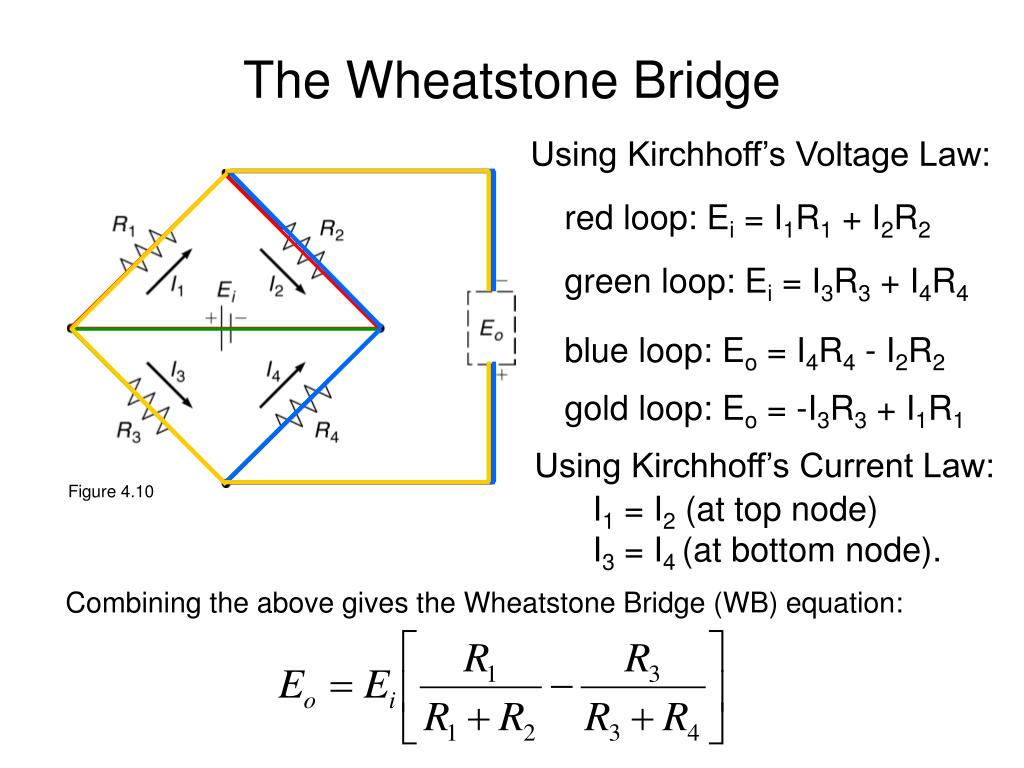

Аналогично рассмотренным выше измерениям при постоянном токе, с помощью моста Уитстона при переменном токе определяются емкость витой пары (шлейфа) и емкость каждой из жил пары относительно экрана. Длина жил может быть вычислена по их погонной емкости. Погонная емкость (нФ/км) витой пары зависит от сечения жил, типа скрутки, вида и материала изоляции и определяется табличным способом по типу кабеля.

Резкое увеличение емкости витой пары по сравнению с ее паспортным значением, как правило, свидетельствует о наличии воды в сердечнике кабеля. Для локализации повреждений этого типа применяются другие методы, прежде всего зондирование поврежденной пары с помощью рефлектометра.

Отметим, что, в отличие от сопротивления, погонная емкость слабо зависит от температуры, что существенно упрощает измерения.

Мост Уитстона — конструкция, принцип работы, ошибки, ограничения и применение

30 мая 2021 г.

Мост Уитстона — наиболее распространенный, точный и надежный метод, используемый для измерения среднего сопротивления. Принцип работы моста Уитстона основан на нулевом прогибе. Он используется для определения неизвестного сопротивления путем сравнения его с известным сопротивлением.

Строительство моста Уитстона :

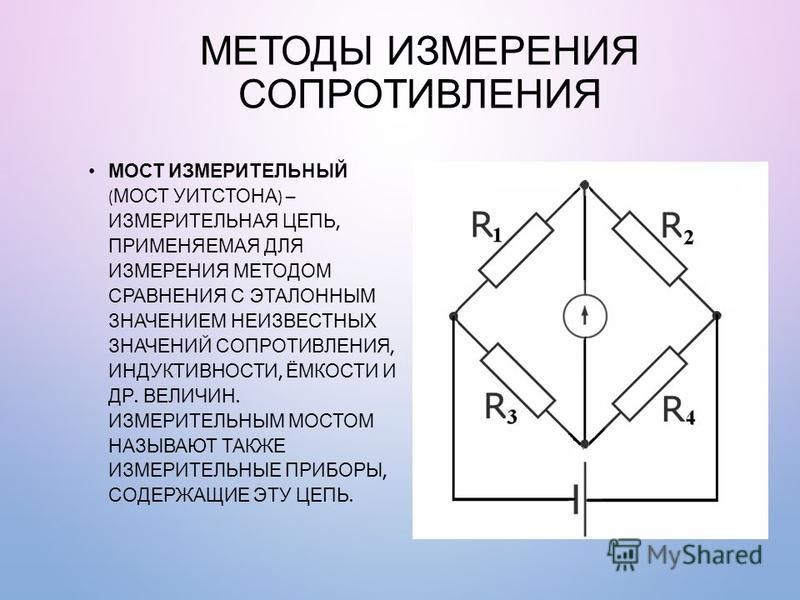
Ниже показаны электрические соединения моста Уитстона. Он состоит из четырех плеч, в которых соединены четыре сопротивления (по одному в каждом плече). Источник ЭДС и нуль-детектор (гальванометр) подключаются между точками AC и BD соответственно.

Рычаги с сопротивлениями R ₁ и R ₂ называются передаточными рычагами. Сопротивление R ₃ — это стандартное сопротивление рычага, а R ₄ — неизвестное измеряемое сопротивление.

Работа моста Уитстона :

Принцип работы моста Уитстона заключается в нулевом отклонении или нулевом показании, т. е. когда мост уравновешен, отношение их сопротивлений равно и ток через гальванометр не течет.

Если мост неуравновешен, между B и D будет разность потенциалов, которая вызывает протекание тока через гальванометр. Для достижения сбалансированного состояния следует варьировать известное сопротивление и переменное сопротивление. Базовая схема моста Уитстона показана ниже.

let,

• P = сопротивление плеча AB
• Q = сопротивление BC
• R = сопротивление AD
• S = сопротивление CD
• E = источник (батарея)
• G = Гальванометр (детектор).

Мост называется уравновешенным, если разность потенциалов между точками А и В равна напряжению на точках А и D (т. е. разность потенциалов на гальванометре или BD равна нулю). Следовательно, через гальванометр не протекает ток, следовательно, в нем нет отклонения (нулевое отклонение).

В условиях балансировки напряжение на AB будет равно напряжению на AD, т.е.

I ₁ P = I ₂ Ч …(1)

Когда мост уравновешен, также существуют следующие условия: Где Е — ЭДС источника. Подставляя значения I ₁ и I ₂ в уравнение 1, мы получаем, Где,

• R = неизвестное сопротивление
• S = стандартное сопротивление плеча
• P, Q = соотношение плеч.

Приведенное выше выражение является уравнением моста Уитстона в сбалансированном состоянии. Следовательно, из приведенного выше уравнения можно определить значение неизвестного сопротивления R, если известны сопротивления в трех других плечах, то есть P, Q и S.

Чувствительность моста Уитстона:

В состоянии равновесия гальванометр показывает нулевой ток. Но он отклоняется из-за небольшого дисбаланса моста, т. е. отклонение гальванометра зависит от его чувствительности, которая определяется как

Предположим,

• В _г = Напряжение на гальванометре.

Чувствительность моста определяется как отношение отклонения гальванометра к единице долевого изменения неизвестного сопротивления, т. е.

Для того, чтобы получить чувствительность моста, предположив небольшой разбаланс в мосту, т.е. разбаланс ΔR находится на сопротивлении R. Из-за этого разбаланса в мосте возникает ЭДС V _o поперек BD, т. е. гальванометр, как показано ниже.

Используя метод Тевенина для определения напряжения, напряжение на гальванометре или клеммах BD определяется как Отклонение гальванометра определяется как Таким образом, чувствительность моста составляет

Ошибки в мосте Уитстона:

При точном измерении сопротивления среды с помощью моста Уитстона необходимо учитывать следующие факторы.

• Сопротивление соединительных проводов — соединительный провод длиной 25 см из провода 22 SWG имеет сопротивление около 0,012 Ом, что составляет более 1 части на 1000 для сопротивления 10 Ом.
• Термоэлектрические эффекты. На отклонение гальванометра влияет термоэлектрическая ЭДС, которая присутствует в измерительной цепи из-за дисбаланса моста. Термоэлектрический эффект можно свести к минимуму (или) устранить, поменяв местами соединения батареи с помощью быстродействующего переключателя и регулируя гальванометр до тех пор, пока не будет наблюдаться изменение отклонения. Результаты получаются путем усреднения двух показаний. Таким образом, термоэлектрический эффект может быть устранен.
• Влияние температуры. Повышение температуры сопровождается повышением сопротивления всех медных и алюминиевых деталей. Ошибки, вызванные изменением сопротивления из-за изменения температуры, приводят к серьезным ошибкам в измерениях. В случае меди с температурным коэффициентом 0,004%C изменение температуры на 33,8°F вызовет ошибку 0,4%.
• Контактное сопротивление — Ошибки в измерении возникают также из-за контактных сопротивлений переключателей. Циферблат может иметь контактное сопротивление около 0,003 Ом, и, таким образом, коробка сопротивления с четырьмя циферблатами имеет контактное сопротивление около 0,012 Ом. Это значение высокое, особенно при измерении малых сопротивлений. Этого можно избежать, используя мост Кельвина для точного измерения сопротивления.

Ограничения моста из пшеничных камней:

• Эффект нагрева, вызванный током, протекающим через резисторы, приводит к изменению сопротивления плеч моста. Это можно проверить, если заранее рассчитать рассеиваемую мощность в плечах моста. Это обеспечивает ограничение тока до безопасного значения и, таким образом, снижает эффект нагрева.
• При использовании моста Уитстона для измерения малых сопротивлений нагрузочное и контактное сопротивления становятся более значительными, что вносит погрешность. Для устранения этого недостатка используется двойной мост Кельвина.
• При измерении высокого сопротивления гальванометр не показывает дисбаланс моста. Это связано с тем, что сопротивление моста становится настолько высоким, что гальванометр становится нечувствительным к дисбалансу. Этого можно избежать, заменив батарею с помощью источника питания и гальванометра на VTVM постоянного тока (вакуумный вольтметр).

Однако измерение сопротивлений в диапазоне мегаом невозможно с помощью моста Уитстона.

Применение моста из пшеничного камня:

• Точное измерение низкого сопротивления можно выполнить с помощью моста Уитстона.
• Для определения места повреждения кабеля в телефонных компаниях.
• Конфигурация моста Уитстона может использоваться с электрическими датчиками, такими как тензодатчик, LDR и термистор для измерения деформации, света и температуры.
• Его также можно использовать для измерения емкости и индуктивности.

Что такое мост Уитстона? Глубокое погружение в его принцип, теорию и доказательство

Мост Уитстона — это базовая схема, используемая для измерения неизвестного сопротивления в малых количествах. Измерение сопротивления выполняется путем соединения резистора неизвестного номинала с тремя резисторами известного номинала в четырехугольной схеме. Затем между одной парой противоположных углов подается напряжение, а к другой паре противоположных точек подключается гальванометр и производятся расчеты. Теперь, когда мы знаем, что такое мост Уитстона, давайте разберемся с его основной теорией и доказательством.

Далее, давайте узнаем, каково сбалансированное состояние моста Уитстона?

Каково сбалансированное состояние моста Уитстона?

Сбалансированный мост Уитстона — это мост, в котором через катушку не протекает ток, и, следовательно, разность потенциалов на гальванометре равна нулю.

Это условие имеет место, когда разности потенциалов между точками AB и точками AD равны. Точно так же остаются неизменными и разности потенциалов между точками BC и CD.

Рассмотрим схему моста Уитстона, в которой сопротивления P и R соединены последовательно друг с другом, а также S и Q. Но комбинация сопротивлений P и R соединена параллельно с сопротивлениями S и Q. Токи I1 , I3, I2 и I4 протекают через резисторы P, Q, R и S соответственно.

В этой цепи ток I поступает в гальванометр и делится на I1 и I2. Если гальванометр показывает нулевое значение, это означает, что эти токи имеют одинаковую величину. Такое состояние называется сбалансированным состоянием моста Уитстона.

То же самое можно математически выразить для токов I1 и I2 следующим образом:

Теперь в цепи потенциал точки B относительно точки C равен падению напряжения на Q. В этом сценарии уравнение будет

Аналогично, потенциал точки D по отношению к C равен падению напряжения на резисторе S, тогда получается уравнение0009

На приведенном ниже рисунке показан вариант моста Уитстона, в котором сопротивление R4 заменено неизвестным сопротивлением Rx. Rx прикреплен к чувствительному рычагу между точками BD, а R3 отрегулирован так, чтобы придать мосту Уитстона сбалансированное состояние. Теперь ожидается, что схема будет давать нулевой выходной сигнал на гальванометре в соответствии с принципом моста Уитстона.

Таким образом, когда мост уравновешен, сопротивления в цепи могут быть указаны как:

Теперь давайте рассмотрим уравнение баланса моста Уитстона для неизвестного сопротивления Rx. Здесь номиналы резисторов R1 и R2 известны или заданы заранее.

Его можно рассчитать, как показано ниже:

Где:

Vout указывает общее выходное напряжение.

Vc и Vd — выходы напряжения в точках C и D соответственно.

R1, R2, R3 и R4 (Rx) — четыре резистора, как показано на рисунке.

Тогда как Rc и Rd — сопротивления в точках C и D.

Этот вывод доказывает, что при замене R4 неизвестным сопротивлением Rx в сбалансированном состоянии значение Rx становится таким же, как значение R4.