Объемная скорость течения жидкости в разных сечениях: 2.Течение жидкости. Линейная и объемная скорости, соотношение между ними

2.Течение жидкости. Линейная и объемная скорости, соотношение между ними

2.Течение жидкости. Линейная и объемная скорости, соотношение между ними. Уравнение неразрывности струи. Закон Бернулли, его практическое значение.

Основной характеристикой любого движения является его скорость. Выделяют 2 разных скорости.

Скорость перемещения самих частиц жидкости (или плывущих вместе с жидкостью мелких тел — например, эритроцитов в крови) обозначают v и называют линейной скоростью. V=x/t.

Объём V жидкости, протекающей в данном потоке (в трубе, в русле реки, в кровеносном сосуде и т.п.) за единицу времени. Эту величину называют объёмной скоростью и обозначают Q.

Между линейной скоростью v и объёмной скоростью Q существует простая связь. Рассмотрим трубку с площадью поперечного сечения S.

Выделим поперечный слой жидкости, который в момент времени t = 0 занимает положение 1.

Через некоторое время t он переместится в положение 2, отстоящее на расстояние x= v*t. При этом через трубку пройдёт объём жидкости V = S*x . Объёмная скорость жидкости Q при этом будет равна Q =v/t=s*x/t. Но x/t=v, тогда

Q = S*V

В реальных жидкостях всегда существуют силы трения. В отличие от твёрдых тел, где силы трения действуют между двумя разными телами, в жидкостях силы трения возникают внутри жидкости (между разными её слоями). Поэтому трение в жидкостях называют внутренним трением или вязкостью.

Термин „идеальная жидкость» подразумевает, что при движении такой жидкости не происходит диссипация энергии (переход механической, энергии в тепло). Считалось, что таких жидкостей не существует, но в 1938 году академик П Л.Капица обнаружил, что при температурах, очень близких к абсолютному нулю, подобными свойствами обладает жидкий гелий (Капица назвал такое поведение гелия «сверхтекучестью».

Хотя во всех остальных случаях движение жидкости обязательно сопровождается диссипацией энергии, понятие идеальной жидкости (как, например, и понятие идеального газа) имеет большое практическое значение, потому что во многих случаях формулы, выведенные для идеальной жидкости, можно без больших ошибок применять для движения реальных жидкостей и газов. Наиболее интересным примером является теорема Бернулли, Рассмотрим горизонтальную трубку переменного сечения, по которой течёт жидкость или газ.

Легко видеть, что кинетическая энергия жидкости а правой части трубки больше, чем в левой, потому что линейная скорость жидкости справа больше, чем слева. Откуда взялось это увеличение энергии ? Оно произошло потому, что сила давления Кл при перемещении какого-то объема жидкости V производит некоторую работу А. По общей формуле но сила давления

равна самому давлению р, умноженному на площадь S, то есть . Отсюда

В левой части трубки соответственно, в правой части трубки Разность работ слева и справа есть

но мы уже несколько раз говорили, что через любое сечение неразветвлённой трубки проходит одинаковый объём жидкости, то 10

есть V, =V2- Обозначая объём просто V и вынося его за скобку, получим:

Так как мы считаем жидкость идеальной (потерь энергии нет), то разность работ равна приросту кинетической энергии;

Если разделить это равенство на объём, то справа вместо массы будет стоять плотность:

Перенося члены с индексом 1 влево, а с индексом 2 направо,

получаем:

Члены р и соединены знаком „плюс»; отсюда следует, что

их размерность одинакова, то есть величина тоже имеет

смысл давления. Её называют динамическим давлением, а член р – статическим давлением. Сумма статического и динамического давлений, стоящая в формуле называется полным давлением;

Так как при выводе мы положения сечений 1 и 2 взяли произвольно,- то из равенства (4) следует, что во всем потоке жидкости или газа полное давление (то есть сумма статического и динамического давлений) есть величина постоянная:

Это положение и, соответственно, формулы (4) и (5) и принято называть теоремой. Бернулли.

Статическое давление — это то давление, которое движущаяся жидкость оказывает на стенки трубки. Его можно измерить, если плоскость отверстия трубки манометра расположить параллельно линиям тока жидкости (рисунок 4-а). Если же плоскость отверстия трубки-манометра будет перпендикулярна линям тока, (рис. 4-6), то манометр покажет полное давление. При расположении манометра, как показано на рис. 4-в, мы будем измерять разность между полным и статическим давлениями, то есть динамическое давление.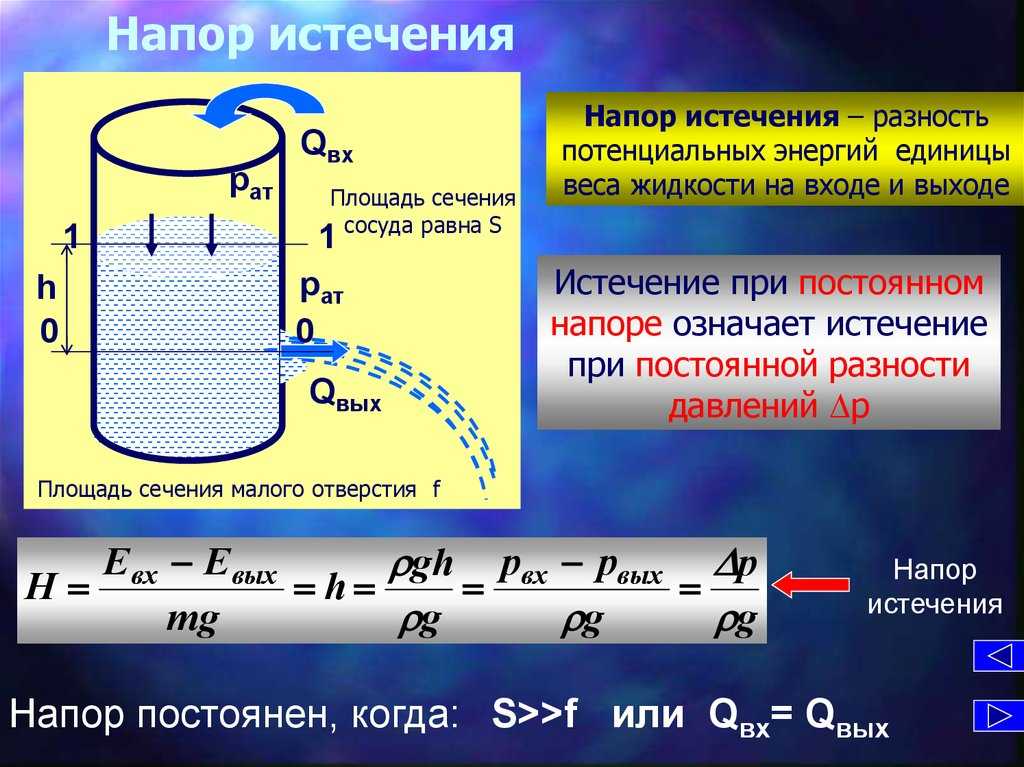

Из теоремы Бернулли следует, что там, где скорость жидкости или газа больше, статическое давление меньше, и наоборот.

Как объемная скорость установившегося течения жидкости в трубе переменного сечения зависит от площади поперечного сечения трубы? — КиберПедия

Как объемная скорость установившегося течения жидкости в трубе переменного сечения зависит от площади поперечного сечения трубы?

А. Чем меньше площадь сечения, тем меньше объемная скорость.

Б. Чем меньше площадь сечения, тем больше объемная скорость.

В. Чем больше площадь сечения, тем меньше объемная скорость.

Г. Объемная скорость не зависит от площади поперечного сечения трубы.

Как линейная скорость движения жидкости в трубе переменного сечения при установившемся течении зависит от диаметра трубы?

А. Чем меньше диаметр трубы, тем меньше скорость.

Б. Чем меньше диаметр трубы, тем больше скорость.

В.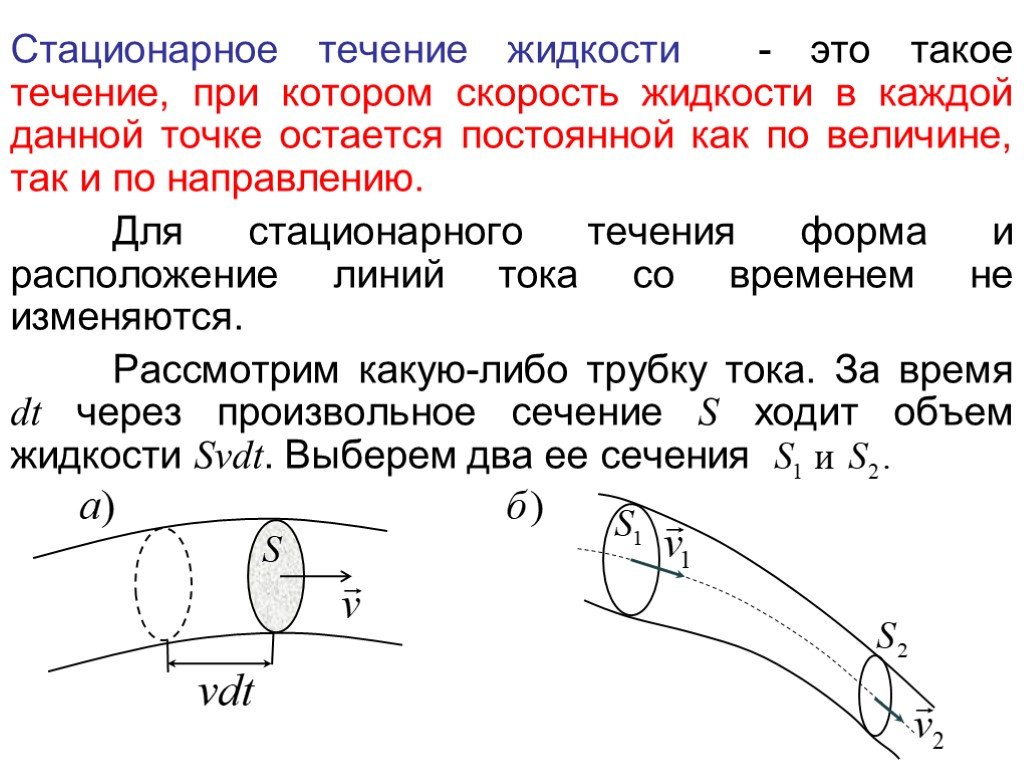 Чем больше диаметр, тем больше скорость.

Г. Линейная скорость не зависит от диаметра трубы.

54. Градиентом скорости течения жидкости g называют отношение:

А. g = dv/dt

Б. g = dv/dx

В. g = dv/ds

Г. g = dx/dt

55. Сила трения между двумя слоями движущейся жидкости (основной закон вязкого течения жидкости — закон Ньютона) с вязкостью h , площадью S, и градиентом скорости dv/dx имеет вид:

А. F = — h×(dv/dx)×l

Б. F = — h×(dv/dx)×S

В. F = h×(dv/dt)×S

Г. F = h×(dv/dx)×S

56. Единица измерения вязкости в системе СИ:

А. Па×с

Б. Па×с²В. Па/с Г. Па×м²

Как изменяется вязкость жидкости при повышении температуры?

А. Вязкость не меняется.

Б. Вязкость увеличивается.

В. Вязкость уменьшается.

Г. У одних жидкостей вязкость уменьшается, у других увеличивается.

Какое течение жидкости называется ламинарным?

А. Течение, при котором линейная скорость постоянна во всех точках

потока.

Б. Течение, при котором объемная скорость одинакова во всех сечениях

потока.

В. Течение, при котором скорость потока постепенно падает до нуля.

Г. Упорядоченное течение, при котором отдельные слои жидкости текут не

перемешиваясь друг с другом.

 

 

61. Какое движение жидкости (или газа) называется турбулентным?

А. Движение, при котором линейная скорость частиц жидкости различна в

различных сечениях потока.

Б. Движение, при котором температура жидкости различна в различных

сечениях потока.

В. Любое движение жидкости с высокой скоростью.

Г. Движение, при котором в жидкости возникают многочисленные

завихрения.

Какой параметр в формуле числа Рейнольдса выступает в качестве

Критического размера при течении жидкости по трубе?

А. Длина трубы, по которой течет жидкость.

Б. Диаметр трубы, по которой течет жидкость.

В. Размеры молекул жидкости.

Г. Отношение длины трубы к диаметру.

 

Известно, что кровь является неньютоновской жидкостью, то есть ее вязкость

Изменяется в зависимости от градиента скорости в потоке.

Это прежде всего объясняется тем, что:

А. Плазма крови обладает высокой вязкостью.

Б. Форменные элементы крови образуют крупные агрегаты – «монетные столбики».

В. Форменные элементы крови разнообразны по форме и размерам.

Г. Плазма крови обладает низкой вязкостью.

68. Идеальной жидкостью называется:

А. Несжимаемая и не имеющая вязкости жидкость

Б. Жидкость, течение которой подчиняется уравнению Ньютона

В. Жидкость, молекулы которой не взаимодействуют между собой

Г. Жидкость, состоящая из однородных недеформируемых частиц.

69. Уравнение неразрывности струи имеет вид:

А.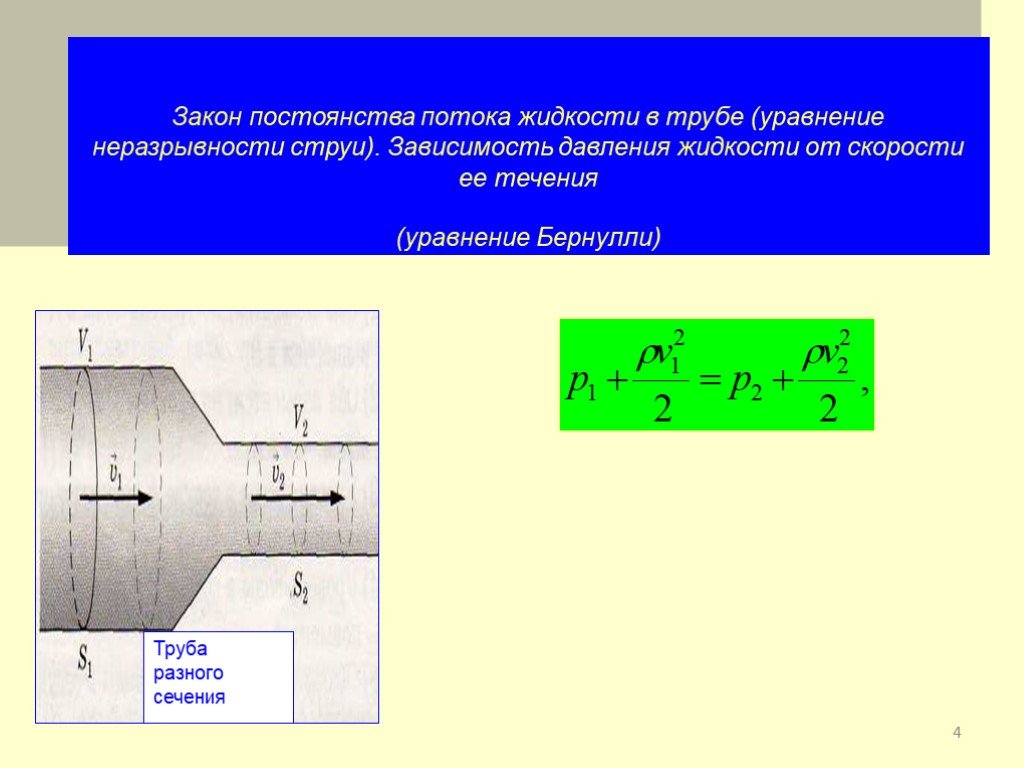 v₁×Q₁ = v₂×Q₂

Б. v₁×S₁ = v₂×S₂

В. S₁×S₁ = S₂×S₂

Г. v₁ / S₁ = v₂ / S₂

×

При движении тел сферической формы в жидкости или газе сила сопротивления F

равна:

А. F = – 9×h×R⁴×^v

Б. F = 3×v²×R×r

В. F = — 6×p×h×R×v

Г. F = 8×p× R²×v×r

 

72. Жидкости – это вещества, для которых соотношение между средней кинетической энергией частиц и их потенциальной энергией имеет вид:

А. W_пот » W_кин

Б. W_пот << W_кин

В. W_пот >> W_кин

Г. W_пот ¹ 0, W_кин » 0

Вязкость крови

А. В мелких сосудах меньше, чем в крупных.

Б. В мелких сосудах больше, чем в крупных.

В. Постоянна во всех отделах сосудистого русла.

75. Течение крови по сосудам является:

А. Всегда ламинарным.

Б. Всегда турбулентным.

В. Преимущественно ламинарным и лишь в некоторых случаях – турбулентным.

Г. Преимущественно турбулентным и лишь в некоторых случаях – ламинарным.

76. В каком отделе сосудистого русла линейная скорость кровотока минимальна:

А. В аорте.

Б. В артериях.

В. В артериолах.

Г. В капиллярах.

77. Основной движущей силой кровотока является:

А. Кровяное давление, обусловленное превышением давления, вызванного работой сердца,

над атмосферным давлением.

Б. Гидростатическое давление.

В. Сила тяжести.

Г. Статическое давление.

78. Ламинарное течение жидкости переходит в турбулентное при:

А. Повышении температуры.

Б. При увеличении скорости течения.

В. При повышении давления.

Г. При уменьшении скорости течения жидкости.

 

81. Число Рейнольдса R_e зависит от плотности жидкости r, скорости ее течения v, критического размера d, вязкостижидкости и определяется формулой:

А. R_e = r v d /h

Б. R_e = r v/hd

В. R_e = r /hv d

Г. R_e = r h/v d

 

82. Если число Рейнольдса превышает критическое значение, то:

А. Течение жидкости имеет ламинарный характер.

Б. Характер течения жидкости определить нельзя.

В. Течение жидкости называется установившимся.

Г. Течение жидкости имеет турбулентный характер.

 

Как объемная скорость установившегося течения жидкости в трубе переменного сечения зависит от площади поперечного сечения трубы?

А. Чем меньше площадь сечения, тем меньше объемная скорость.

Б. Чем меньше площадь сечения, тем больше объемная скорость.

В. Чем больше площадь сечения, тем меньше объемная скорость.

Г. Объемная скорость не зависит от площади поперечного сечения трубы.

Измерение объемного расхода жидкости и газа ~ Изучение приборостроения и техники управления

В этом блоге мы обсуждали в прошлом различные технологии расходомеров, где требуется объемный расход. Также важно, чтобы мы обсудили единицы измерения расхода в некоторых из этих технологий расходомеров. Этот пост предназначен для расширения вашего понимания объемных расходов жидкости и особенно измерения расхода газа.

Как мы могли видеть, большинство технологий расходомеров работают по принципу интерпретации потока жидкости на основе скорости жидкости. Некоторые из технологий расходомеров, использующих этот принцип, включают:

(a) Ультразвуковые расходомеры
(b) Турбинные расходомеры
(c) Расходомеры с диафрагмой и т. д.

В этих расходомерах, основанных на скорости, скорость жидкости можно легко преобразовать в объемный расход, используя приведенное ниже уравнение непрерывности:

                              Q = AV
Где:
Q = объемный расход
A = площадь поперечного сечения горловины расходомера
V = средняя скорость жидкости в секции горловины

0014
Многие приложения для измерения расхода промышленных сред, включающие жидкости, измеряются в объемных единицах, поскольку измерение жидкости относительно просто. Измерения объемного расхода жидкостей в основном измеряются в кубических футах в единицу времени (например, фут3/мин), кубических метрах в единицу времени (например, м3/мин) или галлонах в единицу времени (например, галлонах/мин). Жидкости по существу несжимаемы: то есть они не уступают по объему приложенному давлению. Это делает измерение объемного расхода жидкостей относительно простым: один кубический метр жидкости при высоком давлении и температуре внутри технологического сосуда будет занимать примерно такой же объем (≈ 1 м3), когда хранится в другом технологическом сосуде при атмосферном давлении и температуре.

То есть объемные скорости потока в большинстве жидких систем практически не зависят от изменений давления и температуры.

Объемный расход при измерении расхода газа

Газы и пары легко изменяют свой объем под воздействием давления и температуры. Другими словами, газ будет уступать увеличивающемуся давлению за счет уменьшения объема, поскольку молекулы газа сближаются, и он будет уступать при понижении температуры за счет уменьшения объема по мере уменьшения кинетической энергии отдельных молекул.

Это делает измерение объемного расхода газов и паров более запутанным и сложным, чем для жидкостей. Один кубический метр газа при высоком давлении и температуре внутри технологического сосуда не займет один кубический метр при различных условиях давления и температуры в том же сосуде. Это означает, что измерение объемного расхода газа практически бессмысленно без сопутствующих данных о давлении и температуре.

Стандартизированное измерение объемного расхода

Поскольку газ занимает разные объемы при различных условиях температуры и давления, объемы газа указываются при некотором согласованном наборе давления и температуры, известных как стандартные условия, а объемы газа называются стандартизированными.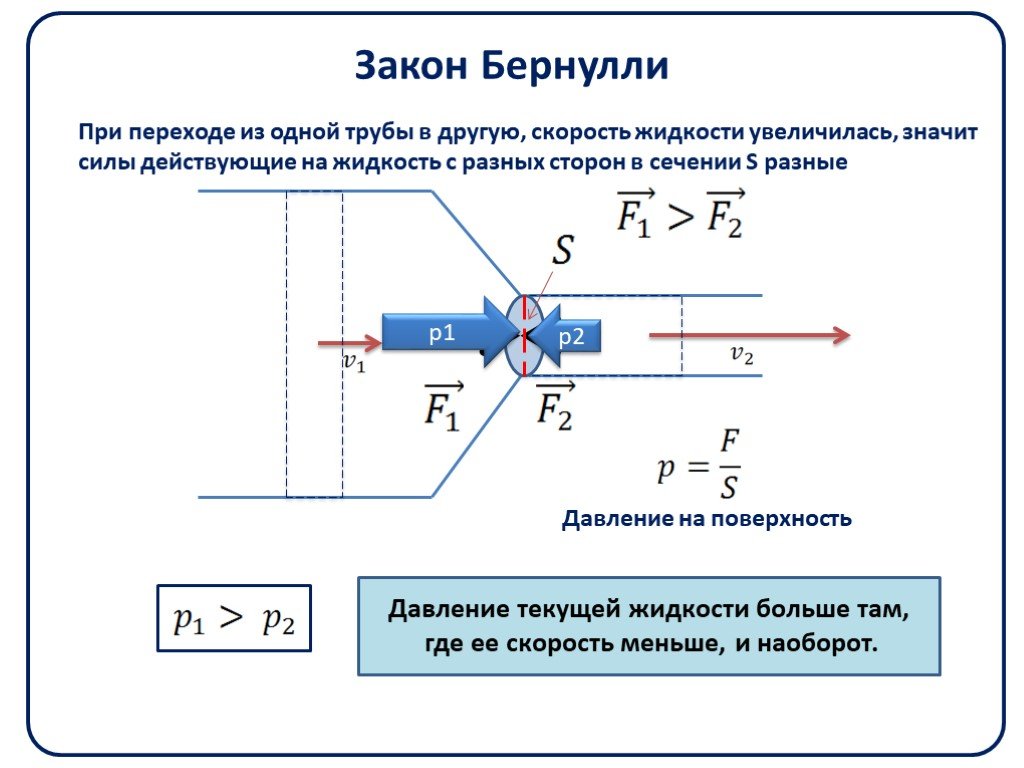

измерение объемного расхода.

Чтобы отличить фактический объемный расход от стандартного объемного расхода, мы обычно предваряем каждую единицу буквой «A» или буквой «S», в зависимости от случая, например. АКФМ и СКФМ. Здесь ACFM означает фактический кубический фут в минуту, который представляет собой объем газа при текущих условиях. SCFM означает стандартный кубический фут в минуту, который представляет собой объем того же газа в настоящее время при стандартных условиях температуры и давления.

Стандартные условия, используемые для определения стандартизированного объемного расхода

Существуют различные стандартные условия для определения стандартизированного расхода в большинстве приложений коммерческого учета газов по всему миру, особенно природного газа:

(a) Использует API (Американский институт нефти) 14,7 фунтов на квадратный дюйм и 60 градусов по Фаренгейту, эквивалентные 519,67 градусов по Ранкину, в качестве стандартных условий для расчета объемного расхода газа для расчета

объемный расход газа.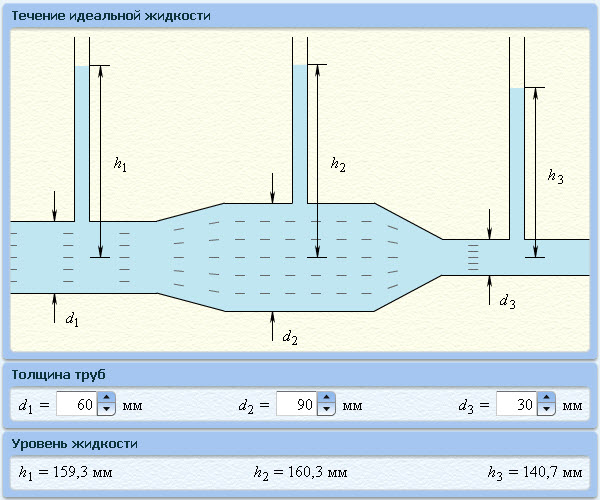

(c) Американский CAGI (Институт сжатого воздуха и газа) использует 14,5 PSIA и 68 градусов по Фаренгейту (527,67 градусов по Ренкину) в качестве стандартных условий для расчета объемного расхода газа.

Фактический расход по сравнению со стандартным объемным расходом

Как показано выше, рассмотрим газ с фактическим расходом VA, давлением PA и температурой TA в условиях потока. Предположим, что газу позволили расшириться до стандартных условий, и теперь мы хотим определить объем газа VS при данных условиях давления PS и температуры TS. Мы можем использовать уравнение идеального газа, чтобы определить это:

                     
PV = ZnRT

Где:
P = давление
V = объем
Z = коэффициент сжимаемости газа
R = универсальная газовая постоянная
T = температура

В условиях, далеких от критических точек фазового перехода, большинство реальных газов ведут себя как идеальные газы, т.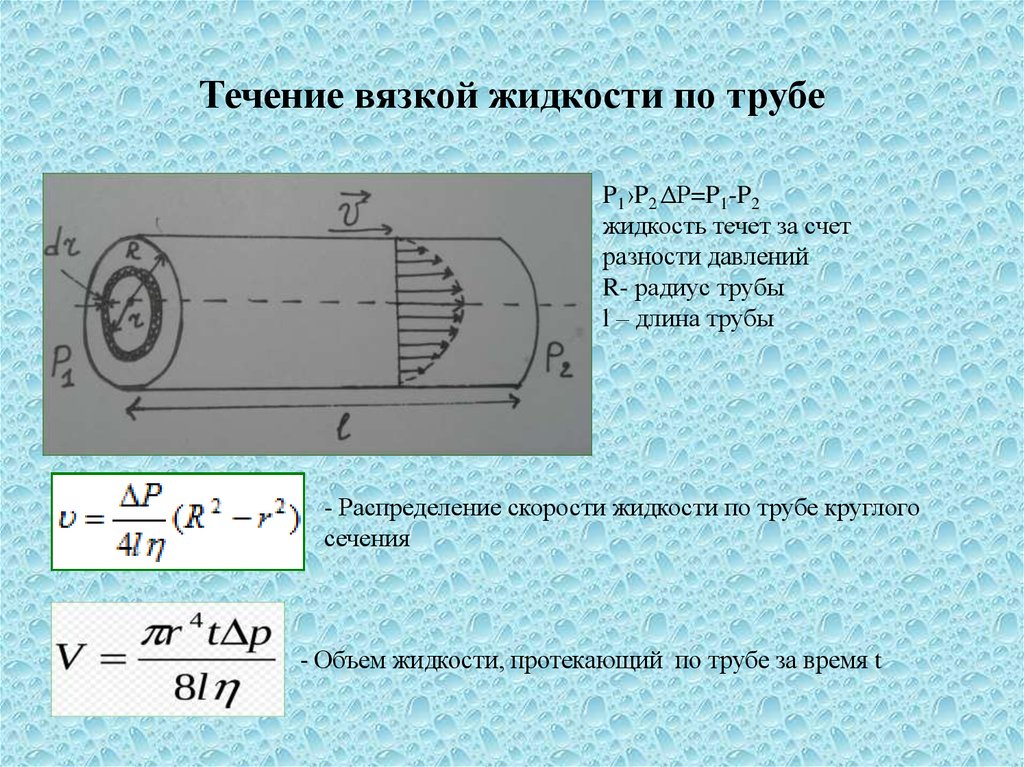 е. Z = 1, следовательно, мы имеем хорошее приближение к закону идеального газа:
                       $PV = nRT$ имеют:

 $P_AV_A = nRT_A $  ————(1)
При стандартных условиях имеем: 

$P_SV_S = nRT_S$ ————-( 2)
Разделив уравнение (2) на (1), получим:
 $\frac{P_SV_S}{P_AV_A} = \frac{nRT_S}{nRT_A}$            

Что теперь сводится к:
 $\frac{V_S}{ V_A} = \frac{P_AT_S}{P_ST_A}$              

Поскольку мы знаем, что определением объемного расхода (Q) является изменение объема во времени (V/t), мы можем разделить каждую переменную Volume ,V, на t, чтобы преобразовать это в объемный расход таким образом:

 $\frac{Q_S}{Q_A} = \frac{P_AT_S}{P_ST_A}$                 

Приведенное выше уравнение дает нам отношение стандартизированного объемного расхода (Qs) к фактическому объемному расходу (Q) для любого известных давлений и температур.
Из этого уравнения видно, что стандартный объемный расход определяется по формуле:

 $Q_S = Q_A\frac{P_AT_S}{P_ST_A}$    

         
Чтобы использовать приведенную выше формулу, давление и температура должны быть выражены в абсолютных единицах. как следует из закона идеального газа.
Давайте рассмотрим пример, чтобы проиллюстрировать применение приведенной выше формулы в приложении коммерческого учета природного газа:
Станция учета природного газа производит 200 000 кубических футов в час (фактических кубических футов в час) газа при средней температуре 350°C и давлении 18бар изб.
(a) Какова объемная скорость потока в стандартных кубических футах в час (SCFH)
(b) Какой объем газа может быть доставлен за два (2) дня в
(i) SCF (стандартные кубические футы) (ii ) SCM (стандартные кубические метры) 90R$
Примечание (градусы F = 1,8*C + 32) и (градусы R = F + 459,67)
$P_S$ = 14,7 фунтов на квадратный дюйм
$T_S$  = 68 + 459,67 = 527,67 градусов Ренкина Следовательно:
$Q_S$  = 200 000 x (279,3*527,67)/(14,7*554,67) = 3 615 025,15008 стандартных кубических футов в час =     
             = 3,615025 млн стандартных кубических футов в час = 3 615 025,15008 x 2 x 24 = 173 521 207,20384 стандартных кубических футов [1 день = 24 часа]
         = 173,521 млн стандартных кубических футов
(b)(ii) Общий объем газа в SCM, поставленный за два (2) дня:
= 173 521,207.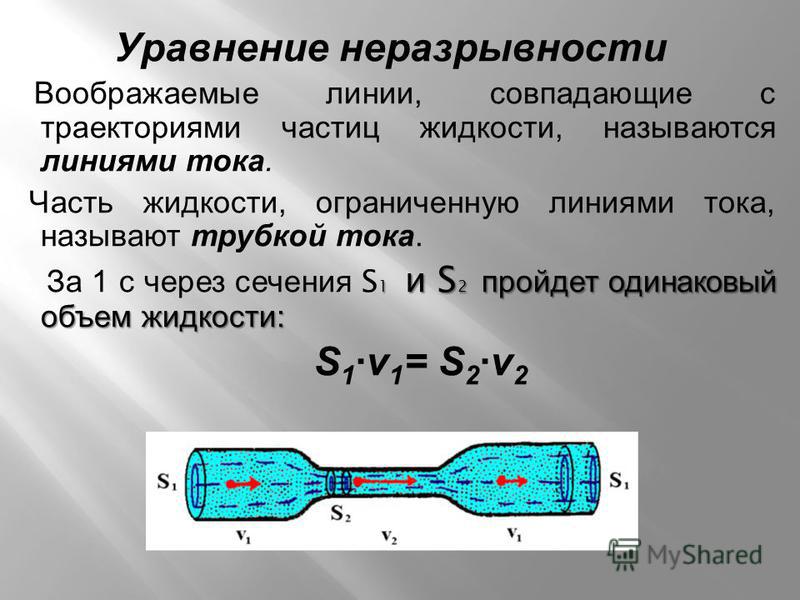 203844SCF x 0,0283168466SCM/SCF
= 4,913,573.40624SCM = 4,9136MMSCM

Факторы конверсии :
в зависимости от того, что вы можете найти в следующих факторах.
1 станд. куб. м = 35,314666711 станд. куб. футов
MSCF = 1000 станд. куб.

Градус F = 1,8*C + 32  , F обозначает градусы Фаренгейта, C обозначает 9 градусов Цельсия.0004

Градус R = F + 459,67
Абсолютное давление (фунт/кв. дюйм) = манометрическое давление (фунт/кв. дюйм абс.) + 14,7 фунт/кв. термин в физике, который описывает, сколько материи — с точки зрения физических размеров, а не массы — перемещается в пространстве в единицу времени. Например, когда вы включаете кухонный кран, определенное количество воды (которое вы можете измерить в жидких унциях, литрах или чем-то еще) вытекает из отверстия крана за определенное время (обычно секунды или минуты). Это количество считается объемным расходом.

Термин «объемный расход» почти всегда применяется к жидкостям и газам; твердые тела не «текут», даже если они тоже могут двигаться в пространстве с постоянной скоростью.

Уравнение объемного расхода

Основное уравнение для задач такого рода: занята текущим материалом, а V — средняя скорость потока. V считается средним, потому что не все части текущей жидкости движутся с одинаковой скоростью. Например, когда вы наблюдаете, как воды реки неуклонно текут вниз по течению с заданным количеством галлонов в секунду, вы замечаете, что здесь течение на поверхности более медленное, а там более быстрое.

Поперечное сечение часто представляет собой круг в задачах объемного расхода, потому что эти задачи часто касаются круглых труб. В этих случаях площадь A находится путем возведения в квадрат радиуса трубы (который составляет половину диаметра) и умножения результата на константу пи (π), которая имеет значение около 3,14159..

Обычными единицами измерения расхода в системе СИ (от французского «международная система», эквивалентная «метрической системе») являются литры в секунду (л/с) или миллилитры в минуту (мл/мин).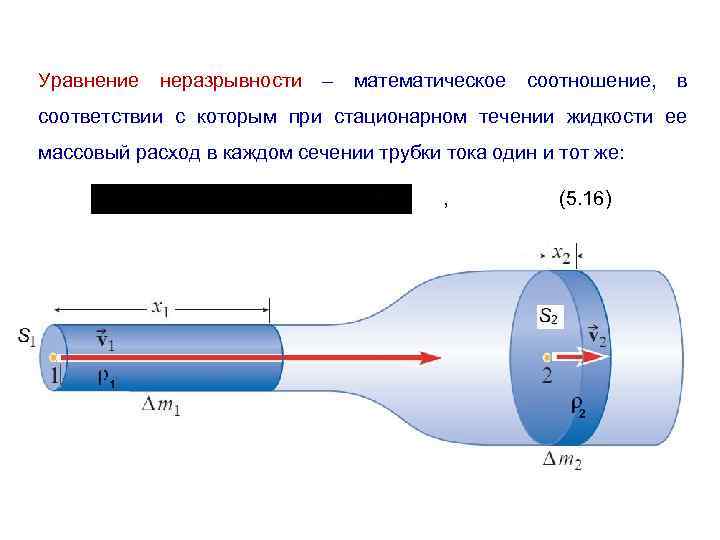 Однако, поскольку в США уже давно используются имперские (английские) единицы измерения, объемный расход по-прежнему гораздо чаще выражается в галлонах в день, галлонах в минуту (галлонах в минуту) или кубических футах в секунду (кубических футах в секунду). Чтобы найти объемный расход в единицах, которые обычно не используются для этой цели, вы можете использовать онлайн-калькулятор расхода, такой как тот, что находится в Ресурсах.

Массовый расход

Иногда вам нужно знать не только объем жидкости, движущейся в единицу времени, но и количество массы, которое она представляет. Это, очевидно, имеет решающее значение в технике, когда необходимо знать, какой вес может безопасно выдержать данная труба или другой трубопровод или резервуар для жидкости.

Формула массового расхода может быть получена из формулы объемного расхода путем умножения всего уравнения на плотность жидкости ​ ρ ​. Это следует из того факта, что плотность — это масса, деленная на объем, что также означает, что масса равна плотности, умноженной на объем.