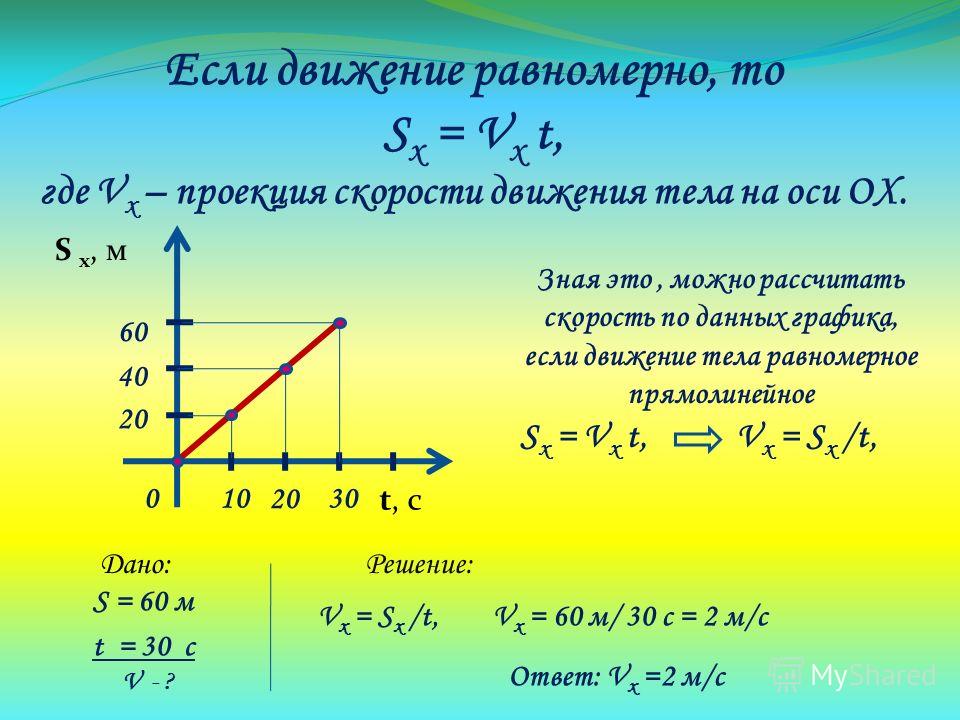
Средняя скорость, теория и онлайн калькуляторы
Средняя скорость, теория и онлайн калькуляторыПеремещение материальной точки
Пусть материальная точка совершает движение по оси X все время в одном направлении. Тогда перемещением этой материальной точки за отрезок времени $\Delta t=t_2-t_1$ будет отрезок $\Delta x=x_2-x_1$. Если материальная точка все время своего движения перемещалась в одном направлении, то пройденный путь ($\Delta s$) равен по модулю величине перемещения:
\[\Delta s=\left|\Delta x\right|\left(1\right).\]
Если точка движется сначала в одном направлении, затем останавливается и движется в противоположном направлении, (например, так движется тело брошенное вертикально вверх) то путь равен сумме модулей перемещений в обоих направлениях:
\[\Delta s=\left|\Delta x_1\right|+\left|\Delta x_2\right|+\dots \left(2\right).\]
Определение средней скорости
Определение
Средней скоростью ($\left\langle v\right\rangle $) материальной точки за промежуток времени $\Delta t$ называют физическую величину, которая равна отношению перемещения, которое совершило тело к этому промежутку времени:
\[\left\langle v\right\rangle =\frac{\Delta x}{\Delta t}\left(3\right). 2\left(4\right).\]
2\left(4\right).\]
Для моментов времени $t_1=0,1\ $c координата тела (подставим время $t_1$ в формулу (4)) равна: $x_1=0,049\ $м; для $t_2=0,2\ $c$\ x_2=0,196$ м, тогда $\left\langle v\right\rangle $в промежутке времени от $t_1=0,1$ с до $t_2=0,2\ $c будет:
\[\left\langle v\right\rangle =\frac{0,196-0,049}{0,2-0,1}=1,47\ \left(\frac{м}{с}\right).\]
Если взять для того же свободно падающего тела промежуток времени от $t_1=0,7$ с до $t_2=0,8\ $c, то средняя скорость получится равной $\left\langle v\right\rangle =7,4\frac{м}{с}$.
Средняя скорость равномерного движения
Только при равномерном движении средняя скорость является постоянной величиной и не зависит от выбора промежутка времени, в который движется тело. При равномерном движении материальной точки по оси X кинематические уравнения для перемещения запишем как:
\[x=x_0+vt\ \left(5\right).\]
Тогда:
\[x_1\left(t_1\right)=x_0+vt_1;;\ x_2\left(t_2\right)=x_0+vt_2\left(6\right). \]
\]
Найдем среднюю скорость движения, используя определение (3) и выражения (6):
\[\left\langle v\right\rangle =\frac{x_0+vt_2-x_0-vt_1}{t_2-t_1}=v\frac{t_2-t_1}{t_2-t_1}=v.\]
Для оценки численной величины средней скорости на практике используют следующее определение $\left\langle v\right\rangle $: средняя скорость равна отношению пройдённого пути (s) ко времени (t), которое было затрачено на движение:
\[\left\langle v\right\rangle =\frac{s}{t}\left(7\right).\]
Определяемая таким образом средняя скорость является скалярной величиной.
Примеры задач с решением
Пример 1
Задание. Пешеход, потратил первую половину времени своего движения, двигаясь со скоростью $v_1=5\frac{км}{ч}$, вторую половину времени он шел со скоростью $v_3=3\frac{км}{ч}$. Какова средняя скорость движения человека?
Решение. Сделаем рисунок.
Для решения задачи используем формулу, определяющую среднюю скорость:
\[\left\langle v\right\rangle =\frac{s}{t}\ \left(1.1\right),\]
где путь складывается из двух участков движения:
\[s=s_1+s_2\left(1.2\right).\]
Причем по условию задачи:
\[s_1=v_1t_1=v_1\frac{t}{2}\left(1.3\right)\ и\ \] \[s_2=v_2t_2=v_2\frac{t}{2}\left(1.4\right).\]
Подставим в определение средней скорости (1.1) правые части выражений (1.2) — (1.4), и учтем, что $t=t_1+t_2$ имеем:
\[\left\langle v\right\rangle =\frac{v_1\frac{t}{2}+v_2\frac{t}{2}}{t}=\frac{v_1+v_2}{2}.\]
Вычислим среднюю скорость пешехода:
\[\left\langle v\right\rangle =\frac{5+3}{2}=4\ (\frac{м}{с}).\]
Ответ. $\left\langle v\right\rangle =4\frac{м}{с}$
Пример 2
Задание. 2}{3}$
2}{3}$
Читать дальше: статика.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Формула средней скорости движения
|
|
|
|||||||||||||||||||||
| На главную
Теория
Задачи
Учёные
Интересные статьи
Шкала скоростей
Средняя скорость – не
самое сложное понятие в кинематике. 2. Как правильно
рассчитать среднюю скорость тела, которое начало движение в пункте А, окончило
его в пункте В, но по дороге из А в В поворачивало назад (может быть ни
один раз!), а затем вновь продолжало движение к пункту В? Пример 1. Найти среднюю скорость человека на пути от дома до станции, расстояние между которыми l =800 м, если, пройдя четверть пути, он вернулся домой (например, проверить, хорошо ли закрыта дверь) и через мин продолжил путь на станцию. Скорость движения человека постоянна и равна v =4 км/ч. Решение. Началом движения человека, конечно, следует считать момент времени,
когда он первый раз вышел из дома. S = 2l1/4 + l =400 + 800 =1200 м =1,2 км. Время t, которое затрачено на преодоление этого пути, складывается из времени пребывания дома и времени Т, в течение которого человек двигался по маршруту “из дома–к дому–на станцию”. Поскольку скорость движения человека постоянна (v =4 км/ч) и проделанный путь известен, то время движения составляет: 1,2 км : 4
км/ч =0,3 ч =18 мин. t =+ T = 2 + 18 =20 мин =1/3 ч. 1,2 км : ч =3,6 км/ч. Ответ: vср =3,6 км/ч. Среднюю скорость движения человек оценивает
довольно часто, но судит о ней, глядя на часы. Вернемся к рассмотренному примеру. Будем считать, что скорость v0 =4 км/ч выбрана человеком не случайно. проходя от дома до станции ежедневно, человек замечает, что расстояние l ==800 м, он проходит за время t0 =12 мин =0,2 ч: = 0,8 км : 0,2 ч =4 км/ч. По существу, это – средняя скорость,
поскольку доподлинно неизвестно, с какой скоростью человек идет в каждый момент
времени. Двигаясь с такой скоростью и затрачивая время t0,
человек ежедневно успевает на станцию вовремя. Если приходится возвращаться
домой (увеличивать путь, который надо преодолеть и на это требуется
дополнительное время) или останавливаться (увеличивая время, необходимое на
преодоление пути), выбранная скорость движения v0 не
подходит: можно опоздать на станцию. Пример 2. Человек обычно доходит из дома до станции за время t0 =12 мин, проходя расстояние l =800 м. Однажды, пройдя четверть пути, он вспоминает, что не выключил электроприборы, и возвращается домой, выключает электроприборы, затрачивая время= 2 мин, и снова идет на станцию. С какой наименьшей скоростью надо двигаться человеку, после того как он повернул домой, чтобы успеть на станцию в обычное время (и не опоздать на электричку). Решение. 1. Обычно человек двигается со скоростью м/мин =4 км/ч. 2. Пройдя с такой скоростью четверть пути, он затратил время : 4 км/ч =0,05 ч =3 мин. Значит, в его распоряжении осталось время Т2 =t0 – T1 =12 – 3 =9 мин. 3. За время Т2 человек должен
преодолеть путь до дома, а затем снова до станции: ч, то есть со скоростью, не меньшей, чем 1 км : ч =км/ч =км/ч » 8,6 км/ч. Проверьте, что добежав до дома со скоростью км/ч, а
затем шагая со скоростью v2 =2v0 =8 км/ч,
человек придет на станцию вовремя. м/мин =100 м/мин =6 км/ч. Найденное значение vср в полтора раза выше, чем v0, и показывает, с какой начальной скоростью следует выходить человеку из дома, если он забывчив. На рис.1 показан график зависимости скорости человека от
времени для примера 2 в случае, если человек бежит домой со скоростью v1
=3v0 ==12 км/ч, а затем идет до станции очень быстрым
шагом со скоростью v2 =2v0 =8 км/ч. Подсчитаем среднее арифметическое для значений скорости v0, v1, v2: км/ч. Это значение не равно значению средней скорости vср. Убедитесь в этом и не совершайте в дальнейшем распространенную ошибку: не пытайтесь искать среднюю скорость как среднее арифметическое значение (оно не имеет физического смысла!). Пример 3. Автомобиль проезжает первую треть пути равномерно со
скоростью v1 =108 км/ч, а остальные две трети пути – со
скоростью v2 =72 км/ч. Найти среднюю скорость автомобиля. км/ч. 1. Найдем время t1 движения
со скоростью v1, полагая, что весь путь равен L [км].
Из условия ясно, что 2. Время t2 движения на оставшемся участке пути составляет 3. Итак, время на продолжение пути L составляет 4. По определению средней скорости км/ч. Ответ: средняя скорость vср =81 км/ч. Значение средней скорости совпадает со
средним арифметическим значением скорости только в одном частном случае,
когда тело двигается с различными скоростями так, что между последовательными
моментами изменения (переключения) скорости проходит одинаковое время Т.
Таким образом, тело двигается со скоростью v1 в течение
времени t1=T, со скоростью v2 в
течение времени t2=T, со скоростью v3
в течение времени t3=T и т. S =v1t1 + v2t2 + v3t3 + … +vntn =T(v1 + v2 + v3 + … +vn). Время t, за которое пройден путь, составляет t =t1 + t2 + t3 + … + tn =T*n. По определению: . Не запрещено для этого частного случая двигаться со скоростью v0=0, т.е. делать остановки. Но время остановки должно составлять t0 =T. Пример 4. Вертолет пролетает без остановок равномерно и
прямолинейно над пунктами А, В, С (в указанном порядке) и
возвращается в А. Пункты А, В, С являются как бы вершинами треугольника. Решение. 1. Находим скорость движения вертолета на каждом участке: км/ч; км/ч; км/ч. 2. Поскольку t =0,5 ч одинаково для всех участков движения, то км/ч. 3. Если расстояние LСА =200
км и tCA=1ч, то не меняется vCA=200
км/ч. Но в этом случае нельзя подсчитывать (для простоты) среднюю скорость как
среднее арифметическое, так как tCА ? tAB ==tBC. км/ч. Ответ: 1) vcp1 =300 км/ч; 2) vcp2 =275 км/ч. Контрольные задания на эту тему
|
Средняя скорость. Ускорение | 7 класс Онлайн
Конспект по физике для 7 класса «Средняя скорость. Ускорение». ВЫ УЗНАЕТЕ: Как можно определить среднюю скорость при неравномерном прямолинейном движении тела. Что такое ускорение. ВСПОМНИТЕ: В каком случае тело движется неравномерно? Что такое путь? Что такое скорость? Каковы единицы скорости? Как определить скорость тела при равномерном движении?
В окружающем нас мире мы крайне редко сталкиваемся с равномерным движением. Обычно скорость тела изменяется с течением времени, и за одинаковые промежутки времени тетю проходит неодинаковые пути. Такое движение является неравномерным. Однако никого не удивляет, когда мы говорим, что ехали на автомобиле со скоростью 60 км/ч, хотя при этом подразумевается, что мы и тормозили, и останавливались перед светофорами, и вновь ускорялись. О какой же скорости тогда идёт речь?
О какой же скорости тогда идёт речь?
СРЕДНЯЯ СКОРОСТЬ
Для характеристики неравномерного движения вводят понятие средней скорости. Средняя скорость тела при неравномерном движении находится так же, как и скорость при равномерном движении, т. е. весь пройденный телом путь необходимо разделить на полное время движения тела, включая остановки.
путь
———— = средняя скорость
время
Полученное значение показывает среднюю скорость движения тела на всём пути, и оно может не совпадать со значением скорости в различные моменты времени движения.
Предположим, что автомобиль проехал путь s, состоящий из участков s1, s2, и s3, причём прохождение каждого из них заняло соответственно время t1, t2и t3. Для определения средней скорости движения автомобиля надо весь пройденный путь разделить на общее время движения:
ʋср = (s1 + s2 + s3) / (t1 + t2 + t3)
Зная среднюю скорость движения тела и время движения, можно найти пройденный за это время путь по формуле s = t ʋср.
Если нам известны средняя скорость движения и пройденный путь, мы можем определить время движения по формуле t = s ʋср.
ГРАФИКИ ЗАВИСИМОСТИ ПУТИ И СКОРОСТИ ОТ ВРЕМЕНИ
В отличие от графиков прямолинейного равномерного движения при неравномерном движении графики зависимости скорости и пути от времени могут выглядеть совершенно по-разному в зависимости от конкретной задачи.
Рассмотрим пример. Пусть велосипедист при движении из одного города в другой сначала проехал 8 км за 20 мин. Затем, отдохнув 10 мин, проехал ещё 6 км за 30 мин, а оставшиеся 2,5 км прошёл пешком за 30 мин. Как будут выглядеть соответствующие графики, если в пределах каждого временного интервала велосипедист двигался с постоянными скоростями?
РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ
Предположим, в начале определённого отрезка времени мы движемся в автомобиле со скоростью ʋ0. Автомобиль начинает увеличивать скорость, и через время t его скорость становится равной ʋ. Если за любые одинаковые промежутки времени скорость этого автомобиля увеличивалась на одно и то же значение, то в течение времени t автомобиль двигался равноускоренно.
Автомобиль начинает увеличивать скорость, и через время t его скорость становится равной ʋ. Если за любые одинаковые промежутки времени скорость этого автомобиля увеличивалась на одно и то же значение, то в течение времени t автомобиль двигался равноускоренно.
Прямолинейным равнопеременным движением называется движение, при котором траекторией тела является прямая линия и за любые равные промежутки времени скорость тела изменяется (увеличивается или уменьшается) на одно и то же значение.
УСКОРЕНИЕ
В физике существует величина, характеризующая изменение скорости тела при равнопеременном движении. Она называется ускорением и обозначается латинской буквой а. Для того чтобы вычислить ускорение, необходимо найти отношение изменения скорости ко времени, в течение которого это изменение произошло, т. е. от значения его конечной скорости нужно отнять значение начальной скорости и полученный результат разделить на рассматриваемое время движения.
В Международной системе единиц (СИ) за единицу ускорения принимают ускорение такого равнопеременного движения, при котором скорость движущегося тела за время 1 с изменяется на 1 м/с.
Эту единицу называют 1 метр на секунду в квадрате и обозначают 1 м/с2.
Ускорение может принимать как положительное, так и отрицательное значение. Действительно, если скорость тела в начале движения (ʋ0) меньше скорости тела в конце движения (ʋ), то при нахождении ускорения положительное число (ʋ — ʋ0) мы делим на положительное число (t) и получаем положительное значение ускорения. Если же тело замедляется, то значение начальной скорости оказывается больше значения скорости в конце движения, разность ʋ — ʋ0 становится отрицательной и значение ускорения тоже оказывается меньше нуля.
Вы смотрели Конспект по физике для 7 класса «Средняя скорость. Ускорение»: Как можно определить среднюю скорость при неравномерном прямолинейном движении тела. Что такое ускорение. Вернуться к Списку конспектов по физике (оглавление).
Ускорение»: Как можно определить среднюю скорость при неравномерном прямолинейном движении тела. Что такое ускорение. Вернуться к Списку конспектов по физике (оглавление).
Фиксация средней скорости и опасного вождения — как это будет работать?
- Главная
- Новости
- Фиксация средней скорости и опасного вождения: как это будет работать
Автор: Максим Берёзкин
На следующий год Росстандарт и МВД обещают подготовить новые стандарты и типы дорожных камер, которые снова начнут фиксировать среднюю скорость и уличать нас в опасном вождении. Ничего удивительного: вся мощь технического прогресса нацелена на то, чтобы заставить автомобилистов либо ездить медленно, либо вообще отказаться от своих колес. Что сулят нам эти нововведения? С таким вопросом мы обратились к эксперту, который занимается сертификацией автомобильной техники, – ГК «Серконс».
Партнерский материал
Помните, недавно на нескольких патрульных машинах в Москве повесили суперсовременные и очень недешевые «мигалки», которые помимо основной своей функции стали фиксировать нарушения в движении? Так вот, эти кибер-комплексы, судя по официальной статистике ГИБДД, в особенной эффективности не были замечены. За первый месяц работы они обнаружили всего лишь 79 случаев нарушений скоростного режима.
Но заскучать за рулем нам не дадут. Для новых комплексов фотовидеофиксации будут разработаны новые стандарты ГОСТ и программное обеспечение. Эти камеры будут наделены новым правом фиксировать среднюю скорость, а вдобавок – ещё и такое спорное нарушение, как «опасное вождение».
Согласно действующему на данный момент ГОСТ Р 57144-2016 (касающемуся специальных технических средств, имеющих функции фото- и киносъемки для обеспечения контроля за дорожным движением), имеется определение, что такое «средняя скорость». «Однако это определение связано с процессом измерения радарной части, а не со способом фиксации нарушения скорости на протяженном участке», – объясняет руководитель органа по сертификации колесно-транспортных средств и автомобильных компонентов ГК «Серконс» Дмитрий Хохлов.
Вот как это звучит в источнике: «Средняя скорость движения ТС – характеристика, равная отношению длины контролируемого участка ко времени, затраченному транспортным средством на преодоление данного участка».
«Конечно, прежде всего изменения должны быть внесены в ПДД и законодательные нормы КоАП, – продолжает эксперт крупнейшего органа сертификации «Серконс». – Понятие «средняя скорость» и штраф за ее превышение в нормативно-правовых документах отсутствуют. У любого нарушения должно быть место и время. Но как быть в случае достаточно протяженного участка и длительности по времени? Фактически у органов наказания имеются лишь косвенные доказательства превышения скоростного режима: нет конкретного места и времени нарушения, а превышение скоростного порога не соответствует реальному и неоднозначно назначено в плане сетки штрафа, установленного лишь для истинной скорости автомобиля».
Словом, без изменений нормативно-правовой базы эффективности от фиксации средней скорости ожидать не стоит.
Но самую бурную дискуссию в обществе вызвала предусмотренная возможность фиксации в автоматическом режиме такого преступления, как опасное вождение. Среди перечня потенциальных угроз – торможение, несоблюдение дистанции, «шашки» на дороге и препятствие обгону.
Согласно правилам ПДД, опасной ездой считается совокупность определенных маневров, которая совершилась водителем более одного раза и могла повлечь реальную угрозу для жизни людей. Норма введена еще в 2016 году, но практического применения до сих пор не находит. Конечно, возможно «обучить» камеры наблюдения отслеживать движение автомобилей с превышением скорости потока и многократными перестроениями, сопряженными с нарушением безопасной дистанции и боковых интервалов. И теоретически достаточно было бы заменить программное обеспечение в комплексах видеофиксации, но не всё так просто.
«Проблема в том, что в связи с неоднократной повторяемостью опасных действий согласно определению «опасного вождения» их нужно зафиксировать на протяженном участке, – говорит эксперт «Серконс» Дмитрий Хохлов. –То есть, длительное нарушение требует столь же длительной фиксации. А ведь этот «состав преступления», как правило, сопряжен с высокой скоростью. Соответственно, на этом участке должна быть целая сеть камер или высотные камеры для обзора сверху-вниз в режиме «полёт птицы» (например, с беспилотного дрона) для контроля траектории движения и точек создания помех в движении другому транспорту. И тогда возможно было бы собрать доказательный материал, свидетельствующий о таком нарушении, как «опасное вождение». В любом случае, конечное решение будет за инспектором.
–То есть, длительное нарушение требует столь же длительной фиксации. А ведь этот «состав преступления», как правило, сопряжен с высокой скоростью. Соответственно, на этом участке должна быть целая сеть камер или высотные камеры для обзора сверху-вниз в режиме «полёт птицы» (например, с беспилотного дрона) для контроля траектории движения и точек создания помех в движении другому транспорту. И тогда возможно было бы собрать доказательный материал, свидетельствующий о таком нарушении, как «опасное вождение». В любом случае, конечное решение будет за инспектором.
Где-то на заре становления нашего испытательного центра «ПромМаш Тест» у нас был проект с комплексом «Ураган», когда мы испытывали и измеряли скорость с помощью бесконтактных датчиков, средств метрологии и видеокамер, – рассказывает основатель ГК «Серконс» Ихсан Бозкурт. – Мы еще тогда убедились в том, насколько все зависит от уровня и возможностей современных средств измерения и видеофиксации для самого понятия «автоматическая фиксация». Даже при наличии нормативно-правовой базы для того, чтобы схема реально стала рабочей, нужно больше денег и больше времени. Думаю, только на тестирование и введение в эксплуатацию таких продвинутых комплексов понадобится около 2-х лет».
Даже при наличии нормативно-правовой базы для того, чтобы схема реально стала рабочей, нужно больше денег и больше времени. Думаю, только на тестирование и введение в эксплуатацию таких продвинутых комплексов понадобится около 2-х лет».
При этом, по словам эксперта из «Серконс» Дмитрия Хохлова, в городе уже существует единая нейросеть, которая объединяет все камеры. И если чья-то машина хронически «цепляет» много штрафов, то такой водитель и сегодня может расцениваться как потенциально опасный. Может, стоит использовать эти алгоритмы и давать оперативно информацию патрульным службам на дороге, а не искать новые поводы для штрафов в автоматическом режиме? С учетом того, что мы достаточно быстро движемся к беспилотной эре, необходимость штрафов в будущем отпадет сама собой, а камеры займут роль пассивных наблюдателей.
ГИБДД законы
Новые статьи
Статьи /
Владимир Шмаков, Chery: в ценообразовании важна не только разница курсов валют
По итогам прошлого года марка Chery оказалась в лидерах по продажам среди китайских брендов. В этом году в Chery намерены повторить успех, а суббренд Exeed продолжает набирать обороты. Но це…
340
1
0
25.09.2022
В этом году в Chery намерены повторить успех, а суббренд Exeed продолжает набирать обороты. Но це…
340
1
0
25.09.2022
Статьи / Практика Снижаем октан: действительно ли можно ли ездить на 95-м бензине вместо 98-го В Сети можно найти немало случаев, когда «серьёзный технический эксперт» утверждает, что нет ничего страшного в том, чтобы в целях экономии ездить на бензине, октановое число которого чуть н… 3749 0 1 23.09.2022
Статьи / Популярные вопросы
Как оформить ДТП по европротоколу через Госуслуги
Мы уже рассказывали о том, как оформить ДТП по европротоколу, а также о том, что с 2019 года стало возможным оформить европротокол даже при наличии разногласий о причинах и виновнике у уча. ..
377
0
1
21.09.2022
..
377
0
1
21.09.2022
Популярные тест-драйвы
Тест-драйвы / Тест-драйв Полный привод, самый мощный мотор и силы в запасе: первый тест Chery Tiggo 8 PRO MAX Появление в российской линейке Chery модели Tiggo 8 PRO MAX можно назвать знаковым для бренда. Почему? Да хотя бы потому, что это первый с 2014 года полноприводный кроссовер Chery, приехавши… 18444 13 44 29.04.2022
Тест-драйвы / Тест-драйв
Haval Dargo против Mitsubishi Outlander: собака лает, чужестранец идет
В дилерском центре Haval на юге Москвы жизнь кипит: покупатели разглядывают машины, общаются с менеджерами и подписывают какие-то бумаги. Пока я ждал выдачи тестового Dargo, такой же кроссов…
11372
6
95
13.09.2022
Пока я ждал выдачи тестового Dargo, такой же кроссов…
11372
6
95
13.09.2022
Тест-драйвы / Тест-драйв Мотор от Mercedes, эмблема от Renault, сборка от Dacia: тест-драйв европейского Logan 1,0 Казалось бы, что нового можно рассказать про Renault Logan второго поколения, известный каждому российскому таксисту, что называется, вдоль и поперёк? Однако конкретно в этом автомобиле есть… 10343 10 41 13.08.2022
|
|||||||||||||||||||||||
|
При неравномерном движении тело может за равные промежутки времени проходить как равные, так и разные пути. Для описания неравномерного движения вводится понятие средней скорости.
Средняя скорость, по данному определению, величина скалярная потому, что путь и время величины скалярные. Однако среднюю скорость можно определять и через перемещение согласно уравнению В этом случае среднюю скорость следует считать величиной векторной потому, что она определяется через отношение векторной величины к скалярной. Средняя скорость прохождения пути и средняя скорость перемещения – это две разные величины, которые могут характеризовать одно и то же движение. При расчете средней скорости очень часто допускается ошибка, состоящая в том, что понятие средней скорости подменяется понятием среднего арифметического скоростей тела на разных участках движения. Чтобы показать неправомерность такой подмены рассмотрим задачу и проанализируем ее решение.
Движение поезда на участке AC и на участке CB равномерное. Взглянув на текст задачи, нередко сразу хочется дать ответ: υср = 40 км/ч. Почему? Да потому, что нам кажется, что для вычисления средней скорости вполне подходит формула, используемая для расчета среднего арифметического. Давайте разберемся: можно ли использовать эту формулу и рассчитывать среднюю скорость путем нахождения полусуммы заданных скоростей. Для этого рассмотрим несколько иную ситуацию. Допустим, мы правы и средняя скорость действительно равна 40 км/ч. Тогда решим другую задачу.
Как видно, тексты задач очень похожи, есть только «очень маленькая» разница. Если в первом случае речь идет о половине пути, то во втором случае речь идет о половине времени. Очевидно, что точка C во втором случае находится несколько ближе к точке A, чем в первом случае, и ожидать одинаковых ответов в первой и второй задаче, вероятно, нельзя. Если мы, решая вторую задачу, так же дадим ответ, что средняя скорость равна полусумме скоростей на первом и втором участке, мы не можем быть уверены, что мы решили задачу правильно. Выход из положения следующий: дело в том, что средняя скорость не определяется через среднее арифметическое. Есть определяющее уравнение для средней скорости, согласно которому для нахождения средней скорости на некотором участке, надо весь путь, пройденный телом, поделить на все время движения: Начинать решение задачи нужно именно с формулы, определяющей среднюю скорость, даже если нам кажется, что мы в каком-то случае можем использовать более простую формулу. Будем двигаться от вопроса к известным величинам. Неизвестную величину υср выражаем через другие величины – L0 и Δt0. Оказывается, что обе эти величины неизвестны, поэтому мы должны выразить их через другие величины. Например, в первом случае: L0 = 2 ∙ L, а Δt0 = Δt1 + Δt2. Подставим эти величины, соответственно, в числитель и знаменатель исходного уравнения. Во втором случае мы поступаем точно так же. Нам не известен весь путь и все время. Выражаем их: и Очевидно, что время движения на участке AB во втором случае и время движения на участке AB в первом случае различны. В первом случае, поскольку нам неизвестны времена и мы попытаемся выразить и эти величины: а во втором случае мы выражаем и : Подставляем выраженные величины в исходные уравнения. Таким образом, в первой задаче имеем: После преобразования получаем: Во втором случае получаем а после преобразования: Ответы, как и было предсказано, различны, но во втором случае мы получили, что средняя скорость действительно равняется полусумме скоростей. Может возникнуть вопрос, а почему сразу нельзя воспользоваться этим уравнением и дать такой ответ? Дело в том, что записав, что средняя скорость на участке AB во втором случае равна полусумме скоростей на первом и на втором участках, мы бы представили не решение задачи, а готовый ответ. При неравномерном движении скорость тела может непрерывно меняться. При таком движении скорость в любой последующей точке траектории будет отличаться от скорости в предыдущей точке. Скорость тела в данный момент времени и в данной точке траектории называют мгновенной скоростью. Чем больше промежуток времени Δt, тем средняя скорость больше отличается от мгновенной. И, наоборот, чем меньше промежуток времени, тем меньше средняя скорость отличается от интересующей нас мгновенной скорости.
Определим мгновенную скорость как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени: Если речь идет о средней скорости перемещения, то мгновенная скорость является величиной векторной: Если речь идет о средней скорости прохождения пути, то мгновенная скорость является величиной скалярной: Часто встречаются случаи, когда при неравномерном движении скорость тела меняется за равные промежутки времени на одну и ту же величину.
При равнопеременном движении скорость тела может, как уменьшаться, так и увеличиваться. Если скорость тела увеличивается, то движение называется равноускоренным, а если уменьшается – равнозамедленным. Характеристикой равнопеременного движения служит физическая величина, называемая ускорением.
Зная ускорение тела и его начальную скорость, можно найти скорость в любой наперед заданный момент времени: В проекции на координатную ось 0X уравнение примет вид: υx = υ0x + ax ∙ Δt. |
Формула средней скорости — Что такое формула для средней скорости? Примеры
Средняя скорость — это среднее значение скорости тела за определенный период времени. Формула для средней скорости необходима, поскольку скорость движущегося тела непостоянна и меняется с течением времени. Даже при различной скорости можно использовать значения общего времени и общего пройденного расстояния, а с помощью формулы для средней скорости мы можем найти одно значение для представления всего движения.
Что такое формула средней скорости?
Средняя скорость тела равна общему пройденному расстоянию, деленному на общее время. Формула для средней скорости имеет следующий вид:
Формула средней скорости:
Средняя скорость = общее пройденное расстояние ÷ общее затраченное время
Формула средней скорости. скорость \(s_1 \) за время \( t_1 \) и скорость \(s_2 \) за время \( t_2 \), формула для средней скорости приведена в приведенном ниже выражении. Произведение \(s_1 \times t_1 \) и \(s_2 \times t_2 \) дает расстояния, пройденные за интервалы времени \(t_1 \) и \(t_2 \) соответственно.
Формула средней скорости \(= \frac{s_1 \times t_1 + s_2 \times t_2}{t_1 + t_2}\)
Случай 2: Аналогично, когда ‘n’ различных скоростей, \(s_{1} , s_{2}, s_{3},… s_{n}\), даны для ‘n’ соответствующих отдельных интервалов времени, \(t_{1}, t_{2}, t_{3},. .. t_{n}\) соответственно, формула средней скорости задается как:
Формула средней скорости \(= \frac{s_1 t_1 + s_2 t_2 + . .. + s_n t_n}{t_1 + t_2 +… + t_n}\)
.. + s_n t_n}{t_1 + t_2 +… + t_n}\)
Случай 3: Средняя скорость при прохождении разных расстояний \(d_{1}, d_{2}, d_{3},… d_{n}\) за разные интервалы времени, \(t_{1}, t_{2}, t_{3},… t_{n}\) соответственно задается как:
Формула средней скорости \(S_{avg}\) \(= \frac{d_1 + d_2 + d_3 +…+ d_n} {t_1 + t_2 + t_3 +….+ t_n}\)
Случай 4: Средняя скорость, когда разные скорости, \(s_{1}, s_{2}, s_{3},… s_{n}\), даны для разных расстояний, \(d_{1}, d_{2}, d_{3},… d_{n}\) соответственно задается как:
Формула средней скорости \(S_{avg}\) \(= \frac{d_1 + d_2 + d_3 +. ..+ d_n} {\dfrac{d_1}{s_1} + \dfrac{d_2}{s_2} + \dfrac{d_3}{s_3} +….+ \dfrac{d_n}{s_n}}\)
Корпус 5: Формула средней скорости, когда заданы две или более скоростей (\(s_{1}, s_{2}, s_{3},… s_{n}\)) так, что эти скорости были пройдены за одинаковое количество времени (\(t_{1} = t_{2} = t_{3} =… t_{n} = t)\) задается как:
Формула средней скорости, \(S_{avg}\) \( = \frac{s_{1} t + s_{2} t +. ..+ s_{n} t} {t\times n} = \frac{s_{1} + s_{2} +…+ s_{n}} {n} \)
..+ s_{n} t} {t\times n} = \frac{s_{1} + s_{2} +…+ s_{n}} {n} \)
Случай 6: Средняя скорость при заданных разных скоростях (\(s_{1}, s_{2}, s_{3},… s_{n})\ ) для того же расстояния (\(d_{1} = d_{2} = d_{3} =… d_{n} = d)\) задается как:
Формула средней скорости \(S_{avg}\) \(= \frac{ n \times d} { d \times \left[ \dfrac{1}{s_1} + \dfrac{1}{s_2} + \ dfrac{1}{s_3} +….+ \dfrac{1}{s_n}\right]} = \frac{n} {\left[\dfrac{1}{s_1} + \dfrac{1}{ s_2} + \dfrac{1}{s_3} +….+ \dfrac{1}{s_n}\right]}\)
Хотите находить сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Забронировать бесплатный пробный урок
Примеры формулы средней скорости
Давайте рассмотрим несколько примеров, чтобы лучше понять формулу средней скорости.
Пример 1: Используя формулу средней скорости, найдите среднюю скорость Сэма, который проходит первые 200 километров за 4 часа, а следующие 160 километров еще за 4 часа.
Решение:
Чтобы найти среднюю скорость, нам нужно общее расстояние и общее время.
Общее расстояние, пройденное Сэмом = 200 км + 160 км = 360 км
Общее время, затраченное Сэмом = 4 часа + 4 часа = 8 часов
Средняя скорость = общее пройденное расстояние ÷ общее затраченное время
Средняя скорость = 360 ÷ 8 = 45 км/ч
Ответ: Средняя скорость Сэма составляет 45 км/ч.
Пример 2: Поезд движется со скоростью 80 миль в час в течение первых 4 часов и со скоростью 110 миль в час в течение следующих 3 часов. Найдите среднюю скорость поезда по формуле средней скорости.
Решение:
Дано, что поезд движется со скоростью 80 миль в час в течение первых 4 часов.
Здесь \(S_1\) = 80 и \(T_1\) = 4.
И поезд движется со скоростью 110 миль в час следующие 3 часа.
Отсюда \(S_2 \) = 110 и \(T_2\) = 3,
.
Формула средней скорости = \(\frac{S_1 \times T_1 + S_2 \times T_2}{T_1 + T_2}\)
Средняя скорость = (80 × 4 + 110 × 3) ÷ (4 + 3)
= (650) ÷ (7) = 92,86 миль/ч
Ответ: Средняя скорость поезда 92,86 мили/час.
Пример 3: Автомобиль движется со скоростью 45 км/ч в течение 5 часов, а затем решает снизить скорость до 40 км/ч в течение следующих 2 часов. Рассчитайте среднюю скорость, используя формулу средней скорости.
Решение:
Расстояние I = 45 × 5 = 225 миль
Расстояние II = 40 × 2 = 80 миль
Общее расстояние = расстояние 1 + расстояние 2
D = 225 + 80 = 305 миль
Используя формулу средней скорости = Общее пройденное расстояние ÷ Общее затраченное время
Средняя скорость = 305 ÷ 7 = 43,57 м/с.
Ответ: Средняя скорость автомобиля 43,57 м/с.
Часто задаваемые вопросы о формуле средней скорости
Как рассчитать расстояние с помощью формулы средней скорости?
Общая формула для средней скорости задается как [Средняя скорость = Пройденное расстояние ÷ Общее затраченное время]
Чтобы рассчитать расстояние, формулу средней скорости можно представить в виде [Расстояние = Средняя скорость × Время].
Как рассчитать время, используя формулу средней скорости?
Формула общей средней скорости задается как [Средняя скорость = Расстояние ÷ Время]
Для расчета времени формула средней скорости будет иметь вид [Время = Пройденное расстояние ÷ Средняя скорость].
Как использовать формулу для средней скорости?
Чтобы понять, как пользоваться формулой средней скорости, рассмотрим пример.
Пример. Бегун пробегает 100 м за 40 сек. После финиша первого круга он вернулся к исходной точке. Вычислите среднюю скорость бегуна.
Решение: общее расстояние, пройденное бегуном = 100 метров
.
Общее время = 40 сек
Итак, применяя общую формулу для средней скорости
у нас есть,
Средняя скорость = расстояние ÷ время
Средняя скорость = 100 ÷ 40 = 2,5 м/с.
Средняя скорость бегуна 2,5 м/с.
Какой будет формула общей средней скорости для объекта?
Общая формула средней скорости для объекта задается как [Средняя скорость = Общее пройденное расстояние ÷ Общее затраченное время]. Единицей средней скорости в СИ является м/с.
Единицей средней скорости в СИ является м/с.
Объяснение урока: Средняя скорость | Nagwa
В этом объяснении мы узнаем, как различать постоянную скорость и Средняя скорость.
Мы можем вспомнить, что скорость объекта является мерой пройденного расстояния этим объектом в единицу времени.
Можно также вспомнить, что если объект движется с постоянной скоростью, это означает значение этой скорости не меняется. Другими словами, объект, движущийся со с постоянной скоростью проходит равные расстояния за равные промежутки времени.
Например, автомобиль, показанный на диаграмме ниже, движется с постоянной скоростью.
В этом случае автомобиль проезжает равное расстояние 20 м в каждом интервал времени 1 с.
Для объекта, движущегося с постоянной скоростью 𝑣 и преодолевающего расстояние 𝑑 за время 𝑡, у нас есть следующее уравнение, которое связывает эти три количества: 𝑣=𝑑𝑡.
Это уравнение применимо как к путешествию в целом, так и к каждому отдельному
участок этого путешествия.
Полезно проверить это для автомобиля на диаграмме выше и показать, что скорость автомобиля всегда будет равна 20 м/с независимо от того, какая часть пути используется для расчета этого скорость.
Это верно для любого объекта, который движется с постоянной скоростью. Не важно что часть пути мы используем для расчета, для объекта с постоянной скорость, мы всегда будем находить одно и то же значение для этой скорости.
Однако не все объекты всегда движутся с постоянной скоростью.
В качестве конкретного примера снова рассмотрим движение автомобиля. Изначально эта машина должна была быть где-то припаркована. Другими словами, в некоторых точка, она стартовала из состояния «неподвижности»; мы бы описали это как говоря, что машина завелась с места. Объект в состоянии покоя имеет скорость 0 м/с.
Если у нас есть машина, которая стартует со скоростью
0 м/с и после
какое-то время движется со скоростью
20 м/с, мы знаем
что его скорость не может быть постоянной. На протяжении всего интервала времени, в котором
скорость автомобиля изменилась с
от 0 м/с до
20 м/с, было
не двигаясь с постоянной скоростью
0 м/с и не движется с постоянной скоростью
20 м/с. В разных
раз в пределах этого интервала, скорость должна иметь все значения между
0 м/с и
20 м/с.
На протяжении всего интервала времени, в котором
скорость автомобиля изменилась с
от 0 м/с до
20 м/с, было
не двигаясь с постоянной скоростью
0 м/с и не движется с постоянной скоростью
20 м/с. В разных
раз в пределах этого интервала, скорость должна иметь все значения между
0 м/с и
20 м/с.
Когда скорость объекта непостоянна, это означает, что он не преодолевать равные расстояния за равные промежутки времени. В этом случае мы говорим, что объект имеет непостоянную или изменяющуюся скорость.
Независимо от того, постоянна ли скорость объекта, мы всегда можем говорить о средняя скорость объекта на заданном интервале.
Когда мы говорим о средних значениях в физике, мы часто имеем в виду
усреднение нескольких повторных измерений. В этом контексте мы могли бы представить себе
автомобиль, который проезжает одинаковое расстояние по одному и тому же участку дороги кратно
раз. Мы могли бы каждый раз измерять скорость автомобиля, а затем брать среднее значение. всех этих измерений, чтобы получить среднюю скорость.
всех этих измерений, чтобы получить среднюю скорость.
Однако в контексте непостоянных скоростей, когда мы говорим о среднем скорость, мы имеем в виду что-то другое. Мы рассматриваем объект, который движется некоторое расстояние в течение некоторого интервала времени, изменяя при этом свою скорость. среднее, о котором мы говорим, не является усреднением по повторным измерениям. Скорее, это усреднение всех различных скоростей, которые имеет объект. во время этого движения.
Рассмотрим автомобиль, который движется следующим образом:
Из диаграммы видно, что автомобиль не проходит одинаковое расстояние за каждый 1-секундный интервал. Следовательно, мы знаем, что автомобиль имеет непостоянную скорость.
Чем больше расстояние, пройденное за заданный интервал времени 1 с, больше средней скорости на этом интервале.
В этом случае автомобиль проходит большее расстояние в промежутке между
1 с и
2 с, чем в
два других интервала, поэтому мы можем сказать, что он имеет наибольшую среднюю скорость в этом
второй интервал.
Давайте рассмотрим пару примеров задач.
Пример 1. Поиск участка пути с наибольшим средним значением Скорость
Скорость игрушечной машинки измеряется путем записи ее положения каждый раз. второй. Между в какой из следующих моментов времени средняя скорость автомобиля наибольшая?
- С момента начала измерения до через 1 секунду после начало измерения
- Через 1 секунду после измерение начинается с 2 секунд после начала измерения
- Через 2 секунды после измерение начинается с 3 секунд после начала измерения
Ответ
Вопрос заключается в том, чтобы найти, в течение какого из показанных интервалов времени
игрушечная машинка имеет наибольшую среднюю скорость. Все временные интервалы показаны
иметь одинаковую длину
1 с. Это означает, что к
найти интервал с наибольшей средней скоростью, нам нужно найти время
интервал, за который игрушечная машинка проходит наибольшее расстояние.
Глядя на диаграмму, мы видим, что в течение первого интервала, с которого измерение начинается с 1 с затем автомобиль проходит расстояние 1 м.
Во время второго интервала, с 1 с до 2 с после измерения заводится, автомобиль проходит расстояние более 1 м. Мы можем видеть это из диаграмма выглядит следующим образом: В начале временного интервала автомобиль выровнен с отметкой 1 м. В конце временного интервала, машина вышла за пределы следующего отметка 1 м — значит, она должна иметь пройдено расстояние, превышающее 1 м в этот промежуток времени.
Во время третьего интервала, с
2 с до
3 с после измерения
заводится, автомобиль проходит расстояние менее
1 м. Мы можем видеть это из
диаграмма, поскольку он начинает этот интервал перед
1 м и заканчивается
интервал, совпадающий со следующим
отметка 1 м.
Мы знаем, что автомобиль проезжает наибольшее расстояние за интервал времени через 1 с после начало измерения и 2 с после начала измерения. Это означает, что мы знаем, что он имеет наибольшее среднее значение. скорость на этом интервале.
Следовательно, наш ответ на вопрос состоит в том, что средняя скорость автомобиля равна наибольший из через 1 секунду после измерение начинается через 2 секунды после начинается измерение. Это ответ, данный в варианте B.
Пример 2: Определение интервалов непостоянной скорости
Показанная игрушечная машинка двигалась с постоянной скоростью до того, как мы начали измерять ее скорость. скорость, записывая свое положение каждую секунду. Когда было машина определенно , а не , равномерно движущихся со скоростью 1 метр в секунду?
- Через 1 секунду после начинается измерение и через 3 секунды после начало измерения
- Между началом измерения и через 1 секунду после начало измерения
- За все время движения автомобиля
Ответ
Вопрос заключается в том, чтобы выяснить, когда игрушечная машинка, показанная на
диаграмма никак не могла иметь постоянную скорость
1 м/с.
Автомобиль может иметь скорость только 1 м/с в течение заданной 1 с интервал времени, если он прошел общее расстояние 1 м во время этого интервал. Если он двигался на другое расстояние от этого, он двигался на другое количество метров, чем один во время этого во-вторых, поэтому он должен был иметь средняя скорость отличается от 1 метр в секунду.
Глядя на диаграмму, мы видим, что на первом интервале машина перемещается на расстояние 1 м. Следовательно, это возможно, что автомобиль имел постоянную скорость 1 м/с во время этот интервал.
Обратите внимание, что это не гарантия того, что автомобиль имел постоянную скорость
1 м/с во время
этот интервал, только то, что это не невозможно. Все, что мы знаем наверняка, это то, что
среднее значение за этот интервал было
1 м/с; Это
может быть дело в том, что скорость изменилась во время
интервал 1 с.
Во время следующего интервала (между 1 с и 2 с после измерения начинается), автомобиль проходит расстояние, превышающее 1 м. Он начинает интервал, выровненный с 1 м, но заканчивается интервал перед следующим отметка 1 м.
Следовательно, в промежутке между 1 с и 2 с после измерения начинается, автомобиль не может иметь среднюю скорость 1 м/с. Его средняя скорость должна быть больше.
В промежутке между 2 с и 3 с после измерения начинается, автомобиль проходит расстояние, которое меньше, чем 1 м. Он начинает интервал впереди 1 м отмечать, но заканчивает интервал, выровненный со следующим отметка 1 м.
Следовательно, в промежутке между
2 с и
3 с после измерения
начинается, автомобиль не может иметь среднюю скорость
1 м/с. Его
средняя скорость должна быть меньше.
Его
средняя скорость должна быть меньше.
Следовательно, наш ответ: машина определенно не движется со скоростью постоянная скорость 1 метр в секунду между через 1 секунду после начинается измерение и через 3 секунды после начинается измерение. Это ответ, данный в варианте А.
Мы видели, что подразумевается под средней скоростью объекта. Мы также можем опишите эту среднюю скорость математически.
Средняя скорость объекта на заданном расстоянии равна общему расстоянию пройдено им, деленное на общее время, затраченное на это расстояние.
Чтобы понять, что это значит, давайте рассмотрим автомобиль, который движется, как показано на рисунке. диаграмма ниже:
На диаграмме показаны два интервала времени: между 0 секундами и более поздним временем
𝑡, а между 𝑡 и далее раз
𝑡. На схеме также показаны
расстояние, пройденное автомобилем за каждый из этих двух интервалов, начиная с
0 метров за 0 секунд. Через время 𝑡 автомобиль проехал
расстояние 𝑑. Через время 𝑡 автомобиль проехал общее расстояние
𝑑.
Через время 𝑡 автомобиль проехал
расстояние 𝑑. Через время 𝑡 автомобиль проехал общее расстояние
𝑑.
Предположим, мы хотим найти среднюю скорость этого автомобиля во время показан второй интервал, то есть между временем 𝑡 и временем 𝑡. Мы можем сделать это следующим образом.
Мы знаем, что средняя скорость за интервал равна общему расстоянию, пройденному за этот интервал, разделенный на общее время, необходимое для перемещения на это расстояние. Это означает нам нужно выражение длительности второго интервала, а также выражение для расстояния, пройденного за этот интервал.
Интервал времени начинается в момент времени 𝑡 и заканчивается в момент времени 𝑡. Таким образом, можно сказать, что продолжительность этого интервал равен 𝑡−𝑡.
В конце интервала автомобиль проехал общее расстояние
𝑑 с его позиции в
0 секунд. Однако,
к началу интервала машина уже проехала расстояние
𝑑. Таким образом, расстояние, пройденное за второй интервал, равно
𝑑−𝑑.
Таким образом, расстояние, пройденное за второй интервал, равно
𝑑−𝑑.
Тогда средняя скорость 𝑣 — это расстояние, пройденное за время интервал, 𝑑−𝑑, деленный на продолжительность этого интервал, 𝑡−𝑡.
Математически мы можем записать это как 𝑣=𝑑−𝑑𝑡−𝑡.
В этом выражении 𝑑−𝑑 представляет собой изменение общего расстояние, пройденное автомобилем за промежуток времени 𝑡−𝑡.
Мы можем записать это более компактно, используя следующие обозначения: Δ𝑑=𝑑−𝑑,Δ𝑡=𝑡−𝑡.
Символ Δ используется для обозначения того, что мы рассматриваем изменение расстояния и изменение времени в течение данного интервала.
С помощью этих обозначений мы можем определить среднюю скорость объекта математически следующим образом.
Уравнение: средняя скорость
Для объекта, который проходит расстояние Δ𝑑 за время
интервал
Δ𝑡, средняя скорость 𝑣 этого объекта
в течение этого промежутка времени определяется
𝑣=Δ𝑑Δ𝑡.
Вообще, 𝑑 и 𝑑 могут быть любым расстоянием значения, отмечая начало и конец любой части движения объекта нас интересует. Между тем 𝑡 — это время, в которое объект прошел расстояние 𝑑 и 𝑡 это время, за которое объект прошел расстояние 𝑑.
Иногда нас интересует среднее значение интервала, начинающегося с точку, в которой мы начинаем измерение (т. е. в 0 метров и 0 секунд). В этом случай, 𝑑=0m и Δ𝑑=𝑑−𝑑=𝑑. Сходным образом, 𝑡=0s и Δ𝑡=𝑡−𝑡=𝑡.
Рассмотрим автомобиль, который движется, как показано на диаграмме ниже:
Предположим, мы хотим вычислить среднюю скорость в течение первого второй движения.
Раздел начинается одновременно
𝑡=0 с и заканчивается за один раз
𝑡=1с. В начале этого участка автомобиль проехал
0 метров от
точка, с которой мы начинаем измерение, поэтому мы имеем
𝑑=0м. В конце этого участка автомобиль двинулся
6 метров от своего положения, когда
начинается измерение, поэтому имеем
𝑑=6м.
Затем мы можем рассчитать среднюю скорость автомобиля на этом участке как следует: 𝑣=6−01−0=61𝑣=6/.mmssmsms
Теперь предположим, что мы хотим узнать среднюю скорость автомобиля во время последующий 1-секундный интервал. Этот раздел начинается во время 𝑡=1 с и заканчивается во время 𝑡=2с. В начале этого раздела автомобиль 6 метров от начала положение, поэтому имеем 𝑑=6м. В конце секция, машина есть 16 метров от исходное положение, поэтому 𝑑=16м.
Тогда средняя скорость 𝑣=16−62−1=101𝑣=10/.mmssmsms
Мы рассчитали разные средние скорости для каждого из двух участков
движение, показанное на схеме. Это говорит нам о том, что скорость автомобиля не может
быть постоянным на протяжении всего путешествия. Мы также можем видеть это непосредственно из
диаграмме, так как мы можем сказать, что автомобиль не перемещается на равные расстояния за равные
интервалы времени – расстояние, пройденное автомобилем за второй интервал, равно
больше, чем расстояние, пройденное за первый интервал.
Рассмотрим другой автомобиль, который проезжает столько же дистанции 16 м, как первый, но этот второй автомобиль движется с постоянной скоростью. Движение Второй автомобиль показан на диаграмме ниже:
Опять же, мы можем рассчитать среднюю скорость по каждому из Показаны интервалы в 1 секунду.
Для первого интервала имеем 𝑡=0s и 𝑡=1с, что дает Δ𝑡=1−0=1сс. Автомобиль стартует с 0 метров и заканчивается интервал на 8 метрах, так что мы имеем 𝑑=0m и 𝑑=8м. Это дает нам Δ𝑑=8−0=8ммм.
Вычисляя среднюю скорость на этом интервале, имеем 𝑣=81=8/.msms
Для второго интервала имеем 𝑡=1s и 𝑡=2s, что дает Δ𝑡=2−1=1сс. Автомобиль начинается этот интервал в 8 метров и заканчивается это на 16 метрах, так что у нас есть 𝑑=8м и 𝑑=16м. Это дает Δ𝑑=16−8=8мм.
Средняя скорость на втором интервале определяется выражением
𝑣=81=8/. msms
msms
Итак, для этого автомобиля, который движется с постоянной скоростью, мы нашли то же самое средняя скорость на обоих участках его движения.
Этот результат имеет более общее значение. Для любого объекта, движущегося с постоянной скоростью, значения расстояния и времени находятся в одинаковой пропорции для любой части движение. Это означает, что уравнение постоянной скорости 𝑣=𝑑𝑡 может быть применяется к любому участку движения объекта и даст тот же результат для скорости независимо от того, какой раздел мы рассматриваем.
Давайте рассмотрим еще пару примеров задач.
Пример 3: Сравнение средних скоростей
Скорость игрушечной машинки измеряется путем записи ее положения каждый раз. второй. Как изменилась средняя скорость автомобиля в первом второй по сравнению с его средним скорость на всем пути?
- Средняя скорость в первом
второй больше, чем
средняя скорость за время измерения скорости.
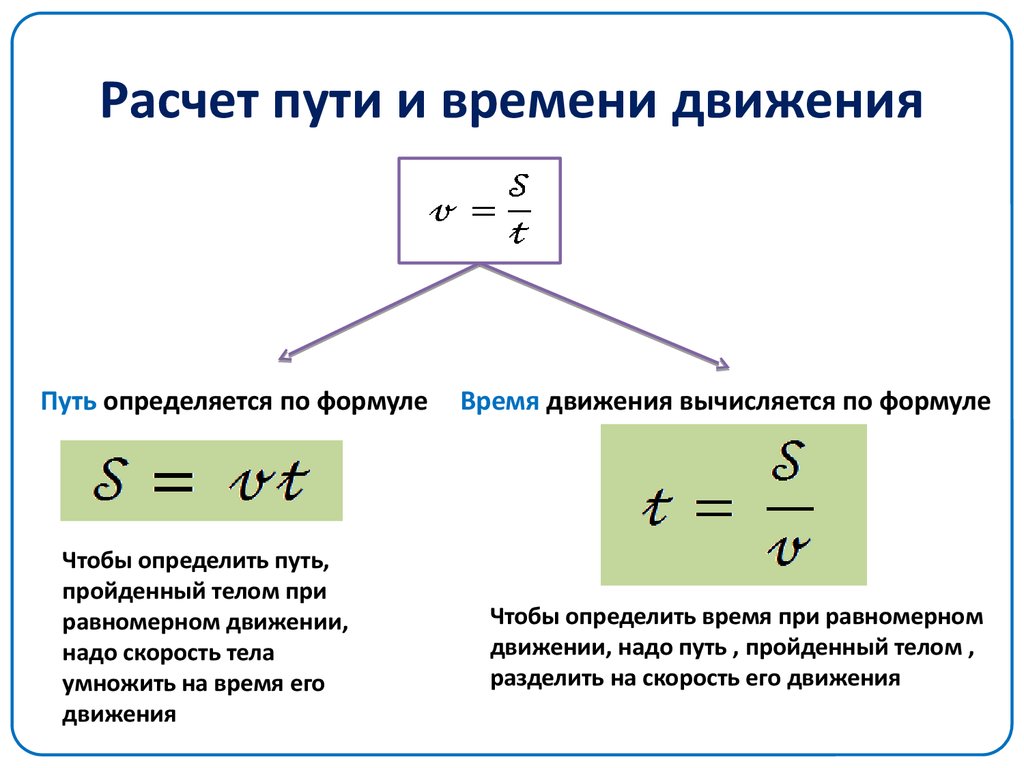
- Средняя скорость в первой второй равна средней скорости за время измерения скорости.
- Средняя скорость в первом второй меньше средней скорости за время измерения скорости.
Ответ
В этом вопросе нас просят выяснить, как средняя скорость машина в первом второй сравнивает к средней скорости за все время измерения скорости.
Для этого вычислим, какова средняя скорость автомобиля в течение этот первый интервал. Затем вычисляем среднюю скорость на все время, за которое измеряется скорость. Наконец, мы сравним два значения.
На первом интервале из диаграммы видно, что машина движется расстояние 1 м. Это означает, что, для этого интервала имеем Δ𝑑=1м и Δ𝑡=1с.
Мы использовали индекс «1», чтобы указать, что эти значения
для первого интервала.
Можно вспомнить наше уравнение для средней скорости 𝑣: 𝑣=Δ𝑑Δ𝑡.
Замена в Δ𝑑=1м и Δ𝑡=1с, мы получаем, что 𝑣, средняя скорость на первом интервале, дан кем-то 𝑣=11𝑣=1/.msms
Теперь рассмотрим все время, за которое измеряется скорость.
Из диаграммы видно, что скорость измеряется за общее время 3 с и что машина за это время проходит расстояние 3 м. Это означает, что у нас есть Δ𝑑=3Tm и Δ𝑡=3Ts.
Мы использовали нижний индекс «T», чтобы указать, что эти значения относятся к общему времени, за которое измеряется скорость.
Замена Δ𝑑=3Tm и Δ𝑡=3Ts в уравнение для средней скорости, мы получаем, что 𝑣T, средняя скорость за все время определяется выражением 𝑣=33𝑣=1/.TTmsms
Итак, мы нашли, что 𝑣=1/мс и 𝑣=1/Tms. Другими словами, обе эти средние скорости имеют одинаковое значение.
Следовательно, наш ответ на вопрос состоит в том, что средняя скорость в
первый
второй
равна средней скорости за время измерения скорости. Это
ответ дан в варианте B.
Это
ответ дан в варианте B.
Пример 4. Выяснение того, какой из двух объектов имеет большее среднее значение Скорость
Синий объект и оранжевый объект перемещаются по сетке из равноотстоящих друг от друга линий. Оба объекта перемещаются в течение 5 секунд. Стрелки показывают расстояния, пройденные каждым второй. Объект какого цвета имеет большую среднюю скорость?
- Синий объект
- Оба объекта имеют одинаковую среднюю скорость.
- Оранжевый объект
Ответ
сетка. Нас просят определить, какой объект имеет большее среднее значение. скорость.
Мы видим, что два объекта движутся по-разному в течение указанного времени. Оранжевый объект перемещается на расстояние 1 квадрат в каждом
второй;
следовательно, он движется с постоянной скоростью. Тем временем синий объект не двигается
одинаковое количество квадратов в каждом
секунда времени;
следовательно, он не движется с постоянной скоростью.
Однако мы видим, что общее расстояние, пройденное каждым из объектов то же самое. Он равен 5 квадратам на сетке. Мы не знаем, сколько каждый квадрат в метрах, но мы знаем, что линии на сетке на равном расстоянии. Поэтому можно говорить о расстоянии в единицах из «квадратов».
Вопрос говорит нам, что каждый объект перемещается на 5 с.
Поскольку каждый объект перемещается на одинаковое расстояние (5 клеток) и занимает в то же время, чтобы сделать это (5 секунд), мы известно, что все объекты должны иметь одинаковую среднюю скорость.
Мы можем явно вычислить эту среднюю скорость, в единицах квадратов в секунду. второй, используя уравнение для средней скорости: 𝑣=Δ𝑑Δ𝑡.
В этом случае Δ𝑑=5 квадратов и Δ𝑡=5 секунд. Это дает нам среднюю скорость 𝑣=55𝑣=1.squaressecondssquarepersecond
Подчеркнем, что общее расстояние
Δ𝑑=5 квадратов и общее время
Δ𝑡=5 секунд
одинаковы как для оранжевого объекта, так и для синего объекта. Итак, это среднее
расчет скорости применяется для обоих объектов.
Итак, это среднее
расчет скорости применяется для обоих объектов.
Таким образом, наш ответ на вопрос состоит в том, что оба объекта имеют одинаковую Средняя скорость. Это ответ, данный в варианте B.
Пример 4 подчеркивает интересный момент, касающийся средней скорости. Среднее скорость объекта за заданный интервал времени определяется с помощью суммарной пройденное расстояние и общая продолжительность интервала. Это не независимо от того, как скорость изменяется в течение этого интервала времени; все, что имеет значение среднее значение.
Это означает, что два объекта могут иметь одинаковую среднюю скорость как друг друга в течение определенного интервала времени, даже если в течение этого интервала скорость каждого объекта меняется по-разному.
Мы видели, как можно вычислить среднюю скорость 𝑣
объект, учитывая общее расстояние Δ𝑑, пройденное этим объектом
за общий временной интервал Δ𝑡.
Мы также можем изменить уравнение, чтобы сделать либо Δ𝑑 или Δ𝑡 предмет. Эти перестановки работают точно так же, как и при перестановке уравнения для движения с постоянной скоростью.
Делая Δ𝑑 предметом, мы имеем следующее уравнение: Δ𝑑=𝑣×Δ𝑡.
Если мы знаем среднюю скорость объекта и знаем, сколько времени объект ходов за, это уравнение позволяет нам рассчитать общее расстояние, пройденное этот объект. Это справедливо независимо от того, равна ли скорость объекта постоянный; нам нужно только знать среднюю скорость 𝑣 по интервал времени Δ𝑡.
Сделав Δ𝑡 предметом, мы получим следующее уравнение: Δ𝑡=Δ𝑑𝑣.
Тогда, если мы знаем среднюю скорость объекта и общее расстояние, которое
объект движется, это уравнение позволяет нам рассчитать, сколько времени он
требуется, чтобы пройти это расстояние. Как и прежде, не имеет значения,
скорость постоянна; нам нужно знать только среднее расстояние
путешествовал.
Давайте рассмотрим конкретный пример, где нам нужно использовать один из этих переставил уравнения.
Предположим, у нас есть бегун, который соревнуется в бег на 400 м и бег на средняя скорость 8 м/с. Мы хотим выяснить, как много времени требуется им, чтобы завершить гонку.
В этом случае мы имеем среднюю скорость 𝑣=8/мс и общее расстояние, пройденное Δ𝑑=400м. Мы хотите найти значение Δ𝑡. Это означает, что нам нужен наш уравнение средней скорости перестроено так, что Δ𝑡 предмет: Δ𝑡=Δ𝑑𝑣.
Затем мы можем заменить наши значения Δ𝑑=400м и 𝑣=8/мс: Δ𝑡=4008/.мм
Наконец, оценивая правую часть, мы имеем, что Δ𝑡=50.s
Таким образом, мы обнаружили, что бегуну требуется время 50 с, чтобы завершить гонка.
Давайте теперь обобщим то, что было изучено в этом объяснителе.
Ключевые точки
- Если объект не проходит равные расстояния за равные промежутки времени,
то он не движется с постоянной скоростью.
 В этом случае мы говорим, что
объект имеет непостоянную или изменяющуюся скорость.
В этом случае мы говорим, что
объект имеет непостоянную или изменяющуюся скорость. - Средняя скорость объекта равна общему пройденному расстоянию объектом за все время.
- Для объекта, который проходит общее расстояние Δ𝑑 за общее время Δ𝑡 средняя скорость 𝑣 объекта во время этого движения можно рассчитать, используя 𝑣=Δ𝑑Δ𝑡. Это уравнение применимо независимо от того, скорость тела постоянна во время движения.
- Это уравнение можно изменить так, чтобы Δ𝑡 или Δ𝑑 предмет. Тогда, если мы зная среднюю скорость объекта и общее расстояние, которое он проходит, мы можем рассчитать затраченное время. Или, если мы знаем среднюю скорость и общее время взято, мы можем вычислить пройденное расстояние.
2.2 Скорость и скорость — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Рассчитать среднюю скорость объекта
- Соотнесите перемещение и среднюю скорость
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (4) Научные концепции.
 Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:- (B) описывают и анализируют движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Кроме того, в Руководстве по физике для средней школы рассматривается содержание этого раздела лабораторной работы под названием «Положение и скорость объекта», а также следующие стандарты:
- (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (Б) описывать и анализировать движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Основные термины раздела
| средняя скорость | средняя скорость | мгновенная скорость |
| мгновенная скорость | скорость | скорость |
Поддержка учителей
Поддержка учителей
В этом разделе учащиеся будут применять полученные знания о расстоянии и перемещении к понятиям скорости и скорости.
[BL][OL] Прежде чем учащиеся прочитают этот раздел, попросите их привести примеры того, как они слышали употребление слова «скорость». Затем спросите их, слышали ли они слово «скорость». Объясните, что эти слова часто взаимозаменяемы в повседневной жизни, но их научные определения различны. Скажите студентам, что они узнают об этих различиях, когда будут читать этот раздел.
[AL] Объясните учащимся, что скорость, как и перемещение, является векторной величиной. Попросите их предположить, чем скорость отличается от скорости. После того, как они поделятся своими идеями, задайте вопросы, которые углубят их мыслительный процесс, например: Почему вы так думаете? Что такое пример? Как можно применить эти термины к движению, которое вы видите каждый день?
Скорость
Движение — это нечто большее, чем расстояние и смещение. Такие вопросы, как «Сколько времени занимает пеший забег?» и «Какова была скорость бегуна?» нельзя ответить без понимания других понятий. В этом разделе мы рассмотрим время, скорость и скорость, чтобы расширить наше понимание движения.
В этом разделе мы рассмотрим время, скорость и скорость, чтобы расширить наше понимание движения.
Описание того, насколько быстро или медленно движется объект, называется его скоростью. Скорость — это скорость, с которой объект меняет свое местоположение. Как и расстояние, скорость является скаляром, поскольку имеет величину, но не направление. Поскольку скорость — это скорость, она зависит от временного интервала движения. Вы можете рассчитать прошедшее время или изменение во времени ΔtΔt движения как разницу между временем окончания и временем начала
Δt=tf−t0.Δt=tf−t0.
Единицей времени в СИ является секунда (с), а единицей скорости в СИ является метр в секунду (м/с), но иногда километры в час (км/ч), мили в час (миль в час) или другие единицы скорости.
Когда вы описываете скорость объекта, вы часто описываете среднее значение за определенный период времени. Средняя скорость, v avg , представляет собой пройденное расстояние, деленное на время, в течение которого происходит движение.
vavg=расстояние-времяavg=расстояние-время
Вы, конечно, можете изменить уравнение, чтобы решить либо расстояние, либо время
время = distancevavg.time = distancevavg.
Distance = Vavg × TimeDistance = Vavg × Time
Предположим, например, что автомобиль проезжает 150 километров за 3,2 часа. Его средняя скорость за поездку
ср=расстояние/время=150 км3,2 ч=47 км/ч. ср=расстояние/время=150 км3,2 ч=47 км/ч.
Скорость автомобиля может увеличиваться и уменьшаться во много раз за 3,2-часовую поездку. Однако его скорость в конкретный момент времени является его мгновенной скоростью. Спидометр автомобиля описывает его мгновенную скорость.
Поддержка учителей
Поддержка учителей
[OL][AL] Предупредите учащихся, что средняя скорость не всегда является средним значением начальной и конечной скоростей объекта. Например, предположим, что автомобиль проехал расстояние 100 км. Первые 50 км он едет со скоростью 30 км/ч, а вторые 50 км – со скоростью 60 км/ч. Его средняя скорость будет равна расстоянию /(интервал времени) = (100 км)/[(50 км)/(30 км/ч) + (50 км)/(60 км/ч)] = 40 км/ч. Если бы автомобиль проехал одинаковое время 30 км и 60 км, а не равное расстояние на этих скоростях, его средняя скорость была бы 45 км/ч.
Первые 50 км он едет со скоростью 30 км/ч, а вторые 50 км – со скоростью 60 км/ч. Его средняя скорость будет равна расстоянию /(интервал времени) = (100 км)/[(50 км)/(30 км/ч) + (50 км)/(60 км/ч)] = 40 км/ч. Если бы автомобиль проехал одинаковое время 30 км и 60 км, а не равное расстояние на этих скоростях, его средняя скорость была бы 45 км/ч.
[BL][OL] Предупредите учащихся, что термины «скорость», «средняя скорость» и «мгновенная скорость» в повседневном языке часто называются просто скоростью. Подчеркните важность использования правильной терминологии в науке, чтобы избежать путаницы и правильно передать идеи.
Рисунок 2,8 За 30-минутную поездку туда и обратно до магазина общее пройденное расстояние составляет 6 км. Средняя скорость 12 км/ч. Перемещение для кругового рейса равно нулю, потому что нет чистого изменения положения.
Рабочий пример
Вычисление средней скорости
Мрамор катится на 5,2 м за 1,8 с. Какова была средняя скорость шарика?
Какова была средняя скорость шарика?
Стратегия
Мы знаем расстояние, которое проходит шарик, 5,2 м, и интервал времени, 1,8 с. Мы можем использовать эти значения в уравнении средней скорости.
Решение
vavg=distancetime=5,2 м1,8 с=2,9 м/svavg=distancetime=5,2 м1,8 с=2,9 м/с отвечать. Мы можем проверить разумность ответа, оценив: 5 метров разделить на 2 секунды равно 2,5 м/с. Поскольку 2,5 м/с близко к 2,9м/с, ответ разумный. Речь идет о скорости быстрой ходьбы, так что это тоже имеет смысл.
Практические задачи
9.
Питчер бросает бейсбольный мяч с насыпи питчера на домашнюю тарелку за 0,46 с. Расстояние 18,4 м. Какова была средняя скорость бейсбольного мяча?
- 40 м/с
- — 40 м/с
- 0,03 м/с
- 8,5 м/с
10.
Кэсси шла к дому своей подруги со средней скоростью 1,40 м/с. Расстояние между домами 205 м. Сколько времени заняла у нее поездка?
Расстояние между домами 205 м. Сколько времени заняла у нее поездка?
146 с
0,01 с
2,50 мин
287 с
Скорость
Векторная версия скорости — это скорость. Скорость описывает скорость и направление объекта. Как и в случае со скоростью, полезно описывать либо среднюю скорость за период времени, либо скорость в конкретный момент. Средняя скорость равна смещению, деленному на время, в течение которого происходит смещение.
vavg=displacementtime=ΔdΔt=df−d0tf−t0vavg=displacementtime=ΔdΔt=df−d0tf−t0
Скорость, как и скорость, измеряется в единицах СИ в метрах в секунду (м/с), но поскольку это вектор, вы также должен включать направление. Кроме того, переменная v для скорости выделена жирным шрифтом, потому что это вектор, в отличие от переменной v для скорости, которая выделена курсивом, потому что это скалярная величина.
Советы для успеха
Важно помнить, что средняя скорость — это не то же самое, что средняя скорость без направления. Как мы видели со смещением и расстоянием в предыдущем разделе, изменения направления во временном интервале оказывают большее влияние на скорость и скорость.
Предположим, что пассажир двигается к задней части самолета со средней скоростью –4 м/с. Мы не можем сказать по средней скорости, остановился ли пассажир на мгновение или дал задний ход, прежде чем он добрался до задней части самолета. Чтобы получить больше деталей, мы должны рассмотреть меньшие сегменты пути за более короткие интервалы времени, такие как те, что показаны на рис. 2.9. Если вы рассматриваете бесконечно малые интервалы, вы можете определить мгновенную скорость, то есть скорость в определенный момент времени. Мгновенная скорость и средняя скорость одинаковы, если скорость постоянна.
Чтобы получить больше деталей, мы должны рассмотреть меньшие сегменты пути за более короткие интервалы времени, такие как те, что показаны на рис. 2.9. Если вы рассматриваете бесконечно малые интервалы, вы можете определить мгновенную скорость, то есть скорость в определенный момент времени. Мгновенная скорость и средняя скорость одинаковы, если скорость постоянна.
Рисунок 2,9 На диаграмме показана более подробная запись пассажира самолета, направляющегося к задней части самолета, с указанием меньших сегментов его поездки.
Ранее вы читали, что пройденное расстояние может отличаться от величины перемещения. Точно так же скорость может отличаться от величины скорости. Например, вы едете в магазин и через полчаса возвращаетесь домой. Если одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, значит, ваша средняя скорость составила 12 км/ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение за кругосветное путешествие равно нулю.
Смотреть физику
Вычисление средней скорости или скорости
В этом видео рассматриваются векторы и скаляры, а также описывается, как вычислить среднюю скорость и среднюю скорость, когда известны перемещение и изменение во времени. В видео также рассматривается, как преобразовать км/ч в м/с.
Что из следующего полностью описывает вектор и скалярную величину и правильно дает пример каждого из них?
Скалярная величина полностью описывается своей величиной, тогда как для полного описания вектору необходимы и величина, и направление. Перемещение является примером скалярной величины, а время — примером векторной величины.
Скалярная величина полностью описывается своей величиной, тогда как для полного описания вектору необходимы и величина, и направление.
 Время — пример скалярной величины, а перемещение — пример векторной величины.
Время — пример скалярной величины, а перемещение — пример векторной величины.Скалярная величина полностью описывается своей величиной и направлением, в то время как вектору для полного описания требуется только величина. Перемещение является примером скалярной величины, а время — примером векторной величины.
Скалярная величина полностью описывается своей величиной и направлением, в то время как вектору для полного описания требуется только величина. Время — пример скалярной величины, а перемещение — пример векторной величины.
Поддержка учителей
Поддержка учителей
В этом видео хорошо показано различие между векторами и скалярами. Студент знакомится с идеей использования «s» для обозначения перемещения, которое вы можете поощрять или не поощрять. Прежде чем учащиеся посмотрят видео, обратите внимание на то, что преподаватель использует s→s→ для смещения вместо d, как в этом тексте. Объясните, что использование маленьких стрелок над переменными является распространенным способом обозначения векторов в курсах физики более высокого уровня. Предупредите учащихся, что в этом видео не используются общепринятые сокращения для часов и секунд. Напомните учащимся, что в своей работе они должны использовать сокращения h для обозначения часов и s для обозначения секунд.
Студент знакомится с идеей использования «s» для обозначения перемещения, которое вы можете поощрять или не поощрять. Прежде чем учащиеся посмотрят видео, обратите внимание на то, что преподаватель использует s→s→ для смещения вместо d, как в этом тексте. Объясните, что использование маленьких стрелок над переменными является распространенным способом обозначения векторов в курсах физики более высокого уровня. Предупредите учащихся, что в этом видео не используются общепринятые сокращения для часов и секунд. Напомните учащимся, что в своей работе они должны использовать сокращения h для обозначения часов и s для обозначения секунд.
Рабочий пример
Вычисление средней скорости
Студент переместился на 304 м к северу за 180 с. Какова была средняя скорость студента?
Стратегия
Мы знаем, что смещение 304 м на север и время 180 с. Для решения задачи можно использовать формулу средней скорости.
Решение
ср=ΔdΔt=304 м180 с=1,7 м/с север vср=ΔdΔt=304 м180 с=1,7 м/с север
2,1
Обсуждение
Поскольку средняя скорость является векторной величиной, вы должны указать в ответе не только величину, но и направление. Обратите внимание, однако, что направление можно опустить до конца, чтобы не загромождать задачу. Обратите внимание на значащие цифры в задаче. Расстояние 304 м имеет три значащих цифры, а временной интервал 180 с — только две, поэтому частное должно иметь только две значащие цифры.
Советы для успеха
Обратите внимание на способ представления скаляров и векторов. В этой книге d представляет собой расстояние и перемещение. Точно так же v представляет скорость, а v представляет скорость. Переменная, не выделенная жирным шрифтом, указывает на скалярную величину, а переменная, выделенная жирным шрифтом, указывает на векторную величину. Векторы иногда представляются маленькими стрелками над переменной.
Поддержка учителей
Поддержка учителей
Используйте это задание, чтобы подчеркнуть важность использования правильного количества значащих цифр в вычислениях. Некоторые учащиеся склонны включать много цифр в свои окончательные расчеты. Они ошибочно полагают, что повышают точность своего ответа, записывая многие из цифр, показанных на калькуляторе. Обратите внимание, что это приводит к ошибкам в расчетах. В более сложных расчетах эти ошибки могут распространяться и приводить к неправильному окончательному ответу. Вместо этого напомните учащимся всегда использовать одну или две дополнительные цифры в промежуточных вычислениях и округлять окончательный ответ до правильного количества значащих цифр.
Рабочий пример
Решение для смещения, когда известны средняя скорость и время
Лейла бежит трусцой со средней скоростью 2,4 м/с на восток. Каково ее водоизмещение через 46 секунд?
Стратегия
Мы знаем, что средняя скорость Лейлы составляет 2,4 м/с на восток, а временной интервал равен 46 секундам. Мы можем изменить формулу средней скорости, чтобы найти смещение.
Мы можем изменить формулу средней скорости, чтобы найти смещение.
Решение
vср=ΔdΔtΔd=vaсрΔt=(2,4 м/с)(46 с)=1,1×102 м истср=ΔdΔtΔd=vaсрΔt=(2,4 м/с)(46 с)=1,1×102 м восток
2.2
Обсуждение
Ответ примерно 110 м на восток, что является разумным смещением для чуть менее минуты бега трусцой. Калькулятор показывает ответ как 110,4 м. Мы решили написать ответ, используя экспоненциальную запись, потому что хотели, чтобы было ясно, что мы использовали только две значащие цифры.
Советы для успеха
Анализ размерностей — хороший способ определить, правильно ли вы решили задачу. Запишите расчет, используя только единицы измерения, чтобы убедиться, что они совпадают по разные стороны от знака равенства. В рабочем примере у вас есть
м = (м/с)(с). Поскольку секунды находятся в знаменателе средней скорости и в числителе времени, единица измерения сокращается, оставляя только m и, конечно же, m = m.
Рабочий пример
Решение для времени, когда известны перемещение и средняя скорость
Филипп идет по прямой дорожке от своего дома до школы. Сколько времени потребуется ему, чтобы добраться до школы, если он пройдет 428 м на запад со средней скоростью 1,7 м/с на запад?
Стратегия
Мы знаем, что перемещение Филиппа составляет 428 м к западу, а его средняя скорость — 1,7 м/с к западу. Мы можем рассчитать время, необходимое для поездки, изменив уравнение средней скорости.
Solution
vavg=ΔdΔtΔt=Δdvavg=428 m1.7 m/s=2.5×102 svavg=ΔdΔtΔt=Δdvavg=428 m1.7 m/s=2.5×102 s
2.3
Discussion
Here again we пришлось использовать научную запись, потому что ответ мог иметь только две значащие цифры. Поскольку время является скаляром, ответ включает только величину, а не направление.
Практические задачи
11.
Дальнобойщик едет по прямому шоссе 0,25 ч со смещением 16 км на юг. Какова средняя скорость дальнобойщика?
4 км/ч на север
4 км/ч на юг
64 км/ч север
64 км/ч юг
12.
Птица перелетает со средней скоростью 7,5 м/с на восток с одной ветки на другую за 2,4 с. Затем он делает паузу перед полетом со средней скоростью 6,8 м/с на восток в течение 3,5 с к другой ветке. Каково полное перемещение птицы от исходной точки?
Каково полное перемещение птицы от исходной точки?
- 42 м на запад
- 6 м на запад
- 6 м на восток
- 42 м на восток
Виртуальная физика
Ходячий человек
В этой симуляции вы будете наводить курсор на человека и перемещать его сначала в одном направлении, а затем в противоположном. Держите вкладку Introduction активной. Вы можете использовать вкладку Charts после того, как узнаете о построении графиков движения позже в этой главе. Внимательно следите за знаком чисел в полях положения и скорости. На данный момент игнорируйте поле ускорения. Посмотрите, сможете ли вы сделать положение человека положительным, а скорость отрицательной. Затем посмотрите, можете ли вы сделать наоборот.
Проверка захвата
Какая ситуация правильно описывает ситуацию, когда положение движущегося человека было отрицательным, но его скорость была положительной?
- Человек движется к 0 слева от 0
- Человек движется к 0 справа от 0
- Человек уходит от 0 слева от 0
- Человек уходит от 0 справа от 0
Поддержка учителей
Поддержка учителей
Это мощная интерактивная анимация, которую можно использовать на многих уроках. На этом этапе его можно использовать, чтобы показать, что смещение может быть как положительным, так и отрицательным. Это также может показать, что когда смещение отрицательно, скорость может быть как положительной, так и отрицательной. Позже его можно использовать, чтобы показать, что скорость и ускорение могут иметь разные знаки. Настоятельно рекомендуется, чтобы вы удерживали учащихся на уровне 9.0514 Введение табл. Вкладку Charts можно использовать после того, как учащиеся узнают о построении графиков движения позже в этой главе.
На этом этапе его можно использовать, чтобы показать, что смещение может быть как положительным, так и отрицательным. Это также может показать, что когда смещение отрицательно, скорость может быть как положительной, так и отрицательной. Позже его можно использовать, чтобы показать, что скорость и ускорение могут иметь разные знаки. Настоятельно рекомендуется, чтобы вы удерживали учащихся на уровне 9.0514 Введение табл. Вкладку Charts можно использовать после того, как учащиеся узнают о построении графиков движения позже в этой главе.
Проверьте свое понимание
13.
Два бегуна, движущиеся по одной и той же прямой дорожке, начинают и заканчивают свой бег в одно и то же время. На полпути они имеют разные мгновенные скорости. Могут ли их средние скорости за весь путь быть одинаковыми?
Да, потому что средняя скорость зависит от чистого или полного водоизмещения.

Да, потому что средняя скорость зависит от общего пройденного пути.
Нет, потому что скорости обоих бегунов должны оставаться одинаковыми на протяжении всего пути.
Нет, потому что мгновенные скорости бегунов должны оставаться одинаковыми в средней точке, но могут различаться в других точках.
14.
Если разделить общее расстояние, пройденное за поездку на автомобиле (определяемое одометром), на время в пути, вычисляете ли вы среднюю скорость или величину средней скорости и при каких обстоятельствах эти две величины такой же?
- Средняя скорость.
 Оба одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление.
Оба одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление. - Средняя скорость. Оба одинаковы, когда скорость постоянна и автомобиль не меняет своего направления.
- Величина средней скорости. Оба одинаковы, когда автомобиль движется с постоянной скоростью.
- Величина средней скорости. Оба одинаковы, когда автомобиль не меняет своего направления.
15.
Может ли средняя скорость быть отрицательной?
Да, если чистый водоизмещение отрицательное.
Да, если направление объекта меняется во время движения.
Нет, потому что средняя скорость описывает только величину, а не направление движения.

Нет, потому что средняя скорость описывает величину только в положительном направлении движения.
Поддержка учителей
Поддержка учителей
Используйте Проверьте свое понимание вопросов для оценки достижений учащихся по разделам целей обучения. Если учащиеся испытывают трудности с выполнением определенной задачи, тест «Проверка понимания» поможет определить, какие именно, и направит учащихся к соответствующему содержанию. Элементы оценки в TUTOR позволят вам переоценить.
Скорость в зависимости от скорости
Точно так же, как расстояние и перемещение имеют совершенно разные значения (несмотря на их сходство), так же и скорость и скорость. Скорость — это скалярная величина, которая относится к тому, «как быстро движется объект». Скорость можно рассматривать как скорость, с которой объект преодолевает расстояние. Быстро движущийся объект имеет высокую скорость и преодолевает относительно большое расстояние за короткий промежуток времени. Сравните это с медленно движущимся объектом с низкой скоростью; он покрывает относительно небольшое расстояние за то же время. Объект без движения имеет нулевую скорость.
Скорость можно рассматривать как скорость, с которой объект преодолевает расстояние. Быстро движущийся объект имеет высокую скорость и преодолевает относительно большое расстояние за короткий промежуток времени. Сравните это с медленно движущимся объектом с низкой скоростью; он покрывает относительно небольшое расстояние за то же время. Объект без движения имеет нулевую скорость.
Скорость как векторная величина
Скорость — это векторная величина, которая относится к «скорости, с которой объект меняет свое положение». Представьте себе человека, который быстро движется — один шаг вперед и один шаг назад — и всегда возвращается в исходное исходное положение. Хотя это может привести к безумной активности, это приведет к нулевой скорости. Поскольку человек всегда возвращается в исходное положение, движение никогда не приведет к изменению положения. Поскольку скорость определяется как скорость изменения положения, это движение приводит к нулевой скорости. Если человек в движении хочет максимизировать свою скорость, то этот человек должен приложить все усилия, чтобы максимизировать величину, на которую он смещен от своего исходного положения. Каждый шаг должен быть направлен на то, чтобы продвинуть этого человека дальше от того, с чего он начал. Наверняка человек ни в коем случае не должен менять направления и начинать возвращаться в исходное положение.
Если человек в движении хочет максимизировать свою скорость, то этот человек должен приложить все усилия, чтобы максимизировать величину, на которую он смещен от своего исходного положения. Каждый шаг должен быть направлен на то, чтобы продвинуть этого человека дальше от того, с чего он начал. Наверняка человек ни в коем случае не должен менять направления и начинать возвращаться в исходное положение.
Скорость является векторной величиной. Таким образом, скорость равна направлениям . При оценке скорости объекта необходимо следить за направлением. Было бы недостаточно сказать, что объект имеет скорость 55 миль в час. Необходимо включить информацию о направлении, чтобы полностью описать скорость объекта. Например, вы должны описать скорость объекта как 55 миль/час, восток . Это одно из существенных различий между скоростью и скоростью. Скорость является скалярной величиной и не следить за направлением ; скорость является векторной величиной и знает направление .
Определение направления вектора скорости
Задача описания направления вектора скорости проста. Направление вектора скорости совпадает с направлением движения объекта. Не имеет значения, ускоряется объект или замедляется. Если объект движется вправо, то его скорость описывается как направленная вправо. Если объект движется вниз, то его скорость описывается как нисходящая. Таким образом, самолет, летящий на запад со скоростью 300 миль/час, имеет скорость 300 миль/час на запад. Обратите внимание, что скорость не имеет направления (это скаляр), а скорость в любой момент времени — это просто значение скорости с направлением.
Расчет средней скорости и средней скорости
Когда объект движется, его скорость часто меняется. Например, во время обычной поездки в школу происходит много изменений скорости. Вместо того, чтобы измеритель скорости поддерживал устойчивые показания, стрелка постоянно движется вверх и вниз, отражая остановку и запуск, ускорение и замедление. В один момент машина может двигаться со скоростью 50 миль в час, а в другой момент она может остановиться (т. е. 0 миль в час). Тем не менее, во время поездки в школу человек может проехать в среднем 32 мили в час. Среднюю скорость во время всего движения можно рассматривать как среднее значение всех показаний спидометра. Если бы показания спидометра можно было собирать с интервалом в 1 секунду (или с интервалом в 0,1 секунды, или…), а затем усреднять вместе, можно было бы определить среднюю скорость. Теперь это будет много работы. И, к счастью, есть короткий путь. Читать дальше.
В один момент машина может двигаться со скоростью 50 миль в час, а в другой момент она может остановиться (т. е. 0 миль в час). Тем не менее, во время поездки в школу человек может проехать в среднем 32 мили в час. Среднюю скорость во время всего движения можно рассматривать как среднее значение всех показаний спидометра. Если бы показания спидометра можно было собирать с интервалом в 1 секунду (или с интервалом в 0,1 секунды, или…), а затем усреднять вместе, можно было бы определить среднюю скорость. Теперь это будет много работы. И, к счастью, есть короткий путь. Читать дальше.
Средняя скорость во время движения часто рассчитывается по следующей формуле:
В отличие от этого, средняя скорость часто вычисляется по этой формуле
Давайте начнем реализовывать наше понимание этих формул со следующей задачи:
В: Во время отпуска Лиза Карр преодолела в общей сложности 440 миль. Ее поездка заняла 8 часов. Какова была ее средняя скорость?
Какова была ее средняя скорость?
Чтобы вычислить ее среднюю скорость, мы просто делим пройденное расстояние на время в пути.
Это было просто! Лиза Карр в среднем разгонялась до 55 миль в час. Возможно, она не двигалась с постоянной скоростью 55 миль в час. Она, несомненно, была остановлена в какой-то момент времени (возможно, для перерыва в ванной или на обед), и, вероятно, в другие моменты времени она двигалась со скоростью 65 миль в час. Тем не менее, она развивала среднюю скорость 55 миль в час. Приведенная выше формула представляет собой сокращенный метод определения средней скорости объекта.
Средняя скорость по сравнению с мгновенной скоростью
Поскольку движущийся объект часто меняет свою скорость во время движения, принято различать среднюю скорость и мгновенную скорость. Различие заключается в следующем.
- Мгновенная скорость — скорость в любой данный момент времени.
- Средняя скорость — среднее значение всех мгновенных скоростей; находится просто по соотношению расстояние/время.

Вы можете думать о мгновенной скорости как о скорости, которую показывает спидометр в любой данный момент времени, а о средней скорости как о среднем значении всех показаний спидометра в ходе поездки. Поскольку задача усреднения показаний спидометра была бы достаточно сложной (а может быть, и опасной), среднюю скорость чаще рассчитывают как отношение расстояния к времени.
Движущиеся объекты не всегда движутся с неустойчивой и меняющейся скоростью. Иногда объект будет двигаться с постоянной скоростью с постоянной скоростью. То есть объект будет преодолевать одно и то же расстояние каждый регулярный интервал времени. Например, бегун по пересеченной местности может бежать с постоянной скоростью 6 м/с по прямой в течение нескольких минут. Если ее скорость постоянна, то расстояние, пройденное за каждую секунду, одинаково. Бегун будет преодолевать расстояние 6 метров каждую секунду. Если бы мы могли измерять ее положение (расстояние от произвольной начальной точки) каждую секунду, то мы бы заметили, что положение меняется на 6 метров каждую секунду. Это будет резко контрастировать с объектом, который меняет свою скорость. Объект с изменяющейся скоростью будет перемещаться на разное расстояние каждую секунду. В приведенных ниже таблицах данных изображены объекты с постоянной и изменяющейся скоростью.
Это будет резко контрастировать с объектом, который меняет свою скорость. Объект с изменяющейся скоростью будет перемещаться на разное расстояние каждую секунду. В приведенных ниже таблицах данных изображены объекты с постоянной и изменяющейся скоростью.
Теперь давайте снова рассмотрим движение этого учителя физики. Учитель физики проходит 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север. Все движение длилось 24 секунды. Определить среднюю скорость и среднюю скорость.
Учитель физики прошел 12 метров за 24 секунды; таким образом, ее средняя скорость составила 0,50 м/с. Однако, поскольку ее перемещение равно 0 м, ее средняя скорость равна 0 м/с. Помните, что смещение относится к изменению положения, а скорость зависит от этого изменения положения. В этом случае движения учителя происходит изменение положения на 0 метров и, следовательно, средняя скорость равна 0 м/с.
Вот еще один пример, аналогичный тому, что мы видели ранее при обсуждении расстояния и смещения. На приведенной ниже диаграмме показано положение лыжника в разное время. В каждый из указанных моментов времени лыжник поворачивается и меняет направление движения. Другими словами, лыжник перемещается из пункта А в пункт В, затем в пункт С и затем в пункт D. 90 899
На приведенной ниже диаграмме показано положение лыжника в разное время. В каждый из указанных моментов времени лыжник поворачивается и меняет направление движения. Другими словами, лыжник перемещается из пункта А в пункт В, затем в пункт С и затем в пункт D. 90 899
Используйте диаграмму, чтобы определить среднюю скорость и среднюю скорость лыжника в течение этих трех минут. Когда закончите, нажмите кнопку, чтобы просмотреть ответ.
В качестве последнего примера рассмотрим футбольного тренера, расхаживающего взад-вперед вдоль боковой линии. На приведенной ниже диаграмме показаны несколько позиций тренера в разное время. В каждой отмеченной позиции тренер делает «разворот» и движется в обратном направлении. Другими словами, тренер перемещается из позиции A в B, затем в C и затем в D.
Какова средняя скорость и средняя скорость тренера? Когда закончите, нажмите кнопку, чтобы просмотреть ответ.
В заключение, скорость и скорость являются кинематическими величинами, которые имеют совершенно разные определения. Скорость, будучи скалярной величиной, представляет собой скорость, с которой объект преодолевает расстояние. Средняя скорость — это расстояние (скалярная величина) за отношение времени. Скорость не знает направления . С другой стороны, скорость — векторная величина; это с учетом направления . Скорость – это скорость изменения положения. Средняя скорость — это смещение или изменение положения (векторная величина) за отношение времени.
Скорость, будучи скалярной величиной, представляет собой скорость, с которой объект преодолевает расстояние. Средняя скорость — это расстояние (скалярная величина) за отношение времени. Скорость не знает направления . С другой стороны, скорость — векторная величина; это с учетом направления . Скорость – это скорость изменения положения. Средняя скорость — это смещение или изменение положения (векторная величина) за отношение времени.
Мы хотели бы предложить …
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактива Name That Motion. Он находится в разделе «Интерактивная физика» и позволяет учащемуся применять понятия скорости, скорости и ускорения.
Посетите назовите это движение.
Следующий раздел:
Перейти к следующему уроку:
Скорость и скорость – Гиперучебник по физике
[закрыть]
скорость
В чем разница между двумя одинаковыми объектами, движущимися с разной скоростью? Почти все знают, что тот, кто движется быстрее (тот, у кого больше скорость), пройдет дальше, чем тот, кто движется медленнее, за то же время. Либо так, либо вам скажут, что тот, кто движется быстрее, доберется до места раньше, чем тот, кто медленнее. Какой бы ни была скорость, она включает в себя и расстояние, и время. «Быстрее» означает «дальше» (большее расстояние) или «скорее» (меньше времени).
Удвоение скорости означает удвоение пройденного расстояния за заданный промежуток времени. Удвоение скорости также означало бы сокращение вдвое времени, необходимого для преодоления заданного расстояния. Если вы немного разбираетесь в математике, эти утверждения будут значимыми и полезными. (Символ v используется для обозначения скорости из-за связи между скоростью и скоростью, которая будет вскоре обсуждаться.)
(Символ v используется для обозначения скорости из-за связи между скоростью и скоростью, которая будет вскоре обсуждаться.)
- Скорость прямо пропорциональна расстоянию, когда время постоянно: v ∝ с ( t константа)
- Скорость обратно пропорциональна времени при постоянном расстоянии: v ∝ 1 t ( с константа)
Объединение этих двух правил дает определение скорости в символической форме.
| v = | с |
| т |
| ☞ Это не окончательное определение. |
Не нравятся символы? Тогда вот еще один способ определить скорость. Скорость скорость изменения расстояния со временем.
Чтобы вычислить скорость объекта, мы должны знать, как далеко он ушел и сколько времени потребовалось, чтобы добраться туда. «Дальше» и «ранее» соответствуют «быстрее». Допустим, вы поехали на машине из Нью-Йорка в Бостон. Расстояние по дороге составляет примерно 300 км (200 миль). Если поездка занимает четыре часа, какова была ваша скорость? Применение приведенной выше формулы дает…
«Дальше» и «ранее» соответствуют «быстрее». Допустим, вы поехали на машине из Нью-Йорка в Бостон. Расстояние по дороге составляет примерно 300 км (200 миль). Если поездка занимает четыре часа, какова была ваша скорость? Применение приведенной выше формулы дает…
| v = | с | ≈ | 300 км | = 75 км/ч |
| т | 4 часа |
Это ответ, который дает нам уравнение, но насколько он верен? Было ли 75 км/ч 90 885 скоростью автомобиля 90 515? Да, конечно, это было… Ну, может быть, я предполагаю… Нет, это не могло быть на скорости . Если только вы не живете в мире, где автомобили имеют какой-то исключительный круиз-контроль и транспортные потоки регулируются каким-то идеальным образом, ваша скорость во время этого гипотетического путешествия, безусловно, должна была варьироваться. Таким образом, число, рассчитанное выше, не равно 9. 0885 скорость автомобиля, это средняя скорость за весь путь. Чтобы подчеркнуть этот момент, уравнение иногда модифицируют следующим образом…
0885 скорость автомобиля, это средняя скорость за весь путь. Чтобы подчеркнуть этот момент, уравнение иногда модифицируют следующим образом…
| v = | ∆ с |
| ∆ т |
Черта между и указывает на среднее или среднее значение, а символ ∆ (дельта) указывает на изменение. Прочитайте это как «Vee bar — это дельта-эсс над дельта-тройником». Это количество мы рассчитали для нашей гипотетической поездки.
Напротив, спидометр автомобиля показывает его мгновенную скорость , то есть скорость, определяемую за очень небольшой интервал времени — мгновение. В идеале этот интервал должен быть как можно ближе к нулю, но на самом деле мы ограничены чувствительностью наших измерительных приборов. Мысленно, однако, можно представить вычисление средней скорости за все меньшие интервалы времени, пока мы не вычислим мгновенную скорость. Эта идея записывается символически как…
Эта идея записывается символически как…
| v = |
| ∆ с | = | дс | ||
| ∆ т | дт |
или на языке исчисления скорость есть первая производная расстояния по времени.
Если вы не занимались исчислением, не парьтесь слишком сильно с этим определением. Есть и другие, более простые способы определения мгновенной скорости движущегося объекта. На графике расстояние-время скорость соответствует наклону, и, таким образом, мгновенная скорость объекта с непостоянной скоростью может быть найдена по наклону линии, касательной к его кривой. Мы займемся этим позже в этой книге.
скорость
Чтобы вычислить скорость объекта, нам нужно знать, как далеко он ушел и сколько времени потребовалось, чтобы туда добраться. Тогда мудрый человек спросил бы…
Тогда мудрый человек спросил бы…
Что вы подразумеваете под как далеко ? Вам нужно расстояние или смещение ?
Мудрый человек, когда-то давно
Ваш выбор ответа на этот вопрос определяет, что вы будете вычислять — скорость или скорость.
- Средняя скорость — скорость изменения расстояния со временем.
- Средняя скорость — скорость изменения смещения со временем.
А для любителей исчисления…
- Мгновенная скорость является первой производной расстояния по времени.
- Мгновенная скорость является первой производной перемещения по времени.
Скорость и скорость связаны почти так же, как связаны расстояние и перемещение. Скорость — это скаляр, а скорость — это вектор. Скорость получает символ v (курсив), а скорость получает символ v (жирный шрифт). Средние значения получают полосу над символом.
Средние значения получают полосу над символом.
| средняя скорость |
| ||||||||||
| мгновенная скорость |
|
| средний скорость |
| ||||||||||
| мгновенная скорость |
|
Смещение измеряется по кратчайшему пути между двумя точками, и его величина всегда меньше или равна расстоянию. Величина смещения приближается к расстоянию, когда расстояние приближается к нулю. То есть расстояние и смещение фактически одинаковы (имеют одинаковую величину), когда исследуемый интервал «небольшой». Поскольку скорость основана на расстоянии, а скорость основана на смещении, эти две величины фактически одинаковы (имеют одинаковую величину), когда временной интервал «небольшой» или, говоря языком исчисления, величина средней скорости объекта приближается. его средняя скорость по мере приближения интервала времени к нулю.
Величина смещения приближается к расстоянию, когда расстояние приближается к нулю. То есть расстояние и смещение фактически одинаковы (имеют одинаковую величину), когда исследуемый интервал «небольшой». Поскольку скорость основана на расстоянии, а скорость основана на смещении, эти две величины фактически одинаковы (имеют одинаковую величину), когда временной интервал «небольшой» или, говоря языком исчисления, величина средней скорости объекта приближается. его средняя скорость по мере приближения интервала времени к нулю.
| ∆ t → 0 | ⇒ | против → | против | |
Мгновенная скорость объекта равна величине его мгновенной скорости.
против = | против |
Скорость говорит вам, насколько быстро. Скорость говорит вам, как быстро и в каком направлении.
шт.
Скорость и скорость измеряются в одних и тех же единицах измерения. Единицей расстояния и перемещения в СИ является метр. Единицей времени в СИ является секунда. Единицей скорости и скорости в СИ является отношение двух — 9.1043 метра в секунду .
Единицей времени в СИ является секунда. Единицей скорости и скорости в СИ является отношение двух — 9.1043 метра в секунду .
| ⎡ ⎢ ⎣ | м | = | м | ⎤ ⎥ ⎦ |
| с | с |
Этот прибор редко используется за пределами научных и академических кругов. Большинство людей на этой планете измеряют скорость в километров в час (км/ч или км/ч). Соединенные Штаты являются исключением в том смысле, что мы используем более старую мили в час (миль/ч или миль в час). Давайте определим коэффициенты преобразования, чтобы мы могли связать скорость, измеренную в м/с, с более привычными единицами измерения.
| 1 км/ч = | 1 км | 1000 м | 1 час | |||
| 1 час | 1 км | 3600 с | ||||
| 1 км/ч = | 0,2777… м/с ≈ ¼ м/с | |||||
| 0476 | 1 миля | 1609 м | 1 час | |||
| 1 час | 1 миля | 3600 с | ||||
| 1 час в час = | 0,4469… м/с ≈ ½ м/с | |||||
Десятичные значения, показанные выше, точны до четырех значащих цифр, но дробные значения следует рассматривать только как эмпирические правила (1 км/ч на самом деле больше похож на 2 7 м/с, чем 1 4 м/с и 1 миль/ч больше похоже на 4 9 м/с, чем на 1 20519 м/с).
Отношение любой единицы расстояния к любой единице времени является единицей скорости.
- Скорость кораблей, самолетов и ракет часто указывается в узлах . Один узел равен одной морской миле в час — морская миля составляет 1852 м или 6076 футов, а час — 3600 с. НАСА до сих пор сообщает скорость своих ракет в узлах и расстояние до них в морских милях. Один узел составляет примерно 0,5144 м/с.
- Самые низкие скорости измеряются в течение самых длительных периодов времени. Континентальные плиты ползут по поверхности Земли с геологически медленной скоростью 1–10 см/год или 1–10 м/столетие — примерно с такой же скоростью растут ногти и волосы.
- Аудиокассета движется со скоростью 1⅞ дюйма в секунду (ips). Когда магнитная лента была впервые изобретена, ее наматывали на открытые катушки, как кинопленку. Эти ранние катушечные магнитофоны воспроизводили ленту со скоростью 15 кадров в секунду.
 Более поздние модели также могли записывать с половиной этой скорости (7½ дюймов в секунду), затем с половиной этой скорости (3¾ дюймов в секунду), а затем с половиной этой скорости (1⅞ дюймов в секунду). Когда формулировался стандарт аудиокассет, было решено, что последнего из этих значений будет достаточно для нового носителя. Один дюйм в секунду по определению равен 0,0254 м/с.
Более поздние модели также могли записывать с половиной этой скорости (7½ дюймов в секунду), затем с половиной этой скорости (3¾ дюймов в секунду), а затем с половиной этой скорости (1⅞ дюймов в секунду). Когда формулировался стандарт аудиокассет, было решено, что последнего из этих значений будет достаточно для нового носителя. Один дюйм в секунду по определению равен 0,0254 м/с.
Иногда скорость объекта описывается относительно скорости чего-то другого; желательно какое-то физическое явление.
- Аэродинамика — это изучение движущегося воздуха и того, как объекты взаимодействуют с ним. В этой области скорость объекта часто измеряется относительно скорости звука . Это отношение известно как число Маха . Скорость звука составляет примерно 295 м/с (660 миль/ч) на высоте, на которой обычно летают коммерческие реактивные самолеты. Выведенный из эксплуатации сверхзвуковой Concorde British Airways и Air France двигался со скоростью 600 м/с (1340 миль в час).
 Простое деление показывает, что эта скорость примерно вдвое превышает скорость звука или 2,0 Маха, что является исключительно быстрым. Для сравнения, Боинг 777 развивает крейсерскую скорость 248 м/с (555 миль в час) или 0,8 Маха, что только кажется медленным по сравнению с Конкордом.
Простое деление показывает, что эта скорость примерно вдвое превышает скорость звука или 2,0 Маха, что является исключительно быстрым. Для сравнения, Боинг 777 развивает крейсерскую скорость 248 м/с (555 миль в час) или 0,8 Маха, что только кажется медленным по сравнению с Конкордом. - скорость света в вакууме определяется в системе СИ как 299 792 458 м/с (около миллиарда км/ч). Обычно это указывается с более разумной точностью как 3,00 × 10 8 м/с. Скорость света в вакууме обозначается символом c (курсивом) при использовании в уравнении и c (римским шрифтом) при использовании в качестве единицы измерения. Скорость света в вакууме является универсальным пределом, поэтому реальные объекты всегда движутся медленнее, чем c . Он часто используется в физике элементарных частиц и астрономии далеких объектов. Самые далекие наблюдаемые объекты — квазары; сокращение от «квазизвездные радиообъекты». Визуально они похожи на звезды (приставка «квази» означает «похожие»), но излучают гораздо больше энергии, чем любая звезда.
 Они лежат на окраинах наблюдаемой Вселенной и с невероятной скоростью уносятся от нас. Самые далекие квазары удаляются от нас почти на 0,9в. Кстати, символ c был выбран не потому, что скорость света является универсальной константой (которой она и является), а потому, что это первая буква латинского слова, обозначающего быстроту — celeritas .
Они лежат на окраинах наблюдаемой Вселенной и с невероятной скоростью уносятся от нас. Самые далекие квазары удаляются от нас почти на 0,9в. Кстати, символ c был выбран не потому, что скорость света является универсальной константой (которой она и является), а потому, что это первая буква латинского слова, обозначающего быстроту — celeritas .
| м/с | км/ч | устройство, событие, явление, процесс |
|---|---|---|
| 10 −9 ~10 −8 | континентальных пластин, рост волос, рост ногтей | |
| 10 −4 | человеческие сперматозоиды | |
| 10 −3 | улиток | |
| 0,013 | 0,045 | розлив кетчупа из бутылки |
| 10 −1 | ленивцы, черепахи, черепахи | |
| 0,65–1,29 | 2,34–4,64 | тараканы |
| 1 | 3,6 | нервные импульсы, немиелиновые клетки |
| 1 | 3,6 | океанские течения |
| 0,06–1,14 | 0,22–4,10 | ламантинов |
| 1,3 | 4,8 | человек, типичный темп ходьбы |
| 2,391 | 8,608 | самый быстрый человек: плавание (Сезар Сьело) |
| 8 | 30 | максимальная комфортная скорость лифта |
| 10 | 40 | дельфины, морские свинки, киты |
| 10 | 40 | падающие капли дождя |
10. 422 422 | 37,520 | самый быстрый человек: бег (Усэйн Болт) |
| 12 | 43 | волна стадиона |
| 12 | 44 | пробка для шампанского |
| 15.223 | 54.803 | самый быстрый человек: катание на коньках (Павел Кулижников) |
| 20 | 70 | кролики, зайцы, лошади, борзые, тунец, акулы |
| 30 | 100 | типичное ограничение скорости на автостраде |
| 33 | 118 | гепарды |
| 34,42 | 123,9 | самый быстрый человек: поле для софтбола (Моника Эбботт) |
| 40 | 140 | падающий град |
| 42,47 | 152,9 | самый быстрый человек: метание летающего диска (Саймон Лизотт) |
| 46,98 | 169,1 | самый быстрый человек: бейсбольное поле (Арольдис Чепмен) |
| 55 | 200 | конечная скорость типичного парашютиста |
| 70,8217 | 254,958 | самый быстрый человек: катание на лыжах (Иван Оригон) |
| 73,06 | 263 | самый быстрый человек: подача в теннисе (Сэм Грот) |
| 80 | 290 | сапсан в пикировании |
| 82 | 295 | очень быстрый мяч для гольфа |
82. 211 211 | 296.00 | самый быстрый человек: велосипедист (Дениз Коренек Мюллер) |
| 33–83 | 120–300 | ураган, максимальная устойчивая скорость ветра |
| 30–90 | 105–330 | торнадо, максимальная устойчивая скорость ветра |
| 100 | 360 | нервные импульсы, миелинизированные клетки |
| 113,2 | 407,5 | максимальный порыв приземного ветра (остров Барроу, Австралия) |
| 118,3 | 426 | самый быстрый человек: победа в бадминтоне (Мадс Пилер Колдинг) |
| 124,22 | 447,19 | самый быстрый дорожный автомобиль (Koenigsegg Agera RS) |
| 142,89 | 511,11 | самый быстрый корабль (Дух Австралии) |
| 159,7 | 574,8 | самый быстрый поезд (Train à Grande Vitesse) |
| 168,249 | 605,697 | самый быстрый мотоцикл (Top 1 Ack Attack) |
| 200 | 700 | цунами |
| 250 | 900 | коммерческий реактивный самолет |
| 331 | 1 190 | скорость звука в воздухе, СТП |
| 340 | 1 225 | скорость звука в воздухе на уровне моря |
341. 4031 4031 | 1 229,051 | самый быстрый экспериментальный автомобиль (Thrust SSC) |
| 343 | 1 235 | скорость звука в воздухе при комнатной температуре |
| 377,1 | 1 357,6 | самый быстрый человек: прыжки с парашютом (Феликс Баумгартнер) |
| 980.433 | 3 529,56 | самый быстрый самолет (SR-71 Blackbird) |
| 180–1 200 | 650–4400 | пуль |
| 1 500 | 5 400 | скорость звука в воде |
| 2000 | 6000 | сейсмические волны |
| 6900 | 25 000 | скорость детонации тротила |
| 8000 | 29 000 | космический шаттл на орбите |
| 11 094 | 39 938 | самый быстрый пилотируемый космический корабль (Аполлон 10) |
| 11 180 | 40 250 | космическая скорость на поверхности Земли |
| 13 790 | 49 600 | Космический зонд New Horizons |
| 15 400 | 55 400 | Космический зонд «Вояджер-2» |
| 17 000 | 61 200 | Космический зонд «Вояджер-1» |
| 29 790 | 107 200 | Земля на орбите |
| 201 000 | 724 000 | самый быстрый беспилотный космический корабль (Parker Solar Probe) |
| 248 000 | 892 000 | Солнце движется по Млечному Пути |
| 300 000 | 1 100 000 | солнечный ветер у земли |
| 370 000 | 1 330 000 | Млечный Путь сквозь космический микроволновый фон |
| 60 000 000 | 216 000 000 | Project Starshot, предлагаемый межзвездный космический зонд | .
| 124 000 000 | 446 000 000 | скорость света в алмазе |
| 225 000 000 | 810 000 000 | скорость света в воде |
| 299 792 369 | 1 079 252 530 | протонов и антипротонов в Тэватроне, Фермилаб |
| 299 792 455 | 1 079 252 840 | протонов в Большом адронном коллайдере, ЦЕРН |
| 299 792 458 | 1 079 252 850 | скорость света в вакууме |
3.3 Время, скорость и скорость – биомеханика движения человека
Рисунок 1. Движение этих гонщиков на лонгборде можно описать их скоростями и скоростями. (кредит: Альтернативный скейт, Unsplash).
Движение — это нечто большее, чем расстояние и смещение. Такие вопросы, как «Сколько времени занимает пеший забег?» и «Какова была скорость бегуна?» нельзя ответить без понимания других понятий. В этом разделе мы добавляем определения времени, скорости и скорости, чтобы расширить наше описание движения.
Как обсуждалось ранее, самые фундаментальные физические величины определяются тем, как они измеряются. Так обстоит дело со временем. Каждое измерение времени связано с измерением изменения некоторой физической величины. В биомеханике время определяется просто: время равно изменению или интервалу, в течение которого происходит изменение. Невозможно узнать, что время прошло, если что-то не изменится.
Количество времени или изменения калибруется путем сравнения со стандартом. Стандартной единицей времени является секунда, сокращенно «с».
Как время связано с движением? Обычно нас интересует время, затраченное на определенное движение, например, сколько времени требуется пассажиру самолета, чтобы добраться от своего места до задней части самолета. Чтобы найти прошедшее время, мы отмечаем время в начале и в конце движения и вычитаем два. Например, лекция может начаться в 11:00. и закончить в 11:50, так что прошедшее время будет 50 мин. Прошедшее время Δ t – разница между временем окончания и временем начала,
Прошедшее время Δ t – разница между временем окончания и временем начала,
Δ t = t f – t i where Δ t is the change in time or elapsed time, t f is the time at the end of the motion, and t i is the time at начало движения. (Как обычно, дельта-символ Δ означает изменение величины, следующей за ним.) Жизнь проще, если время начала t i принять за ноль, как при использовании секундомера. Если бы мы использовали секундомер, он просто показывал бы ноль в начале лекции и 50 минут в конце. Если t i = 0 , то ∆ t = t f ≡ 9,0515 ≡ 9,0518 90 В этом тексте для простоты Ваше представление о скорости, вероятно, совпадает с ее научным определением. Средняя скорость равна смещению (изменению положения), деленному на время движения , [латекс]\overrightarrow{\mathbf{v}}_{average} = \frac{\Delta\overrightarrow{ \mathbf{p}}}{\Delta\mathbf{t}} = \frac{\overrightarrow{\mathbf{p_f}}-\overrightarrow{\mathbf{p_i}}}{\mathbf{t_f-t_i}}[ /latex] , где [latex]\overrightarrow{\mathbf{v}}[/latex] — скорость, [latex]\Delta\overrightarrow{\mathbf{p}}[/latex] — изменение положения (или смещения), а [latex]\overrightarrow{\mathbf{p_f}}[/latex] и [latex]\overrightarrow{\mathbf{p_i}}[/latex] — конечная и начальная позиции в моменты времени т ф и т и соответственно. Если начальное время t i принять равным нулю, то средняя скорость равна просто [латекс]\overrightarrow{\mathbf{v}}_{average} = \frac{\Delta \overrightarrow{\mathbf{p}}}{\Delta\mathbf{t}} = \frac{\overrightarrow{\mathbf{p_f}}-\overrightarrow{\mathbf{p_i}}}{\mathbf{t_f}} [/латекс] Обратите внимание, что это определение указывает, что скорость — это вектор, потому что смещение — это вектор . [латекс]\overrightarrow{\mathbf{v}}_{среднее} = \frac{\mathbf{смещение}}{\mathbf{время}} = \frac{-4\textbf{m}}{5\textbf { с}}=-0,8 \textbf{ м/с}[/латекс] Знак минус указывает, что средняя скорость также направлена к задней части самолета. Однако средняя скорость объекта ничего не говорит нам о том, что происходит с ним между начальной и конечной точками. Например, по средней скорости мы не можем сказать, остановился ли пассажир самолета на мгновение или дал задний ход перед тем, как подойти к задней части самолета. Чтобы получить больше деталей, мы должны рассмотреть меньшие отрезки пути за меньшие промежутки времени. Чем меньше временных интервалов, учитываемых в движении, тем детальнее информация. Когда мы доводим этот процесс до его логического завершения, остается бесконечно малый интервал. Средняя скорость на таком интервале становится равной мгновенная скорость или скорость в конкретный момент времени . Автомобильный спидометр, например, показывает величину (но не направление) мгновенной скорости автомобиля. (Полиция выдает билеты на основе мгновенной скорости, но при расчете времени, которое потребуется, чтобы добраться из одного места в другое во время дорожного путешествия, вам необходимо использовать среднюю скорость.) Мгновенная скорость, [латекс]\overrightarrow{\mathbf{ v}}[/latex], — это средняя скорость в конкретный момент времени (или за бесконечно малый интервал времени). Математически нахождение мгновенной скорости, [латекс]\overrightarrow{\mathbf{v}}[/латекс] , в точный момент времени t может включать в себя принятие предела, вычислительную операцию, выходящую за рамки этого текста. . Однако во многих случаях мы можем найти точные значения мгновенной скорости без вычислений. В повседневном языке большинство людей используют термины «скорость» и «скорость» как синонимы. Однако в биомеханике они не имеют одинакового значения и представляют собой разные понятия. Одним из основных отличий является то, что скорость не имеет направления. Таким образом скорость является скаляром . Точно так же, как нам нужно различать мгновенную скорость и среднюю скорость, нам также необходимо различать мгновенную скорость и среднюю скорость. Мгновенная скорость — величина мгновенной скорости. Например, предположим, что пассажир самолета в какой-то момент имел мгновенную скорость -3,0 м/с (минус означает по направлению к задней части самолета). Мы заметили, что пройденное расстояние может быть больше, чем перемещение. Таким образом, средняя скорость может быть больше, чем средняя скорость, которая равна смещению, деленному на время. Например, если вы добежали до магазина и через полчаса вернулись домой, а общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км/ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение за кругосветное путешествие равно нулю. (Перемещение — это изменение положения и, таким образом, равно нулю для кругового рейса.) Таким образом, средняя скорость равна не просто величина средней скорости. График Другой способ визуализации движения объекта — использование графика. График зависимости положения или скорости от времени может быть очень полезен. Например, для этой поездки в магазин на рис. 4 ниже показаны графики положения, скорости и зависимости скорости от времени. (Обратите внимание, что эти графики изображают очень упрощенную модель поездки. Мы предполагаем, что скорость во время поездки постоянна, что нереально, учитывая, что мы, вероятно, остановимся в магазине.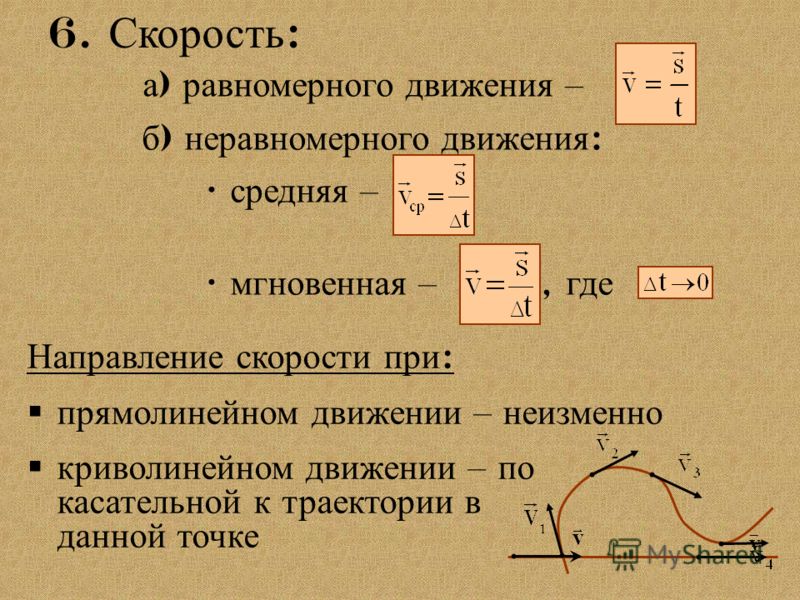 Вы знаете, что если у вас есть большое перемещение за небольшой промежуток времени, у вас будет большая скорость, и эта скорость имеет единицы измерения расстояния, деленные на время, такие как километры в час.
Вы знаете, что если у вас есть большое перемещение за небольшой промежуток времени, у вас будет большая скорость, и эта скорость имеет единицы измерения расстояния, деленные на время, такие как километры в час. СРЕДНЯЯ СКОРОСТЬ
 Она имеет как величину, так и направление. Стандартной единицей измерения скорости является метр в секунду или м/с, но широко используются многие другие единицы, такие как км/ч, мили/ч (также пишется как миль/ч) и см/с. Предположим, например, что пассажиру самолета потребовалось 5 секунд, чтобы переместиться на -4 м (знак минус указывает, что перемещение происходит в направлении задней части самолета). Его средняя скорость будет
Она имеет как величину, так и направление. Стандартной единицей измерения скорости является метр в секунду или м/с, но широко используются многие другие единицы, такие как км/ч, мили/ч (также пишется как миль/ч) и см/с. Предположим, например, что пассажиру самолета потребовалось 5 секунд, чтобы переместиться на -4 м (знак минус указывает, что перемещение происходит в направлении задней части самолета). Его средняя скорость будет

 При этом его мгновенная скорость была 3,0 м/с. Или предположим, что в какой-то момент во время похода по магазинам ваша мгновенная скорость составляет 40 км/ч строго на север. Ваша мгновенная скорость в этот момент будет 40 км/ч — та же величина, но без указания направления. Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, деленное на прошедшее время.
При этом его мгновенная скорость была 3,0 м/с. Или предположим, что в какой-то момент во время похода по магазинам ваша мгновенная скорость составляет 40 км/ч строго на север. Ваша мгновенная скорость в этот момент будет 40 км/ч — та же величина, но без указания направления. Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, деленное на прошедшее время.


 Первые полторы тысяч разложений.
Первые полторы тысяч разложений. Итак немного теории
Итак немного теории п.) то, учитывая что сумма таких частей будет равна всему пути ( равной единице), то средняя скорость будет определятся как
п.) то, учитывая что сумма таких частей будет равна всему пути ( равной единице), то средняя скорость будет определятся как

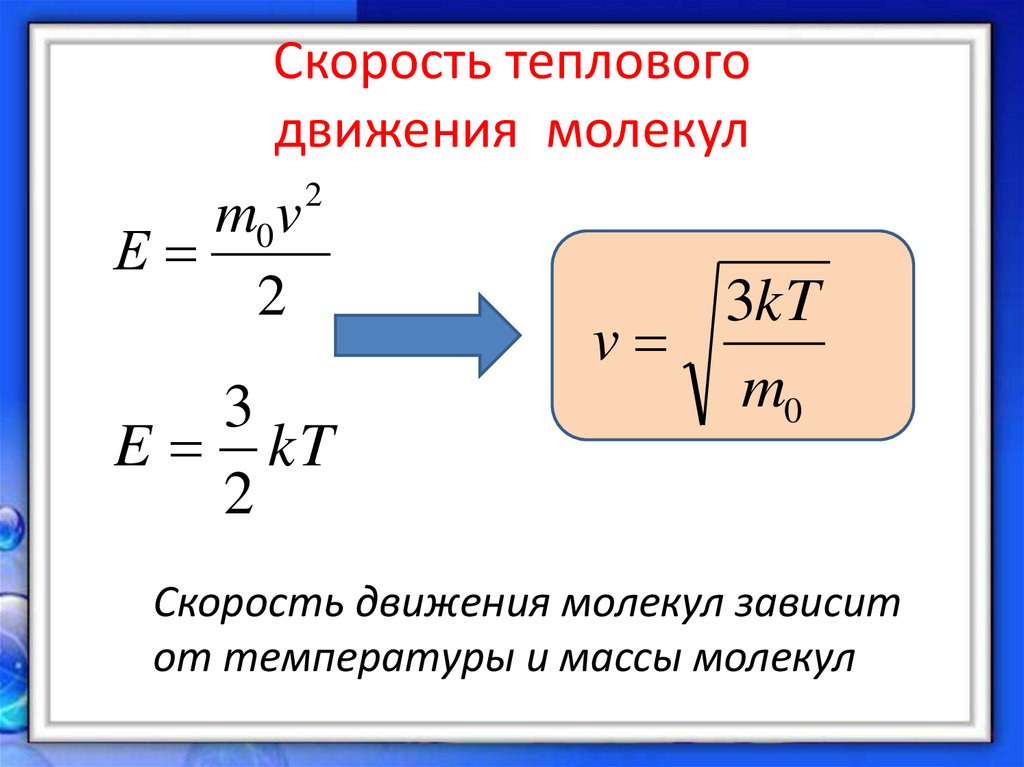 Настройка.
Настройка. Подробно
Подробно Однако для многих учащихся простота этого
понятия оказывается обманчивой.
Однако для многих учащихся простота этого
понятия оказывается обманчивой. 
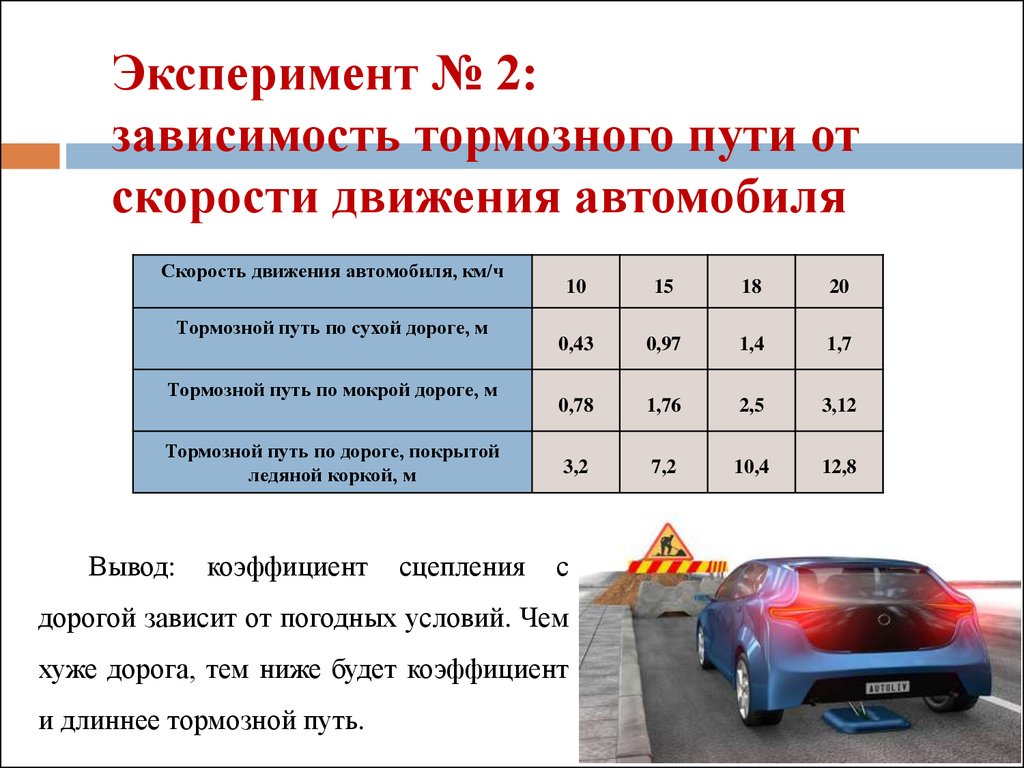 Четверть пути составляет расстояние l1/4
=l : 4 =800 : 4 =200 м. При возвращении домой человек прошел путь 2l1/4
=400 м. После этого он вышел из дома второй раз и дошел до станции.
Путь, пройденный человеком с начала движения, составит:
Четверть пути составляет расстояние l1/4
=l : 4 =800 : 4 =200 м. При возвращении домой человек прошел путь 2l1/4
=400 м. После этого он вышел из дома второй раз и дошел до станции.
Путь, пройденный человеком с начала движения, составит: Торопящийся человек соотносит
расстояние, которое ещё осталось преодолеть, и время, отпущенное ему на это,
после чего делает вывод (хотя числовое значение средней скорости вряд ли при
этом находится): “Ну, теперь можно идти помедленнее” или “Придется еще
поднажать, иначе не успею”.
Торопящийся человек соотносит
расстояние, которое ещё осталось преодолеть, и время, отпущенное ему на это,
после чего делает вывод (хотя числовое значение средней скорости вряд ли при
этом находится): “Ну, теперь можно идти помедленнее” или “Придется еще
поднажать, иначе не успею”. Значит, надо увеличивать скорость
движения. Но как это сделать без напрасных затрат сил?
Значит, надо увеличивать скорость
движения. Но как это сделать без напрасных затрат сил? Поэтому путь S человеку придется преодолевать за время
Поэтому путь S человеку придется преодолевать за время

 2
2 Половину всего времени (до точки C) он движется со скоростью 30 км/ч, а вторую половину времени – со скоростью 50 км/ч.
Половину всего времени (до точки C) он движется со скоростью 30 км/ч, а вторую половину времени – со скоростью 50 км/ч. Как быть?
Как быть?
 Решение же, как видно, достаточно длинное, и начинается оно с определяющего уравнения. То, что мы в данном случае получили уравнение, которое хотели использовать изначально – чистая случайность.
Решение же, как видно, достаточно длинное, и начинается оно с определяющего уравнения. То, что мы в данном случае получили уравнение, которое хотели использовать изначально – чистая случайность.