Средняя скорость (примеры решения) — Знаешь как
Средняя скорость это общее расстояние, пройденное этим объектом, деленное на общее время, затраченное на преодоление указанного расстояния.
Средняя скорость объекта говорит вам о средней скорости, с которой он преодолеет расстояние, то есть объект имеет скорость 30 км/час, его положение будет меняться в среднем на 30 км каждый час.
Средняя скорость-это скорость, то есть величина, деленная на время, затраченное на получение этой величины. Единицей измерения скорости в СИ являются метры в секунду.
Содержание статьи
- 0.1 Что такое средняя скорость
- 1 Скорость
- 1.1 Примеры определения средней скорости
- 2 Средняя скорость объекта
- 2.1 Примеры определения средней скорости объекта
- 3 Различия и сходства между средней скоростью и средней скоростью
- 3.1 Примеры определения со средней скоростью так и со средней скоростью
- 4 Часто задаваемые вопросы и ответы?
Средняя скорость рассчитывается по формуле S = d/t, где S равна средней скорости, d равно общему расстоянию, а t равно общему времени.
Чтобы узнать о средней скорости и средней скорости, сначала должны знать некоторые термины и их значения.
Пройденное расстояние
Пройденное расстояние, как ясно видно из названия, — это общее расстояние, пройденное объектом.
Затраченное время
Время, необходимое объекту для перемещения на заданное расстояние.
Смещение
Смещение это кратчайшее расстояние между начальной точкой, в которой находился объект, и конечной точкой, в которой объект оказался.
Скорость
Скорость это расстояние, пройденное объектом за единицу времени. Скорость-это скалярная величина. Это означает, что у него нет определенного направления. Скорость относится к тому, как быстро движется объект, или, по сути, к скорости, с которой преодолевается расстояние.
СкоростьСкорость это полное перемещение объекта в заданном направлении в единицу времени. Скорость-это векторная величина. Это означает, что он имеет определенное направление.
Скорость относится к скорости перемещения объекта во времени. Представьте себе человека, который проходит некоторое расстояние, прежде чем вернуться в исходное положение.
Поскольку скорость-это скорость перемещения, это движение приводит к нулевой скорости. Если человек хочет максимизировать свою скорость, он должен максимизировать смещение от своего первоначального положения.
Поскольку скорость является векторной величиной, при ее оценке мы должны отслеживать направление.
Основное различие между скоростью и скоростью заключается в том, что скорость не учитывает направление, поскольку она является скалярной величиной.
А скорость зависит от пройденного расстояния, в то время как скорость является векторной величиной, которая учитывает направление, а скорость зависит от перемещения.
Примеры определения средней скорости1). Автомобиль преодолевает расстояние в 70 км за 2 часа. Какова средняя скорость?
Ответ: средняя скорость = расстояние/время
Таким образом, средняя скорость автомобиля составляет 70 км/2 часа = 35 км/час
2). Человек может ходить со скоростью 1,5 метра в секунду. Как далеко он пройдет за 4 минуты?
Человек может ходить со скоростью 1,5 метра в секунду. Как далеко он пройдет за 4 минуты?
Ответ: средняя скорость = расстояние/время
Расстояние = средняя скорость(время)
Расстояние = 1,5(4) (60)
Расстояние = 360 метров.
- Поезд движется по прямой линии с постоянной скоростью 60 км/ч на определенное расстояние d, а затем проходит еще одно расстояние, равное 2d, в том же направлении с постоянной скоростью 80 км/ч в том же направлении, в котором он ехал ранее. а) Какова средняя скорость поезда в течение всего пути?
Решение а) Время t1 для преодоления расстояния
t1 = d / 60
Время t2 для преодоления расстояния 2d со скоростью 80 км/ч определяется как
t2 = 2d / 80
Средняя скорость = расстояние/время = (d + 2d) / (d/60) + (2d/80) = 3d / (80d + 2d×60)/ (60×80)
= 3 d/(200d/4800) = 3d (4800)/200d = 72 км/ч
Средняя скорость объектаСредняя скорость объекта может быть определена как смещение относительно исходного положения, деленное на время. Другими словами, это скорость, с которой объект совершает перемещения со временем.
Другими словами, это скорость, с которой объект совершает перемещения со временем.
Как и средняя скорость, единица измерения СИ составляет метры в секунду. Можно также сказать, что средняя скорость-это отношение общего перемещения объекта к общему времени, за которое должно произойти это действие.
Направление средней скорости-это направление перемещения. Даже если скорость объекта колеблется и его величина меняется, его направление все равно будет таким же, как и направление перемещения.
Величина средней скорости всегда либо меньше, либо равна средней скорости, поскольку смещение всегда меньше или равно пройденному расстоянию.
Средняя скорость рассчитывается по формуле V = D/t, где V равна средней скорости, D равно полному перемещению, а t равно общему времени.
Примеры определения средней скорости объекта- Водитель грузовика проезжает 20 км по дороге за 5 минут. Затем он разворачивается и проезжает 12 км обратно по дороге за 3 минуты.
 Какова его средняя скорость?
Какова его средняя скорость?
Решение: V = D/t
В = (20 – 12)/ (5+3)
V = 8/8
V = 1 километр в минуту
- Мальчик проходит 10 км на восток за 2 часа, а затем 2,5 км на запад за 1 час. Вычислить общую среднюю скорость этого мальчика?
Решение: V = D/t
V = (10 -2,5)/2+1
V = 7,5/3
V = 2,5 км / ч
- Вычислите среднюю скорость на определенном временном интервале человека, если он перемещается на 7 м за 4 с и на 18 м за 6 с вдоль оси х?
Решение: Начальное расстояние, пройденное человеком, xi = 7 м,
Конечное пройденное расстояние, xf = 18 м,
Начальный интервал времени ti = 4 с,
Конечный интервал времени tf = 6 с,
Средняя скорость V = xi − xf / ti − tf = 18-7 / 6-4 = 11 / 2 = 5.5 м/с.
Различия и сходства между средней скоростью и средней скоростьюСходство
Оба этих термина имеют в среднем некоторую продолжительность по времени. Единица СИ и другие стандартные единицы измерения как средней скорости, так и средней скорости одинаковы.
Единица СИ и другие стандартные единицы измерения как средней скорости, так и средней скорости одинаковы.
Формула, используемая для расчета средней скорости и средней скорости, практически одинакова,
v = D/t, s = d/t,
с той лишь небольшой разницей, что в первом случае следует упомянуть направление.
Различия
Средняя скорость является скаляром и не зависит от наличия или отсутствия направления, в то время как средняя скорость, являющаяся вектором, нуждается в направлении.
Средняя скорость зависит от расстояния, то есть общей длины, пройденной во время измерения, в то время как средняя скорость зависит от перемещения, то есть от прямого расстояния от исходного положения до конечного положения.
Примеры определения со средней скоростью так и со средней скоростьюПример 1. Автомобиль проедет по прямой дороге на восток 120 метров за 5 секунд, затем проедет на запад 60 метров за 1 секунду. Определите среднюю скорость и среднюю скорость.
Решение:
Расстояние = 120 метров + 60 метров = 180 метров
Смещение = 120 метров – 60 метров = 60 метров, на восток.
Прошедшее время = 5 секунд + 1 секунда = 6 секунд.
Средняя скорость = Пройденное расстояние / время = 180 метров / 6 секунд = 30 метров/сек.
Средняя скорость = Перемещение / прошедшее время = 60 метров / 6 секунд = 10 метров/сек.
Пример 2. Бегун бегает по прямоугольной дорожке длиной = 50 метров и шириной = 20 метров. Он дважды объезжает прямоугольную дорожку и, наконец, возвращается в исходную точку.
Если общее время, необходимое ему для пробежки по трассе, составляет 100 секунд, определите среднюю скорость и среднюю скорость.
Решение:
Окружность прямоугольника, которая представляет собой расстояние, пройденное за один раунд = 2(50 метров) + 2(20 метров) = 100 метров + 40 метров = 140 метров.
Обегает прямоугольник дважды = 2(140 метров) = 280 метров.
Расстояние = 280 метров.
Смещение = 0 метров. (С тех пор, как бегун вернулся в исходную точку)
Средняя скорость равна пройденному расстоянию / времени = 280 метров / 100 секунд = 2,8 метра/сек.
Средняя скорость равна перемещению / затраченному времени = 0/100 секунд = 0.
Пример 3. Человек начинает ходить из точки на круговом поле радиусом 0,5 км и через 1 час оказывается в той же точке, откуда он изначально начал.
(а) Какова средняя скорость за все время его путешествия? Какова средняя скорость этого человека для того же самого?
Решение: а) Если этот человек обойдет круговое поле и вернется в ту же точку, он преодолел расстояние, равное окружности круга.
Таким образом, средняя скорость, с которой он путешествовал = Расстояние / время = окружность / время = Pi (0,5) (2) / 1 час = 3,14 км/час (приблизительно)
б) Если он ходит по кругу и возвращается в ту же точку, с которой начал по кругу, то изменение его положения равно нулю.
Поскольку изменение его положения равно нулю, смещение также равно нулю. Это означает, что средняя скорость также равна нулю.
Это означает, что средняя скорость также равна нулю.
Что такое средняя скорость движения?
Скорость движения при этом не обязана быть постоянной. Здесь – средняя скорость, – весь путь, пройденный телом, – время прохождения пути. Единица измерения скорости – м/с (метр в секунду).
Средняя скорость – скалярная величина.
Как найти среднюю скорость?
Чтобы найти среднюю скорость, надо:
1) найти весь пройденный путь;
2) найти все время движения;
3) весь пройденный путь разделить на все время движения: На примерах посмотрим, как находить среднюю скорость.
1) Пешеход прошел 2 часа со скоростью 7 км/ч и 3 часа со скоростью 5 км/ч.
Что называется средней скоростью за промежуток времени?
Δ s = | Δ x 1 | + | Δ x 2 | + … ( 2). Средней скоростью ( ⟨ v ⟩ ) материальной точки за промежуток времени Δ t называют физическую величину, которая равна отношению перемещения, которое совершило тело к этому промежутку времени.
Как найти среднюю скорость имея только две скорости?
Сложите значения двух скоростей.
Затем сумму разделите на два. Вы найдете среднюю скорость на всем протяжении пути.
Таким образом, если автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч, средняя скорость автомобиля на всем протяжении пути составила 50 км/ч.
Чему равна средняя скорость движения?
Скажем, если половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч (а не 100 км/ч).
В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках.
Мгновенная и средняя скорость | Физика
1. Мгновенная скорость
В этом параграфе мы будем рассматривать неравномерное движение. Однако при этом нам пригодится то, что мы знаем о прямолинейном равномерном движении.
На рисунке 4.1 показаны положения разгоняющегося автомобиля на прямом шоссе с интервалом времени 1 с. Стрелка указывает на зеркальце заднего вида, положение которого мы рассмотрим далее более подробно.
Мы видим, что за равные интервалы времени автомобиль проходит разные пути, то есть движется неравномерно.
Уменьшим теперь последовательные интервалы времени в 20 раз – до 0,05 с – и проследим за изменением положения автомобиля в течение половины секунды (это нетрудно сделать, например, с помощью видеосъемки).
Чтобы не загромождать рисунок 4.2, на нем изображены только два положения автомобиля с промежутком времени 0,5 с. Последовательные положения автомобиля с интервалом 0,05 с отмечены положением его зеркальца заднего вида (показано красным цветом).
Мы видим, что когда последовательные равные промежутки времени достаточно малы, то пути, проходимые автомобилем за эти промежутки времени, практически одинаковы. А это означает, что движение автомобиля в течение столь малых промежутков времени можно с хорошей точностью считать прямолинейным равномерным.
Оказывается, этим замечательным свойством обладает любое движение (даже криволинейное): если рассматривать его за достаточно малый промежуток времени Δt, оно очень похоже на прямолинейное равномерное движение! Причем чем меньше промежуток времени, тем больше это сходство.
Скорость тела за достаточно малый промежуток времени и называют его скоростью в данный момент времени t, если этот момент времени находится в промежутке Δt. А более точное ее название – мгновенная скорость.
Насколько малым должен быть промежуток времени Δt, чтобы в течение этого промежутка движение тела можно было считать прямолинейным равномерным, зависит от характера движения тела.
В случае разгона автомобиля это доли секунды. А, например, движение Земли вокруг Солнца можно с хорошей точностью считать прямолинейным и равномерным даже в течение суток, хотя Земля за это время пролетает в космосе больше двух с половиной миллионов километров!
Говоря далее о скорости, мы будем (если это особо не оговорено) подразумевать обычно мгновенную скорость.
? 1. По рисунку 4.2 определите мгновенную скорость автомобиля. Длину автомобиля примите равной 5 м.
Значение мгновенной скорости автомобиля показывает спидометр (рис. 4.3).
Как найти мгновенную скорость по графику зависимости координаты от времени
На рисунке 4.4 изображен график зависимости координаты от времени для автомобиля, который движется по прямолинейному шоссе.
Мы видим, что он движется неравномерно, потому что график зависимости его координаты от времени – это кривая, а не отрезок прямой.
Покажем, как определить по этому графику мгновенную скорость автомобиля в какой-либо момент времени – скажем, при t = 3 с (точка на графике).
Для этого рассмотрим движение автомобиля за столь малый промежуток времени, в течение которого его движение можно считать прямолинейным равномерным.
На рисунке 4.5 показан интересующий нас участок графика при десятикратном увеличении (см., например, шкалу времени).
Мы видим, что этот участок графика практически неотличим от отрезка прямой (красный отрезок). За последовательные равные промежутки времени по 0,1 с автомобиль проходит практически одинаковые расстояния – по 1 м.
За последовательные равные промежутки времени по 0,1 с автомобиль проходит практически одинаковые расстояния – по 1 м.
2. Чему равна мгновенная скорость автомобиля в момент t = 3 с?
Возвращаясь к прежнему масштабу чертежа, мы увидим, что прямая красного цвета, с которой практически совпадал малый участок графика, – касательная к графику зависимости координаты от времени в данный момент времени (рис. 4.6).
Итак, о мгновенной скорости тела можно судить по угловому коэффициенту касательной к графику зависимости координаты от времени: чем больше угловой коэффициент касательной, тем больше скорость тела. (Описанный способ определения мгновенной скорости с помощью касательной к графику зависимости координаты от времени связан с понятием производной функции. Это понятие вы будете изучать в курсе «Алгебра и начала аиализа».) А в тех точках графика, где угол наклона касательной равен нулю, то есть касательная параллельна оси времени t, мгновенная скорость тела равна нулю.
? 3. Рассмотрите рисунок 4.6.
а) В каких точках графика угол наклона касательной наибольший? наименьший?
б) Найдите наибольшую и наименьшую мгновенную скорость автомобиля в течение первых 6 с его движения.
2. Средняя скорость
Во многих задачах используют среднюю скорость, связанную с пройденным путем:
vср = l/t. (1)
Определенная таким образом средняя скорость является скалярной величиной, так как путь – это скалярная величина. (Иногда во избежание недоразумений ее называют средней путевой скоростью.)
Например, если автомобиль в течение трех часов проехал по городу 120 км (при этом он мог разгоняться, тормозить и стоять на перекрестках), то его средняя скорость равна 40 км/ч.
? 4. Насколько уменьшится средняя скорость только что упомянутого автомобиля, если из-за остановок в пробках общее время движения увеличится на 1 ч?
Средняя скорость на двух участках движения
Во многих задачах рассматривается движение тела на двух участках, на каждом из которых движение можно считать равномерным.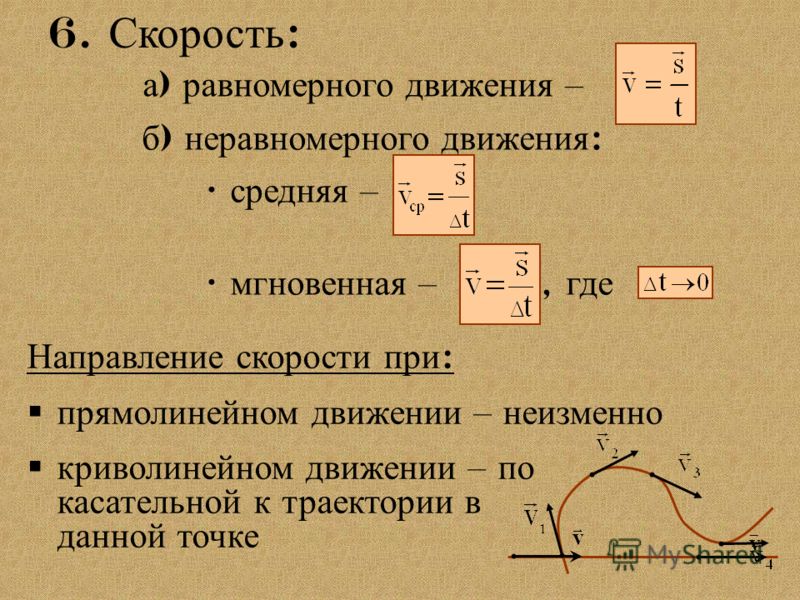 В таком случае, согласно определению средней скорости (1), можно записать:
В таком случае, согласно определению средней скорости (1), можно записать:
vср = (l1 + l2)/(t1 + t2), (2)
где l1 и t1 – путь и время для первого участка, а l2 и t2 – для второго. Рассмотрим примеры.
Саша выехал из поселка на велосипеде со скоростью 15 км/ч и ехал в течение часа. А потом велосипед сломался, и Саша еще час шел пешком со скоростью 5 км/ч.
? 5. Найдите:
а) путь, пройденный Сашей за все время движения;
б) общее время движения Саши;
в) среднюю скорость Саши.
В рассмотренном случае средняя скорость оказалась равной среднему арифметическому скоростей, с которыми Саша ехал и шел. Всегда ли это справедливо? Рассмотрим следующий пример.
Пусть Саша ехал на велосипеде в течение часа со скоростью 15 км/ч, а потом прошел такое же расстояние пешком со скоростью 5 км/ч.
? 6. Найдите:
а) путь, который Саша прошел пешком;
б) путь, пройденный Сашей за все время движения;
в) общее время движения Саши;
б) среднюю скорость Саши.
Рассмотрев этот случай, вы увидите, что на этот раз средняя скорость не равна среднему арифметическому скоростей езды и ходьбы. А если присмотреться еще внимательнее, то можно заметить, что во втором случае средняя скорость меньше, чем в первом. Почему?
? 7. Сравните промежутки времени, в течение которых Саша ехал и шел пешком в первом и втором случаях.
Обобщим рассмотренные выше ситуации.
Рассмотрим сначала случай, когда тело двигалось с разными скоростями в течение равных промежутков времени.
Пусть первую половину всего времени движения тело двигалось со скоростью v1, а вторую половину – со скоростью v2. Можно ли найти среднюю скорость движения на всем участке, если не известны ни общее время движения, ни путь, пройденный телом за все время движения?
Можно: для этого введем обозначения для всех нужных нам величин независимо от того, известны они или неизвестны. Это распространенный прием при решении многих задач.
Обозначим все время движения t, весь путь l, а пути, пройденные за первую и вторую половину времени движения, обозначим соответственно) l1 и l2.
? 8. Выразите через v1, v2 и t:
a) l1 и l2; б) l; в) среднюю скорость.
Найдя ответы на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках с разными скоростями в течение равных промежутков времени, то его средняя скорость на всем пути равна среднему арифметическому скоростей движения на двух участках.
Рассмотрим теперь случай, когда тело двигалось с разными скоростями первую и вторую половину пути.
Пусть теперь первую половину всего пути тело двигалось со скоростью v1, а вторую половину – со скоростью v2. Обозначим снова все время движения t, весь путь l, а промежутки времени, в течение которых тело двигалось на первом и втором участке, обозначим соответственно t1 и t2.
? 9. Выразите через v1, v2 и l:
а) t1 и t2; б) t; в) среднюю скорость.
Ответив на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках равной длины с разными скоростями, то его средняя скорость на всем пути не равна среднему арифметическому этих скоростей.
? 10. Докажите, что средняя скорость тела, которое двигалось на двух участках равной длины с разными скоростями, меньше, чем если бы оно двигалось на двух участках с теми же скоростями в течение равных промежутков времени.
Подсказка. Выразите для каждого из двух случаев среднюю скорость через скорости на первом и втором участках и сравните полученные выражения.
? 11. На первом участке пути тело двигалось со скоростью v1, а на втором – со скоростью v2. Чему равно отношение длин этих участков, если средняя скорость движения оказалась равной среднему арифметическому v1 и v2?
Дополнительные вопросы и задания
12. Одну треть всего времени движения поезд ехал со скоростью v1, а оставшееся время – со скоростью v2.
а) Выразите пройденный поездом путь через v1, v2 и все время движения t.
б) Выразите среднюю скорость поезда через v1 и v2.
в) Найдите числовое значение средней скорости при v1 = 60 км/ч, v2 = 90 км/ч.
13. Автомобиль ехал три четверти всего пути со скоростью v1, а оставшийся участок пути – со скоростью v2.
а) Выразите все время движения автомобиля через v1, v2 и весь пройденный путь l.
б) Выразите среднюю скорость движения автомобиля через v1 и v2.
в) Найдите числовое значение средней скорости при v1 = 80 км/ч, v2 = 100 км/ч.
14. Автомобиль ехал 2 ч со скоростью 60 км/ч. Сколько времени после этого он должен ехать со скоростью 80 км/ч, чтобы его средняя скорость на всем пути стала равной 66,7 км/ч?
15. Перенесите в тетрадь (по клеточкам) график зависимости координаты автомобиля от времени, изображенный на рисунке 4.4. Считайте, что автомобиль едет вдоль оси x.
а) Определите графически среднюю скорость за 6 с.
б) Используя касательную, определите, в какие примерно моменты времени мгновенная скорость автомобиля была равна его средней скорости за 6 с.
16. Тело движется вдоль оси x. Зависимость координаты тела от времени выражается формулой x = 0,2 * t2.
а) Выберите удобный масштаб и изобразите график зависимости x(t) в течение первых 6 с.
б) С помощью этого графика найдите момент времени, в который мгновенная скорость тела была равна средней скорости за все время движения.
Скорость
СкоростьСредняя скорость объекта определяется как пройденное расстояние, деленное на прошедшее время. Скорость является векторной величиной, а среднюю скорость можно определить как перемещение, деленное на время. Для частного случая прямолинейного движения в направлении x средняя скорость принимает вид: Из определения можно предположить, что единицами измерения скорости являются метры в секунду или вообще любая единица измерения расстояния в любую единицу времени. Вы можете приблизиться к выражению для мгновенной скорости в любой точке пути, взяв предел по мере того, как временной интервал становится все меньше и меньше.
| Индекс Концепции движения | ||
| Назад |
Средняя скорость объекта определяется как пройденное расстояние, деленное на прошедшее время. Скорость является векторной величиной, а среднюю скорость можно определить как перемещение, деленное на время. Для частного случая прямолинейного движения в направлении x средняя скорость принимает вид:  Пример непостоянного ускорения | Индекс Концепции движения | ||
| Назад |
| Средняя скорость объекта определяется как пройденное расстояние, деленное на прошедшее время. Скорость является векторной величиной, а среднюю скорость можно определить как перемещение, деленное на время. Для общих случаев, связанных с непостоянным ускорением, это определение должно применяться напрямую, потому что выражения средней скорости по прямой не работают. | Индекс Концепции движения | ||
| Вернуться |
Средняя скорость | Определение средней скорости, формула и разница
Наука является одним из самых динамичных предметов, с помощью которых студенты изучают и понимают концепцию основных, но важных вещей нашей вселенной, которая окружает нас в нашей повседневной жизни. Наука облегчает учащимся изучение того, что стоит за всем, что и как. Это наполняет их сердца радостью и волнением, поскольку ученики могут непосредственно увидеть актуальность своего обучения в повседневной жизни. Для студентов наука делится на три основных подпредмета, а именно: физику, химию и биологию.
Наука облегчает учащимся изучение того, что стоит за всем, что и как. Это наполняет их сердца радостью и волнением, поскольку ученики могут непосредственно увидеть актуальность своего обучения в повседневной жизни. Для студентов наука делится на три основных подпредмета, а именно: физику, химию и биологию.
Физика — это наука о материи, включающая наблюдение за поведением Вселенной. Физика — самый динамичный предмет в потоке естественных наук. Этот предмет касается важных тем повседневной жизни, таких как отражение и преломление света, линза и зеркало, энергия и ресурсы, изучение углерода и так далее. В результате студенты считают физику одним из самых интересных и увлекательных предметов для учащихся.
Что такое средняя скорость – определение и формула
Термин «движение» может быть описан с использованием некоторых терминов физических величин, таких как скорость, скорость, расстояние, смещение и ускорение. Правильное описание движения дал сэр Исаак Ньютон. Все эти величины описываются относительно одного параметра — времени. Здесь мы обсуждаем среднюю скорость и ее математическое представление, а также графическое представление.
Все эти величины описываются относительно одного параметра — времени. Здесь мы обсуждаем среднюю скорость и ее математическое представление, а также графическое представление.
Средняя скорость Определение
Слово «средняя» просто означает отношение суммы величин к общему количеству величин. В физике используется другой подход. Теперь, прежде чем понять среднюю скорость, давайте разберемся, что такое скорость и что такое скорость, и как они связаны.
Скорость объекта относится к изменению положения этого объекта во времени. С другой стороны, скорость — это не что иное, как скорость, определяемая относительно направления, в котором движется объект.
Мы подробно рассмотрим разницу между скоростью и скоростью, а пока вернемся к средней скорости.
Теперь средняя скорость согласно определению есть отношение перемещения объекта из точки а в точку b ко времени, которое требуется для перемещения из точки а в точку b. Можно отметить, что мы используем термин «движение» вместо «расстояние», чтобы подчеркнуть направление.
Можно отметить, что мы используем термин «движение» вместо «расстояние», чтобы подчеркнуть направление.
Алгебраически и средняя скорость определяется как v = \[\frac{d}{t}\]
, где d — смещение, а t — время, необходимое для этого смещения.
Для короткого интервала времени среднюю скорость можно рассчитать следующим образом: положение объекта в момент времени t, а (y0+Δy) — его положение в том же направлении после увеличения времени на Δt.
Когда мы берем предел как Δt→0, то он становится dy/dt, средняя скорость превращается в мгновенную скорость в момент времени t.
Когда скорость объекта изменяется в разное время, средняя скорость определяется как общая сумма всех скоростей в разные моменты времени, разделенная на общее количество раз. Например, если объект имеет разные скорости v1, v2, v3, vn в моменты времени t = t1, t2, t3, tn, то средняя скорость определяется выражением
VA = \[\frac{[v_1+v_2 +v_3. ….+v_n]}{n}\]
….+v_n]}{n}\]
Разница между средней скоростью и средней скоростью
Ранее мы объяснили, что такое скорость и что такое скорость и в чем разница между ними.
Скорость — это скалярная величина, а скорость — векторная величина.
Теперь, например, мы говорим об автомобиле, движущемся со скоростью 80 миль в час без привязки к его направлению, тогда мы говорим о его скорости. Если же мы говорим, что автомобиль движется со скоростью 80 миль в час в направлении на северо-восток, то мы имеем в виду его скорость. Время всегда будет скалярной величиной, а направление смещения будет направлением скорости.
Давайте возьмем еще один пример, чтобы лучше понять эту концепцию.
Возьмем, к примеру, автомобиль, движущийся на восток со скоростью 80 км в час в течение 2 часов и с той же скоростью в течение одного часа, но в направлении на запад, которое противоположно предыдущему.
Теперь общее пройденное расстояние равно 80 × 2 + 80 × 1 = 180 км, а общее время равно 3 часам. Следовательно, средняя скорость 1803 = 80 км в час. Но когда вы вычисляете водоизмещение автомобиля, чистое перемещение составляет 80 × 2 — 80 × 1 = 80 км в восточном направлении. Следовательно, средняя скорость 803 = 20 км/ч в восточном направлении.
Следовательно, средняя скорость 1803 = 80 км в час. Но когда вы вычисляете водоизмещение автомобиля, чистое перемещение составляет 80 × 2 — 80 × 1 = 80 км в восточном направлении. Следовательно, средняя скорость 803 = 20 км/ч в восточном направлении.
Формула средней скорости
Когда мы извлекаем среднее значение заданного числа скоростей, оно называется средней скоростью. Средняя скорость — это смещение объекта во времени. Чтобы найти среднюю скорость тела, делим пройденное расстояние на затраченное время. Мы знаем, что скорость является векторной величиной, и среднюю скорость можно найти, разделив перемещение на время.
Единицы, используемые для скорости, могут быть получены из ее определения, т. е. метры в секунду (стандартная единица СИ) или любая единица расстояния в любой единице времени.
Если скорость тела постоянно меняется в течение заданного периода, может быть очень полезно определить среднюю скорость этого объекта, чтобы получить представление о его полном пути.
Формула средней скорости Математическое описание
Дано Вав. Формула средней скорости включает полное перемещение и общее время, затраченное на это перемещение.
Для любых позиций заданы xi и xf вместе с соответствующими им временными интервалами ti и tf, мы используем формулу, приведенную ниже
Формула здесь
x I = начальная позиция,
x F = окончательная позиция,
T F — T I = временной интервал
. нам нужно узнать чистое перемещение данного объекта во время всего его движения. Начальное направление движения объекта, указанное в вопросе, принимается за его направление на всем протяжении до уточнения.
Следующая диаграмма прояснит понятие средней скорости.
Предположим, что объект перемещается на расстояние d 1 за заданное время t 1 , d 2 за время t 2 и d 3 за время 8 как показано выше.
 Должно быть хорошо известно, что пройденные расстояния не совпадают в направлениях. d 1 + d 2 + d 3 — это общее расстояние, но не чистое перемещение. Чистое смещение выступов d 2 и d 3 в направлении d 1 равно d 2 + d 3 и, следовательно, чистое перемещение равно d 1 + d 1 1 + d 1 8 130 8 Следовательно, в приведенном выше случае среднюю скорость можно найти по формуле ,
Должно быть хорошо известно, что пройденные расстояния не совпадают в направлениях. d 1 + d 2 + d 3 — это общее расстояние, но не чистое перемещение. Чистое смещение выступов d 2 и d 3 в направлении d 1 равно d 2 + d 3 и, следовательно, чистое перемещение равно d 1 + d 1 1 + d 1 8 130 8 Следовательно, в приведенном выше случае среднюю скорость можно найти по формуле ,Вср= \[\frac{[d_1+d_2+……+d_n]}{[t_1+t_2+……+t_n]}\] .
Здесь следует отметить, что если скорость, сформированная на диаграмме, принимает форму тупого угла, то указанная скорость будет иметь отрицательные значения.
Величина средней скорости
Векторные величины всегда имеют направление и величину, а поскольку мы определили скорость как векторную величину, следовательно, она имеет и величину, и направление. Если в любом случае направление объекта игнорируется, за значение средней скорости принимается величина средней скорости. Здесь следует помнить, что при расчете средней скорости для заданного объекта, где данные о скоростях даны за разные промежутки времени, нужно игнорировать направление не при расчете, а только на конечном этапе.
Здесь следует помнить, что при расчете средней скорости для заданного объекта, где данные о скоростях даны за разные промежутки времени, нужно игнорировать направление не при расчете, а только на конечном этапе.
Теперь вспомните формулу, которую мы вывели для вычитания средней скорости из последнего раздела.
Средняя скорость
Для объекта, имеющего n скоростей за n последовательных интервалов времени, величина средней скорости может быть определена как
Величина Vav = \[\frac{[ d_1+d_2+……+d_n]}{[t_1+t_2+……+t_n]}\]
Средняя угловая скорость
До сих пор мы обсуждали средние скорости в случае линейные движения, т. е. объекты, движущиеся от или к заданной точке по прямой линии. Но изучение кругового движения не менее важно. При круговом движении объект движется вокруг точки по круговой траектории. Лучшим примером этого является движение вращающихся колес.
В случае кругового движения можно определить термин, называемый угловой скоростью. Угловая скорость может быть измерена с точки зрения угла, покрываемого объектом при круговом движении за единицу времени. Обычно мы обозначаем угловую скорость греческой буквой ω. Направление угловой скорости ограничено направлением по часовой стрелке или против часовой стрелки. Данные будут называться угловой скоростью в случае отсутствия направления.
Таким образом, определение средней угловой скорости:
ω = \[\frac{\theta}{t}\],
где θ — угол поворота за время t
скорость проще. Он либо из двух: положительный или отрицательный. По соглашению, направление против часовой стрелки считается положительным, а направление по часовой стрелке — отрицательным. Основной единицей угловой скорости является радиан в единицу времени, чаще всего радиан в секунду. Следует иметь в виду, что один оборот означает охват угла в 2π радиан.
И в этом случае, когда разные угловые скорости имеют место в разное время, средняя угловая скорость находится по данной формуле.
ωср = \[\frac{[\theta _1+\theta _2+…..+\theta _n]}{[t_1+t_2+….+t_n]}\] (если временные интервалы идут последовательно.)
Ключевые точки не забывать делать заметки и преуспевать в средней скорости и других связанных темах физики 11 класса
Учащиеся, которые хотят получить высокие оценки на экзаменах, но им трудно понять процесс, всегда ищут некоторые лайфхаки и простые способы, чтобы получить хорошие оценки в экзамены через обучение творчески и эффективно. Тем не менее, постоянство и ежедневная практика не сравнится ни с чем, чтобы получить высокие оценки на экзаменах. Но для чтения в последнюю минуту и для перерыва между экзаменационными днями ниже приведены некоторые стратегии, которые учащиеся могут использовать, чтобы узнать больше за меньшее время и получить больше баллов.
1) Прочтите еще раз
Прочтите понятие средней скорости на своем языке, чтобы понять и узнать о средней скорости.
2) Пишите и делайте свои собственные заметки
Это важная часть обучения средней скорости, так как она требует, чтобы учащиеся решали уравнения и запоминали важные формулы, которые можно запомнить, только записывая и делая свои собственные заметки.
3) Повторение и решение контрольных работ
Повторение помогает учащимся подготовиться к экзамену и подготовиться к экзамену. Студентам также рекомендуется прочитать важные вопросы по средней скорости за день до экзамена, доступные в Vedantu бесплатно.
Поэтому важно питать и развивать их творческие способности с помощью наиболее подходящего и подходящего учебного материала. С этой целью Vedantu предоставляет качественные учебные материалы, чтобы учиться у лучших и опытных учителей. Заинтересованные студенты могут скачать приложение Vedantu или зарегистрироваться на сайте vedantu.

 Такой предельный процесс называется производной, а мгновенная скорость может быть определена как
Такой предельный процесс называется производной, а мгновенная скорость может быть определена как