Определите минимальную скорость при которой автомобиль: Желательно с рисунком. Показать направление сил.Определите минимальную скорость, при которой автомобиль успеет остановиться перед препятствием, если он начинает тормозить на расстоянии 25 м от препятс...

3 кг движется с постоянной скоростью v = 36 км/ч: а) по горизонтальному мосту; б) по выпуклому мосту; в) по вогнутому мосту. Радиус кривизны моста в последних двух случаях R = 60 м. С какой силой давит автомобиль на мост (в последних двух случаях) в тот момент, когда линия, соединяющая центр кривизны моста с автомобилем, составляет угол а = 10 с вертикалью? 5096. По выпуклому мосту, радиус кривизны которого R = 90 м, со скоростью v = 54 км/ч движется автомобиль массой m = 2 т. В точке моста, направление на которую из центра кривизны моста составляет с направлением на вершину моста угол а, автомобиль давит с силой F = 14 400 Н. Определить угол а. 5097. Шарик массой m = 100 г подвешен на нити длиной 1=1 м. Шарик раскрутили так, что он начал двигаться по окружности в горизонтальной плоскости. При этом угол, составляемый нитью с вертикалью, а = 60°. Определить полную работу, совершаемую при раскручивании шарика. 5098. 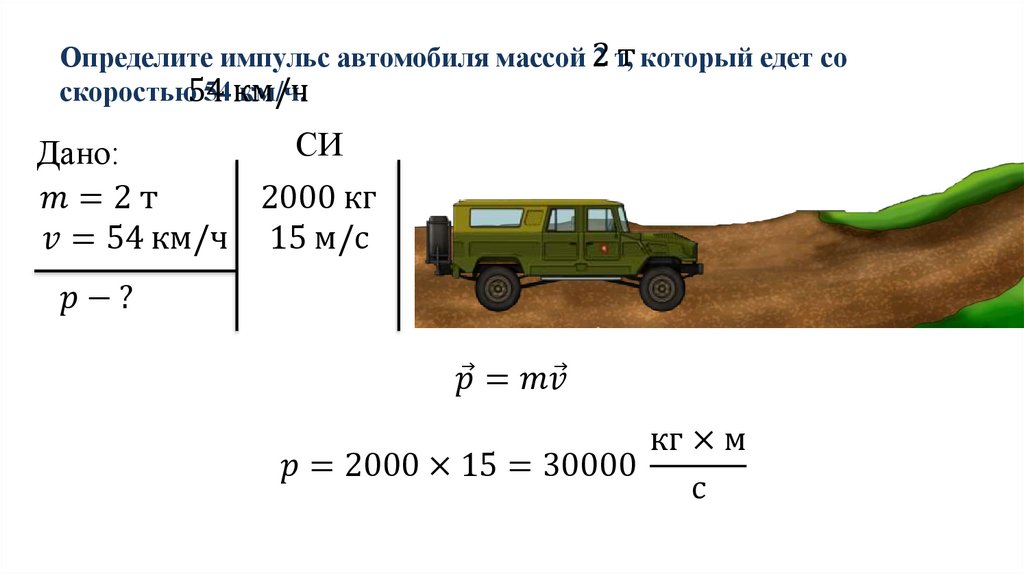С какой наибольшей скоростью может двигаться автомобиль на повороте с радиусом закругления R = 150 м, чтобы его не «занесло», если коэффициент трения скольжения шин о дорогу k = 0,42 ? 5099. 1. Каким должен быть максимальный коэффициент трения скольжения к между шинами автомобиля и асфальтом, чтобы автомобиль мог пройти закругление радиусом R = 200 м при скорости v = 100 км/ч? 2. Автомобиль со всеми ведущими колесами, трогаясь с места, равномерно набирает скорость, двигаясь по горизонтальному участку дороги, представляющему собой дугу окружности а = 30° радиусом R = 100 м. С какой максимальной скоростью автомобиль может выехать на прямой участок пути? Коэффициент трения колес о землю k = 0,3. 5100. Поезд движется по закруглению радиусом R = 800 м со скоростью v = 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего, чтобы на колесах не возникало бокового усилия. Расстояние между рельсами по горизонтали принять равным d = 1,5 м.

5101. Мотоциклист едет по горизонтальной дороге со скоростью 72 км/ч, делая поворот радиусом кривизны 100 м. На сколько при этом он должен наклониться, чтобы не упасть на повороте? 5102. 1. С какой максимальной скоростью v может ехать по горизонтальной плоскости мотоциклист, описывая дугу радиусом R = 90 м, если коэффициент трения скольжения k = 0,4? 2. На какой угол ф от вертикального направления он должен при этом отклониться? 3. Чему будет равна максимальная скорость мотоциклиста, если он будет ехать по наклонному треку с углом наклона а = 30° при том же радиусе закругления и коэффициенте трения? 4. Каким должен быть угол наклона трека а0 для того, чтобы скорость мотоциклиста могла быть сколь угодно большой? 5103. Самолет совершает поворот, двигаясь по дуге окружности с постоянной скоростью v = 360 км/ч. Определить радиус R этой окружности, если корпус самолета повернут вокруг направления полета на угол а = 10°.

5104. На повороте дороги радиусом R = 100 м равномерно движется автомобиль. Центр тяжести автомобиля находится на высоте h = 1 м, ширина колеи автомобиля а = 1,5 м. Определить скорость v, при которой автомобиль может опрокинуться. В поперечном направлении автомобиль не скользит. 5105. Шофер, едущий на автомобиле, внезапно заметил впереди себя забор, перпендикулярный направлению его движения. Что выгоднее сделать, чтобы предотвратить аварию: затормозить или повернуть в сторону? 5106. В вагоне поезда, идущего равномерно по криволинейному пути со скоростью v = 12 км/ч, производится взвешивание груза на пружинных весах. Масса груза m = 5 кг, а радиус закругления пути R = 200 м. Определить показание пружинных весов (силу натяжения пружины Т).

5107. Найти силу Fед.об., отделяющую сливки (плотность рс = 0,93 г/см3) от снятого молока (рм = 1,03 г/см3) в расчете на единицу объема, если отделение происходит: а) в неподвижном сосуде; б) в центробежном сепараторе, вращающемся с частотой 6000 мин-1, если жидкость находится на расстоянии r = 10 см от оси вращения.

5108. Самолет делает «мертвую петлю» с радиусом R = 100 м и движется по ней со скоростью v = 280 км/ч. С какой силой F тело летчика массой М = 80 кг будет давить на сиденье самолета в верхней и нижней точках петли? 5109. Определить силу натяжения Г каната гигантских шагов, если масса человека М = 70 кг и канат при вращении образует со столбом угол а = 45°. С какой угловой скоростью со будут вращаться гигантские шаги, если длина подвеса l = 5 м? 5110. Найти период Т вращения маятника, совершающего круговые движения в горизонтальной плоскости. Длина нити l. Угол, образуемый нитью с вертикалью, а. 5111. Грузик, подвешенный на нити, вращается в горизонтальной плоскости так, что расстояние от точки подвеса до плоскости, в которой происходит вращение, равно h Найти частоту n вращения груза, считая ее неизменной. 5112. 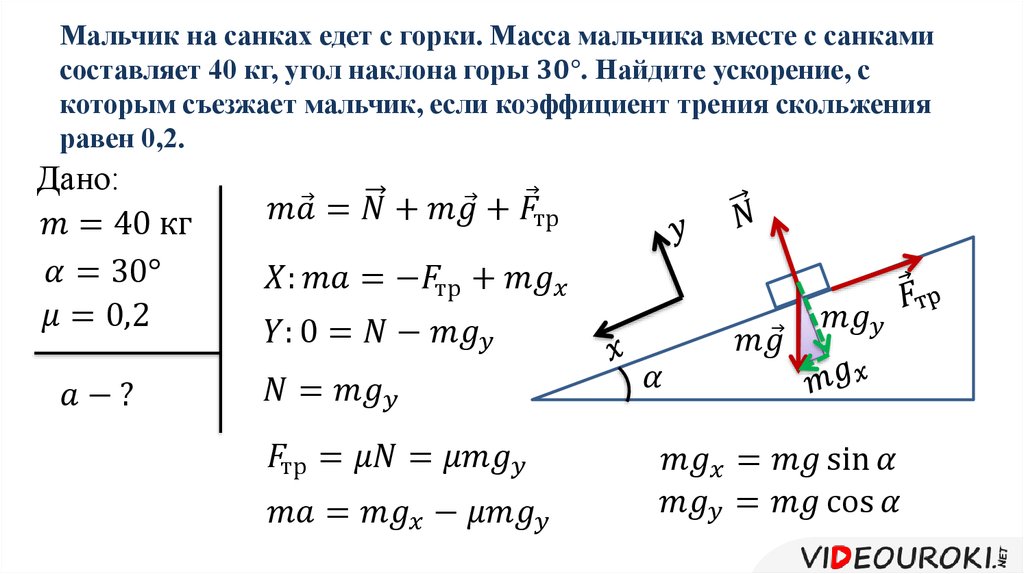Люстра массой m = 100 кг подвешена к потолку на металлической цепи, длина которой l = 5м. Определить высоту h, на которую можно отклонить люстру, чтобы при последующих качениях цепь не оборвалась? Известно, что разрыв цепи наступает при силе натяжения Т > 1960 Н.

5113. Шарик массой т подвешен на нерастяжимой нити. На какой минимальный угол амин надо отклонить шарик, чтобы при дальнейшем движении нить оборвалась, если максимально возможная сила натяжения нити 1,5 mg? 5114. Маятник отклоняют в горизонтальное положение и отпускают. При каком угле а с вертикалью сила натяжения нити будет равна по величине действующей на маятник силе тяжести? Маятник считать математическим. 5115. Груз массой m, привязанный к нерастяжимой нити, вращается в вертикальной плоскости. Найти максимальную разность сил натяжений нити. 5116. Гимнаст «крутит солнце» на перекладине.

Масса гимнаста m. Считая, что вся его масса сосредоточена в центре тяжести, а скорость в верхней точке равна нулю, определить силу, действующую на руки гимнаста в нижней точке.

5117. Один грузик подвешен на нерастяжимой нити длиной l, а другой — на жестком невесомом стержне такой же длины. Какие минимальные скорости нужно сообщить этим грузикам, чтобы они вращались в вертикальной плоскости? 5118. Шарик массой М подвешен на нити. В натянутом состоянии нить расположили горизонтально и отпустили шарик. Вывести зависимость силы натяжения нити Т от угла а, который образует в данный момент нить с горизонтальным направлением. Проверить выведенную формулу, решив задачу для случая прохождения шарика через положение равновесия, при a = 90°. 5119. Математический маятник длиной l и массой М отвели на угол ф0 от положения равновесия и сообщили ему начальную скорость v0, направленную перпендикулярно к нити вверх.

Найти силу натяжения нити маятника Т в зависимости от угла ф нити с вертикалью. 5120. Грузик, подвешенный на нити, отводят в сторону так, что нить принимает горизонтальное положение, и отпускают. Какой угол с вертикалью а образует пить в тот момент, когда вертикальная составляющая скорости грузика наибольшая? 5121. Одинаковые упругие шарики массой m, подвешенные на нитях равной длины к одному крючку, отклоняют в разные стороны от вертикали на угол а и отпускают. Шарики ударяются и отскакивают друг от друга. Какова сила F, действующая на крючок: а) при крайних положениях нитей; б) в начальный и конечный моменты удара шариков; в) в момент наибольшей деформации шариков? 5122. Математическому маятнику с гибкой нерастяжимой нитью длиной l сообщают из положения равновесия горизонтальную скорость v0. Определить максимальную высоту его подъема h при движении по окружности, если v02 = 3gl.

По какой траектории будет двигаться шарик маятника после того, как он достиг максимальной высоты подъема h на окружности? Определить максимальную высоту H, достигаемую при этом движении маятника. 5123. Маленький шарик подвешен в точке А на нити длиной l. В точке О на расстоянии l/2 ниже точки А в стену вбит гвоздь. Шарик отводят так, что нить занимает горизонтальное положение, и отпускают. В какой точке траектории исчезает сила натяжения нити? Как дальше будет двигаться шарик? До какой наивысшей точки поднимется шарик? 5124. Сосуд, имеющий форму расширяющегося усеченного конуса с диаметром дна D = 20 см и углом наклона стенок a = 60°, вращается вокруг вертикальной оси 001. При какой угловой скорости вращения сосуда со маленький шарик, лежащий на его дне, будет выброшен из сосуда? Трение не учитывать.

5125. Сфера радиусом R = 2 м равномерно вращается вокруг оси симметрии с частотой 30 мин-1.

Внутри сферы находится шарик массой m = 0,2 кг. Найти высоту h, соответствующую положению равновесия шарика относительно сферы, и реакцию сферы N. 5126. Внутри конической поверхности, движущейся с ускорением а, вращается шарик по окружности радиусом R. Определить период Т движения шарика по окружности. Угол при вершине конуса 2а. 5127. Небольшое тело массой m соскальзывает вниз по наклонному скату, переходящему в мертвую петлю радиусом R (рис. 31). Трение ничтожно мало. Определить: а) какова должна быть наименьшая высота h ската, чтобы тело сделало полную петлю, не выпадая; б) какое давление F при этом производит тело на помост в точке, радиус-вектор которой составляет угол а с вертикалью. 5128. Лента конвейера наклонена к горизонту под углом а. Определить минимальную скорость ленты Vмин, при которой частица руды, лежащая на ней, отделяется от поверхности ленты в месте набегания ее на барабан, если радиус барабана равен R.

5129. Небольшое тело скользит с вершины сферы вниз. На какой высоте h от вершины тело оторвется от поверхности сферы радиусом R? Трением пренебречь. 5130. Найти кинетическую энергию обруча массой m, катящегося со скоростью v. Проскальзывания нет. 5131. Тонкий обруч без проскальзывания скатывается в яму, имеющую форму полусферы. На какой глубине h сила нормального давления обруча на стенку ямы равна его силе тяжести? Радиус ямы R, радиус обруча r. 5132. Маленький обруч катится без скольжения по внутренней поверхности большой полусферы. В начальный момент у ее верхнего края обруч покоился. Определить: а) кинетическую энергию обруча в нижней точке полусферы; б) какая доля кинетической энергии приходится на вращательное движение обруча вокруг его оси; в) нормальную силу, прижимающую обод к нижней точке полусферы. Масса обруча равна m, радиус полусферы R.

5133. Вода течет по трубе, расположенной в горизонтальной плоскости и имеющей закругление радиусом R = 2 м. Найти боковое давление воды. Диаметр трубы d = 20 см. Через поперечное сечение трубы в течение одного часа протекает М = 300 т воды. 5134. Тело соскальзывает из точки А в точку В по двум искривленным наклонным поверхностям, проходящим через точки А и В один раз по выпуклой дуге, второй — по вогнутой. Обе дуги имеют одинаковую кривизну и коэффициент трения в обо их случаях один и тот же (рис. 32). В каком случае скорость тела в точке больше? 5135. Стержень ничтожной массы длиной l с двумя маленькими шариками m1 и m2 (m1 > m2) на концах может вращаться около оси, проходящей через середину стержня перпендикулярно к нему. Стержень приводят в горизонтальное положение и отпускают. Определить угловую скорость со и силу давления F на ось в момент прохождения стержнем с шариками положения равновесия.

5136. На виток цилиндрической спирали, ось которой вертикальна, надевают маленькое колечко массой m. Колечко без трения начинает скользить по спирали. С какой силой F будет колечко давить на спираль после того, как оно пройдет n полных витков? Радиус витка R, расстояние между соседними витками h (шаг витка). Считать h << R. 5137. Замкнутая металлическая цепочка лежит на гладком горизонтальном диске, будучи свободно насажена на центрирующее ее кольцо, соосное с диском. Диск приведен во вращение. Принимая форму цепочки за горизонтальную окружность, определить силу натяжения Т вдоль цепочки, если ее масса m = 150 г, длина l = 20 см и цепочка вращается с частотой n = 20 с-1 5138. Реактивный самолет m = 30 т летит вдоль экватора с запада на восток со скоростью v = 1800 км/ч. На сколько изменится подъемная сила, действующая на самолет, если он будет лететь с той же скоростью с востока на запад? 5139. 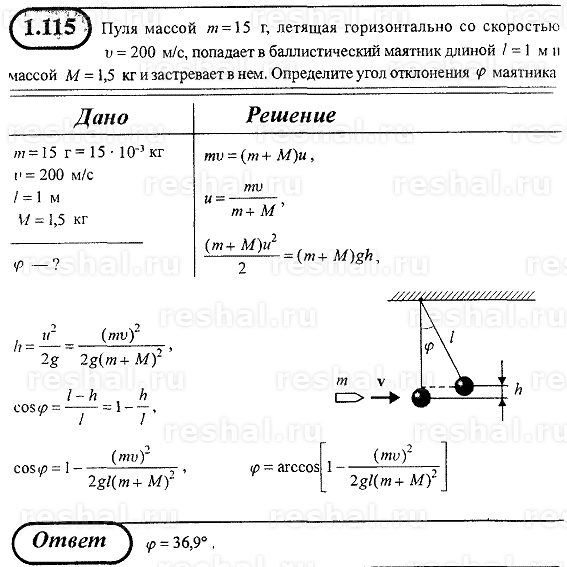Найти размерность гравитационной постоянной y в СИ. По ее значению и ускорению силы тяжести найти массу Земли М. Радиус Земли R = 6400 км. 5140. Определить силы, с которыми действуют друг на друга вследствие тяготения два соприкасающихся свинцовых шара диаметром по метру каждый. Плотность свинца 11,3 г/см3. 5141. В свинцовом шаре радиусом R сделана сферическая полость, поверхность которой касается поверхности шара и проходит через его центр. Масса шара М. Используя закон всемирного тяготения, определить, с какой силой свинцовый шар будет притягивать маленький шарик массой m, находящийся на расстоянии d > R от центра свинцового шара на прямой, соединяющей центры шара и полости, со стороны полости? 5142. На каком расстоянии от поверхности Земли ускорение тяжести равно 1 м/с2? 5143. Определить ускорение g силы тяжести на высоте h = 20 км над Землей, принимая ускорение силы тяжести на поверхности Земли g0 = 981 см/с2, а радиус Земли R = 6400 км.

11 м. 5154. Может ли спутник двигаться по орбите, плоскость которой не проходит через центр Земли? 5155. Спутник движется вокруг Земли на расстоянии h от ее поверхности. Радиус Земли R. Считая орбиту спутника круговой, выразить скорость движения и период обращения спутника через h, R и ускорение силы тяжести g на поверхности Земли. 5156. Найти среднюю угловую w и линейную v скорости орбитального движения искусственного спутника Земли, если период обращения его вокруг Земли составляет 105 мин. 5157. Какими должны быть радиус обращения искусственного спутника Земли по круговой орбите и его линейная скорость, чтобы период обращения спутника был таким же, как у Земли? Какую траекторию будет описывать спутник при наблюдении с Земли? В какой плоскости должна находиться траектория полета спутника, чтобы наблюдателю, находящемуся на Земле, спутник казался неподвижным? 5158. 10 Дж. Найти массу спутника. Радиус Земли R3 принять равным 6400 км. 5161. Найти отношение затрат энергии на поднятие спутника на высоту h2 = 3200 км и на запуск его по круговой орбите на той же высоте. Тот же вопрос для высоты h3 = 6400 км. 5162. В какой стадии движения межпланетного корабля космонавт почувствует состояние невесомости? 5163. Как изменяется ход маятниковых («ходиков») и пружинных (наручных) часов в межпланетном корабле? 5164. Как измерить массу тела в условиях невесомости? 5165. Можно ли создать весомость внутри космического корабля? 5166. Изменяется ли потенциальная энергия тел относительно Земли, если они перемещаются внутри движущегося по орбите искусственного спутника Земли? 5167. Справедливы ли в условиях невесомости законы Паскаля и Архимеда? 5168. Как будут изменяться линейная и угловая скорости спутника, движущегося в условиях слабого трения. Считать орбиту спутника круговой. 5169. В каком случае и почему при трении о воздух космическая ракета нагревается сильнее: при ее запуске или при падении на Землю. 5170. Фонарь массой М = 10 кг подвешен над серединой улицы шириной l = 10 м на канатике, допустимая сила натяжения которого Т= 500 Н. Определить высоту Я крепления концов канатика, если точка крепления фонаря должна находиться на высоте h = 5 м? 5171. Можно ли натянуть трос горизонтально так, чтобы он не провисал? 5172. Какова должна быть сила F, чтобы можно было равномерно двигать ящик массой М = 60 кг вдоль горизонтальной поверхности, если коэффициент трения между ящиком и площадкой k = 0,27, а сила действует под углом а = 30° к горизонту? 5173. Какой угол ос должно составлять направление силы с горизонтом, чтобы при равномерном перемещении груза по горизонтальной плоскости сила F была наименьшей? Сила приложена в центре тяжести груза, коэффициент трения равен k. 5174. Катушка находится на столе (рис. 33). В какую сторону она будет двигаться, если нить натягивается силой F1, F2 или F3 (продолжение линии действия силы F2 проходит через точку, лежащую на линии соприкосновения катушки со столом)? 5175. Стержень АВ, шарнирно закрепленный в точке А, опирается концом В на платформу (рис. 34). Какую минимальную силу F нужно приложить для того, чтобы сдвинуть платформу с места? Масса стержня m, коэффициент трения стержня о платформу k и угол, образуемый стержнем с вертикалью, равен а. Трением качения колес платформы и трением в осях пренебречь. 5176. К вертикальной гладкой стене в точке A на веревке длиной l подвешен шар массой m (рис. 3 кг лежит на земле. Какое усилие F надо приложить, чтобы приподнять краном трубу за один из ее концов? 5181. Автомобиль массой 1,35 т имеет колесную базу длиной 3,05 м. Центр тяжести расположен на расстоянии 1,78 м позади передней оси. Определить силу, действующую на каждое из передних колес и на каждое из задних колес со стороны горизонтальной поверхности земли. 5182. К двум одинаковым пружинам, соединенным один раз последовательно, а другой — параллельно (рис. 36), подвешивают один и тот же груз массой m. Найти удлинение dх пружин в обоих случаях, если жесткость каждой пружины k. Будет ли одинаковым в обоих случаях расстояние dl, на которое опустится груз? 5183. Две пружины с коэффициентами упругости k1 и k2 соединяют один раз последовательно, другой раз — параллельно (см. рис. 36). Какой должна быть жесткость kэкв пружины, которой можно было бы заменить эту систему из двух пружин? 5184. К концу пружины, первоначальная длина которой равна l, подвешивают груз массой m. При этом длина пружины увеличивается на 0,1 l. В какой точке нерастянутой пружины нужно было подвесить груз массой 2m, чтобы точка его подвеса оказалась на одинаковом расстоянии от концов пружины? Груз m по-прежнему прикреплен к нижнему концу пружины. Массой пружины пренебречь. 5185. Каков должен быть минимальный коэффициент трения kмин материала стенок куба о горизонтальную плоскость, чтобы его можно было опрокинуть через ребро горизонтальной силой, приложенной к верхней грани? Чему должна быть равна приложенная сила F? Масса куба М. 5186. Какой минимальной силой Fмин можно опрокинуть через ребро куб, находящийся на горизонтальной плоскости? Каков должен быть при этом минимальный коэффициент трения k куба о плоскость? Масса куба M. 5187. Высокий прямоугольный брусок с квадратным основанием стоит на горизонтальной поверхности. Как приблизительно определить коэффициент трения между бруском и поверхностью, располагая для этой цели только линейкой? 5188. Железный прут массой М изогнут пополам так, что его части образуют прямой угол (рис. 37). Прут подвешен за один из концов на шарнире. Найти угол а, который образует с вертикалью верхний стержень в положении равновесия. 5189. Однородная балка массой М и длиной l подвешена за концы на двух пружинах (рис. 38). Обе пружины в ненапряженном состоянии имеют одинаковую длину, но жесткость левой пружины в n раз больше жесткости правой (при действии одинаковой нагрузки удлинение у правой пружины в n раз больше, чем у левой). На каком расстоянии х от левого конца балки надо подвесить груз массой m, чтобы она приняла горизонтальное положение? Считать, что n = 2. 5190. Шар массой m = 4,9 кг опирается на две гладкие плоскости, образующие угол, причем левая образует с горизонтом угол а = 35°, а правая — b = 20°. Определить силы F1 и F2, с которыми шар давит на плоскости. Решить задачу двумя способами: а) разложением сил и б) правилом момента. 5191. Колесо радиусом R и массой m стоит перед ступенькой высотой h. Какую наименьшую горизонтальную силу F надо приложить к оси колеса О, чтобы оно могло подняться на ступеньку? Трением пренебречь. 5192. Как легче сдвинуть с места железнодорожный вагон: прилагая силу к корпусу вагона или к верхней части обода колеса? 5193. При резком торможении автомобиля его передок опускается. Почему?
Содержание

Дистанция и боковой интервал — какими они должны быть? — журнал За рулем
Скорость надвое
Правило двух секунд
Боковой интервал
Правила дорожного движения требуют соблюдать безопасные дистанцию и боковой интервал — но без конкретики. «За рулем» напоминает несколько простых, но эффективных способов, позволяющих сориентироваться в потоке и избежать аварийной ситуации.
Правила дорожного движения требуют соблюдать безопасные дистанцию и боковой интервал — но без конкретики.
Решения для домашних заданий
Глава 6, Круговое движение
Ч. 6, Круговое движение
Расчет скорости, необходимой для противодействия силе тяжести в петле
Эта статья из книги:
Об авторе книги:
Дистанция и боковой интервал — какими они должны быть? — журнал За рулем

LADA
УАЗ
Kia
Hyundai
Renault
Toyota
Volkswagen
Skoda
Nissan
ГАЗ
BMW
Mercedes-Benz
Mitsubishi
Mazda
Ford
Все марки
Правила дорожного движения требуют соблюдать безопасные дистанцию и боковой интервал — но без конкретики. «За рулем» напоминает несколько простых, но эффективных способов, позволяющих сориентироваться в потоке и избежать аварийной ситуации.
Материалы по теме
Не делайте так! 9 ДТП, которых не должно было случиться
Любопытно, что пункт 9.10 ПДД, в отличие от многих прочих, за последние 25 лет ни разу не менялся — хотя это не говорит о его совершенстве. Скорее уж — о невозможности четко указать значения безопасных бокового интервала и дистанции. Поэтому формулировка этого пункта довольно абстрактная: «9.10. Водитель должен соблюдать такую дистанцию до движущегося впереди транспортного средства, которая позволила бы избежать столкновения, а также необходимый боковой интервал, обеспечивающий безопасность движения».
Особенно сложно с дистанцией (расстоянием до впереди идущего автомобиля). Чтобы определить безопасную дистанцию, нужно учитывать и скорость движения, и погодные условия, и техническое состояние машины… Однако есть пара простых распространенных методик.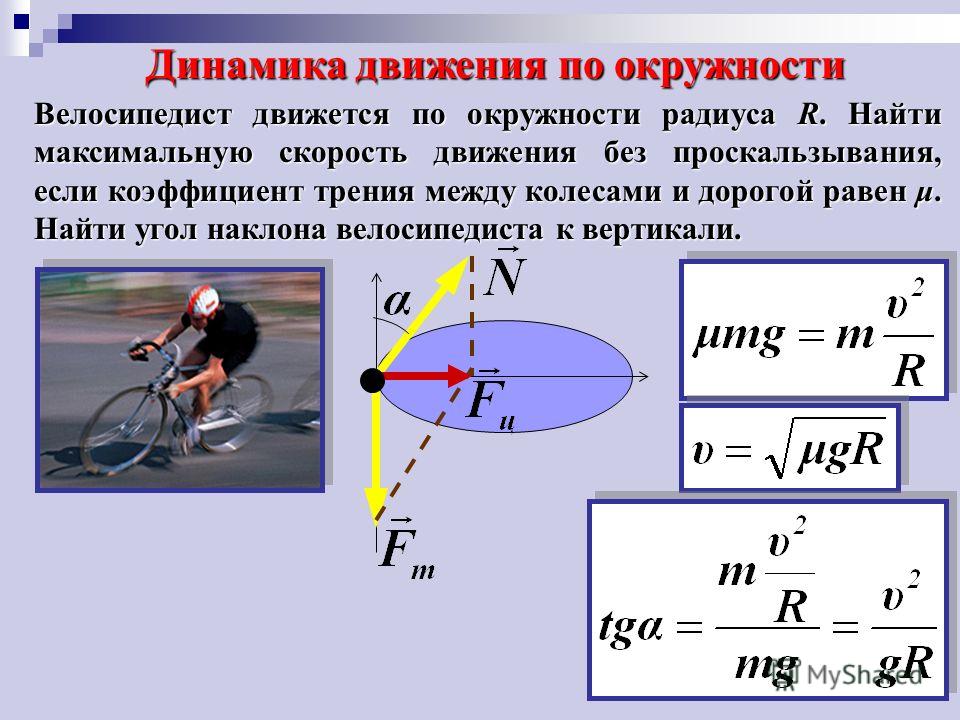
Водители машин, попавших в «паровозик», явно нарушили пункты 9.10 и 10.1 ПДД (о безопасной скорости).
Водители машин, попавших в «паровозик», явно нарушили пункты 9.10 и 10.1 ПДД (о безопасной скорости).
Скорость надвое
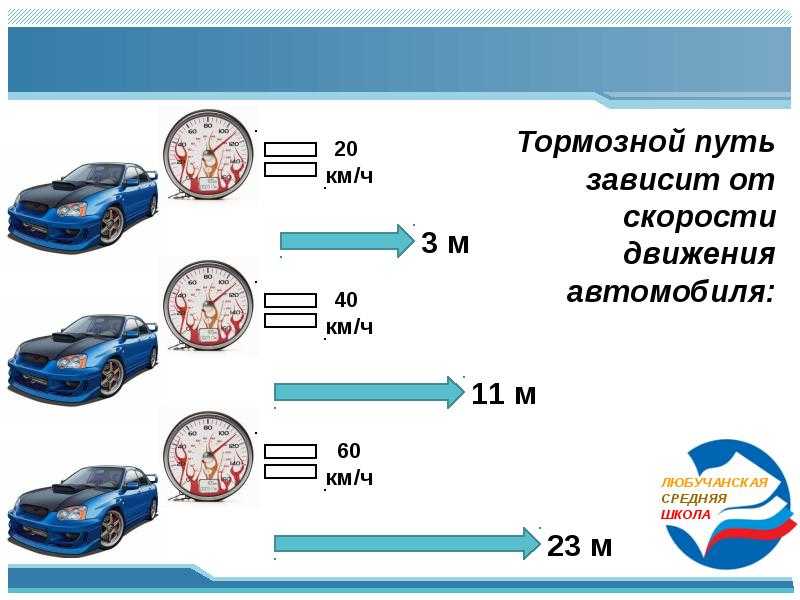
Чтобы определить безопасную дистанцию на сухой дороге, для простоты предлагается делить скорость надвое. То есть: едешь 100 км/ч — безопасная дистанция 50 метров, едешь 60 км/ч — дистанция 30 метров, и так далее. Эта методика описывалась в старых водительских учебниках, о ней рассказывал журнал «За рулем» еще полвека назад, и время от времени ее до сих пор вспоминают на всевозможных автофорумах.
Но эта методика применима только для сухого покрытия. В дождь коэффициент сцепления с дорогой снижается примерно в 1,5 раза. Зимой — в 2 раза. Так что едешь 100 по снежной каше — и дистанция должна равняться 100. Не меньше!
Правило двух секунд
Чем плох предыдущий метод? Приблизительностью. Глазомер у всех разный, и один водитель будет считать, что держит дистанцию в 50 метров, тогда как между машинами нет и 30, а другой будет держать 75, принимая их за 50.
Опытные водители предлагают использовать правило двух секунд. Нужно заметить место, которое проехал впередиидущий автомобиль, и сосчитать до двух. Если за это время вы проскочили ориентир — дистанцию нужно увеличить.
Вы можете считать дистанцию в метрах или секундах. Самое главное — не жадничать!
Вы можете считать дистанцию в метрах или секундах. Самое главное — не жадничать!
Материалы по теме
Мотоциклист между рядами: что он на самом деле нарушает
Откуда взялись эти две секунды? Да все просто. Давно установлено, что среднестатистическому водителю требуется 0,8 секунды на осознание экстренной ситуации и принятие решения, еще 0,2 секунды — на удар по педали и срабатывание тормозов. И еще одна секунда — хороший запас для нерасторопных.
Опять же, это правило действует только для сухой дороги. На мокрой дороге стоит применять правило трех секунд, на зимней — отсчитывать до 6 секунд. А в темноте двигаться так, чтобы иметь возможность остановиться до границы светового пятна фар вашего автомобиля. Помните, что за этими границами может оказаться неподвижный объект (пешеход, сломанный автомобиль, собака или лось). Остановочный путь на скорости 100 км/ч равняется примерно 70 метрам: 40 метров — средний тормозной путь современного легкового автомобиля, и 27,78 метра — путь, который автомобиль проходит на 100 км/ч за 1 секунду (время реакции водителя на экстренную ситуацию).
Боковой интервал
Здесь правило еще проще: чем больше — тем лучше. Фактически следует всегда держаться ровно в середине своей полосы (если нет колейности, глубоко утопленных люков и прочих препятствий).
Система предупреждения об объектах в «мертвой» зоне дисциплинирует, отучает шарахаться по полосе.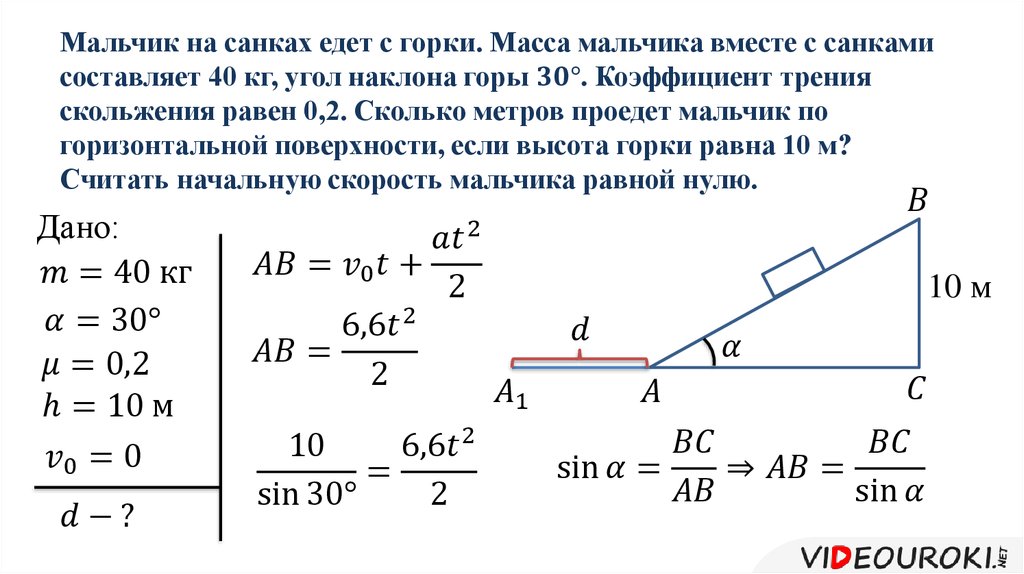
Система предупреждения об объектах в «мертвой» зоне дисциплинирует, отучает шарахаться по полосе.
Говорят, что безопасный боковой интервал на высокой скорости (при движении по загородной дороге) должен равняться примерно половине ширины машины. В городе он может быть меньше, но не стоит забывать о мотоциклистах, ездящих между рядами, и не только на узких эндуро, но и на круизерах — широченных и очень дорогих. При аварии вам вполне могут приписать несоблюдение бокового интервала. Если будете ехать ровно в середине своей полосы, оснований для этого не возникнет.
Раз уж заговорили о двухколесных, напомню, что тормозной путь у среднестатистического мотоцикла на городских скоростях больше, чем у среднестатистической машины — и это нужно учитывать при выборе дистанции.
Раз уж заговорили о двухколесных, напомню, что тормозной путь у среднестатистического мотоцикла на городских скоростях больше, чем у среднестатистической машины — и это нужно учитывать при выборе дистанции.
Материалы по теме
Вы попали в ДТП: 10 самых важных шагов
Правило бокового интервала применимо не только к машинам и мотоциклам. От велосипедистов и пешеходов стоит ехать не ближе чем в полутора метрах. И это будет вполне безопасно.
Последний совет — думать не только за себя, но и за других участников движения, пытаться предусматривать их дальнейшие действия, а также прислушиваться к интуиции. Если вам хочется увеличить дистанцию или боковой интервал — не нужно сопротивляться этому чувству. Безопасность не может быть лишней.
Правило двух секунд — вы про него помните?
Правила дорожного движения требуют соблюдать безопасные дистанцию и боковой интервал — но без конкретики. «За рулем» напоминает несколько простых, но эффективных способов, позволяющих сориентироваться в потоке и избежать аварийной ситуации.
Правило двух секунд — вы про него помните?
Правило двух секунд — вы про него помните?
Правила дорожного движения требуют соблюдать безопасные дистанцию и боковой интервал — но без конкретики.
«За рулем» напоминает несколько простых, но эффективных способов, позволяющих сориентироваться в потоке и избежать аварийной ситуации.
Правило двух секунд — вы про него помните?
Наше новое видео
Большой кроссовер Lada, почти VW из Калуги, «родные» Москвичи: раскрыты планы автопрома
Так вот в чем дело! 7 незаметных причин перерасхода топлива
Рама, вечный дизель, светодиоды, куча фишек… — такой ГАЗ всем нужен!
Понравилась заметка? Подпишись и будешь всегда в курсе!
За рулем в Дзен
Новости smi2.ru
Решения для домашних заданий
Глава 6, Круговое движение

Домашнее задание
Ч. 6, Круговое движение
Гл.6: 7, 9, 19, 21, 24, 48, 51, 63, 67
Вопросы 4, 5, 6, 7, 8, 9
| Хмвк, ч. 5 | Домашнее задание Назначение Страница | Домашняя страница PHY 1350 Страница | Hmwk, ч. 7 |

Дополнительные задачи из четвертого издания Serway
(4 изд) 6.1 Автомобиль движется с постоянной скоростью по гребню холма. Водитель движется по вертикальному кругу радиусом 18,0 м. В верхней части холме, она замечает, что едва остается в контакте с сиденьем. Найди скорость транспортного средства.

(4 изд.) 6.2 Автомобиль огибает кривую с уклоном, как показано на рис. 6.5. Радиус Кривизна дороги равна R, угол крена равен , а коэффициент статического трения равен .
(a) Определить диапазон скоростей автомобиля без буксования вверх или вниз по дороге.
(b) Найдите формулу минимального значения, при которой минимальная скорость равна нулю.
(c) Какой диапазон скоростей возможен, если R = 100 м, = 10 ^o и = 0,10 (скользкие условия)?

Концептуальные вопросы
Q6.4 Почему грязь слетает с быстро вращающейся автомобильной шины?
Чтобы грязь двигалась по кругу, на нее должна действовать (результат) сила — направленная к центру круга. Значение этой силы F _c = m v ² / р. По мере увеличения скорости (или скорости) эта сила должна увеличить, если кусок грязи будет продолжать двигаться по кругу. Как скорость увеличивается, сила, прижимающая грязь к колесу, достигает своего предела. предел и грязь больше не может ходить по кругу. Когда этот предел достиг, грязь отделяется от шины.
Q6.5 Представьте, что вы прикрепляете тяжелый предмет к одному концу пружины и затем вращайте пружину и объект по горизонтальному кругу (удерживая свободный конец пружины). Растягивается пружина? Если да, то почему? Обсудить это с точки зрения силы, вызывающей круговое движение.
Для того, чтобы тяжелый объект двигался по кругу, должна быть (суммарная) сила на это, направленное к центру. Эта сила обеспечивается пружиной. Для пружина, чтобы обеспечить силу, она должна быть растянута.
Q6.6 Было высказано предположение, что вращающиеся цилиндры около 16 км в длину и 8 км в диаметре разместить в космосе и использовать как колонии. Цель вращения — имитировать гравитацию для жителей. Объясните эту концепцию создания эффективной гравитации.
Чтобы обитатель двигался по кругу, внешний край (или «пол») придется приложить силу, направленную к центру. Эта сила очень очень похоже на силу, которую обычный пол оказывает на человека, так что это было бы создают иллюзию гравитации.
Q6.7 Почему пилот теряет сознание при сходе с крутого склона? нырять?
Выход из крутого пике прикладывает большие силы ко всему — в том числе кровь пилота. Эти силы, часто называемые «силами инерции». — заставить кровь пилота двигаться от его мозга к его нижней части тела. Если это происходит достаточно долго или если силы достаточно велики — мозг лишается кислорода в крови и пилот теряет сознание.
Обычно это происходит, когда силы превышают вес примерно в шесть раз. — называется «шесть g». Герметичные костюмы могут «сжимать» ноги и живот пилота и поддерживать приток крови к мозгу. Некоторый американские горки настолько близки к этим условиям, что некоторые жертвы — э, я имею в виду «гостей» — может потерять сознание. Некоторые из этих роликов подставки делают паузу на несколько секунд в конце, чтобы кровь вернулась к мозгу прежде чем позволить «гостям» сойти с горки.
Q6.8 Опишите ситуацию, в которой у водителя автомобиля может возникнуть центростремительная ускорение, но не тангенциальное ускорение.
Равномерное круговое движение (UCM) как раз такая ситуация. Всегда будет быть центростремительным ускорением при круговом движении из-за изменения направление. Если движение равномерное, если скорость постоянна, будет нет тангенциальное ускорение.
Q6.9 Опишите путь движущегося объекта, если его ускорение постоянно по величине во все времена и
(а) перпендикулярно скорости; и
Равномерное круговое движение (UCM).
(б) параллельно скорости.
Это прямолинейное движение.

Задачи из текущего (5-го) издания Serway and Beichner.
6.7 Пока два астронавта находились на поверхности Луны, третий астронавт вращался вокруг Луны. Предположим, что орбита круговая и находится на высоте 100 км над поверхностью. Луны. Если масса и радиус Луны равны 7,40 х 10 ²² кг и 1,70 x 10 ⁶ м, определите
(a) ускорение космонавта на орбите,
(b) его орбитальная скорость и
(в) период обращения.
Радиус орбиты
r = 100 км + 1,70 х 10 ⁶ м = 0,10 х 10 ⁶ м + 1,70 х 10 ⁶ м = 1,80 x 10 ⁶ м
F _г = Г М м/р ² = м а _с
Г М/р ² = а _в
(6,672 x 10 ^-11 Н·м ² / кг ² ) ( 7,40 x 10 ²² ) / ( 1,80 х 10 ⁶ м) ² = а _в
а _с = 1,524 м/с ²
а _с = v ² / r
v ² = a _c r = (1,524 м/с ² ) (1,80 х 10 ⁶ м)
v ² = 2,743 x 10 ⁶ м ²/с ²
v = 1,656 х 10 ³ м/с
v = D / t = C / t = 2 О r / t
t = 2 r / v = 2 ( 1,80 х 10 ⁶ м) / (1,656 х 10 ³ м/с)
t = 6,829 x 10 ³ с [ мин / 60 с] [ ч / 60 мин ]
т = 1,897 ч
6,9 Монета, расположенная на расстоянии 30 см от центра вращающейся горизонтали. поворотный стол проскальзывает, когда его скорость составляет 50 см/с.
(a) Что обеспечивает силу в радиальном направлении, когда перед монетой проскальзывает?
(b) Каков коэффициент статического трения между монетой и поворотным столом?
Как всегда, не начинайте без хороших, четких схем. Что такое все силы, действующие на монету?
w — вес, n — «нормальная» сила — сила перпендикулярно поверхности — и F _fr сила трения — параллельно поверхности. Именно эта сила трения F _fr что обеспечивает центростремительную силу F _c .
Теперь, что такое коэффициент трения ?
Ф _из = п
н = вес = мг
Ф _из = мг
F _fr = F _{c = m v ² /r}
м г _{= м v ² /r}
г _{=
v ² /r}
_{= v ² /(г
г)}
Будьте осторожны с юнитами. Мы знаем v в см/с и знаем r в см. Обычно мы указываем g как 9,8 м/с ² . Если вы просто подключите соответствующий числа ответ будет ужасным — потому что единицы не то же самое. Мы можем серьезно заняться преобразованием единиц или просто использовать g как 980 см/с ² .
₌ (50 см/с) ² /[(980 см/с ² )(30 см)]
₌ (50) ² /[(980)(30)]
₌ 0,085
6.19 Ведро с водой вращается по вертикальной окружности радиусом 1,0 м. Какой должна быть минимальная скорость ведра в верхней части круга, если нет вода должна вылиться?
В верхней части круга гравитация тянет вниз — к центру круга — с силой w = m g . Если вода просто на грани выплескивания, это только силу на воду так, чтобы также должна быть центростремительной силы.
F _c = m v ² /r = m g = w
м v ² /r = м г
v ² /r = г
v ² = г р
v ² = (9,8 м/с ² )(1,0 м)
v ² = 9,8 м ² /с ²
v = 3,13 м/с
6.21 Транспортное средство для американских горок имеет массу 500 кг при полной загрузке пассажиры.
(a) Если транспортное средство имеет скорость 20,0 м/с в точке А, какова сила воздействие гусеницы на транспортное средство в этот момент?
(b) Какую максимальную скорость может иметь транспортное средство в точке B, оставаясь при этом На дороге?

(a) Если транспортное средство имеет скорость 20,0 м/с в точке А, какова сила воздействие гусеницы на транспортное средство в этот момент?

Силы, воздействующие на массу m автомобиля с американскими горками, равны его весу в мг вниз и сила, которую оказывает гусеница F _n, указывающая вверх . Таким образом, чистая сила F _чистая равна
F _нетто = F _n — м г
Эта результирующая сила равна центральной центральной силе F _c ,
F _с = м v ² / р
F _нетто = F _c
F _n — m g = m v ² / r
F _n = (m v ² / r) + m g
F _n = m [( v ² / r) + g ]
F _n =(500 кг) [( (20 м/с) ² / 10 м) + 9,8 м/с ² ]
F _n =(500 кг) [ 49,8 м/с ² ]
Ф _н = 24,900 Н
Это примерно пять раз его вес 5000 Н.

(b) Какую максимальную скорость может иметь транспортное средство в точке B, оставаясь при этом На дороге?
«Все еще оставаться на пути» означает, что нормальная сила F _n имеет только что обнулился, F _n = 0,
При нормальной силе, равной нулю, доступен только вес мг для подачи центростремительной силы F _с ,
F _c = F _нетто
м v ² / r = м г
v ² / г = г
v ² = g r = (9,8 м/с ² ) (15 м) = 147 м ² / с ²
v = 12,12 м/с
6,24 Груз массой 5,00 кг, закрепленный на пружинных весах, лежит на горизонтальной поверхности без трения. поверхность как на рисунке P6.26. Пружинная шкала, прикрепленная к переднему концу товарный вагон, показывает 18,0 Н, когда вагон находится в движении.
(a) Если шкала пружины показывает ноль, когда кабина находится в состоянии покоя, определите ускорение автомобиля во время движения.
(б) Что будет показано на пружинной шкале, если автомобиль будет двигаться с постоянной скоростью?
(c) Опишите силы, действующие на массу, наблюдаемые кем-то в машине и кем-то в состоянии покоя, вне автомобиля.
(a) Если шкала пружины показывает ноль, когда кабина находится в состоянии покоя, определите ускорение автомобиля во время движения.

F _нетто = F _весы = 18 N = (5 кг) a = ma
а = 18 Н/5 кг
а = 3,6 м/с ²
(б) Что будет показано на пружинной шкале, если автомобиль будет двигаться с постоянной скоростью?
При постоянной скорости результирующая сила на блоке должна быть равна нулю. Только весы воздействуют на блок горизонтальной силой , поэтому на нем должно быть ноль .
(c) Опишите силы, действующие на массу, наблюдаемые кем-то в машине и кем-то в состоянии покоя, вне автомобиля.
Наблюдатель, находящийся в состоянии покоя, снаружи видит пружинную шкалу, прилагающую силу вправо, что заставляет блок ускоряться вправо. Сила весенней шкалы только горизонтальное усилие на блоке и это сила net , которая заставляет блок ускоряться.
Наблюдатель, едущий вместе с блоком внутри автомобиля, видит блок в остальные в ее системе отсчета. Пружинная шкала оказывает усилие на правильно, но блок остается в покое. Поэтому наш попутный наблюдатель придем к выводу, что есть дополнительная сила слева от , действующая на блоке. Мы называем это «силой инерции» или «фиктивной силой». к ускорению системы отсчета.
6.48 В атоме водорода электрон на орбите вокруг протона чувствует сила притяжения около 8,20 х 10 ^-8 Н. Если радиус «орбита» 5,30 х 10 ^-11 м, какова частота в оборотах в секунду?
F _c = m v ² / r
v ² = F _c об/м = (8,20 х 10 ^-8 N)(5,30 x 10 ^-11 м) / (1,67 x 10 ^-27 кг)
v ² = 2,60 x 10 ⁹ м ²/с ²
v = 5,101 x 10 ⁴ м/с
v = г
= v / r = (5,101 х 10 ⁴ м/с) / (5,30 х 10 ^-11 м) = 9,625 х 10 ¹⁴ рад/сек
f = 9,625 х 10 ¹⁴ рад/сек [об/2 рад]
f = 1,532 х 10 ¹⁴ об/сек
6. 51 Воздушная шайба массой 0,25 кг привязана к веревке и вращается по кругу радиусом 1,0 м на горизонтальном столе без трения. Другой конец нити проходит через отверстие в центре стола и груз к нему привязано 1,0 кг (рис. P6.38). Подвешенная масса остается в равновесии пока шайба на столешнице вращается. Что такое
(а) натяжение струны,
(b) центральная сила, действующая на шайбу, и
(с) скорость шайбы?

Что такое (а) натяжение струны,
Посмотрите на силы, действующие на подвешенную массу . Из тех, что вы можете легко следите за тем, чтобы натяжение нити было равно весу подвески масса,
Т = м ₂ г
T = (1,0 кг) ((9,8 м/с ² )
Т = 9,8 Н
(b) центральная сила, действующая на шайбу, и
Единственная горизонтальная сила , действующая на шайбу, представляет собой натяжение в струны, так что это натяжение равно центральной силе и равно центростремительной сила,
F _c = T = m ₂ г
Ф _с = Т = 9,8 Н
(с) скорость шайбы?
F _c = m ₁ v ² / R = m ₂ г
(0,25 кг) v ² / 1,0 м = 90,8 Н
v ² = (m ₂ / m ₁ ) г R
v ² = (9,8 / 0,25) м ²/с ² = 39,2 м ² / с ²
v = SQRT [ (m ₂ / m ₁ ) g R ]
v = 6,26 м/с
6. 63 Аттракцион состоит из большого вертикального цилиндра, который вращается вокруг своей оси достаточно быстро, чтобы любой человек внутри был прижат к стене когда пол упадет (рис. P6.49). Коэффициент статического трения между человек и стена равны _s , а радиус цилиндра стоит р.

Six Flags — Сент-Луис — называется эта поездка «Твистер Тома». На ярмарках у Midways часто есть такой, который называется «Ротор». Еще один вариант, часто называемый «Сводка новостей», тильтует жертв — я имею в виду гостей. — под углом. Смотреть на них.
(a) Покажите, что максимальный период оборота, необходимый для удержания человека от падения Т = (4 ² R _с/г) ^1/2 .

F _x = — F _n = — m v ² / R = — F _c
F _n = m v ² / R
F _у = F _f — m g = 0 = m a _y
Ф _Ф = м г
Ф _Ф = Ф _п
F _f = F _n = ( m v ² / R) = m g
( м v ² / R) = м г
v = С/Т = 2 Р/Т
v ² = 4 ² Р ² / Т ²
([4 ² R ² / T ² ] / R) = г
Т ² = 4 ² Р/г
Т = [4 ² Р/г] ^1/2
(b) Получите числовое значение fo T, если R = 4,00 м и _s = 0,4.
Т = [4 ² Р/г] ^1/2
T = [(0,4)(4 ² )(4,0 м) / (9,8 м/с ² ) ] ^1/2
Т = 2,5 с
(c) Сколько оборотов в минуту делает цилиндр?
f = 1 / T = (1 об) / (2,5 с) [60 с/мин] = 24 об/мин
f = 24 об/мин
Решения дополнительных проблем из четвертого издания Serway.
(4 изд) 6.1 Автомобиль движется с постоянной скоростью по гребню холма. Водитель движется по вертикальному кругу радиусом 18,0 м. В верхней части холме, она замечает, что едва остается в контакте с сиденьем. Найди скорость транспортного средства.

Поскольку водитель «едва соприкасается с сиденьем», нормальный сила F _n , между здесь и седлом, равна ноль . Она движется по кругу, поэтому действующая на нее чистая сила должна обеспечивать центростремительную сила и единственная сила доступная ее масса, мг.
F _c = m v ² / r
F _с = м г
м v ² / r = м г
v ² / г = г
v ² = g r = (9,8 м/с ²) (18 м) = 176.r м ² / с ²
v = 13,28 м/с
(4 изд.) 6.2 Автомобиль огибает кривую с уклоном, как показано на рис. 6.5. Радиус Кривизна дороги равна R, угол крена равен , а коэффициент статического трения равен .
(a) Определить диапазон скоростей автомобиля без буксования вверх или вниз по дороге.
(b) Найдите формулу минимального значения, при которой минимальная скорость равна нулю.
(c) Какой диапазон скоростей возможен, если R = 100 м, = 10 ^o и = 0,10 (скользкие условия)?
Во-первых, предостережение. Это очень легко — почти «автоматически» — чтобы выбрать оси X и Y таким образом,
с осью x вдоль плоскости. Но не делайте этого здесь! Центростремительный сила и ускорение будут направлены к центру окружности . И центр круга , а не , лежит вдоль этой оси x. Скорее, выберите ось x так, чтобы центр окружности лежал на ней.
Теперь с этими осями результирующая сила в направлении Y будет равна нулю, F _net,y = 0 и результирующая сила в направлении x будет центростремительная сила, F _нетто,x = — F _c = — m v ² / р
Трение всегда противостоит движению поэтому мы должны рассмотреть две возможности для силы трения. Мы должны использовать отдельные диаграммы свободного тела для два чемодана
, когда автомобиль вот-вот соскользнет «вверх» по берегу
, когда автомобиль вот-вот соскользнет «вниз» с берега
F _{нетто,у} = 0
F _n cos — m g — F _f sin = 0
F _n cos — m g — F _n sin = 0
F _n (cos — sin ) = м г
F _n = м г / (cos — sin )
F _нетто,x = — F _c = — m v ² / р
F _net,x = — F _n sin — F _f cos
m v ² / r = F _n sin + F _f cos
m v ² / r = F _n sin + F _n cos
м v ² / r = F _н (грех + косинус)
v ² = F _n (sin + cos )(r / m)
v ² = [1 / (cos — sin)] [sin+ cos] x [(r / m) (m g)]
v ² = [1/(cos-sin)][sin+ cos](rg)
v ² = [sin+ cos]/[(cos-sin)](rg)
F _{нетто,у} = 0
F _n cos + F _f sin — m g = 0
F _n cos + F _n sin — m g= 0
F _n (cos + sin ) = мг г
F _n = м г / (cos + sin )
F _нетто,x = — F _c = — m v ² / р
F _net,x = — F _n sin + F _f cos
м v ² / r = F _n sin — F _f cos
м v ² / r = F _n sin — F _n cos
м v ² / r = F _n (sin-cos)
v ² = F _n (sin — cos)(r/m)
v ² = [1 / (cos + sin)] [sin-cos] x [(r / m) (m g)]
v ² = [1/(cos-sin)][sin+ cos](rg)
v ² = [sin-cos]/[(cos+sin)](rg)
(c) Теперь, с конкретными числовыми значениями, это
v ² = {[sin 10 ^o + 0,10 cos 10 ^o ]/[cos 10 ^o — 0,10 sin 10 ^o ]}(100 м)(9,8 м/с ² )
v ² = {[0,174 + 0,10 (0,985)]/[0,985 — 0,10 (0,174)]}(100 м)(9,8 м/с ² )
v ² = {[0,174 + 0,099]/[0,985 — 0,0174]}(100 м)(90,8 м/с ² )
v ² = {[0,272]/[0,968]}(980 м ² /с ² )
v ² = 275 м ² /с ²
v = 16,6 м/с
Это максимум скорость.
(c) Теперь, с конкретными числовыми значениями, это
v ² = {[sin 10 ^o — 0,10 cos 10 ^o ]/[cos 10 ^o + 0,10 sin 10 ^o ]}(100 м)(9,8 м/с ² )
v ² = {[0,174 — 0,10 (0,985)]/[0,985 + 0,10 (0,174)]}(100 м)(9,8 м/с ² )
v ² = {[0,174 — 0,099]/[0,985 + 0,0174]}(100 м)(9,8 м/с ² )
v ² = {[0,075]/[1,002]}(980 м ² /с ² )
v ² = 73,3 м ² /с ²
v = 8,6 м/с
Это минимум скорость.
(a) Определить диапазон скоростей автомобиля без буксования вверх или вниз по дороге.
(b) Найдите минимальное значение для такое, что минимальная скорость равна нулю.
Можно положить v = 0. На самом деле проще положить v ² = 0
v ² = [sin-cos] / [(cos+sin)](rg) = 0
sin-cos = 0
sin= cos
= sin/cos
= желтовато-коричневый
(c) Какой диапазон скоростей возможен, если R = 100 м, = 10 ^o и = 0,10 (скользкие условия)?
Эти значения находятся в конце таблицы выше.
| Хмвк, ч. 5 | Домашнее задание Назначение Страница | Домашняя страница PHY 1350 Страница | Hmwk, ч. 7 |
(с) Дуг Дэвис, 2001 г.; все права защищены
Расчет скорости, необходимой для противодействия силе тяжести в петле
Если известен радиус круговой дорожки, вы можете использовать физику для расчета скорости, с которой должен двигаться объект, чтобы оставаться в контакте с дорожкой без падает, когда достигает вершины петли.
Возможно, вы смотрели по телевизору экстремальные виды спорта и задавались вопросом, как байкеры или скейтбордисты могут въезжать в петлю на трассе и переворачиваться вверх ногами, не падая на землю. Разве гравитация не должна их сбить? Как быстро они должны идти? Ответы на эти вопросы о вертикальном круговом движении лежат в центростремительной силе и силе гравитации.
Сила и скорость мяча на круговой дорожке.
Взгляните на рисунок, на котором мяч движется по круговой дорожке. Вопрос, с которым вы можете столкнуться на вводных уроках физики, звучит так: «Какая скорость необходима, чтобы мяч безопасно прошел петлю?» Важнейшая точка находится в самом верху дорожки — если мяч собирается оторваться от своей круговой дорожки, то вершина — это то место, куда он упадет. Чтобы ответить на ключевой вопрос, вы должны знать, какому критерию должен соответствовать мяч, чтобы удержаться. Спросите себя: «Какому ограничению должен соответствовать мяч?»
Чтобы двигаться по петле, на объект должна действовать результирующая сила, равная центростремительной силе, необходимой для движения по кругу заданного радиуса и скорости. В верхней части своего пути, как вы можете видеть на рисунке, мяч почти не соприкасается с дорожкой. Другие точки на трассе обеспечивают нормальную силу из-за скорости и того факта, что трасса искривлена. Если вы хотите узнать, какая минимальная скорость должна быть у объекта, чтобы оставаться на петле, вам нужно посмотреть, где объект едва касается дорожки — другими словами, на грани выпадения из своей окружности. путь.
Нормальная сила, которую гусеница прикладывает к объекту наверху, почти равна нулю. Единственная сила, удерживающая объект на его круговой траектории, — это сила тяжести, а это означает, что в вершине скорость объекта должна быть такой, чтобы центростремительная сила равнялась весу объекта, чтобы он двигался по кругу, радиус которого равен такой же, как радиус петли. Это означает, что если это сила, необходимая
, то сила тяжести в верхней части петли равна
.
F _г = м _г
А поскольку F _g должны равняться F _c , можно написать
Вы можете упростить это уравнение до следующей формы:
Масса любого объекта, такого как мотоцикл или гоночный автомобиль, который движется по круговой трассе, не учитывается в уравнении.
Квадратный корень из r раз г — это минимальная скорость, необходимая объекту в верхней части цикла, чтобы продолжать двигаться по кругу. Любой более медленный объект оторвется от дорожки в верхней части петли (он может упасть обратно в петлю, но в этой точке он не будет следовать по круговой дорожке). Для практического примера, если петля на рисунке имеет радиус 20,0 метров, с какой скоростью должен двигаться мяч в верхней части петли, чтобы оставаться в контакте с дорожкой? Просто введите цифры:
В верхней части дорожки мяч для гольфа должен двигаться со скоростью 14,0 метров в секунду, что составляет примерно 31 милю в час.
Эта статья из книги:
Физика I для чайников,
Об авторе книги:
Доктор Стивен Хольцнер написал более 40 книг по физике и программированию.