Первое правило термодинамики: Первый закон термодинамики

Содержание

Первый закон термодинамики — формула, формулировка и применение

Определение и понятие

Термодинамика — это раздел физики, который занимается взаимоотношениями между теплом и другими формами энергии. В частности, он описывает, как тепловая энергия преобразуется в другие виды и влияет на материю. Основные принципы термодинамики содержат три закона:

I закон термодинамики гласит, что тепло является формой энергии, поэтому термодинамические процессы подчиняются принципу ее сохранения. Это означает, что тепловая энергия не может быть создана или уничтожена, однако ее можно перенести из одного места в другое и преобразовать в другие виды. Изменение энергии неизолированной термодинамической системы равно разности между количеством теплоты, переданной системе, и работой, совершенной системой над внешними силами.
Второе начало термодинамики гласит, что энтропия любой замкнутой изолированной системы всегда увеличивается. Изолированные системы самопроизвольно эволюционируют в направлении теплового равновесия — состояния максимальной энтропии (мера упорядоченности) системы. Энтропия Вселенной (предельно изолированная система) только увеличивается и никогда не уменьшается. Кратко описать этот простой закон можно так: комната, если её не убирать, со временем неизменно становится более грязной и беспорядочной, даже если постоянно поддерживать ее в чистоте. Когда происходит уборка в помещении, его изолированная система уменьшается, но усилия по очистке приводят к ее увеличению за пределами комнаты, которое превышает потерянную энтропию.
Третье начало термодинамики гласит, что энтропия системы приближается к постоянному значению, когда температура снижается к абсолютному нулю. Предельно изолированная система обычно равна нулю и во всех случаях определяется только количеством различных основных состояний, которые она имеет. В частности, энтропия чистого кристаллического вещества (идеальный порядок) при абсолютной нулевой температуре равна нулю.
Это выражение верно, если идеальный кристалл имеет только одно состояние с минимальной энергией.

Эти законы не имеют особого отношения к тому, как и почему происходит теплообмен, что имеет смысл для открытий, которые были сформулированы до того, как атомная теория была полностью принята. Они имеют дело с общей суммой энергетических и тепловых переходов внутри системы и не учитывают специфическую природу теплопередачи на атомном или молекулярном уровне.

Математическое представление

Физики обычно используют единообразные условные обозначения для представления величин в I законе термодинамики. Они выглядят так:

U 1 (или Ui) — начальная внутренняя энергия в начале процесса.
U 2 (или Uf) — конечная внутренняя энергия в конце процесса.
Дельта U = U 2 — U 1 — изменение внутренней энергии (используется в тех случаях, когда особенности начальной и конечной внутренних энергий не имеют значения).
Q — тепло, передаваемое в (Q > 0) или из (Q <0) системы.
W — работа, выполненная системой (W > 0) или в системе (W <0).

Формула первого закона термодинамики выглядит следующим образом: ∆U=Q+A. Это даёт математическое представление первого закона, который оказывается очень полезным и может быть переписан несколькими способами:

Анализ термодинамического процесса в классе физики обычно включает анализ ситуации, когда одна из этих величин либо равна 0, либо контролируется разумным образом. Например, в адиабатном процессе теплообмен (Q) равен 0, в изохорном работа (W) тоже имеет значение 0.

История открытия

История термодинамики начинается с Отто фон Герике, который в 1650 году построил первый в мире вакуумный насос и продемонстрировал его действие, используя свои магдебургские полушария. Ученый был вынужден произвести такой эксперимент, чтобы опровергнуть давнее предположение Аристотеля о том, что «природа не терпит вакуума».

Вскоре после этого в 1656 году английский физик и химик Роберт Бойль узнал о конструкции Герике и по согласованию с учёным Робертом Гуком построил воздушный насос. Используя его, они заметили корреляцию между давлением, температурой и объёмом. Со временем был сформулирован закон Бойля, согласно которому давление и объём обратно пропорциональны.

Изучение тепла как отдельной формы энергии началось примерно в 1798 году, когда сэр Бенджамин Томпсон (также известный как граф Румфорд), британский военный инженер, заметил, что тепло может генерироваться пропорционально количеству проделанной работы. Эта фундаментальная концепция в итоге стала следствием I закона термодинамики.

Французский физик Сади Карно впервые сформулировал базовый принцип термодинамики в 1824 году. Его учёный использовал для определения своего теплового двигателя цикла Карно. В итоге этот принцип перешел во второй закон термодинамики немецкого физика Рудольфа Клаузиуса. Ему нередко приписывают и формулировку первого закона.

Одной из причин быстрого развития термодинамики в XIX веке была необходимость разработки эффективных паровых двигателей во время промышленной революции.

Термодинамические системы

По словам профессора физики университета штата Миссури Макки, энергию можно разделить на две части. К одной из них принадлежит поршень, движущийся и толкающий газ.

Макки объясняет: «Когда я приставляю два образца металла друг к другу, два атома сталкиваются, одна из частиц отрывается быстрее другой, я не могу удержаться от наблюдения за этим процессом. Это происходит в очень маленьком масштабе времени, на небольшом расстоянии и много раз в секунду. Итак, мы просто делим всю передачу энергии на две группы: то, что мы будем отслеживать, и то, что не будем. Последний из них называется теплом». Термодинамические системы обычно рассматриваются как открытые, закрытые или изолированные:

Открытая система, в отличие от закрытой или изолированной, свободно обменивается энергией и веществом с окружающей средой. Например, кастрюля с кипящим супом получает энергию из печи, излучает тепло из емкости и выделяет вещество в виде пара. Это открытая система.

Если поставить крышку на горшок плотно, он всё равно будет излучать тепловую энергию, но больше не станет выделять вещество в виде пара. Это закрытая система.
Если налить суп в идеально изолированный термос и закрыть крышку, не будет никакой энергии или вещества. Это изолированная система.

Однако на практике совершенно изолированные системы не могут существовать. Все системы передают энергию в окружающую среду посредством излучения независимо от того, насколько они изолированы. Суп в термосе останется горячим только в течение нескольких часов и достигнет комнатной температуры на следующий день.

В другом примере звёзды белых карликов, которые больше не производят энергию, могут быть изолированы световыми годами почти до идеального вакуума в межзвёздном пространстве, но в итоге они будут охлаждаться с нескольких десятков тысяч градусов почти до абсолютного нуля в связи с потерей энергии из-за излучения. Хотя этот процесс занимает больше времени, чем нынешний век Вселенной, его не остановить.

Применение на практике

Наиболее распространённым практическим применением I закона является тепловой двигатель. Он преобразует тепловую энергию в механическую и наоборот. Большинство таких двигателей попадает в категорию открытых систем. Их основной принцип использует взаимосвязь между теплом, объёмом и давлением рабочей жидкости, которая обычно является газом. В некоторых случаях она может подвергаться фазовым переходам от газа к жидкости и обратно во время цикла.

Если газ подвергается нагреванию, он расширяется, но когда он ограничен, давление увеличивается.

Если нижняя стенка удерживающей камеры является верхом подвижного поршня, то давление оказывает силу на поверхность, заставляя его двигаться вниз. Это движение затем можно использовать для выполнения работы, равной суммарному усилию, приложенному к верхней части поршня, умноженному на расстояние, на которое он перемещается.

Существуют многочисленные вариации основного теплового двигателя. Например, паровые двигатели полагаются на внешнее сгорание, чтобы нагреть бак котла, содержащий рабочую жидкость, обычно воду. Она превращается в пар, а затем давление используется для привода поршня, который преобразует тепловую энергию в механическую. Однако в автомобильных двигателях используется внутреннее сгорание, когда жидкое топливо испаряется, смешивается с воздухом и воспламеняется внутри цилиндра над подвижным поршнем, приводящим его в движение вниз.

Холодильники и тепловые насосы — это двигатели, которые преобразуют механическую энергию в тепло. Большинство из них попадает в категорию закрытых систем. Когда газ сжимается, его температура увеличивается. Он может затем передавать тепло в окружающую среду. Затем, когда сжатому газу позволяют расширяться, его температура становится ниже, чем была до сжатия, потому что часть его тепловой энергии оказалась удалена во время горячего цикла. Холодный газ может затем поглощать тепловую энергию из окружающей среды. Это принцип работы кондиционера.

Кондиционеры на самом деле не производят холод, они удаляют тепло. Рабочая жидкость переносится наружу механическим насосом, где нагревается компрессией. После этого он передаёт это тепло наружной среде через теплообменник с воздушным охлаждением. Затем он возвращается в помещение, где ему разрешается расширяться и охлаждаться, чтобы он мог поглощать тепло из воздуха через другой теплообменник.

Тепловой насос — это просто кондиционер, работающий в обратном направлении. Тепло от сжатой рабочей жидкости используется для обогрева здания. После этого он переносится наружу, где расширяется и становится холодным, что позволяет ему поглощать тепло из наружного воздуха, который даже зимой обычно теплее, чем холодная рабочая жидкость.

В геотермальных или наземных системах кондиционирования воздуха и тепловых насосах используются длинные U-образные трубки в глубоких скважинах или набор горизонтальных труб, погруженных в большую площадь, по которой циркулирует рабочая жидкость, а тепло передаётся на землю или из нее. Другие системы используют реки или океаническую воду для нагрева или охлаждения рабочей жидкости.

Основные изопроцессы

Поскольку тепловые двигатели могут пройти сложную последовательность шагов, упрощённая модель часто используется для иллюстрации принципов термодинамики. В частности, можно рассмотреть газ, который расширяется и сжимается в цилиндре с подвижным поршнем при заданном наборе условий. Применение первого закона термодинамики к изопроцессам содержит два таких набора:

Одно условие, известное как изотермическое расширение, включает в себя поддержание постоянной температуры газа. Поскольку он работает против сдерживающей силы поршня, то должен поглощать тепло для сохранения энергии. В противном случае он будет охлаждаться при расширении или, наоборот, нагреваться при сжатии. Это пример, в котором поглощённое тепло полностью превращается в работу со стопроцентной эффективностью. Однако этот процесс не нарушает фундаментальных ограничений по эффективности, поскольку само по себе расширение не является циклическим процессом.
Второе условие, известное как адиабатическое расширение (от греческого «адиабатос», что означает «непроходимый»), — это состояние, при котором предполагается, что цилиндр идеально изолирован, так что тепло не может течь внутрь него или наружу. При применении первого начала термодинамики для адиабатического процесса газ охлаждается при расширении, потому что работа, выполняемая против сдерживающей силы на поршне, может исходить только от внутренней энергии газа. Таким образом, изменение этого показателя должно быть ΔU = -W, о чём свидетельствует снижение его температуры. 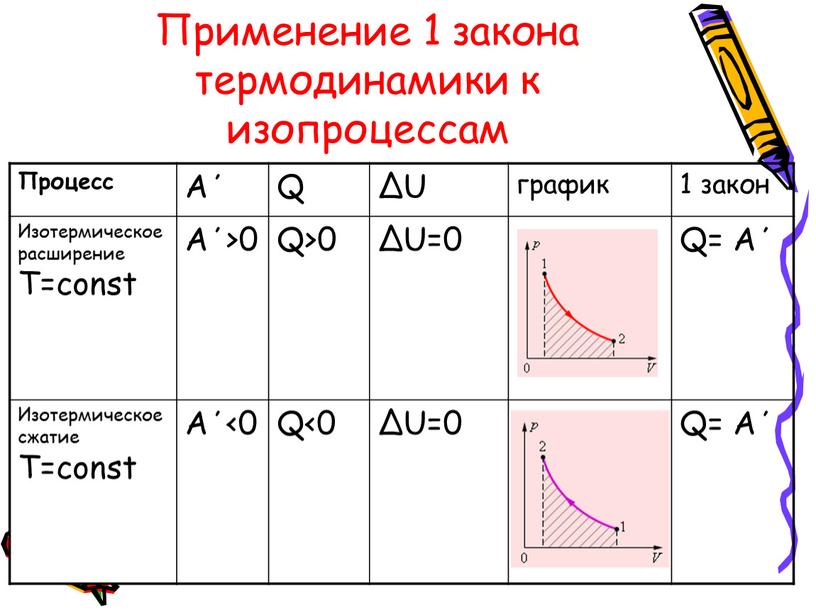Газ остывает, хотя теплового потока нет, потому что он работает за счёт собственной внутренней энергии. Точное количество охлаждения можно рассчитать по теплопроводности газа.

Многие природные явления адиабатны, потому что времени для значительного теплового потока недостаточно. Например, когда тёплый воздух поднимается в атмосферу, он расширяется и охлаждается по мере того, как давление падает при наборе высоты. Но он является хорошим теплоизолятором, поэтому нет значительного теплового потока от него. В этом случае окружающий воздух играет роль стенок изолированного цилиндра и подвижного поршня.

Тёплый воздух работает против давления, создаваемого окружающим воздухом при его расширении, поэтому его температура должна падать. Более подробный анализ этого адиабатического расширения объясняет бо́льшую часть понижения температуры с высотой, учитывая известный факт, что на вершине горы холоднее, чем у её основания.

Тепло, подаваемое при постоянном давлении, также известно как изобарный процесс.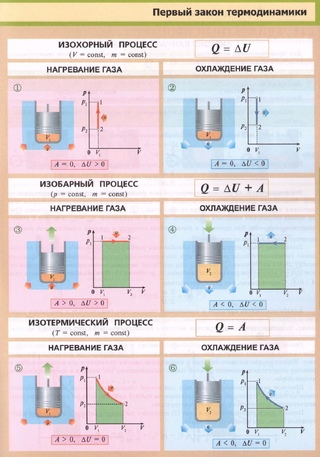 При нем не происходит изменения давления во время подачи тепла в систему.

Первое начало термодинамики рассматривается многими как основа концепции сохранения энергии. В основном это говорит о том, что энергия, которая поступает в систему, не может быть потеряна по пути, но должна быть использована для того, чтобы изменить внутреннюю энергию, либо выполнить работу. С этой точки зрения он является одним из самых обширных научных понятий, когда-либо обнаруженных.

Первое начало термодинамики 🐲 СПАДИЛО.РУ

Первое начало термодинамики (первый закон термодинамики) представляет собой закон сохранения энергии в тепловых процессах.

Первое начало термодинамики

Внутренняя энергия идеального газа изменяется двумя способами: за счет теплопередачи или при совершении работы.

±ΔU=±Q±A‘

Пояснение:

+∆U — внутренняя энергия газа увеличивается.
–∆U — внутренняя энергия газа уменьшается.
+Q — газ нагревают (газу передают количество теплоты).
–Q — газ охлаждается (газ отдает тепло окружающей среде).
+A’ — газ сжимает внешняя сила.
–A’ — газ расширяется, совершая работу.

Внимание! Знак перед работой показывает, как процесс совершения работы влияет на изменение внутренней энергии газа.

Пример №1. В некотором процессе внутренняя энергия газа уменьшилась на 300 Дж, а газ совершил работу 500 Дж. Какое количество теплоты было сообщено газу?

Чтобы рассчитать количество теплоты, сообщенное газу, нужно найти разность между изменением внутренней энергии и работой, совершенным газом. Для этого нужно правильно определить их знаки. Так как внутренняя энергия уменьшилась, она отрицательна. Но работа положительна. Поэтому газу было сообщено следующее количество теплоты:

Q = A – U = 500 – 300 = 200 (Дж)

Зависимость физических величин

Выясним, от чего зависят величины, входящие в формулу первого начала термодинамики. Изменение внутренней энергии идеального газа зависит от изменения температуры:

ΔU=32..νRΔT

Работа идеального газа зависит от изменения его объема:

A‘=pΔV

Первое начало термодинамики для изопроцессов

Изотермический процесс (T = const)	ΔU=0, Q=A‘
Изохорный процесс (V = const)	A‘=0, ΔU=Q
Изобарное расширение газа (p = const)	ΔU=Q−pΔV ΔU=Q−νRΔT
Адиабатный (система не получает тепло извне и не отдает его окружающей среде, или Q = 0)	Q=0, ΔU=A‘

Пример №2. Идеальный одноатомный газ находится в сосуде с жесткими стенками объемом 0,6 куб. м. При нагревании его внутренняя энергия увеличилась на 18 кДж. На сколько возросло давление газа?

18 кДж = 18000 Дж

Внутреннюю энергию газа можно определить по формуле:

ΔU=32..νRΔT

Отсюда изменение температуры равно:

ΔT=2ΔU3νR. .

Уравнение состояния идеального газа для 1 и 2 состояния:

p1V=νRT1

p2V=νRT2

Отсюда давления равны:

p1=νRT1V..

p2=νRT2V..

Разность давлений:

p2−p1=νRT2V..−νRT1V..=νRV..ΔT=νRV..·2ΔU3νR..=2ΔU3V..

p2−p1=2·180003·0,6..=20000 (Па)=20 (

Первый и второй законы термодинамики — Студопедия

Первый закон термодинамики является частным случаем закона сохранения и превращения энергии. Этот закон утверждает, что энергия не исчезает и не возникает вновь, а лишь переходит из одного вида в другой в различных процессах. Значит, если телу сообщить количество теплоты Q, то оно израсходуется на изменение внутренней энергии тела ?U и на совершение внешней работы L:

Это соотношение представляет собой аналитическое выражение первого закона термодинамики для неподвижных тел.

В дифференциальной форме этот закон можно записать:

, или , или . (1)

Если в уравнение (1) подставить (связь между механической и технической работой), то получим:

Выражение (u+pv) является калориметрическим параметром состояния тела. В технической термодинамике этот параметр называют энтальпией и обозначают буквой Н и измеряют в Дж, удельную энтальпию обозначают h и измеряют в Дж/кг, то есть

Энтальпия – это сумма внутренней энергии и упругостной энергии газа (потенциальной энергии давления).

Следовательно, первый закон термодинамики может быть записан так:

В изобарном процессе (р = const) vdp = 0, следовательно .

Для идеальных газов справедливы соотношения:

и .

Тогда .

Второй закон термодинамики связан с необратимостью всех естественных процессов и является опытным законом, основывающимся на многовековых наблюдениях ученых, однако установлен он был только в середине XIX века. Являясь статическим законом, второй закон термодинамики отражает поведение большого числа частиц, входящих в состав изолированной системы. В системах, состоящих из малого количества частиц, могут иметься отклонения от второго закона термодинамики.

Самым вероятным состоянием изолированной термодинамической системы является состояние ее внутреннего равновесия, которому соответствует достижение максимального значения энтропии. Поэтому второй закон называют законом возрастания энтропии. В этой связи его можно сформулировать в виде следующего принципа: энтропия изолированной системы не может убывать.

Энтропия – это параметр состояния рабочего тела, устанавливающий связь между количеством теплоты и температурой. Для ее определения запишем уравнение первого закона термодинамики в таком виде

Разделим данное выражение на Т, а р заменим на , получим:

или .

Выражение говорит о том, что является полным дифференциалом некоторой функции s, являющейся параметром состояния, поскольку она зависит только от двух параметров состояния газа и не зависит от того, каким путем газ перешел из одного состояния в другое. Энтропию обозначают буквой S и измеряют в Дж/К. Энтропию, отнесенную к 1 кг газа, называют удельной энтропией и обозначают буквой s и измеряют в кДж/(К?кг).

Таким образом, .

Второй закон термодинамики представляет собой обобщение изложенных положений и постулатов, применительных к тепловым двигателям и заключается в следующем:

1. Самопроизвольное протекание естественных процессов возникает и развивается при отсутствии равновесия между участвующей в процессе термодинамической системой и окружающей средой.

2. Самопроизвольно происходящие в природе естественные процессы, работа которых может быть использована человеком, всегда протекает лишь в одном направлении от более высокого потенциала к более низкому.

3. Ход самопроизвольно протекающих процессов происходит в направлении, приводящем к установлению равновесия термодинамической системы с окружающей средой, и по достижении этого равновесия процессы прекращаются.

4. Процесс может протекать в направлении, обратном самопроизвольному процессу, если энергия для этого заимствуется из внешней среды.

Все эти формулировки, различающиеся по форме, эквивалентны друг другу по существу, так как они напрямую связаны с принципом невозможности убывания энтропии: .

Законы термодинамики

Энергия и ее перевоплощения всегда была одним из самых интересных вопросов, который заботил научный мир. Одновременно с раскрытием закона о сохранении энергии появился и бесконечный интерес к исследованиям в области термодинамики, а также законы термодинамики. Само понятие термодинамика представляет собой теорию тепловых процессов в количественной интерпретации. Несмотря на то, что термодинамика рассматривается как часть молекулярной физики, она рассматривает процессы в большом масштабе, на уровне макроскопических явлений. Исследование процессов на гранях различных масштабов позволяет лучше понимать и объяснять различные процессы, поэтому различные методы имеют места быть.

Основное понятие для изучения в термодинамике это энергия, основные процессы – ее превращение и способы передачи. Большая часть процессов происходит с выделением тепла и, исходя из этого появляется еще один параметр, которого нужно учитывать и носит он название температура. Современная наука термодинамика основана на постулатах, которые появились долгое время тому назад и были подтверждены, так как временем, так и заявлениями различных ученых. Различные законы термодинамики были озвучены известными физиками в конкретных формулировках. Те заявления, которые были достаточно изучены и подтверждены различными заявлениями и стали законами термодинамики.

Всего существует три закона термодинамики, некоторые из них известны в несколько интерпретациях. Понятие закон означает, что явление происходит с определенной регулярностью и без существенных изменений условий. Термодинамические наблюдения можно применять в отношении любого вещества в любом состоянии. Правда обобщенность больше мешает, когда не известны свойства конкретного вещества, так как от его свойств будут зависеть определенные параметры. Это единственный серьезный минус метода термодинамики в изучении отдельных процессов. Недостаток проявляется тем, что приходится тратить больше времени на изучение всей информации о веществе.

Законы термодинамики: первый, второй и третий закон термодинамики

Первый закон термодинамики сформулировал М.В. Ломоносов: Энергия не исчезает и не теряется в никуда, она всего лишь переходит из одного состояния в другое. (Закон известен также как «закон сохранения энергии»).

Второй закон термодинамики известен в несколько интерпретациях: Больцмана, Клаузиуса, Томсона и Кельвина. Первая формулировка принадлежит Клаузиусу, поэтому именно ее необходимо озвучить в первую очередь: Любое холодное тело не способно передавать тепло другому телу с более высокой температурой.

Томсон заявил: «Никакой процесс не может считаться возможным, если для его исполнения требуется тепло другого тела».

Согласно Больцману: «Энергия может превратиться в энное количество тепла, но только в одно направление, так как в обратное направление речь уже только о частичной трансформации».

Кельвин считал что: «Невозможны те процессы, которые должны повторяться и происходить с учетом использования тепла от конкретного тела. Не реально создать тепловой двигатель на основе принципа использования тепла постороннего тела.»

Третий закон термодинамики известен также как теорема Нернста, ссылается на то же состояние энтропии, о которой упоминал Больцман при формулировке второго закона термодинамики. «Состояние энтропии будет стремиться к пределу в том случае, когда изменения температуры в системе направлены к нулю. Это происходит, потому что энтропия перестает зависеть от любых других параметров состояния. »

Законы термодинамики и их практическое применение

Термодинамика играет особую роль в различных областях науки и повседневной жизни. Ее закономерности и правила применяются для решения задач в области теплотехники, энергетики, космических исследований, биологии, машиностроении и много других областей. Гораздо проще свершать какие-то новые открытия, когда уже есть общеизвестные и неоспоримые факты. Великие открытия в прошлом всегда продолжают решать задачи человечества, несмотря на наступающий прогресс, потому что он не был бы возможным без всех тех свершений в прошлом.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Первое начало термодинамики — Википедия

Пе́рвое нача́ло термодина́мики (первый закон термодинамики) — один из основных законов этой дисциплины, представляющий собой конкретизацию общефизического закона сохранения энергии для термодинамических систем, в которых необходимо учитывать термические, массообменные и химические процессы^[1]^[2]^[3]. В форме закона сохранения (уравнения баланса энергии) первое начало используют в термодинамике потока и в неравновесной термодинамике. В равновесной термодинамике под первым законом термодинамики обычно подразумевают одно из следствий закона сохранения энергии, из чего проистекает отсутствие единообразия формулировок первого начала, используемых в учебной и научной литературе (К. А. Путилов в своей монографии^[4] приводит шесть формулировок, которые он считает наиболее удачными).

Историческая справка

Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера, распространившего закон сохранения механической энергии сначала на термические (1842), а затем (1845) и на все немеханические явления, английского физика Дж. П. Джоуля (1843), экспериментально обосновавшего новый закон, и немецкого физика Г. Гельмгольца (1847), который — не зная о работах Майера — распространил закон сохранения энергии на все её виды и сыграл решающую роль в том, что этот закон стал общепризнанным^[5].

Особенности различных формулировок первого начала термодинамики

Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя (перпетуум мобиле) первого рода, который совершал бы работу, не черпая энергию из какого-либо источника^[1]^[2]^[3]. Связь этого утверждения с законом сохранения энергии самоочевидна.

Для феноменологической термодинамики важны те формулировки первого начала, которые вводят в физику представление о внутренней энергии^[2] как об аддитивной величине^[6]^[7], являющейся однозначной, непрерывной и конечной скалярной функцией состояния термодинамической системы^[8]. Как и для любой другой функции состояния, изменение внутренней энергии U{\displaystyle U} в бесконечно малом процессе есть полный дифференциал dU{\displaystyle dU}, а изменение внутренней энергии в круговом процессе равно нулю^[9]^[10]^[11]^[12]:

ΔU=∮⁡dU=0.

{\displaystyle \Delta U=\oint dU=0.}

Математическое выражение, служащее дефиницией внутренней энергии, зависит от выбора термодинамических величин, используемых в качестве независимых переменных теории. Традиционно внутреннюю энергию выражают с использованием в качестве фундаментальных понятий, которым термодинамика даёт описание без дефиниций, теплоту и термодинамическую работу^[1]^[3] (заимствуя понятие работы из других разделов физики^[13]^[14]). Согласно Г. Кирхгофу сумма количества теплоты q{\displaystyle q} и работы w{\displaystyle w} для бесконечно малого^[15]равновесного процесса^[16] в закрытой системе (при использовании термодинамического правила знаков для теплоты и работы) равна изменению внутренней энергии системы в данном процессе dU{\displaystyle dU}^[17]^[18]^[19]^[20]^[21]:

dU≡q+w.{\displaystyle dU\equiv q+w.

}

(Дефиниция внутренней энергии по Кирхгофу)

Первое начало термодинамики в формулировке Кирхгофа утверждает, что существует функция состояния U{\displaystyle U}, называемая внутренней энергией и представляющая собой часть полной энергии системы, изменение которой в любом процессе в закрытой системе равно сумме работы и теплоты; каждое состояние термодинамической системы характеризуется определённым значением U{\displaystyle U}, независимо от того, каким путём система приведена в данное состояние^[1]^[2]^[3]; dU{\displaystyle dU} есть полный дифференциал внутренней энергии U{\displaystyle U}^[2] (величины q{\displaystyle q} и w{\displaystyle w} в общем случае есть функционалы пути, по которому совершается процесс^[22]^[23], численные значения которых различны для различных способов проведения процесса при одинаковом исходном и конечном состояниях системы, иначе говоря, зависят от пути процесса^[1]^[2]^[24]). Из первого начала в формулировке Кирхгофа вытекает, что те составные части полной энергии системы, которые не изменяются в рассматриваем процессе, во внутреннюю энергию системы не входят и, следовательно, внутренняя энергия есть изменяемая часть полной энергии системы.

Для функции состояния естественен вопрос о её аргументах. Из дефиниции Кирхгофа следует, что внутренняя энергия зависит от переменных, входящих в выражение для работы, то есть обобщённых термодинамических координат, и температуры как движущей силы теплопередачи.

Традиционно теплоту и работу трактуют как формы передачи энергии, то есть их характеризуют посредством описательных дефиниций. Именно по этой причине как математические объекты теплота и работа в дефиницию внутренней энергии по Кирхгофу входят в виде неопределяемых переменных. Давать дефиницию фундаментальной физической величине — энергии — посредством величин менее фундаментальных — теплоты и работы — есть методологический недостаток подхода Кирхгофа. Наконец, в формулировке Кирхгофа внутренняя энергия как функция состояния привязана к функциям процесса — теплоте и работе. Фактически это означает привязку внутренней энергии к равновесным процессам в закрытых системах, когда возможна однозначная трактовка понятий теплоты и работы.

Важно, что ни масса системы, ни массы (количества) составляющих систему веществ не относятся к обобщённым термодинамическим координатам, а поэтому в традиционном подходе к обоснованию термодинамики массы (количества) веществ не входят в перечень переменных, от которых зависит внутренняя энергия (или, что то же самое, масса является адиабатно заторможенной величиной^[25]). Из аддитивности внутренней энергии вытекает, однако, что для флюидов (газов и жидкостей) внутренняя энергия обладает свойством экстенсивности, то есть внутренняя энергия однородной системы пропорциональна массе этой системы. Если же учесть, что масса системы равна сумме масс составляющих систему веществ, то становится понятным, что, во-первых, массы (количества) веществ могут входить в формулы термодинамики закрытых систем, и что, во-вторых, в эти формулы (например, в выражения для удельной теплоёмкости и других удельных величин) массы (количества) веществ входят не как переменные состояния, а в качестве числовых параметров, детализирующих характеристики конкретных систем. Из сказанного следует, что термодинамическое описание открытых систем постоянного состава ничем не отличается от описания свойств закрытых систем^[26].

Для открытых систем переменного состава, с которыми имеют дело в химической термодинамике, первое начало формулируют в виде аксиомы о существовании внутренней энергии как функции состояния, в перечень постулируемых свойств которой входит её функциональная зависимость от масс составляющих систему веществ^[27]^[24]^[28]^[29]. Так, К. Каратеодори (1909) выразил первое начало термодинамики в форме утверждения о существовании внутренней энергии — составной части полной энергии системы — как функции состояния, зависящей для простых систем^[30] от объёма V{\displaystyle V}, давления P{\displaystyle P}, масс составляющих систему веществ m1,m2,…,mi,…{\displaystyle m_{1},m_{2},…,m_{i},…}^[31]

U=U(P,V,{mi}){\displaystyle U=U\left(P,V,\left\{m_{i}\right\}\right)}

(Первое начало в формулировке Каратеодори)

(выражение {mi}{\displaystyle \{m_{i}\}} есть сокращение для перечисления m1,m2,. ..,mi,…{\displaystyle m_{1},m_{2},…,m_{i},…}) и обладающей следующими свойствами:

для бесконечно малого адиабатного процесса изменение внутренней энергии равно работе процесса

dU=w;{\displaystyle dU=w;}

(Изменение внутренней энергии в адиабатном процессе)

количество теплоты для бесконечно малого равновесного процесса в закрытой системе согласно Клаузиусу полагают (при использовании термодинамического правила знаков для теплоты и работы) равным разности между изменением внутренней энергии системы в данном процессе и работой процесса^[32]^[33]:

q≡dU−w.{\displaystyle q\equiv dU-w.}

(Дефиниция теплоты по Клаузиусу — Каратеодори — Борну)

В формулировке Каратеодори внутренняя энергия не представляет собой характеристическую функцию своих независимых переменных.

В случае открытых систем переменного состава изменение внутренней энергии вследствие изменения масс составляющих систему веществ несводимо ни к теплоте, ни к работе^[27], поэтому «…для открытой системы являются беспредметными как классическая точка зрения (эквивалентность теплоты и работы), так и точка зрения Каратеодори (определение теплоты)»^[25]. Формальное распространение дефиниции Кирхгофа на внутреннюю энергию открытых систем переменного состава выполняют, добавляя в выражение для дефиниции внутренней энергии ещё одно слагаемое — энергию перераспределения масс составляющих систему веществ (химическую работу^[34]) z{\displaystyle z}^[1]^[24]^[35]:

dU≡q+w+z,{\displaystyle dU\equiv q+w+z,}

однако ни практического, ни теоретического значения это выражение не имеет. Дело в том, что однозначности разделения изменения внутренней энергии на теплоту и работу в традиционном подходе к термодинамике достигают, заимствуя понятие работы из других разделов физики и используя представление об адиабатной изоляции для трактовки теплоты как энергии, передаваемая без совершения работы и без изменения масс составляющих систему веществ^[36] (поскольку любая адиабатная оболочка/перегородка непроницаема для вещества). Это означает, что работа и теплота представляют собой независимо измеряемые величины^[1]^[3], тогда как способы независимого измерения химической работы отсутствуют в традиционном подходе к построению термодинамики.

Дж. У. Гиббс в своей работе «О равновесии гетерогенных веществ» (1875—1878)^[37] строит термодинамику простых открытых систем, рассматривая внутреннюю энергию как функцию энтропии S{\displaystyle S}, объёма V{\displaystyle V} и масс составляющих систему веществ m1,m2,…,mi,…{\displaystyle m_{1},m_{2},…,m_{i},…}:

U=U(S,V,{mi}).{\displaystyle U=U\left(S,V,\left\{m_{i}\right\}\right).}

(Первое начало в формулировке Гиббса)

Распространяя термодинамику Гиббса на сложные системы^[38], внутреннюю энергию полагают функцией энтропии S{\displaystyle S}, обобщённых координат x1,x2,…,xi,…{\displaystyle x_{1},x_{2},…,x_{i},…} и масс составляющих систему веществ^[39]^[40]:

U=U(S,{xi},{mi}).{\displaystyle U=U\left(S,\left\{x_{i}\right\},\left\{m_{i}\right\}\right).}

(Фундаментальное уравнение Гиббса в энергетическом выражении)

В неравновесной термодинамике выражение для первого начала термодинамики выглядит так (см. {e}} — поток энергии.

Правила знаков для теплоты и работы

В научной и учебной литературе можно встретить варианты математического выражения для первого начала термодинамики, отличающиеся знаками (+{\displaystyle +} или

2. Первое начало термодинамики

Первое начало термодинамики — один из трех основных законов термодинамики, представляющий собой закон сохранения энергии для систем, в которых существенное значение имеют тепловые процессы.

Согласно первому началу термодинамики, термодинамическая система (например, пар в тепловой машине) может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии.

Первое начало термодинамики объясняет невозможность существования вечного двигателя 1-го рода, который совершал бы работу, не черпая энергию из какого-либо источника.

Сущность первого начала термодинамики заключается в следующем:

При сообщении термодинамической системе некоторого количества теплоты Q в общем случае происходит изменение внутренней энергиисистемы DU и система совершает работу А:

Q = DU + A (4)

Уравнение (4), выражающее первое начало термодинамики, является определением изменения внутренней энергии системы (DU), так как Q и А — независимо измеряемые величины.

Внутреннюю энергию системы U можно, в частности, найти, измеряя работу системы в адиабатном процессе (то есть при Q = 0): А_ад = — DU, что определяет U с точностью до некоторой аддитивной постоянной U₀:

U = U + U₀(5)

Первое начало термодинамики утверждает, что U является функцией состояния системы, то есть каждое состояние термодинамической системы характеризуется определённым значением U, независимо от того, каким путём система приведена в данное состояние (в то время как значения Q и А зависят от процесса, приведшего к изменению состояния системы). При исследовании термодинамических свойств физической систем первое начало термодинамики обычно применяется совместно со вторым началом термодинамики.

3. Второе начало термодинамики

Второе начало термодинамики является законом, в соответствии с которым макроскопические процессы, протекающие с конечной скоростью, необратимы.

В отличие от идеальных (без потерь) механических или электродинамических обратимых процессов, реальные процессы, связанные с теплообменом при конечной разности температур (т. е. текущие с конечной скоростью), сопровождаются разнообразными потерями: на трение, диффузию газов, расширением газов в пустоту, выделением джоулевой теплоты и т.д.

Поэтому эти процессы необратимы, то есть могут самопроизвольно протекать только в одном направлении.

Второе начало термодинамики возникло исторически при анализе работы тепловых машин.

Само название «Второе начало термодинамики» и первая его формулировка (1850 г. ) принадлежат Р. Клаузиусу: «…невозможен процесс, при котором теплота переходила бы самопроизвольно от тел более холодных к телам более нагретым».

Причем такой процесс невозможен в принципе: ни путем прямого перехода теплоты от более холодных тел к более теплым, ни с помощью каких–либо устройств без использования каких-либо других процессов.

В 1851 году английский физик У. Томсон дал другую формулировку второго начала термодинамики: «В природе невозможны процессы, единственным следствием которых был бы подъем груза, произведенный за счет охлаждения теплового резервуара».

Как видно, обе приведённые формулировки второго начала термодинамики практически одинаковы.

Отсюда следует невозможность реализации двигателя 2-го рода, т.е. двигателя без потерь энергии на трение и другие сопутствующие потери.

Кроме того, отсюда следует, что все реальные процессы, происходящие в материальном мире в открытых системах, необратимы.

В современной термодинамике второе начало термодинамики изолированных систем формулируется единым и самым общим образом как закон возрастания особой функции состояния системы, которую Клаузиус назвал энтропией (S).

Физический смысл энтропии состоит в том, что в случае, когда материальная система находится в полном термодинамическом равновесии, элементарные частицы, из которых состоит эта система, находятся в неуправляемом состоянии и совершают различные случайные хаотические движения. В принципе можно определить общее число этих всевозможных состояний. Параметр, который характеризует общее число этих состояний, и есть энтропия.

Рассмотрим это на простом примере.

Пусть изолированная система состоит из двух тел «1» и «2», обладающих неодинаковой температурой T₁>T₂. Тело «1» отдает некоторое количество тепла Q , а тело «2» его получает. При этом идет тепловой поток от тела «1» к телу «2». По мере уравнивания температур увеличивается суммарное количество элементарных частиц тел «1» и «2», находящихся в тепловом равновесии. По мере увеличения этого количества частиц увеличивается и энтропия. И как только наступит полное тепловое равновесие тел «1» и «2», энтропия достигнет своего максимального значения.

Таким образом, в замкнутой системе энтропия S при любом реальном процессе либо возрастает, либо остаётся неизменной, т. е. изменение энтропии dS ³ 0. Знак равенства в этой формуле имеет место только для обратимых процессов. В состоянии равновесия, когда энтропия замкнутой системы достигает максимума, никакие макроскопические процессы в такой системе, согласно второму началу термодинамики, невозможны.

Отсюда следует, что энтропия — физическая величина, количественно характеризующая особенности молекулярного строения системы, от которых зависят энергетические преобразования в ней.

Связь энтропии с молекулярным строением системы первым объяснил Л. Больцман в 1887 году. Он установил статистический смысл энтропии (формула 1.6). Согласно Больцману (высокая упорядоченность имеет относительно низкую вероятность)

S = k lnP, (6)

где k — постоянная Больцмана, P – статистический вес.

k = 1.37·10^-23Дж/К.

Статистический вес Р пропорционален числу возможных микроскопических состояний элементов макроскопической системы (например, различных распределений значений координат и импульсов молекул газа, отвечающих определённому значению энергии, давления и других термодинамических параметров газа), т. е. характеризует возможное несоответствие микроскопического описания макросостояния.

Для изолированной системы термодинамическая вероятность W данного макросостояния пропорциональна его статистическому весу и определяется энтропией системы:

W = exp (S/k). (7)

Таким образом, закон возрастания энтропии имеет статистически-вероятностный характер и выражает постоянную тенденцию системы к переходу в более вероятное состояние. Отсюда следует, что наиболее вероятным состоянием, достижимым для системы, является такое, в котором события, происходящие в системе одновременно, статистически взаимно компенсируются.

Максимально вероятным состоянием макросистемы является состояние равновесия, которого она может в принципе достичь за достаточно большой промежуток времени.

Как было указано выше, энтропия является величиной аддитивной, то есть она пропорциональна числу частиц в системе. Поэтому для систем с большим числом частиц даже самое ничтожное относительное изменение энтропии, приходящейся на одну частицу, существенно меняет её абсолютную величину; изменение же энтропии, стоящей в показателе экспоненты в уравнении (7), приводит к изменению вероятности данного макросостояния W в огромное число раз.

Именно этот факт является причиной того, что для системы с большим числом частиц следствия второго начала термодинамики практически имеют не вероятностный, а достоверный характер. Крайне маловероятные процессы, сопровождающиеся сколько-нибудь заметным уменьшением энтропии, требуют столь огромных времён ожидания, что их реализация является практически невозможной. В то же время малые части системы, содержащие небольшое число частиц, испытывают непрерывные флуктуации, сопровождающиеся лишь небольшим абсолютным изменением энтропии. Средние значения частоты и размеров этих флуктуаций являются таким же достоверным следствием статистической термодинамики, как и само второе начало термодинамики.

Буквальное применение второго начала термодинамики к Вселенной как целому, приведшее Клаузиуса к неправильному выводу о неизбежности «тепловой смерти Вселенной», является неправомерным, так как в природе в принципе не может существовать абсолютно изолированных систем. Как будет показано далее, в разделе неравновесной термодинамики, процессы, протекающие в открытых системах, подчиняются другим законам и имеют другие свойства.

Первый закон термодинамики

18.2 Первый закон термодинамики

Цель обучения

Для расчета изменения внутренней энергии.

Связь между изменением энергии системы и ее окружением определяется первым законом термодинамики. Энергия Вселенной постоянна: ΔEuniverse = ΔEsystem + ΔEsurroundings = 0., что означает, что энергия Вселенной постоянна. .Используя уравнение 18.1, мы можем выразить этот закон математически следующим образом:

Уравнение 18.6

ΔEuniv = ΔEsys + ΔEsurr = 0ΔEsys = −ΔEsurr

, где индексы univ , sys и surr относятся к вселенной, системе и окружению соответственно. Таким образом, изменение энергии системы идентично по величине, но противоположно по знаку изменению энергии ее окружения.

Важным фактором, определяющим исход химической реакции, является тенденция всех систем, химических или иных, двигаться к самому низкому возможному общему энергетическому состоянию.Когда кирпич падает с крыши, его потенциальная энергия преобразуется в кинетическую энергию; когда он достигает уровня земли, он достигает состояния с более низкой потенциальной энергией. Любой, кто находится поблизости, заметит, что энергия передается в окружающую среду, поскольку шум от удара отражается, и пыль поднимается, когда кирпич падает на землю. Точно так же, если искра воспламеняет смесь изооктана и кислорода в двигателе внутреннего сгорания, диоксид углерода и вода образуются спонтанно, в то время как потенциальная энергия (в виде относительного положения атомов в молекулах) выделяется в окружающую среду в виде тепла и Работа.Содержание внутренней энергии смеси продуктов CO ₂ / H ₂ O меньше, чем у смеси реагентов изооктан / O ₂. Однако эти два случая различаются по форме передачи энергии в окружающую среду. В случае падающего кирпича энергия передается в виде работы, совершаемой над всем, что оказывается на пути кирпича; в случае сжигания изооктана энергия может выделяться исключительно в виде тепла (если реакция осуществляется в открытом контейнере) или в виде смеси тепла и работы (если реакция осуществляется в цилиндре двигателя внутреннего сгорания. ).Поскольку тепло и работа — единственные два способа передачи энергии между системой и ее окружением, любое изменение внутренней энергии системы представляет собой сумму переданного тепла ( q ) и проделанной работы ( w ):

Уравнение 18.7

Δ E _sys = q + w

Хотя q и w сами по себе не являются функциями состояния, их сумма (Δ E _sys) не зависит от пройденного пути и, следовательно, является функцией состояния.Основная задача разработчиков любой машины, которая преобразует энергию в работу, состоит в том, чтобы максимально увеличить объем выполняемой работы и минимизировать количество энергии, выделяемой в окружающую среду в виде тепла. Примером может служить сжигание угля для производства электроэнергии. Хотя максимальное количество энергии, доступной для процесса, фиксируется содержанием энергии в реагентах и продуктах, доля

Термодинамика | Физика для идиотов

Есть четыре закона термодинамики, и они являются одними из самых важных законов во всей физике.Законы следующие

Нулевой закон термодинамики — Если две термодинамические системы каждая находится в тепловом равновесии с третьей, то они находятся в тепловом равновесии друг с другом.
Первый закон термодинамики — Энергия не может быть ни создана, ни разрушена. Он может менять только формы. В любом процессе общая энергия Вселенной остается неизменной. Для термодинамического цикла чистое тепло, подводимое к системе, равно чистой работе, выполненной системой.
Второй закон термодинамики — энтропия изолированной системы, не находящейся в равновесии, будет иметь тенденцию увеличиваться со временем, приближаясь к максимальному значению в состоянии равновесия.
Третий закон термодинамики — Когда температура приближается к абсолютному нулю, энтропия системы приближается к постоянному минимуму.

Прежде чем я рассмотрю эти законы более подробно, будет проще, если я сначала расскажу об энтропии.

Энтропия — очень важная вещь в области термодинамики. Это основная идея второго и третьего законов, которая проявляется повсюду. По сути, энтропия — это мера беспорядка и случайности в системе. Вот 2 примера

Допустим, у вас есть контейнер с молекулами газа.Если все молекулы находятся в одном углу, это будет состояние с низкой энтропией (высокоорганизованное). По мере того, как частица перемещается и заполняет остальную часть контейнера, энтропия (беспорядок) увеличивается.
Если у вас есть мяч, летящий по воздуху, он начнет движение с организованной энергией, то есть кинетической энергией движения. Однако, когда он движется по воздуху, часть кинетической энергии распределяется между частицами воздуха, поэтому общая энтропия системы увеличилась (однако общая энергия сохраняется благодаря первому закону)

Чтобы получить более подробную картину энтропии, нам нужно взглянуть на концепцию фазового пространства.Некоторые из концепций этого могут быть немного запутанными, но потерпите меня, если вы разберетесь, все не так уж и плохо.

Фазовое пространство похоже на график, но точка на этом графике представляет все состояние системы. Приведем пример. Представьте, что у меня есть ящик с 4 частицами газа внутри. Каждая точка в фазовом пространстве этой системы сообщает вам, где находятся все 4 шара в коробке.

В нашем примере нас интересуют только положения 4 частиц, поэтому каждая точка в фазовом пространстве должна содержать координаты x, y и z для каждой частицы, чтобы наше фазовое пространство было 3N-мерным, где N — число частиц в системе.Таким образом, в нашем случае фазовое пространство 12-мерное, чтобы каждая точка могла описывать расположение 4 тел.

На всех диаграммах я изображу фазовое пространство как 2D, чтобы было легче передать то, что оно на самом деле представляет. Для наших целей нам не нужно учитывать размеры.

Если мы представим, что каждая из частиц имеет разный цвет, чтобы нам было легче отслеживать их положение. Если мы представим случай, когда все частицы расположены в одном углу контейнера, мы получим ситуацию

С точки зрения системы существует множество других комбинаций из 4 частиц, которые будут организованы так же, как и состояние выше

и так далее.Каждая из этих установок будет соответствовать разному положению в фазовом пространстве, поскольку все они представляют собой различные схемы системы из 4-х частиц. Если мы добавим их в фазовое пространство вместе с оригиналом, мы получим что-то вроде

Эти 5 макетов из 4 частиц вместе с 11 другими комбинациями образуют набор состояний, которые (помимо цветов) неразличимы. Таким образом, в фазовом пространстве мы могли бы поместить рамку вокруг 16 состояний, которая определяет все состояния внутри него как макроскопически неразличимые.

Общее фазовое пространство системы будет иметь множество областей разных форм и размеров и может выглядеть следующим образом:

Но как все это абстрактное представление связано с энтропией? Энтропия, указанная в уравнениях как символ, определяется как

Где — постоянная Больцмана (), а — объем прямоугольника в фазовом пространстве. Все точки в области фазового пространства имеют одинаковую энтропию, и значение энтропии связано с логарифмом объема (первоначально Больцман никогда не вставлял константу в формулу, поскольку его не интересовали единицы измерения.Буква k была введена Планком).

Энтропия также может быть определена как изменение при передаче энергии при постоянной температуре

Где — изменение энтропии, — это энергия или тепло, а T — постоянная температура.

Нулевой закон назван так, потому что он появился после остальных 3. Законы 1, 2 и 3 существовали некоторое время, прежде чем важность этого закона была полностью осознана. Оказалось, что этот закон был настолько важен и фундаментален, что он должен был пойти раньше остальных трех, и вместо того, чтобы переименовать уже известные три закона, они назвали новый закон Нулевым и поместили его в начале списка.

Но что это на самом деле означает? Закон гласит

«Если две термодинамические системы каждая находится в тепловом равновесии с третьей, то они находятся в тепловом равновесии друг с другом».

В основном, если A = B и C = B, то A = C. Это может показаться настолько очевидным, что об этом не нужно говорить, но без этого закона мы не смогли бы определить температуру и не смогли бы построить термометры.

Первый закон термодинамики в основном утверждает, что энергия сохраняется; он не может быть ни создан, ни уничтожен, просто заменен с одного на другой,

«Общее количество энергии в изолированной системе сохраняется.”

Энергия в системе может быть преобразована в тепло, работу или другие вещи, но у вас всегда будет та же сумма, с которой вы начали.

В качестве аналогии подумайте об энергии как о неразрушимых блоках. Если у вас есть 30 блоков, то что бы вы ни делали с блоками или с ними, у вас всегда будет 30 из них в конце. Вы не можете уничтожить их, только переместите их или разделите, но всегда будет 30. Иногда вы можете потерять один или несколько, но их все равно нужно учитывать, потому что энергия сохраняется.

Фундаментальное термодинамическое соотношение

Из второго закона мы можем записать, что изменение внутренней энергии системы равно количеству тепла, подаваемого в систему, за вычетом любой работы, выполняемой системой,,

(1)

Из определения энтропии, приведенного выше, мы можем заменить, и мы также можем сделать замену, дав нам

(2)

Теперь, если у нас есть система различных частиц, мы можем получить протекающие химические реакции, поэтому нам нужно добавить еще один член, чтобы учесть это

(3)

Это, вероятно, самый известный (по крайней мере, среди ученых) и важный закон всей науки.Говорится;

«Энтропия Вселенной стремится к максимуму».

Другими словами, энтропия либо остается прежней, либо увеличивается, энтропия вселенной никогда не может снизиться.

Проблема в том, что этот грех не всегда правда. Если вы возьмете наш пример с 4 атомами в коробке, то все они, находящиеся в одном углу, представляют собой высокоупорядоченную систему и, следовательно, будут иметь низкую энтропию, а затем со временем они будут двигаться, становясь более неупорядоченными и увеличивая энтропию.Но ничто не мешает им беспорядочно возвращаться в угол. Это невероятно маловероятно, но не невозможно.

Если вы посмотрите на проблему с точки зрения фазового пространства, вы увидите, что со временем более вероятно, что вы переместитесь в более крупный блок, что означает более высокую энтропию, но на самом деле нет никаких препятствий, мешающих вам вернуться в меньший блок.

Третий закон обеспечивает абсолютную точку отсчета для измерения энтропии, говоря, что

«Когда температура системы приближается к абсолютному нулю (−273.15 ° C, 0 K), то значение энтропии приближается к минимуму ».

Значение энтропии обычно равно 0 при 0K, однако в некоторых случаях в системе все еще остается небольшое количество остаточной энтропии.

Когда вы нагреваете что-либо, в зависимости от того, из чего оно сделано, для нагрева требуется разное время. Если предположить, что мощность, количество энергии, передаваемой за единицу времени, остается постоянной, это должно означать, что некоторым материалам требуется больше энергии для повышения их температуры на 1 К (1 К фактически то же самое, что 1 ° C, они просто начинаются в другом месте. .Для получения дополнительной информации щелкните здесь), чем другие. Если задуматься, в этом есть смысл. Деревянная ложка нагревается намного дольше, чем металлическая. Мы говорим, что металл является хорошим проводником тепла, а дерево — плохим проводником тепла. Энергия, необходимая для подъема 1 кг вещества на 1 К, называется удельной теплоемкостью. Формула, которую мы используем, чтобы найти, сколько энергии требуется, чтобы поднять 1 кг вещества на 1K:

где = энергия, = масса, = удельная теплоемкость и = изменение температуры.

1а. Лора готовит завтрак перед работой в воскресенье утром (пожалуйста, отправьте сообщения с сочувствием, что мне пришлось работать в воскресенье здесь). Она больше не хочет мыть посуду, если это абсолютно необходимо, поэтому решает помешать спагетти, которые готовит, вилкой, вместо того чтобы мыть деревянной ложкой. Она оставляет вилку на сковороде, намазывает тост маргарином и натирает сыр. Плита выдает вилке 1000 Дж энергии за то время, когда она оставляет ее без присмотра.Каким будет повышение температуры вилки, если предположить, что половина выделяемой энергии будет потеряна для окружающей среды, а начальная температура вилки составляла 20 ° C, а масса вилки 50 г и изготовлена из материала со специфическим тепловая мощность 460 Джкг-1К-1

Хотя я почти уверен, что где-то читал, что попытка проработать энергетические изменения в вилках первым делом утром была симптомом безумия, я время от времени делаю это. Для этого вопроса нам понадобится уравнение Q = mcΔT. Это уравнение, которое вам, вероятно, понадобится, так что стоит попытаться запомнить его.Это также возникает в химии. Прежде всего, нам нужно изменить уравнение, чтобы сделать ΔT объектом. После перестановки этого вопроса вы должны получить ΔT = Q / (mc). Подставляя данные нам значения в вопрос, вы получаете:

ΔT = 1000 / (50 x 10-3 x 460)
ΔT = 43K
Итак, поскольку начальная температура вилки была 20 ° C, конечная температура вилки будет 63 ° C.

Внутренняя энергия:
Бесплатная энергия Гельмгольца:
Энтальпия:
Свободная энергия Гиббса:

Maxwell’s Relations

(4)

(5)

(6)

(7)

Термодинамика

Термодинамика — это раздел физики, который занимается и работа системы.Он родился в 19 веке как ученые. впервые открыли, как строить и эксплуатировать паровые машины. Термодинамика имеет дело только с крупномасштабный ответ системы которые мы можем наблюдать и измерять в экспериментах. Маломасштабный газ взаимодействия описываются кинетической теория газов. Методы дополняют друг друга; некоторые принципы легче понимаются с точки зрения термодинамики, и некоторые принципы более легко объясняется кинетической теорией.

Есть три основных закона термодинамики, которые описаны на отдельных слайдах. Каждый закон приводит к определению термодинамические свойства, которые помогают нам понимать и прогнозировать работу физической системы. Мы будем представим несколько простых примеров этих законов и свойств для разнообразие физических систем, хотя мы больше всего интересуется термодинамикой при изучении движение системы и высокоскоростные потоки.К счастью, многие из классических примеров термодинамики связаны с газом. динамика. К сожалению, система нумерации трех законов термодинамика немного сбивает с толку. Начнем с нулевого закона.

Нулевой закон термодинамики включает некоторые простые определения термодинамического равновесия . Термодинамическое равновесие приводит к крупномасштабному определению температура, в отличие от мелкомасштабной определение, связанное с кинетической энергией молекул.В первый закон термодинамики связывает различные формы кинетической и потенциальной энергии в системе с работа, которую может выполнять система, и передача тепла. Этот закон иногда принимают как определение внутренней энергии, и вводит дополнительный переменная состояния, энтальпия. Первый закон термодинамики позволяет множеству возможных состояний системы существовать. Но опыт показывает, что бывают только определенные состояния. Этот приводит к второй закон термодинамики и определение другая переменная состояния, называемая энтропия.Второй закон гласит, что полная энтропия системы плюс ее окружающая среда не может уменьшаться; он может оставаться постоянным для обратимого процесс, но всегда должен увеличиваться для необратимого процесса .

Деятельность:

Экскурсии с гидом

Термодинамика:

Навигация..

Руководство для начинающих Домашняя страница