Площадь лобового сопротивления: Расчет лобового сопротивления автомобиля УАЗ

Содержание

Аэродинамический тест: седан ВАЗ-2110, универсал ВАЗ-2111 и хэтчбек ВАЗ-2112 | Блог по доработке,тюнингу и обслуживанию автомобиля и скутера

Опубликовать

Отправить

Распечатать

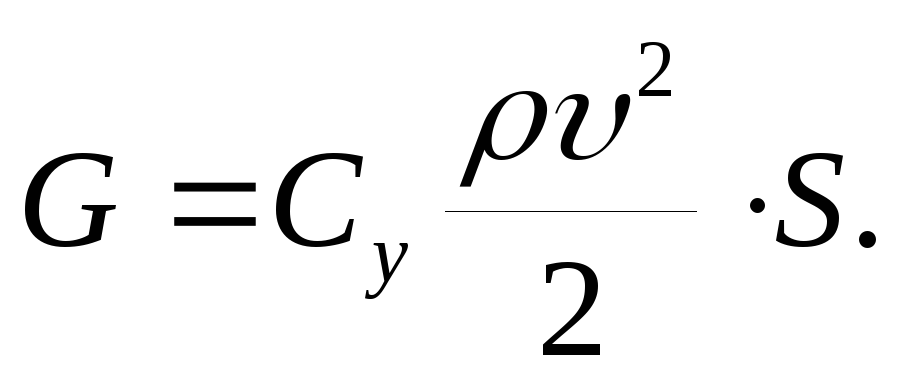
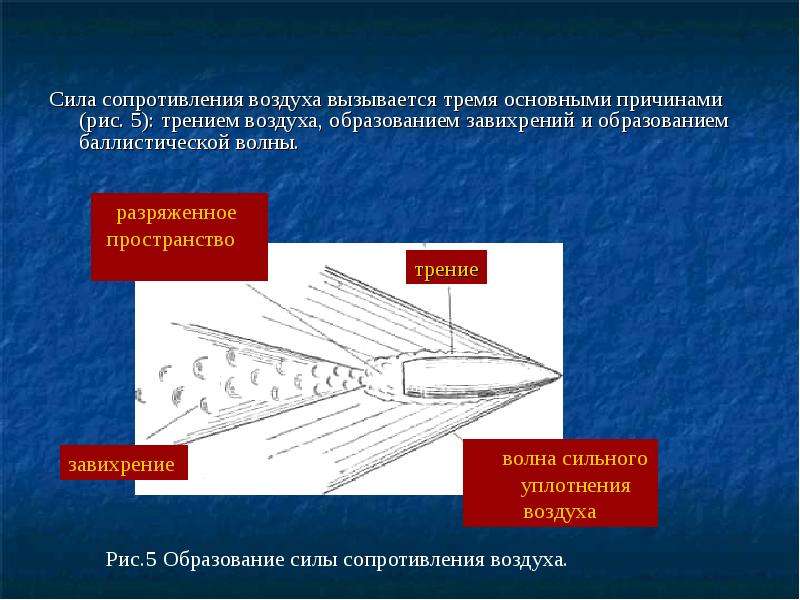
В среде физиков бытует поговорка: «Эксперимент надо ставить только тогда, когда заранее известен результат». Затевая этот сравнительный аэродинамический тест, мы, в принципе, тоже догадывались о его исходе. Но желание самим проверить, какой тип кузова предпочтительнее с точки зрения аэродинамики, все же оказалось сильнее. Именно поэтому в аэродинамической трубе Дмитровского полигона оказались три автомобиля: седан ВАЗ-2110, универсал ВАЗ-2111 и хэтчбек ВАЗ-2112.

Сх «десятки» чуть выше — из-за небольшой зоны разрежения, возникающей над крышкой багажника

Первое, о чем должен позаботиться настоящий экспериментатор, — соблюдение корректности поставленного опыта. Если мы станем сравнивать характер обтекаемости, например, хэтчбека ВАЗ-2109 и универсала ВАЗ-2104, то выясним лишь отличия в аэродинамике этих конкретных моделей, но не сможем сделать из этого каких-либо общих выводов. Это совершенно разные автомобили! Но сравнение трех машин одного «десятого» семейства позволит нам уже смелее интерпретировать результаты.

Ведь дизайн этих машин выполнен в одном стиле, а их передки и вовсе одинаковы. Так что разницу в обтекаемости, обусловленную именно разными типами кузовов, в этом случае «поймать» будет гораздо проще.
Кстати, для пущей корректности все три автомобиля отправились в Дмитров в одинаковой, стандартной комплектации — со стальными штампованными дисками, брызговиками за задними колесами и всеми полагающимися стеклоочистителями. И никаких дополнительных молдингов, накладок или антенн.
Занятно, что хэтчбек ВАЗ-2112 оказался в аэродинамической трубе Дмитровского автополигона впервые. Нет-нет, машину «продували», но не в Дмитрове, а уже в Тольятти, в недавно построенной вазовской трубе. А в руках дмитровских специалистов по аэродинамике «двенадцатая» успела побывать только в виде пластилинового макета. И каким именно окажется коэффициент аэродинамического сопротивления Сх хэтчбека ВАЗ-2112, дмитровчане только догадывались.

..
Зато и седан, и универсал ВАЗ-2111 прошли в Дмитрове полные циклы доводочных работ. Так что наш тест только подтвердил уже известные специалистам автополигона результаты.

Над пятой дверью ВАЗ-2112 воздушный поток протекает безотрывно, что улучшает характер обтекаемости

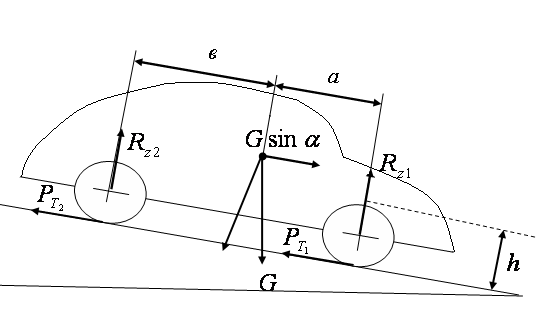
Обтекаемость универсала заметно хуже, нежели у седана. Если у «десятки» коэффициент аэродинамического сопротивления Сх равен 0,347, то у универсала он вырос до 0,381! Объясняется это просто. При движении за любым автомобилем возникает зона разрежения. Естественно, что за вертикальной задней стенкой универсала разрежение оказывается намного больше, нежели за багажником седана. А чем обширнее зона пониженного давления за автомобилем, тем существенней она «оттягивает» машину назад, увеличивая аэродинамическое сопротивление.

Несмотря на вполне закономерное и ожидаемое ухудшение обтекаемости универсала, полигоновцы все же сокрушались.

«Зачем вазовские дизайнеры поставили этот спойлер в задней части крыши? Ведь был у нас гораздо более удачный вариант в виде дефлектора, отсекающего часть воздуха с крыши на дверь багажника. Он и зону разрежения уменьшал, и заднее стекло меньше грязью забрасывало…»
Зато с хэтчбеком тольяттинцы не подкачали — Сх «двенадцатой» модели оказался равным 0,335, что чуть меньше, чем у седана. Секрет успеха в том, что заднее стекло хэтчбека установлено с гораздо большим наклоном — угол к горизонтали составляет менее «пограничных» 28 градусов, и поэтому воздух стекает с машины ровно и безотрывно. А если бы щетка заднего стеклоочистителя «двенадцатой» в состоянии покоя лежала не горизонтально, а фиксировалась бы на стекле в вертикальном положении, то Сх удалось бы еще немного уменьшить.

«Успокоившись» на длинной крыше универсала, воздух сходит с него ровной горизонтальной струей. Но за почти вертикальной задней дверью образуется обширная зона разрежения, увеличивающая Сх

Кстати, если вы помните, на первых фотографиях предсерийный хэтчбек представал то с небольшим антикрылышком над стеклом пятой двери, то с мощным лопатообразным антикрылом. В серию пошла последняя, самая серьезная с точки зрения аэродинамики конструкция — очевидно, она эффективнее снижает подъемную силу, действующую на заднюю часть кузова. В результате вазовцам удалось добиться того, что по значению подъемной силы хэтчбек ВАЗ-2112 лишь чуть-чуть проигрывает обычной «десятке».

Зато на универсал ВАЗ-2111 действует не подъемная, как обычно, а прижимающая сила! Вдобавок, она великолепно распределена между передними и задними колесами. Кольцевой болид, да и только! В чем секрет? Оказалось, что в длинной крыше. Как протекает воздух над седаном или над хэтчбеком? Взметнувшись за лобовым стеклом, он дугообразно огибает крышу и падает на заднее стекло.

Эту дугу хорошо видно, если пустить на лобовое стекло машины тонкую струйку дыма (такую процедуру специалисты называют визуализацией воздушных потоков). В зоне этой дуги создается разрежение — точно так же, как и над самолетным крылом (см. схему внизу). А под днищем автомобиля, как правило, образуется зона повышенного давления. Именно эта разница давлений и обусловливает появление подъемных сил.

А на длинной крыше универсала, особенно если ее должным образом спрофилировать, воздух успевает успокоиться и протекает по-другому, не образуя столь обширной зоны разрежения. Поэтому и подъемная сила у универсала меньше.
Можно ли соотношение аэродинамических характеристик вазовских седанов, хэтчбеков и универсалов считать закономерным и распространять на другие семейства автомобилей? Специалисты дмитровской трубы согласны дать положительный ответ только применительно к седанам и универсалам — практически всегда последние будут иметь худшую обтекаемость и большее значение Сх, нежели трехобъемные машины одного и того же семейства.

Кстати, благодаря большей «парусности» боковин универсалы, как правило, лучше «держат дорогу» на высокой скорости, нежели седаны и хэтчбеки (обратите внимание на то, как мал поворачивающий момент Mz у ВАЗ-2111).
А вот с хэтчбеками все не так однозначно. Здесь все зависит от геометрии задней части кузова — в основном от угла наклона заднего стекла. Если оно стоит почти вертикально, как, например, у хэтчбека VWGolfIV, то лобовое сопротивление такой машины будет больше, чем у седана. Ведь такой хэтчбек — почти универсал! Ну, а если стекло задней двери хэтчбека будет установлено столь же отлого, как на вазовской «двенадцатой» модели, то обтекаемость такой машины будет или такой же, как у седана, или лучшей. Впрочем, как показывает практика, лишь продувка в аэродинамической трубе может дать иногда неожиданный, но всегда точный ответ.

Аэродинамические характеристики автомобилей
	ВАЗ-2110	ВАЗ-2111	ВАЗ-2112
Площадь фронтальной проекции, м2	1,931	1,962	1,944
Сила лобового сопротивления Рх, Н	536	598	521
Коэффициент аэродинамического сопротивления Сх	0,347	0,381	0,335
Подъемная сила Pz, Н	332	-33	295
Опрокидывающий момент Му, Нм	-229	21	-264
Момент крена Мх, Нм	406	661	498
Поворачивающий момент Mz, Нм	571	339	499

Кстати. ..

Отличный пример грамотной организации аэродинамики задней части универсала — новый Volvo V70, который мы «продували» в Дмитрове прошлой зимой. Над его пятой дверью расположен дефлектор, очень похожий на тот, от установки которого на ВАЗ-2111 в Тольятти отказались. Дефлектор отсекает часть воздушного потока, сходящего с крыши, и направляет его вниз. Какова польза такого приспособления? Во-первых, заднее стекло из-за этого меньше загрязняется. А во-вторых, разрежение позади автомобиля намного падает, что приводит к снижению Сх.

Профиль крыла

Природу возникновения подъемной силы при движении автомобиля проще всего проиллюстрировать на примере самолетного крыла. Ведь оно создает подъемную силу не только потому, что направляет поток вниз, как думают многие (хотя, конечно, подъемная сила и зависит от угла атаки). Все дело в профиле крыла. Форма его сечения такова, что поток воздуха над плоскостью проходит больший путь, чем поток под плоскостью. Поэтому скорость протекания воздуха над крылом и под ним неодинакова — над плоскостью поток течет быстрее, что, согласно закону Бернулли, и создает над крылом зону разрежения и, в конечном итоге, подъемную силу.

Лобовое сопротивление самолета — Энциклопедия по машиностроению XXL

Посадку на фюзеляж производят только на грунт. При расчете посадки учитывается уменьшенное лобовое сопротивление самолета за счет убранного шасси. Перед приземлением выключают двигатели, закрывают пожарные краны, обесточивают бортовую электрическую сеть, открывают аварийные люки. При возникновении пожара на самолете или ранения пассажиров экипаж под руководством командира корабля организует тушение пожара и оказание помощи пострадавшим. [c.38]
Поляра самолета — зависимость коэффициента лобового сопротивления самолета Сх от коэффициента подъемной силы Су. [c.149]

Лобовое сопротивление самолета (потребная тяга) в горизонтальном полете Qt. п. зависит от скорости и высоты полета. Величина лобового сопротивления в горизонтальном полете определяется формулой [c.157]

Выдерживание — горизонтальный полет на высоте 0,5— 1,0 м, или полет с постепенным снижением. Режим работы двигателя на этом этапе — Малый газ . Так как тяга двигателя практически отсутствует, то под действием лобового сопротивления самолет уменьшает скорость. Для поддержания горизонтального полета летчик постепенно выбирает ручку на себя для увеличения угла атаки. По достижении самолетом посадочного положения летчик прекращает увеличение угла атаки — подъемная сила уменьшается и происходит приземление. [c.177]

Лобовое сопротивление самолета [c.55]

Лобовое сопротивление самолета можно для удобства изучения делить на составные части (рис. 2.13). Названия их зависят от признака деления. С одним из них мы уже знакомы в зависимости [c.55]

Индуктивное сопротивление О ИНД — часть лобового сопротивления самолета, связанная с образованием подъемной силы.

[c.56]

Расчет лобового сопротивления самолета выполняется по одной из следующих двух формул, аналогичных формулам подъемной силы [c.63]

Коэффициент лобового сопротивления самолета с.х — это выраженное в долях скоростного напора лобовое сопротивление самолета, приходящееся на каждый квадратный метр площади крыла. [c.63]

Сопротивление давления и подъемная сила являются составляющими равнодействующей сил давления. Поэтому коэффициент сопротивления давления зависит от тех же трех факторов (формы самолета, угла атаки и числа М), что и коэффициент подъемной силы. Если бы при изменении сопротивления давления (за счет скорости, плотности воздуха, размеров самолета, угла атаки я т. д.) пропорционально ему изменялось и сопротивление трения, то и коэффициент лобового сопротивления самолета зависел «бы только от указанных трех факторов. Но для такой пропорциональности нужно, во-первых, одно и то же состояние поверхности самолета и, во-вторых, неизменное число Рейнольдса. Учитывая, что эти условия могут быть нарушены, делаем вывод, что на коэффициент лобового сопротивления самолета должны влиять следующие факторы 1) форма самолета 2) угол атаки 3) число М 4) состояние поверхности самолета [c.63]

Основная причина сильного снижения аэродинамического качества при сверхзвуковом обтекании — отсутствие подсасывающей силы, котосилу лобового сопротивления самолета (см. гл. 2, 4 и 13), особенно на больших углах атаки. [c.87]

Примером такого приспособления формы одних частей самолета к наилучшей работе совместно с другими является применение правила площадей с целью уменьшения лобового сопротивления самолета при сверхзвуковых скоростях полета. [c.100]

Проще всего рассчитать продольную перегрузку Пх, если известны тяга и лобовое сопротивление самолета, по формуле (5.06). Допустим, что необходимо рассчитать Пх при заданных Пу, числе М и высоте полета на режиме располагаемой тяги, которая известна, а также известны полетный вес самолета, площадь крыла и имеется поляра для данного числа М. [c.133]

Если тяга двигателя превосходит лобовое сопротивление самолета, то силы, действующие на самолет, производят положительную работу и его суммарная энергия возрастает. В случае превышения лобового сопротивления над тягой, наоборот, суммарная энергия летящего самолета будет уменьшаться. Ее изменение может происходить как за счет одновременно, обоих слагаемых (т. е, за счет высоты и скорости), так и одного из них, причем одно из слагаемых может расти, а другое уменьшаться. [c.6]

Лобовое сопротивление колес при у = =тах составляет в среднем 8—10% от полного лобового сопротивления самолета. Для уменьшения лобового сопротивления колес их рас-Фиг. 94. [c.576]

Здесь X — С qS — лобовое сопротивление самолета, Г == j, — подъемная сила, G — вес самолета, Ф — тяга винта, М,,, Му, M — моменты сил X, Y, Ф относительно горизонтальной оси, проходящей через ц. т. самолета. Moa — момент сил, действующих на горизонтальное оперение относительно той же оси q = — скоростной напор (р — массовая плотность воздуха кг/ск то-, v — скорость л /ск). Моменты Му, должны быть уравновешены моментом Мд , другими словами, для того чтобы удерживать самолет на некоторой траектории, летчик, действуя ручкой управления, должен отклонить рули высоты в ту или другую сторону и тем вызвать момент надлежащего знака и величины. Т. о. в А. р. рассматривают ур-ия (1) и (2), предполагая, что ур-ие (3) удовлетворяется. Эти ур-ия часто упрощают, полагая для небольших а и у, sin (а + 7) IS О, os (а + у) is 1 в этом случае [c.18]

Уже в первых, выполненных еще в 1939 г., эскизах будущего Ме 262 Мессершмитт предусмотрел установку реактивных двигателей в крыле, чтобы таким образом снизить лобовое сопротивление самолета и его вес. С самого начала этот замысел провалился из-за постоянно меняющихся размеров первых специальных двигателей . [c.92]

Предположим, что самолет летит со скоростью 288 кж/час или 80 ж/сек. Пусть обш,ее сопротивление воздуха или лобовое сопротивление самолета равно 450 %г. [c. 234]

На рис. 35 показан бак, который подвешивается под фюзеляжем самолета на замках бомбодержателей. Обтекаемая форма сбрасываемого бака уменьшает лобовое сопротивление самолета. [c.46]

С. В. Ильюшин считал, что достичь заданной дальности на скоростном самолете можно и при крыле с умеренным геометрическим удлинением, так как доля индуктивного сопротивления в общем балансе лобового сопротивления самолета зависит от подъемной силы крыла и уменьшается на малых углах атаки, характерных для полета со скоростью 350—400 км/ч. Снизить возросшую при этом долю профильного сопротивления можно было применением тонкого двояковыпуклого профиля, а также сокращением площади крыла вследствие увеличения удельной нагрузки на него. В связи с этим для скоростного дальнего бомбардировщика ЦКБ-26 было спроектировано крыло, параметры которого для самолета такого назначения были [c.340]

Всесоюзная конференция по скоростной авиации, проведенная в 1935 г. , показала значение и роль аэродинамических исследований и средств по уменьшению лобового сопротивления самолетов, в значительной степени обусловивших резкое улучшение летных данных самолетов того времени. [c.287]

Разработкой рациональных туннельных, крыльевых радиаторов и капотов для двигателей воздушного охлаждения был завершен комплекс аэродинамических исследований и поиск конструктивных мероприятий, направленных на коренное уменьшение лобового сопротивления самолета и создание его идеальных форм. Эти результаты, естественно, вначале были применены на опытных и рекордных самолетах, а затем начали широко внедряться на боевых самолетах уже во время Великой Отечественной войны. [c.290]

На рис. 18 показаны взлетные тяговооруженности самолетов, на которых установлен рекорд. Нанесены линии равных значений обобщенного баллистического коэффициента S/rjG, который определяет уровень аэродинамики скоростного самолета.

Видно, что застой в аэродинамике продолжался в течение 10 лет, только в 1934 г. рекорд скорости был увеличен за счет снижения сопротивления самолета и совершенствования воздушных винтов (были внедрены убирающиеся шасси и винты изменяемого шага), что позволило значительно уменьшить лобовое сопротивление самолета и реализовать полную располагаемую мощность мотора на всех режимах полета. Рекордный самолет 1932 г. обладал менее совершенной аэродинамикой, чем самолет 1924 г. (В работе [13] отмечено, что его конструктором было допущено бесцеремонное обращение с аэродинамикой .) Прирост максимальной скорости АК 25,6 км/ч был достигнут за счет увеличения взлетной энерговооруженности N/G на 37% (от 0,53 до 0,73). Следующий рекорд (1935 г.) был установлен на самолете с ВИШ и закрылками, что обеспечило не только увеличенную тягу винта на взлете, но и позволило существенно увеличить нагрузку на крыло, т. е. снизить лобовое сопро- [c.386]

Удельная сила тяги — важная характеристика ТРД, определяющая степень совершенства использования воздуха (газа) в процессе создания тяги. Чем выше удельная тяга, тем меньше при заданной величине тяги потребный расход воздуха через двигатель и тем меньше диаметр и масса двигателя. Меньшие поперечные размеры двигателя позволяют уменьшить площадь поперечного сечения (мидель) фюзеляжа самолета (если двигатель расположен в фюзеляже), или гондол двигателя, если он крепится к крылу. Это приводит к уменьшению лобового сопротивления самолета и потребной силы тяги двигателя, а следовательно, к увеличению дальности и продолжительности полета. Уменьшение массы (силы тяжести) двигателя позволяет увеличить полезную нагрузку самолета. [c.476]

Для уменьшения лобового сопротивления самолета двигатели заключаются в специальные капоты. [c.223]

Новый метод подвески самых больших ракет под фюзеляжем по две тандемом позволил значительно уменьшить лобовое сопротивление самолета. Ракеты отделяются от самолета вертикально вниз при помощи толкателей. Запуск двигателя ракеты и включение головки самонаведения происходит только после удаления ракет от траектории полета самолета на большое расстояние. Два крыльевых пилона могут нести по одной ракете средней дальности, по две малой или по одному ПТБ емкостью 2500 л. [c.261]

Первые и вторые режимы горизонтального полета определяют области скоростей, отличающиеся друг от друга тем, что при установившемся полете на первом режиме самолет в определенных условиях выдерживает исходную скорость, а при полете на втором режиме не выдерживает. Особенности полета на первом и втором режимах анализируются с помощью кривых Н. Е. Жуковского—зивисимостей лобового сопротивления самолета и тяги двигателя от скорости (рис. 4.27). [c.168]

Чем меньше лобовое сопротивление самолета при данной подъемной силе (или чем больше подъемная сила при данном лобовом сопротивлении), тем более совершенен в аэродинамическом отношении самолет. Поэтому одним из основных показателей аэродинамического совершенства самолета является отношение подъемной силы к лобо вому сопротивлению, называемое аэродинамическим качеством самолета [c. 65]

Иногда ведомые сохраняют свое место в строю изменением не тяги, а сопротивления, периодически выпуская тормозные щитки, И в этом случае требуется резерв тяги, так как среднее лобовое сопротивление самолета ведомого при этом больше, чем самолета ведущего, у которого щитки убраны. Некоторое повышение сопротивления у самолета ведомого получается также за счет отклонений руля натравления и скольжений в процессе сохранения заданного интервала. Дополнительный резерв тяги требуется иметь ведомым при выполнении разворотов, но этот случай мы покл рассматривать не будем. [c.113]

Силу лобового сопротивления самолета преодолевает сила тяги Р. Тяга Р создается или вращающимся винтом, или реактивным двигателем. Сила тяги реактивного дви1ателя, как уже было сказано в 27, определяется ежесекундным расходом воздуха и скоростью, с которой этот воздух выбрасывается дви- [c.406]

Так как при переходе с режима полета Ущах на V меняются коэфициент полезного действия винта, лобовое сопротивление самолета и удельный расход топлива, что оказывает влияние на общий расход топлива, то для учета этого обстоятельства полученное количество топлива увеличивают на 6—8%. Следует отметить, что полученные зависимости дают только приближенное значение расходуемого количества топлива на самолете, так как они не учитывают ряда факторов, влияющих на расход топлива (атмосферные условия, режим работы двигателя и др.)- [c.13]

Первоначально для самолета ДАР была разработана оригинальная, ранее не встречавшаяся в практике мирового самолетостроения, компоновочная схема силовой установки, обеспечивавшая повышение тяговых характеристик винтов и снижение лобового сопротивления самолета. По этой схеме силовая установка ДАР должна была состоять из двух двигателей Испано-Сюиза 12, которые устанавливались над лодкой в тандем, но носками друг к другу так, что их толкающий и тянущий воздушные винты образовывали систему соосных воздушных винтов, вращающихся в ра.эные стороны. При этом диски винтов работали в профилированном кольце, нижняя часть которого образовывалась вогнутой верхней палубой лодки и полукольцевым центропланом крыла с горизонтальными стой- [c.268]

Чем меньше поперечный глбарит двигателя, тем меньше лобовое сопротивление самолета. [c.42]

Что же касается основного свойства — уменьшения суммарного лобового сопротивления самолета, то капот NA A эффективнее кольца Тоуненда. [c.407]

Следовательно, величина силы сопротивлений воздуха прйм(> пропорциональна а) плотности воздуха — р б) несущей поверхности й и в) скорости полета в квадрате 1 кроме того, она зависит от профиля крыльев, размаха и ширины их, угла атаки, формы и размеров остальных частей самолета. Последнее учиты вается коэфициентом лобового сопротивления самолета С в [c.62]

КАИ АВТОВАЗа. Повелители ветра

Вазовскому КАИ (комплексу аэродинамических испытаний) всего 4 года. Здесь пока не получил завершения ни один из новых проектов, принятых к реализации. Но отдача уже есть

Сергей Жуков

Вазовскому КАИ (комплексу аэродинамических испытаний) всего 4 года. Здесь пока не получил завершения ни один из новых проектов, принятых к реализации. Но отдача уже есть.

Борьба за снижение аэродинамических потерь (а в конечном счете, «обучение» автомобиля более быстрой езде при меньших затратах мощности и расходе топлива) не могла не привести разработчиков волжских малолитражек к постройке собственного комплекса аэродинамических испытаний. И его появление не замедлило сказаться. Вот лишь один пример реальной отдачи.

Известно, что 106-ю модель ВАЗа тщательно доводят в многочисленных спортивных «конюшнях», улучшая ее динамику и управляемость. Для этого изменяются характеристики силового агрегата, трансмиссии и ходовой части. В то же время вопросам аэродинамики уделяется внимания гораздо меньше.

Между тем понижение клиренса спортивной машины (как один из способов оптимизации воздушного потока под днищем автомобиля), без соответствующей доводки остальных элементов кузова, может привести к ухудшению коэффициента аэродинамического сопротивления (Сх). Именно это и произошло с представленной на фотографиях 106-й. После продувки в аэродинамической трубе в навеску автомобиля пришлось вносить изменения. В частности, были трансформированы передний бампер с нижним спойлером и антикрыло, тем самым создана отрицательная подъемная сила, равномерно распределяемая на колеса автомобиля.

Ну а теперь — о собственно комплексе аэродинамических испытаний. Все его составляющие — иностранного производства, приобретенные у ведущих в этой области фирм.

Лазерный стенд по определению площади поперечного сечения, обошедшийся ВАЗу почти в 1 млн DEM, спроектирован компанией ISRA Sistemtechnik GmbH, а изготовлен при содействии компании Carl Schenck AG. На стенде можно замерять поперечное сечение (до 4 м2) легковых автомобилей и микроавтобусов в натуральную величину, макетов автобусов и грузовиков в масштабе от 1:2 до 1:5, а также архитектурных сооружений.

Использование HeNe-лазера на специальной подвеске, чувствительного экрана и видеокамер с двумя режимами разрешения обеспечивает высокую точность измерений. Они могут проводиться автоматически, процесс занимает от 15 до 30 минут. При этом информация отображается на экране монитора, а затем распечатывается на принтере.

Самое грандиозное сооружение комплекса — аэродинамическая труба (АДТ) для образцов в натуральную величину. (Есть и модельная АДТ — для работы с макетами. Обе — производства канадской компании DSMA International Inc.)

АДТ (усовершенствованный вариант той, что используется в исследовательском центре Porsche) позволяет оценивать аэродинамические характеристики натуральных объектов или их макетов. Здесь помимо значения Сх с помощью специальных весов можно получать и все шесть аэродинамических составляющих, действующих на автомобиль (трех сил — лобовой Рх, боковой Ру, подъемной Рz и трех моментов — крена Мх, опрокидывающего Му, поворачивающего Мz). Можно определять параметры воздушного потока на поверхности объекта и вокруг него, визуализировать обтекание объекта воздухом и определять уровень шумов. Специалисты выдают не только результаты измерений, но и рекомендации по доводке образцов.

Главный вентилятор полноразмерной АДТ обладает колоссальной мощностью — 2,3 МВт. С его помощью воздушный поток разгоняется до 60 м/с, что соответствует скорости движения автомобиля в 216 км/ч. Изменив угол атаки лопаток, можно добиться прироста скорости еще на 10-15%. Впрочем, опытные специалисты уже при скорости потока в 10 м/с достаточно достоверно прогнозируют поведение объекта в более мощном воздушном потоке.

Интересно, что АДТ, по сути, — огромный аэрогриль. Прирост температуры каждые полчаса работы трубы — 10 °С. Расплавить пластилиновый макет в таких условиях ничего не стоит. Чтобы этого не произошло, в системе охлаждения постоянно циркулирует 15 тонн этиленгликоля, и рабочая температура в чреве АДТ поддерживается на уровне 20-25 °С.

Особую гордость инженеров ВАЗа составляют упомянутые шестикомпонентные тензометрические весы. Других таких в России нет. Они также изготовлены фирмой Carl Schenck AG, а смонтированы рабочими тольяттинского завода.

Хотя главный объект комплекса — полномасштабная АДТ, гораздо больший объем работ приходится на модельную, позволяющую экономить средства на проведение испытаний и вносить изменения в проект на ранней стадии.

Например, подготавливаемый к производству пикап ВАЗ-2323 необходимо было оснастить съемным тентом. Его оптимальную конфигурацию удалось подобрать, используя макет, обойдясь без изготовления нескольких образцов тента и каркаса в натуральную величину.

В другом случае уменьшенную модель перспективного минивэна исследовали на предмет забрызгивания грязью при движении, чтобы выяснить, будет машина «грязнушкой» или «чистюлей». Визуализировав потоки воздуха, обтекающие автомобиль, узнали, что с «опрятностью» не все в порядке, и теперь специалисты решают эту проблему.

Оценка аэродинамических качеств полномасштабных объектов может принести весьма неожиданные результаты, как было с «Консулом». Оказалось, на скорости свыше 120 км/ч виниловое покрытие на крыше лимузина (не приклеенное к плоскости крыши) вздувается, ухудшая Сх и увеличивая шумы.

Полный цикл аэродинамических испытаний — с выдачей отчета и соответствующих рекомендаций — автомобиль проходит в течение одного рабочего дня. Современное оборудование — лишь инструмент. Главное достояние КАИ, конечно, — специалисты. Их подготовка началась задолго до появления собственного центра. Знания и опыт приобретались на Дмитровском полигоне (в единственном тогда месте, располагающем АДТ для испытаний автомобилей) и при доводке семейства «восьмерок» в исследовательском центре Porsche.

Результат очевиден: у «копейки» Сх равнялся 0,55, у «девяносто девятой» — 0,438, а у «десятки» — уже 0,33 (мы привели показатели седанов, чтобы сравнение было корректным). Конечно, это еще далеко от лучших характеристик зарубежных машин, но надо учитывать, что в рекламных целях данные иномарок частенько завышаются.

Специалисты Управления специальных испытаний ВАЗа планируют со временем перейти к исследованиям математических моделей и глубже заняться изучением аэродинамики подкапотного пространства, днища автомобиля, системы приточной и вытяжной вентиляции.

Сейчас комплекс аэродинамических испытаний занят лишь на треть, то есть работы ведутся в одну смену, тогда как можно было бы организовать три. Заказов со стороны не счесть — и от других автозаводов, и от строителей, которых интересует ветровая нагрузка архитектурных сооружений. Проблема в одном — в кадрах. Судя по всему, тольяттинским «повелителям ветра» необходимо создавать собственную школу.

Значения коэффициентов аэродинамического сопротивления некоторых моделей (данные производителя)

Модель — Сх
ВАЗ-2101 — 0,55
ВАЗ-2106 — 0,524
ВАЗ-2104 — 0,531
ВАЗ-2109 — 0,459
ВАЗ-21099 — 0,438
ВАЗ-2110 — 0,33
ВАЗ-2111 — 0,362
ВАЗ-21109 — 0,35
ВАЗ-2118 — 0,366
ВАЗ-2121 — 0,536
ВАЗ-2120 — 0,417

Редакция рекомендует:

Хочу получать самые интересные статьи

Факторы, влияющие на силу воздушного сопротивления в велосипедном спорте

Известно, что аэродинамическая сила сопротивления возрастает пропорционально квадрату скорости набегающего потока и площади проекции системы велосипедист—велосипед на плоскость, перпендикулярную потоку (миделевая площадь, рис. 1).

Аэродинамическая сила сопротивления зависит от коэффициента лобового сопротивления, который, в свою очередь, зависит от формы тела и числа Рейнольдса Re, выражающего связь между характерными размерами тела, скоростью потока и кинематической вязкостью воздуха.

где X — сила сопротивления воздуха;
Сх — коэффициент лобового сопротивления;
V — скорость потока, м/сек;
S — миделевая площадь, м²;
ρ — плотность воздуха,
I — характерный линейный размер, м;
v — коэффициент кинематической вязкости,

Первая часть работы, проведенная авторами, заключалась в определении аэродинамического сопротивления в зависимости от различных посадок велосипедиста (положение головы, рук, локтей) и его экипировки (каска, шлем, обтекаемый костюм, а также обычная спортивная одежда).

Вторая часть работы состояла в поиске посадки, при которой спортсмен испытывает воздушное сопротивление меньшее, чем то, которое возникает при прохождении соревновательной дистанции, а также в выявлении возможности получить наименьшее сопротивление в привычной позе за счет индивидуальных особенностей (телосложение, расположение рук, кистей и головы).

Третья часть работы была направлена на количественное определение силы воздушного сопротивления в зависимости от одежды велосипедиста.

Исследования проводились в аэродинамической трубе.

Для закрепления велосипеда на аэродинамических весах применялся специальный кронштейн, который с одной стороны прикреплялся к весам, а с другой — к каретке и наклонной трубе рамы. Колеса велосипеда находились в 2—3 см от поверхности экрана, имитирующего поверхность, по которой движется велосипедист (рис. 2).

Спортсмен во время исследования находился без движения, так как регистрировать силу воздушного сопротивления при движении ног было невозможно из-за действия на весы инерционных сил, возникающих при педалировании. Измерения проводились при различном положении ног и при скоростях потока воздуха 10, 15, 20 м/сек. Замерялись определенные позы спортсменов, которые затем фотографировались.

В результате исследования было выявлено следующее. Коэффициент лобового сопротивления (Сх) при одной и той же посадке и скорости потока воздуха 10—20 м/сек менялся для разных велосипедистов в пределах 0.185—0,299. На аэродинамическую силу сопротивления влияло изменение не только положения туловища, но и положения отдельных частей тела и даже кистей рук.

Аэродинамическое сопротивление зависит:
1) от антропометрических характеристик спортсмена. Сопротивление воздуха в наилучшей посадке гонщиков для скорости потока 20 м/сек было в пределах от 44 до 73 Н. Различие этого параметра достигало 29 Н. Причем разность силы воздушного сопротивления в наилучшей посадке и посадке, имеющей наибольшее воздушное сопротивление, составляла у одного гонщика 7, а другого—19Н. В зависимости от особенностей телосложения гонщиков приблизительно одного роста и веса сила сопротивления воздуха в одной и той же посадке была различной;
2) от одежды велосипедиста (обычная, различные обтекаемые велосипедные костюмы, различные шлемы и каски). Результаты эксперимента приводятся в табл. 1 и 2. Были выявлены спортсмены, имеющие благоприятное с точки зрения аэродинамики телосложение, и спортсмены, для которых совершенствование посадки в аэродинамической трубе имеет первостепенное значение.

Из сказанного можно сделать вывод, что применение одного и того же костюма, шлема и другой экипировки различными гонщиками изменяет воздушное сопротивление по-разному (табл. 3). Поэтому подбирать их следует одновременно и индивидуально и обязательно в сочетании с выгодной посадкой.

Р. Е. Варгашкин, А. В. Рудченко, Б. А. Яковлев, Москва

Рекордная аэродинамика и 770 километров без подзарядки: чего ждать от флагманского электро-Мерседеса

Коэффициент лобового сопротивления Mercedes-Benz EQS составит 0,20 при площади фронтальной проекции в 2,51 квадратного метра. Производитель утверждает, что это значение на данный момент является рекордом. Аналогичная характеристика у седана Lucid Air — 0,21, однако ещё в середине прошлого десятилетия концерн Volkswagen разработал «однолитровый» XL1, коэффициент аэродинамического сопротивления которого составлял 0,189. Впрочем, тираж последнего поколения XL1 не превысил сотни экземпляров.

В Mercedes-Benz добились такого результата благодаря не только обтекаемому силуэту, но и ряду более мелких деталей — скажем, плоскому днищу, выдвижным дверным ручкам, продуманному дизайну колёс (от 19 до 21 дюйма), заднему спойлеру и сотням часов компьютерного моделирования. При этом работа над аэродинамикой ещё продолжается — уже с использованием полноразмерных физических моделей. Производитель уверяет, что низкий коэффициент сопротивления критически важен не только для запаса хода, но и для акустического комфорта в салоне.

Проезжать EQS сможет до 770 километров по циклу WLTP, а обеспечивать запас хода будет батарея на 107,8 кВт⋅ч (это меньше, чем у Lucid, но больше, чем у Tesla). Более доступные модификации укомплектуют более компактными аккумуляторами на 90 кВт⋅ч, но Mercedes-Benz особо отмечает, что, во-первых, сами батареи — нового поколения с высокой плотностью, а во-вторых, разработаны и будут производиться самой компанией. Обещанный срок работы — 10 лет или 250 тысяч километров. Заряжать батареи планируется от станций мощностью до 200 кВт, при этом для преодоления расстояния в 300 километров аккумулятор наберёт энергии всего за 15 минут.

Младшая модификация EQS 450 получит одномоторную силовую установку на 333 л.с. и 568 Нм крутящего момента. Более дорогой EQS 480 оснастят двумя двигателями совокупной отдачей 524 л.с. и 855 Нм, а также возможностью распределения крутящего момента между осями. Максимальная скорость в обоих случаях ограничена отметкой 210 км/ч. Однако в Mercedes-Benz уже уточнили, что этим моторная гамма не ограничится. У EQS будет и более мощная и быстрая модификация. Возможно, её выпустят под суббрендом AMG.

Ранее компания Mercedes-Benz рассказала о нюансах оформления интерьера электрического флагмана, в том числе и о гигантской 56-дюймовой панели, которая займёт всю переднюю часть электрокара и спрячет в себе три больших монитора. Производить EQS будут на предприятии в Зиндельфингене, а на европейском рынке роскошный электромобиль появится уже в августе нынешнего года.

АЭРОДИНАМИКА

Статьи об аэродинамике обычно фокусируются на восхвалении достоинств низкого лобового сопротивления и сопутствующих эффектов по эффективности и экономии топлива. Но создание «гладких мотоциклов», возможно, легкий случай. Обычно при рассмотрении всех средств достижения высоких скоростей эффект воздушного давления необходимо учитывать, но вовсе не неожиданно это становится очень сложным на байке по сравнению с такими самобалансирующимися машинами, как автомобили. Наша старый приятельница, сила гироскопической прецессии и ее взаимодействие с рулением, является причиной многих проблем стабильности, отсутствующих у автомобилей, грузовиков и т.д. Давайте взглянем на некоторые их этих проблем и рассмотрим, можно ли что-нибудь сделать для их ослабления.

ЛОБОВОЕ СОПРОТИВЛЕНИЕ

Вначале давайте рассмотрим, что же вызывает лобовое сопротивление – которое, в конце концов, является самым крупным вором выходной мощности нашего двигателя на всех скоростях, кроме самых медленных. Лобовое сопротивление – сила, стремящаяся предотвратить быстрое движение байка через воздух, эта сила генерируется разностью давления между передом и задом машины. Эта разность давления действует на фронтальную зону байка и вызывает тормозную силу, следовательно чем больше фронтальная зона, тем больше лобовое сопротивление. Так как байк движется через воздух, он должен раздвигать молекулы воздуха в стороны, и если это происходит мягко на более низких скоростях, молекулы следуют за байком недалеко от очертания машины и генерируется небольшое сопротивление. Малое сопротивление возможно только при хорошо обтекаемой форме, как классическая капля. При таких условиях поток воздуха будет ламинарным и большинство лобового сопротивления будет возникать от сил трения, так как частички воздуха фактически трутся одна о другую вдоль поверхности корпуса. На практике поток обычно турбулентный, а не ламинарный, и лобовое сопротивление значительно выше. Как подсказывает само название, такой режим потока (турбулентный) запутан и состоит из многих вихрей около поверхности. Эти вихри возникают из-за неспособности воздуха следовать резким изменениям формы, которые изобилуют на байке или автомобиле. Момент инерции частичек воздуха стремится удержать их на прямолинейном пути, но когда форм корпуса отходит слишком далеко от идеала, воздух больше не следует за формой, и трение между соседними слоями воздуха, движущимися с разной скоростью, стремится завернуть поток воздуха в вихри. Объект, движущийся через воздух, оставляет в таком случае за собой турбулентную струю, и исследования показали, что сила лобового сопротивления приблизительно прямо пропорциональна площади этой струи. Размер и форма объекта, а также скорость – наиболее существенные факторы, влияющие на площадь этой струи. Для того, чтобы в цифрах сравнить аэродинамические качества разных форм, используется безразмерный параметр, известный как Cd (коэффициент лобового сопротивления). Иногда некорректно утверждается, что плоская пластина, толкаемая через воздух, имеет Cd в 1,0. это относится только к особому теоретическому случаю, когда воздух перед пластиной выталкивается непосредственно вперед ее, и совсем не распределяется по сторонам. В действительности Cd плоской пластины зависит от ее размера и может быть ближе к 0.5. Сам вопрос размера очень интересен, так как он влияет на достоверность при экстраполировании результатов от теста моделей к реальной машине. Аэродинамические трубы, достаточно большие, чтобы вместить полноразмерный байк или автомобиль, очень дороги в постройке и работе, и поэтому тесты моделей могут быть сильно значимыми в плане экономии денег, что всегда является приоритетом производителей. Тем не менее, использование моделей не всегда просто. Есть вполне очевидные проблемы, такие как точность, например, допуск в 1 мм на полноразмерной машине становится допуском в 0,2 мм на модели в одну пятую величины. Менее очевидным, но столь же важным обстоятельством является число Рейнольдса. Г-н Рейнольдс, ранний исследователь потоков жидкости, открыл, что скорость воздуха, при которой турбулентные характеристики объекта такой же формы, но другого размера зависят от его размера. Фактически, если вы возьмете половинный размер объекта, вам нужно увеличить скорость воздуха вдвое, этот эффект был формализован в математическое выражение, известное как число Рейнольдса. Для того, чтобы достичь аналогичных условий потока в моделях с разными размерами, на нужно стараться сохранить это число неизменным. Но во многих случаях это очень трудно. Допустим мы хотим исследовать аэродинамику мотоцикла в аэродинамической трубе при 100 милях в час (≈ 160 км/ч), используя модель в одну шестую величины. Для аналогичного числа Рейнольдса это потребует, чтобы скорость потока воздуха в трубе была примерно 600 миль в час (≈ 960 км/ч), что немедленно приводит к еще бОльшим проблемам. Огромная мощность требуется для создания потока такой скорости, и силы, действующие на модель, будут исключительно высоки, создавая возрастающие трудности. Вдобавок ко всему, 600 миль/час очень близко к скорости звука, а когда мы подбираемся к этой скорости, проблемы сжимаемости выходят на первый план и нарушают все характеристики потока. Конечным результатом этого является то, что небольшие модели тестируются при небольших числах Рейнольдса и требуется много умения и тщательности при интерпретации этих тестов.

Значимость уменьшенного лобового сопротивления было ясно показано в пятидесятых, когда журнал «Motor Cycle» заказал постройку полузакрытого обтекаемого корпуса на пятилетнем 350-кубовом Royal Enfield. Это вылилось в увеличении общего веса на 45 фунтов. Но значение лобового сопротивления было таково, что даже ускорение в диапазоне от 15 до 40 миль/час было значительно улучшено, как показывает таблица результатов.

Эти тесты проводились Виком Виллоубай в MIRA с использованием электронного счетного привода. Попытка свести эти результаты в процентное уменьшение лобового сопротивления имеет свои проблемы, во многом из-за того, что все тесты проводились на одной передаче. Следовательно обороты двигателя, а значит и выходная мощность, возможно, были бы разными при максимальных скоростях, в зависимости от того, был ли прикреплен обтекатель или нет. Тем не менее, делая одно или пару допущений, я просчитал, что лобовое сопротивление с обтекателем было примерно 75-85% от лобового сопротивления машины без обтекателя. Так что если этот порядок совершенствования отдачи возможен при таком корпусе, просто представьте, чего можно достичь с постройкой целевого аппарата – хорошо обтекаемого FF, например, с уменьшенной фронтальной зоной, а также с возможностью лучшей формы. Ну да ладно, так какая же форма является наилучшей с точки зрения лобового сопротивления? Положим, классическую каплеобразную форму было бы трудно победить, и приближение к ней было очень успешно использовано в NSU при достижении многих мировых рекордах скорости в малых классах еще в пятидесятых. Однако отношение длины к ширине, требуемое для минимального лобового сопротивления, сделало бы обычный мотоцикл слишком длинным. Сокращение длины корпуса путем увода зада под более крутым углом только вызовет турбулентность и увеличение лобового сопротивления, гораздо лучше создать длинный тонкий кузов и просто обрезать его хвост для получения желаемой длины, это как бы обманывает воздух и действует, как если бы остаток хвоста все еще присутствовал. Такая задняя часть известна как хвост Камма – по имени человека, впервые додумавшегося до этого. Даже с хвостом Кама обычный байк трудно сделать действительно эффективно обтекаемым из-за разных вырезов, нужных по практическим причинам, например, посадка на байк, опускание ноги вниз при остановке и т.д. И все же усовершенствования определенно можно сделать, и, несмотря на многие современные аргументы, начинать надо с задней части машины – поток вокруг зон повышенного давления спереди может сам о себе позаботиться, но все, что сглаживает поток сзади и помогает уменьшить площадь струи, будет действительно выигрышным. Фактически многие остроконечные спереди формы создавали бы меньшее лобовое сопротивление, если их развернуть наоборот, как показано на рис. 1

ПОДЪЕМ

Аэродинамический подъем, в особенности над передним колесом, потенциально опасен, так как он уменьшает сцепление шины(шин) с дорогой. Не всегда понимают, что даже если форма корпуса не создает самостоятельной подъемной силы, все равно остается тенденция для переноса веса от переднего колеса на заднее полностью из-за эффекта лобового сопротивления. Рассмотрим рис. 2: силу лобового сопротивления Fd можно считать действующей через одну точку на ограниченном расстоянии от земли h. Эта сила создает вращающий момент, стремящийся повернуть байк вокруг его заднего колеса, таким образом, поднимая перед.

Итак, при прочих равных условиях все, что уменьшает лобовое сопротивление и/или эффективную высоту его действия, поможет уменьшить этот перенос веса. Дополнительно к простому уменьшению лобового сопротивления идеальная ситуация для формы корпуса была бы в создании прижимающей силы спереди и подъемной силы сзади, чтобы точно сбалансировать вышерассмотренный эффект. Во главе с БМВ с их обтекателем для R 100 RS производители обращают сейчас больше внимания на эту проблему. Иногда предполагают, что, раз гоночные автомобили в настоящее время выигрывают так много от огромного прижимающего аэродинамического давления, создаваемого их корпусами, то можно использовать те же преимущества на байках при поворотах. Но здесь снова, как и во многих других аспектах, наша потребность наклонять байк для поворота усложняет вопрос. На прямой линии любые аэродинамические черты, создающие дополнительную прижимающую силу, будут сильнее нагружать шины и давать большее сцепление. При условии, что наши тормоза достаточно хороши и у нас достаточно мощности, это повышенное сцепление позволит лучше разгоняться и тормозить. Но когда мы говорим о повороте, ситуация меняется. Предположим, что мы получили дополнительную прижимающую силу от использования антикрыла, как на рис. 3. Тогда при наклоне в поворот эта сила будет действовать по линии байка и, следовательно, увеличит горизонтальную силу в прямой пропорции с увеличением вертикальной составляющей на шины. Следовательно, любое увеличение способностей шин поддерживать увеличенную боковую реакцию расходуется горизонтальной составляющей аэродинамической силы. На практике скорость прохождения поворота может фактически уменьшиться. Так как коэффициент сцепления шин, скорее всего, уменьшится из-за увеличенной нагрузки. Гоночный автомобиль выигрывает потому, что он не наклоняется на значительный угол и сила действует вертикально вниз, а получить то же самое на байке означает, что антикрыло должно было бы наклоняться, оставаясь в положении, близком к горизонтальному, при наклоне байка, или не давать байку наклоняться – возможно, путем экстремального использования наколенных слайдеров и стиля езды со смещением пятой точки вбок.

ОСНОВЫ ПУТЕВОЙ УСТОЙЧИВОСТИ

Одно из первых требований для нее – чтобы Центр бокового Давления был позади Центра тяжести. ЦД – мы можем считать, что это точка, через которую действует сила ветра на боковую поверхность байка. Именно этот критерий устойчивости требует, чтобы у самолетов были вертикальные стабилизаторы в задней части, а у дротиков и стрел – оперение. Это работает так: при воздействии бокового ветра, если ЦД сзади, задняя часть машины отталкивается ветром, заставляя, таким образом, перед приводиться к ветру и автоматически корректировать сбивание с курса. С другой стороны, когда ЦД расположен спереди, то перед отклоняется ветром и байк будет сдувать с начального курса – в своей основе не стабильное условие и только вмешательство водителя сможет удержать все под контролем. Получить ЦД, расположенный сзади, труднее, чем говорить о нем. У обычных мотоциклов есть склонность иметь большинство, если не весь свой обвес спереди водителя – наследство недальновидного решения ММФ в 1957 г. Значительно ограничить дизайн обтекаемости гоночных байков, и поэтому расположенный спереди ЦД неизбежен в обычной конструкции. Как ни иронично, но даже если задаться целью создания обтекаемого корпуса с большой боковой зоной сзади, часто этого сложнее достичь. Чтобы это понять, нам нужно немного ближе рассмотреть подробности потока воздуха вокруг такой машины.

Рис. 4 показывает как на скорости боковой ветер действует вовсе не как боковой, а в сочетании со встречным ветром от движения байка, и создает поток воздуха под углом к машине. Например, если байк едет со скоростью 75 миль/ч, а боковой ветер дует со скоростью 15 миль/ч, то результирующий ветер будет действовать со скоростью 76,5 миль/ч под углом около 10°. Хорошо обтекаемая часть, как самолетное крыло, будет создавать очень высокие силы при таком угле атаки. На самолете эти силы действуют как подъемные, и их величина наглядно демонстрируется каждый раз, когда взлетает 747-й. На наземной машине эти силы действуют как боковые, и мы хотим уменьшить их величину, чтобы минимизировать отклоняющий эффект. Плохо обтекаемая форма стала бы очень плохим самолетным крылом, потому что степень подъема была бы низкой и те же самые соображения применяются на дороге, величина боковых отклоняющих сил обычно уменьшается при дизайне с высоким лобовым сопротивлением. Реальный мотоцикл попадает где-то посередине между идеальной формой капли (по причинам лобового сопротивления) и кирпичом с колесами. Поток воздуха вокруг фронтальной части машины разумно желателен, но в каком-то месте вдоль нее произойдет разделение, и поток позади этой точки будет турбулентным. Случай, когда это происходит на стороне, подверженной этому завихренному потоку, не будет эффективен в сохранении ЦД сзади. При возрастании скорости точка разделения будет сдвигаться вперед вместе с ЦД, так что вместо улучшения аэродинамической устойчивости при возрастании скорости обычная тенденция как раз противоположна. У обтекаемых машин-рекордсменов часто есть высокие хвостовые стабилизаторы для восстановления баланса. Если говорить о балансе, он также нарушается боковым ветром, как показывает вид сзади на рис. 5

Боковая сила создает момент, стремящийся опрокинуть байк в сторону от ветра, для удержания баланса, следовательно, необходимо наклонить байк к ветру. При этих условиях вес машины теперь действует сбоку от центральной линии и создает момент, балансирующий момент силы ветра. Для уменьшения требуемой степени наклона нам требуется вызывать небольшую боковую силу в сочетании с низко расположенным ЦД, чтобы получить минимальный нарушающий эффект, и требуется тяжелый байк с высоким расположением ЦТ для минимизации реакции байка на такой дисбаланс.

ДИНАМИЧЕСКАЯ ПУТЕВАЯ УСТОЙЧИВОСТЬ

Вышесказанное относится к устойчивым условиям постоянного бокового ветра. На практике это случается редко и более обычны условия порывистого ветра. Помимо меняющегося ветра, прогалины в окружающих защитных лесопосадках, а также завихрения и ударные волны от грузовиков на шоссе также добавляют свой вклад в наши проблемы. Полный динамический эффект всего этого набора на байк исключительно сложен, но мы можем рассмотреть некоторые основные моменты. Как я уже подчеркивал в предыдущих статьях боковые движения или движения наклона байка переплетаются с курсовыми движениями или рулением. Это может привести к дисбалансу при условиях порывистого ветра. Рассмотрим резкий порыв ветра слева, байк отреагирует неожиданным наклоном от ветра вправо, это в свою очередь, посредством эффекта прецессии, вызовет поворот руля вправо, а значит байк будет стремиться увернуться от ветра, вместо того, чтобы привестись к нему, как было бы желательно. Но это стремление повернуть вправо, через центробежную силу, будет наклонять машину влево, что нам и нужно для удержания баланса. – Понимаете, что я имею в виду, говоря о сложности всего этого дела!

В 1986 г. я переделал Gold Wing – вместо телескопических вилок я поставил одну из своих подвесок с центральной ступицей – для его владельца, Уейна Бойза. Спустя некоторое время после переделки мы обсудили разные эффекты, замеченные при обычной езде, многие наблюдения соответствовали моим ожиданиям, но я был слегка удивлен, когда он подчеркнул, что машина стала гораздо более устойчива при порывистом боковом ветре. Сначала я подумал, что это произошло, возможно, из-за увеличенной боковой жесткости новой подвески, которая обычно в любом случае более устойчива. Но еще немного размышлений о различиях двух конструкций пролило свет на то. Почему они должны вести себя так по-разному в этих условиях. Было три основных отличия в дополнение к уже упомянутой жесткости: 1) 16” колесо, вместо 19”, 2) уменьшенный вынос (трейл), 3) угол наклона рулевой колонку в 17°, который требовал нулевого смещения между осью рулевой колонки и центральной линией колеса для получения желаемого выноса. Вполне можно оспорить то, что все три изменения работают как улучшение поведения при порывистом ветре.

Уменьшенное колесо: Силы прецессии уменьшаются, одновременно с уменьшением веса, в месте посадки шины на обод. Это уменьшает связь между курсовыми и наклонными движениями.
Уменьшенный вынос: Составляющая силы бокового ветра, действующая спереди машины, переносится на поверхность дороги через шину посредством рулевой колонки, но ось рулевой колонки проходит перед пятном контакта шины на расстоянии выноса, а следовательно, боковая сила на байке стремится повернуть колесо по ветру. Именно та ситуация, которую мы хотели бы избежать.
Нулевое смещение: При обычной геометрии рулевой колонки со смещением около 1-2” основная часть боковой зоны колеса находится впереди оси рулевой колонки, что в сочетании с эффектом увеличенных современных шин и дисков означает, что существенная сила руления может возникать от действия бокового ветра на колесо. Но при геометрии с нулевым смещением, примененной на конструкции с центральной ступицей, эта боковая сила сбалансирована относительно оси рулевой колонки и не создает поворачивающего эффекта.

Интересной особенностью, которую я заметил при езде на своем QL на прошлогоднем шоу в Милане, был эффект давления воздуха в шинах. У QL обтекаемый корпус с довольно большой боковой зоной, а значит можно ожидать, что величина сил бокового ветра будет большой. Но если машина показала себя стабильной в отношении курсовой аэродинамической устойчивости, она начинала опасно вилять, если давление в шинах снижалось. Это происходило из-за того, что позже обнаружилось как медленная утечка воздуха в золотнике переднего колеса. Похоже, что уменьшенная боковая жесткость шин, когда они недокачаны, позволяло машине значительно уходить в стороны от направления движения под действием большой силы бокового ветра. Фото «Flying Hammok»

ЗАКЛЮЧЕНИЕ

Аэродинамический дизайн мотоциклов – нечто большее, чем просто средство уменьшить лобовое сопротивление, подъем корпуса с ЦД позади ЦТ. Труднее достичь устойчивости с хорошо обтекаемым корпусом из-за увеличенной боковой поверхности с таким обтекателем и из-за более эффективного вызывания «бокового подъема», возникающего от угла потока воздуха к направлению движения. Так что в идеале мы бы хотели получить комбинацию иногда конфликтующих условий: минимальное лобовое сопротивление для улучшенной отдачи и экономии топлива; низко расположенный передний ЦД для уменьшения переноса веса. Вызываемого лобовым сопротивлением; расположенный низко и сзади боковой ЦД для уменьшения дестабилизирующих моментов и получения курсовой устойчивости; форма и размер боковой поверхности, минимизации создаваемой боковой силы; расположенный высоко и спереди ЦТ в сочетании с большим весом для минимизации эффекта любых боковых сил.

Если кто-либо из вас думает о создании собственного обтекателя, не дайте всей этой информации сбить вас с толку. Часто любитель с ограниченными ресурсами повергает в смущение большие компании, которые не всегда получают правильный результат даже со своими аэродинамическими трубами. Вспомните попытку компании Форд с Сиеррой, когда вначале были проблемы с устойчивостью, пока они не прикрепили спойлер над задними фонарями. В мире байков в 1981 году дорожный тест полностью обтекаемого концепт байка БМВ Футуро также очень плохо показал себя в этом отношении.

Сайт создан в системе uCoz

Аэродинамика автомобиля — RacePortal.ru

Современная автомобильная аэродинамика решает множество задач. Специалисты должны не только добиться минимального сопротивления воздуха, но и отследить величину и распределение по осям подъемной силы, ведь нынешние автомобили достигают тех скоростей, на которых самолеты уже отрываются от земли. Необходимо предусмотреть и доступ воздуха для охлаждения двигателя и тормозных дисков, продумать вентиляцию салона, расположив в нужных местах отверстия для забора и вытяжки воздуха. Аэродинамика определяет уровень шумов в салоне, заботится о том, чтобы захватывающие грязь воздушные потоки не попадали на стекла, зеркала, фонари и ручки дверей. С ростом скорости не должно меняться и качество очистки лобового стекла.

В общем, круг задач необычайно широк, а решение одной проблемы тесно связано с другой: например, необходимость делать воздухозабрники для охлаждения тормозов или борьба с подъемной силой ведет к увеличению лобового сопротивления. И разобраться в этой головоломке, найти оптимум под силу лишь настоящим мастерам своего дела. Мы же рассмотрим только два главных аспекта автомобильной аэродинамики: проблему сопротивления воздуха и прижимной силы.

Аэродинамическое сопротивление

Наверное, каждый слышал о том, что сила сопротивления воздуха пропорциональна квадрату скорости – столь быстро нарастает противодействие движению в процессе разгона. Впечатляет, но как это соотнести с параметрами автомобиля? Для этого нужно лишь перейти в термины механической работы, и тогда получится, что отбираемая от двигателя мощность находится аж в кубической зависимости от скорости! Только представьте, с каким трудом даются автомобилю последние десятки километров в час. В таких условиях даже значительная прибавка мощности мотора не в состоянии существенно увеличить максимальную скорость.

Таким образом, задача снижения лобового сопротивления – приоритетная задача не только для аэродинамики, но, в свете борьбы за экологию, и для всего автомобилестроения в целом.

Сила сопротивления — так рассчитывается сила аэродинамического сопротивления. S – площадь поперечного сечения (м2), V – скорость воздушного потока (м/c), p – плотность воздуха (1,23 кг/м3), Cx — коэффициент аэродинамического сопротивления. То есть повлиять на величину силы при заданной скорости можно только двумя путями: изменив либо Cx, либо площадь S.

Решение можно искать по двум направлениям. Первое – это уменьшение площади поперечного сечения автомобиля, иными словами, создание более узкого и низкого кузова. Путь весьма эффективный, ибо сопротивление воздуха напрямую зависит от размеров объекта, но, к сожалению, совершенно расходящийся с нынешней тенденцией к увеличению габаритов автомобилей. И увеличению, стоит отметить, немалому, ведь в моду активно входят кроссоверы, вторгающиеся даже в совершенно чуждый им сегмент спортивных, скоростных автомобилей, где требования к аэродинамике предельно высоки.

А значит остается второй и единственный вариант – оптимизация процесса обтекания кузова, критерием совершенства которого как раз и является коэффициент аэродинамического сопротивления Cx (или Cw, как иногда встречается в литературе).

Величина Cx определяется опытным путем. Например, у так называемого обтекаемого тела, похожего на вытянутую каплю воды, Cx равен 0,04, у сферы – 0,47, у куба, грань которого перпендикулярна потоку, — 1,05, а если его повернуть, так чтобы угол между воздушным потоком и гранями составлял 45 градусов, то Сх снизится до 0,8. Примерно в том же диапазоне находится и Сх практически всех автомобилей, разве что нижняя граница поднимается примерно до 0,25.

Факторов, влияющих на Cx автомобиля, несколько: во-первых, это внутреннее сопротивление, возникающее при прохождении воздуха через подкапотное пространство и салон, во-вторых, сопротивление трения между воздушным потоком и поверхностью кузова, и, в-третьих, сопротивление формы, проявляющееся главным образом в избыточном давлении перед автомобилем и разряжением позади него. Внутреннее сопротивление составляет около 12% от общей величины, и пока особых успехов в этой области не наблюдается: напротив, все более и более мощные моторы современных автомобилей требуют все больше воздуха для охлаждения. Например, в пределе 300-сильный бензиновый двигатель выделяет в виде тепла около 450кВт – этого хватило бы для отопления нескольких особняков! Соответственно, растут размеры радиаторов, уплотняются моторные отсеки, увеличивается сопротивление воздуха… Существенные же улучшения здесь возможны лишь при переходе на более эффективные электродвигатели, но пока они так и остаются технологией будущего.

Красные стрелки – вектора, показывающие направление и скорость движения отдельных частиц. В данном случае они параллельны друг другу, а потому поток находится в ламинарном состоянии.

Сопротивление поверхностного трения так же вносит свой 10-процентный вклад в величину Cx. Вообще, наличие столь ощутимого трения между воздухом и кузовом может показаться странным, но оно действительно имеет место: прилегающий к поверхности слой воздуха сталкивается с микронеровностями покрытия и тормозиться — образуется так называемый пограничный слой. Пока это течение находится в ламинарном состоянии, то есть все его частицы движутся в одном направлении, толщина пограничного слоя невелика (около нескольких миллиметров) и сопротивление трения небольшое. Но с переходом в турбулентное состояние, когда поток «спотыкается» о более крупное препятствие, и траектории его частиц становятся хаотичными, пограничный слой расширяется, а вместе с ним увеличивается и трение – воздух словно становится более вязким. Таким образом, от разработчиков в данном случае требуется обеспечение гладкости кузова, дабы пограничный слой дольше оставался ламинарым. А для этого нужно уменьшать зазоры кузовных элементов, закрывать уплотнителями щели между деталями. Помогает и придание поверхностям небольшой кривизны – прилегающий поток ускоряется, давление в нем падает, и траектории частиц упорядочиваются. К сожалению, в целях экономии этими мерами в последнее время частично пренебрегают, например, уплотнители по периметру лобового стекла или вокруг фар сейчас встретишь нечасто.

Рсопротивление давления Распределение давления воздуха на движущийся автомобиль. Красному соответствуют зоны высокого давления, синему – низкого. Обратите внимание на возникающее разряжение позади заднего стекла и, в особенности, за крышкой багажника и бампером – именно эта область главным образом и определяет аэродинамику кузова. И чем меньше она, тем лучше.

И, наконец, сопротивление формы или сопротивление давления – главный фактор, определяющий значение Cx. Причина его возникновения понятна – спереди на автомобиль давит набегающий поток воздуха, а позади его «оттягивает» назад зона разряжения, образующаяся в результате отрыва потока от резко заканчивающегося кузова. Решение проблемы тоже, казалось бы, очевидно – нужно придать автомобилю такую форму, чтобы он плавно рассекал воздух и опять-таки плавно, без отрыва потока от поверхности, позволял ему сойтись позади себя. Но загвоздка в том, что в соответствии с такими требованиями автомобиль должен напоминать дирижабль (точнее, его половину, отрезанную в продольной плоскости), то есть иметь минимум граней и, главное, очень длинную, постепенно сужающуюся заднюю часть. Разумеется, о рациональной компоновке в данном случае говорить трудно. Так что задача перед инженерами стояла непростая…

Ретроспектива

Первый автомобиль, преодолевший отметку в 100 км/ч (1899 г.). Приводился в движение двумя электромоторами суммарной мощностью 67 л.с. Масса – 1000 кг. Максимальная скорость 105 км/ч.

В начале прошлого века, когда автомобили только зарождались, их скорость едва превышала 40км/ч, а форма походила на карету, об аэродинамике, естественно, не задумывались – при величине Cx около единицы те модели едва ли могли поспорить по обтекаемости даже с пресловутым кирпичом. Однако все же находились энтузиасты, уделявшие этому внимание. Главным образом, то были разработчики рекордных автомобилей и тех, что мы бы сейчас назвали «концепт-карами».

Над формой долго не думали – её перенимали из других областей техники, таких как мореплавание или авиация. Соответственно, автомобили напоминали корабли, дирижабли, торпеды и другие тела вращения. Самым же первым представителем этой плеяды была машина Камилла Дженатци, на которой сам создатель впервые в истории преодолел рубеж в 100км/ч – произошло это аж в 1899 году. Cx того автомобиля, конечно, не известен, но, учитывая немалую мощность в 67 л.с., можно предположить, что его аэродинамика все же была далека от совершенства – сопротивление увеличивал водитель, возвышавшийся над кузовом, и совершенно неприкрытые элементы подвески и шасси.

Более удачной попыткой создать обтекаемый автомобиль стала Alfa Romeo 40-60 HP – спортивная машина 1913 года, на шасси которой был установлен кузов в форме дирижабля. Полностью укрывающий пассажиров корпус, интегрированное шасси и компактные узлы подвески позволили при мощности 70 л.с. достигать уже 139 км/ч, что свидетельствует о весьма неплохой, а по тем временам и вовсе выдающейся, аэродинамике.

Уникальность автомобиля Tropfenwagen (1921 г.) состояла не только в потрясающе низком Сх (0,28), но и необычной компоновке с W-образным 6-цилиндровым двигателем в хвостовой части. Всего было выпущено около 100 таких моделей.

Но постепенно подход к проектированию обтекаемых кузовов менялся. Опыт в самолетостроении, накопленный за время Первой мировой войны, помог разработчикам взглянуть на проблему шире — они уже не стремились просто перенять удачные с точки аэродинамики формы, а начали их комбинировать, совмещать, пытаясь получить приемлемое для автомобиля решение. И быстро преуспели в этом деле.

В 1921 году инженером Эдмундом Румплером был создан Tropfenwagen – «машина-капля». Необычный автомобиль имел сильно зауженную в горизонтальной проекции переднюю и заднюю части, плавный изгиб крыши и овальную, вытянутую кабину – набегающий воздух он направлял не вверх и вниз, а в стороны. Проведенные в последствии, в 1979 году, компанией Volkwagen испытания показали, что Cx Tropfenwagen равнялся 0,28! И это при том, что выступающие за габариты колеса увеличивали сопротивление примерно на 50%. К сожалению, спросом экстравагантный автомобиль не пользовался – не помогал ни низкий расход топлива, ни появление удлиненной версии. идеальная форма — Сх =0,16

Одна из идеальных аэродинамических форм автомобиля – Cx равен 0,14-0,16. Возможны и другие, но их Cх будет так же находится в окрестности 0,15.

Сравнение форм задка. 1 – укороченная форма, характерная для серийных автомобилей 20-40-годов; 2 – «оптимальная» форма предложенная в 1934 г; 3 – идеальная форма. В последнем случае имеет место безотрывное обтекание кузова, а в 1-ом и 2-ом – точка отрыва располагается в месте расхождения с оптимальной формой. Таким образом, 2-ой вариант с крутым срезом задка оказывается предпочтительнее наклонной формы 1, ибо поток отрывается от кузова заметно позже.

Тем временем Институтом аэродинамических исследований в Геттингене (Германия) была выведена «идеальная» форма, Сх которой равнялся 0,16. В профиль такой кузов походил на современные Porsche 911, но имел более заостренную и узкую переднюю и заднюю часть. Однако если для спортивных двухместных автомобилей эта форма еще подходила — можно вспомнить великолепный Adler Triumph 1934 года – то для «гражданских» она казалась почти бесполезной – слишком нерационально использовался внутренний объем длинного «хвоста».

И все же попытки приблизиться к такому идеалу в серийном производстве предпринимались долго, а одной из самых успешных стала Tatra-87 1940 года. Угол наклона задка у неё был больше, но сильно зауженная сзади кабина и плавно спадающая подоконная линия позволили снизить Сх до 0,38.

Впрочем, к тому времени смысла в подобных хитростях уже не было – в 1934-ом исследователи пришли к выводу, что выгоды от покатой, вытянутой задней части кузова нет, если она не повторяет идеальную форму – как только наклон задка превышает определенное значение, поток срывается, и продолжающаяся часть хвоста оказывается в зоне разряжения. Следовательно, её можно просто отбросить без ущерба для аэродинамики, а в некоторых случаях даже на этом и выиграть, ведь в зоне разряжения оказывается меньшая площадь поверхности. Что, собственно, чуть позже и продемонстрировал автомобиль конструктора Камма под индексом К5 – его Сх равнялся 0,37. А это означало, что впервые аэродинамика и практичность нашли точку пересечения, но началась война…

Первым автомобилем с оптимизированной формой укороченного задка был опытный К5 конструктора Камма, построенный на шасси Mercedes-Benz 170V в 1938 году. Его Сх равнялся 0,37 (в отличие от донора 170V, у которого Cx был 0,55)

Надо отметить, что все упомянутые наработки почти не коснулись серийных автомобилей 20-40-ых годов. Конечно, за этот период Сх в среднем снизилися с 0,8 до 0,55, но в основе этого лежали лишь компоновочные и стилистические изменения – сохраняя выступающие крылья и фары, автомобили становились более вытянутыми и округлыми. Те же модели, что внешне казались обтекаемыми, только подражали реально эффективным кузовам.

Не сильно изменилась ситуация и послевоенные годы. Целенаправленные работы по созданию обтекаемых автомобилей почти остановились, а Cx серийных моделей снижался в основном за счет объединения отдельно выступающих фар и крыльев в единую форму кузова. И все же к 60-ому году некоторые автопроизводители обратили внимание на аэродинамику. Так, в 1955-ом вышел Citroen DS, потрясший мир не только множеством неординарных конструктивных решений, но и великолепной обтекаемостью – Cx составлял всего 0,38. Отличился и Porsche со своей моделью 356, второе поколение которой в 1959 году достигло Cx равного 0,39. И это в то время, когда для большинства автомобилей была характерна величина около 0,5.

Постепенно стали подтягиваться и остальные автопроизводители – росла мощность моторов, увеличивались скорости, и к 70-ому году вместе с модой на угловатые кузова окончательно утвердилась и роль аэродинамики, как одной из приоритетных областей совершенствования автомобилей.

Оптимизация

Однако задача перед инженерами стояла уже другая: если раньше они трудились над созданием оптимальной аэродинамической формы, то отныне их работа заключалась в оптимизации предложенного дизайнерами проекта. То есть в последовательном изменении отдельных частей кузова, таких, как переходы, выступы, спойлеры, с целью снижения сопротивления воздуха при минимальном вмешательстве в дизайн. И хотя это означало гораздо меньшую свободу действий, тем не менее, на практике такой подход оказался весьма эффективным. В частности, в 70-ых он помог удержать Cx на уровне 0,45, несмотря на переход к более угловатым формам кузова, а в дальнейшем, особенно с появлением мощных суперкомпьютеров, позволил неизменно совершенствовать аэродинамику автомобилей вплоть до наших дней.

Но как же при столь ограниченном вмешательстве удалось достичь почти такой же обтекаемости, что и у кузовов, изначально спроектированных с учетом аэродинамики? Оказывается, факторов, принципиально влияющих на обтекаемость, не так уж и много. Их мы сейчас и рассмотрим.

Передний спойлер Передний спойлер уменьшает воздушный поток под днищем автомобиля, а вместе с ним и общее аэродинамическое сопротивление. Правда, справедливо это лишь для маленького спойлера – большой уже увеличивает Cx и работает на создание прижимной силы, создавая существенную зону разряжения под передком.

К носовой части автомобиля (оформлению бампера, фар и решетки радиатора) требований предъявляется немного, и различные формы могут обеспечивать почти одинаковое сопротивление – все же «разрезать» воздушный поток не составляет больших проблем. Однако в этом месте важно придать воздуху правильно направление, ведь от этого зависит характер обтекания остальной поверхности кузова. В частности, нужно избегать отрыва потока от передней кромки капота – образующая за ней зона разряжения может протянуться аж до лобового стекла и увеличить Cx примерно на 0,05 единиц. Для этого, особенно при сильном наклоне передка, необходимо сглаживать переход к капоту, избегая резких граней.

Дополнительно можно отыграть несколько сотых, установив небольшой передний спойлер. Сам по себе он, конечно, увеличивает Cx, частично препятствуя затеканию воздуха под автомобиль, но это компенсируется падением сопротивления днища, где уже гораздо меньший поток сталкивается с полосой препятствий в виде рычагов подвески, картеров агрегатов и выхлопной системой. Нередко подобного эффекта добиваются и за счет небольшого наклона автомобиля вперед – достаточно даже 2 градусов, чтобы понизить Cx на пару-тройку процентов.

А вот наклон лобового стекла, как ни странно, однозначного влияния не оказывает – в пределах стандартых 30-40 градусов четкая связь с величиной Cx не прослеживается. Зато положительную роль играет небольшая выпуклость крыши – снижение Cx может составить две-три сотых. Правда, это верно лишь при условии сохранения высоты кузова – кривизна должна достигаться вследствие увеличения наклона лобового и заднего стекла, ибо в противном случае уменьшение Cx нивелируется увеличением площади поперечного сечения.

Главный же элемент, определяющий аэродинамику автомобиля, – задняя часть кузова. Здесь счет идет уже не на сотые, а на десятые доли Cx!

Хэтчбеки и универсалы Характер обтекания универсалов и хэтчбеков с большим наклоном пятой двери (коих подавляющее большинство) одинаков – поток отрывается от задней кромки крыши.

Автомобили с углом наклона задка около 30 градусов Уменьшение угла наклона задней части до 30 градусов приводит к образованию кромочных вихрей, создающих дополнительное разряжение позади автомобиля. При дальнейшем же уменьшении наклона вихри ослабевают, и примерно на 23 градусов достигается плавное и безотрывное течение потока по наклонной поверхности.

Наименее эффективной оказывается форма с крутым срезом, то есть кузов типа универсал – поток срывается прямо с кромки крыши, и за машиной образуется обширная зона разряжения, увеличивающая сопротивление движению. Сопутствующей неприятностью является и быстрое загрязнение заднего стекла, ибо в «пустующее» позади пространство активно устремляется поднятая пыль и грязь. И поправить положение никак нельзя, разве что установить дефлектор на крыше, над пятой дверью, отсекающий часть потока вниз – так и стекло будет медленнее пачкаться и разряжение слегка упадет. Подобное решение часто встречается на современных универсалах.

Кузова со скошенной задней частью (как правило, хэтчбеки) выглядят, на первый взгляд, предпочтительнее – поток стекает по наклонной поверхности и отрывается внизу пятой двери, оставляя гораздо меньшую область разряжения. Однако справедливо это лишь при малом наклоне задка, не более 23-х градусов. Среди современных гражданских автомобилей такой формой обладают, пожалуй, только Audi A5 Sportback да Porsche Panamera. Большинство же остальных хэтчбеков и близко не подбираются к этой цифре, а потому по обтекаемости они эквивалентны универсалам и точно так же оснащаются задним стеклоочистителем. Попытки же приблизиться к оптимальному углу чреваты еще большими проблемами. А дело в том, что при уменьшении наклона до 28-32 градусов воздушный поток оказывается в неком переходном состоянии – точка отрыва уже перемещается на нижнюю кромку задка, но плавного обтекания еще наблюдается. При этом на наклонной поверхности возникают так называемые кромочные вихри – потоки с боков кузова начинают попадать на наклонный задок и, закручиваясь по спирали, создают значительное разряжение позади автомобиля. И хотя заднее стекло уже не пачкается, ибо вихри направлены вниз, Cx получается наихудшим. В свое время именно с такой проблемой столкнулся Москвич 2141, который при всей своей визуальной обтекаемости, имел Cx около 0,47.

А что же делать инженерам, если им на стол лег такой неудачный дизайнерский проект с наклоном близким к 30 градусам? Если поменять угол никак не нельзя, то можно пойти на крайние меры и установить на торце крыши спойлер — он сорвет поток, предотвратив образование кромочных вихрей, и по обтекаемости такой автомобиль хотя бы приблизится к универсалам. Впрочем, при небольшом наклоне (< 28 градусов) есть и менее радикальный способ – разместить в том же месте спойлер чуть поменьше, который не сорвет поток, а лишь переведет в турбулентное состояние, что поможет ему лучше удерживаться на наклонной поверхности.

Современные седаны и купе, как правило, демонстрируют наилучшие показатели обтекаемости среди остальных типов кузовов. А в некоторых случаях даже удается добиться безотрывного течения потока по заднему стеклу.

Описанные проблемы встречаются и на автомобилях со ступенчатым задком, например, седанах и купе, но последствия уже не столь страшны – отовравшийся с крыши поток или закрутившийся на стекле кромочных вихрь «приземляется» на крышку багажника, успокаивается, а затем вновь и уже окончательно отрывается от задней кромки. В результате разряжение за задним стеклом получается небольшим, а вихревой след за автомобилем — почти как у хэтчбека с малым наклоном задка. Кроме того, увеличивая высоту и длину багажника, можно дополнительно понизить Cx на несколько сотых – чем раньше поток коснется поверхности, и чем дольше он будет пребывать в стационарном состоянии, тем лучше. Почти так же эффективно и небольшое сужение задней части. В общем, возможностей для оптимизации в данном случае предостаточно, а потому на практике именно седаны или купе, особенно больших размеров, и демонстрируют наилучшую обтекаемость.

А дальше?

Возможность достижения значений Сх ниже 0,2 для рядовых автомобилей была доказана еще в 1977 году дизайн-студией Pininfarina. Представленный ими макет седана имел Cx 0,18!

Читая пресс-релизы и отслеживая презентации новых моделей, трудно усомниться в прогрессе автомобильной аэродинамики – столь восторженно автопроизводители докладывают о своих достижениях. Однако если посмотреть на такие дорогие машины как BMW и Mercedes, то с удивлением можно обнаружить, что за последние 15-20 лет улучшений практически нет. Например, Cx «семерки» BMW образца 1986 года равнялся 0,34, а последней модели – только 0,31. Более того, новый Mercedes E-класса с его Сх равным 0,27, кстати, весьма неплохой величиной по нынешним меркам, оказывается на одном уровне с E-классом 1995-го модельного года! Аналогичная картина и c «пятеркой» BMW.

Таким образом, нижняя граница Сх нащупана уже давно, а наблюдаемый прогресс объясняется лишь снижением стоимости исследований, что позволило менее именитым брендам подтянуться к компаниям, изначально не жалевшим денег на проработку аэродинамики.

А как же двигаться дальше? Об этом уже давно говорят многие специалисты – необходимо вновь пересматривать роль аэродинамики в процессе создания автомобиля. Нужны новые формы, новые пропорции, главенство инженерной мысли над фантазией дизайнера. И потенциал здесь скрыт немалый – речь не только о выведенной еще в 20-ых годах идеальной форме с Сх 0,16, но и о более поздних исследованиях, подтвердивших, что обтекаемость и рациональная компоновка – понятия не взаимоисключающие.

Прижимная сила

Благодаря несимметричному профилю поток над плоскостью крыла течет быстрее, что, согласно закону Бернулли, создает над крылом зону разрежения а, в конечном итоге, и подъемную силу.

Почему крыло самолета создает подъемную силу? Отнюдь не из-за угла между ним и набегающим потоком, как кажется на первый взгляд – угол этот может быть и нулевым (хотя при его увеличении подъемная сила и возрастает). Секрет крыла кроется в его особом профиле. Оказывается, будучи несимметричным, оно разрезает набегающий воздух таким образом, что верхний поток проходит больший путь, чем нижний. С учетом несжимаемости воздуха (на малых скоростях) это означает, что над крылом скорость потока выше, а статическое давление, соответственно, ниже. Эта разность давлений и создает подъемную силу.

При чем же здесь автомобиль? А притом, что характер его обтекания воздухом практически тот же: нижний поток, ныряя под днище, обходит кузов по прямой, а верхний вынужден ускоряться, дабы успеть обогнуть автомобиль сверху. Отсюда все та же разница в давлении и подъемная сила. Правда, во многом она компенсируется динамическим давлением воздуха на капот и лобовое стекло — отталкивая поток вверх, автомобиль, согласно закону сохранения импульса, сам дополнительно прижимается к земле.

В итоге подъемная сила получается невелика – как правило, даже на предельной скорости автомобиль разгружается не более чем на 100 кг.

Характер обтекания автомобиля во многом повторяет ситуацию с крылом — все так же воздух сверху ускоряется, а его давление падает.

В общем-то, этой величиной можно и пренебречь, но беда в том, что по осям она распределяется неравномерно – если передок автомобиля, как уже было сказано, догружается встречным воздухом, то задняя часть кузова нередко оказывается еще и в области сильного разряжения из-за отрыва потока. В результате с набором скорости постепенно меняется баланс автомобиля: задняя ось разгружается, увеличивая риск заноса. С этой неприятностью в основном и борются производители массовых автомобилей, тем более что до некоторого момента снижение подъемной силы не противоречит уменьшению лобового сопротивления.

Например, стремление к безотрывному обтеканию кузова воздухом понижает не только Сx, но и подъемную силу, ведь над автомобилем в таком случае не возникает локальных зон резко пониженного давления. Аналогично две цели преследует и выравнивание поверхности днища – поток воздуха под автомобилем меньше «цепляется» за неровности, его скорость возрастает, а давление, наоборот, падает. То, что нужно!

Задний спойлер

В отличие заднего спойлера, «работающего» на улучшение Cx, спойлер, увеличивающий прижимную силу, имеет большие размеры и заметный наклон по отношению к воздушному потоку.

С целью снижения подъемной силы, действующей на заднюю ось, часто применяется небольшой спойлер. Размещенный на задней кромке кузова, в месте отрыва потока, он не только уменьшит Cx, ослабив вихри позади автомобиля, но и прижмет автомобиль к дороге, отталкивая вверх набегающий поток воздуха. Правда, здесь уже важно знать меру – слишком большой спойлер негативно скажется на обтекаемости, увеличив и без того обширную зону разряжения за автомобилем. Из-за этого на некоторых машинах он даже делается выдвижным, чтобы вступать в работу лишь при необходимости.

Таков инструментарий инженеров при разработке «гражданского» автомобиля. А как же быть со спортивными или тем более гоночными моделями? Чтобы удержать болид в повороте нужен уже гораздо более серьезный арсенал, превращающий подъемную силу в прижимную. Причем подчас такую, что автомобиль смог бы ездить и по потолку!

Передний спойлер

Чтобы добиться заметного эффекта, передний спойлер должен быть очень большим,что неизбежно увеличивает лобовое сопротивление.

Одним из подобных радикальных средств является передний спойлер. Идея проста – не пустить воздух по днище, создав тем самым область пониженного давления, присасывающую автомобиль к дороге. Для большего эффекта и равномерного распределения прижимной силы одновременно может применяться и специальный обвес вдоль порогов, «герметизирующий» днище по бокам. Простое и эффективное это решение почти повсеместно применяется на гоночных автомобилях, однако на суперкарах, предназначенных все же для дорог общего пользования, массивный спойлер встретишь нечасто. Причин тому две: первая – снижение геометрической проходимости, ведь спойлер должен едва ли не касаться земли, вторая – увеличение лобового сопротивления. А, разумеется, для большинства покупателей суперкаров важнее круглая цифра максимальной скорости, нежели цепкость в повороте на 200км/ч.

К тому же есть и другие решения, почти не портящие обтекаемость. Правда, без серьезного вмешательства в конструкцию автомобиля тут уже не обойтись…

Форма кузова

Помимо низкого центра тяжести такая форма кузова дает и выигрыш в прижимной силе при минимальном лобовом сопротивлении.

Речь, прежде всего, об особой форме кузова, примером которой могут послужить суперкары Lamborghini. Минимальная высота, смещенная вперед кабина, сильно наклоненное лобовое стекло и почти горизонтальная задняя часть – автомобиль словно приплюснут сверху. А, как мы помним, чем меньше кривизна верхней части кузова, тем ниже скорость воздушного потока над ней, и тем больше прижимная сила. И все это при низком лобовом сопротивлении, ведь с такими линиями отрыв потока почти исключен, а площадь поперечного сечения минимальна.

К сожалению, воспользоваться всеми перечисленными преимуществами дано лишь избранным – среднемоторным суперкарам с очень низкой крышей. В остальных случаях придание задней части автомобиля столь малого наклона приведет к увеличению лобового сопротивления, ибо кромка задка, с которой отрывается поток, окажется слишком высоко. Предельный случай – кузова типа универсал: в сравнении с седанами или хэтчбеками их Cx максимален, хотя, с точки зрения прижимной силы, они по-прежнему впереди всех!

Граунд-эффект

Даже столь быстрые суперкары, как Ferrari Enzo, не ограничивают доступ воздуха под днище спойлером. Наоборот, они «подминают» поток под себя…

…чтобы ускорить и понизить давление, а затем выпустить его через диффузор позади.

Более хитрым способом прижать автомобиль к земле является так называемый граунд-эффект. В его основе лежит все та же обратная зависимость между скоростью потока и давлением: если под днищем автомобиля разогнать воздух, то его статическое давление упадет, а прижимающая сила, соответственно, вырастет. Но как ускорить воздух? Для этого необходимо так спрофилировать днище, чтобы оно вместе с поверхностью дороги представляло собой сужающийся канал – в простейшем случае дно можно сделать не плоским, а немного выгнутым. Кроме того, нужно обеспечить более-менее свободный доступ воздуха под автомобиль, то есть, как минимум, не преграждать ему путь спойлером, а так же правильно организовать его выход позади автомобиля, применив диффузор. Задача последнего – помочь «вытягиванию» воздуха из-под днища, используя область низкого давления, образующуюся за автомобилем, а параллельно и уменьшить саму область разряжения, направив в неё воздух. Собранные же воедино все эти элементы могут дать совершенно поразительный результат, выражающийся в большой прижимной силе при низком лобовом сопротивлении. Например, в болидах Формулы-1, даже несмотря на строгий регламент, ограничивающий форму днища, на долю граунд-эффекта приходится около 40% от общей величины создаваемой прижимающей силы.

А откуда берутся оставшиеся 60? Их обеспечивают антикрылья.

Антикрылья

Составное антикрыло помогает сильнее прижать автомобиль к дороге, избежав сильного вихреобразования позади себя – поток проникает в щели между планками, уменьшая образующуюся зону разряжения.

Впервые появившиеся в 60-ых годах в Формуле-1 антикрылья стали неотъемлемым атрибутом гоночных автомобилей всех мастей. Конструктивно это те же крылья, о которых шла речь в начале статьи, только перевернутые. Соответственно, область пониженного статического давления образуется не сверху, а снизу, и крыло уже не стремиться взлететь, а тянет вниз. Правда, при установке параллельно воздушному потоку, как того требуют соображения о минимизации лобового сопротивления, заметный эффект достигается лишь на очень большой скорости, в то время как прижимная сила нужна в поворотах, где темп, наоборот, невысок. В связи с этим антикрылья обычно устанавливаются под некоторым углом к потоку (углом атаки), дабы прижимать автомобиль и за счет динамического давления встречного воздуха. Но опять незадача – при этом возрастает лобовое сопротивление! И чем выше нужна прижимная сила, тем больше угол атаки, и тем хуже обтекаемость.

С этого момента и начинается инженерное искусство. Например, вместо антикрыла с одним профилем применяются двойные или даже тройные конструкции – так при заданных габаритах удается увеличить общую поверхность антикрыла и получить бОльшую прижимную силу, не прибегая к повышению угла атаки. Если же без наклона пластин все-таки не обойтись, то дополнительно изгибают и сам профиль – теперь, разместив пластины многоярусного антикрыла с небольшим смещением, можно развернуть поток так, чтобы уменьшить разряжение позади них. Отдельное внимание уделяется торцам антикрыльев – в этом месте происходит смешивание попавшего и не попавшего на крыло потоков, а потому велик риск образования вихрей. Во избежание этого устанавливаются специальные торцевые пластины, разделяющие эти потоки. Казалось бы, простой элемент, но взгляните, сколь сложна форма этих пластин на болидах Формулы-1 – описанию она просто не поддается, но именно в этом – вся красота аэродинамики.

Руководство по аэродинамике для начинающих: уравнение сопротивления — уровень -1

Начинающий Руководство по аэродинамике
Drag Equation — Level 1
Answers

Нажмите на Перетащите уравнение, чтобы открыть соответствующий слайд. Изучите уравнение и прочтите объяснение этой концепции. Затем используйте информацию, чтобы ответьте на вопросы ниже.

В следующем В таблице определите каждую переменную в уравнении. Укажите соответствующий единиц для каждого значения:

переменная	Личность	Метрическая система Единицы	Английский Единицы
D	Перетащите	Ньютонов	фунтов
Кд	Коэффициент сопротивления	Нет единиц	Нет единиц
r	Плотность воздуха	кг / м ³	снарядов / фут ³
В	Скорость	м / с	фут \ с
А	Учетная площадка	м ²	футов ²

А.Какие возможные справочные области (A) можно использовать для расчета сопротивления?
Общая площадь ЛА, лобовая площадь самолета или площадь крыла.

Б. Если мы хотим вычислить L / D (коэффициент подъемной силы к сопротивлению), площадь, которую мы хотели бы использовать? Почему?
Площадь крыла, поскольку подъемная сила рассчитывается с использованием площадь крыла.

С.Помимо контрольной площади, плотности воздуха и скорости, сопротивление зависит от несколько других значений. Какая переменная используется для моделирования многих сложных зависимости перетаскивания? Каковы некоторые из зависимостей встроенного перетаскивания в этом значении?
Cd — коэффициент аэродинамического сопротивления. Некоторые зависимости сопротивления включены в это значение форма, наклон и некоторые условия потока.

Рассчитайте следующее проблемы, связанные с лобовым сопротивлением самолета: ( Перед вычислением, убедитесь, что все единицы согласны)
А.Предположим, вы летят на самолете со следующей формой и размерами крыла. Какая общая площадь крыла?

A = 1 / 2h (b ₁ + b ₂) = 1/2 x 76,48 (25,3 + 48,9) = 2834,44 фута ² для одного крыла
= 5668,88 футов ² для обоих крыльев

Б.Тяга самолета составляет 120 000 фунтов, а плотность воздуха составляет 0,00048 снарядов / куб. фут. Текущая крейсерская скорость составляет 450 футов / сек, и нам нужно определить сопротивление. коэффициент самолета. Найдите компакт-диск. (Подсказка: вы можете захотеть преобразовать сначала исходное уравнение)
Cd = 2D / (г x V ² x A) = 2 (120 000) / (. 00048) (450) ² (5668,88) = . 436

С.Погода условия вынуждают самолет снижаться до уровня, при котором плотность воздуха составляет .00076 слизней / куб. фут. Тяга двигателя увеличивается до 250 000 фунтов. Какова скорость самолета на новой крейсерской высоте? (Намекать: еще раз, вы можете сначала преобразовать уравнение)
В = sqrt (2D / Cd x r x A) = sqrt (2x (250 000) / (. 436 x 0,00076 x 5668,88)) = 516 фут / сек

Drag Queens: сравнение аэродинамики

Из июньского выпуска Автомобиль и водитель

Подобно ночному вору, сопротивление ветра — это незаметный злоумышленник, который снижает вашу скорость и убивает ваш километраж, не оставляя отпечатков пальцев.Мягкое журчание воздуха, струящегося над вашей машиной, под ней и сквозь нее, противоречит отвратительным течениям ветра.

Даже если нет альтернативы движению в атмосфере Земли, мы, по крайней мере, можем бороться с сопротивлением ветру с помощью науки. Аэродинамика — изучение движения воздуха — может поднять нашу максимальную скорость, сократить расход топлива и, если мы будем в этом разбираться, удержать наши шины прилипшими к асфальту.

Задолго до того, как автомобильные инженеры начали беспокоиться об аэродинамике, пионеры авиации определили основные принципы сопротивления и подъемной силы.Вдохновленные птицами и дирижаблями, демоны ранней скорости также играли с обтекаемыми формами. Первым автомобилем, который разогнался до скорости 60 миль в час (в 1899 году), была электрическая торпеда на колесах, которую весело назвали «La Jamais Contente» («Неудовлетворенные»). Гонщики Гран-при взялись за дело в начале 1920-х годов; В следующем десятилетии Auto Union и Mercedes-Benz разогнались до 300 миль в час с обтекаемыми моделями, разработанными в немецких аэродинамических трубах. Спустя полвека после того, как Чак Йегер преодолел звуковой барьер в полете, Энди Грин на своем Thrust SSC проехал 763 миль в час по пустыне Блэк-Рок в Неваде.

МАРК БРЭМЛИ, А.Дж. МЮЛЛЕР, РОЙ РИТЧИ, МАРК УРБАНО, ПРОИЗВОДИТЕЛЬ

Теперь наша очередь. Автомобиль и водитель собрал пять скользких автомобилей, чтобы изучить их характеристики сопротивления и подъемной силы в аэродинамической трубе, название и местонахождение которой мы поклялись не раскрывать. У нас были две цели: во-первых, изучить тонкости обдува автомобиля воздухом в испытательной камере; во-вторых, чтобы определить, какая марка лучше всех оптимизирует аэродинамические характеристики своего автомобиля.

Есть причины, по которым вы раньше не читали эту историю. Каждый крупный автопроизводитель владеет и эксплуатирует аэродинамическую трубу, но эти объекты загружены круглосуточно, поскольку инженеры работают над тем, чтобы опережать быстро растущую тенденцию к увеличению пробега EPA. Другой проблемой, мешающей легкому доступу, является соперничество между компаниями. В то время как производители часто рекламируют скользкость своей продукции, сравнения с конкурирующими моделями случаются редко.

Ответственный эксперт на нашем подпольном испытательном полигоне объясняет: «Все аэродинамические трубы стремятся точно оценить аэродинамику автомобиля в реальном мире.Транспортное средство и туннель составляют систему со сложными взаимодействиями. В результате измерения сопротивления и подъемной силы на конкретном транспортном средстве могут варьироваться от одного туннеля к другому ».

По его словам, группа транспортных средств может по-разному размещаться в разных туннелях. Вот почему большинство производителей так мало верят в показатели аэродинамики, измеряемые за пределами их собственных предприятий. Тестирование на выбеге, при котором регистрируется скорость автомобиля при его замедлении, часто рекламируется как лучший «реальный» способ измерения аэродинамических свойств автомобиля.«В принципе, это может быть правдой, но на практике трудно получить точные результаты, потому что на результаты влияют колебания ветра, температуры трансмиссии и качества шин. Прелесть аэродинамических труб в том, что они жестко контролируют переменные ».

Этот контент импортирован с YouTube. Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.

Нашим победителем здесь будет автомобиль с наименьшей площадью лобового сопротивления, которая является произведением площади лобовой части формы и ее коэффициента аэродинамического сопротивления и истинным показателем способности автомобиля противостоять ветру [см. «Немного многословный глоссарий» ниже] .На этом мы смиренно представляем наше первое в истории аэросравнение.

НЕКОТОРЫЙ ГЛОССАРИЙ С ДЛИННЫМ ОБОРОТОМ

Аэродинамическая мощность в лошадиных силах: Мощность, необходимая для движения транспортного средства в атмосфере (без учета трансмиссии и потерь при качении шин). Она увеличивается вместе с кубом скорости, так что аэродинамическая мощность на 100 миль в час в 2,9 раза превышает требуемую мощность на скорости 70 миль в час.

Площадь сопротивления: Произведение коэффициента лобового сопротивления и площади лобовой части является лучшим показателем аэродинамических характеристик любого автомобиля, поскольку оно прямо пропорционально горизонтальной силе, измеренной в аэродинамической трубе и испытанной на дороге.

Коэффициент сопротивления (CD): Безразмерный параметр, используемый для количественной оценки аэродинамической эффективности в горизонтальной плоскости (лобовое сопротивление).

Фронтальная область: Самый крупный горизонтальный вид автомобиля. Мы использовали 200-миллиметровый объектив камеры, расположенный в 150 футах от транспортного средства, чтобы сделать цифровую фотографию, которую мы проанализировали с помощью программного обеспечения Siemens Solid Edge CAD.

Лифт: Воздух, проходящий над автомобилем и под ним, а также через решетку, может уменьшить нагрузку на колеса и, в крайних случаях, ухудшить управляемость.Воздушные дамбы и интерцепторы — эффективные средства противодействия.

Сопротивление ветру (сопротивление): Сила, пропорциональная площади сопротивления, увеличивается пропорционально квадрату скорости автомобиля.

Линии обтекания: Операторы аэродинамической трубы добавляют небольшое количество дыма в воздушный поток, чтобы показать, как ветер движется вокруг, под или сквозь тестируемое транспортное средство.

Площадь сопротивления = 7,8 фут²
Лист — самая квадратная форма, которую мы катили в аэродинамической трубе, и у него вторая по величине лобовая площадь в этом тесте — 24.5 квадратных футов. В сочетании с коэффициентом лобового сопротивления 0,32 это дает площадь лобового сопротивления 7,8 квадратных футов. Это разумная цифра для пятиместного универсала и всего на 30 процентов больше, чем у двухместной пулевидной модели Honda Insight 2001 года, которую мы привезли с собой и проверили для справки.

МАРК БРЭМЛИ, А.Дж. МЮЛЛЕР, РОЙ РИТЧИ, МАРК УРБАНО, ПРОИЗВОДИТЕЛЬ

Фары с «глазками» гордо возвышаются над V-образным носом Leaf, чтобы отводить воздух от наружных зеркал, которые часто являются источником турбулентности, сопротивления и шума.Чтобы максимально увеличить пространство в кабине, боковые окна приподняты, а крыша плоская, как лист фанеры. Хвост этого люка больше похож на защищающую от ветра телефонную будку, чем на гладкую каплю дождя.

МАРК БРЭМЛИ, А.Дж. МЮЛЛЕР, РОЙ РИТЧИ, МАРК УРБАНО, ПРОИЗВОДИТЕЛЬ

Нижняя часть кузова Leaf плоская и скользкая (что все чаще встречается в новых автомобилях), а полосы диффузора встроены в его заднюю панель. В чистом электромобиле нет необходимости в большом радиаторе, поэтому единственный воздух, попадающий в нижнюю решетку, — это охлаждение электрооборудования и вентиляция аккумулятора и салона.Воздух, проходящий через внутренние полости автомобиля, является основным источником сопротивления и подъемной силы.

Nissan инвестировал 5 миллиардов долларов в разработку первого серийного электромобиля, продаваемого по всей Америке. Если повезет, у котенка осталось несколько иен, чтобы снизить сопротивление в следующем поколении.

Площадь перетаскивания = 7,0 фут²
У CLA 250 самая маленькая лобная площадь в этом тесте. Измеренный нами коэффициент лобового сопротивления — 0,30 — выше, чем ожидалось для того, что Mercedes называет эталоном аэродинамики для серийных автомобилей.Но стоит отметить, что Mercedes не поддерживает специальные функции, такие как автоматические жалюзи решетки радиатора, на американских моделях. И хотя этот спортивный седан оснащен двигателем с турбонаддувом и автоматической коробкой передач, чтобы сохранять хладнокровие, его площадь лобового сопротивления в 7,0 квадратных футов конкурентоспособна с гибридами и электрикой.

МАРК БРЭМЛИ, А.Дж. МЮЛЛЕР, РОЙ РИТЧИ, МАРК УРБАНО, ПРОИЗВОДИТЕЛЬ

Оба конца CLA агрессивно сужены, чтобы избежать ветра.Фары заворачиваются назад, как глаза королевы ботокса, слишком туго затянутой в хвост. Мини-спойлеры под автомобилем направляют воздух вокруг передних шин, а обтекатели сглаживают поток воздуха под двигателем и задней подвеской.

Крыша CLA жертвует некоторой задней высотой, но следует отдать должное Mercedes за то, что он придал своей модели начального уровня аэродинамический дизайн, обеспечивающий высокую топливную экономичность.

МАРК БРЭМЛИ, А.Дж. МЮЛЛЕР, РОЙ РИТЧИ, МАРК УРБАНО, ПРОИЗВОДИТЕЛЬ

Область перетаскивания = 6.7 футов²
Коэффициент аэродинамического сопротивления среднего блока Volt (0,28) и площадь лобовой части (23,7 квадратных фута) дают ему оценку площади лобового сопротивления, которая, в общем, соответствует среднему уровню. Традиционно выглядящая решетка этого подключаемого гибрида почти полностью заблокирована, чтобы отводить воздух сверху и по бокам. Это дает увеличение нагрузки на переднюю ось на 15 фунтов на скорости 70 миль в час, что способствует устойчивости на шоссе.

Передние фары Volt простираются до колес, а от верхней части решетки до задней кромки люка есть лыжный магнат красивой формы, обеспечивающий плавный ход для скольжения.Боковые зеркала заднего вида, установленные на стойках, пропускают ветер. GM создал Volt так, чтобы воздушный поток оставался на боковых поверхностях как можно дольше, чтобы уменьшить турбулентность. Плоский удлинитель люка помогает стабилизировать кильватерный след автомобиля.

МАРК БРЭМЛИ, А.Дж. МЮЛЛЕР, РОЙ РИТЧИ, МАРК УРБАНО, ПРОИЗВОДИТЕЛЬ

Но даже если хвосты Prius и Volt выглядят примерно одинаково, мы измерили на 50 процентов больше подъемной силы сзади у Chevy. Снижение нагрузки на задние колеса Volt на 26 фунтов не вызывает беспокойства, но именно такая разница говорит вам, что вы должны доверять аэродинамической трубе, а не визуальной оценке формы любого автомобиля.

МАРК БРЭМЛИ, А.Дж. МЮЛЛЕР, РОЙ РИТЧИ, МАРК УРБАНО, ПРОИЗВОДИТЕЛЬ

Площадь лобового сопротивления = 6,2 фута²
Многолетний представитель Toyota в области гибридных технологий занял второе место в нашем тестировании с аккуратной лобовой площадью 23,9 квадратных фута и чистым коэффициентом аэродинамического сопротивления 0,26. Подключаемые модули Prius, Prius C и Prius третьего поколения — самые эффективные гибриды на рынке, во многом потому, что они отдают ветру так мало энергии.Это приводит к 50 милям на галлон в комбинированных оценках экономии топлива EPA и только 42 лошадиным силам (по сравнению с уже низкими 45 у Volt), необходимыми для преодоления аэродинамического сопротивления на скорости 100 миль в час.

МАРК БРЭМЛИ, А.Дж. МЮЛЛЕР, РОЙ РИТЧИ, МАРК УРБАНО, ПРОИЗВОДИТЕЛЬ

Верхняя поверхность этого автомобиля имитирует аэродинамический профиль — одну из самых эффективных форм для пробивания чистой дыры в атмосфере. Лобовое стекло сливается с крышей без дополнительных молдингов, препятствующих воздушному потоку.Зеркала в форме яйца хорошо отделены от почти плоских боковых поверхностей. Спицы колесных колпаков гладкие, чтобы свести к минимуму отток.

Круто наклоненный капот и контролируемый поток воздуха через двигатель / моторный отсек обеспечивают 4 фунта передней прижимной силы на скорости 70 миль в час. Задний подъемник составляет всего 17 фунтов.

Площадь сопротивления = 6,2 фута²
Предел победы Tesla над Prius кроется в погрешности, характерной для аэродинамических труб. S занимает наш верхний слот благодаря своим большим 25.2 квадратных фута и более низкий коэффициент лобового сопротивления 0,24, что дает такую же площадь лобового сопротивления 6,2 квадратных фута, как у Prius. Низкое лобовое сопротивление — более сложная задача с большей лобовой площадью, отсюда и общая победа Tesla. Будьте осторожны при проверке наших математических расчетов, потому что в конце вычислений измерения были округлены.

В Model S есть нечто большее, чем красивое лицо и гладкий внешний вид. Пневматическая подвеска снижает дорожный просвет на скоростях по шоссе (мы тестировали в нижнем положении). Контурный подбородок под решеткой помогает удерживать воздушный поток, проходящий под плоским днищем автомобиля.Внешние углы передней панели отклоняют воздух вокруг шин. Жалюзи закрывают три отверстия решетки до тех пор, пока внутренние теплообменники не потребуют воздушного потока. Спойлеры и ограждения отводят воздух от передних колесных арок, а выходящий воздух направляется под автомобиль, а не через колесные отверстия. Задний диффузор выравнивает поток, чтобы минимизировать подъемную силу и сопротивление, а сверху дополнительный спойлер из углеродного волокна уменьшает подъемную силу, не снижая сопротивления.

МАРК БРЭМЛИ, А.Дж. МЮЛЛЕР, РОЙ РИТЧИ, МАРК УРБАНО, ПРОИЗВОДИТЕЛЬ

Аэродинамика Model S стала результатом компьютерного моделирования, дополненного посещениями в аэродинамической трубе.Наши дорожные испытания Model S показали максимальную скорость 134 миль в час и реальный запас хода 211 миль. С более высокой передачей P85 Model S может разогнаться до 200 миль в час. Очевидно, что это аэродинамический электромобиль, заслуживающий пристального внимания мировых автопроизводителей. Это доказывает, что вы можете выглядеть гладко и одновременно.

Цена 9005 $ 34,9950004 9225

0048

Автомобиль

2014 Chevrolet Volt

2014 Mercedes-
Benz CLA250

2012 Nissan Leaf SL

2012 Tesla Model S P85

2014 Toyota Prius

$ 30,825

$ 38,100

$ 93,390

$ 29,245

Цена по результатам испытаний

$ 35,995

$ 35,855

$ 38,290

177.1 дюйм

182,3 дюйма

175,0 дюйма

196,0 дюйма

176,4 дюйма

Ширина

70,4 дюйма

70,0 дюйма

69,7 дюйма

77,3 дюйма

68,7 дюйма 56,6 дюйма

56,6 дюйма

61,0 дюйма

56,5 дюйма

58,7 дюйма

Колесная база

105,7 дюйма

106.3 дюйма

106,3 дюйма

116,5 дюйма

106,3 дюйма

Вес

3766 фунтов

3374 фунта

3353 фунта

4785 фунтов

3180 фунтов

Силовой агрегат

DOHC 1,4-литровый рядный 4 + электродвигатель переменного тока, вариатор

DOHC 2,0-литровый рядный 4-цилиндровый с турбонаддувом, 7-ступенчатая автоматическая коробка передач с двойным сцеплением

Электродвигатель переменного тока, одинарный скоростной привод

Электродвигатель переменного тока, односкоростной привод

DOHC 1.8-литровый рядный 4 + электродвигатель переменного тока, вариатор

Мощность л.с. при об / мин

84 при 4800 (двигатель)

208 при 5500

107 при 10000

416 при 8600

98 при 5200 (двигатель )

Крутящий момент LB-FT при об / мин

271 при 0 (двигатель)

258 при 1250

187 при 0

443 при 0

153 при 0 (двигатель)

Ведомые колеса

передний

задний

передний

Производительность

Ускорение

9008 с

6,3 с

10,2 с

4,6 с

10,0 с

¼-мили при MPH

16,7 с при 85

14,9 с при 95

17,7 с при 78

13,3 с 104

17,6 с при 79

Максимальная скорость

101 миль / ч (ограничено губернатором
)

133 миль / час (ограничено регулятором)

94 миль / час (ограничено регулятором)

134 миль / час (ограничено красной линией)

115 миль / час (ограниченное сопротивление)

Топливо

EPA City / Hwy

35/40 миль на галлон

Результаты работы по результатам отчета C / D , ноябрь 2011 г.

26/38 миль на галлон

Результаты производительности для C / D , декабрь 2013 г.

126/101 миль на галлон

Результаты производительности для C / D , март 2014.

88/90 миль на галлон

Результаты производительности от C / D , январь 2013 г.

51/48 миль на галлон

Результаты производительности по C / D , июль 2009 г.

Результаты тестирования аэродинамической трубы

Коэффициент сопротивления

0.28

0,30

0,32

0,24

0,26

Фронтальная площадь

23,7 квадратных футов

23,2 квадратных футов

24,5 квадратных футов

квадратных 25,2

Площадь перетаскивания
(фронтальная зона CD X)

6,7 квадратных футов

7,0 квадратных футов

7,8 квадратных футов

6,2 квадратных футов

6.2 квадратных фута

Drag Force
@ 70 миль в час

84 фунта

88 фунтов

97 фунтов

77 фунтов

78 фунтов

Aero Power

при

70 миль в час

16 л.с.

18 л.с.

14 л.с.

Aero Power
@ 100 миль в час

45 л.с. 42 л. миль / ч

26 фунтов

44 фунта

11 фунтов

17 фунтов

МАРК БРЭМЛИ, А.Дж. МЮЛЛЕР, РОЙ РИТЧИ, МАРК УРБАНО, ПРОИЗВОДИТЕЛЬ

Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты. Вы можете найти больше информации об этом и подобном контенте на сайте piano.io.

Что такое коэффициент лобового сопротивления — Площадь лобового сопротивления — Автомобили

Коэффициент лобового сопротивления широко используется в автомобильной конструкции. Коэффициент аэродинамического сопротивления CD — это обычно публикуемый рейтинг аэродинамического сопротивления автомобиля.

Коэффициент лобового сопротивления — Площадь сопротивления — Легковые автомобили

Коэффициент аэродинамического сопротивления является стандартной мерой в автомобильной конструкции . Коэффициент аэродинамического сопротивления C _D — это обычно публикуемый рейтинг аэродинамического сопротивления автомобиля , связанный с формой автомобиля. Умножение C _D на площадь лобовой части автомобиля дает индекс общего сопротивления. Результат называется площадью перетаскивания .

Поскольку аэродинамическое сопротивление и сила сопротивления возрастают пропорционально квадрату скорости, это свойство становится критически важным на более высоких скоростях.Уменьшение коэффициента лобового сопротивления в автомобиле улучшает характеристики автомобиля, поскольку это касается скорости и топливной экономичности. Средний современный автомобиль достигает коэффициента лобового сопротивления от C _D = 0,30 до 0,35.

Коэффициент сопротивления — характеристики сопротивления

Как было написано, характеристики сопротивления тела представлены безразмерным коэффициентом сопротивления , C _D, , определенным как:

Контрольная область A равна определяется как площадь ортогональной проекции объекта на плоскость, перпендикулярную направлению движения.Для полых объектов контрольная площадь может быть значительно больше, чем площадь поперечного сечения, но для неполых объектов она точно такая же, как и площадь поперечного сечения. Как можно видеть, коэффициент лобового сопротивления в первую очередь зависит от формы тела и учитывает как поверхностное трение, так и сопротивление формы. Это также может зависеть от числа Рейнольдса и шероховатости поверхности.

Когда доступны коэффициенты сопротивления и , общий коэффициент сопротивления определяется простым их сложением:

При низких числах Рейнольдса наибольшее сопротивление возникает из-за сопротивления трения .Это особенно актуально для обтекаемых тел, таких как аэродинамические поверхности. С другой стороны, при высоком числе Рейнольдса падение давления является значительным, что увеличивает сопротивление от сопротивления .

Ссылки:

Физика реакторов и тепловая гидравлика:

Дж. Р. Ламарш, Введение в теорию ядерных реакторов, 2-е изд., Эддисон-Уэсли, Ридинг, Массачусетс (1983).
Дж. Р. Ламарш, А. Дж. Баратта, Введение в ядерную инженерию, 3-е изд., Прентис-Холл, 2001, ISBN: 0-201-82498-1.
У. М. Стейси, Физика ядерных реакторов, John Wiley & Sons, 2001, ISBN: 0-471-39127-1.
Glasstone, Сесонске. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4-е издание, 1994 г., ISBN: 978-0412985317
Тодреас Нил Э., Казими Муджид С. Ядерные системы, том I: теплогидравлические основы, второе издание. CRC Press; 2 издание, 2012 г., ISBN: 978-0415802871
Зохури Б., МакДэниел П. Термодинамика в системах атомных электростанций. Springer; 2015, ISBN: 978-3-319-13419-2
Моран Михал Дж., Шапиро Ховард Н. Основы инженерной термодинамики, пятое издание, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
Кляйнштройер К. Современная гидродинамика. Springer, 2010 г., ISBN 978-1-4020-8670-0.
Министерство энергетики США, ТЕРМОДИНАМИКА, ТЕПЛООБМЕН И ПОТОК ЖИДКОСТИ. Справочник по основам DOE, том 1, 2 и 3. Июнь 1992 г.
Уайт Фрэнк М., Механика жидкости, McGraw-Hill Education, 7-е издание, февраль 2010 г., ISBN: 978-0077422417

Мы надеемся, что эта статья, Коэффициент перетаскивания — Область перетаскивания — Автомобили , поможет вам.Если это так, даст нам на боковой панели. Основная цель этого сайта — помочь общественности узнать интересную и важную информацию о теплотехнике.

% PDF-1.5 % 853 0 объект > эндобдж xref 853 75 0000000016 00000 н. 0000002415 00000 н. 0000002536 00000 н. 0000003233 00000 н. 0000003270 00000 н. 0000003384 00000 н. 0000003508 00000 н. 0000004326 00000 н. 0000004667 00000 н. 0000004886 00000 н. 0000005346 00000 п. 0000005693 00000 п. 0000006082 00000 н. 0000006426 00000 н. 0000006758 00000 н. 0000007088 00000 н. 0000007595 00000 н. 0000008025 00000 н. 0000008467 00000 н. 0000008872 00000 н. 0000008965 00000 н. 0000009328 00000 н. 0000009452 00000 н. 0000009857 00000 н. 0000010213 00000 п. 0000010674 00000 п. 0000010711 00000 п. 0000014872 00000 п. 0000016016 00000 п. 0000017914 00000 п. 0000018626 00000 п. 0000021275 00000 п. 0000023850 00000 п. 0000025794 00000 п. 0000026149 00000 п. 0000026547 00000 п. 0000026622 00000 п. 0000027032 00000 п. 0000027107 00000 п. 0000027519 00000 п. 0000027594 00000 п. 0000029228 00000 п. 0000029303 00000 п. 0000030939 00000 п. 0000031014 00000 п. 0000032650 00000 п. 0000032725 00000 п. 0000034361 00000 п. 0000034436 00000 п. 0000036072 00000 п. 0000036147 00000 п. 0000037781 00000 п. 0000037856 00000 п. 0000039488 00000 п. 0000039563 00000 п. 0000041198 00000 п. 0000041273 00000 п. 0000041684 00000 п. 0000041759 00000 п. 0000042187 00000 п. 0000042262 00000 п. 0000042681 00000 п. 0000042756 00000 п. 0000043185 00000 п. 0000043260 00000 п. 0000043672 00000 п. 0000043747 00000 п. 0000044165 00000 п. 0000044240 00000 п. 0000045874 00000 п. 0000045949 00000 п. 0000047584 00000 п. 0000057838 00000 п. 0000093694 00000 п. 0000001796 00000 н. трейлер ] / Назад 1508798 >> startxref 0 %% EOF 927 0 объект > поток hb««eb`d> ̀

Коэффициент сопротивления трения — обзор

4.11 Безразмерные формы уравнений и динамическое подобие

Для правильно определенной задачи или ситуации потока жидкости дифференциальные уравнения движения жидкости, основные и термодинамические свойства жидкости, а также граничные условия могут использоваться для определения безразмерных параметров, которые определяют ситуация представляет интерес еще до попытки решения уравнений. Определенные таким образом безразмерные параметры устанавливают важность различных членов в основных дифференциальных уравнениях и, таким образом, указывают, какие явления будут важны в результирующем потоке.В этом разделе описаны и представлены основные безразмерные параметры или числа, необходимые в оставшейся части текста. Многие другие, не упомянутые здесь, определены и используются в широкой области механики жидкости.

Безразмерные параметры для любой конкретной задачи можно определить двумя способами. Их можно вывести непосредственно из основных дифференциальных уравнений, если эти уравнения известны; этот метод проиллюстрирован здесь. Однако, если основные дифференциальные уравнения неизвестны или интересующий параметр не входит в известные уравнения, безразмерные параметры могут быть определены из анализа размеров (см. Раздел 1.11). Преимущество использования первой стратегии состоит в том, что безразмерные параметры, определяемые из уравнений движения, легче интерпретируются и связаны с физическими явлениями, происходящими в потоке. Таким образом, знание соответствующих безразмерных параметров часто помогает процессу решения, особенно когда для достижения решения необходимы допущения и приближения.

Кроме того, безразмерные параметры, полученные из уравнений движения жидкости, задают условия, при которых тестирование масштабной модели окажется полезным для прогнозирования производительности более мелких или крупных устройств.В частности, два поля потока считаются динамически подобными, если: (1) их геометрия подобна масштабам и (2) их безразмерные параметры совпадают. Первое требование подразумевает, что любой масштаб длины в первом поле потока может быть отображен на его аналог во втором поле потока путем умножения на единичный коэффициент масштабирования. Второе требование позволяет делать прогнозы для потока большего или меньшего масштаба на основе количественных данных о потоке в масштабе модели, когда учитывается масштабное соотношение.Более того, использование стандартных безразмерных параметров обычно уменьшает количество параметров, которые необходимо варьировать в эксперименте или вычислении, и значительно облегчает сравнение измеренных или вычисленных результатов с предыдущими работами, выполненными в потенциально других условиях.

Чтобы проиллюстрировать эти преимущества, рассмотрим силу сопротивления F _D на сфере диаметром d , движущейся со скоростью U в жидкости с плотностью ρ и вязкостью μ .Анализ размеров (раздел 1.11) с использованием этих пяти параметров дает следующие возможные безразмерные законы масштабирования:

(4,99) FDρU2d2 = Ψ (ρUdμ) или FDρμ2 = Φ (μρUd).

Оба действительны, но предпочтительнее первый, потому что он содержит безразмерные группы, которые либо исходят из уравнений движения, либо традиционно определяются при изучении гидравлического сопротивления жидкости. Если бы безразмерные группы не использовались, необходимо было бы провести эксперименты для определения F _D как функции d , сохраняя фиксированные значения U , ρ и μ .Затем необходимо провести эксперименты, чтобы определить F _D как функцию U , сохраняя фиксированными d , ρ и μ , и так далее. Однако в таком дублировании усилий нет необходимости при использовании безразмерных групп. Фактически, использование первого безразмерного закона, приведенного выше, позволяет просто отображать экспериментальные результаты для широкого диапазона условий с двумя осями (см. Рис. 4.23), даже если полный набор экспериментов мог включать вариации всех пяти размерных параметров.

Рисунок 4.23. Коэффициент лобового сопротивления C _D для сферы в зависимости от числа Рейнольдса Re, основанного на диаметре сферы. При низком числе Рейнольдса C _D ∼ 1 / Re и выше Re ∼ 10 ³, C _D ∼ константа (за исключением провала между Re = 10 ⁵ и 10 ⁶). Такое поведение (за исключением провала) можно объяснить простыми рассуждениями о размерах. Причина провала — переход ламинарного пограничного слоя в турбулентный, как объясняется в главе 10.

Идея размерного анализа тесно связана с концепцией подобия. Фактически, коллапс всех данных на одном графике, таком как на рис. 4.23, возможен только потому, что в этой задаче все потоки имеют одно и то же значение безразмерной группы, известной как число Рейнольдса Re = ρUd / μ динамически подобны. Это динамическое подобие обеспечивается, потому что число Рейнольдса появляется, когда уравнения движения приводятся в безразмерной форме.

Использование безразмерных параметров проникает в механику жидкости до такой степени, что эта глава и этот текст будут считаться неполными без этого раздела, даже несмотря на то, что эта тема хорошо освещена в текстах первого курса по механике жидкости, где содержание этого раздела обычно в сочетании с тем, что в Разделе 1.11. Для ясности нижеследующее обсуждение сначала охватывает безразмерные группы, связанные с уравнением импульса, а затем переходит к уравнениям неразрывности и энергии.

Рассмотрим поток жидкости с номинальной плотностью ρ и вязкостью μ через поле потока, характеризуемое шкалой длины l , шкалой скорости U и частотой вращения или колебаний Ω. Ситуация здесь должна быть общей, так что размерные параметры, полученные в результате этих усилий, будут широко применимы. Конкретные ситуации, которые могут включать все пять параметров, включают пульсирующий поток через трубу, поток через волнообразное самоходное тело или поток через турбомашину.

Отправной точкой является уравнение количества движения Навье-Стокса (4.39), упрощенное для несжимаемого потока. (Влияние сжимаемости выводится из уравнения неразрывности в следующем подразделе.)

(4.39b) ρ (∂u∂t + (u · ∇) u) = — ∇p + ρg + μ∇2u

Это уравнение можно сделать безразмерным путем определения безразмерных переменных:

(4.100) xi ∗ = xi / l, t ∗ = Ωt, uj ∗ = uj / U, p ∗ = (p − p∞) / ρU2 и gj ∗ = gj / g,

, где g — ускорение свободного падения. Когда используются эти безразмерные переменные, граничные условия могут быть сформулированы в терминах чистых чисел и не зависят от , , U, и Ω.Например, рассмотрим вязкое течение по круговому цилиндру радиусом R . Если шкала скорости U представляет собой скорость набегающего потока, а шкала длины — радиус R , то в терминах безразмерной скорости u ^∗ = u / U и безразмерной координаты r ^∗ = r / R , граничное условие на бесконечности равно u ^∗ → 1 при r ^∗ → ∞, а условие на поверхности цилиндра равно u ^∗ = 0 при r ^∗ = 1.Кроме того, поскольку давление входит в (4.39b) только как градиент, само давление не имеет значения; важны только перепады давления. Обычно p — p _∞ делают безразмерным, где p _∞ — это подходящим образом выбранное эталонное давление. В зависимости от характера потока, p — p _∞ можно сделать безразмерным с общим вязким напряжением μU / l , гидростатическим давлением ρgl или как в (4.100), динамическое давление ρU ². Подстановка (4.100) в (4.39) дает:

(4.101) [ΩlU] ∂u ∗ ∂t ∗ + (u ∗ · ∇ ∗) u ∗ = — ∇ ∗ p ∗ + [glU2] g ∗ + [μρUl ] ∇ ∗ 2u ∗,

где ∇ ∗ = l∇. Форма этого уравнения подразумевает, что два потока с разными значениями Ω, U , l , g или μ , будут подчиняться точно одному и тому же уравнению дифференциального импульса, если значения безразмерных групп Ω l / U , gl / U ² и μ / ρUl идентичны.Поскольку безразмерные граничные условия также идентичны в двух потоках, следует, что , они будут иметь одинаковые безразмерные решения . Произведения этих безразмерных групп появляются как коэффициенты перед различными членами, когда предполагается, что давление имеет альтернативные масштабные значения (см. Упражнение 4.71).

Группы параметров, показанные в [,] — скобках в (4.100), имеют следующие названия и интерпретации:

(4.102) St = число Струхаля нестационарное ускорение, адвективное ускорение ∂u / ∂tu (∂u / ∂x) ∝ΩUU2 / l = ΩlU,

(4.103) Re = число Рейнольдса инерция силы вязкая сила ρu (∂u / ∂x) μ (∂2u / ∂x2) ∝ρU2 / lμU / l2 = ρUlμ, и

(4,104) Fr = число Фруда [сила инерции силы тяжести] 1 / 2∝ [ρu (∂u / ∂x) ρg] 1 / 2∝ [ρU2 / lρg] 1/2 = Ugl.

Число Струхаля определяет важность нестационарного ускорения жидкости в потоках с колебаниями. Это актуально, когда нестабильность потока возникает естественным образом или из-за заданной частоты. Число Рейнольдса — наиболее распространенное безразмерное число в механике жидкости. Потоки с низким содержанием Re предполагают малые размеры, низкие скорости и высокую кинематическую вязкость, например, бактерии, плавающие через слизистые.Потоки с высоким содержанием Re связаны с большими размерами, высокими скоростями и низкой кинематической вязкостью, например, при движении океанского лайнера на полной скорости.

St, Re и Fr должны быть равны для динамического сходства между двумя потоками, в которых важны нестационарность, вязкие и гравитационные эффекты. Обратите внимание, что простое присутствие гравитации не делает гравитационные эффекты динамически важными. Для обтекания объекта в однородной несжимаемой жидкости сила тяжести важна только при возникновении поверхностных волн.В противном случае эффект силы тяжести заключается в простом добавлении гидростатического давления ко всей системе, которое изменяет местное опорное давление (см. «Пренебрежение силой тяжести в потоках с постоянной плотностью» в разделе 4.9).

Интересно, что в стратифицированной по плотности жидкости гравитация может играть значительную роль без наличия свободной поверхности. Эффективная сила тяжести на единицу объема в двухслойной ситуации составляет ( ρ ₂ — ρ ₁) г , где ρ ₁ и ρ ₂ плотности жидкости в двух слоях.В таком случае внутреннее число Фруда определяется как:

(4.105) Fr′≡ [инерционная сила плавучести] 1 / 2∝ [ρ1U2 / l (ρ2 − ρ1) g] 1/2 = Ug′l,

где г ′ ≡ г ( ρ ₂ — ρ ₁) / ρ ₁ — это уменьшенная сила тяжести . Для непрерывно стратифицированной жидкости, имеющей максимальную частоту плавучести N (см. 1.35), эквивалент (4.105) равен Fr′≡U / Nl. В качестве альтернативы внутреннее число Фруда может быть заменено числом Ричардсона = Ri≡1 / Fr′2 = g′l / U2, которое также может быть уточнено до градиентного числа Ричардсона ≡N2 (z) / (dU / dz) 2 это важно при изучении нестабильности и турбулентности в стратифицированных жидкостях.

При динамическом подобии безразмерные числа в потоке в масштабе модели сопоставляются со своими аналогами в потоке большего или меньшего масштаба, и это обеспечивает идентичность безразмерных решений. Кроме того, согласованность размеров уравнений движения гарантирует, что все величины потока могут быть заданы в безразмерной форме. Например, локальное давление в точке x = ( x , y , z ) можно сделать безразмерным в виде:

(4.106) p (x, t) −p∞12ρU2≡Cp = Ψ (St, Fr, Re; xl, Ωt),

, где C _p = ( p — p _∞) / (½) ρU ² называется коэффициентом давления (или числом Эйлера = Eu), а Ψ представляет собой безразмерное решение для коэффициента давления в терминах безразмерных параметров и переменных. Коэффициент ½ в (4.106) условен, но не обязателен. Аналогичные соотношения справедливы и для любой другой безразмерной переменной потока, такой как скорость u / U .Отсюда следует, что в динамически подобных потоках безразмерные переменные потока идентичны в соответствующих точках и временах (то есть для одинаковых значений x / l и Ω t ). Конечно, есть много случаев, когда геометрия потока может потребовать двух или более шкал длины: l , l ₁, l ₂,… l _n. В этом случае соотношения сторон l ₁/ l , l ₂/ l ,… l _n/ l обеспечивают безразмерное описание геометрии, и также появится как аргумент функции Ψ в соотношении типа (4.106). Здесь следует отметить разницу между соотношениями (4.99) и (4.106). Уравнение (4.99) является соотношением между общими параметрами потока, тогда как (4.106) удерживает локально в точке.

Между прочим, в потоках жидкости, когда p _∞ в (4.106) заменяется давлением пара жидкости, p _υ , безразмерное отношение известно как число кавитации . Нулевое или отрицательное число кавитации в любой точке потока указывает на вероятное образование паровых пузырьков в этом месте, и наличие таких пузырьков может полностью изменить характер потока, часто пагубно.Например, кавитация часто устанавливает пределы производительности и / или диктует срок службы гидродинамического оборудования, такого как водяные насосы, гидроэлектрические турбины и гребные винты судов.

В предшествующем анализе наложенная неустойчивость граничных условий считалась важной. Однако время также можно сделать безразмерным с помощью t ^* = Ut / l , что было бы подходящим для потока с установившимися граничными условиями. В этом случае производная по времени в (4.39) по-прежнему следует сохранять, потому что результирующий поток все еще может быть естественно неустойчивым, поскольку колебания потока могут возникать самопроизвольно, даже если граничные условия устойчивы. Но, исходя из соображений размеров, такая неустойчивость должна иметь временной масштаб, пропорциональный l / U .

В предшествующем анализе мы также предположили, что заданная скорость U имеет значение. Рассмотрим теперь ситуацию, когда наложенные граничные условия являются чисто нестационарными.Чтобы быть конкретным, рассмотрим объект, имеющий характерный масштаб длины -1, колеблющийся с частотой Ω в покоящейся на бесконечности жидкости. Это проблема, имеющая наложенный масштаб длины и временной масштаб 1 / Ом. В таком случае можно построить шкалу скоростей U = l Ом. Затем проводится предыдущий анализ и делается вывод, что St = 1, Re = Ul / v = Ω l ²/ v , и Fr = U / ( gl ) ^1/2 = Ω ( l / g ) ^1/2 должны быть продублированы для динамического сходства.

Все безразмерные величины идентичны в динамически подобных потоках. Для обтекания погруженного тела, такого как сфера, мы можем определить (безразмерные) коэффициенты сопротивления и подъемной силы:

(4.107, 4.108) CD≡FD12ρU2A иCL≡FL12ρU2A,

, где A — эталонная площадь, а F _D и F _L — силы сопротивления и подъемная сила, соответственно, действующие на тело; как в (4.106) множитель 1/2 в (4.107) и (4.108) условны, но не обязательны. Для затупленных тел, таких как сферы и цилиндры, A принимается как максимальное поперечное сечение, перпендикулярное потоку. Следовательно, A = πd ²/4 для сферы диаметром d и A = bd для цилиндра диаметром d и длиной b , ось которой перпендикулярна поток. С другой стороны, для обтекания плоских пластин и профилей A принимается равной площади в плане , то есть A = sl ; здесь l — средняя длина пластины или хорды аэродинамического профиля в направлении потока, а s — ширина, перпендикулярная потоку, иногда называемая размахом .

Значения коэффициентов лобового сопротивления и подъемной силы идентичны для динамически подобных потоков. При обтекании постоянно движущегося корабля сопротивление вызывается как гравитационными, так и вязкими эффектами, поэтому мы должны иметь функциональную связь вида C _D = C _D (Fr, Re) . Однако во многих потоках гравитационные эффекты не важны. Примером может служить обтекание тела, которое находится далеко от свободной поверхности и не генерирует гравитационные волны.В этом случае Fr не имеет значения, поэтому C _D = C _D (Re) — это все, что нужно, когда эффекты сжимаемости не важны. Это ситуация, изображенная первым членом (4.99) и проиллюстрированная на рис. 4.23.

Повторяющимся ограничением при тестировании масштабной модели является невозможность сопоставить числа Рейнольдса для достижения полного динамического сходства между моделью и более крупным и / или более быстрым полномасштабным устройством. Эта ситуация обычно известна как неполное сходство , и ею можно управлять разными способами.Прежде всего, если модельные и полномасштабные числа Рейнольдса не могут быть сопоставлены с одной и той же жидкостью, то для модельных испытаний возможно использование специальной жидкости с желаемой плотностью или вязкостью. Таким образом, гидродинамические испытания иногда проводят на аэродинамических устройствах, поскольку кинематическая вязкость воды составляет примерно 1/15 вязкости воздуха, поэтому меньшие устройства, испытанные на более низких скоростях в воде, могут достичь того же числа Рейнольдса, что и более крупные, испытанные в более быстро движущемся воздухе. Сжатый воздух и жидкий гелий — это другие жидкости, которые позволяют проводить испытания устройств в модельном масштабе с использованием высоких чисел Рейнольдса.Во-вторых, тесты масштабной модели могут показать, что важные показатели производительности ( C _L и C _D, возможно) не зависят от того, что Re превышает пороговое значение числа Рейнольдса. В этом случае экстраполяция результатов производительности от модели к полномасштабной может быть успешной, но такая экстраполяция по своей сути рискованна. Однако такую неопределенность экстраполяции и риск неполного сходства в тестах на масштабной модели можно уменьшить, если модели Рейнольдса и полномасштабные числа Рейнольдса будут как можно ближе.На практике это означает, что тесты масштабных моделей обычно проводятся с максимально возможными моделями с максимально возможной скоростью, которую позволяют доступные ресурсы. Оба примера в конце этого подраздела описывают прогнозы производительности, основанные на неполном сходстве.

Теперь вернемся к развитию безразмерных групп, которые естественным образом возникают из уравнений движения. Безразмерная форма уравнения неразрывности должна указывать, когда вызванные потоком перепады давления вызывают значительные отклонения от потока несжимаемой жидкости.Однако простейшее возможное масштабирование не дает никакой информации, потому что уравнение неразрывности само по себе не содержит давления. Таким образом, более плодотворной отправной точкой для определения относительного размера ∇ · u является (4.9):

(4.9) · u = −1ρDρDt = −1ρc2DpDt,

вместе с предположением, что изменения плотности, вызванные давлением, будут изэнтропический, dp = c ² dρ , где c — скорость звука, см. (1.25). Используя следующие безразмерные переменные:

(4.109) xi ∗ = xi / l, t ∗ = Ut / l, uj ∗ = uj / U, p ∗ = (p − p∞) / ρoU2 и ρ ∗ = ρ / ρo,

, где ρ _o — эталонная плотность, внешние члены (4.9) можно переписать:

(4.110) ∇ ∗ · u ∗ = — [U2c2] 1ρ ∗ Dp ∗ Dt ∗,

, что, в частности, показывает, что квадрат :

(4.111) M = Число Маха≡ [сила инерции сжимаемости] 1 / 2∝ [ρU2 / lρc2 / l] 1/2 = Uc

устанавливает размер изоэнтропических отклонений от потока несжимаемой жидкости. В инженерной практике потоки газа считаются несжимаемыми при M <0.3, и из (4.110) это соответствует отклонению ∼10% от идеального поведения несжимаемой жидкости, когда (1/ ρ ^∗) ( Dp ^∗/ Dt ^∗) равно единице. Конечно, могут быть и неизэнтропические изменения плотности, и они рассматриваются Томпсоном (1972, стр. 137–146). Потоки, в которых M <1, называются дозвуковыми , тогда как потоки, в которых M > 1 называются сверхзвуковыми . На высоких дозвуковых и сверхзвуковых скоростях согласование числа Маха между потоками требуется для динамического подобия.

Существует много возможных тепловых граничных условий для уравнения энергии, поэтому полностью общее масштабирование (4.60) невозможно. Вместо этого предоставляется простое масштабирование на основе постоянной удельной теплоемкости, пренебрежения μ _υ и постоянных температур набегающего потока и стенки, T _o и T _w, соответственно. . Кроме того, для простоты не учитывается навязанная частота колебаний потока.Отправной точкой приведенного здесь масштабирования является небольшая переработка (4.60), которая включает энтальпию ч на единицу массы:

(4.112) ρDhDt = DpDt + ρε + ∂∂xi (k∂T∂xi),

, где ε определяется формулой (4.58). Используя dh≅cpdT, следующие безразмерные переменные:

(4.113) ε ∗ = ρol2ε / μoU2, μ ∗ = μ / μo, k ∗ = k / ko, T ∗ = (T − To) / (Tw − To) ,

, а те, которые определены в (4.106), (4.107), становятся:

(4.114) ρ ∗ DT ∗ Dt ∗ = [U2cp (Tw − To)] Dp ∗ Dt ∗ + [U2cp (Tw − To) μoρoUl] ρ ∗ ε ∗ + [kocpμoμoρoUl] ∇ ∗ (k ∗ ∇ ∗ T ∗).

Здесь релевантные безразмерные параметры:

(4,115) Ec = число Эккерта кинетическая энергия, тепловая энергия = U2cp (Tw − To),

(4,116) Pr = число Прандтлина импульсная диффузия, теплопроводность = νκ3 = ρko7 / ρoko / νκ3 и мы узнаем ρoUl / μo как число Рейнольдса в (4.114). В низкоскоростных потоках, где число Эккерта мало, средние члены выпадают из (4.109), а уравнение полной энергии (4.107) сводится к (4.89). Таким образом, для приближения Буссинеска требуется низкое значение Ec.

Число Прандтля — это соотношение двух свойств молекулярного транспорта. Следовательно, это свойство жидкости и не зависит от геометрии потока. Для воздуха при обычных температурах и давлениях Pr = 0,72, что близко к значению 0,67, предсказанному с помощью упрощенной модели кинетической теории, предполагающей твердые сферы и одноатомные молекулы (Hirschfelder, Curtiss, & Bird, 1954, стр. 9–16). Для воды при 20 ° C Pr = 7,1. Для динамического подобия потоков с тепловыми эффектами требуется равенство чисел Эккерта, Прандтля и Рейнольдса.

И, наконец, для потоков с поверхностным натяжением σ существует несколько соответствующих безразмерных чисел:

(4,117) We = число Вебера инерция силы поверхностного натяжения ρU2l2σl = ρU2lσ,

(4,118) Bo = число связи сила силы тяжести ρlg ,

(4.119) Ca = число капилляров вязкие напряжения напряжения поверхностного натяжения μU / lσ / l = μUσ.

Здесь для чисел Вебера и Бонда отношение строится на основе соотношения сил, как в (4.107) и (4.108), а не силы на единицу объема, как в (4.103), (4.104) и (4.111). При высоком числе Вебера капли и пузырьки легко деформируются за счет ускорения или замедления жидкости, например, при ударе о твердую поверхность. При высоких числах Бонда эффекты поверхностного натяжения относительно не важны по сравнению с гравитацией, как в случае длинноволновых поверхностных волн океана. При высоком капиллярном числе силы вязкости преобладают над силами поверхностного натяжения; это обычно имеет место в потоках смазки оборудования.Однако для медленного пузырькового потока через пористую среду или узкие трубки (с низким содержанием Ca) верно обратное.

Пример 4.16

Ожидается, что судно длиной 100 м ( л ) будет курсировать со скоростью 10 м / с ( U ). Он имеет затопленную поверхность 300 м ² ( A ). Найдите скорость модели для модели в масштабе 1/25, пренебрегая эффектами трения. Сила сопротивления F _D измеряется как 60 Н, когда модель испытывается в буксирном баке на этой скорости модели.Оцените полное сопротивление, если коэффициент сопротивления поверхностного трения для модели равен 0,003, а для полномасштабного корабля — 0,0015.

Решение

Корпус корабля будет взаимодействовать с поверхностью воды и непосредственно с водой, поэтому будут возникать как волновое сопротивление, так и сопротивление трения. В безразмерной форме это требует, чтобы безразмерная сила сопротивления зависела от числа Фруда, числа Рейонльдса и соотношения сторон:

FD / (12ρU2A) = Ψ (U / gl, ρUl / μ, A / l),

где Ψ — неопределенная функция.Здесь не удастся совместить Fr и Re между моделью и полноразмерным устройством. Однако соотношение сторон автоматически подбирается для теста истинной масштабной модели, поэтому в дальнейшем оно не рассматривается.

Чтобы найти скорость испытания модели, приравняйте числа Фруда модели и корабля:

(U / gl) m = (U / gl) s, что подразумевает: Um = Usglm / gls = (10 м / с) 1/25 = 2 м / с.

Здесь нижние индексы « m » и « s » обозначают параметры модели и корабля , соответственно.

Измеренное полное сопротивление модели составляет 60 Н на этой скорости модели, и частично это сопротивление трения. Здесь мы можем использовать гипотезу Фруда о том, что неизвестная функция Ψ является суммой члена фрикционного сопротивления Ψ _f, который зависит только от числа Рейнольдса (и коэффициента шероховатости поверхности), и члена волнового сопротивления Ψ _w это зависит только от числа Фруда.

FD / (12ρU2A) = Ψw (U / gl) + Ψf (ρUl / μ).

Более того, относитесь к погруженной части корпуса как к плоской пластине, для которой коэффициент сопротивления трения C _D является функцией числа Рейнольдса, т.е.е., установить C _D = Ψ _f. В постановке задачи коэффициенты сопротивления трения устанавливаются как C _{D, m} = 0,003 и C _{D, s} = 0,0015, и они согласуются с основанными на длине значениями Re для модели и корабль, 8 × 106 и 10 ⁹ соответственно. Используя значение ρ = 1000 кг / м ³ для воды, можно оценить сопротивление трения модели:

(12ρU2ACD) m = (0.5) (103 кг / м3) (2 м / с) 2 (300 м2 / 252) (0,003) = 2,88 Н.

Таким образом, из общего сопротивления модели 60 Н, волновое сопротивление модели составляет ( F _WD) _м = 60 — 2,88 = 57,12 Н. И это волновое сопротивление подчиняется закон масштабирования выше, что означает, что:

(Ψw) m = (Ψw) s = (FWD12ρU2A) m = (FWD12ρU2A) s.

Таким образом, волновое сопротивление корабля ( F _WD) _s можно оценить следующим образом:

(FWD) s = (FWD) mρsρmUs2Um2AsAm = (57.12N) (1) (10 м / с2 м / с) 2 (25) 2 = 8,925 × 105 N,

, где отношение площадей является квадратом отношения масштаба длины. К этому следует добавить сопротивление трения корабля:

(12ρU2ACD) s = (0,5) (103 кг / м3) (10 м / с) 2 (300 м2) (0,0015) = 0,225 × 105 Н.

Следовательно, общее сопротивление судна прогнозируется равным: (8,925 + 0,225) × 10 ⁵ = 9,15 × 10 ⁵ Н. волновых эффектов, то прогнозируемое сопротивление корабля будет:

(FD) s = (FD) mρsρmUs2Um2AsAm = (60N) (1) (10 м / с2 м / с) 2 (25) 2 = 9.37 × 105N,

, что на несколько процентов выше оценки с поправкой на трение.
Пример 4.17
Настольный центробежный вентилятор диаметром d ₁ испытывается при частоте вращения Ω ₁ и генерирует объемный расход Q ₁ при перепаде давления Δ p ₁ при движении воздуха с плотностью ρ ₁ и вязкостью μ ₁. Каковы три релевантные безразмерные группы? Подобный масштабу центробежный водяной насос диаметром d ₂ = 2 d ₁ работает с частотой вращения Ω ₂ = Ω ₁/10.Если производительность турбомашины не зависит от Re в рабочем диапазоне этих устройств, каковы объемный расход насоса Q ₂ и рост давления Δ p ₁, если Re не совпадает, но два других безразмерных параметра равны ?
Решение
Анализ размеров с использованием шести параметров дает следующие безразмерные группы:
Коэффициент расхода = QΩd3, коэффициент напора = ΔpρΩ2d2 и Re = ρΩd2μ.
Эти три, наряду с эффективностью устройства, обычно используются при масштабировании производительности турбомашин.Согласование коэффициентов потока дает:
Q1Ω1d13 = Q2Ω2d23 = Q2 (Ω1 / 10) 8d13 или Q2 = 45Q1.
Коэффициенты согласования напора дают:
Δp1ρ1Ω12d12 = Δp2ρ2Ω22d22 = Δp2825ρ1 (Ω1 / 10) 24d12, или Δp2 = 825 · 4102Δp1 = 33Δp1,
где отношение плотности воды / воздуха и давления составляет 825 при комнатной температуре. Для этих условий мощность водяного насоса составляет Q ₂ Δ p ₂ = 26,4 Q ₁ Δ p ₁, что значительно превышает мощность вентилятора.Соотношение чисел Рейнольдса:
Re2Re1 = Ω2d22 / ν2Ω1d12 / ν1≅ (Ω1 / 10) 4d12 / (ν1 / 15) Ω1d12 / ν1 = 6,
, где ν — кинематическая вязкость, а ν _2./ ν ₁ ≈ 1/15 при комнатной температуре и давлении.
Площадь сопротивления, измеренная в полевых условиях, является ключевым коррелятом результатов испытаний на время при езде на велосипеде.
, , , , и
Джеймс Э. Петерман
Департамент интегративной физиологии, Университет Колорадо в Боулдере , Боулдер, Колорадо, США
Аллен К.Лим
Кафедра интегративной физиологии, Колорадский университет в Боулдере, Боулдер, Колорадо, США
Райан И. Игнатц
Кафедра интегративной физиологии, Колорадский университет в Боулдере, Боулдер, Колорадо, США
Эндрю Г. Эдвардс
Кафедра of Integrative Physiology, University of Colorado Boulder, Boulder, CO, USA
William C. Byrnes
Департамент интегративной физиологии, Университет Колорадо в Боулдере, Боулдер, Колорадо, США
Академический редактор: Венбинг Чжао
Департамент интегративной физиологии , Университет Колорадо в Боулдере, Боулдер, Колорадо, США
Автор, ответственный за переписку.
Поступило 11 мая 2015 г .; Принято, 2015 г. 10 июля.
Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение, воспроизведение и адаптацию на любом носителе и для любых целей при условии правильной ссылки на нее. Для указания авторства необходимо указать автора (авторов), название, источник публикации (PeerJ) и либо DOI, либо URL-адрес статьи.
Дополнительные материалы
Приложение S1: Методологические детали
DOI: 10.7717 / peerj.1144 / supp-1
Приложение S2: Исходные данные исследования
DOI: 10.7717 / peerj.1144 / supp-2
Аннотация
Область перетаскивания ( A _d ) является основным фактором, определяющим аэродинамическое сопротивление во время езды на велосипеде по уровню, и, следовательно, ключевым фактором, определяющим эффективность гонок на время в горизонтальных гонках. Однако A _d традиционно было трудно измерить. Наша цель состояла в том, чтобы определить ценность добавления измеренного в полевых условиях A _d в качестве коррелята с показателями в гонке на время на велосипеде по уровню.На поле 19 велосипедистов-мужчин выполнили гонку на время в горизонтальном (22,1 км) режиме. Отдельно были рассчитаны полевые A _d и сопротивление качению для испытуемых вместе с прогнозируемой фронтальной площадью, оцененной напрямую ( A _P ) и косвенно (Est A _P ). Кроме того, для определения пика V˙O2, лактатного порога (LT) и экономичности был проведен дифференцированный тест с физической нагрузкой. Пик V˙O2 (lmin − 1) и мощность в LT значительно коррелировали с мощностью, измеренной во время испытания на время ( r = 0.83 и 0,69 соответственно), но существенно не коррелировали со временем выполнения ( r = -0,42 и -0,45). Корреляция со временем выполнения значительно улучшилась ( p <0,05), когда эти переменные были нормализованы до A _d . Следует отметить, что только A _d лучше коррелировал со временем выполнения ( r = 0,85, p <0,001), чем любая комбинация ненормализованных физиологических показателей. Лучшая корреляция со временем производительности была измерена в полевых условиях во время испытания на время, нормированная на A _d ( r = — 0.92). A _P приходится только 54% изменчивости в A _d . Соответственно, корреляция со временем производительности была значительно ниже при использовании мощности, нормированной на A _P ( r = — 0,75) или Est A _P ( r = — 0,71). В заключение, если не нормализовать до A _d , результаты испытаний на время в полевых условиях не сильно коррелировали с общими лабораторными измерениями.Кроме того, наш измеренный в полевых условиях A _d легко определить и был единственным лучшим средством предсказания уровня производительности в гонках на время.
Ключевые слова: Коэффициент сопротивления, Измеритель мощности, Полевые испытания, Выходная мощность, Прогнозирование производительности, Физиология упражнений , лактатный порог (LT) и экономия (Coyle et al., 1988; Койл, 1995). В лаборатории, где силы сопротивления контролируются или минимизируются, эти физиологические факторы успешно использовались для прогнозирования результатов моделирования испытаний на время (Coyle et al., 1988; Loftin & Warren, 1994; Coyle, 1995; Bishop et al., 2000; Bentley et al., 2001; Lamberts et al., 2012). Однако в поле при езде по ровной местности с постоянной скоростью (> 40 км / ч ⁻¹) более 90% общего сопротивления ( R _TOT) препятствует прямому движению системы велосипедист-гонщик. определяется аэродинамическим сопротивлением ( R _a ) (Pugh, 1974; Di Prampero et al., 1979; Мартин и др., 1998; Olds & Olive, 1999). Таким образом, измерения способности велосипедиста обеспечивать механическую мощность не всегда позволяют прогнозировать время выступления в гонках на время (Hoogeveen & Schep, 1997; Balmer, Davison & Bird, 2000). Например, Balmer, Davison & Bird (2000) продемонстрировали, что, хотя пиковая выходная механическая мощность, оцененная во время поэтапного стресс-теста, действительно сильно коррелирует ( r = 0,99, p <0,001) со средней выходной мощностью механической мощности в течение 16 лет.Полевые испытания на время 1 км, ни пиковая выходная механическая мощность в лаборатории, ни средняя выходная механическая мощность во время испытаний на время хорошо коррелировали со временем работы ( r = 0,46, p > 0,05). Одно из возможных объяснений этих результатов заключается в том, что сопротивление, препятствующее движению вперед, с которым сталкиваются соревнующиеся велосипедисты, достаточно изменчиво, чтобы выходная механическая мощность сама по себе не могла предсказать производительность (Jeukendrup & Martin, 2001).
Измерение силы аэродинамического сопротивления ( R _a ) во время езды на велосипеде может быть сложной задачей.Прямые меры включают испытания в аэродинамической трубе (Davies, 1980; Kyle, 1991; Martin et al., 1998), моторизованную буксировку (Di Prampero et al., 1979; Capelli et al., 1993) и методы замедления движения накатом (De Groot , Sargeant & Geysel, 1995; Candau et al., 1999). Несмотря на то, что эти прямые измерения точны, они непрактичны для большинства исследователей и практиков. Например, испытательные центры в аэродинамической трубе недоступны и дороги. Кроме того, во время испытаний в аэродинамической трубе велосипеды физически не движутся по воздуху, и движение педалей вызывает шум в системе измерения силы во время каждого хода педали.Моторизованные методы буксировки и торможения накатом также сложны в их настройке и исполнении, что означает, что они не являются идеальной заменой аэродинамической трубе.
Поскольку измерение силы аэродинамического сопротивления может быть сложной задачей, иногда предполагается, что оно прямо пропорционально измерениям или оценкам прогнозируемой фронтальной площади ( A _P ) велосипеда и гонщика (Di Prampero et al., 1979 ; De Groot, Sargeant & Geysel, 1995; Olds & Olive, 1999; Heil, 2001; Anton et al., 2007). Однако это предполагает, что у разных людей аэродинамическое сопротивление изменяется предсказуемо с изменениями в A _P . Однако существуют доказательства обратного. Предыдущие исследования показывают отсутствие соразмерности между измеренным человеком A _P и аэродинамическим сопротивлением (Kyle, 1991; De Groot, Sargeant & Geysel, 1995). Это несоответствие должно быть связано с изменчивостью коэффициента лобового сопротивления ( C _d , см. Уравнение (2)), который зависит от формы велосипеда и водителя, сильно различается у разных людей и не меняется пропорционально изменения в проекции лобной области (Debraux et al., 2011).
Недавно было продемонстрировано, что измерение выходной механической мощности и скорости в полевых условиях с помощью измерителей мощности, установленных на велосипеде, является жизнеспособным и доступным методом определения аэродинамического сопротивления и сопротивления качению человека (Martin et al., 2006; Debraux et al., 2011; Лим и др., 2011). Этот метод в сочетании со стандартным физиологическим профилированием может улучшить нашу способность прогнозировать полевые показатели, поскольку утверждалось, что физические факторы, препятствующие движению вперед, играют большую роль в результативности, чем физиологические переменные (Jeukendrup & Martin, 2001).Антон и др. (2007) ранее показали, что одна только проекция фронтальной площади коррелирует со временем выступления во время равнинной гонки на время ( r = -0,73). Тем не менее, их оценочная площадь лобной поверхности не улучшила прогноз производительности в горизонтальных гонках на время по сравнению с максимальной выходной механической мощностью, измеренной в лаборатории. Как описано выше, A _P не прямо пропорционально аэродинамическому сопротивлению. Таким образом, аэродинамические характеристики велосипедиста (площадь сопротивления ( A _d )), которая включает как A _P , так и C _d , могут обеспечить лучшую корреляцию для результатов гонки на время.
Соответственно, целью этого исследования было количественное определение физиологических детерминант выносливости в сочетании с физическими факторами, которые способствуют сопротивлению во время езды на велосипеде. Затем сравнивались корреляции между различными детерминантами / факторами и результатами в гонках на время. Мы предположили, что физиологические возможности велосипедиста или средняя выходная мощность не будут предсказывать время выполнения обычных гонок на время, если они не нормированы к некоторому представлению аэродинамического сопротивления.Кроме того, мы предположили, что оценки аэродинамического сопротивления, такие как прямые и косвенные оценки прогнозируемой лобовой площади, не будут коррелировать с характеристиками так сильно, как фактические аэродинамические характеристики велосипедиста.
Методы
Субъекты
Девятнадцать соревнующихся велосипедистов-мужчин добровольно приняли участие в этом исследовании. Все испытуемые были лицензированными велосипедистами (Федерация велосипедного спорта США категории Pro / 1/2 Road или Pro / Expert MTB), которые жили, тренировались и участвовали в гонках в Колорадо, США, в течение как минимум двух месяцев.Все тесты проводились в разгар местного соревновательного велосезона. Описательные характеристики наших девятнадцати субъектов и результаты лабораторных испытаний представлены в. Все субъекты были проинформированы о рисках, связанных с участием в исследовании, и дали письменное информированное согласие перед участием. Комитет по исследованиям на людях Университета Колорадо в Боулдере одобрил протокол, использованный для этого исследования (ссылочный номер 0600.20).
Таблица 1
Среднее ± стандартное отклонение, минимальная и максимальная описательная информация для всех 19 субъектов и значения для основных показателей физиологической работоспособности, оцененных во время лабораторного градуированного теста с физической нагрузкой.
6,0 Мощность LT 1 мМ (Вт)
Среднее значение ± стандартное отклонение Мин. Макс.
Возраст (лет) 27,6 ± 4,6 20 36
Рост 164 184
Масса тела (кг) 70,0 ± 8,0 59,5 87,3
Жир (%) 10,4 ± 2,64 6,0 5
Плотность костной ткани (г см ^-2) 1,22 ± 0,11 1,03 1,41
Годы гонок 8 ± 5 3 20
20
₂ пик (л мин ^-1) 4,67 ± 0,40 3,91 5,47
VO ₂ пик (мл кг ^-1 мин ^-1) 67,6 ± 6,4 54.2 76,5
Мощность при VO ₂ пиковая (Вт) 362 ± 30 308 410
Пиковая мощность при VO _{(Вт кг 9001) −1 )} 5,15 ± 0,51 4,21 5,95
LT 1 мМ в% от VO ₂ пик 76 ± 4,5 65 82
271 ± 29 230 331
Отношение мощности к массе при LT 1 мМ (Вт кг ⁻¹) 3.87 ± 0,48 3,03 4,53
Economy Wl O2−1 73,5 ± 3,1 69,1 78,9
Макс.
Устройства для измерения мощности и калибровка
Все испытуемые использовали измеритель мощности на задней втулке (CycleOps PowerTap, Мэдисон, Висконсин, США), установленный для записи внешней выходной мощности, скорости хода, частоты вращения педалей и времени, измеренных с частотой 61 Гц с усредненными данными, записанными в эпохах 1.26 с для всех переменных. Пульс регистрировался с помощью нагрудного ремня пульсометра CycleOps, который передавался на компьютер измерителя мощности. На протяжении всего исследования использовались девятнадцать различных измерителей мощности, по одному для каждого испытуемого. Каждый испытуемый использовал один и тот же измеритель мощности для испытаний на время, лабораторных испытаний и измерений аэродинамического сопротивления / сопротивления качению. Перед началом испытаний все блоки, использованные во время испытаний, были откалиброваны по нулевому эталонному крутящему моменту, в то время как педали были неподвижны и разгружены в соответствии с указаниями производителя.
Лабораторные измерения и протокол
Лабораторные измеренные предикторы выносливости, включая пиковое потребление кислорода (пик V˙O2), лактатный порог (LT) и экономию (ватт102-1 мин-1 в LT), были измерены во время поэтапного теста с физической нагрузкой, проведенного в течение три дня испытания на время подопытного. Каждый тест проводился на личном шоссейном велосипеде испытуемого, прикрепленном к тренажеру с электронным тормозом (CompuTrainer ^®, Сиэтл, Вашингтон, США), при этом мощность измерялась с помощью измерителя мощности задней ступицы, предоставленного испытуемому в начале исследования.Протокол начинался с выходной мощности от 100 до 150 ватт и увеличивался примерно на 30 ватт каждые 4 минуты до тех пор, пока не наступило волевое утомление. Все испытания проводились на высоте 1625 м (5330 футов) при среднем атмосферном давлении, температуре и влажности 630,5 ± 3,4 мм рт. Ст., 22,9 ± 1,4 ° C и 37,1 ± 6,9% соответственно. Кроме того, вентилятор использовался для охлаждения испытуемых на протяжении каждого теста с физической нагрузкой.
Среднее потребление кислорода и производство углекислого газа определяли каждые 15 с с помощью компьютерной непрямой калориметрии с использованием программного и аппаратного обеспечения Parvomedics для интеграции входных данных от датчика давления Validyne и масс-спектрометра Perkin Elmer.Датчик давления был связан с пневмотахом Ганса Рудольфа, измеряющим вдыхаемую вентиляцию, и масс-спектрометром Perkin Elmer, отобранным из 4-литровой смесительной камеры. Процедуры калибровки кратко изложены в Приложении S1.
Пиковое потребление кислорода было определено как наивысшая скорость потребления кислорода за интервал выборки в одну минуту во время поэтапного стресс-теста. Субъектам настоятельно рекомендовалось приложить максимум усилий, и во всех случаях коэффициент респираторного обмена превышал 1.15 и лактат крови 7 мМ при волевом истощении. В целях экономии использовался только кислород, израсходованный за последние две минуты каждой 4-минутной стадии, чтобы обеспечить меры в установившемся режиме. Экономия измерялась как отношение между выходной мощностью и потреблением кислорода ватт102-1 на пороге лактата на основе регрессии зависимости потребления кислорода от мощности. У всех испытуемых зависимость между потреблением кислорода и выходной мощностью была линейной ( r > 0,99) на предпоследнем этапе.
Концентрация лактата в крови измерялась в состоянии покоя и в течение последней минуты каждого 4-минутного этапа. Для каждого образца примерно 50 мкл крови отбирали через уколы пальцем в капиллярную трубку объемом 75 мкл. Затем двадцать пять мкл смешивали с «коктейлем», содержащим 50 мкл буфера, лизирующего (Triton XL-100) и антигликолитического (фторид натрия) раствора. Наконец, лактат анализировали с помощью анализатора лактата YSI 2300 (Yellow Springs, Огайо, США). Перед каждым тестом анализатор лактата калибровался по известному стандарту и повторно калибровался каждые 15 минут.Порог лактата был определен как точка на 1 мМ выше исходного уровня, который включал лактат в состоянии покоя (Coyle et al., 1988). Этот процесс включает в себя некоторую субъективную интерпретацию при определении базовых значений, оставляя место для возможной человеческой ошибки. Таким образом, при анализе данных использовалось среднее значение для этих точек, полученное от восьми независимых наблюдателей. Между наблюдателями не было обнаружено значительных различий.
Частота сердечных сокращений во время лабораторных испытаний измерялась с помощью радиотелеметрии (Polar ^®, Lake Success, Нью-Йорк, США) каждую минуту, в то время как воспринимаемое напряжение измерялось с использованием шкалы Borg 6–20 через 3 минуты на каждом этапе.В течение двух дней после лабораторного испытания состав тела оценивали с помощью двухэнергетической рентгеновской абсорбциометрии (система GE LUNAR DXA, Фэрфилд, Коннектикут, США).
Гонка на время
Гонка на время на ровном месте проводилась на двух кругах четырехугольной петли в Хигиене, штат Колорадо. Общая дистанция гонки на время составила 22,1 км. В течение каждого круга испытуемые набирали и теряли 79 м высоты, в результате чего чистый прирост высоты составлял 0 м. Схема трассы позволяла испытуемым ехать непрерывно, без знаков остановки или светофоров, мешающих их усилиям.Испытуемым разрешалось использовать велосипеды для гонок на время, оборудованные планками для гонок на время и аэродинамическим передним колесом. Шесть испытуемых ехали на стандартном шоссейном велосипеде без дополнительного аэродинамического оборудования. Еще четыре испытуемых ехали на стандартном шоссейном велосипеде с аэродинамическим рулем. Остальные девять испытуемых использовали велосипед для гонок на время, оборудованный аэродинамическим рулем с аэродинамической глубокой тарелкой или трехспицевым передним колесом.
В течение двух недель до гонки на время испытуемых просили предварительно проехать курс, чтобы ознакомить их с маршрутом.Все испытуемые имели предыдущий опыт обучения по выбранному курсу. Непосредственно перед гонкой на время испытуемые выполняли личную предсоревновательную разминку. В это время шины были накачаны до 8,3 бар, когда гонщики не ехали на велосипеде. Непосредственно перед гонкой на время индивидуальная масса испытуемого ( M _R ) и масса системы велосипедиста ( M _BRS) были измерены с помощью электронных весов, предварительно откалиброванных по лабораторным весам (Detecto Scales, Webb City. , Штат Миссури, США).На старте бортовые компьютеры были очищены, а измерители мощности откалиброваны по нулевой нагрузке. Во время гонок на время испытуемые не видели свою выходную мощность, но позволяли видеть скорость, время, расстояние, частоту вращения педалей и частоту сердечных сокращений. Помимо времени, измеренного бортовым компьютером, время выступления измерялось также с помощью внешнего секундомера.
Все тесты на время проводились с 9 до 11 часов утра. Плотность воздуха рассчитывалась на основе измерений температуры окружающей среды, давления на станции и относительной влажности, собранных с помощью модельного погодного прибора Vantage Pro (Digital Instruments, Enterprise, Орегон, США).Хотя была сделана попытка запланировать как можно больше испытуемых в один и тот же день для контроля ветра, условий окружающей среды и атмосферы соревнований, в общей сложности было проведено десять отдельных испытаний на время с семью испытуемыми, выполняющими испытания на время в одиночку, а остальные — на один из трех случаев. В дни, когда несколько испытуемых проводили испытание на время, между началом каждого предмета давалось достаточно времени, чтобы испытуемые не могли двигаться или сбрасывать друг друга во время испытания.Во время этих отдельных случаев испытания на время разрешались при условии, что ветер не превышал 3 балла или «легкий ветерок» по шкале ветра Бофорта. Это эквивалентно скорости ветра менее 19 км / ч ^–1, характеризующейся окружающей средой, в которой дым поднимается вертикально (0) со скоростью ветра, когда листья и маленькие веточки постоянно движутся (3).
Обработка и анализ данных
Сразу после испытания на время данные, собранные с измерителя мощности и пульсометра CycleOps, были загружены с бортового компьютера на компьютер Apple G4.Загруженные данные включали время, выходную мощность, скорость, частоту вращения педалей и частоту сердечных сокращений с интервалом 1,26 секунды. Используя программное обеспечение Power Coach ™ (Kochli Sport, Сонвилье, Швейцария), управляемое компьютерами Apple G4, время работы, измеренное внешним секундомером, было локализовано на данных и изолировано. Затем проверялось расстояние от этих изолированных данных, чтобы убедиться, что оно соответствует фактическому расстоянию на трассе. Выделенные таким образом данные не отличались более чем на 50 м (7,26 ± 4,26 с) от фактического расстояния курса.Каждую строку данных также проверяли на наличие любых потенциальных проблем с записью с любыми ошибочными (потеря сигнала или надфизиологическими) данными, интерполированными между соседними точками данных. В среднем, приблизительно четыре секунды данных были интерполированы в любом данном испытании на время (диапазон = 0–24 с), при этом никогда не было более 2 ошибочных точек данных, появляющихся последовательно. Наконец, интересующие статистические данные были рассчитаны с использованием специального кода, написанного для Matlab ^® (Mathworks Inc., Беркли, Калифорния, США).
Профилирование аэродинамики и сопротивления качению, измеренное в полевых условиях
В течение трех недель после испытания на время аэродинамическое сопротивление и сопротивление качению были определены на основе полевых измерений мощности и скорости (Edwards & Byrnes, 2007; Lim et al., 2011). Используя методологию, описанную Di Prampero et al. (1979), площадь сопротивления ( A _d ) и сопротивление качению ( R _r ) были рассчитаны для каждого объекта (см. Приложение S1).
Спроектированная фронтальная площадь
Спроектированная фронтальная площадь была определена на основе рекомендаций Olds & Olive (1999).Цифровые фотографии (Nikon Cool Pix 4300, Мелвилл, Нью-Йорк, США) были сделаны, когда испытуемые сидели в положении для езды на велосипеде, который они использовали во время гонки на время, который был установлен на стационарном тренажере. Фотографии анализировали с помощью программы NIH Image 1.62. Это программное обеспечение после калибровки по известному расстоянию или площади автоматически вычисляет площадь данной трассы. Спроецированная фронтальная площадь рассчитывалась только на основе контуров тела и шлема испытуемого, за исключением велосипеда.В дополнение к фактическим измерениям проектируемой фронтальной площади были также сделаны оценки проектируемой фронтальной площади. В литературе приводятся многочисленные уравнения для прогнозирования или учета некоторых аспектов аэродинамического сопротивления или площади лобовой поверхности велосипедистов (Pugh, 1974; Davies, 1980; McLean, 1993; Olds, Norton & Craig, 1993; Olds et al. , 1995; Heil, 2001; Heil, 2002). Некоторые из уравнений основаны на предположении, что A _P представляет собой постоянную долю площади поверхности тела (BSA), в то время как другие выводят более сложные алгоритмы для прогнозирования A _P на основе различных антропометрических качеств велосипедиста ( я.е., рост и вес). Было проведено сравнение десяти различных уравнений из предыдущих исследований (DuBois & DuBois, 1916; Pugh, 1974; Davies, 1980; McLean, 1993; Olds, Norton & Craig, 1993; Olds et al., 1995; Heil, 2001).
Статистический анализ
Двумерные корреляции были выполнены для оценки взаимосвязи между физическими, физиологическими и нормализованными переменными со временем и средней мощностью, измеренной во время испытания на время. Кроме того, были выполнены пошаговые множественные регрессии, чтобы найти лучшую одиночную или комбинацию переменных, предсказывающих время и среднюю выходную мощность.Затем были обнаружены различия между коэффициентами корреляции с помощью теста Хотеллинга. Коэффициенты корреляции «произведение-момент» Пирсона использовались для определения взаимосвязи между фактическими и прогнозируемыми значениями A _p и A _d . Для определения наличия средних различий между фактическими и прогнозируемыми значениями A _p были проведены дисперсионные анализы с повторными измерениями. Если значимость была обнаружена, использовался более консервативный апостериорный тест Шеффе, чтобы определить, какие переменные различаются.Значимость для всех расчетов была установлена на уровне p <0,05. Описательные данные представлены в виде среднего, стандартного отклонения, минимума и максимума.
Результаты
Основные компоненты сопротивления во время езды на велосипеде представлены в. Поскольку A _P был рассчитан только с гонщиком, тогда как A _d был рассчитан для всей системы велосипеда и водителя, было бы технически некорректно рассчитывать C _d для велосипеда и система наездника или один наездник.Тем не менее, деление A _d на A _P даст оценку C _d , равную 1,03 ± 0,12. Корреляция 0,735 была обнаружена между A _P и A _d . Однако не было обнаружено никакой связи между A _P и C _d ( r = — .170, p = 0,486).
Таблица 2
Основные факторы, определяющие аэродинамическое сопротивление и сопротивление качению, измеренные на велосипеде, и положение тела, использованное во время гонки на время.
постоянная (Н · м ⁻² с ²)
Среднее ± SD Мин. Макс.
Плотность воздуха (кг · м ^-3) 1,00 ± 0,02 0,98 9002 1,06 0,170 ± 0,028 0,126 0,228
A _d (м ²) 0,349 ± 0,059 258 0,462
A _P (м ²) 0,338 ± 0,050 0,272 0,444
Est A _P 900 (м) (м) et al., 1995) 0,342 ± 0,017 0,32 0,375
Est A _P (м ²) (Heil, 2002) 0,327 ± 0,027 0,293
R _R (N) 4.88 ± 1,27 2,71 7,39
C _r (безразмерный) 0,006 ± 0,002 0,004 0,009
Общая масса (кг) 99,7
Результаты гонки на время представлены в. Из измеренных физиологических переменных: пик V˙O2 (l мин ^-1) ( r = 0,83, p <0,001), мощность при пике V˙O2 ( r = 0.67, p <0,001), и мощность в LT ( r = 0,69, p <0,001) значимо коррелировали с измеренной в полевых условиях выходной мощностью во время испытания на время. Эти физиологические показатели, однако, не были сильно или существенно связаны с временем выполнения гонок на время (пик V˙O2 r = -0,42, p = 0,08; мощность при пике V˙O2 r = -0,43, p = 0,07; мощность при LT r = — 0,45, p = 0,06). Вдобавок, хотя и значимо, измеренная в полевых условиях выходная мощность во время испытаний на время была коррелирована со временем работы со значением r , равным только -0.59. Таким образом, как предполагалось, ненормализованные физиологические показатели не были сильно связаны со временем выполнения гонок на время.
Таблица 3
Производительность и переменные среды, измеренные во время гонок на время.
5,9
Среднее ± SD Мин. Макс.
Общее время (мин: сек) 31:24 ± 2:15 28:05:00 34: 52:00
Температура (° C) 26.2 ± 4,5 20 35
Влажность (%) 30,7 ± 9,5 14 50
Давление воздуха (мм рт.
Плотность воздуха (кг · м ⁻³) 0,97 ± 0,02 0,95 1
Средняя мощность (Вт) 303 ± 26 259 354
Стандартное отклонение мощность во время гонки на время (Вт) 80 ± 14 61 113
Мощность (Вт кг ⁻¹) 4.32 ± 0,44 3,27 4,98
Мощность (% от LT) 112,4 ± 9,2 96,1 133
Мощность (% от VO ₂ пиковая) 84 69,6 92,5
ЧСС (уд / мин) 173 ± 6 161 183
Стандартное отклонение частоты сердечных сокращений во время испытания на время (уд / мин) 8 ± 2 4 11
Частота сердечных сокращений (% от LT HR) 111.9 ± 3,8 101,5 117,6
ЧСС (% от макс. ЧСС _r) 95,5 ± 1,1 93,3 96,8
Макс. ) 180 ± 6,3 167 192
Соотношение физиологических показателей и времени выполнения значительно увеличилось при приведении к аэродинамическим характеристикам. При нормировании на A _d , мощность на пике V˙O2 (Вт · м ⁻²) ( r = — 0.92, p <0,001) и мощность в LT ( r = — 0,85, p <0,001) лучше коррелировали со временем выполнения (). Другие нормализованные лабораторные измерения физиологических показателей либо не были значимыми, либо, если они были значимыми, коррелировали лишь умеренно. Корреляция со временем работы была наилучшей, когда измеренная средняя выходная мощность была нормализована либо до k ( r = — 0,92, p <0,001) или A _d ( r = — 0.92, p <0,001). отображает взаимосвязь между временем работы относительно средней выходной мощности, измеренной полем, а также средней выходной мощностью, измеренной в полевых условиях, нормированной на массу тела, A _P и A _d . Сопротивление качению само по себе или когда оно используется для нормализации мощности или физиологических показателей, не связано со временем выполнения.
Взаимосвязь между временем выполнения гонок на время относительно ненормализованных и нормализованных лабораторных показателей.
(A) Время работы относительно мощности при пике V˙O2. (B) Время работы относительно мощности на пороге лактата (LT). (C) Время работы относительно мощности на пике V˙O2, нормированное на определяемую полем площадь сопротивления ( A _d ). (D) Время работы относительно мощности при LT, нормализованное к определенному в полевых условиях A _d .
Взаимосвязь между временем проведения испытаний на время относительно ненормализованной и нормированной выходной мощности, измеренной в полевых условиях.
(A) Время работы относительно средней выходной мощности, измеренной в полевых условиях. (B) Время работы относительно средней выходной мощности, измеренной в полевых условиях, нормированной на массу тела. (C) Время работы относительно средней выходной мощности, измеренной в полевых условиях, нормированной на фронтальную область ( A _P ). (D) Время работы относительно средней выходной мощности, измеренной в полевых условиях, нормированной на определенную в полевых условиях площадь сопротивления ( A _d ).
Оба k ( r = — 0,32, p = 0.18) и A _d ( r = — 0,32, p = 0,17) не коррелировали с измеренной в полевых условиях выходной мощностью во время испытания на время. Однако только k ( r = 0,85, p <0,001) и A _d ( r = 0,85, p <0,001) были значительно связаны со временем выполнения. Хотя и значимо ( p = 0,04), измеренное значение A _P само по себе имело более низкую корреляцию ( r = 0.47), а методы определения Est A _P не коррелируют со временем выполнения ( r = 0,010–0,099). Кроме того, измеренная в полевых условиях выходная мощность, нормированная на A _P , лишь незначительно коррелировала со временем работы ( r = — 0,75).
Предполагая, что все сопротивление, с которым столкнулись велосипедисты во время гонки на время, было вызвано аэродинамическим сопротивлением и сопротивлением качению, даны оценки мощности для каждого компонента. Аэродинамическая мощность рассчитывалась на основе k, измеренного для положения велосипеда каждого испытуемого, в то время как сопротивление качению принималось как оставшаяся часть мощности.Во время гонок на время аэродинамическое сопротивление и сопротивление качению составили 89,77% и 10,23% от общей мощности при 272 ± 23 и 31 ± 12 Вт соответственно.
За исключением Olds et al. (1995) и Heil (2001) ( P > 0,999 и 0,322, соответственно), среднее значение для A _P (0,338 ± 0,049 м ²) было значительно выше предсказанного всеми другими оценками . A _P в процентах от BSA ( p <0,001; Пью (34), P = 0.011). Диапазон значений Est A _P в процентах от BSA составлял от 0,306 ± 0,020 м ² до 0,495 ± 0,032 м ². Для прогнозов A _P , основанных на антропометрических алгоритмах, за исключением метода Heil (2002) ( P = 0,983), все другие методы значительно ( p <0,001) превысили прогноз, сделанный нашим оцифрованным A _P. . Эти Est A _P варьировались от 0,399 ± 0,025 м ² до 0.550 ± 0,028 м ². Не было обнаружено корреляции между общей массой и A _P ( r = 0,302, p = 0,208).
Пошаговая регрессия была также выполнена для прогнозирования времени и мощности в гонке на время. В этом многомерном анализе наилучшими коррелятами времени уровня была средняя мощность, измеренная полем, к A _d ( r = — 0,92, p <0,001, y = — 0,53 × мощность испытания на время для площадь сопротивления + 2358.6). Коэффициент корреляции для этой связи существенно не отличался от коэффициента корреляции для мощности k ( r = — 0,92, p <0,001), что указывает на то, что колебания плотности окружающего воздуха между разными днями испытаний на время маловероятны. оказали большое влияние на время успеваемости в нашей группе испытуемых. Если мощность на пике V˙O2 и LT нормализованы к параметрам, влияющим на сопротивление, лучшим коррелятом времени производительности была мощность на пике V˙O2, нормализованная до A _d ( r = — 0.92, p <0,001, y = — 0,48 × мощность при пике V˙O2 до A _d + 2394,8). Эта корреляция существенно не отличалась от корреляции, полученной с использованием средней измеренной мощности поля, нормированной на A _d или k . Для выходной мощности во время испытания на время наилучшим коррелятом всех переменных, измеренных в лаборатории, является пик V˙O2 (l мин ⁻¹) ( r = 0,83, p <0,001, y = 54,67 × V ˙O2 пик + 48.8).
Обсуждение
Как и предполагалось, средняя выходная мощность велосипедиста, измеренная в полевых условиях, нормализованная к нашему определенному в полевых условиях аэродинамическому сопротивлению (например, k или A _d), была наилучшим коррелятом времени выступления в горизонтальной гонке на время ( r = — 0,92, p <0,001). Эти результаты демонстрируют и подтверждают, что аэродинамическое сопротивление является основным сопротивлением, с которым сталкивается при езде на велосипеде по ровной местности. Соответственно, измеренные в лаборатории физиологические показатели работоспособности (например,g., мощность при пике V˙O2), хотя и существенно коррелировали с измеренной в полевых условиях выходной мощностью ( r = 0,64), не были существенно связаны со временем работы ( r = — 0,43), если не нормировать на аэродинамическое сопротивление ( r = — 0,92). Следует отметить, что только наша определенная в поле площадь сопротивления была единственной лучшей корреляцией со временем выполнения на уровне ( r = 0,85, p <0,001), подтверждая, что аэродинамическое сопротивление в нашей популяции играло наиболее значительную роль во времени на уровне. пробное исполнение.Кроме того, наша определенная в полевых условиях площадь сопротивления улучшила корреляцию со временем работы лучше, чем A _P или Est A _P . Кроме того, сопротивление качению не было отличительным показателем производительности, отражая его меньший вклад в сопротивление движению вперед во время езды на велосипеде.
В согласии с Balmer, Davison & Bird (2000), мы обнаружили, что большинство лабораторных измерений не коррелировали в значительной степени с временем выполнения стандартных гонок на время.Однако, в отличие от наших результатов, ряд исследователей продемонстрировали более сильную корреляцию между лабораторными показателями производительности и уровнями показателей в гонках на время в полевых условиях (Hawley & Noakes, 1992; Nichols, Phares & Buono, 1997; Smith, Dangelmaier & Hill, 1999). ; Антон и др., 2007). Вполне вероятно, что эти противоречивые результаты связаны с различиями в привлеченных популяциях. Например, в исследовании Anton et al. (2007), исследуемая популяция имела относительно однородную площадь лобной поверхности (0.35 ± 0,02 м ²) и относительно неоднородной максимальной выходной механической мощностью (490 ± 56 Вт) по сравнению с испытуемыми из нашего исследования (0,34 ± 0,05 и 362 ± 30, соответственно). Эта однородность площади фронтальной поверхности, вероятно, привела к большей корреляции между лабораторными измерениями и результатами испытаний на время. Поскольку характеристики в гонке на время на уровне, по сути, представляют собой баланс между силами сопротивления (в первую очередь аэродинамическим сопротивлением) и движущими силами (выходная механическая мощность), однородность одного фактора приводит к тому, что другой неоднородный фактор имеет большую корреляцию.Кроме того, мы полагаем, что корреляции в этих предыдущих исследованиях были бы сильнее, если бы измерения лабораторных показателей были нормализованы к фактической площади аэродинамического сопротивления объекта. Например, в нашем исследовании мощность в LT имела корреляцию -0,45 со временем выполнения, но когда этот же лабораторный показатель был нормализован до A _d , корреляция стала -0,85.
Наш вывод о том, что время выполнения обычных гонок на время лучше всего прогнозируется путем нормализации выходной мощности, измеренной в полевых условиях, до k или A _d ( r = — 0.92, p <0,001), хотя, возможно, самоочевидно, но подчеркивает значительное отсутствие реальных аэродинамических показателей в исследованиях, пытающихся предсказать результаты велотренировок на время в полевых условиях. Martin et al. (2006) обнаружили, что измеренное аэродинамическое сопротивление можно использовать для прогнозирования скорости бега велосипедистов. Наше исследование поддерживает эти результаты и является первым, кто подчеркивает важность измеренной аэродинамики во время более длительных соревнований на более медленных скоростях по сравнению с теми, которые наблюдаются во время спринта.В нашем исследовании средняя мощность, измеренная в полевых условиях, значимо коррелировала со временем уровня ( r = — 0,59, p <0,01), но объясняла только 35% изменчивости во времени уровня. Однако, когда мощность, измеренная в полевых условиях, была приведена к аэродинамике, 85% изменчивости было объяснено тем, что различия в аэродинамике являются решающим фактором, определяющим характеристики.
Мы обнаружили, что только аэродинамическое сопротивление, представленное как k или A _d , значительно коррелировало со временем работы ( r = 0.85, p <0,001), что объясняет 72% вариабельности во времени выполнения. Разнородное оборудование и позиции испытуемых, использованные в гонке на время, могли способствовать этому выводу. Из девятнадцати испытуемых девять использовали велосипеды для гонок на время, четыре использовали стандартные дорожные велосипеды с аэродинамическими рулями, а остальные шесть использовали стандартный дорожный велосипед без специального аэродинамического оборудования. Однако, хотя в каждой группе были значительно разные средние значения для A _d , у девяти испытуемых, использовавших велосипеды для гонок на время, наши результаты были аналогичными со средней измеренной мощностью поля, нормированной на аэродинамику, единственным лучшим показателем времени выполнения ( r = — 0.88, p <0,001), аэродинамика является следующим лучшим предсказателем ( r = 0,72, p <0,001), а мощность, измеренная в полевых условиях, не предсказывает время работы ( r = — 0,33, p > 0,05 ). Диапазон в A _d между участниками, едущими на велосипеде для гонок на время (от 0,258 до 0,355 м ²), также мог помочь в этом открытии. Этот диапазон в A _d , тем не менее, также подчеркивает различия, которые существуют между людьми с аналогичным оборудованием, и важность определения площади сопротивления для прогнозирования результатов горизонтальных гонок на время.
Поскольку в прошлом было трудно измерить аэродинамическое сопротивление, во многих исследованиях предпринимались попытки использовать оценки прогнозируемой фронтальной площади (Est A _P ) или фактические измерения прогнозируемой фронтальной площади ( A _P ) для представления аэродинамического сопротивления ( A _d ) (Swain, 1994; Anton et al., 2007). Оценка A _d таким образом предполагает постоянный коэффициент лобового сопротивления ( C _d ), который вместе с A _P составляет A _d .Однако в настоящем исследовании на A _P приходилось только 54% изменчивости в A _d . Это несоответствие во многом связано с индивидуальными различиями в C _d . Если принять постоянное значение C _d , необходимо, чтобы гонщики ехали в одних и тех же условиях окружающей среды, используя одинаковые велосипеды, геометрию, одежду и оборудование. Однако диапазон значений C _d между нашими испытуемыми (0.823 до 1,262) подчеркивает индивидуальную изменчивость этого показателя. Кроме того, в соответствии с предыдущей работой (Kyle, 1991; De Groot, Sargeant & Geysel, 1995; Debraux et al., 2011), мы не обнаружили связи между A _P и C _d ( r = — 0,17, p = 0,49), демонстрируя их независимость и индивидуальную важность при определении A _d . Соответственно, при нормализации выходной мощности, измеренной полем во время испытания на время, мы обнаружили, что корреляция со временем производительности была значительно ниже при использовании A _P ( r = — 0.75) или Est A _P (-0,71) по сравнению с нормализацией с использованием нашего полевого A _d ( r = — 0,92). Таким образом, фактическая проецируемая фронтальная площадь или оценка прогнозируемой фронтальной площади не объясняют всей изменчивости в A _d , и при использовании для нормализации мощности не обязательно лучше для прогнозирования производительности горизонтальных испытаний на время, чем A _d. отдельно ( r = — 0,85).
Результаты настоящего исследования показывают, что полевые испытания с измерителем мощности могут быть лучшей альтернативой традиционным лабораторным испытаниям (т.е., V˙O2 пик, LT, экономия) для спортсменов и тренеров, желающих спрогнозировать результаты в гонках на время. Измеренная в полевых условиях площадь лобового сопротивления в сочетании с измеренной в полевых условиях выходной мощностью обеспечили лучший прогноз характеристик во время испытаний на время по сравнению с любой комбинацией лабораторных испытаний. Кроме того, мы демонстрируем, что определение площади сопротивления не должно быть трудным. Наше определение площади лобового сопротивления, измеренное в полевых условиях, было единственным лучшим предиктором результатов испытаний на время и требует только измерителя мощности, спидометра и ровной дороги, что делает его гораздо более экономичным, чем другие инструменты (т.э., аэродинамическая труба). Таким образом, спортсмены могут легко количественно оценить и улучшить результаты в соревнованиях, таких как заезды на время, используя нашу методику измерения площади сопротивления в полевых условиях, чтобы оптимизировать взаимосвязь между аэродинамическим сопротивлением и выходной мощностью.
В заключение, чтобы предсказать результативность езды на велосипеде в полевых условиях, необходимо учитывать способность велосипедиста производить мощность по отношению к силам, которые сопротивляются движению вперед. Соответственно, характеристики в горизонтальных гонках на время лучше всего спрогнозировать путем нормализации средней выходной мощности, измеренной в полевых условиях, на аэродинамическое сопротивление на квадрат скорости ( k ) или площадь сопротивления ( A _d ).Несмотря на то, что физиологические переменные обычно считаются наиболее важным фактором, определяющим производительность, мы обнаружили, что одни только показатели аэродинамического сопротивления лучше связаны с уровнем производительности, чем пиковое значение V˙O2, LT или экономия. Более того, использование прогнозируемой фронтальной площади ( A _P ) или оценок прогнозируемой фронтальной площади (Est A _P ) не так точно, как прямые измерения A _d .
Дополнительная информация
Приложение S1
Методологические детали:
Приложение S2
Исходные данные исследования:
Отчет о финансировании
Это исследование финансировалось CycleOps PowerTap.Высказанные мнения принадлежат авторам и не отражают точку зрения CycleOps PowerTap. Финансирующие организации не играли никакой роли в дизайне исследования, сборе и анализе данных, принятии решения о публикации или подготовке рукописи.
Дополнительная информация и заявления
Конкурирующие интересы
Авторы заявляют об отсутствии конкурирующих интересов.
Вклад авторов
Джеймс Э. Питерман проанализировал данные, внес в него реагенты / материалы / инструменты анализа, написал статью, подготовил рисунки и / или таблицы, рассмотрел черновики статьи.
Аллен С. Лим и Уильям К. Бирнс задумали и спланировали эксперименты, провели эксперименты, проанализировали данные, предоставили реагенты / материалы / инструменты анализа, написали документ, подготовили рисунки и / или таблицы, рассмотрели черновики статьи.
Райан И. Игнатц проводил эксперименты, анализировал данные, вносил реагенты / материалы / инструменты для анализа, писал статью, рецензировал черновики статьи.
Эндрю Дж. Эдвардс провел эксперименты, проанализировал данные, предоставил реагенты / материалы / инструменты для анализа, просмотрел черновики статьи.
Человеческая этика
В отношении этических разрешений была предоставлена следующая информация (например, утверждающий орган и любые ссылочные номера):
Все субъекты были проинформированы о рисках, связанных с участием в исследовании, и дали письменное информированное согласие перед участием. Комитет по исследованиям на людях Университета Колорадо в Боулдере одобрил протокол, использованный для этого исследования (ссылочный номер 0600.20).
Ссылки
Anton et al. (2007) Антон М, Искьердо М, Ибанез Дж, Азиайн Х, Мендигучия Дж, Горостяга Э.Прогнозирование результатов гонок на время и в гору для элитных велосипедистов-любителей. Международный журнал спортивной медицины. 2007. 28 (4): 306–313. DOI: 10,1055 / с-2006-6. [PubMed] [CrossRef] [Google Scholar] Балмер, Дэвисон и Берд (2000) Балмер Дж., Дэвисон Р.С., Берд С.Р. Пиковая мощность определяет мощность во время гонки на время на велосипеде 16,1 км на открытом воздухе. Медицина и наука в спорте и физических упражнениях. 2000; 32: 1485–1490. DOI: 10.1097 / 00005768-200008000-00018. [PubMed] [CrossRef] [Google Scholar] Bentley et al.(2001) Bentley DJ, McNaughton LR, Thompson D, Vleck VE, Batterham AM. Пиковая выходная мощность, лактатный порог и результаты гонок на время у велосипедистов. Медицина и наука в спорте и физических упражнениях. 2001; 33: 2077–2081. DOI: 10.1097 / 00005768-200112000-00016. [PubMed] [CrossRef] [Google Scholar] Бишоп и др. (2000) Епископ Д., Дженкинс Д.Г., Макинери М., Кэри М.Ф. Связь между параметрами лактата плазмы и характеристиками мышц у женщин-велосипедистов. Медицина и наука в спорте и физических упражнениях. 2000; 32: 1088–1093.DOI: 10.1097 / 00005768-200006000-00008. [PubMed] [CrossRef] [Google Scholar] Candau et al. (1999) Candau R, Grappe F, Menard M, Barbier B, Millet GY, Hoffman MD, Belli AR, Rouillon JD. Упрощенный метод замедления для оценки сил сопротивления при езде на велосипеде. Медицина и наука в спорте и физических упражнениях. 1999. 31 (10): 1441–1447. DOI: 10.1097 / 00005768-199^{0-00013. [PubMed] [CrossRef] [Google Scholar] Capelli et al. (1993) Капелли К., Роза Дж., Бутти Ф, Ферретти Дж., Вейштайнас А., Ди Прамперо П. Энергозатраты и эффективность езды на аэродинамических велосипедах.Европейский журнал прикладной физиологии. 1993. 67: 144–149. DOI: 10.1007 / BF00376658. [PubMed] [CrossRef] [Google Scholar] Coyle (1995) Coyle EF. Интеграция физиологических факторов, определяющих выносливость. Обзоры науки о спорте. 1995; 23: 25–63. DOI: 10.1249 / 00003677-199500230-00004. [PubMed] [CrossRef] [Google Scholar] Койл и др. (1988) Койл Э. Ф., Когган А. Р., Хоппер М. К., Уолтерс Т. Дж.. Детерминанты выносливости у хорошо подготовленных велосипедистов. Журнал прикладной физиологии. 1988; 64: 2622–2630.[PubMed] [Google Scholar] Дэвис (1980) Дэвис К. Влияние сопротивления воздуха на метаболические затраты и эффективность езды на велосипеде. Европейский журнал прикладной физиологии. 1980; 45: 245–254. DOI: 10.1007 / BF00421332. [PubMed] [CrossRef] [Google Scholar] Debraux et al. (2011) Дебро П., Граппе Ф, Манолова А. В., Бертуччи В. Аэродинамическое сопротивление при езде на велосипеде: методы оценки. Спортивная биомеханика. 2011; 10 (3): 197–218. DOI: 10.1080 / 14763141.2011.5. [PubMed] [CrossRef] [Google Scholar] Де Гроот, Сарджант и Гейзель (1995) Де Гроот Дж., Сарджант А., Гейзель Дж.Воздушное трение и сопротивление качению при езде на велосипеде. Медицина и наука в спорте и физических упражнениях. 1995; 27: 1090–1095. DOI: 10.1249 / 00005768-199507000-00020. [PubMed] [CrossRef] [Google Scholar] Ди Прамперо и др. (1979) Ди Прамперо П. Е., Кортили Г., Моньони П., Сайбене Ф. Уравнение движения велосипедиста. Журнал прикладной физиологии. 1979; 47: 201–206. [PubMed] [Google Scholar] DuBois & DuBois (1916) DuBois D, DuBois E. Формула для оценки приблизительной площади поверхности, если известны рост и вес.Архивы внутренней медицины. 1916; 17: 863–871. DOI: 10.1001 / archinte.1916.00080130010002. [PubMed] [CrossRef] [Google Scholar] Эдвардс и Бирнс (2007) Эдвардс А.Г., Бирнс В.К. Аэродинамические характеристики как определяющие факторы тягового эффекта при езде на велосипеде. Медицина и наука в спорте и физических упражнениях. 2007. 39 (1): 170–176. DOI: 10.1249 / 01.mss.0000239400.85955.12. [PubMed] [CrossRef] [Google Scholar] Хоули и Ноукс (1992) Хоули Дж. А., Ноукс Т. Д.. Пиковая выходная мощность предсказывает максимальное потребление кислорода и время тренировки у тренированных велосипедистов.Европейский журнал прикладной физиологии и физиологии труда. 1992. 65: 79–83. DOI: 10.1007 / BF01466278. [PubMed] [CrossRef] [Google Scholar] Heil (2001) Heil DP. Масштабирование массы тела проектируемой лобной области у соревнующихся велосипедистов. Европейский журнал прикладной физиологии. 2001. 85 (3–4): 358–366. DOI: 10.1007 / s004210100424. [PubMed] [CrossRef] [Google Scholar] Heil (2002) Heil DP. Масштабирование массы тела в лобной области у соревнующихся велосипедистов, не использующих руль. Европейский журнал прикладной физиологии.2002. 87: 520–528. DOI: 10.1007 / s00421-002-0662-9. [PubMed] [CrossRef] [Google Scholar] Hoogeveen & Schep (1997) Hoogeveen AR, Schep G. Реакция лактата в плазме на упражнения и выносливость: отношения у элитных триатлонистов. Международный журнал спортивной медицины. 1997. 18: 526–530. DOI: 10,1055 / с-2007-972676. [PubMed] [CrossRef] [Google Scholar] Jeukendrup & Martin (2001) Jeukendrup AE, Martin J. Повышение эффективности езды на велосипеде: как мы должны тратить свое время и деньги. Спортивная медицина.2001. 31: 559–569. DOI: 10.2165 / 00007256-200131070-00009. [PubMed] [CrossRef] [Google Scholar] Кайл (1991) Кайл CR. Испытания аэровелосипедов в аэродинамической трубе. Велосипедная наука. 1991. 3 (3–4): 57–61. [Google Scholar] Lamberts et al. (2012) Ламбертс Р.П., Ламберт М.И., Сварт Дж., Ноукс Т.Д. Аллометрическое масштабирование пиковой выходной мощности точно предсказывает результаты гонок на время и максимальное потребление кислорода тренированными велосипедистами. Британский журнал спортивной медицины. 2012. 46 (1): 36–41. DOI: 10.1136 / bjsm.2010.083071. [PubMed] [CrossRef] [Google Scholar] Лим и др.(2011) Лим AC, Homestead EP, Edwards AG, Carver TC, Kram R, Byrnes WC. Измерение изменений аэродинамического сопротивления / сопротивления качению с помощью навесных измерителей мощности. Медицина и наука в спорте и физических упражнениях. 2011. 43 (5): 853–860. DOI: 10.1249 / MSS.0b013e3181fcb140. [PubMed] [CrossRef] [Google Scholar] Лофтин и Уоррен (1994) Лофтин М., Уоррен Б. Сравнение смоделированной гонки на время 16,1 км, VO ₂ max и связанных факторов у велосипедистов с разными порогами вентиляции. Международный журнал спортивной медицины.1994; 15: 498–503. DOI: 10,1055 / с-2007-1021094. [PubMed] [CrossRef] [Google Scholar] Мартин и др. (2006) Мартин Дж. К., Гарднер А. С., Баррас М., Мартин Д. Т.. Моделирование спринтерского цикла с использованием параметров, полученных из поля, и прямого интегрирования. Медицина и наука в спорте и физических упражнениях. 2006. 38 (3): 592–597. DOI: 10.1249 / 01.mss.0000193560.34022.04. [PubMed] [CrossRef] [Google Scholar] Мартин и др. (1998) Мартин Дж. К., Милликен Д. Л., Кобб Дж. Э., Макфадден К. Л., Когган А. Р.. Валидация математической модели мощности езды на велосипеде.Журнал прикладной биомеханики. 1998. 14: 276–291. [PubMed] [Google Scholar] Маклин (1993) Маклин Б. Взаимосвязь между площадью фронтальной поверхности и антропометрическими параметрами у гонщиков-велосипедистов. Международное общество биомеханики, XIV конгресс, 4–8 июля; Париж. 1993. [Google Scholar] Nichols, Phares & Buono (1997) Nichols JF, Phares SL, Buono MJ. Взаимосвязь между реакцией лактата в крови на упражнения и выносливостью у соревнующихся женщин-велогонщиков. Международный журнал спортивной медицины.1997; 18: 458–463. DOI: 10,1055 / с-2007-972664. [PubMed] [CrossRef] [Google Scholar] Олдс, Нортон и Крэйг (1993) Олдс Т., Нортон К., Крейг Н. Математическая модель велосипедной езды. Журнал прикладной физиологии. 1993. 75 (2): 730–737. [PubMed] [Google Scholar] Olds et al. (1995) Олдс Т., Нортон К., Лоу Э, Олив С., Рей Ф., Ли С. Моделирование езды на велосипеде по дороге. Журнал прикладной физиологии. 1995. 78 (4): 1596–1611. [PubMed] [Google Scholar] Olds & Olive (1999) Olds T, Olive S. Методологические соображения при определении прогнозируемой фронтальной площади у велосипедистов.Журнал спортивной науки. 1999. 17: 335–345. DOI: 10.1080 / 026404199366046. [PubMed] [CrossRef] [Google Scholar] Пью (1974) Пью LG. Соотношение потребления кислорода и скорости в соревнованиях по велоспорту и сравнительные наблюдения на велоэргометре. Журнал физиологии. 1974; 241: 795–808. DOI: 10.1113 / jphysiol.1974.sp010685. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] Smith, Dangelmaier & Hill (1999) Smith JC, Dangelmaier BS, Hill DW. Критическая мощность связана с показателями велоспорта в гонках на время.Международный журнал спортивной медицины. 1999. 20: 374–378. DOI: 10,1055 / с-2007-971147. [PubMed] [CrossRef] [Google Scholar] Суэйн (1994) Суэйн Д.П. Влияние массы тела на выносливость на велосипеде. Медицина и наука в спорте и физических упражнениях. 1994; 26: 58–63. [PubMed] [Google Scholar]
40 CFR § 1037.528 — Процедуры выбега для расчета площади сопротивления (CdA). | CFR | Закон США
§ 1037.528 Процедуры выбега для расчета площади сопротивления (CdA).
Процедуры выбега в этом разделе описывают, как рассчитать площадь сопротивления, CdA, для тракторов, прицепов и профессиональных транспортных средств Фазы 2 с учетом положений §§ 1037.С 525 по 1037. 527. Эти процедуры считаются эталонным методом для тракторов, но альтернативным методом для прицепов. Следуйте положениям разделов 1–9 SAE J2263 (включенного в качестве ссылки в § 1037.810) с пояснениями и исключениями, описанными в этом разделе. Некоторые из этих исключений взяты из SAE J1263 (включенного в качестве ссылки в § 1037.810). Процедуры выбега в 40 CFR 1066.310 применяются вместо положений этого раздела для тракторов Фазы 1.
(a) Термины и переменные, указанные в этом разделе, имеют значение, указанное в SAE J1263 и SAE J2263, если не указано иное.
(b) Чтобы определить значения CdA для трактора, выполните испытание выбегом с комбинацией трактор-прицеп с использованием трактора производителя и стандартного прицепа. Чтобы определить значения CdA для прицепа, выполните испытание выбегом с комбинацией трактор-прицеп с использованием стандартного трактора. Подготовьте тракторы и прицепы к испытаниям следующим образом:
(1) Установите приборы для выполнения указанных измерений.
(2) После добавления контрольно-измерительных приборов убедитесь, что отсутствует тормозное сопротивление или другое условие, препятствующее свободному вращению колес.Не включайте стояночный тормоз ни в какой момент между этой проверкой и окончанием процедуры измерения.
(3) Установите шины, смонтированные на стальных дисках, в двойной конфигурации (кроме управляемых шин). Шины должны —
(i) иметь сертификат SmartWay или иметь коэффициент сопротивления качению не более 5,1 кг / метрическую тонну.
(ii) Накопили не менее 2000 миль, но имеют не менее 50 процентов исходной глубины протектора, как указано для кабин грузовиков в SAE J1263.
(iii) Не иметь восстановленных протекторов или каких-либо явных следов трещин или неравномерного износа.
(iv) быть размером 295 / 75R22,5 или 275 / 80R22,5.
(v) Накачать шину до надлежащего давления, как указано в разделах 6.6 и 8.1 SAE J2263.
(vi) Использовать шины той же модели для данной оси.
(4) Выполните осмотр или регулировку углов установки колес как трактора, так и прицепа, чтобы убедиться, что положение колес соответствует спецификациям производителя.
(c) Спецификации условий испытаний, описанные в Разделах 7.Применяются с 1 по 7.4 SAE J1263 с некоторыми исключениями и дополнительными положениями, как описано в этом параграфе (c). Эти условия применяются к каждому запуску отдельно.
(1) Мы рекомендуем не проводить испытания на выбеге, если ожидается, что скорость ветра превысит 6,0 миль / час.
(2) Среднее значение составляющей скорости ветра параллельно дороге не должно превышать 6,0 миль / ч. Это ограничение является дополнительным к ограничениям, указанным в разделе 7.3 SAE J1263.
(3) Если уклон дороги больше 0.02% по длине тестовой поверхности, вы должны определить высоту как функцию расстояния по длине тестовой поверхности и включить это в анализ.
(4) Уклон дороги может превышать 0,5% на ограниченных участках испытательной поверхности при условии, что это не влияет на результаты выбега, в соответствии с хорошей инженерной оценкой.
(5) Температура поверхности дороги должна быть не ниже 50 ° C. При измерении температуры дорожного покрытия руководствуйтесь здравым техническим расчетом.
(d) Расчеты CdA основаны на измеренных значениях скорости, когда транспортное средство движется по инерции в диапазоне высоких скоростей от 70 до 60 миль / ч и в диапазоне низких скоростей от 20 до 10 миль / ч.Отключите все ограничители скорости автомобиля, которые не позволяют двигаться со скоростью более 72 миль / ч. Измерьте скорость автомобиля с минимальной частотой записи 10 Гц вместе с данными времени суток. Определите скорость автомобиля одним из следующих методов:
(1) Завершить выбег. Управляйте автомобилем с максимальной скоростью выше 72,0 миль / ч и дайте ему возможность двигаться по инерции до 8,0 миль / ч или ниже. Соберите данные для диапазона высоких скоростей в тестовом сегменте, который включает скорости от 72,0 до 58,0 миль / ч, и соберите данные для диапазона низких скоростей в тестовом сегменте, включающем скорости от 22.0 до 8,0 миль / час.
(2) Разделенные выбеги. Собирайте данные во время выбега на высокой скорости, пока автомобиль движется по инерции через тестовый сегмент, который включает скорости от 72,0 миль / ч до 58,0 миль / ч. Точно так же собирайте данные во время выбега на низкой скорости, когда транспортное средство движется по инерции через тестовый сегмент, который включает скорости от 22,0 миль / ч до 8,0 миль / ч. Выполните один сегмент выбега на высокой скорости или два последовательных сегмента выбега на высокой скорости в одном направлении, за которыми следует такое же количество сегментов выбега на низкой скорости в том же направлении, а затем выполните такое же количество измерений в противоположном направлении.Вы не можете разделять прогоны, как описано в разделе 9.3.1 SAE J2263, за исключением случаев, разрешенных этим параграфом (d) (2).
(e) Измеряйте скорость ветра, направление ветра, температуру воздуха и давление воздуха с частотой регистрации 10 Гц вместе с данными времени суток. Используйте по крайней мере один стационарный анемометр и подходящие регистраторы данных, соответствующие спецификациям SAE J1263, с учетом следующих дополнительных спецификаций для анемометра, размещенного вдоль испытательной поверхности:
(1) Вы должны начать измерение выбега в течение 24 часов после завершения калибровки нулевого ветра и нулевого угла.
(2) Поместите анемометр на расстоянии не менее 50 футов от ближайшего дерева и не менее 25 футов от ближайшего куста (или аналогичных элементов). Разместите анемометр рядом с испытательной поверхностью, около средней точки длины дорожки, на расстоянии 2,5–3,0 ширины тела от предполагаемого местоположения центральной линии испытуемого транспортного средства, когда он проходит анемометр. Запишите местоположение анемометра на испытательном треке с точностью до 10 футов.
(3) Установите анемометр на высоте в пределах 6 дюймов от половины высоты тела тестируемого автомобиля.
(4) Высота растительности вокруг анемометра не должна превышать 10% от установленной высоты анемометра в пределах радиуса, равного высоте установленного анемометра.
(f) Измерьте воздушную скорость и относительное направление ветра (угол рыскания) на борту транспортного средства с минимальной частотой регистрации 10 Гц в сочетании с данными времени суток, используя анемометр и подходящие регистраторы данных, которые соответствуют требованиям Разделов 5.4 SAE J2263. Угол рыскания должен измеряться с разрешением и точностью ± 0.5 °. Установите анемометр так, чтобы он измерял скорость воздуха на высоте 1,5 метра над передней кромкой прицепа. Если препятствия на испытательной площадке не позволяют обеспечить такую высоту установки, установите анемометр так, чтобы он измерял скорость воздуха на высоте не менее 0,85 метра над верхней кромкой передней кромки прицепа.
(g) Выполните следующие вычисления, чтобы отфильтровать и исправить измеренные данные:
(1) Для любых измеренных значений, не определенных как выбросы, используйте эти измеренные значения непосредственно в расчетах, указанных в этом разделе.Отфильтруйте измерения скорости воздуха, угла рыскания, скорости ветра, направления ветра и скорости транспортного средства, чтобы заменить выбросы для каждого измеренного значения следующим образом:
(i) Определите среднее измеренное значение, представляющее точку измерения, и измерения за 3 секунды до и после этой точки. В первые и последние три секунды выбега используйте все доступные данные для определения среднего измеренного значения. Окно измерений для определения среднего значения будет соответственно включать 61 измерение в большинстве случаев и всегда будет включать как минимум 31 измерение (для частоты записи 10 Гц).
(ii) Определите среднее абсолютное отклонение, соответствующее каждому окну измерения из параграфа (g) (1) (i) этого раздела. Обычно это происходит в результате вычисления 61 абсолютного отклонения от среднего измеренного значения и определения среднего из этих 61 отклонений. Рассчитайте стандартное отклонение для каждого окна измерения, умножив среднее абсолютное отклонение на 1,4826; рассчитайте три стандартных отклонения, умножив среднее абсолютное отклонение на 4,4478. Обратите внимание, что коэффициент 1.4826 — статистическая константа, которая связывает средние абсолютные отклонения со стандартными отклонениями.
(iii) Измеренное значение является выбросом, если измеренное значение в данной точке отличается от среднего измеренного значения более чем на три стандартных отклонения. Замените каждый выброс средним измеренным значением из пункта (g) (1) (i) этого раздела. Этот метод фильтрации выбросов известен как метод Хэмпеля.
(2) Для каждого высокоскоростного и каждого низкоскоростного сегментов исправьте измеренную скорость воздуха, используя измерения скорости и направления ветра, описанные в параграфе (e) этого раздела, следующим образом:
(i) Рассчитайте теоретическую воздушную скорость, vair, th, для каждого набора измерений с частотой 10 Гц, используя следующее уравнение:
vair, th = w2 + v2 + 2 · v · w · cos (ϕw + ϕveh) Ур.1037.528-1
Пример:
Вт = 7,1 миль / ч
v = 64,9 миль / ч
øw = 47,0 °
øveh = 0 °
vair, th = 7,12 + 64,92 + 2 · 64,9 · 7,1 · cos⁡ (47 + 0)
vair, th = 69,93 миль / ч
(ii) Выполните линейную регрессию с использованием парных значений vair, th и измеренной воздушной скорости, vair, Meas, для определения поправочных коэффициентов воздушной скорости a0 и a1 на основе следующего уравнения:
vair, th = α0 + α1 · vair, mesEq. 1037.528-2
(iii) Исправьте каждое измеренное значение скорости воздуха, используя следующее уравнение:
vair = α0 + α1 · vair, mesEq.1037.528-3
(3) Исправьте измеренное направление воздуха со всех высокоскоростных сегментов, используя измерения скорости и направления ветра, описанные в параграфе (e) этого раздела, следующим образом:
(i) Рассчитайте теоретическое направление воздуха, c; воздух, th, используя следующее уравнение:
ψair, th = arctan (w · sin⁡ (ϕw + ϕveh) v + w · cos⁡ (ϕw + ϕveh)) Ур. 1037.528-4
Пример:
Вт = 7,1 миль / ч
v = 64,9 миль / ч
øw = 47,0 °
øveh = 0 °
ψair, th = arctan (7.1 · sin⁡ (47,0 + 0) 64,9 + 7,1 · cos⁡ (47,0 + 0))
каир, th = 4,26 °
(ii) Выполните линейную регрессию с использованием парных значений cair, th и измеренного направления воздуха, cair, Meas, для определения поправочных коэффициентов направления воздуха, b0 и b1, на основе следующего уравнения:
ψair, th = β0 + β1 · ψair, изм. 1037.528-5
(iii) Исправьте каждое измеренное значение направления воздуха, используя следующее уравнение:
ψair = β0 + β1 · ψair, изм. 1037.528-6
(h) Определите площадь сопротивления CdA, используя следующую процедуру вместо процедуры, указанной в разделе 10 SAE J1263:
(1) Вычислите эффективную массу автомобиля Me, чтобы учесть инерцию вращения, добавив 56.7 кг к измеренной массе транспортного средства M (в кг) для каждой шины, контактирующей с дорогой.
(2) Управляйте транспортным средством и собирайте данные в диапазоне высоких и низких скоростей, как указано в параграфе (d) (1) или (2) этого раздела. Если на автомобиле есть ограничитель скорости, который не позволяет ей превышать 72 миль / ч, вы должны отключить ограничитель скорости для тестирования.
(3) Рассчитайте среднюю скорость автомобиля в каждой начальной точке скорости (70 и 20 миль / час) и конечной точке (60 и 10 миль / час) следующим образом:
(i) Вычислить среднюю скорость транспортного средства, чтобы представить начальную точку каждого диапазона скоростей как среднее арифметическое измеренных скоростей в течение непрерывного временного интервала, который начинается, когда измеренная скорость транспортного средства меньше 2.На 00 миль / час выше номинальной начальной скорости и заканчивается, когда измеренная скорость транспортного средства достигает 2,00 миль / час ниже номинальной начальной скорости, выраженной как минимум с двумя десятичными знаками. Вычислите отметку времени, соответствующую начальной точке каждого диапазона скорости, как среднюю отметку времени интервала.
(ii) Повторите вычисления, описанные в параграфе (h) (3) (i) этого раздела, соответствующие конечной скорости (60 или 10 миль / час), чтобы определить время, в которое транспортное средство достигает конечной скорости, и средняя скорость транспортного средства, представляющая конечную точку каждого диапазона скоростей.
(iii) Если вы включаете уклон в свои расчеты, используйте средние значения высоты и пройденного расстояния за каждый интервал.
(4) Рассчитайте силу дорожной нагрузки F для каждого диапазона скоростей, используя следующее уравнение:
F = -Me · v — начало-v-конец-начало-t-конец + M · ag · h-начало-ч-конец∣D-начало-D-конец∣Ур. 1037.528-7
Пример:
Me = 17,129 кг (18 шин, контактирующих с дорожным покрытием) v
начало = 69,97 миль / ч = 31,28 м / с v
конец = 59.88 миль / ч = 26,77 м / с M = 16,108 кг
ag = 9,8061 м / с
2 D
начало = 706,8 футов = 215,4 м D
конец = 2230,2 футов = 697,8 м F = −17129 · 31,28−26,773,05−19,11 + 16108 · 9,8061 · 0,044−0,547∣215,4−697,8∣
F = 4645,5 Н
(5) Для испытаний трактора вычислите усилие потери вращения ведущего моста на высоких и низких скоростях, Fspin [скорость], и определите ΔFspin следующим образом:
(i) Используйте результаты проверки эффективности оси, описанной в § 1037.560, для модели ведущей оси, установленной на тракторе, испытываемом для этой процедуры выбега.
(ii) Выполните регрессию второго порядка потери мощности оси в Вт только по контрольным точкам с нулевым крутящим моментом со скоростью колеса fnwheel в об / с из теста эффективности оси, чтобы определить коэффициенты c0, c1 и c2.
Ploss = c0 + c1 · fnwheel + c2 · fnwheel2Eq. 1037.528-8
(iii) Рассчитайте Fspin [скорость], используя следующее уравнение:
Fspin [скорость] = 1v — сегмент [скорость] [c0 + c1 · v — сегмент [скорость] · TRPM + c2 · (v — сегмент [скорость] · TRPM) 2] Ур. 1037.528-9
Пример:
TRPM = 508 об / мин = 0.315657 п / м
c0 = −206,841 Вт
c1 = 239,8279 Вт · с / об
c2 = 21,27505 Вт · с
2 / г
2
Fspinhi = 128,86 · [-206,841 + 239,8279 · 28,86 · 0,315657 + 21,27505 · (28,86 · 0,315657) 2]
Fspinhi = 129,7 Н
Fspinlo = 52,7 N
(iv) Рассчитайте ΔFспин, используя следующее уравнение:
ΔFspin = Fspinhi − FspinloEq. 1037.528-10
Пример:
ΔFспин = 129,7−52,7 = 77,0 Н
(6) Для испытаний трактора вычислите силу сопротивления качению шины на высоких и низких скоростях для рулевого управления, ведущей оси и осей прицепа, FTRR [скорость, ось], и определите ΔFTRR, разность сопротивления качению между 65 милями / час и 15 миль / час для каждой шины следующим образом:
(i) Провести ступенчатое испытание шин на сопротивление качению с использованием трех шин для каждой модели шин, установленных на транспортном средстве, с использованием стандарта SAE J2452 (включенного посредством ссылки в § 1037.810) для следующих контрольных точек (которые заменяют контрольные точки в таблице 3 SAE J2452):
Таблица 1 § 1037.528 — Контрольные точки ступенчатого выбега для определения сопротивления качению шины в зависимости от скорости
Номер шага Нагрузка
(% от макс.) Инфляция
давление
(% от макс.)
1 20 100
2 55 70
3 85 120
4 85 100
5 100 95
(ii) Рассчитайте FTRR [скорость, ось], используя следующее уравнение:
Пример:
нт, рулить = 2
psteer = 758.4 кПа
Lsteer = 51421,2 Н
αsteer = −0,2435
βsteer = 0,9576
звездочек = 0,0434
bsteer = 5,4 · 10−5
csteer = 5,53 · 10-7
нт, диск = 8
л.с. = 689,5 кПа
Ldrive = 55958,4 Н
αдвиг = -0,3146
βдвиг = 0,9914
adrive = 0,0504
привод = 1,11 · 10−4
cdrive = 2,86 · 10-7
нт, трейлер = 8
птрейлер = 689.5 кПа
L прицеп = 45727,5 Н
αtrailer = −0,3982
βtrailer = 0,9756
прицеп = 0,0656
btrailer = 1,51 · 10−4
ctrailer = 2,94 · 10−7
всеги = 28,86 м / с = 103,896 км / час
всегло = 5,84 м / с = 21,024 км / час
FTRRhi, рулевое управление = 365,6 Н
FTRRhi, привод = 431,4 Н
FTRRhi, прицеп = 231,7 Н
FTRRlo, рулевое управление = 297,8 Н
FTRRlo, привод = 350,7 Н
FTRRlo, прицеп = 189.0 N
(iii) Рассчитайте FTRR [скорость] путем суммирования расчетов сопротивления качению шины при заданной скорости для каждого положения оси:
Пример:
FTRRhi = 365,6 + 431,4 + 231,7 = 1028,7 N
FTRRlo = 297,8 + 350,7 + 189,0 = 837,5 N
(iv) Отрегулируйте FTRR [скорость] в соответствии с температурой окружающей среды во время участка выбега следующим образом:
Пример:
FTRRhi = 1028,7 Н
FTRRlo = 837,5 Н
Цеги = 25.5 ° C
Цегло = 25,1 ° C
FTRRhi, adj = 1 + 0,006 · (24−25,5)] = 1019,4 Н
FTRRlo, adj = 837,5 · [1 + 0,006 · (24−25,1] = 832,0 N
(v) Определите разницу в сопротивлении качению между 65 и 15 милями в час, ΔFTRR, для каждой шины. Принимайте во внимание множественные результаты с хорошей инженерной оценкой. Например, вы можете проигнорировать результаты испытаний шин с наибольшей и наименьшей разницей и использовать результат для оставшейся шины. Определите ΔFTRR следующим образом:
Пример:
ΔFTRR = 1019.4−832.0 = 187.4 N
(7) Для испытания прицепа определите ΔFTRR, используя значение по умолчанию, скорректированное с учетом температуры окружающей среды, вместо проведения испытания сопротивления качению, как показано ниже:
ΔFTRR = ΔFTRR, def [1 + 0,006 · (24-T — выбег)] Ур. 1037.528-15
Пример:
ΔFTRR, по умолчанию = 215 Н
ΔFTRR = 215 · [1 + 0,0006 · (24−25,5)] = 213,1 N
(8) Возвести в квадрат измерения скорости воздуха и вычислить средний квадрат скорости воздуха в каждом диапазоне скоростей для каждого пробега, v
2air, привет и v
2air, вот.
(9) Среднее значение Flo и v
2air, lo значения для каждой пары прогонов в противоположных направлениях. Если выполняется полный выбег, как описано в параграфе (d) (1), или один высокоскоростной сегмент в каждом направлении, как описано в параграфе (d) (2), усреднять каждые два Flo и v
2air, lo значения. При прохождении двух высокоскоростных сегментов в каждом направлении, как описано в параграфе (d) (2), усредните каждые четыре Flo и v
2air, lo значения. Используйте эти значения как Flo, pair и v.
2air, lo, pair в расчетах в этом параграфе (h) для применения к каждому из двух или четырех высокоскоростных сегментов из тех же пробегов, что и низкоскоростные сегменты, используемые для определения Flo, pair и v.
2аир, вот, пара.
(10) Рассчитать среднюю температуру воздуха T и давление воздуха P
действовать во время каждого скоростного бега. (11) Рассчитать площадь сопротивления, CdA, в м
2 для каждого высокоскоростного сегмента с использованием следующего уравнения, выраженного как минимум с тремя десятичными знаками:
CdA = 2 · (Fhi-Flo, пара-ΔFspin-ΔFTRR) (v-воздух, hi2-v-воздух, lo, пара2) · R · T-p-actEq. 1037.528-16
Пример:
Fhi = 4645,5 Н
Flo, пара = 1005.0 N
ΔFспин = 77,0 Н
ΔFTRR = 187.4 с.ш. v
2air, hi = 933,4 м
2 / с
2
v
2air, lo, пара = 43,12 м
2 / с
2 R = 287,058 Дж / (кг · К) п
act = 101,727 кПа = 101727 Па CdA = 2 · (4640,5−1005,0−77,0−187,4) (933,4−43,12) · 287,058 · 285,97101727
CdA = 6,120 м
2
(12) Рассчитайте окончательное значение CdA для высокоскоростных сегментов следующим образом:
(i) Удалите все точки, где были известные проблемы с оборудованием или другие проблемы с измерениями.
(ii) Из оставшихся точек вычислите медианное значение абсолютного значения углов рыскания, cmed, и удалите все значения CdA, которые отличаются более чем на 1.0 ° от cmed.
(iii) Из оставшихся точек вычислите среднее и стандартное отклонение CdA и удалите все значения, которые отличаются более чем на 2,0 стандартных отклонения от среднего значения.
(iv) Должно быть не менее 24 очков. Из оставшихся точек пересчитайте средний угол рыскания. Округлите средний угол рыскания с точностью до 0,1 °. Этот конечный результат — эффективный угол рыскания ceff для испытания на выбеге.
(v) Для того же набора точек пересчитайте среднее значение CdA.Это окончательный результат теста на выбег, CdAcoastdown (ψeff).
(i) [Зарезервировано]
(j) Включите в заявку на сертификацию следующую информацию:
(1) Название, расположение и описание ваших испытательных центров, включая предысторию / историю, оборудование и возможности, а также трассу и высоту объекта, а также уклон и размер / длину трассы.
(2) Условия испытаний для каждого результата испытания, включая дату и время, скорость и направление ветра, температуру и влажность окружающей среды, скорость транспортного средства, расстояние в пути, название производителя, испытываемое транспортное средство / тип модели, год модели, применимое семейство, тип шин и сопротивление качению, вес тягача с прицепом (по результатам испытаний) и идентификатор (-ы) водителя.}

Аэродинамический тест: седан ВАЗ-2110, универсал ВАЗ-2111 и хэтчбек ВАЗ-2112 | Блог по доработке,тюнингу и обслуживанию автомобиля и скутера

Лобовое сопротивление самолета — Энциклопедия по машиностроению XXL

КАИ АВТОВАЗа. Повелители ветра

Редакция рекомендует:

Хочу получать самые интересные статьи

Факторы, влияющие на силу воздушного сопротивления в велосипедном спорте

Рекордная аэродинамика и 770 километров без подзарядки: чего ждать от флагманского электро-Мерседеса

АЭРОДИНАМИКА

Аэродинамика автомобиля — RacePortal.ru

Аэродинамическое сопротивление

Ретроспектива

Прижимная сила

Руководство по аэродинамике для начинающих: уравнение сопротивления — уровень -1

Drag Queens: сравнение аэродинамики

Что такое коэффициент лобового сопротивления — Площадь лобового сопротивления — Автомобили

Коэффициент лобового сопротивления — Площадь сопротивления — Легковые автомобили

Коэффициент сопротивления — характеристики сопротивления

Коэффициент сопротивления трения — обзор

4.11 Безразмерные формы уравнений и динамическое подобие

Пример 4.16

Решение

Пример 4.17

Решение

Площадь сопротивления, измеренная в полевых условиях, является ключевым коррелятом результатов испытаний на время при езде на велосипеде.

Джеймс Э. Петерман

Аллен К.Лим

Райан И. Игнатц

Эндрю Г. Эдвардс

William C. Byrnes

Аннотация

Методы

Субъекты

Таблица 1

Устройства для измерения мощности и калибровка

Лабораторные измерения и протокол

Гонка на время

Обработка и анализ данных

Профилирование аэродинамики и сопротивления качению, измеренное в полевых условиях

Спроектированная фронтальная площадь

Статистический анализ

Результаты

Таблица 2

Таблица 3

Обсуждение

Дополнительная информация

Приложение S1

Приложение S2

Отчет о финансировании

Дополнительная информация и заявления

Ссылки

40 CFR § 1037.528 — Процедуры выбега для расчета площади сопротивления (CdA). | CFR | Закон США

Добавить комментарий Отменить ответ