Правило помехи справа пдд: как работает правило, кто должен уступить, исключения, штрафы

Содержание

как понять, кто должен уступить

Помеха справа — правило ПДД

Правило ПДД «помеха справа» введено как специальный термин, для того, чтобы участники движения придерживались элементарных норм безопасности в ситуациях, в основном предназначенных для безопасного проезда авто в качестве подсказки – как себя вести в кажущейся нештатной дорожной ситуации.
Давайте разбираться, что значит помеха справа на дороге. Особенно нагляден пример при проезде нерегулируемых перекрёстков равнозначных дорог, если траектории транспортных средств пересекаются.
На рисунке сверху водитель жёлтого авто имеет первым проехать перекрёсток, так как второе авто приближается к нему слева. Кто должен уступить в этой ситуации — понятно – ведь жёлтое авто является помехой справа для синего. То, что пересекающиеся дороги равнозначны, отмечено соответствующими знаками.
Но это, так сказать, хрестоматийный, упрощенный случай.

«Помеха справа» на перекрёстках

Как правило, все перекрёстки оборудованы дорожными знаками, не допускающими «разночтений» правила «Помеха справа».

Проезд регулируемых перекрёстков со знаком «Главная дорога»
В таких случаях, транспортное средство, находящееся на главной дороге, имеет право продолжать движение, если транспортные средства, даже приближающиеся к нему справа, находятся на второстепенной дороге.
Когда ещё действует это правило? В случаях, если траектории ТС, движущихся одновременно по дороге, обозначенном знаком «Главная дорога», пересекаются, то принцип «помехи справа» распространяется на них так же, как при движении по равнозначной дороге.
Проезд перекрёстков, оборудованных дополнительными секциями («стрелками»). При проезде на разрешающий сигнал дополнительной секции, если горит основной разрешающий сигнал, водители, движущиеся «под стрелку», обязаны пропустить транспортные средства, движущиеся с любых других направлений.
«Помеха справа на кольце». Проезд перекрёстков с круговым (кольцевым) движением. Применение правила «помеха справа» совершенно не должно вызывать у водителей каких-либо затруднений. Если вы движетесь «по кольцу», то все авто, пытающиеся вклиниться в поток кольцевого движения, обязаны уступать вам дорогу. Это правило, скорее, является исключением пункта «помеха справа» — ведь все авто будут приближаться к кольцу именно с правой стороны. Впрочем, такие перекрёстки оборудованы соответствующими дорожными знаками, не допускающими «разночтений». Говоря короче – кольцо – это «главная дорога», и применение принципа «помехи справа» здесь «не работает».
Правило помехи справа неукоснительно должно соблюдаться при выезде во дворе и с частных территорий.

Правило «помеха справа» на парковках так же актуально, как и автостоянках, и при «разборе полётов» инспекторами ДПС нарушение этого правила наказывается штрафом.

Движение при одновременном перестроении

Правило «Помеха справа» на полосе разгона «не работает».

Читайте по теме:

Что означает восклицательный знак на автомобиле

В наше время появилось много наклеек на машины, среди них есть и информационные, и шуточные. Рассмо…

Реверсивное движение на дороге — что это такое

Большинство автовладельцев знает, что представляет из себя реверсивное движение на дороге ли…

Разделы

Интересное
- Автодокументы
- Автострахование
- Выхлопная система
- Двигатель
- Кузов
- Купля и продажа авто
- Нарушения и штрафы
- Разное
- Салон
- Топливная система
- Тормозная система
- Трансмиссия
- Ходовая часть
- Электрика и электроника
Обзор автомобилей

ВНИМАНИЕ: ПОМЕХА СПРАВА! | ОТДЕЛ ГИБДД УМВД РОССИИ ПО ГОРОДУ БРЯНСКУ

Все водители и даже некоторые пешеходы, слышали о том, что на дороге действует так называемое правило «помехи справа». Причем, каждый трактует это правило по-своему. Например, многие считают, что нужно уступать дорогу всем автомобилям, приближающимся справа не зависимо от других условий, что, конечно же, в корне неверно. Так что же такое на самом деле «помеха справа»?

Правило «помехи справа» применяется в двух ситуациях: при одновременном перестроении и при движении на нерегулируемых перекрестках или в других местах, где очередность проезда не оговорена правилами. По сути, правило «помехи справа» это последнее (а не первое) правило, которое нужно применять на дороге. Последнее не в том смысле, что его не нужно знать, а в том, что применяется оно после других правил.

Кстати, такого понятия, как «помеха справа« в правилах дорожного движения вообще нет.

Одновременное перестроение

В правилах дорожного движения про перестроение говорится следующее:

«При перестроении водитель должен уступить дорогу транспортным средствам, движущимся попутно без изменения направления движения. При одновременном перестроении транспортных средств, движущихся попутно, водитель должен уступить дорогу транспортному средству, находящемуся справа».

Рассмотрим все по порядку, т.к. случаев перестроения может быть множество.

1. Вы едете по своей полосе, а автомобиль перестраивается с соседней полосы. Уступать ему Вы не обязаны, независимо от того, движется автомобиль справа от Вас или слева. Можете сделать это только по собственному желанию. Правило «помехи справа» не действует.

2. Вы хотите перестроиться на соседнюю полосу. Другие автомобили не перестраиваются. В этом случае придется подождать, пока автомобили на соседней полосе не закончатся. Правило «помехи справа» не действует.

3. Вы перестраиваетесь на полосу, которая находится слева от Вас. Автомобиль на левой полосе также выполняет перестроение. По правилам дорожного движения автомобиль должен уступить Вам дорогу, причем это не зависит от того, куда перестраивается он. Действует правило «помехи справа». Хотя в данной ситуации Вы имеете преимущество, врываться на левую полосу с криком «Ура! Правило помехи справа действует!» не стоит. Лучше немного подождать и убедиться, что дорогу Вам действительно уступают.

4. Вы перестраиваетесь на полосу, которая находится справа от Вас. Автомобиль на правой полосе выполняет перестроение. В этом случае дорогу должны уступить Вы. Действует правило «помехи справа».

Обобщенные правила перестроения

На основе всего вышесказанного можно получить обобщенные правила перестроения:

1. Если я не перестраиваюсь, то и уступать никому не должен.

2. Если я перестраиваюсь направо, то уступить дорогу должен всем.

3. Если я перестраиваюсь налево, то меня должны пропустить (могут и не пропустить) только те, кто перестраивается одновременно со мной.

логика — Разница между логическими аксиомами и правилами вывода

По сути, это вопрос точки зрения.

Идея логических аксиом восходит к « Begriffsschrift » Фреге (1879 г.). Для Фреге логика — это наука, в частности, та отрасль знания, которая имеет дело с истиной. Следовательно, необходимо иметь совокупность законов, регулирующих предмет, а именно понятие истины. Это то, что мы знаем как логические аксиомы.

Представляется естественным выводить более сложные из этих суждений [чистого мышления] из более простых не для того, чтобы сделать их более достоверными, что в большинстве случаев было бы излишним, а для того, чтобы выявить отношения суждений к друг друга. Просто знать законы — это, очевидно, не то же самое, что знать их вместе со связями одних с другими. Таким образом, мы приходим к небольшому числу законов, в которые, если добавить содержащиеся в правилах, включается содержание всех законов, хотя и в неразвитом состоянии. (Фреге 1879 г., §13)

Также важно отметить, что для Фреге (и Рассела) не было четкой разницы между логикой и математикой, поэтому современная практика, представленная в таких теориях множеств, как ZFC, включения логических принципов в качестве правил вывода и -конкретные математические факты как аксиомы было немыслимо.

Книга Генцена Untersuchungen über das logische Schließen (1934/1935) ознаменовала собой поворотный момент от этой ранней аксиоматики к современной выводной концепции логики. По сути, идея Генцена состояла в том, чтобы разработать понятие формального доказательства, которое более точно отражает фактические математические рассуждения:0003

Моя отправная точка была такой: формализация логической дедукции, особенно в том виде, в каком она была разработана Фреге, Расселом и Гильбертом, довольно далека от форм дедукции, используемых на практике в математических доказательствах. Взамен достигаются значительные формальные преимущества. Напротив, я намеревался сначала установить формальную систему, максимально приближенную к реальному мышлению. В результате получилось «

исчисление естественного вывода ». (Гентцен, 1934/1935)

Действительно, с исчислениями в стиле Гильберта не очень приятно работать, так как формальные доказательства простых тавтологий в этих системах часто основаны на крайне искусственных аргументах.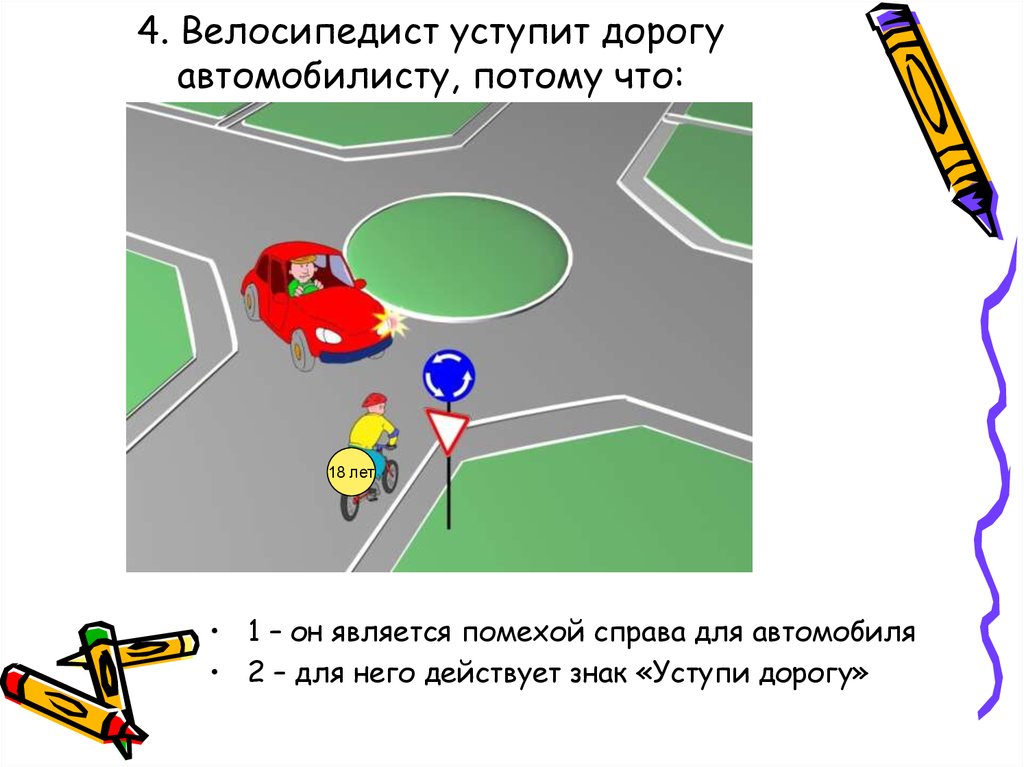 Стоит упомянуть, что сам Фреге не заметил, что его шесть аксиом для исчисления высказываний не являются независимыми:

$A \rightarrow (B \rightarrow A)$
$(A \стрелка вправо (B \стрелка вправо C)) \стрелка вправо ((A \стрелка вправо B) \стрелка вправо (A \стрелка вправо C))$
$(A \стрелка вправо (B \стрелка вправо C)) \стрелка вправо (B \стрелка вправо (A \стрелка вправо C))$
$(A \стрелка вправо B) \стрелка вправо (\neg B \стрелка вправо \neg A)$
$\neg \neg A \rightarrow A$
$A \rightarrow \neg \neg A$

То есть, аксиому 3 можно получить из modus ponens и аксиом 1 и 2. Этот результат был впервые установлен Лукасевичем в 1929 году. Более того, аксиомы 3, 4 и 5 можно свести к одной аксиоме:

$$ (\neg B \rightarrow \neg A) \rightarrow (A \rightarrow B)$$

Это тоже не заметил Фреге.

Исчисления по методу Генцена уделяют больше внимания правилам вывода, которые представляют процесс рассуждения с помощью логических связок, объясняя, как их можно получить (правила введения) и что мы можем с ними делать (правила исключения). Как правило, они опираются только на несколько аксиом, таких как аксиома отражения:

$$p \in \Gamma \vdash p$$

, но даже это можно рассматривать как правило вывода без каких-либо предположений!

Правила вывода и логические доказательства

доказательство

является аргументом из гипотез (предположений) к заключению . Каждый шаг рассуждения подчиняется законам логики. В математике утверждение не считается действительным или правильным, если оно не сопровождается доказательством. Эта настойчивость в доказательстве — одна из вещей, что отличает математику от других предметов.

Писать доказательства сложно; нет никаких процедур, которые вы можете следуйте которым гарантирует успех. Шаблоны, подтверждающие следовать сложны, и их много. Вы не можете рассчитывайте делать доказательства, следуя правилам, запоминая формулы или глядя на несколько примеров в книге.

По этой причине я начну с обсуждения логики . пруфы . Поскольку они более структурированы, чем большинство доказательств, они являются хорошим местом для начала. Они будут записаны в формате

столбцов , где каждый шаг будет оправдан правилом вывода . Большинство правил вывода будет исходить из тавтологии. Так как тавтология – это утверждение, которое «всегда верно», имеет смысл использовать их в рисовании выводы.

Как и большинство доказательств, логические доказательства обычно начинаются с . помещения — заявления, которые вам разрешено делать. Заключение — это утверждение, которое вам нужно доказывать. Идея состоит в том, чтобы работать в помещении, используя правила вывод, пока не придешь к заключению.

Правил помещений. Вы можете записать посылку в любой момент доказательства.

Второе правило вывода — это то, которое вы будете использовать в большинстве логических доказательства. Иногда его называют modus ponendo. ponens

, но я буду использовать более короткое имя.

Модус Поненс. Если вы знаете P и , вы можете записать Q.

В правилах вывода подразумевается, что такие символы, как «P» и «Q» можно заменить на любой высказывания, в том числе составные высказывания. Я скажу больше об этом позже.

Вот простое доказательство с использованием modus ponens:

Я напишу логические доказательства в 3 столбца. Утверждения в логических доказательствах пронумерованы, чтобы вы могли обратиться к ним, и номера идут в первый столбец. Фактические заявления идут во втором столбце. третья колонка содержит ваше обоснование записи заявление.

Таким образом, утверждения 1 (P) и 2 ( ) являются помещения, поэтому правило помещения позволяет мне их записать. Модус поненс говорит, что если я уже записал P и — на любые предыдущих строк в любом порядке — тогда я могу написать Q. Я сделал это в строке 3, сославшись на правило («Modus ponens») и строки (1 и 2), содержащие утверждения, необходимые мне для применения modus ponens.

Как я уже отмечал, буквы «P» и «Q» в modus ponens правило может фактически означать составные операторы — они не имеют быть «одними буквами». Например:

Здесь следует отметить несколько вещей. Во-первых, занимает место P в модусе правило поненс, и занимает место Q. То есть, и 9соединение 0005 операторы , которые заменены на «P» и «Q» в modus ponens.

Обратите также внимание на то, что оператор if-then указан первым, а Часть «если» указана второй. Это не независимо от того, какая из них была записана первой, и пока обе части уже записаны, вы можете применить modus ponens.

Наконец, заявление не приняло участие на шаге modus ponens. Возможно, это часть более крупного доказательства, и будет использоваться позже. Тот факт, что он пришел между двумя частями modus ponens не имеет значения.

Как обычно в математике, вы должны обязательно применять правила ровно . Например, это , а не допустимое использование модус поненс:

Вы понимаете, почему? Чтобы использовать modus ponens в операторе if-then, вам нужна часть «if», которая является . У вас есть только P, что составляет всего часть «если»-часть. Этого недостаточно.

Двойное отрицание. В любом заявлении вы можете замените P на или вместо P (и запишите новое утверждение).

Например, в этом случае я применяю двойное отрицание с P заменен на :

Вы также можете применить двойное отрицание «внутри» другого заявление:

Двойное отрицание встречается достаточно часто, поэтому мы нарушаем правила и разрешить его использование, не делая этого в качестве отдельного шага или упоминая это явно. Я продемонстрирую это на примерах для некоторых другие правила вывода.

Модус Толленс. Если вы знаете и , вы можете записать .

Это простой пример modus tollens:

В следующем примере я применяю modus tollens с заменой P на C. и Q заменен на:

Последний пример показывает, как вам разрешено «подавлять» шаги двойного отрицания. Вы видите, как это было сделано? Если бы я написал шаг двойного отрицания явно, это будет выглядеть так:

Когда вы применяете modus tollens к оператору if-then, убедитесь, что у тебя есть отрицание части «тогда». следующий вывод неверен:

Чтобы использовать modus tollens, вам нужен , а не Q.

Это тоже неверно:

Это похоже на modus ponens, но наоборот. Нет такого правила позволяет сделать это: Вычет недействителен.

Дизъюнктивный силлогизм. Если вы знаете и , вы можете написать Q.

Вот простой пример дизъюнктивного силлогизма:

В следующем примере я применяю дизъюнктивный силлогизм с заменой P и D вместо Q в правиле:

Обратите внимание, что в следующем примере P совпадает с , так что это отрицание .

Это еще один случай, когда я пропускаю шаг двойного отрицания. Без пропуска шага доказательство будет выглядеть так:

Закон ДеМоргана. В любом заявлении вы можете заменять:

1. для .

2. для .

3. для .

4. для .

Как обычно, после замены вы записываете новое утверждение.

Закон ДеМоргана говорит вам, как распределять по или или как выносить из или. Чтобы распространить, вы прикрепляете к каждому термину, а затем меняете на или на . Чтобы факторизовать, вы факторизуете каждый член, а затем меняете на или на .

Обратите внимание, что это относится только (напрямую) к «или» и «и». Мы увидим, как свести на нет «если-то» позже.

Вот пример применения ДеМоргана к оператору «или»:

Обратите внимание, что буквальное применение ДеМоргана дало бы . Я изменил это на , еще раз подавив шаг двойного отрицания.

Условная дизъюнкция. Если знаете, можете написать.

Если знаете, то можете написать.

Вот первое направление:

И вот второй:

Первое направление является ключевым: условная дизъюнкция позволяет вам преобразовать операторы «если-то» в «или» заявления.

Ниже мы увидим, что биусловные операторы могут быть преобразованы в пары условных операторов. Вместе с условным дизъюнкции, это позволяет в принципе сократить пять логических связки на три (отрицание, конъюнкция, дизъюнкция). Но ДеМорган позволяет нам превращать конъюнкции в дизъюнкции (или наоборот). наоборот), поэтому в принципе мы могли бы сделать все, «или» и «не». Причина, по которой мы этого не делаем, заключается в том, что это сделало бы наши заявления намного длиннее: использование другого связки — это как стенография, которая избавляет нас от необходимости писать.

Кроме того, мы можем решить проблему отрицания условного что мы упоминали ранее.

Мы вывели новое правило! Давайте запишем это.

Отрицание условного предложения. Если знаете, можете написать.

Если знаете, то можете написать.

Первое направление полезнее второго. Лично я обычно забывают об этом правиле и просто применяют условную дизъюнктию и ДеМорган, когда мне нужно отрицать условное выражение. Но вы можете использовать это, если ты хочешь.

Построение соединения. Если вы знаете P и Q, вы можете записать .

Подумайте об этом, чтобы убедиться, что это имеет смысл для вас. Если истинно, вы говорите, что P истинно, а Q истинно. истинный. Так что, с другой стороны, вам нужны как P true, так и Q true, чтобы сказать, что это правда.

Вот пример. Обратите внимание, что я помещаю части в круглые скобки, чтобы сгруппируйте их после построения союза.

Правило силлогизма. Если вы знаете и , то вы можете написать вниз .

Правило силлогизма гласит, что силлогизмы можно «сцеплять». вместе. Например:

Определение бикондиционала. Если знаете, то можете записывать и можете записывать. Если вы знаете и , вы можете написать .

Сначала простой пример:

Кстати, стандартная ошибка — применять modus ponens к биусловный («»). Modus ponens применяется к условные («»). Так это недействительно:

С такими же помещениями вот что нужно сделать:

Разложение соединения. Если вы знаете , вы можете записать P и Q.

Это правило гласит, что вы можете разложить конъюнкцию, чтобы получить отдельные части:

Обратите внимание, что вы не можете разложить дизъюнкт!

Что не так с этим? Если вы знаете, что это правда, вы знаете, что один P или Q должен быть истинный. Проблема в том, что вы не знаете , какое из верно, так что вы не можете предполагать что либо в частности правда.

С другой стороны, легко построить дизъюнкций.

Построение дизъюнкции. Если вы знаете P и Q is любой оператор , вы можете записать.

Это говорит о том, что если вы знаете утверждение, вы можете «или» его с любой другой оператор для построения дизъюнкции.

Обратите внимание, что не имеет значения, какое другое утверждение! Как только вы известно, что P истинно, любое утверждение «или» с P должно быть true: утверждение «или» истинно, если хотя бы одно из штук правда.

Следующие два правила сформулированы для полноты. Они достаточно легкие что, как и в случае с двойным отрицанием, мы позволим вам использовать их без отдельный шаг или явное упоминание.

Коммутативность союзов. В любом утверждение, вы можете заменить (и записать новое утверждение).

Коммутативность дизъюнкций. В любом утверждение, вы можете заменить (и записать новое утверждение).

Вот коммутативность конъюнкции:

Вот коммутативность для дизъюнкции:

Прежде чем я приведу несколько примеров логических доказательств, я объясню, где исходят из правил вывода. Вы, наверное, заметили, что правила вывода соответствуют тавтологии. На самом деле, вы можете начать с тавтологии и использовать небольшое число простой правила вывода для получения всех остальных правил вывода.

Выше были сформулированы три простых правила: Правило предпосылок, Modus Ponens и построение соединения. Вот два других. Мы использовали их без упоминания в некоторых наших примерах, если вы посмотрите внимательно.

Эквивалентность Вы можете заменить утверждение на другой, который логически эквивалентен. (Напомним, что P и Q логически эквивалентны тогда и только тогда, когда это тавтология.)

Например, поскольку P и логически эквивалентны, вы можете заменить P на или на P.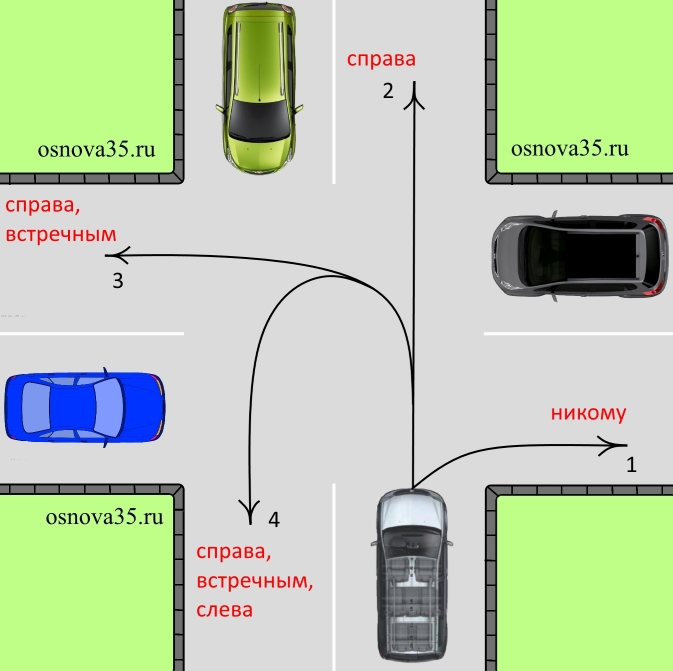 Это является двойным отрицанием. Как я уже говорил, мы экономим время, не пишем вне этого шага.

Замена. Вы можете взять известную тавтологию и заменить простые утверждения.

Это сводится к моему замечанию в начале: в утверждении правила вывод, простые утверждения («P», «Q» и и так далее) может обозначать составные утверждения. «Может стоять за» это то же самое, что сказать «можно заменить на». Мы были делать это без явного упоминания.

Вот пример. Тавтология дизъюнктивного силлогизма гласит:

Предположим, у вас есть и в качестве помещения. Вот как вы применяете простые правила вывода и тавтология дизъюнктивного силлогизма:

Обратите внимание, что я использовал четыре из пяти простых правил вывода: Правило предпосылок, Modus Ponens, построение соединения и Замена. В строке 4 я использовал тавтологию дизъюнктивного силлогизма. заменив

(Некоторые люди используют слово «инстанциация» для такого рода замена. )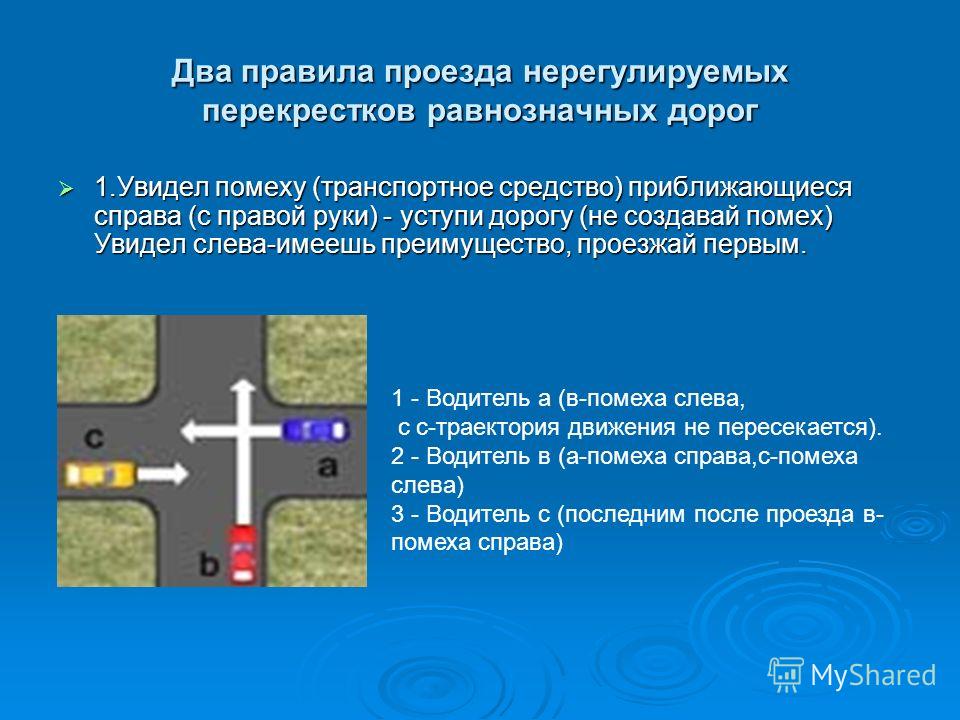

Преимущество этого подхода в том, что у вас есть только пять простых правила вывода. Недостатком является то, что доказательства, как правило, дольше. С подходом, который я буду использовать, Дизъюнктивный силлогизм является правилом. вывод, а доказательство таково:

Подход, который я использую, превращает тавтологии в правила вывода. заранее, и по этой причине вам не нужно будет использовать Эквивалентность и правила замены, которые часто. Но ты разрешено используйте их, и вот где они могут быть полезны. Предположим, вы пишете доказательство, и вы хотели бы использовать правило вывода — но это выше не упоминалось. Запишите соответствующие логические утверждение, затем построить таблицу истинности, чтобы доказать, что это тавтология (если его нет в списке тавтологии). Затем используйте замену для использования Ваша новая тавтология.

Если вы идете на рынок за пиццей, один из способов — купить пиццу.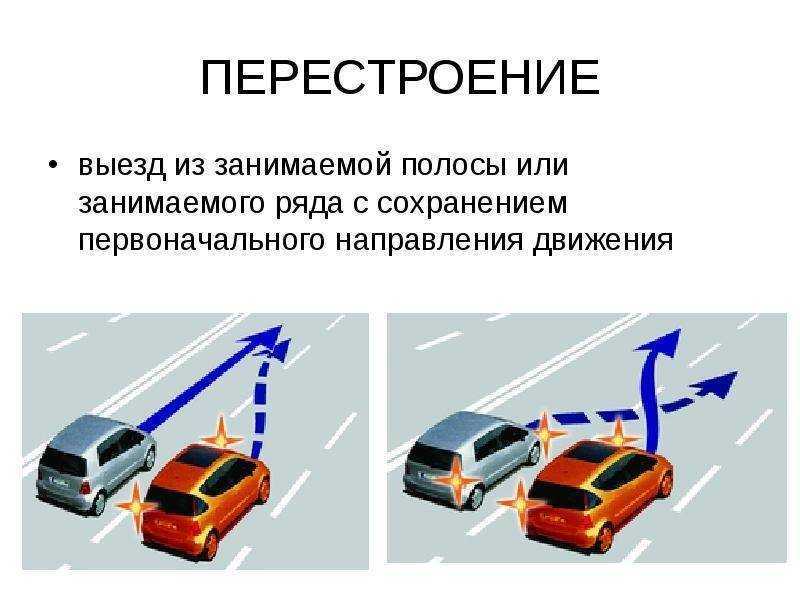 ингредиенты — корочка, соус, сыр, начинка — возьмите все домой, соберите пиццу и поставьте ее в духовку. Использование тавтологии вместе с пятью простыми правилами вывода как сделать пиццу с нуля. Но вы также можете пойти в рынок и купить замороженную пиццу, взять ее домой, и поставить ее в духовку. Используя множество правил вывода, происходящих из тавтологии, — подход, который я буду использовать — это как получить замороженную пиццу.

Вот несколько доказательств, использующих правила вывода. В каждом случае, около предпосылок — заявлений, которые предполагаются чтобы быть правдой — приведены, а также заявление для доказательства. Доказательство состоит в использовании правил вывода для получения утверждения о доказать из помещения.

Пример. Помещения: .

Докажите: С.

Одно дело видеть, что шаги верны; это другое дело чтобы увидеть, как вы думаете, чтобы сделать их. я использовал свой опыт работы с логическими формами в сочетании с работает в обратном направлении .

Я пытаюсь доказать C, поэтому искал утверждения, содержащие C. Только первая посылка содержит С. Я видел, что С содержится в следствие если-то; согласно modus ponens, следствие следует, если ты знаешь предысторию.

Часть «если» первой посылки. Следовательно, я искал другую посылку, содержащую А или . Единственная другая посылка, содержащая А, это второй. В этом случае A появляется как часть «если» если-то. По modus tollens следует из отрицание «тогда» — части Б. Но я заметил, что в качестве предпосылки, поэтому оставалось только запустите все эти шаги вперед и запишите все.

Обычно в логических доказательствах (и в математических доказательствах) работает назад от того, что вы хотите на бумаге для заметок, затем напишите настоящую доказательство вперед. Вторая часть важна!

Для этого мне нужно было иметь практическое знакомство с основные правила вывода: Modus ponens, modus tollens и т.

Правило помехи справа пдд: как работает правило, кто должен уступить, исключения, штрафы :: Autonews