4 Кинематика и динамика автомобильного колеса
План лекции
3.1. Общие сведения
3.2. Упугое проскальзывание и скольжение колеса. Радиус качения колеса.
3.3. Момент сопротивления качению эластичного колеса в ведомом режиме
3.4. Влияние конструктивных и эксплутационных факторов на коэффициент сопротивления качению
3.1.Общие сведения
Энергия вращения, вырабатываемая двигателем автомобиля, преобразуется в поступательное движение транспортного средства движетелем, в качестве которого в автомобиле выступает система колес с эластичными пневматическими шинами.
Пневматическая шина представляет собой оболочку, наполненную сжатым воздухом. При качении колеса по дороге происходит деформация этой оболочки и проскальзывание элементов протектора относительно поверхности дороги.
Размер автомобильного колеса в свободном, ненагруженном состоянии характеризуется свободным радиусом rc. Свободный радиус колеса — половина наружного диаметра Dн;
Свободный радиус колеса — половина наружного диаметра Dн;
rc =0.5 Dн.
Рекомендуемые файлы
Под наружным диаметром колеса понимается диаметр наибольшего окружного сечения беговой дорожки колеса при отсутствии контакта с дорогой. Наружный диаметр колеса зависит от давления воздуха в шине и, как правило, возрастает с его увеличением, определяется непосредственно замером. Значение наружного диаметра колеса при номинальном давлении воздуха в шине указывается в ГОСТах или каталогах.
При действии на колесо вертикальной нагрузки происходит деформация части шины, соприкасающейся с опорной поверхностью. При этом расстояние от оси колеса до опорной поверхности становится меньше свободного радиуса. Это расстояние, замеренное у неподвижного колеса, называется статическим радиусом rст. Статический радиус при номинальных нагрузках и давлении воздуха в шинах также указывается в их характеристиках. Обычно шины конструируют таким образом, чтобы при номинальных нагрузке и давлении прогиб шины составлял 13… 20 % от высоты профиля. Статический радиус при известных конструктивных параметрах шин можно находить из соотношения:
Обычно шины конструируют таким образом, чтобы при номинальных нагрузке и давлении прогиб шины составлял 13… 20 % от высоты профиля. Статический радиус при известных конструктивных параметрах шин можно находить из соотношения:
rст =0,5d+lzH,
где d — посадочный диаметр обода шины;
lz —коэффициент вертикальной деформации, зависящий от типа шин:
для тороидных шин lz =0,85…0,87;
для шин с регулируемым давлением и арочных lz =0,8…0,85;
Н — высота профиля.
При качении нагруженного колеса в силу ряда причин (динамическое действие нагрузки, передаваемый колесом крутящий момент, скорость вращения и др.) расстояние между осью колеса и опорной поверхностью меняется. Это расстояние называют динамическим радиусом rд. При качении колеса по твердой опорной поверхности с малой скоростью статический и динамический радиусы его практически одинаковы. Поэтому при приближенных расчетах динамический радиус часто принимают равным статическому.
Поэтому при приближенных расчетах динамический радиус часто принимают равным статическому.
3.2. Упугое проскальзывание и скольжение колеса. Радиус качения колеса.
Реальное автомобильное колесо в тангенциальном направлении не является абсолютно жестким. Под воздействием передаваемого крутящего момента протектор деформируется в тангенциальном направлении. Если направление передаваемого момента совпадает с направлением угловой скорости колеса, элементы шины, находящиеся в набегающей полуокружности, подвергаются сжатию, а с противоположной стороны — растяжению, как это показано на рис. 3.4. На этом же рисунке показана эпюра тангенциальных напряжений в протекторе шины.
Рис. 3.4. Деформация шины (а) и эпюра напряжений в протекторе (б) при приложении к колесу крутящего момента:+ —зона сжатия; — —зона растяжения
Элементы шины, находящиеся в контакте с опорной поверхностью, нагружены в тангенциальном направлении неодинаково: элементы, входящие в контакт, сжимаются, а выходящие — растягиваются. При возрастании передаваемого крутящего момента увеличивается площадь, в пределах которой происходит проскальзывание шины относительно дороги (рис. 3.5).
При возрастании передаваемого крутящего момента увеличивается площадь, в пределах которой происходит проскальзывание шины относительно дороги (рис. 3.5).
Рис. 3.5. Зависимость площади скольжения колеса (заштрихованная зона) от передаваемого им момента Мк
При некотором значении момента начинается одновременное перемещение всех находящихся в зоне контакта точек колеса. Перемещение части точек колеса, находящихся в контакте с дорожным покрытием, относительно опорной поверхности, когда в зоне контакта есть точки, неподвижные относительно этой поверхности, называется упругим проскальзыванием колеса. Одновременное же перемещение всех находящихся в контакте точек колеса называется скольжением колеса.
Вследствие упругого проскальзывания или скольжения путь, проходимый колесом за один оборот, оказывается меньшим, чем путь, проходимый в ведомом режиме. При возрастании передаваемого крутящего момента увеличивается тангенциальная деформация шины и скольжение, а путь, проходимый колесом за один оборот, уменьшается.
Радиус качения колеса можно представить как радиус условного недеформируемого кольца, которое, катясь без скольжения, совершит число оборотов и пройдет путь, одинаковый с реальным колесом. Радиус качения колеса является условной величиной и непосредственно не связан с его размерами. Он определяется как отношение поступательной скорости колеса к угловой скорости его вращения rk = vx /wk.
В соответствии с принятым выше определением, уменьшение пути центра колеса за определенное число его оборотов равносильно уменьшению радиуса качения.
Если направление передаваемого момента будет противоположным направлению угловой скорости вращения колеса (тормозящее колесо), при увеличении момента радиус качения будет возрастать.
Рис. 3.6. Зависимость радиуса качения колеса от передаваемого ему крутящего момента
Зависимость радиуса качения колеса от передаваемого ему крутящего момента показана на рис. 3.6. На участке 2—3 радиус качения линейно зависит от передаваемого момента, и его изменение определяется упругим проскальзыванием колеса. Акад. Е. А. Чудаковым, впервые установившим эту зависимость, предложена следующая формула для нахождения радиуса качения по передаваемому колесу моменту:
3.6. На участке 2—3 радиус качения линейно зависит от передаваемого момента, и его изменение определяется упругим проскальзыванием колеса. Акад. Е. А. Чудаковым, впервые установившим эту зависимость, предложена следующая формула для нахождения радиуса качения по передаваемому колесу моменту:
rk=rk0—ltMk
где rk0 — радиус качения при нулевом крутящем моменте, который соответствует радиусу качения колеса в ведомом режиме;
lt — коэффициент тангенциальной эластичности шины, зависящий от типа и конструкции шины.
На участках 1—2 и 3—4 изменение радиуса качения определяется как упругим проскальзыванием, так и скольжением колеса. Пунктирной линией на графике показано, как изменялся бы радиус качения при отсутствии скольжения. Очевидно, что на участках 1—2 и 3—4 он может находиться также по формуле (1. 2). В последующем радиус качения, определенный при отсутствии скольжения, будем называть радиусом качения без скольжения и обозначать r0.
2). В последующем радиус качения, определенный при отсутствии скольжения, будем называть радиусом качения без скольжения и обозначать r0.
На участках 0—1 и 4—5 происходит полное скольжение элементов шины относительно опорной поверхности. Точка 5 соответствует буксующему колесу при неподвижном автомобиле, а точка 0—колесу, движущемуся юзом.
Если обозначить радиусы качения и передаваемые колесом моменты в начале и в конце линейного участка соответственно через М2, rк2 и М3, rк3, то коэффициент тангенциальной эластичности шины определим как
Экспериментально радиус качения находят путем определения числа оборотов колеса N на отрезке пути s при заданном режиме движения:
rk=s/(2pN).
Рис. 3.7.
3.7.
Согласно рис. 3.7, скорость точки В (скорость vs) можно рассматривать как скорость скольжения элементов шины относительно опорной поверхности. В соответствии с принятыми обозначениями
vs = vx — voB=wк(rк—rо).
Отсюда следует, что при rк=rо колесо катится без скольжения. Если rк>rо, скорость скольжения положительна и ее направление совпадает с направлением поступательной скорости колеса (колесо движется юзом). При rк<rо скорость скольжения отрицательна и направлена в сторону, противоположную вектору поступательной скорости центра колеса (колесо движется с буксованием).
Рис. 3.8. Положения мгновенных центров вращения колеса
На рис. 3.8 показаны планы скоростей для рассмотренных трех случаев качения колеса. Из рисунка следует, что радиус качения является расстоянием от центра колеса до его мгновенного центра вращения Оt и в зависимости от режима движения может изменяться от нуля (буксующее колесо при неподвижном автомобиле) до бесконечности (заблокированное колесо при движущемся автомобиле).
3.8 показаны планы скоростей для рассмотренных трех случаев качения колеса. Из рисунка следует, что радиус качения является расстоянием от центра колеса до его мгновенного центра вращения Оt и в зависимости от режима движения может изменяться от нуля (буксующее колесо при неподвижном автомобиле) до бесконечности (заблокированное колесо при движущемся автомобиле).
3.3. Момент сопротивления качению эластичного колеса в ведомом режиме
Шина деформируется под действием нормальной к опорной поверхности составляющей нагрузки на колесо. Площадь контакта ее с дорогой увеличивается до тех пор, пока не наступит равновесие между нормальной реакцией дороги и нагрузкой. У неподвижной шины контактная поверхность имеет форму, близкую к эллипсу, большая ось которого находится в плоскости симметрии шины. Распределение давления по площади контактной поверхности неравномерное, оно примерно пропорционально деформации шины. Характерная эпюра давлений под неподвижной шиной показана на рис.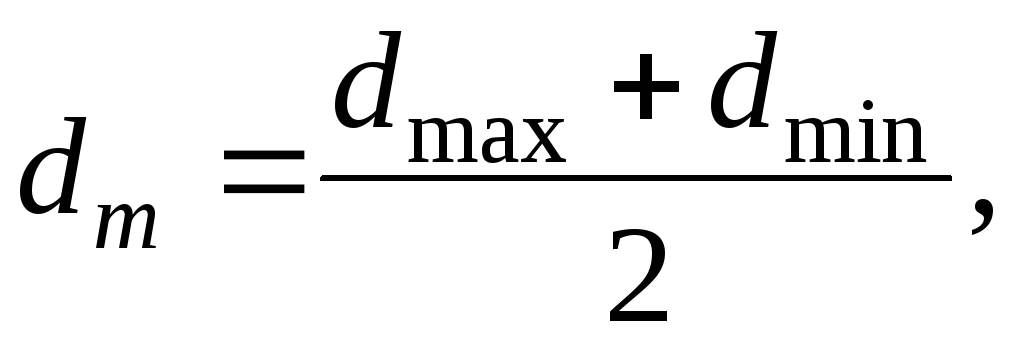 3.9, а.
3.9, а.
Рис. 3.9. Эпюры давлений: о—неподвижной шины; б—катящейся. |
Рис. 3.10. Деформация элементов шины при качении |
При движении автомобильного колеса в работе участвуют все элементы шины. За один оборот колеса каждый элемент профиля шины, например элемент b—b (рис. 3.10, а), подвергается полному циклу нагружения и разгрузки.
С достаточной для практической цели точностью можно считать, что нагружение (деформирование) элементов шины происходит в зоне полуокружности 0—1—2, а восстановление формы — полуокружности 2—3—0. При этом наиболее интенсивное деформирование и восстановление происходят в зонах полудуг 1—2 и 2—3 соответственно.
По мере перемещения элемента шины от точки 1 к точке 2 увеличивается его деформация и, следовательно, воспринимаемая им нагрузка. Зависимость нагрузки DF, передающейся на элемент, от его деформации представлена на графике рис. 3.10, б (линия 1—2). При перемещении элемента от точки 2 к точке 3 происходит уменьшение деформации (уменьшение нагрузки, приходящейся на элемент). На графике линия, характеризующая зависимость DF=f(h) вследствие неизбежных гистерезисных потерь пройдет ниже линии, показывающей ту же зависимость при увеличении деформации (линия 2—3). Площадь, заключенная между линиями нагружения и разгрузки, пропорциональна потерям энергии на деформацию элемента шины при одном обороте колеса.
Зависимость нагрузки DF, передающейся на элемент, от его деформации представлена на графике рис. 3.10, б (линия 1—2). При перемещении элемента от точки 2 к точке 3 происходит уменьшение деформации (уменьшение нагрузки, приходящейся на элемент). На графике линия, характеризующая зависимость DF=f(h) вследствие неизбежных гистерезисных потерь пройдет ниже линии, показывающей ту же зависимость при увеличении деформации (линия 2—3). Площадь, заключенная между линиями нагружения и разгрузки, пропорциональна потерям энергии на деформацию элемента шины при одном обороте колеса.
Вследствие того, что при одинаковых прогибах в зонах увеличения и уменьшения деформации на элементы шины приходится разная нагрузка, эпюра давлений для катящегося колеса оказывается несимметричной относительно середины контактной поверхности: в передней части контактной поверхности нормальные давления будут большими, нежели в задней. Поэтому равнодействующая нормальных реакций смещена на расстояние а от середины контактной поверхности (см. рис. 3.9, б). За счет этого смещения создается момент относительно оси колеса
Поэтому равнодействующая нормальных реакций смещена на расстояние а от середины контактной поверхности (см. рис. 3.9, б). За счет этого смещения создается момент относительно оси колеса
Mf=aRz,
где Rz — нормальная к опорной поверхности составляющая реакции дороги.
Этот момент препятствует качению колеса. Поэтому его можно считать моментом сопротивления качению колеса. Отметим, что на недеформируемой поверхности момент сопротивления качению обусловлен внутренними (гистерезисными) потерями энергии на деформацию шины.
В дальнейшем вместо момента сопротивления качения колеса мы будем рассматривать силу сопротивления качению колеса Ff=Mf / r0=aRz/ r0= fRz.
Здесь f=a/r0 – коэффициент сопротивления качению колеса. Коэффициент сопротивления качению колеса характеризует потери энергии, возникающие при качении колеса.
Коэффициент сопротивления качению колеса характеризует потери энергии, возникающие при качении колеса.
3.4. Влияние конструктивных и эксплутационных факторов на коэффициент сопротивления качению.
На коэффициент сопротивления качению влияют:
1. тип покрытия дороги и ее состояние;
2. скорость движения;
3. давление воздуха в шинах;
4. температура шины;
5. нагрузка на колесо;
6. его размеры;
7. конструктивные особенности шины.
Увеличение скорости движения. Как правило, коэффициент f при увеличении v возрастает. На ровных дорогах при изменении скорости от нуля до некоторого значения, зависящего от конструктивных особенностей шины, нормальной нагрузки на колесо и внутреннего давления воздуха, возрастание коэффициента f невелико. Поэтому для большинства шин грузовых автомобилей связь коэффициента f и скорости v достаточно точно аппроксимируется линейной зависимостью. На неровных дорогах даже при средних скоростях с увеличением v коэффициент f может расти довольно сильно. Начиная с некоторого значения v даже на ровных дорогах коэффициент f начинает быстро увеличиваться (рис. 3.11).
Поэтому для большинства шин грузовых автомобилей связь коэффициента f и скорости v достаточно точно аппроксимируется линейной зависимостью. На неровных дорогах даже при средних скоростях с увеличением v коэффициент f может расти довольно сильно. Начиная с некоторого значения v даже на ровных дорогах коэффициент f начинает быстро увеличиваться (рис. 3.11).
Рис.3.11. Зависимость коэффициента сопротивления качению при различных значениях рВ: 1-3 соответственно 15, 25 и 30 МПа
При номинальных нагрузках на колесо и давлениях воздуха в шине интенсивный рост коэффициента f начинается при v=20…30 м/с.
Существуют различные эмпирические формулы, позволяющие приближенно подсчитать коэффициент f при различных скоростях движения; удобной является формула
f=f0+kfv2,
где f0 — коэффициент сопротивления качению при малой скорости. В тех случаях, когда действительное значение kf неизвестно, рекомендуется принимать kf=7×10-6
В тех случаях, когда действительное значение kf неизвестно, рекомендуется принимать kf=7×10-6
Температура шины. С увеличением температуры шины ее сопротивление качению снижается, во-первых, за счет уменьшения гистерезисных потерь в резине, во-вторых, в результате повышения внутреннего давления воздуха.
Рис. 3.12. Зависимость коэффициента сопротивления качению от температуры шины
При этом снижается коэффициент f в результате уменьшения деформаций шины (рис. 3.12). Приводимые в литературе значения f относятся обычно к полностью прогретой шине.
Давление воздуха в шине рв. Коэффициент f на различных дорогах в различной степени зависит от рв. На дорогах с твердым покрытием он уменьшается с увеличением давления рв, достигая минимального значения при давлении рв, близком к рекомендованному для данной шины. При чрезмерном давлении рв возрастают динамические нагрузки, возникающие в результате взаимодействия колеса с неровностями дороги, что может привести к некоторому возрастанию коэффициента f.
При чрезмерном давлении рв возрастают динамические нагрузки, возникающие в результате взаимодействия колеса с неровностями дороги, что может привести к некоторому возрастанию коэффициента f.
Рис. 3.13. Зависимость коэффициента сопротивления качению от внутреннего давления воздуха в шине на разных поверхностях: 1- песок; 2- пашня; 3- асфальт
Если движение происходит по деформируемым дорогам, при уменьшении давления рв увеличиваются потери, связанные с деформацией шины, но уменьшаются потери, связанные с деформацией дороги. Можно подобрать такое давление рв.опт, при котором сопротивление качению будет минимальным (рис. 3.13). Оптимальное давление тем меньше, чем больше деформируемость дорожного полотна. Такая зависимость коэффициента сопротивления качению используется для повышения проходимости автомобилей с центральной системой регулирования давления в шинах.
Нагрузка на колесо Рz. При неизменном давлении рв увеличение Рz приводит к возрастанию коэффициента f. На дорогах с твердым покрытием при изменении нагрузки в пределах 80…110 % номинальной увеличение коэффициента f несущественно. При превышении нагрузки на 20 % номинального значения коэффициент возрастает приблизительно на 5 %, а при дальнейшей перегрузке — более интенсивно. Сильно возрастает коэффициент f с увеличением нагрузки Рz на деформируемой опорной поверхности.
При неизменном давлении рв увеличение Рz приводит к возрастанию коэффициента f. На дорогах с твердым покрытием при изменении нагрузки в пределах 80…110 % номинальной увеличение коэффициента f несущественно. При превышении нагрузки на 20 % номинального значения коэффициент возрастает приблизительно на 5 %, а при дальнейшей перегрузке — более интенсивно. Сильно возрастает коэффициент f с увеличением нагрузки Рz на деформируемой опорной поверхности.
Конструктивные параметры шины. Значение коэффициента f зависит от большого числа конструктивных параметров.
Увеличение толщины протектора повышает коэффициент f, особенно у диагональных шин. В связи с этим по мере износа шин сопротивление качению падает. При полностью изношенном протекторе сопротивление качению может уменьшиться на 20…25 % по сравнению с неизношенным. У шин с вездеходным рисунком протектора, имеющих толщину протектора почти в 2 раза большую, чем у шины с дорожным рисунком, при качении по дорогам с твердым покрытием коэффициент f на 25.
Уменьшение отношения высоты Н профиля шины к его ширине В приводит к снижению коэффициента сопротивления качению. Снижение Н/В уменьшает также зависимость коэффициента f от скорости движения.
Люди также интересуются этой лекцией: КРЁБЕР Алфред Луис.
Внутреннее строение каркаса шины оказывает существенное влияние на коэффициент сопротивления качению. При v<30… 35 м/с наименьшим сопротивлением качению обладают радиальные шины (коэффициент f у них меньше, чем у диагональных на 15…20 %). При больших скоростях наименьшим коэффициентом обладают диагонально-опоясанные и низкопрофильные диагональные шины. По мере износа преимущество радиальных шин по сравнению с диагональными уменьшается.
Увеличение диаметра колеса приводит к уменьшению коэффициента f. На ровных дорогах с твердым покрытием уменьшение небольшое. Чем больше размеры и число неровностей на дороге и чем больше на таких дорогах скорость движения, тем значительнее влияние диаметра колеса на коэффициент f. Особенно сильно снижается коэффициент f на деформируемых опорных поверхностях.
Особенно сильно снижается коэффициент f на деформируемых опорных поверхностях.
Увеличение ширины колеса на дорогах с твердым покрытием незначительно увеличивает коэффициент f, а на большинстве деформируемых опорных поверхностях существенно снижает.
Совершенствование качества резины позволяет значительно снизить сопротивление качению.
На автомобилях со сдвоенными колесами (грузовые автомобили, автопоезда и др.) дополнительные потери на качение возникают также в результате неравномерного распределения между шинами сдвоенных колес нормальных нагрузок и крутящих моментов. Причиной неравномерности являются неодинаковые геометрические размеры и износ шин, различие в температуре, наличие поперечного уклона дороги, прогиб балки моста, неодинаковость внутреннего давления воздуха и др. Вся совокупность конструктивных мероприятий, улучшающих энергетические свойства шин, позволяет снизить их сопротивление качению в 2…3 раза.
Что это — сила трения качения и по какой формуле ее можно вычислить?
Современное состояние техники выглядело бы совершенно иначе, если бы человечество в далеком прошлом не научилось использовать для своих благ силу трения качения. Что она собой представляет, почему появляется и как ее можно рассчитать, эти вопросы рассматриваются в статье.
Под ним понимают физическую силу, которая появляется во всех случаях, когда один предмет не скользит, а катится по поверхности другого. Примерами силы трения качения являются движение деревянного колеса телеги по грунтовой дороге или перемещение колеса автомобиля по асфальту, качение металлических шариковых и игольчатых подшипников по стальной оси, перемещение малярного валика по стене и так далее.
В отличие от сил трения покоя и скольжения, причиной которых являются взаимодействия на атомном уровне шероховатых поверхностей тела и поверхности, причина появления трения в результате качения заключается в гистерезисе деформации.
Объясним названный факт на примере колеса. Когда оно контактирует с абсолютно любой твердой поверхностью, то в зоне контакта происходит его микродеформация в упругой области. Как только колесо повернется на некоторый угол, то эта упругая деформация исчезнет, и тело восстановит свою форму. Тем не менее в результате качения колеса происходит повторение циклов сжатия и восстановления формы, которые сопровождаются потерей энергии и микроскопическими нарушениями в структуре поверхностных слоев колеса. Эти потери называются гистерезисом. Они при движении проявляются в возникновении силы трения качения.
Тем не менее в результате качения колеса происходит повторение циклов сжатия и восстановления формы, которые сопровождаются потерей энергии и микроскопическими нарушениями в структуре поверхностных слоев колеса. Эти потери называются гистерезисом. Они при движении проявляются в возникновении силы трения качения.
Качение недеформируемых тел
Рассмотрим идеальный случай, когда колесо, двигаясь по абсолютно твердой поверхности, не испытывает микродеформаций. В этом случае зона его контакта с поверхностью будет соответствовать прямому отрезку, площадь которого равна нулю.
При движении на колесо действуют четыре силы. Это сила тяги F, сила реакции опоры N, вес колеса P и трение fr. Первые три силы носят центральный характер (действуют на центр масс колеса), поэтому крутящего момента они не создают. Сила fr действует по касательной к ободу колеса. Момент трения качения равен:
M = fr*r.
Здесь радиус колеса обозначен буквой r.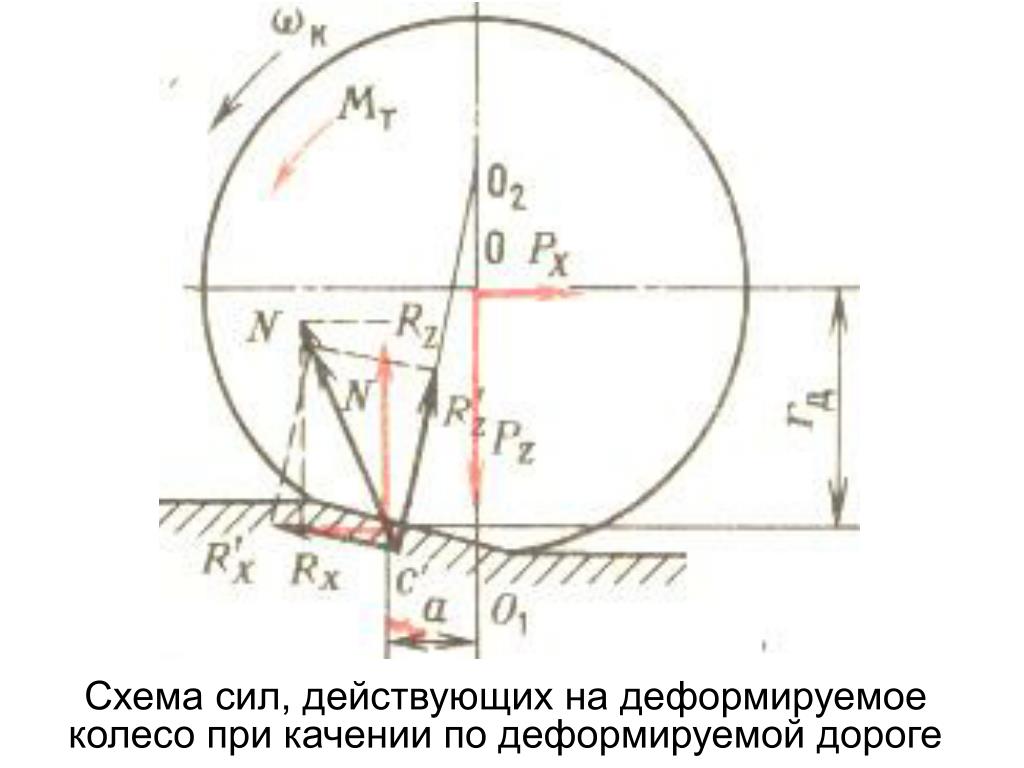
Силы N и P действуют по вертикали, поэтому в случае равномерного движения сила трения fr будет равна силе тяги F:
F = fr.
Любая бесконечно маленькая сила F будет способна преодолеть величину fr, и колесо начнет движение. Этот вывод приводит к тому, что в случае недеформируемого колеса сила трения качения равна нулю.
Качение деформируемых (реальных) тел
В случае реальных тел в результате деформации колеса его площадь опоры на поверхность не равна нулю. В первом приближении она представляет собой прямоугольник, со сторонами l и 2*d. Где l — ширина колеса, которая нас сильно не интересует. Появление же силы трения качения обязано именно значению 2*d.
Как и в случае с недеформируемым колесом, на реальный объект также действуют четыре названные выше силы. Все соотношения между ними сохраняются за исключением одного: сила реакции опоры в результате деформации будет действовать не через ось на колесо, а будет смещена относительно нее на расстояние d, то есть она будет принимать участие в создании крутящего момента. Формула для момента M в случае реального колеса принимает вид:
Формула для момента M в случае реального колеса принимает вид:
M = N*d — fr*r.
Равенство нулю величины M является условием равномерного качения колеса. В результате приходим к равенству:
fr = d/r*N.
Поскольку N равно весу тела, получаем конечную формулу для силы трения качения:
fr = d/r*P.
Это выражение содержит полезный результат: с увеличением радиуса r колеса уменьшается сила трения fr.
Коэффициент сопротивления качению и коэффициент качения
В отличие от сил трения покоя и скольжения, качение характеризуется двумя зависимыми друг от друга коэффициентами. Первый из них — это величина d, описанная выше. Она называется коэффициентом сопротивления качению, поскольку чем больше ее значение, тем больше сила fr. Для колес поездов, автомобилей, металлических подшипников значение d лежит в пределах десятых долей миллиметра.
Второй коэффициент — это собственно качения коэффициент. Он является безразмерной величиной и равен:
Cr = d/r.
Во многих таблицах приводят именно эту величину, поскольку его удобнее применять для решения практических задач, чем значение d. В большинстве практических случаев величина Cr не превышает нескольких сотых (0,01- 0,06).
Условие качения реальных тел
Выше мы получили формулу для силы fr. Запишем ее через коэффициент Cr:
fr = Cr*P.
Видно, что ее форма аналогична таковой для силы трения покоя, в которой вместо Cr используется величина µ — коэффициент трения покоя.
Сила тяги F приведет к качению колеса только в том случае, если она будет больше fr. Однако, тяга F может привести и к скольжению, если она превысит соответствующую силу покоя. Таким образом, условие качения реальных тел заключается в том, чтобы сила fr была меньше силы трения покоя.
В большинстве случаев значения коэффициента µ на 1-2 порядка превышают величину Cr. Тем не менее, в некоторых ситуациях (наличие на поверхности качения снега, льда, маслянистых жидкостей, грязи) µ может становиться меньше Cr. В последнем случае будет наблюдаться проскальзывание колеса.
Блог › То, что крутит колеса. Все о дифференциалах: крутящий момент истины
Когда известно изменение силы тяги на колесах в зависимости от скорости движения автомобиля и суммарной силы сопротивления движению, можно определить максимальную скорость. На рис. 26 показано изменение силы тяги на колесах автомобиля я (верхняя кривая) и сумма сил сопротивления движению (нижняя кривая) в зависимости от скорости движения. На графике сила дана в ньютонах, чтобы выразить ее в килограммах, достаточно разделить на 9,8.
Кривая изменения суммы сил сопротивления построена по точкам, соответствующим значениям величин, полученным при равномерном движении автомобиля с заданной скоростью. Так как движение равномерное, то, естественно, сюда не включена сила инерции. Поэтому в сумму сопротивления входят: сила сопротивления качению Р к, сопротивление подъема Р п и сила сопротивления воздушной среды Р в.
Так как движение равномерное, то, естественно, сюда не включена сила инерции. Поэтому в сумму сопротивления входят: сила сопротивления качению Р к, сопротивление подъема Р п и сила сопротивления воздушной среды Р в.
Если бы в каждый отдельный момент сила тяги на колесах была равна суммарным значениям сил сопротивления для данной скорости, то автомобиль двигался бы равномерно. Однако, как видно из рисунка, значение силы тяги совпадает с суммарным значением сил сопротивления только в одной точке А, соответствующей определенному значению скорости автомобиля. Влево от этой точки сила тяги превышает значение сил сопротивления. Этот избыток сил, обозначенный Р′ п, позволяет преодолеть инерцию и сообщает автомобилю ускорение.
Поэтому при полном открытии дроссельной заслонки автомобиль движется на скоростях, лежащих влево от точки А, т. е. с ускорением. Вправо от точки пересечения кривых сила тяги меньше сил сопротивления движению, и автомобиль начинает замедлять ход. Точка пересечения этих кривых А обозначает максимальную скорость движения автомобиля, которую можно достичь при заданных условиях и полном открытии дроссельной заслонки.
Зная ориентировочно вес будущего автомобиля, его лобовую площадь и коэффициент сопротивления воздуха, состояние дорожного полотна и тип покрытия, а также максимально возможный угол подъема на тех дорогах, на которых в дальнейшем он будет эксплуатироваться, можно подсчитать суммарную величину всех сил сопротивления движению и построить кривую этих сил. Возникает вопрос, где же взять значение силы тяги Р т?
Сила тяги на колесах зависит от величины крутящего момента, который подводится к ним через передачу от двигателя. Следовательно, значение крутящего момента на колесах зависит от величины его на валу двигателя и от передаточного отношения трансмиссии, т. е. передаточного числа той механической связи, посредством которой вал двигателя связан с ведущими колесами.
Обычно число оборотов вала двигателя бывает больше требуемого числа оборотов колеса, когда последние были бы соединены без передачи — напрямую. Поэтому для снижения оборотов между двигателем и осью ведущих колес используют коробку передач и главную передачу.
где М кр — крутящий момент на валу двигателя, кгм;
i к — передаточное число включенной передачи в коробке передач;
i г.п. — передаточное число главной передачи;
r к — радиус качения колеса, м.
Максимальную скорость автомобиль развивает на горизонтальном участке дороги с твердым покрытием, когда значение коэффициента сопротивления качения наименьшее, а сила сопротивления подъему отсутствует (угол а равен нулю). В этот момент машина обычно движется на прямой передаче, величина передаточного отношения в трансмиссии равна только передаточному числу главной передачи i г.п. Уравнение тягового баланса автомобиля в этом случае примет более простой вид
Чтобы определить необходимый крутящий момент на валу двигателя для данных условий движения, нужно знать: вес автомобиля, максимальную скорость движения, радиус качения колеса, т. е размер шин, передаточное отношение главной передачи и коэффициент полезного действия трансмиссии.
е размер шин, передаточное отношение главной передачи и коэффициент полезного действия трансмиссии.
В «Технических требованиях к микролитражным автомобилям и мотоколяскам, изготовляемым в индивидуальном порядке» указано, что самостоятельно можно изготавливать микролитражные автомобили и трехколесные мотоколяски с рабочим объемом двигателя не более 900 см 3 . Таким образом, на основе анализа существующих конструкций можно предположить, что масса этих автомобилей с полной нагрузкой не будет более 800 кг (7850 ньютонов), а у мотоколясок с двигателем объемом в 300 см 3 — 400÷450 кг (3900÷4400 ньютонов). Для двухместных микролитражных автомобилей масса должна быть равна примерно 600 кг (5870 ньютонам). Для четырехместных автомобилей при расчетах следует принимать массу 650÷700 кг (6360÷6850 ньютонов). Следовательно, приступая к расчету, можно ориентировочно установить вес (массу) автомобиля.
Величина радиуса качения колеса зависит от размеров шин. Колеса и шины для самодельных автомобилей берутся от мотороллеров, мотоколясок, малолитражных автомобилей, выпускаемых промышленностью. Основные сведения по шинам, которые можно устанавливать на самодельные микролитражные автомобили, приведены в таблице 3.
Основные сведения по шинам, которые можно устанавливать на самодельные микролитражные автомобили, приведены в таблице 3.
В обозначении размеров шин первое число показывает величину профиля шины в дюймах, а второе — диаметр обода колеса также в дюймах. По этим размерам можно определить номинальный радиус колеса r′ к, находящегося в свободном состоянии,
где b — наибольшая ширина профиля накаченной шины в дюймах;
d — диаметр обода колеса в дюймах.
Под действием веса автомобиля и пассажиров шина деформируется, в результате чего расстояние от центра колеса до поверхности контакта протектора с дорогой изменяется. Новый радиус колеса будет меньше номинального. Он называется радиусом качения колеса и определяется непосредственным измерением или рассчитывается по формуле, в которую вводится коэффициент радиальной деформации шины
где r к — радиус качения колеса;
r′ к — номинальный радиус колеса;
λ — коэффициент деформации шины, принимаемый в пределах 0,94-0,96.
Во время движения автомобиля расстояние от оси его колес до поверхности дороги не всегда будет соответствовать статическому радиусу качения, но для наших расчетов изменение радиуса качения при движении можно не учитывать. Следовательно, выбрав размер шин, можно узнать и радиус качения колеса.
Когда автомобиль движется на прямой передаче, передаточное число коробки передач равно 1. Передаточное число главной передачи можно определить, если известны числа оборотов двигателя и колеса, соответствующие заданной скорости. Отношение количества оборотов вала двигателя и колеса будет необходимым числом главной передачи.
Для определения числа оборотов колеса при заданной скорости ν в км/час следует вначале скорость движения из км/час перевести в м/мин
Затем разделить полученное значение скорости на длину окружности выбранного колеса, чтобы получить число оборотов колеса в минуту
После чего определить передаточное число главной передачи
Расчет передаточного числа главной передачи дан применительно к автомобилям, где коленчатый вал непосредственно соединен с ведущим валом коробки передач. При установке мотоциклетных двигателей следует иметь в виду, что у них в передаче коленчатый вал соединен с ведущим валом коробки передач через цепную передачу, передаточное число которой можно взять из справочных книг. Таким образом, чтобы получить передаточное число главной передачи, необходимо полученное расчетное число i′ г.п. разделить на передаточное число передней цепной передачи силового агрегата мотоцикла i п
При установке мотоциклетных двигателей следует иметь в виду, что у них в передаче коленчатый вал соединен с ведущим валом коробки передач через цепную передачу, передаточное число которой можно взять из справочных книг. Таким образом, чтобы получить передаточное число главной передачи, необходимо полученное расчетное число i′ г.п. разделить на передаточное число передней цепной передачи силового агрегата мотоцикла i п
По техническим условиям максимальная скорость самодельных автомобилей установлена 75 км/час, а мотоколясок — 50 км/час. Число же оборотов вала двигателя при максимальной мощности (значение приводится в технических характеристиках) не соответствует числу оборотов его при максимальной скорости движения и бывает примерно на 15-20% меньше последнего. Следовательно, при определении передаточного числа главной передачи необходимо число оборотов вала двигателя при максимальной мощности увеличить на 15-20%.
Число оборотов коленчатого вала в минуту при максимальной мощности двигателей самодельных автомобилей бывает в пределах 4800-5000 (если они взяты от мотоциклов) и около 4000 (если двигатель мотоколяски или микролитражного автомобиля).
Коэффициент полезного действия η, учитывающий потери мощности и крутящего момента в трансмиссии автомобиля, при тяговых расчетах берется по аналогии с уже существующими моделями. Для легковых автомобилей к. п. д. можно принимать равным 0,9.
Установив значения коэффициента качения ƒ, исходя из возможных дорожных условий, максимальной скорости, лобовой площади и коэффициента сопротивления воздуха, можно рассчитать необходимую тяговую силу для равномерного движения автомобиля на горизонтальном участке дороги
Значение силы по этому уравнению получается в единицах кгс. Для перевода в ньютоны (единицы силы в системе СИ) полученное значение необходимо умножить на 9,8.
Затем по формуле:
определить величину необходимого крутящего момента на валу двигателя для скорости, которую автомобиль развивает при числе оборотов двигателя, соответствующих максимальной мощности.
В приложении 2 в конце книги приведена таблица, в которой даны основные характеристики выпускаемых двигателей, устанавливаемых на мотоциклах, мотороллерах, мотоколясках и микроавтомобилях. По полученному значению крутящего момента двигателя при оборотах, соответствующих максимальной мощности, можно подобрать необходимый силовой агрегат для проектируемого автомобиля.
Конечно, весь рассмотренный выше расчет приближенный, но все же по нему можно произвести первоначальный подбор двигателя.
В конструкторских бюро двигатель для автомобиля выбирают с учетом различных факторов. Так, с увеличением или уменьшением числа оборотов коленчатого вала мощность его, а также крутящий момент изменяются. Кроме того, мощность карбюраторных двигателей зависит от величины открытия дроссельной заслонки.
Изменение мощности и крутящего момента в зависимости от числа оборотов коленчатого вала двигателя при полностью открытой дроссельной заслонке изображается графически на основе проведенных испытаний двигателя а иногда расчетным путем. Называется оно внешней характеристикой двигателя.
Называется оно внешней характеристикой двигателя.
На рис. 27 показаны внешние характеристики двух мотоциклетных двигателей — М-53 и Иж-Ю. Как видно из этих характеристик, максимальные значения мощности и крутящего момента получаются при различных числах оборотов коленчатого вала. Причем с изменением их мощность двигателя значительно изменяется, тогда как крутящий момент изменяется более плавно. В дальнейшем, при определении динамических качеств создаваемого автомобиля, мы вновь вернемся к внешней характеристике двигателя.
В графике (рис. 27) показана взаимосвязь крутящего момента и мощности на валу в зависимости от количества оборотов двигателя. Она позволяет нам при известном числе оборотов перейти от значений крутящего момента, получаемых при расчете, к мощности.
Теперь рассмотрим, как можно подобрать двигатель?
Вы, например, решили построить четырехместный микроавтомобиль с кузовом из стеклопластика, рассчитанный на перевозку двоих взрослых и двух детей. Поскольку он будет в основном эксплуатироваться на дорогах с асфальтобетонным и асфальтовым покрытием, при расчете коэффициент сопротивления качению можно принять равным 0,02.
Поскольку он будет в основном эксплуатироваться на дорогах с асфальтобетонным и асфальтовым покрытием, при расчете коэффициент сопротивления качению можно принять равным 0,02.
Такой автомобиль по своим размерам ближе подходит к легковым микролитражкам и, следовательно, лобовую площадь, не зная еще ее размеров, примем по аналогии с существующими моделями равной 1,4 м 2 , а коэффициент сопротивления воздуха — 0,03.
Максимальную скорость автомобиля выбираем на основании технических условий — до 75 км/час.
Анализируя существующие конструкции, приходим к выводу, что сухой вес автомобиля должен быть около 500 кг, вес взрослых пассажиров в среднем составит 75×2=150 кг, а двух детей — 37,5×2=75 кг. Итого: вес пассажиров равен 225 кг. Добавим еще 25 кг на снаряжение автомобиля. Тогда полный вес автомобиля окажется равным 750 кгс. Это и будет расчетный вес.
Чтобы автомобиль двигался на горизонтальном участке дороги с коэффициентом сопротивления качению 0,02 и скоростью 75 км/час, на его колесах должна развиваться тяговая сила, равная
Теперь можно перейти к определению крутящего момента двигателя или его мощности. Но для этого необходимо знать радиус качения колеса и передаточное число главной передачи. Конечно, проще всего использовать колеса от мотороллера, так мы и сделаем и примем радиус качения колеса для расчета 0,22.
Но для этого необходимо знать радиус качения колеса и передаточное число главной передачи. Конечно, проще всего использовать колеса от мотороллера, так мы и сделаем и примем радиус качения колеса для расчета 0,22.
Так как на автомобиле, вероятно, придется использовать двигатель от мотороллера или мотоцикла, то за расчетное число оборотов двигателя примем максимальную мощность 4800 об/мин. Чтобы получить число оборотов при максимальной скорости, увеличим его на 15-20%. Затем определим число оборотов ведущего колеса при расчетной скорости в 75 км/час, и далее передаточное число главной передачи
Приняв коэффициент полезного действия трансмиссии 0,9, подсчитаем, какой крутящий момент двигателя необходим для того, чтобы обеспечить на колесах рассчитанную выше тяговую силу
По таблице в приложении 2 найдем более близкую величину по значению крутящего момента. Для нашего приближенного расчета подойдет двигатель от мотороллера Т-250, который при максимальной скорости развивает на валу крутящий момент, равный 1,57 кгм. Двигатель снабжен устройством принудительного охлаждения, и нам не нужно рассчитывать и проектировать вентилятор, направляющий кожух. Следует только в передачу вращения от двигателя к ведущим колесам включить устройство заднего хода.
Двигатель снабжен устройством принудительного охлаждения, и нам не нужно рассчитывать и проектировать вентилятор, направляющий кожух. Следует только в передачу вращения от двигателя к ведущим колесам включить устройство заднего хода.
На детских микроавтомобилях, полный вес которых не более 200 кг, достаточно установить двигатели от мопедов Ш-50, Д-4 и Д-5.
На одноместные или двухместные микроавтомобили, полный вес которых превышает 400 кг, можно поставить двигатели мотороллеров и легких мотоциклов ВП-150 ВП-175, М-1, К-125, М-103 и К-58. А двигатели типа Т-200, ТГ-200, К-175 и К-175А от мотоколяски СЗЛ подойдут к автомобилям, вес которых составляет 400-800 кг.
Для четырехместных автомобилей с легким кузовом, имеющих вес с полной нагрузкой примерно 600-700 кг, подойдут двигатели мотороллера Т-250 и мотоцикла М-101.
На автомобилях, полный вес которых равен 700-850 кг, можно установить двигатели от мотороллера 1-250, мотоколяски СЗА, мотоциклов Иж-56, «Ява-250». А двигатели тяжелых мотоциклов, таких как К-750, М-72M, М-62, М-52, «Ява-350», а также малолитражных автомобилей рекомендуем устанавливать на более мощных автомобилях (четырехместных), вес которых составляет свыше 900 кг.
А двигатели тяжелых мотоциклов, таких как К-750, М-72M, М-62, М-52, «Ява-350», а также малолитражных автомобилей рекомендуем устанавливать на более мощных автомобилях (четырехместных), вес которых составляет свыше 900 кг.
Мы перестали спорить в курилках на технические темы. А жаль. Какой нормальный мужик откажется побазарить о том, как распределяется по колесам крутящий момент мотора? Или хотя бы постоять рядом, храня молчанье в важном споре. Не сериалы же нам обсуждать!
Про мощности и скорости спорить неинтересно, а вот момент — дело другое! Разброд мнений здесь гарантирован. По секрету скажем, что даже «доценты с кандидатами» сгоряча давали противоположные ответы на простые, казалось бы, вопросы. В итоге истину удалось постичь только после длительной дискуссии с представителями заводов ГАЗ и УАЗ и нескольких профильных вузов, а также в результате консультаций с зарубежными коллегами.
Предлагаем всем желающим попытаться найти правильные ответы в предложенных нами ситуациях. А предварительно перечислим условия, которые следует учитывать при выборе правильного варианта.
А предварительно перечислим условия, которые следует учитывать при выборе правильного варианта.
Во всех ситуациях условно считаем, что трение и прочие потери отсутствуют как класс. Нагрузки на колеса — одинаковые. Продольная и поперечная развесовки — равномерные. Условия сцепления шин с покрытием — одинаковые, если иное не оговорено. Все дифференциалы — симметричного типа. Момент, передаваемый двигателем на конкретный дифференциал, условно принимаем за 100%.* Для разминки — первый вопрос. В нем скрыта маленькая «нехорошесть»: если ответ на него останется непонятен, то ко второму вопросу переходить бессмысленно.
Условные обозначения.
ВОПРОС № 1
Автомобиль сел на брюхо и беспомощно крутит ведущими колесами в воздухе. Чему при этом приблизительно равен момент на маховике двигателя?
Б — зависит от оборотов
В — заявленной паспортной величине
Г — зависит от включенной передачи
Правильный ответ : А
Тем, кому непонятен ответ, поясняем: момента без сопротивления не бывает! Представьте себе электрическую розетку, рядом с которой стоит неподключенный утюг. Напряжение в розетке есть, но отдаваемый ток — нулевой. Так и здесь: двигатель не совершает никакой полезной работы, колеса не встречают сопротивления, а потому и момент отсутствует.
Напряжение в розетке есть, но отдаваемый ток — нулевой. Так и здесь: двигатель не совершает никакой полезной работы, колеса не встречают сопротивления, а потому и момент отсутствует.
* Если это понятно, то даем задание более сложное — уже с участием дифференциала. Тем, кто подзабыл, что это такое, рекомендуем заглянуть в подсказку ниже.
C чем его едят
Автомобиль ВАЗ‑2107 едет по кругу на четвертой передаче. Как приблизительно распределены моменты на его задних колесах?
А — поровну
Б — обратно пропорционально частоте вращения каждого из колес
В — в зависимости от силы сцепления с дорогой и от нагрузок
Г — прямо пропорционально частоте вращения каждого из колес
Правильный ответ : А
Моменты распределены поровну: по-другому симметричный дифференциал просто не умеет себя вести. Напоминаем, что трение и прочие потери мы условились не учитывать
*Если и это понятно, то усложняем вопросы.
ВОПРОС № 3
У ВАЗ‑2107 при включенной передаче одно ведущее колесо вывешено в воздухе. Как приблизительно распределены моменты на задних колесах, если принять момент, поступающий от двигателя, за 100%?
Как приблизительно распределены моменты на задних колесах, если принять момент, поступающий от двигателя, за 100%?
А — 100% на вращающемся колесе и 0% на неподвижном
Б — на обоих колесах момент равен нулю
В — в зависимости от сцепления неподвижного колеса с дорогой
Г — пропорционально оборотам двигателя
Правильный ответ: Б
Почему нулю, если колесо крутится? Дело в том, что полезной работы двигатель не совершает. Висящее колесо не испытывает сопротивления, а потому и момент на нем нулевой. На неподвижном колесе, само собой, момент также равен нулю.
*Теперь переходим к полноприводным автомобилям : здесь к межколесным дифференциалам добавлен межосевой.
ВОПРОС № 4
Chevrolet Niva едет по кругу на четвертой передаче. Включена блокировка межосевого дифференциала. Каково приблизительное соотношение моментов на всех колесах, если принять момент, поступающий от двигателя, за 100%?
А — по 25% на каждом
Б — по 50% на каждом
В — пропорционально оборотам двигателя
Г — на колесах каждой оси моменты делятся поровну, а распределение по осям — в зависимости от нагрузок и сил сцепления
Правильный ответ : Г
Межколесные дифференциалы на каждой из осей делят моменты поровну, как и в предыдущих примерах. Если бы межосевой дифференциал оставался свободным, каждому колесу досталось бы по 25% крутящего момента. Но водитель его заблокировал, а потому распределение между осями стало зависеть от конкретной дорожной ситуации. В пределе (колеса одной из осей стоят на сухом асфальте, а колеса другой — на гладком льду) практически весь момент реализуется на асфальте.
Если бы межосевой дифференциал оставался свободным, каждому колесу досталось бы по 25% крутящего момента. Но водитель его заблокировал, а потому распределение между осями стало зависеть от конкретной дорожной ситуации. В пределе (колеса одной из осей стоят на сухом асфальте, а колеса другой — на гладком льду) практически весь момент реализуется на асфальте.
*А теперь предположим, что мы немножко застряли.
ВОПРОС № 5
У вседорожника Chevrolet Niva при включенной передаче одно ведущее колесо вывешено в воздухе. Водитель заблокировал межосевой дифференциал. Как приблизительно распределены моменты на всех четырех колесах?
А — на вывешенном колесе 0%, на втором колесе той же оси 0%; на другой оси моменты на каждом из колес равны половине момента, поступающего на ее дифференциал от двигателя
Б — на вывешенном колесе 0%, на остальных — по 33,3% момента, поступающего от двигателя
В — на всех колесах по 25% момента, поступающего от двигателя
Г — в зависимости от нагрузок и сил сцепления
Правильный ответ : А
Висящее в воздухе колесо не работает — следовательно, момент на нем нулевой. То же относится к другому колесу на этой оси: незаблокированный межколесный дифференциал обеспечил равенство. А вот другая ось работает в штатном режиме. И ненулевые моменты на ее колесах при свободном межколесном дифференциале равны между собой.
То же относится к другому колесу на этой оси: незаблокированный межколесный дифференциал обеспечил равенство. А вот другая ось работает в штатном режиме. И ненулевые моменты на ее колесах при свободном межколесном дифференциале равны между собой.
*Теперь попробуем заблокировать межколесный дифференциал!
ВОПРОС № 6
Полноприводный вседорожник едет по кругу на четвертой передаче. Включена блокировка заднего дифференциала. Межосевой дифференциал не заблокирован. Каково приблизительное соотношение моментов на колесах?
А — на каждом по 25% момента, поступающего к межосевому дифференциалу от двигателя
Б — на каждом по 50% момента, поступающего от двигателя
В — зависит от оборотов мотора
Г — на передних колесах по 25%. Остальные 50% распределяются между задними колесами пропорционально нагрузке на них и силам сцепления.
Правильный ответ : Г
Благодаря работающему межосевому дифференциалу задний мост получает столько же ньютон-метров, сколько и передний. Но реальное соотношение моментов на его колесах уже зависит от конкретной дорожной ситуации, поскольку блокированный межколесный дифференциал ничего не выравнивает. Если одно из колес зависнет в воздухе, то всё достанется второму колесу, а если сцепление одинаковое, то и дележ будет равным. Поэтому соотношение моментов определяется нагрузками и силами сцепления. ;
Но реальное соотношение моментов на его колесах уже зависит от конкретной дорожной ситуации, поскольку блокированный межколесный дифференциал ничего не выравнивает. Если одно из колес зависнет в воздухе, то всё достанется второму колесу, а если сцепление одинаковое, то и дележ будет равным. Поэтому соотношение моментов определяется нагрузками и силами сцепления. ;
*Попытаемся застрять еще раз.
ВОПРОС № 7
У полноприводного вседорожника при включенной передаче одно заднее колесо вывешено в воздухе. Включена блокировка заднего дифференциала. Межосевой дифференциал не заблокирован. Каково примерное соотношение моментов на колесах, если условно принять момент, поступающий от двигателя, за 100%?
А — 100% на колесе, касающемся земли, 0% на вывешенном и по 25% на передних колесах
Г — 50% на колесе, касающемся земли, 0% на вывешенном и по 25% на передних колесах
Правильный ответ : Г
Межосевой дифференциал поделил моменты между осями поровну. Висящее колесо не испытывает сопротивления, а потому его момент равен нулю.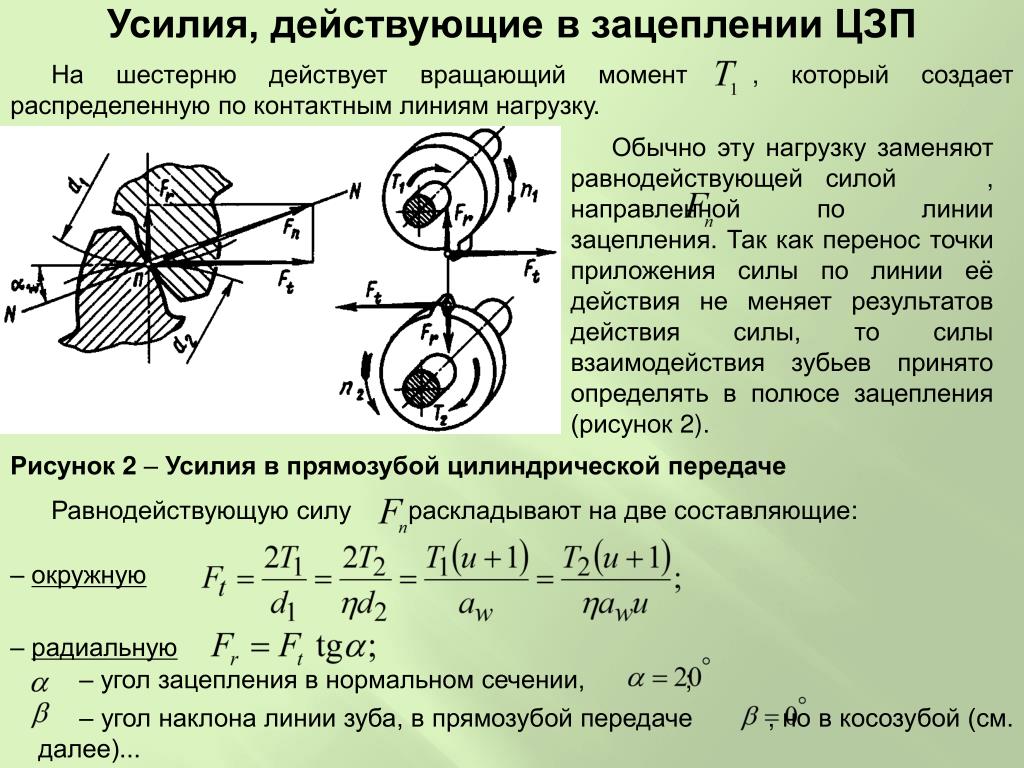 За него отдувается другое колесо на этой оси, толкающее машину, — и весь передающийся назад крутящий момент (50% общего) достается именно второму колесу.
За него отдувается другое колесо на этой оси, толкающее машину, — и весь передающийся назад крутящий момент (50% общего) достается именно второму колесу.
*Напоследок напомним основные принципы, которые помогут разобраться в моментах, осях и дифференциалах.
- Там, где нет сопротивления, момент всегда равен нулю.
- Заблокированный межколесный дифференциал фактически превращает ось автомобиля в аналог колесной пары железнодорожного вагона. Но даже при этом момент на вывешенном колесе равен нулю.
- На вывешенном колесе момент равен нулю независимо от того, блокирован дифференциал или нет.
- Симметричный дифференциал всегда выравнивает моменты: межосевой — на осях, межколесный — на колесах.
Всем удачи на дорогах — без зависших колес и нулевых моментов!
Как работает дифференциал
Дифференциал состоит из корпуса (1), шестерен-сателлитов (2) и полуосевых шестерен (3). Корпус обычно совмещен с ведомой шестерней главной передачи (4). Шестерни-сателлиты играют роль планетарного механизма и соединяют полуосевые шестерни с корпусом дифференциала. Полуосевые (солнечные) шестерни соединены с ведущими колесами через полуоси.
Шестерни-сателлиты играют роль планетарного механизма и соединяют полуосевые шестерни с корпусом дифференциала. Полуосевые (солнечные) шестерни соединены с ведущими колесами через полуоси.
Ведомая шестерня главной передачи вращает корпус с сателлитами, который в свою очередь вращает шестерни полуосей. Когда автомобиль движется идеально прямо, сателлиты неподвижны относительно своих осей. Но как только движение становится неравномерным (например, при повороте), сателлиты начинают собственные фуэте, ускоряя одну полуось и замедляя другую.
Если сцепление колес с покрытием разное, то крутящий момент, реализуемый на скользком покрытии, ограничен коэффициентом сцепления шины с дорогой. Чем меньше сопротивление, тем ниже момент на этом колесе. Но таким же становится момент и на другом колесе той же оси. А вот если заблокировать дифференциал, то дележка моментов между колесами происходит в соответствии с силами их сопротивлений (или сцеплений) с дорогой.
В так называемых дифференциалах повышенного трения сателлиты изначально лишены возможности вращаться свободно. Это сделано как раз для того, чтобы при вывешивании или проскальзывании одного колеса машина беспомощно не застревала. Если с обычным дифференциалом в таких случаях моменты на колесах падают до нуля, то его «коллега» с повышенным трением оставляет им запас, равный заложенному в него моменту трения! Получается эдакий облегченный вариант полной блокировки, помогающий выбраться из неприятных ситуаций, если это позволяет сила трения на колесе с лучшим сцеплением.
Это сделано как раз для того, чтобы при вывешивании или проскальзывании одного колеса машина беспомощно не застревала. Если с обычным дифференциалом в таких случаях моменты на колесах падают до нуля, то его «коллега» с повышенным трением оставляет им запас, равный заложенному в него моменту трения! Получается эдакий облегченный вариант полной блокировки, помогающий выбраться из неприятных ситуаций, если это позволяет сила трения на колесе с лучшим сцеплением.
Как выбрать подходящие двигатели для колесного робота? Ответить точно на этот вопрос в начале конструирования робота непросто. Для этого нужно знать вес робота, а он еще не построен. Однако, технические характеристики и размеры двигателей значительно влияют на окончательные параметры мобильного робота. Для того, чтобы получить полную информацию, необходимо учесть вращающий момент, скорость и мощность. Для колесного робота также необходимо подобрать диаметр колес и определить правильное передаточное число зубчатой передачи для расчета скорости его движения.
Крутящий момент
Крутящий момент двигателя — это сила, с которой он воздействует на вращаемую ось. Для того, чтобы робот мог двигаться, необходимо, чтобы эта сила превышала вес робота (выражаемый в Н/м ).
Некоторые употребляют вместо понятия крутящий момент , термин вращающий момент . По сути это одно и то же. И то и другое являются моментами, просто в технике крутящий момент — это нагрузка на колесе, а вращающий момент — нагрузка в технической науке под названием «Сопротивление материалов» .
Рассмотрим сильно упрощенную идеализированную модель колесного робота.
В нашем случае, вес робота равен 1кг , и мы хотим добиться максимальной скорости его движения 1м/с при радиусе колеса равном 20мм .
При движении по прямой на расстояние 1м , рассчитаем ускорение, необходимое для достижения скорости в 1м/с .
где — расстояние, пройденное роботом, — его начальная скорость (стартуем с места, поэтому ),
где — скорость робота, -его ускорение.
Подставим значения, принятые в нашей модели, получим
м/с 2
Вращающий момент, который необходим для перемещения робота и получения им ускорения, необходимого для достижения максимальной скорости рассчитывается следующим образом:
При — момент инерции и — угловое ускорение, получим
Здесь м/с 2 — ускорение свободного падения (округлим его до 10), — радиус колеса, — масса всего робота
Подставив значения, получим
мН·м
Для перевода величины, выраженной в Н·м в кг·см нужно учесть, что 1Н = 0.102 кг и 1м = 100 см. Поэтому 50 мН·м = 50 · 0.102: 1000 * 100 = 0.51 кг · см.
Полученный крутящий момент распределяется между двумя двигателями робота и его еще нужно поделить на передаточное число используемой зубчатой передачи (подробнее про зубчатые передачи можно почитать ).
Мощность
Для расчета максимальной мощности двигателей нам понадобится частота вращения, которая выражается в оборотах в минуту
(об/мин ) =
или в радианах в секунду
(рад/с ) =
через круговую частоту
Подставив радиус колеса, получим
рад/с
об/мин .
Мощность двигателей пропорциональна крутящему моменту и частоте вращения:
Подставив сюда формулы для крутящего момента и частоты, получим:
Используя собственные значения, получим
Опять же, мы получили суммарную мощность для всех двигателей, в нашем случае двигателя два, поэтому необходимо разделить результат на два и, как и в случае с расчетом крутящего момента, если используются зубчатые передачи, разделить на передаточное число зубчатых передач.
Обратите внимание, что мы рассчитали механическую мощность вырабатываемую двигателями, а не электрическую мощность , которую они потребляют. Необходимо учитывать КПД двигателей, который будет отличаться в зависимости от модели двигателя. Выбирать нужно двигатели, естественно, с бóльшим КПД.
Просмотров: 8197При характеристике как двигателей внутреннего сгорания, так и электродвигателей транспортных средств, применяется такой термин, как крутящий момент, который в целом является критерием оценки тяговых возможностей двигателя. Как оказалось, выражение «крутячий момент» понятно не всем. Людей, изучающих технические характеристики того или иного электродвигателя в первую очередь интересует мощность, энергозатратность и максимальная скорость. О крутящем моменте мало кто спрашивает, и зря. Мы расскажем вам о нем подробно, поскольку не думаем, что вы правильно сможете оценить петенциал электродвигателя, располагая лишь скупыми техническими
Как оказалось, выражение «крутячий момент» понятно не всем. Людей, изучающих технические характеристики того или иного электродвигателя в первую очередь интересует мощность, энергозатратность и максимальная скорость. О крутящем моменте мало кто спрашивает, и зря. Мы расскажем вам о нем подробно, поскольку не думаем, что вы правильно сможете оценить петенциал электродвигателя, располагая лишь скупыми техническими
параметрами его работоспособности. Для того, чтобы в должной степени оценить покупку, а также не пожалеть о сделанном выборе в пользу определенной мощности мотор-колеса, предлагаем вам ознакомится с нижеизложенным.
Сначала попробуем разобраться с определениями, поэтому вернемся к школьному курсу физики. Крутящий момент — это произведение силы на плечо рычага, к которому она приложена: Мкр = F х L. При этом Сила измеряется в ньютонах, рычаг – в метрах. 1 Нм – крутящий момент, который создает сила в 1 Н, приложенная к концу рычага длиной в 1 м. Единица измерения крутящего момента — Ньютон-метр. Получить больший крутящий момент можно двумя путями – увеличив длину рычага или вес груза.
Получить больший крутящий момент можно двумя путями – увеличив длину рычага или вес груза.
Издавна для путешествия людей и транспортировки грузов использовались всевозможные механизмы. Сначала, роль колеса сводилась лишь к уменьшению сопротивления и переводу силы трения в движение (качение). Существенное изменение механизма применения колеса произошло благодаря появлению такого гениального изобретения, как двигатель. Кроме пассивной трансформации трения из одного вида в другой, колесо стало создавать тяговую (движущую) силу.
Мощность, развиваемая мотор-колесом – это его способность вращаться как можно быстрее, одновременно создавая на оси колеса крутящий момент. При контакте колеса с дорожным покрытием крутящий момент мотор-колеса электровелосипеда становится тяговой силой.
Существуют такие параметры мотор-колеса , как число оборотов электродвигателя при максимальной мощности и максимальном крутящем моменте, а также величина этой мощности и крутящего момента. Эти показатели измеряются в оборотах в минуту, киловаттах (кВт), ньютометрах (Нм).
Существует прямая зависимость показателя крутящего момента мотор колеса от силы тока и числа его оборотов, поэтому крутящий момент – величина не постоянная. Производители мотор-колес ведут борьбу за то, чтобы максимальный крутящий момент электродвигателя развивался в как можно более широком диапазоне оборотов.
При вращательном движении мотор-колеса его мощность определяется как производящее крутящего момента на угловую скорость вращения. Мощность показывает, сколько раз на единицу времени электродвигатель создает крутящий момент, то есть мощность прямо зависит от количества оборотов мотор-колеса. Мощность электродвигателя указывается в Вт, кВт.
Номинальный крутящий момент электродвигателя велосипеда вычисляют за формулой:
Mном=Pном / nном, где Pном – номинальная мощность мотор-колеса (кВт) , а nном – номинальная частота вращения (об/мин).Данная формула наглядно демонстрирует взаимосвязь мощности и крутящего момента мотор-колеса электровелосипеда.
Максимальный крутящий момент мотор-колеса электровелосипеда – это наибольший момент вращения, развиваемый электродвигателем в установленном режиме при номинальном напряжении и частоте, соединении обмоток, соответствующем номинальным условиям работы, номинальному току возбуждения.
На практике высокий крутящий момент мотор-колеса особенно заметен при разгонах и при передвижении по бездорожью. От крутящего момента зависит время достижение электродвигателем максимальной мощности, а значит и динамика разгона при старте.
Минимальный вращающий момент электродвигателя — наименьший момент вращения, развиваемый двигателем в процессе разгона с неподвижного состояния до частоты вращения, соответствующей максимальному моменту при номинальных напряжении и частоте, при соединении обмоток, соответствующем номинальным условиям работы электродвигателя.
Крутящий момент мотор-колеса электрического велосипеда отвечает за способность ускорятся и преодолевать препятствия. Каждому значению частоты оборотов мотор-колеса соответствует свое значение мощности и крутящего момента.
Не стоит путать понятия «вращающий момент» и «крутячий момент», поскольку они совершенно не тождественны. В технике «вращающий момент» ассоциируется со внешним усилием, прилагаемым к объекту, а понятие «крутячий момент» подразумевает внутреннее усилие, возникающее в обьекте под влиянием приложенных нагрузок.
Если вы желаете получить более высокую скорость и вместе с тем хорошую тягу, тогда вам стоит остановить свой выбор на мотор-колесах минимум в 500 W. Сочетание отличного показателя крутящего момента и большой скорости делают электровелосипеды с 500 W мотор-колесами одним из лучших предложений на мировом рынке при хорошем соотношении: приемлемая цена — качество — технические характеристики. Использование мотор-колес мощностью больше, чем в 500 Вт, оправдано в тех случаях, если велосипедисту приходится преодолевать крутые подъемы, или если он желает увеличить грузоподъемность своего электровелосипеда. Стоит учитывать, что вместе с мощностью электровелосипеда будет возрастать и его вес, поскольку в таком случае необходимо будет комплектовать свой электрический велосипед ещё и более мощными и, соответственно, более тяжелыми аккумуляторами. Существенное увеличение веса может чрезмерно перегрузить раму.
Чем больше мощность электродвигателя, тем большим является его крутящий момент. Соответственно, увеличивается опасность и того, что дропауты велосипедной вилки, где установлено переднеприводное мотор-колесо, могут разогнуться, и колесо просто выпадет при эксплуатации электровелосипеда. В случае покупки велосипедного электродвигателя большой мощности, не забудьте побеспокоится о приобретении велосипедного крепежа для надежной фиксации переднеприводного мотор-колеса в велосипедной вилке. Если вы используете 250 W или 350 W электродвигатель, то, думаю, что у вас, скорое всего, никогда и не возникнет подобных проблем, чего не скажешь о 500W или, скажем, 1000W мотор-колесах. При комплектации электровелосипеда электрическим двигателем, нужно брать во внимание эксплуатационное состояние и сплав велосипедной вилки, поскольку большинство из тех, что поставляются на рынок страны, не рассчитаны на дополнительные тяговые нагрузки мотор-колеса, и попросту могут сломаться в случае установки на них мощного мотор-колеса. К примеру, алюминиевая велосипедная вилка не совсем подходит для комплектиования электровелосипеда, хотя по иронии судьбы велосипеды алюминиевой конструкции обычно дороже своих стальных аналогов из-за преимущества в весе.
Соответственно, увеличивается опасность и того, что дропауты велосипедной вилки, где установлено переднеприводное мотор-колесо, могут разогнуться, и колесо просто выпадет при эксплуатации электровелосипеда. В случае покупки велосипедного электродвигателя большой мощности, не забудьте побеспокоится о приобретении велосипедного крепежа для надежной фиксации переднеприводного мотор-колеса в велосипедной вилке. Если вы используете 250 W или 350 W электродвигатель, то, думаю, что у вас, скорое всего, никогда и не возникнет подобных проблем, чего не скажешь о 500W или, скажем, 1000W мотор-колесах. При комплектации электровелосипеда электрическим двигателем, нужно брать во внимание эксплуатационное состояние и сплав велосипедной вилки, поскольку большинство из тех, что поставляются на рынок страны, не рассчитаны на дополнительные тяговые нагрузки мотор-колеса, и попросту могут сломаться в случае установки на них мощного мотор-колеса. К примеру, алюминиевая велосипедная вилка не совсем подходит для комплектиования электровелосипеда, хотя по иронии судьбы велосипеды алюминиевой конструкции обычно дороже своих стальных аналогов из-за преимущества в весе. Для электрического велосипеда больше подойдет качественная стальная вилка, поскольку при установке мотор-колеса показатель прочности велосипедной вилки более важен, нежели весовой. Чтобы проверить, является ли ваша вилка стальной, посмотрите, притягивается ли к ней магнит.
Для электрического велосипеда больше подойдет качественная стальная вилка, поскольку при установке мотор-колеса показатель прочности велосипедной вилки более важен, нежели весовой. Чтобы проверить, является ли ваша вилка стальной, посмотрите, притягивается ли к ней магнит.
© Сергей Вольтер 2013
Любое копирование, перепечатка и распространение материалов статей без разрешения правообладателя запрещены и преследуются по закону. Нарушение авторских прав будет рассматриваться согласно статьи 52 Закона Украины «О авторском праве и смежных правах», статьи 176 Криминального Кодекса Украины, статьи 432 Гражданского кодекса Украины, статьи 51-2 Кодекса Украины об административных правонарушениях.
Я упоминал такие узлы, как главная передача и дифференциал. А потому, возможно, есть смысл чуть подробнее рассказать и о них, чтобы сложилось полное представление о работе трансмиссии.
Как известно, вращение выходного вала КПП не передается напрямую на колеса автомобиля. Передача крутящего момента происходит через такой важный узел как главная передача, которая устанавливает соответствующее режиму соотношение крутящего момента и мощности.
Передача крутящего момента происходит через такой важный узел как главная передача, которая устанавливает соответствующее режиму соотношение крутящего момента и мощности.
Главная передача – это, по сути, набор шестерен (обычно две, но в некоторых конструкциях может быть и более одной пары).
В первую очередь она предназначена для увеличение крутящего момента, получаемого на выходе из коробки переключения передач.
Во вторую — для изменения направления вращения, «поворота» — когда двигатель и ведущая ось расположены перпендикулярно друг к другу, как в классических авто с продольным расположением силового агрегата.
Понятно, что данный блок шестерен должен быть вмеру компактен, обладать изрядным запасом прочности и не быть шумным в работе.
Таким требованиям вполне отвечает стандартная главная передача переднеприводных автомобилей с поперечным расположениям двигателя. Это, пожалуй, самая простая конструкция, поскольку в ее функции не входит изменение направления вращения, и при правильной технологии изготовления и установки она не требует обслуживания весь срок эксплуатации.
Данную конструкцию главной передачи называют цилиндрической . Стандартная цилиндрическая главная передача представляет собой пару шестерен, нарезанных на цилиндрических поверхностях. При этом зубья ведущей шестерни, передавая усилие, не «вгрызаются» жестко в зазоры зубьев ведомой, а как бы катаются друг по другу, поскольку профили зубьев шестерен не прямоугольные, а эвольвентные, то есть округлые (чем-то похожие на синусоиды). Получается, что в цилиндрических главных передачах используется трения качения вместо трения скольжения, а это является более щадящим для механизма, к тому же, и мощности отбирает заметно меньше. При этом, зубья ведущей и ведомой шестерен нарезаны не перпендикулярно оси вращения, а под углом к ней, то есть, шестерни в цилиндрической главной паре косозубые, что делает их надежнее простых прямозубых.
В автомобилях с продольным расположением двигателя помимо увеличения крутящего момента требуется еще и поворот вращения, так как ведущая ось расположена под углом 90 град. Для этого обычно применяют так называемую гипоидную главную передачу, в которой ведущая и ведомая шестерни расположены перпендикулярно друг к другу, а зубья нарезаются на поверхностях, имеющих форму гиперболоидов вращения.
Для этого обычно применяют так называемую гипоидную главную передачу, в которой ведущая и ведомая шестерни расположены перпендикулярно друг к другу, а зубья нарезаются на поверхностях, имеющих форму гиперболоидов вращения.
При этом ведущий вал шестерни ориентирован не по центру ведомой шестерни.
Когда-то эту роль выполнял система конический узел. Это была довольно массивная система, забирающая на себя немалый процент мощности, шумная, требующая постоянного контроля сальников, чтобы не было течи. Но при всех своих недостатках у конического узла было одно неоспоримое достоинство – это очень надежное и неприхотливое устройство.
В современных легковых авто гипоидные главные передачи уже давно вытеснили конический узел. И уже постепенно вытесняют его из сектора грузового автомобилестроения. Эта передача имеет гораздо более высокий КПД, меньший размер и массу, более продуманную систему смазки и пр., пр., пр.
Однако следует помнить, что у гипоидных главных передач есть три существенных недостатка:
1. Они требуют дорогостоящих конических подшипников.
Они требуют дорогостоящих конических подшипников.
2. В случае ремонта очень сложно добиться точности работы.
3. Они требовательны к качеству смазки – для них необходимо дорогостоящее противозадирное масло (тогда как в конический узел достаточно было залить дешевый нигрол). Если в редуктор гипоидной главной передачи не залить специальное (гипоидное) масло, то при включении передач устройство можно испортить, особенно при включении задней передачи, когда шестерни работают в наиболее «загруженном» режиме.
Гипоидная главная передача, как правило, одинарная, то есть состоит из пары шестерен. А вот вышеупомянутые цилиндрические главные передачи нередко бывают и двойными. Действуя в два этапа, они более эффективно изменяют крутящий момент.
Схема простая — ведомая шестерня первой пары приводит в движение находящуюся с ней на одном валу ведущую шестерню второй пары, которая вращает свою ведомую деталь, непосредственно работающую с дифференциалом.
Замечу, не следует путать двойные главные передачи с двухступенчатыми – это, как говорится, две большие разницы.
Ну и поскольку был упомянут дифференциал, то нужно сказать и о нем.
Дифференциал – узел, который, получая вращение, преобразованное главной передачей, распределяет его между колесами. без него – никак. Если не применять дифференциал, то при любом повороте ведущие колеса будут получать одинаковое вращение. А ведь известно, что в момент поворота внутреннее колесо проходит меньший путь, так как имеет меньший радиус поворота, чем колесо, движущееся по внешнему радиусу. Таким образом, на заднеприводной машине при прохождении поворота резку ухудшится управляемость, внутреннее к повороту колесо станет пробуксовывать и снашивать резину.
Что касается переднеприводного авто, то тут повернуть будет вообще практически невозможно (разве что рывками). Так что дифференциал служит именно для получения разных угловых скоростей на ведущих колесах, потому его иногда называют «системой межколесного обгона».
Межколесные дифференциалы называются симметричными, так как при прямолинейном движении всегда распределяют крутящий момент поровну.
Классический дифференциал (то есть, не оснащенный блокировками) – узел, получающий крутящий момент от ведомой шестерни главной передачи. Его конические шестерни (сателлиты) передают вращение шестерням полуосей. Когда автомобиль движется по прямой, сателлиты дифференциала не вращаются, а в случае начала поворота они приходят во вращение и перераспределяют крутящий момент.
Следует отметить, что дифференциал по одному и тому же принципу вращает не только полуоси зависимой подвески, ни и карданные шарниры равных угловых скоростей (ШРУСы) независимой подвески.
Кроме классических конических дифференциалов, массово также применяют цилиндрические и планетарные. Правда, последние используют только в качестве межосевых, а вот цилиндрические устройства могут быть и межколесными.
Говоря о дифференциале, нельзя не упомянуть о системе его блокировки.
Дело в том, что дифференциал распределяет крутящий момент симметрично только при равной нагрузке на колеса – движении по прямой. Но вот если одно из двух ведущих колес попадает в грязь или на ледовый участок, и сцепление с дорогой уменьшается, то резко уменьшается и его сопротивление вращению. В итоге, дифференциал «воспринимает» его как колесо, движущееся по внешнему радиусу поворота, передавая ему больший крутящий момент, тогда как второе ведущее колесо «воспринимает» как движущееся по внутреннему радиусу, уменьшая крутящий момент плоть до полной остановки. Каждому приходилось видеть картину, когда завязнувшее в грязи или застрявшее в яме колесо стоит «колом», тогда как вывешенное бешено раскручивается не в силах ничем помочь автомобилю выбраться. В такой пробуксовке и состоит основной недостаток дифференциалов без блокировок.
Но вот если одно из двух ведущих колес попадает в грязь или на ледовый участок, и сцепление с дорогой уменьшается, то резко уменьшается и его сопротивление вращению. В итоге, дифференциал «воспринимает» его как колесо, движущееся по внешнему радиусу поворота, передавая ему больший крутящий момент, тогда как второе ведущее колесо «воспринимает» как движущееся по внутреннему радиусу, уменьшая крутящий момент плоть до полной остановки. Каждому приходилось видеть картину, когда завязнувшее в грязи или застрявшее в яме колесо стоит «колом», тогда как вывешенное бешено раскручивается не в силах ничем помочь автомобилю выбраться. В такой пробуксовке и состоит основной недостаток дифференциалов без блокировок.
Но проблема решаема. Задача блокировки – достичь жесткого соединения одной из полуосевых шестерен с корпусом дифференциала, чтобы «насильно» передать крутящий момент колесу, находящемуся в хорошем зацеплении с дорогой.
Повышенное внутреннее трение лежит в основе принципа действия самоблокирующихся дифференциалов. Простой конический дифференциал легко превратить в самоблокирующийся с помощью комплекта фрикционных шайб.
Простой конический дифференциал легко превратить в самоблокирующийся с помощью комплекта фрикционных шайб.
Если использовать вместо шайб электромагнитную фрикционную муфту – тогда блокировку можно будет включать принудительно. Принудительные блокировки – удел серьезных внедорожников. Однако водителям таких автомобилей следует помнить о необходимости после преодоления тяжелого участка пути вовремя выключать блокировку и не в коем случае не разгоняться с заблокированным дифференциалом (на многих моделях вендорожников установлены: или специальный ограничитель скорости при включенной блокировке, или функция автоматического разблокирования при повышении скорости). Блокировка приводит к возрастанию нагрузки на ведущие оси и рулевое управление, и, к тому же, сокращает срок службы покрышек. Так что использовать постоянно не только расточительно, но и опасно.
Вот, пожалуй, и все, что можно сказать о конструкции и принципе работы главной передачи и дифференциала в общих чертах.
Всем удачных поездок!
1 год
1.3 Определение передаточных чисел трансмиссии. Проектирование карданной передачи
Похожие главы из других работ:
Выбор прототипа автомобиля общего назначения на основании заданных технических характеристик
4.1 Определение передаточных чисел трансмиссии
Общее передаточное число трансмиссии на I-ой передаче должно обеспечивать движение машины в самых трудных условиях, т.е максимальное сопротивление дороги при полной нагрузке: , (4.1) где Pkmax — максимальная сила тяги…
Двигатели внутреннего сгорания и базовые тягачи
Определение передаточных чисел трансмиссии
Общее передаточное число трансмиссии на первой передаче определяется по заданному номинальному тяговому усилию…
Двигатель внутреннего сгорания. Расчёт тягача
3. Определение скоростей тягача и передаточных чисел трансмиссии на различных передачах
Максимальная скорость Umax трактора (тягача) для гусеничных машин с полужесткой подвеской принимается равной 10?12 км/ч; для гусеничных машин с эластичной подвеской равна 15?20 км/ч; для колесных машин составляет 40?60 км/ч. Следует иметь в виду…
Определение основных параметров автомобиля
4. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНЫХ ЧИСЕЛ ТРАНСМИССИИ, СКОРОСТЕЙ ДВИЖЕНИЯ, ПАРАМЕТРОВ ПРОХОДИМОСТИ
Цель расчета: определить передаточные числа трансмиссии, определить скорости движения, определить параметры проходимости. Исходные данные: максимальная скорость на первой рабочей передаче Vmax = 26,7 м/с…
Подвеска легкового автомобиля
1.8 Определение передаточных чисел трансмиссии
…
Проектирование автомобиля на базе ЗИЛ ММЗ 4413
1.4 Расчет передаточных чисел трансмиссии
…
Проектирование автомобиля с бензиновым двигателем
3. Расчет передаточных чисел трансмиссии
Передаточное число трансмиссии автомобиля определяется выражением: iTP=ik* io, (13) где iK и io — передаточные числа соответственно КПП и главной передачи. Следовательно…
Проектирование карданной передачи
1.
 3 Определение передаточных чисел трансмиссии
3 Определение передаточных чисел трансмиссииДинамические качества автомобиля определяются во многом числом ступеней КПП, передаточными числами КПП и главной передачи…
Расчёт основных параметров лесотранспортной машины
2. Выбор передаточных чисел трансмиссии. Построение и анализ тяговой и динамической характеристик машины. Выбор основных узлов трансмиссии.
…
Расчёт сцепления и коробки передач автомобиля ВАЗ 21213
3.1 Определение передаточных чисел высшей и низшей передач и диапазона передаточных чисел КП
…
Ремонт автомобиля
1.1 Определение передаточных чисел трансмиссии проектируемого автомобиля
Передаточное число главной передачи определяется исходя из обеспечения заданной максимальной скорости движения автомобиля: i0=0,377rnncmax/[ikVmax]=0,3770,336485005/[1135]=4,703 где rn — радиус качения колеса, м; ncmax — максимальные обороты колен. Вала…
Тяговая динамика автомобиля
4.
 Определение передаточных чисел трансмиссии
Определение передаточных чисел трансмиссии…
Тяговый расчет трактора и автомобиля
1.9 Определение передаточных чисел трансмиссии основного ряда
Передаточное число трансмиссии на первой передаче основного ряда определяется согласно заданной теоретической скорости трактора , по формуле (1…
Тяговый расчет трактора и автомобиля
2.5 Определение передаточных чисел трансмиссии
Передаточное число главной передачи определяем из условия движения автомобиля на высшей (прямой) передаче с максимальной заданной скоростью : (2.6) где — передаточное число главной передачи…
Эксплуатационные свойства автомобиля
1.3 Определение передаточных чисел трансмиссии.
Динамические качества автомобиля определяются во многом числом ступеней КПП, передаточными числами КПП и главной передачи…
Эффективный радиус качения — обзор
Ширина пятна контакта оказывает значительное влияние на крутящий момент и косвенно на боковую силу из-за поглощения некоторой части трения участвующими продольными силами. Кроме того, для реальной шины с податливостью каркаса крутящий момент будет вызывать дополнительное искажение каркаса, что приводит к дальнейшему изменению эффективного угла скольжения (помимо искажения, уже вызванного выравнивающим крутящим моментом, возникающим из-за боковых сил).Среди прочего, эти вопросы могут быть учтены в имитационной модели протектора, которая рассматривается в разделе 3.3.
В следующей части мы покажем сложность, возникающую при рассмотрении продольного скольжения помимо вращения и бокового скольжения. Чтобы учесть влияние ширины пятна контакта, рассмотрим модель с левым и правым рядом элементов протектора, расположенными на расстоянии y L = — b ряд и y R = b ряд от центральной плоскости колеса.Фактически, мы можем предположить, что мы имеем дело с двумя колесами, прикрепленными друг к другу на одном валу на расстоянии 2 b ряда друг от друга. Колеса подвергаются одинаковым скоростям бокового скольжения и проскальзывания при повороте, V sy и ψ˙, и имеют одинаковый угол развала γ . Однако скорости продольного скольжения для случая развала различаются из-за разницы в эффективных радиусах качения. Для скорости продольного скольжения левого или правого колеса, расположенного на расстоянии y L, R от центральной плоскости,
(3.88) VsxL, R = Vsx − yL, R {ψ˙− (1 − ɛγ) Ωsinγ}
Это выражение получается путем рассмотрения уравнения (2.55), в котором конусность не учитывается, предполагается установившееся состояние и изгиб введен понижающий коэффициент ɛ γ . Коэффициенты θ определяются как (как в (3.54, 3.55))
(3.89) θγx (y) = — ɛγ, θy (x, y) = — ɛγxresinγ
Из уравнений (2.55, 2.56) с использованием ( 3.88) получаются составляющие скорости скольжения:
(3.90) VgxL, R = VsxL, R − ∂uL, R∂xVr
(3.91) Vgy = Vsy − ∂v∂xVr + x {ψ˙− (1 − ɛγ) Ωsinγ}
После введения теоретических величин скольжения для двух прикрепленных колес
(3.92) σxL, R = −VsxL, RVr, σy = −VsyVr, σψ = −ψ˙Vr
находим для градиентов прогибов в зоне адгезии (где V g = 0), если рассматривать малое вращение (скольжение только сзади),
(3.93) ∂uL, R∂x = −σxL, R
(3.94) ∂v∂x = −σy − x {σψ + (1 − ɛγ) 1resinγ}
, что дает после интегрирования прогибов в зона сцепления ( x < x т ):
(3.95) uL, R = (a − x) σxL, R
(3.96) v = (a − x) σy + 12 (a2 − x2) {σψ + (1 − ɛγ) 1resinγ}
Точка перехода от адгезия к скольжению при x = x t может быть оценена с помощью условия
(3,97) cpeL, R = μqz
с величиной прогиба
(3,98) eL, R = | eL, R | = uL, R2 + v2
Решение для x t и выполнение интегрирования по диапазону адгезии может быть выполнено численно. В диапазоне скольжения направление прогибов варьируется в пределах x .В качестве приближения можно предположить, что все эти отклонения e (для изотропной модели) направлены противоположно скорости скольжения V sL, R . Результаты таких интеграций, дающие значения F x , F y и M z , здесь отображаться не будут. Мы обращаемся к Сакаи (1990) за аналитическими решениями модели однорядной щетки при комбинированном скольжении с изгибом.
Окружность качения
Окружность качения — это расстояние, которое колесо преодолевает без проскальзывания за один оборот; Для автомобилей скорость 60 км / ч должна приниматься за основу в соответствии с DIN 70020. Вымышленный динамический радиус качения (геометрически не измеряемый) рассчитывается по длине окружности качения.
Окружность качения изменяется незначительно в результате нагрузки и скорости. Радиальные шины, распространенные в легковых автомобилях, характеризуются ремнем, который лишь слегка растягивается и раскручивается один раз за оборот. [1] Динамический радиус качения rD {\ displaystyle r _ {\ mathrm {D}}} больше под нагрузкой, чем расстояние от центра колеса до поверхности дороги (статический радиус rS {\ displaystyle r _ {\ mathrm { S}}}). В частности, динамический радиус качения изменяется под нагрузкой значительно меньше, чем статический радиус. [2] Для динамического радиуса качения можно сделать следующее приближение : [3]
- rD≈23r0 + 13rS {\ displaystyle r _ {\ mathrm {D}} \ приблизительно {\ frac {2} { 3}} r_ {0} + {\ frac {1} {3}} r _ {\ mathrm {S}} \;} с r0 {\ displaystyle r_ {0}}… радиус разгруженной шины
Автомобили
В Германии окружность качения колес автотранспортных средств измеряется при скорости 60 км / ч. Ровная проезжая часть является предпосылкой для правильного измерения. В директиве 107-01 Немецкой ассоциации резиновой промышленности (WdK) рассматривается зависимость длины окружности качения автомобильных шин от скорости, а в части 02 — процедура испытаний на статический радиус и окружность качения. Расстояние, преодолеваемое за один оборот колеса, в гораздо большей степени зависит от скорости шин диагонального типа, чем шин радиального типа.На скорости 180 км / ч диагональные шины «растут» прим. 5% по сравнению с 60 км / ч, радиальные шины только прим. 1%.
Окружность качения автомобильной шины определяется размером обода R и соотношением высоты H, которая выходит за край обода. H не указывается непосредственно в обозначении размера шины, а только соотношение H и ширины B протектора. Расчет также очень прост с соотношением H / B. Информация о размере шины структурирована таким образом, что сначала указывается ширина B, а после косой черты — отношение H / B, умноженное на 100, а затем an R и предполагаемый диаметр обода в дюймах.Например, шина размером 245/45 R 18 имеет ширину 245 мм, В / Ш соответствует 0,45, и шина предназначена для 18-дюймового обода. В этом случае к окружности U применимо следующее: U = π (R + 2 (H / B) / 100 B)
Следует отметить, что характеристики диаметра обода все равно должны быть преобразованы в метры или производные от него единицы. . Например, один дюйм соответствует 2,54 см или 25,4 мм.
Для шин размером 245/45 R 18 получается следующая окружность: U = π · (18 · 25.4 мм + 2 · 45/100 · 245 мм) = 2129 мм = 212,9 см = 2,129 м
Отклонения из-за износа профиля и изменения давления воздуха
Радиус без нагрузки изменяется в результате износа профиля. Согласно расчетной формуле, приведенной выше, изменение радиуса влияет только на 2/3 окружности качения. Согласно этому расчету, износ протектора в 7 мм на средней автомобильной шине приведет только к отклонению от 1,3% до 2% вместо отклонения в 2-3%. При изменении давления воздуха изменяется статический радиус.Влияние на окружность качения значительно меньше. Поскольку формула оценки является только ориентировочной, применима информация производителя.
При раскручивании ремень сохраняет свою длину и является гибким только по форме. Он скатывается один раз за оборот, как бронированная цепь. В области точки контакта частицы профиля прилипают и легко деформируются, но это не влияет на длину ремня в области области контакта. Таким образом, изменение давления воздуха или глубины протектора оказывает незначительное влияние на длину окружности качения.Тем не менее, незначительные изменения оцениваются в блоках управления ESP и используются для предупреждения по крену .
Циклы
Окружность качения также является решающим параметром для правильного определения скорости движения и пройденного расстояния для велосипедных тахометров. Кроме того, окружность качения имеет прямое влияние на развитие, то есть расстояние, преодолеваемое за один оборот кривошипа.
Справочная информация о диаметре шины и диаметре обода
Размер шины в дюймах является лишь приблизительным показателем внешнего диаметра шины.В течение долгого времени шины практически не отличались по ширине, а это означало, что размер обода также можно было определить на основе дюймовой спецификации диаметра шины. В результате такие выражения, как «обод диаметром 28 мм», стали обычным явлением, что означает обод с внешним диаметром 622 мм (= 24,5 дюйма), поскольку он в основном использовался для шин диаметром 28 мм — и используется до сих пор. С появлением все большего числа шин различной ширины для «специальных» применений, таких как гоночные велосипеды или горные велосипеды, взаимосвязь между размером шины и размером обода становится все более и более устаревшей (см. Также велосипедные шины # Размеры шин и ободов).
Например, обода для 27-дюймовых дорожных шин имеют больший внешний диаметр на 630 мм, чем обода для обычных 28-дюймовых шин с 622 мм. Пояснение: Из-за тонких шин гоночного велосипеда общий диаметр колеса с 630 ободами остается около 27 дюймов, тогда как колесо с 622 ободами и более толстыми обычными шинами имеет внешний диаметр примерно 28 дюймов:
- Внешний диаметр колеса ≈ 630 мм обод + шина 2 × 28 мм = 686 мм ≈ 27 ″
- Внешний диаметр колеса ≈ 622 мм обода + 2 × 44 мм шины = 710 мм ≈ 28 ″
Колеса для гоночных велосипедов, состоящие из 622 обода и тонкие 23-миллиметровые шины, обычно используемые для этой цели, имеют внешний диаметр всего около 26 с половиной дюймов, хотя эти обода иногда все еще называют ободами «28», потому что многие люди называют их 28-дюймовыми. Используются шины:
- Наружный диаметр колесо ≈ 622 мм обод + шина 2 × 23 мм = 668 мм ≈ 26.3 ″
Приблизительный расчет длины окружности качения
Один из методов расчета длины окружности качения — через внешний диаметр колеса, то есть шины / каркаса. Велосипедные шины имеют разные названия, в основном устаревшие, но все еще распространенные, дюймовые спецификации (например, 26 × 1 3 ⁄ 8 ) и более свежие спецификации ISO (например, 32-571). Хотя первая цифра в дюймах уже указывает на внешний диаметр шины, это можно рассматривать только как приблизительную классификацию.Поскольку шины имеют разную ширину (последнее число в дюймах), это приводит к разным внешним диаметрам, которые в конечном итоге отличаются от указанных, например, 26 дюймов (см. Выше).
Информация ISO согласно ETRTO лучше подходит для приблизительного расчета окружности качения, чем таможенная информация. Размер ETRTO состоит из шины , ширины в миллиметрах и внешнего диаметра обода {\ displaystyle d} (= внутренний диаметр шины).Внешний диаметр крыльчатки получается из d {\ displaystyle d} и высоты шины над ней a {\ displaystyle a}. Чтобы иметь возможность рассчитать длину окружности качения на основе информации ETRTO, используется тот факт, что накачанная камера / шина велосипеда образует примерно круг в своем поперечном сечении. Следовательно, можно предположить, исходя из приближения, что высота шины примерно соответствует ширине шины . В результате получается окружность качения l {\ displaystyle l}:
- l≈ (2⋅a + d) ⋅Pi {\ displaystyle l \ приблизительно (2 \ cdot a + d) \ cdot \ pi \,}
28-дюймовое колесо ETRTO размера 35-622 имеет ширину шины (≈ высота шины) 35 мм и, следовательно, диаметр колеса 35 + 622 + 35 = 692 мм {\ displaystyle 35 + 622 + 35 = 692 \, \ mathrm {мм}}.Это дает длину окружности качения l≈Pi⋅692 мм = 2174 мм {\ displaystyle l \ приблизительно \ pi \ cdot 692 \, \ mathrm {mm} = 2174 \, \ mathrm {mm}}.
Измерение окружности качения
Существует два обычных метода измерения длины окружности качения вместо ее вычисления. Один работает путем измерения радиуса крыльчатки (= половине диаметра) путем измерения расстояния между ступицей и землей в нагруженном состоянии. Затем это расстояние удваивается и умножается на число пи, что дает длину окружности качения.
Второй метод измеряет длину окружности качения напрямую, поэтому он является наиболее точным из всех перечисленных здесь методов. Его иногда называют «методом кетчупа», который включает отметку точки на колесе с помощью кетчупа или мелом, затем перемещение колеса вперед на один полный оборот и измерение расстояния между двумя отметками мела на полу. Хотя метод кетчупа кажется очень простым, он дает лучший результат.
Веб-ссылки
Индивидуальные доказательства
- ↑ Михаил Тжесневски: шасси .Springer Vieweg, 2017 г., ISBN 978-3-658-15544-5, стр. 12. (ограниченный предварительный просмотр в поиске Google Book)
- ↑ http://elib.uni-stuttgart.de/opus/volltexte/2007/3196/pdf/disssment_rau_magnus_abgabe.pdf
- ↑ C. Rill: Vehicle Dynamics. С. 15. http://www.autogumi.com/FDV_Skript.pdf.
Загруженный и динамический радиус качения (r l и r d) как функция …
Контекст 1
… z — радиальное расстояние до каркаса под датчиком.Следовательно, продольные и поперечные перемещения увеличивают расстояние D. Кроме того, в OTS расстояние D обратно пропорционально корню сигнала датчика для данной интенсивности светодиода, которая зависит от направления луча: смещение светодиода снижает интенсивность (смещение 10 ◦ или угловое смещение снижает интенсивность примерно на 1 — 3% для рассматриваемого широкоугольного светодиода). Лазерный триангуляционный датчик непосредственно измеряет расстояние z, а не D (рисунок 2). На рисунке также показано направление прокатки, т.е.грамм. минусовые значения указывают период до контакт-центра. Ожидается, что точность и воспроизводимость результатов улучшатся с новым датчиком по сравнению с OTS. Это позволяет сравнивать незначительные различия в конструкции шин, а не только сравнивать поведение каркаса шины в различных условиях движения. Например, ранее [13, 14] можно было изучить явление аквапланирования на разных этапах аквапланирования, но теперь характеристики немного разных шин можно сравнивать в одних и тех же условиях, таких как частичное или полное аквапланирование.Это поможет разработчикам шин глубоко понять поведение шин, а не просто эмпирически сравнивать характеристики готовой продукции. Датчик шины был испытан на стенде для испытания шин на барабане динамометра шасси (радиус 1,219 м) [19]. Следует отметить, что кривизна барабана влияет на измеряемый сигнал, но легкая воспроизводимость и возможность регулировки состояния шины оправдывают испытание барабана. Автомобильные испытания также проводились с VW Golf V. Во всех тестах использовалась шина NokianTyres WRG2 205 / 65R16.Давление в шинах поддерживалось постоянным во время измерения, что на практике реализовывалось путем регулировки давления после прогрева шины. Это важный аспект, потому что прогрев шины увеличивает давление в шине и ее жесткость, что немедленно влияет на смещение каркаса. Исследование деформации грунта и испытания на аквапланирование проводились на испытательной машине, поэтому кривизна вальца не повлияла на них. Датчик был протестирован на скорости до 130 км / ч без каких-либо проблем с качеством сигнала или долговечностью компонентов.Во время тестовой сессии примерно на 1000 км не было никаких проблем с долговечностью. Нагрузка на колесо и давление в шине сильно влияют на прогиб каркаса шины. Следовательно, влияние этих параметров можно наблюдать по смещению внутренней облицовки (z-сигнал). На рисунке 3 показаны семейства кривых для различных колесных нагрузок и давления накачки. Кажется, что измерения полностью соответствуют физической модели шины, представленной в [20]. Каждое семейство кривых содержит данные за 6 с, что включает примерно 56 оборотов.Увеличение показывает повторяемость и незначительное изменение нагрузки на колесо в условиях измерения. Увеличение нагрузки на колесо естественным образом увеличивает вертикальное перемещение каркаса (z-сигнал). На рисунке 4 показано, как амплитуда (разница между минимальным и максимальным значениями) и среднее значение одного полного оборота имеют примерно линейную зависимость от нагрузки на колесо для всех соответствующих давлений накачки. На рисунке 5 показан рассчитанный наклон (своего рода коэффициент податливости) и смещение для данных амплитуды, показанных на рисунке 4.Остаток также наносится на график, чтобы показать, насколько чуть более сильная линейность получается при увеличении внутреннего давления. Легко оценить нагрузку на колесо шины с помощью линейной модели, если известна жесткость каркаса шины (обратная податливость). Кроме того, жесткость каркаса шины можно оценить по измерению давления в шинах, которое в соответствии с законодательством становится обычным оборудованием в транспортных средствах. Это открывает возможность использования любого измерения смещения каркаса для оценки нагрузки на колесо даже в серийном автомобиле для улучшения систем активной безопасности.Однако жесткость каркаса шины также зависит от свойств каркаса, даже если давление преобладает. На рис. 6 показаны не данные датчиков шины (данные, полученные исключительно с испытательного стенда), а динамический радиус нагрузки r l и динамический радиус качения r d как функция нагрузки на колесо для различных давлений накачивания. Он представлен здесь для пояснения терминологии радиуса шины, которая может сбивать с толку. Радиус динамической нагрузки — это просто расстояние от центра колеса до дороги, которое измеряется датчиком линейного движения на стенде для испытаний шин.Динамический радиус качения …
(PDF) Продольная упругость и эффективный радиус качения шины: экспериментальный метод и данные
10
18. Гл. Р. Карлсон, Дж. Ч. Гердес, Определение изменения давления в шине
с помощью нелинейной оценки
продольной жесткости и эффективного радиуса,
Proceedings of AVEC 2002, Hiroshima, Japan,
Sept. 2002, pp. 899-906.
19. Я. Накао, Х. Кавасаки, Д. Дж. Майор, Оценка
уровней трения между шиной и дорогой, SAE
Технический документ, 2002-01-1198.
20. Я. Накадзима, Аналитическая модель продольной шины
Сцепление на снегу, Журнал Terramechanics, 40
(2003), с. 63 — 82.
21. DD Filiatrault, PJ Cooper, YY Zheng, PN
Liebetreu, TL Wright, Влияние качения шины
Радиусна усиление педали и склонность к опрокидыванию
легкового грузовика, SAE Технический доклад, 2002-
01-3062.
22. П. Кисс, Радиусы качения пневматической шины на деформируемом грунте
, Biosystems Engineering, 2003,
85 (2), с.153 — 161.
Литература
1. Вирабов Р.В. Тяговые характеристики трения
Трансмиссии, Москва, Машиностроение
, Издательство
, 263 с.
2. Левин М.А., Фуфаев Н.А. Теория качения деформируемого колеса
. Москва, Наука,
272 с.
3. Пацейка Х. Б., Шины и динамика транспортных средств. SAE,
ISBN 076011264, 627 стр.
4. Высококачественные сельскохозяйственные шины. SAE Off-Highway
Engineering, апрель 2002 г., стр.41 — 46.
5. Рвачев В.Л., Шевченко А.Н., Intelligent
Инструменты для моделирования физико-механических полей,
International Journal Pattern Recognition and
Image Analysis, 1992, 2., с. 234-237.
6. Ю. В. Пирковский, С. Б. Шухман, Теория движения многоприводного автомобиля
, Москва,
Издательство UNITY и ELIT, 230 с.
7. Петрушов В.А., Шуклин С.А., Московкин В.В.,
Сопротивление качению автомобилей и грузовиков,
Москва, Машиностроение, 225 с.
8. Ванцевич В.В., Ломако Г., Опейко А., Взаимодействие
между автономными транспортными средствами и дорожным покрытием,
Int. Журнал автономных систем транспортных средств (Великобритания),
2003, Vol. 1, № 3/4, спецвыпуск, приглашенный редактор
— Ванцевич В.В.
9. Ванцевич В.В., Высоцкий М.С., Харитончик С.В.,
Управление динамикой колеса, SAE Технический документ
Серия— 980242, Междунар. Конгресс и выставка,
Детройт, Мичиган, 23-26 февраля 1998 г.
10. Ванцевич В.В. Новое эффективное исследование
Направление в области исполнительных систем для
многоприводных транспортных средств, Междунар. Journal of Vehicle Design
(Великобритания), Vol. 15, № 3/4/5, стр. 337-347.
11. В. В. Ванцевич, М. С. Высоцкий, Д. А. Дубовик,
Контроль движущих сил колес как основа управления динамикой внедорожников
,
Транзакции SAE 2002 — Коммерческий журнал
Транспортные средства, стр.452-459.
12. В. В. Гуськов и др., Тракторы: теория, Москва,
Издательство «Машиностроение», 376с.
13. В. Ф. Милликен, Д. Л. Милликен, Race Car Vehicle
Dynamics, SAE ISBN 1560915269, 890p.
14. А. Ф. Андреев, В. В. Ванцевич, А. Х. Лефарова,
Дифференциалы колесной техники, Москва,
Издательство «Машиностроение», 240 с.
15. В.П. Бойков, В.В. Ванцевич, А.Х. Лефаров, С.
И.Стригунов, Тяговые характеристики Ti res для сельскохозяйственных тракторов
классов 1,4 и 2,0, тракторов
и сельскохозяйственных машин, 1986, №1 (Москва).
16. Чудаков Е. А. Катание автомобильного колеса.
Москва, Мачгиз Издательство, 72 стр.
17. В. В. Ванцевич, М. С. Высоцкий, Л. Х. Gileles,
Мобильные транспортные машины: взаимодействие с
окрестностями. Минск: Беларуская навука
Издательство, 303с.
920-343e-07.05.indd 10920-343e-07.05.indd 10 20.07.2005 12: 32: 3520.07.2005 12:32:35
Сопротивление качению
Сила, которая сопротивляется движению тела, катящегося по поверхности, называется качением . сопротивление или трение качения .
Сопротивление качению может быть выражено общим уравнением
F r = c W (1)
где
F r = сопротивление качению или трение качения (Н , фунт f )
c = коэффициент сопротивления качению — безразмерный (коэффициент трения качения — CRF)
W = ma г
= нормальная сила — или вес — тела ( Н, фунт f )
m = масса тела (кг, фунт)
a g = ускорение свободного падения ( 9.81 м / с 2 , 32,174 фут / с 2 )
Обратите внимание, что коэффициент сопротивления качению — c — зависит от различных переменных, таких как конструкция колеса, поверхность качения, размеры колеса и многое другое.
Сопротивление качению также можно выразить как
F r = c l W / r (2)
где
c l = коэффициент сопротивления качению — размерная длина ( коэффициент трения качения) (мм, дюйм)
r = радиус колеса (мм, дюйм)
Коэффициенты трения качения
Некоторые типичные коэффициенты качения:
| Коэффициент сопротивления качению | ||
|---|---|---|
| c | c l (мм) | |
| 0.001 — 0,002 | 0,5 | железнодорожные стальные колеса на стальных рельсах |
| 0,001 | велосипедная шина на деревянной гусенице | |
| 0,002 — 0,005 | бескамерные шины с низким сопротивлением | 905 905 шина на бетоне |
| 0,004 | велосипедная шина на асфальтовой дороге | |
| 0,005 | грязные трамвайные рельсы | |
| 0.006 — 0,01 | грузовая шина на асфальте | |
| 0,008 | велосипедная шина на неровной асфальтированной дороге | |
| 0,01 — 0,015 | обычные автомобильные шины на бетоне, новый асфальт, булыжники маленькие новые | |
| автомобильные шины на гудроне или асфальте | ||
| 0,02 | автомобильные шины на гравии — накатанные новые | |
| 0,03 | автомобильные шины на брусчатке — большие изношенные | |
| 0.04 — 0,08 | автомобильная шина на твердом песке, гравий рыхлый, грунт средней твердости | |
| 0,2 — 0,4 | легковая шина на рыхлом песке | |
Коэффициенты качения Легковые автомобили
Коэффициенты качения для воздухонаполненных шины на сухих дорогах можно оценить
c = 0,005 + (1 / p) (0,01 + 0,0095 (v / 100) 2 ) (3)
где
c = коэффициент качения
p = давление в шинах (бар)
v = скорость (км / ч)
Пример — давление в колесе и коэффициент сопротивления качению
Стандартное давление в колесе в Tesla Model 3 составляет 2.9 бар (42 фунта на кв. Дюйм) . Коэффициент трения качения при 90 км / ч (56 миль / ч) можно рассчитать из (3) как
c = 0,005 + (1 / (2,9 бар)) (0,01 + 0,0095 ((90 км / ч) / 100) 2 )
= 0,011
Повышение давления до 3,5 бар снижает коэффициент сопротивления качению до
c = 0,005 + (1 / (3,5 бар)) (0,01 + 0,0095 ((90 км / ч) / 100) 2 )
= 0,010
— или
((0.011 — 0,10) / 0,011) 100% = 9%
- 1 бар = 10 5 Па = 14,5 фунтов на кв. Дюйм
- 1 км / ч = 0,6214 миль / ч
Пример — сопротивление качению автомобиля по асфальту
Сопротивление качению всех четырех колес автомобиля общей массой 1500 кг по асфальту с коэффициентом трения качения 0,03 можно оценить с помощью общего уравнения 1 как
F r = 0.03 (1500 кг) (9,81 м / с 2 )
= 441 Н
= 0,44 кН
Сопротивление качению для одного колеса можно рассчитать как
F r = 0,03 (1500 кг / 4) (9,81 м / с 2 )
= 110 Н
= 0,11 кН
Калькулятор размера шин
Воспользуйтесь нашим калькулятором размеров шин, чтобы рассчитать диаметр, ширину, боковину, окружность и количество оборотов на милю любой шины.Просто введите метрическую или стандартную шину и нажмите рассчитать. Шины с дюймовыми измерениями довольно просты для понимания, однако метрические шины используют более сложную систему для чтения. Первое число на метрической шине — это ширина. Разделите это на 25,4, чтобы получить эквивалент в дюймах. Третье число, которому обычно предшествует буква «R», — это диаметр колеса. Боковина и соотношение сторон используются в шинах метрического размера для определения общей высоты шины. Второе число на метрической шине предназначено для расчета размера боковой стенки.Высота боковины — это процент от ширины шины. Это второе число и есть тот процент. Высота боковины или «соотношение сторон» шины 285/75 / R16 составляет 75% от 285 мм.
Чтобы рассчитать высоту метрической шины в дюймах: (# 1 x # 2/2540 x 2) + (# 3)
Пример: 285 / 75R16 (285 X 75/2540 x 2) + 16 = 32,8 дюйма в высоту.
Наш калькулятор шин сделает это за вас. Просто введите метрические поля и нажмите «преобразовать в дюймы». Это также решает проблему выбора шины, которую вы хотели бы использовать, если вы имеете в виду дюймовые размеры, но не можете найти компанию, которая производит эту шину дюймового размера.Просто введите нужные размеры в дюймах, и он рассчитает точную метрическую версию этой шины. Есть еще много возможностей и вариантов выбора метрических шин, поэтому использование калькулятора размера шин может пригодиться.
Калькулятор для сравнения размеров шин измеряет две шины и сравнивает диаметр, ширину, боковину, окружность и количество оборотов на милю. Затем, в качестве бонуса, он показывает примеры показаний вашего спидометра с первой шиной и фактическую скорость, с которой вы движетесь, если бы вы установили вторую шину.Очень полезный калькулятор шин при поиске шин, размер которых отличается от стандартного.
Калькулятор преобразования размера шин или калькулятор диаметра шин — лучший способ получить ответы, которые вы ищете. Что нас отличает, так это наше руководство по выбору шин. Для каждого размера шины, который вы вводите, наш калькулятор шин предлагает несколько размеров шин, которые на один дюйм больше или меньше введенного размера шины. Сделайте как можно проще найти шину, которая подходит именно вам.
Также просмотрите наши категории шин и страницы со скидками на шины для Jeep, шины 4X4, новые дешевые шины, всесезонные шины, дешевые грузовые шины, всесезонные шины и шины с бесплатной доставкой.
Расчет сопротивления качению с помощью параметрического уравнения
В этом блоге мы удостоили чести Пера Ландебека как специального приглашенного автора нашего блога. Пер написал этот замечательный блог о параметрическом уравнении для расчета сопротивления качению автомобильной шины.
Инженер по испытаниям и моделированию на пенсии с большим опытом работы с различными транспортными средствами, такими как автомобили, автобусы, грузовики и поезда.Учился в Технологическом университете Чалмерса и защитил кандидатскую диссертацию по военному двигателю Volvo Aero. Ранее занимал должности сотрудника / консультанта в SAAB, Volvo Truck, Volvo Bus, Bombardier, Scania Truck и NEVS (National Electric Vehicle Sweden). Технические аспекты в области комфорта, управляемости, торможения, рулевого управления, подвески, опор двигателя, шин и расчета / моделирования общих компонентов
«Спасибо за приглашение написать о сопротивлении качению шин и особенно о моем разработанном параметрическом уравнении сопротивления качению.Это считается первой публикацией, и очень вероятно, что статья будет опубликована. Следовательно, применяются общие правила авторской записи ».
Введение
За годы тестирования и моделирования различных транспортных средств (автомобилей, автобусов, грузовиков и поездов) меня
интересовало, как описать сопротивление качению колеса, и я прочитал много опубликованных отчетов. С
1970 г. количество опубликованных статей о сопротивлении качению увеличилось в 400 раз.
опубликованных статей варьируются от простых уравнений до сложных моделей.
Общее параметрическое уравнение, которое учитывает наиболее важные параметры, необходимо для того, чтобы
можно было использовать в качестве аналитических или исходных данных для моделей шин. Модель измерений FTIRE, используемая в нескольких программах моделирования
(например, Msc Adams), плохо отображает сопротивление качению. Другим моделям шин, таким как
PAC2002, которые могут быть настроены для работы так же хорошо, как и модель FTIRE, для работы требуются соответствующие данные.
Здесь я представлю общее параметрическое уравнение, которое охватывает все необходимые параметры и демонстрирует хорошее соответствие измеренным данным шины
. Но прежде чем это показать, я хотел бы описать, что такое сопротивление качению.
Что такое сопротивление качению?
Основная функция шины — обеспечивать связь между транспортным средством и дорогой. Несколько сил
сопротивляются движению транспортного средства; силы сопротивления качению от самой шины, аэродинамические силы, внутренние силы трения
транспортного средства, силы тяжести при движении вверх по склону и силы инерции при разгоне / торможении
.
Сопротивление качению шины зависит от трех основных причин; изгиб до и после зоны контакта,
сжатие и сдвиг в зоне контакта (80-95%), микропроскальзывание шины относительно дороги (менее 5%) и аэродинамическое сопротивление
из-за вращающейся шины, функционирующей как сопротивление вентилятора движению (0- 15%), см. Рисунок ниже. Аэродинамическое сопротивление
зависит от ширины и радиуса шины и является почти квадратом функции скорости.
Наиболее важной причиной сопротивления качению является потеря энергии в шине при повышении температуры.Хотя на этот
больше всего влияет потеря энергии вязкоупругого материала, также играет роль жесткость, определяя площадь
зоны контакта. Чтобы это наглядно представить, на рисунке 1c показано жесткое деревянное колесо. Как видно, область контакта
состоит только из точки без потерь энергии. У этого колеса будет нулевое сопротивление качению, но ужасная комфортность езды
.
В обычной шине легкового / грузового автомобиля корона вносит 70% потерь энергии, а боковины и площадь борта
— по 15% каждая.Коронка выполнена в виде композитной конструкции с центральным металлическим поясом и двумя слоями вязкоупругого материала
(внутренний вкладыш и протектор), см. Рисунок 2.
Потери энергии в шине возникают гистерезисом, когда композитный материал (резина и др.)
сжимается / растрескивается и изгибается во время прокатки. Результирующая сила будет расположена немного впереди центра шины
, как показано на рисунке 3.
Поверхность дороги влияет на сопротивление качению.Шероховатое дорожное покрытие имеет сопротивление
на 40% больше, чем гладкое шоссе, рисунок 4.
Очень важным фактором является температура окружающей среды и создаваемая в шине температура. Шина
работает при температуре от 20 до 60 градусов C в зависимости от типа шины, типа вождения и температуры окружающей среды. При повышении температуры окружающей среды
сопротивление качению снижается. Для того, чтобы автомобильная шина достигла стабильной температуры
° С, требуется около 30 минут, а для шины автобуса / грузовика — до 3 часов.Согласно ISO 8767 шина должна пройти примерно 20
мин перед каждой измеренной скоростью.
Непрерывное развитие производителей шин привело к снижению сопротивления качению и приближается к асимптотическому уровню
, как показано на рисунке 6 [D.E. Холл, Дж. Морленд, Основы сопротивления качению.
Вдобавок ко всему существуют разные классы скорости, как и для легковых автомобилей: S (180 км / ч), T (190 км / ч), U (200 км / ч),
H (210 км / ч), V (240 км / ч), W (270 км / ч) и Y (300 км / ч).Композитный материал шин класса Speed
немного отличается. В более высоких скоростных классах сопротивление качению обычно выше.
Как измеряется сопротивление качению?
Для измерения сопротивления качению используются четыре стандартных метода;
• Усилие на оси шины
• Крутящий момент, прикладываемый к валу барабана
• Мощность двигателя
• Выбег (качение вниз)
Измерения вальца являются наиболее распространенными и должны быть скорректированы для получения значений, аналогичных измерению на платформе
.
Используются разные стандарты, в Европе в основном ISO8767 для автомобильных шин и ISO9948 для грузовых / автобусных шин. Производители US
соответствуют двум стандартам SAE; SAE1269 (барабанный тест) и SAE2452 (ступенчатый выбег).
Самый простой способ — это движение по инерции. Если выполняется пошаговое выполнение, температура стабильна в каждом интервале
оборотов. Непрерывный выбег будет иметь слегка повышенную температуру на более низких скоростях. Обычно сила сопротивления
измеряется на шпинделе шины, однако, если кто-то хочет провести какое-то исследование (частное или профессиональное
), я представлю здесь несколько полезных уравнений.2. CD и эти два часто рассматриваются вместе как одна константа.
Сопротивление качению, представленное ниже.
Для расчета замедления и изменения скорости необходимо определить эффективный радиус качения. Либо используйте уравнение
, представленное здесь, либо определите модель PAC2002. Представленные уравнения взяты из
различных источников и немного изменены или развиты.
Для расчета эффективного радиуса качения необходима статическая жесткость шины.2 для наката от 100 км / ч. Это немного повлияет на сопротивление качению, но также небольшая слишком высокая температура при более низких скоростях снизит сопротивление качению.
Силы сопротивления трению, возникающие из-за подшипников и других факторов, можно определить отдельно, используя жесткое колесо или чрезмерно накачанную шину (асимптотическое значение) и выбегая с более низких скоростей до нуля.
Параметрическое уравнение сопротивления качению
Это общее параметрическое уравнение постепенно разрабатывалось в течение многих лет.Последняя версия, представленная здесь, обновлена в этом 2021 году.
Сопротивление качению напрямую зависит от радиуса без нагрузки, ширины шины, давления, нагрузки и скорости.
Кроме того, зависит от классов скорости (разные композиты), по сути, от жесткости ремня.
RR в сравнении с классами скорости, радиусом и шириной Больший радиус и ширина дают меньшее сопротивление качению, что подтверждается несколькими опубликованными статьями. Кроме того, шины с разными скоростными классами напрямую влияют на сопротивление качению.Класс скорости ST (180-190 км / ч) несколько ниже, чем класс скорости HV (210-240 км / ч), а класс скорости WYZ (240-300 км / ч) имеет большее сопротивление качению. Это связано с требованиями к дизайну и выбором композитного материала.
Большое количество шин в трех скоростных классах измеряется в соответствии со стандартом SAE J1269. Стандарт
предписывает 80 км / ч при 80% нагрузке и соответствующем давлении производителя. Из-за этого в этих данных немного разные нагрузки и давление.
Ширина имеет прямое влияние на показатель мощности диаметра, показанный ссылкой [7], так что маленькие узкие шины дают большее сопротивление качению (рисунок 9).
Как показано на рисунке 9, ширина влияет на сопротивление качению, но в сочетании с радиусом. Rhyne & Cron
[7] ограниченное и простое моделирование показывает прямую зависимость между диаметром и шириной. Данные об использованных шинах имеют большой шум из-за немного другой нагрузки и давления, и можно определить только RRC в зависимости от диаметра. Отдельно оценивалась зависимость от ширины.
Если бы можно было доказать соотношение между диаметром и шириной, показанное Rhyne & Cron, уравнение было бы таким:
Сила RR и коэффициент RR в зависимости от давления и нагрузки, квазистатический
Квазистатическое сопротивление качению из-за давления и нагрузки.Сопротивление качению быстро увеличивается по мере уменьшения давления
. Причина в том, что более низкое давление уменьшает сжатие блоков протектора, но увеличивает площадь основания и
изгиб и срезание блоков протектора. Следовательно, сопротивление качению обратно зависит от давления.
Сила сопротивления качению увеличивается почти линейно с увеличением нагрузки, в то время как коэффициент сопротивления качению обычно уменьшается с увеличением нагрузки. Причина в том, что повышенная нагрузка снижает вязкоупругость при повышении температуры
(большая нагрузка) и создает больший изгиб и сдвиг.Многие опубликованные статьи рассматривают зависимость сопротивления качению от нагрузки как линейную, в то время как Michelin сообщает о слабой нелинейности с показателем 0,85. На рисунке 13 показано обобщенное поведение Michelin при увеличении нагрузки.
Это описание является только квазистатическим, и зависимость от скорости будет рассматриваться отдельно.
Зависимость силы RR и коэффициента RR от скорости
Увеличение скорости увеличивает сопротивление качению. Существует несколько причин, однако преобладающим фактором
является изменение вязкоупругих свойств из-за повышения температуры с увеличением скорости и аэродинамического сопротивления
вокруг колеса (описанного выше).
Предполагается, что только доминирующие параметры, такие как давление и нагрузка, будут влиять на сопротивление качению
, увеличиваясь со скоростью. Больший радиус и ширина будут иметь немного большее сопротивление качению из-за повышенного аэродинамического сопротивления
, см. Рисунок 14. Для простоты это не учитывается в параметрическом уравнении
сопротивления качению. Другие параметры, такие как влияние радиуса и ширины на увеличенную скорость, считаются небольшими, а
не учитываются (влияние только на квазистатику).
Давление оказывает прямое влияние на увеличение скорости. На это может повлиять другой размер шин, однако,
опубликовано мало статей об этом. Чтобы сделать это простым, но при этом иметь эффект, данные
, представленные в ссылке [10], используются для соответствующего масштабирования при изменении давления. На рисунке 15 показано
влияние давления для шины 185 / 65R15 (эталонная шина).
Больше нагрузки влияет на компонент скорости. Большая нагрузка снижает коэффициент сопротивления качению, но увеличивает общую силу сопротивления
(немного меньший коэффициент, умноженный на большую нагрузку).Для автомобильной шины 185 / 65R15
с двойной нагрузкой RRC примерно на 10% ниже на скорости 80 км / ч, но усилие на 80% больше.
Кроме того, разные классы скорости будут влиять на более высокую скорость, особенно класс скорости WYZ
выше 160 км / ч. Этим эффектом скоростных классов на большей скорости пренебрегают.
Эта часть параметрического сопротивления качению, относящаяся к скорости, имеет следующую форму;
Сопротивление качению при разгоне и торможении
Во время разгона и торможения возникает дополнительная деформация протектора шины, которая влияет на сопротивление качению
.Возникновение продольных сил сопровождается некоторым скольжением в части зоны контакта
. Это означает, что теряется больше энергии и увеличивается коэффициент сопротивления качению.
Это очень мало опубликованных работ, исследующих это, одна из них является справочной [11]. Сопротивление качению
будет минимальным при небольшом ускорении.
Зависимость нагрузки не очень доминирующая, поэтому, создавая прирост сопротивления качению от нуля
тяги / торможения, усредняя для всей нагрузки и создавая функцию против Fx / Fz, эта часть параметрического сопротивления качению
принимает форму;
Уравнение полного параметрического сопротивления качению
Пройдя через все вышеизложенное, можно составить все общее уравнение.Это уравнение является аналитическим инструментом
и дает разумные приблизительные значения сопротивления качению. Преимущества:
• Влияние диаметра на сопротивление качению
• Влияние ширины на сопротивление качению
• Влияние давления на сопротивление качению в квазистатическом режиме и зависимость от скорости
• Влияние нормальной нагрузки на сопротивление качению в квазистатическом режиме и зависимость от скорости
• Классы скорости
• Торможение и тяга влияние на сопротивление качению
Однако есть пределы возможностей параметрического уравнения.На соотношение между радиусом и шириной
могут влиять различные вязкоупругие свойства, и это не является гарантией, что уравнение
будет давать правильное в некоторых случаях при экстремальных значениях, но все же является хорошей оценкой. Кроме того, на скорости более 150 км / ч некоторые шины
могут иметь резкое увеличение сопротивления качению.
Где константа K SPCL — коэффициент класса скорости. Эталонная шина имеет размерный класс скорости 185 / 65R15 ST (макс.180 км / ч). При правильной установке всех коэффициентов достигается хорошее совпадение с измеренными значениями, такими как
, как показано на рисунке 19.
Используя это уравнение для различных классов скорости в базе данных шин, достигается близкое соответствие. Коэффициенты
для различных классов скорости оцениваются как ST 1.0, HV 1.08 и WYZ 1.165.
Калькулятор сопротивления качению учитывает трение в подшипниках, двигателе, колесах и аэродинамическое сопротивление. Фрикционная часть обычно зависит от скорости.
При измерении выбегом и использовании приведенных выше уравнений очень хорошее согласие достигается для электромобиля.
Фрикционная часть оценивается с использованием вышеуказанного общего уравнения (старая версия) и обратной оценки фрикционной части, см. Рисунок 22.
Заключение
Общее параметрическое уравнение сопротивления качению может относительно хорошо оценить силу сопротивления качению для всех автомобильных шин. Сравнение с измерением показывает хорошее соответствие.
Это параметрическое уравнение сопротивления качению может использоваться в качестве входных данных для моделей шин, таких как PAC2002 или других.Общее уравнение также можно использовать в качестве аналитического инструмента для выбора наилучших автомобильных шин. Можно изменить общее уравнение для других шин, таких как шины для мотоциклов и грузовых автомобилей. Возможно, придется изменить некоторые константы и показатели.
Список литературы
1. Бхарат Мохан Редруту Сидхарт Дас, «Моделирование шин для определения сопротивления качению, подразделение машиностроения
и автономной системы, Технологический университет Чалмерса
2. Мишлен, 2013,« Сопротивление качению и экономия топлива », Société de Technologie Michelin
3.Ульф Сандберг, 2011 г., «Сопротивление качению — основная информация и современное состояние по методам измерения
», Шведский национальный научно-исследовательский институт дороги и транспорта (VTI)
4. Ф. Коутны, 2007 г., «Геометрия и механика пневматики. Шины »,
5. Ульрико Пекельсен, 2017,« Объективная разработка шин », Karlsruher Institut für Technologie (KIT)
6. Ф. Коутны,« Геометрия и механика пневматических шин », Zlín, CZE, 2007
7. TB Райн и С. Cron, 2012, «Исследование минимального сопротивления качению», том 40, Tire Science и
Technology
8.Юкио Накадзима, 2019, «Продвинутая механика шин», Департамент механических наук и
инженерии, Университет Когакуин, Япония
9.
