Расчет аэродинамического сопротивления: Репозиторий Самарского национального исследовательского университета имени академика С.П. Королёва: Недопустимый идентификатор

Содержание

Расчет сопротивления сети вентиляции пример. Аэродинамический расчет воздуховодов приточной системы вентиляции

где R — потери давления на трение в расчете на 1 погонный метр воздуховода, l — длина воздуховода в метрах, z — потери давления на местные сопротивления (при переменном сечении).

1. Потери на трение:

Pтр = (x*l/d) * (v*v*y)/2g,

z = Q* (v*v*y)/2g,

Метод допустимых скоростей

При расчете сети воздуховодов по методу допустимых скоростей за исходные данные принимают оптимальную скорость воздуха (см. таблицу). Затем считают нужное сечение воздуховода и потери давления в нем.

Данный метод предполагает постоянную потерю напора на 1 погонный метр воздуховода. На основе этого определяются размеры сети воздуховодов. Метод постоянной потери напора достаточно прост и применяется на стадии технико-экономического обоснования систем вентиляции:

В диаграмме потерь напора указаны диаметры круглых воздуховодов . Если вместо них используются воздуховоды прямоугольного сечения, то необходимо найти их эквивалентные диаметры с помощью приведенной ниже таблицы.

Примечания:

Если места недостаточно (например, при реконструкции), выбирают прямоугольные воздуховоды . Как правило, ширина воздуховода в 2 раза больше высоты).

Этим материалом редакция журнала „Мир Климата“ продолжает публикацию глав из книги „Системы вентиляции и кондиционирования. Рекомендации по проектированию для произ-
водственных и общественных зданий“. Автор Краснов Ю.С.

Аэродинамический расчет воздуховодов начинают с вычерчивания аксонометрической схемы (М 1: 100), проставления номеров участков, их нагрузок L (м 3 /ч) и длин I (м). Определяют направление аэродинамического расчета — от наиболее удаленного и нагруженного участка до вентилятора. При сомнениях при определении направления рассчитывают все возможные варианты.

Расчет начинают с удаленного участка: определяют диаметр D (м) круглого или площадь F (м 2) поперечного сечения прямоугольного воздуховода:

Скорость растет по мере приближения к вентилятору.

По приложению Н из принимают ближайшие стандартные значения: D CT или (а х b) ст (м).

Гидравлический радиус прямоугольных воздуховодов (м):

где — сумма коэффициентов местных сопротивлений на участке воздуховодов.

Местные сопротивления на границе двух участков (тройники, крестовины) относят к участку с меньшим расходом.

Коэффициенты местных сопротивлений даны в приложениях.

Схема приточной системы вентиляции, обслуживающей 3-этажное административное здание

Пример расчета

Исходные данные:

№ участков	подача L, м 3 /ч	длина L, м	υ рек, м/с	сечение а × b, м	υ ф, м/с	D l ,м	Re	λ	Kmc	потери на участке Δр, па
решетка рр на выходе				0,2 × 0,4	3,1	—	—	—	1,8	10,4
1	720	4,2	4	0,2 × 0,25	4,0	0,222	56900	0,0205	0,48	8,4
2	1030	3,0	5	0,25× 0,25	4,6	0,25	73700	0,0195	0,4	8,1
3	2130	2,7	6	0,4 × 0,25	5,92	0,308	116900	0,0180	0,48	13,4
4	3480	14,8	7	0,4 × 0,4	6,04	0,40	154900	0,0172	1,44	45,5
5	6830	1,2	8	0,5 × 0,5	7,6	0,50	234000	0,0159	0,2	8,3
6	10420	6,4	10	0,6 × 0,5	9,65	0,545	337000	0,0151	0,64	45,7
6а	10420	0,8	ю.	Ø0,64	8,99	0,64	369000	0,0149	0	0,9
7	10420	3,2	5	0,53 × 1,06	5,15	0,707	234000	0,0312 ×n	2,5	44,2
Суммарные потери: 185
Таблица 1. Аэродинамический расчет

Воздуховоды изготовлены из оцинкованной тонколистовой стали, толщина и размер которой соответствуют прил. Н из. Материал воздухозаборной шахты — кирпич. В качестве воздухораспределителей применены решетки регулируемые типа РР с возможными сечениями: 100 х 200; 200 х 200; 400 х 200 и 600 х 200 мм, коэффициентом затенения 0,8 и максимальной скоростью воздуха на выходе до 3 м/с.

Сопротивление приемного утепленного клапана с полностью открытыми лопастями 10 Па. Гидравлическое сопротивление калориферной установки 100 Па (по отдельному расчету).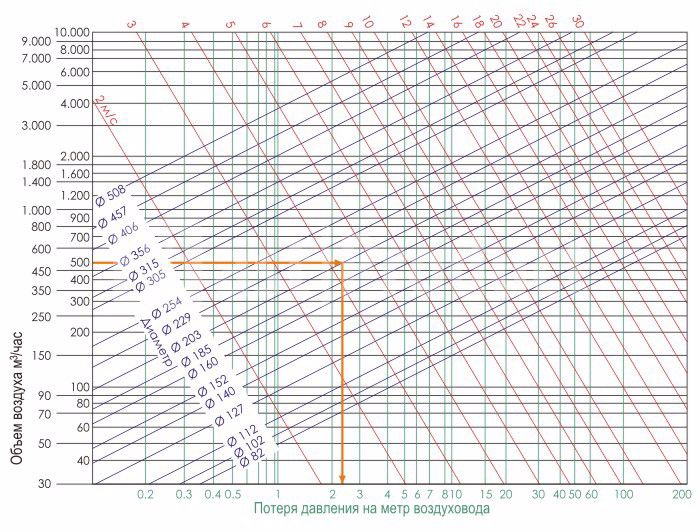 Сопротивление фильтра G-4 250 Па. Гидравлическое сопротивление глушителя 36 Па (по акустическому расчету). Исходя из архитектурных требований проектируют воздуховоды прямоугольного сечения.

Сечения кирпичных каналов принимают по табл. 22.7 .

Коэффициенты местных сопротивлений

Участок 1. Решетка РР на выходе сечением 200×400 мм (рассчитывают отдельно):

№ участков	Вид местного сопротивления	Эскиз	Угол α, град.	Отношение			Обоснование	КМС
№ участков	Вид местного сопротивления	Эскиз	Угол α, град.	F 0 /F 1	L 0 /L ст	f прох /f ств	Обоснование	КМС
1	Диффузор		20	0,62	—	—	Табл. 25.1	0,09
	Отвод		90	—	—	—	Табл.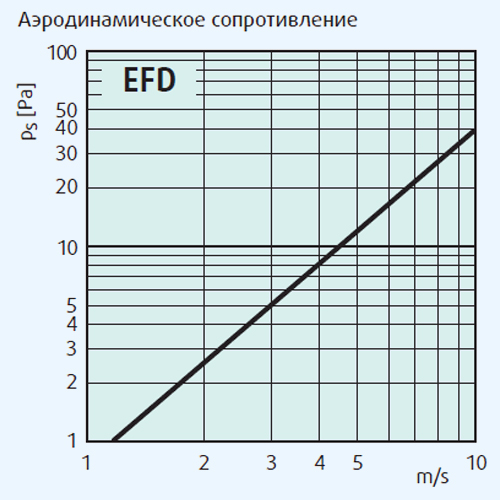 25.11	0,19
	Тройник-проход		—	—	0,3	0,8	Прил. 25.8	0,2
							∑ =	0,48
2	Тройник-проход		—	—	0,48	0,63	Прил. 25.8	0,4
3	Тройник-ответвление		—	0,63	0,61	—	Прил. 25.9	0,48
4	2 отвода	250 × 400	90	—	—	—	Прил. 25.11
	Отвод	400 × 250	90	—	—	—	Прил. 25.11	0,22
	Тройник-проход		—	—	0,49	0,64	Табл. 25.8	0,4
							∑ =	1,44
5	Тройник-проход		—	—	0,34	0,83	Прил. 25.8	0,2
6	Диффузор после вентилятора		h=0,6	1,53	—	—	Прил. 25.13	0,14
	Отвод	600 × 500	90	—	—	—	Прил. 25.11	0,5
							∑=	0,64
6а	Конфузор перед вентилятором			D г =0,42 м			Табл. 25.12	0
7	Колено		90	—	—	—	Табл.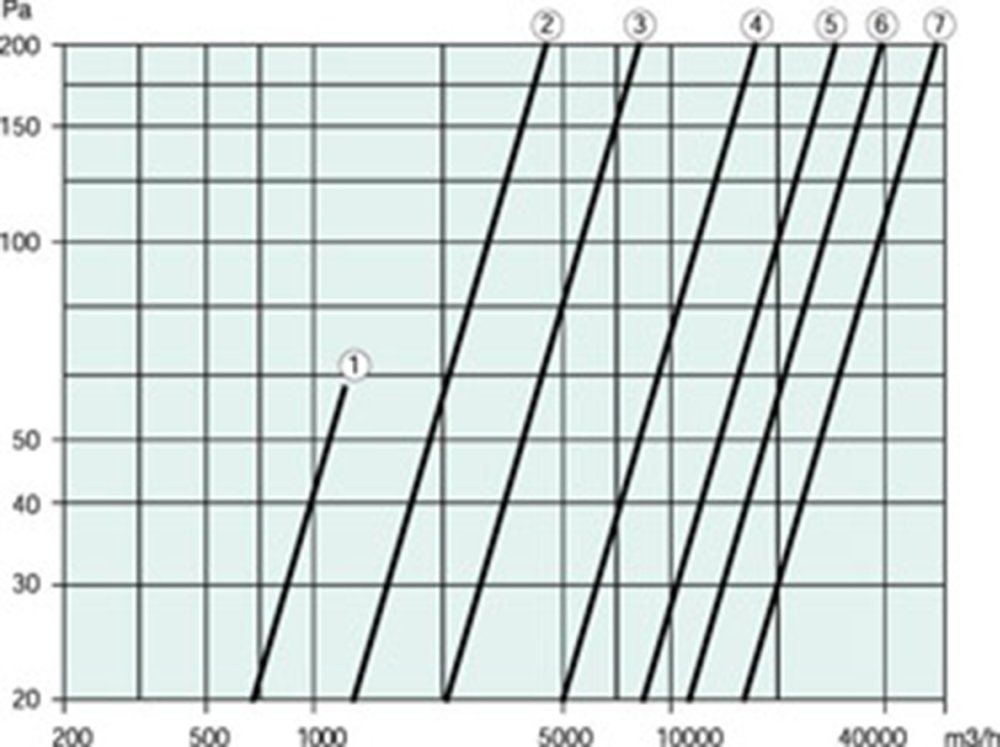 25.1	1,2
	Решетка жалюзийная						Табл. 25.1	1,3
							∑ =	1,44
Таблица 2. Определение местных сопротивлений

Краснов Ю.С.,

Когда известны параметры воздуховодов (их длина, сечение, коэффициент трения воздуха о поверхность), можно рассчитать потери давления в системе при проектируемом расходе воздуха.

Общие потери давления (в кг/кв.м.) рассчитываются по формуле:

1. Потери на трение:

В круглом воздуховоде потери давления на трение P тр считаются так:

Pтр = (x*l/d) * (v*v*y)/2g,

где x — коэффициент сопротивления трения, l — длина воздуховода в метрах, d — диаметр воздуховода в метрах, v — скорость течения воздуха в м/с, y — плотность воздуха в кг/куб. м., g — ускорение свободного падения (9,8 м/с2).

Замечание: Если воздуховод имеет не круглое, а прямоугольное сечение, в формулу надо подставлять эквивалентный диаметр, который для воздуховода со сторонами А и В равен: dэкв = 2АВ/(А + В)

2. Потери на местные сопротивления:

Потери давления на местные сопротивления считаются по формуле:

z = Q* (v*v*y)/2g,

где Q — сумма коэффициентов местных сопротивлений на участке воздуховода, для которого производят расчет, v — скорость течения воздуха в м/с, y — плотность воздуха в кг/куб.м., g — ускорение свободного падения (9,8 м/с2). Значения Q содержатся в табличном виде.

Метод допустимых скоростей

Порядок действий при аэродинамическом расчете воздуховодов по методу допустимых скоростей:

Начертить схему воздухораспределительной системы. Для каждого участка воздуховода указать длину и количество воздуха, проходящего за 1 час.
Расчет начинаем с самых дальних от вентилятора и самых нагруженных участков.
Зная оптимальную скорость воздуха для данного помещения и объем воздуха, проходящего через воздуховод за 1 час, определим подходящий диаметр (или сечение) воздуховода.
Вычисляем потери давления на трение P тр.
По табличным данным определяем сумму местных сопротивлений Q и рассчитываем потери давления на местные сопротивления z.
Располагаемое давление для следующих ветвлений воздухораспределительной сети определяется как сумма потерь давления на участках, расположенных до данного ветвления.

В процессе расчета нужно последовательно увязать все ветви сети, приравняв сопротивление каждой ветви к сопротивлению самой нагруженной ветви. Это делают с помощью диафрагм. Их устанавливают на слабо нагруженные участки воздуховодов, повышая сопротивление.

Таблица максимальной скорости воздуха в зависимости от требований к воздуховоду

Примечание: скорость воздушного потока в таблице дана в метрах в секунду

Метод постоянной потери напора

В зависимости от назначения помещения по таблице допустимых скоростей воздуха выбирают скорость на магистральном участке воздуховода.
По определенной в п.1 скорости и на основании проектного расхода воздуха находят начальную потерю напора (на 1 м длины воздуховода). Для этого служит нижеприведенная диаграмма.
Определяют самую нагруженную ветвь, и ее длину принимают за эквивалентную длину воздухораспределительной системы. Чаще всего это расстояние до самого дальнего диффузора.
Умножают эквивалентную длину системы на потерю напора из п.2. К полученному значению прибавляют потерю напора на диффузорах.

Теперь по приведенной ниже диаграмме определяют диаметр начального воздуховода, идущего от вентилятора, а затем диаметры остальных участков сети по соответствующим расходам воздуха.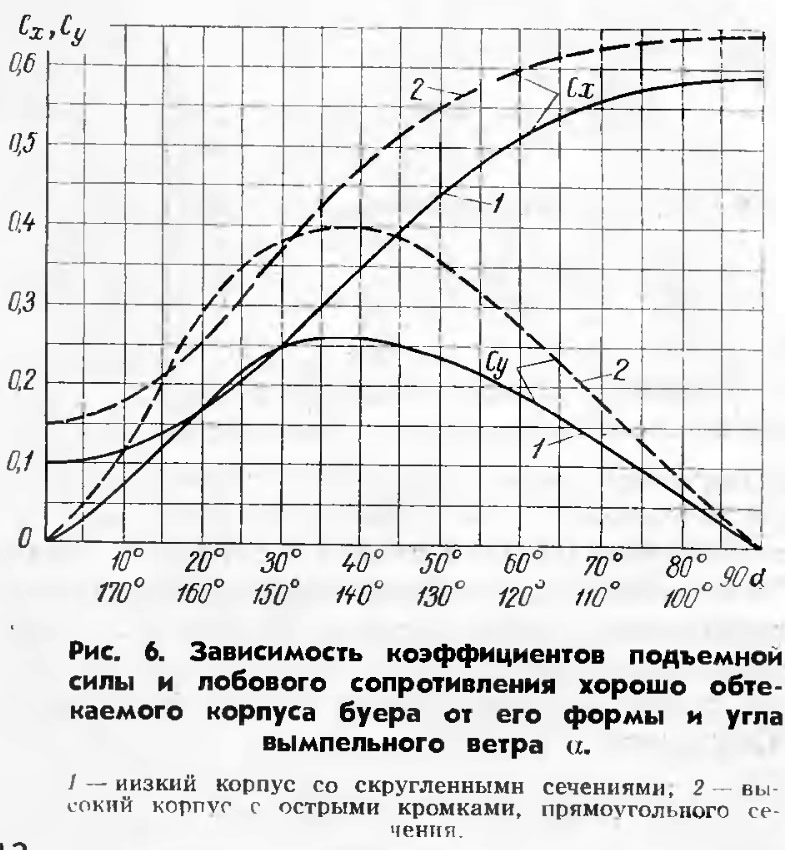 При этом принимают постоянной начальную потерю напора.

Диаграмма определения потерь напора и диаметра воздуховодов

Использование прямоугольных воздуховодов

В диаграмме потерь напора указаны диаметры круглых воздуховодов. Если вместо них используются воздуховоды прямоугольного сечения, то необходимо найти их эквивалентные диаметры с помощью приведенной ниже таблицы.

Примечания:

Если позволяет пространство, лучше выбирать круглые или квадратные воздуховоды;
Если места недостаточно (например, при реконструкции), выбирают прямоугольные воздуховоды. Как правило, ширина воздуховода в 2 раза больше высоты).

В таблице по горизонтальной указана высота воздуховода в мм, по вертикальной — его ширина, а в ячейках таблицы содержатся эквивалентные диаметры воздуховодов в мм.

Таблица эквивалентных диаметров воздуховодов

Целью аэродинамического расчета является определение потерь давления (сопротивления) движению воздуха во всех элементах системы вентиляции — воздуховодах, их фасонных элементах, решетках, диффузорах, воздухонагревателях и других.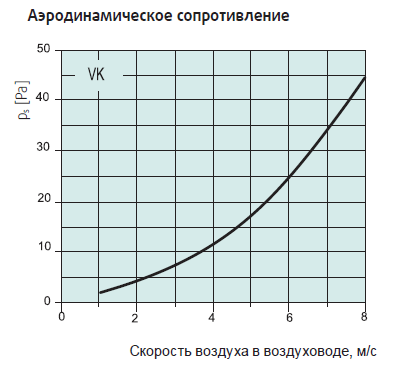 Зная общую величину этих потерь, можно подобрать вентилятор, способный обеспечить необходимый расход воздуха. Различают прямую и обратную задачи аэродинамического расчета. Прямая задача решается при проектировании вновь создаваемых систем вентиляции, состоит в определении площади сечения всех участков системы при заданном расходе через них. Обратная задача – определение расхода воздуха при заданной площади сечения эксплуатируемых или реконструируемых систем вентиляции. В таких случаях для достижения требуемого расхода достаточно изменения частоты вращения вентилятора или его замены на другой типоразмер.

Аэродинамический расчет начинают после определения кратности воздухообмена помещений и принятия решения по трассировке (схеме прокладки) воздуховодов и каналов. Кратность воздухообмена является количественной характеристикой работы системы вентиляции, показывает, сколько раз в течение 1-го часа объем воздуха помещения полностью заменится новым. Кратность зависит от характеристик помещения, его назначения и может отличаться в несколько раз. Перед началом аэродинамического расчета создается схема системы в аксонометрической проекции и масштабе М 1:100. На схеме выделяют основные элементы системы: воздуховоды, их фасонные части, фильтры, шумоглушители, клапана, воздухонагреватели, вентиляторы, решетки и другие. По этой схеме, строительным планам помещений определяют длину отдельных ветвей. Схему делят на расчетные участки, которые имеют постоянный расход воздуха. Границами расчетных участков являются фасонные элементы – отводы, тройники и прочие. Определяют расход на каждом участке, наносят его, длину, номер участка на схему. Далее выбирают магистраль – наиболее длинную цепь последовательно расположенных участков, считая от начала системы до самого удаленного ответвления. Если в системе несколько магистралей одинаковой длины, то главной выбирают с большим расходом. Принимается форма поперечного сечения воздуховодов – круглая, прямоугольная или квадратная. Потери давления на участках зависят от скорости воздуха и состоят из: потерь на трение и в местных сопротивлениях.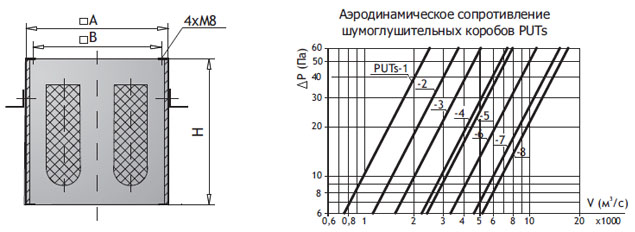 Общие потери давления системы вентиляции равны потерям магистрали и состоят из суммы потерь всех ее расчетных участков. Выбирают направление расчета – от самого дальнего участка до вентилятора.

По площади F определяют диаметр D (для круглой формы) или высоту A и ширину B (для прямоугольной) воздуховода, м. Полученные величины округляют до ближайшего большего стандартного размера, т.е. D ст , А ст и В ст (справочная величина).

Пересчитывают фактические площадь сечения F факт и скорость v факт .

Для прямоугольного воздуховода определяют т.н. эквивалентный диаметр DL = (2A ст * B ст ) / (A ст + B ст ), м.

Определяют величину критерия подобия Рейнольдса Re = 64100* D ст * v факт. Для прямоугольной формы D L = D ст .

Коэффициент трения λ тр = 0,3164 ⁄ Re-0,25 при Re≤60000, λ тр = 0,1266 ⁄ Re-0,167 при Re>60000.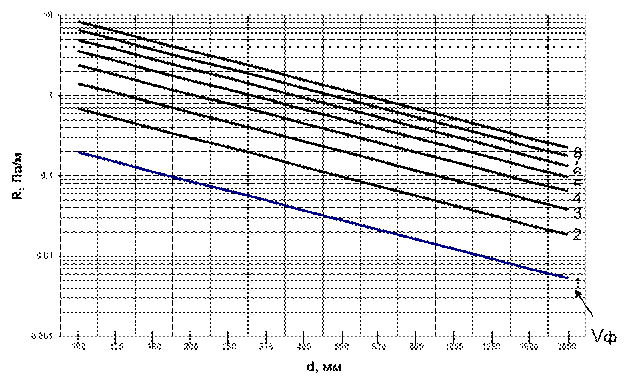

Коэффициент местного сопротивления λм зависит от их типа, количества и выбирается из справочников.

Сопротивление прохождению воздуха в вентиляционной системе, в основном, определяется скоростью движения воздуха в этой системе. С увеличением скорости возрастает и сопротивление. Это явление называется потерей давления. Статическое давление, создаваемое вентилятором, обуславливает движение воздуха в вентиляционной системе, имеющей определенное сопротивление. Чем выше сопротивление такой системы, тем меньше расход воздуха, перемещаемый или . Расчет потерь на трение для воздуха в воздуховодах, а также сопротивление сетевого оборудования (фильтр, шумоглушитель, нагреватель, клапан и др.) может быть произведен с помощью соответствующих таблиц и диаграмм, указанных в каталоге. Общее падение давления можно рассчитать, просуммировав показатели сопротивления всех элементов вентиляционной системы.

Рекомендуемая скорость движения воздуха в воздуховодах:

Определение скорости движения воздуха в воздуховодах:

V= L / 3600*F (м/сек)

где L — расход воздуха, м 3 /ч;
F — площадь сечения канала, м 2 .

Рекомендация 1.
Потеря давления в системе воздуховодов может быть снижена за счет увеличения сечения воздуховодов, обеспечивающих относительно одинаковую скорость воздуха во всей системе. На изображении мы видим, как можно обеспечить относительно одинаковую скорость воздуха в сети воздуховодов при минимальной потере давления.

Рекомендация 2.
В системах с большой протяженностью воздуховодов и большим количеством вентиляционных решеток целесообразно размещать вентилятор в середине вентиляционной системы. Такое решение обладает несколькими преимуществами. С одной стороны, снижаются потери давления, а с другой стороны, можно использовать воздуховоды меньшего сечения.

Пример расчета вентиляционной системы:
Расчет необходимо начать с составления эскиза системы с указанием мест расположения воздуховодов, вентиляционных решеток, вентиляторов, а также длин участков воздуховодов между тройниками, затем определить расход воздуха на каждом участке сети.

Выясним потери давления для участков 1-6, воспользовавшись графиком потери давления в круглых воздуховодах, определим необходимые диаметры воздуховодов и потерю давления в них при условии, что необходимо обеспечить допустимую скорость движения воздуха.

Участок 1: расход воздуха будет составлять 220 м 3 /ч. Принимаем диаметр воздуховода равным 200 мм, скорость — 1,95 м/с, потеря давления составит 0,2 Па/м х 15 м = 3 Па (см. диаграмму определение потерь давления в воздуховодах).

Участок 2: повторим те же расчеты, не забыв, что расход воздуха через этот участок уже будет составлять 220+350=570 м 3 /ч. Принимаем диаметр воздуховода равным 250 мм, скорость — 3,23 м/с. Потеря давления составит 0,9 Па/м х 20 м = 18 Па.

Участок 3: расход воздуха через этот участок будет составлять 1070 м 3 /ч.
Принимаем диаметр воздуховода равным 315 мм, скорость 3,82 м/с. Потеря давления составит 1,1 Па/м х 20= 22 Па.

Участок 4: расход воздуха через этот участок будет составлять 1570 м 3 /ч.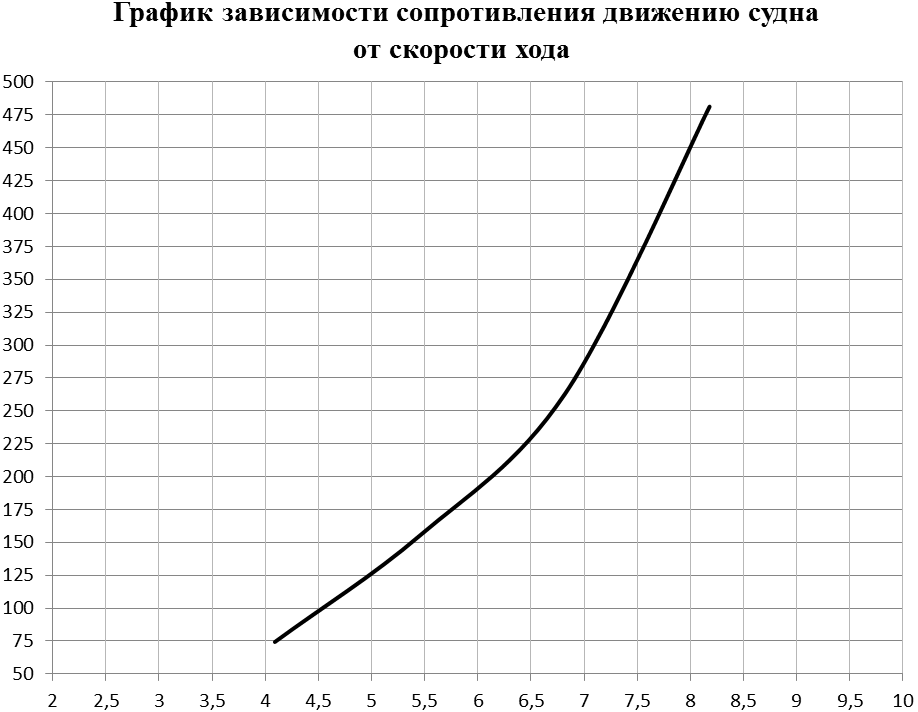 Принимаем диаметр воздуховода равным 315 мм, скорость — 5,6 м/с. Потеря давления составит 2,3 Па х 20 = 46 Па.

Участок 5: расход воздуха через этот участок будет составлять 1570 м 3 /ч. Принимаем диаметр воздуховода равным 315 мм, скорость 5,6 м/с. Потеря давления составит 2,3 Па/м х 1= 2,3 Па.

Участок 6: расход воздуха через этот участок будет составлять 1570 м 3 /ч. Принимаем диаметр воздуховода равным 315 мм, скорость 5,6 м/с. Потеря давления составит 2,3 Па х 10 = 23 Па. Суммарная потеря давления в воздуховодах будет составлять 114,3 Па.

Когда расчет последнего участка завершен, необходимо определить потери давления в сетевых элементах: в шумоглушителе СР 315/900 (16 Па) и в обратном клапане КОМ 315 (22 Па). Также определим потерю давления в отводах к решеткам (сопротивление 4-х отводов в сумме будут составлять 8 Па).

Определение потерь давления на изгибах воздуховодов

График позволяет определить потери давления в отводе, исходя из величины угла изгиба, диаметра и расхода воздуха.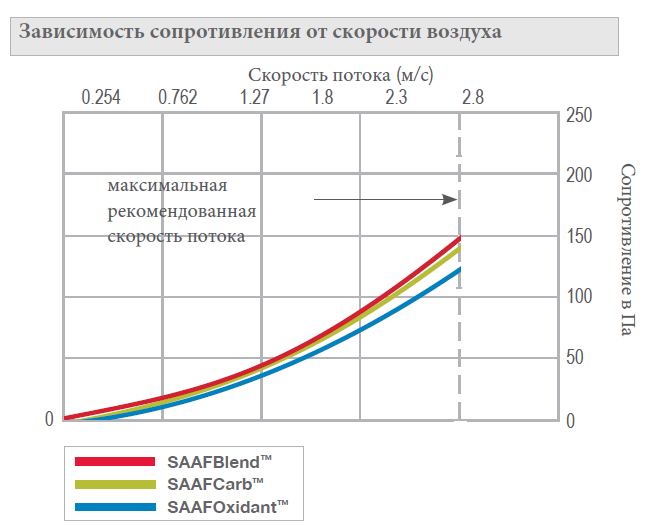

Пример. Определим потерю давления для отвода 90° диаметром 250 мм при расходе воздуха 500 м3/ч. Для этого найдем пересечение вертикальной линии, соответствующей нашему расходу воздуха, с наклонной чертой, характеризующей диаметр 250 мм, и на вертикальной черте слева для отвода в 90° находим величину потери давления, которая составляет 2Па.

Принимаем к установке потолочные диффузоры серии ПФ, сопротивление которых, согласно графику, будет составлять 26 Па.

Теперь просуммируем все величины потери давления для прямых участков воздуховодов, сетевых элементов, отводов и решеток. Искомая величина 186,3 Па.

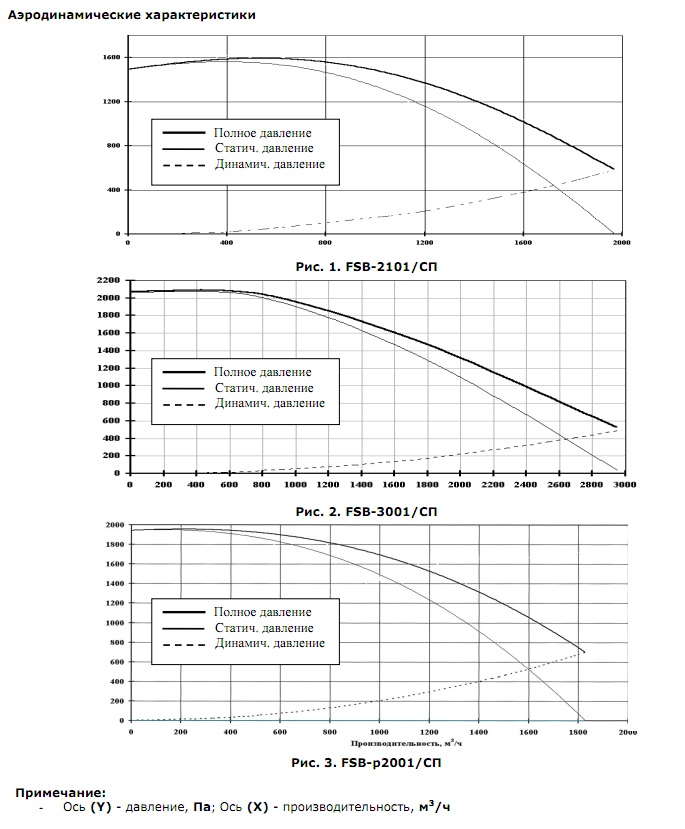
Мы рассчитали систему и определили, что нам нужен вентилятор, удаляющий 1570 м3/ч воздуха при сопротивлении сети 186,3 Па. Учитывая требуемые для работы системы характеристики нас устроит вентилятор требуемые для работы системы характеристики нас устроит вентилятор ВЕНТС ВКМС 315.

Определение потерь давления в воздуховодах.

Определение потерь давления в обратном клапане.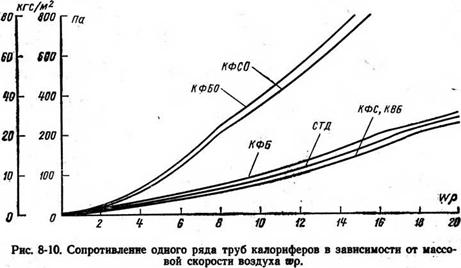

Подбор необходимого вентилятора.

Определение потерь давления в шумоглушителях.

Определение потерь давления на изгибах воздухуводов.

Определение потерь давления в диффузорах.

Основой проектирования любых инженерных сетей является расчет. Для того чтобы правильно сконструировать сеть приточных или вытяжных воздуховодов, необходимо знать параметры воздушного потока. В частности, требуется рассчитать скорость потока и потери давления в канале для правильного подбора мощности вентилятора.

В этом расчете немаловажную роль играет такой параметр, как динамическое давление на стенки воздуховода.

Поведение среды внутри воздухопровода

Вентилятор, создающий воздушный поток в приточном или вытяжном воздуховоде, сообщает этому потоку потенциальную энергию. В процессе движения в ограниченном пространстве трубы потенциальная энергия воздуха частично переходит в кинетическую. Этот процесс происходит в результате воздействия потока на стенки канала и называется динамическим давлением.

Кроме него существует и статическое давление, это воздействие молекул воздуха друг на друга в потоке, оно отражает его потенциальную энергию. Кинетическую энергию потока отражает показатель динамического воздействия, именно поэтому данный параметр участвует в расчетах .

При постоянном расходе воздуха сумма этих двух параметров постоянна и называется полным давлением. Оно может выражаться в абсолютных и относительных единицах. Точкой отсчета для абсолютного давления является полный вакуум, в то время как относительное считается начиная от атмосферного, то есть разница между ними — 1 Атм. Как правило, при расчете всех трубопроводов используется величина относительного (избыточного) воздействия.

Вернуться к оглавлению

Физический смысл параметра

Если рассмотреть прямые отрезки воздуховодов, сечения которых уменьшаются при постоянном расходе воздуха, то будет наблюдаться увеличение скорости потока. При этом динамическое давление в воздуховодах будет расти, а статическое — снижаться, величина полного воздействия останется неизменной. Соответственно, для прохождения потока через такое сужение (конфузор) ему следует изначально сообщить необходимое количество энергии, в противном случае может уменьшиться расход, что недопустимо. Рассчитав величину динамического воздействия, можно узнать количество потерь в этом конфузоре и правильно подобрать мощность вентиляционной установки.

Обратный процесс произойдет в случае увеличения сечения канала при постоянном расходе (диффузор). Скорость и динамическое воздействие начнут уменьшаться, кинетическая энергия потока перейдет в потенциальную. Если напор, развиваемый вентилятором, слишком велик, расход на участке и во всей системе может вырасти.

В зависимости от сложности схемы, вентиляционные системы имеют множество поворотов, тройников, сужений, клапанов и прочих элементов, называемых местными сопротивлениями. Динамическое воздействие в этих элементах возрастает в зависимости от угла атаки потока на внутреннюю стенку трубы. Некоторые детали систем вызывают значительное увеличение этого параметра, например, противопожарные клапаны, в которых на пути потока установлены одна или несколько заслонок. Это создает повышенное сопротивление потоку на участке, которое необходимо учитывать в расчете. Поэтому во всех вышеперечисленных случаях нужно знать величину динамического давления в канале.

Вернуться к оглавлению

Расчеты параметра по формулам

На прямом участке скорость движения воздуха в воздуховоде неизменна, постоянной остается и величина динамического воздействия. Последняя рассчитывается по формуле:

Рд = v2γ / 2g

В этой формуле:

Рд — динамическое давление в кгс/м2;
V — скорость движения воздуха в м/с;
γ — удельная масса воздуха на этом участке, кг/м3;
g — ускорение силы тяжести, равное 9.81 м/с2.

Получить значение динамического давления можно и в других единицах, в Паскалях. Для этого существует другая разновидность этой формулы:

Рд = ρ(v2 / 2)

Здесь ρ — плотность воздуха, кг/м3. Поскольку в вентиляционных системах нет условий для сжатия воздушной среды до такой степени, чтобы изменилась ее плотность, она принимается постоянной — 1.2 кг/м3.

Далее, следует рассмотреть, как участвует величина динамического воздействия в расчете каналов. Смысл этого расчета — определить потери во всей системе приточной либо вытяжной вентиляции для подбора напора вентилятора, его конструкции и мощности двигателя. Расчет потерь происходит в два этапа: сначала определяются потери на трение о стенки канала, потом высчитывается падение мощности воздушного потока в местных сопротивлениях. Параметр динамического давления участвует в расчете на обоих этапах.

Сопротивление трению на 1 м круглого канала рассчитывается по формуле:

R = (λ / d) Рд, где:

Рд — динамическое давление в кгс/м2 или Па;
λ — коэффициент сопротивления трению;
d — диаметр воздуховода в метрах.

Потери на трение определяются отдельно для каждого участка с различными диаметрами и расходами.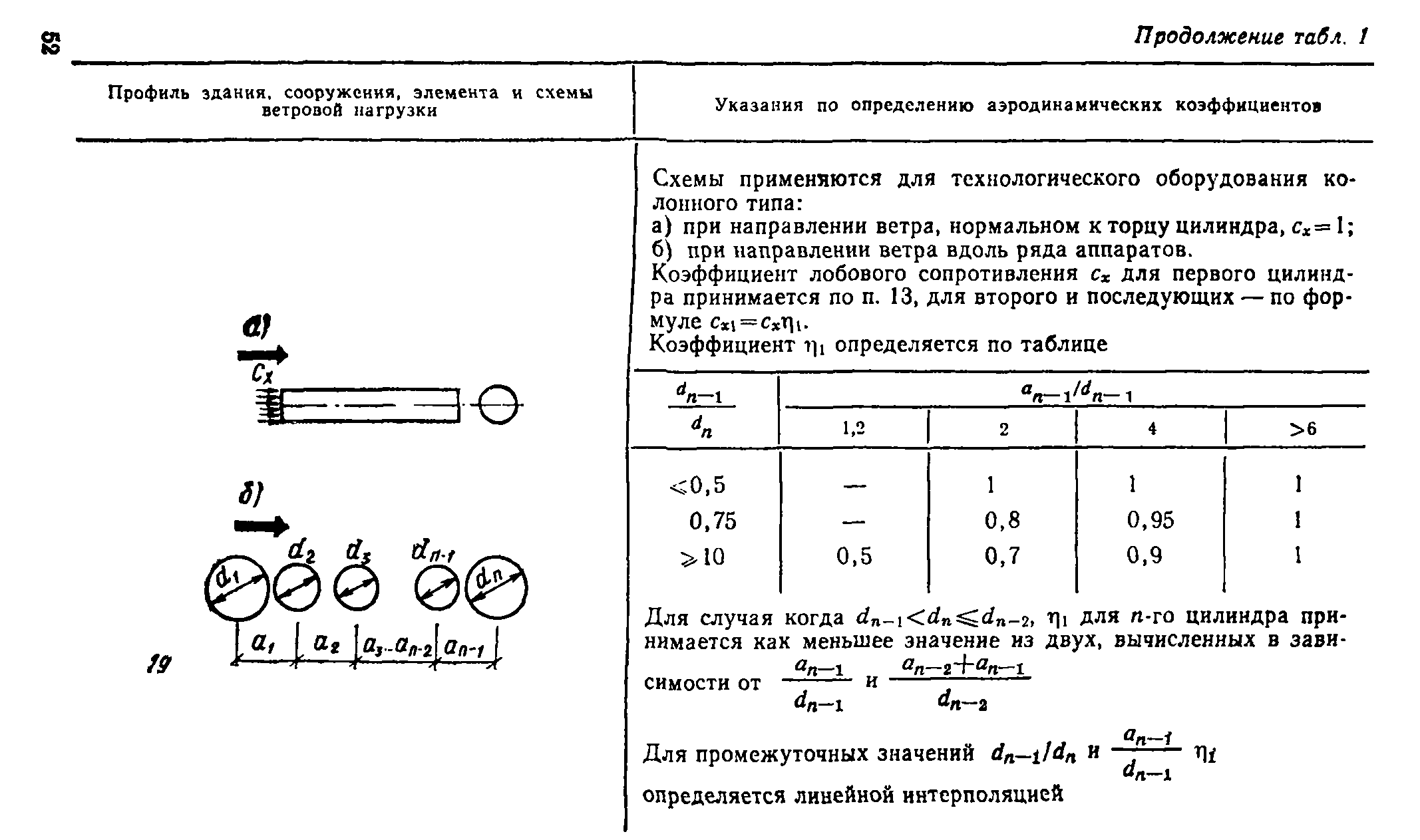 Полученное значение R умножают на общую длину каналов расчетного диаметра, прибавляют потери на местных сопротивлениях и получают общее значение для всей системы:

HB = ∑(Rl + Z)

Здесь параметры:

HB (кгс/м2) — общие потери в вентиляционной системе.
R — потери на трение на 1 м канала круглого сечения.
l (м) — длина участка.
Z (кгс/м2) — потери в местных сопротивлениях (отводах, крестовинах, клапанах и так далее).

Вернуться к оглавлению

Определение параметров местных сопротивлений вентиляционной системы

В определении параметра Z также принимает участие величина динамического воздействия. Разница с прямым участком заключается в том, что в разных элементах системы поток меняет свое направление, разветвляется, сходится. При этом среда взаимодействует с внутренними стенками канала не по касательной, а под разными углами. Чтобы это учесть, в расчетную формулу можно ввести тригонометрическую функцию, но тут есть масса сложностей. Например, при прохождении простого отвода 90⁰ воздух поворачивает и нажимает на внутреннюю стенку как минимум под тремя разными углами (зависит от конструкции отвода). В системе воздуховодов присутствует масса более сложных элементов, как рассчитать потери в них? Для этого существует формула:

Z = ∑ξ Рд.

Для того чтобы упростить процесс расчета, в формулу введен безразмерный коэффициент местного сопротивления. Для каждого элемента вентиляционной системы он разный и является справочной величиной. Значения коэффициентов были получены расчетами либо опытным путем. Многие заводы-производители, выпускающие вентиляционное оборудование, проводят собственные аэродинамические исследования и расчеты изделий. Их результаты, в том числе и коэффициент местного сопротивления элемента (например, противопожарного клапана), вносят в паспорт изделия или размещают в технической документации на своем сайте.

Для упрощения процесса вычисления потерь вентиляционных воздуховодов все значения динамического воздействия для разных скоростей также просчитаны и сведены в таблицы, из которых их можно просто выбирать и вставлять в формулы. В Таблице 1 приведены некоторые значения при самых применяемых на практике скоростях движения воздуха в воздуховодах.

Поделитесь статьей с друзьями:

Сопротивление аэродинамическое — Энциклопедия по машиностроению XXL

Расчет сопротивления аэродинамической трубы (рис. 1-23) [c.56]

Совместная работа насосов на общую сеть 438 Соединение труб тройниковое 498 Солесодержание 552 Сопротивление аэродинамическое 623 [c.643]

Практическое значение изложенных в этом параграфе условий подобия заключается в том, что они позволяют установить, от каких безразмерных параметров зависят величины, характеризующие аэродинамику данного тела (его сопротивление, аэродинамический момент, распределение давлений и т.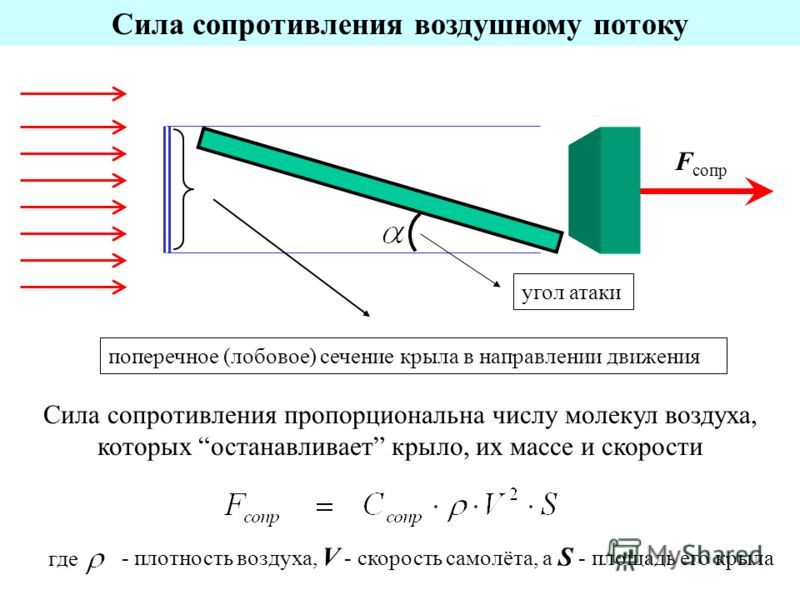 д.). Мы видели, например, что коэффициент сонротивления трубы X зависит от числа Рейнольдса. [c.460]

Измерение аэродинамического сопротивления. Аэродинамическое сопротивление оребренной трубки равно разности статических давлений в начале и конце рабочего участка. При незначительном сопротивлении входного коллектора (коэффициент сопротивления = 0,02) статическое давление перед оребрением практически равно барометрическому поэтому в опытах без ощутимой погрешности аэродинамическое сопротивление определялось как разность барометрического давления и статического в конце рабочего участка. Перепад давлений в зависимости от его величины измерялся либо U-образным манометром 7, либо микроманометром 8. Относительная погрешность в определении перепада не превосходила 1-1,5%. [c.118]

Физически продуваемый снизу плотный слой частиц теряет устойчивость потому, что сопротивление фильтрующемуся сквозь него газу становится равным весу столба материала на единицу площади поддерживающей решетки.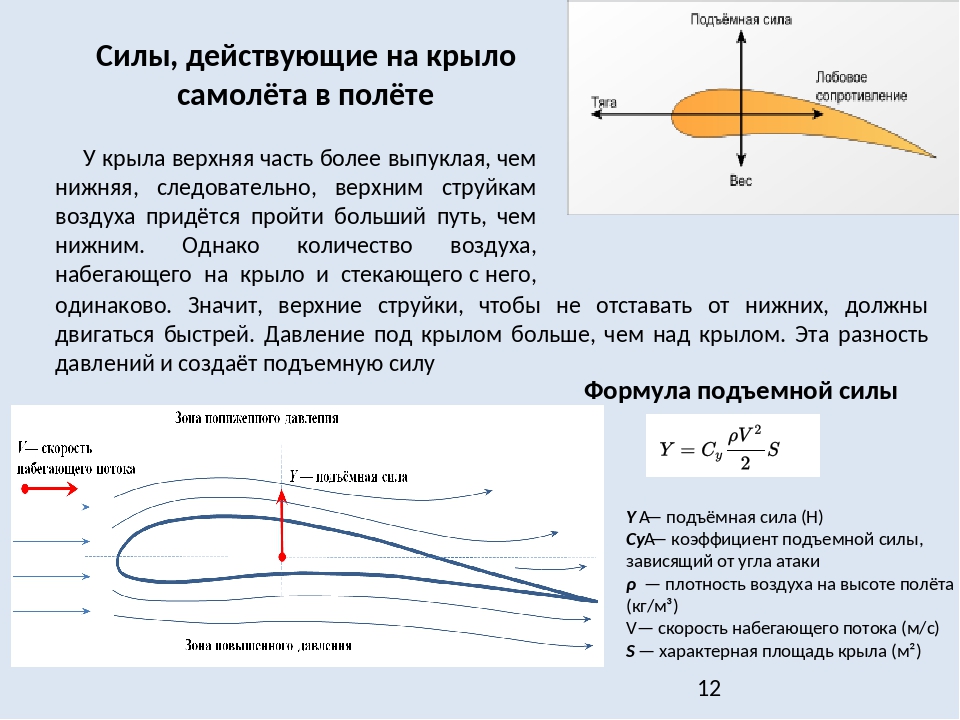 Поскольку аэродинамическое сопротивление есть сила, с которой газ действует на частицы (и соответственно по третьему закону Ньютона —частицы на газ), то при равенстве сопротивления и веса слоя частицы (если рассматривать идеальный случай) опираются не на решетку, а на газ. [c.143]

В реальных условиях все процессы в ГТУ являются неравновесными, что связано с потерями работы в турбине и компрессоре, а также с аэродинамическими сопротивлениями в тракте ГТУ. На рис. 20.10 действительный процесс сжатия в компрессоре изображен линией /—2, а процесс расширения в турбине — линией, 3—4. Точками 2а и 4а отмечено состояние рабочего тела соответственно в конце равновесного адиабатного сжатия и расширения, точкой О — параметры окружающей среды. [c.174]

Исследование аэродинамического сопротивления этих двух правильных укладок с одинаковым значением т = 0,259 пока- [c.52]

Шар, к которому по форме приближаются многие твердые компоненты потоков газовзвеси, является плохо обтекаемым телом. Безотрывное обтекание сохраняется лишь при невысоких числах Rex, а положение точки отрыва пограничного слоя от поверхности зависит от режима обтекания, т. е. от Ret- Соответственно меняется и закон сопротивления, который оценивается коэффициентом аэродинамического сопротивления Сш, учитывающим как силы трения, так и разность сил давления в лобовой и кормовой частях шара. [c.47]

Определив экспериментально Va, можно затем оценить коэффициент аэродинамического сопротивления по выражению (2-1) [c.50]

При противоточном падении частиц в камере с тормозящими элементами общий коэффициент аэродинамического сопротивления можно оценить по правилам оценки местного сопротивления, представив его как сумму трех слагаемых [c.131]

Коэффициент аэродинамического сопротивления, вызванного наличием движущейся насадки, [c.134]

На рис. 5-7 четко различаются две области теплообмена переходная область при 50400- 500. Эти границы согласуются с диапазоном первой переходной и автомодельной областей аэродинамического сопротивления движущихся частиц неправильной формы (гл. 2). [c.165]

Величина А в формуле (6-17) раскрыта на основе обработки данных работ [Л. 225, 309, 362, 380], поскольку в них наряду с теплообменом изучалось и аэродинамическое сопротивление (см. 6-11). [c.191]

Для флюидных дисперсных потоков, формирующихся при 0,03плотным слоем. Вопросы аэродинамического расчета кратко рассматриваются в (Л. 255, 289, 322]. По данным [Л. 225,] для 60[c.249]

В зависимостях (8-16)—(8-18) удивляет полное отсутствие скоростей компонентов потока газа и твердых частиц. Из предыдущего анализа данных об аэродинамическом сопротивлении и теплообмене известно влияние на них чисел Рейнольдса и Фруда для компонентов потока. В рассматриваемой обработке они отсутствуют, хотя пределы изменения плотности смеси охватывают и обычный пневмотранспорт. Наличие числа Ргв в формуле (8-18) не исправляет положения, так как этот критерий построен не по абсолютной, а по взвешивающей скорости движения частиц. Само определение этой скорости в [Л. 51] по закону Стокса также вызывает серьезные возражения. Дело не только в том, что, частицы, близкие к верхней границе указанных пределов (dt 0,45 мм), никак не подчиняются закону Стокса. Более важна сильная зависимость взвешивающей скорости от объемной концентрации. При концентрациях, охватываемых формулой (8-18), возможно значительное (в 2 и более раз ) падение скорости Va по сравнению 260 [c.260]

Для расчета аэродинамического сопротивления восходящего плотного слоя выражение (4-36 ) упрощается и видоизменяется. Коэффициентом сопротивления чистого газа можно пренебречь. Тогда, по-прежнему относя для удобства расчета коэффициенты сопротивления к скорости несущей фазы, определенной на полное входное сечение, имеем [c.280]

Помимо задач выравнивания неоднородных потоков в аппаратах и других различных устройствах, часто возникает необходимость преобразовать одну форму профиля скорости в другую. Например, в аэродинамических трубах с равномерным (прямолинейным) потоком иногда требуется создать для испытуемой в рабочей части модели кинематически подобную схему полета по кривой траектории. Этого можно достичь [26, 37], во-первых, изогнув особым образом модель и, во-вторых, создав поперек рабочего сечения трубы постоянный градиент скорости. Такое распределение скоростей может быть получено, например, при испытании решетки с переменным по сечению сопротивлением (переменной густотой). [c.11]

Однако многочисленные наблюдения и исследования показывают, что при определенных условиях роторы начинают вибрировать и при скоростях, отличных от критических.. 9ти гямовоз-буждающиеся колебания не связаны непосредственно с наличием неуравновешенности или других возмущающих воздействий. Причинами, вызывающими эти вибрации, являются силы трения между поверхностями движущихся твердых тел, силы внутреннего трения в материале, силы сопротивления аэродинамического и электромагнитного происхождения и т. д. Эти силы в зависимости от характера их действия, скорости вращения ротора и ряда других причин могут или стабилизировать движение и ограничивать амплитуды колебаний при резонансе, или, наоборот, вызывать раскачку колебаний. По существу их нельзя называть силами сопротивления, так как при одном виде движения они могут быть силами сопротивления, при другом — движущими силами. Исследованию этих вопросов посвящена обширная отечественная и зарубежная литература. [c.196]

Коэффициент сопротивления диффузора определяется выражением (388), в котором угол р находится по формуле (391) при к = . Перейдем теперь к оценке обратного сопротивления аэродинамического клапана. Это сопротивление складывается из сопротивления конфузора, расширения потока в камере, входа, и расширения потока за сжатым сечением с — с. Следовательно, коэффициент обратного сопротивления может быть представлен как сумма коэфпциептов перечисленных сопротивлений [c.283]

Поляра самолета, определяемая величинами и Л, изменяется в зависимости от внешней конфигурации самолета. Подвеска внешних объектов типа ракет и бомб, выпуск шасси, закрылков, тормозных щитков и т. п. могут привести к существенным изменениям величины коэффициента лобовош сопротивления, аэродинамического качества, а также к изменениям несущих свойств и других характеристик самолета. Так, например, за счет подвески внешних объектов, которые увеличивают коэффициент самолета на величину ДС , относительное изменение максимального аэродинамического качества /Стах и наивыгоднейшего коэффициента подъемной силы может быть оценено по сле- [c.22]

Более полное использование теплоты продуктов сгорания привело к значительному снижению температуры уходящих газов, и установка дополнительных поверхностей нагрева (водяного экономайзера и воздухоподогревателя) и золоуловителей увеличила аэродинамическое сопротивление тракта уходящих газов. В этих условиях удаление газов стало возможным только за счет работы дымососа, а функция дымовой трубы свелась к рассеянию вредных веществ (золы, токсичных газов) с больщой высоты по-возможности над большей территорией для уменьщения их концентрации. [c.217]

Коэффициент аэродинамического сопротивления винтовых сетчатых вставок вс на основе полученных в [Л. 21] опытных данных три / = 0,30- 0,66% dold = = 3,35н-7,7 Re = (1,98 3,2) 10 , п = 5,33 может быть определен по формуле [c.134]

Согласно данным гл. 2 о коэффициентах аэродинамического сопротивления (рис. 2-7), кварцевые частицы, использованные в опытах по теплообмену А. М. Николаевым и 3. Ф. Чухановым, Г. Н. Худяковым н 3. Ф. Чухановым, 3. Р. Горбисом [Л. 222, 307, 71], относятся к первой группе неправильных частиц. Поэтому коэффициент геометрической формы этих частиц принимается равным 1,2. При обработке данных [Л. 71] в области Reкоэффициенте сопротивления кварцевых частиц, использованных, в этой работе. [c.162]

Несмотря на определенное восполнение наших знаний о флюидных дисперсных потоках, последние нуждаются в специальных и всесторонних исследованиях. В первую очередь важно детально выяснить качественные изменения в структуре системы.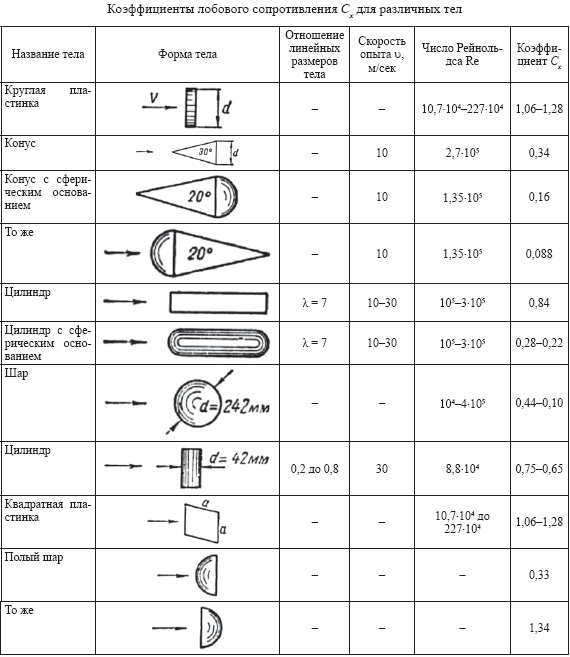 Здесь при повышенных концентрациях необходимо в новых условиях вернуться к проблеме возможного вырождения турбулентности несущей среды, к задаче о распределении локальной и средней истинных концентраций, к необходимости оценить вид и значение критического и оптимального обобщающего критерия (включающего и соответствующие концеИтрации), к методам расчета аэродинамического сопротивления и реологических свойств системы и пр. Иначе говоря, лишь знание гидромеханических свойств флюидных потоков позволит надежно и на основе достаточно общих закономерностей вести их расчет в качестве массо- и теплоносителей. Важность этих задач определяется тем, что именно здесь возможно 264 [c.264]

При этом скорость СЛОЯ, обеспечивающую движение в режиме плотного слоя, следует проверить по критическому числу Фруда Ргкр (гл. 9), а потерю давления можно рассчитывать по данным, приведенным в гл. 9. Диаметры теплообменных камер зависят от выбора величины скорости газа. Для камер типа слой эта величина в основном ограничивается допустимым аэродинамическим сопротивлением. Для прямоточных аппаратов типа газовзвесь скорость газа ограничена условиями беззавальной работы, а в противоточных — коэффициентом аэродинамического торможения А = у/ув, который должен быть из-за опасности уноса частиц меньше еди- [c.363]

Обнаружено, что в изотермических и неизотермических условиях сопротивление движущегося слоя практически не зависит от его скорости и близко к аэродинамическому сопротивлению неподвижного слоя с такой же пористостью. Режимные характеристики теплообменника расход греющих газов Gi = 300 2 ООО кг/ч расход нагреваемого воздуха 02 = 50 800 кг/ч расход насадки Gx = 200- 2 ООО кг/ч средние температуры греющих газов на входе / i =б00ч-1 400° С температуры нагрева насадки f x = 600-b 1 200° С температуры воздуха /»2 = = 200-ь980°С средние скорости фильтрации i = 3-v-8 л/се/с, воздуха г 2 = 0,5- 6,2 м1сек, насадки г т = 0,05- [c.380]

Для котла ТП-230 в ОТИЛ был проведен расчет компоновки всей конвективной части котла при замене газового обогрева обогревом кварцевым дисперсным теплоносителем.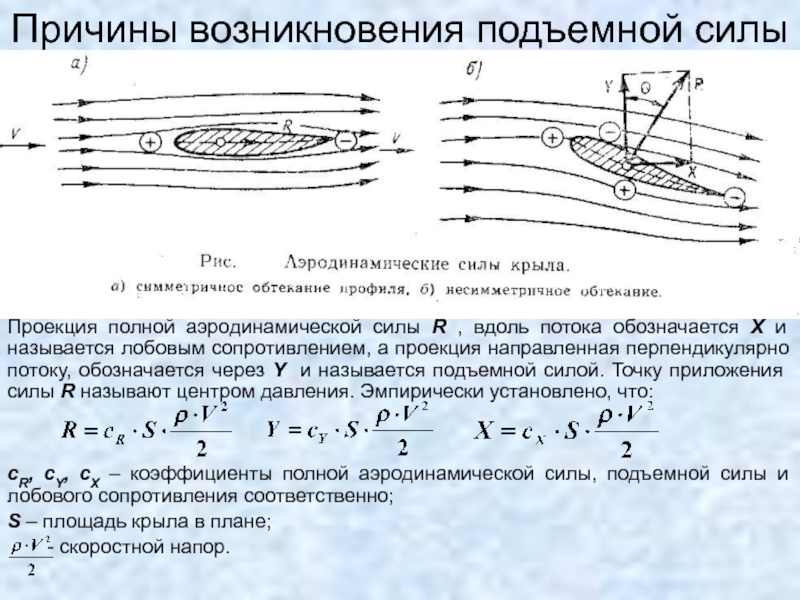 Согласно рис. 2-3 продукты сгорания топлива после пароперегревателя должны направляться не в опускную шахту, как обычно, а вверх — в камеру свободной газовзвеси, которая является не только противо-точной камерой нагрева дисперсной насадки, но и существенной частью дымовой трубы. При этом аэродинамическое сопротивление оо газовому тракту падает (до 130 кг м ), так как сопротивление противоточ- [c.387]

Стремление уменьшить поверхности регенераторов газотурбинных установок иривело к ряду схем с использованием промежуточного дисперсного теплоносителя. Разработка предложенной автором схемы по рис. 12-1 для ГТУ-50-800 показала принципиальную возможность уменьшения требуемой поверхности нагрева, заметного снижения аэродинамического сопротивления по газовому тракту и достижения компактности при расположении камеры газовзвеси в вытяжной дымовой трубе. Габаритные характеристики улучшаются заметно, если рекуперативную камеру для нагрева воздуха расположить над камерой противоточной газовзвеси.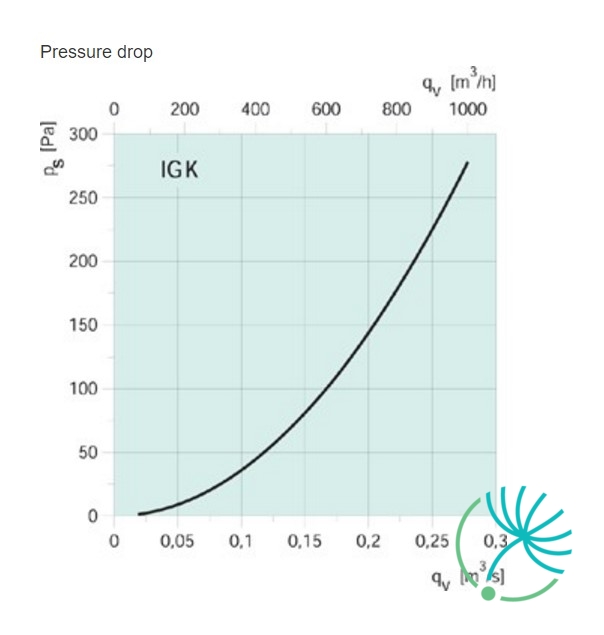 [c.389]

В раздающих коллекторах постоянного или переменного сечения с обычными ответвлениями (рис. 10.42) даже при выборе характеристики коллектора 4 = I 1 — ькР/к. обеспечивающей равномерное распределение скоростей (расходов) по всем ответвлениям, концентрация взвешенных в потоке частиц, особенно грубой пыли, распределяется неравномерно. Так как частицы обладают малым аэродинамическим сопротивлением, ответвляющийся поток не может их полностью увлечь за собой. Только в конце колл(жтора частицы, ударяясь о заглушенную стенку, теряют скорость и подхватываются потоком, идущим в последнее ответвление. Таким образом, в коллекторах указанного типа концентрация пыли в первых ответвлениях значительно меньще, чем в последнем, что не всегда желательно. Чтобы получить равномерное распределение взвешенных в потоке частиц, необходимо притормаживать их движение перед каждым ответвлением. Для этого можно использовать, например, устройство, изображенное на рис. 10.42, в. Внутри коллектора у каждого ответвления с помощью плавных козырьков, установленных над выходным отверстием, отсекается некоторая доля иылегазового потока. В работе [157] предложено выиустигь из боковых ответвлений в коллектор скошенные концы [c.320]

Расчет и подбор водяного калорифера для приточной установки

Коэффициент теплопередачи водяных калориферов КСк (предприятие-производитель ООО Т.С.Т., ТУ 4863-002-55613706-02) характеризуется интенсивностью и количеством теплового потока, передаваемого от греющего теплоносителя нагреваемому воздуху, в условиях вынужденной механической конвекции в обеих средах. В целях улучшения коэффициентов теплопередачи водовоздушных калориферов типа КСк 02 ХЛ3, и в целом процесса теплоотдачи, на металлические тепло несущие элементы в виде трубок, накатывается алюминиевое оребрение. Механическое деформирование наружной алюминиевой трубы приводит к увеличению теплонагревательной поверхности со стороны воздуха и обеспечивает надежный контакт между стальной трубкой и развитым алюминиевым оребрением. Улучшению значений коэффициентов теплоотдачи и процессов внешнего теплообмена способствует и расположение биметаллических трубок калорифера КСк в шахматном порядке. Это приводит к большей турбулизации воздушного потока, исключению из теплообмена застойных зон и увеличению коэффициентов теплопередачи водяного теплообменника модели КСк.

Расчет коэффициента теплопередачи водяных калориферов КСК

Коэффициент теплопередачи воздухонагревателей типа КСк находится двумя способами. Первый – по формуле, используя числовые коэффициенты данных приточных нагревателей, полученные при теплотехнических испытаниях. Второй способ определения – по рассчитанным показателям в таблице, принимая известные данные по массовой скорости воздуха во фронтальном сечении и скорости теплоносителя в трубках. Следует принять во внимание, что наиболее оптимальная массовая скорость для водяных калориферов КСк составляет 3.5 – 5.0 кг/м²•с, допустимые значения – от 2 до 8 кг/м²•с. Выбор массовой скорости воздуха зависит от многих факторов, среди которых: температура входящего воздуха, технические характеристики установленного вентилятора, разница температур на который необходимо нагреть воздух, схема компоновки калориферов и др.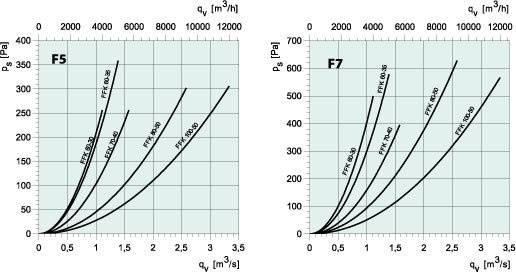 Оптимальные показатели скорости воды в трубках 0.2 – 0.5 м/сек. Превышение этого значения не приводит к значительному увеличению коэффициента теплопередачи, в то время, как гидравлическое сопротивление возрастает значительно. Также не рекомендуется принимать скорость теплоносителя менее 0.12 м/сек, из-за увеличения вероятности замораживания калориферов.

Формула для расчета коэффициента теплопередачи имеет вид:
К Вт/(м²•°С) = A • Vⁿ • Wᵐ
V — принятая массовая скорость воздуха, кг/м²•с; W — скорость движения горячей воды в трубках, м/сек; A, n, m — значение модуля и степеней из таблицы.

Расчетные значения для подсчета коэффициентов теплопередачи
КСк2 (2-х рядная модель)	A	n	m	КСк3 (3-х рядная модель)	A	n	m	КСк4 (4-х рядная модель)	A	n	m
КСк2 (2-х рядная модель)	33.3	0.383	0.175	КСк3 (3-х рядная модель)	29.3	0.437	0.168	КСк4 (4-х рядная модель)	25.5	0.496	0.160

Пример расчета 1.

Рассчитать коэффициент теплопередачи водяного калорифера КСк 4-9 с принятой массовой скоростью воздуха в фронтальном сечении – 4.2 кг/м²•с, и средней скоростью теплоносителя в трубках – 0.48 м/сек.
К Вт/(м²•°С) = 25.5 • 4.2^0.496 • 0.48^0.160 = 25.5 • 2.0377 • 0.8892 = 46.204 Вт/(м²•°C)
4.2 – принятая массовая скорость воздуха, кг/м²•с; 0.48 — скорость движения горячей воды в трубках, м/сек; 25.5, 0.496, 0.160 — значение модуля и степеней для калориферов КСк4 из таблицы.

Аэродинамическое сопротивление калориферов КСК

Формула для расчета аэродинамического сопротивления имеет вид:
ΔPa (Па) = B • Vʳ
V — действительная массовая скорость воздуха, кг/м²•с; B, r — значение модуля и степеней из таблицы.

Расчетные значения для подсчета аэродинамического сопротивления
КСк2 (2-х рядная модель)	B	r	КСк3 (3-х рядная модель)	B	r	КСк4 (4-х рядная модель)	B	r
КСк2 (2-х рядная модель)	4.23	1.832	КСк3 (3-х рядная модель)	6.05	1.832	КСк4 (4-х рядная модель)	8.63	1.833

Пример расчета 2.

Рассчитать аэродинамическое сопротивление двухрядного водяного калорифера КСк 2-7 при массовой скорости воздуха в фронтальном сечении равным 4.28 кг/м²•с
ΔPa (Па) = 4.23 • 4.28^1.832 = 60.7 Па
4.28 — действительная массовая скорость воздуха в фронтальном сечении, кг/м²•с; 4.23, 1.832 — значение модуля и степени из таблицы значений двухрядного воздухонагревателя.

Нахождение коэффициента теплопередачи и аэродинамического сопротивления по табличным данным

Пример расчета 3.

Рассчитать коэффициент теплопередачи и аэродинамическое сопротивление водяного воздухонагревателя КСк 3-6 с принятой массовой скоростью воздуха в фронтальном сечении – 3.5 кг/м²•с, и средней скоростью теплоносителя в трубках – 0.45 м/сек.
По таблице коэффициентов теплопередачи для калориферов трехрядных КСк3, находим графу с массовой скоростью 3.5 кг/м²•с. Опускаемся по колонке вниз до перекрестного пересечения с принятыми данными скорости воды. Берем значение 0.4 м/сек – 43.4 и значение 0.5 м/сек – 45.1, складываем эти показатели и делим полученную сумму пополам. Получается 44.25 Вт/(м²•°C). Это и есть искомое значение коэффициента при скорости водяного потока 0.45 м/сек.

В таблицах представлены числовые значения коэффициентов теплопередачи водяных калориферов КСк2 02 ХЛ3, КСк3 02 ХЛ3 и КСк4 02 ХЛ3 производства ООО Т.С.Т., в зависимости от массовой скорости воздуха в набегающем потоке и скорости движения теплоносителя по трубкам. Отдельной строкой выложены данные по аэродинамическому сопротивлению воздухонагревателей. Как видно из представленных таблиц, с увеличением рядности калориферов и массовой скорости аэродинамические потери возрастают.

Прилагаются формулы и таблицы, технические данные всех моделей воздухонагревателей. Каждый шаг подсчетов и вычислений сопровождается конкретным примером.

Описание, теплотехнические характеристики, сравнительные габаритные размеры, фотографии, чертежи, основные параметры.

Таблицы с выложенными данными по коэффициентам гидравлического сопротивления теплообменников данного вида.

Уравнение сопротивления

Перетаскивание зависит от плотности воздуха, квадрат скорости, вязкость и сжимаемость воздуха, размер и форма тело, и склонность тела к поток. В целом зависимость от формы тела, наклона, воздуха вязкость и сжимаемость очень сложны.

Один из способов справиться со сложными зависимостями — охарактеризовать зависимость от одной переменной.2

Для данного воздуха условий, формы и наклона объекта, мы должны определить значение Cd для определения сопротивления. Определение стоимости коэффициент лобового сопротивления сложнее, чем определение коэффициент подъемной силы из-за многократного источники сопротивления. Приведенный выше коэффициент лобового сопротивления включает форму сопротивление, сопротивление поверхностного трения, волновое сопротивление и компоненты индуцированного сопротивления. Торможение поршня обычно включается в чистую тягу, потому что оно зависит от воздушный поток через двигатель.Коэффициенты сопротивления почти всегда определенный экспериментально используя ветер туннель.

Обратите внимание, что площадь (A), указанная в уравнении сопротивления, задается как эталонный участок . Сопротивление напрямую зависит от размера тела. Поскольку мы имеем дело с аэродинамическими сил, зависимость может характеризоваться некоторой площадью. Но какой район мы выбираем? Если мы думаем, что сопротивление вызвано трение между воздухом и телом, логичным выбором будет общая площадь поверхности тела.Если мы думаем о перетаскивании как о сопротивление потоку, более логичным выбором будет фронтальная площадь тела, перпендикулярная направлению потока. А также наконец, если мы хотим сравнить с коэффициентом подъемной силы, мы должны использовать ту же площадь крыла, что и для расчета коэффициента подъемной силы. Поскольку коэффициент лобового сопротивления обычно определяется экспериментально путем измерения перетащите и область, а затем выполните деление, чтобы получить коэффициент, мы можем использовать любую область , которая может быть легко измеряется.Если выбрать площадь крыла, а не поперечное сечение области вычисленный коэффициент будет иметь другое значение. Но сопротивление такое же, а коэффициенты связаны соотношением области. На практике коэффициенты сопротивления сообщаются на основе большое разнообразие площадей объектов. В отчете аэродинамик должен указать используемую площадь; при использовании данных читателю, возможно, придется преобразовать коэффициент лобового сопротивления, используя соотношение площадей.

В приведенном выше уравнении плотность обозначена буква «р.»Мы не используем» d «для обозначения плотности, так как» d «часто используется указать расстояние. Во многих учебниках по аэродинамике плотность равна дается греческим символом «ро» (по-гречески «р»). Сочетание термин «плотность, умноженная на квадрат скорости, деленной на два»: называется динамическое давление и появляется у Бернулли уравнение давления.

Вы можете исследовать различные факторы, влияющие на перетаскивание, используя Java-апплет FoilSim III. (Удачи!) Используйте кнопку браузера «Назад», чтобы вернуться на эту страницу.если ты хотите, чтобы ваша собственная копия FoilSim поиграйте, вы можете скачать его на бесплатно.

Вы можете просмотреть короткий кино из «Орвилла и Уилбура Райтов» обсуждают силу сопротивления и как это повлияло на полет их самолета. Файл фильма может можно сохранить на свой компьютер и просмотреть как подкаст на проигрывателе подкастов.

Действия:

Экскурсии

Навигация..

Руководство для начинающих Домашняя страница

Уравнение сопротивления

Между 1900 и 1905 годами братья Райт спроектировали и построили три безмоторные планеры и три приведенный в действие самолет. В процессе проектирования им пришлось сделать некоторые математические оценки. подъемной силы и сопротивления их транспортных средств. Братья Райт были велосипедными механиками и имел хорошее практическое знание математики и естественных наук.Они знали о Законы Ньютона движения и о силы. Они знали, что им нужно произвести достаточно аэродинамический подъемник преодолеть масса своих самолетов. Они также знали математические уравнения который можно использовать для прогнозирования количества поднимать а также тащить, тянуть что объект сгенерирует.

На этой странице мы представляем современную версию уравнения сопротивления. Величина сопротивления, создаваемого объектом, зависит от количества факторы, включая плотность воздуха, скорость между объектом и воздух, вязкость и сжимаемость воздуха, размер и форма тела, и наклон тела к потоку.2 * А

В целом зависимость от формы тела, наклона, вязкость воздуха и сжимаемость очень сложны. Один из способов справиться со сложными зависимостями — охарактеризовать зависимость от одной переменной. Для перетаскивания эта переменная называется коэффициент лобового сопротивления, обозначенный «Cd». Во времена братьев Райт обычно ссылались на коэффициент лобового сопротивления. сопротивлению плоской пластины равной площади проекции. На другой странице мы показываем некоторые типичные значения коэффициента лобового сопротивления.Для самолета Райта базовый коэффициент лобового сопротивления был равен примерно 0,045.

Для заданных условий воздуха, формы и наклон объекта, мы должны определить значение Cd для определить сопротивление. Коэффициент лобового сопротивления состоит из двух частей; базовый коэффициент лобового сопротивления, который включает эффекты поверхностного трения и формы (формы) , и дополнительный коэффициент лобового сопротивления, связанный с подъемной силой самолета. Дополнительный источник сопротивления называется индуцированным сопротивлением . и производится на законцовках крыла за счет подъемной силы самолета.Из-за давления перепады выше и ниже крыла, воздух внизу крыла нарисованный сверху возле кончиков крыльев. Это создает закрученный поток который изменяет эффективный угол атаки по крылу и «наводит» тормоз на крыле. Коэффициент индуцированного сопротивления равен квадрат коэффициента подъемной силы (Cl) , деленный на количество: пи (3,14159) -кратное соотношение сторон (Ar) -кратное увеличение КПД (e) .В соотношение сторон это квадрат размах, деленный на площадь крыла. Для Прямоугольное крыло это сводится к соотношению размаха к хорде. Длинные, тонкие крылья с большим удлинением имеют меньшее индуцированное сопротивление, чем короткие толстые крылья с низким удлинением. Теория подъемной линии показывает, что оптимальное (наименьшее) индуцированное сопротивление возникает для эллиптического распределения подъема от кончика к кончику. Коэффициент полезного действия (е) равен 1,0. для эллиптического распределения и имеет значение меньше 1.2 / (пи * Ар * е)

Братья Райт узнали о индуцированном сопротивлении на собственном горьком опыте. Следующий их первые полеты на планерах 1900 г., они знали, что им нужно увеличить размер крыльев, чтобы позволить летать в разумные ветры. Для 1901 г. увеличили хорду крыла, но сохранил размах почти одинаковым. В результате получилось крыло с удлинением 3,0 и высокое индуцированное сопротивление. В братья сделали математические прогнозы характеристик своих самолетов.Но самолет 1901 года не оправдал своих прогнозов по дальности из-за того, что ожидаемый подъем и сопротивление выше ожидаемого. Зимой с помощью их в аэродинамической трубе они начали понимать роль вызванное лобовое сопротивление из-за плохих характеристик их самолета. Затем они разработали Крыло самолета 1902 года будет иметь больший размах и более короткую хорду чем самолет 1901 года. Соотношение сторон было изменено на 6.0 с почти таким же площадь крыла. Удвоив соотношение сторон, братья вдвое уменьшили индуцированное сопротивление.Самолет 1902 года смог выполнить поставленные задачи. и они смогли достичь высоты более 650 футов.

Помните, что определение сопротивления только часть дизайнерской проблемы. Вы обнаружите, что более высокий угол атаки создает большую подъемную силу, но также увеличивает сопротивление. Вы также обнаружите, что увеличение площади крыла увеличивает подъемную силу. Но в целом увеличение площади крыла также увеличивает вес и сопротивление. Дизайнеры обычно стараются оптимизировать отношение подъемной силы к лобовому сопротивлению.Это коэффициент полезного действия для самолета и обратно связан с угол скольжения. Самолет с высокой подъемной силой и лобовым сопротивлением может лететь на большие расстояния. при этом теряя лишь небольшую высоту. Райт понимал, что им нужен как высокий подъемник, так и низкое лобовое сопротивление.

Навигация ..

Возрождение пути Райта
Руководство по воздухоплаванию для новичков
Домашняя страница НАСА: http://www.nasa.gov

Аэродинамическое сопротивление — обзор

4.2 Аэродинамическое сопротивление маховикам

Момент аэродинамического сопротивления с обеих сторон вращающегося диска может быть выражен как: ^†

(4.1) Ma = ρgω2ro5Cm

Безразмерный коэффициент C _m является функцией трех других безразмерных параметров, а именно числа Рейнольдса R _e, числа Маха M и числа Кнудсена. К _№.

Число Рейнольдса настолько широко используется в технике, что не требует объяснения. В случае вращающихся устройств его значение обычно выражается как:

(4.2) Re = ro2ω / v = ρgro2ω / η

Также число Маха:

(4.3) M = roω / Vs

, где V _s — скорость звука, не требует дополнительных объяснений.

Число Кнудсена — это отношение длины свободного пробега молекул λ к размеру рассматриваемого объекта. В случае вращающихся дисков используется значение

(4.4) Kn = λ / ro

Если число Кнудсена очень низкое, как в случае маховика, работающего при атмосферном давлении, газ, окружающий диск, можно рассматривать как непрерывную среду.Если, наоборот, значение K _n высокое, можно предположить поток свободных молекул.

Соответствующее уравнение газа используется для расчета трех вышеупомянутых безразмерных параметров. Если газ ведет себя как «идеальный газ», можно использовать уравнение:

(4.5) p = ρgR * T

Значение константы R * = R / м _м для некоторых газов, которые могут использоваться в маховике, указано в таблице 4.1 вместе со значениями молекулярной массы m _m. Значение универсальной газовой постоянной R составляет:

ТАБЛИЦА 4.1. Параметры для расчета чисел Рейнольдса, Маха и Кнудсена с воздухом и другими газами

901 4,81 301 4,8

Газ	R * (Дж / кг · К)	м _м (кг / моль)	м (кг)	a (20 ° C) (м)	a _∞ (м)	T _c (K)	λ (20 ° C) , 1 торр) (m = 032)	η (20 ° C) (кг / мс) = (Pl)
Воздух	287.2	0,028 8	4,782 × 10 ⁻²⁶	3,68 × 10 ⁻¹⁰	—	113	4,56 × 10 ⁻⁵	1,81 × 10 ⁻⁵
O ₂	259,9	0,032	5,313 × 10 ⁻²⁶	3,60 × 10 ⁻¹⁰	2,96 × 10 ⁻¹⁰	132	2,03 × 10 ⁻⁵
N ₂	296.8	0,028 016	4,652 × 10 ⁻²⁶	3,70 × 10 ⁻¹⁰	3,20 × 10 ⁻¹⁰	112	4,50 × 10 ⁻⁵	1,50 × 10 ⁻⁵	−5
H ₂	4124,5	0,002016	3,347 × 10 ⁻²⁷	2,70 × 10 ⁻¹⁰	2.42 × 9024 −10	2.42 × 9024 −10 8,81 × 10 ⁻⁵	0.91 × 10 ⁻⁵
He	2077,2	0,004 003	6,646 × 10 ⁻²⁷	2,26 × 10 ⁻¹⁰	1,94 × 10 ⁻¹⁰	1,94 × 10 ⁻¹⁰	13,32 × 10 ⁻⁵	0,84 × 10 ⁻⁵

R = 8,315 Дж / моль K

Плотность газа можно легко вычислить из уравнения (4.5).

Динамическая вязкость газа η может быть рассчитана как функция длины свободного пробега молекул по соотношению:

(4.6) η = 13ρgυ¯λ

, полученное в предположении, что равновесное распределение скоростей является максвелловским. Поскольку это не совсем так для реальных газов, уравнение (4.6) может быть изменено как ^†:

(4.7) η≃12ρgυ¯λ

Средняя длина свободного пробега λ определяется как:

(4.8) λ = m / (2a2ρgπ)

, а средняя скорость по:

(4.9) υ¯ = 8KTπm

, где m — масса молекул ( m = m _m/ N _a, где N _a постоянная Авогадро

Na = 6.023 × 1023 моль − 1

и K — постоянная Больцмана

K = R / Na = 1,38 × 10−23 Дж / K

Эффективный диаметр молекулы a не совсем постоянный, но немного изменяется с температурой . Значения a при 20 ° C для различных газов приведены в Таблица 4.1 вместе со значением a _∞, относящимся к бесконечно высокой температуре, и постоянной Сазерленда T _c, необходимой для расчета. из a при разных температурах по формуле:

(4.10) a = a∞ (1 + Tc / T)

Средняя длина свободного пробега для различных газов при 20 ° C показана как функция температуры на Рис. 4.1 . Такие значения можно использовать для быстрого вычисления числа Кнудсена и вязкости, а следовательно, и числа Рейнольдса. Вязкость рассчитывается по формуле:

Рисунок 4.1. Зависимость длины свободного пробега некоторых газов от давления. Значения, рассчитанные для температуры 20 ° C

(4.11) η≃λρg (2KTπm) = KmTa2π3 / 2

Уравнение (4.11) выводится из уравнения (4.7) и исправлено отклонение распределения скоростей от максвелловского.

Другой формулой, которая позволяет рассчитать вязкость газа, является формула Сазерленда:

(4,12) η = AT3 / 2 / (B + T)

, где константы A и B зависят от типа газа. газ. Вязкость некоторых обычных газов при 20 ° C приведена в Таблица 4.1 .

Когда поток представляет собой реальный свободномолекулярный поток , то есть когда число Кнудсена превышает единицу, вязкость зависит как от давления, так и от температуры.Эта зависимость становится важной, однако, для значений давления, которые ниже, чем те, которые обычно встречаются в технологии маховиков.

Скорость звука, необходимая для вычисления числа Маха, составляет:

(4,13) Vs = (kR * T)

, где константа k — это отношение между удельной теплотой при постоянном давлении и удельная теплоемкость при постоянном объеме газа и принимает значение 1,4 для двухатомного газа и 1,66 для одноатомного.

В случае малых значений числа Кнудсена ( K _n ≪ 1), т.е.е. когда газ можно рассматривать как непрерывную среду, можно легко получить значение коэффициента крутящего момента C _м. Если можно предположить ламинарный поток в пограничном слое, следующая формула обычно принимается для тонких дисков постоянной толщины.

Если поток в пограничном слое является турбулентным, приближенная формула, полученная фон Карманом, имеет следующий вид:

(4,15) Cm = 0,146Re − 1/5

Эти уравнения построены на рис. 4.2 вместе с уравнением:

Рисунок 4.2. Коэффициент крутящего момента для тонкого диска постоянной толщины как функция числа Рейнольдса. Сообщалось также о некоторых экспериментальных точках.

(4,16) 1Cm = 1,97log (ReCm) +0,03

, которое можно использовать вместо уравнения (4.15) для случая турбулентного пограничного слоя. Также сообщается о некоторых экспериментальных результатах.

Переход между двумя типами потока в пограничном слое происходит при числе Рейнольдса 5 × 10 ⁴, но ламинарный поток может существовать во многих случаях даже при более высоких значениях, и экспериментальные результаты в переходной области вполне приемлемы. разбросанный.

Аэродинамическое сопротивление не зависит от числа Маха, но это верно только для маховика с тонкими дисками. Если число Кнудсена велико ( K _n> 10), поток можно рассматривать как свободномолекулярный поток, и была предложена следующая формула [74–6]:

(4,17) Ma = ρgωr4 / 2KTm

Отношение между «крутящим моментом» лобового сопротивления (вычисленным по уравнению (4.16) для ламинарной области и уравнением (4.15) для турбулентной области) и моментом, полученным из уравнения (4.17) был нанесен на , рис. 4.3, как функция числа Кнудсена.

Рисунок 4.3. Отношение между аэродинамическим крутящим моментом на тонком диске при различных значениях числа Кнудсена и крутящим моментом, вычисленным с помощью уравнения (4.17) для свободномолекулярного потока. Параметр кривых — M *, определяемый уравнением (4.19).

(Gu, A. [74–6])

В области, где число Кнудсена принимает значения 0,1 < K _n <10, поток нельзя рассматривать ни как непрерывный, ни как поток свободных молекул.В [74–6] пунктирные линии, нанесенные на рис. 4.3 , показаны для этой промежуточной области.

Кривые приведены с параметром M *, который строго связан с числами Маха:

(4.18) M * = roω / R * T = M / √k

Число Маха, по-видимому, влияет на сопротивление крутящий момент в области непрерывного потока, но это связано с тем, что момент в свободномолекулярной зоне, используемый для нормализации значений, полученных для различных условий, зависит от числа Маха.

На практике обтекание маховика является турбулентным при более высоких давлениях в корпусе и ламинарным в области среднего вакуума: 130 Па> p > 0,13 Па (1 Торр> p > 10 ⁻³ Торр). Только при очень низких значениях давления становится важным определенный эффект свободномолекулярного потока. Рисунок 4.3 дает первое приближение сопротивления.

Уравнение (4.1) часто перестраивается, чтобы позволить прямой расчет сопротивления, по крайней мере, при комнатной температуре.Вводя уравнения (4.15) и (4.16) в уравнение (4.1), можно получить следующие формулы:

(4.19) Ma = 3.87ro4√ (ρgηω3) (ламинарный, Re <5 × 104)

(4.20) Ma = 0,146ρg4 / 5ω9 / 5ro23 / 5η1 / 5 (турбулентный, Re≥5 × 104)

Приведенные выше уравнения действительны только в том случае, если диск вращается на открытом воздухе. Если, с другой стороны, диск заключен в кожух, то обычно можно предположить более низкое значение тормозящего момента.

Если зазор между диском и стенками корпуса очень мал, т.е.е. меньше толщины пограничного слоя, а число Рейнольдса достаточно низкое, чтобы предположить ламинарный поток, можно предположить течение Куэтта, и выражение коэффициента момента сопротивления становится очень простым:

(4,21) Cm = 2πrod1Re

где d — ширина зазора между боковыми поверхностями диска и стенками корпуса.

Это уравнение нанесено на Рис. 4.2 и, похоже, согласуется с экспериментальными результатами в полевых условиях вплоть до числа Рейнольдса, равного примерно 1.6 × 10 ⁴.

Линия и это значение R _o были получены с учетом значения d / r _o = 0,02 и зависят от значения этого отношения. В случае, показанном на рис. 4.21 , наличие корпуса снижает аэродинамическое сопротивление, если число Рейнольдса превышает 7 × 10 ³.

Рисунок 4.21. Система маховика для автомобильного применения, в которой весь корпус подвешен таким образом, что вращение после удара не сдерживается.

(1) Обод из композитного материала; (2) ступица; (3) Вал; (4) подшипники и корпус уплотнения; (5) втулка; (6) Монтажные кронштейны; (7) Стороны вакуумного кожуха; (8) Шов для уплотнения и разборки; (9) Радиальные элементы жесткости / аэродинамические тормоза. (10) Защитное кольцо из спиральной стальной ленты.

(Саповит, AD и др. . [80–68])
Толщина пограничного слоя для случая диска в набегающем потоке с ламинарным пограничным слоем составляет:
(4,22) δ = √ (v / ω )
и, следовательно, не зависит от радиуса.
Если число Рейнольдса больше, чем ранее вычисленное, и зазор между диском и контейнером меньше, чем толщина пограничного слоя, значение коэффициента C _m может быть вычислено с использованием простых формул :
(4,23) Cm = 2,67Re − 1/2 (ламинарный поток, Re <3 × 105)
(4,24) Cm = 0,0622Re − 1/5 (турбулентный поток, Re> 3 × 105)
значение числа Рейнольдса, при котором происходит переход между течением Куэтта (уравнение (4.21)) и имеет место ламинарный поток (уравнение (4.23)), можно получить из пересечения двух линий (, рис. 4.2, ).
Эти уравнения соответствуют экспериментальным результатам, за исключением ошибки около 17% при высоких значениях числа Рейнольдса; это можно отнести к сделанным предположениям.
Следует отметить, что сопротивление не зависит от ширины зазора d при условии, что зазор меньше толщины пограничного слоя.В случае турбулентного пограничного слоя его толщина составляет:
(4,25) δ = r3 / 5 (v / ω) 1/5
Толщина пограничного слоя в этом случае не зависит от радиуса, а увеличивается мощностью 3/5.
Следует отметить, что пограничный слой, который довольно тонкий при высоких значениях числа Рейнольдса, становится толще, если диск эксплуатируется в вакууме. Тогда можно получить зазор, который меньше толщины пограничного слоя, даже если между ротором и корпусом должен быть оставлен большой зазор, например.грамм. если ротор подвешен на системе с низкой жесткостью.
Вводя плотность энергии маховика и отношение ζ между радиусом инерции r _j и внешним радиусом маховика, уравнения (4.19) и (4.20) дают момент сопротивления как функцию энергии плотность:
(4,26) млн лет = 3,87 (ro5ρgηζ3) (2em) 3/4
(4,27) млн лет = 0,146 (ro14ρ4ηζ) 1/5 (2em) 9/10
Уравнения (4.26) и (4.27), которые справедливы только в случае тонкого диска в набегающем потоке с числом Кнудсена меньше примерно 0.1, показывают, что момент сопротивления увеличивается почти линейно с плотностью энергии и сильно зависит от радиуса (с мощностью 5/2 для ламинарного пограничного слоя и 14/5 для турбулентного потока).
С точки зрения аэродинамического сопротивления предпочтительны небольшие быстрые маховики. Если диск имеет постоянную толщину, но не очень тонкий, необходимо учитывать аэродинамическое сопротивление боковой поверхности цилиндра. Простой способ учесть влияние боковой поверхности диска — это умножить коэффициент момента, полученный в предположении тонкости диска, на коэффициент:
(ro + 52h) / ro
, где h — толщина диск (55–1).
Все эти уравнения относятся к дискам постоянной толщины, и, похоже, очень мало работы было сделано с дисками определенной формы. Если изменения толщины не очень велики, в расчетах можно принять диск постоянной толщины с таким же внешним радиусом и толщиной. Роторы со спицами или частями, выступающими из обода, представляют более серьезные проблемы; но насколько известно, этот случай не изучался в контексте технологии маховиков.
Необходимо экспериментально измерить коэффициент момента сопротивления в каждом конкретном приложении и исследовать его зависимость от всех трех параметров — чисел Рейнольдса, Кнудсена и Маха.Это может быть довольно сложно в случае работы в высоком вакууме, когда необходимо измерять очень малые значения сопротивления. Один из методов проведения этих испытаний — контролировать замедление вращения маховика в контролируемых условиях. Из измеренного закона скорости-времени можно оценить аэродинамическое сопротивление:
(4,28) Ma = dωdt (Jf + Js) −Ms
M _s и J _s, соответственно, общий момент сопротивления, действующий на систему, кроме аэродинамического (из-за подшипников, уплотнений и т. д.), и момент инерции всех вращающихся частей, соединенных с маховиком. Насколько известно в настоящее время, основные проблемы связаны с точностью, с которой возможно выполнить функцию производной уравнения (4.28), и, прежде всего, с оценкой момента сопротивления M _s.
M _s можно оценить, выполнив серию тестов на замедление вращения системы без маховика. Однако необходимо использовать некоторый балласт, чтобы нагружать подшипники с силой, равной той, которая присутствует во время фактического испытания.Однако в этом испытании энергия, рассеиваемая в амортизаторах, не учитывается точно, поскольку динамическое поведение системы с маховиком не совпадает с поведением системы с балластом, и легко могут быть внесены другие ошибки. Обычно они не имеют большого значения, если аэродинамическое сопротивление намного больше, чем сопротивление из-за других компонентов системы, но может стать настолько большим, что результаты будут совершенно бесполезными в случае работы в высоком вакууме.
Результаты некоторых тестов на замедление вращения, проведенных автором на маховике, аналогичном показанному на Рис. 3.34 показаны на Рис. 4.4 (а) . Значения являются результатом наилучшего соответствия по многим экспериментальным точкам. Следует отметить, что точность можно считать хорошей в турбулентной области, в то время как линия, полученная в ламинарной области, должна рассматриваться только для оценки порядка величины, особенно при низких значениях числа Рейнольдса. Для сравнения приведены теоретические кривые для тонкого диска постоянной толщины.
Рисунок 4.4. Момент аэродинамического сопротивления на субциркульном маховике, аналогичном показанному на рис. 3 .34 .
(a)
Экспериментальные значения, полученные в результате испытаний на замедление вращения при очень малых значениях числа Кнудсена и M _a ≪ 1. Эффект стенки не учитывается. Из-за использованной экспериментальной техники значения для очень малых чисел Рейнольдса являются только ориентировочными.
(b)
Потери мощности из-за аэродинамического сопротивления, вакуумных насосов и системы управления, измеренные на экспериментальной установке для выравнивания пиков Pirelli-CNR ( Рисунок 2.6 ). Устройство рассчитано на 100 кВт и хранит 5 кВтч. Поскольку система не оптимизирована, потери, отличные от аэродинамических, могут быть уменьшены.
Мощность, теряемая из-за аэродинамического сопротивления ротора Pirelli – C.N.R. Экспериментальная система выравнивания нагрузки на маховике (см. , рис. 2.6, ) показана как функция скорости на , рис. 4.4, ( b ). Также показаны потери мощности по другим причинам.
Коэффициент сопротивления
Любой объект, движущийся в жидкости, испытывает сопротивление — чистую силу в направлении потока из-за давления и сил касательного напряжения на поверхности объекта.
Сила сопротивления может быть выражена как:
F _d = c _d 1/2 ρ v ² A (1)
где
F _d = сила сопротивления (Н)
c _d = коэффициент лобового сопротивления
ρ = плотность жидкости (1,2 кг / м ³ для воздуха в NTP)
v = скорость потока (м / с)

A = характерная фронтальная площадь кузова (м ²)

Коэффициент лобового сопротивления является функцией нескольких параметров, таких как форма тела , Число Рейнольдса для потока, число Фруда, число Маха и шероховатость поверхности.
Характеристика лобовой поверхности — А — зависит от кузова.
Коэффициенты сопротивления объектов в большинстве своем являются результатами экспериментов. Коэффициенты лобового сопротивления для некоторых распространенных кузовов указаны ниже:
0,15 передняя часть мотоцикла 1,8
Тип объекта Коэффициент сопротивления
— c _d — Фронтальная площадь
Ламинарная плоская пластина (Re = 106) 0,001
Дельфин 0.0036 смачиваемая зона
Плоская турбулентная пластина (Re = 106) 0,005
Дозвуковой транспортный самолет 0,012
Сверхзвуковой истребитель, M = 2,5 0,025 Обтекаемый корпус 0,04 π / 4 d2
Крыло самолета, нормальное положение 0,05
Половина обтекаемой формы 0.09
Длинный обтекаемый кузов 0,1
Веломобиль — обтекаемый Веломобиль 0,12 5 футов ² (0,47 м ²)
Современный автомобиль, такой как модель Tesla 3 или модель Y 0,23
Toyota Prius, модель Tesla S 0,24 лобовая зона
Tesla модель X 908 Спорткар, наклонная задняя часть 0.2 — 0,3 передняя часть
Обычный автомобиль, такой как Opel Vectra (класс C) 0,29 передняя часть
Полая полусфера, обращенная к потоку 0,38
Bird передняя часть
Solid Hemisphere 0,42 π / 4 d2
Sphere 0,5
Седан со ступенчатой задней частью 0.4 — 0,5 спереди
Велосипед — тяга за другим велосипедистом 0,5 3,9 фута ² (0,36 м ²)
Кабриолет с открытым верхом 0,6 — 0,7 Фронтальная зона
Автобус 0,6 — 0,8 Фронтальная зона
Старый автомобиль как Т-брод 0,7 — 0,9 Фронтальная зона
Cube 0.8 s2
Велосипед — гоночный 0,88 3,9 фута ² (0,36 м ²)
Велосипед Грузовик 0,9
Тягач передний площадь
Грузовик 0,8 — 1,0 передняя часть
Стоящий человек 1,0 — 1,3
Велосипед — вертикальный пригородный поезд 1.1 5,5 футов ² (0,51 м ²)
Тонкий диск 1,1 π / 4 d2
Поток в твердом полусфере перпендикулярно плоской стороне 2 1,17 π
Квадратная плоская пластина под углом 90 градусов 1,17
Провода и кабели 1,0 — 1,3
Человек (вертикальное положение) 1,0 — 1,3 9024 Полый полуцилиндр против течения 1.2
Лыжный джемпер 1,2 — 1,3
Полусфера, противоположная потоку 1,42
Пассажирский поезд 1,8 передняя часть
Длинная плоская пластина под углом 90 градусов 1,98
Прямоугольная коробка 2,1
Пример — Сила сопротивления воздуха
, действующая на нормальную силу сопротивления 9128 Требуется для преодоления сопротивления воздуха нормальному семейному автомобилю с коэффициентом аэродинамического сопротивления 0.29 и площадь лобовой части 2 м ² дюйм 90 км / ч можно рассчитать как:
F _d = 0,29 1/2 (1,2 кг / м ³) ((90 км / ч) (1000 м / км) / (3600 с / ч)) ² (2 м ²)

= 217,5 Н
Работа по преодолению сопротивления воздуха за один час движение (90 км) можно рассчитать как
Вт _d = (217,5 Н) (90 км) (1000 м / км)
= 19575000 (Нм, Дж)
Мощность, необходимая для преодоления Сопротивление воздуха при движении 90 км / ч можно рассчитать как
P _d = (217.5 Н) (90 км / ч) (1000 м / км) (1/3600 ч / с)
= 5436 (Нм / с, Дж / с, Вт)
= 5,4 (кВт)
Аэродинамическое сопротивление
Аэродинамическое сопротивление
Брэдфорд Зеллер
B / Z Motorsports
Когда вы устанавливаете крыло на гоночную машину, и она движется по воздуху, крыло прижимает машину к поверхности трассы, обеспечивая большее сцепление. Но помните, что в жизни нет ничего бесплатного. Этим вы также увеличили коэффициент лобового сопротивления автомобиля, и двигатель должен преодолеть это сопротивление.Неважно, болид это Formula Vee или Indy, двигатель теперь должен делать больше работы, чтобы толкать машину по воздуху. Все предметы, включая тело, имеют тот же эффект, что и крыло. Каждый маленький предмет, застрявший в воздушном потоке, вызывает сопротивление. Насколько важна головка болта? Посмотрим на цифры.
Существует основное уравнение силы, необходимой для проталкивания чего-либо в воздухе:
Аэродинамическое сопротивление = 1 / 2DAV²
В этом уравнении D — это плотность воздуха, A — фронтальная площадь, а V — скорость.
Для реальных форм тела, воздуха при стандартных условиях, V в милях в час и сопротивления в фунтах силы это уравнение принимает вид: Drag = 1/391 CdAV²
Это уравнение показывает, что для расчета сопротивления вам необходимо знать три вещи: Cd сопротивление коэффициент, A — площадь лобовой части того, что проходит через воздух, и скорость воздуха, проходящего мимо него. Это уравнение показывает важный момент. Аэродинамические силы пропорциональны квадрату скорости. Другими словами, вы увеличиваете сопротивление в четыре раза, когда удваиваете скорость.
Коэффициент аэродинамического сопротивления Cd важен, потому что вместе с площадью лобовой части он определяет затраты энергии на проталкивание фигуры через воздух с определенной скоростью.Автомобиль с небольшой площадью лобовой части и низким Cd будет иметь более высокую максимальную скорость, чем квадратный автомобиль с такой же мощностью.
Вы тратите тысячи долларов на двигатель, чтобы получить больше лошадиных сил. Сколько ты тратишь зря? Посмотрите на свою машину и посмотрите, сколько вещей торчит в воздушном потоке.
Об авторе:
Брэд Зеллер занимается разработкой гоночных автомобилей более 50 лет. Его аэродинамический опыт был применен к победам на чемпионате мира WKA и на последних этапах SCCA.С ним можно связаться по адресу [email protected]
. Для получения дополнительной информации об аэродинамике щелкните здесь. Для получения дополнительной информации: [email protected] Дизайн: B / Z Technologies. Авторское право, 1999 — 2021 гг., B / Z Technologies. Все права защищены.
Aerodynamic Drag — веб-сайт Крейга на Backfire.ca
Аэродинамическое сопротивление
Из http://craig.backfire.ca/pages/autos/drag
Введение
Все объекты обладают определенным аэродинамическим сопротивлением. В этой статье я рассмотрю, как перетаскивание влияет на способность автомобиля ускоряться и максимальная скорость.Я не буду освещать фактическое изучение автомобильная аэродинамика в деталях.

Теория
Мощность
Мощность определяется как скорость передачи энергии, или темп работы. Двигатель автомобиля производит определенное количество силы, которое может быть использовано для достижения определенного количество силы на определенной скорости. Я буду использовать лошадиных сил как единица измерения мощности.
Одна лошадиных сил составляет 33000 фут-фунт-сила в минуту, как определено Джеймсом Ваттом.Агрегаты для лошадиных сил могут быть изменены, пока они остаются продуктом силы и расстояние с течением времени, и используются любые необходимые константы преобразования единиц. Ниже приведены единицы измерения мощности, наиболее подходящие для работа с аэродинамикой.
Определение одной лошадиных сил в единицах измерения преобразовано, чтобы показать силу на определенной скорости в миль в час.
Из приведенного выше уравнения видно, что двигатель мощность в одну лошадиную силу может составлять 375 фунтов силы на 1 милю в час, или 1 фунт-сила при 375 милях в час или любое другое равное произведение силы и скорости.Затем формулу можно изменить, чтобы получить сила от скорости и мощности, как показано ниже.
Силу можно рассчитать, когда мощность и скорость известны.
Перетащите
Сила сопротивления объекта зависит от следующего:
Плотность жидкости, ρ .
Плотность зависит от температуры и давления жидкости ρ (T, p) .
Квадрат скорости жидкости, v .
Коэффициент лобового сопротивления объекта, C _d , безразмерный параметр.
Фронтальная площадь объекта, А .
Коэффициент лобового сопротивления, C _d , является безразмерным параметром. который описывает, какое сопротивление вызывает поток жидкости на объекте. Большее значение C _d означает, что объект имеет большее сопротивление.
Свойства перетаскивания объекта зависят от форма и размер объекта.
Сила перетаскивания объекта происходит от его перетаскивания. коэффициент умноженный на площадь лобовой части вместе со скоростью и плотность жидкости, как показано ниже в уравнении сопротивления :
Уравнение сопротивления, модифицированное для использования с юнитами обычно используется с автомобилями.
Сила сопротивления присутствует на скорости, что означает, что сопротивление использует силу. В то же время, двигатель производит мощность на скорости, а это значит, что он проявляет силу. Сила, которую может использовать автомобиль ускорение — это сила, доступная после некоторого был использован для давления на воздух. Потому что скорость воздуха такая же, как и скорость автомобиля (в условиях безветренной погоды), силу двигателя и силу воздуха можно сравнить напрямую.
Двигатель проявляет силу, в то время как аэродинамическое сопротивление противостоит силе двигателя.Оставшаяся сила от двигателя используется для разгона.
Разгон и максимальная скорость
На очень низких скоростях эффекты аэродинамического сопротивления минимальны. В то же время двигатель может очень большое усилие на низких скоростях, а это означает, что сила ускорения будет высокой. На более высоком скорости, сопротивление увеличивается, и двигатель сила уменьшается. В конце концов, сила сопротивления и сила двигателя станет равной, не оставив силы уехал на разгон. Именно с такой скоростью автомобиль, как говорят, достиг своего ограниченного сопротивления максимальная скорость.
На приведенном выше графике показано усилие, которое двигатель может проявить, а сила за счет аэродинамического тащить, тянуть. Когда сила сопротивления станет равной сила, которую может проявить двигатель, автомобиль достигает максимальной скорости с ограничением по лобовому сопротивлению. В этом случае максимальная скорость автомобиля составляет примерно 150 миль в час.
На приведенном выше графике показана сила, доступная для добавлено ускорение после перетаскивания. Когда сила равна нулю, ускорения больше нет.
Если мощность и лобовое сопротивление автомобиля известны, ограниченное сопротивление максимальная скорость может быть рассчитана путем объединения уравнения сопротивления с уравнением мощности, как показано ниже:
Максимальную скорость можно определить по мощности и сопротивление транспортного средства, установив силу сопротивления равной к силе двигателя.
Сравнение
Чтобы показать эффект сопротивления транспортного средства, я сделаю простое сравнение. На этот раз я буду использовать автомобили прямо из автопарка моей семьи: супра 87 года моего отца и мой Caprice 82 года.
Претенденты: Toyota Supra Turbo 1987 года выпуска со скользким кузовом. против Chevy Caprice 1982 года с квадратным кузовом.
Для этого сравнения я добавлю немного мощности к Каприз. Сейчас у него 180 л.с., но я его дам 247 л.с. для этого эксперимента, чтобы получить такую же удельную мощность соотношение, как у Supra.Это будет сделано, чтобы убрать эффекты разница в весе между машинами. Я также сделаю предположение что машины могут сбрасывать максимальную мощность на любой скорости, что устранит влияние трансмиссии. Наконец, силы ускорения отображаться не будут, потому что все значения были бы бессмысленны при применении этих предположений.
Ниже представлена таблица с соответствующими значениями для автомобилей.
Supra Caprice
Мощность 230 л.с. 247 л.с.
Масса 3500 фунтов (1.75тонн) 3760 фунтов (1,88 тонны)
Удельная масса 131 л.с. / тонну 131 л.с. / тонну
Коэффициент сопротивления (Cd) 0,340 0,410
Фронтальная зона (A) 20,56 футов ² 24,66 футов ²
Перетащите (CdA) 6,99 кдфут ² 10.11Cdft ²
Функция перетаскивания 32,90 л.с. / куб. Фут ² 24,43 л.с. / куб. Фут ²
Используя значения из приведенной выше таблицы и приведенные ранее уравнения, производительность автомобилей может быть определена на любой скорости транспортного средства. Ниже это таблица, в которой сравниваются два автомобиля рядом. Способность к ускорению относится к соотношению доступной мощности для ускорения и веса автомобиля.
Supra Caprice
Скорость (миль / ч) Перетяжка HP Ускорение HP Accel HP: Масса (л.с. / тонна) Перетяжка HP Ускорение HP Accel HP: Масса (л.с. / тонна)
1 0,00 230 131 л.с. / тонну 0.00 247 131 л.с. / тонну
20 0,40 229.60 131 л.с. / тонну 0,58 246,42 131 л.с. / тонну
50 6,27 223,73 128 л.с. / тонну 9,21 237,79 126 л.с. / тонна
70 17.21 212,79 122 л.с. / тонну 24,89 222,11 118 л.с. / тонну
100 50,18 179,82 103 л.с. / тонну 72,58 174,42 93 л.с. / тонну
140 137,69 92,31 53 л.с. / тонну 199,15 47.85 25 л.с. / тонна
150 169,36 60,64 35 л.с. / тонна 244,95 Нет Нет
166 229,54 Нет Нет –
Из таблицы выше видно, что обе машины имеют одинаковое ускорение на низких скоростях, но по мере увеличения скорости и увеличения сопротивления менее аэродинамичный автомобиль начинает падать. позади.Несмотря на то, что разница в максимальной скорости составляет всего 16 миль в час, Caprice проигрывает гонка со скоростью около 100 миль в час, что намного ниже максимальной скорости любого автомобиля.
Графическое сравнение Supra и Caprice.
Чтобы Caprice разогнал Supra до максимальной скорости, потребуется около 332 л.с. 166 миль / ч. Конечно, если бы Caprice обладал такой мощностью, он бы сдул Supra. на более низких скоростях. Это показывает, что Caprice тратит много сил на борьбу с воздухом.
Практичность
Зубчатая передача
До сих пор в этой статье я предполагал, что автомобиль может показать свой пик. мощность независимо от того, с какой скоростью он движется.В реальной жизни это не так потому что двигатель автомобиля не всегда работает на максимальной мощности. Таким образом, автомобиль максимальная скорость может быть намного ниже ожидаемой. Как правило, автомобиль с множеством трансмиссий передачи на выбор смогут приблизиться к теоретической максимальной скорости, в то время как автомобиль с очень небольшим количеством передач может быть далеко, потому что двигатель будет далеко от своего пиковая мощность.
Некоторые автомобили, особенно очень старые высокопроизводительные, не достигают максимальной аэродинамической скорости. а скорее кончатся передачи.Если автомобиль на высшей передаче врезался в красную черту, не доехав до его максимальная скорость ограничена сопротивлением, автомобиль, как говорят, имеет максимальную скорость с ограничением передачи . Это не очень распространено в современных автомобилях, у которых много шестерен трансмиссии и осевой редуктор. настроен на экономию топлива.
Автомобиль всегда будет иметь максимальную скорость, равную максимальной скорости с ограничением передачи , или его максимальная скорость с ограниченным сопротивлением , в зависимости от того, что ниже.
Газ Пробег
Автомобилю требуется определенное количество лошадиных сил, чтобы двигаться в воздухе на скорости.Мощность в газовом двигателе вырабатывается за счет сжигания топлива, поэтому автомобиль с большим сопротивлением потребуется сжигать больше топлива, чтобы двигаться с той же скоростью, что и более аэродинамический автомобиль.
Аэродинамическое сопротивление зависит от квадрата скорость автомобиля, поэтому, если скорость автомобиля увеличивается вдвое, сопротивление увеличивается в четыре раза. Из этого следует, что сопротивление на скорости 70 миль в час вдвое превышает сопротивление на скорости 50 миль в час.
Сказав это, автомобиль не обязательно будет иметь лучший расход топлива на скорости 50 миль в час. чем 70 миль в час. Расход бензина зависит от многих других факторов, выходящих за рамки Объем этой статьи.
Торможение
Аэродинамическое сопротивление может использоваться для остановки автомобиля. Если бы кто-то водил их машина очень быстро, а затем внезапно включала сцепление, машина начинала замедляться, потому что сила аэродинамического сопротивления противодействует движению автомобиля. Сочетание силы сопротивления с силой торможения (и силы от трения) позволяет автомобилю замедляться на очень высокой скорость при движении на высоких скоростях. Вот почему некоторые спортивные автомобили имеют закрылки, которые поднимаются при торможении на высокой скорости.Откидные створки также могут помочь в устойчивость при торможении, помогая прижать задние колеса к тротуар.
Другие факторы
Есть много вещей, которые могут помешать проезду автомобиля это теоретическая максимальная скорость. Ниже представлен неполный список.
Трение между дорогой и шинами.
Мощность, используемая для создания импульса в колесах и другие движущиеся части.
Неустойчивость на высоких скоростях.
Отсутствие подходящего объекта (холмы и т. Д.).
Ветер.
Закон.
Заключение
Аэродинамическое сопротивление — важный фактор, влияющий на способность автомобиля ускоряться. На очень высоких скоростях, соотношение выходной мощности двигателя к сопротивлению кузова становится более важным, чем удельная мощность, что важно на более низких скоростях, когда сопротивление не является значительным. Предполагая, что у автомобиля подходящая передача, единственный способ Увеличение максимальной скорости должно улучшить аэродинамику или прибавить мощности. В идеальных условиях вес автомобиля составляет почти не влияет на максимальную скорость, только время, необходимое, чтобы добраться туда.
См. Также
Как я могу измерить сопротивление автомобиля?
Это отличный вопрос, который объединяет многое из того, о чем мы говорили в других статьях HowStuffWorks о перетаскивании. И, как оказалось, есть относительно простой способ узнать, сколько сопротивления имеет ваша машина.
В статье «Как работают сила, мощность, крутящий момент и энергия» вы узнали о втором законе Ньютона, который мы можем переформулировать следующим образом: сила ( F ) равна массе ( м ), умноженной на ускорение ( a ).
F = ma или a = F / m
F = ma или a = F / m
Это уравнение означает, что сила, приложенная к автомобилю, будет вызывать ускорение вашего автомобиля. Когда вы едете с постоянной скоростью, мощность, производимая двигателем, преобразуется в силу, действующую на шины. Сила сопротивления действует в противоположном направлении и равна силе, создаваемой двигателем на шинах. Поскольку эти силы равны и противоположны, суммарная сила , действующая на автомобиль, равна нулю, поэтому автомобиль сохраняет постоянную скорость.Если вы уберете силу, создаваемую двигателем (например, переведя автомобиль в нейтральное положение), то единственной силой, действующей на автомобиль, будет сопротивление. Поскольку на автомобиль действует чистая сила, он начинает замедляться.
Если вы можете измерить массу автомобиля и ускорение, то вы можете определить силу. Вы можете взвесить автомобиль на свалке, чтобы определить массу. И вы можете определить ускорение, измерив, сколько времени требуется автомобилю, чтобы замедлиться, когда вы включаете нейтраль.
Это поможет вам немного понять силы, действующие на машину, прежде чем вы начнете эксперимент.
Сила, толкающая машину по дороге, зависит от ее скорости. Оно следует уравнению следующего вида:
сила дорожной нагрузки = a + bv + cv2
сила дорожной нагрузки = a + bv + cv ²
Буква v представляет скорость движения car, а буквы a , b и c представляют три разные константы:
Компонент a не зависит от скорости.В основном это происходит из-за сопротивления качению шин и трения в компонентах автомобиля, например, сопротивления тормозных колодок или трения в ступичных подшипниках.
Компонент b также возникает из-за трения в компонентах и из-за сопротивления качению в шинах.
Компонент c в основном связан с такими факторами, которые влияют на аэродинамическое сопротивление, как лобовая поверхность, коэффициент лобового сопротивления и плотность воздуха.
Важным аспектом этого уравнения является то, что сила, действующая на автомобиль, очень быстро увеличивается на высоких скоростях.Сила, действующая на автомобиль на скорости 70 миль в час, намного выше, чем сила на скорости 60 миль в час.
Это означает, что мы хотим измерить ускорение в очень узком диапазоне скоростей. Что-то вроде 3 или 5 км / ч должно работать. Мы будем делать этот расчет в метрических единицах, потому что с ними легче работать.
Допустим, ваша машина имеет массу 2000 килограммов (кг), включая вас и вашу мать, и вы собираетесь проверить ускорение между 100 и 95 км / ч (что дает среднюю скорость 97,5 км / ч или около 60 миль / ч, так что сделайте это). это на автостраде, где ограничение скорости достаточно высоко).Вам следует выбрать ровный участок дороги с небольшой проходимостью и делать это в день, когда ветер спокойный и нет дождя.
Пусть ваша мама разгонит машину до 105 км / ч и приготовит секундомер. Скажите матери, чтобы она поставила машину на нейтраль, чтобы вы начали движение по инерции. Когда автомобиль замедлится до 100 км / ч, запустите таймер и остановите его, когда автомобиль разгонится до 95 км / ч. Вы можете повторить это несколько раз, возможно, двигаясь в другом направлении на одном и том же участке автострады. Записывайте все время и усредняйте их.
Допустим, среднее время составляло 10 секунд. Теперь у вас есть вся информация, необходимая для расчета силы сопротивления. Вам просто нужно сделать несколько преобразований. Вам нужно ваше ускорение в метрах в секунду, в секунду (м / с ²).
Ваш автомобиль замедлился на 5 км / ч, что составляет 5000 метров в час или 1,389 метра в секунду. Чтобы так сильно замедлиться, потребовалось 10 секунд, поэтому скорость ускорения составила 0,1389 м / с ^2.
Чтобы найти силу, просто подставьте массу и ускорение в уравнение F = ma .Здесь есть удобный преобразователь измерений.
Таким образом, сила этой гипотетической машины на скорости 60 миль в час составляет примерно 60 фунтов. Это также означает, что для того, чтобы автомобиль разогнался до 60 миль в час, двигатель должен производить достаточно мощности, чтобы создать силу на колесах в 60 фунтов.
Мы также можем выяснить, сколько это мощности. Мощность равна силе, умноженной на скорость. Итак, все, что нам нужно сделать, это умножить силу в ньютонах на скорость в метрах в секунду, это даст нам мощность в ваттах.
Средняя скорость вашего тестового запуска составила 97.5 км / ч, что составляет 27 метров в секунду. Таким образом, ваша мощность составляет 278 Н, умноженные на 27 м / с = 7500 ватт, или 7,5 киловатт, что составляет 10 лошадиных сил.

Расчет сопротивления сети вентиляции пример. Аэродинамический расчет воздуховодов приточной системы вентиляции

Схема приточной системы вентиляции, обслуживающей 3-этажное административное здание

Коэффициенты местных сопротивлений

Метод допустимых скоростей

Метод постоянной потери напора

Поведение среды внутри воздухопровода

Физический смысл параметра

Расчеты параметра по формулам

Определение параметров местных сопротивлений вентиляционной системы

Сопротивление аэродинамическое — Энциклопедия по машиностроению XXL

Расчет и подбор водяного калорифера для приточной установки

Расчет коэффициента теплопередачи водяных калориферов КСК

Аэродинамическое сопротивление калориферов КСК

Уравнение сопротивления

Уравнение сопротивления

Аэродинамическое сопротивление — обзор

4.2 Аэродинамическое сопротивление маховикам

Коэффициент сопротивления

Пример — Сила сопротивления воздуха

Аэродинамическое сопротивление

Aerodynamic Drag — веб-сайт Крейга на Backfire.ca

Введение

Теория

Мощность

Перетащите

Разгон и максимальная скорость

Сравнение

Практичность

Зубчатая передача

Газ Пробег

Торможение

Другие факторы

Заключение

См. Также

Как я могу измерить сопротивление автомобиля?

F = ma или a = F / m

сила дорожной нагрузки = a + bv + cv2

Добавить комментарий Отменить ответ