Расчет средней скорости автомобиля: Какова средняя скорость автомобиля , если за первые 3ч он проехал 80км , а следующие…

Как найти среднюю скорость автомобиля после поездки в разных режимах?

Часто водителю необходимо отыскать такой важный показатель, как средняя скорость автомобиля после той или иной поездки. Иногда эта цифра будет важным фактом для водителя транспорта компании, а в иных случаях — просто интересное число для владельца транспортного средства. В любом случае, расчет средней скорости важен для многих водителей. В современных автомобилях, оснащенных эффективными компьютерными системами управления, достаточно просто выбрать нужный режим отображения информации на экране компьютера, чтобы узнать среднюю скорость за определенный промежуток времени или пробег.

Для вычисления средней скорости поездки на современной машине достаточно подготовиться заранее, сбросив показатели суточного пробега на нуль, а также обнулив средние данные расхода и скорости. После этого вы сможете не засекать никакого времени, а также не продумывать формулы по расчету средней скорости поездки. Тем не менее, такой вариант не всегда подходит, да и не все автомобили оснащены хорошим бортовым компьютером. Потому следует разобраться с тем, как определять среднюю скорость и прочие параметры.

Находим среднюю скорость и средний расход поездки по факту

Если замеры средней скорости поездки важны для вас в коммерческих целях или в качестве отчетности для фирмы, в которой вы работаете, то проще всего купить GPS-навигатор, который обладает функцией учета скорости и времени, проведенного в дороге. Этот прибор полностью заменит бортовой компьютер и сможет без применения различных формул показать вам среднюю скорость поездки.

В иных случаях можно пользоваться более грубыми методами определения. Для замеров вам потребуется секундомер, который будет определять рабочее время поездки. То есть, для нас важна каждая секунда, которую автомобиль проводит в дороге. Время, проведенное на заправках или в придорожных кафе зачастую в расчет не входит. Задачи для точного замера следующие:

• перед поездкой сбросьте суточный счетчик километров на нуль, начните новый отчет пробега;
• установите на приборной панели автомобиля секундомер и не забывайте включать его каждый раз, когда трогаетесь;
• как только вы остановились не по причине дорожной обстановки, а по собственному желанию, выключайте секундомер;
• после прибытия в пункт назначения выпишите данные суточного счетчика с точностью до одного километра;
• также выпишите данные секундомера с точностью до минуты — это даст вам возможность развязать уравнение;
• подставьте полученные данные в формулу Vсредняя = S / t, где V — это средняя скорость, S — пройденное расстояние, а t — затраченное на поездку время.

Предположим, на поездку у вас ушло ровно 5 часов, а пройденное по спидометру расстояние оказалось 300 километров. Это значит, что средняя скорость вашего автомобиля во время движения составила 60 км/ч. Если вы будете практиковать определение средней скорости для каждой дальней поездки, то будете удивлены низкими показателями.

Часто создается впечатление, что средняя скорость должна быть около 120 километров в час, но на деле оказывается меньше 60. Подобным образом вы сможете просчитать средний расход топлива. Нужно затраченные литры поделить на сотни километров пройденного расстояния. К примеру, если вы проехали 300 километров, то делать сумму литров нужно на 3.

Какой должна быть средняя скорость машины в поездке?

Многие задаются вопросом, а какой же на самом деле должна быть средняя скорость автомобиля. Просчитав удивительный факт того, что средняя скорость авто в трассовом режиме составила всего 80 километров в час, водитель начинает сомневаться в том, что он эффективно использует ресурс транспортного средства. На самом деле, такая скорость вполне допустима.

Оптимальной скоростью при движении по трассе является 90 км/ч, но далеко не всегда получает держать крейсерскую скорость постоянно. Иногда происходят ситуации, которые заставляют в течение нескольких минут ехать медленно. К примеру, можно тянуться за фурой, ожидая возможности обгона. Оптимальная средняя скорость на трассе будет зависеть от таких факторов:

• дорожные условия и состояние дороги, по которой выполняется поездка в нужное вам место;
• количество транспорта, загруженность и сложность трассы для совершения обгонов медленных авто;
• наличие дополнительных полос для совершения маневров без снижения скорости машины;
• позволенная скорость и наличие средств автоматической фиксации нарушения ПДД или постов ГИБДД;
• соображения личной безопасности, которые исходят из состояния собственного автомобиля;
• тип транспорта, на котором вы преодолеваете дистанцию, его технические возможности и ограничения;
• погодные условия, наличие корки льда на трассе или мокрая дорога, снижающая хорошее сцепление.

Это лишь базовые факторы, которые влияют на среднюю скорость машины при трассовой поездке. На практике при отсутствии нарушений ПДД средняя скорость автомобиля на трассе составляет 75-80 километров в час. Достичь средней скорости в 90 км/ч можно только на определенном отрезке трассы. Потому не огорчайтесь, увидев небольшие значения на экране бортового компьютера.

Первым фактором, который нужно оценивать при выборе скоростного режима на трассе, является безопасность. Именно этот важный критерий иногда становится жертвой нехватки времени или желания показать достойные цифры средней скорости. На деле такие цели никогда не приводят к хорошим последствиям, потому всегда выбирайте безопасные режимы поездки.

Оптимальная скорость для автомобиля — второй фактор выбора режима поездки

Главным критерием выбора скоростного режима являются далеко не возможности машины, а ваши соображения о безопасности и уверенности поездки. Если вы считаете, что ехать со скоростью 90 км/ч при данных условиях опасно, то лучше выбрать более комфортный и уверенный режим.

Тем не менее, существуют определенные рекомендации от производителей.

Первое, о чем стоит вспомнить в таком контексте разговора, является средний расход. Если вы будете поддерживать скорость машины на уровне 90 километров в час, то расход будет максимально близким к паспортным показателям расхода на трассе. Многие водители переживают по поводу того, что их машина на трассе расходует больше топлива, чем указано в документах. Происходит это по таким причинам:

• на обгоне автомобиль вынужден потреблять в разы больше топлива в силу необходимости быстрого разгона;
• постоянное торможение и трогание с места в пробке или на различных преградах также дает плюс к расходу;
• движение на скорости свыше 100 километров в час начинает значительно увеличивать расход бензина;
• производитель рассчитывает трассовые режимы поездки на среднюю скорость 90 километров в час;
• под данный показатель происходит настройка всех функций и узлов автомобиля, передаточных чисел и двигателя.

Именно по этим причинам средние показатели расхода часто оказываются на порядок больше паспортных замеров. При определении расхода в трассовом режиме для технических характеристик машины производитель выполняет тестирование транспорта не треке, где машина едет с постоянной одной рекомендованной скоростью. Именно это позволяет достичь столь занимательных цифр расхода топлива.

Для получения максимальных выгод в расходе топлива и прочих характеристиках вашего автомобиля экспериментируйте и пробуйте разные режимы поездки. Не лишни будет и почитать отзывы о том, как люди эксплуатируют ваш тип транспорта. Это поможет максимально упростить эксплуатацию машины, сделать меньшим расход топлива и предсказать любые особенности поведения транспортного средства. Помните, что скорость должна быть оправданной. Предлагаем подборку видео ДТП, случившихся в частности из-за высокой скорости:

Подводим итоги

Средняя скорость автомобиля — важный показатель, который может объяснить повышенный расход и задержки по времени, которые вы испытываете в той или иной поездке. Нужно уметь рассчитывать среднюю скорость и знать параметры эксплуатации своего транспорта для выбора оптимальных режимов поездки. Такие знания никогда вам не помешают, а также помогут понять многие тонкости эксплуатации автомобиля.

Если вы решили учитывать особенности вашей эксплуатации транспорта, следует начать с учета средней скорости при движении, а также средних показателей расхода. Если вы сможете учитывать эти показатели постоянно, вы также сможете улучшать средний расход, ведь в данном случае проснется спортивный интерес. Занимаетесь ли вы учетом средних показателей эксплуатации вашего авто?

Формула расчета скорости и расстояния. Как вычислить среднюю скорость

Все задачи, в которых присутствует движение объектов, их перемещение или вращение, так или иначе связаны со скоростью.

Данный термин характеризует перемещение объекта в пространстве за определенный отрезок времени – число единиц расстояния за единицу времени. Он является частым «гостем» как разделов математики, так и физики. Исходное тело может менять свое расположение как равномерно, так и с ускорением. В первом случае величина скорости статична и в ходе движения не меняется, во втором наоборот – увеличивается или уменьшается.

Как найти скорость – равномерное движение

Если скорость движения тела оставалась неизменной от начала перемещения и до окончания пути, то речь идет о перемещении с постоянным ускорением – равномерном движении. Оно может быть прямолинейным или же криволинейным. В первом случае траекторией перемещения тела является прямая.

Тогда V=S/t, где:

• V – искомая скорость,
• S – пройденное расстояние (общий путь),
• t – общее время движения.

Как найти скорость – ускорение постоянно

Если объект двигался с ускорением, то его скорость по мере движения менялась. В таком случае найти искомую величину поможет выражение:

V=V (нач) + at, где:

• V (нач) – первоначальная скорость движения объекта,
• a – ускорение тела,
• t – общее время пути.

Как найти скорость – неравномерное движение

В данном случае имеет место ситуация, когда разные участки пути тело проходило за разное время.
S(1) – за t(1),
S(2) – за t(2) и т.д.

На первом участке движение происходило в “темпе” V(1), на втором – V(2) и т.д.

Чтобы узнать скорость перемещения объекта на всем пути (ее среднее значение) воспользуйтесь выражением:

Как найти скорость – вращение объекта

В случае вращения речь идет об угловой скорости, определяющей угол, на который поворачивается элемент за единицу времени. Обозначается искомая величина символом ω (рад/с).

• ω = Δφ/Δt, где:

Δφ – пройденный угол (приращение угла),
Δt – прошедшее время (время движения – приращение времени).

• В случае, если вращение равномерное, искомая величина (ω) связана с таким понятием как период вращения – за какое время наш объект совершит 1 полный оборот. В таком случае:

ω = 2π/T, где:
π – константа ≈3,14,
T – период.

Или ω = 2πn, где:
π – константа ≈3,14,
n – частота обращения.

• При известной линейной скорости объекта для каждой точки на пути движения и радиусе окружности, по которой она перемещается, для нахождения скорости ω потребуется следующее выражение:

ω = V/R, где:
V – численное значение векторной величины (линейной скорости),
R – радиус траектории следования тела.

Как найти скорость – сближение и отдаление точек

В подобного рода задачах уместным будет использование терминов скорость сближения и скорость отдаления.

Если объекты направляются друг к другу, то скорость сближения (отдаления) будет следующей:
V (сближ) = V(1) + V(2), где V(1) и V(2) – скорости соответствующих объектов.

Если одно из тел догоняет другое, то V (сближ) = V(1) – V(2), V(1) больше V(2).

Как найти скорость – движение по водоему

Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т. е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?

В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).

В предложенном задании нас просят объяснить, как найти скорость, время и расстояние в задаче. Задачи с такими величинами относят к задачам на движение.

Задачи на движение

Всего в задачах на движение используются три основные величины, как правило, одна из которых, является неизвестной и её надо найти. Сделать это можно с помощью формул:

• Скорость. Скоростью в задаче называют величину, которая обозначает, какое расстояние проделал объект за единиц времени. Следовательно, она находится по формуле:

скорость = расстояние / время.

• Время. Временем в задаче называют величину, которая показывает, какое время затратил объект на путь при определённое скорости. Соответственно, оно находится по формуле:

время = расстояние / скорость.

• Расстояние. Расстоянием или путём в задаче называют величину, которая показывает, какое расстояние преодолел субъект при определённой скорости за какой-либо промежуток времени. Таким образом, оно находится по формуле:

расстояние = скорость * время.

Итог

Таким образом, подводим итог. Задачи на движения могут решаться по вышеуказанным формулам. В заданиях также может быть несколько движущихся объектов или несколько отрезков пути и времени. В таком случае решение будет состоять из нескольких отрезков, которые в итоге складываются или вычитываются в зависимости от условий.

Чтобы вычислить среднюю скорость, воспользуйтесь простой формулой: Скорость = Пройденный путь Время {\displaystyle {\text{Скорость}}={\frac {\text{Пройденный путь}}{\text{Время}}}} . Но в некоторых задачах даются два значения скорости — на разных участках пройденного пути или в различные промежутки времени. В этих случаях нужно пользоваться другими формулами для вычисления средней скорости. Навыки решения подобных задач могут пригодиться в реальной жизни, а сами задачи могут встретиться на экзаменах, поэтому запомните формулы и уясните принципы решения задач.

Шаги

По одному значению пути и одному значению времени

• длина пути, пройденного телом;
• время, за которое тело прошло этот путь.
• Например: автомобиль проехал 150 км за 3 ч. Найдите среднюю скорость автомобиля.

1. Формула: , где v {\displaystyle v} — средняя скорость, s {\displaystyle s} — пройденный путь, t {\displaystyle t} — время, за которое пройден путь.

   В формулу подставьте пройденный путь. Значение пути подставьте вместо s {\displaystyle s} .

   • В нашем примере автомобиль проехал 150 км. Формула запишется так: v = 150 t {\displaystyle v={\frac {150}{t}}} .

2. В формулу подставьте время. Значение времени подставьте вместо t {\displaystyle t} .

   • В нашем примере автомобиль ехал в течение 3 ч. Формула запишется так: .

3. Разделите путь на время. Вы найдете среднюю скорость (как правило, она измеряется в километрах в час).

4. Вычислите общий пройденный путь. Для этого сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).

   • В нашем примере автомобиль проехал 150 км, 120 км и 70 км. Общий пройденный путь: .

5. T {\displaystyle t} ).

   • . Таким образом, формула запишется так: .
6. • В нашем примере:
     v = 340 6 {\displaystyle v={\frac {340}{6}}}

     Таким образом, если автомобиль проехал 150 км за 3 ч, 120 км за 2 ч, 70 км за 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).

По нескольким значениям скоростей и нескольким значениям времени

1. Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:

   Запишите формулу для вычисления средней скорости. Формула: v = s t {\displaystyle v={\frac {s}{t}}} , где v {\displaystyle v} — средняя скорость, s {\displaystyle s} — общий пройденный путь, t {\displaystyle t} — общее время, за которое пройден путь.

2. Вычислите общий путь. Для этого умножьте каждую скорость на соответствующее время. Так вы найдете длину каждого участка пути. Чтобы вычислить общий путь, сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).

   • Например:
     50 км/ч в течение 3 ч = 50 × 3 = 150 {\displaystyle 50\times 3=150} км
     60 км/ч в течение 2 ч = 60 × 2 = 120 {\displaystyle 60\times 2=120} км
     70 км/ч в течение 1 ч = 70 × 1 = 70 {\displaystyle 70\times 1=70} км
     Общий пройденный путь: 150 + 120 + 70 = 340 {\displaystyle 150+120+70=340} км. Таким образом, формула запишется так: v = 340 t {\displaystyle v={\frac {340}{t}}} .

3. Вычислите общее время в пути. Для этого сложите значения времени, за которые был пройден каждый участок пути. В формулу подставьте общее время (вместо t {\displaystyle t} ).

   • В нашем примере автомобиль ехал в течение 3 ч, 2 ч и 1 ч. Общее время в пути: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6} . Таким образом, формула запишется так: v = 340 6 {\displaystyle v={\frac {340}{6}}} .

4. Разделите общий путь на общее время. Вы найдете среднюю скорость.

   • В нашем примере:
     v = 340 6 {\displaystyle v={\frac {340}{6}}}
     v = 56 , 67 {\displaystyle v=56,67}
     Таким образом, если автомобиль двигался со скоростью 50 км/ч в течение 3 ч, со скоростью 60 км/ч в течение 2 ч, со скоростью 70 км/ч в течение 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).

По двум значениям скоростей и двум одинаковым значениям времени

1. Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины и условия:

   • два или несколько значений скоростей, с которыми двигалось тело;
   • тело двигалось с определенными скоростями в течение равных промежутков времени.
   • Например: автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч. Найдите среднюю скорость автомобиля на всем протяжении пути.

2. Запишите формулу для вычисления средней скорости, если даны две скорости, с которыми тело движется в течение равных промежутков времени. Формула: v = a + b 2 {\displaystyle v={\frac {a+b}{2}}} , где v {\displaystyle v} — средняя скорость, a {\displaystyle a} — скорость тела в течение первого промежутка времени, b {\displaystyle b} — скорость тела в течение второго (такого же, как первый) промежутка времени.

   • В таких задачах значения промежутков времени не важны — главное, чтобы они были равны.
   • Если дано несколько значений скоростей и равные промежутки времени, перепишите формулу так: v = a + b + c 3 {\displaystyle v={\frac {a+b+c}{3}}} или v = a + b + c + d 4 {\displaystyle v={\frac {a+b+c+d}{4}}} . Если промежутки времени равны, сложите все значения скоростей и разделите их на количество таких значений.

3. В формулу подставьте значения скоростей. Неважно, какое значение подставить вместо a {\displaystyle a} , а какое — вместо b {\displaystyle b} .

   • Например, если первая скорость равна 40 км/ч, а вторая скорость равна 60 км/ч, формула запишется так: .

4. Сложите значения двух скоростей. Затем сумму разделите на два. Вы найдете среднюю скорость на всем протяжении пути.

   • Например:
     v = 40 + 60 2 {\displaystyle v={\frac {40+60}{2}}}
     v = 100 2 {\displaystyle v={\frac {100}{2}}}
     v = 50 {\displaystyle v=50}
     Таким образом, если автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч, средняя скорость автомобиля на всем протяжении пути составила 50 км/ч.

t = S: V

15: 3 = 5 (с)

Составим выражение: 5 3: 3 = 5 (с) Ответ: 5 с потребуется слепню.

Реши задачу.

1. Катер, двигаясь со скоростью 32 км/ч, про­шёл путь между пристанями за 2 ч. Сколько потребуется времени, чтобы пройти этот же путь на лодке, если она движется со скорос­тью 8 км/ч?

2. Велосипедист, двигаясь со скоростью 10 км/ч, проехал путь между деревнями за 4 ч. Сколько

потребуется времени пешеходу, чтобы пройти этот же путь, если он движется со скоростью 15 км/ч?

Составные задачи на время. II тип.

Образец:

Многоножка сначала бежала 3 мин со скоростью 2 дм/м, а потом она побежала со скоростью 3 дм/м. За какое время мно­гоножка пробежала оставшийся путь, если всего она пробежала 15 дм? Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.

Скорость (V) Время (t) Расстояние (S)

С. — 2 дм/мин З мин?дм

П.-3 дм/мин? ? мин?дм 15дм

Составим план решения этой задачи. Что­бы узнать, время многоножки потом, надо узнать какое расстояние она пробежала потом, а для этого надо знать, какое рас­стояние она пробежала сначала.

t п S п S с

S с = V с · t

2 3 = 6 (м) — расстояние, которое пробе­жала многоножка сначала.

S п = S — S с

15 — 6 = 9 (м) — расстояние, которое пробежала многоножка потом.

Чтобы найти время, надо расстояние раз­делить на скорость.

9: 3 = 3(мин)

Ответ: за 3 мин многоножка пробежала оставшийся путь.

Реши задачу.

1. Волк бежал по лесу 3 ч со скоростью 8 км/ч. По полю он бежал со скоростью 10 км/ч. Сколько времени волк бежал по полю, если он пробежал 44 км?

2. Рак до коряги полз 3 мин со скоростью 18 м/мин. Остальной путь он полз со скоростью 16 м/мин. Сколько времени потребовалось раку на остальной путь, если он прополз 118м?

3. Гена добежал до футбольной площадки за 48 с со скоростью 6 м/с, а потом он побежал к школе со скоростью 7 м/с. Через какое время Гена добежит до школы, если он пробежал 477 м?

4. Пешеход шёл до остановки 3 ч со скоростью 5 км/ч, после остановки он пошёл со скорос­тью 4 км/ч. Сколько времени пешеход был в пути после остановки, если он прошёл 23 км?

5. Уж плыл до коряги 10с со скоростью 8 дм/с, а потом он поплыл до берега со скоростью 6 дм/с. За какое время доплыл уж до берега, если он проплыл 122дм?

Составные задачи на скорость. I тип

Образец:

Из норки побежали два ёжика. Один бе­жал 6 с со скоростью 2 м/с. С какой ско­ростью должен бежать другой ёжик, чтобы преодолеть это расстояние за 3 с? Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.

Скорость (V) Время (1) Расстояние (8)

I — 2 м/с 6 с одинаковое

II — ?м/с 3 с

Составим план решения этой задачи. Что­бы найти скорость второго ёжика, надо найти расстояние, которое пробежал пер­вый ёжик.

Чтобы найти расстояние, надо скорость умножить на время.

S = V I · t I

2 · 6 = 12 (м) – расстояние, которое пробежал первый ежик.

Чтобы найти скорость, надо расстояние разделить на время.

V II = S: t II

12:3 = 4(м/с)

Составим выражение: 2 6:3 = 4 (м/с)

Ответ; 4м/с скорость второго ёжика.

Реши задачу.

1. Один кальмар плыл 4 с со скоростью 10 м/с. С какой скоростью должен плыть другой кальмар, чтобы преодолеть это расстояние за 5 с?

2. Трактор, двигаясь со скоростью 9 км/ч, прошёл путь между деревнями за 2 ч. С какой скоростью должен идти пешеход, чтобы пре­одолеть это расстояние за 3 ч?

3. Автобус, двигаясь со скоростью 64 км/ч, про­шёл путь между городами за 2 ч. С какой скоростью должен ехать велосипедист, что­бы преодолеть это расстояние за 8 ч?

4. Чёрный стриж летел 4 мин со скоростью 3 км/мин. С какой скоростью должна лететь утка кряква, чтобы преодолеть это расстоя­ние за 6 мин?

Составные задачи на скорость. II тип

Лыжник до горки ехал 2 ч со скоростью 15 км/ч, а потом по лесу он ехал ещё 3 ч. С какой скоростью лыжник будет ехать по лесу, если всего он проехал 66км?

Давайте школьный урок физики превратим в увлекательную игру! В этой статье нашей героиней станет формула «Скорость, время, расстояние».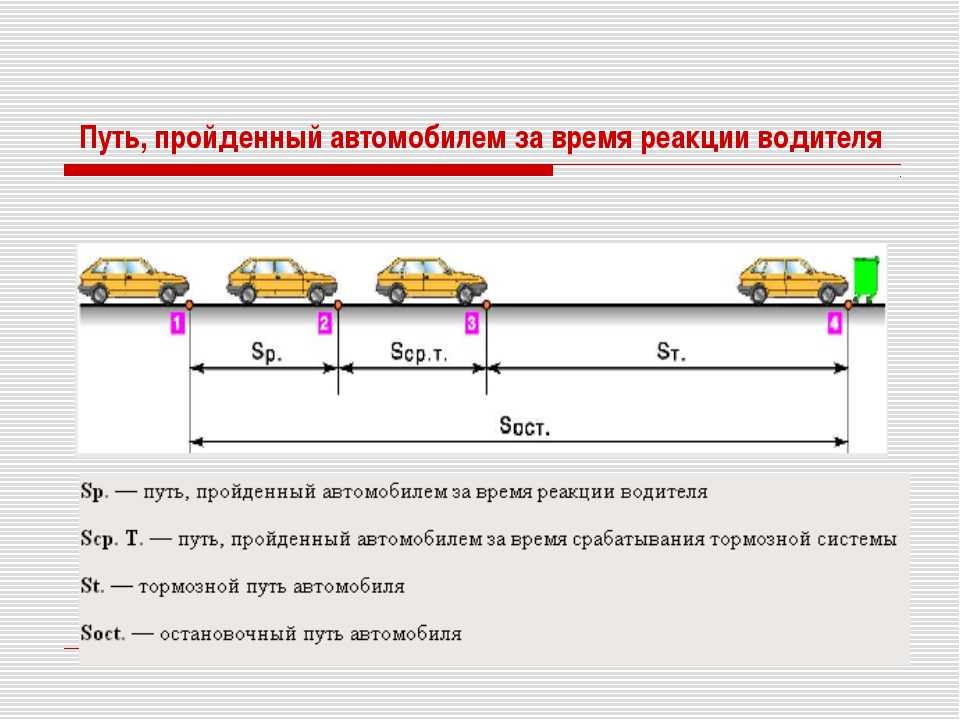 Разберем отдельно каждый параметр, приведем интересные примеры.

Скорость

Что же такое «скорость»? Можно наблюдать, как одна машина едет быстрее, другая -медленее; один человек идет быстрым шагом, другой — не торопится. Велосипедисты тоже едут с разной скоростью. Да! Именно скоростью. Что же под ней подразумевается? Конечно же, расстояние, которое прошел человек. проехала машина за какое-то Допустим, что 5 км/ч. То есть за 1 час он прошел 5 километров.

Формула пути (расстояния) — произведение скорости и времени. Конечно же, самый удобный и доступный параметр — это время. Часы есть у всех. Скорость пешехода не строго 5 км/ч, а приблизительно. Поэтому здесь может быть погрешность. В таком случае, вам лучше взять карту местности. Обратите внимание, какой масштаб. Должно быть указано, сколько километров или метров в 1 см. Приложите линейку и замерьте длину. Например, от дома до музыкальной школы прямая дорога. Отрезок получился 5 см. А в масштабе указано 1 см = 200 м. Значит, реальное расстояние — 200*5=1000 м=1 км. За сколько вы проходите это расстояние? За полчаса? Выражаясь техническим языком, 30 мин=0,5 ч=(1/2) ч. Если мы решим задачу, то получится, что идете со скоростью 2 км/ч. Всегда вам поможет решить задачу формула «скорость, время, расстояние».

Не упустите!

Советую вам не упускать очень важные моменты. Когда вам дается задача, смотрите внимательно, в каких единицах измерения даны параметры. Автор задачи может схитрить. Напишет в дано:

Человек проехал по тротуару на велосипеде 2 километра за 15 минут. Не спешите сразу решать задачу по формуле, иначе у вас получится ерунда, а учитель ее вам не засчитает. Помните, что ни в коем случае нельзя делать так: 2 км/15 мин. У вас единица измерения получится км/мин, а не км/ч. Вам нужно добиться последнего. Переведите минуты в часы. Как это сделать? 15 минут — это 1/4 часа или 0,25 ч. Теперь можете смело 2км/0,25ч=8 км/ч. Теперь задача решена верно.

Вот так легко запоминается формула «скорость, время, расстояние».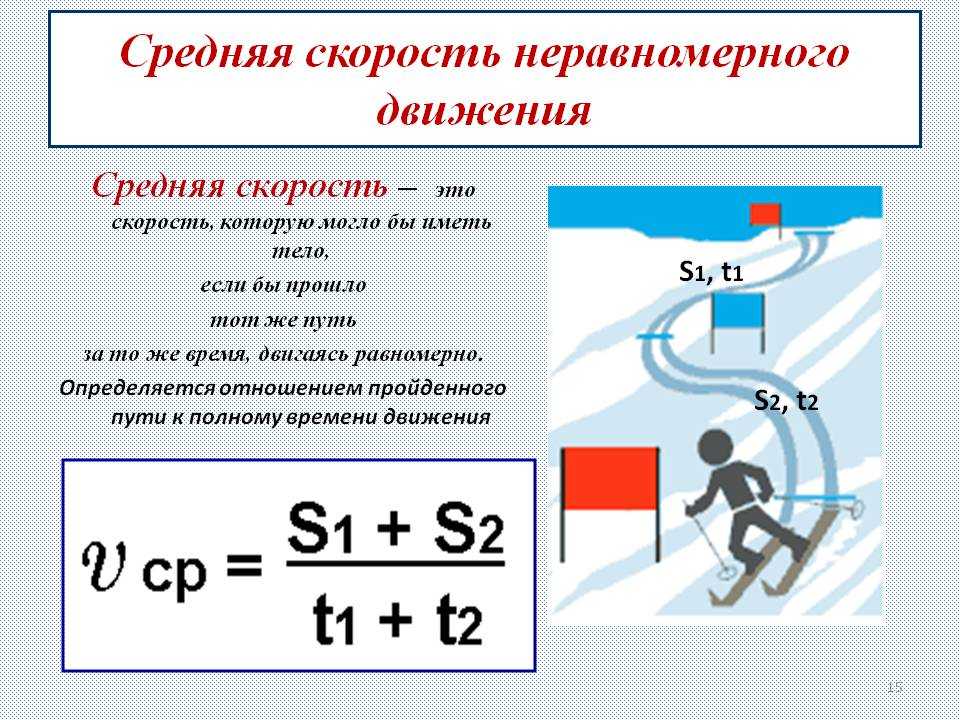 Только соблюдайте все правила математики, обращайте внимание на единицы измерения в задаче. Если есть нюансы, как в рассмотренном чуть выше примере, сразу же переводите в систему единиц СИ, как положено.

Средняя скорость — Физика — Университет Висконсин-Грин-Бей

• Домашний
• Характеристики
• Практическое руководство
• Проблемы

Вы едете на машине со скоростью 64 км/ч 21 км, затем разгоняетесь до 96 км/ч и еще . Какая у вас средняя скорость?

• Идентифицировать
• Нарисуй картинку
• Выберите отношение
• Решить
• Понять

• В этой задаче вам дается информация о скорости, смещении и времени автомобиля на разных участках пути, а также запрашивается средняя скорость . v, x и t связаны через определение скорости, так что это проблема определения.

  В общем, если вам говорят о скорости, с которой изменяется какая-либо переменная (в данном случае x), вы должны проверить, сможете ли вы решить задачу, просто используя соответствующее определение.

  
  

• В большинстве задач с определением изображения нет необходимости. Однако в этом случае изображение может помочь вам визуализировать движение и понять важность использования определяющего уравнения для определения средней скорости. Это, однако, не требуется, если вас устраивает скорость. Вам предоставляется информация о расстоянии, времени и скорости по двум этапам пути и запрашивается средняя скорость всего пути. Рисунок не даст никакой дополнительной организации сверх того, что уже присутствует в задаче.

  
  

• В форме уравнения определение средней скорости дается как

  
  Это единственное соотношение, которое вам нужно для этой задачи.

  
  

• В этот момент вам нужно использовать остальную информацию, приведенную в задаче, чтобы найти расстояние, пройденное на втором этапе пути, и время, необходимое для первого этапа пути:

  
  

  Теперь можно вернуться к уравнению средней скорости за всю поездку:

  
  

  Средняя скорость автомобиля 86 км/ч на север. Дальнейшее решение не требуется.

  
  

• Средняя скорость является одним из наиболее часто пропускаемых типов задач определения. Если объект не тратит одинаковое количество времени на каждой скорости, вы . Вместо этого вы должны использовать определение средней скорости и разделить общее расстояние, пройденное автомобилем, на общее количество необходимого времени.

  
  

  Поскольку автомобиль ехал со скоростью 96 км/ч больше времени, чем со скоростью 64 км/ч, логично предположить, что средняя скорость ближе к 96, чем к 64. Средняя скорость — это средняя скорость и направление, или 86 км/ч на север.

 

• Дом
• Характеристики
• Практическое руководство
• Проблемы
• Висконсинский университет Грин Бэй
• 2420 Николет Доктор
• Грин Бэй, Висконсин, 54311

Как рассчитать среднюю скорость в милях в час

••• TongRo Images/TongRo Images/Getty Images

Обновлено 25 апреля 2017 г. рассчитать среднюю скорость в милях в час, с которой ехал автомобиль. Полученная информация может повлиять на ваш подход к проблеме. Если вы можете определить общее пройденное расстояние и общее время, проведенное в пути, вы можете рассчитать среднюю скорость автомобиля, используя простую формулу.

Что такое среднее?

Среднее значение — это вычисление, которое показывает, какое число является центральным или наиболее распространенным в наборе чисел. Например, можно сказать, что средний возраст всех старшеклассников составляет шестнадцать лет. Это центральное значение в возрастном диапазоне от 14 до 18 лет, к которому относится большинство старшеклассников.

Формула средней скорости

Чтобы рассчитать любое среднее значение, вы сложите все числа в наборе и разделите сумму на количество чисел в наборе. Хотя это можно сделать и таким образом, расчет средней скорости обычно немного отличается от расчета большинства других средних значений. Чтобы вычислить среднюю скорость, вы обычно делите общее пройденное расстояние на общее количество времени, затраченного на поездку. Несмотря на то, что автомобиль мог двигаться с разными скоростями на разных участках общего расстояния, это учитывается в расчете за общее время. Формула средней скорости выглядит так:

Средняя скорость = общее расстояние ÷ общее время

Расчет средней скорости по общему расстоянию и общему времени

Представьте, что кто-то едет на машине из города А в город Б. Если вы знаете, что два города находятся на расстоянии 350 миль друг от друга, а поездка заняла шесть часов, вы можете просто подставить эти значения в формулу для средней скорости, например:

Средняя скорость = 350 миль ÷ 6 часов = 58,3 мили/час

Ответ говорит вам, что автомобиль двигался со средней скоростью 58,3 миль в час. Автомобиль, вероятно, двигался то быстрее, то медленнее, при этом 58,3 мили в час были центральной или наиболее распространенной скоростью.

Расчет средней скорости на основе нескольких расстояний и времени

Вы все равно можете выполнить расчет, если дано несколько расстояний и времени. Предположим, вам сказали, что водитель совершал поездку между городом X и городом Y в течение трех дней, причем поездка за каждый день описывалась следующим образом:

День 1: Водитель выехал из города X и проехал 100 миль за три часа. День 2: Водитель проехал 250 миль за четыре часа. День 3: Водитель проехал 300 миль за пять часов и прибыл в город Y.

Самый простой способ рассчитать среднюю скорость в этом случае — просуммировать все расстояния в верхней части уравнения средней скорости и просуммировать все времена в нижняя часть, вот так:

Средняя скорость = (100 миль + 250 миль + 300 миль) ÷ (3 часа + 4 часа + 5 часов) = 650 миль ÷ 12 часов = 54,2 мили/час

Средняя скорость водителя в этой поездке составила 54,2 мили в час.