Равномерное движение жидкости: Равномерное и неравномерное движение — Основы гидродинамики

Равномерное и неравномерное движение — Основы гидродинамики

Равномерное и неравномерное движение Живым сечением потока называют поперечное сечение потока, перпендикулярное его направлению. Расходом потока Q называют объем жидкости, проходящей в единицу времени через живое сечение потока. Расход жидкости измеряют в м3/с или л/с. Иногда пользуются понятием весового расхода G, под которым подразумевают вес жидкости, проходящей в единицу времени через сечение потока. Между весовым и объемным расходами существует такая зависимость: G=yQ, где у — удельный вес жидкости. Равномерным называют такое установившееся движение жидкости, при котором живые сечения и средняя скорость потока не меняются по его длине. Примером равномерного движения служит движение жидкости в цилиндрической трубе или канале неизменного сечения и постоянной глубины. Неравномерным называют такое установившееся движение жидкости, при котором живые сечения и средние скорости потока изменяются по его длине. Примером неравномерного движения служит движение жидкости в конической трубе, в естественном русле, на перепаде. При равномерном движении линии тока представляют собой систему прямых параллельных линий. Такое движение называется параллельноструйным. При движении жидкости в естественных руслах живое сечение обычно непрерывно изменяется вдоль потока как по форме, так и по площади. Такое движение жидкости является установившимся неравномерным. Для облегчения изучения такого движения в гидравлике введено понятие плавно изменяющегося движения, которое характеризуется следующими свойствами: – кривизна линий тока в потоке считается весьма незначительной; – угол расхождения между отдельными линиями тока очень мал; – живые сечения потока являются плоскими; – давление распределяется по живому сечению по гидростатическому закону. Читать далее: Гидравлический удар в трубопроводах Режимы движения жидкостей Виды движения жидкостей

Равномерное движение — жидкость — Большая Энциклопедия Нефти и Газа, статья, страница 1

Равномерное движение — жидкость

Cтраница 1

Равномерное движение жидкости возможно лишь при отсутствии местных сопротивлений. Следовательно, в этом случае существуют только линейные потери напора.  [1]

Равномерное движение жидкости в открытых каналах или в трубопроводах с частично заполненным поперечным сечением устанавливается, когда геометрический уклон трубопровода или дна канала имеет постоянное значение по всей длине и форма поперечного сечения не меняется. Шероховатость стенок канала также должна иметь постоянное значение.  [2]

Равномерное движение жидкости — такое, когда вдоль любой линии тока скорость жидкости остается неизменной. Для неравномерного движения характерно изменение скоростей вдоль потока.  [3]

Равномерное движение жидкости является частным случаем плавно изменяющегося движения.  [4]

Равномерным движением жидкости называется такое, при котором средняя скорость и живое сечение по длине потока не изменяются.  [5]

Равномерным движением жидкости в канале называется такое движение, при котором живое сечение со, глубина наполнения канала h и средняя скорость и, а также эпюра распределения, н осредненной скорости по жи — — вому сечению — не изменяются вдоль потока.  [6]

Равномерным движением жидкости называется такое, при котором линейная скорость потока не меняется от одного сечения к другому. Движение несжимаемой жидкости в простом трубопроводе постоянного сечения при полном заполнении его является равномерным, так как линейная скорость постоянна по всей длине трубопровода.  [7]

Равномерным движением жидкости называется такое движение, при котором живые сечения потока одинаковы по всей его длине и скорость потока в соответствующих точках всех живых сечений также одинакова. Движение жидкости, при котором эти условия не выполняются, называется неравномерным.  [8]

Равномерным движением жидкости в открытом русле будем называть такое, когда скорость движения частиц жидкости по оси каждой элементарной струйки не изменяется по длине. Следовательно, средние скорости в различных живых сечениях русла будут равны между собой. Такое движение возможно при условии постоянства расхода, размеров и формы живого сечения потока, шероховатости русла и гидравлического ( пьезометрического) уклона.  [9]

Равномерным движением жидкости в открытом русле будем называть такое, когда скорость движения частиц жидкости на оси каждой элементарной струйки не изменяется по ее длине. Следовательно, средние скорости в различных живых сечениях потока будут равны между собой. Такое движение возможно при условии постоянства расхода, размеров и формы живого сечения, шероховатости русла и гидравлического ( а также пьезометрического) уклона по длине потока.

 [10]

Равномерным движением жидкости называют такое установившееся движение, при котором живые сечения и средняя скорость потока не изменяются по его длине. Примером равномерного движения служит движение жидкости в цилиндрической трубе или в канале, глубина потока в котором не изменяется и поперечное сечение которого постоянно.  [11]

Рассмотрим равномерное движение жидкости, например, в канале. Так как при равномерном движении жидкости все живые сечения потока одинаковы, то и глубины h в соответственных точках дна одинаковы по длине потока. При равномерном движении во всех живых сечениях средние скорости v течения потока одинаковы, а поэтому и удельная кинетическая энергия потока v2 ( 2g) тоже одинакова.  [12]

Рассмотрим равномерное движение жидкости, напри — р, в канале. Так как при равномерном движении идкости все живые сечения потока одинаковы, то и 1убины — А в соответственных точках дна одинаковы по 1ине потока.  [13]

Рассмотрим равномерное движение жидкости в прямой горизонтальной трубе ( рис. IV.  [14]

Рассмотрим равномерное движение жидкости в открытом русле при ламинарном режиме.  [15]

Страницы:      1    2    3    4

2 Равномерное движение жидкости в открытых руслах

2.1 Особенности движения жидкости в открытых руслах. Уравнение равномерного движения

Движение жидкости в открытых руслах характеризуется наличием свободной поверхности и является безнапорным.

Вертикальное расстояние в живом сечении безнапорного потока, измеряемое от свободной поверхности жидкости до наинизшей точки дна русла называется глубиной потока и обозначается h.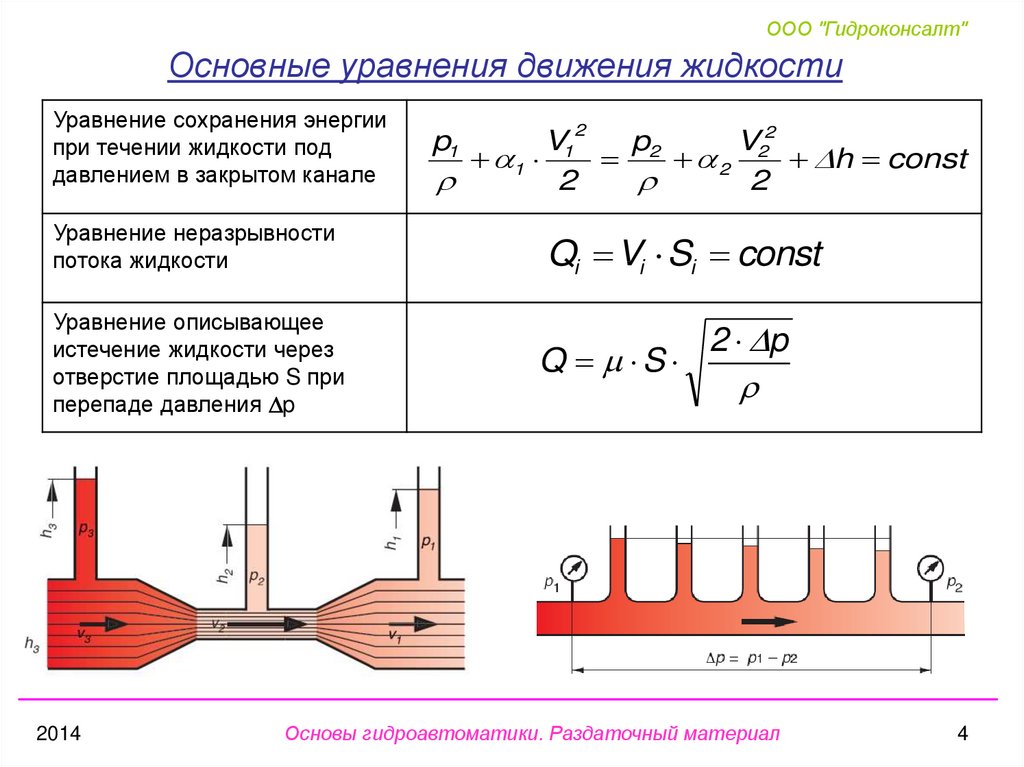 Различают глубину нормальную и критическую (соответствующую минимальному значению удельной энергии сечения).

Глубина равномерного движения называется нормальной глубиной и обозначается h₀.

Равномерным движением называется такое установившееся движение, при котором соблюдены следующие условия:

1) средняя скорость v постоянна вдоль движения;

2)живые сечения (площадь и форма) по всей длине потока не изменяются;

3) эпюры скоростей во всех живых сечениях одинаковы.

В виду постоянства средней скорости v, площади  и формы живого сечения вдоль движения будут постоянны также глубина h₀, ширина, смоченный периметр , гидравлический радиус R и другие характеристики движения.

Равномерное движение встречается в каналах, лотках, безнапорных трубах постоянного сечения.

Разность отметок (z₁  z₂) в двух расчётных сечениях, отнесённая к расстоянию между этими сечениями l называется уклоном дна русла (рис. 1)

i₀ = = sin , (1)

где   угол наклона дна русла к горизонту.

Рисунок 1 – Уклон дна русла

Так как уклон дна обычно невелик, то условно считают живые сечения и глубины вертикальными, а не перпендикулярными линии дна. Отсюда следует, что

i₀ = i_p = i, (2)

где i₀ – уклон дна,

i_p – пьезометрический уклон,

i – гидравлический уклон.

Уравнение (2) называют уравнением равномерного движения в открытых

руслах.

Скорость течения при равномерном движении в открытых руслах определяется по формуле Шези

v = С  = W  , (3)

где С – скоростной множитель, или коэффициент Шези. С = ;

R – гидравлический радиус трубопровода, м;

i₀ – уклон дна;

W – скоростная характеристика. W = С  .

Расход равен

Q =   W  . (4)

Для определения С и W предложен ряд эмпирических формул.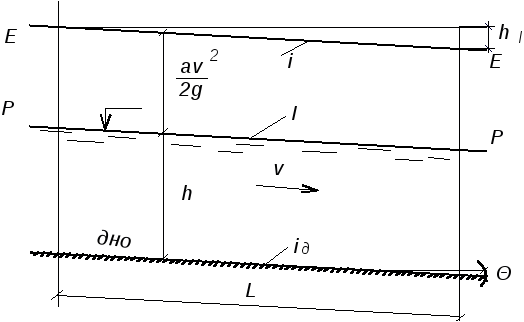

2.2 Гидравлически наивыгоднейшее сечение канала

Расход в открытом канале или лотке может быть выражен формулой

Q = , (11)

где   смоченный периметр.

Русла различных форм поперечного сечения (рис. 2) при одинаковой площади  имеют различный смоченный периметр  и гидравлический радиус R = . При заданных уклоне дна i₀, площади сечения  и коэффициенте шероховатости n наибольшая пропускная способность будет у русла, имеющего максимальный гидравлический радиус или минимальный смоченный периметр. Сечения таких русел называются гидравлически наивыгоднейшими. Другими словами гидравлически наивыгоднейшим сечением называется такое, у которого при заданном расходе Q, уклоне дна i₀ и коэффициенте шероховатости n будет наименьшая площадь живого сечения.

Рисунок 2 – Поперечные сечения русел

На сооружение каналов с гидравлически наивыгоднейшими сечениями затрачивается минимум земляных работ (площадь сечения) или минимум работ по укреплению дна и берегов (смоченный периметр).

Из различных форм живого сечения (рис. 2) наиболее выгодным будет полукруглое сечение. В этом случае при заданной площади будет наименьший смоченный периметр. Из прямоугольных сечений наиболее выгодным является полуквадрат, то есть ширина b = 2h. На практике чаще встречаются трапецеидальные или параболические сечения.

Для определения гидравлически наивыгоднейшего сечения необходимо найти величину максимального гидравлического радиуса R_max.

R_max = . (14)

где функция  представляет собой отношение  = = .

Таким образом, для нахождения R_max необходимо знать расход Q, уклоне дна i₀, коэффициенте шероховатости n, значение величины  _г.н. и показатель степени z.

Осреднённые значение z приведены в таблицах. Величина  _г.н. зависит от формы сечения русла.

Движение жидкости равномерное — Справочник химика 21

    Жидкость подводится сверху к вращающемуся разбрызгивающему устройству 1, которое вращается на валу, приводимом в движение электромотором 2. Жидкость равномерно разбрызгивается на поверхность нагрева испарителя 4 и пленкой стекает вниз. Тепло подводится греющим кожухом 5, имеющим каналы. Сгущенный раствор через патрубок отводится из конусообразного днища испарителя. Пары испаряемой жидкости конденсируются на охлаждающей поверхности конденсатора 6 конденсат собирается в водосборных желобах 7, установленных по периметру на определенной высоте. Из отдельных желобов конденсат собирается в нижний желоб, откуда удаляется через патрубок. [c.236]
    На рис. У-2 показано строение двойного электрического слоя для растворов электролитов средней концентрации. Отрицательно заряженные ионы адсорбируются на поверхности твердого тела, образуя тонкий внутренний слой. Положительно заряженные ионы образуют внешний слой, причем концентрация этих ионов в нем убывает в направлении от поверхности твердого тела. Такой характер внешнего слоя объясняется взаимным влиянием электростатического поля, концентрирующего положительно заряженные ионы вблизи внутреннего слоя, и теплового движения молекул, равномерно распределяющего эти ионы во всем объеме жидкости. [c.192]

    Для повышения равномерности движения жидкости во всасывающем и напорном трубопроводах на них устанавливают воздушные колпаки (заполнен( ые воздухом объемы), примыкающие к всасывающему и нагнетательному клапанам. В воздушном колпаке воздух сжимается, когда расход жидкости превышает средний, а соответствующая часть воздушного колпака заполняется жидкостью, которая выталкивается вновь в трубопровод в результате расширения воздуха в воздушном колпаке, когда расход оказывается меньше среднего. [c.97]

    Влияние размеров насадки на массообмен представляет собою равнодействующую ее влияния на диаметр капли и скорость ее движения. Эти величины определяют удерживающую способность и поверхность контакта [уравнение (4-9)]. Скорость движения жидкости равномерно уменьшается с сокращением размеров насадки, например диаметра колец Рашига, и оказывается наименьшей для насадки наименьших размеров. Это влияние обычно сильнее сказывается на скорости движения, чем на диаметре капель, и поэтому, если размеры насадок ниже критических, поверхность контакта фаз наибольшая и массообмен идет быстрее всего, несмотря на увеличение диаметра капель. Такая зависимость установлена для колец Рашига и [c. 327]

    Для процессов разделения, в которых требуется обеспечить низкое гидравлическое сопротивление используется ситчатая тарелка с отбойными элементами (рис. 3.18). По принципу действия тарелка относится к классу перекрестно-прямоточных конструкций. Основание тарелки выполнено из просечно-вытяжного листа, ячейки которого имеют наклон 30 и обраш,ены в сторону слива жидкости, благодаря чему часть энергии пара используется для организации движения жидкости по тарелке, обеспечивая равномерную работу по всей ее плоскости. Для предотвращения уноса жидкости на тарелке поперек движения жидкости установ- [c.331]

    В направлении, перпендикулярном движению жидкости, равномерность барботажа зависит от горизонтальности установки полотна тарелки, отсутствия волн и прогибов самого полотна, а также горизонтальности установки приемной (распределительной) и сливной планки, через которую жидкость сливается с тарелки. Горизонтальность тарелки приобретает решающее значение особенно для тарелок большого диаметра (5-10 м), поскольку допустимая разница высот от горизонтали по диаметру тарелки не должна превышать 3 мм. Установка с такой точностью крупных несущих балок, на которые опирается полотно тарелки, представляет непростую задачу. [c.512]

    Принимая движение жидкости равномерным, т. е. без инерционных явлений, выделенный элемент будет находиться под действием только двух сил — силы тяжести жидкости G и силы трения Т. [c.15]

    Эти реакторы имеют механическую мешалку с центральным валом и лопастями (лопатками), число которых обычно равно 6, реже 8 (рис.2). Лопасти могут быть прямыми или изогнутыми, часто их располагают в несколько ярусов, что обеспечивает более эффективное перемешивание больших объемов жидкости. В систему входят также отражательные перегородки — узкие металлические пластинки, прикрепленные к внутренним стенкам биореактора. Они предотвращают возникновение водоворотов и обеспечивают вихревое движение жидкости, равномерно распределяемое но всему объему реактора. Однако в ряде случаев они не могут быть применены (культивирование мицелиальных грибов), так как обрастают микроорганизмами (мицелием).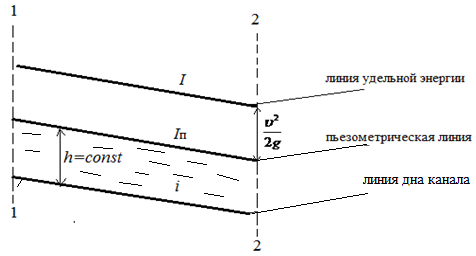 Нежное и медленное перемешивание создается в биореакторах, предназначаемых для выращивания ьслеток животных и (в меньшей степени) растений. [c.37]

    Основные сведения. Центробежные насосы относятся к группе лопастных насосов, в которых жидкость перекачивается под действием центробежной силы вращающегося лопастного рабочего колеса. Движение жидкости равномерное, без пульсаций. [c.100]

    Равномерным движением жидкости называется такое движение, при котором живые сечения потока одинаковы по всей его длине и скорость потока в соответствующих точках всех живых сечений также одинакова. Движение жидкости, при котором эти условия не выполняются, называется неравномерным. [c.13]

    Чем больше разность — р, тем сильнее колебание скорости жидкости, вытекающей из газового колпака в нагнетательный трубопровод. Движение жидкости в нагнетательном трубопроводе считают равномерным при тк 0,025. При определенном значении коэффициента неравномерности давления т, = 0,025 объем нагнетательного газового колпака определяют по формулам для пасоса одинарного действия [c.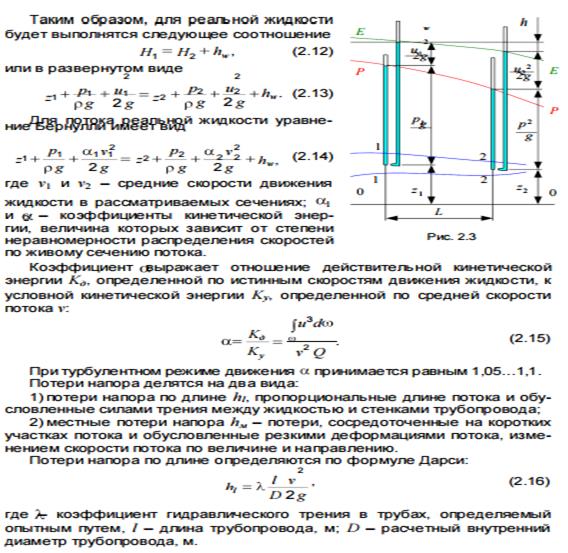 111]

    К аппаратам промышленных масштабов предъявляются требования, определяемые условиями их изготовления и эксплуатации. Прежде всего, промышленные аппараты для осуществления мембранных процессов, в том числе и для обратного осмоса и ультрафильтрации, должны иметь большую рабочую поверхность мембран в единице объема аппарата. Они должны быть простыми в сборке и монтаже ввиду необходимости периодической смены мембран. При движении жидкости по секциям или элементам аппарата она должна равномерно распределяться над мембранной поверхностью и иметь достаточно высокую скорость течения для снижения влияния концентрационной поляризации (см. стр. 170). При этом перепад давления в аппарате должен быть по возможности небольшим. Кроме того, необходимо выполнение всех требований, связанных с работой аппаратов при повышенных давлениях обеспечение механической прочности, герметичности и т. д. Создать аппарат, который в полной мере удовлетворяет всем требованиям, по-видимому, невозможно. Поэтому для каждого конкретного процесса разделения следует подбирать конструкцию аппарата, обеспечивающую наиболее выгодные условия проведения именно этого процесса. [c.115]

    Шарик термометра в приборе Тиле должен находиться на равном» удалении от стенок примерно посередине вертикального участка — там, где движение жидкости наиболее равномерное. Капилляр с веществом можно прикреплять непосредственно к термометру, например при помощи резинового колечка, [c.177]

    Организация движения жидкости на тарелке. Критериями правильной организации движения жидкости на тарелке являются малый градиент уровня жидкости на тарелке и нормальная работа сливных устройств. Равномерное распределение пара по сечению колпачковой тарелки достигается, если градиент уровня жидкости не превышает 20—25 мм, а нагрузка но жидкости 65 м /(м-ч). Если основные потери давления происходят в контактных элементах тарелки, то изменение градиента жидкости не оказывает решающего влияния на распределение паров по сечению. Рекомендуется соблюдать следующее соотношение между градиентом уровня жидкости и сопротивлением сухой тарелки АР с А = 2. [c.86]

    Чем меньше поршней (плунжеров), тем проще схема насоса и тем меньше сменных деталей, что очень важно в условиях интенсивного их износа. С другой стороны, увеличением рядов, в которых использованы стандартные детали, достигается повышение подачи и равномерности движения жидкости в трубопроводах (см. 39). [c.97]

    Работа по схеме г осуществлена на тарелке, у которой колпачки имеют отогнутые прорези. Проходя через такие прорези, газ создает направленный ноток жидкости и обеспечивает тем самым движение жидкости по тарелке единым потоком между колпачками. Достоинство подобной тарелки — равномерная работа и высокая эффективность ввиду большого пути жидкости однако такая тарелка пригодна лишь для работы с незначительными расходами жидкости. [c.133]

    Характерным и отличительным признаком в работе перекрестно-прямоточных тарелок является использование энергии пара для организации движения жидкости по тарелке и сепарации жидкости после осуществления контакта. Перекрестно-прямоточное движение пара и жидкости по тарелке обеспечивает равномерную работу тарелки по всей ее плоскости, т. е. исключает поперечную неравномерность, полностью или частично исключает обратное перемешивание жидкости на тарелке, улучшает сепарацию жидкости после осуществления контакта с помощью центробежных сил и, следовательно, применимы более высокие скорости пара. [c.135]

    При установившемся движении и одинаковой величине средних скоростей во всех поперечных сечениях потока имеем равномерное движение жидкости при изменении величин скоростей потока от сечения к сечению — неравномерное движение. [c.39]

    Сопротивление при равномерном движении жидкости по трубопроводу. При равномерном движении жидкости возникают силы [c.49]

    Из сказанного следует, что при турбулентном режиме скорости распределены более равномерно по сечению потока по сравнению с распределением скоростей при ламинарном режиме. Характерное распределение скоростей для каждого режима движения жидкости устанавливается на протяжении некоторого участка трубопровода, называемого начальным, длину которого рассчитывают по формулам  [c.54]

    При достаточном объеме воздушных колпаков движение жидкости в трубопроводах можно считать практически равномерным. [c.97]

    Объем воздуха в колпаке гораздо больше объема поступающей жидкости. Поэтому давление воздуха в колпаке при сжатии и расщирении воздуха изменяется незначительно, и движение жидкости в нагнетательном трубопроводе близко к равномерному. [c.211]

    При выводе формулы (8-23) не учитывался характер движения жидкости в отстойнике (возможность вихреобразований) и допускалось, что потоки равномерно распределяются по всей площади аппарата. Для Определения необходимой поверхности отстаивания следует теоретическую поверхность, рассчитанную по формуле (8-23), умножить на некоторый коэффициент, учитывающий влияние неравномерности отстаивания, вихреобразований и других факторов на реальный процесс отстаивания. Ориентировочно этот коэффициент можно принять равным 1,3. [c.250]

    Для нормальной работы барботажной тарелки должно быть обеспечено равномерное распределение потока паров по всей рабочей площади тарелки, т.е. гидравлическое сопротивление каждого контактного элемента (колпачка, клапана, отверстия) должно быть одинаковым. Этого можно достичь погружением контактных элементов в слой жидкости на одну и ту же глубину. Если высота слоя жидкости на тарелке меняется незначительно, что характерно для колонн относительно небольшого диаметра (обычно менее 1 м), то колпачки могут быть установлены на одном горизонтальном уровне. Для колонн большого диаметра и при значительных расходах жидкости, когда высота слоя жидкости на тарелке существенно меняется (более 10 мм), применяют разный уровень установки колпачков (более высокий у колпачков, расположенных ближе к входу жидкости на тарелку). Кроме того, устраивают несколько каскадов по пути движения жидкости или делят общий поток жидкости на несколько потоков (см. рис. У11-2, а-г). [c.230]

    Другим примером, иллюстрирующим различие времен пребывания, может служить рассмотрение профиля скоростей при движении жидкости по трубе (см. рис. II-10, стр. 45). Различия в скоростях по сечению наиболее велики при ламинарном течении. Поэтому частицы, движущиеся вблизи оси трубы, обгоняют частицы, движущиеся ближе к ее стенкам, и находятся в трубе значительно меньшее время, чем последние. При турбулентном течении скорости распределены по сечению трубы более равномерно. Однако и в данном случае время пребывания разных частиц жидкости неодинаково, что обусловлено турбулентными пульсациями, под действием которых происходит перемешивание частиц, или турбулентная диффузия различные частицы движутся в разных направлениях по отношению к движению основной массы потока, в том числе и в поперечном (радиальная диффузия), и в продольном (осевая диффузия). Осевая диффузия может как совпадать по направлению с движением основной массы потока, так и быть направлена в обратную сторону, в результате чего возникают различия во времени пребывания частиц жидкости. Радиальная же диффузия, выравнивая профиль скоростей, наоборот, сближает время пребывания разных частиц. [c.117]

    При этом давление воздуха, находящегося в колпаке, изменяется незначительно (поскольку его объем гораздо больше объема поступающей жидкости) и движение жидкости в нагнетательном (или всасывающем) трубопроводе становится близким к равномерному. [c.143]

    Измерения начинают через 5 мин после замыкания электрической цепи (для установления равномерного движения жидкости через диафрагму). За это время, наблюдая за направлением пере- [c.89]

    Как известно, в смесях газов и в растворах частицы равномерно распределяются по всему объему. Например, если на концентрированный раствор сахара осторожно налить слой чистой воды, то молекулы сахара, совершая хаотическое тепловое движение, постепенно равномерно распределяются по всему объему жидкости. Одновременно в молекулы воды проникают в раствор сахара, разбавляя его. Оба эти процесса идут самопроизвольно и до тех пор, пока не произойдет полное выравнивание концентрации [c.97]

    Аппараты с неподвижным слоем твердого материала. В этих аппаратах скорость движения жидкости при ее фильтровании сквозь слой практически совпадает по величине и направлению со скоростью обтекания. Простейшим аппаратом такого типа является открытый резервуар с ложным днищем (решеткой), подобный открытому нутч-фильтру (см. стр. 199). На решетку загружается слой твердого материала, через который сверху вниз протекает растворитель. При таком направлении движения жидкость равномерно заполняет сечение аппарата и не происходит смешения более концентрированного раствора с раствором низкой концентрации, приводящего к снижению движущей силы. Выгрузку выщелаченного твердого остатка производят периодически, чаще всего гидравлическим способом — вымывая твердый материал из аппарата водой. [c.556]

    ВНИЗ протекает растворитель. При таком направлении движения жидкость равномерно заполняет сечение аппарата и не происходит смешения более концентрированного раствора с раствором низкой концентрации, приводящего к сниженйю1 движущей силы. Выгрузку выщелоченного твердого остатка производят периодически, чаще всего гидравлическим способом — вымывая твердый материал из аппарата водой. [c.586]

    Отмечена сложность исследования равномерности проникания твердых ча стйц в пористый слой при разделении малоконцентрированных суспензий с тонкодисперсными частицами и вязкой жидкой фазой, что объяснено совместным влиянием ряда микрофакторов и небольшой глубиной проникания [128]. Распределение частиц по толщине слоя исследовано с помощью установки для фотометрирования интенсивности свечения люминофорных частиц, аккумулированных слоем. На фильтре с горизонтальной перегородкой из лавсановой ткани поверхностью 22,4 см формировался слой перлита путем разделения его суспензии в кремнийорганической жидкости при концентрации 2,5%. Затем на фильтре разделялась суспензия люминофорных частиц в той же жидкости при концентрации 0,01—0,25% и постоянной разности давлений. Установлено, что аккумулирование частиц в пористом слое происходит на относительно небольшой глубине, которая не зависит от времени фильтрования при данной концентрации, но существенно увеличивается при ее уменьшении с повышением вязкости жидкой фазы глубина проникания частиц также увеличивается. Последнее объяснено следующим образом. При изменении направления движения жидкости в извилистой поре сила инерции приближает твердую частицу к стенкам поры, что сопровождается торможением частицы и уменьшением глубины ёе проникания в пористый слой. При увеличении силы трения, обусловленной повышением вязкости жидкости, приближение твердой частицы к стенкам поры затрудняется и глубина ее проникания в пористый слой увеличивается. [c.111]

    В дифференциальном насосе (см. рис. 8.1,з) объем Кз такой же, как в на сосе одностороннего действия, но движение жидкости в отводящей трубе более равномерное. Кроме того, в той же степени снижено усилие по штоку. Если / = f/2, то нагрузка на шток одинаковая независимо от направления движения поршня. В этом достоинство дифференциального насоса. Вследствие недостатков — наличия сальника и непроточной штоковой камеры, являющейся местом накапливания осадков (песка, утяжелителя и т. п.) и усложнения конструкции дифференциальный насос (см. рис. 8.1,з) распространения не получил. Однако в скважинном исполнении плунжерный вариант дифференциального насоса (см. рис. 8.1, г) оказался наиболее экономичным. [c.97]

    Для обычных технических целей задача об определении параметров пневмокомпенсатора удовлетворительно решается описанным методом. При правильном выборе и настройке гасители пульсаций придают возвратно-поступательным насосам положительные свойства машин вращательного действия — почти равномерное движение жидкости в присоединяемых к ним трубопроводах. [c.115]

    Тарелки, которые можно отнести также к перекрестно-прямоточным, изображены на рис. 60. В данных конструкциях ввиду наличия составляющей скорости газа, направленной в сторону движения жидкости, достигается увеличение производительности по сравнению с обычными ситчатыми тарелками. В последнем случае одностороннее направление потока паров осуществляется за счет отверстий, расположенных преимущественно с одной стороны 5-образного элемента. Отогнутые кромки элемента иод отверстиями создают увеличенную скорость газа при входе в отверстие, что способствует более равномерному вступлению тарелки в работу. К перекрестно-прямоточным провальным тарелкам можно отнести тарелки тииа Киттеля [164]. Движение жидкости на одной такой тарелке происходит по спирали от центра к периферии, на другой — ио радиусу от периферии к центру. Столь сложное движение жидкости осуществляется за счет кинетической энергии паров, так как пары выходят под определенным углом к основанию тарелки благодаря направлению просечки у листов основания. Слив жидкости на одной тарелке осуществляется у периферии, на другой — в центре. Организованное движение жидкости создает места ее скопления и увеличивает статическое давление жидкости в этих местах, что так же, как и на ситчатых волнистых тарелках, повышает их производительность. Кроме того, круговое движение пара в межтаре-лочном пространстве создает благоприятные условия для сепарации жидкости. Тарелки Киттеля в США имеют ограниченное применение и широко используются в других капиталистических странах. Текущие затраты на колонну с тарелками Киттеля составляют в среднем 65— [c.136]

    Перекрестноточные тарелки характеризуются наибольшей разделительной способностью, поскольку время пребывания жидкости на них наибольшее по сравнению с другими типами тарелок. Перекрестнопрямоточные тарелки по сравнению с перекрестноточными обладают (благодаря организации направленного движения жидкости по тарелке) повышенной производительностью и лучшей равномерностью работы по сечению колонны. Как перекрестноточные, так и перекрестнопрямоточные тарелки можно подразделить еще на два подтипа с нерегулируемым и регулируемым сечением контакта фаз. Последние (особенно балластные) по сравнению с таре лками с нерегулируемым сечением контакта фаз (колпачкового, желобчатого, 5-образного, ситчатого, струйного и др. типов) обладают значительно более широким диапазоном эффективной работоспособности и находят в последние годы преимущественное применение. [c.36]

    Роль распределительной головки в злектродегидраторе весьма разнообразна она должна не только обеспечивать веерообразное поступление сырья в зону между электродами, но и сообщать вытекающей из нее жидкости значительную скорость, чтобы эта жидкость, получив соответствующий запас кинетической энергии, двигалась в межэлектродном пространстве от центра к стенкам аппарата. При этом обеспечивается, во-первых, равномерная загрузка эмульсией всего электрического поля, создаваемого электродамп, во-вторых, поперечное движение жидкости в зоне между электродами. При движении по горизонтали, перпендикулярно электрическим силовым линиям поля разрушаются водяные цепочки, образующиеся вдоль этих линий и отрицательно влияющие на процесс деэмульгирования нефти. При наличии большого количества цепочек значительно повышается электропроводность столба жидкости между электродами, следовательно, резко увеличивается сила тока. При образовании сплошных цепочек от электрода к электроду возникает короткое замыкание. [c.53]

    Над решеткой находится слс(й подвижной пены, в котором движение газа происходит снизу вверх, а движение жидкости — по го-рйзонтали вдоль решетки с поступательной скоростью 0,02—1,0 м/с. Жидкость подают на решетку через патрубок в приемную коробку, которая обеспечивает равномерное поступление жидкости по всей ширине (или дуге сектора) решетки. Газ подают в подрешеточную часть через патрубок или диффузор. После взаимодействия с жидкостью газ выводится из аппарата через верхний штуцер, прнчем важно обеспечить равномерный отвод со всей плой ади сечения аппарата. Пройдя решетку, жидкость в виде пены поступает череа порог и сливное отверстие в сливную коробку, где пена разрушается и жидкость стекает через патрубок в гидравлический затвор. Освободившийся газ возвращается в аппарат. [c.17]

    Задачам свободной конвекции на изотермических или равномерно обогреваемых вертикальных пластинах уделялось большое внимание, поскольку они ие только отличаются простотой, ио и имеют практическое значение. Теоретические решения задач для этой геометрии большей частью основаны на предположениях о том, что пластина, погруженная в бесконечно большой объем жидкости, имеет бесконечную ширину и полуограничена по длине вверх по потоку движение жидкости ниже нижней кромки пластины отсутствует. iIeeмoтpя на эти упрощения получаемые решения дают правильные по структуре зависимости для корреляции экспериментальных данных. Аналогичный вид зависимостей оказывается пригодным и для других геометрий и условий. Поэтому сначала рассматриваются теоретические решения, а затем экспериментальные результаты. [c.274]

---

Основное уравнение равномерного движения. Статьи компании «ООО Гидро-Максимум»

Равномерным движением называется установившееся движение, при котором скорости частиц жидкости не изменяются вдоль траекторий. При равномерном движении жидкости в водопроводах, а также в открытых руслах живые сечения, средние скорости течения и глубины по длине потока остаются постоянными.

Выведем основное уравнение равномерного движения, на основании которого выявим факторы, влияющие на величину гидравлических потерь по длине трубопровода.

Рассмотрим поток жидкости произвольной формы площадью , имеющий по длине постоянное живое сечение и наклоненный к горизонту под углом(рис. 5.1). Выделим в потоке сечениями 1-1 и 2-2 отсек длинойl. Действие отброшенной жидкости слева и справа заменим давлениями р₁ и р₂, которые создают внешние силы, приводящие жидкость в движение: ;. К ним относятся и сила тяжести отсека жидкости:

.

Рис.5.1

На жидкость действуют также силы сопротивления движению. Эти силы приложены вдоль поверхности стенок. Обозначим через удельную силу трения, через– длину смоченного периметра. Тогда сила трения

.

Составим уравнение равновесия сил, действующих на выделенный отсек.

По условию равномерного движения, внешние силы, приводящие жидкость в движение, должны быть равны силам сопротивления, т.е. если спроектировать все силы на ось потока, получим

,

где  .

Тогда получим

.

 

Разделим все слагаемые на  и сгруппируем

. (5.1)

Сравним выражение (5.1) с уравнением Бернулли для потока реальной жидкости:

.

 

 

 

Так как V₁ = V₂, то

. (5.2)

Так как — гидравлический радиус, то выражение (5.2) представим в виде

. (5.3)

разделим левую и правую часть выражения (5.3) на l:

 или

. (5.4)

Выражения (5.2), (5.3) и (5.4) являются уравнениями равномерного движения.

 

Формулы для определения гидравлических потерь

Линейные потери. Основной формулой линейных потерь, наиболее полно вскрывающей их суть, является формула Дарси – Вейсбаха:

, (5.5)

где — коэффициент гидравлического трения, он зависит от режима движения жидкости и относительной шероховатости, т.е.;- соответственно длина и диаметр трубопровода;- скорость движения жидкости.

Формула (5.5) является универсальной. По ней можно подсчитать линейные потери в трубопроводах любого назначения, но в настоящее время этой формулой пользуются при расчете объемного гидравлического привода.

при расчете водопроводных систем широко используются табличные методы. Так линейные потери можно определить по формуле

, (5.6)

где — гидравлический уклон, т.е. потери, приходящиеся на единицу длины трубопровода, берется из таблиц в зависимости от материала трубопровода, его диаметра и расхода;l — длина расчетного участка трубопровода.

Линейные потери водопроводных систем определяются так же по зависимости

, (5.7)

где l — длина расчетного участка; Q — расход по участку; К — расходная характеристика, берется из таблиц в зависимости от материала трубопровода и его диаметра.

рассмотрим особенности расчета безнапорных систем, каковыми являются каналы, лотки и т.п. устройства.

Рис.5.2

При равномерном движении жидкости в подобных системах уравнение Бернулли для потока реальной жидкости, составленное для сечений 1-1 и 2-2 (рис.5.2) имеет вид

,

т.е. разница геометрических напоров затрачивается на преодоление линейных потерь. Таким образомт движение жидкости обеспечивается наличием гидравлического уклона i, который в данном случае равен геометрическому:

Поэтому при проектировании каналов большой протяженности используют естественный уклон местности и в этом случае определяют пропускную способность канала и его размеры по формуле Шези:

 (5.8)

где — живое сечение канала;R — гидравлический радиус; С — коэффициент Шези, который зависит от гидравлического радиуса и коэффициента шероховатости.

Коэффициент Шези берется из таблиц или определяется по формулам, например, по формуле Маннинга

.

 

 

При необходимости решаются и другие задачи.

Местные потери. Для их определения пользуются единственной формулой

, (5.9)

где — коэффициент местного сопротивления, берется из таблиц и графиков, вычисляется по специальным формулам в зависимости от вида местного сопротивления;V — скорость движения жидкости в трубопроводе, где установлено местное сопротивление.

 

Основное уравнение равномерного движения жидкости

Содержание:

Основное уравнение равномерного движения жидкости

Основное уравнение равномерного движения жидкости. Рассмотрим устойчивое, равномерное (продольно равномерное) движение жидкости в произвольной поперечной цилиндрической трубе Длина секции b (рис. 5.11).Используйте уравнения, представляющие законы изменения импульса. Это векторная форма любого объема V, заключенного в поверхность A、 Проекция членов этого уравнения на ось совпадает с направлением скорости жидкости. Где; проекция вектора скорости на ось C, очевидно, и= И = |и|; проекция вектора плотности распределения внешних объемных сил на ось B I. определить напряжения pn/, принимая во внимание N ca1 в противоположном направлении от 1U a и u в том же направлении (и принимая во внимание раздел 5.1 леммы 1).

Если сторона потока представляет собой неподвижную твердую поверхность, то знак минус вводится таким образом, чтобы касательное напряжение m было положительным. Людмила Фирмаль

• В этом случае pn /-тангенциальное напряжение, действующее со стороны Abok (перпендикулярно этой поверхности n) и ориентированное вдоль оси (pn и pn-нормальные напряжения поверхности сечение O и ω соответственно).в результате это выглядит так: Внутрь!»: РП= РПП = ПП на СО2 ’■Пн; = + Р»= » П2; А6 (Вт: РШ-напряжение сдвига. Поскольку движение является устойчивым, локальная составляющая реальной производной равна нулю, а при равномерном (продольно равномерном) движении плотность распределения импульса ri вдоль потока не изменяется, и, следовательно, конвективная составляющая реальной производной также равна нулю. = M. Поскольку движения равномерны, можно взять полосу 1lZX в качестве элемента B. где b-длина выделенного управляющего объема, а 6X-основная длина смачиваемого участка (см. рис. 5.11).

Форма интеграла в этом случае имеет вид (5.63) если вы подставляете (5.65) в исходное уравнение (5.62)、 поскольку bx и r2 соответствуют любым соответствующим точкам в разделах 1-1 и 2-2, мы предполагаем, что это вертикальные координаты центроида разделов 1-1 и 2-2.Если разделить все члены уравнения (5.66) на p&W. Если движение в разрезе равномерное, как описано выше、 Где H-потенциальное давление. Имея это в виду, он представляет(5.67) в виде: Где I-пьезоэлектрическое смещение. Это общий вид основных уравнений равномерного движения.

Более широко эта формула используется в некоторых случаях, когда m является постоянным во всех точках вокруг увлажненной области. Людмила Фирмаль

• Это условие выполняется точно в цилиндрической форме и почти точно в прямоугольных каналах, которые очень широки. Уравнение(5.69) преобразуется в следующий вид Уравнения (5.71) и (5.72) используются не только для описанных выше случаев, но и для каналов с различными формами поперечного сечения, вводя в эти уравнения среднее касательное касательное напряжение вместо X. В заключение отметим, что при равномерном движении она равна 3 = 1e. при использовании формул (571) и (572) это учитывается далее.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Геометрическая и энергетическая интерпретации слагаемых, входящих в уравнение Бернулли.
2. Потенциальный и полный (гидродинамический) напоры. Пьезометрическая и напорная линии.
3. Два режима движения жидкости.
4. Потери напора при установившемся равномерном движении жидкости (потери по длине).

Основное уравнение равномерного движения жидкости

Формула Шези

Равномерное движение жидкости мы можем наблюдать во многих случаях жизни. Это может быть установившееся движение жидкости в каналах, водопроводных трубах и т.п. Условием равномерного движения является постоянство живого сечения, скорости течения и глубины по длине по длине потока.

Для вывода основного уравнения движения жидкости необходимо рассмотреть часть потока, ограниченного сечениями 1 – 1 и 2 – 2 и составить уравнение баланса сил, спроектированных на ось движения потока

Р₁ – Р₂ + G sin α – T_тр = 0 . (3.48)

Здесь Р₁ = р₁ω и Р₂ = р₂ω – суммарные силы гидростатического давления в соответствующих сечениях; G – сила тяжести части потока в объёме W = ωl

G = ρ∙g∙ω∙l, (3.49)

α – угол наклона оси потока;

Рис.3.9 sin α = . (3.50)

Т_тр– суммарная сила трения потока о стенки

Т_тр = τ₀ S = τ₀ f l , (3.51)

где τ₀∙ – касательные напряжения между жидкостью и стенкой трубы; f – смоченный периметр; l – длина участка трубы, ограниченного сечениями 1- 1 и 2-2.

Если подставить соответствующие значения суммарных сил давления, а также (3.49), (3.50) в уравнение (3.48) и поделить на ρgω, то получим

. (3.52)

Перегруппируем составляющие уравнения (3.53)

. (3.54)

Левая часть уравнения (3.54) в условиях равномерного движения выражает потерю напора на рассматриваемом участке движения жидкости, тогда

,

или

. (3.55)

Поскольку (гидравлический радиус), а (гидравлический уклон), окончательно получим

. (3.56)

Зависимость (3.56) есть основное уравнение равномерного движения жидкости, которое показывает, что касательные напряжения, отнесённые к удельному весу жидкости, равны произведению гидравлического радиуса на гидравлический уклон.

Из уравнения (3.56) можно вывести формулу Шези для определения средней скорости потока.

Многочисленными опытами подтверждается, что при развитом турбулентном движении жидкости, отношение пропорционально средней скорости потока, то есть

, (3.57)

где b – коэффициент пропорциональности, тогда

RI = bv².^(3.58)

 

или средняя скорость равна

. (3.59)

Обозначим , тогда

. (3.60)

 

Формулу (3.60) называют формулой Шези для определения средней скорости потока. Для определения расхода жидкости используют формулу Шези в следующем виде

, (3.61)

где С – скоростной множитель или коэффициент Шези. Он может быть определён по формуле академика Н.Н. Павловского или по формуле Базена.

 

Узнать еще:

Uniform Flow — обзор

V Inviscid Incompressible Flow

Несжимаемый поток — это поток с постоянной плотностью. Невязкий поток — это течение, в котором явления переноса диффузии массы, вязкости и теплопроводности пренебрежимо малы. При этих двух предположениях, основные уравнения движения, уравнения. (1) — (5) существенно упрощаются: уравнение (1) сводится к

(6) ∇⋅V = 0,

, что является уравнением неразрывности для несжимаемого потока. (2) — (4) объединить — и уменьшить до

(7) p1 + 12ρV12 = p2 + 12ρV22.

Уравнение (7) — это знаменитое уравнение Бернулли, которое связывает давление и скорость в двух разных точках вдоль линии тока. Другой способ записи уравнения Бернулли:

(8) p + 12ρV2 = постоянная

вдоль линии тока. Если все линии тока потока происходят из однородного резервуара (например, резервуара аэродинамической трубы или атмосферы далеко впереди движущегося летательного аппарата), то постоянная inEq. (8) одинаково для всех линий тока, а формула (7) затем связывает давление и скорость в любых двух точках потока, не обязательно на одной и той же линии тока.Для невязкого несжимаемого потока уравнение энергии [Ур. (5)] также сведется к уравнению Бернулли; следовательно, уравнение энергии для такого потока является избыточным и не требуется. Следовательно, уравнение Бернулли можно рассматривать как утверждение второго закона Ньютона, F ​​ = ma , и как утверждение сохранения механической энергии в невязком несжимаемом потоке.

Уравнение Бернулли используется во многих приложениях низкоскоростной аэродинамики: обтекание аэродинамических поверхностей, обтекание воздуховодов и использование трубки Пито для измерения воздушной скорости, и это лишь некоторые из них.Рассмотрим подробнее последний пункт, упомянутый выше, а именно трубку Пито.

В 1732 году француз Анри Пито пытался измерить скорость течения реки Сены в Париже. Одним из инструментов, которые он использовал, было его собственное изобретение — трубка странного вида, изогнутая в форме, как показано на рис. 6. Пито сориентировал один из открытых концов трубки так, чтобы он смотрел прямо в поток. В свою очередь, он использовал давление внутри этой трубки для измерения скорости потока воды. Это был первый случай в истории, когда было произведено правильное измерение скорости жидкости, и изобретение Пито сохранилось до наших дней в виде трубки Пито — одного из наиболее распространенных и часто используемых инструментов в любой современной аэродинамической лаборатории.Кроме того, трубка Пито — наиболее распространенный прибор для измерения скорости полета самолетов. Цель этого раздела — описать основной принцип работы трубки Пито.

РИСУНОК 6. Иллюстрация измерений Пито и статического давления. [Из Андерсона, Дж. Д., младшего (2001). «Основы аэродинамики», 3-е изд., МакГроу-Хилл, Нью-Йорк]

Рассмотрим поток с давлением p ₁ , движущийся со скоростью V ₁ , как показано слева на Рис.6. Рассмотрим подробнее значение давления p ₁ . Давление связано со скоростью изменения количества движения молекул газа, ударяющихся о поверхность или пересекающих ее; то есть давление явно связано с движением молекул. Это движение очень случайное, молекулы движутся во всех направлениях с разными скоростями. Теперь представьте, что вы запрыгиваете на жидкий элемент потока и едете с ним со скоростью V ₁ .Молекулы газа из-за своего беспорядочного движения все равно будут сталкиваться с вами, и вы почувствуете давление газа p ₁ . Теперь мы даем этому давлению конкретное название: статическое давление. Статическое давление — это мера чисто случайного движения молекул в газе; это давление, которое вы чувствуете, когда едете вместе с газом с местной скоростью потока. Все значения давления, использованные до сих пор в этой статье, были статическими; давление p , фигурирующее во всех наших предыдущих уравнениях, было статическим давлением.В технике всякий раз, когда делается ссылка на «давление» без дополнительных уточнений, это давление всегда интерпретируется как статическое давление. Кроме того, рассмотрите границу потока, например стену, в которой просверливается небольшое отверстие перпендикулярно поверхности. Плоскость отверстия параллельна потоку, как показано в точке А на рис. 6. Поскольку поток движется над отверстием, давление, ощущаемое в точке A, возникает только из-за беспорядочного движения молекул; то есть в точке А измеряется статическое давление.Такое маленькое отверстие в поверхности называется отверстием статического давления или отводом статического давления.

Напротив, примите во внимание, что трубка Пито теперь вставлена ​​в поток с открытым концом, обращенным непосредственно в поток. То есть плоскость отверстия трубки перпендикулярна потоку, как показано в точке B на фиг. 6. Другой конец трубки Пито подсоединяется к манометру, например к точке C на Рис. 6; то есть трубка Пито закрыта в точке C. В течение первых нескольких миллисекунд после того, как трубка Пито вставлена ​​в поток, газ устремляется в открытый конец и заполняет трубку.Однако в точке C трубка закрыта; газу некуда идти, а значит, после непродолжительного периода регулировки газ внутри трубки застаивается; то есть скорость газа внутри трубки будет равна нулю. Действительно, газ в конечном итоге будет скапливаться и застаиваться повсюду внутри трубы, в том числе в открытом отверстии в точке B. видит это лицо как препятствие для потока.Элементы жидкости вдоль линии тока DB замедляются по мере приближения к трубке Пито и переходят к нулевой скорости прямо в точке B. Любая точка в потоке, где V = 0, называется точкой торможения потока; следовательно, точка B на открытой поверхности трубки Пито является точкой торможения, где V _B = 0. В свою очередь, из уравнения Бернулли мы знаем, что давление увеличивается с уменьшением скорости. Следовательно, p _B > p ₁ . Давление в точке застоя называется давлением застоя или общим давлением и обозначается как p ₀ .Следовательно, в точке B p _B = p ₀ .

Из приведенного выше обсуждения мы видим, что для данного потока можно определить два типа давления: статическое давление, которое представляет собой давление, которое вы ощущаете при движении с потоком с его локальной скоростью V ₁ , и полное давление. , которое представляет собой давление, которое достигает поток, когда скорость изоэнтропически уменьшается до нуля.

Как трубка Пито используется для измерения скорости потока? Чтобы ответить на этот вопрос, сначала обратите внимание, что полное давление p ₀ , оказываемое потоком на входе в трубку (точка B), воздействует на всю трубку (внутри трубки нет потока; следовательно, давление повсюду внутри трубки). трубка р ₀ ).Следовательно, манометр в точке C показывает p ₀ . Это измерение вместе с измерением статического давления p ₁ в точке A дает разность между полным и статическим давлением, p ₀ — p ₁ , и именно это давление разница, которая позволяет вычислить В ₁ с помощью уравнения Бернулли. В частности, примените уравнение Бернулли между точкой A, где давление и скорость равны p ₁ и V ₁ , соответственно, и точкой B, где давление и скорость равны p ₀ и V = 0 соответственно:

pA + 12ρVA1 = pB + 12ρVB2

или

p1 + 12ρV12 = p0 + 0.

Решая для V ₁ , получаем

V1 = 2 (p0 − p1) ρ.

Приведенное выше уравнение позволяет вычислить скорость просто по измеренной разнице между общим и статическим давлением. Общее давление p ₀ получается из трубки Пито, а статическое давление p ₁ получается из подходящим образом размещенного отвода статического давления.

Можно объединить измерение как полного, так и статического давления в одном приборе, статическом датчике Пито.Датчик статического давления Пито измеряет p ₀ на носике зонда и p ₁ при подходящем размещении отвода статического давления на поверхности зонда ниже по потоку от носа.

InEq. (8) группа 12ρ V ² называется по определению динамическим давлением и используется во всех потоках, несжимаемых до гиперзвуковых:

Динамическое давление 12ρV2.

Однако для несжимаемого потока динамическое давление имеет особое значение; это как раз разница между общим и статическим давлением:

q = p0 − p.

Важно помнить, что это соотношение исходит из уравнения Бернулли и, следовательно, справедливо только для несжимаемого потока. Для сжимаемого потока, где уравнение Бернулли не действует, перепад давления p ₀ — p не равен q . Скорости сжимаемых потоков, как дозвуковых, так и сверхзвуковых, можно измерить с помощью трубки Пито, но уравнения отличаются от приведенных выше. (Измерения скорости в дозвуковых и сверхзвуковых сжимаемых потоках обсуждаются в разделе VI.)

В аэродинамике полезно определить безразмерное давление как

(9) Cp≡p − p∞q∞,

, где q _∞ = 12ρ _∞ V _∞ ² , где C _p определяется как коэффициент давления , используемый во всей аэродинамике, от несжимаемого до гиперзвукового потока. В аэродинамической литературе очень часто встречаются значения давления, выраженные в единицах C _p , а не само давление.Для расход несжимаемой жидкости , C _p можно выразить только через скорость. Применяя уравнение Бернулли к уравнению. (9) результат для несжимаемого потока

(10) Cp = 1− (V / V∞) 2.

Коэффициент давления — это больше, чем просто безразмерное давление; это параметр подобия в том же смысле, что и C _L и C _D , и для данной формы тела, угла атаки и геометрически подобного местоположения в потоке C _p = f ( M _∞ , Re _∞ , Pr _∞ ).

При общем рассмотрении невязких, несжимаемых, безвихревых потоков основные управляющие уравнения сводятся к уравнению Лапласа в терминах потенциала скорости. Комбинирование (6) с безвихревым выражением V = ▿ϕ, мы непосредственно получаем

(11) ∇2ϕ = ∂2ϕ∂x2 + ∂2ϕ∂y2 + ∂2ϕ∂z2 = 0,

, что составляет уравнение Лапласа —one из самых знакомых уравнений из математической физики. Следовательно, решения несжимаемых, невязких, безвихревых потоков называются решениями потенциальных потоков.

В теоретической аэродинамике иногда используется концепция функции тока. По определению функция тока ψ¯ является постоянной вдоль данной линии тока, а изменение ψ¯, Δψ¯ между двумя линиями тока равно потоку массы между этими линиями тока. Для несжимаемого потока определена модифицированная функция тока ψ так, что Δψ¯ между двумя линиями тока равняется объемному расходу между линиями тока. Из определения функции тока можно показать, что скорость потока может быть найдена путем дифференцирования ψ, например,

(12) ∇2ψ = ∂2ψ∂x2 + ∂2ψ∂y2 + ∂2ψ∂z2 = 0.

Следовательно, для таких потоков уравнение Лапласа управляет как ϕ, так и ψ. Более того, в поле течения линии постоянного ψ (т. Е. Линии тока) всюду ортогональны линиям постоянного ϕ (т. Е. Эквипотенциальным линиям).

Уравнение Лапласа является линейным, и, следовательно, любое количество частных решений, например ϕ ₁ , ϕ ₂ , ϕ ₃ и ϕ ₄ , может быть добавлено для получения другого решения, скажем ϕ ₅ :

ϕ5 = ϕ1 + ϕ2 + ϕ3 + ϕ4.

Это позволяет синтезировать решение данного потенциального потока путем наложения ряда других, более элементарных потоков.Это основная стратегия, лежащая в основе решения невязких несжимаемых безвихревых потоков. При синтезе таких потоков полезны следующие элементарные потоки.

1.

Равномерный поток. Поток с постоянными свойствами при скорости V _∞ , с прямыми линиями тока, ориентированными в одном направлении (например, направление x ),

ϕ1 = V∞x = V∞rcosθψ1 = V∞y = V∞rsinθ

, где r и θ — полярные координаты.

2.

Исходный поток (в двух измерениях).Линии тока — это прямые линии, исходящие из центральной точки (скажем, начала системы координат), где скорость вдоль каждой линии тока изменяется обратно пропорционально расстоянию от центральной точки. В полярных координатах

ϕ2 = Λ2πlnrψ2 = Λ2πθ,

, где Λ — мощность источника, определяемая как скорость объемного потока из источника. Отрицательное значение Λ обозначает сток , где поток движется к центральной точке.

3.

Исходный поток (в трех измерениях).Поток с прямыми линиями тока, исходящий в трех измерениях из начала координат, где скорость изменяется обратно пропорционально квадрату расстояния от начала координат, и

ϕ3 = −λ4πr,

, где λ — сила источника, то есть скорость объемный расход от источника. Для стока λ отрицательно.

4.

Дублетный поток (в двух измерениях). Суперпозиция источника и стока равной, но противоположной силы, Λ и — Λ, где расстояние l между ними приближается к нулю, в то время как произведение Λ l остается постоянным.Прочность дублета κ ≡ Λ l . В полярных координатах

ϕ4 = (κ2π) cosθrψ4 = — (κ2π) sinθr.

5.

Дублетный поток (в трех измерениях). Суперпозиция трехмерного источника и стока равной, но противоположной силы, λ и -λ, где расстояние l между ними приближается к нулю, в то же время произведение μ = λ l остается постоянным. В сферических координатах

ϕ5 = — (μ4π) cosθr2.

6.

Вихревой поток (в двух измерениях). Линии тока представляют собой концентрические круги вокруг данной центральной точки, где скорость вдоль любой данной круговой линии тока постоянна, но изменяется от одной линии тока к другой обратно пропорционально расстоянию от общего центра. В полярных координатах с началом в центральной точке,

ϕ6 = −Γ2πθψ6 = Γ2πlnr,

, где Ɣ — сила вихря, определяемая как циркуляция вокруг вихря.

Термин «циркуляция», введенный выше, является общим понятием в аэродинамике и особенно полезен при анализе низкоскоростных аэродинамических поверхностей и крыльев.Тираж определен как

Γ = −∮V⋅ds.

То есть циркуляция — это линейный интеграл скорости потока, проинтегрированный по замкнутой кривой C, проведенной в потоке. Для вихревого потока сила вихря Ɣ — это циркуляция, взятая вокруг любой замкнутой кривой, охватывающей центральную точку.

Шесть описанных выше элементарных потоков сами по себе не являются практическими полями потоков. Однако они могут быть наложены различными способами для синтеза практических потоков в двух и трех измерениях, таких как потоки над цилиндрами, сферами, аэродинамическими профилями, крыльями и целыми самолетами.Например, ниже описаны три таких потока. Имейте в виду, что выражения, приведенные для ϕ и ψ для элементарных потоков, являются решениями уравнения Лапласа для этих потоков, и поэтому такие решения можно складывать вместе (накладывать друг на друга) для получения других решений.

1.

Неподъемный поток над круговым цилиндром. Этот симметричный поток синтезируется путем суперпозиции однородного потока с дублетом, что дает функцию тока для цилиндра радиусом R в набегающем потоке со скоростью V _∞ :

ψ = (V∞rsinθ) (1 − R2r2).

Результирующее изменение коэффициента давления по поверхности цилиндра симметрично и равно

Cp = 1−4sin2θ.

Поскольку изменение давления является симметричным, для цилиндра теоретически не прогнозируется подъемная сила или сопротивление.

2.

Подъемный поток над круговым цилиндром. Фактически, круговой цилиндр, вращающийся вокруг своей оси и погруженный в поток со скоростью V _∞ , будет испытывать подъемную силу. Это связано с тем, что эффект трения между жидкостью и вращающимся цилиндром имеет тенденцию увеличивать скорость потока на одной стороне цилиндра и уменьшать скорость потока на другой стороне.Согласно уравнению Бернулли, эти неравные скорости приводят к неравным давлениям с обеих сторон цилиндра, вызывая создание подъемной силы. Это явление иногда называют «эффектом Магнуса». Кривая вращающегося бейсбольного мяча и крючок или кусочек вращающегося мяча для гольфа являются примерами эффекта Магнуса. В этом случае для цилиндра радиуса R в потоке со скоростью V _∞ подъемный поток синтезируется суперпозицией равномерного потока, дублета и вихря, что дает

ψ = ( V∞rsinθ) (1 − R2r2) + Γ2πlnrR.

Полученное распределение коэффициента давления не является симметричным и определяется как

Cp = 1− [4sin2θ + 2ΓsinθπRV∞ + (Γ2πRV∞)].

В свою очередь, это дает теоретическое значение подъемной силы и сопротивления на единицу пролета цилиндра как

L = ρ∞V∞ΓD = 0,

, где Ɣ — величина циркуляции вокруг цилиндра, которая также равна силе элементарного вихря, используемого в процессе суперпозиции.

3.

Неподъемное течение по сфере. Этот поток синтезируется суперпозицией однородного потока и трехмерного дублета, давая результат для изменения коэффициента давления по сферической поверхности как

Cp = 1−94sin2θ.

Это симметричное распределение давления, которое приводит к теоретическим результатам нулевой подъемной силы и нулевого сопротивления.

Теоретический результат, заключающийся в том, что сопротивление равно нулю для всех вышеупомянутых потоков, называется парадоксом Даламбера и является следствием пренебрежения трением в теории. В действительности поверхностное трение и отрыв потока от поверхности — оба эффекта вязкости — создают конечное сопротивление любому реальному аэродинамическому телу.

Однако теоретический результат для подъемной силы, полученный для подъемного цилиндра, вполне реален, а именно:

L = ρ∞V∞Γ.

Этот результат является общим результатом для невязкой несжимаемой жидкости над цилиндрическим телом любой произвольной формы и называется теоремой Кутта – Жуковского . В нем говорится, что подъемная сила на единицу пролета вдоль тела прямо пропорциональна циркуляции вокруг тела. Этот результат является основным направлением теории циркуляции подъемной силы, впервые разработанной в начале 1900-х годов и до сих пор использующейся для прогнозирования подъемных характеристик низкоскоростных тел.

Для источников, вихрей и дублетных потоков, описанных выше, центр потока может рассматриваться как -точечный -источник, -точечный -вихрь или -точечный -дублет, где точка является сингулярностью, поскольку скорость идет до бесконечность в центре.Это приводит к общему теоретическому подходу, в котором поле потока над телом общей формы вычисляется путем распределения таких сингулярностей по поверхности и вычисления силы этих сингулярностей таким образом, что в сочетании с однородным набегающим потоком форма тела становится линией тока. потока. Более того, для профиля с острой задней кромкой поток должен плавно уходить на задней кромке; это по сравнению с другими возможными решениями, когда он может покинуть поверхность в какой-либо другой точке профиля.Действительно, место, где поток покидает поверхность, является функцией количества циркуляции Ɣ, имеющейся вокруг аэродинамического профиля. Природа выбирает только правильное значение Ɣ, чтобы поток всегда плавно уходил на острой задней кромке. Это называется условием Кутта . Если аэродинамический профиль достаточно тонкий и угол атаки мал, приближенная теория, основанная на идее распределенных сингулярностей, упомянутых выше (теория тонкого аэродинамического профиля), приводит к следующему результату для скорости изменения коэффициента подъемной силы c ₁ в зависимости от угла атаки: dc ₁ / d α = 2π (на радиан).То есть для малых углов атаки коэффициент подъемной силы изменяется линейно с углом атаки — результат, подтвержденный экспериментом.

Чтобы дополнительно проиллюстрировать аэродинамические свойства крыльев на малых скоростях, на рис. 7a и 7b показаны экспериментальные данные для профиля 2412 Национального консультативного комитета по аэронавтике (NACA); здесь коэффициент подъемной силы c ₁ и коэффициент момента около четверти хорды cmc / 4 показаны как функция угла атаки α (рис. 7a), а коэффициент лобового сопротивления c _d и коэффициент момента около аэродинамический центр CMA.c. показаны как функции от c ₁ (рис. 7b). Аэродинамический центр определяется как точка на профиле, в которой моменты не меняются в зависимости от угла атаки, как это ясно видно на рис. 7b.

РИСУНОК 7. Коэффициенты подъемной силы и момента в зависимости от угла атаки для обычного профиля. (b) Коэффициенты сопротивления и момента в зависимости от коэффициента подъемной силы для обычного профиля.

Для трехмерных тел. также используется концепция распределенных особенностей по поверхности тела.Исторически для конечного крыла эти особенности имели форму ряда вихревых нитей (дискретных линий завихренности) в форме подковы, причем один сегмент проходил по размаху крыла (так называемая «линия подъема»). ), а другие сегменты уходят вниз по потоку в след за крылом. Эта теория подъемной линии, разработанная Людвигом Прандтлем (1875–1953), привела к первому разумному расчету подъемной силы и сопротивления крыла самолета. Он также выявил компонент лобового сопротивления, называемый индуцированным сопротивлением , который связан с изменением распределения давления по крылу, вызванным сильными вихрями, тянущимися вниз по потоку от законцовок крыла.Эти вихри на концах крыла вызывают общий направленный вниз компонент скорости над крылом (называемый потоком вниз), который, в свою очередь, изменяет распределение давления таким образом, чтобы увеличить сопротивление. Это увеличение сопротивления является индуцированным сопротивлением. Индуцированное сопротивление прямо пропорционально квадрату коэффициента подъемной силы; следовательно, индуцированное сопротивление быстро увеличивается с увеличением подъемной силы. Для всего самолета коэффициент полного сопротивления C _D на низких скоростях можно выразить как

(13) CD = CD0 + CDi,

, где

CDi = CL2 / πAR.

InEq. (13), который называется поляром сопротивления , CD0 — коэффициент сопротивления паразита при нулевой подъемной силе; Сопротивление паразита создается чистым эффектом поверхностного трения о поверхность тела плюс дополнительное сопротивление давлением, создаваемое областями отрыва потока по поверхности (иногда называемое сопротивлением формы). Также в формуле (13) CDi — коэффициент сопротивления, обусловленный подъемной силой, и обусловлен увеличением паразитного сопротивления (выше нулевого значения подъемной силы), которое происходит, когда самолет находится под более высокими углами атаки, связанными с созданием подъемной силы, плюс индуцированная подъемная сила. сопротивление из-за завихрений на кончике, отсюда и размывка.В приведенном выше примере AR — удлинение, AR = b ² / S , где b — размах крыла, а S — площадь платформы крыла. Кроме того, e представляет собой коэффициент полезного действия, где e ≤ 1, и частично связан с математической формой распределения подъемной силы по размаху крыла.

В современной аэродинамике трехмерный потенциальный поток над низкоскоростными телами рассчитывается с помощью сингулярностей, распределенных на небольших плоских панелях, которые, в свою очередь, покрывают поверхность тела.Разработка «панельного метода» с использованием либо источников, вихрей или дублетных панелей или их комбинации была хорошо развита с 1965 года.

Жидкости в движении твердого тела

Жидкости в движении твердого тела

Жидкости в движении твердого тела

Введение

• Напомним, для случая движения твердого тела уравнение движение потока жидкости (уравнение Навье-Стокса) сводится к
  
  Обратите внимание, что новый вектор «эффективной гравитации», G , был определен как векторная сумма силы тяжести и отрицательного вектора ускорения.Этот новый эффективный вектор гравитации можно получить с помощью небольшой тригонометрии в качестве результирующего вектора прибавления г и — и .
  
  
• Рассмотрим два случая движения твердого тела: равномерное линейное ускорение твердого тела и жесткое вращение корпуса .

Равномерное линейное ускорение твердого тела

• Рассмотрим случай, когда жидкость ускоряется равномерно в каком-то направлении.Другими словами, каждая частица жидкости в контейнер ощущает точно такой же вектор ускорения, который постоянная во времени. В таком случае, поскольку вектор гравитации и вектор ускорения постоянны, эффективная сила тяжести вектор, G , также должен быть постоянным.
• Обратите внимание, что уравнение движения идентично уравнение гидростатики, за исключением того, что гравитация г заменяется эффективной силой тяжести G . Это делает проблемы такого типа не сложнее простой гидростатики.Фактически, для униформы линейное ускорение твердого тела, решение идентично гидростатики, но с г заменен на G , и с z (параллельно g , т.е. вниз) заменено на s (параллельно G ). Хороший способ запомнить это — представить, что ускоряющая жидкость вместо этого находится на планете, где сила тяжести действует в каком-то странном направлении (вектор G ) и с некоторая величина G. Одним из следствий этого является то, что изобары должны быть перпендикулярно к G , т.е.е. перпендикулярно направлению с. Фактически, давление увеличивается линейно с расстоянием s, скорее чем с z.
  
  
• В качестве примера рассмотрим стакан воды в лифте, который ускоряется:
  
  Здесь эффективная гравитация все еще направлена ​​вниз, но с большей силой. величина, чем г. Изобары по-прежнему являются горизонтальными поверхностями, поскольку в гидростатике. По сути все идентично гидростатике кроме большей силы тяжести (представьте, например, что стекло сидит на планете Юпитер).Наше простое гидростатическое давление соотношение по-прежнему применяется, но с заменой g на G и заменой z на s, т.е.
  
  Также обратите внимание, что «внизу» и «вверху» являются относительными для координации s, а не z. При прочих равных давление внизу ускорительного стакана будет больше чем на дне неподвижного стакана (поскольку G больше чем g).
  • Теперь рассмотрим стакан воды в лифте, который ускоряется. равномерно вправо. Опять же, эффективный вектор гравитации может быть построенным, как показано:
    
    Теперь, поскольку эффективная гравитация наклонена под некоторым углом к внизу слева изобары должны быть перпендикулярны этому направлению.Таким образом, изобары названы вниз и вправо, как показано на рисунке. Обратите внимание, что поверхность остается изобарой постоянного давления p _a , и поэтому также наклонен, как показано на рисунке. В какой-то момент 1 в жидкости, давление можно определить по пересмотренной гидростатической соотношение давления следующим образом:
    
    

Вращение жесткого тела

• Рассмотрим емкость с некоторой жидкостью, которая вращается вокруг вертикальная ось с некоторой постоянной угловой скоростью, как показано на эскиз:
• Для любого вида движения твердого тела уравнение движения для потока жидкости (уравнение Навье-Стокса) сводится к При линейном ускорении твердого тела, эффективный вектор силы тяжести, G , была постоянной везде в жидкости.Здесь этого больше нет случай, поскольку ускорение вращающейся частицы жидкости относительно некоторой оси изменяется с расстоянием от оси. Фактически, для круговое движение, ускорение всегда внутрь, в сторону центр вращения (центростремительное ускорение). Это ускорение линейно увеличивается с радиусом (см. текст для вывода): Таким образом, эффективный вектор гравитации G непостоянен, но зависит от радиуса. На рисунке ниже эффективная сила тяжести вектор в точке A строится: Локально изобары вблизи точки A, конечно, по-прежнему перпендикулярны G , и они показано.
• Однако в других точках потока местная эффективная вектор силы тяжести другой, так как местное ускорение другое. Например, в точке B (на большем радиусе, чем точка A) вектор ускорения внутрь больше, и G наклоняется дальше справа, как показано ниже: Локальные изобары вокруг точки B перпендикулярны местным изобарам. эффективный вектор гравитации, таким образом, наклонены в верхний правый угол даже сильнее, чем в точке A. На средней линии (точка C) местное ускорение равно нулю, а эффективная сила тяжести идентична до стандартной плотности; изобары рядом с осевой линией вращающегося жидкости горизонтальные, как и в гидростатике:
• Если этот вид анализа выполняется повсюду в потоке, изобары оказываются параболоидами, которые строятся вращением парабола вокруг своей оси для создания осесимметричной поверхности: Свободная поверхность, конечно, изобара, так как ее давление атмосферный.Давление увеличивается перпендикулярно изобарам.
• В тексте приводится более подробный математический вывод уравнений для давления и изобар. Если происхождение определяется в самой низкой точке свободной поверхности, как показано на рисунок выше, уравнения для давления и для изобар находятся:
• Когда p = p _a , второе уравнение выше становится уравнение, описывающее свободную поверхность. Когда p больше, чем p _a , это уравнение описывает изобары под поверхностью (при более высоком давлении).Обозначим теперь h как разницу между высота по центру свободной поверхности и по краю свободной поверхность. Оказывается, по сравнению с исходной свободной поверхностью (емкость вообще не вращается) поверхность опускается на в центре на величину (h / 2), равную величине, на которую поднимается поверхность обод (также h / 2). Это показано ниже:
• Рассмотрим числовой пример. Емкость с водой радиуса 4,0 дюйма вращается с фиксированной угловой скоростью 100 об / мин. Оценивать час: Простой эксперимент с вращающейся чашкой с водой может показать, что это предсказание достаточно точное.
• Обратите внимание, что плотность не появляется в уравнении для изобары или в уравнении для h. Таким образом, воду можно было заменить с любой другой жидкостью, и результат будет идентичным. Давление будет увеличиваться быстрее с глубиной для более плотной жидкости, но форма свободной поверхности останется прежней, независимо от используемой жидкости. Кроме того, поскольку это вращение твердого тела, части жидкости можно даже удалить или заменить твердый материал. Таким образом, любой вращающийся кусок жидкости, независимо от его формы, можно проанализировать, как если бы он был частью большого контейнера вращение вокруг оси z, как на рисунках выше.

Неравномерный поток — современная промышленная гидравлика

Поток жидкости можно классифицировать следующим образом:
• Устойчивые и нестационарные потоки
• Равномерные и неоднородные потоки
• Ламинарные и турбулентные потоки
• Вращательные и невращательные потоки.

Устойчивый поток
Поток жидкости считается устойчивым, если в любой точке текущей жидкости важные характеристики, такие как давление, плотность, скорость, температура и т. Д., Которые используются для описания поведения жидкости, не меняются. с течением времени.Другими словами, скорость потока через любое поперечное сечение трубы в установившемся потоке постоянна.

Неустойчивый поток
Поток жидкости считается неустойчивым, если в любой точке текущей жидкости одна или все характеристики, описывающие поведение жидкости, такие как давление, плотность, скорость и температура, изменяются со временем. Нестационарный поток — это такой тип потока, при котором характеристики жидкости меняются во времени или, другими словами, скорость потока через любое поперечное сечение трубы непостоянна.

Равномерный поток
Поток называется однородным, если скорость потока не изменяется ни по величине, ни по направлению в любой точке текущей жидкости в течение заданного времени. Например, течение жидкости под давлением по длинным трубопроводам постоянного диаметра называется равномерным потоком.

Неоднородный поток
Говорят, что поток неоднороден, когда есть изменение скорости потока в различных точках текущей текучей среды в течение заданного времени.Например, течение жидкости под давлением по длинным трубопроводам переменного диаметра называется неравномерным потоком. Все эти типы потоков могут существовать независимо друг от друга. Таким образом, может быть любая из четырех возможных комбинаций потоков:
1. Устойчивый однородный поток
2. Устойчивый неравномерный поток
3. Неустойчивый однородный поток
4. Неустойчивый неравномерный поток.

Ламинарный поток
Поток называется ламинарным, если частицы жидкости движутся слоями, так что один слой жидкости плавно скользит по соседнему слою.Вязкость жидкости играет важную роль в развитии ламинарного течения. Картина течения, демонстрируемая высоковязкой жидкостью, в общем, может рассматриваться как ламинарный поток.

Турбулентный поток
Если скорость потока превышает определенное значение, поток становится турбулентным. Движение частиц жидкости в турбулентном потоке будет случайным. Это смешивающее действие сталкивающихся частиц жидкости создает турбулентность, что приводит к большему сопротивлению потоку жидкости и, следовательно, большим потерям энергии по сравнению с ламинарным потоком.

14.5 Гидравлическая динамика | Университетская физика, том 1,

Цели обучения

К концу этого раздела вы сможете:

• Опишите характеристики потока
• Рассчитать расход
• Опишите взаимосвязь между расходом и скоростью
• Объясните последствия уравнения неразрывности для сохранения массы

Первая часть этой главы посвящена статике жидкости, изучению жидкости в состоянии покоя.Остальная часть этой главы посвящена гидродинамике, изучению движущихся жидкостей. Даже самые простые формы движения жидкости могут быть довольно сложными. По этой причине мы ограничиваем наше исследование идеальной жидкостью s во многих примерах. Идеальная жидкость — жидкость с незначительной вязкостью. Вязкость — это мера внутреннего трения в жидкости; мы исследуем его более подробно в разделе «Вязкость и турбулентность». На нескольких примерах мы исследуем несжимаемую жидкость — ту, для которой требуется чрезвычайно большая сила для изменения объема — поскольку плотность в несжимаемой жидкости постоянна на всем протяжении.

Характеристики потока

Векторы скорости часто используются для иллюстрации движения жидкости в таких приложениях, как метеорология. Например, ветер — жидкое движение воздуха в атмосфере — может быть представлен векторами, указывающими скорость и направление ветра в любой заданной точке на карте. (Рисунок) показывает векторы скорости, описывающие ветры во время урагана Артур в 2014 году.

Рис. 14.24 Векторы скорости показывают поток ветра во время урагана Артур.Обратите внимание на циркуляцию ветра вокруг очага урагана. Самые высокие скорости ветра у глаз. Цвета представляют относительную завихренность, меру вращения или вращения воздуха.

Другой метод представления движения жидкости — это линия тока . Линия тока представляет путь небольшого объема жидкости, когда она течет. Скорость всегда тангенциальна к линии тока. На схемах (Рисунок) линии тока используются для иллюстрации двух примеров движения флюидов по трубе.Первая жидкость демонстрирует ламинарный поток (иногда описываемый как устойчивый поток), представленный плавными параллельными линиями тока. Обратите внимание, что в примере, показанном в части (а), скорость жидкости наибольшая в центре и уменьшается у стенок трубы из-за вязкости жидкости и трения между стенками трубы и жидкостью. Это особый случай ламинарного потока , где трение между трубой и жидкостью велико, что известно как граничные условия отсутствия проскальзывания. Вторая диаграмма представляет турбулентный поток, в котором линии тока нерегулярны и меняются со временем.В турбулентном потоке пути потока текучей среды нерегулярны, поскольку разные части текучей среды смешиваются вместе или образуют небольшие круглые области, напоминающие водовороты. Это может произойти, когда скорость жидкости достигает определенной критической скорости.

Рис. 14.25 (a) Ламинарный поток можно представить как слои жидкости, движущиеся параллельными регулярными путями. (b) В турбулентном потоке области жидкости движутся по нерегулярным, сталкивающимся траекториям, что приводит к перемешиванию и завихрению.

Расход и его связь со скоростью

Объем жидкости, проходящей через заданное место через область в течение периода времени, называется расходом Q , или, точнее, объемным расходом .В символах это записывается как

.

[латекс] Q = \ frac {dV} {dt} [/ латекс]

, где В, — объем, а т, — прошедшее время. На (Рисунок) объем цилиндра равен Ax , поэтому расход равен

.

[латекс] Q = \ frac {dV} {dt} = \ frac {d} {dt} (Ax) = A \ frac {dx} {dt} = Av. [/ латекс]

Рисунок 14.26 Скорость потока — это объем жидкости, протекающей мимо точки через площадь A в единицу времени. Здесь заштрихованный цилиндр жидкости обтекает точку P по однородной трубе за время t.{3}). [/ латекс]

Расход и скорость связаны, но совершенно разными физическими величинами. Чтобы сделать различие ясным, рассмотрим скорость течения реки. Чем больше скорость воды, тем больше скорость течения реки. Но скорость потока также зависит от размера и формы реки. Стремительный горный ручей несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. (Рисунок) показывает объемный расход. Объемный расход [латекс] Q = \ frac {dV} {dt} = Av, [/ latex], где [латекс] A [/ латекс] — это площадь поперечного сечения трубы, а v — величина скорости.

Точное соотношение между расходом Q и средней скоростью v составляет

[латекс] Q = Av, [/ латекс]

, где A — площадь поперечного сечения, а [латекс] v [/ латекс] — средняя скорость. Это соотношение говорит нам, что скорость потока прямо пропорциональна средней скорости жидкости и площади поперечного сечения реки, трубы или другого водовода. Чем больше размер трубы, тем больше площадь его поперечного сечения. (Рисунок) иллюстрирует, как получается это соотношение.Заштрихованный цилиндр имеет объем [латекс] V = Ad [/ ​​латекс], который проходит мимо точки P за время t . Разделив обе стороны этого отношения на т , получим

[латекс] \ frac {V} {t} = \ frac {Ad} {t}. [/ латекс]

Отметим, что [latex] Q = V \ text {/} t [/ latex], а средняя скорость равна [latex] v \ text {} = d / t [/ latex]. Таким образом, уравнение становится [латекс] Q = Av [/ латекс].

(рисунок) показывает несжимаемую жидкость, текущую по трубе с уменьшающимся радиусом.Поскольку жидкость несжимаема, одно и то же количество жидкости должно пройти через любую точку трубы за заданное время, чтобы обеспечить непрерывность потока. Поток является непрерывным, поскольку они не являются источниками или стоками, которые добавляют или удаляют массу, поэтому масса, текущая в трубу, должна быть равна массе, вытекающей из трубы. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы.В частности, для произвольных точек 1 и 2

[латекс] \ begin {array} {ccc} \ hfill {Q} _ {1} & = \ hfill & {Q} _ {2}, \ hfill \\ \ hfill {A} _ {1} {v} _ {1} & = \ hfill & {A} _ {2} {v} _ {2}. \ Hfill \ end {array} [/ latex]

Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости (с постоянной плотностью). Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью — это и есть цель форсунки.И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется, возможно, снова набирая скорость, когда она покидает другой конец водохранилища. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда увеличивается площадь поперечного сечения.

Рисунок 14.27 Когда труба сужается, тот же объем занимает большую длину. Для того, чтобы тот же объем прошел точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс в точности обратим.Если жидкость течет в противоположном направлении, ее скорость уменьшается при расширении трубки. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости не масштабированы.)

Поскольку жидкости по существу несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.

Пример

Расчет скорости жидкости через сопло

Сопло диаметром 0.{2}} \, 1,96 \, \ text {m / s} = 25,5 \, \ text {m / s} \ text {.} [/ Latex]

Значение

Скорость 1,96 м / с примерно подходит для воды, выходящей из шланга с форсункой. Сопло создает значительно более быстрый поток, просто сужая поток до более узкой трубки.

Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что дает большие эффекты при изменении радиуса. Мы можем задуть свечу на большом расстоянии, например, поджав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.

Сохранение массы

Скорость потока жидкости также может быть описана массовым расходом или массовым расходом. Это скорость, с которой масса жидкости движется мимо точки. Еще раз обратитесь к (Рисунок), но на этот раз рассмотрите массу в заштрихованном объеме. Масса определяется по плотности и объему:

[латекс] m = \ rho V = \ rho Ax. [/ латекс]

Тогда массовый расход будет

[латекс] \ frac {dm} {dt} = \ frac {d} {dt} (\ rho Ax) = \ rho A \ frac {dx} {dt} = \ rho Av, [/ latex]

, где [латекс] \ rho [/ latex] — это плотность, A — это площадь поперечного сечения, а v — величина скорости.Массовый расход является важной величиной в гидродинамике и может использоваться для решения многих задач. Рассмотрим (рисунок). Труба на рисунке начинается у входа с площадью поперечного сечения [латекс] {A} _ {1} [/ latex] и сужается до выхода с меньшей площадью поперечного сечения [латекс] {A} _ {2 } [/ латекс]. Масса жидкости, поступающей в трубу, должна быть равна массе жидкости, покидающей трубу. По этой причине скорость на выходе [латекс] ({v} _ {2}) [/ latex] больше, чем скорость на входе [латекс] ({v} _ {1}) [/ latex].Используя тот факт, что масса жидкости, поступающей в трубу, должна быть равна массе жидкости, покидающей трубу, мы можем найти связь между скоростью и площадью поперечного сечения, взяв скорость изменения массы в трубе и массы из:

[латекс] \ begin {array} {ccc} \ hfill {(\ frac {dm} {dt})} _ {1} & = \ hfill & {(\ frac {dm} {dt})} _ {2 } \ hfill \\ \ hfill {\ rho} _ {1} {A} _ {1} {v} _ {1} & = \ hfill & {\ rho} _ {2} {A} _ {2} { v} _ {2}. \ hfill \ end {array} [/ latex]

(рисунок) также известно как уравнение неразрывности в общем виде.Если плотность жидкости остается постоянной из-за сужения, то есть жидкость несжимаема, тогда плотность сокращается из уравнения неразрывности,

[латекс] {A} _ {1} {v} _ {1} = {A} _ {2} {v} _ {2}. [/ латекс]

Уравнение сокращается, чтобы показать, что объемный расход в трубе равен объемному расходу из трубы.

Рисунок 14.28 Геометрия для вывода уравнения неразрывности. Количество жидкости, поступающей в площадь поперечного сечения (заштрихованную), должно равняться количеству жидкости, покидающей площадь поперечного сечения, если жидкость несжимаема.{3} \ text {/ s,} [/ latex], но можно использовать другие скорости, например л / мин.

Расход и скорость связаны соотношением [латекс] Q = Av [/ латекс], где A — площадь поперечного сечения потока, а v — его средняя скорость.

Уравнение неразрывности гласит, что для несжимаемой жидкости масса, втекающая в трубу, должна равняться массе, вытекающей из трубы.

Концептуальные вопросы

На многих рисунках в тексте показаны обтекаемые формы.Объясните, почему скорость жидкости максимальна там, где линии тока находятся ближе всего друг к другу. ( Подсказка: Учитывайте взаимосвязь между скоростью жидкости и площадью поперечного сечения, через которую она течет.)

Показать решение

Рассмотрим две разные трубы, подключенные к одной трубе меньшего диаметра, при этом жидкость течет из двух труб в меньшую трубу. Поскольку жидкость проталкивается через меньшую площадь поперечного сечения, она должна двигаться быстрее по мере того, как линии потока становятся ближе друг к другу.{3} \ text {/ s} [/ latex]?

Водопад Хука на реке Вайкато — одна из самых посещаемых природных достопримечательностей Новой Зеландии. В среднем река имеет скорость потока около 300 000 л / с. В ущелье река сужается до 20 метров в ширину и в среднем до 20 метров в глубину. а) Какова средняя скорость реки в ущелье? b) Какова средняя скорость воды в реке ниже водопада, когда она расширяется до 60 м, а глубина увеличивается в среднем до 40 м?

(a) Оцените время, которое потребуется для наполнения частного бассейна емкостью 80 000 л с использованием садового шланга со скоростью 60 л / мин.{3} \ text {/ s} [/ латекс]; c. Нет, расход и скорость не зависят от плотности жидкости.

Вода движется со скоростью 2,00 м / с по шлангу с внутренним диаметром 1,60 см. а) Какая скорость потока в литрах в секунду? (b) Скорость жидкости в сопле этого шланга составляет 15,0 м / с. Каков внутренний диаметр сопла?

Докажите, что скорость несжимаемой жидкости через сужение, например, в трубке Вентури, увеличивается в раз, равный квадрату коэффициента уменьшения диаметра.{3} \ text {/ s} [/ latex]? (б) Каков диаметр ручья на 0,200 м ниже крана? Пренебрегайте эффектами поверхностного натяжения.

Глоссарий

расход

сокращенно Q , это объем V , который проходит мимо определенной точки в течение времени t , или [латекс] Q = dV \ text {/} dt [/ latex]

идеальная жидкость

жидкость с пренебрежимо малой вязкостью

ламинарный поток

тип потока жидкости, в котором слои не смешиваются

турбулентный поток

Тип потока жидкости, в котором слои смешиваются друг с другом посредством завихрений и завихрений

вязкость

Измерение внутреннего трения в жидкости

механика жидкости | физика | Britannica

гидромеханика , наука, изучающая реакцию жидкостей на действующие на них силы.Это раздел классической физики, имеющий большое значение в гидравлической и авиационной технике, химической инженерии, метеорологии и зоологии.

Самая известная жидкость — это, конечно, вода, и энциклопедия 19 века, вероятно, рассмотрела бы этот предмет под отдельными заголовками: гидростатика, наука о воде в состоянии покоя и гидродинамика, наука о воде в движении. Архимед основал гидростатику примерно в 250 г. до н. Э., Когда, согласно легенде, он выпрыгнул из своей ванны и побежал голым по улицам Сиракуз с криком «Эврика!»; с тех пор он претерпел довольно небольшое развитие.С другой стороны, основы гидродинамики не были заложены до 18 века, когда математики, такие как Леонард Эйлер и Даниэль Бернулли, начали исследовать последствия для практически непрерывной среды, такой как вода, динамических принципов, которые Ньютон провозгласил для систем. состоит из дискретных частиц. Их работа была продолжена в 19 веке несколькими математиками и физиками первого ранга, в частности Г.Г. Стокса и Уильяма Томсона. К концу века были найдены объяснения множеству интригующих явлений, связанных с потоком воды через трубы и отверстия, волнами, которые корабли, движущиеся в воде, оставляют после себя, каплями дождя на оконных стеклах и т. Д.Однако до сих пор не было должного понимания таких фундаментальных проблем, как проблема протекания воды мимо фиксированного препятствия и приложения к нему силы сопротивления; теория потенциального потока, которая так хорошо работала в других контекстах, дала результаты, которые при относительно высоких расходах сильно расходились с экспериментом. Эта проблема не понималась должным образом до 1904 года, когда немецкий физик Людвиг Прандтль представил концепцию пограничного слоя (см. Ниже Гидродинамика: пограничные слои и разделение).Карьера Прандтля продолжилась в период разработки первых пилотируемых самолетов. С тех пор поток воздуха представляет такой же интерес для физиков и инженеров, как поток воды, и, как следствие, гидродинамика превратилась в гидродинамику. Термин «механика жидкости», используемый здесь, охватывает как гидродинамику, так и предмет, который все еще обычно называют гидростатикой.

Британская викторина

Викторина «Все о физике»

Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.

Еще один представитель 20-го века, заслуживающий упоминания, помимо Прандтля, — это Джеффри Тейлор из Англии. Тейлор оставался классическим физиком, в то время как большинство его современников обращали свое внимание на проблемы атомной структуры и квантовой механики, и он сделал несколько неожиданных и важных открытий в области механики жидкости. Богатство механики жидкости во многом объясняется нелинейным членом в основном уравнении движения жидкости — i.е., , который включает в себя двойную скорость жидкости. Для систем, описываемых нелинейными уравнениями, характерно то, что при определенных условиях они становятся нестабильными и начинают вести себя таким образом, который на первый взгляд кажется полностью хаотическим. В случае жидкостей хаотическое поведение очень распространено и называется турбулентностью. Математики начали распознавать закономерности в хаосе, которые можно плодотворно анализировать, и это развитие предполагает, что механика жидкости останется областью активных исследований и в 21 веке.(Обсуждение концепции хаоса см. В разделе «Физическая наука, принципы».)

Механика жидкости — это предмет с почти бесконечными разветвлениями, и последующее описание обязательно является неполным. Потребуются некоторые знания основных свойств жидкостей; обзор наиболее подходящих свойств приведен в следующем разделе. Для получения дополнительных сведений см. Термодинамика и жидкость.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Основные свойства жидкостей

Жидкости не являются строго непрерывными средами, как предполагали все последователи Эйлера и Бернулли, поскольку они состоят из дискретных молекул.Однако молекулы настолько малы, и, за исключением газов с очень низким давлением, количество молекул на миллилитр настолько велико, что их не нужно рассматривать как отдельные объекты. Есть несколько жидкостей, известных как жидкие кристаллы, в которых молекулы упакованы вместе таким образом, чтобы сделать свойства среды локально анизотропными, но подавляющее большинство жидкостей (включая воздух и воду) изотропны. В механике жидкости состояние изотропной жидкости может быть полностью описано путем определения ее средней массы на единицу объема или плотности (ρ), ее температуры ( T ) и ее скорости ( v ) в каждой точке пространства. , и то, какова связь между этими макроскопическими свойствами и положением и скоростью отдельных молекул, не имеет прямого значения.

Пожалуй, нужно сказать несколько слов о разнице между газами и жидкостями, хотя разницу легче уловить, чем описать. В газах молекулы расположены достаточно далеко друг от друга, чтобы двигаться почти независимо друг от друга, а газы имеют тенденцию расширяться, чтобы заполнить любой доступный им объем. В жидкостях молекулы более или менее соприкасаются, и силы притяжения на коротком расстоянии между ними заставляют их сцепляться; молекулы движутся слишком быстро, чтобы образовать упорядоченные массивы, характерные для твердых тел, но не настолько быстро, чтобы разлетаться.Таким образом, образцы жидкости могут существовать в виде капель или струй со свободной поверхностью, или они могут находиться в лабораторных стаканах, ограниченных только силой тяжести, в отличие от образцов газа. Такие образцы могут со временем испаряться, поскольку молекулы одна за другой набирают достаточную скорость, чтобы ускользнуть через свободную поверхность и не заменяются. Однако время жизни жидких капель и струй обычно достаточно велико, чтобы не учитывать испарение.

Существует два вида напряжений, которые могут существовать в любой твердой или текучей среде, и разницу между ними можно проиллюстрировать на примере кирпича, удерживаемого двумя руками.Если держатель сдвигает руки друг к другу, он оказывает давление на кирпич; если он перемещает одну руку к своему телу, а другую — от него, то он создает так называемое напряжение сдвига. Твердое вещество, такое как кирпич, может выдерживать нагрузки обоих типов, но жидкости, по определению, поддаются напряжениям сдвига, независимо от того, насколько малы эти напряжения. Они делают это со скоростью, определяемой вязкостью жидкости. Это свойство, о котором подробнее будет сказано позже, является мерой трения, которое возникает, когда соседние слои жидкости скользят друг по другу.Отсюда следует, что касательные напряжения всюду равны нулю в жидкости в покое и в равновесии, и из этого следует, что давление (то есть сила на единицу площади), действующее перпендикулярно всем плоскостям в жидкости, одинаково независимо от их ориентации. (Закон Паскаля). Для изотропной жидкости в равновесии существует только одно значение местного давления ( p ), соответствующее заявленным значениям для ρ и T . Эти три величины связаны вместе так называемым уравнением состояния жидкости.

Для газов при низких давлениях уравнение состояния простое и хорошо известное. Здесь R — универсальная газовая постоянная (8,3 джоулей на градус Цельсия на моль), а M — молярная масса или средняя молярная масса, если газ представляет собой смесь; для воздуха соответствующее среднее значение составляет около 29 × 10 ⁻³ килограмм на моль. Для других жидкостей знание уравнения состояния часто является неполным. Однако, за исключением очень экстремальных условий, все, что нужно знать, это то, как изменяется плотность, когда давление изменяется на небольшую величину, и это описывается сжимаемостью жидкости — либо изотермической сжимаемостью, β _T , или адиабатическая сжимаемость, β _S , в зависимости от обстоятельств.Когда элемент жидкости сжимается, проделанная с ним работа имеет тенденцию нагревать его. Если тепло успевает уйти в окружающую среду, а температура жидкости остается практически неизменной, тогда β _T является соответствующей величиной. Если тепло практически не уходит, как это чаще бывает в случае проблем с потоком, потому что теплопроводность большинства текучих сред низкая, тогда поток называют адиабатическим, и вместо него требуется β _S .( S относится к энтропии, которая остается постоянной в адиабатическом процессе при условии, что он протекает достаточно медленно, чтобы считаться «обратимым» в термодинамическом смысле.) Для газов, которые подчиняются уравнению (118), очевидно, что p и ρ пропорциональны друг другу в изотермическом процессе, а

В обратимых адиабатических процессах для таких газов, однако, температура повышается при сжатии со скоростью, такой, что и где γ составляет около 1,4 для воздуха и принимает аналогичные значения для других распространенных газы.Для жидкостей соотношение изотермической и адиабатической сжимаемостей намного ближе к единице. Для жидкостей, однако, обе сжимаемости обычно намного меньше, чем p ^-1 , и упрощающее предположение, что они равны нулю, часто оправдано.

Коэффициент γ — это не только отношение между двумя сжимаемостями; это также соотношение двух основных удельных теплоемкостей. Молярная теплоемкость — это количество тепла, необходимое для повышения температуры одного моля на один градус.Это больше, если веществу позволяют расширяться при нагревании и, следовательно, выполнять работу, чем если бы его объем был фиксированным. Основные молярные удельные теплоты, C _P и C _V , относятся к нагреванию при постоянном давлении и постоянном объеме, соответственно, и

для воздуха, C _P составляет около 3,5 R .

Твердые тела можно растягивать без разрушения, а жидкости, но не газы, тоже могут выдерживать растяжение.Таким образом, если давление в образце очень чистой воды постоянно снижается, пузырьки в конечном итоге появятся, но они могут не появиться до тех пор, пока давление не станет отрицательным и будет значительно ниже -10 ⁷ ньютон на квадратный метр; это в 100 раз больше по величине, чем (положительное) давление атмосферы Земли. Вода обязана своей высокой идеальной силой тому факту, что разрыв включает разрыв связей притяжения между молекулами по обе стороны от плоскости, на которой происходит разрыв; необходимо проделать работу, чтобы разорвать эти ссылки.Однако его сила резко снижается из-за того, что образует ядро, в котором может начаться процесс, известный как кавитация (образование полостей, заполненных паром или газом), и жидкость, содержащая взвешенные частицы пыли или растворенные газы, склонна к кавитации довольно легко. .

Работа также должна быть выполнена, если свободная капля жидкости сферической формы должна быть вытянута в длинный тонкий цилиндр или деформирована любым другим способом, увеличивающим площадь ее поверхности. Здесь снова необходима работа, чтобы разорвать межмолекулярные связи.Поверхность жидкости фактически ведет себя, как если бы она была эластичной мембраной при натяжении, за исключением того, что натяжение, создаваемое эластичной мембраной, увеличивается, когда мембрана растягивается таким образом, как натяжение, оказываемое поверхностью жидкости. Поверхностное натяжение — это то, что заставляет жидкости подниматься по капиллярным трубкам, что поддерживает висящие капли жидкости, что ограничивает образование ряби на поверхности жидкости и так далее.

Механическая среда клеток и основание меридианов

Используя информацию, полученную в результате глубокого рассечения, микронаблюдений и измерения акупунктурных точек в верхних и нижних конечностях человеческого тела, мы разработали трехмерную модель пористой среды для моделирования потока. поле с помощью программного обеспечения FLUENT и для изучения напряжения сдвига на поверхности интерстициальных клеток (тучных клеток), вызванного потоком интерстициальной жидкости.Результаты численного моделирования показывают следующее: (i) параллельная природа капилляров приведет к направленному потоку интерстициальной жидкости, что может объяснить длинные межклеточные тканевые каналы или меридианы, наблюдаемые в некоторых экспериментах; (ii) когда распределение капилляров неравномерно, скорость увеличивается поочередно, и скорость имеет тенденцию быть однородной, что благоприятно для обмена веществ; (iii) поток интерстициальной жидкости вызывает напряжение сдвига величиной в несколько Па на мембранах интерстициальных клеток, которое активирует клетки и приводит к биологической реакции; (iv) капиллярные и интерстициальные параметры, такие как плотность капилляров, кровяное давление, проницаемость капилляров, интерстициальное давление и интерстициальная пористость, влияют на напряжение сдвига на поверхности клеток.Результаты численного моделирования показывают, что поток интерстициальной жидкости in vivo составляет механическую среду клеток и играет ключевую роль в управлении клеточной деятельностью, что может объяснить меридиональные явления и эффекты акупунктуры, наблюдаемые в экспериментах.

1. Введение

Интерстициальный поток жидкости — это движение жидкости через внеклеточный матрикс тканей, часто между кровеносными и лимфатическими сосудами. Этот поток обеспечивает необходимый механизм для транспортировки крупных белков через интерстиций и составляет важный компонент микроциркуляции [1].Помимо своей роли в переносе массы, поток интерстициальной жидкости также обеспечивает особую механическую среду, которая важна для физиологической активности интерстициальных клеток [2, 3]. Несколько экспериментов in vitro показали, что поток интерстициальной жидкости очень важен для клеточной активности и что поток величиной мкм и м / с вызывает физиологические реакции клеток [4-8]. Численное моделирование in vitro того, как архитектура внеклеточных волокон влияет на напряжение сдвига на клеточных мембранах, также показало, что поток интерстициальной жидкости важен для воздействия жидкости на клетку, заключенную в трехмерную матрицу [9, 10].Кровоток играет важную роль в управлении физиологической активностью эндотелиальных клеток (ЭК) и гладкомышечных клеток (ГМК), а также во время ремоделирования кости [11–13]. Однако исследования влияния потока интерстициальной жидкости на интерстициальные клетки (тучные клетки) проводятся редко. Тучные клетки — это тип иммунных клеток, обнаруженных в соединительных тканях. Когда тучные клетки стимулируются, они высвобождают химические медиаторы из своих клеточных гранул во внеклеточный матрикс и инициируют серию биологических ответов; многие ответы коррелируют с эффектами иглоукалывания [14].

До настоящего времени прямых измерений потока межклеточной жидкости in vivo не проводилось, а информация о потоке межклеточной жидкости была получена только из других, возможно, коррелированных измерений. Например, Ли и др. визуализировали региональные подкожные каналы миграции в интерстициальной жидкости человека с помощью магнитно-резонансной томографии (МРТ) [15]. Эти каналы отличались от лимфатических или кровеносных сосудов и частично совпадали с характеристиками меридианов.Считается, что поток интерстициальной жидкости можно использовать для иллюстрации современного физиологического механизма меридианов. В другом эксперименте нуклид вводили в акупунктурную точку «Тайюань» недавно умершей обезьяны (в течение получаса после смерти). Следа передачи вдоль меридиана не было обнаружено, но оно появилось, когда физиологический раствор с гепарином вводился одновременно через подмышечную артерию и вену [16]. Это явление демонстрирует, что движение изотопа по меридианам требует толчка, который обеспечивается циркулирующей кровью в живых существах.Мы предложили динамическую модель для моделирования межклеточного потока жидкости вблизи меридианов и обнаружили, что источником прямого толчка для этого потока было проникновение плазмы между капиллярами и межклеточной жидкостью [17]. Кроме того, мы разработали двумерную (2D) модель для изучения поля потока в соединительных тканях и наблюдали направленный поток жидкости [18, 19].

МРТ показало, что кончик иглы для акупунктуры обычно помещается рядом с межкостной перепонкой. В этой статье мы исследуем трехмерную (3D) картину потока интерстициальной жидкости в межкостной мембране человека, влияние физиологических параметров на скорость потока и физиологическое влияние потока на интерстициальные клетки.Оставшаяся часть теста организована следующим образом. В разделе 2 мы представляем трехмерную модель пористой среды для описания межкостной мембраны. Результаты, полученные с помощью предложенной модели, представлены в Разделе 3. Обсуждение и резюме настоящего исследования представлены в Разделе 4.

2. Модель и методы

2.1. 3D-модель

Межкостная перепонка имеет длину 25 см, ширину 2 см и толщину 0,2 см. Анатомические наблюдения показали, что капилляры образовывали кластеры и располагались чередующимися слоями.В каждом кластере капилляры были почти параллельны. Рисунок 1 (а) представляет собой схематическую карту одного мембранного блока. Передние концы капилляров подсоединены к прекапилляру, а нижние концы — к венуле. Средняя длина группы капилляров составляет 2000 мкм м (см. Ось на рисунке 1 (а)), а средняя ширина составляет 400 мкм м (см. Ось на рисунке 1 (а)). Расстояние между соседними кластерами составляет примерно 1875 мкм м по оси -оси и примерно 315 мкм м по оси -оси.Предположим, что расстояние между капиллярами в кластере равно примерно 50 мкм м. По этим характеристикам мы разрабатываем 3D-модель, показанную на рисунке 1 (б). Сплошные толстые линии представляют капилляры, а черный и серый цвета указывают на разные слои. Пунктирным прямоугольником отмечена расчетная область.

Чтобы изучить влияние потока на интерстициальные клетки, мы помещаем тучную клетку (сферу диаметром 16 мкм м) в центр домена (центр сферы находится в мм, мм) (рис. 1 (б)).Увеличенная тучная клетка на рисунке 1 (b) показывает местные декартовы координаты. Начало координат () находится в центре сферы, а -axis, -axis и -axis параллельны -axis, -axis и -axis соответственно. Для тучных клеток в интерстиции существует тонкий пограничный слой около поверхности клетки, называемый пограничным слоем Бринкмана. Таким образом, во время создания сетки есть уточненная зона около поверхности тучной клетки, показанная на рисунке 1 (b) [20].

2.2. Управляющие уравнения

Поскольку число Рейнольдса межклеточного потока жидкости мало, инерцией можно пренебречь.Предполагается, что пространство в интерстиции, состоящее из параллельных фибрилл коллагена, является пористой средой. Основными уравнениями являются уравнения Бринкмана и неразрывности [20]: где — оператор градиента, — оператор Лапласа, — вектор локальной скорости потока, — внутреннее давление, — вязкость межклеточной жидкости, — проницаемость по Дарси матрицы коллагеновых фибрилл. Член в левой части (1) — это градиент давления. Первый член в правой части представляет вязкий член, а последний член в правой части представляет член Дарси-Форххаймера, который характеризует течение в пористой среде.

Безразмерные переменные определяются как; ; ; где — характеристическая скорость, — диаметр капилляров, — плотность жидкости, — вектор положения. Уравнения (1) и (2) переписываются в безразмерном виде как: где Re — число Рейнольдса, определяемое как. В нашей модели она мала (10 ⁻¹⁶ м ² ), а безразмерный параметр составляет примерно 10 ⁻⁶ . Следовательно, вязкий член мал по сравнению с членом Дарси-Форхгеймера, и им можно пренебречь.Уравнение (3) сводится к закону Дарси [20]:

Для тучной клетки в интерстиции следующие результаты покажут, что поле потока около клетки почти симметрично относительно оси -оси. Поэтому мы используем сферические координаты для анализа напряжения сдвига на тучной клетке (), и доминирующим напряжением является

2.3. Влияние капилляров на поток внутриклеточной жидкости

Гипотеза Старлинга о том, что движение жидкости через стенки микрососудов определяется трансмуральной разницей гидростатического и онкотического давления, стала общим принципом физиологии [21]: где — коэффициент проницаемости стенок капилляров, — гидростатическое давление в крови, — интерстициальное гидростатическое давление на стенке капилляра, — это осмотическое давление в крови, — это интерстициальное осмотическое давление на стенке капилляра.Ху и Вайнбаум определили, что и (гидростатическое и коллоидно-осмотическое давление, соответственно, за поверхностным гликокаликсом в их модели) могут сильно отличаться от соответствующих давлений в межклеточном пространстве [25]. Как правило, предполагается, что только изменяется и линейно уменьшается от прекапиллярной стороны к стороне венулы по длине капилляра. Остальные параметры (, и) предполагаются постоянными [21]. Определив характеристическую скорость, где — внутрисосудистое капиллярное давление на верхнем конце потока, и используя значения параметров, перечисленных в таблице 1, трансмуральная капиллярная скорость равна где — расстояние от входного конца, а — длина капилляра.

212.4. Влияние коллагеновых фибрилл на поток интерстициальной жидкости

Параллельные коллагеновые фибриллы могут влиять на поток интерстициальной жидкости. Chen et al. разработали 2D и 3D модели конечных элементов, аналогичные параллельным массивам коллагеновых фибрилл в связках и сухожилиях, для моделирования поперечных и продольных межклеточных потоков жидкости [22]. Поток вдоль фибрилл коллагена определяется как продольный поток, при этом поток, перпендикулярный фибриллам коллагена, определяется как поперечный поток. Результаты расчетов предоставили эмпирические выражения проницаемости по Дарси как функции пористости.Рассматривая жидкость как ньютоновскую жидкость, эмпирические выражения показаны следующим образом: где [22]. Физиологический диапазон пористости связок составляет [22]. Структура межкостной перепонки аналогична связке. Следовательно, продольная проницаемость составляет приблизительно 1,0 × 10 ⁻¹⁶ м ² , а отношение to (ratio =) составляет приблизительно 10.

2,5. Граничные условия

Расчетная область показана на рисунке 1 (b) и содержит один целый и два полукапиллярных кластера.Стенка капилляра определяется как граница скорости на входе, а скорость на входе определяется UDF (8). Кроме того, из-за периодического геометрического характера мы определяем периодические граничные условия, как показано на рисунке 1 (b). Выходящий поток (на нижней границе) полностью развит, производная по направлению равна нулю (). Поток вверх по потоку не учитывается, а скорость на входе (верхняя граница) определяется равной нулю. Расчетная область представляет собой пористую зону, а вязкое сопротивление составляет.

Когда тучная клетка присутствует в интерстиции, область тучной клетки (сфера в центре) удаляется из исходной расчетной области. Предполагается, что поверхность сферы представляет собой стену; поэтому используются граничные условия противоскольжения (,). Пограничный слой Бринкмана () имеет толщину.

2.6. Вычислительный метод

Программный пакет CFD FLUENT (версия 6.0) используется для численного моделирования. Сетка формируется с помощью программного комплекса GAMBIT.Модель является ламинарной, решатель сегрегирован и устойчив, а метод решения — ПРОСТАЯ схема. Основные уравнения решаются итерацией. Когда итерация сходится (ошибка повторных результатов), получается поле скорости.

2.7. Физиологические параметры

В таблице 1 показаны физиологические параметры, использованные в численном моделировании.

3. Результаты

3.1. Поле потока без промежуточной ячейки

Рисунок 2 (а) представляет собой поле потока в плоскости — (, масштаб отображения::,:: 2.5). Толстые черные линии представляют капилляры, стрелки указывают направление скорости, длина стрелки указывает величину скорости, а цветные линии — контуры скорости. Межклеточная жидкость течет из капилляра к интерстиции на верхней (левой) стороне. Вблизи оси -оси направление потока стремится стать параллельным капиллярам. На стороне венулы небольшое количество жидкости абсорбируется капиллярами, в то время как большая часть жидкости выходит наружу. В первом кластере скорость на входе равна нулю.Однако проникающий поток через стенку капилляра больше, чем поглощающий поток. Следовательно, жидкость вытекает в конце первого кластера. Во втором кластере, поскольку из первого кластера выходят потоки жидкости, скорость на входе больше не равна нулю. Сравнение скорости межузельной жидкости в первом кластере со скоростью во втором кластере показывает, что скорость во втором кластере явно больше. Эта разница возникает из-за того, что скорость на входе второго кластера, который генерируется из первого кластера капилляров, ускоряет межклеточную жидкость.Отток второго кластера больше, чем оттока первого кластера. Следовательно, скорость в третьем кластере будет еще больше. На рис. 2 (b) показаны линии пути от капилляров в межузельном пространстве (масштаб отображения:: 2,5,:: 2,5). Цветные линии представляют собой линии пути, которые почти параллельны капиллярам, ​​а максимальная скорость составляет приблизительно 1,5 × 10 ⁻⁶ м / с (~ 2,5 U).

3.2. Поле потока вокруг промежуточной ячейки

Используя эту модель, мы также исследуем поле потока с ячейкой в ​​промежуточном пространстве.Промежуточная ячейка мало влияет на поле потока, за исключением поверхности ячейки. Максимальная скорость наблюдается на поверхности ячейки (3,25 × 10 ⁻⁶ м / с, 5 U) и намного больше, чем скорость в других местах. Поле течения около ячейки почти симметрично относительно оси. На рисунке 3 показаны линии тока вокруг ячейки: (a) показаны линии тока в локальной плоскости (, представляет поперечное сечение), (b) показаны линии тока в локальной плоскости (, представляют собой плоскость) и (c) показаны линии тока в локальной плоскости ().Рисунки 3 (б) и 3 (в) почти идентичны. Направление скорости — вдоль оси -оси, максимальная скорость — в мм.

3.3. Механическая среда интерстициальной клетки

Поток интерстициальной жидкости обеспечивает механические стимулы для интерстициальной клетки. Напряжение сдвига на поверхности тучной клетки () рассчитывается с использованием (6). Напряжение сдвига зависит от проницаемости по Дарси. На рисунке 4 показано распределение на поверхности ячейки для (а) изотропного условия (отношение = 1) и (б) анизотропного условия (отношение = 10).Результаты показывают, что он имеет двустороннюю симметрию и что максимум () находится в мм для отношения ≥ 1 (отношение = 1 и отношение = 10). увеличивается по мере уменьшения. По мере увеличения соотношения близость существенно меняется. Распределение на поверхности ячейки на рисунке 4 также показано для (c) фиксированного (m ² ) и (d) фиксированного (m ² ). Результаты показывают, что это главный фактор. Когда фиксировано, увеличивается по мере уменьшения (Рисунок 4 (c)). Когда фиксируется, по мере уменьшения распределение становится более неравномерным (рис. 4 (г)).

3.4. Влияние физиологических параметров на

Плотность капилляров в интерстиции может влиять на поток интерстициальной жидкости и. С площадью поперечного сечения, определенной как, Рисунок 5 показывает взаимосвязь между и. Очевидно, что при увеличении уменьшается, и зависимость нелинейная. Для меньшего размера происходят большие изменения.

Коэффициент проницаемости стенки капилляра () также может влиять на поток внутриклеточной жидкости и. Как показано на рисунке 6, увеличивается линейно с.

Как внутрисосудистое капиллярное давление (), так и внутреннее гидростатическое давление на стенке капилляра () может влиять на скорость проницаемости стенки капилляра (7) и, следовательно, на поток внутриклеточной жидкости и. На рис. 7 показано, как влияют изменения внутрисосудистого капиллярного давления на верхнем конце () и внутрисосудистого капиллярного давления на нижнем конце (). По оси абсцисс отложено изменение, и по сравнению со стандартными значениями, и, соответственно; то есть, .линейно возрастает с увеличением и, линейно убывает с увеличением. Эффект наибольший, а эффект наименьший.

На основании численных результатов можно сделать следующие наблюдения. Капилляры в параллельном ряду могут вызывать параллельный межклеточный поток жидкости. Поток интерстициальной жидкости может вызвать напряжение сдвига на поверхности клетки. Отношение определяет распределение напряжения сдвига и сильно влияет на максимальное напряжение сдвига.Напряжение сдвига можно увеличить за счет уменьшения площади поперечного сечения, что соответствует увеличению плотности капилляров. Напряжение сдвига также может быть увеличено за счет увеличения проницаемости капилляров, увеличения внутрисосудистого капиллярного давления и уменьшения межклеточного давления.

4. Обсуждение

4.1. Направленный поток внутриклеточной жидкости может объяснить некоторые экспериментальные наблюдения

Поле скоростей показывает, что направление потока внутриклеточной жидкости параллельно ориентации капилляров.Первый кластер капилляров может генерировать внутриклеточный поток жидкости со скоростью приблизительно 0,75 × 10 ^-6 м / с. Затем этот поток входит в пространство, окружающее второй кластер капилляров, и ускоряется до 1,25 × 10 ^-6 м / с. Максимальная скорость в пространстве, окружающем второй кластер капилляров, составляет 1,5 × 10 ^-6 м / с. Если жидкость не абсорбируется лимфатической системой, она будет течь вниз по потоку и ускоряться нижележащими капиллярами.В прошлом считалось, что большая часть просачивания со стороны артериол капилляра абсорбируется на стороне венулы, а избыток немедленно абсорбируется лимфатическими сосудами. В действительности капилляры не всегда находятся рядом с лимфатическими сосудами, и количество жидкости, которая просачивается из капилляров, всегда превышает количество жидкости, поглощаемой капиллярами. Следовательно, неабсорбированная жидкость пройдет некоторое расстояние или даже большое расстояние, прежде чем снова будет поглощена кровеносными или лимфатическими сосудами.Возможно, что длинные межузельные треки, наблюдавшиеся в предыдущем эксперименте, на самом деле представляют собой межузельный поток жидкости [16]. Индикатор (Gd-DTPA), вводимый в акупунктурную точку, перемещается с потоком межклеточной жидкости. Следовательно, наблюдение за потоком по меридиану, отличным от кровотока и лимфы, может быть интерстициальным потоком жидкости [15].

4.2. Ступенчатое распределение капилляров приводит к равномерной скорости внутриклеточной жидкости

Распределение капилляров может влиять на распределение скорости внутриклеточного потока жидкости.Рисунок 2 (а) показывает это влияние. В первом кластере капилляры расположены дальше от -оси, и, таким образом, скорость промежуточной жидкости дальше от -оси увеличивается быстрее, чем скорость около -оси. Напротив, капилляры во втором кластере расположены вблизи оси -оси, и эта промежуточная скорость жидкости около -оси увеличивается быстрее, чем поток дальше от -оси. При таком шахматном распределении капилляров увеличение скорости чередуется, и скорость имеет тенденцию быть равномерной, что благоприятно для обмена веществ.Поток интерстициальной жидкости влияет на биоактивность клеток. Когда ткани плохо васкуляризованы, такие как связки и сухожилия, поток интерстициальной жидкости более важен для метаболизма, чем для тканей с хорошей васкуляризацией.

4.3. Напряжение сдвига, вызванное потоком межклеточной жидкости, будет влиять на биоактивность клеток

Численное моделирование показывает, что поток имеет скорость величиной 10 ^-6 м / с и что поток вызывает напряжения сдвига в несколько Па на поверхности тучных ячеек.Многие исследования показали, что тонкая жидкая механическая среда играет важную роль в способности клеток пролиферировать, дифференцироваться, формировать функциональные структуры и высвобождать химические медиаторы [26, 27]. Недавние исследования показали, что интерстициальный поток влияет на иммунную микросреду при раке [28]. Иммунное микроокружение опухоли состоит из нескольких типов клеток, цитокинов и стромальных компонентов, которые могут дополнительно привлекать иммунные клетки и определять их судьбу. Civelek et al. представили первое прямое доказательство того, что SMCs с сократительным фенотипом действительно будут сокращаться при воздействии 2D сдвигового напряжения жидкости [29].Исследования показывают, что как ламинарное напряжение сдвига (2D), так и интерстициальный поток (3D) могут вызывать сокращение SMC [30]. Эти исследования предлагают другую точку зрения на механизм миогенного контроля кровотока, который регулирует распределение кровотока в ответ на изменения артериального давления. Ван обнаружил, что внутриклеточный Ca ²⁺ увеличивается в тучных клетках, а медиаторы высвобождаются сразу после механической стимуляции [31]. Дальнейшие исследования показали, что механочувствительный Ca ²⁺ канал TRPV ₂ может участвовать в этом процессе [32].

Механизм влияния интерстициального потока на биоактивность клеток до сих пор неизвестен. Когда-то считалось, что напряжение сдвига, вызванное потоком, является основным фактором. Дальнейшие исследования предполагают, что рецепторы, связанные с клеточной мембраной, ионные каналы, гликокаликс клеточной поверхности, интегрины и сигнальные мессенджеры — все они вовлечены в этот процесс. Недавняя работа показывает, что напряжение сдвига жидкости в клетках довольно мало и что твердое напряжение, вызванное интерстициальным потоком через гликокаликс клеточной поверхности, намного выше [33].Сильный стресс, скорее всего, играет важную роль в регулировании функции и поведения клеток. Однако оценить твердый стресс сложно, потому что для этого требуется детальное знание микроструктуры гликокаликса и свойств внеклеточного матрикса. В этой статье мы не сосредотачиваемся на сложном механизме активации мембранного ионного канала и твердого стресса, вызванного интерстициальным потоком через гликокаликс клеточной поверхности. Вместо этого мы сравниваем только напряжения сдвига на поверхности тучных клеток в различных условиях.

4.4. Изменение физиологических параметров влияет на

Продольная проницаемость и соотношение определяют распределение. Из (9) мы знаем, что и являются функциями пористости. Следовательно, влияет. На самом деле, чем меньше, тем больше эффект. При нормальных физиологических значениях оказывает гораздо меньшее влияние, чем при значениях, выходящих за пределы нормального физиологического диапазона [19]. Может увеличиваться внутрисосудистое капиллярное давление или проницаемость капилляров.Следовательно, микроциркуляция крови может влиять на условия жизни интерстициальных клеток, и изменение кровоснабжения является эффективным методом регулирования циркуляции межклеточной жидкости. Снижение интерстициального давления также может увеличиваться, и это имеет большее влияние, чем изменение внутрисосудистого капиллярного давления.

4.5. Процедуры ТКМ и эффект иглоукалывания

С помощью традиционных китайских процедур, таких как массаж и купирование, межклеточное давление может быть изменено путем периодического или отрицательного давления на поверхность тела [34].Приведенные выше результаты показывают, что межклеточное давление является основным фактором, влияющим на межклеточный поток, и, следовательно, может существовать корреляция между этими обработками и межклеточным потоком.

Иглоукалывание — это терапевтическое лечение, при котором игла вводится в определенные части (акупунктурные точки). Когда игла вращается, поднимается и толкается, наматывание коллагена на иглу для акупунктуры изменяет интерстициальную микросреду [35, 36], что вызывает механическую стимуляцию. Стимуляция вызывает дегрануляцию местных тучных клеток и высвобождение биологических медиаторов, таких как гистамин, вещество P и лейкотриен C ₄ и так далее [14].Эти медиаторы могут дополнительно активировать тучные клетки и возбуждать нервные окончания, что может привести к «Де-ци» (местное ощущение тяжести, онемения, болезненности или парестезии, которое считается важным аспектом лечения иглоукалыванием). Более того, эти медиаторы обладают мощным эффектом, увеличивая проницаемость капилляров и увеличивая интерстициальный кровоток [24]. Увеличенный поток не только увеличивает активацию локальных тучных клеток, но также транспортирует биологические медиаторы, секретируемые тучными клетками, чтобы активировать другие тучные клетки по пути потока [2, 37].Таким образом, меридиональные явления и ощущения «Де-ци» вдоль меридиана во время иглоукалывания могут быть тесно связаны с интерстициальным потоком.

Благодарности

Эта работа была поддержана Национальным фондом естественных наук Китая (11202053), Шанхайским научным фондом (12ZR1401100) и проектом 973 (2012CB518502).

Эссе по потоку жидкости — 1126 слов

Лекция № 5
КЛАССИФИКАЦИЯ ПОТОКА ЖИДКОСТИ И УРАВНЕНИЕ НЕПРЕРЫВНОСТИ

5.1 Классификация потока жидкости
Равномерный поток
Если скорость жидкости одинакова по величине и направлению в каждой точке жидкости, поток называется однородным. Неоднородный поток
Неоднородный поток — это поток, скорости которого в разных точках в данный момент не совпадают. Каждая жидкость, которая течет около твердой границы, будет неоднородной, потому что жидкость на границе принимает скорость границы, которая обычно равна нулю. Устойчивый поток

Устойчивый поток — это такой поток, при котором условия (т.е., скорость, давление, поперечное сечение) могут изменяться от точки к точке, но не изменяются со временем. Нестабильный поток
Если в какой-либо точке жидкости условия меняются со временем, поток неустойчивый. На самом деле всегда есть небольшие колебания скорости и давления; однако, если средние значения постоянны, поток можно считать устойчивым. Устойчивый равномерный поток

При устойчивом однородном потоке условия не меняются в зависимости от положения в потоке или со временем.
Пример: поток воды в трубе постоянного диаметра при постоянной скорости

Устойчивый неравномерный поток
В этой классификации потока условия меняются от точки к точке в потоке, но не меняются со временем.
Пример: поток жидкости в сужающейся трубе с постоянной скоростью на входе. Скорость будет меняться по мере того, как жидкость движется по длине трубы к выходу. Неустойчивый равномерный поток
В этом потоке условия во всех точках одинаковы в любой данный момент, но меняются со временем.
Пример: поток жидкости через трубу постоянного диаметра, подключенную к насосу, перекачивающему с постоянной скоростью, который затем отключается. Неустойчивый неравномерный поток
Если каждое состояние потока меняется от точки к точке и изменяется со временем в каждой точке, поток является неустойчивым и неравномерным.
Пример: Волны в канале

Классификация, основанная на сдерживающем эффекте твердой границы Поток в закрытом канале
Потоки, которые полностью закрыты ограничением твердой поверхности (например, поток через трубы и трубки) Поток в открытом канале
Потоки, при которых одна поверхность жидкости подвергается воздействию атмосферы (например, поток реки, поток воды при орошении) Поток со свободной поверхностью
Поток, при котором жидкость не контактирует с твердой поверхностью (например, струя воды из шланга, дождь)

5.2 Поток несжимаемой и сжимаемой жидкости

Поток несжимаемой жидкости: поток, в котором плотность жидкости постоянна;
можно принять для потока жидкости
Поток сжимаемой жидкости: поток, в котором плотность жидкости изменяется
практически для всех газов

5.3 Трехмерный поток
В целом поток жидкости является трехмерным с давлением, скоростью и другими условиями потока, изменяющимися во всех направлениях. Однако во многих случаях наиболее существенные изменения происходят только в двух направлениях или даже только в одном.Одномерный поток. Пример: поток в трубе (см. Рисунок 5.1)

Рисунок 5.1. Одномерное течение в трубе

Двумерное течение. Пример: Обтекание водослива, типичные линии тока которого показаны на рисунке 5.2.

Рисунок 5.2. Двумерный поток над водосливом

5.4 Линии тока и трубки потока

Линии тока
Линии тока представляют собой воображаемые кривые, проведенные через жидкость, чтобы указать направление движения в различных участках потока жидкости системы.По сути, они представляют собой визуализацию схем течения, которые нарисованы путем соединения точек с одинаковой скоростью. На рис. 5.3 показан простой пример линий тока в поперечном сечении корпуса в форме крыла самолета.

Рисунок 5.3. Линии тока вокруг крыловидного тела

Линии тока, близкие к границе, параллельны этой границе. Во всех точках направление линии тока соответствует направлению скорости жидкости. В случае нестационарного течения положение линий тока может со временем меняться.В установившемся потоке положение линий тока не меняется. Жидкость движется в том же направлении линий тока; следовательно, жидкость не может пересечь …

Продолжить чтение

Присоединяйтесь к StudyMode, чтобы прочитать полный документ

.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт

Параметр Значение Вязкость межклеточной жидкости / (кг · м −1 909 −1 · 1 0 · с −3 [22] Коэффициент проницаемости стенки капилляра / (м 2 · с · кг −1 ) 5 × 10 −10 [23] Коллоидно-плазменный осмотический давление / мм рт. ст. 28 [24] Осмотическое давление интерстициального коллоида на стенке капилляра / мм рт. Длина капилляра / мкм м 2000 Диаметр капилляра / мкм м 8 [19] Расстояние между соседними капиллярами / 912 мкм м 48 [19] Интерстициальное гидростатическое давление на стенке капилляра / мм рт. давление на выходе / мм рт. Ширина расчетной области ( μ м) 784 Высота расчетной области ( μ м) 632