Размерность объемной скорости течения жидкости – 2.Течение жидкости. Линейная и объемная скорости, соотношение между ними

2.Течение жидкости. Линейная и объемная скорости, соотношение между ними

2.Течение жидкости. Линейная и объемная скорости, соотношение между ними. Уравнение неразрывности струи. Закон Бернулли, его практическое значение.

Основной характеристикой любого движения является его скорость. Выделяют 2 разных скорости.

Скорость перемещения самих частиц жидкости (или плывущих вместе с жидкостью мелких тел — например, эритроцитов в крови) обозначают v и называют линейной скоростью. V=x/t.

Объём V жидкости, протекающей в данном потоке (в трубе, в русле реки, в кровеносном сосуде и т.п.) за единицу времени. Эту величину называют объёмной скоростью и обозначают Q.

Между линейной скоростью v и объёмной скоростью Q существует простая связь. Рассмотрим трубку с площадью поперечного сечения S.

Выделим поперечный слой жидкости, который в момент времени t = 0 занимает положение 1. Через некоторое время t он переместится в положение 2, отстоящее на расстояние x= v*t. При этом через трубку пройдёт объём жидкости V = S*x . Объёмная скорость жидкости Q при этом будет равна Q =v/t=s*x/t. Но x/t=v, тогда

Q = S*V

В реальных жидкостях всегда существуют силы трения. В отличие от твёрдых тел, где силы трения действуют между двумя разными телами, в жидкостях силы трения возникают внутри жидкости (между разными её слоями). Поэтому трение в жидкостях называют внутренним трением или вязкостью.

Термин „идеальная жидкость» подразумевает, что при движении такой жидкости не происходит диссипация энергии (переход механической, энергии в тепло). Считалось, что таких жидкостей не существует, но в 1938 году академик П Л.Капица обнаружил, что при температурах, очень близких к абсолютному нулю, подобными свойствами обладает жидкий гелий (Капица назвал такое поведение гелия «сверхтекучестью».

Хотя во всех остальных случаях движение жидкости обязательно сопровождается диссипацией энергии, понятие идеальной жидкости (как, например, и понятие идеального газа) имеет большое практическое значение, потому что во многих случаях формулы, выведенные для идеальной жидкости, можно без больших ошибок применять для движения реальных жидкостей и газов. Наиболее интересным примером является теорема Бернулли, Рассмотрим горизонтальную трубку переменного сечения, по которой течёт жидкость или газ.

Легко видеть, что кинетическая энергия жидкости а правой части трубки больше, чем в левой, потому что линейная скорость жидкости справа больше, чем слева. Откуда взялось это увеличение энергии ? Оно произошло потому, что сила давления Кл при перемещении какого-то объема жидкости V производит некоторую работу А. По общей формуле но сила давления

равна самому давлению р, умноженному на площадь S, то есть . Отсюда

В левой части трубки соответственно, в правой части трубки Разность работ слева и справа есть

но мы уже несколько раз говорили, что через любое сечение неразветвлённой трубки проходит одинаковый объём жидкости, то 10

есть V, =V2- Обозначая объём просто V и вынося его за скобку, получим:

Так как мы считаем жидкость идеальной (потерь энергии нет), то разность работ равна приросту кинетической энергии;

Если разделить это равенство на объём, то справа вместо массы будет стоять плотность:

Перенося члены с индексом 1 влево, а с индексом 2 направо,

получаем:

Члены р и соединены знаком „плюс»; отсюда следует, что

их размерность одинакова, то есть величина тоже имеет

смысл давления. Её называют динамическим давлением, а член р – статическим давлением. Сумма статического и динамического давлений, стоящая в формуле называется полным давлением;

Так как при выводе мы положения сечений 1 и 2 взяли произвольно,- то из равенства (4) следует, что во всем потоке жидкости или газа полное давление (то есть сумма статического и динамического давлений) есть величина постоянная:

Это положение и, соответственно, формулы (4) и (5) и принято называть теоремой. Бернулли.

Статическое давление — это то давление, которое движущаяся жидкость оказывает на стенки трубки. Его можно измерить, если плоскость отверстия трубки манометра расположить параллельно линиям тока жидкости (рисунок 4-а). Если же плоскость отверстия трубки-манометра будет перпендикулярна линям тока, (рис. 4-6), то манометр покажет полное давление. При расположении манометра, как показано на рис. 4-в, мы будем измерять разность между полным и статическим давлениями, то есть динамическое давление.

Из теоремы Бернулли следует, что там, где скорость жидкости или газа больше, статическое давление меньше, и наоборот.

studfiles.net

Расчет скорости течения жидкости в трубопроводе

Скорость потока жидкости в трубе формула

Диаметр трубопроводов, скорость течения и расход теплоносителя.

Данный материал предназначен понять, что такое диаметр, расход и скорость течения. И какие связи между ними. В других материалах будет подробный расчет диаметра для отопления.

Для того чтобы вычислить диаметр необходимо знать:

Вот необходимые формулы, которые нужно знать:

Сопротивление движению теплоносителя.

Любой движущийся внутри трубы теплоноситель, стремиться к тому, чтобы прекратить свое движение. Та сила, которая приложена к тому, чтобы остановить движение теплоносителя – является силой сопротивления.

Это сопротивление, называют – потерей напора. То есть движущийся теплоноситель по трубе определенной длины теряет напор.

Напор измеряется в метрах или в давлениях (Па). Для удобства в расчетах необходимо использовать метры.

Для того, чтобы глубже понять смысл данного материла, рекомендую проследить за решением задачи.

В трубе с внутренним диаметром 12 мм течет вода, со скоростью 1м/с. Найти расход.

Решение: Необходимо воспользоваться вышеуказанными формулами:

S=3.14•0,012 2 /4=0,000113 м 2

Q=0,000113•1=0,000113 м 3 /с = 0,4 м 3 /ч.

Имеется насос, создающий постоянный расход 40 литров в минуту. К насосу подключена труба протяженностью 1 метр. Найти внутренний диаметр трубы при скорости движения воды 6 м/с.

Q=40л/мин=0,000666666 м 3 /с

Из выше указанных формул получил такую формулу.

Каждый насос имеет вот такую расходно-сопротивляемую характеристику:

Это означает, что наш расход в конце трубы будет зависеть от потери напора, которое создается самой трубой.

Более детально потеря напора по длине трубопровода рассматривается в этой статье:

А теперь рассмотрим задачу из реального примера.

Стальная (железная) труба проложена длиной 376 метров с внутренним диаметром 100 мм, по длине трубы имеются 21 отводов (угловых поворотов 90°С). Труба проложена с перепадом 17м. То есть труба относительно горизонта идет вверх на высоту 17 метров. Характеристики насоса: Максимальный напор 50 метров (0,5МПа), максимальный расход 90м 3 /ч. Температура воды 16°С. Найти максимально возможный расход в конце трубы.

Найти максимальный расход = ?

Для решения необходимо знать график насосов: Зависимость расхода от напора.

В нашем случае будет такой график:

Смотрите, прерывистой линией по горизонту обозначил 17 метров и на пересечение по кривой получаю максимально возможный расход: Qmax.

По графику я могу смело утверждать, что на перепаде высоты, мы теряем примерно: 14 м 3 /час. (90-Qmax=14 м 3 /ч).

Ступенчатый расчет получается потому, что в формуле существует квадратичная особенность потерь напора в динамике (движение).

Поэтому решаем задачу ступенчато.

Поскольку мы имеем интервал расходов от 0 до 76 м 3 /час, то мне хочется проверить потерю напора при расходе равным: 45 м 3 /ч.

Находим скорость движения воды

Q=45 м 3 /ч = 0,0125 м 3 /сек.

V = (4•0,0125)/(3,14•0,1•0,1)=1,59 м/с

Находим число рейнольдса

ν=1,16•10 -6 =0,00000116. Взято из таблици. Для воды при температуре 16°С.

Δэ=0,1мм=0,0001м. Взято из таблицы, для стальной (железной) трубы.

Далее сверяемся по таблице, где находим формулу по нахождению коэффициента гидравлического трения.

У меня попадает на вторую область при условии

10•D/Δэ 0.25 =0,11•( 0,0001/0,1 + 68/137069) 0,25 =0,0216

Далее завершаем формулой:

h=λ•(L•V 2 )/(D•2•g)= 0,0216•(376•1,59•1,59)/(0,1•2•9,81)=10,46 м.

Как видите, потеря составляет 10 метров. Далее определяем Q1, смотри график:

Теперь делаем оригинальный расчет при расходе равный 64м 3 /час

Q=64 м 3 /ч = 0,018 м 3 /сек.

V = (4•0,018)/(3,14•0,1•0,1)=2,29 м/с

λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/197414) 0,25 =0,021

h=λ•(L•V 2 )/(D•2•g)= 0,021•(376•2,29 •2,29)/(0,1•2•9,81)=21,1 м.

Отмечаем на графике:

Qmax находится на пересечении кривой между Q1 и Q2 (Ровно середина кривой).

Ответ: Максимальный расход равен 54 м 3 /ч. Но это мы решили без сопротивления на поворотах.

Для проверки проверим:

Q=54 м 3 /ч = 0,015 м 3 /сек.

V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с

λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/164655) 0,25 =0,0213

h=λ•(L•V 2 )/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.

Итог: Мы попали на Н_пот=14,89=15м.

А теперь посчитаем сопротивление на поворотах:

Формула по нахождению напора на местном гидравлическом сопротивление:

ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. Для больших диаметров он уменьшается. Это связано с тем, что влияние скорости движения воды по отношению к повороту уменьшается.

Смотрел в разных книгах по местным сопротивлениям для поворота трубы и отводов. И приходил часто к расчетам, что один сильный резкий поворот равен коэффициенту единице. Резким поворотом считается, если радиус поворота по значению не превышает диаметр. Если радиус превышает диаметр в 2-3 раза, то значение коэффициента значительно уменьшается.

Скорость 1,91 м/с

h=ζ•(V 2 )/2•9,81=(1•1,91 2 )/( 2•9,81)=0,18 м.

Это значение умножаем на количество отводов и получаем 0,18•21=3,78 м.

Ответ: при скорости движения 1,91 м/с, получаем потерю напора 3,78 метров.

Давайте теперь решим целиком задачку с отводами.

При расходе 45 м 3 /час получили потерю напора по длине: 10,46 м. Смотри выше.

При этой скорости (2,29 м/с) находим сопротивление на поворотах:

h=ζ•(V 2 )/2•9,81=(1•2,29 2 )/(2•9,81)=0,27 м. умножаем на 21 = 5,67 м.

Складываем потери напора: 10,46+5,67=16,13м.

Отмечаем на графике:

Решаем тоже самое только для расхода в 55 м 3 /ч

Q=55 м 3 /ч = 0,015 м 3 /сек.

V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с

λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/164655) 0,25 =0,0213

h=λ•(L•V 2 )/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.

h=ζ•(V 2 )/2•9,81=(1•1,91 2 )/( 2•9,81)=0,18 м. умножаем на 21 = 3,78 м.

Складываем потери: 14,89+3,78=18,67 м

Рисуем на графике:

Ответ: Максимальный расход=52 м 3 /час. Без отводов Qmax=54 м 3 /час.

В итоге, на размер диаметра влияют:

Если расход в конце трубы меньше, то необходимо: Либо увеличить диаметр, либо увеличить мощность насоса. Увеличивать мощность насоса не экономично.

Данная статья является частью системы: Конструктор водяного отопления

Скорость потока жидкости в трубе формула
Скорость потока жидкости в трубе формула Диаметр трубопроводов, скорость течения и расход теплоносителя. Данный материал предназначен понять, что такое диаметр, расход и скорость течения. И

Источник: infobos.ru

Скорость потока жидкости в трубе формула

При движении жидкости в круглой трубе скорость равна нулю у стенок трубы и максимальна на оси трубы. Полагая течение ламинарным, найдем закон изменения скорости с расстоянием от оси трубы.

Выделим воображаемый цилиндрический объем жидкости радиуса и длины l (рис. 77.1). При стационарном течении в трубе постоянного сечения скорости всех частиц жидкости остаются неизменными. Следовательно, сумма внешних сил, приложенных к любому объему жидкости, равна нулю. На основания рассматриваемого цилиндрического объема действуют силы давления, сумма которых равна Эта сала действует в направлении движения жидкости. Кроме того, на боковую поверхность цилиндра действует сила трения, равная (Имеется в виду значение на расстоянии от оси трубы). Условие стационарности имеет вид

Скорость убывает с расстоянием от оси трубы. Следовательно, отрицательна и Учтя это, преобразуем соотношение (77.1) следующим образом:

Разделив переменные, получим уравнение:

Интегрирование дает, что

Постоянную интегрирования нужно выбрать так, чтобы скорость обращалась в нуль на стенках трубы, т. е. — радиус трубы).

Из этого условия

Подстановка значения С в (77.2) приводит к формуле

Значение скорости на оси трубы равно

С учетом этого формуле (77.3) можно придать вид

Таким образом, при ламинарном течении скорость изменяется с расстоянием от оси трубы по параболическому закону (рис. 77.2).

При турбулентном течении скорость в каждой точке меняется беспорядочным образом. При неизменных внешних условиях постоянной оказывается средняя (по времени) скорость в каждой точке сечения трубы. Профиль средних скоростей при турбулентном течении изображен на рис. 77.3. Вблизи стенок трубы скорость изменяется гораздо сильнее, чем при ламинарном течении, в остальной же части сечения скорость изменяется меньше.

Полагая течение ламинарным, вычислим поток жидкости Q, т. е. объем жидкости, протекающий через поперечное сечение трубы за единицу времени. Разобьем поперечное сечение трубы на кольца ширины (рис. 77.4). Через кольцо радиуса пройдет за секунду объем жидкости, равный произведению площади кольца на скорость течения в точках, находящихся на расстоянии от оси трубы.

Приняв во внимание формулу (77.5), получим:

Чтобы получить поток Q, нужно проинтегрировать выражение (77.6) по в пределах от нуля до R: я 9

— площадь сечения трубы). Из формулы (77.7) следует, что при ламинарном течении среднее (по сечению) значение скорости равно половине значения скорости на. оси трубы.

Подставив в (77.7) значение (77.4) для

получим для потока формулу

Эта формула называется формулой Пуазейля. Согласно (77.8) поток жидкости пропорционален перепаду давления на единице длины трубы, пропорционален четвертой степени радиуса трубы и обратно пропорционален коэффициенту вязкости жидкости. Напомним, что формула Пуазейля применима только при ламинарном течении.

Соотношение (77.8) используется для определения вязкости жидкостей. Пропуская жидкость через капилляр известного радиуса и измеряя перепад давления и поток Q, можно найти

Скорость потока жидкости в трубе формула
Научная библиотека популярных научных изданий

Источник: scask.ru

Расход воды через трубу при нужном давлении

Содержание статьи

Основная задача расчёта объёма потребления воды в трубе по её сечению (диаметру) – это подобрать трубы так, чтобы водорасход не был слишком большой, а напор оставался хороший. При этом необходимо учесть:

• диаметры (ДУ внутреннего сечения),
• потери напора на рассчитываемом участке,
• скорость гидропотока,
• максимальное давление,
• влияние поворотов и затворов в системе,
• материал (характеристики стенок трубопровода) и длину и т.д..

Подбор диаметра трубы по расходу воды с помощью таблицы считается более простым, но менее точным способом, чем измерение и расчёт по давлению, скорости воды и прочим параметрам в трубопроводе, сделанный по месту.

Табличные стандартные данные и средние показатели по основным параметрам

Для определения расчётного максимального расхода воды через трубу приводится таблица для 9 самых распространённых диаметров при различных показателях давления.

Среднее значение давления в большинстве стояках находится в интервале 1,5-2,5 атмосфер. Существующая зависимость от количества этажей (особенно заметная в высотных домах) регулируется путём разделения системы водообеспечения на несколько сегментов. Водонагнетение с помощью насосов влияет и на изменение скорости гидропотока. Кроме того, при обращении к таблицам в расчёте водопотребления учитывают не только число кранов, но и количество водонагревателей, ванн и др. источников.

Способы вычисления зависимостей водорасхода и диаметра трубопровода

С помощью нижеприведённых формул можно как рассчитать расход воды в трубе, так и, определить зависимость диаметра трубы от расхода воды.

В данной формуле водорасхода:

• под q принимается расход в л/с,
• V – определяет скорость гидропотока в м/с,
• d – внутреннее сечение (диаметр в см).

Зная водорасход и d сечения, можно, применив обратные вычисления, установить скорость, или, зная расход и скорость – определить диаметр. В случае наличия дополнительного нагнетателя (например, в высотных зданиях), создаваемое им давление и скорость гидропотока указываются в паспорте прибора. Без дополнительного нагнетания скорость потока чаще всего варьируется в интервале 0,8-1,5 м/сек.

Для более точных вычислений принимают во внимание потери напора, используя формулу Дарси:

Для вычисления необходимо дополнительно установить:

• длину трубопровода (L),
• коэффициент потерь, который зависит от шероховатостей стенок трубопровода, турбулентности, кривизны и участков с запорной арматурой (λ),
• вязкость жидкости (ρ).

Зависимость между значением D трубопровода, скоростью гидропотока (V) и водорасходом (q) с учётом угла уклона (i) можно выразить в таблице, где две известные величины соединяются прямой линией, а значение искомой величины будет видно на пересечении шкалы и прямой.

Для технического обоснования также строят графики зависимости эксплуатационных и капитальных затрат с определением оптимального значения D, которое устанавливается в точке пересечения кривых эксплуатационных и капитальных затрат.

1. способа расчёта сопротивления,
2. материала и вида трубопроводных систем (сталь, чугун, асбоценмент, железобетон, пластмасса), где принимается во внимание, что, например, пластиковые поверхности менее шероховатые, чем стальные, и не подвергаются коррозии,
3. внутреннего диаметры,
4. длины участка,
5. падения напора на каждый метр трубопровода.

В некоторых калькуляторах учитываются дополнительные характеристики трубопроводных систем, например:

• новые или не новые с битумным покрытием или без внутреннего защитного покрытия,
• с внешним пластиковым или полимерцементным покрытием,
• с внешним цементно-песчаным покрытием, нанесённым разными методами и др.

Расход воды через трубу при нужном давлении
Определение зависимости расхода объёма воды, диаметра трубы, давления и скорости потока 3 способами: с помощью таблицы, формул или расчётов онлайн-калькулятором.

Источник: hitropop.com

Расчет расхода воды по диаметру трубы и давлению по таблице и СНИПу 2.04.01-85

Предприятия и жилые дома потребляют большое количество воды. Эти цифровые показатели становятся не только свидетельством конкретной величины, указывающей расход.

Помимо этого они помогают определить диаметр трубного сортамента. Многие считают, что расчет расхода воды по диаметру трубы и давлению невозможен, так, как эти понятия совершенно не связаны между собой.

Но, практика показала, что это не так. Пропускные возможности сети водоснабжения зависимы от многих показателей, и первыми в этом перечне будут диаметр трубного сортамента и давление в магистрали.

Выполнять все расчеты рекомендуют еще на стадии проектирования строительства трубопровода, потому, что полученные данные определяют ключевые параметры не только домашнего, но и промышленного трубопровод. Обо всем этом и пойдет далее речь.

Калькулятор для расчета воды онлайн

Какие факторы влияют на проходимость жидкости через трубопровод

Критерии, оказывающие влияние на описываемый показатель, составляют большой список. Вот некоторые из них.

1. Внутренний диаметр, который имеет трубопровод.
2. Скорость передвижения потока, которая зависит от давления в магистрали.
3. Материал, взятый для производства трубного сортамента.

Определение расхода воды на выходе магистрали выполняется по диаметру трубы, ведь эта характеристика совместно с другими влияет на пропускную способность системы. Так же расчитывая количество расходуемой жидкости, нельзя сбрасывать со счетов толщину стенок, определение которой проводится, исходя из предполагаемого внутреннего напора.

Можно даже заявить, что на определение «трубной геометрии» не влияет только протяженность сети. А сечение, напор и другие факторы играют очень важную роль.

Помимо этого, некоторые параметры системы оказывают на показатель расхода не прямое, а косвенное влияние. Сюда относится вязкость и температура прокачиваемой среды.

Подведя небольшой итог, можно сказать, что определение пропускной способности позволяет точно установить оптимальный тип материала для строительства системы и сделать выбор технологии, применяемой для ее сборки. Иначе сеть не будет функционировать эффективно, и ей потребуются частые аварийные ремонты.

Расчет расхода воды по диаметру круглой трубы, зависит от его размера. Следовательно, что по большему сечению, за определенный промежуток времени будет выполнено движение большего количества жидкости. Но, выполняя расчет и учитывая диаметр, нельзя сбрасывать со счетов давление.

Если рассмотреть этот расчет на конкретном примере, то получается, что через метровое трубное изделие сквозь отверстие в 1 см пройдет меньше жидкости за определенный временной период, чем через магистраль, достигающей в высоту пару десятков метров. Это закономерно, ведь самый высокий уровень расхода воды на участке достигнет максимальных показателей при самом высоком давлении в сети и при самых высоких размера ее объема.

Вычисления сечения по СНИП 2.04.01-85

Прежде всего, необходимо понимать, что расчет диаметра водопропускной трубы является сложным инженерным процессом. Для этого потребуются специальные знания. Но, выполняя бытовую постройку водопропускной магистрали, часто гидравлический расчет по сечению проводят самостоятельно.

Данный вид конструкторского вычисления скорости потока для водопропускной конструкции можно провести двумя способами. Первый – табличные данные. Но, обращаясь к таблицам необходимо знать не только точное количество кранов, но и емкостей для набора воды (ванны, раковины) и прочего.

Только при наличии этих сведений о водопропускной системе, можно воспользоваться таблицами, которые предоставляет СНИП 2.04.01-85. По ним и определяют объем воды по обхвату трубы. Вот одна из таких таблиц:

Расчет расхода воды по диаметру трубы и давлению по таблице и СНИПу -85
Расчет расхода воды по диаметру трубы и давлению необходимо произвести перед тем как … но на определение расхода воды влияет так же температура и вязкость среды, а так же материал, из которого состоит магистраль

Источник: trubanet.ru

Расчет скорости течения жидкости в трубопроводе

Автоклав объёмом 25,0 л наполнен жидкостью и закрыт герметически. Коэффициент температурного расширения жидкости , её модуль упругости Е. Определить повышение давления в автоклаве при увеличении температуры жидкости на величину Т. Объёмной деформацией автоклава пренебречь.

V0 = 25,0л = 25*10-3 м3

Из-за повышения температуры объем жидкости увеличится на величину.

V = 536*10-6*25*10-3*21=0,2814*10-3 м3

Коэффициент объемного сжатия сведем с модулем упругости.

Он представляет собой относительное изменение объема жидкости, приходящееся на единицу давления.

Величина повышения давления.

Вертикальная цилиндрическая цистерна с полусферической крышкой до самого верха заполнена жидкостью, плотность которой . Диаметр цистерны D, высота её цилиндрической части Н. Манометр М показывает манометрическое давление Рм. Определить силу, растягивающую болты А, и горизонтальную силу, разрывающую цистерну по сечению 1-1.

Силой тяжести крышки пренебречь. Векторы сил показать на схеме.

Вертикальная сила Fz, растягивающую болты.

где V – объем тела давления

Расстояние по вертикали до пьезометрической плоскости (пп).

Объем тела давления как разность объемов цилиндра и полусферы.

Сила растягивающая болты.

Fz =*g*=998*9,81*=5249 Н

Горизонтальная сила, действующая на вертикальную полуцилиндрическую часть.

где p1 = рм+gh = g*0,288 D

– давление в центре тяжести С1 вертикальной проекции верхней полуцилиндрической части,

– площадь этой проекции (полукруг).

F1 = g *0,288D* = 0,036 П* g = 0,036П*998*9,81*1,63=4535Н

Горизонтальная сила, действующая на цилиндрическую часть.

– давление в центре тяжести вертикальной проекции цилиндрической части.

А2 – площадь этой проекции.

F2 = g ( НD =998*9,81*(.

Полная горизонтальная сила равна.

FX = F1 + F2 = 4535+120304=124839 Н.

Ответ: Fz = 5249H, Fx = 124839H.

Центробежный насос, перекачивающий жидкость Ж при температуре 20С, развивает подачу Q. Определить допустимую высоту всасывания hв, если длина всасывающего трубопровода l, диаметр d, эквивалентная шероховатость э, коэффициент сопротивления обратного клапана к, а показание вакуумметра не превышало бы pв.

Построить пьезометрическую и напорную линии. Данные в соответствии с вариантом задания выбрать из табл. 4.

Q = 1,9 л/с=1,9*10-3 м3/с

– кинематическая вязкость Ж

= 808 кг/м3 – плотность Ж

Выбираем два живых сечения в потоке, где известно наибольшее число входящих в уравнение Бернулли гидравлических параметров. За первое сечение 1-1 берем свободную поверхность жидкости в резервуаре А, за второе сечение 2-2 принимаем место подключения вакуумметра.

3. Для выбранных сечений уравнение Бернулли будет иметь вид:

Намечаем горизонтальную плоскость сравнения проходящую через центр тяжести сечения 1-1.

Геометрическая высота: Z1 = 0, Z2 = hв.

Давление: р1 = Ратм, р2 = Ратм – рв.

h=hтр+hм (сумма потерь на трение и местные потери)

Скорость течения жидкости в трубопроводе

Определяем режим течения жидкости, исходя из значения числа Рейнольдса по формуле:

– режим течения турбулентности.

Коэффициента гидравлического трения по формуле Альтшуля.

Потери напора от трения по длине трубопровода

Местные гидравлические потери.

– сумма коэффициентов местных сопротивлений (вход в трубу, клапан, поворот). жидкость пьезометрический гидравлический трение

Допустимая высота всасывания

Ответ: hв = 7,40 м.

Рабочая жидкость масло Ж, температура которого 50С, из насоса подводится к гидроцилиндру Ц через дроссель ДР. Поршень цилиндра со штоком перемещается против нагрузки Fсо скоростью п. Вытесняемая поршнем жидкость со штоковой полости попадает в бак Б через сливную линию, длина которой равна lc, а диаметр равен dc.

Определить внешнюю силу F, преодолеваемую штоком при его движении. Давление на входе в дроссель определяется показанием манометра М, а противодавление в штоковой полости цилиндра потерями давления в сливной линии. Коэффициент расхода дросселя принять равным = 0,64, а диаметр отверстия дросселя dд. Диаметр поршня Dп, а диаметр штока Dш. К.п.д. гидроцилиндра: объёмный 0 = 1,0, механический м.

Расчет скорости течения жидкости в трубопроводе
Расчет скорости течения жидкости в трубопроводе Автоклав объёмом 25,0 л наполнен жидкостью и закрыт герметически. Коэффициент температурного расширения жидкости , её модуль упругости Е.

Источник: studwood.ru

trubyisantehnika.ru

Понятие идеальной жидкости. Уравнение неразрывности струи и следствие этого уравнении. Объёмная скорость течения жидкости, единицы её измерения.

Стр 1 из 5Следующая ⇒

БИЛЕТ 1

Понятие идеальной жидкости. Уравнение неразрывности струи и следствие этого уравнении. Объёмная скорость течения жидкости, единицы её измерения.

Уравнение Бернулли, статическое, гидростатическое, динамическое и полное -давления

Текущей жидкости.

Идеа́льная жи́дкость — в гидродинамике — воображаемая (идеализированная) жидкость, в которой, в отличие от реальной жидкости, отсутствуют вязкость и теплопроводность. В идеальной жидкости отсутствует внутреннее трение, то есть, нет касательных напряжений между двумя соседними слоями.

Уравнение неразрывности — соотношение между скоростью течения, объемным расходом среды и расстоянием между линиями тока. Это уравнение выражает один из основных законов гидроаэромеханики, согласно которому объемный расход во всякой трубке тока, ограниченной соседними линиями тока, должен быть в любой момент времени одинаков во всех ее поперечных сечениях. Поскольку объемный расход Q равен произведению скорости текущей среды V на площадь A поперечного сечения трубки тока, уравнение неразрывности имеет следующий вид:

Q = V₁A₁ = V₂A₂ или же vS = const ( v — скорость жидкости, S — площадь сечения трубы, по которой течёт жидкость. Смысл — сколько воды вливается — столько и должно вылиться, если условия течения неизменны).

Поэтому там, где сечение велико и линии тока разрежены, скорость должна быть мала, и наоборот. (Все три части этого двойного равенства должны выражаться в одной и той же системе единиц. Так, если величина Q выражена в м³/с, то скорость V должна выражаться в м/с, а площадь A — в м².)

Уравнение Бернулли имеет вид: р + рv² + pgh = const.

где р — давление жидкости, р — её плотность, V — скорость движения, g — ускорение свободного падения, h — высота, на которой находится элемент жидкости.

Согласно уравнению Бернулли, в случае установившегося течения, для которого не имеют существенного значения все другие характеристики текущей среды, кроме плотности (удельного веса), полный напор одинаков во всех поперечных сечениях трубки тока. Если к отверстию в стенке трубы присоединить манометрическую трубку, то жидкость в такой трубке поднимется на высоту, равную гидростатическому напору. Если манометрическую трубку выставить навстречу потоку, то жидкость в манометре поднимется на дополнительную высоту, равную скоростному напору. Трубка, имеющая одновременно торцевое и боковые манометрические отверстия, называется трубкой Пито и используется для определения скорости течения по измеренному скоростному напору. Трубки Пито входят в комплект измерительного оборудования всех самолетов, а также широко применяются для измерений скорости течения в трубопроводах, вентиляционных воздуховодах, в аэро- и гидродинамических трубах.

Если скорость течения равна нулю (т.е. среда не движется), то уравнение Бернулли сводится к простому уравнению гидростатики.

Согласно этому уравнению, увеличению высоты в неподвижной среде жидкости или газа соответствует равное уменьшение гидростатического напора. Поэтому давление в любой точке неподвижной жидкости равно глубине этой точки под свободной поверхностью, умноженной на удельный вес жидкости. На основе этого соотношения вычисляется давление жидкости на стенки резервуаров, а также проводится анализ плавучести и остойчивости морских и речных судов.

В тех случаях, когда скорость течения отлична от нуля, уравнение Бернулли совместно с уравнениями неразрывности и закона сохранения количества движения позволяет решать практически важные задачи — о расходе среды, текущей через измерительные диафрагмы, поверх измерительных и водосбросных водосливов и под затворы шлюзовых галерей; о траектории струи жидкости; о форме, скорости и силе волн, действующих на суда и волноломы. Хотя в таких задачах обычно рассматривается течение воды под атмосферным слоем воздуха, аналогичные процессы гравитационного характера имеют место в случае течения более холодной (и, следовательно, более плотной) воды под более теплой, как и других жидкостей и газов разной плотности. Таким образом, водным потокам в реках аналогичны океанские течения и ветры, поскольку все гравитационные явления подчиняются одним и тем же законам гидроаэромеханики.

Мембранный потенциал клеток. Биологические потенциалы тканей и органов. Физические основы электрокардиографии и вектор электрографии (ЭКГ и ВЭКГ).

Функционирование клеток биологических тканей сопровождается изменением концентрации ионов калия и натрия, входящих в состав цитоплазмы и межклеточной жидкости. При этом изменение концентрации ионов по обе стороны клеточной мембраны приводит к изменению мембранного потенциала. Ткань или орган, состоящие из клеток, создают в каждый момент электрическое поле, потенциал которого является геометрической суммой всех мембранных потенциалов отдельных клеток (в соответствии с принципом сложения электрических полей).

В состоянии покоя наружная поверхность клеточной мембраны имеет положительный заряд, а внутренняя — отрицательный. Это состояние называют состоянием поляризации клетки. При возбуждении клетки меняется проницаемость мембраны, и внутрь клетки устремляются положительные ионы натрия. Нейтрализация внутреннего отрицательного заряда клетки при­водит к изменению знака мембранного потенциала, в результате чего внеш­няя поверхность клетки становится отрицательно заряженной. Это состояние называют деполяризацией. Обратный переход из состояния возбуждения в состояние покоя называют реполяризацией.

Из всех органов сердечная мышца — миокард обладает способностью автоматического чередования состояний покоя и возбуждения, благодаря наличию в ней не только мускульных клеток, но и системы специфических нервно-мышечных элементов, называемых проводящей системой сердца. Автоматизм сердечных сокращений задаёт входящий в эту систему синусный узел, расположенный в правом предсердии. От него процесс возбуждения в определённой последовательности охватывает остальные участки миокарда с периодичностью, определяющей цикл сердечных сокращений.

Процесс возбуждения каждого участка сердечной мышцы сопровождается изменением знака поверхностного заряда клеток. При этом происходит непрерывное перемещение границы положительно и отрицательно заряженных клеток, что приводит к изменению электрического поля сердца.

Электрокардиография — диагностический метод, основанный на измерении потенциалов электрического поля работающего сердца. Изменение потенциала электрического поля всей сердечной мышцы связано с последовательность возбуждения определённых её участков в течение цикла сокращений сердца. В этом и заключена принципиальная возможность связать вид кривой изменения биопотенциалов сердца (ЭКГ) с состоянием отдельных его участков.

В настоящее время наибольшее признание получила дипольная теория образования ЭКГ. предложенная Эйнтховеном. Согласно этой теории, на границе возбуждённого и невозбуждённого участков миокарда возникают разноимённые заряды или элементарные диполи. В сердце одновременно возникает множество таких диполей с различными направлениями моментов. Векторная сумма моментов всех диполей образует мгновенное значе­ние суммарного электрического вектора сердца — (ЭВС). ориентация и вели­чина которого меняется во времени. Принято считать, что начало ЭВС всё время находится в одной точке, называемой электрическим центром сердца.

За время сердечного цикла конец ЭВС описывает три замкнутые кривые с общей точкой в электрическом центре сердца, соответствующие: деполяризации предсердий, деполяризации желудочков, реполяризации предсердий. Направление ЭВС, соответствующее моменту деполяризации желудочков, называют электрической осью сердца.

Для регистрации кривой изменения биопотенциалов сердца Эйнтховеном было предложено снимать разности потенциалов между тремя точками, расположенными на: запястьях левой руки (ЛР) и правой руки (ИР) и на щиколотке левой ноги (ЛН). Эти точки образуют равносторонний треугольник. центр которого совпадает с электрическим центром сердца.

Этот треугольник получил название треугольника Эйнтховена, а варианты снимаемых разностей потенциалов называются стандартными отведениями:

ЛР — ПР — I отведение.

ЛН — ПР — II отведение.

ЛН — ЛР — III отведение.

ЭКГ, снимаемые в каждом из отведений, представляют собой проекции мгновенных значений ЭВС на соответствующую сторону треугольника Эйнтховена.

При этом Р-зубец ЭКГ является проекцией первой петли, описываемой концом ЭВС (деполяризации предсердий). QRS-зубец- проекция второй большой петли (деполяризация желудочков), Т-зубец — проекция третьей малой петли (реполяризация предсердий).

Можно наблюдать и сами петли па экране Электронно-лучевой трубки. Их получают при одновременной подаче напряжений двух отведений: на отклоняющие пластины ЭЛТ (одного на вертикально, другого на горизонтально отклоняющие пластины). Этот метод диагностики получил название вектор электрокардиографии (ВЭКГ).

БИЛЕТ 2

Для медицины.

БИЛЕТ 3

БИЛЕТ 4

1. Физические основы рефрактометрии. Рефрактометр, назначение и принцип действия. Его применение для определения концентрации раствора

БИЛЕТ 5

Импульсный ток

БИЛЕТ 6

БИЛЕТ 7

БИЛЕТ 8

БИЛЕТ 9

БИЛЕТ 10

БИЛЕТ 11

1. Физические основы рефрактометрии (законы» преломление и Т.Д.). Рефрактометр, назначение и принцип действия. Его применение для определения

БИЛЕТ 12

БИЛЕТ 13

Неполяризованный свет;)

БИЛЕТ 14

БИЛЕТ 15

1. Законы преломления. Рефрактометр. ( Законы преломления. Абсолютный и относительный показатели преломления света. Переход света из среды более плотной в среду менее плотную, Явление полного внутреннего отражения. Предельный угод полного внутреннего отражения. Физические основы рефрактометрии. Рефрактометр, назначение и принцип действия. Его применение для определения концентрации раствора),

БИЛЕТ 16

УВЧ-терапия. Сущность процедуры, воздействующий фактор, первичный эффекты от воздействия этого фактора на организм человека, оценка теплового эффекта. Принципиальная схема УВЧ — аппарата. Условие согласования генератора УВЧ — аппарата и контура пациента.

БИЛЕТ 17

БИЛЕТ 18

БИЛЕТ 19

1. Физическне основы рефрактометрии. Рефрактометр, назначение и принцип действия, его применение для определения концентрации раствора

БИЛЕТ 20

Оптическая схема микроскопа

Изображение предмета, полученное с помощью объектива и двух систем Галилея, поочередно включаемых в ход лучей, фокусируется объективами в фокальную плоскость окуляров. Системы Галилея работают в прямом и обратном ходе, давая в сочетании с объективами четыре варианта увеличений объективной части микроскопа. Пятый вариант увеличения получается при выключенных из хода лучей систем Галилея. Значения увеличений объективной части микроскопа приведены в таблице 1. К микроскопу прилагаются две пары сменных окуляров и один окуляр 8х со сменными шкалой и сеткой и диоптрийной наводкой, с помощью которых рассматривается изображение, даваемое оптической частью микроскопа. Округленные значения увеличений окуляров нанесены на их корпусах. Оптические характеристики микроскопа с каждой парой сменных окуляров и при всех увеличениях объективной части приведены в таблице 2. Призмы Шмидта дают прямое изображение предмета и позволяют изменять межзрачковое расстояние прибора от 56 до 72 мм в соответствии с базой глаз наблюдателя.

 

Описание конструкции

Микроскоп состоит из следующих основных частей: оптической головки, стола микроскопа, блока питания. Оптическая головка включает в себя: корпус с барабаном, объектив f=90 мм, бинокулярную насадку, осветитель. Стол микроскопа состоит из столика для работы в проходящем свете и столика для работы в отраженном свете. Установка нужного увеличения осуществляется вращением рукояток до совмещения цифры на рукоятке с индексом на кольце. Фокусировка микроскопа на объект производится перемещением оптической головки относительно стола микроскопа по направляющей типа «ласточкин хвост» вращением рукояток.

 

Импедансометрия (Цепи переменного тока с омическим (активным) сопротивлением, с индуктивностью, с емкостью. Мгновенные значения силы тока и напряжения в этих цепях. Сущность метода векторных диаграмм при вычислении импеданса цепей переменного тока.).

Импедансометрией называют методы исследование объектов различной природы путем измерения их полного сопротивления (импеданса) на пере­менном токе. Часто при этом исследуется частотная зависимость этого со­противления.

Импедансометрия широко применяется в медицине для диагностики ря­да заболеваний и оценке эффективности лечебных мероприятий. Достоинство этих методов состоит в том, что с их помощью можно исследовать живой объект, не нарушая его структуры и функций. Они позволяют регистрировать изменения физико-химической структуры живых тканей при различных внешних воздействиях. Импедансометрия включает в себя такие методы ди­агностики как реокардиография, реоплетизмография, реоэнцефалография и другие.

В импедансометрии вводится понятие эквивалентной схемы исследуе­мого объекта. Под эквивалентной схемой понимают электрическую схему, состоящую из R,L,C- элементов (сопротивлений, индуктивностей, конденса­торов), которая имеет такую же величину и частотную зависимость импедан­са, как и исследуемый объект.

 

УЗ излучение ( Ультразвуковые волны. Особенности ультразвуковых волн по сравнению с волнами звуковых частот. Закон поглощения ультразвукового излучения ( УЗИ). Акустический импеданс. Отражение ультразвука. Явление кавитации. Воздействие УЗИ на биологические ткани. Применение (УЗИ) в терапии и хирургии. Физические основы применения УЗИ в диагностике (теневой метод и метод бирэхолокации))

Распространение ультразвука

Распространение ультразвука — это процесс перемещения в пространстве и во времени возмущений, имеющих место в звуковой волне.

Звуковая волна распространяется в веществе, находящемся в газообразном, жидком или твёрдом состоянии, в том же направлении, в котором происходит смещение частиц этого вещества, то есть она вызывает деформацию среды. Деформация заключается в том, что происходит последовательное разряжение и сжатие определённых объёмов среды, причём расстояние между двумя соседними областями соответствует длине ультразвуковой волны. Чем больше удельное акустическое сопротивление среды, тем больше степень сжатия и разряжения среды при данной амплитуде колебаний.

Частицы среды, участвующие в передаче энергии волны, колеблются около положения своего равновесия. Скорость, с которой частицы колеблются около среднего положения равновесия называется колебательной скоростью. Колебательная скорость частиц изменяется согласно уравнению: V = U sin (2pift + G), где V — величина колебательной скорости; U — амплитуда колебательной скорости; f — частота ультразвука; t — время; G — разность фаз между колебательной скоростью частиц и переменным акустическим давлением. Амплитуда колебательной скорости характеризует максимальную скорость, с которой частицы среды движутся в процессе колебаний, и определяется частотой колебаний и амплитудой смещения fA,pчастиц среды. U = 2

Дифракция, интерференция

При распространении ультразвуковых волн возможны явления дифракции, интерференции и отражения.

Дифракция (огибание волнами препятствий) имеет место тогда, когда длина ультразвуковой волны сравнима (или больше) с размерами находящегося на пути препятствия. Если препятствие по сравнению с длиной акустической волны велико, то явления дифракции нет.

При одновременном движении в ткани нескольких ультразвуковых волн в определённой точке среды может происходить суперпозиция этих волн. Такое наложение волн друг на друга носит общее название интерференции. Если в процессе прохождения через биологический объект ультразвуковые волны пересекаются, то в определённой точке биологической среды наблюдается усиление или ослабление колебаний. Результат интерференции будет зависеть от пространственного соотношения фаз ультразвуковых колебаний в данной точке среды. Если ультразвуковые волны достигают определённого участка среды в одинаковых фазах (синфазно), то смещения частиц имеют одинаковые знаки и интерференция в таких условиях способствует увеличению амплитуды ультразвуковых колебаний. Если же ультразвуковые волны приходят к конкретному участку в противофазе, то смещение частиц будет сопровождаться разными знаками, что приводит к уменьшению амплитуды ультразвуковых колебаний.

Интерференция играет важную роль при оценке явлений, возникающих в тканях вокруг ультразвукового излучателя. Особенно большое значение имеет интерференция при распространении ультразвуковых волн в противоположных направлениях после отражения их от препятствия.

БИЛЕТ 22

БИЛЕТ 23

БИЛЕТ 24

БИЛЕТ 25

Магнитное поле. Индукция и напряженность магнитного поля. Вектор индукции магнитного поля. Графическое изображение магнитного поля. Закон Био-Савара-Лапласа. Поток магнитной индукции. Проводник с током в магнитном поле. Закон Ампера-Действие магнитного поля на заряженные частицы. Сила Лоренца. Энергия магнитного поля.

БИЛЕТ 26

Построения).

БИЛЕТ 27

БИЛЕТ 28

Рентгенография

— исследование внутренней структуры объектов, которые проецируются при помощи рентгеновских лучей на специальную плёнку или бумагу. Наиболее часто термин используется в медицинском контексте, описывающий неинвазивное исследование, основанное на изучении костных структур и мягких тканей, при помощи суммационного проекционного изображения.

Получение изображения основано на ослаблении рентгеновского излучения при его прохождении через различные ткани с последующей регистрацией его на рентгеночувствительную плёнку. Таким образом, на плёнке получается усреднённое, суммационное изображение всех тканей (тень).

В современных цифровых аппаратах регистрация выходного излучения может производиться на специальную кассету с плёнкой или на электронную матрицу. При этом печать плёнок производится только при необходимости, а диагностическое изображение выводится на монитор и, в некоторых системах, сохраняется в базе данных вместе с остальными данными о пациенте.

Рекомендуется проведение снимков не менее чем в двух проекциях.

БИЛЕТ 29

Импедансометрия.

Импедансометрией называют методы исследование объектов различной природы путем измерения их полного сопротивления (импеданса) на пере­менном токе. Часто при этом исследуется частотная зависимость этого со­противления.

Импедансометрия широко применяется в медицине для диагностики ря­да заболеваний и оценке эффективности лечебных мероприятий. Достоинство этих методов состоит в том, что с их помощью можно исследовать живой объект, не нарушая его структуры и функций. Они позволяют регистрировать изменения физико-химической структуры живых тканей при различных внешних воздействиях. Импедансометрия включает в себя такие методы диагностики как реокардиография, реоплетизмография, реоэнцефалография и другие.

В импедансометрии вводится понятие эквивалентной схемы исследуемого объекта. Под эквивалентной схемой понимают электрическую схему, состоящую из R,L,C- элементов (сопротивлений, индуктивностей, конденсаторов), которая имеет такую же величину и частотную зависимость импеданса, как и исследуемый объект.

Целью настоящей работы является изучение законов прохождения переменного тока через электрические цепи и знакомство с основами импедансометрии биологических объектов

Рентгенодиагностика.

БИЛЕТ 30

УЗИ

БИЛЕТ 31

Электрический ток.

БИЛЕТ 1

Понятие идеальной жидкости. Уравнение неразрывности струи и следствие этого уравнении. Объёмная скорость течения жидкости, единицы её измерения.

Рекомендуемые страницы:

lektsia.com

13.Расход жидкости(виды расходов) и средняя скорость. Способы их определения

Расходом называется количество жидкости, протекающей через живое сечение потока в единицу времени.

Различают:

объемный (Q) :

массовый (Qm) :

весовой (G)

расходы жидкости. Где V— объем жидкости; m — масса жидкости; ? — время.

Объемный расход потока с живым сечением F определим с использованием понятия средней скорости потока wcp:

Средняя скорость — это условная скорость потока, которая считается одинаковой для всех частиц данного сечения, но подобрана так, что расход, определенный по ее значению, равен истинному значению расхода.

14. Уравнения неразрывности для элементарной струйки и потоки жидкости.

Если несжимаемая жидкость движется без разрывов, то при установившемся движении объемный расход для всех живых сечений потока постоянен, т.е. можно записать, что вдоль потока

Это уравнение называют уравнением неразрывности потока, оно является первым основным уравнением гидродинамики. Из него следует, что средние скорости обратно пропорциональны площадям соответствующих живых сечений потока.

14(2). Уравнение неразрывности для элементарной струйки и потока жидкости при установившемся движении. В гидравлике обычно рассматривают потоки, в которых не образуются разрывы и не заполненные жидкостью пустоты, т.е. жидкость сплошь заполняет пространство.

Рассмотрим элементарную струйку несжимаемой жидкости при установившемся движении. Выделим сечение 1-1 и 2-2, расположенные на расстоянии l одно от другого (рис.1.23). Здесь Δs1 и Δs2 — площади живых сечений соответственно; u 1 и u2 — скорости; ΔQ1 и ΔQ2 — расходы элементарной струйки в сечениях.

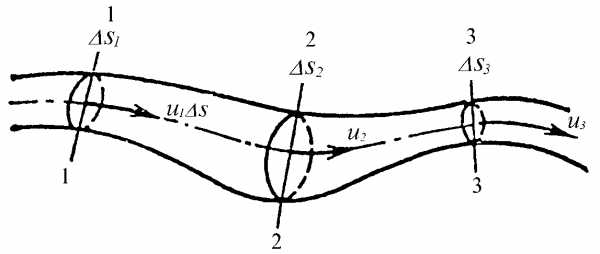
Рис. 1.23. Элементарные струйки несжимаемой жидкости при установившемся режиме движения

Очевидно, что ΔQ1 = Δs1u1 и ΔQ2 = Δs2u2, причем ΔQ1 втекает в рассматриваемый отсек, а ΔQ 2 — вытекает.

Учитывая, что форма элементарной струйки не изменяется с течением времени, поперечный приток и отток невозможен, так как скорости на боковой поверхности струйки направлены по касательным к линиям тока, из которых состоит эта боковая поверхность, получаем, что расходы ΔQ1 и ΔQ2 равны, т.е.

Δs1u 1 = Δs2u2. (1.50)

Аналогичные соотношения можно написать для любых двух сечений элементарной струйки, расположенных вдоль нее:

u1Δs1 = u2Δs2 =…= uΔs = ΔQ = const (1.51)

Это и есть уравнение неразрывности для элементарной струйки несжимаемой жидкости при установившемся движении.

Если выделить в потоке два любых сечения, отстоящих на некотором расстоянии, то, просуммировав по каждому из живых сечений обе части в уравнении (1.50)

Таким образом, в отмеченных условиях расход, проходящий через все живые сечения потока, неизменен, несмотря на то что в каждом сечении средняя скорость и площадь живого сечения могут быть различны.

Из (1.52) получим также важное соотношение

т.е. средние скорости обратно пропорциональны площадям живых сечений потока, которым соответствуют эти средние скорости.

Уравнение неразрывности (1.52) является одним из основных уравнений гидродинамики.

studfiles.net

§4. Течение вязкой жидкости по цилиндрическим трубам.

Формула Пуазейля. Ламинарное и турбулентное течение жидкости.

Понятие о числе Рейнольдса.

Жидкость, протекающую по цилиндрической трубе радиуса R, можно представить разделенной на концентрические слои (рис.10).В каждом таком слое

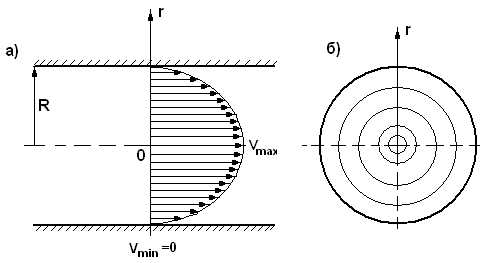
Рис.10

скорость течения постоянна, но от слоя к слою изменяется. Слой, прилипший к стенкам трубы, имеет скорость равную нулю, V_min=0. Слой, текущий вдоль оси трубы, имеет максимальную скорость V_max. Профиль скорости в этом случае является параболой (рис.10 а). Вдоль радиуса трубы (ось r) скорость изменяется, и это изменение характеризуется величиной .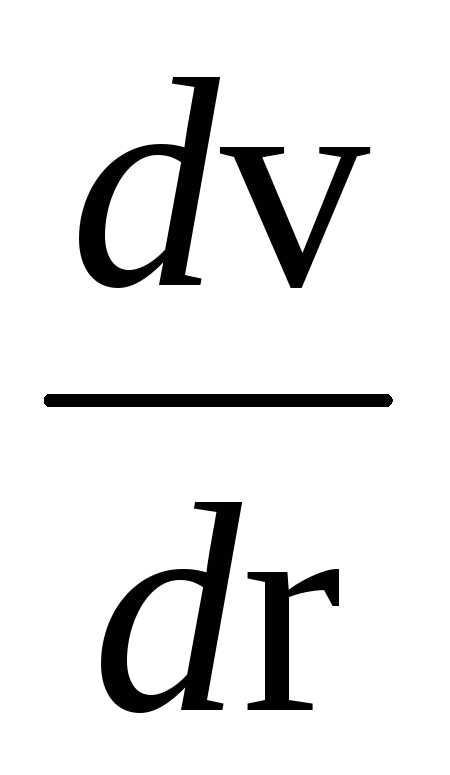

Задача о течении вязкой жидкости по цилиндрическим трубам имеет исключительно важное значение для физиологии, так как кровеносная система является системой из многократно разветвляющихся цилиндрических сосудов различных диаметров.

Важнейшей закономерностью течения вязкой жидкости по цилиндрическим трубам является формула Пуазейля, позволяющая рассчитать объем жидкости, протекающий через поперечное сечение трубы за одну секунду.

,

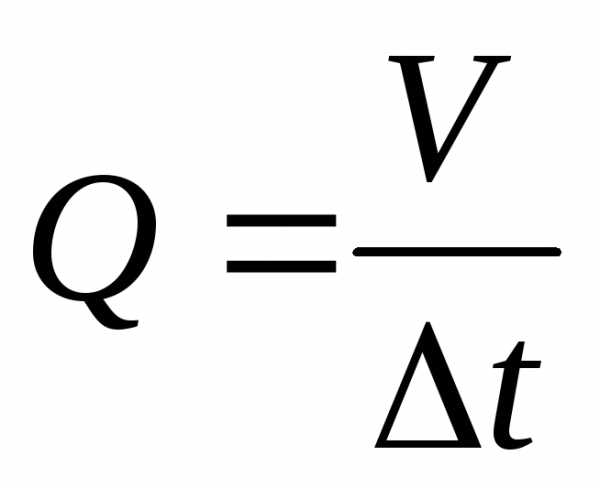где — объем жидкости, протекающей через поперечное сечение трубыза время. Используя формулу (1), можно записать

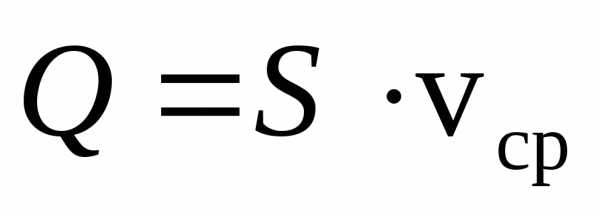
где — средняя скорость течения жидкости в трубе. Тогда, учитывая, чтоS=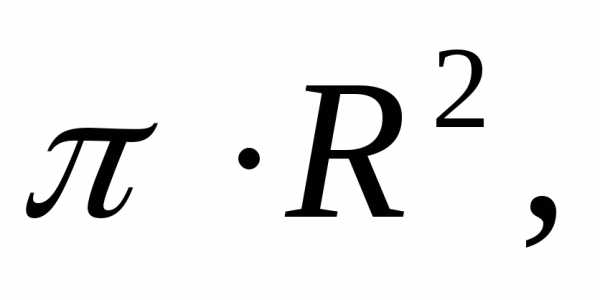запишемQ=

Для вычисления выделим в объеме текущей жидкости малый цилиндр произвольного радиусаr длиной l (рис.II). Обозначив давление в жидкости слева от выбранного цилиндра через Р₁, а справа через Р₂.На малый цилиндр в потоке действуют две силы: _1, обусловленная разностью давлений — Р₂, сообщающая цилиндру ускорение, и сила — сила трения (вязкости), которую испытывает этот цилиндр, перемещаясь в потоке жидкости.

Рис.11

Для силы F₁ запишем

F₁=

где S₁= 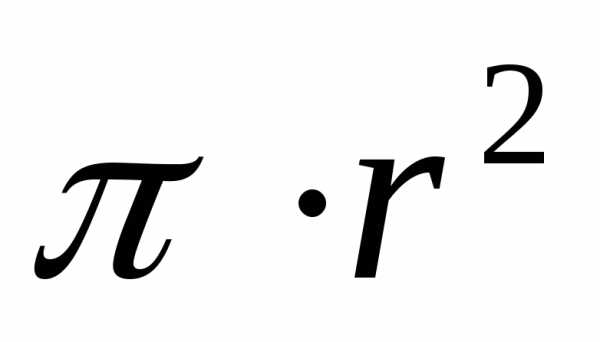— площадь поперечного сечения малого цилиндра.

Используя формулу Ньютона, для силы F₂ получим:

F₂ =,

где S₂ = 2 боковая поверхность малого цилиндра / поверхность соприкосновения этого цилиндра с остальным объемом жидкости /.

Чтобы цилиндр двигался с постоянной скоростью, надо, чтобы силы иуравновешивали друг друга, т.е. должно выполняться условие:

(15)

Условие (15) через модули сил запишем в виде F₁=-F₂ или, подставив значение сил, получим

(Р₁-Р₂)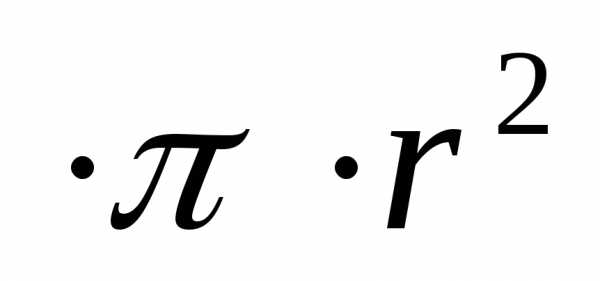= —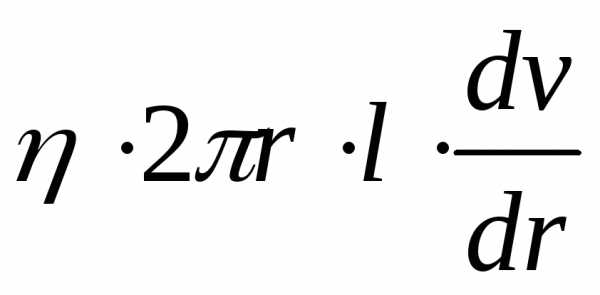(16)

Произведем сокращения и выразим из этого уравнения :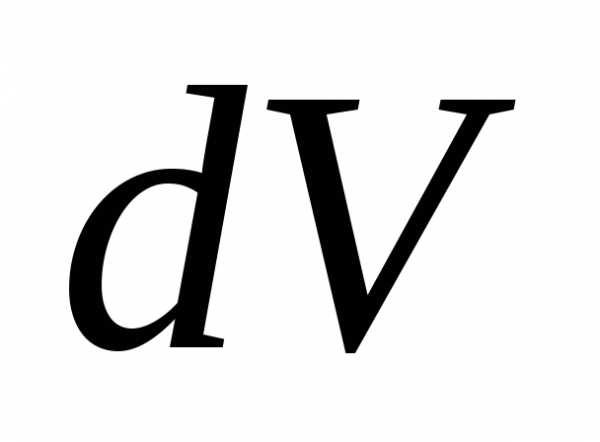

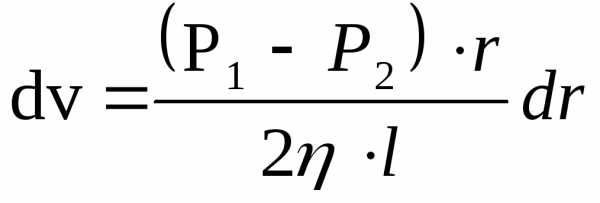
Проинтегрируем полученное уравнение, подставив предел интегрирования:

или

_. (17)

На осевой линии трубы r=0, а скорость 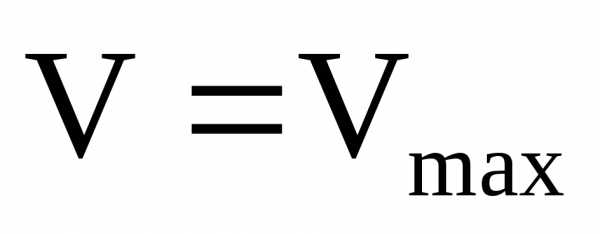тогда (17) можно переписать в виде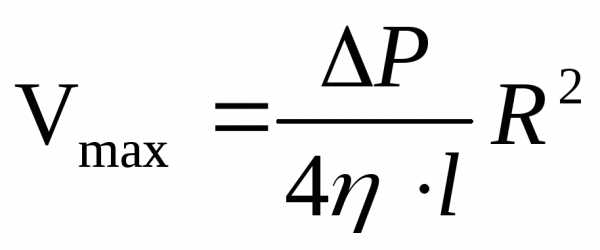(18)

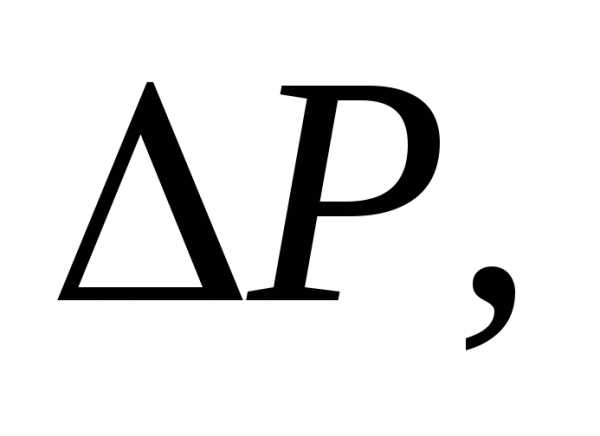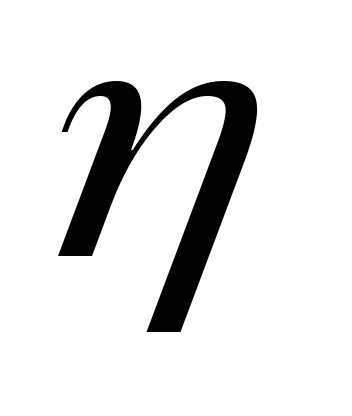Формула (18) была получена французским физиком и физиологом Пуазейлем в 1841 году. Из (18) видно, что максимальная скорость течения жидкости по трубе прямо пропорциональна перепаду давления квадрату радиуса трубыR и обратно пропорциональна коэффициенту вязкости жидкости и длине цилиндраl.Подставляя (18) в (14),получим Q=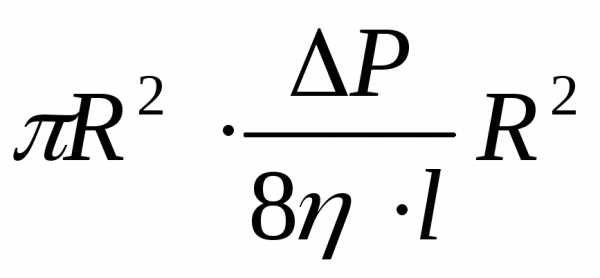или в окончательном виде

(19)

Q=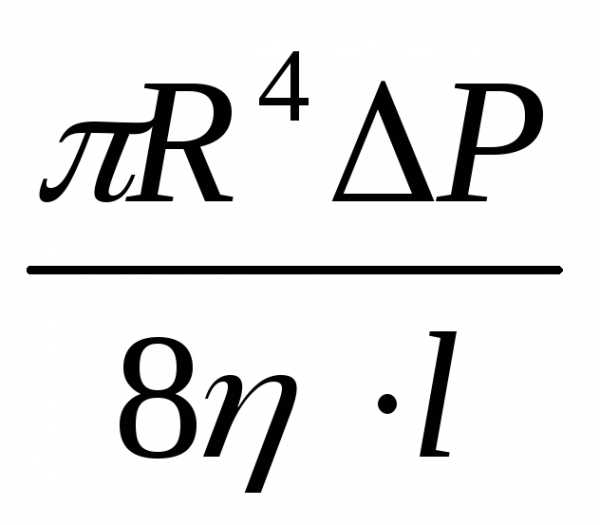

Полученное выражение носит название формулы Гагена-Пуазейля, или формулы Пуазейля.

Таким образом, объем жидкости Q, ежесекундно протекающей через поперечное сечение трубы, прямо пропорционален четвертой степени радиуса трубы R (Q~R⁴), разности давлений 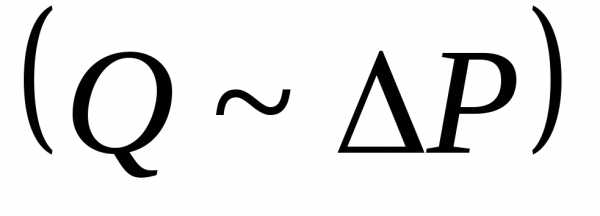и обратно пропорционален коэффициенту вязкости и длине трубы.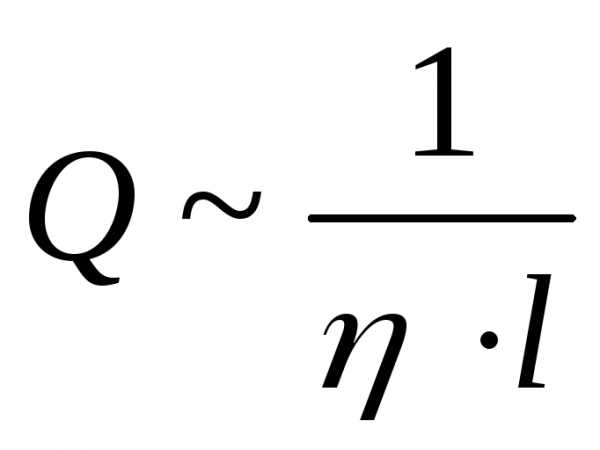

Часто проводят аналогию между формулой Пуазейля и законом Ома для однородного участка цепи 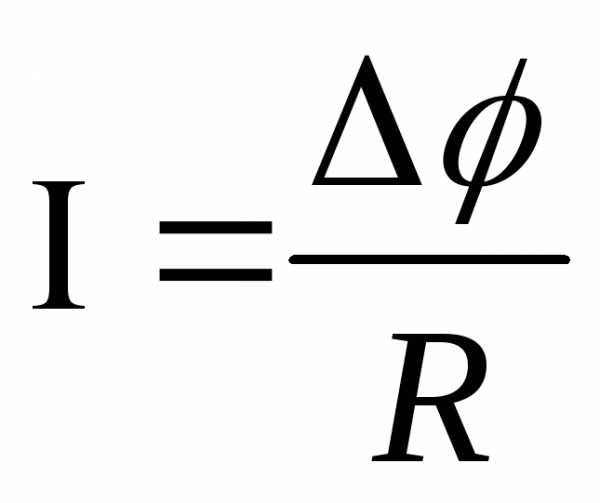(сила токапрямо пропорциональна разности потенциалов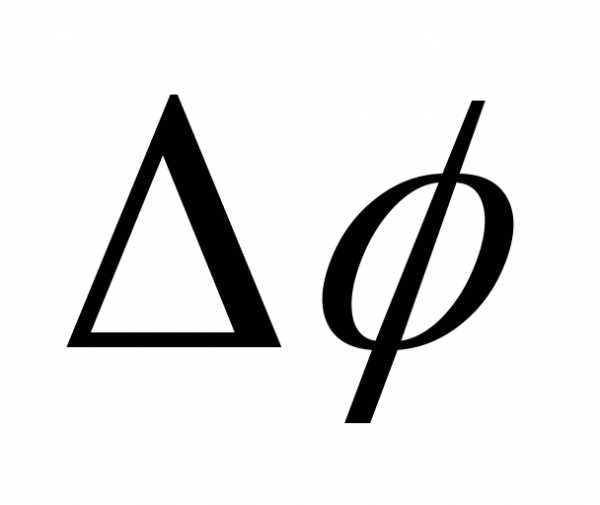на участке цепи и обратно пропорциональна сопротивлениюR этого участка.) Формулу (19) представим в виде:

Q =.

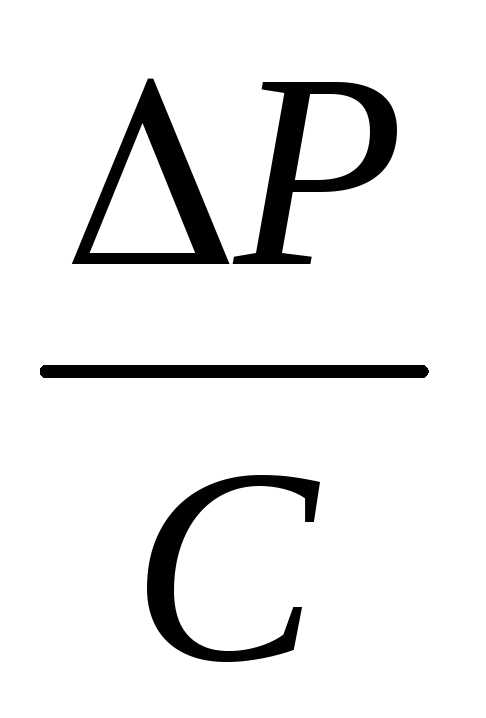Величину С =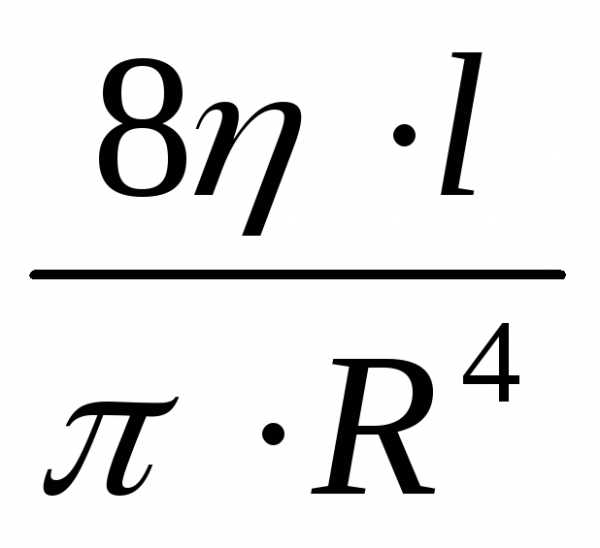называютгидравлическим сопротивлением. Оно тем больше, чем больше вязкость жидкости 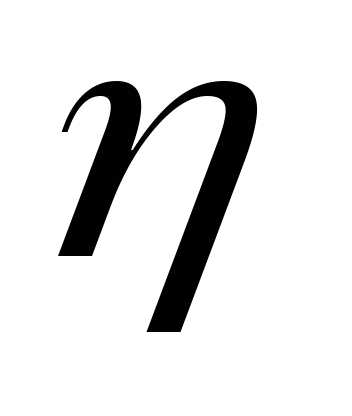и длина трубыl, и зависит обратно пропорционально от четвёртой степени радиуса трубы R.

Таким образом, объём жидкости, ежесекундно протекающей через поперечное сечение трубы, прямо пропорционален разности давлений и обратно пропорционален гидравлическому сопротивлению С.

Аналогия между сопротивлением в электрической цепи и гидравлическим сопротивлением позволяет использовать правила для расчета сопротивления при последовательном и параллельном соединении труб с различными сопротивлениями.

Общее гидравлическое сопротивление труб, соединённых последовательно, рассчитывается по формуле:

С=С₁+С₂+С₃+… , а соединённых параллельно, по формуле

.

Формула Пуазейля справедлива не для любого течения вязкой жидкости, а только для ламинарного течения.

В гидродинамике различают два вида течения жидкости – ламинарное и турбулентное. Ламинарным называют слоистое течение, при котором слои не перемешиваются друг с другом. Для цилиндрического профиля трубы профиль скорости такого течения дан на рис.10а.

Турбулентным называют течение, при котором происходит интенсивное перемешивание слоёв, образуются завихрения жидкости.

Рис.12

Турбулентность увеличивает гидравлическое сопротивление. Профиль скорости такого движения в цилиндрической трубе показан на рис.12 .Вблизи стенок трубы наблюдается большой перепад скорости, скорость быстро нарастает от 0 до V – некоторого среднего значения скорости частиц, что позволяет считать такое течение в среднем однородным.

Характер течения жидкости (ламинарное или турбулентное) определяется целым рядом факторов: вязкостью жидкости, сечением трубы, скоростью течения и плотностью жидкости.

Как уже рассматривалось выше, на любой малый объём жидкости в потоке действуют ускоряющая сила и сила вязкого трения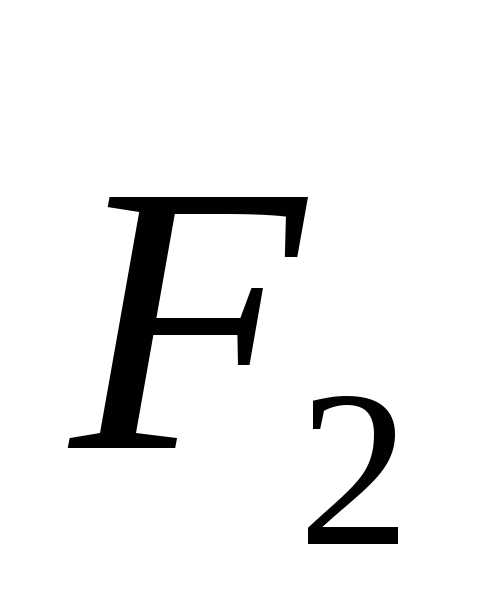. Характер течения будет определяться отношением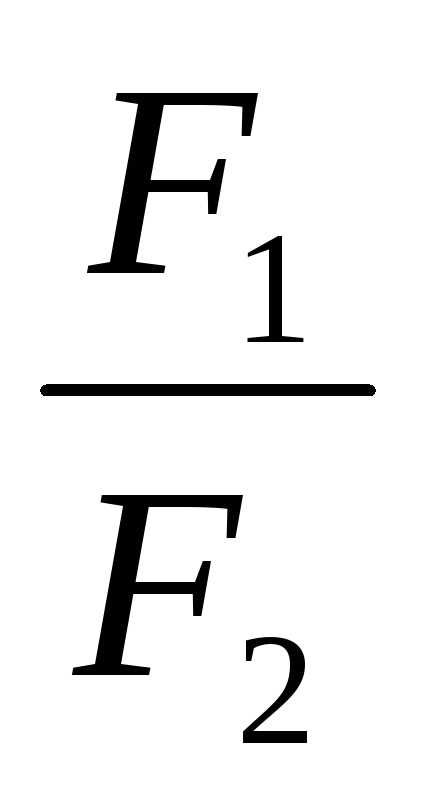. Чем больше это отношение, тем больше вероятность возникновения вихрей, а следовательно, и турбулентного течения. Английский физик и инженер Рейнольдс рассчитал безразмерное отношениеF₁/F₂. Это отношение получило название числа Рейнольдса Re. Очевидно, число Re есть величина безразмерная.

Re =

=

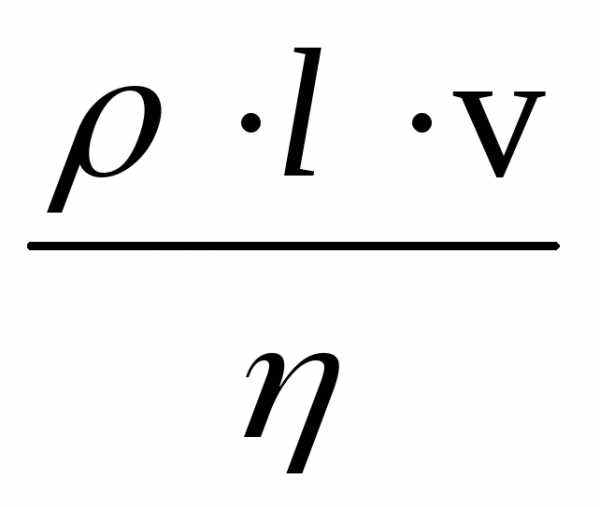
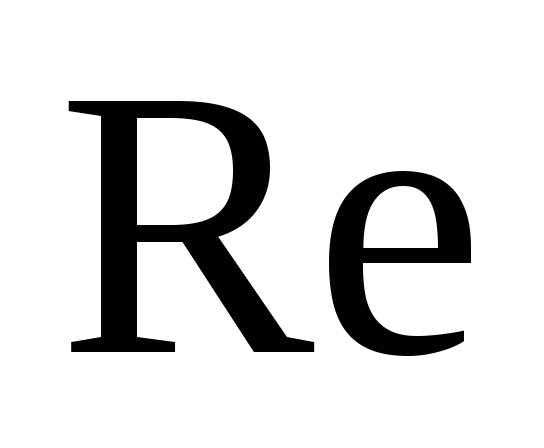(20)

где плотность жидкости,l –характерный линейный размер сечения трубы (диаметр или радиус для цилиндрического сечения трубы, высота – для треугольного, сторона – для квадратного), 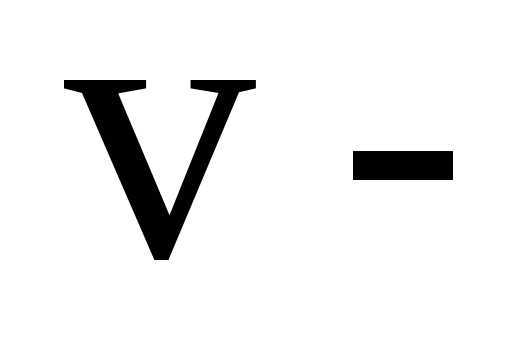скорость потока,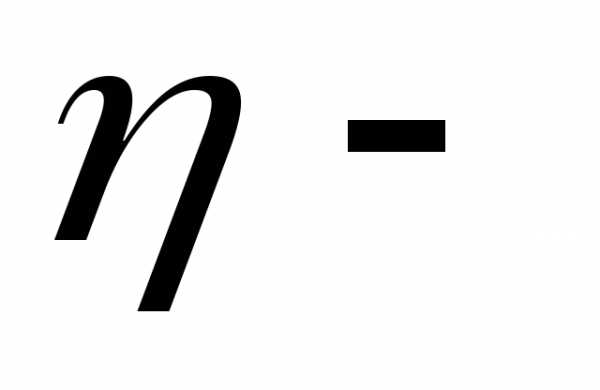коэффициент вязкости.

Так как число Рейнольдса зависит от двух характеристик жидкости – вязкости 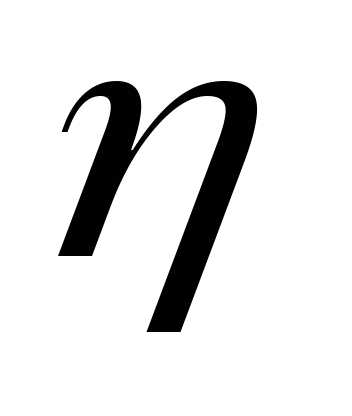и плотности, то целесообразно ввести в это число величину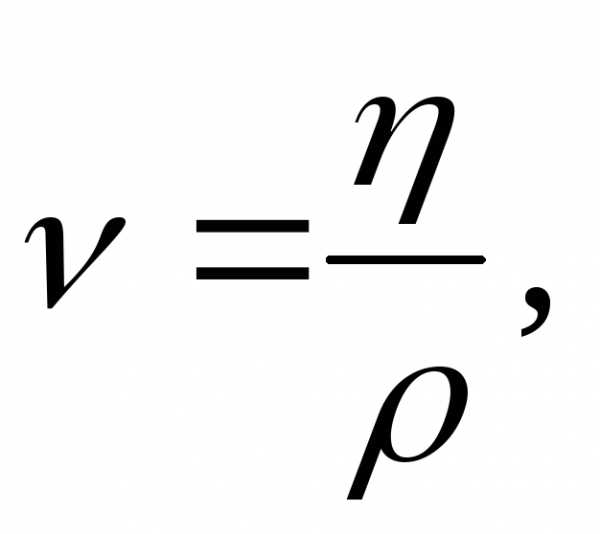называемую кинематической вязкостью. Тогда (20) принимает вид

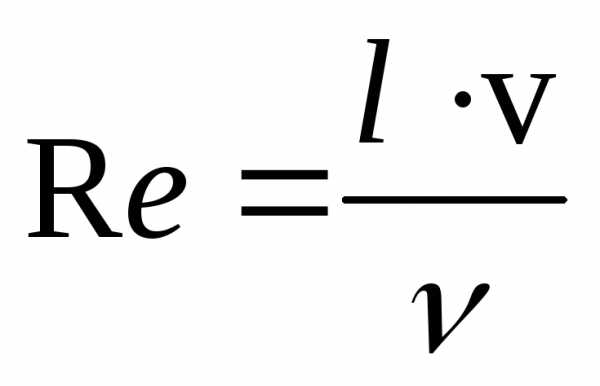
Переход от ламинарного течения к турбулентному определяется критическим числом Рейнольдса.

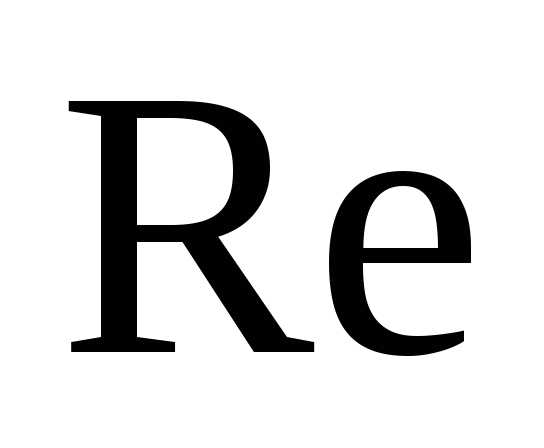
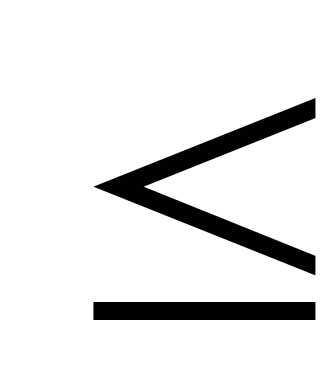
При числах 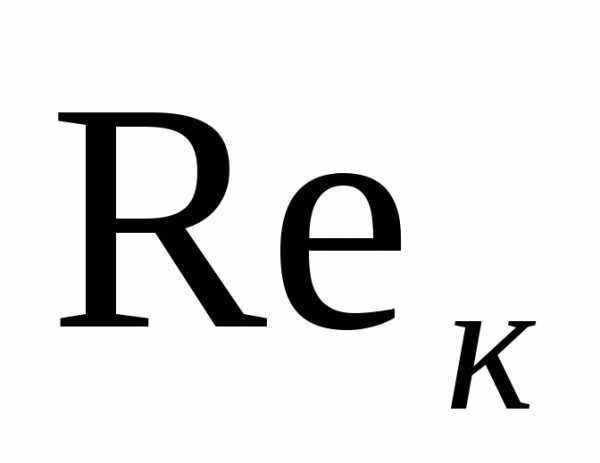течение носит ламинарный характер, при>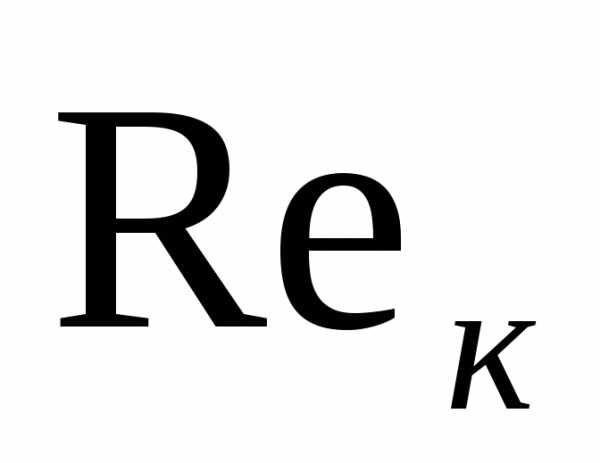течение становится турбулентным. Критические значения числа Рейнольдса определяются только экспериментально. Для гладких цилиндрических труб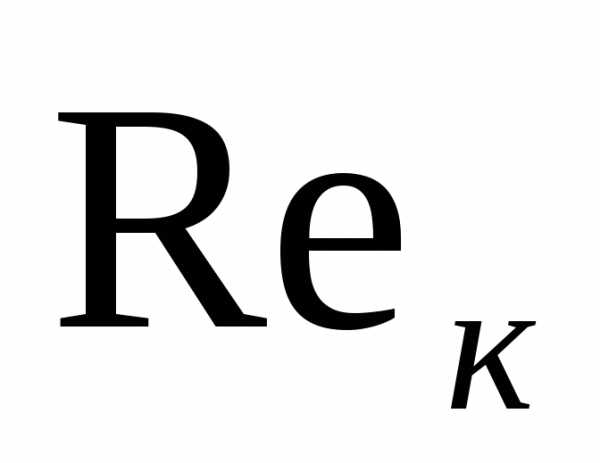1000, если за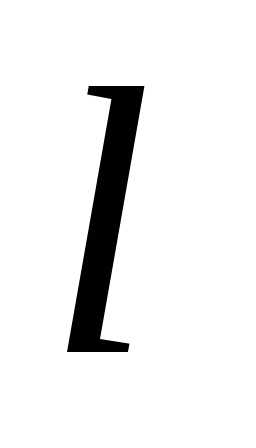принять радиус трубы. Число Рейнольдса играет большую роль во многих количественных исследованиях течения жидкости и газа. Оно является критерием подобия при создании моделей гидро- и аэродинамических систем и, в частности, кровеносной системы. Важно, чтобы модель имела то же число Рейнольдса, что и сама система. Это достигается соответствующим подбором скорости, вязкости и линейного размера сечения модели. 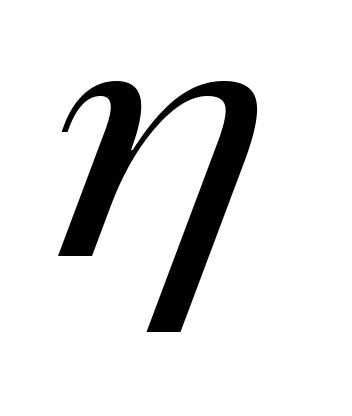Из (20) видно, что увеличение размеров сечения можно скомпенсировать уменьшением скорости теченияили подбором жидкости с соответствующими значениями вязкостии плотности.

Течение крови в сосудах носит в норме ламинарный характер, небольшая турбулентность наблюдается вблизи клапанов сердца. При патологии число Re может превысить критическое значение и течение станет турбулентным, что можно обнаружить по характерным шумам и использовать в диагностике заболеваний.

II. ПРАКТИЧЕСКАЯ ЧАСТЬ

А. Определение коэффициента вязкости методом Стокса

Приборы и принадлежности: стеклянный цилиндр с кольцевыми метками, исследуемая жидкость, дробинки, микрометр, секундомер, линейка, термометр.

Английским физиком и математиком Стоксом было установлено, что сила вязкого трения F_с, действующая в жидкости на движущееся тело при небольших скоростях прямо пропорциональна скорости, т.е.

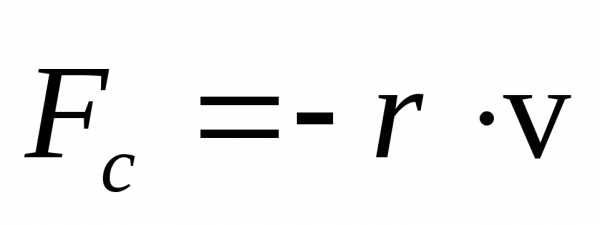(21)

где r-коэффициент сопротивления, зависящий от размеров и формы тела, а также от вязкости среды, в которой оно движется. Для твёрдого тела шарообразной формы радиуса R, движущего в жидкости с коэффициентом вязкости 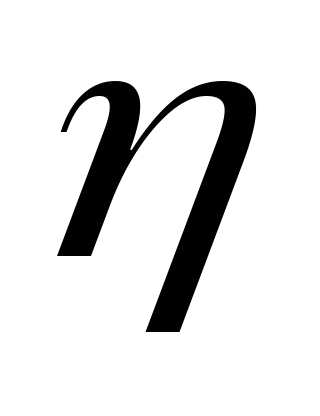, коэффициент сопротивления

r = 6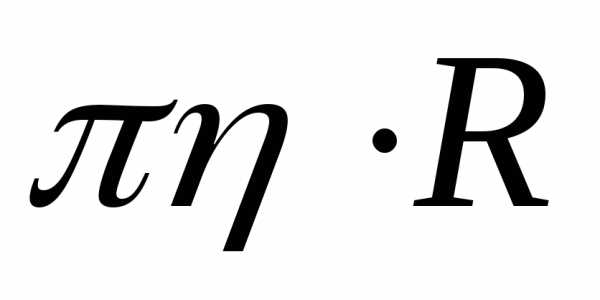

Тогда по закону Стокса для модуля силы сопротивления, действующей на шарообразное тело, можно записать выражение

F_c = 6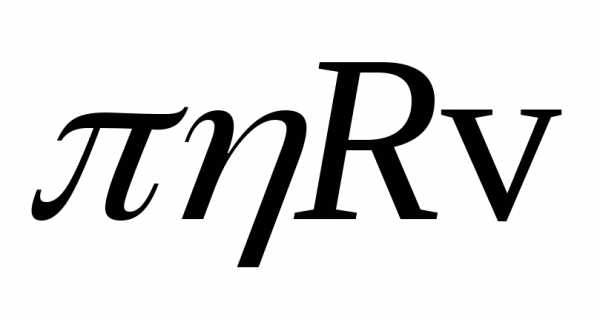 (22)

Метод Стокса позволяет определить вязкость жидкости. На шар B массой m, объёмом V, падающий в жидкости с коэффициентом вязкости действуют три силы: сила тяжестивыталкивающая сила(сила Архимеда) и сила сопротивления(рис.13). Сила тяжести рассчитывается по формуле

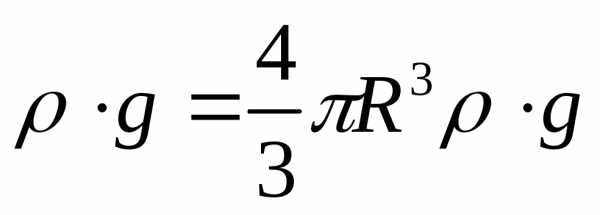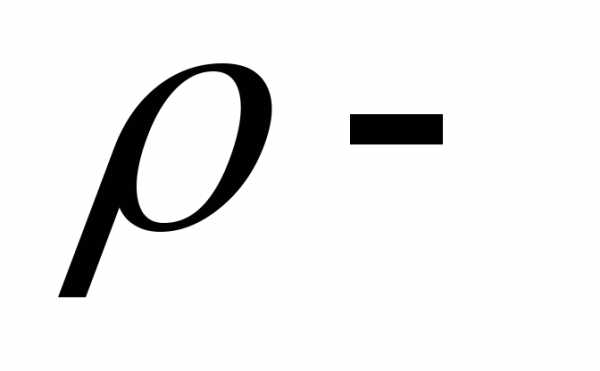F_т = mg=V , где плотность шара,g – ускорение свободного падения. Силу Архимеда можно рассчитать как

Рис.13

здесь m_ж – масса жидкости, вытесненной шаром, плотность этой жидкости. Сила сопротивленияF_c вычисляется по формуле (22). Так как сила ипостоянны, а силавозрастает с увеличением скорости движения шара, то с некоторого момента времени эти три силы могут уравновесить друг друга, и движение шара станет равномерным. В векторной форме закон движения шара запишется в виде

,

или через модули сил этот закон можно записать таким образом

F_T= F_A+ F_C.

Подставим в последнее уравнение выражения для сил и получим:

откуда после соответствующих преобразований получим выражение,

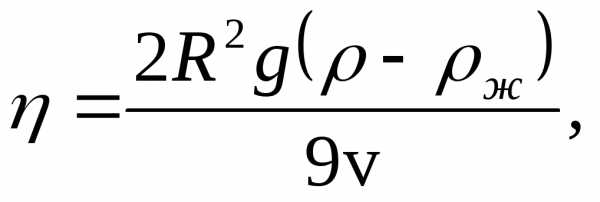
или, учитывая, что гдеD- диаметр шара, последнюю формулу запишем в виде

(23)

studfiles.net

15) Элементарная струйка, поток жидкости, живое сечение. Гидравлический радиус, расход и средняя скорость.

Часть потока, заключенная внутри трубки тока, называется элементарной струйкой. Поток Ж – представляет собой совокупность элементарных струек.

Живым сечением – сечение потока Ж, перпендикулярное направлению скорости ее сечения. При плавно изменяющемся движении Ж сечение считается плоским и равным площади поперечного сечения потока ().

Площадь живого сечения S= dS

Расход потока Q — объем жидкости V, протекающей за единицу времени t через живое сечение ω.

Средняя скорость потока υ — скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Гидравлический радиус потока R — отношение живого сечения к смоченному периметру Смоченный периметр χ («хи») — часть периметра живого сечения, ограниченное твердыми стенками.

16) Уравнение неразрывности. Понятие расхода.

Течение жидкости называют стационарным, если в каждой точке пространства, занимаемого жидкостью, ее скорость с течением времени не изменяется.Жидкости практически несжимаемы, т. е. можно считать, что данная масса жидкости всегда имеет неизменный объем. Поэтому одинаковость объемов жидкости, проходящих через разные сечения трубы, означает, что скорость течения жидкости зависит от сечения трубы. Пусть скорости стационарного течения жидкости через сечения трубы S₁ и S₂ равны соответственно v₁ и v₂. Объем жидкости, протекающей за промежуток времени t через сечение S₁, равен V₁=S₁v₁t, а объем жидкости, протекающей за то же время через сечение S2, равен V₂=S₂v₂t. Из равенства V₁=V₂ следует, что уравнением неразрывности. Из него следует, что Следовательно, при стационарном течении жидкости скорости движения ее частиц через разные поперечные сечения трубы обратно пропорциональны площадям этих сечений.

Расходом называется количество жидкости, протекающее через живое течение потока (струйки) в единицу времени. Различают объёмный Q (м³/с), весовой Q_G(Н/с) и массовый Q_m(кг/с) расходы.

;

17) Распределение сил в сплошной среде. Объемные и поверхностные силы.

Внешние силы: массовые (объемные) и поверхностные.

Массовые силы в соответствии со вторым законом Ньютона про­порциональны массе жидкости или, для однородной жидкости, — ее объему. К ним относятся сила тяжести и сила инерции переносного движения.

Поверхностные силы непрерывно распределены по поверхности жидкости и при равномерном их распределении пропорциональны площади этой поверхности.

Массо­вые силы относят к единице мас­сы, а поверхностные к единице площади

Сплошна́я среда́ — механическая система, обладающая бесконечным числом внутренних степеней свободы. Её движение в пространстве, в отличие от других механических систем, описывается не координатами и скоростями отдельных частиц, а скалярным полем плотности и векторным полем скоростей.

Если плотность сплошной среды постулируется равной константе, то такая сплошная среда называется несжимаемой.

18) Уравнение Бернулли для установившегося движения жидкости.

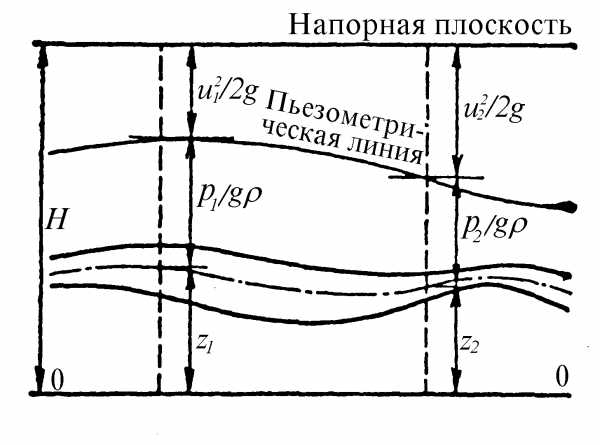
Напорная линия – линия показывающая изменение гидродинамического напора Ж по длине потока

Линия, соединяющая уровни Ж в пьезометрах наз-ся пьезометрической линией

Отметим, что в такой записи члены уравнения выражают удельную энергию, отнесенную к весу (Mg = G).

Как и в гидростатике, величину z называют высотой положения, а величину p/gρ — пьезометрической высотой. 

Сумма первых двух членов уравнения  z + p/gρ — пьезометрический напор. 

Третий член уравнения u²/2g линейная величина. Как известно, начавшаяся двигаться вертикально со скоростью u при отсутствии сопротивления движению, поднялась бы на высоту u²/2g. Этот член уравнения Бернулли называется скоростной высотой или скоростным напором.

studfiles.net

Объемная скорость — Справочник химика 21

    Объемная скорость газа в условиях контакта рассчитывается по формуле [c.159]

    Рассчитать объемную скорость газа в контактном аппарате, если объем катализатора в нем 15 м , а расход газа 9000 м ч. [c.138]

    Для газообразного сырья объемную скорость выражают как количество газовой смеси У(, отнесенное к 0° С и 760 мм рт. ст., пропускаемой через 1 м реакционного объема в час м м ч или ч- )  [c.265]

    Объемная скорость подачи, считая на жидкую фракцию 4, объем С4/1Ш объем катализатора [c.88]

    Объемная скорость (нагрузка катализатора по свежему газу) [c.106]

    При нормальном ходе процесса температура реакции должна быть равной примерно 25°. Скорость сульфохлорирования зависит от силы источника света. Последняя в лабораторных условиях может быть взята весьма большой, если только принять меры, чтобы при большой объемной скорости газа не происходило сильного вспенивания реакционной жидкости, нарушающего протекание процесса. Вспенивание наступает из-за большой скорости подачи газа. При большой интенсивности облучения и проведении реакции в кварцевой трубке превращение может быть закончено за 30—60 мин. [c.402]

    МПа- -равной 50 000 — 60 000 ч . В промышленных конверторах метана (в производство аммиака) при температуре 600— 1000° С объемную скорость принимают равной 250—400 ч . [c.120]

    Поскольку время реакции т не всегда можно определить точно, в формулу (3.1) вместо времени реакции вводят так называемое фиктивное время реакции или величину, обратно пропорциональную фиктивному времени, — объемную скорость. Объемной скоростью называется количество кубических метров исходного газа, проходящего через 1 м катализатора в 1 ч. Объемная скорость выражается в м (м ч), или ч . [c.120]

    То обстоятельство, что допустимая удельная нагрузка катализатора или допустимая объемная скорость для синтеза при нормальном и среднем (9 ат) давлениях остается одинаковой, несмотря на значительно большее время контакта при работе под давлением, может быть объяснено тем, что лимитирующими общую скорость синтеза процессами являются адсорбция и десорбция на катализаторе, а эти процессы протекают приморено одинаково п при нормальном и при среднем давлениях. [c.87]

    Сравнительно недавно удалось получить фумаровую кислоту пропусканием см еси 1 г-мол паров дихлорпентана со 188 г-мол воздуха над пятиокисью ванадия при 425° и объемной скорости 50—60 час (около 57 л газа на 1 л катализатора в час в пересчете на органическое вещество). Выход достигает около 28,4% вес. [208]. [c.229]

    Способы приготовления и составы катализаторов сильно отличались. Синтез велся в одну ступень без циркуляции. Температура синтеза 200° и максимальная 225°, да вление 10 ат, состав синтез-газа 1,25 Нг 1,0 СО с 12% инертных компонентов. Объемная скорость составляла 105—ПО объемов на объем катализатора в час, т. е. была примерно такой же, как и при синтезе над кобальтовым Катализатором. Использованные для испытаний катализаторы могут быть разделены на катализаторы на носителе и на катализаторы без носителя. Катализаторы первого типа аналогичны кобальтовым с той разницей, что на носитель, например кизельгур, наносится вместо кобальта железо. Они имеют значительно меньший насыпной вес, чем катализаторы без носителя. [c.113]

    Оно может быть выражено также через массовую либо объемную скорость  [c.269]

    Добавки кислорода, хлора или их обоих при одновременном варьировании температуры, объемной скорости и молярном отношении углеводорода к нитрующему агенту позволяют при газофазном нитровании парафиновых углеводородов получать различные выходы каждого из нитропроизводного, смотря по потребностям в них. [c.573]

    Рассчитать объемную скорость ш и производи ель-иость катализатора ири синтезе аммиака, если через колонну синтеза пропускают азотоводородную смесь со скоростью 6800 м ч- В колонне синтеза получается газовая смесь с объемной долей КЧЬ 0,22. Объем, занимаемый катализатором в коло[[не, составляет 1,28 м . [c.151]

    Объемная скорость ло свежему газу составляет примерно 270 объемов газа на 1 объем катализатора в час. С 1 л катализатора получают примерно 0,8 кг/сутки продукта. При работе в две ступени выход составляет 92—93% [56]. [c.114]

    Радикалы метил и этил образуются, по-видимому, при распаде пропильных и пропокси-радикалов. Относительно низкие температуры и большие объемные скорости при нитровании делают невероятной непосредственную диссоциацию пропана на радикалы. [c.571]

    Для проведения синтеза достаточно одной ступени, так как при работе на газе состава СО Н2=1,2 (и больше) 1, превращение СОЧ-Нг при объемной скорости 700 достигает 90%. При газе, более богатом водородом или окисью углерода, применяют циркуляцию остаточного газа. [c.119]

    Из результатов различных опубликованных исследований можно сделать следующие выводы. Чем выше давление при окислении, тем выше выходы спиртов и тем ниже выходы альдегидов и органических кислот. Высокие объемные скорости реагирующих газов благоприятствуют получению спиртов с более длинной цепью, а низкие скорости способствуют образованию низкомолекулярных спиртов и кислот, воды и двуокиси углерода. Повышение температуры влияет почти так же, как и уменьшение объемных скоростей. [c.436]

    Объем катализатора определяется исходя из объемной скорости (и  [c.120]

    Кайзер [97] провел обширную работу по определению оптимальных условий гидратации на ионитах. Он исследовал зависимость между соотношением вода олефины, давлением и временем контакта на ионитах Амберлит-15 и Амберлит IR-120. Было показано, что на ионитах можно достичь таких же значений конверсии и селективности, как при гидратации на неорганических катализаторах. Максимальная конверсия составляла 72,9% при объемной скорости жидкости 0,6 и селективности 96,4%. Ниже будет показано, что реакция протекает по псевдопервому порядку и существенно зависит от давления и температуры. [c.65]

    При проведении первой стадии важно рассчитать время контактирования т, напряженность катализатора рн, скорость окисления аммиака и и объемную скорость Уоб в условиях контакта. [c.159]

    Задача 7.2. Определить время работы (в часах) ьа- 1НОИИТОВОЙ колонки, используемой для умягчения воды. Объем катионита 0,53 м , общая емкость его поглощения 1 000 моль/м , объемная скорость потока воды 8 м ч. Жесткость вод з1 составляет 13,8 ммоль/л и обусловлена катионами кальция. [c.119]

    Для жидких продуктов объемную скорость выражают как количество холодного сьгрья Уе. пропускаемого через 1 реакционного объема в час ч или ч )  [c.265]

    Менаду массовой и объемной скоростью сутцествует следующая [c.266]

www.chem21.info