Измерение работы, мощности и объемной скорости потока
Поиск по вики-сайту о сжатом воздухе
Изучив основы физики здесь, вы сможете узнать больше о физических единицах, используемых для измерения различных состояний материи. Это может быть очень полезно при работе со сжатым воздухом. В этой статье мы расскажем об основах измерения работы, мощности и объемной скорости потока.
Что такое механическая работа? Как она измеряется?
Механическую работу можно определить в виде произведения силы и расстояния, с которого сила воздействует на тело. В частности, что касается тепла, работа — это энергия, которая передается от одного тела другому.
Такой перенос энергии осуществляется в термодинамическом смысле слова. Результат работы может быть выражен в разных формах, таких как изменения потенциальной, кинетической или тепловой энергии. Механическая работа, связанная с изменениями объема газовой смеси, является одним из важнейших процессов в инженерной термодинамике. В системе СИ единицей работы является джоуль: 1 Дж = 1 Нм = 1 Вт*с.
Как измерить мощность?
Мощность — это работа, выполняемая за единицу времени. Это показатель того, насколько быстро можно выполнить работу. Единицей СИ для измерения мощности является ватт: 1 Вт = 1 Дж/с.
Как измеряется объемная скорость потока?
Объемный расход системы представляет меру объема жидкости, протекающего за единицу времени. Его можно рассчитать в виде произведения площади поперечного сечения потока и средней скорости потока. В системе СИ единицей объемной скорости потока является м3/с. Тем не менее, часто используется единица литры в секунду (л/с), когда речь идет об объемной скорости потока (также называемой производительностью) компрессора. Она обозначается в виде нормальных литров в секунду (н.л/с), либо в виде подачи атмосферного воздуха (л/с). При использовании н.л/с расход воздуха пересчитывается для «нормального состояния», т.
Для подачи атмосферного воздуха (FAD) выходной расход компрессора пересчитывается до объема атмосферного воздуха при стандартном состоянии на входе (входное давление 1 бар (a) и температура на входе 20 °C). Соотношение между двумя объемными скоростями потока (обратите внимание, что упрощенная формула, показанная выше, не учитывает влажность).
Что такое подача атмосферного воздуха?
FAD или подача атмосферного воздуха. Объясним этот термин на следующем примере. Что означает FAD = 39 л/с для компрессора, работающего при давлении 13 бар? Сколько времени необходимо для того, чтобы заполнить резервуар 390 л при давлении 13 бар? Чтобы вычислить это, нам нужно вернуться к условиям давления на входе, которое составляет 1 бар.
Если мы начинаем с пустого сосуда, то через 1 секунду в емкости будет объем 39 литров при давлении 1 бар. Через 10 секунд давление внутри сосуда составляет 1 бар. Через 20 секунд давление составляет 2 бар. Таким образом, через 130 секунд сосуд будет заполнен до 13 бар. Затем определяем разницу между исходными и нормальными условиями. Исходные условия характеризуются давлением 1 бар, температурой 20 °C и относительной влажностью 0% (RH). Нормальные условия характеризуются давлением 1 атм = 1,01325 бар, температурой 0 °C и влажностью 0% RH. Следующее определение — SER или удельное потребление энергии. Эта величина обозначает количество энергии, которое требуется для подачи 1 литра FAD при определенном давлении.
Другие статьи по этой теме
Измерение давления, температуры и теплоемкости
Чтобы понять процесс обработки сжатого воздуха, необходимо определить некоторые базовые физические понятия. Мы определим различные физические единицы измерения давления, температуры и теплоемкости. Узнайте больше.
Мы определим различные физические единицы измерения давления, температуры и теплоемкости. Узнайте больше.
Структура и различные состояния материи
Чтобы понять процесс получения сжатого воздуха, необходимо определить некоторые базовые физические понятия. Начнем с объяснения структуры и четырех различных состояний материи. Узнайте больше.
2.Течение жидкости. Линейная и объемная скорости, соотношение между ними
2.
Основной характеристикой любого движения является его скорость. Выделяют 2 разных скорости.
Скорость перемещения самих частиц жидкости (или плывущих вместе с жидкостью мелких тел — например, эритроцитов в крови) обозначают v и называют линейной скоростью. V=x/t.
Объём V жидкости, протекающей в данном потоке (в трубе, в русле реки, в кровеносном сосуде и т.п.) за единицу времени. Эту величину называют объёмной скоростью и обозначают Q.
Между линейной скоростью v и объёмной скоростью Q существует простая связь. Рассмотрим трубку с площадью поперечного сечения S.
Выделим
поперечный слой жидкости, который в
момент времени t = 0 занимает положение
1. Через некоторое время t он переместится
в положение 2, отстоящее на расстояние
x= v*t.
Q = S*V
В реальных жидкостях всегда существуют силы трения. В отличие от твёрдых тел, где силы трения действуют между двумя разными телами, в жидкостях силы трения возникают внутри жидкости (между разными её слоями). Поэтому трение в жидкостях называют внутренним трением или вязкостью.
Термин „идеальная жидкость» подразумевает, что при движении такой жидкости не происходит диссипация энергии (переход механической, энергии в тепло). Считалось, что таких жидкостей не существует, но в 1938 году академик П Л.Капица обнаружил, что при температурах, очень близких к абсолютному нулю, подобными свойствами обладает жидкий гелий (Капица назвал такое поведение гелия «сверхтекучестью».
Хотя
во всех остальных случаях движение
жидкости обязательно сопровождается
диссипацией энергии, понятие идеальной
жидкости (как, например, и понятие
идеального газа) имеет большое практическое
значение, потому что во многих случаях
формулы, выведенные для идеальной
жидкости, можно без больших ошибок
применять для движения реальных жидкостей
и газов. Наиболее интересным примером
является теорема Бернулли, Рассмотрим
горизонтальную трубку переменного
сечения, по которой течёт жидкость или
газ.
Наиболее интересным примером
является теорема Бернулли, Рассмотрим
горизонтальную трубку переменного
сечения, по которой течёт жидкость или
газ.
Легко видеть, что кинетическая энергия жидкости а правой части трубки больше, чем в левой, потому что линейная скорость жидкости справа больше, чем слева. Откуда взялось это увеличение энергии ? Оно произошло потому, что сила давления Кл при перемещении какого-то объема жидкости V производит некоторую работу А. По общей формуле но сила давления
равна самому давлению р, умноженному на площадь S, то есть . Отсюда
В левой части трубки соответственно, в правой части трубки Разность работ слева и справа есть
но мы уже несколько раз говорили, что через любое сечение неразветвлённой трубки проходит одинаковый объём жидкости, то 10
есть V, =V2- Обозначая объём просто V и вынося его за скобку, получим:
Так как мы считаем жидкость идеальной (потерь энергии нет), то разность работ равна приросту кинетической энергии;
Если разделить это равенство на объём, то справа вместо массы будет стоять плотность:
Перенося члены с индексом 1 влево, а с индексом 2 направо,
Члены р и соединены знаком „плюс»; отсюда следует, что
их размерность одинакова, то есть величина тоже имеет
смысл
давления. Её называют динамическим
давлением, а член р – статическим
давлением. Сумма статического и
динамического давлений, стоящая в
формуле называется полным давлением;
Её называют динамическим
давлением, а член р – статическим
давлением. Сумма статического и
динамического давлений, стоящая в
формуле называется полным давлением;
Так как при выводе мы положения сечений 1 и 2 взяли произвольно,- то из равенства (4) следует, что во всем потоке жидкости или газа полное давление (то есть сумма статического и динамического давлений) есть величина постоянная:
Это положение и, соответственно, формулы (4) и (5) и принято называть теоремой. Бернулли.
Статическое
давление — это то давление, которое
движущаяся жидкость оказывает на стенки
трубки. Его можно измерить, если плоскость
отверстия трубки манометра расположить
параллельно линиям тока жидкости
(рисунок 4-а). Если же плоскость отверстия
трубки-манометра будет перпендикулярна
линям тока, (рис. 4-6), то манометр покажет
полное давление. При расположении
манометра, как показано на рис. 4-в, мы
будем измерять разность между полным
и статическим давлениями, то есть
динамическое давление.
Из теоремы Бернулли следует, что там, где скорость жидкости или газа больше, статическое давление меньше, и наоборот.
| Чем отличается объемный расход от массового? Рисунок схематично показывает, в чем состоит разница между объемным и массовым расходом. Допустим, в первой трубе давление P1, плотность газа р1, (молекулы газа расположены редко). Выделим единичный объем газа — цилиндр, который движется со скоростью V1. F1об = S *V1, где S -площадь поперечного сечения трубопровода, Массовый же расход равен количеству газа Fмасс, который переносится в единицу времени в единичном объеме. F1масс = S * V1 * р1 Допустим, давление в трубе подняли в 2 раза до P2, плотность газа тоже возросла в 2 раза и стала р2. Молекулы в трубопроводе стали располагаться плотнее (на нижнем рисунке). Скорость же V1 единичного объема не изменилась. При этом объемный расход не изменится, а массовый расход увеличится вдвое. F2масс = S * V* р2 = F1масс*р2/ р1= 2*F1масс Отсюда вывод: массовый расход — вот что реально показывает «затраты» газа. Как правило при изменяющихся давлении и температуре газа, пользователю требуются дополнительные датчики давления и температуры, чтобы с их помощью компенсировать изменения. Массовый расходомер не нуждается в дополнительных датчиках, т.к. измеряет скорость массы газа. Почему же массовый расход измеряется в объемных единицах? Иногда вместо массовых единиц измерения ( г/мин, кг/ч) для удобства используют объемные единицы измерения. | Новости: 14.03.2020 Высокоточные ±0,25% расходомеры эконом-класса подробнее…08.02.2020 Вниманию центров стандартизации и метрологии (ЦСМ): компактный калибровочный стенд
ООО «АвесТех» представляет компактный калибровочный стенд. 17.02.2018 Новое решение: расходомеры для факельных, дымовых и топливных газов Факельный, дымовой, топливный газ – нефтегазовая отрасль может успешно использовать термомассовый расходомер для измерения расхода газа… подробнее…12.06.2017 Выпущен программный продукт для измерения расхода газовых смесей Новая функция создания газовых смесей Кумикс (qMix) в расходомерах Сьерра QuadraTherm 640i/780i позволяют оператору заносить необходимый состав газовой смеси в расходомер прямо на месте. подробнее. .. ..14.05.2017 Выпрямители-формирователи потока Вопрос: как можно снизить требования к прямым участкам, не теряя в точности измерений? Ответ: использовать формирователи (выпрямители) потока. подробнее…07.05.2017 Калибровка и самодиагностика Самодиагностика вихревого расходомера 240i /241i на месте БЕЗ извлечения расходомера может показать нужна ли калибровка. подробнее…08.02.2017 Сенсор из Хастеллоя Для дымовых и факельных газов с агрессивными примесями CO, CO2, SO2, NOx, CO3 — расходомер из Хастеллоя. 14.12.2016 Расходомер для агрессивных газов Расходомер теперь и для влажного хлора. Гарантия 1 год. подробнее… |
Архив документации
Настоящая книга основана на курсе лекций по физической океанографии, в течение многих лет читаемом одним из авторов книги студентам 3-го курса кафедры термогидромеханики океана Московского физико-технического института (государственного университета).
Задача курса состоит в сообщении студентам основных сведений об океане, необходимых для более живого вос- приятия последующих теоретических курсов по динамике океана. В связи с этим особенно большое внимание уделяется географическим распределениям океанографических характеристик, следствием чего является обилие в книге иллюстраций, более 80% из которых представляют собой карты, океанские разрезы и вертикальные кривые свойств океана.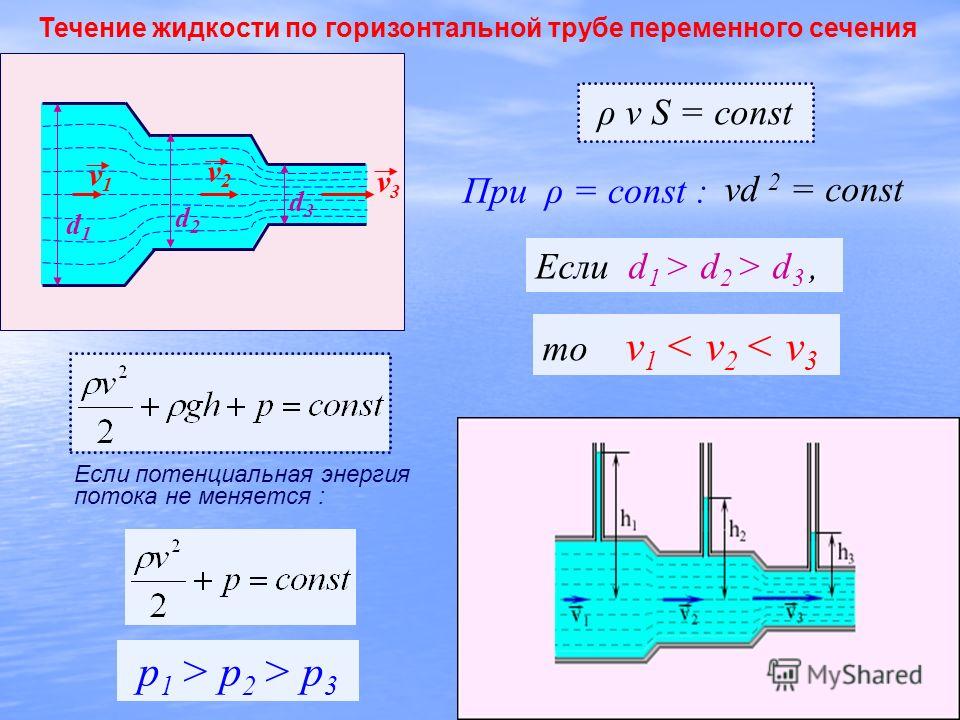
В этом отношении предлагаемую книгу с равной степенью обоснованности можно рассматривать и как учебный текст, богато иллюстрированный рисунками, и как атлас с поясняющим текстом. При этом везде, где только это возможно, авторы стараются дать простое, с минимальным употреблением математики, физическое объяснение наблюдаемым в океане географическим распределениям океанографических характеристик.
Следование книги годовому курсу лекций накладывает жесткие ограничения на ее объем и содержание, которое сводится исключительно к проблемам макроокеанографии с упором на крупномасштабную термохалинную структуру океана и океанскую циркуляцию. Ограниченность объема книги определяет и лаконичный стиль изложения материала.
Так как книга предлагаемого типа не должна иметь большого списка литературы, ссылки на оригинальные работы в большинстве случаев даются для указания источника иллюстративного материала или количественной оценки того или иного явления. Авторы оказывают некоторое предпочтение описанию реультатов отечественных исследований, что представляется особенно обоснованным для последней главы книги.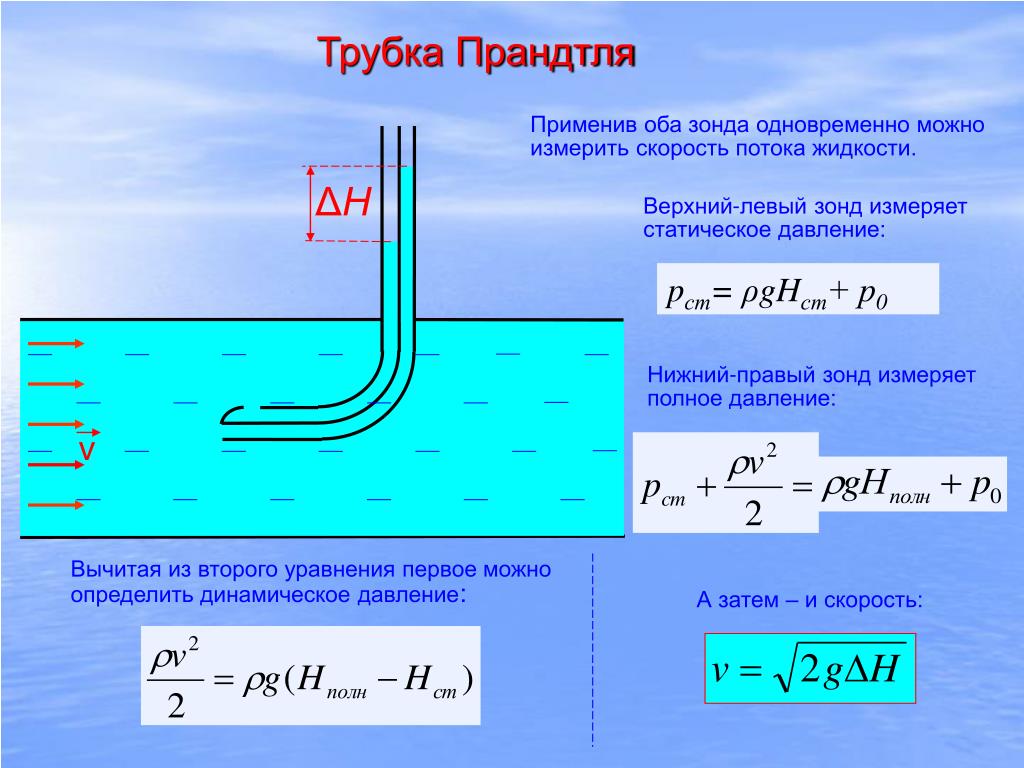
Авторы выражают глубокую благодарность выпускникам кафедры термогидромеханики океана МФТИ: кандидату физико-математических наук Н. А. Максименко (выпуск 1983 г.) за помощь в подборе данных спутниковых наблюдений и численного моделирования океана, кандидату физико-математических наук Е. М. Кошлякову (выпуск 1987 г.) за тщательное прочтение рукописи и ряд важных замечаний и заведующему кафедрой термогидромеханики океана профессору В. В. Жмуру (выпуск 1973 г.) за поддержку работы над книгой и ее издания. Авторы благодарят также доктора географических наук П.Н. Маккавеева за просмотр раздела 1.2 и сделанные замечания.
ХиМиК.ru — XuMuK.ру — 4.1 Вязкость жидкостей и вискозиметрия как метод характеристики коллоидных систем и растворов полимеров 4.1.1. Вязкость жидкостей
Вязкой называют жидкость, в которой между отдельными частицами (молекулами) существуют такие силы притяжения, которые при перемещении одной части жидкости относительно другой сдерживают движение слоев. Очевидно, что все жидкости должны быть вязкими, так как между реальными молекулами всегда существуют силы не только притяжения, но и отталкивания. Равновесие между этими силами и обусловливает равновесное состояние жидкости. Если один из слоев жидкости вывести из состояния равновесия и перемещать его с некоторой скоростью относительно другого, то силы притяжения частиц будут тормозить это движение.
Очевидно, что все жидкости должны быть вязкими, так как между реальными молекулами всегда существуют силы не только притяжения, но и отталкивания. Равновесие между этими силами и обусловливает равновесное состояние жидкости. Если один из слоев жидкости вывести из состояния равновесия и перемещать его с некоторой скоростью относительно другого, то силы притяжения частиц будут тормозить это движение.
При теоретическом описании вязкости жидкость рассматривают как непрерывную бесструктурную среду. В равновесном состоянии частицы (молекулы) будут располагаться таким образом, что равновесная сила (разность между силами притяжения и отталкивания) равна нулю. Если это не соблюдается, то молекулы будут перемещаться относительно друг друга до тех пор, пока вновь не наступит состояние равновесия. Если под действием какой-либо силы жидкость привести в движение (как показано на рис. 2.26) таким образом, что один из слоев, например АB, будет перемещаться с ускорением dU по отношению к слою MN, то между слоями возникнет сила трения, стремящаяся выравнять скорости движения слоев АВ и MN и вернуть их в состояние равновесия. Можно ожидать, что сила трения Ff прямо пропорциональна относительной скорости движения dU и площади контакта слоев dA и обратно пропорциональна расстоянию между слоями dx (между центрами движущихся слоев).
Можно ожидать, что сила трения Ff прямо пропорциональна относительной скорости движения dU и площади контакта слоев dA и обратно пропорциональна расстоянию между слоями dx (между центрами движущихся слоев).
Тогда
Ff= hdА dU/dx (2.4.1)
или
Ff /dA = P = hdU/dх, (2.4.1,а)
где Р– напряжение течения, h– коэффициент пропорциональности, называемый коэффициентом вязкости или вязкостью,dU/dx– градиент скорости течения.
Рис. 2.26. Схема течения жидкости в капилляре. Площадь контакта слоев dA, расстояние между слоями dx |
Уравнение (2.4.1) было получено Ньютоном в 1687 г. Вязкость при ламинарном течении является функцией исключительно сил межмолекулярного взаимодействия в жидкости, поэтому может служить характеристикой интенсивности этих сил и зависит от температуры.
По физическому смыслу вязкость соответствует силе (выраженной в ньютонах) при площади контакта слоев dA (1 м2) и градиенте скорости (1 м/с) в системе СИ имеет размерность h = [Па×с]. В честь ученого Пуазейля, который посвятил много работ изучению вязкости и предложил метод ее измерения, часто используется единица, называемая «пуаз» 1П = 0,1 Па×с. Жидкости, подчиняющиеся при течении закону Ньютона называют ньютоновскими, или нормальными.
В честь ученого Пуазейля, который посвятил много работ изучению вязкости и предложил метод ее измерения, часто используется единица, называемая «пуаз» 1П = 0,1 Па×с. Жидкости, подчиняющиеся при течении закону Ньютона называют ньютоновскими, или нормальными.
Из уравнения (2.4.1) вытекают два следствия:
1. При течении жидкости вдоль неподвижной стенки, прилегающий к ней, слой должен иметь наименьшую скорость течения, так как молекулы жидкости притягиваются к твердой поверхности. По мере удаления слоев жидкости от твердой стенки скорость течения будет увеличиваться. Максимальная скорость будет у слоя жидкости, наиболее удаленного от твердой стенки. Поэтому при течении жидкости в ее объеме повсюду имеется градиент скорости. Во всем объеме жидкости коэффициент вязкости будет одинаковым и лишь при перемещении слоя, прилегающего непосредственно к твердой стенке, коэффициент трения будет характеризовать межмолекулярное взаимодействие молекул жидкости и твердого тела, из которого сделана стенка. Эта сила при достаточном объеме жидкости обычно пренебрежимо мала.
Эта сила при достаточном объеме жидкости обычно пренебрежимо мала.
2. Если рассматривать не движение жидкости относительно неподвижной стенки, а движение твердой частицы через стационарную жидкость, то картина будет такой: слой жидкости, прилегающей непосредственно к твердой частице, будет перемещаться с той же скоростью, что и частица. По мере удаления от поверхности частицы слои жидкости будут перемещаться со все меньшей скоростью. Жидкость должна двигаться вместе с частицей и общая сила трения будет складываться в основном из сил трения слоев жидкости друг о друга, а силой трения жидкости о частицу можно пренебречь.
|
Рис. 2.27. Схема капилляра, использованная при выводе уравнения Пуазейля |
В 1842 г. Пуазейль вывел уравнение, связывающее вязкость жидкости со скоростью ее истечения через капилляр из какого-либо сосуда. Схема капилляра показана на рис. 2.27. Если течение жидкости происходит под давлением Р, то жидкость движется ускоренно до тех пор, пока силы трения не уравновесят это давление. Такое течение носит название стационарного. По мере удаления от стенки капилляра скорость течения будет увеличиваться и достигнет наибольшего значения в его центре, а возле стенок — будет равна нулю. В промежуточных точках скорость будет зависеть только от расстояния до центра. Считается, что в стационарном режиме градиент скорости течения будет неизменным. Следовательно, через любое поперечное сечение капилляра должен всегда проходить один и тот же объем жидкости.
2.27. Если течение жидкости происходит под давлением Р, то жидкость движется ускоренно до тех пор, пока силы трения не уравновесят это давление. Такое течение носит название стационарного. По мере удаления от стенки капилляра скорость течения будет увеличиваться и достигнет наибольшего значения в его центре, а возле стенок — будет равна нулю. В промежуточных точках скорость будет зависеть только от расстояния до центра. Считается, что в стационарном режиме градиент скорости течения будет неизменным. Следовательно, через любое поперечное сечение капилляра должен всегда проходить один и тот же объем жидкости.
Рассмотрим элемент объема, заключенный между концентрическими цилиндрами, как показано на рис. 2.27. Радиусы цилиндров различаются на малую величину dr. Один цилиндр отстоит от центра капилляра на расстояние r, а другой r+dr. Элемент объема проходит вдоль всего капилляра длиной l. При ламинарном (пластинчатом) режиме течения этот элемент объема жидкости в капилляре не смешивается с другими.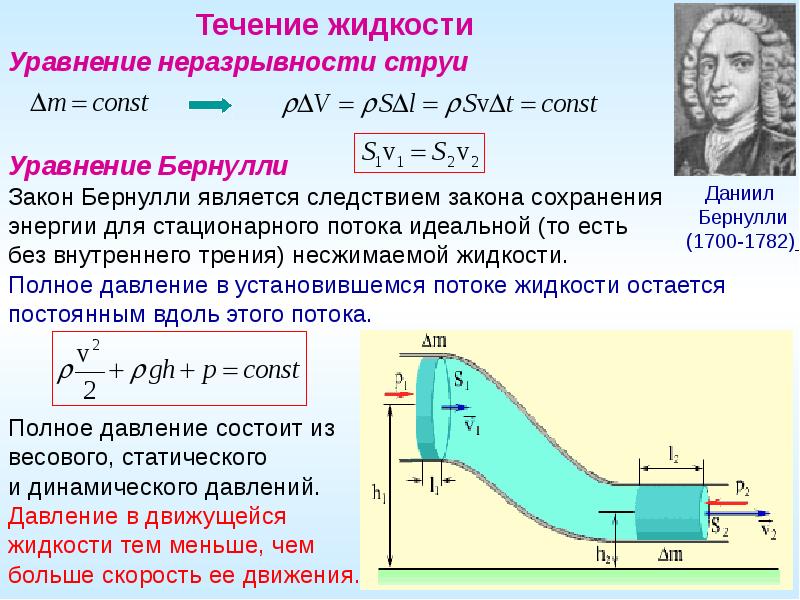 Площадь его соприкосновения с внутренним элементом объема составляет 2rl, а с наружным 2l(r+dr). Жидкость во внешнем элементе объема движется медленнее, а во внутреннем – быстрее выделенного нами элемента. Поэтому на условно выделенный нами объем действуют две силы: одна (со стороны внутреннего элемента) ускоряет движение, а другая (со стороны внешнего элемента объема) замедляет.
Площадь его соприкосновения с внутренним элементом объема составляет 2rl, а с наружным 2l(r+dr). Жидкость во внешнем элементе объема движется медленнее, а во внутреннем – быстрее выделенного нами элемента. Поэтому на условно выделенный нами объем действуют две силы: одна (со стороны внутреннего элемента) ускоряет движение, а другая (со стороны внешнего элемента объема) замедляет.
В стационарном режиме течения эти противоположные по направлению силы будут равны по величине и представляют собой произведение давления на элемент площади, т.е. Р(2prdr).
Сила трения задается уравнением (2.4.1).
Тогда
(2.4.2)
Знак «минус» в правой части уравнения объясняется тем, что по внешней поверхности элемента жидкости движение будет затормаживаться, а «плюс» – тем, что по внутренней его поверхности движение ускоряется.
Разлагая в ряд Тэйлора правую часть уравнения (2.4.2) и учитывая, что dU/dx (при х=r+dr) равно dU/dx (при x=r) плюс (d2U/dr2)dr, и деля каждую часть уравнения (2. 4.2) на 2p dr, получаем
4.2) на 2p dr, получаем
, (2.4.3)
гдеdU/dr– градиент скорости на расстоянии r от центра капилляра.
Первое интегрирование дает
, (2.4.4)
где А1 – постоянная интегрирования.
Второе интегрирование приводит к уравнению зависимости линейной скорости течения слоя жидкости от расстояния до центра капилляра
, (2.4.5)
где А2 – постоянная второго интегрирования.
Постоянная А1 =0, что следует из уравнения (2.4.4) при условии, что r=0. Физический смысл постоянной А2вытекает из уравнения (2.4.5) при условии, что при r=R U=0.
Тогда
А2= РR2/(4lh) , (2.4.6)
поэтому
U = P(R2 – r2)/(4lh). (2.4.7)
Это уравнение дает параболическое распределение скоростей течения жидкости в зависимости от расстояния до центра капилляра.
Более удобной для практического использования является объемная скорость течения, т. е. объем жидкости, протекающей через капилляр с радиусом поперечного течения r за одну секунду. Объем протекающей жидкости будет разным для каждого из элементов объема капилляра, зависит от линейной скорости U и будет равен произведению U на площадь поперечного сечения элемента объема:
е. объем жидкости, протекающей через капилляр с радиусом поперечного течения r за одну секунду. Объем протекающей жидкости будет разным для каждого из элементов объема капилляра, зависит от линейной скорости U и будет равен произведению U на площадь поперечного сечения элемента объема:
Vi=Ui2hrldr . (2.4.8)
Общий объем жидкости, протекающей за одну секунду получают интегрированием по всем элементам объема:
. (2.4.9)
Уравнение (2.4.9) известно как уравнение Пуазейля. Его часто записывают в форме
, (2.4.10)
где V – объем жидкости, вытекающей через капилляр длиной l и радиусом r за время t (с) под давлением Р.
Уравнение Пуазейля используют при определении вязкости с помощью капиллярных вискозиметров. Пример наиболее популярного капиллярного вискозиметра Оствальда-Пинкевича приведен на рис. 2.28. Здесь a и b– метки, ограничивающие объем А; bс– длина капилляра; В –сосуд.
Если жидкость вытекает под действием собственной тяжести, то в капиллярных вискозиметрах фиксируется начальный h1 и конечный h2 уровень жидкости за промежуток времени от 0 до t. В капиллярных вискозиметрах давление Р в процессе течения не остается постоянным, изменяясь от Р0 = rgh1 до Рt = rgh2, где r– плотность жидкости; g– ускорение свободного падения.
В капиллярных вискозиметрах давление Р в процессе течения не остается постоянным, изменяясь от Р0 = rgh1 до Рt = rgh2, где r– плотность жидкости; g– ускорение свободного падения.
Общее время, необходимое для понижения уровня жидкости от h1 до h2 ,
. (2.4.11)
|
Рис. 2.28. Вискозиметр Оствальда — Пинкевича |
Интеграл в правой части уравнения (2.4.11) представляет собой постоянную вискозиметра, также как r и l. Объединяя все постоянные в одну, можем получить для каждого капиллярного вискозиметра
t = сonsth/r. (2.4.12)
Отношение h/r называют кинематической вязкостью. Постоянная вискозиметра определяется путем измерения времени истечения между метками на капилляре жидкости с известными значениями h и r.
Если скорость истечения жидкости из капилляра велика (т. е. мало время истечения), то необходимо учитывать поправку на разность кинетической энергии жидкости, входящей в капилляр и вытекающей из нее, так как часть давления DР=grDh приходится на ускорение жидкости.
е. мало время истечения), то необходимо учитывать поправку на разность кинетической энергии жидкости, входящей в капилляр и вытекающей из нее, так как часть давления DР=grDh приходится на ускорение жидкости.
Градиент скорости (или скорость) течения ньютоновских жидкостей линейно растет при повышении давления, приводящего жидкость в движение, до того критического значения Ркр, когда режим течения из ламинарного переходит в турбулентное.
Вязкость этих жидкостей не зависит от давления вплоть до той же величины Ркр. При турбулентном режиме течения h теряет свой смысл. Схема зависимости вязкости и градиента скорости от давления показана на рис. 2.29.
|
Модуль Вычислительная гидродинамика для моделирования течений жидкости и газа
Геометрия
Вокруг импортированной из CAD геометрической модели можно создавать области течения. Можно автоматически или вручную убрать из геометрической модели элементы, не влияющие на структуру течения.
Можно автоматически или вручную убрать из геометрической модели элементы, не влияющие на структуру течения.
Материалы
В модуле Вычислительная гидродинамика имеется Библиотека материалов, содержащая самые распространенные газы и жидкости. В сочетании с модулем Химические реакции вы получаете доступ к общему описанию физических свойств газов (вязкость, плотность, коэффициент диффузии и теплопроводность).
Сетка
При автоматическом построении сетки учитываются заданные граничные условия для решения гидродинамической задачи с требуемой точностью. Погранслойные элементы сетки строятся автоматически. Этот тип элементов необходим для расчета градиентов скорости, которые, обычно, возникают вблизи твердых стенок.
Дискретизация
В гидродинамических интерфейсах для дискретизации уравнений и построения расчетной двумерной, двумерной осесимметричной или трехмерной пространственных моделей используется метод наименьших квадратов Галеркина. Тестовые функции подобраны так, чтобы стабилизировать в уравнениях переноса гиперболические члены и члены, содержащие давление. Методы расчета с учетом разрывов параметров сокращают паразитные осцилляции решения. Кроме того, для обеспечения сохранения импульса, массы и энергии на внутренних и внешних границах используются разрывные методы Галеркина.
Тестовые функции подобраны так, чтобы стабилизировать в уравнениях переноса гиперболические члены и члены, содержащие давление. Методы расчета с учетом разрывов параметров сокращают паразитные осцилляции решения. Кроме того, для обеспечения сохранения импульса, массы и энергии на внутренних и внешних границах используются разрывные методы Галеркина.
Решатели
Уравнения гидродинамики обычно сильно нелинейны. Для их решения система автоматически подбирает подходящий демпфированный метод Ньютона. Для масштабных задач линейные итерации в рамках метода Ньютона ускоряются с помощью новейших алгебраических или геометрических многосеточных методов, специально разработанных для решения уравнений переноса.
В нестационарных задачах для наиболее точного вычисления полей скорости и давления в сочетании с вышеперечисленными нелинейными решателями используются методы дискретизации по времени с автоматическим выбором шага и определением порядка полиномов.
Обработка результатов
При использовании гидродинамических интерфейсов создаются ряд стандартных графиков для анализа полей скорости и давления. Доступен также обширный список производных значений и переменных, к которым можно быстро получить доступ и вывести результаты анализа.
Доступен также обширный список производных значений и переменных, к которым можно быстро получить доступ и вывести результаты анализа.
Как рассчитать объемный расход
Обновлено 15 декабря 2020 г.
Кевин Бек
Объемный расход — это физический термин, который описывает, сколько вещества — с точки зрения физических размеров, а не массы — перемещается в пространстве за единицу времени . Например, когда вы запускаете смеситель на кухне, определенное количество воды (которое вы можете измерить в жидких унциях, литрах или чем-то еще) выходит из отверстия крана за заданный промежуток времени (обычно секунды или минуты).Это количество считается объемным расходом.
Термин «объемный расход» почти всегда применяется к жидкостям и газам; твердые тела не «текут», даже если они тоже могут двигаться с постоянной скоростью в пространстве.
Уравнение объемного расхода
Основное уравнение для задач такого рода:
Q = AV
, где Q — объемный расход, A — площадь поперечного сечения занята текущим материалом, а V — средняя скорость потока. V считается средним значением, потому что не каждая часть текущей жидкости движется с одинаковой скоростью. Например, когда вы наблюдаете, как воды реки неуклонно спускаются вниз по течению с заданным количеством галлонов в секунду, вы замечаете, что на поверхности здесь более медленные течения, а там — более быстрые.
V считается средним значением, потому что не каждая часть текущей жидкости движется с одинаковой скоростью. Например, когда вы наблюдаете, как воды реки неуклонно спускаются вниз по течению с заданным количеством галлонов в секунду, вы замечаете, что на поверхности здесь более медленные течения, а там — более быстрые.
Поперечное сечение часто представляет собой круг из-за проблем с объемным расходом, потому что эти проблемы часто связаны с круглыми трубами. В этих случаях вы найдете площадь A , возведя в квадрат радиус трубы (который составляет половину диаметра) и умножив результат на константу пи (π), которая имеет значение около 3.14159.
Обычная система СИ (от французского «международная система», что эквивалентно «метрической») единицы расхода — это литры в секунду (л / с) или миллилитры в минуту (мл / мин). Однако, поскольку в США давно используются имперские (английские) единицы измерения, по-прежнему гораздо чаще можно увидеть объемный расход, выраженный в галлонах / день, галлонах / мин (gpm) или кубических футах в секунду (cfs). Чтобы найти объемный расход в единицах, которые обычно не используются для этой цели, вы можете использовать онлайн-калькулятор расхода, подобный тому, что указан в разделе «Ресурсы».
Чтобы найти объемный расход в единицах, которые обычно не используются для этой цели, вы можете использовать онлайн-калькулятор расхода, подобный тому, что указан в разделе «Ресурсы».
Массовый расход
Иногда вам нужно знать не только объем жидкости, движущейся в единицу времени, но и величину массы, которую он представляет. Это, очевидно, критически важно в инженерии, когда необходимо знать, какой вес может безопасно выдержать данная труба, другой трубопровод или резервуар для жидкости.
Формула массового расхода может быть получена из формулы объемного расхода путем умножения всего уравнения на плотность жидкости, ρ .Это следует из того факта, что плотность равна массе, разделенной на объем, что также означает, что масса равна плотности, умноженной на объем. В уравнении объемного расхода уже есть единицы объема в единицу времени, поэтому, чтобы получить массу в единицу времени, вам просто нужно умножить на плотность.
Таким образом, уравнение массового расхода имеет следующий вид:
\ dot {m} = \ rho AV
ṁ , или «м-точка», является обычным обозначением массового расхода.
Проблемы с объемным расходом
Допустим, вам дали трубу с радиусом 0.2} = 0,52 \ text {m / s} = 52 \ text {cm / s}
Вода должна проходить через трубу с быстрой, но вероятной скоростью около полуметра или чуть более 1,5 футов в секунду. правильно слить воду из бака.
Расход и его отношение к скорости
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте расход.
- Определите единицы объема.
- Опишите несжимаемые жидкости.
- Объясните последствия уравнения неразрывности.
Расход Q определяется как объем жидкости, проходящей через некоторое место через область в течение периода времени, как показано на рисунке 1. В символах это может быть записано как
В символах это может быть записано как
[латекс] Q = \ frac {V} {t} \\ [/ latex],
, где V — объем, а t — прошедшее время. Единица измерения скорости потока в системе СИ — 3 / с, но обычно используются другие единицы измерения для Q .Например, сердце взрослого человека в состоянии покоя перекачивает кровь со скоростью 5 литров в минуту (л / мин). Обратите внимание, что литровый (L) равен 1/1000 кубического метра или 1000 кубических сантиметров (10 -3 м 3 или 10 3 см 3 ). В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации.
Рис. 1. Скорость потока — это объем жидкости в единицу времени, проходящий мимо точки через область A . Здесь заштрихованный цилиндр жидкости проходит через точку P по однородной трубе за время t .Объем цилиндра составляет Ad , а средняя скорость составляет [латекс] \ overline {v} = d / t \\ [/ latex], так что скорость потока составляет [латекс] Q = \ text {Ad} / t = A \ overline {v} \\ [/ latex].
Пример 1. Расчет объема по скорости потока: сердце накачивает много крови за всю жизнь
Сколько кубических метров крови перекачивает сердце за 75 лет жизни, если средняя скорость потока составляет 5,00 л / мин?
СтратегияВремя и расход Q даны, поэтому объем V можно рассчитать из определения расхода.{3} \ end {array} \\ [/ latex].
ОбсуждениеЭто количество около 200 000 тонн крови. Для сравнения, это значение примерно в 200 раз превышает объем воды, содержащейся в 6-полосном 50-метровом бассейне с дорожками.
Расход и скорость связаны, но совершенно разными физическими величинами. Чтобы сделать различие ясным, подумайте о скорости течения реки. Чем больше скорость воды, тем больше скорость течения реки. Но скорость потока также зависит от размера реки.Быстрый горный ручей несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. Точное соотношение между расходом Q и скоростью [латекс] \ bar {v} \\ [/ latex] составляет
Точное соотношение между расходом Q и скоростью [латекс] \ bar {v} \\ [/ latex] составляет
[латекс] Q = A \ overline {v} \\ [/ latex],
, где A — площадь поперечного сечения, а [latex] \ bar {v} \\ [/ latex] — средняя скорость. Это уравнение кажется достаточно логичным. Это соотношение говорит нам, что скорость потока прямо пропорциональна величине средней скорости (далее называемой скоростью) и размеру реки, трубы или другого водовода.Чем больше размер трубы, тем больше площадь его поперечного сечения. На рисунке 1 показано, как получается это соотношение. Заштрихованный цилиндр имеет объем
.V = Ad,
, который проходит через точку P за время t . Разделив обе стороны этого отношения на т дает
[латекс] \ frac {V} {t} = \ frac {Ad} {t} \\ [/ latex].
Отметим, что Q = V / t и средняя скорость [latex] \ overline {v} = d / t \\ [/ latex]. Таким образом, уравнение принимает вид [латекс] Q = A \ overline {v} \\ [/ latex]. На рис. 2 показана несжимаемая жидкость, текущая по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, одно и то же количество жидкости должно пройти через любую точку трубы за заданное время, чтобы обеспечить непрерывность потока. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, для точек 1 и 2,
Таким образом, уравнение принимает вид [латекс] Q = A \ overline {v} \\ [/ latex]. На рис. 2 показана несжимаемая жидкость, текущая по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, одно и то же количество жидкости должно пройти через любую точку трубы за заданное время, чтобы обеспечить непрерывность потока. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, для точек 1 и 2,
[латекс] \ begin {case} Q_ {1} & = & Q_ {2} \\ A_ {1} v_ {1} & = & A_ {2} v_ {2} \ end {cases} \\ [/ latex ]
Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости.Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью — это и есть назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется, возможно, снова набирая скорость, когда она покидает другой конец водохранилища. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда увеличивается площадь поперечного сечения.
Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда увеличивается площадь поперечного сечения.
Рисунок 2.Когда трубка сужается, тот же объем занимает большую длину. Для того, чтобы тот же объем проходил через точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс в точности обратим. Если жидкость течет в обратном направлении, ее скорость будет уменьшаться при расширении трубки. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости не масштабированы.)
Поскольку жидкости по существу несжимаемы, уравнение неразрывности справедливо для всех жидкостей.Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.
Пример 2. Расчет скорости жидкости: скорость увеличивается, когда труба сужается
Насадка радиусом 0,250 см присоединяется к садовому шлангу радиусом 0,900 см. {2}} \ bar {v} _ {1} \\ [/ latex].{2}} 1,96 \ text {m / s} = 25,5 \ text {m / s} \\ [/ latex].
{2}} \ bar {v} _ {1} \\ [/ latex].{2}} 1,96 \ text {m / s} = 25,5 \ text {m / s} \\ [/ latex].
Скорость 1,96 м / с примерно подходит для воды, выходящей из шланга без сопел. Сопло создает значительно более быстрый поток, просто сужая поток до более узкой трубки.
Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что дает большие эффекты при изменении радиуса. Мы можем задуть свечу на большом расстоянии, например, поджав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.Во многих ситуациях, в том числе в сердечно-сосудистой системе, происходит разветвление потока. Кровь перекачивается из сердца в артерии, которые подразделяются на более мелкие артерии (артериолы), которые разветвляются на очень тонкие сосуды, называемые капиллярами. В этой ситуации непрерывность потока сохраняется, но сохраняется сумма , скоростей потока в каждом из ответвлений на любом участке вдоль трубы. Уравнение неразрывности в более общем виде принимает вид
Уравнение неразрывности в более общем виде принимает вид
[латекс] {n} _ {1} {A} _ {1} {\ overline {v}} _ {1} = {n} _ {2} {A} _ {2} {\ overline {v} } _ {2} \\ [/ latex],
, где n 1 и n 2 — количество ответвлений в каждой из секций вдоль трубы.
Пример 3. Расчет скорости потока и диаметра сосуда: разветвление сердечно-сосудистой системы
Аорта — это главный кровеносный сосуд, по которому кровь покидает сердце и циркулирует по телу. (а) Рассчитайте среднюю скорость кровотока в аорте, если скорость потока составляет 5,0 л / мин. Аорта имеет радиус 10 мм. (б) Кровь также течет через более мелкие кровеносные сосуды, известные как капилляры. Когда скорость кровотока в аорте составляет 5,0 л / мин, скорость кровотока в капиллярах составляет около 0.33 мм / с. Учитывая, что средний диаметр капилляра составляет 8,0 мкм м, рассчитайте количество капилляров в системе кровообращения.
Стратегия Мы можем использовать [latex] Q = A \ overline {v} \\ [/ latex] для расчета скорости потока в аорте, а затем использовать общую форму уравнения непрерывности для расчета количества капилляров как всех другие переменные известны. {2} \ left (0.{9} \ text {capillaries} \\ [/ latex].
{2} \ left (0.{9} \ text {capillaries} \\ [/ latex].
Обратите внимание, что скорость потока в капиллярах значительно снижена по сравнению со скоростью в аорте из-за значительного увеличения общей площади поперечного сечения капилляров. Эта низкая скорость предназначена для того, чтобы дать достаточно времени для эффективного обмена, хотя не менее важно, чтобы поток не становился стационарным, чтобы избежать возможности свертывания. Кажется ли разумным такое большое количество капилляров в организме? В активной мышце обнаруживается около 200 капилляров на мм 3 , или около 200 × 10 6 на 1 кг мышцы.На 20 кг мышц это составляет примерно 4 × 10 9 капилляров.
Сводка раздела
- Расход Q определяется как объем V , протекающий через момент времени t , или [латекс] Q = \ frac {V} {t} \ [/ latex], где V объем и т время.
- Единица объема в системе СИ — м 3 .

- Другой распространенной единицей измерения является литр (л), который составляет 10 -3 м 3 .
- Расход и скорость связаны соотношением [латекс] Q = A \ overline {v} \\ [/ latex], где A — площадь поперечного сечения потока, а [латекс] \ overline {v} \\ [ / латекс] — его средняя скорость.
- Для несжимаемых жидкостей скорость потока в различных точках постоянна. То есть
[латекс] \ begin {case} Q_ {1} & = & Q_ {2} \\ A_ {1} v_ {1} & = & A_ {2} v_ {2} \\ n_ {1} A_ {1 } \ bar {v} _ {1} & = & n_ {2} A_ {2} \ bar {v} _ {2} \ end {case} \\ [/ latex].
Концептуальные вопросы
1. В чем разница между расходом и скоростью жидкости? Как они связаны?
2. На многих рисунках в тексте показаны линии тока. Объясните, почему скорость жидкости максимальна там, где линии тока находятся ближе всего друг к другу.(Подсказка: рассмотрите взаимосвязь между скоростью жидкости и площадью поперечного сечения, через которую она течет. )
)
3. Определите некоторые вещества, которые несжимаемы, а некоторые — нет.
Задачи и упражнения
1. Каков средний расход бензина в см 3 / с на двигатель автомобиля, движущегося со скоростью 100 км / ч, если он составляет в среднем 10,0 км / л?
2. Сердце взрослого человека в состоянии покоя перекачивает кровь со скоростью 5,00 л / мин. (a) Преобразуйте это в см 3 / с.(b) Какова эта скорость в м 3 / с?
3. Кровь перекачивается из сердца со скоростью 5,0 л / мин в аорту (радиусом 1,0 см). Определите скорость кровотока по аорте.
4. Кровь течет по артерии радиусом 2 мм со скоростью 40 см / с. Определите скорость потока и объем, который проходит через артерию за 30 с.
5. Водопад Хука на реке Вайкато — одна из самых посещаемых природных достопримечательностей Новой Зеландии (см. Рис. 3).В среднем река имеет скорость потока около 300 000 л / с. В ущелье река сужается до 20 м в ширину и в среднем 20 м в глубину. а) Какова средняя скорость реки в ущелье? b) Какова средняя скорость воды в реке ниже водопада, когда она расширяется до 60 м, а глубина увеличивается в среднем до 40 м?
а) Какова средняя скорость реки в ущелье? b) Какова средняя скорость воды в реке ниже водопада, когда она расширяется до 60 м, а глубина увеличивается в среднем до 40 м?
Рис. 3. Водопад Хука в Таупо, Новая Зеландия, демонстрирует скорость потока. (Источник: RaviGogna, Flickr)
6. Основная артерия с площадью поперечного сечения 1.00 см 2 разветвляется на 18 артерий меньшего размера, каждая со средней площадью поперечного сечения 0,400 см 2 . Во сколько раз снижается средняя скорость крови при переходе в эти ветви?
7. (a) Когда кровь проходит через капиллярное русло в органе, капилляры соединяются, образуя венулы (маленькие вены). Если скорость кровотока увеличивается в 4 раза, а общая площадь поперечного сечения венул составляет 10,0 см 2 , какова общая площадь поперечного сечения капилляров, питающих эти венулы? (б) Сколько вовлечено капилляров, если их средний диаметр равен 10.0 мкм м?
8. Система кровообращения человека насчитывает примерно 1 × 10 9 капиллярных сосудов. Каждый сосуд имеет диаметр около 8 мкм м. Предполагая, что сердечный выброс составляет 5 л / мин, определите среднюю скорость кровотока через каждый капиллярный сосуд.
Система кровообращения человека насчитывает примерно 1 × 10 9 капиллярных сосудов. Каждый сосуд имеет диаметр около 8 мкм м. Предполагая, что сердечный выброс составляет 5 л / мин, определите среднюю скорость кровотока через каждый капиллярный сосуд.
9. (a) Оцените время, которое потребуется для наполнения частного бассейна емкостью 80 000 л с использованием садового шланга со скоростью 60 л / мин. (b) Сколько времени потребуется для заполнения, если вы сможете перенаправить в него реку среднего размера, текущую на высоте 5000 м 3 / с?
10.Скорость потока крови через капилляр с радиусом 2,00 × 10 -6 составляет 3,80 × 10 9 . а) Какова скорость кровотока? (Эта малая скорость дает время для диффузии материалов в кровь и из нее.) (B) Если предположить, что вся кровь в организме проходит через капилляры, сколько их должно быть, чтобы нести общий поток 90,0 см 3 / с? (Полученное большое количество является завышенной оценкой, но все же разумно. )
)
11. (a) Какова скорость жидкости в пожарном шланге с 9.Диаметр 00 см, пропускающий 80,0 л воды в секунду? б) Какая скорость потока в кубических метрах в секунду? (c) Вы бы ответили иначе, если бы соленая вода заменила пресную воду в пожарном шланге?
12. Диаметр главного всасывающего воздуховода воздухонагревателя составляет 0,300 м. Какова средняя скорость воздуха в воздуховоде, если его объем равен объему внутри дома каждые 15 минут? Внутренний объем дома эквивалентен массивному прямоугольному массиву шириной 13,0 м на 20.0 м в длину на 2,75 м в высоту.
13. Вода движется со скоростью 2,00 м / с по шлангу с внутренним диаметром 1,60 см. а) Какая скорость потока в литрах в секунду? (b) Скорость жидкости в сопле этого шланга составляет 15,0 м / с. Каков внутренний диаметр сопла?
14. Докажите, что скорость несжимаемой жидкости через сужение, например, в трубке Вентури, увеличивается на коэффициент, равный квадрату коэффициента уменьшения диаметра. (Обратное применимо к потоку из сужения в область большего диаметра.)
(Обратное применимо к потоку из сужения в область большего диаметра.)
15. Вода выходит прямо из крана диаметром 1,80 см со скоростью 0,500 м / с. (Из-за конструкции крана скорость потока не меняется.) (A) Какова скорость потока в см 3 / с? (б) Каков диаметр ручья на 0,200 м ниже крана? Пренебрегайте эффектами, связанными с поверхностным натяжением.
16. Необоснованные результаты Горный ручей имеет ширину 10,0 м и в среднем 2,00 м в глубину. Во время весеннего стока сток в ручье достигает 100 000 м 3 / с.а) Какова средняя скорость потока в этих условиях? б) Что неразумного в этой скорости? (c) Что является необоснованным или непоследовательным в помещениях?
Глоссарий
- расход:
- сокращенно Q , это объем V , который проходит мимо определенной точки в течение времени t , или Q = V / t
- литр:
- единица объема, равная 10 −3 м 3
Избранные решения проблем и упражнения
1. 2,78 см 3 / с
2,78 см 3 / с
3. 27 см / с
5. (а) 0,75 м / с (б) 0,13 м / с
7. (а) 40.0 см 2 (б) 5.09 × 10 7
9. (а) 22 ч (б) 0,016 с
11. (а) 12,6 м / с (б) 0,0800 м 3 / с (в) Нет, не зависит от плотности.
13. (а) 0,402 л / с (б) 0,584 см
15. (а) 128 см 3 / с (б) 0,890 см
Fluid Mechanics — британские единицы измерения и размеры в системе СИ
Fluid Mechanics — размеры в британских единицах и единицах СИEngineering ToolBox — ресурсы, инструменты и основная информация для проектирования и проектирования технических приложений!
— поиск — самый эффективный способ навигации по Engineering ToolBox!
Британская (USCS) и терминология единиц измерения и единиц измерения в механике жидкости
Механика жидкости в системе
- Имперская система или USCS — общепринятые единицы США
- Международная система единиц — система СИ
| Терминология | Размеры | Имперские единицы (USCS) | СИ-единицы | ||||
|---|---|---|---|---|---|---|---|
| Ускорение под действием силы тяжести | L / T 2 | фут / с 2 | м 2|||||
| Площадь | L 2 | футов 2 | м 2 | ||||
| Коэффициент шероховатости Шези | L 900футов 1/2 / с | м 1/2 / с | |||||
| Критическая глубина | L | футов | м | ||||
| Плотность | FT 2 / L 4 | 905 футов 2 2 905 футовН с 2 / м 4 | |||||
| Глубина | L | футов | м | ||||
| футов | м | ||||||
| Диаметр | L | футов | м | ||||
| Расход | л 3 / т | футов 3 / с | м 3 / с | ||||
| Усилие | F | фунтов | N | фунтов | N | ||
| Коэффициент шероховатости Хазена Вильямса | L 0. 37 / T 37 / T | футов 0,37 / с | м 0,37 / с | ||||
| Потеря напора из-за трения | L | футов | футов | ||||
| Высота напора | L | футов | м | ||||
| Головка водослива | L | футов | м над м надL | футов | м | ||
| Гидравлический радиус | L | футов | T | футов 2 / с | м 2 / с 9 0567 | ||
| Длина | L | футов | м | ||||
| Коэффициент шероховатости Мэннинга | T / L 1/3 | s / L 1/3 с /с / м 1/3 | |||||
| Масса | FT 2 / L | фунтов с 2 / фут | Н с 2 / м | ||||
| Модуль упругости | F / L 2 | фунтов / дюйм 2 (psi) | Па | ||||
| Периметр | Высота | Высота футовм | |||||
| Давление | F / L 2 | фунт / фут 2 | 9056 9 Па | ||||
| Радиус | L | футов | м | ||||
| Напряжение сдвига | F / L 2 | 2 2 9005Па | |||||
| Размер шероховатости | L | фут | м | ||||
| Удельный вес | 905 / L 3 9005 905 9005 905 9005 | кг / м 3 | |||||
| Поверхностное натяжение | F / L | фунт / фут | кг / м | s | s | ||
| Толщина | L | футов | м | ||||
| Время | T | s | s | ||||
| Общий напор | 905 905 905 905 905 Расход агрегата | л 3 / TL | футов 3 / (с фут) | м 3 / (с фут) | |||
| Скорость | л / т | фут / с | м / с | ||||
| Вязкость | фут / л 2 | фунт / фут | Па с | Па с | F | фунт-сила | N |
- L — длина
- F — fo rce
- T — время
Связанные темы
Связанные документы
Поиск тегов
- en: размеры единицы британские si uscs
Перевести эту страницу на
О Engineering ToolBox!
Мы не собираем информацию от наших пользователей. В нашем архиве хранятся только письма и ответы. Файлы cookie используются в браузере только для улучшения взаимодействия с пользователем.
В нашем архиве хранятся только письма и ответы. Файлы cookie используются в браузере только для улучшения взаимодействия с пользователем.
Некоторые из наших калькуляторов и приложений позволяют сохранять данные приложений на локальном компьютере. Эти приложения — из-за ограничений браузера — будут отправлять данные между вашим браузером и нашим сервером. Мы не сохраняем эти данные.
Google использует файлы cookie для показа нашей рекламы и обработки статистики посетителей. Пожалуйста, прочтите Условия использования Google для получения дополнительной информации о том, как вы можете контролировать показ рекламы и собираемую информацию.
AddThis использует файлы cookie для обработки ссылок на социальные сети. Пожалуйста, прочтите AddThis Privacy для получения дополнительной информации.
Цитирование
Эту страницу можно цитировать как
- Engineering ToolBox, (2005). Механика жидкости — размеры в британской системе и системе СИ . [онлайн] Доступно по адресу: https://www.
 engineeringtoolbox.com/terminology-units-d_963.html [день доступа, пн. год].
engineeringtoolbox.com/terminology-units-d_963.html [день доступа, пн. год].
Изменить дату доступа.
. .закрыть
Научный онлайн-калькулятор
4 15
.Объемный расход | Справочник единиц и констант в KnowledgeDoor
Характеристика | cumec | Примечания | ||
|---|---|---|---|---|
Метрический (СИ) эквивалент | 1 метр3 / сек | Этот эквивалент рассчитывается на основе точных значений. | ||
Метрическая система (СИ) Размеры | длина4 × время-1 | |||
Описание в терминах других единиц и констант | м3 / с | |||
Характеристика | cusec | Примечания | ||
Метрический (SI) эквивалент | 28. | Этот эквивалент и приведенный ниже рассчитаны на основе точных значения. | ||
Другой метрический эквивалент (СИ), эквивалентный другим основным единицам | 0,028316846592 метра3 / сек | |||
Метрическая система (СИ) Размеры | длина 4 × time-1 | |||
Описание в терминах других единиц и констант | фут3 / второй | |||
Характеристика | галлонов в минуту | Банкноты | ||
|---|---|---|---|---|
Метрический эквивалент (СИ) | 3. | Этот эквивалент и приведенный ниже рассчитаны на основе точных значений. | ||
Другой эквивалент в метрической системе (СИ) с другими базовыми единицами измерения | 63.04 см3 / сек | |||
Метрическая система (СИ) Размеры | длина 4 × время-1 | |||
Описание в терминах других единиц и констант | галлонов в минуту | |||
Характеристика | лусек | 1| 9055 9055 9055 9055 9055 9055 9055 9055 | | |||
|---|---|---|---|---|---|---|
Метрический (СИ) Эквивалент | 1 литр / сек | Этот эквивалент и приведенный ниже рассчитываются на основе точных значений. | ||||
Другой эквивалент в метрической системе (СИ) с другими базовыми единицами измерения | 0,001 м3 / сек | |||||
Метрическая система (СИ) Размеры | длина4 × время-1 | |||||
Описание в терминах других единиц и констант | л / сек | |||||
Характеристика | sverdrup | Примечания | ||
|---|---|---|---|---|
Метрический (СИ) эквивалент | 1 × 106 м3 / сек | Этот эквивалент рассчитывается на основе точных значений. | ||
Метрическая система (СИ) Размеры | длина 4 × время-1 | |||
Описание в терминах других единиц и констант | 1 × 106 метров3 / сек 4 905 | |||
гидродинамика — Почему электрический ток и объемный расход не выражают единицы / размеры площади в их знаменателях?
Определение тока — $ I = \ frac {dq} {dt} $, а определение объемного расхода — $ Q = \ frac {dV} {dt} $.
На письменном, нематематическом языке, я видел ток, описанный как: « Электрический ток определяется как скорость, с которой заряд протекает через поверхность (например, поперечное сечение провода) » (источник: https://physics.info/electric-current/)
Точно так же я видел объемный расход, описанный как: « Объемный расход Q жидкости определяется как объем жидкости, который проходит через данную площадь поперечного сечения в единицу времени. «(источник: https://www.khanacademy.org/science/physics/fluids/fluid-dynamics/a/what-is-volume-flow-rate)
«(источник: https://www.khanacademy.org/science/physics/fluids/fluid-dynamics/a/what-is-volume-flow-rate)
В обоих случаях мы видим, что эти концепции устанавливаются со ссылкой на площадь поперечного сечения.
Теперь я недавно узнал о концепции плотности тока , которая представляет собой количество заряда в единицу времени, которое проходит через единицу площади выбранного поперечного сечения . Хотя я не встречал эквивалентного термина в контексте гидродинамики, можно легко представить себе аналогичный полученный термин (т.2} $.
Итак, мой вопрос: «Что именно здесь происходит?» . Кажется, что все термины описаны относительно некоторой площади поперечного сечения, но только плотность тока (и составленный термин «объемная плотность потока») содержит единицы площади в знаменателе.
Сначала я подумал, что член поперечного сечения в плотности тока ведет себя как процент. то есть диаметр провода, по которому течет ток в цепи, можно рассматривать как «вселенную». ..или $ 100 \ text {%} $ области. Если бы я хотел узнать, сколько тока проходит через 50 \ text {%} $ провода, я бы разделил этот «универсальный ток» на 2 доллара. Однако ясно, что этот термин — , а не , который ведет себя как процент, потому что он имеет фактические единицы!
..или $ 100 \ text {%} $ области. Если бы я хотел узнать, сколько тока проходит через 50 \ text {%} $ провода, я бы разделил этот «универсальный ток» на 2 доллара. Однако ясно, что этот термин — , а не , который ведет себя как процент, потому что он имеет фактические единицы!
Будем признательны за любые идеи! Ура ~
12.1: Скорость потока и ее связь со скоростью
Скорость потока \ (Q \) определяется как объем жидкости, проходящей через определенное место через область в течение периода времени, как показано на рисунке \ (\ PageIndex {1 } \).3 \, см \)). В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации.
Рисунок \ (\ PageIndex {1} \): Скорость потока — это объем жидкости в единицу времени, проходящий мимо точки через область \ (A \). Повторно заштрихованный цилиндр жидкости течет мимо точки \ (P \) в однородной трубе во времени \ (t \). Объем цилиндра равен \ (Ad \), а средняя скорость равна \ (\ overline {v} = d / t \), так что расход равен \ (Q = Ad / t = A \ overline {v} \ ).
Пример \ (\ PageIndex {1} \): Расчет объема по скорости потока: Сердце накачивает много крови за всю жизнь
Сколько кубических метров крови перекачивает сердце за 75 лет жизни при средней скорости потока 5.3 \ end {align *} \]
Обсуждение
Это количество около 200 000 тонн крови. Для сравнения, это значение примерно в 200 раз превышает объем воды, содержащейся в 6-полосном 50-метровом бассейне с дорожками.
Расход и скорость связаны, но совершенно разными физическими величинами. Чтобы сделать различие ясным, подумайте о скорости течения реки. Чем больше скорость воды, тем больше скорость течения реки. Но скорость потока также зависит от размера реки.Быстрый горный ручей несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. Точное соотношение между расходом \ (Q \) и скоростью \ (\ overline {v} \) составляет
\ [Q = A \ overline {v}, \]
где \ (A \) — площадь поперечного сечения, а \ (\ overline {v} \) — средняя скорость. Это уравнение кажется достаточно логичным. Это соотношение говорит нам, что скорость потока прямо пропорциональна величине средней скорости (далее называемой скоростью) и размеру реки, трубы или другого водовода.Чем больше размер трубы, тем больше площадь его поперечного сечения. На рисунке \ (\ PageIndex {1} \) показано, как получается эта взаимосвязь. Заштрихованный цилиндр имеет объем
Это уравнение кажется достаточно логичным. Это соотношение говорит нам, что скорость потока прямо пропорциональна величине средней скорости (далее называемой скоростью) и размеру реки, трубы или другого водовода.Чем больше размер трубы, тем больше площадь его поперечного сечения. На рисунке \ (\ PageIndex {1} \) показано, как получается эта взаимосвязь. Заштрихованный цилиндр имеет объем
\ [V = Ad, \]
, который проходит мимо точки \ (P \) за время \ (t \). Разделив обе стороны этого отношения на \ (t \), получим
\ [\ dfrac {V} {t} = \ dfrac {Ad} {t}. \]
Отметим, что \ (Q = V \ t \), а средняя скорость равна \ (\ overline {v} = d / t \). Таким образом, уравнение становится \ (Q = A \ overline {v} \).
На рисунке \ (\ PageIndex {2} \) показана несжимаемая жидкость, текущая по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, одно и то же количество жидкости должно пройти через любую точку трубы за заданное время, чтобы обеспечить непрерывность потока. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, для точек 1 и 2,
В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, для точек 1 и 2,
\ [Q_1 = Q_2 \]
\ [A_1 \ overline {v} _1 = A_2 \ overline {v} _2 \]
Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости.Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью — это и есть назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется, возможно, снова набирая скорость, когда она покидает другой конец водохранилища. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда увеличивается площадь поперечного сечения.
Рисунок \ (\ PageIndex {2} \): Когда труба сужается, тот же объем занимает большую длину.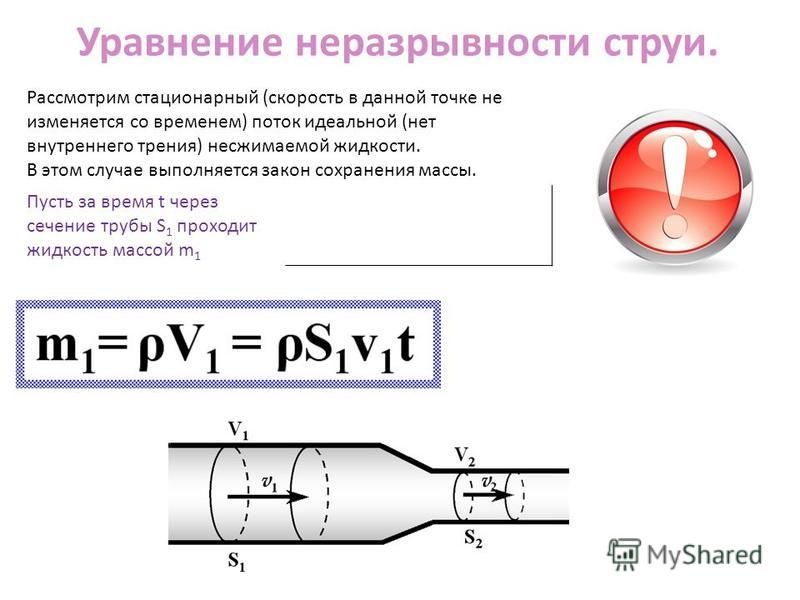 Для того, чтобы тот же объем проходил через точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс в точности обратим. Если жидкость течет в обратном направлении, ее скорость будет уменьшаться при расширении трубки. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости не в масштабе.)
Для того, чтобы тот же объем проходил через точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс в точности обратим. Если жидкость течет в обратном направлении, ее скорость будет уменьшаться при расширении трубки. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости не в масштабе.)Поскольку жидкости по существу несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.
Пример \ (\ PageIndex {2} \): Расчет скорости жидкости: скорость увеличивается, когда труба сужается
Насадка радиусом 0,250 см присоединяется к садовому шлангу радиусом 0,900 см. Расход через шланг и насадку составляет 0,500 л / с. Рассчитайте скорость воды (а) в шланге и (б) в форсунке.
Стратегия
Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. Мы будем использовать индекс 1 для шланга и 2 для сопла.2} 1,96 \, м / с = 25,5 \, м / с. \ nonumber \]
Мы будем использовать индекс 1 для шланга и 2 для сопла.2} 1,96 \, м / с = 25,5 \, м / с. \ nonumber \]
Обсуждение
Скорость 1,96 м / с примерно подходит для воды, выходящей из шланга без сопел. Сопло создает значительно более быстрый поток, просто сужая поток до более узкой трубки.
Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что дает большие эффекты при изменении радиуса. Мы можем задуть свечу на большом расстоянии, например, поджав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.
Во многих ситуациях, в том числе в сердечно-сосудистой системе, происходит разветвление потока. Кровь перекачивается из сердца в артерии, которые подразделяются на более мелкие артерии (артериолы), которые разветвляются на очень тонкие сосуды, называемые капиллярами. В этой ситуации непрерывность потока сохраняется, но сохраняется сумма расходов в каждом из ответвлений в любой части вдоль трубы.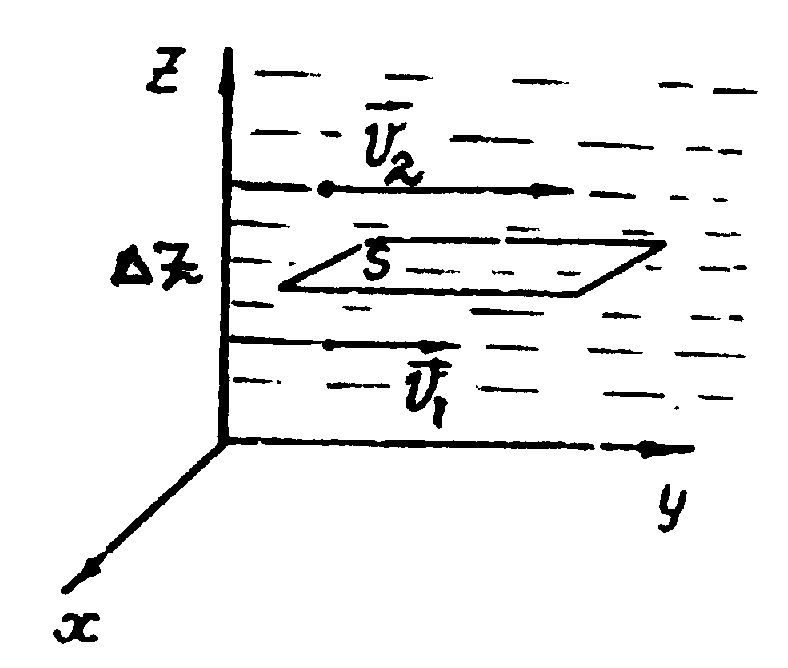 Уравнение неразрывности в более общем виде принимает вид
Уравнение неразрывности в более общем виде принимает вид
\ [n_1A_1 \ overline {v} _1 = n_2A_2 \ overline {v} _2, \]
, где \ (n_1 \) и \ (n_2 \) — количество ответвлений в каждой из секций вдоль трубы.
Пример \ (\ PageIndex {3} \): Расчет скорости потока и диаметра сосуда: ветвление в сердечно-сосудистой системе
Аорта — это главный кровеносный сосуд, по которому кровь покидает сердце и циркулирует по телу. (а) Рассчитайте среднюю скорость кровотока в аорте, если скорость потока составляет 5,0 л / мин. Аорта имеет радиус 10 мм. (б) Кровь также течет через более мелкие кровеносные сосуды, известные как капилляры. Когда скорость кровотока в аорте составляет 5,0 л / мин, скорость кровотока в капиллярах составляет около 0.33 мм / с. Учитывая, что средний диаметр капилляра составляет \ (8,0 \, \ мкм \), рассчитайте количество капилляров в системе кровообращения.
Стратегия
Мы можем использовать \ (Q = A \ overline {v} \) для вычисления скорости потока в аорте, а затем использовать общую форму уравнения непрерывности для вычисления количества капилляров, поскольку все другие переменные известны. 6 \) на 1 кг мышцы.3 \)
6 \) на 1 кг мышцы.3 \)
\ [Q_1 = Q_2 \]
\ [A_1 \ overline {v} _1 = A_2 \ overline {v} _2 \]
\ [n_1A_1 \ overline {v} _1 = n_2A_2 \ overline {v} _2 \]
Глоссарий
- расход
- сокращенно Q , это объем V , который проходит мимо определенной точки за время t , или Q = V / t
- литр
- единица объема, равная 10 −3 м 3
Авторы и авторство
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет).Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Преобразование линейной скорости в объемный расход или в массовый расход
Обычно используемые параметры для расхода жидкости
Три различных параметра, обычно используемых в качестве меры расхода жидкости для потока в трубе или в открытом канале, — это объемный расход, масса расход и средняя скорость. Объемный расход — наиболее широко используемый для жидкостей.Как следует из названия, его единицей будет объем потока в единицу времени. Для газов температура и давление оказывают значительное влияние на плотность газа и, следовательно, на объемный расход, поэтому иногда вместо объемного расхода для газов используется массовый расход. Для потока текучей среды в трубах, воздуховодах или открытых каналах скорость не будет постоянной по площади поперечного сечения потока, тем не менее, некоторая мера скорости текучей среды часто представляет интерес. Наиболее широко используемым параметром скорости является средняя скорость, определяемая как объемный расход, деленный на площадь поперечного сечения потока.Суммируя эти три параметра с использованием символов и типичных единиц измерения, мы получаем:
- Объемный расход; Символ: Q; Единицы: фут3 / сек, галлоны в минуту, м3 / сек и т. Д.
- Массовый расход; Символ: м; Единицы: фунт / час, кг / мин и т. Д.
- Средняя скорость; Символ: V; Единицы: фут / сек или м / сек
Уравнения для преобразования линейной скорости в объемный расход и в массовый расход
Уравнение для преобразования линейной скорости (средней скорости) в объемный расход происходит из определения среднего скорость, упомянутая выше:
V = Q / A или Q = VA,
, где V — средняя скорость, а A — площадь поперечного сечения жидкости, перпендикулярная потоку.
Массовый расход — это просто плотность жидкости, умноженная на объемный расход, или:
м = ρQ = ρVA, где ρ = плотность жидкости. Это показано на рисунке слева.
Уравнение непрерывности механики жидкости
Основной принцип сохранения массы применительно к жидкостной системе обычно называется уравнением неразрывности. В своей наиболее общей форме
, нестационарном состоянии, уравнение неразрывности сжимаемого потока утверждает, что общая скорость массового потока в системе за вычетом общей скорости массового потока из этой системы в любой момент времени должна равняться скорости изменения. массы в системе.В виде уравнения это:
Σmin -Σmout — dM / dt, где M — масса жидкости в системе.
Многие системы потока жидкости работают в условиях стационарного потока. То есть общий массовый расход в системе и общий массовый расход из системы остаются постоянными со временем. В этом случае количество массы в системе не меняется, поэтому dM / dt = ноль, и форма стационарного состояния уравнения неразрывности сжимаемого потока принимает следующий вид:
Σmin = Σmout или ΣρQin = ΣρQout или ΣρVAin = ΣρVAout
Еще одно упрощение уравнения неразрывности — его приложение к потоку несжимаемой жидкости.В механике жидкости термин «несжимаемый поток» на самом деле не относится к жидкости, которую нельзя сжимать. Скорее это относится к ситуации, в которой плотность текучей среды не изменяется для данного набора условий потока текучей среды. В общем, поток жидкостей можно рассматривать как несжимаемый поток, а во многих случаях текущие газы следует рассматривать как сжимаемый поток. Для несжимаемого потока плотность ρ остается постоянной, поэтому уравнение неразрывности несжимаемого потока принимает следующий вид:
ΣQin = ΣQout или ΣVAin = ΣVAout.
Примеры расчетов
Постановка проблемы № 1: Расход воды через трубу диаметром 4 дюйма, приближающуюся к переходному фитингу, со средней скоростью
5 футов / сек. Фитинг сокращается до диаметра трубы 3 дюйма. i) Каков объемный расход через эту трубу? и ii) Какова средняя скорость воды в трубе диаметром 3 дюйма? См. Рисунок справа.
Решение: i) Преобразование линейной скорости в объемный расход:
Q = VA = V (πD2 / 4) = (5 футов / сек) [π (4/12) 2/4) футов], или Q = 0.4363 фута 3 / сек
ii) Объемный расход через 3-дюймовую трубу должен быть одинаковым, поэтому:
(V3) [π (3/12) 2] / 4 = 0,436 фут3 / сек. Решение для V3 дает: V3 = 8,88 фут / сек
Постановка проблемы # 2: Открытый канал трапециевидной формы с шириной дна 2 фута и боковыми уклонами в горизонт: верт = 3: 1 (как показано на диаграмме слева), несет 20 фут3 / сек, когда течет на глубине 1 фут. Какова средняя скорость в канале в этих условиях?
Решение: Из статьи «Расчет гидравлического радиуса для потока в открытом канале» трапецеидальное поперечное сечение потока можно рассчитать по формуле: A = by + zy2, где b — ширина дна канала, y — глубина потока, а z — горизонтальный: вертикальный боковой наклон.Таким образом, A = (2) (1) + 3 (12) = 5 футов2, а V = Q / A = (20 футов3 / сек) / 5 футов2), или V = 4 фута / сек .

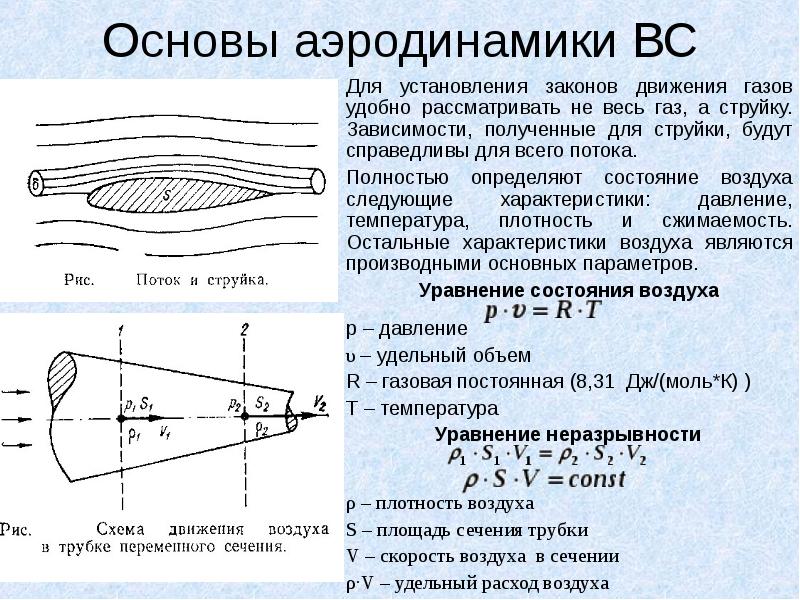
 Он выражается в единицах массы г/мин, кг/час и пропорционален плотности газа р.
Он выражается в единицах массы г/мин, кг/час и пропорционален плотности газа р.  Но это не значит, что измеряется объемный расход. Пользователь также может выбрать на дисплее прибора и л/мин, м3/ч или см3/мин.
Но это не значит, что измеряется объемный расход. Пользователь также может выбрать на дисплее прибора и л/мин, м3/ч или см3/мин.  Его элементами являются: калибратор, тестовый расходомер, источник газа, ноутбук, соединительные гибкие трубки, кабели.
Его элементами являются: калибратор, тестовый расходомер, источник газа, ноутбук, соединительные гибкие трубки, кабели.
 316846592 л / с
316846592 л / с 785411784 л / мин
785411784 л / мин
