Сила сопротивления рисунок: Сила трения и сила сопротивления — урок. Физика, 7 класс.

Сила сопротивления при движении тел в жидкостях и газах. Школьный курс физики

Главная | Физика 10 класс | Сила сопротивления при движении тел в жидкостях и газах

Сила сопротивления.

При движении твёрдого тела в жидкости или газе или при движении одного слоя жидкости (газа) относительно другого возникает сила, тормозящая движение, — сила вязкого трения, или сила сопротивления. Она направлена параллельно поверхности соприкосновения твёрдого тела с жидкостью (газом) в сторону, противоположную скорости тела относительно среды, и тормозит его движение. Сила сопротивления обычно значительно меньше силы сухого трения. Именно поэтому для уменьшения сил трения между движущимися деталями машин применяют смазку.

Особенность силы сопротивления состоит в том, что она появляется только при относительном движении тела и окружающей среды. Сила трения покоя в жидкостях и газах полностью отсутствует. Это приводит к тому, что усилием рук можно сдвинуть тяжёлое тело, например баржу.

Сила сопротивления зависит от размеров, формы и состояния поверхности тела, свойств (вязкости) среды (жидкости или газа), в которой движется тело, и, наконец, от относительной скорости движения тела и среды. Для того чтобы уменьшить силу сопротивления среды, телу придают обтекаемую форму. Наиболее выгодна в этом отношении сигарообразная форма (рис. 3.56, а), близкая к форме падающей капли дождя или рыбы.

Рис. 3.56

Влияние формы тела на силу сопротивления наглядно показано на рисунке 3.56, б. Модуль силы сопротивления цилиндра обозначим через F₀.

Конусообразная насадка к цилиндру уменьшает силу сопротивления от 1/2 до 1/4 F₀ в зависимости от размера угла при вершине конуса. Сглаженная насадка доводит силу сопротивления до 1/5 F₀. Наконец, если придать телу сигарообразную форму, то при том же поперечном сечении сила сопротивления уменьшается до 1/25

F₀.

По этой причине фюзеляж самолёта имеет обтекаемую сигарообразную форму, при которой сопротивление воздуха мало. Наоборот, парашютист должен достигать поверхности Земли с небольшой скоростью. В этом случае необходимо, чтобы воздух оказывал значительное сопротивление движению парашюта. Этого можно добиться, если парашюту придать форму полусферы (рис. 3.57).

Рис. 3.57

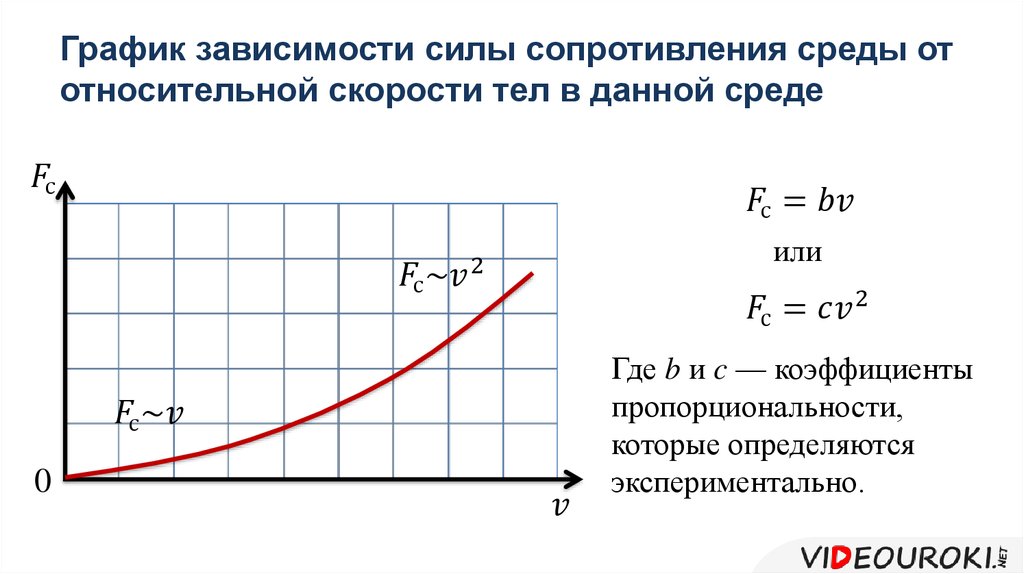
Примерный характер зависимости модуля силы сопротивления среды F_с от модуля относительной скорости и тела приведён на рисунке 3.58.

Рис. 3.58

Если тело неподвижно относительно вязкой среды (относительная скорость равна нулю), то сила сопротивления равна нулю. C увеличением относительной скорости сила сопротивления растёт медленно, а затем всё быстрее. При малых скоростях движения в жидкости (газе) модуль силы сопротивления среды можно считать приближённо прямо пропорциональным модулю скорости движения тела относительно среды:

F_с = k₁υ,          (1)

где k₁ — коэффициент сопротивления, зависящий от формы, размеров, состояния поверхности тела и свойств среды (её вязкости).

Коэффициент k₁ в СИ выражается в H • с/м = кг/с.

При больших скоростях относительного движения модуль силы сопротивления среды пропорционален квадрату скорости тела относительно среды:

F_с = k₂υ²,          (2)

где k₂ — коэффициент сопротивления, который в СИ выражается в H ∙ c²∕м² = кг/м.

При этом k₂ не равен k₁. Какую именно формулу — (1) или (2) — следует применять в конкретном случае, устанавливают опытным путём.

Установившееся движение тел в вязкой среде.

Благодаря тому, что сила сопротивления растёт с увеличением скорости, любое тело в вязкой среде при действии на него какой-либо постоянной силы, например силы тяжести, в конце концов, начинает двигаться равномерно. Модуль этой постоянной скорости зависит от модуля постоянной силы, действующей на тело, и от того, как быстро сила сопротивления растёт с увеличением скорости (т. е. от коэффициента сопротивления). Так, при падении шарика в вязкой жидкости (например, глицерине) уже при малых скоростях сила сопротивления достигает заметного значения. Модуль этой силы можно считать прямо пропорциональным модулю скорости. C учётом этого запишем уравнение движения шарика:

mα = F — k₁υ,

где F — модуль постоянной силы, равной векторной сумме силы тяжести m и архимедовой силы _A.

В самом начале движения сила сопротивления незначительна (скорость мала), и ускорение а почти равно по модулю g, если архимедова сила невелика. В дальнейшем скорость движения увеличивается, и с ней вместе растёт сила сопротивления. Наконец, при

F = k₁υ_y,

ускорение тела обращается в нуль, и, начиная с этого момента, тело будет двигаться с постоянной скоростью, модуль которой равен

υ_y = F / k₁.

Чем тяжелее тело при прочих равных условиях, тем больше модуль установившейся скорости.

В воздухе тяжёлые тела падают с большей установившейся скоростью, чем лёгкие тела. Соответственно они должны пролетать большее расстояние, прежде чем их скорость станет постоянной. Так, капли дождя имеют установившуюся скорость порядка нескольких метров в секунду, а авиационная бомба — несколько сотен метров в секунду. Такая большая скорость достигается лишь при падении с высоты, равной 5 — 6 км.

Вопросы:

1. В каких случаях возникает сила сопротивления среды? Приведите примеры.

2. Как можно уменьшить силу сопротивления среды?

3. Как зависит модуль силы сопротивления среды от модуля скорости тела относительно среды?

4. Проанализируйте график, показанный на рисунке 3.58.

Рис. 3.58

5. Почему любое тело в вязкой среде при действии на него какой-либо постоянной силы, например силы тяжести, в конце концов, начинает двигаться равномерно?

Вопросы для обсуждения:

1. Почему пловцы, бросаясь в воду, выставляют вперёд сложенные вместе руки?

2.

Почему крылышки анемометра (в метеорологии этот прибор используют для измерения скорости ветра) сделаны в виде полусфер, а не в виде плоских лопаток (рис. 3.59)?

Рис. 3.59

Упражнения:

1. Какую массу балласта необходимо сбросить с равномерно опускающегося аэростата, чтобы он начал равномерно подниматься с той же по модулю скоростью? Масса аэростата с балластом равна 1200 кг. Модуль архимедовой силы, действующей на аэростат, равен 8000 Н.

2. Парашют сконструирован таким образом, чтобы модуль скорости приземления женщины массой 50 кг составлял 6,5 м/с. C какой по модулю скоростью приземлится мужчина массой 100 кг, если по ошибке воспользуется этим парашютом?

3. При скоростном спуске лыжник шел по склону с углом наклона 45° к горизонту, не отталкиваясь палками. Коэффициент трения скольжения лыж о снег равен 0,1. Модуль силы сопротивления воздуха пропорционален квадрату скорости

F_c = k₂υ², где k₂ — 0,7 кг/м. Какую максимальную по модулю скорость смог развить лыжник, если его масса равна 90 кг?

4. Коэффициент трения колёс велосипеда о дорогу равен 0,1. При этом модуль максимальной скорости велосипедиста составляет 10 м/с. Модуль силы сопротивления воздуха, действующей на велосипедиста, пропорционален квадрату его скорости. Оцените величину коэффициента сопротивления. Масса велосипедиста вместе с велосипедом составляет 100 кг.

Это любопытно…

Из истории развития физики и техники

Считается, что идея создания парашюта принадлежит Леонардо да Винчи. Он же исследовал механизм полёта птицы и впервые спроектировал летательный аппарат. В 1483 г. Леонардо да Винчи нарисовал эскиз пирамидального парашюта (рис. 3.60) и описал его следующим образом. «Если сделать из полотна шатёр шириной 12 локтей (6 метров) и глубиной 12 локтей, законопатить в нём все щели, то любой человек сможет броситься с любой высоты с ним вниз, не причинив себе вреда». Кстати говоря, современные парашюты имеют почти такие размеры, как предсказывал Леонардо да Винчи.

Рис. 3.60

Используя эскизы Леонардо, хорватский учёный Фауст Вранчич (1551 — 1617) собрал свою модель парашюта. В 1597 г. он прыгнул с колокольной башни высотой 87 м и успешно приземлился на рыночную площадь в Братиславе. Именно Вранчич считается первым человеком, успешно испытавшим парашют.

26 декабря 1783 г. французский физик, изобретатель и пионер в области прыжков с парашютом Луи-Себастьян Ленорман (1757—1837) прыгнул с башни в Монпелье на сконструированном им парашюте. Он представлял собой деревянную раму, обтянутую льняной прорезиненной тканью. Ленорману приписывают и введение самого термина «парашют» .

2 марта 1784 г. в Париже французский изобретатель, пионер авиации и воздухоплаватель Жан-Пьер Франсуа Бланшар (1753—1809) совершил первый успешный полёт на заполненном водородом воздушном шаре. Он предложил использовать для парашютов шёлковую ткань и выдвинул идею использования парашютов для прыжков с воздушного шара. Свою идею Бланшар осуществил в 1793 г. , когда его воздушный шар потерпел аварию. Первый человек, который добровольно прыгнул с воздушного шара, был французский аэронавт Андре-Жак Гарнерен (1769—1823). Это случилось 22 октября 1797 г. Его прыжок с высоты 400 м над парижским парком Монсо стал первым парашютным прыжком в Европе.

Более подробно на сайте «История техники»

Предыдущая страницаСледующая страница

как найти, в каких единицах выражается, от каких параметров зависит

Содержание:

• Что такое сила сопротивления
• Разновидности сил сопротивления
• Как определить силу сопротивление воздуха
• Изменение силы в зависимости от скоростей

Содержание

• Что такое сила сопротивления
• Разновидности сил сопротивления
• Как определить силу сопротивление воздуха
• Изменение силы в зависимости от скоростей

Что такое сила сопротивления

При совершенно любом движении будет фиксироваться появление между поверхностями тел или в среде, где оно осуществляется, сил сопротивления. Второе свойственное им название — силы трения.

Определение

Сила трения — сила, которая появляется в момент передвижения одного тела вдоль другого либо в какой-то среде, ведущая к замедлению действия.

Препятствие движению объясняется тем, что силы трения имеют противоположное направление, и в момент, когда движущая сила и силы сопротивления уравновесятся, скорость станет равна 0.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Схематически действие силы трения можно представить на рисунке:

 

Изображенное здесь тело массой m лежит на ровной поверхности, и на него действуют сила тяжести и уравновешивающая ее сила опоры (N). Направления этих двух сил противоположные, однако, обе — перпендикулярны поверхности.

Сила опоры по своей величине определяется по формуле:

\(N=m\times g\)

С позиций механики понятно, что для того, чтобы сдвинуть это тело с места, необходимо приложить усилие (P), превосходящее силу трения (F).

Определение

Основателем закона трения считается француз Гийом Амонтон. Согласно его постулатам, F_тр пропорциональна давлению, которое тело оказывает на опору либо на другое тело. Кроме этого, она определяется физическими свойствами контактирующих материалов, но не зависит от величины поверхности соприкосновения.

Как любая другая, сила трения измеряется в Ньютонах (Н).

Разновидности сил сопротивления

Причинами возникновения силы трения являются:

• неровный характер соприкасающихся поверхностей;
• действие межмолекулярных связей (применимо для гладких поверхностей).

В зависимости от этих факторов, а также с учетом характера движения силы сопротивления бывают:

1. Силой качения, которая находится в зависимости от физических свойств опоры, скорости движения, сопротивления воздуха. В формулу для определения силы качения вводится коэффициент f, который уменьшается при росте температуры и давления.
2. Сила сопротивления воздуха (если идет лобовое взаимодействие). Причина ее появления — разница давлений. Чем выше вихреобразование, тем выше этот показатель. Вихреобразование же, в свою очередь, зависит от формы самого движущегося тела.

Пример

Передняя часть движущегося тела будет всегда испытывать большее сопротивление воздуха. При закруглениях спереди и сзади плоскостенного тела сопротивление уменьшается на 72%.

Существует понятие электрического сопротивления, под которым понимается свойство проводника препятствовать прохождению тока. Величина, с которой это происходит, равняется частному от деления напряжения на концах к силе тока, протекающему в последовательной цепи.

Как определить силу сопротивление воздуха

При движении тела на него действует лобовое сопротивление воздуха (обозначение — Р_вл). Для его измерения существует формула:

\(P_{вл}=С_х\times p\times F_в\times V^2\div2\)

где C_x — коэффициент обтекаемости (при лобовом сопротивлении воздуха), p — плотность среды (в данной ситуации — воздуха), F_в — площадь миделевого сечения.

Наибольшая концентрация силы сопротивления наблюдается в точке, которая не совпадает с центром массы тела. Это — центр парусности.

\(P_j=m\times dV\div dt\)

В этой формуле m обозначает массу автомобиля, а частное изменения скорости по истечению времени — ускорение центра инерции (или центра масс).

Изменение силы в зависимости от скоростей

На малых скоростях движения сила сопротивления всегда определяется вязкостью жидкости, физическими характеристиками движения (в частности — скоростью), размерами самого тела.

Движение при больших скоростях имеет свои особенности. Например, в случае жидкой либо воздушной среды закономерности трения вязкости не работают. Даже при скоростях в 1 см/с их можно применить только для тел, размеры которых измеряются в мм.

Медленно движущееся тело по всей своей длине постепенно обтекается жидкостью, а сила сопротивления, действующая на него, называется силой вязкого трения. 2\)

где p — плотность среды, L — размеры тела, V — скорость движения.

Насколько полезной была для вас статья?

Рейтинг: 1.86 (Голосов: 14)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

5.2 Силы сопротивления – College Physics

Глава 5 Дополнительные применения законов Ньютона: трение, сопротивление и упругость

Резюме

• Выразите математически силу сопротивления.
• Обсудите применение силы сопротивления.
• Задайте конечную скорость.
• Определить конечную скорость данной массы.

 

Другой интересной силой в повседневной жизни является сила сопротивления объекта, когда он движется в жидкости (газе или жидкости). Вы чувствуете силу сопротивления, когда проводите рукой по воде. Вы также можете почувствовать это, если пошевелите рукой во время сильного ветра. 2}}.[/latex] Принимая во внимание другие факторы, это отношение становится равным 9.2},[/latex], где [latex]{b}[/latex] — константа, эквивалентная [latex]{0,5C\rho{A}}.[/latex] Мы установили показатель степени для этих уравнений равным 2. потому что, когда объект движется с высокой скоростью в воздухе, величина силы сопротивления пропорциональна квадрату скорости. Как мы увидим через несколько страниц гидродинамики, для малых частиц, движущихся в жидкости с малыми скоростями, показатель степени равен 1,

.

СИЛА СОПРОТИВЛЕНИЯ

Установлено, что сила сопротивления [латекс]{F_{\text{D}}}[/латекс] пропорциональна квадрату скорости объекта. Математически 92,}[/latex]

, где [latex]{C}[/latex] – коэффициент сопротивления, [latex]{A}[/latex] – площадь объекта, обращенного к жидкости, а [latex]{ \rho}[/latex] — плотность жидкости.

 

Спортсмены, а также конструкторы автомобилей стремятся уменьшить силу сопротивления, чтобы сократить время своих гонок. (См. рис. 1). «Аэродинамическая» форма автомобиля может уменьшить силу сопротивления и, таким образом, увеличить расход топлива автомобиля.

Рисунок 1. От гоночных автомобилей до гонщиков бобслея аэродинамическая форма имеет решающее значение для достижения максимальной скорости. Бобслей создан для скорости. Они имеют форму пули с коническими плавниками. (кредит: армия США, Wikimedia Commons)

Значение коэффициента аэродинамического сопротивления, [латекс]{C},[/латекс] определяется опытным путем, обычно с использованием аэродинамической трубы. (См. рис. 2).

Рис. 2. Исследователи НАСА тестируют модель самолета в аэродинамической трубе. (кредит: НАСА/Эймс)

Коэффициент лобового сопротивления может зависеть от скорости, но мы будем считать, что здесь он является константой. В таблице 2 перечислены некоторые типичные коэффициенты сопротивления для различных объектов. Обратите внимание, что коэффициент сопротивления является безразмерной величиной. На скоростях шоссе более 50% мощности автомобиля используется для преодоления сопротивления воздуха. Наиболее экономичная крейсерская скорость составляет около 70–80 км / ч (около 45–50 миль / ч). По этой причине в течение 19Во время нефтяного кризиса 70-х годов в США максимальная скорость на шоссе была установлена ​​​​на уровне около 90 км / ч (55 миль / ч).

[латекс]\текст{Объект}[/латекс]	[латекс]\текст{С}[/латекс]
Аэродинамический профиль	0,05
Тойота Камри	0,28
Форд Фокус	0,32
Хонда Сивик	0,36
Феррари Тестаросса	0,37
Пикап Dodge Ram	0,43
Сфера	0,45
Внедорожник Hummer h3	0,64
Парашютист (ноги вперед)	0,70
Велосипед	0,90
Парашютист (горизонтальный)	1,0
Круглая плоская пластина	1,12
Таблица 2. Значения коэффициента сопротивления Типичные значения коэффициента сопротивления [латекс]{C}[/латекс].

В мире спорта проводятся серьезные исследования по минимизации сопротивления. Ямочки на мячах для гольфа переделываются, как и одежда, которую носят спортсмены. Велогонщики, а также некоторые пловцы и бегуны носят полные боди. Австралийка Кэти Фриман носила полный костюм на Олимпийских играх 2000 года в Сиднее и выиграла золотую медаль в беге на 400 метров. Многие пловцы на Олимпийских играх 2008 года в Пекине носили комбинезоны (спидометры); это могло бы иметь значение для побития многих мировых рекордов (см. рис. 3). Большинство элитных пловцов (и велосипедистов) бреют волосы на теле. Такие инновации могут сократить миллисекунды в гонке, иногда определяя разницу между золотой и серебряной медалью. Одним из следствий этого является то, что для поддержания целостности спорта необходимо постоянно разрабатывать тщательные и точные правила.

Рисунок 3. Боди-костюмы, такие как этот LZR Racer Suit, установили множество мировых рекордов после их выпуска в 2008 году. Более гладкая «кожа» и большее усилие сжатия на теле пловца обеспечивают как минимум на 10 % меньшее сопротивление. (Фото: НАСА/Кэти Барнсторфф)

Некоторые интересные ситуации, связанные со вторым законом Ньютона, возникают при рассмотрении воздействия сил сопротивления на движущийся объект. Например, рассмотрим парашютиста, падающего в воздухе под действием силы тяжести. На него действуют две силы: сила тяжести и сила сопротивления (без учета выталкивающей силы). Нисходящая сила тяжести остается постоянной независимо от скорости, с которой движется человек. Однако по мере увеличения скорости человека величина силы сопротивления увеличивается до тех пор, пока величина силы сопротивления не сравняется с силой гравитации, что приводит к нулевой чистой силе. Нулевая результирующая сила означает, что ускорение отсутствует, как указано во втором законе Ньютона. В этот момент скорость человека остается постоянной, и мы говорим, что человек достиг своего конечная скорость ([латекс]{вт}[/латекс]). Поскольку [латекс]{F_{\text{D}}}[/латекс] пропорционален скорости, более тяжелый парашютист должен двигаться быстрее, чтобы [латекс]{F_{\текст{D}}}[/латекс] был равен его вес. Давайте посмотрим, как это работает более количественно.

На предельной скорости,

[латекс] {F _ {\ text {net}} = мг-F _ {\ text {D}} = ma = 0.} [/ латекс]

Таким образом,

[латекс] {мг = F _ {\ текст {D}}.} [/латекс]

Используя уравнение для силы сопротивления, мы имеем

92)}}}[/латекс]

[латекс]{=98\текст{ м/с}}[/латекс]

[латекс]{=350\текст{ км/ч}}.[/латекс]

Это означает, что парашютист массой 75 кг достигает максимальной конечной скорости около 350 км/ч, путешествуя в положении согнувшись (головой вперед), сводя к минимуму площадь и сопротивление. В расправленном положении эта конечная скорость может уменьшиться примерно до 200 км/ч по мере увеличения площади. Эта конечная скорость становится намного меньше после раскрытия парашюта. 2}[/латекс] в зависимости от массы. Какая из этих зависимостей более линейна? Какой вывод вы можете сделать из этих графиков? 92)}}}[/latex]

[latex]{=44\text{ м/с}}.[/latex]

Обсуждение

Этот результат согласуется со значением для [latex]{v_ {\text{t}}}[/latex], упомянутый ранее. 75-килограммовый парашютист, идущий ногами вперед, имел [латекс]{v=98\text{ м/с}}.[/латекс] Он весил меньше, но имел меньшую лобную площадь и, следовательно, меньшее сопротивление воздуха.

Размер объекта, падающего в воздухе, представляет собой еще одно интересное применение сопротивления воздуха. Если вы упадете с 5-метровой ветки дерева, вы, скорее всего, поранитесь — возможно, сломаете кость. Однако маленькая белка делает это все время, не причиняя себе вреда. Вы не достигаете конечной скорости на таком коротком расстоянии, но белка достигает.

Следующая интересная цитата о размерах животных и конечной скорости взята из эссе 1928 года британского биолога Дж. Б.С. Холдейна под названием «О том, чтобы быть подходящего размера».

Для мышей и любых мелких животных [гравитация] практически не представляет опасности. Вы можете бросить мышь в шахту длиной в тысячу ярдов; и, достигнув дна, он получает легкий толчок и уходит, при условии, что земля достаточно мягкая. Крыса убита, человек разбит, а лошадь забрызгана. Ибо сопротивление воздуха движению пропорционально поверхности движущегося объекта. Разделите длину, ширину и высоту животного на десять; его вес уменьшен в тысячную, а поверхность только в сотые. Таким образом, сопротивление падению маленького животного относительно в десять раз превышает движущую силу.

Приведенная выше квадратичная зависимость сопротивления воздуха от скорости не выполняется, если объект очень мал, движется очень медленно или находится в более плотной среде, чем воздух. Тогда мы находим, что сила сопротивления прямо пропорциональна скорости. Это соотношение задается законом Стокса , который гласит, что

[латекс] {F_{\text{s}}=6\pi{r}\eta{v}},[/латекс]

, где [латекс]{r}[/латекс] — радиус объекта, [латекс]{\эта}[/латекс] — вязкость жидкости, а [латекс]{v}[/латекс] — скорость объекта.

ЗАКОН СТОКА

[латекс] {F_{\text{s}}=6\pi{r}\eta{v}},[/latex]

, где [латекс]{r}[/латекс] радиус объекта, [latex]{\eta}[/latex] — вязкость жидкости, а [latex]{v}[/latex] — скорость объекта.

Хорошими примерами этого закона являются микроорганизмы, пыльца и частицы пыли. Поскольку каждый из этих объектов очень мал, мы обнаруживаем, что многие из этих объектов движутся без посторонней помощи только с постоянной (конечной) скоростью. Конечная скорость для бактерий (размером примерно [латекс]{1\:\mu}[/латекс] ) может быть примерно [латекс]{2\:\мю\текст{/с}}.[/латекс] Чтобы двигаться со С большей скоростью многие бактерии плавают с помощью жгутиков (органелл в форме маленьких хвостов), которые приводятся в действие маленькими двигателями, встроенными в клетку. Отложения в озере могут двигаться с большей конечной скоростью (около [latex]{5\:\mu\text{/s}}[/latex] ), поэтому может пройти несколько дней, прежде чем они достигнут дна озера после отложения. на поверхности.

Если мы сравним животных, живущих на суше, с животными, живущими в воде, то увидим, как сопротивление повлияло на эволюцию. Рыбы, дельфины и даже массивные киты имеют обтекаемую форму, чтобы уменьшить силы сопротивления. Птицы имеют обтекаемую форму, а мигрирующие виды, которые летают на большие расстояния, часто имеют особые черты, такие как длинная шея. Стаи птиц летят в форме наконечника копья, формируя обтекаемый рисунок (см. рис. 4). У людей одним из важных примеров упорядочения является форма сперматозоидов, которые должны эффективно использовать энергию 9.0021 .

Рисунок 4. Гуси летят V-образным строем во время своих длительных миграционных путешествий. Эта форма снижает сопротивление и потребление энергии для отдельных птиц, а также позволяет им лучше общаться. (Фото: Julo, Wikimedia Commons)

ЭКСПЕРИМЕНТ ГАЛИЛЕЯ

Говорят, что Галилей сбросил с Пизанской башни два объекта разной массы. Он измерил, сколько времени потребовалось каждому, чтобы достичь земли. Поскольку секундомеры были недоступны, как, по-вашему, он измерял время их падения? Если бы объекты были одного размера, но разной массы, что, по вашему мнению, он должен был бы наблюдать? Был бы этот результат другим, если бы это было сделано на Луне?

ИССЛЕДОВАНИЯ PHET: МАССЫ И ПРУЖИНЫ

Реалистичная лаборатория масс и пружин. Подвесьте грузы к пружинам и отрегулируйте жесткость пружины и демпфирование. Вы даже можете замедлить время. Перевозите лабораторию на разные планеты. Диаграмма показывает кинетическую, потенциальную и тепловую энергию для каждой пружины.

Рис. 5. Массы и пружины

• Силы сопротивления, действующие на объект, движущийся в жидкости, противодействуют движению. Для более крупных объектов (таких как бейсбольный мяч), движущихся со скоростью [латекс]{v}[/латекс] в воздухе, сила сопротивления определяется выражением 92},[/латекс]

  , где [латекс]{C}[/латекс] — коэффициент сопротивления (типичные значения приведены в таблице 2), [латекс]{А}[/латекс] — площадь объекта, обращенная к жидкости, а [латекс] {\rho}[/latex] — плотность жидкости.

• Для небольших объектов (таких как бактерия), движущихся в более плотной среде (такой как вода), сила сопротивления определяется законом Стокса,

  [латекс] {F_{\text{s}}=6\pi\eta{rv}},[/латекс]

  , где [latex]{r}[/latex] — радиус объекта, [latex]{\eta}[/latex] — вязкость жидкости, а [latex]{v}[/latex] — скорость объекта. . 92},[/латекс]

  , где [латекс]{C}[/латекс] — коэффициент сопротивления, [латекс] {А}[/латекс] — площадь объекта, обращенного к жидкости, а [латекс] {\ rho} [/латекс] — плотность жидкости

  Закон Стокса

  [латекс]{F_{\text{s}}=6\pi{r}\eta{v}},[/latex], где [латекс]{r}[/латекс] — радиус объекта, [ latex]{\eta}[/latex] — вязкость жидкости, а [latex]{v}[/latex] — скорость объекта

   

  Калькулятор уравнения сопротивления

  Создано Miłosz Panfil, PhD

  Отзыв от Dominik Czernia, PhD и Adena Benn

  Последнее обновление: 22 декабря 2022 г.

  Содержание:
  • Что такое уравнение для силы сопротивления калькулятор

  Калькулятор уравнения сопротивления помогает вам вычислить силу, действующую на движущийся объект, погруженный в жидкость . Читая текст ниже, вы узнаете, что такое уравнение для силы сопротивления, как форма объекта влияет на силу и каков коэффициент сопротивления.

  Какое уравнение для силы сопротивления

  Если объект движется в жидкости, он испытывает силу сопротивления, силу сопротивления . Величина этой силы зависит от размера и формы объекта, плотности жидкости и относительной скорости объекта и жидкости. Уравнение

  Fd = 1/2 × ρ × u² × A × Cd ,

  где:

  • Fd – сила сопротивления;
  • ρ – Плотность жидкости;
  • u – относительная скорость;
  • A – Контрольная зона; и
  • Cd – Коэффициент аэродинамического сопротивления.

  Базовая площадь A для объекта простой формы представляет собой площадь поперечного сечения, ортогонального направлению движения. Например, для сферы радиусом r мы просто возьмем A = π × r² . Для объекта более сложной формы, такого как автомобиль, опорную площадь указать сложнее, но обычно она больше, чем площадь поперечного сечения.

  Для приложения силы сопротивления вы можете проверить свободное падение с помощью калькулятора сопротивления воздуха и калькулятора закона Стокса.

  Коэффициент сопротивления

  Уравнение силы сопротивления зависит от коэффициента сопротивления Cd . Что это? Коэффициент сопротивления — это безразмерное число, которое зависит от формы объекта . Если объект имеет гладкую форму, то Cd — малое число, и результирующая сила сопротивления также мала. Например, он равен 0,04 для обтекаемого тела, тогда как для куба оно равно 1,05 .

  Сам коэффициент аэродинамического сопротивления зависит от числа Рейнольдса Re . Зависимость мягкая для достаточно малых чисел Рейнольдса (несколько тысяч и меньше), а коэффициент лобового сопротивления примерно постоянен.