Силы действующие на тело: Физические основы механики

Тело на наклонной плоскости | Физика

1. Тело на гладкой наклонной плоскости

Напомним: когда говорят о гладкой поверхности, подразумевают, что трением между телом и этой поверхностью можно пренебречь.

На тело массой m, находящееся на гладкой наклонной плоскости, действуют сила тяжести m и сила нормальной реакции (рис. 19.1).

Удобно ось x направить вдоль наклонной плоскости вниз, а ось y – перпендикулярно наклонной плоскости вверх (рис. 19.1). Угол наклона плоскости обозначим α.

Уравнение второго закона Ньютона в векторной форме имеет вид

? 1. Объясните, почему справедливы следующие уравнения:

? 2. Чему равна проекция ускорения тела на ось x?

? 3. Чему равен модуль силы нормальной реакции?

? 4. При каком угле наклона ускорение тела на гладкой плоскости в 2 раза меньше ускорения свободного падения?

? 5. При каком угле наклона плоскости сила нормальной реакции в 2 раза меньше силы тяжести?

При выполнении следующего задания полезно заметить, что ускорение тела, находящегося на гладкой наклонной плоскости, не зависит от направления начальной скорости тела.

? 6. Шайбу толкнули вверх вдоль гладкой наклонной плоскости с углом наклона α. Начальная скорость шайбы v₀.
а) Какой путь пройдет шайба до остановки?
б) Через какой промежуток времени шайба вернется в начальную точку?
в) С какой скоростью шайба вернется в начальную точку?

? 7. Брусок массой m находится на гладкой наклонной плоскости с углом наклона α.
а) Чему равен модуль силы, удерживающей брусок на наклонной плоскости, если сила направлена вдоль наклонной плоскости? Горизонтально?
б) Чему равна сила нормальной реакции, когда сила направлена горизонтально?

2. Условие покоя тела на наклонной плоскости

Будем теперь учитывать силу трения между телом и наклонной плоскостью.

Если тело покоится на наклонной плоскости, на него действуют сила тяжести m, сила нормальной реакции и сила трения покоя _тр.пок (рис. 19.2).

Сила трения покоя направлена вдоль наклонной плоскости вверх: она препятствует соскальзыванию бруска. Следовательно, проекция этой силы на ось x, направленную вдоль наклонной плоскости вниз, отрицательна:

F_{тр.пок x} = –F_тр.пок

? 8. Объясните, почему справедливы следующие уравнения:

? 9. На наклонной плоскости с углом наклона α покоится брусок массой m. Коэффициент трения между бруском и плоскостью равен μ. Чему равна действующая на брусок сила трения? Есть ли в условии лишние данные?

? 10. Объясните, почему условие покоя тела на наклонной плоскости выражается неравенством

μ ≥ tgα.

Подсказка. Воспользуйтесь тем, что сила трения покоя удовлетворяет неравенству F_тр.пок ≤ μN.

Последнее неравенство можно использовать для измерения коэффициента трения: угол наклона плоскости плавно увеличивают, пока тело не начинает скользить по ней (см. лабораторную работу 4).

? 11.Лежащий на доске брусок начал скользить по доске, когда ее угол наклона к горизонту составил 20º. Чему равен коэффициент трения между бруском и доской?

? 12. Кирпич массой 2,5 кг лежит на доске длиной 2 м. Коэффициент трения между кирпичом и доской равен 0,4.
а) На какую максимальную высоту можно поднять один конец доски, чтобы кирпич не сдвинулся?
б) Чему будет равна при этом действующая на кирпич сила трения?

Сила трения покоя, действующая на тело, находящееся на наклонной плоскости, не обязательно направлена вдоль плоскости вверх. Она может быть направлена и вниз вдоль плоскости!

? 13. Брусок массой m находится на наклонной плоскости с углом наклона α. Коэффициент трения между бруском и плоскостью равен μ, причем и μ < tg α. Какую силу надо приложить к бруску вдоль наклонной плоскости, чтобы сдвинуть его вдоль наклонной плоскости:

а) вниз? б) вверх?

3. Движение тела по наклонной плоскости с учетом трения

Пусть теперь тело скользит по наклонной плоскости вниз (рис. 19.3). При этом на него действует сила трения скольжения, направленная противоположно скорости тела, то есть вдоль наклонной плоскости вверх.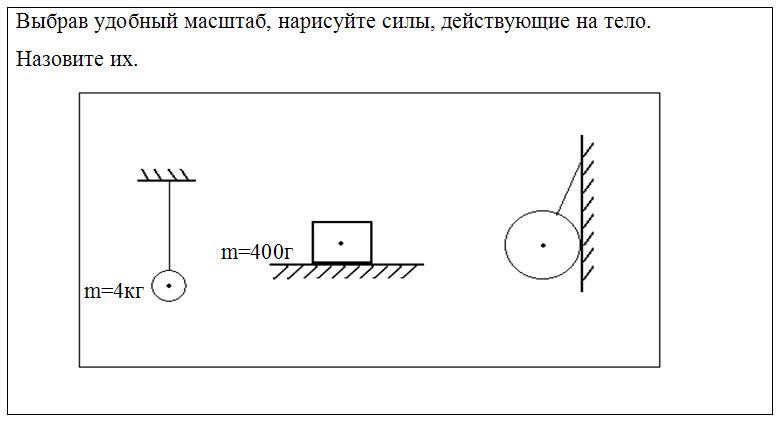

? 15. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:

? 16. Чему равна проекция ускорения тела на ось x?

? 17. Брусок скользит по наклонной плоскости вниз. Коэффициент трения между бруском и плоскостью равен 0,5. Как изменяется со временем скорость бруска, если угол наклона плоскости равен:
а) 20º? б) 30º? в) 45º? г) 60º?

? 18. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Чему ранен коэффициент трения между бруском и доской? С каким по величине и направлению ускорением будет скользить брусок вниз по доске, наклоненной на угол 30º? 15º?

Пусть теперь начальная скорость тела направлена вверх (рис. 19.4).

? 19. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:

? 20. Чему равна проекция ускорения тела на ось x?

? 21. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту.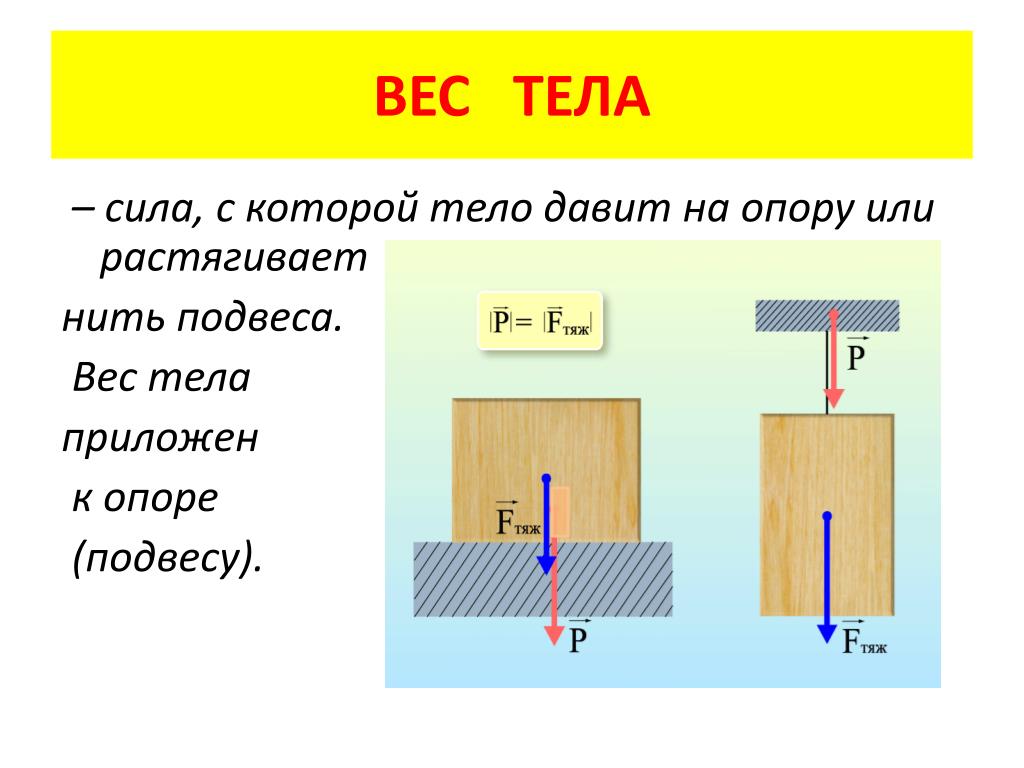 Брусок толкнули вверх по доске. С каким ускорением он будет двигаться, если доска наклонена на угол: а) 30º? б) 15º? В каком из этих случаев брусок остановится в верхней точке?

? 22.Шайбу толкнули вверх по наклонной плоскости с начальной скоростью v₀. Угол наклона плоскости α, коэффициент трения между шайбой и плоскостью μ. Спустя некоторое время шайба вернулась в начальное положение.
а) Сколько времени двигалась шайба вверх до остановки?

б) Какой путь прошла шайба до остановки?
в) Сколько времени после этого шайба возвращалась в начальное положение?

? 23. После толчка брусок двигался в течение 2 с вверх по наклонной плоскости и затем в течение 3 с вниз до возвращения в начальное положение. Угол наклона плоскости 45º.
а) Во сколько раз модуль ускорения бруска при движении вверх больше, чем при движении вниз?
б) Чему равен коэффициент трения между бруском и плоскостью?

Зацените!! Езда Электро-Велосипеда по воде

Дополнительные вопросы и задания

24. Брусок соскальзывает без начальной скорости с гладкой наклонной плоскости высотой h (рис. 19.5). Угол наклона плоскости равен α. Какова скорость бруска в конце спуска? Есть ли здесь лишние данные?

25. (Задача Галилея) В вертикальном диске радиуса R просверлен прямолинейный гладкий желоб (рис. 19.6). Чему равно время соскальзывания бруска вдоль всего желоба из состояния покоя? Угол наклона желоба α, в начальный момент брусок покоится.

26. По гладкой наклонной плоскости с углом наклона α скатывается тележка. На тележке установлен штатив, на котором на нити подвешен груз. Сделайте чертеж, изобразите силы, действующие на груз. Под каким углом к вертикали расположена нить, когда груз покоится относительно тележки?

27. Брусок находится на вершине наклонной плоскости длиной 2 м и высотой 50 см.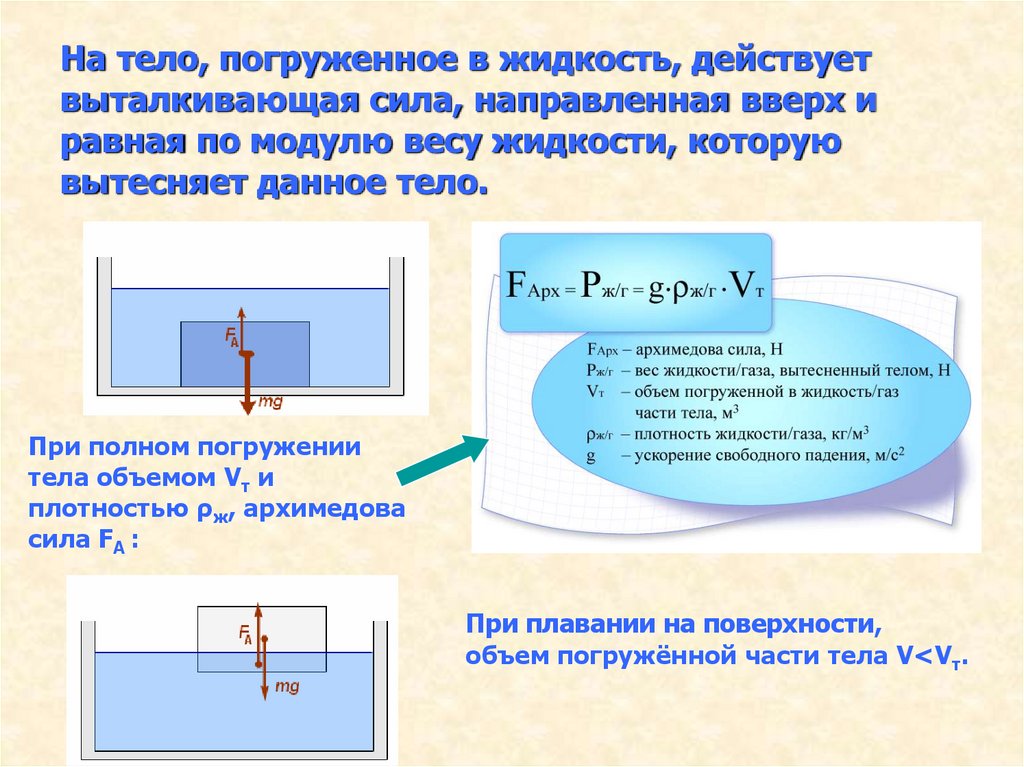 Коэффициент трения между бруском и плоскостью 0,3.
а) С каким по модулю ускорением будет двигаться брусок, если толкнуть его вниз вдоль плоскости?
б) Какую скорость надо сообщить бруску, чтобы он достиг основания плоскости?

28. Тело массой 2 кг находится на наклонной плоскости. Коэффициент трения между телом и плоскостью 0,4.
а) При каком угле наклона плоскости достигается наибольшее возможное значение силы трения?
б) Чему равно наибольшее значение силы трения?

в) Постройте примерный график зависимости силы трения от угла наклона плоскости.
Подсказка. Если tg α ≤ μ, на тело действует сила трения покоя, а если tg α > μ – сила трения скольжения.

Движение тела под действием нескольких сил по окружности

Из кодификатора по физике, 2020.

«1.2.4. Второй закон Ньютона: для материальной точки в ИСО

1.2.8. Сила упругости. Закон Гука:

1.2.9. Сила трения. Сухое трение. Сила трения скольжения:

Сила трения покоя:

Коэффициент трения. »

3. Определите значения проекций всех величин.

4. Решите полученные уравнения. При необходимости, исходя из физиче-ской природы, выразите силы через величины, от которых они зависят.

Задача 1. Мальчик массой 50 кг качается на качелях с длиной подвеса 4 м. Определите силу, с которой он давит на сиденье при прохождении нижнего положения со скоростью 6 м/с.

Решение. При использовании второго закона Ньютона, мы применяем силы, действующие на тело. Сила Fдавл – это сила, с которой мальчик давит на сиденье качелей. По третьему закону Ньютона, с такой же по величине силой, но противоположной по направлению, качели будут действовать на мальчика – это сила реакции опоры (N). Тогда

На мальчика действуют сила тяжести и сила реакции опоры (N). При движении по дуге окружности в нижней точке ускорение направлено к центру окружности (вверх). Ось Y направим вверх (рис. 1). Запишем второй закон Ньютона:

где , R=l.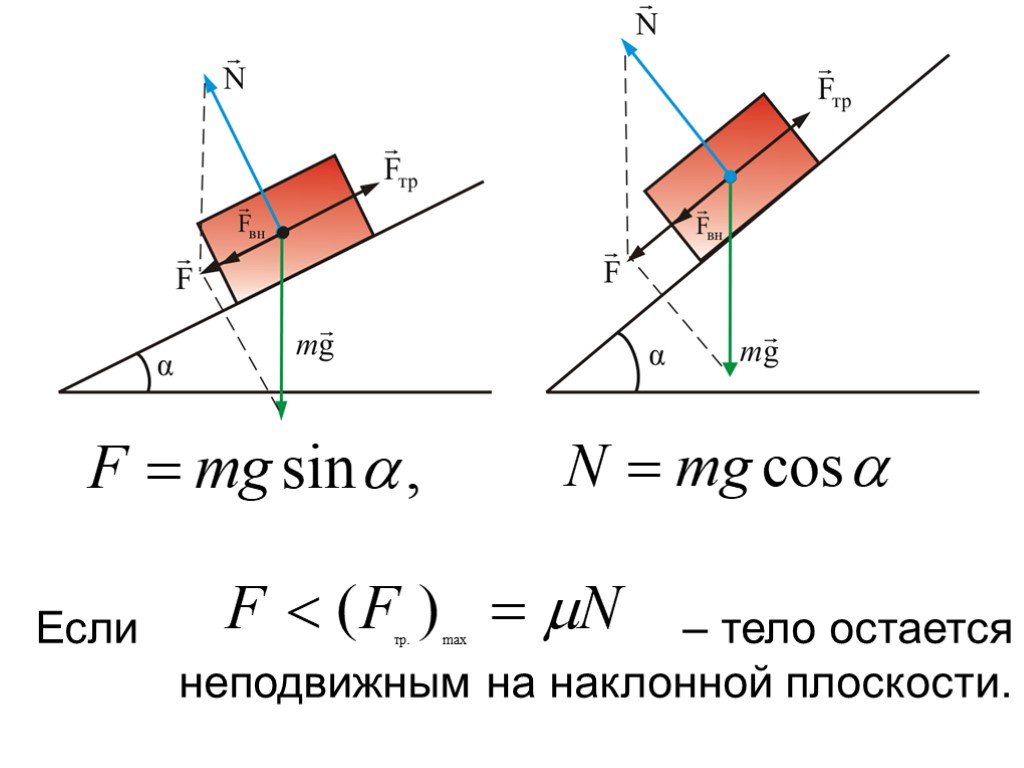 С учетом уравнений (1) и (2) получаем

Задача 2. На горизонтальном диске, который равномерно вращается вокруг вертикальной оси, проходящей через центр диска, лежит небольшая монета. Коэффициент трения между монетой и поверхностью диска равен 0,25. Угловая скорость вращения диска 5,0 рад/с. Определите максимальное расстояние (в см) между центром монеты и осью вращения, при котором монета не соскальзывает с диска.

Решение. На монету, лежащую на диске, действуют: сила тяжести и сила реакции опоры (N) — они направлены по вертикали (вдоль оси 0Y на рис. 2), сила трения (Fтр) — она направлена по горизонтали. Так как тело не движется, то сила трения — это сила трения покоя.

Монета вращается вместе с диском, поэтому у тела есть центростреми-тельное ускорение, направленное к центру диска. А так как на тело действует только одна горизонтальная сила (Fтр), то она будет направлена в ту же сторону, что и ускорение, т.е. к центру дис-ка.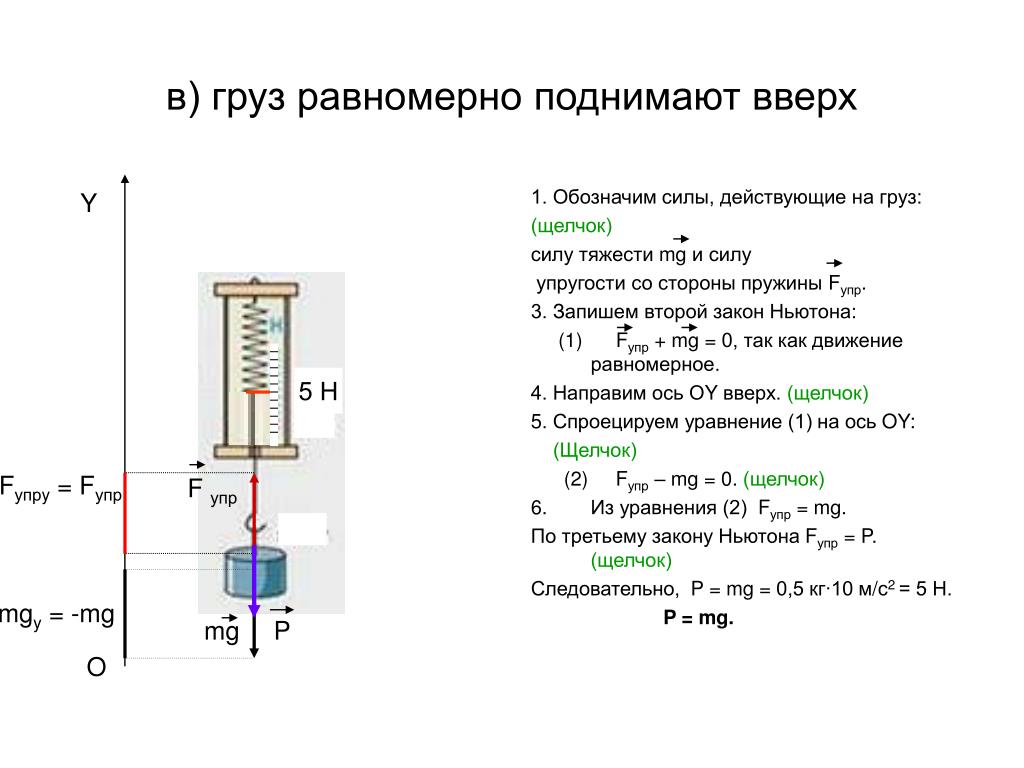

Оси координат направим так, как показано на рис. 2. Запишем второй закон Ньютона:

При любом расстоянии тело начнет скользить по диску к краю. Тогда

Задача 3. Груз, подвешенный на нити длиной 1,4 м, двигаясь равно-мерно, описывает в горизонтальной плоскости окружность (конический ма-ятник). Определите скорость, с которой движется груз, если во время его движения нить образует с вертикалью постоянный угол в 30º.

Решение. На груз действуют сила тяжести и сила натяжения подвеса (T). При равномерном движении по окружности возникает центростремительное ускорение, направленное горизонтально. Оси координат выберем так, как показано на рис. 3. Запишем второй закон Ньютона:

Задача 4. По выпуклому мосту, радиус кривизны которого 90 м, со скоростью 54 км/ч движется автомобиль массой 2,0 т. В точке моста, направление на которую из центра кривизны моста составляет с направле-нием на вершину моста угол α, автомобиль давит с силой 14,4 кН. Определите угол α.

Решение. Сила Fд — это сила, с которой автомобиль давит на дорогу. По третьему закону Ньютона, с такой же по величине силой, но противоположной по направле-нию, дорога будет действовать на автомобиль, а это сила реакции опоры (N). Тогда

На автомобиль действуют сила тяжести , сила реакции опоры (N), сила трения (Fтр) и сила тяги (F). При движении по дуге окружности возникает центростремительное ускорение, которое направлено к центру кривизны (перпендикулярно поверхно-сти). Ось 0Y направим вдоль ускорения, чтобы не учитывать тангенциальное ускорение (рис. 4).

Запишем второй закон Ньютона:

Автор Сакович А.Л.

Сила

Цели обучения:

• Понять, что такое сила и как сила может воздействовать на тело человека
• Уметь различать силу и массу
• Понимание различных классификаций или типов сил и того, как каждая из них может по-разному влиять на человеческое тело. Эти различные классификации сил включают: (1) внутреннюю и внешнюю силу, (2) контактную и бесконтактную силу и (3) трение и нормальную силу
.
• Понимать коэффициенты статического и динамического трения и уметь использовать следующее уравнение для количественной оценки силы трения, нормальной силы и/или коэффициента трения: F _F = F _N × µ
• Уметь определять результирующее (чистое) воздействие двух или более сил с помощью сложения векторов
• Уметь разлагать результирующую (результирующую) силу на ортогональные (перпендикулярные) составляющие, используя векторное разрешение
• Понимание концепции статического равновесия. Знать, как определить, находится ли объект в статическом равновесии, путем суммирования сил, действующих на объект. Уметь определять неизвестную силу, действующую на неподвижный объект (если известны все остальные силы, действующие на объект).

Следующий математический обзор может быть полезен для вас перед изучением некоторых из следующих материалов. Сила и масса: Сила — это толчок или притяжение, которые потенциально могут ускорить объект, включая человеческое тело; силы также могут деформировать анатомические структуры. Сила — это векторная величина, которая измеряется в ньютонах (Н) или фунтах (фунтах).

Масса — это скалярная мера инерции или мера количества материи для объекта, включая человеческое тело. Массу часто измеряют в килограммах (кг).

Некоторые полезные преобразования включают 1 Н = 0,225 фунта, 1 фунт = 4,45 Н, 1 кг = 2,214 фунта и 1 Н = 1 кг × 1 м/с ² (F = ma).

Практика: Вес тела – это сила, направленная вниз. Если вы знаете, сколько вы весите в фунтах, используйте третье вышеупомянутое преобразование (1 кг = 2,214 фунта) для расчета массы тела в кг. Затем используйте окончательное вышеупомянутое преобразование (1 Н = 1 кг × 1 м/с ² ), напомнив, что ускорение силы тяжести на Земле равно -90,81 м/с ² , чтобы рассчитать вес вашего тела в Н. Важно помнить, что вес тела — это сила, возникающая в результате гравитации, действующей на массу вашего тела, масса тела — это мера количества вещества. внутри вашего тела (вес тела = масса тела × ускорение под действием земного притяжения).

Классификация сил (различные способы понимания силы)

Один из способов рассмотрения сил состоит в том, чтобы классифицировать их как внутренние или внешние.

1. Внутренние силы:

действуют в пределах исследуемого объекта или системы. Сами по себе эти силы не могут изменить движение центра масс.
Практика: Какие две внутренние силы действовали сегодня на ваше тело?

2. Внешние силы:

Действие на объект или систему в результате ее взаимодействия с внешней средой. Эти силы могут изменить движение центра масс.
Практика: Какие две внешние силы воздействовали на ваше тело сегодня?

Видео, которое может иметь значение, а может и не иметь значения (вероятно, нет).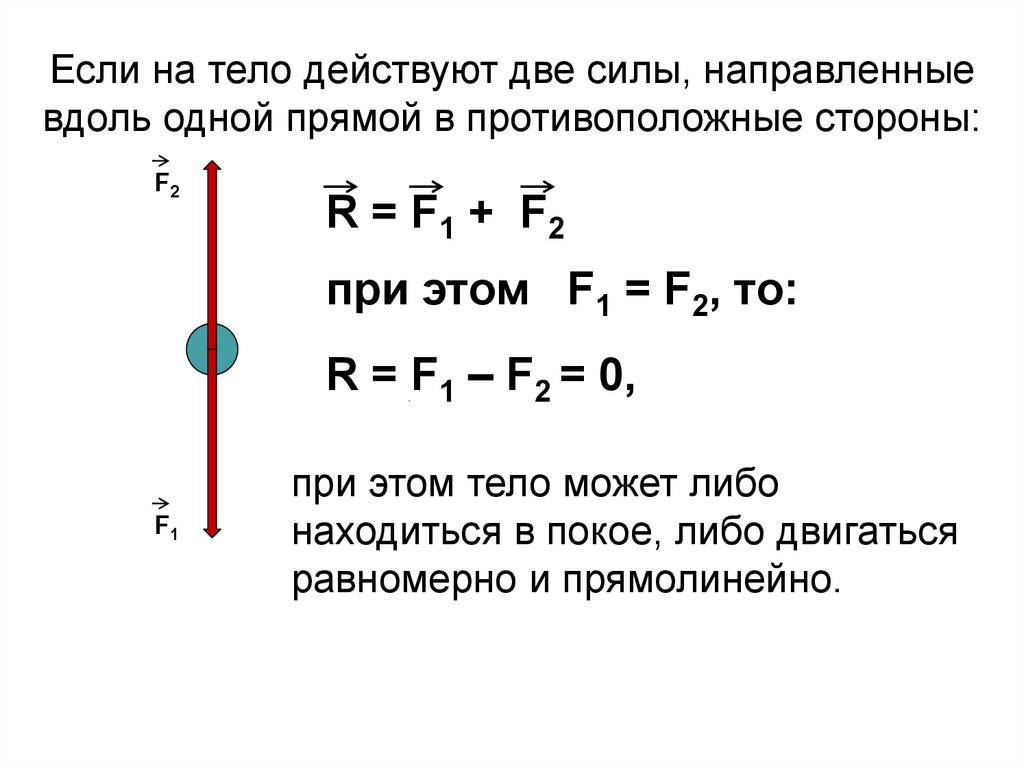 .. Дополнительный способ рассмотрения силы — классифицировать силу как контактную или бесконтактную.

1. Контактные силы:

Большинство сил, которые мы будем рассматривать в этом курсе, будут контактными силами (некоторые внутренние и некоторые внешние). Эти силы возникают, когда объекты контактируют друг с другом, и могут включать твердые тела и жидкости. Мы часто разделяем результирующие контактные силы на две перпендикулярные составляющие силы, которые классифицируются как (1) трение (F _F ) или (2) нормальный (F _N ). Сила реакции грунта является хорошим примером контактной силы, которую можно разложить на трение и нормальную силу.

Сила трения (F _F ) : составляющая контактной силы, действующая параллельно контактирующим поверхностям. Хотя трение часто ассоциируется с противодействием движению, помните, что трение часто способствует движению человека. Трение может быть статическим или динамическим, в зависимости от того, движутся ли контактирующие объекты друг относительно друга.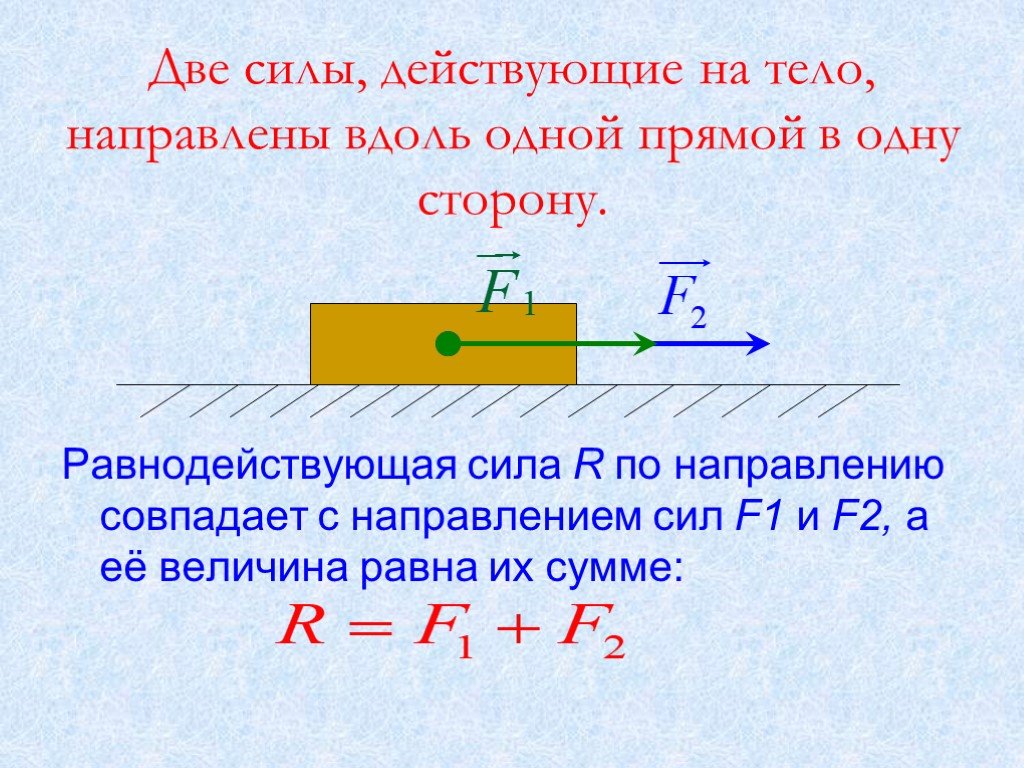 (Статическое трение > динамическое трение).

Коэффициент трения (µ = F _F /F _N ) представляет собой безразмерную величину, зависящую от свойств материала контактирующих поверхностей. Коэффициент различается в зависимости от того, являются ли обстоятельства статическими или динамическими (статический коэффициент > динамический коэффициент).

Интересная дискуссия, связанная с трением шин гоночных автомобилей…

Нормальное контактное усилие (F _N ): составляющая контактной силы, действующая перпендикулярно соприкасающимся поверхностям.

Практика: Коэффициент статического трения между обувью бегуна и землей составляет 0,6. Если земля воздействует на бегуна вертикальной (нормальной) силой реакции земли в 2000 Н, какова максимальная горизонтальная сила, которую бегун может создать под своим ботинком, прежде чем ботинок начнет скользить, и бегун может поскользнуться? Ответ: 1200 Н.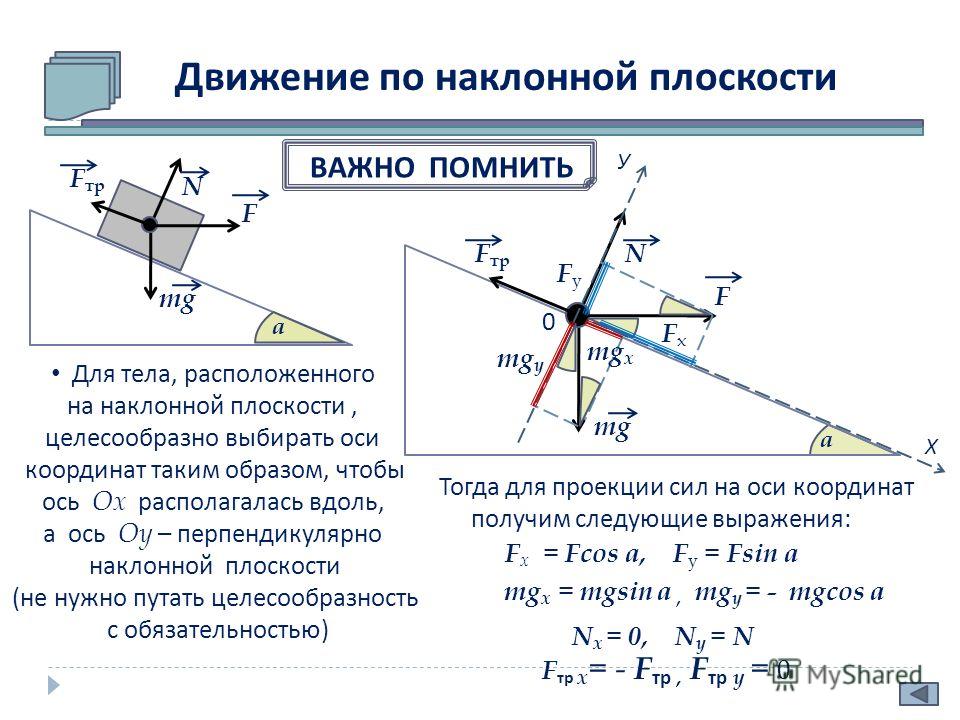 Какие переменные может изменить бегун, чтобы уменьшить вероятность поскользнуться? Точно так же, как вы могли бы уменьшить вероятность поскользнуться на обледенелом тротуаре в этом семестре?

Хранилище Юрченко Замедленная съемка
Силы наземного реагирования и ACLR

2. Бесконтактные силы

Они не требуют контакта между двумя объектами. Для этого курса основной проблемой неконтактной силы является сила тяжести, которая на поверхности земли вызывает вертикальное ускорение около -9,81 м/с/с.

Анализ нескольких одновременных сил: для рассмотрения эффекта нескольких сил, действующих на объект, часто полезно использовать диаграмму свободного тела. На диаграмме свободного тела силы представлены в виде векторов, которые указывают точку приложения силы, величину силы и направление силы.
Краткий обзор добавления вектора : его можно использовать для понимания суммарного воздействия нескольких сил на один объект или систему.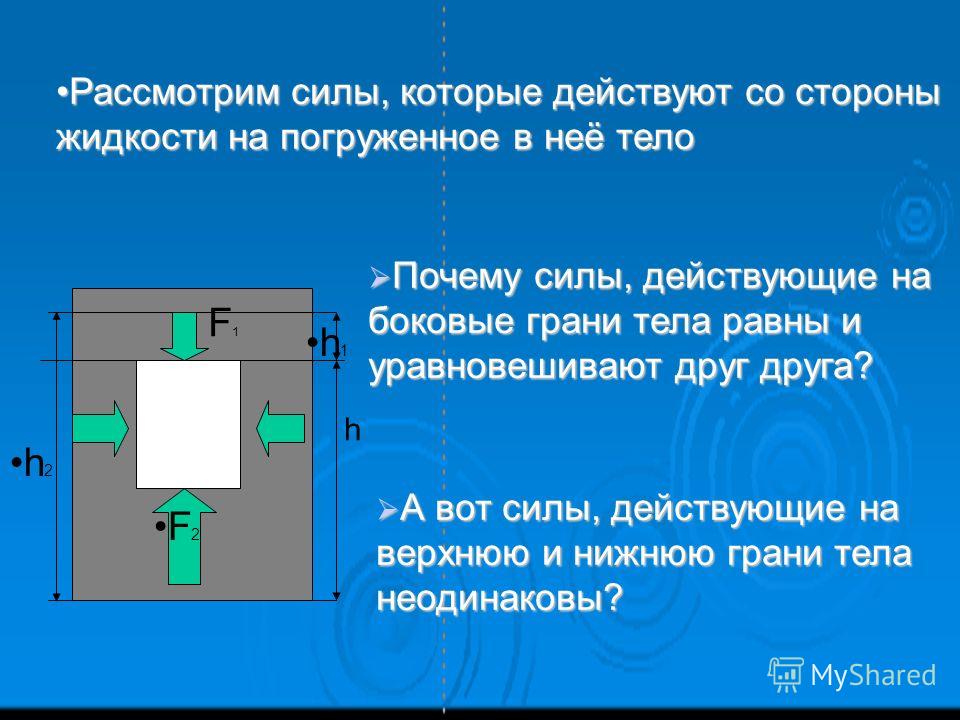 Легко добавить две или более коллинеарных сил: вы можете добавить коллинеарные силы алгебраически. Однако, если силы не коллинеарны, вы не можете алгебраически суммировать каждую из сил. Используйте метод кончика к хвосту и тригонометрию, чтобы добавить неколлинеарные силы.

Некоторые практические задачи на сложение коллинеарных векторов:

Практика: Тяжелоатлет (масса = 100 кг) держит штангу весом (50 фунтов). Вертикальная сила реакции опоры равна 1000 Н. Какая результирующая сила действует на штангиста? Ответ: -203,5 Н. Будет ли центр масс испытывать вертикальное ускорение?
Практика: На спринтера массой 72 кг действует вертикальная сила реакции земли 2200 Н. Какая сила действует на спринтера? Ответ: 1494 N. Как изменится центр масс? (Другими словами, каково будет вертикальное ускорение центра масс бегуна?)
Практика: Используйте сложение векторов, чтобы сложить силы, показанные на вышеупомянутой диаграмме свободного тела бегуна (нормальная сила реакции и сила трения о землю, сопротивление ветра и вес тела). Предположим, что сопротивление воздуха в горизонтальном направлении равно -15 Н, вес тела равен -700 Н, передне-задняя сила реакции на землю (трение) равна 220 Н, а вертикальная сила реакции на землю (в норме) равна 820 Н. Равнодействующая сила? Ответ: 238 Н. И под каким углом по отношению к горизонтальной оси направлена ​​эта равнодействующая сила? Ответ: 30°.
Практика: нарисуйте диаграмму свободного тела, на которой показаны три основные силы (четырехглавая мышца, связка надколенника и бедренная кость), действующие на надколенник. Используйте рентгенограмму ниже, чтобы помочь вам. Эта свободная диаграмма тела и соответствующее обсуждение в классе помогут вам лучше понять данные, представленные Escamilla et al. (2009), MSSE , 41(4), 879-888.

Разрешение вектора также важно при рассмотрении сил, действующих на объект/систему. Векторное разрешение позволяет разложить результирующую или результирующую силу на ортогональные (перпендикулярные) составляющие.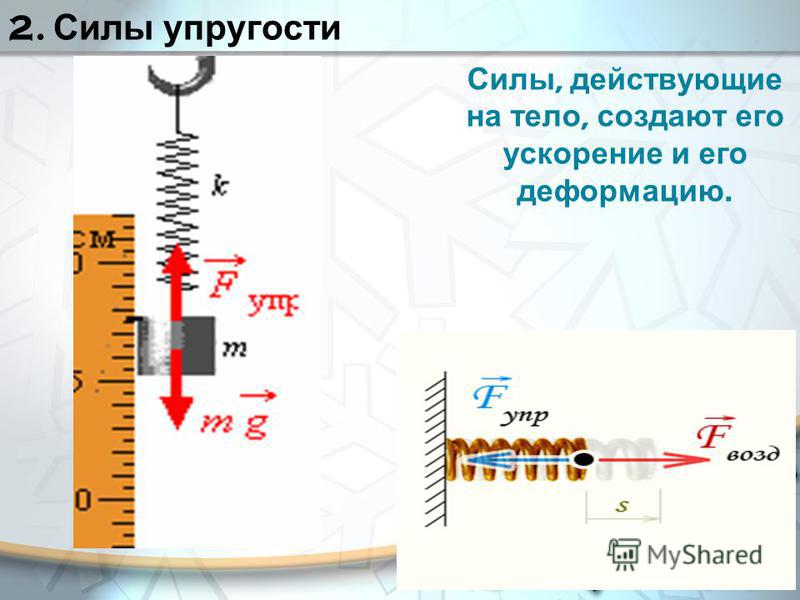
Метод разрешения вектора : На спринтера массой 72 кг действует результирующая сила реакции земли 2124 Н. Сила действует под углом 86 градусов над фиксированной горизонтальной осью (землей). Используя векторное разрешение, каковы вертикальная и горизонтальная составляющие этой результирующей силы реакции земли? Ответы: Вертикальная = 2119 Н; По горизонтали = 148 Н. Каковы последствия этой результирующей силы реакции земли? Восходящее вертикальное ускорение и горизонтальное ускорение в направлении горизонтальной силы.
Еще одна практическая задача на разрешение вектора: Эта учебная задача упрощается благодаря использованию векторного разрешения. Ответы на эту задачу: 68 с.ш. и 43°.

Статическое равновесие (ΣF = 0) Когда объект находится в состоянии покоя и силы, действующие на объект, находятся в равновесии, их результирующая сила равна нулю. Хотя эта концепция не будет часто использоваться в этом классе (движущиеся люди обычно не находятся в статическом равновесии), полезно помнить, поскольку эта концепция закладывает хорошую основу для рассмотрения обстоятельств, не связанных со статическим равновесием. Используйте концепцию статического равновесия, чтобы определить задействованную силу реакции опоры в приведенной ниже задаче. Тяжелоатлет Пример: Ускорение этого тяжелоатлета равно нулю (статическое равновесие). Если масса атлета 80 кг, а масса штанги 70 кг, какой должна быть вертикальная составляющая силы реакции опоры? Ответ: 1471,5 N Помните: F grf + F bw + F bb = 0 Что произойдет, если сила реакции опоры, действующая на штангиста, будет равна 2000 Н? Как это может произойти?

Дополнительные практические задачи:

1. Используя сложение векторов, рассчитайте результирующую силу, действующую на эту гимнастку
2. Рассчитайте силы реакции, действующие на ребенка на качелях, при условии, что ребенок находится в статическом равновесии (ΣF = 0). 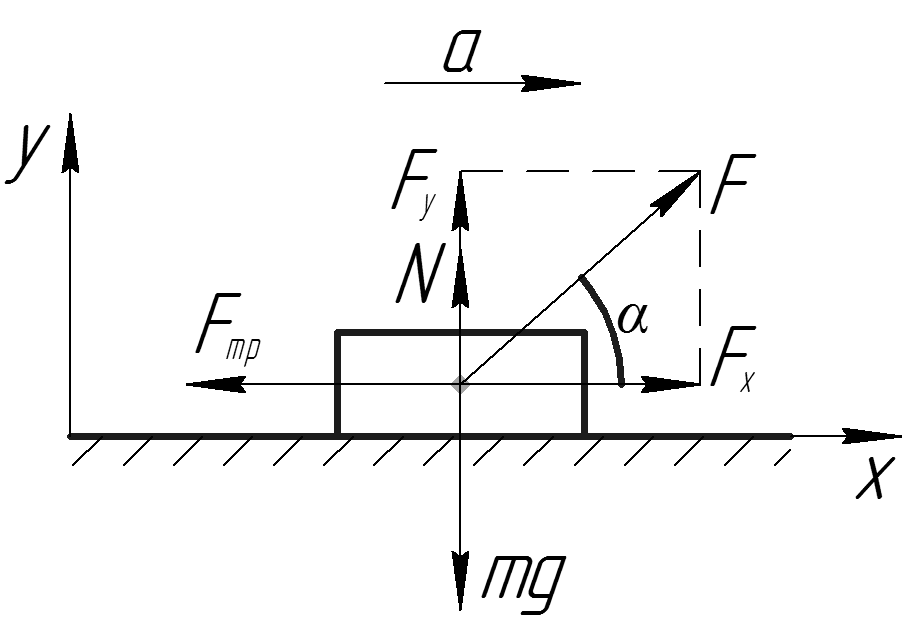Рассчитайте результирующую силу реакции (F _R ), два отдельных компонента результирующей силы реакции (F _RX и F _RY ), и ориентация силы реакции относительно горизонтали (θ). Решения для №1 и №2
3. Вы пытаетесь тащить кого-то на санях за веревку, прикрепленную к саням, по ровному заснеженному полю. Тяговое усилие направлено вперед и вверх под углом 30 градусов над землей. Суммарная масса человека на санях и санях составляет 58 кг, а коэффициент трения покоя между санями и снегом равен 0,10. С какой силой нужно тянуть, чтобы сани начали двигаться? Ответ: ~62N. Решение. Кроме того, какие переменные вы могли бы изменить, чтобы вам было легче тянуть сани?
4. Выполните практические задачи 1–15 из главы 1 учебника МакГинниса (2-е издание).
5. Решите следующие практические задачи.

Ньютоновская механика. Сложение сил, действующих в различных точках тела

спросил 6 лет, 2 месяца назад

Изменено 5 лет, 10 месяцев назад

Просмотрено 3к раз

$\begingroup$

Можно ли векторно сложить и найти равнодействующую нескольких сил, действующих на разные точки протяженного тела? Например, если я приложу пару (равных и противоположных сил) к двум концам жесткого стержня, могу ли я утверждать, что результирующая сила, действующая на стержень, равна нулю? Все, что я знаю о сложении векторов, заключается в том, что можно добавлять векторы, действующие в одной и той же точке/частице.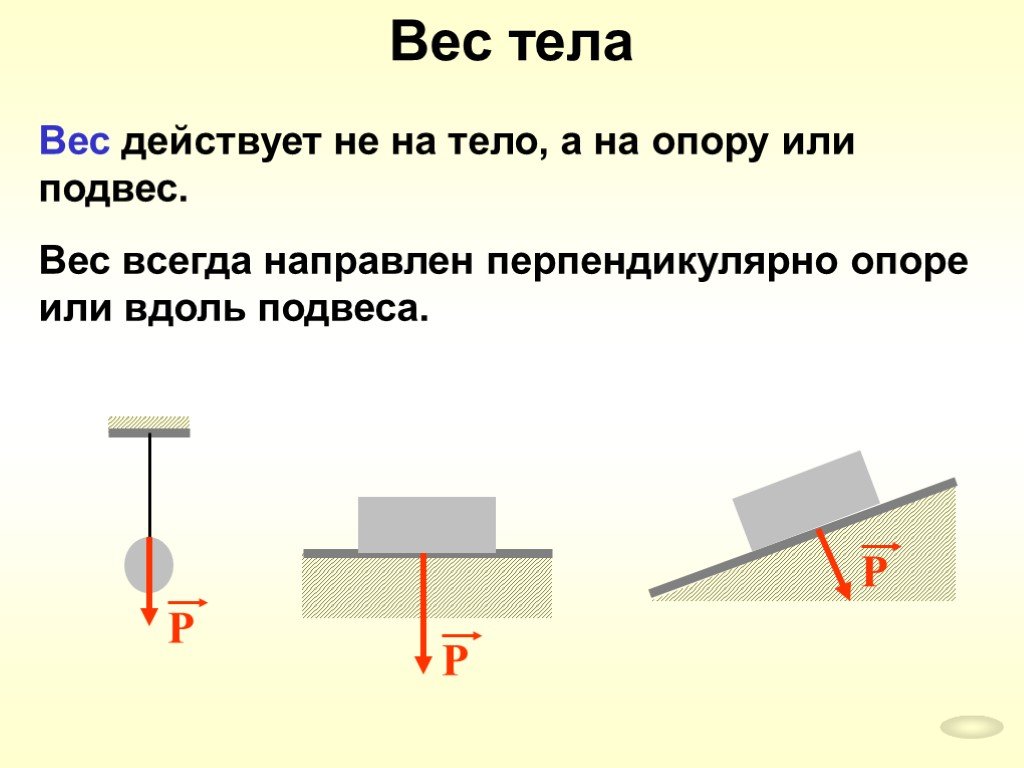

РЕДАКТИРОВАТЬ: я думаю, мы не можем складывать силы на твердом теле, действующие в разных точках. Если бы мы могли, то результирующая сила, действующая на стержень, была бы равна нулю, а если предположить, что применим 2-й закон Ньютона, то ускорение стержня равно нулю. Но стержень вращается, и поэтому различные точки стержня ускоряются. Можно сказать, что центр масс не ускоряется. Однако, если мы применим второй закон Ньютона непосредственно к стержню, никто не поймет, действительно ли ускорение $\textbf{a}$, лежащее в правой части $\textbf{F}=m\textbf{a}$, является ускорением центр масс. И чтобы прийти к понятию центра масс, действительно нужно использовать третий закон Ньютона, независимый от второго закона Ньютона (как это делается для системы N-частиц).

• ньютоновская механика
• классическая механика
• силы
• векторы
• динамика твердого тела

$\endgroup$

5

$\begingroup$

Второй закон Ньютона, примененный к точечным частицам, гласит, что движения не будет, если сумма приложенных сил равна нулю. Поскольку твердое тело состоит из бесконечного числа точечных частиц, движения не будет тогда и только тогда, когда сумма сил, приложенных к каждой точечной частице, из которой состоит тело, равна нулю.

В контексте вашего вопроса утверждение, что результирующая сила, действующая на ваш стержень, равна нулю, может ввести в заблуждение. Математически, если вы суммируете эти векторы, сумма будет равна нулю, но вы считаете, что можете свободно перемещать свои векторы, и ничего не изменится. Поскольку теперь у вас есть набор частиц, каждая из них действует по-своему, поэтому вы не можете отделить эти векторы сил от связанных с ними точек. В самом деле, если вы приложите равные и противоположные силы к противоположным концам стержня, даже если их суммирование даст вам ноль, вы создадите крутящий момент, который будет вращать твердое тело вокруг его центра масс. Суммарная сила, приложенная к системе, равна нулю, но это не означает, что внутренние силы не играют никакой роли, поскольку система состоит из более мелких систем, которые не изолированы (а именно, из частиц).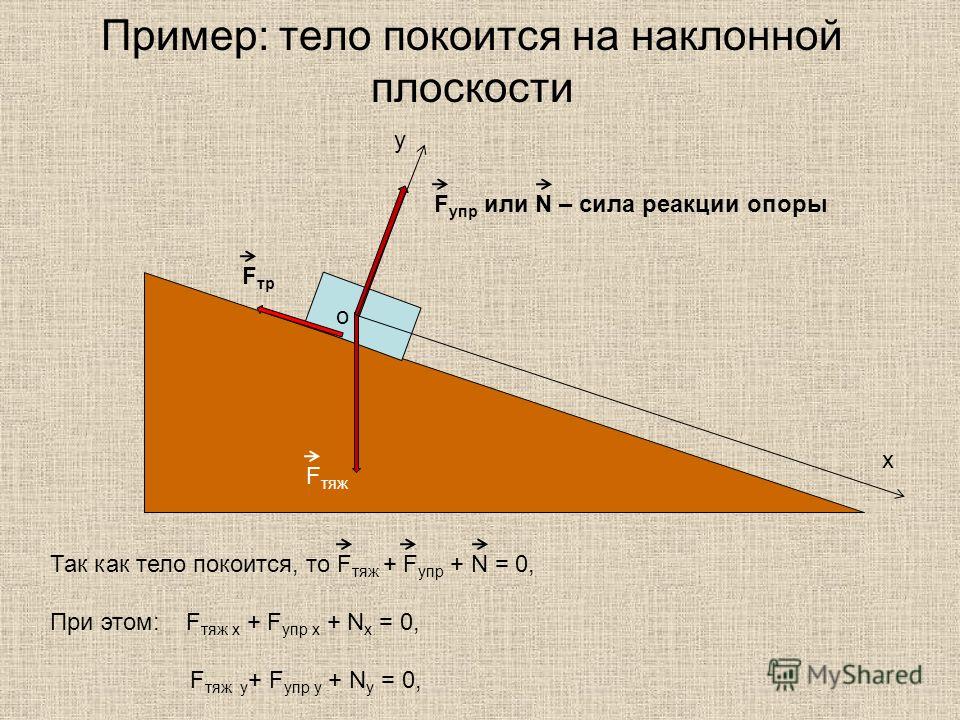

$\endgroup$

$\begingroup$

См. ответ в Крутящий момент в неинерциальной системе отсчета.

Соблюдайте правила движения:

1. Сумма сил равна массе, умноженной на ускорение центра масс : $$ \sum_i \vec{F}_i = m \vec{a}_{cm} $$
2. Сумма крутящих моментов относительно центра масс равна изменению углового момента: $$ \sum_i (M_i + \vec{r}_i \times \vec{F}_i) = I_{cm} \dot{\vec{ \omega}} + \vec{\omega} \times I_{cm} \vec{\omega}$$, где $\vec{r}_i$ — относительное расположение силы $\vec{F}_i$ относительно центр массы.

Ключевым здесь является то, что результирующие силы описывают только движение центра масс, а не всего тела. В вашем случае чистый крутящий момент позволит телу повернуться на вокруг центра масс .

Правила уравнений движения:

1. Если чистый крутящий момент относительно центра масс равен нулю, то тело будет двигаться чисто поступательно
2. Если сумма сил, действующих на тело, равна нулю (но не суммарный крутящий момент), то тело будет вращаться исключительно вокруг своего центра масс.

$\endgroup$

$\begingroup$

 если я приложу пару (равных и противоположных сил) к двум концам жесткого стержня, могу ли я утверждать, что результирующая сила, действующая на стержень, равна нулю?

Да, можете. Вы на самом деле спрашиваете здесь, работают ли законы Ньютона, и да, они работают :

$$\sum \vec F=0 \\ \sum \vec F=m\vec a$$

На стержень действуют равные, но противоположные силы, которые уравновешиваются, поэтому в соответствии с 1-м законом Ньютона не ускоряет .

Ускорение $\vec a$ здесь ключевое. Потому что нет, он не ускоряется, но это не значит, что он не двигается ! Он все еще может вращать на месте.

Давайте посмотрим на вращательные эквиваленты законов Ньютона:

$$\sum \vec \tau=0 \\ \sum \vec \tau =m\vec \alpha$$

Если результирующая сила равна нулю (независимо от того, куда силы атакуют), то объект не ускоряется, $\vec a=0$, а сетевая крутящий момент должен быть равен нулю, чтобы он не вращал , $\vec \alpha =0$.

Таким образом, чтобы быть полностью неподвижным, должны иметь место как $\sum \vec F=0$, так и $\sum \vec \tau=0$. Но если вас интересуют только силы, то вы просто решили не заботиться о наличии вращения.

$\endgroup$

$\begingroup$

Центр тяжести стержня не изменится по импульсу, если две равные силы приложены одновременно к разным (но противоположным) точкам стержня.

$\endgroup$

$\begingroup$

Ответ на ваш вопрос: -Да, мы можем по-разному складывать и находить равнодействующую нескольких сил, действующих на разные точки протяженного тела. Но это сложный процесс, позвольте мне объяснить, но перед этим я хочу перейти к вашему вопросу — в этом конкретном вопросе результирующая будет работать на бесконечности, и вы знаете, если почти нулевая сила работает на бесконечности, то применяя математический предел, мы получаем конечный крутящий момент.

Теперь перейдем к тому, как я это знаю, т.е. как сложить — пусть сначала возьмут 2 силы в плоскости, ПО ПРИНЦИПУ ПЕРЕДАЧИ сил мы знаем, что можем переместить точку приложения силы в любую точку на линии ее действия. Теперь у этих двух сил есть линия действия, которая встретится где-то в любой точке, если они не параллельны, в этом случае сложение двух сил есть не что иное, как равнодействующая этих двух сил (как рассчитано по математической формуле закона параллелограмма), которые будут действовать в точка, где пересекаются линии действия этих двух.

Для 3-х сил мы сначала находим равнодействующую 2-х (как я объяснял во 2-м абзаце), затем это проблема 2-х сил.
Особые случаи — (а) если две силы P и Q подобны параллельным, которые действуют в точках A и B, то их равнодействующая параллельна им, действующим в точке C на линии, соединяющей AB, где (AC)P=(CB)Q [внутреннее деление АВ в соотношении P:Q] (a) если 2 силы P и Q не параллельны и действуют в точках A и B, то их равнодействующая параллельна им, действующим в точке C на продолжении линии, соединяющей AB, где (AC)P=(CB)Q [т.