Скорость движения жидкости: Ваш браузер не поддерживается

Содержание

Средняя скорость — движение — жидкость

Cтраница 1

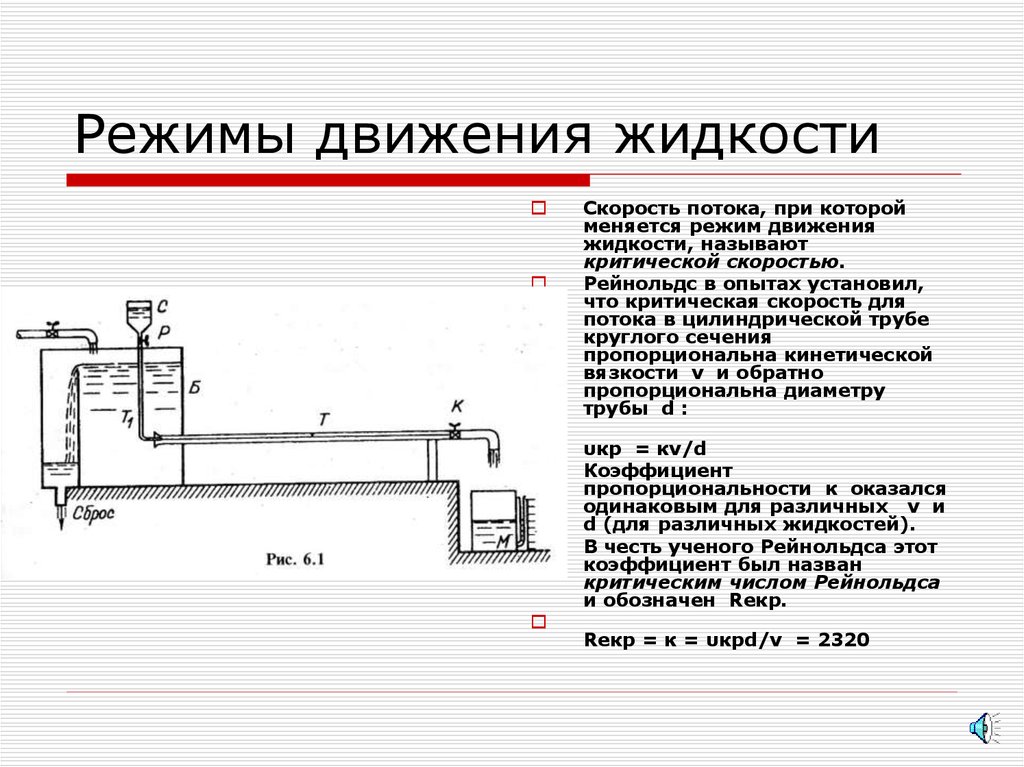
Средняя скорость движения жидкости в трубопроводе должна быть больше 0 5 м / сек во избежание отложений в трубах твердых частиц и в то же время она не должна быть больше 2 5 м / сек во избежание истирания труб песком. [1]

График подачи насоса простого действия. [2]

Средняя скорость движения жидкости и отношение максимальной скорости к средней остаются такими же, как и у насосов простого действия. [3]

Средняя скорость движения жидкости ( газа) не должна превышать критическую. Если эксплуатация скважины по технологическим причинам должна вестись на скоростях выше критической, рекомендуется в нижней части колонны устанавливать центрирующие устройства. [4]

Определим среднюю скорость движения жидкости относительно неподвижной частицы, расположенной на расстоянии г от центра, как путь, проходимый колеблющейся жидкостью в единицу времени, независимо от направления движения.

[5]

К — средняя скорость движения жидкости, м / с; А — площадь живого сечения потока, мг. [6]

По мере приближения средней скорости движения жидкости к критическому значению, как известно [3 ], наблюдается статическая неустойчивость трубопровода. [7]

Установим понятия о средней скорости движения жидкости в рассматриваемом живом сечении потока и расходе целого потока жидкости. Средней скоростью движения жидкости в рассматриваемом живом сечении называется скорость, с которой должны были бы двигаться все частицы жидкости через данное живое, сечение, чтобы расход всего потока был равен расходу, соответствующему действительным скоростям этих частиц. Ввиду важности понятия о средней скорости остановимся на нем несколько подробнее. [8]

Можно полагать, что

средняя скорость движения жидкости на поверхности последней, а, следовательно, и время пробега зависит от величин h, d, Vo, g, о и До р — р, где g, s, р и р — соответственно ускорение силы тяжести, поверхностное натяжение жидкости, плотность жидкости и воздуха.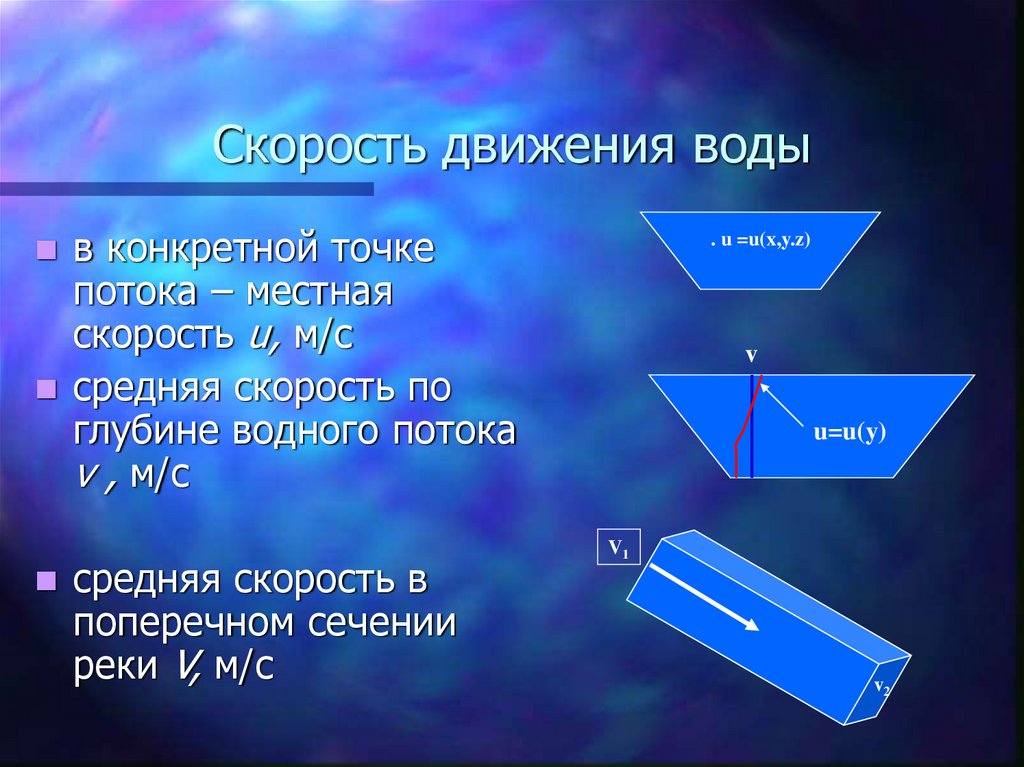

[9]

При проектном расходе сточных вод средняя скорость движения жидкости Б песколовке составляет 0 18 м / сек, а расчетная продолжительность пребывания жидкости в песколовке составляет 67 секунд. [10]

Таким образом, для нахождения средней скорости движения жидкости ( или газа) нужно скорость фильтрации ее разделить на пористость. [11]

Зависимость Qf ( H. для клапанов с ограничителем. и без него.| Экспериментальные зависимости подачи от частоты при аа0 и ал 0 2. [12]

Диаметр трубопровода зависит от величины средней скорости движения жидкости, изменяющейся в пределах 1 0 — 1 5 ж / сек. [13]

Расчет распределителя обычно производят по средним скоростям движения жидкости, что, как будет показано ниже, ведет к значительным ошибкам. Расчет распределителя по фактору время — сечение неправильно отражает физическую сущность явления и не может быть рекомендован для применения.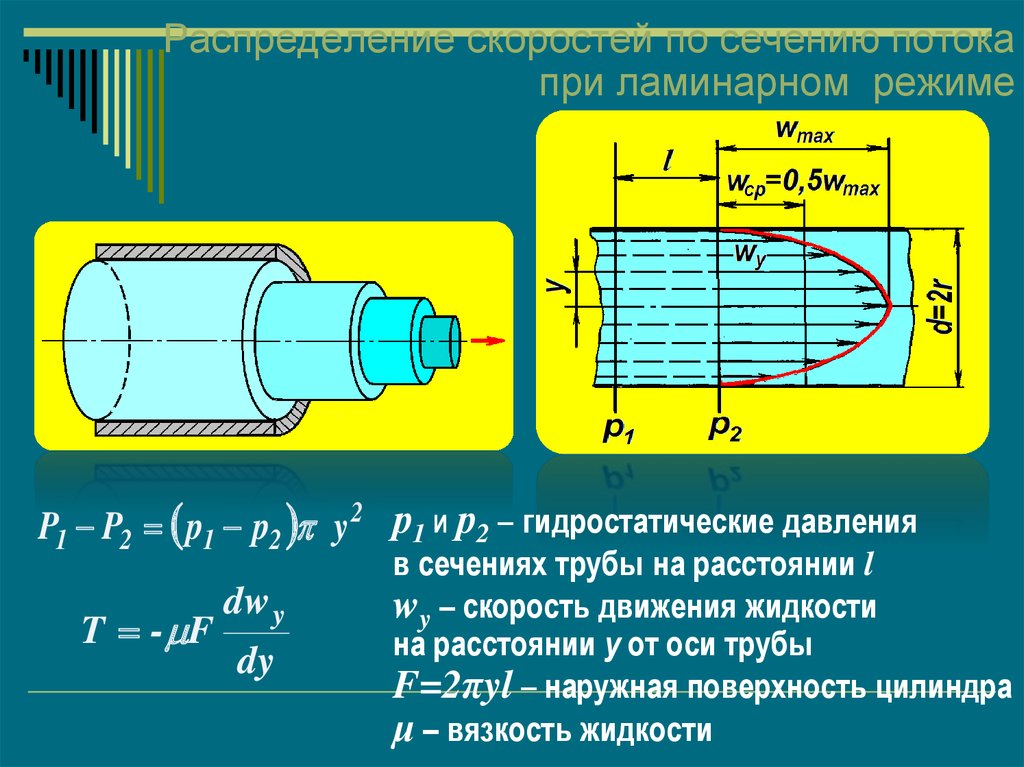 [14]

Зависимость изменения средней скорости движения гравитационной жидкости в осадке от расстояния до фильтрующей перегородки ( полихлорвиниловая смола. hoc 58 мм, закрытые стаканы.| Зависимость средней скорости движения гравитационной жидкости в разных слоях осадка от времени центрифугирования ( полихлорвиниловая смола, закрытые стаканы, Fr 127, й. 58 мм при расстоянии h слоя от фильтрующей перегородки. [15]

Страницы: 1 2 3 4

Средняя скорость движения жидкости — определение термина

Термин и определение

скорость, с которой должны были бы двигаться все частицы жидкости через рассматриваемое плоское сечение, чтобы расход всего потока был равен расходу, соответствующему действительным скоростям этих частиц.

Еще термины по предмету «Процессы и аппараты»

Пьезометрический напор (напор давления)

характеризует удельную потенциальную энергию давления, выраженную в метрах столба жидкости.

Реология

(от греч. rhéos – течение, поток и lógos – слово, учение) – наука о деформациях и текучести вещества; рассматривает процессы, связанные с необратимыми остаточными деформациями и течением разнообразных вязких и пластичных материалов, явления релаксаци напряжений и т.д.; реология тесно связана с гидромеханикой, теориями упругости, пластичности и ползучести; в ней широко используют методы вискозиметрии; вопросы реологии широко рассматриваются в материаловедение, в физике полимеров, в механике грунтов, в физике дисперсных систем и др.

Тепловые процессы

процессы переноса тепла, протекающие со скоростью, определяемой законами теплопередачи.

Научные статьи на тему «Средняя скорость движения жидкости»

Последними считаются физические силы, которые вызывают движение, а искомыми свойствами выступают скорость.

..
движения и внутреннее давление в жидкости….
Кроме того, могут быть ещё следующие виды движения жидкости: вихревое движение – предполагает вращение…
сечения любого потока и средняя скорость одинаковы абсолютно по всей длине; неравномерное движение –…
Необходимо знать также, с какими начальными скоростями движется жидкость в конкретных точках.

Статья от экспертов

С помощью чувствительных торсионных весов определена скорость выхода молекул этанола из жидкого этанола: 2± 0,3 м/с. Оценочная скорость молекул жидкости меньше этой величины. Термодинамическое равновесие пара этанола и окружающего воздуха свидетельствует о столь же низкой скорости поступательного движения молекул воздуха. Экспериментально доказано отсутствие термои бароэффектов в нормальной атмосфере. Выявлено отсутствие связи температуры вещества со скоростью его молекул.

Научный журнал

Creative Commons

Режимы движения жидкости….
Виды движения жидкостей Рисунок 2. Виды движения жидкости….
сечений вдоль потока и средних скоростей по длине потока….
Средняя скорость и площадь поперечного сечения потока при этом могут быть вдоль потока постоянными (пример…
Методы описания движения жидкости В физике существует два способа для описания движения жидкости: способ

Статья от экспертов

Проанализировано разделение частиц на слои в вертикальном потоке жидкости под действием неуравновешенности сил, действующих на частицу, находящуюся среди частиц иного размера и плотности. Рассмотрены два основных типа формул, определяющих распределение скоростей при турбулентном движении: степенной и логарифмический законы. При турбулентном движении жидкости по желобу средняя скорость потока определяется по закону Шези. Экспериментально рассмотрены характеристики водного потока на винтовом се…

Научный журнал

Creative Commons

Повышай знания с онлайн-тренажером от Автор24!

📝 Напиши термин
✍️ Выбери определение из предложенных или загрузи свое
🤝 Тренажер от Автор24 поможет тебе выучить термины, с помощью удобных и приятных карточек

Возможность создать свои термины в разработке

Еще чуть-чуть и ты сможешь писать определения на платформе Автор24. Укажи почту и мы пришлем уведомление с обновлением ☺️

12.1 Расход и его связь со скоростью – College Physics: OpenStax

Глава 12 Динамика жидкости и ее биологические и медицинские приложения

Сводка

Рассчитать скорость потока.
Определить единицы объема.
Опишите несжимаемые жидкости.
Объясните следствия уравнения неразрывности.

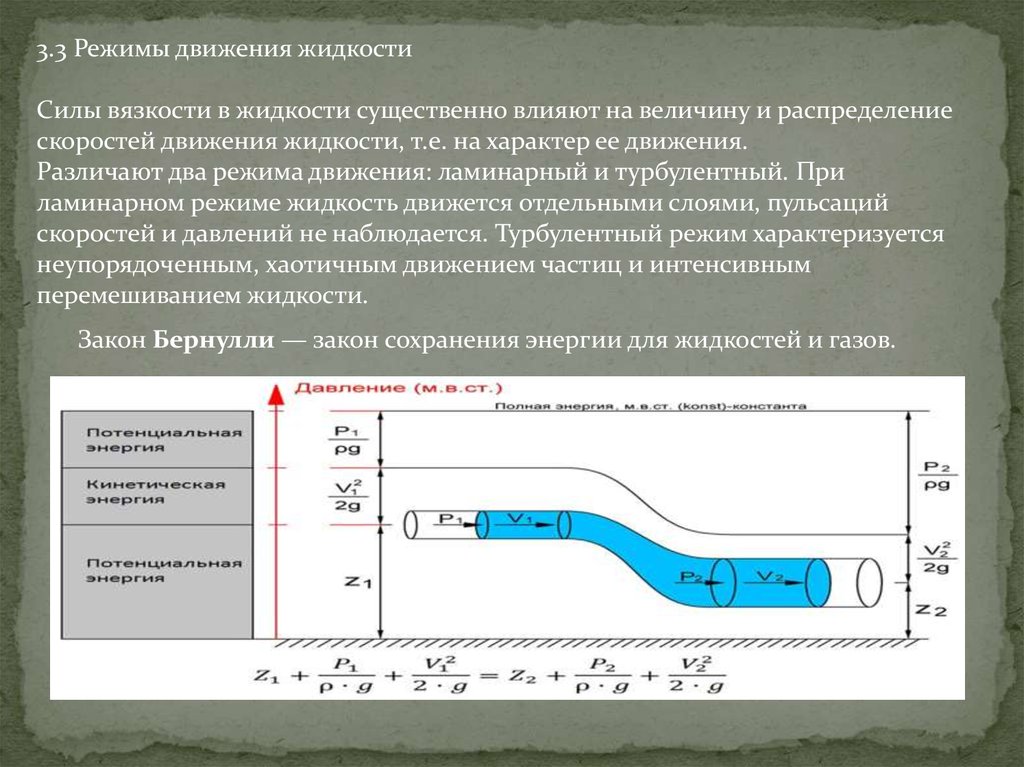
Скорость потока [латекс]\boldsymbol{Q}[/латекс] определяется как объем жидкости, проходящей через некоторое место через область в течение периода времени, как показано на рисунке 1. В символах это может быть пишется как 93}[/латекс]). В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации.

Рисунок 1. Расход – это объем жидкости в единицу времени, протекающий через точку через площадь A . Здесь заштрихованный цилиндр жидкости течет мимо точки P по однородной трубе за время t . Объем цилиндра равен Ad , а средняя скорость равна v̄=d/t , так что расход равен Q=Ad/t=Av̄ .

Пример 1.

Расчет объема по скорости кровотока: сердце перекачивает много крови за всю жизнь

Сколько кубических метров крови перекачивает сердце за 75 лет жизни, если предположить, что средняя скорость кровотока составляет 5,00 л/мин?

Стратегия

Время и скорость потока[latex]\boldsymbol{Q}[/latex] даны, поэтому объем[latex]\boldsymbol{V}[/latex]может быть рассчитан из определения потока оценивать.

Решение 93.} \end{array}[/latex]

Обсуждение

Это количество составляет около 200 000 тонн крови. Для сравнения, это значение примерно в 200 раз превышает объем воды, содержащейся в 50-метровом плавательном бассейне с 6 дорожками.

Расход и скорость являются связанными, но совершенно разными физическими величинами. Чтобы прояснить различие, подумайте о скорости течения реки. Чем больше скорость воды, тем больше расход реки. Но скорость течения также зависит от размера реки. Быстрый горный поток несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. Точное соотношение между скоростью потока[латекс]\жирныйсимвол{Q}[/латекс]и скоростью[латекс]\жирныйсимвол{\бар{в}}[/латекс] равно 9.0005

[латекс]\boldsymbol{Q=A\bar{v}},[/латекс]

, где[латекс]\жирныйсимвол{А}[/латекс]– площадь поперечного сечения, а[латекс]\жирныйсимвол{\бар{в}}[/латекс]– средняя скорость. Это уравнение кажется достаточно логичным. Соотношение говорит нам, что скорость потока прямо пропорциональна как величине средней скорости (далее называемой скоростью), так и размеру реки, трубы или другого водовода. Чем больше трубопровод, тем больше его площадь поперечного сечения. Рисунок 1 иллюстрирует, как получается это соотношение. Заштрихованный цилиндр имеет объем

[латекс]\boldsymbol{V=Ad},[/латекс]

, который проходит мимо точки[latex]\textbf{P}[/latex]за время[latex]\boldsymbol{t}.[/latex]Разделив обе части этого соотношения на[latex]\boldsymbol{t}[ /латекс] дает

[латекс]\boldsymbol{\frac{V}{t}}[/latex][латекс]\boldsymbol{=}[/latex][латекс]\boldsymbol{\frac{Ad}{t}}. [/ латекс]

Заметим, что [латекс]\boldsymbol{Q=V/t}[/latex]и средняя скорость равна[латекс]\boldsymbol{v\bar{v}=d/t}.[/latex] Таким образом, уравнение становится [латекс]\boldsymbol{Q=A\bar{v}}.[/латекс]

На рис. 2 показано течение несжимаемой жидкости по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, через любую точку трубки за заданное время должно пройти одинаковое количество жидкости, чтобы обеспечить непрерывность потока. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, по пунктам 1 и 2

[латекс]\begin{array}{c} \boldsymbol{Q_1=Q_2} \\ \boldsymbol{A_1\bar{v}_1=A_2\bar{v}_2.} \end{array}[/latex] [латекс]\rbrace[/латекс]

Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости. Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью — в этом назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется и, возможно, снова набирает скорость, когда выходит из другого конца водоема. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда площадь поперечного сечения увеличивается.

Рисунок 2. Когда трубка сужается, тот же объем занимает большую длину. Чтобы один и тот же объем прошел точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс точно обратим. Если жидкость течет в противоположном направлении, ее скорость будет уменьшаться при расширении трубы. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости нарисованы не в масштабе.)
Поскольку жидкости практически несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.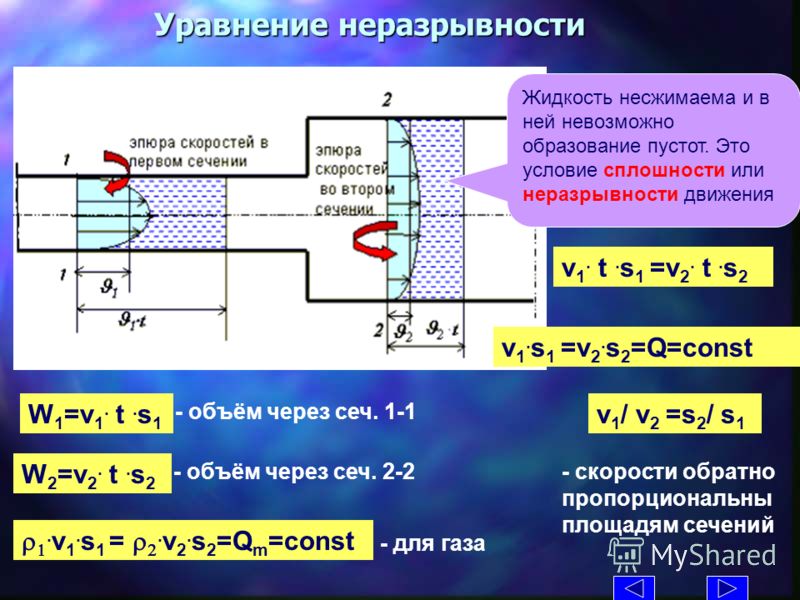
Пример 2. Расчет скорости жидкости: скорость увеличивается при сужении трубы
Насадка с радиусом 0,250 см присоединена к садовому шлангу с радиусом 0,900 см. Скорость потока через шланг и сопло составляет 0,500 л/с. Рассчитайте скорость воды (а) в шланге и (б) в насадке.
Стратегия
Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. Мы будем использовать нижний индекс 1 для шланга и 2 для сопла. 92}}[/latex][latex]\boldsymbol{=\:1.96\textbf{ м/с}}.[/latex]
Решение для (b)
Мы могли бы повторить это вычисление, чтобы найти скорость в сопле [латекс]\boldsymbol{\bar{v}_2},[/латекс], но мы будем использовать уравнение непрерывности, чтобы дать несколько иное представление. Используя уравнение, которое утверждает
[латекс]\boldsymbol{A_1\bar{v}_1=A_2\bar{v}_2},[/latex]
решение для[латекс]\boldsymbol{\bar{v}_2 }[/latex] и подставив [латекс]\boldsymbol{\pi{r}^2}[/latex]вместо площади поперечного сечения, получим 92}}[/latex][latex]\boldsymbol{1,96\textbf{ м/с}=25,5\textbf{ м/с}}.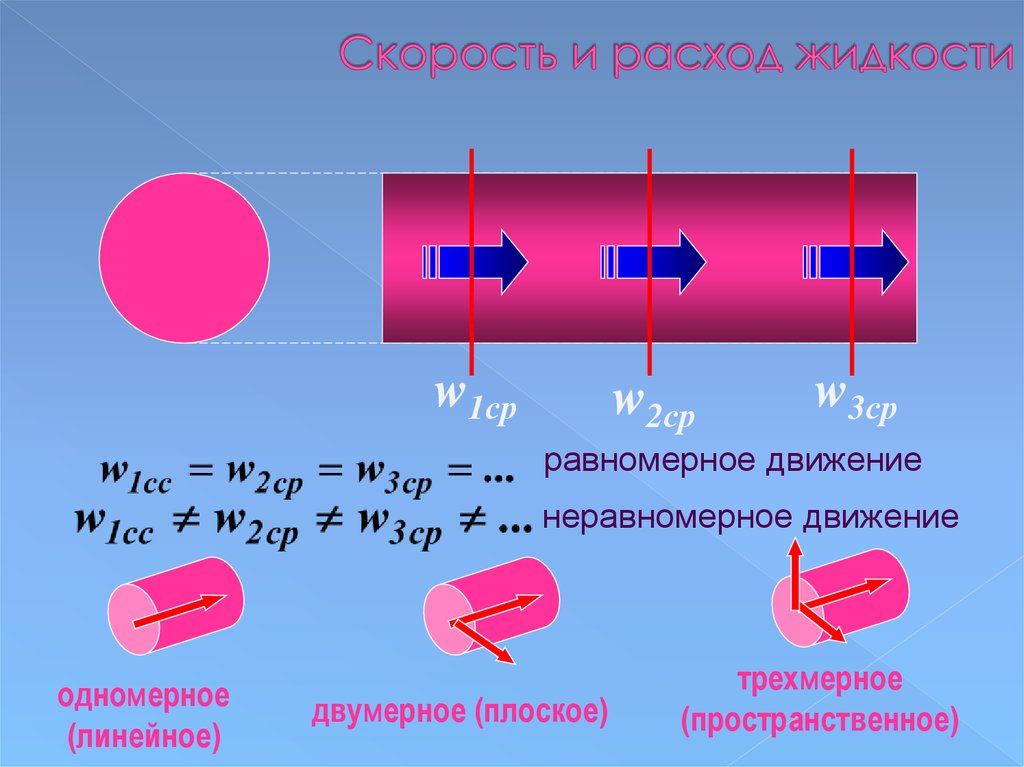 [/latex]
Обсуждение
Скорость 1,96 м/с примерно подходит для воды, вытекающей из шланга без насадок. Форсунка создает значительно более быстрый поток, просто сужая поток в более узкую трубку.
Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что приводит к большим эффектам при изменении радиуса. Мы можем задуть свечу на довольно большом расстоянии, например, сжав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.
Во многих ситуациях, в том числе в сердечно-сосудистой системе, происходит разветвление потока. Кровь перекачивается из сердца в артерии, которые подразделяются на более мелкие артерии (артериолы), которые разветвляются на очень тонкие сосуды, называемые капиллярами. В этой ситуации сохраняется непрерывность потока, но сохраняется сумма расходов расходов в каждой из ветвей на любом участке вдоль трубы. Уравнение неразрывности в более общем виде принимает вид
[латекс]\boldsymbol{n_1A_1\бар{v}_1=n_2A_2\бар{v}_2},[/латекс]
где[latex]\boldsymbol{n_1}[/latex]и[latex]\boldsymbol{n_2}[/latex]количество ответвлений на каждом из участков вдоль трубы.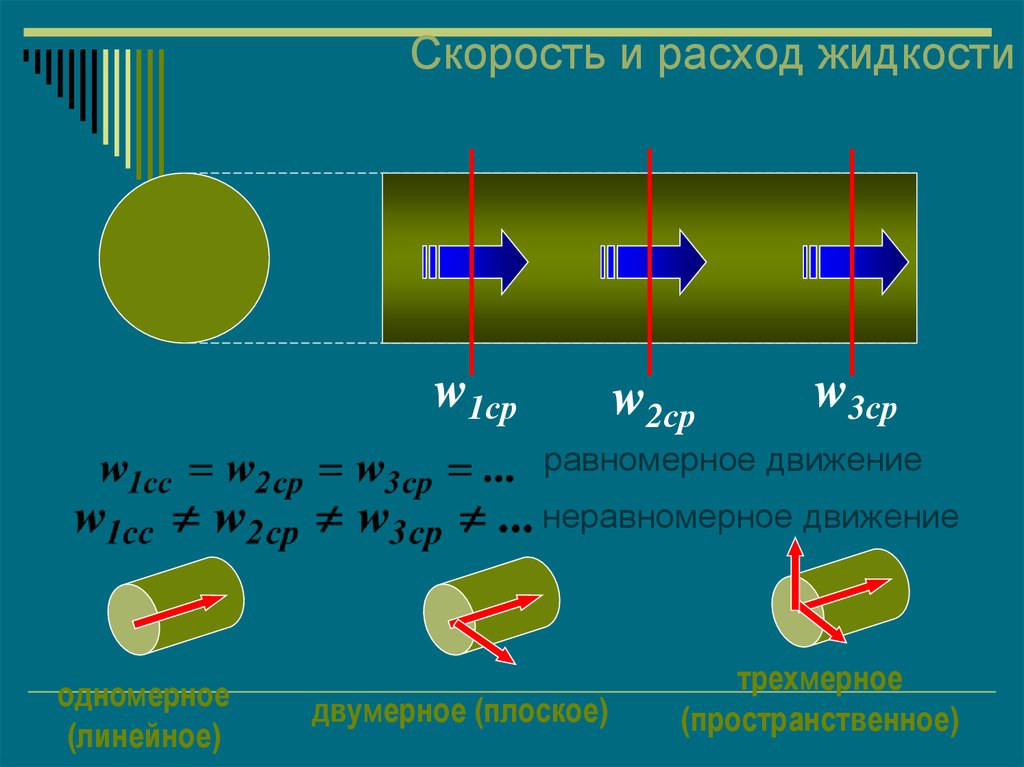
Пример 3: расчет скорости кровотока и диаметра сосуда: разветвления в сердечно-сосудистой системе
Аорта является основным кровеносным сосудом, по которому кровь покидает сердце, чтобы циркулировать по всему телу. а) Рассчитайте среднюю скорость движения крови в аорте при скорости потока 5,0 л/мин. Аорта имеет радиус 10 мм. (б) Кровь также течет через более мелкие кровеносные сосуды, известные как капилляры. При скорости кровотока в аорте 5,0 л/мин скорость крови в капиллярах составляет около 0,33 мм/с. Учитывая, что средний диаметр капилляра составляет[latex]\boldsymbol{8.0\:\mu},[/latex]рассчитайте количество капилляров в системе кровообращения. 92}}[/latex][latex]\boldsymbol{=\:0.27\textbf{ м/с.}}[/latex]
Решение для (b)
Использование[latex]\boldsymbol{n_1A_1\ bar{v}_1=n_2A_2\bar{v}_1},[/latex]присваивая индекс 1 аорте и 2 капиллярам и находя[latex]\boldsymbol{n_2}[/latex](число капилляров) дает[latex]\boldsymbol{n_2=\frac{n_1A_1\bar{v}_1}{A_2\bar{v}_2}}.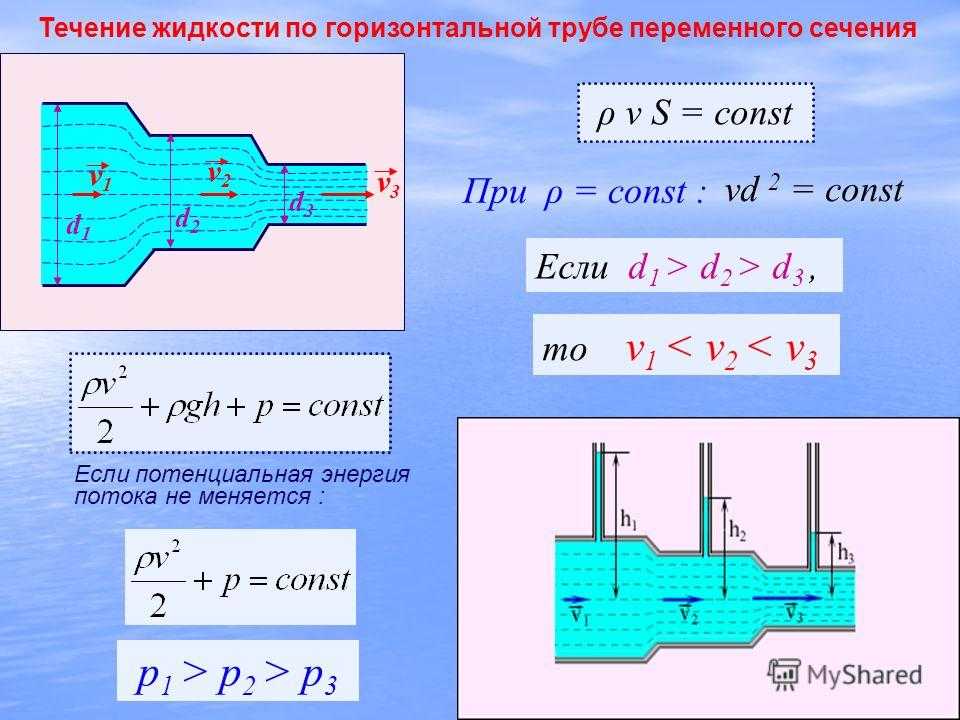 93}.[/латекс]
Расход и скорость связаны соотношением[latex]\boldsymbol{Q=A\bar{v}}[/latex],где[latex]\boldsymbol{A}[/latex]является площадью поперечного сечения потока и [латекс]\boldsymbol{\bar{v}}[/латекс] — его средняя скорость.
Для несжимаемых жидкостей скорость потока в различных точках постоянна. То есть,
[латекс]\begin{array}{c} \boldsymbol{Q_1=Q_2} \\ \boldsymbol{A_1\bar{v}_1=A_2\bar{v}_2} \\ \boldsymbol{n_1A_1\bar{v }_1=n_2A_2\bar{v}_2.} \end{массив}[/latex][latex]\rbrace[/latex]
расход
, сокращенно Q , это объем V , протекающий через определенную точку за время t , или Q = V/t
литр
единица объема, равная 10 ⁻³ м ³

12.1: Расход и его связь со скоростью
Последнее обновление
Сохранить как PDF
Идентификатор страницы
1571
OpenStax
OpenStax
Цели обучения
К концу этого раздела вы сможете:
Рассчитать скорость потока.
Определить единицы объема. 93 \, см\)). В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации.
Рисунок \(\PageIndex{1}\): Расход – это объем жидкости в единицу времени, протекающий через точку через площадь \(A\). re заштрихованный цилиндр жидкости течет мимо точки \(P\) по однородной трубе за время \(t\). Объем цилиндра равен \(Ad\), а средняя скорость равна \(\overline{v} = d/t\), так что скорость потока равна \(Q = Ad/t = A\overline{v}\ ).
Пример \(\PageIndex{1}\): расчет объема по скорости кровотока: сердце перекачивает много крови за всю жизнь
Сколько кубических метров крови перекачивает сердце за 75 лет жизни, если предположить, что средняя скорость кровотока составляет 5,00 л/мин?
Стратегия
Время и расход \(Q\) заданы, поэтому объем \(V\) можно рассчитать из определения расхода.
Решение
Решение \(Q = V/t\) для объема дает
\[V = Qt. 3 \end{align*}\]
Обсуждение
Это количество составляет около 200 000 тонн крови. Для сравнения, это значение примерно в 200 раз превышает объем воды, содержащейся в 50-метровом плавательном бассейне с 6 дорожками.
Расход и скорость являются связанными, но совершенно разными физическими величинами. Чтобы прояснить различие, подумайте о скорости течения реки. Чем больше скорость воды, тем больше расход реки. Но скорость течения также зависит от размера реки. Быстрый горный поток несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. Точное соотношение между расходом \(Q\) и скоростью \(\overline{v}\) составляет
\[Q = A \overline{v},\]
, где \(A\) — площадь поперечного сечения, а \( \overline{v}\) — средняя скорость. Это уравнение кажется достаточно логичным. Соотношение говорит нам, что скорость потока прямо пропорциональна как величине средней скорости (далее называемой скоростью), так и размеру реки, трубы или другого водовода. Чем больше трубопровод, тем больше его площадь поперечного сечения. На рисунке \(\PageIndex{1}\) показано, как получается это отношение. Заштрихованный цилиндр имеет объем
\[V = Ad,\]
, который проходит через точку \(P\) за время \(t\). Разделив обе части этого соотношения на \(t\), мы получим
.
\[\dfrac{V}{t} = \dfrac{Ad}{t}.\]
Заметим, что \(Q = V\t\), а средняя скорость равна \(\overline{v} = d/t\). Таким образом, уравнение принимает вид \(Q = A\overline{v}\).
На рисунке \(\PageIndex{2}\) показана несжимаемая жидкость, текущая по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, через любую точку трубки за заданное время должно пройти одинаковое количество жидкости, чтобы обеспечить непрерывность потока. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться. Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, для пунктов 1 и 2,
\[Q_1 = Q_2\]
\[A_1\overline{v}_1 = A_2\overline{v}_2\]
Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости. Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью — в этом назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется и, возможно, снова набирает скорость, когда выходит из другого конца водоема. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда площадь поперечного сечения увеличивается.
Рисунок \(\PageIndex{2}\): Когда трубка сужается, тот же объем занимает большую длину. Чтобы один и тот же объем прошел точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс точно обратим. Если жидкость течет в противоположном направлении, ее скорость будет уменьшаться при расширении трубы. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости нарисованы не в масштабе.)
Поскольку жидкости практически несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.
Пример \(\PageIndex{2}\): Расчет скорости жидкости: скорость увеличивается при сужении трубы
Насадка с радиусом 0,250 см прикреплена к садовому шлангу с радиусом 0,900 см. Скорость потока через шланг и сопло составляет 0,500 л/с. Рассчитайте скорость воды (а) в шланге и (б) в насадке.
Стратегия
Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. Мы будем использовать нижний индекс 1 для шланга и 2 для сопла. 92} 1,96 \, м/с = 25,5 \, м/с. \номер\]
Обсуждение
Скорость 1,96 м/с соответствует скорости воды, вытекающей из шланга без насадки. Форсунка создает значительно более быстрый поток, просто сужая поток в более узкую трубку.
Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что приводит к большим эффектам при изменении радиуса. Мы можем задуть свечу на довольно большом расстоянии, например, сжав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.
Во многих ситуациях, в том числе в сердечно-сосудистой системе, происходит разветвление потока. Кровь перекачивается из сердца в артерии, которые подразделяются на более мелкие артерии (артериолы), которые разветвляются на очень тонкие сосуды, называемые капиллярами. В этой ситуации непрерывность потока сохраняется, но сохраняется сумма расходов в каждой из ветвей на любом участке вдоль трубы. Уравнение неразрывности в более общем виде принимает вид
\[n_1A_1\overline{v}_1 = n_2A_2\overline{v}_2,\]
, где \(n_1\) и \(n_2\) — количество ответвлений на каждом из участков вдоль трубы.
Пример \(\PageIndex{3}\): расчет скорости кровотока и диаметра сосуда: разветвления в сердечно-сосудистой системе
Аорта является основным кровеносным сосудом, по которому кровь покидает сердце, чтобы циркулировать по всему телу. а) Рассчитайте среднюю скорость движения крови в аорте при скорости потока 5,0 л/мин. Аорта имеет радиус 10 мм. (б) Кровь также течет через более мелкие кровеносные сосуды, известные как капилляры. При скорости кровотока в аорте 5,0 л/мин скорость крови в капиллярах составляет около 0,33 мм/с. Учитывая, что средний диаметр капилляра равен \(8,0 \, \мкм\), рассчитайте количество капилляров в системе кровообращения. 92} \\[5pt] &= 0,27 \, м/с. \end{align*}\]
Решение для (b)
Использование \(n_1A_1\overline{v}_1 = n_2A_2\overline{v}_1\), присвоение индекса 1 аорте и 2 индексу капилляры, и решение для \(n_2\) (количество капилляров) дает \(n_2 = \frac{n_1A_1\overline{v}_1}{A-2\overline{v}_2}.\) Преобразование всех величин в единицах метров и секунд и подстановка в приведенное выше уравнение дает
\[\begin{align*} n_2 &= \dfrac{(1)(\pi)(10 \times 10^{-3} m)^2 (0,27 \, м/с)}{(\pi)(4,0 \times 10^{-6} м)(0,33 \times 10^{-3} м/с)} \\[5pt] &= 5,0 \ раз 10^9\, капилляры. 93\)
Расход и скорость связаны соотношением \(Q = A\overline{v}\), где \(A\) — площадь поперечного сечения потока, а \(v\) — его средняя скорость.
Для несжимаемых жидкостей скорость потока в различных точках постоянна. То есть
\[Q_1 = Q_2\]
\[A_1\overline{v}_1 = A_2\overline{v}_2\]
\[n_1A_1\overline{v}_1 = n_2A_2\overline{v}_2\ ]
Глоссарий
расход
сокращенно Q , это объем V , протекающий через определенную точку за время t , или Q = V/t
литр
единица объема, равная 10 ⁻³ м ³
Эта страница под названием 12.1: Скорость потока и ее связь со скоростью распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или страница
Автор
ОпенСтакс
Лицензия
СС BY
Версия лицензии
4,0
Программа ООР или издатель
ОпенСтакс
Показать оглавление
нет
Метки
поток
расход
литр
источник@https://openstax.