Скорость жидкости: Ваш браузер не поддерживается

Содержание

Об измерении скорости потока жидкостей и газов / Хабр

В нынешнем году мы начали представлять в России компанию IST — швейцарского производителя тонкопленочных датчиков температуры, относительной влажности, проводимости жидкости и скорости потока.

Продукция IST — это не масс-маркет, они не выпускают ~~аналоги DHT22~~ миллионные тиражи дешевых микросхем для стандартных применений. Вместо этого упор делается на специальные задачи: нестандартные конструктивы и диапазоны температур, повышенная точность, минимальное время отклика и так далее.

Среди многообразной продукции IST есть такая интересная штука как flow sensors — датчики скорости потока сплошных сред. Под катом рассказываю как они работают, как выглядят и зачем нужны. Думаю что это будет интересно не только разработчикам расходомеров.

Итак, для измерения расхода жидкостей или газов используются различные физические эффекты. Для измерения скорости потока используют механические, оптические, электромагнитные, ультразвуковые и другие чувствительные элементы, позволяющие по косвенным характеристикам определить расход сплошной среды, проходящей по трубе.

Здесь заметим, что под расходом может подразумеваться как объем потока (литры в минуту или кубические метры в минуту), так и масса потока (килограмм в минуту) или его скорость (метры в секунду). Допуская, что в большинстве приложений известны и характеристики среды, и характеристики трубы, в которой движется поток, мы будем считать все перечисленные понятия тождественными.

Поскольку бОльшую часть продукции IST составляют платиновые датчики температуры (термосопротивления), для определения скорости потока также используются тепловые эффекты.

В тепловых расходомерах измерения производятся либо по охлаждению нагретого тела, помещенного в поток (термоанемометры), либо по переносу тепловой энергии между двумя расположенными вдоль потока точками (калориметрические расходомеры). Посмотрим как используются оба принципа в реальных приложениях.

Термоанемометрические датчики

Расходомеры с термоанемометрическими преобразователями IST применяются преимущественно для потоков газов. В простейшем случае они состоят из нагревательного элемента и датчика температуры. Фактически это два термосопротивления, на базе которых реализуется следующий алгоритм:
При отсутствии потока температура микронагревателя остается неизменной, а при наличии потока нагреватель начинает отдавать тепло внешней среде. Количество тепла, которое отдается потоку, зависит от нескольких факторов: от начальной разности температур нагревателя и среды, от параметров трубы и собственно от скорости потока.

Поскольку разность температур определяется схемой включения датчика расхода, а параметры трубы мы считаем неизменными, теплоотдача нагревательного элемента может использоваться для измерения скорости потока.

Нагреватель и датчик температуры включаются в мостовую схему, которая уравновешена в отсутствии потока и разбалансирована при изменении сопротивления нагревателя. При увеличении скорости потока нагреватель охлаждается, мост разбалансируется и сигнал разбаланса поступает на усилитель. Выходной сигнал усилителя сообщает нагревателю более высокую температуру и приводит мост обратно в равновесное состояние. Этот же сигнал используется как выходной, т.е. как функция скорости потока.

При известных параметрах трубы, положения датчика, типа потока, а также неизменных теплофизических характеристиках газа (состав, давление, температура) такая функция может быть вычислена по одной из общеизвестных методик.

На рисунке приведен пример схемы включения датчика расхода и график зависимости напряжения Uflow от скорости потока.

По такому принципу работают датчики серии FS7. На керамической подложке из диоксида циркония наносятся токопроводящие дорожки – платиновые микронагреватель и датчик температуры, между которыми предусмотрены соединения. Вся конструкция покрыта тонким изолирующим слоем из стекла.

Чувствительные элементы такой конструкции позволяют измерять скорость потока в диапазоне от 0 до 100 м/c с чувствительностью 0.01 м/c и погрешностью менее 3 % от измеряемой величины.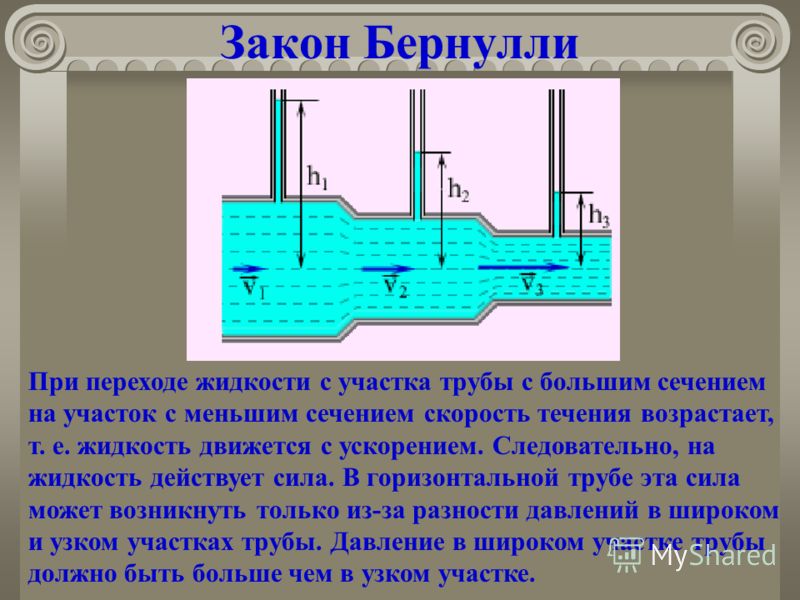 Впрочем, точность измерений определяется не только чувствительным элементом, но и схемой его включения, и способом калибровки конечного устройства.

Диапазон рабочих температур датчика FS7 составляет -20… 150 °C для стандартного исполнения, однако IST практикует изготовление датчиков с допустимой температурой вплоть до +400 °C.
На рисунке показаны два исполнения датчиков FS7 — в корпусе и без него.

Об водосодержащих и агрессивных средах

Важно заметить, что датчики FS7, а также рассмотренный ниже FS2, используются в основном для газов, а также для жидких сред, не содержащих воду — при длительной работе в воде верхний изолирующий слой датчика постепенно разрушается и возникает электролиз.
Для потока воды и других подобных сред предусмотрен модуль Out Of Liquid — анемометрический датчик, элементы которого изолированы от потока. Out Of Liquid — это небольшая трубка из нержавеющей стали, на внешней стенке которой размещены микронагреватель и датчик температуры.

Трубка имеет длину 40 мм и диаметр 4 мм, рабочий температурный диапазон этого решения — от -50 °C до +180 °C.

Об определении направления потока

Термоанемометрические расходомеры имеют некоторые очевидные ограничения. В частности, они не позволяют определить направление потока и не подходят для приложений, требующих высокой чувствительности датчика.

Калориметрические расходомеры, напротив, предназначены для относительно медленных потоков газа с переменным направлением. Калориметрический датчик состоит из трех элементов – микронагревателя и двух датчиков, измеряющих температуру до и после него. В отсутствии потока тепловое пятно, излучаемое нагревателем, неподвижно, поэтому справа и слева от нагревателя сплошная среда имеет одну и ту же температуру. При возникновении потока тепловое пятно «сдвигается» согласно направлению и скорости потока. Таким образом, при известных параметрах трубы и характеристиках среды скорость потока может быть измерена по разности показаний датчиков температуры.

При производстве колориметрического датчика на керамическую подложку также наносятся платиновые дорожки и соединения между ними — микронагреватель и два датчика температуры.

Поскольку при наличии потока нагревательный элемент охлаждается, а для измерений этот процесс уже не используется, на датчике расхода предусматривается дополнительный компенсационный датчик температуры.

По такому принципу построены датчики серии FS2. С их помощью можно определять как направление, так и скорость потока. В диапазоне от 0 до 2.5 м/c датчик имеет чувствительность 0.001 м/c.

Диапазон измерений калориметрических датчиков ограничивается самим принципом его работы – при определенной скорости потока тепловое пятно «сдвигается» слишком далеко и разность показателей правого и левого датчиков уже не позволяет судить о скорости потока.

Это досадное свойство калориметрических датчиков довольно просто обходится. Когда поток достигает определенной скорости, можно «переключиться» на работу в термоанемометрическом режиме — начать использовать пару нагреватель + компенсирующий датчик температуры по уже известному нам термоанемометрическому принципу.

При использовании комбинации двух способов измерения модуль величины скорости потока на большей части диапазона определяется квадратичной функцией от напряжения Uflow (нижний график), а направление потока – по напряжению с полномостовой схемы, состоящей из пары датчиков и микронагревателя.

О работе с «микропотоками»

Если задача вообще не предполагает работы с потоками со скоростью более 1.5 м/c и речь идет о газообразной среде, то можно использовать датчики серии MFS02 (Micro Flow Sense). MFS02 имеет максимальную чувствительность (0,0003 м/с) и скорость срабатывания (время отклика менее 10 мс).

Структурно датчик MFS02 похож на FS2 и состоит из микронагревателя, пары датчиков температуры и дополнительного компенсирующего датчика. Однако MFS02 изготавливаются по другому технологическому процессу: в стеклокерамической подложке датчика выделяется зона, представляющая собой мембрану. Предполагается, что в поток погружается только мембрана, поэтому именно на ней располагаются компоненты для калориметрических измерений, а компенсирующий датчик температуры установлен вне мембраны.

Датчик MFS02 имеет размер всего 3.5 x 5.1 мм, а к контактным площадкам довольно сложно подпаяться, поэтому MFS02 также доступен в составе плат-расширений, предоставляющих доступ к выводам элемента.

Заключение

В заключении поблагодарю читателя за внимание и напомню, что вопросы о применении продукции, о которой мы пишем на хабре, можно также задавать на email, указанный в моем профиле.

upd: все упомянутые датчики и модули доступны со склада. Больше информации на efo-sensor.ru

ЧАРУЮЩИЕ ТАЙНЫ ЖИДКОСТИ | Наука и жизнь

Существует поразительная возможность овладеть предметом математически, не понимая существа дела.

А. Эйнштейн

Эксперимент остается навсегда.
П. Л. Капица

Наука и жизнь // Иллюстрации

‹

›

Открыть в полном размере

Тысячи лет люди наблюдают вечно изменчивое течение воды и пытаются разгадать ее тайну. Первоклассные физики и математики ломали и продолжают ломать головы, стараясь понять природу и прихотливое поведение потока воды. Но вступив в XXI век, мы с сожалением должны констатировать, что с конца XIX столетия — времени наивысшего расцвета науки о движении сплошных сред (гидродинамики в случае жидкости и аэродинамики в случае газа) — мы очень мало продвинулись в понимании природы этого вечно меняющегося течения. Все основные законы течения жидкости (для краткости везде будет говориться о жидкости, хотя, за некоторым исключением, те же закономерности присущи и газу) были открыты до первой половины XIX столетия. Перечислим их.

ПОСТОЯНСТВО ПОТОКА МАССЫ ЖИДКОСТИ

Его еще называют законом неразрывности, законом непрерывности, уравнением сплошности жидкости или законом сохранения вещества в гидродинамике. По существу, этот закон был открыт Б. Кастелли в 1628 году. Он установил, что скорость течения жидкости в трубах обратно пропорциональна площади их поперечного сечения. Другими словами, чем уже сечение канала, тем с большей скоростью движется в нем жидкость.

ВЯЗКОСТЬ ЖИДКОСТИ

И. Ньютон (конец XVII века) экспериментально установил, что любой жидкости свойственна вязкость, то есть внутреннее трение. Вязкость приводит к возникновению сил трения между движущимися с различными скоростями слоями жидкости, а также между жидкостью и омываемым ею телом. Им же было установлено, что сила трения пропорциональна коэффициенту вязкости жидкости и градиенту (перепаду) скорости потока в направлении, перпендикулярном его движению. Жидкости, подчиняющиеся этому закону, называют ньютоновскими в отличие от неньютоновских жидкостей, у которых зависимость между силой вязкого трения и скоростью жидкости имеет более сложный характер.

В силу вязкого трения скорость жидкости на поверхности омываемого ею тела всегда равна нулю. Это совсем не очевидно, но тем не менее подтверждается во множестве экспериментов.

Опыт.

Убедимся, что скорость газа на поверхности обдуваемого им тела равна нулю.

Возьмем вентилятор и припудрим его лопасти пылью. Включим вентилятор в сеть и через несколько минут выключим. Пыль на лопастях как была, так и осталась, хотя вентилятор вращался с довольно большой скоростью и она должна была бы слететь.

Омывая лопасти вентилятора с большой скоростью, поток воздуха на их поверхности имеет нулевую скорость, то есть неподвижен. Поэтому пыль на них и остается. По этой же причине с гладкой поверхности стола легко можно сдуть крошки, а пыль приходится вытирать.

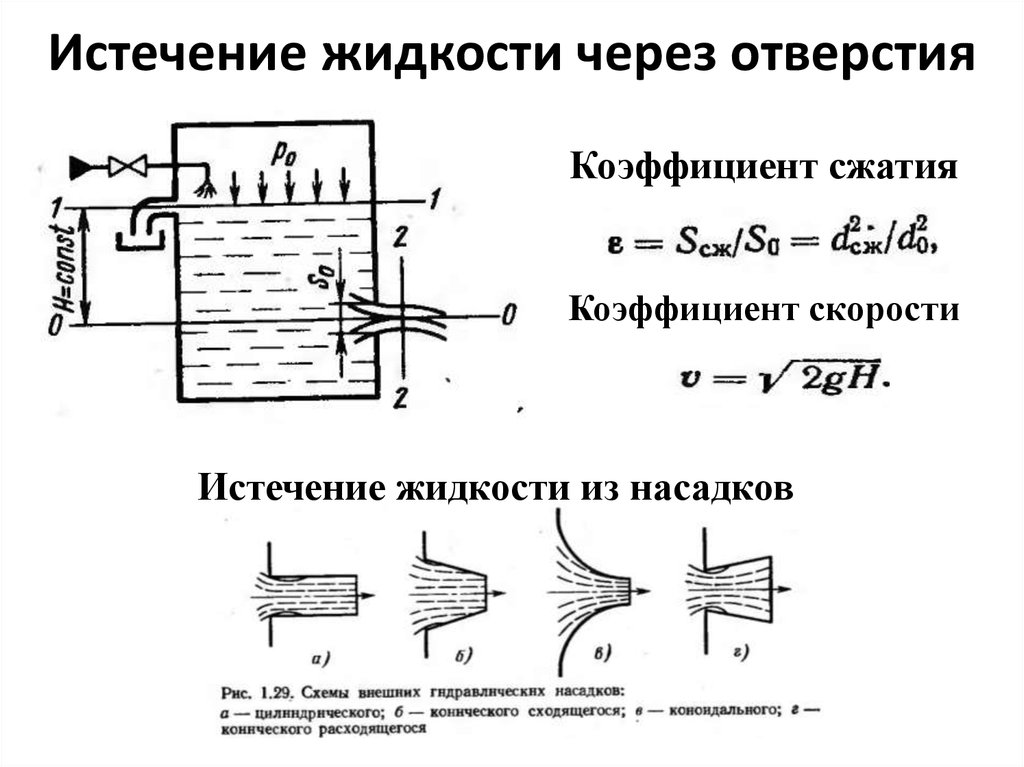
#1# ИЗМЕНЕНИЕ ДАВЛЕНИЯ ЖИДКОСТИ В ЗАВИСИМОСТИ ОТ СКОРОСТИ ЕЕ ДВИЖЕНИЯ.

Д. Бернулли в своей книге «Гидродинамика» (1738) получил для идеальной жидкости, не обладающей вязкостью, математическую формулировку закона сохранения энергии в жидкости, который носит теперь название уравнения Бернулли. Оно связывает давление в потоке жидкости с ее скоростью и утверждает, что давление жидкости при ее движении меньше там, где сечение потока

S меньше, а скорость жидкости соответственно больше.

Вдоль трубки тока, которую можно мысленно выделить в спокойном безвихревом потоке, сумма статического давления , динамического ρV²/2, вызванного движением жидкости плотностью ρ, и давления ρgh столба жидкости высотой h остается постоянной:

#13#

Это уравнение играет фундаментальную роль в гидродинамике, несмотря на то, что оно, строго говоря, справедливо только для идеальной, то есть не имеющей вязкости, жидкости.

#2#

Опыт 1. Убедимся, что чем выше скорость воздуха, тем меньше давление в нем.

Зажжем свечу и через тонкую трубочку, например для коктейля, сильно дунем в нее так, чтобы струйка воздуха прошла примерно на расстоянии 2 см от пламени. Пламя свечи отклонится по направлению к трубочке, хотя на первый взгляд кажется, что воздух должен если и не задуть его, то по крайней мере отклонить в противоположную сторону.

#3# Лабораторный водоструйный насос. В струе воды из крана создается разрежение, которое выкачивает воздух из колбы.

Почему? Согласно уравнению Бернулли, чем выше скорость потока, тем меньше давление в нем. Воздух выходит из трубочки с большой скоростью, так что давление в струе воздуха меньше, чем в окружающем свечу неподвижном воздухе. Перепад давления при этом направлен в сторону выходящего из трубочки воздуха, что и отклоняет к ней пламя свечи.

#4# Принцип работы пульверизатора: атмосферное давление выжимает жидкость в струю воздуха, где давление ниже.

На этом принципе работают пульверизаторы, струйные насосы и автомобильные карбюраторы: жидкость втягивается в поток воздуха, давление в котором ниже атмосферного.

Опыт 2. Возьмем лист писчей бумаги за верхние края, поднесем его к стене и удержим на расстоянии примерно 3-5 см от стены. Подуем в промежуток между стеной и листом. Вместо того, чтобы отклониться от стенки, лист прижимается к ней за счет силы, которую может создавать только возникший перепад давления, направленный к стене. Значит, давление в струе воздуха между листом и стеной меньше, чем в неподвижном воздухе снаружи. Чем сильнее дуть в промежуток, тем плотнее будет прижиматься листок к стене.

#5#

Уравнение Бернулли объясняет также классический опыт с трубой переменного сечения. В силу закона неразрывности для сохранения потока массы жидкости в суженной части трубы ее скорость должна быть выше, чем в широкой. Следовательно, давление выше там, где труба шире, и ниже там, где она уже. На этом принципе работает устройство для измерения скорости или расхода жидкости — трубка Вентури.

Падение внутреннего давления в потоке — хорошо проверенный экспериментальный факт, тем не менее он, вообще говоря, парадоксален. Действительно, интуитивно ясно, что жидкость, «протискиваясь» из широкой части трубы в узкую, «сжимается», а это должно привести к росту давления в ней. Такому поведению жидкости в настоящее время нет объяснения даже на молекулярном уровне, по крайней мере, автор его нигде не обнаружил.

#6# СОПРОТИВЛЕНИЕ, ИСПЫТЫВАЕМОЕ ТЕЛОМ ПРИ ДВИЖЕНИИ В ЖИДКОСТИ

Существование сопротивления среды было обнаружено еще Леонардо да Винчи в XV столетии. Мысль, что сопротивление жидкости движению тела пропорционально скорости тела, впервые высказал английский ученый Дж. Уиллис. Ньютон во втором издании своей знаменитой книги «Математические начала натуральной философии» установил, что сопротивление состоит из двух членов, одного — пропорционального квадрату скорости и другого — пропорционального скорости. Там же Ньютон сформулировал теорему о пропорциональности сопротивления максимальной площади сечения тела, перпендикулярного направлению потока. Силу сопротивления тела, медленно движущегося в вязкой жидкости, рассчитал в 1851 году Дж. Стокс. Она оказалась пропорциональной коэффициенту вязкости жидкости, первой степени скорости тела и его линейным размерам.

Необходимо отметить, что сопротивление жидкости движущемуся в нем телу в значительной мере обусловливается именно наличием вязкости. В идеальной жидкости, в которой вязкость отсутствует, сопротивление вообще не возникает.

Опыт 1. Посмотрим, как возникает сопротивление движущегося в жидкости тела. Хотя в опыте тело неподвижно, а движется воздух, результата это не меняет. Какая разница, что движется — тело в воздухе или воздух относительно неподвижного тела?

#7#

Возьмем свечу и коробок спичек. Зажжем свечу, поставим перед ней на расстоянии примерно 3 см коробок и сильно дунем на него. Пламя свечи отклоняется к коробку. Это означает, что позади коробка давление стало меньше, чем позади свечи, и разность давлений направлена по движению потока воздуха. Следовательно, тело при движении в воздухе или жидкости испытывает торможение.

Поток воздуха набегает на переднюю поверхность коробка, огибает его по краям и не смыкается позади, а отрывается от препятствия. Поскольку давление воздуха меньше там, где его скорость выше, давление по краям коробка меньше, чем позади него, где воздух неподвижен.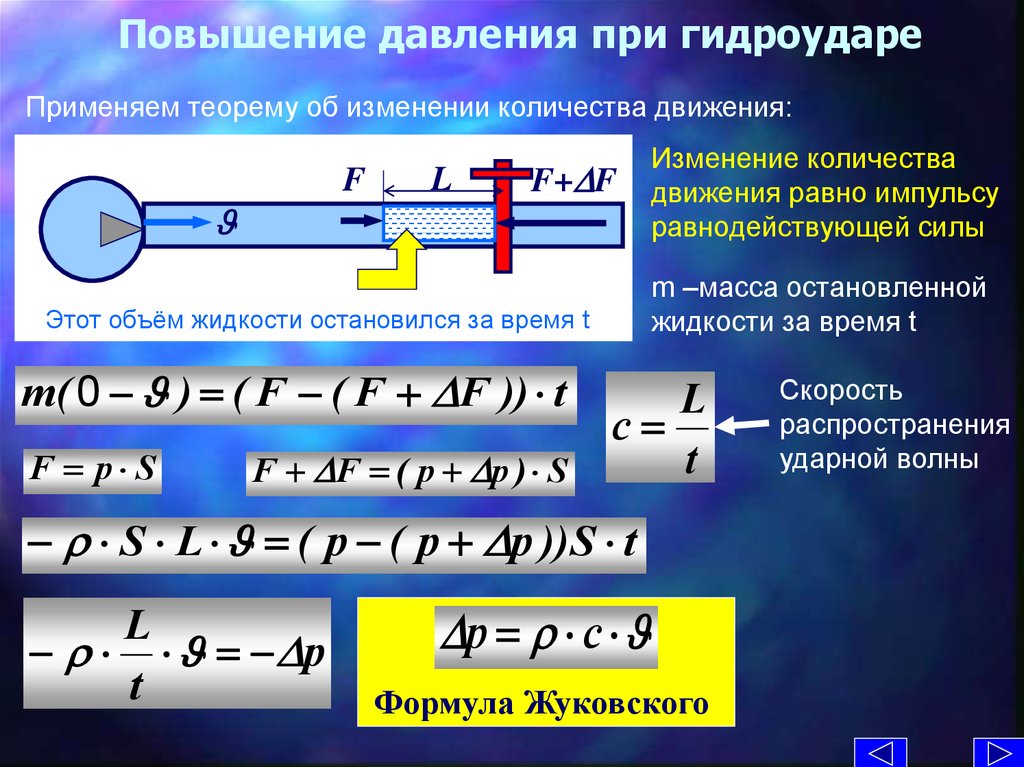 Позади коробка возникает разность давлений, направленная от центра к его краям. В результате воздух за коробком устремляется к его краям, образуя завихрения, что и приводит к уменьшению давления.

Сопротивление зависит от скорости движения тела в жидкости, свойств жидкости, формы тела и его размеров. Важную роль в создании сопротивления играет форма задней стороны движущегося тела. Позади плоского тела возникает пониженное давление, поэтому сопротивление можно уменьшить, предотвратив срыв потока. Для этого телу придают обтекаемую форму. Поток плавно огибает тело и смыкается непосредственно за ним, не создавая области пониженного давления.

Опыт 2. Чтобы продемонстрировать различный характер обтекания, а следовательно, и сопротивле ния тел различной формы, возьмем шар, например мяч для пинг-понга или тенниса, приклеим к нему бумажный конус и поставим за ним горящую свечу.

#8#

Повернем тело шариком к себе и подуем на него. Пламя отклонится от тела. Теперь повернем тело к себе острым концом и снова подуем. Пламя отклоняется к телу. Этот опыт показывает, что форма задней поверхности тела определяет направление перепада давления позади нее, а следовательно , и сопротивление тела в потоке воздуха.

В первом опыте пламя отклоняется от тела; это означает, что перепад давления направлен по потоку. Струя воздуха плавно обтекает тело, смыкается за ним и далее движется обычной струей, которая отклоняет пламя свечи назад и может даже задуть его. Во втором опыте пламя отклоняется к телу — как и в эксперименте с коробком, позади тела создается разрежение, перепад давления направлен против потока. Следовательно, в первом опыте сопротивление тела меньше, чем во втором.

ПАДЕНИЕ ДАВЛЕНИЯ В ВЯЗКОЙ ЖИДКОСТИ ПРИ ЕЕ ДВИЖЕНИИ В ТРУБЕ ПОСТОЯННОГО СЕЧЕНИЯ

Опыт показывает, что давление в жидкости, текущей по трубе постоянного сечения, падает вдоль трубы по течению: чем дальше от начала трубы, тем оно ниже. Чем уже труба, тем сильнее падает давление. Это объясняется наличием вязкой силы трения между потоком жидкости и стенками трубы.

Опыт. Возьмем резиновую или пластиковую трубку постоянного сечения и такого диаметра, чтобы ее можно было насадить на носик водопроводного крана. Сделаем в трубке два отверстия и откроем воду. Из отверстий начнут бить фонтанчики, причем высота ближнего к крану фонтанчика будет заметно выше, чем расположенного дальше по потоку. Это показывает, что давление воды в ближайшем к крану отверстии выше, чем в дальнем: оно падает вдоль трубы в направлении потока.

#9#

Объяснение этого явления на молекулярном уровне автору не известно. Поэтому приведем классическое объяснение. Выделим в жидкости маленький объем, ограниченный стенками трубки и двумя сечениями слева и справа. Так как жидкость течет по трубке равномерно, то разность давлений слева и справа от выделенного объема должна быть уравновешена силами трения между жидкостью и стенками трубки. Следовательно, давление справа, в направлении потока жидкости, будет меньше давления слева. Отсюда заключаем, что давление жидкости уменьшается в направлении течения воды.

На первый взгляд приведенное объяснение удовлетворительно. Однако возникают вопросы, ответа на которые пока нет.

1. Согласно уравнению Бернулли, уменьшение давления в жидкости при ее движении вдоль трубы должно означать, что скорость ее, наоборот, должна расти вдоль потока, то есть течение жидкости должно ускоряться. Но этого не может быть в силу закона неразрывности.

2. Силы трения между стенками трубы и жидкостью должны в принципе тормозить ее. Если это так, то при торможении скорость жидкости вдоль канала должна падать, что в свою очередь приведет к росту давления в ней по потоку. Однако внешнее давление, прокачивающее жидкость по трубе, компенсирует силы трения, заставляя жидкость течь равномерно с одинаковой по всему каналу скоростью. А раз так, то и давление жидкости вдоль канала должно быть везде одинаковым.

Итак, налицо экспериментальный факт, который легко проверить, однако объяснение его остается открытым.

ЭФФЕКТ МАГНУСА

Речь идет о возникновении силы, перпендикулярной потоку жидкости при обтекании ею вращающегося тела. Этот эффект был обнаружен и объяснен Г. Г. Магнусом (около середины XIX столетия) при изучении полета вращающихся артиллерийских снарядов и их отклонения от цели. Эффект Магнуса состоит в следующем. При вращении летящего тела близлежащие слои жидкости (воздуха) увлекаются им и также получают вращение вокруг тела, то есть начинают циркулировать вокруг него. Встречный поток рассекается телом на две части. Одна часть направлена в ту же сторону, что и циркулирующий вокруг тела поток; при этом происходит сложение скоростей набегающего и циркулирующего потоков, значит, давление в этой части потока уменьшается. Другая часть потока направлена в сторону, противоположную циркуляции, и здесь результирующая скорость потока падает, что приводит к увеличению давления. Разность давлений с обеих сторон вращающегося тела и создает силу, которая перпендикулярна к направлению встречного, набегающего потока жидкости (воздуха).

#10#

Опыт. Склеим из листа плотной бумаги цилиндр. Из доски, положенной одним краем на стопку книг, сделаем на столе наклонную плоскость и положим на нее цилиндр. Скатившись, он вроде бы должен дальше двигаться по параболе и упасть дальше от края. Однако вопреки ожидаемому траектория его движения загибается в другую сторону, и цилиндр залетает под стол. Все дело в том, что он не просто падает, а еще и вращается, создавая вокруг себя циркуляцию воздуха. Возникает избыточное давление, направленное в сторону, противоположную поступательному движению цилиндра.

#11#

Эффект Магнуса позволяет игрокам в пинг-понг и теннис отбивать «крученые» мячи, а футболистам — посылать «сухой лист», ударяя мяч по краю.

ЛАМИНАРНЫЙ И ТУРБУЛЕНТНЫЙ ПОТОКИ

Опыт обнаруживает две совершенно разные картины движения жидкости. При низких скоростях наблюдается спокойное, слоистое течение, которое называется ламинарным. При больших скоростях течение становится хаотическим, частицы и отдельные области жидкости движутся беспорядочно, закручиваясь в вихри; такое течение называется турбулентным. Переход от ламинарного течения к турбулентному и обратно осуществляется при определенной скорости жидкости и зависит также от вязкости и плотности жидкости и характерного размера обтекаемого жидкостью тела. До сих пор не ясно, возникают ли вихри с самого начала и имеют просто очень малые размеры, не видимые нами, или вихри возникают начиная с некоторой скорости движения жидкости.

Опыт. Посмотрим, как происходит переход ламинарного потока в турбулентный. Откроем кран и пустим воду сначала тоненькой струйкой, а потом все сильнее и сильнее (конечно, так, чтобы не затопить соседей). Тоненькая струйка движется плавно и спокойно. По мере того, как увеличивается напор воды, скорость струи растет, и, начиная с некоторого момента, вода в ней начинает закручиваться — возникают вихри. Появляясь сначала только в ограниченной области струи, с ростом напора вихри в конце концов охватывают все течение — оно становится турбулентным.

#12# Струя воды падает в поле тяжести, испытывая ускорение. Как только скорость течения возрастает настолько, что число Рейнольдса превышает критическое значение, ламинарное течение (вверху) переходит в турбулентное. Для данного течения Re»2300.

Оценить скорость течения жидкости или газа, при которой возникает турбулентность, можно при помощи так называемого числа Рейнольдса Re = ρvl/μ, где ρ — плотность жидкости или газа, μ — их вязкость (вязкость воздуха, например, 18,5.10^-6Па.с; воды — 8,2.10^-2Па.с), v — скорость потока, l — характерный линейный размер (диаметр трубы, длина обтекаемого тела и пр.). Для каждого вида течений существует такая критическая величина Re_кр, что при Re<Re_кр возможно только ламинарное течение, а при Re>Re_кроно может стать турбулентым. 3/с) 92)

Обратите внимание, что скорость следует измерять в точке трубы, где поток полностью развит и отсутствует значительная турбулентность. Обычно это расстояние не менее 10 диаметров трубы вниз по течению от любых нарушений потока, таких как клапаны или изгибы.

Какова формула скорости потока? Expand

Формула скорости потока жидкости в трубе:

v = Q / A

v скорость жидкости в метрах в секунду (м/с) 92)

Это уравнение утверждает, что скорость потока пропорциональна скорости потока и обратно пропорциональна площади поперечного сечения трубы.

Расход представляет собой объем жидкости, который проходит через данную точку трубы в единицу времени, а площадь поперечного сечения представляет собой пространство, доступное для заполнения жидкостью.

Таким образом, по мере увеличения скорости потока или уменьшения площади поперечного сечения скорость потока будет увеличиваться.

Каково эмпирическое правило для определения скорости потока в трубе? Expand

Типичная скорость воды в трубе обычно составляет 0,7–2,4 м/с:

Скорость холодной воды — 1,5–2,4 м/с или 5–8 футов/с

Скорость потока горячей воды — 1,2-1,5 м/с или 4-5 футов/с

Скорость возврата горячей воды — 0,7-1 м/с или 2-3 фута/с

Зависит от переменных:

Местный стандарт

Например, в США трубы обычно рассчитаны на более высокие скорости по сравнению с Великобританией

Материал трубы

Например, трубы из нержавеющей стали обычно могут быть рассчитаны на более высокие скорости, чем медные трубы

Если труба находится над жилым помещением

Например, если труба находится над комнатой, например спальней, скорость трубы должна быть низкой, чтобы избежать чрезмерного шума

Приложение

Например, трубы с горячей водой в рециркуляционных системах должны быть рассчитаны на более низкую скорость, чем трубы с холодной водой

Скорость обычно не должна опускаться ниже 0,7 м/с, так как это необходимо для поддержания скорости самоочищения. Например, если жидкости содержат твердые частицы, инженеры пытаются добиться более высокой скорости, чтобы тяжелые частицы в жидкости не оседали и не вызывали закупорку трубы.

Увеличивает ли скорость уменьшение размера трубы? Expand

Да, уменьшение размера трубы обычно увеличивает скорость жидкости, протекающей по ней. Согласно принципу сохранения массы, если площадь поперечного сечения трубы уменьшается, скорость жидкости должна увеличиваться, чтобы поддерживать тот же расход. 92)

Скорость будет увеличиваться по мере уменьшения площади поперечного сечения, а по мере увеличения площади поперечного сечения скорость будет уменьшаться. Это известно как уравнение неразрывности и является фундаментальным принципом гидродинамики.

Увеличивается ли скорость с размером трубы? Expand

Нет, скорость жидкости, протекающей по трубе, не увеличивается с размером трубы.

Скорость жидкости в трубе определяется балансом между расходом и площадью поперечного сечения трубы. 92)

Если скорость потока остается постоянной, увеличение площади поперечного сечения трубы уменьшит скорость, а уменьшение площади поперечного сечения трубы увеличит скорость.

Скорость жидкости в трубе напрямую не связана с размером трубы, а скорее с балансом между скоростью потока и площадью поперечного сечения трубы.

Введение в давление Часть II: скорость, скорость потока и сила реакции

В нашем последнем обсуждении мы рассмотрели некоторые основы гидравлической энергии. Если вы еще этого не сделали, ознакомьтесь с этой вводной статьей. Теперь давайте продолжим обсуждение, обратившись к скорости, объему и потоку.

Чтобы определить скорость потока, представленную как Q, мы должны определить как объем V, так и момент времени, через который он течет, представленный t, или Q = V/t. Кроме того, расход и скорость связаны уравнением Q = Av, где A — площадь поперечного сечения потока, а v — его средняя скорость.

В связи с тем, что мы обсуждаем цилиндры, нам потребуется доступ к некоторым ключевым уравнениям, чтобы определить Силу и Скорость. Взгляните на уравнения и диаграмму ниже:

Давайте рассмотрим практический пример. Какая скорость потока в галлонах в минуту (галлонов в минуту) потребуется для питания гидравлического цилиндра с диаметром отверстия 4 дюйма, штоком 2 дюйма и ходом 20 дюймов, работающего со скоростью 10 циклов в минуту? Во-первых, мы знаем, что для того, чтобы цилиндр вращался со скоростью 10 циклов в минуту, цикл не может длиться более шести секунд (60 сек/мин / 10 циклов в минуту = 6 секунд). этой проблемой будет объем, необходимый для расширения цилиндра. Объем = площадь X ход. В этом примере площадь вычисляется с помощью π(r)², и мы знаем, что радиус равен 2 дюймам. Это означает, что площадь равна 12,57 квадратных дюймов. Итак, 12,57 кв. дюймов x 20 дюймов = 251,4 куб. дюймов.

Далее нам нужно рассчитать объем, необходимый для втягивания цилиндра V = A x S. В этом примере площадь находится путем вычитания площади отверстия из площади штока. В этом примере это будет π(2)² — π(1)². Таким образом, V = 9,43 кв. дюймов x 20. Это означает, что V = 188,6 куб. дюймов.

Затем мы складываем эти два объема вместе: 251,4 куб. дюймов + 188,6 куб. дюймов. Это в сумме составляет 440 куб. дюймов. Наш следующий шаг — умножить этот объем на время цикла, которое мы определили как 10 копий в минуту. Когда мы это делаем, то видим, что имеем расход 4400 куб. дюймов/мин. Чтобы выразить это в галлонах в минуту, мы делим это число на 231 куб. дюйм/галлон. Сделав это, мы обнаружим, что 4400 куб. дюймов/мин, деленные на 231 куб. дюйм/гал, равняются 19.0,05 гал/мин.

Также важно понимать роль, которую играет преимущество в механике в обсуждении. Механическое преимущество — это мера усиления силы, достигаемая за счет использования инструмента, механического устройства или системы машин. Мы можем определить механическое преимущество в форме уравнения, выразив его как общую длину штока, деленную на поддерживаемую длину штока — MA = TRL/SRL.

Кроме того, сила реакции, действующая на подшипник шатуна, представляет собой произведение механического преимущества на боковую силу, действующую на конец стержня, или RF = MA x SL.