Способы деформирования тел: Виды деформаций твердых тел | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Виды деформаций твердых тел | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Загрузка…

Известно, что при деформации твердые тела прояв­ляют упругие свойства. Так, было установ­лено, что растяжение или сжатие тела вы­зывает силу упругости, значение которой пропорционально величине деформации (за­кон Гука):

F_упр = —kx,

где x — величина деформации тела, k — ко­эффициент пропорциональности, характе­ризующий жесткость материала.

Жесткость металла k опреде­ляется значением силы F, ко­торую нужно приложить к телу, чтобы деформировать его на единицу длины (1 мм, 1 см или 1 м). В СИ она изменяется в Н/м.

Рис. 3.14. Продольная деформация рас­тяжения и сжатия

Различают разные виды деформации.

Ес­ли сила, приложенная к телу, вызывает его растяжение или сжатие в одном из на­правлений (длины, ширины или высоты), то такая деформация называется продоль­ным растяжением или сжатием. Например, растяжение или сжатие стержня длиной l под действием силы F, приложенной к его концам (рис. 3.14), приведет к дефор­мации растяжения или сжатия. Сила уп­ругости, которая будет возникать при этом, имеет противоположное направление и по закону Гука будет пропорциональна сме­щению Δl.

Рис. 3.15. Деформация изгиба

Приложение силы перпендикулярно оси стержня (рис. 3.15) вызовет его прогибание, вследствие чего возникнет сила упругости, которая будет уравновешивать действующую силу. Этот вид деформации называется де­формацией изгиба. В данном случае сила упругости так же пропорциональна смеще­нию Δ

h: F_ynp ~ Δh.

Загрузка…

Рис. 3.16. Деформация кручения (а) и сдвига (б)

Существуют и другие виды деформации, например деформация кручения, когда под действием приложенных сил различные слои тела смещаются относительно оси, или дефор­мация сдвига, когда различные слои тела под действием силы сдвигаются друг относи­тельно друга (рис. 3.16). Материал с сайта http://worldofschool.ru

Любая из этих деформаций вызывает внутри тела силы, противодействующие ей. Если после прекращения действия внешних сил тело возобновляет свою первоначаль­ную форму и объем, то

деформация на­зывается упругой.

Тем не менее, не всегда можно этого достичь. То есть после прекращения действия сил тело может сохранить (частично или полностью) деформированное состоя­ние. Это свойство твердых тел называют пластичностью.

Остаточная деформация, имею­щая место после снятия ме­ханических нагрузок, называет­ся пластической деформацией.

Учитывание упругих и пласти­ческих деформаций является основой конструирования де­талей машин, строительства, обработки материалов и т. д.

На этой странице материал по темам:

• Механика сплошных сред шпоры

• Деформация твердого тела формула

• Деформация твердых тел доклад

• Скачать реферат деформация , виды и дефрмация твёрдых тел

• Виды деформации тр физика

Вопросы по этому материалу:

• Какие существуют виды деформации?

• Чем виды деформации отличаются друг от друга?

• Что такое упругая деформация?

• Какой закон описывает про­дольную упругую деформацию растяжения (сжатия)?

• Чем отличаются пластичность и хрупкость?

Материал с сайта http://WorldOfSchool.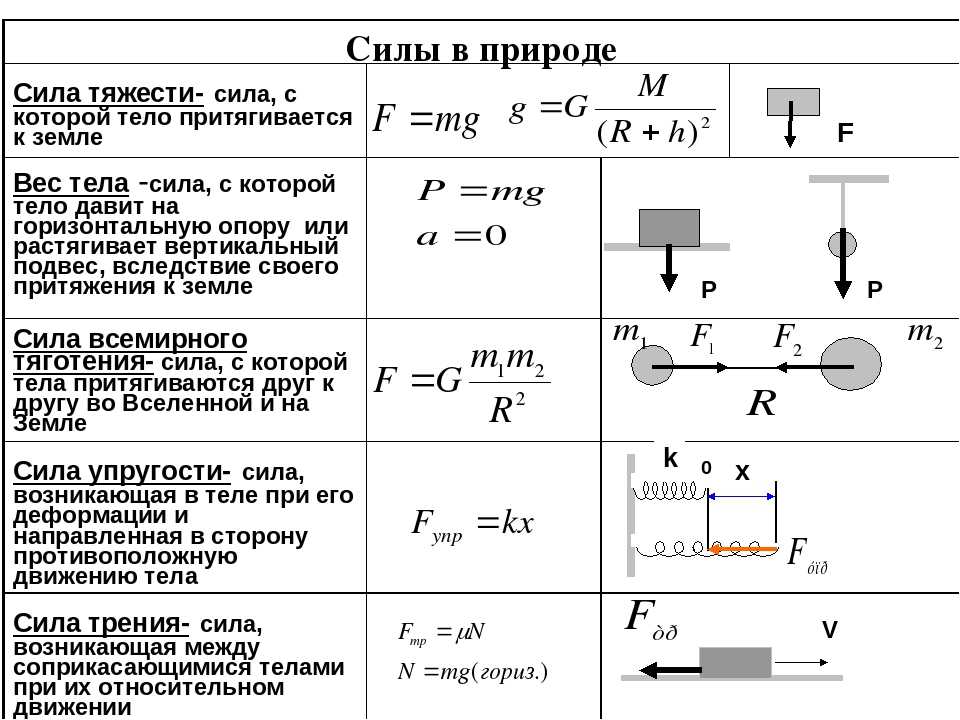 ru

виды деформации, пределы упругости и прочности

Частицы, из которых состоят твердые тела (как аморфные, так и кристаллические) постоянно совершают тепловые колебания около положений равновесия. В таких положениях энергия их взаимодействия минимальная. Если расстояние между частицами уменьшается, начинают действовать силы отталкивания, а если увеличиваться – то силы притяжения. Именно этими двумя силами обусловлены все механические свойства, которыми обладают твердые тела.

Определение 1

Если твердое тело изменяется под воздействием внешних сил, то частицы, из которых оно состоит, меняют свое внутреннее положение. Такое изменение называется

деформацией.

Виды деформации

Различают деформации нескольких видов. На изображении показаны некоторые из них.

Рисунок 3.7.1. Некоторые виды деформаций твердых тел: 1 – деформация растяжения; 2 – деформация сдвига; 3 – деформация всестороннего сжатия.

Первый вид – растяжение или сжатие – является наиболее простым видом деформации. В таком случае изменения, происходящие с телом, можно описать при помощи абсолютного удлинения Δl, которое происходит под действием сил, обозначаемых F→. Взаимосвязь, существующая между силами и удлинением, обусловлена геометрическими размерами тела (в первую очередь толщиной и длиной), а также механическими свойствами вещества.

Определение 2

Если мы разделим величину абсолютного удлинения на первоначальную длину твердого тела, мы получим величину его относительного удлинения (относительной деформации).

Обозначим этот показатель ε и запишем следующую формулу:

ε=∆ll.

Определение 3

Относительная деформация тела растет при его растяжении и соответственно уменьшается при сжатии.

Если учесть, в каком именно направлении внешняя сила действует на тело, то мы можем записать, что F будет больше нуля при растяжении и меньше нуля при сжатии.

Механическое напряжение

Определение 4

Механическое напряжение твердого тела σ – это показатель, равный отношению модуля внешней силы к площади сечения твердого тела.

σ=FS.

Величину механического напряжения принято выражать в паскалях (Па) и измерять в единицах давления.

Важно понимать, как именно механическое напряжение и относительная деформация связаны между собой. Если отобразить их взаимоотношения графически, мы получим так называемую диаграмму растяжения. При этом нам нужно отмерить величину относительной деформации по оси x, а механическое напряжение – по оси y. На рисунке ниже представлена диаграмма растяжения, типичная для меди, мягкого железа и некоторых других металлов.

Рисунок 3.7.2. Типичная диаграмма растяжения для пластичного материала. Голубая полоса – область упругих деформаций.

В тех случаях, когда деформация твердого тела меньше 1% (малая деформация), то связь между относительным удлинением и механическим напряжением приобретает линейный характер. На графике это показано на участке Oa. Если напряжение снять, то деформация исчезнет.

Определение 5

Деформация, исчезающая при снятии напряжения, называется упругой.

Линейный характер связи сохраняется до определенного предела. На графике он обозначен точкой a.

Определение 6

Предел пропорциональности – это наибольшее значение σ=σпр, при котором сохраняется линейная связь между показателями σ и ε.

На данном участке будет выполняться закон Гука:

ε=1Eσ.

В формуле содержится так называемый модуль Юнга, обозначенный буквой E.

Если мы продолжим увеличивать напряжение на твердое тело, то линейный характер связи нарушится. Это видно на участке ab. Сняв напряжение, мы также увидим практически полное исчезновение деформации, то есть восстановление формы и размеров тела.

Предел упругости

Определение 7

Предел упругости – максимальное напряжение, после снятия которого тело восстановит свою форму и размер.

После перехода этого предела восстановления первоначальных параметров тела уже не происходит. Когда мы снимаем напряжение, у тела остается так называемая остаточная (пластическая) деформация.

Определение 8

Обратите внимание на участок диаграммы bc, где напряжение практически не увеличивается, но деформация при этом продолжается. Это свойство называется

текучестью материала.

Предел прочности

Определение 9

Предел прочности – максимальное напряжение, которое способно выдержать твердое тело, не разрушаясь.

В точке e материал разрушается.

Определение 10

Если диаграмма напряжения материала имеет вид, соответствующий тому, что показан на графике, то такой материал называется пластичным. У них обычно деформация, при которой происходит разрушение, заметно больше области упругих деформаций. К пластичным материалам относится большинство металлов.

Определение 11

Если материал разрушается при деформации, которая превосходит область упругих деформаций незначительно, то он называется хрупким. Такими материалами считаются чугун, фарфор, стекло и др.

Деформация сдвига имеет аналогичные закономерности и свойства.

Ее отличительная особенность состоит в направлении вектора силы: он направлен по касательной относительно поверхности тела. Для поиска величины относительной деформации нам нужно найти значение Δxl, а напряжения – FS (здесь буквой S обозначена та сила, которая действует на единицу площади тела). Для малых деформаций действует следующая формула:

∆xl=1GFS

Буквой G в формуле обозначен коэффициент пропорциональности, также называемый модулем сдвига. Обычно для твердого материала он примерно в 2-3 раза меньше, чем модуль Юнга. Так, для меди E=1,1·1011 Н/м2, G=0,42·1011 Н/м2.

Когда мы имеем дело с жидкими и газообразными веществами, то важно помнить, что у них модуль сдвига равен 0.

При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему

V тела. При малых деформациях

∆VV=1Bp

Буквой B обозначен коэффициент пропорциональности, называемый модулем всестороннего сжатия.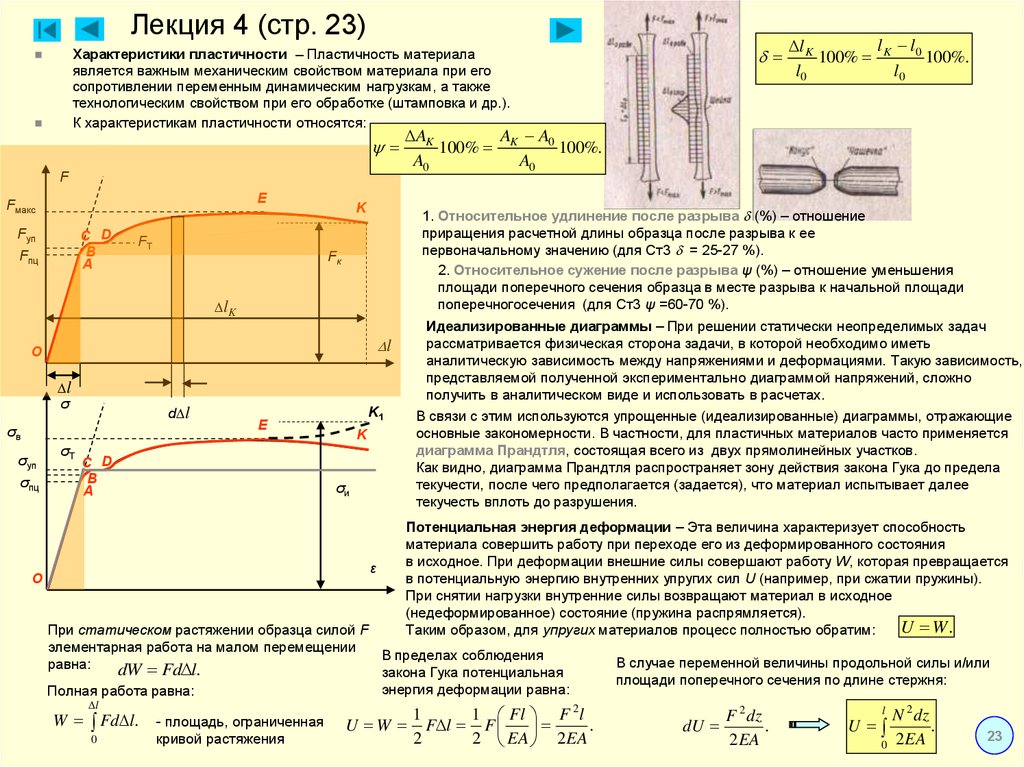 Такому сжатию можно подвергнуть не только твердое тело, но и жидкость и газ. Так, у воды B=2,2·109 Н/м2, у стали B=1,6·1011Н/м2. В Тихом океане на глубине 4 км давление составляет 4·107 Н/м2, а относительно изменения объема воды 1,8 %. Для твердого тела, изготовленного из стали, значение этого параметра равно 0,025 %, то есть оно меньше в 70 раз. Это подтверждает, что твердые тела благодаря жесткой кристаллической решетке обладают гораздо меньшей сжимаемостью по сравнению с жидкостью, в которой атомы и молекулы связаны между собой не так плотно. Газы могут сжиматься еще лучше, чем тела и жидкости.

От значения модуля всестороннего сжатия зависит скорость, с которой звук распространяется в данном веществе.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Деформация тканей – Физика тела: движение к метаболизму

Перейти к содержимому

Если вы нанесете немного на материал и измерите результат, или , наоборот, , вы можете построить кривую зависимости напряжения от деформации, как показано ниже для типичного металла.

Типичный график напряжения-деформации для металла: график заканчивается в точке разрушения. Стрелки показывают направление изменений при постоянно возрастающем напряжении. Точки Н и Е — пределы линейности и эластичности соответственно. Зеленая линия, начинающаяся в точке P, показывает возвращение металла к большей, чем исходная, длине, когда напряжение снимается после входа в область пластичности. Изображение предоставлено: OpenStax University Physics

^[1]

Мы видим, что металл начинает с напряжения, пропорционального деформации, что означает, что материал работает в своей . Мы отобразили напряжение по вертикальной оси, а деформацию по горизонтальной оси, поэтому значение напряжение/деформация равно подъему/пробегу графика. Мы видели в предыдущей главе, что в пределах напряжение/деформация равно , и мы знаем, что подъем/пробег графика является наклоном, поэтому Модуль упругости материала равен наклону линейной части его напряжения относительно кривой .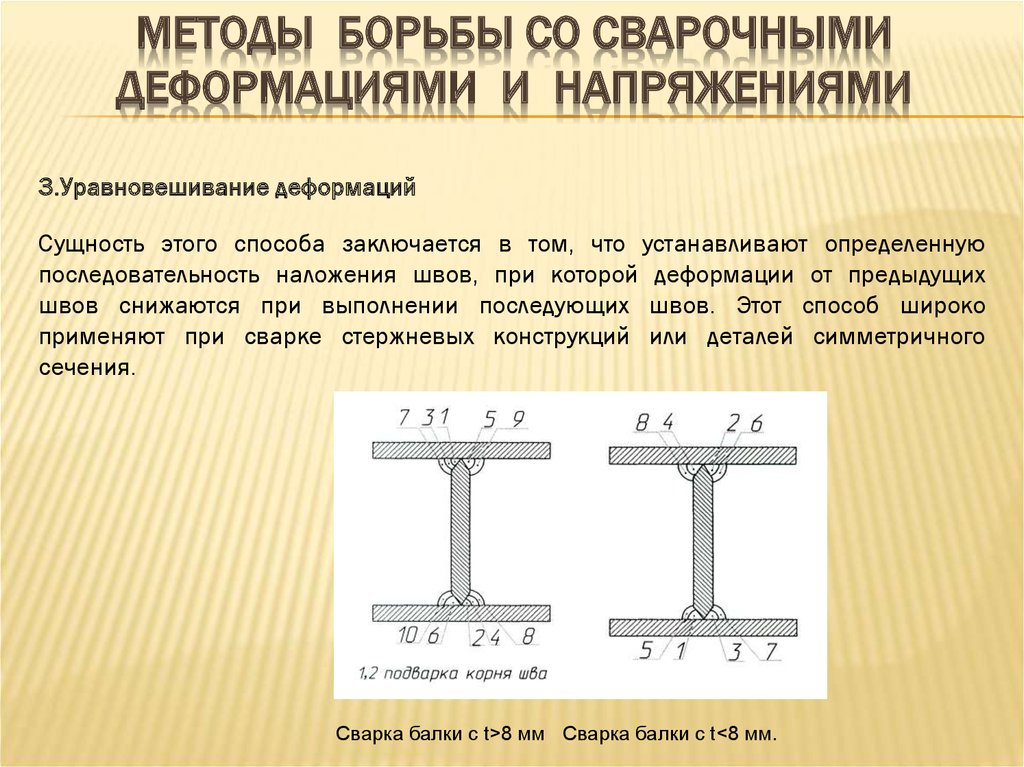 Давайте обсудим важные особенности кривой зависимости напряжения от деформации:

1. Самая высокая точка на графике — это , что указывает на начало отказа в направлении или .
2. Обратите внимание, что после достижения предела прочности, но до полного разрушения, напряжение может фактически уменьшаться по мере увеличения деформации, потому что материал меняет форму, разрушая, а не растягивая или сжимая расстояние между молекулами в материале.
3. В первой части деформация пропорциональна напряжению, это известно как . Уклон этой области равен .
4. После того, как напряжение достигает предела линейности ( H ), наклон больше не является постоянным, но материал по-прежнему ведет себя упруго.
5. Конец и начало в ( E ). В области пластичности небольшое большее напряжение вызывает гораздо большую деформацию, потому что материал меняет форму на молекулярном уровне. В некоторых случаях напряжение может фактически уменьшаться по мере увеличения деформации, потому что материал меняет форму за счет изменения конфигурации молекул, а не просто растяжения или сжатия расстояния между молекулами.
6. Зеленая линия, начинающаяся от P , показывает возвращение металла к ненулевому значению деформации , когда напряжение снимается после того, как оно перешло в пластическую область (постоянная деформация).

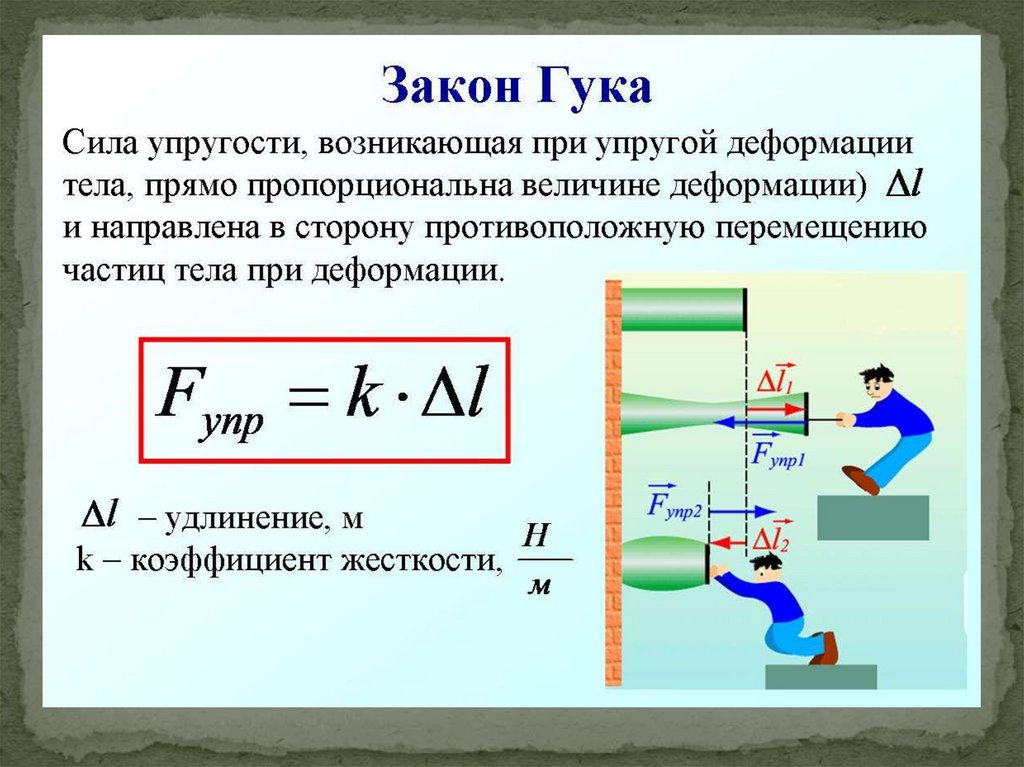
Сухожилия (прикрепляющие мышцы к костям) и связки (прикрепляющие кости к костям) ведут себя несколько уникальным образом при . Функционально сухожилия и связки должны сначала легко растягиваться, чтобы обеспечить гибкость, соответствующую кривой зависимости напряжения от поезда, показанной ниже, но затем сопротивляться значительному растяжению при большом напряжении, чтобы предотвратить чрезмерное растяжение и травмы вывиха, соответствующие линейной области.

Типичная кривая напряжение-деформация для сухожилия млекопитающих. Показаны три области: (1) область носка (2) линейная область и (3) область отказа. Изображение адаптировано из OpenStax College Physics.

^[2]

Структура сухожилия создает такое особое поведение. Чтобы создать область пальца, небольшое напряжение заставляет волокна в сухожилии начать выравниваться в направлении напряжения, или , и повторное выравнивание обеспечивает дополнительную длину. Тогда и сами фибриллы будут растягиваться.

за пределами материала вызовет остаточную деформацию, а область кривой зависимости напряжения от деформации за пределом текучести называется . Стресс выше будет причиной или . Эти явления в тканях тела известны как травмы. Например, s prains возникают, когда связка (соединяющая кость с костью) разрывается под действием напряжения, превышающего ее предельную прочность, или просто растягивается в области разрушения. То же самое событие, происходящее в сухожилии (соединяющем мышцу с костью), называется 9.0005 штамм . ^[3] Мы уже знаем, что это имеет другое, но родственное значение для физиков и инженеров, так что расхождения в терминологии следует остерегаться.

Деятельность по усилению

---

1. OpenStax University Physics, University Physics Volume 1. OpenStax CNX. 2 августа 2018 г. http://cnx.org/contents/[email protected]. ↵
2. OpenStax, Колледж физики. OpenStax CNX. 6 августа 2018 г. http://cnx.org/contents/[email protected]. ↵
3. «Растяжения и растяжения», отдел информации по уходу за пациентами и состоянию здоровья, клиника Майо ↵

License

Body Physics: Motion to Metabolism by Lawrence Davis находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, если не указано иное.

Поделиться этой книгой

Поделиться в Твиттере

деформации и течения | механика

Ключевые люди:

Ганс Клоос

Похожие темы:

напряжение побратимство перелом пластическое течение пластически-вязкая деформация

Просмотреть весь связанный контент →

Резюме

Прочтите краткий обзор этой темы

Понимание явления течения гранулированного материала

Посмотреть все видео к этой статье

деформация и течение , в физике изменение формы или размера тела под действием механических сил. Течение — это изменение деформации, которое продолжается до тех пор, пока действует сила.

Далее следует краткое описание деформации и течения. Для полной обработки см. механика.

Еще из Britannica

осадочные породы: деформационные структуры

Узнайте, как инженеры-строители и инженеры-экологи понимают механику тонких конструкций и как они используют геометрию для изучения процесса деформации

Просмотреть все видео к этой статье

Вещества, используемые в повседневной жизни, обычно классифицируются как твердые, жидкие или газообразные, и при нормальных обстоятельствах газы и жидкости текут относительно свободно, а твердые тела деформируются под воздействием сил. Большинство твердых тел изначально упруго деформируются; то есть они возвращаются к своей первоначальной форме после снятия нагрузки. Твердые материалы, такие как металлы, бетон или камни, выдерживают большие силы, подвергаясь небольшой деформации, но если приложены достаточно большие силы, материалы больше не могут выдерживать их только за счет упругой деформации. Что происходит затем, зависит от внутренней структуры материала. По мере того как к хрупкому веществу, такому как каменный блок или бетон, прикладывается все большая и большая сила, будет достигнута точка, в которой внутренняя конструкция больше не сможет выдерживать приложенную нагрузку только за счет упругой деформации. После этого образец совершенно внезапно разрушится. Такое поведение характерно для хрупких материалов: переход от цельного образца к разрушенному происходит почти мгновенно и практически без предупреждения.

Для пластичного материала, такого как мягкая сталь или алюминий, после начального периода упругой деформации достигается одна и та же критическая точка — предел упругой деформируемости образца. Однако в этом случае материал вместо разрушения приспосабливается к приложенным силам, перестраивая свою внутреннюю структуру. Результатом является пластическая деформация, которая будет продолжаться до тех пор, пока действуют силы. Материал создает впечатление течения под действием приложенных нагрузок, и это течение является пластическим, так как при снятии нагрузки образец сохраняет свою деформацию.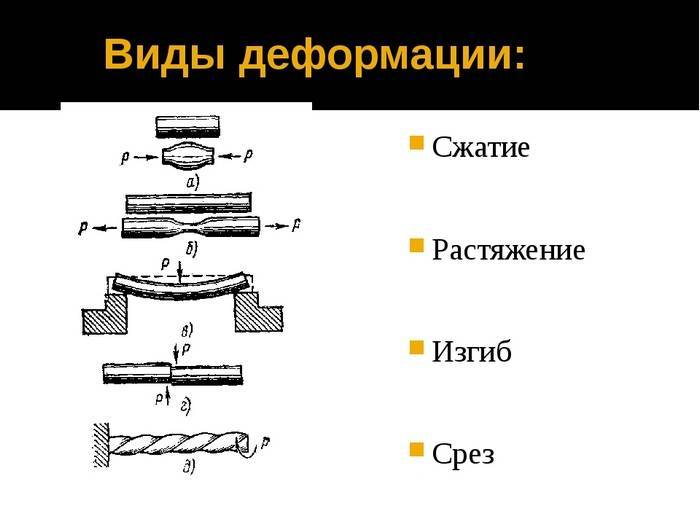 В конце концов, пластическое течение прекратится: деформация в конечном итоге будет стремиться сконцентрироваться в одной области, которая и разорвется.

Эта способность пластичных материалов к пластическому течению под нагрузкой имеет основополагающее значение для их полезности в технике. Как следствие, понимание пластического течения жизненно важно в технологии, особенно при производстве большого количества объектов различных сложных форм. Пластическое течение также является центральным фактором в попытках понять движение и течение горных пород в условиях высокой температуры и давления, которые заставляют их вести себя как пластичные материалы. Такие процессы сформировали поверхность Земли, хотя масштаб времени (миллионы лет) сильно отличается от обычного интереса инженеров.

Простая классификация материалов как твердых, жидких или газообразных теперь может быть расширена на основе корреляции субмикроскопической структуры с механическими свойствами в более сложный набор структурных типов следующим образом:

Получите подписку Britannica Premium и получить доступ к эксклюзивному контенту. Подпишитесь сейчас

Газы имеют беспорядочно движущиеся молекулы, которые не притягиваются друг к другу, скорость которых зависит от температуры газа и которые сталкиваются, как если бы они были упругими сферами незначительного объема. Эти предположения лежат в основе кинетической теории газов, которая предсказывает, что произведение давления и объема, деленное на абсолютную температуру, является константой. Большинство газов вполне соответствуют этому соотношению в удивительно широком диапазоне условий.

Жидкости имеют молекулы, которые находятся в контакте, но способны легко скользить друг по другу. В такой «идеальной жидкости» не может существовать касательных напряжений. (Напряжения сдвига связаны с рассеиванием энергии, когда соседние плоскости молекул скользят друг относительно друга, как в действии карточного игрока, раскладывающего колоду карт по столу.) Вода, самая распространенная жидкость из всех, имеет свойства, очень близкие к свойствам воды. идеальной жидкости.

Вязкие жидкости состоят из молекул, которые, как и молекулы идеальной жидкости, находятся в контакте друг с другом, но действуют друг на друга так, что сдвигающие движения внутри жидкости оказывают сопротивление. Эти внутренние силы сдвига вызывают характерное поведение жидкостей, таких как патока, тяжелые масла или расплавленные пластмассы. Это характерное движение, известное как сдвиговое течение, представляет собой процесс диссипации энергии. Для сравнения, вязкость глицерина (вязкой жидкости) при комнатной температуре составляет 15 пуаз (единица вязкости), по сравнению с 0,01 для воды и 1,8 × 10 ⁻⁴ для воздуха. ( См. гидромеханика.)

Линейно-упругие твердые тела имеют молекулы, которые, как предполагается, скреплены вместе пружинообразными упругими силами. При малых деформациях график зависимости деформации от приложенной нагрузки представляет собой прямую линию. Этот вид деформации представляет собой энергоаккумулирующий процесс, примером которого может служить сжатие пружины. ( См. упругость; закон Гука.) При большей деформации такие упругие твердые тела проявляют либо хрупкость (при которой внутренние упругие силы разрушаются), либо пластичность (при которой определенные внутренние механизмы допускают сдвиговые смещения внутри атомной структуры). Для материалов с кристаллической структурой эти сдвиговые смещения обычно связаны с дефектами кристаллической решетки. Такие дефекты называются дислокациями, и они придают кристаллической структуре способность выдерживать пластические деформации без разрушения. В материаловедении изучение роли дислокаций в пластическом течении составляет основную исследовательскую деятельность.

Вязкоупругие твердые тела имеют молекулы, в которых соотношение нагрузки и деформации зависит от времени. Если к такому материалу внезапно приложить нагрузку, а затем поддерживать ее постоянной, результирующая деформация достигается не сразу. Скорее, твердое тело постепенно деформируется и достигает стационарной деформации только по прошествии значительного периода времени. Такое поведение называется ползучести. И наоборот, внезапное приложение фиксированной деформации к такому материалу создает начальные напряжения, которые могут быть очень большими; затем эти напряжения медленно релаксируют до стационарного значения по мере того, как материал приспосабливается к приложенной деформации. Такая процедура известна как стресс-релаксационный тест. Физические причины такого поведения слишком сложны, чтобы их можно было объяснить какой-либо простой молекулярной моделью. Такое поведение характерно для стекла, резины, многих пластмасс и некоторых металлов.

Твердые пластмассы — это материалы, такие как свинец, степень эластичности которых либо незначительна, либо вообще отсутствует. В таких материалах любая вызванная деформация является постоянной.

Вышеуказанные категории охватывают поведение большинства технических и встречающихся в природе материалов, хотя иногда может быть трудно отнести данное вещество к какой-либо одной категории.