Что Такое Погрешность Простыми Словами? 2022
Определение — Проводя измерение параметров рынка, маркетолог получает результаты в виде таблиц, графиков и пр. Эти данные он предоставляет заказчику. Но в отчетах не все специалисты указывают важную величину — погрешность, о которой клиент не подозревает.
Как объяснить погрешность?
Измерение физических величин основано на том, что физика исследует объективные закономерности, которые происходят в природе. Найти значение физической величины — умножить конкретное число на единицу измерения данной величины, которая стандартизирована ( эталоны ).
расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;физический износ шкалы измерений, что приводит к невозможности распознавания значений.
Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой. Рис. \(1\). Линейка и брусок Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет \(1\) см. Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между \(9\) и \(10\) метками.
У нас есть два варианта определения длины этого бруска. \(1\). Если мы заявим, что длина бруска — \(9\) сантиметров, то недостаток длины от истинной составит более половины сантиметра (\(0,5\) см \(= 5\) мм). \(2\). Если мы заявим, что длина бруска — \(10\) сантиметров, то избыток длины от истинной составит менее половины сантиметра (\(0,5\) см \(= 5\) мм).
Погрешность измерений — это отклонение полученного значения измерения от истинного. Погрешность измерительного прибора равна цене деления прибора. Для первой линейки цена деления составляет \(1\) сантиметр. Значит, погрешность этой линейки \(1\) см. Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями.
Как вычислить погрешность?
Физические величины и погрешности их измерений — Задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Сразу оговоримся, что при выборе измерительного оборудования часто нужно также знать диапазон измерения и какое именно значение интересует: например, среднеквадратическое значение (СКЗ) измеряемой величины в определённом интервале времени, или требуется измерять среднеквадратическое отклонение (СКО) (для измерения переменной составляющей величины), или требуется измерять мгновенное (пиковое) значение.
- При измерении переменных физических величин (например, напряжение переменного тока) требуется знать динамические характеристики измеряемой физической величины: диапазон частот или максимальную скорость изменения физической величины,
- Эти данные, необходимые при выборе измерительного оборудования, зависят от физического смысла задачи измерения в конкретном физическом эксперименте,
Итак, повторимся: задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Эта задача решается с помощью прямых или косвенных измерений, При прямом измерении осуществляется количественное сравнение физической величины с соответствующим эталоном при помощи измерительных приборов.
- Отсчет по шкале прибора указывает непосредственно измеряемое значение.
- Например, термометр дает значения измеряемой температуры, а вольтметр – значение напряжения.
- При косвенных измерениях интересующая нас физическая величина находится при помощи математических операций над непосредственно измеренными физическими величинами (непосредственно измеряя напряжение U на резисторе и ток I через него, вычисляем значение сопротивления R = U / I ).
Точность прямых измерений некоторой величины X оценивается величиной погрешности или ошибки, измерений относительно действительного значения физической величины X Д, Действительное значение величины X Д (согласно РМГ 29-99 ) – это значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
Различают абсолютную (∆ X) и относительную (δ) погрешности измерений. Абсолютная погрешность измерения – это п огрешность средства измерений, выраженная в единицах измеряемой физической величины, характеризующая абсолютное отклонение измеряемой величины от действительного значения физической величины: ∆X = X – X Д,
Относительная погрешность измерения – это п огрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины. Обычно относительную погрешность выражают в процентах: δ = (∆X / Xд) * 100%, При оценке точности косвенных измерений некоторой величины X 1, функционально связанной с физическими величинами X 2, X 3,, X 1 = F (X 2, X 3, ), учитывают погрешности прямых измерений каждой из величин X 2, X 3, и характер функциональной зависимости F (),
Что такое погрешность в математике?
Погре́шность измере́ния — отклонение измеренного значения величины от её истинного (действительного) значения.
Погрешность измерения является характеристикой точности измерения. Выяснить с абсолютной точностью истинное значение измеряемой величины, как правило, невозможно, поэтому невозможно и указать величину отклонения измеренного значения от истинного.
Это отклонение принято называть ошибкой измерения, Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов, На практике вместо истинного значения используют действительное значение величины х д, то есть значение физической величины, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него,
Такое значение обычно вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому при записи результатов измерений необходимо указывать их точность,
Например, запись T = 2,8 ± 0,1 с; P = 0,95 означает, что истинное значение величины T лежит в интервале от 2,7 с до 2,9 с с доверительной вероятностью 95 %.
Количественная оценка величины погрешности измерения — мера «сомнения в измеряемой величине» — приводит к такому понятию, как « неопределённость измерения ».
В то же время иногда, особенно в физике, термин «погрешность измерения» ( англ. measurement error ) используется как синоним термина «неопределённость измерения» ( англ. measurement uncertainty ),
Что такое погрешность измерения своими словами?
Определения погрешности и неопределенности измерений. — Погрешность измерения – это отклонение измеренного значения величины от ее «истинного» значения. По своей природе или характеру проявления погрешность может быть «случайной» и «систематической». Метод выражения погрешности измерений – а ± Δа, где а – измеренная величина, Δа – суммарная абсолютная погрешность, определяемая методикой выполнения измерений.
Для чего нужна погрешность?
Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного.
- Это отклонение принято называть ошибкой измерения.
- В ряде источников, например, в Большой советской энциклопедии, термины ошибка измерения и погрешность измерения используются как синонимы, но согласно РМГ 29-99 термин ошибка измерения не рекомендуется применять как менее удачный).
- Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов,
На практике вместо истинного значения используют действительное значение величины х д, то есть значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него,
- Такое значение, обычно, вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений.
- Это полученное значение не является точным, а лишь наиболее вероятным.
- Поэтому в измерениях необходимо указывать, какова их точность,
- Для этого вместе с полученным результатом указывается погрешность измерений.
Например, запись T=2,8±0,1 c. означает, что истинное значение величины T лежит в интервале от 2,7 с. до 2,9 с. с некоторой оговорённой вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка). В 2004 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов.
Что такое погрешность и виды?
Абсолютная погрешность меры — это значение, вычисляемое как разность между числом, являющимся номинальным значением меры, и настоящим (действительным) значением воспроизводимой мерой величины. Относительная погрешность — это число, отражающее степень точности измерения.
В чем измеряется погрешность?
Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины. Инструментальные и методические погрешности. Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений.
Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.
Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается.
Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены. Инструментальная погрешность обусловлена несовершенством применяемых средств измерений.Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности.
Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях.
Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Как найти погрешность измерений формула?
Абсолютная погрешность Δ измерений, выражаемая в единицах измеряемой величины, представляется разностью между измеренным и истинным (действительным) значениями измеряемой величины: Δ = х изм — х и (х д ).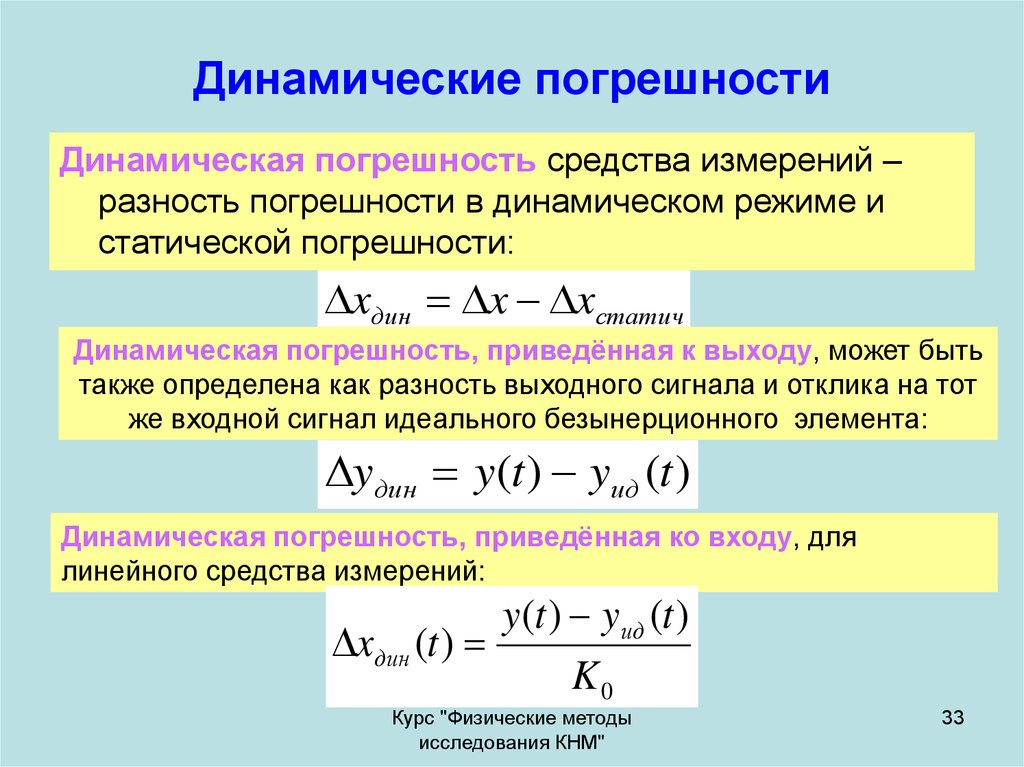
Чему равна абсолютная погрешность?
При измерении каких-либо величин важным понятием является понятие о погрешности. Это связано с тем, что абсолютно точно измерить какую либо величину невозможно. Поэтому вводят понятие погрешности. Есть очень много видов погрешности, связанных с человеческим фактором или процессом измерения.
Что происходит с погрешностью при делении?
| Главная страница УЧЕБНЫЕ МАТЕРИАЛЫ ПРОГРАММА КУРСА КОНСПЕКТЫ ЛЕКЦИЙ ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ВОПРОСЫ К ЗАЧЁТУ РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА | Кафедра физхимии ЮФУ (РГУ) ЧИСЛЕННЫЕ МЕТОДЫ И ПРОГРАММИРОВАНИЕ Материалы к лекционному курсу Лектор – Щербаков И.Н. Пусть X – некоторая величина, истинное значение которой известно или неизвестно и равно x*, Число x, которое можно принять за значение величины X, мы будем называть ее приближенным значением или просто приближенным числом. Число x называют приближенным значением по недостатку, если оно меньше истинного значения ( x x* ). Например, число 3,14 является приближенным значением числа π по недостатку, а 2,72 – приближенным значением числа е (основание натурального логарифма) по избытку. Абсолютная погрешность приближенного числа есть абсолютная величина разности между истинным значением величины и данным ее приближенным значением. Δx = | x * – x | Поскольку истинное значение величины обычно остается неизвестным, неизвестной остается также и абсолютная погрешность. Вместо нее приходится рассматривать оценку абсолютной погрешности, так называемою предельную абсолютную погрешность, которая означает число, не меньшее абсолютной погрешности (далее, в том случае, если это не принципиально, будем под абсолютной погрешностью понимать именно предельную абсолютную погрешность). Абсолютная погрешность приближенного числа не в полной мере характеризует его точность. Действительно, погрешность в 0,1 г слишком велика при взвешивании реактивов для проведения микро-синтеза, допустима при взвешивании 100 г колбасы, и не может быть замечена при измерении массы, например, железнодорожного вагона. Более информативным показателем точности приближенного числа является его относительная погрешность, Относительной погрешностью δx приближенного значения величины X называют абсолютную величину отношения его абсолютной погрешности к истинному значению этой величины. Часто эту относительную погрешность выражают в процентах. C учетом положительности абсолютной погрешности можно записать: δx = Δx / | x* | Ввиду того, что фактически вместо абсолютной погрешности приходится рассматривать предельную, относительную погрешность также заменяют предельной относительной погрешностью, которая означает число, не меньшее относительной погрешности. Более того, при отыскании предельной относительной погрешности приходится заменять неизвестное истинное значение величины x* приближенным – x, Последняя замена обычно не отражается на величине относительной погрешности ввиду близости этих значений и малости абсолютной погрешности. δx = Δx / | x | Например, для приближенного значения π = 3,14 предельная абсолютная погрешность составляет 0,0016, а относительная – 0,00051 или 0,051%. Выражение относительной погрешности в процентах иногда называют процентной погрешностью.Как найти абсолютную погрешность 8 класс?Погрешность и точность приближения. Найдем значение функции у = х 2 при х=1,5 и при х=2,1. Можно найти значение функции двумя способами: по формуле и с помощью графика. С помощью графика приближенные значения функции равны: при х = 1,5 у ≈ 2,3; при х = 2,1 у ≈ 4,4. Что такое основная приведенная погрешность?Приведенная погрешность (средства измерений) – это погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерения к нормирующему значению величины. Чем отличается погрешность от точности? Погрешность и точность — Часто понятия погрешность и точность рассматриваются как синонимы. Однако, эти термины имеют совершенно различные значения. Погрешность показывает, насколько близко измеренное значение к его реальной величине, то есть отклонение между измеренным и фактическим значением.
Ниже, на левом графике показаны эти изменения. Определения неопределенностей. Слева — серия измерений. Справа — значения в виде гистограммы.Почему возникают погрешности измерений?Они возникают из-за конечной точности приборов, ошибок определения, влияния многих случайных факторов, неправильно выбранного способа измерений (систематических ошибок). Что такое абсолютная погрешность примеры? Абсолютная погрешность — Абсолютной погрешностью числа называют разницу между этим числом и его точным значением. Рассмотрим пример : в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой.
Границу абсолютной погрешности называют предельной абсолютной погрешностью. В чем измеряется погрешность?Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений). Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины. Инструментальные и методические погрешности. Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.
Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности. Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статические и динамические погрешности относятся к погрешностям результата измерений. Что представляет собой приведенная погрешность?Приведенная погрешность (средства измерений) – это погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерения к нормирующему значению величины. В чем польза относительной погрешности?4.2 Средняя оценка: 4.2 Всего получено оценок: 1947. Обновлено 11 Января, 2021 4.2 Средняя оценка: 4.2 Всего получено оценок: 1947. Обновлено 11 Января, 2021 Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Опыт работы учителем математики — более 33 лет. Что такое погрешность средств измерений? Погрешность средства измерений — это разность между показаниями СИ и истинным (действительным) значением измеряемой величины. |
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.
Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.
В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Оценка погрешностей измерений на примерах
Оценка погрешностей измерений на примерахПусть измеряемая имеет известное значение величина X. Естественно, отдельные, найденные в процессе измерения значения этой величины x1,x2,…xn заведомо не вполне точны, т.е. не совпадают с X. Тогда величина
будет являться абсолютной погрешностью i-го измерения. Но поскольку истинное значение результата X, как правило, не известно, то реальную оценку абсолютной погрешности используя вместо X среднее арифметическое
,которое рассчитывают по формуле:
(1) |
Однако при малых объемах выборки вместо
предпочтительнее пользоваться медианой.
Медианой (Ме) называют такое значение случайной величины х, при котором половина результатов имеет значение меньшее, а другая большее, чем Ме. Для вычисления Ме результаты располагают в порядке возрастания, то есть образуют так называемый вариационный ряд. Для нечетного количества измерений n мeдиана равна значению среднего члена ряда. Например,
для n=3
Для четных n, значение Ме равно полусумме значений двух средних результатов. Например,
для n=4
Далее рассчитывают среднеквадратичную погрешность (стандартное отклонение выборки), являющуюся мерой разброса и характеризующую случайную погрешность определения:
(2) |
Выборочное стандартное отклонение sзависит от объема выборки n и ее значение колеблется по случайному закону около постоянного значения генерального стандартного отклонения σ
|
Для расчета s пользуются неокругленными результатами анализа с неточным последним десятичным знаком.
При очень большом числе выборки (n>
) случайные погрешности могут быть описаны при помощи нормального закона распределения Гаусса. При малых n распределение может отличаться от нормального. В математической статистике эта дополнительная ненадежность устраняется модифицированным симметричным t-распределением. Существует некоторый коэффициент t, называемый коэффициентом Стьюдента, который в зависимости от числа степеней свободы (f) и доверительной вероятности (Р) позволяет перейти от выборки к генеральной совокупности.
Стандартное отклонение среднего результата
определяется по формуле:
(3) |
Разности между средним
выборки и средним значением генеральной совокупности μ лежат в Р случаях в пределах, которые при помощи нормального распределения и связанного с ним t-распределения определяются следующим выражением:
(4) |
Величина
является доверительным интервалом среднего значения
.
Для серийных анализов обычно полагают Р = 0,95.
Таблица 1. значения коэффициента Стьюдента (t)
f |
Р=0,90 |
Р=0,95 |
Р=0,98 |
Р=0,99 |
1 |
6,31 |
12,7 |
31,8 |
63,6 |
2 |
2,92 |
4,30 |
6,97 |
9,93 |
3 |
2,35 |
3,18 |
4,54 |
5,84 |
4 |
2,13 |
2,78 |
3,75 |
4,60 |
5 |
2,02 |
2,57 |
3,37 |
4,03 |
6 |
1,94 |
2,45 |
3,14 |
3,71 |
7 |
1,90 |
2,36 |
3,00 |
3,50 |
8 |
1,86 |
2,31 |
2,90 |
3,36 |
9 |
1,83 |
2,26 |
2,82 |
3,25 |
10 |
1,81 |
2,23 |
2,76 |
3,17 |
11 |
1,80 |
2,20 |
2,72 |
3,11 |
12 |
1,78 |
2,18 |
2,68 |
3,05 |
Пример 1.
Из десяти определений содержания марганца в пробе требуется подсчитать стандартное отклонение единичного анализа и доверительный интервал среднего значения Mn %: 0,69; 0,68; 0,70; 0,67; 0,67; 0,69; 0,66; 0,68; 0,67; 0,68.
Решение. По формуле (1) подсчитывают среднее значение анализа
|
= 0,679 .
Далее по формуле (2) находят стандартное отклонение единичного результата
|
|
По табл. 1 (приложение) находят для f = n-1= 9 коэффициент Стьюдента (Р = 0,95) t = 2,26 и рассчитывают доверительный интервал среднего значения.
|
По табл. 1 (приложение) находят для f=n-1=9 коэффициент Стьюдента (Р=0,95) t=2,26 и рассчитывают доверительный интервал среднего значения. Таким образом, среднее значение анализа определяется интервалом (0,679 ± 0,009) % Мn.
Пример 2. Среднее из девяти измерений давления паров воды над раствором карбамида при 20°С равно 2,02 кПа. Выборочное стандартное отклонение измерений s = 0,04 кПа. Определить ширину доверительного интервала для среднего из девяти и единичного измерения, отвечающего 95 % — й доверительной вероятности.
Решение. Коэффициент Стьюдента t для доверительной вероятности 0,95 и f = 8 равен 2,31. Учитывая, что
и
, найдем:
— ширина доверит. интервала для среднего значения
— ширина доверит. интервала для единичного измерения значения
Если же имеются результаты анализа образцов с различным содержанием, то из частных средних s путем усреднения можно вычислить общее среднее значение s.
Имея m проб и для каждой пробы проводя nj параллельных определений, результаты представляют в виде таблицы:
Номер |
Номер анализа |
||
1 |
2 |
i…nj |
|
1 |
x11 |
x12 |
x1i… |
2 |
x21 |
x22 |
x2i… |
3 |
x31 |
x32 |
x3i… |
… |
… |
… |
… |
j… |
… |
… |
… |
m |
… |
… |
… |
Средняя погрешность рассчитывают из уравнения:
(5) |
со степенями свободыf = n – m, где n – общее число определений, n = m.
nj.
Пример 2. Вычислить среднюю ошибку определения марганца в пяти пробах стали с различным содержанием его. Значения анализа, % Mn:
1. 0,31; 0,30; 0,29; 0,32.
2. 0,51; 0,57; 0,58; 0,57.
3. 0,71; 0,69; 0,71; 0,71.
4. 0,92; 0,92; 0,95; 0,95.
5. 1,18; 1,17; 1,21; 1,19.
Решение. По формуле (1) находят средние значения в каждой пробе, затем для каждой пробы рассчитывают квадраты разностей, по формуле (5) — погрешность.
1)
= (0,31 + 0,30 + 0,29 + 0,32)/4 = 0,305.
2)
= (0,51 + 0,57 + 0,58 + 0,57)/4 = 0,578.
3)
= (0,71+ 0,69 + 0,71 + 0,71)/4 = 0,705.
4)
= (0,92+0,92+0,95+0,95)/4 =0,935.
5)
= (1,18 + 1,17 + 1, 21 + 1,19)/4 = 1,19.
Значения квадратов разностей
1) 0,0052 +0,0052 +0,0152 +0,0152 =0,500.10-3.
2) 0,0122 +0,0082 +0,0022 +0,0082 =0,276.
10-3.
3) 0,0052 + 0,0152 + 0,0052 + 0,0052 = 0,300.10-3.
4) 0,0152+ 0,0152 + 0,0152 + 0,0152 = 0,900.10-3.
5) 0,012 +0,022 +0,022 + 02 = 0,900.10-3.
Средняя погрешность для f = 4,5 – 5 = 15
|
s = 0,014 % (абс. при f=15 степеням свободы).
Когда проводят по два параллельных определения для каждого образца и находят значения х’ и х», для образцов уравнение преобразуется в выражение:
(6) |
при f = m степеней свободы.
Пример 3. Найти среднюю погрешность в фотометрическом определении хрома в стали по двукратному анализу десяти проб с разным содержанием.
Решение. Расчет производят по таблице (с учетом формулы (6)):
Проба |
х’ |
х» |
х’-х» |
(х’-х»)2 |
1 |
3,77 |
3,75 |
0,02 |
0,0004 |
2 |
2,52 |
2,55 |
0,03 |
0,0009 |
3 |
2,46 |
2,48 |
0,02 |
0,0004 |
4 |
3,25 |
3,20 |
0,05 |
0,0025 |
5 |
1,82 |
1,85 |
0,03 |
0,0009 |
6 |
2,05 |
2,10 |
0,05 |
0,0025 |
7 |
0,88 |
0,90 |
0,02 |
0,0004 |
8 |
1,04 |
1,02 |
0,02 |
0,0004 |
9 |
1,10 |
1,13 |
0,03 |
0,0009 |
10 |
1,52 |
1,48 |
0,04 |
0,0004 |
|
Средняя погрешность по формуле (6) равна
0,023 % Cr |
(при f=10 степеням свободы).
см. также
Математическая обработка результатов химического анализа
- О математической обработке результатов химического анализа
- Оценка погрешностей измерений. Расчет выборочного стандартного отклонения
- Запись результатов измерений
- Сравнение средних результатов химического анализа.
t-критерий Стьюдента - Проблема подозрительно выделяющихся значений
- Погрешности косвенных измерений. Погрешность функций одного или нескольких переменных
Средняя ошибка: Определение — Статистика Как
Статистические определения > Средняя ошибка
Что такое средняя ошибка?
Средняя ошибка — это неофициальный термин , который обычно относится к среднему значению всех ошибок в наборе. «Ошибка» в данном контексте — это неопределенность измерения или разница между измеренным значением и истинным/правильным значением.
Более формальным термином для ошибки является ошибка измерения, также называемая ошибкой наблюдения.
Почему это редко используется
Средняя ошибка обычно приводит к бесполезному числу , потому что положительные и отрицательные значения компенсируют друг друга. Например, две ошибки +100 и -100 дадут среднюю ошибку, равную нулю:
Ноль означает, что ошибки нет, хотя в данном примере это явно не так.
Вместо этого используйте MAE!
Чтобы исправить это, вместо этого использует среднюю абсолютную ошибку (MAE). MAE использует абсолютные значения ошибок в вычислениях, что приводит к более логичным средним ошибкам.
Средняя абсолютная ошибка обычно используется в экспериментах вместо неформальной «средней ошибки».
Формула выглядит немного уродливо, но все, что она требует от вас, это:
- Вычесть одно измерение из другого.
- Найдите абсолютное значение каждой разности из шага 1.
- Сложите все значения из шага 2.
- Разделите шаг 3 на количество измерений.
Пошаговый пример см. в разделе: средняя абсолютная ошибка.
Другие очень похожие термины
Хотя «средняя ошибка» в статистике обычно относится к MAE, она также может относиться к следующим тесно связанным терминам:
- Среднее абсолютное отклонение (среднее абсолютное отклонение): измеряет среднее стандартное отклонение, которое представляет собой разброс значений вокруг центра набора данных. Термины звучат похоже, но они практически не связаны друг с другом, потому что 9Стандартное отклонение 0057 — это единица спреда, а ошибка — это разница в единицах измерения.
- Среднеквадратическая ошибка : используется в регрессионном анализе, чтобы показать, насколько близка линия регрессии к набору точек. «Ошибки» в данном контексте — это расстояния от линии регрессии.
«Ошибки» в данном контексте — это расстояния от линии регрессии. УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Средняя ошибка: определение» от StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/mean-error/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
mean — Средняя стандартная ошибка
спросил
Изменено 7 лет, 5 месяцев назад
Просмотрено 5к раз
$\begingroup$
У меня есть несколько измерений одной и той же популяции в течение нескольких лет, каждый год со своим средним значением и стандартной ошибкой (каждый раз на основе одних и тех же повторов в одном и том же месте), и я хочу вычислить общее среднее и общее стандартная ошибка.
Общее среднее кажется довольно простым (усреднить средние значения?), но я не уверен, смогу ли я рассчитать общее среднее значение SE, усредняющее годовые значения SE. Например: 92 / (n_i — 1)$, выборочная дисперсия в течение года $i$. Однако неясно, что вы будете оценивать с помощью общего среднего, если средние значения также меняются со временем.
$\endgroup$
1
$\begingroup$
Вычисление «большого» среднего и стандартной ошибки может означать несколько разных вещей, в зависимости от точных предположений о ваших данных и того, что вы хотите, чтобы представляла окончательная «ошибка». Это вообще сложная проблема. Например, если некоторые измерения имеют гораздо большие ошибки, чем другие, «общее среднее» должно в большей степени определяться измерениями с высокой степенью достоверности, поэтому мы не хотим просто усреднять средние значения.