Средняя сила сопротивления движения: Силы сопротивления

Физика. 8 класс

Физика. 8 класс

Кикоин И.К., Кикоин А.К. Физика. 8 класс. Учебное пособие. — 4-е изд., перераб. — М.: Просвещение, 1973. — 256 с. Советская фундаментальная наука, и физика в частности, была одной из сильнейших в мире. А по каким учебникам учились в школе и готовились к экзаменам будущие лучшие в мире ученые? Вашему вниманию предлагается учебник по физике для советских восьмиклассников. Охватывает разделы «Кинематика», «Динамика, «Равновесие тел» и «Законы сохранения в механике». Оглавление Глава 1. Общие сведения о движении § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 58. ДВИЖЕНИЕ ПЛАНЕТ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7. Элементы статики § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины Ответы к упражнениям

Сила трения – формула, определение и особенности

4.7

Средняя оценка: 4.7

Всего получено оценок: 235.

4.7

Средняя оценка: 4.7

Всего получено оценок: 235.

В задачах классической механики рассматриваются три основных вида сил, один из которых – силы трения. Они могут нести вред человеку, но и польза от них есть. Чтобы использовать их с толком, либо уменьшать ущерб, наносимый ими, необходимо понимать их природу и уметь находить.

Возникновение трения

Силы трения, причина которых кроется в том, что любая поверхность на микроуровне неровна, действуют на движущиеся и покоящиеся тела. Они могу возникать между твердыми телами, между твердыми и газообразными или жидкими.

Направление сил трения противоположно движению тела (силам, которые движут тело) и лежит в плоскости соприкосновения с поверхностью.

По тому, какая поверхность (со смазкой или без), силы трения делят на сухие и не сухие виды. К первым относят трение покоя (сцепления), скольжения и качения. К не сухим – жидкостное (вязкое).

С помощью подручных средств легко провести опыт. Возьмем любой предмет (например, книгу), положим его на стол и потянем. Если тянуть слабо, книга не сдвинется, ибо на нее действует сила трения покоя. Когда прикладываемся сила станет больше, сцепление также увеличится. Но у него есть максимальное (предельное) значение, и если тянущая сила превысит это значение, тело начнет движение, а покой сменится скольжением.

Рис. 1. Измерение силы трения при помощи динамометра.

Если выстраивать строгую теорию трения скольжения, то придется учитывать ее зависимость от скорости. Но большая часть относительно простых задач решаются в приближении, когда силу трения скольжения считают равной максимальной силе сцепления.

На практике трение часто наносит ущерб. Например, оно вызывают истирание деталей. Эту проблему решают либо добавлением смазки, либо подшипниками. Во втором случае скольжение заменяется качением.

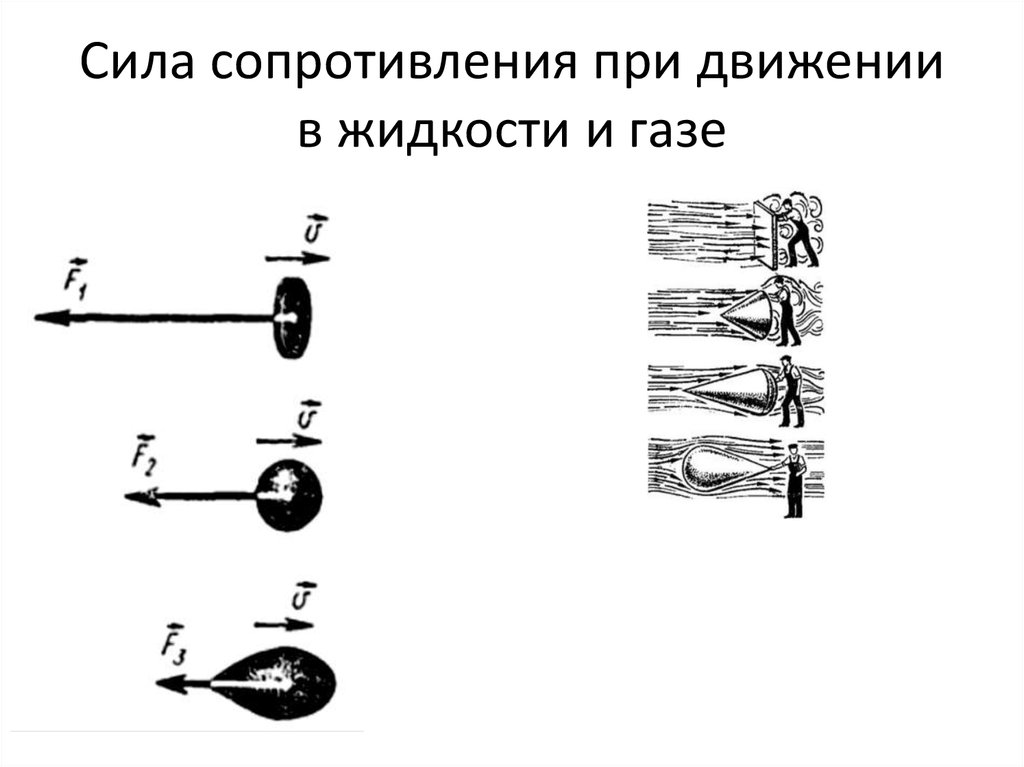
Рис. 2. Возникновение силы трения качения.

При движении в газообразной или жидкой среде возникает вязкое (жидкостное) трение, которое также называются сопротивлением среды. Оно слабее сухого трения, а главная его особенность в том, что оно зависит от скорости. В случае равенства последней нулю, сопротивление также обратится в нуль.

Расчетные формулы

Из экспериментов известно, что сила сцепления $\vec F_{тр} = – \vec F$, где F – внешняя сила.

Максимальное сцепление пропорционально силе нормальной реакции опоры, умноженной на безразмерный коэффициент $\mu$, который определяется характером поверхности трения.

$$F_{тр}= \mu N$$ – (1) формула силы трения покоя

В случае, если тело находится на наклонной поверхности, проекция силы нормальной реакции опоры на ось Оу равна: $N = mgsin \varphi$. И тогда модуль сцепления равен: $F_{тр}= \mu mgsin \varphi$ – (2).

Из вышеприведенной формулы следует, что минимальной сила трения становится, когда угол максимально близок к прямому.

Рис. 3. Сила сцепления на наклонной поверхности.

Силу трения скольжения считают приблизительно равной предельному сцеплению, то есть находится она по формулам (1) и (2). Силой трения качения же на практике часто пренебрегают. При необходимости учета ее влияния пользуются следующей формулой:

$F_{тр} = {\mu \over R}N$,
где R – радиус катящегося (качающегося) тела, а $\mu$ – коэффициент, имеющий размерность радиуса.

Для силы вязкого трения, когда скорости невелики, формула для нахождения записывается так:

$F_{тр1} = k_1v$,
где $k_1$ – коэффициент жидкостного трения.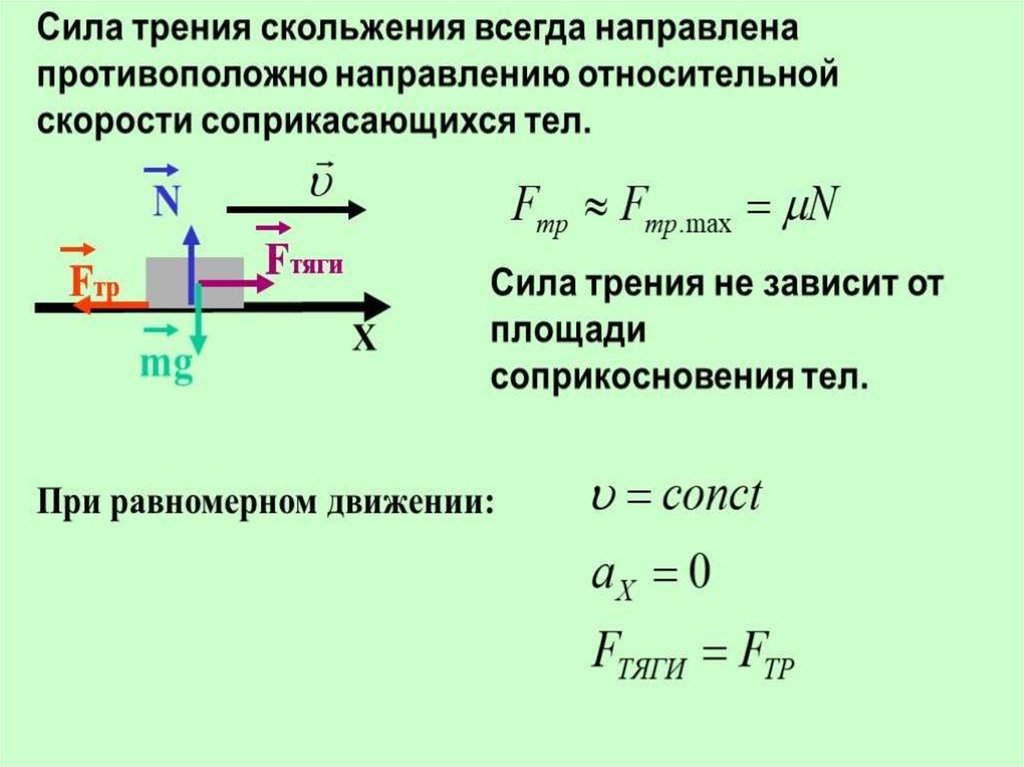 2$$,
где $k_2$ – коэффициент жидкостного трения при больших скоростях.

Задачи

• Кирпич скатывается по деревянной поверхности, которая наклонена к горизонтали под углом 45 градусов. Масса кирпича – 200 грамм, коэффициент трения – 0,5. С каким ускорением он движется?

Решение первой задачи

Схема решения этой задачи та же, по которой решаются большинство задач на основное уравнение динамики.

Ось Оy проведем через вектор силы нормальной реакции опоры, Ось Ох – через вектор ускорения кирпича. Запишем второй закон Ньютона в векторной форме:

$$m \vec a = \vec F_{тр} + m \vec g + \vec N$$

И в проекциях на оси:

Ox: $ma = mgcos \varphi – \mu N$

Oy: $N=mgsin \varphi$

Учитывая уравнение на оси Оу запишем:

$$ma = mgcos \varphi – \mu mgcos \varphi = mg(cos \varphi – \mu sin \varphi)$$

$$a = g(cos \varphi – \mu sin \varphi) = 3,5 м/c$$

• Человек массой 100 кг совершил прыжок с парашютом. 2$$

  Тогда:

  $$v_1 = \sqrt{mg \over k_1} = 14,14 м/с$$

  $$v_2 = \sqrt{mg \over k_2} = 1,38 м/c$$

  Что мы узнали?

  В ходе урока выяснили, как возникают силы трения, установили закон действия этих сил. После чего разделили силы трения на два вида – силы сухого трения и силы жидкостного трения, а также рассмотрели формулы, по которым производится их расчет. В закрепление урока разобрали две несложные задачи.

  Тест по теме

  Доска почёта

  Чтобы попасть сюда — пройдите тест.

  Пока никого нет. Будьте первым!

  Оценка доклада

  4.7

  Средняя оценка: 4.7

  Всего получено оценок: 235.

  ---

  А какая ваша оценка?

  Видео-вопрос: Определение средней силы сопротивления тела, падающего в жидкость

  Стенограмма видео

  Шариковый подшипник массой 150 грамм падает в трубку, заполненную маслом. Шариковый подшипник ударяется о поверхность масла с вертикальной нисходящей скоростью 1,5 метра в секунду. А после провала масла в течение 1,5 секунд скорость шарикоподшипника становится 6,3 метра в секунду. Какая средняя сила сопротивления по вертикали вверх действует на шариковый подшипник?

  Итак, в этом вопросе много информации. Итак, давайте подчеркнем все важные моменты, чтобы ничего не пропустить. Итак, во-первых, мы знаем, что у нас есть шарикоподшипник массой 150 грамм. И мы знаем, что он упал в трубу, наполненную маслом. Нам также говорят, что шарикоподшипник ударяется о поверхность масла с вертикальной нисходящей скоростью 1,5 метра в секунду. И после провала масла в течение 1,5 секунд шарикоподшипник теперь имеет скорость 6,3 метра в секунду.

  Нас попросили рассчитать среднюю вертикально восходящую силу сопротивления, приложенную маслом к ​​шарикоподшипнику. Теперь давайте очень лаконично запишем всю эту важную информацию. Во-первых, мы знаем массу шарикоподшипника, которую назовем 𝑚. А это 150 грамм. Во-вторых, мы знаем скорость, с которой шарикоподшипник ударяется о поверхность масла. Мы назовем это 𝑢. И мы знаем, что это 1,5 метра в секунду. В-третьих, мы знаем, что шарикоподшипник продолжает падать в масло в течение времени, которое мы обозначим 𝑡, равного 1,5 секундам.

  Мы также знаем, что после того, как этот мяч пробыл в масле 1,5 секунды, его скорость стала 6,3 метра в секунду. И мы назовем это 𝑣. Нас попросили рассчитать 𝐹 вспомогательное сопротивление, которое мы будем называть вертикально восходящей силой сопротивления. Мы могли бы также нарисовать небольшую диаграмму, которая поможет нам ответить на этот вопрос. Итак, наша трубка. Вот это масло. А вот шариковый подшипник, когда он впервые попадает на поверхность масла. Мы знаем, что он имеет массу 𝑚. А его начальную скорость мы назовем 𝑢.

  Затем он продолжает движение в течение времени, которое мы назовем 𝑡. И в этот момент у него есть скорость, которую мы назвали 𝑣. Теперь, на данный момент, мы в основном высосали вопрос из любой полезной информации. Так что мы можем избавиться от него. Ах! Так намного лучше! Посмотрите, сколько места у нас теперь для работы! Итак, обо всем по порядку. Заметим, что шарикоподшипник, когда он падает в трубку с маслом, меняет скорость. Первоначально он имел скорость 𝑢, а затем скорость 𝑣.

  Это означает, что шарикоподшипник ускоряется. И мы можем вычислить, каково это ускорение. Ускорение, которое мы будем называть 𝑎, определяется как Δ𝑣, изменение скорости, деленное на время, необходимое для этого изменения скорости, 𝑡. Теперь мы можем сказать, что 𝑎, следовательно, равно, что ж, изменение скорости — это просто конечная скорость, которая равна 𝑣, минус начальная скорость, которая равна 𝑢, и затем мы делим это на время, необходимое для того, чтобы эта скорость достигла изменение, которое является 𝑡.

  Сейчас мы пока не будем подставлять числа, потому что хотим работать с символами как можно дольше, чтобы наша математика не запуталась. Так или иначе, у нас есть формула, которая дает нам ускорение шарикоподшипника через масло. Почему это полезно? Хорошо, если мы знаем ускорение шарикоподшипника, то мы можем вычислить результирующую силу, действующую на шарикоподшипник, используя так называемый второй закон Ньютона. Второй закон Ньютона говорит нам, что результирующая сила, действующая на объект, 𝐹, равна массе объекта 𝑚, умноженной на ускорение объекта 𝑎.

  Вот мы и выяснили, что такое 𝑎. И мы знаем, какова масса объекта, 𝑚. Таким образом, мы можем определить результирующую силу, действующую на объект. В данном случае, конечно, нашим объектом является шарикоподшипник. Поэтому мы говорим, что результирующая сила равна 𝑚𝑎. И мы можем подставить то, что есть 𝑎, в результате чего 𝐹 будет равно 𝑚, умноженному на 𝑣 минус 𝑢 над 𝑡. Итак, мы на шаг ближе к тому, чтобы узнать значение 𝐹 субперетаскивания.

  Однако то, что мы нашли здесь справа, это просто равнодействующая сила. Это чистая сила, действующая на шарикоподшипник. Если мы немного приблизимся к шарикоподшипнику, то сможем рассмотреть силы, действующие на этот шарикоподшипник, когда он ускоряется в масле. Что ж, одной из сил, естественно, должен быть вес шарикоподшипника, который мы назовем 𝑊. И мы можем вспомнить, что вес объекта 𝑊 определяется путем умножения массы объекта на 𝑔, что является силой гравитационного поля Земли. Итак, на подшипник действует еще одна сила — вес 𝑊, который, скажем, равен 𝑚𝑔.

  Другая сила, которая должна воздействовать на шарикоподшипник, называется силой сопротивления. И эта сила противодействует движению шарикоподшипника. Итак, мы знаем, что шарикоподшипник движется в этом направлении вниз. И сила сопротивления будет сопротивляться этому движению. Таким образом, сила сопротивления будет действовать вертикально вверх. Мы назовем это 𝐹 sub drag. И это мы пытаемся выяснить. Теперь важно отметить, что вопрос задавался нам только для того, чтобы найти среднюю силу сопротивления, а это означает, что мы можем технически предположить здесь, в этом вопросе, что сила сопротивления на шарикоподшипнике остается постоянной, 𝐹 вспомогательное сопротивление.

  И мы можем сделать это, потому что мы также предположили, что ускорение 𝑎 шарикоподшипника постоянно. Теперь это технически неверно. Ускорение изменяется, потому что сила сопротивления шарикоподшипнику изменяется, а скорость шарикоподшипника увеличивается. Но чтобы упростить наш сценарий, мы просто предположили, что ускорение постоянно, а вспомогательное сопротивление 𝐹 постоянно. А это средняя сила сопротивления. Мы также знаем, что это средняя сила сопротивления, потому что у нас есть значения скорости шарикоподшипника здесь и здесь, и, как мы уже говорили ранее, мы просто предположили постоянное ускорение между этими двумя точками.

  В любом случае это просто упрощает нашу задачу. Теперь давайте вернемся к рассмотрению двух сил, действующих на шарикоподшипник, веса и силы сопротивления. Ну, эти две силы в основном конкурируют друг с другом. Один действует вниз, что представляет собой вес, а другой действует вверх, что представляет собой силу сопротивления. Итак, если мы объединим эти силы, то сможем узнать, какова результирующая сила. Мы можем сказать, что результирующая сила, которую мы знаем, это то, что мы назвали 𝐹, потому что это то, что мы рассчитали, используя второй закон Ньютона. Это 𝐹 здесь и 𝐹 здесь.

  И мы можем сказать, что это 𝐹 равно равнодействующей двух сил 𝑊 и 𝐹 дополнительного сопротивления. Однако 𝑊 действует в нисходящем направлении. Поэтому мы назовем это положительным 𝑊, а 𝐹 дополнительное сопротивление действует в восходящем направлении. Так что вычитаем. Другими словами, мы предположили, что любая сила, действующая вниз, положительна, а любая сила, действующая вверх, отрицательна. Поэтому также стоит отметить, что мы предположили, что 𝑊 и 𝐹 вспомогательное сопротивление — это просто величины или размеры сил. Другими словами, мы не учли тот факт, что они работают в определенном направлении.

  Но это нормально, потому что мы учли это с помощью стрелок, которые нарисовали на диаграмме. В любом случае, возвращаясь к этому выражению здесь для 𝐹, мы можем изменить порядок, чтобы узнать, что такое субперетаскивание 𝐹. Для этого мы можем сначала добавить вспомогательное перетаскивание 𝐹 к обеим сторонам уравнения, что означает, что вспомогательное перетаскивание 𝐹 отменяется с правой стороны и оставляет нас с дополнительным перетаскиванием 𝐹 плюс 𝐹 равным 𝑊, весу. Тогда мы можем вычесть 𝐹 из обеих частей, что означает, что 𝐹 сокращается из левой части уравнения. И, следовательно, у нас осталось 𝐹 вспомогательное сопротивление, средняя сила сопротивления на шарикоподшипнике, равна 𝑊, весу шарикоподшипника, минус 𝐹, общая результирующая сила на шарикоподшипнике.

  Теперь мы можем подставить все выражения, которые у нас уже есть. 𝐹 дополнительное сопротивление равно 𝑚𝑔, то есть весу, минус 𝑚, умноженному на 𝑣 минус 𝑢 сверх 𝑡, который является результирующей силой. На данный момент мы знаем все значения в правой части уравнения. Мы знаем 𝑚. Мы знаем 𝑔. Мы снова знаем 𝑚. Мы знаем, что такое 𝑣. Мы знаем, что такое 𝑢. И мы знаем, что такое 𝑡. Таким образом, мы могли бы с радостью подставить все значения и выяснить, что такое 𝐹 sub drag. Но прежде чем мы это сделаем, давайте отметим кое-что о значении 𝑚.

  Значение указано в граммах. Теперь это не идеально для нас. Мы хотим преобразовать это в стандартную единицу массы, которая является килограммом. Итак, чтобы сделать это, мы должны вспомнить, что один килограмм равен 1000 граммам. Итак, если мы разделим обе части этого уравнения на 1000, мы получим, что одна тысячная часть килограмма равна одному грамму. Но мы хотим знать, сколько 𝑚 в килограммах. Другими словами, мы хотим знать, сколько 150 граммов в килограммах. К счастью, мы можем узнать это, умножив обе части уравнения на 150. Таким образом, мы находим, что 150 граммов равны 150 на 1000 килограммов. В итоге получается 0,15 кг.

  И на данный момент у нас есть все остальные значения в их стандартных единицах. 𝑢 и 𝑣 в метрах в секунду, а 𝑡 в секундах. Таким образом, мы можем подставить все значения в это уравнение справа. Это дает нам следующее: у нас есть 𝑚, умноженное на 𝑔, что составляет 9,8 метра в секунду в квадрате, это сила гравитационного поля Земли минус 𝑚, умноженная на 𝑣 минус 𝑢 над 𝑡.

  Это все наши ценности. поэтому мы можем оценить это, чтобы дать нам значение 𝐹 sub drag как 0,99 ньютонов. И мы знаем, что это в ньютонах, потому что мы использовали стандартные единицы для всех других величин. Поэтому нам не нужно беспокоиться о единицах измерения. Мы просто поставили ньютоны, которые являются стандартной единицей силы, в конце нашего расчета. И, следовательно, наш окончательный ответ заключается в том, что средняя сила восходящего сопротивления шарикоподшипника составляет 0,99 ньютона.

  6.4 Сила сопротивления и предельная скорость — University Physics Volume 1

  Цели обучения

  К концу этого раздела вы сможете:

  • Выразите силу сопротивления математически
  • Описать применение силы сопротивления
  • Определить конечную скорость
  • Определить конечную скорость объекта по его массе

  Другой интересной силой в повседневной жизни является сила сопротивления объекта, когда он движется в жидкости (газе или жидкости). Вы чувствуете силу сопротивления, когда проводите рукой по воде. Вы также можете почувствовать это, если пошевелите рукой во время сильного ветра. Чем быстрее вы двигаете рукой, тем труднее двигаться. Вы чувствуете меньшую силу сопротивления, когда наклоняете руку так, чтобы только сторона проходила через воздух — вы уменьшили площадь своей руки, обращенную в направлении движения.

  Силы сопротивления

  Как и трение, сила сопротивления всегда противодействует движению объекта. В отличие от простого трения, сила сопротивления пропорциональна некоторой функции скорости объекта в этой жидкости. Эта функциональность сложна и зависит от формы объекта, его размера, его скорости и жидкости, в которой он находится. Для большинства крупных объектов, таких как велосипедисты, автомобили и бейсбольные мячи, движущихся не слишком медленно, величина силы сопротивления FDFD пропорциональна квадрату скорости тела. Мы можем записать это соотношение математически как FD∝v2.FD∝v2. При учете других факторов эта связь становится

  ФД=12CρAv2,ФД=12CρAv2,

  6,5

  , где C — коэффициент сопротивления, A — площадь объекта, обращенного к жидкости, а ρρ — плотность жидкости. (Напомним, что плотность — это масса на единицу объема.) Это уравнение также можно записать в более обобщенном виде: FD=bvn, FD=bvn, где b — константа, эквивалентная 0,5CρA. 0,5CρA. Мы установили показатель степени n для этих уравнений равным 2, потому что, когда объект движется с высокой скоростью в воздухе, величина силы сопротивления пропорциональна квадрату скорости. Как мы увидим в механике жидкости, для малых частиц, движущихся в жидкости с малыми скоростями, показатель степени n равно 1.

  Сила сопротивления

  Сила сопротивления FDFD пропорциональна квадрату скорости объекта. Математически

  FD=12CρAv2,FD=12CρAv2,

  , где C — коэффициент сопротивления, A — площадь объекта, обращенного к жидкости, а ρρ — плотность жидкости.

  Спортсмены, а также конструкторы автомобилей стремятся уменьшить силу сопротивления, чтобы сократить время гонки (рис. 6.29). Аэродинамическая форма автомобиля может уменьшить силу сопротивления и, таким образом, увеличить расход топлива автомобиля.

  Рисунок 6,29 От гоночных автомобилей до гонщиков бобслея аэродинамическая форма имеет решающее значение для достижения максимальной скорости. Бобслей создан для скорости и имеет форму пули с коническими плавниками. (кредит: «Армия США»/Wikimedia Commons)

  Значение коэффициента сопротивления C определяется опытным путем, обычно с применением аэродинамической трубы (рис. 6.30).

  Рисунок 6.30 Исследователи НАСА тестируют модель самолета в аэродинамической трубе. (кредит: НАСА/Эймс)

  Коэффициент лобового сопротивления может зависеть от скорости, но мы предполагаем, что здесь он является константой. В таблице 6.2 перечислены некоторые типичные коэффициенты сопротивления для различных объектов. Обратите внимание, что коэффициент сопротивления является безразмерной величиной. На шоссейных скоростях более 50% 50% мощности автомобиля используется для преодоления сопротивления воздуха. Наиболее экономичная крейсерская скорость составляет около 70–80 км / ч (около 45–50 миль / ч). По этой причине во время нефтяного кризиса 1970-х годов в Соединенных Штатах максимальная скорость на шоссе была установлена ​​на уровне около 9 км/ч.0 км/ч (55 миль/ч).

  Объект	С
  Аэродинамический профиль	0,05
  Тойота Камри	0,28
  Форд Фокус	0,32
  Хонда Сивик	0,36
  Феррари Тестаросса	0,37
  Пикап Додж Рэм	0,43
  Сфера	0,45
  Внедорожник Hummer h3	0,64
  Парашютист (ноги вперед)	0,70
  Велосипед	0,90
  Парашютист (горизонтальный)	1,0
  Круглая плоская пластина	1,12

  Стол 6. 2 Типичные значения коэффициента лобового сопротивления C

  В спортивном мире ведутся масштабные исследования по минимизации сопротивления. Ямочки на мячах для гольфа переделываются, как и одежда, которую носят спортсмены. Велогонщики, а также некоторые пловцы и бегуны носят полные боди. Австралийка Кэти Фриман носила полный костюм на Олимпийских играх 2000 года в Сиднее и выиграла золотую медаль в беге на 400 метров. Многие пловцы на Олимпийских играх 2008 года в Пекине носили комбинезоны (спидометры); это могло бы иметь значение для побития многих мировых рекордов (рис. 6.31). Большинство элитных пловцов (и велосипедистов) бреют волосы на теле. Такие инновации могут сократить миллисекунды в гонке, иногда определяя разницу между золотой и серебряной медалью. Одним из следствий этого является то, что для поддержания целостности спорта необходимо постоянно разрабатывать тщательные и точные правила.

  Рисунок 6.31 Боди-костюмы, такие как этот LZR Racer Suit, помогли установить множество мировых рекордов после их выпуска в 2008 году. Более гладкая «кожа» и большее усилие сжатия на теле пловца обеспечивают как минимум на 10 % 10 % меньше сопротивления. (кредит: НАСА/Кэти Барнсторфф)

  Конечная скорость

  Некоторые интересные ситуации, связанные со вторым законом Ньютона, возникают при рассмотрении действия сил сопротивления на движущийся объект. Например, рассмотрим парашютиста, падающего в воздухе под действием силы тяжести. На него действуют две силы: сила тяжести и сила сопротивления (без учета малой выталкивающей силы). Нисходящая сила тяжести остается постоянной независимо от скорости, с которой движется человек. Однако по мере увеличения скорости человека величина силы сопротивления увеличивается до тех пор, пока величина силы сопротивления не сравняется с силой гравитации, что приводит к нулевой чистой силе. Нулевая результирующая сила означает, что ускорения нет, как показывает второй закон Ньютона. В этот момент скорость человека остается постоянной, и мы говорим, что человек достиг своей конечной скорости (vT). (vT). Поскольку FDFD пропорционален квадрату скорости, более тяжелый парашютист должен двигаться быстрее, чтобы FDFD сравнялся с его весом. Давайте посмотрим, как это работает более количественно.

  На предельной скорости,

  Fnet=mg-FD=ma=0.Fnet=mg-FD=ma=0.

  Таким образом,

  мг=ФД.мг=ФД.

  Используя уравнение для силы сопротивления, мы имеем

  мг=12CρAvT2.мг=12CρAvT2.

  Решая скорость, получаем

  vT=2мгρCA.vT=2мгρCA.

  Предположим, что плотность воздуха ρ=1,21 кг/м3. ρ=1,21 кг/м3. Парашютист весом 75 кг, спускающийся вниз головой вперед, имеет площадь поперечного сечения приблизительно A=0,18 м2, A=0,18 м2 и коэффициент сопротивления приблизительно C=0,70C=0,70. Мы находим, что

  vT=2(75кг)(9,80м/с2)(1,21кг/м3)(0,70)(0,18м2)=98м/с=350км/ч.vT=2(75кг)(9,80м/с2)(1,21кг /м3)(0,70)(0,18м2)=98м/с=350км/ч.

  Это означает, что парашютист массой 75 кг достигает конечной скорости около 350 км/ч, путешествуя головой вперед, сводя к минимуму площадь и сопротивление. В расправленном положении эта конечная скорость может уменьшиться примерно до 200 км/ч по мере увеличения площади. Эта конечная скорость становится намного меньше после раскрытия парашюта.

  Пример 6.17

  Предельная скорость парашютиста

  Найдите конечную скорость парашютиста массой 85 кг, падающего с распростертым орлом. Предположим, что в положении орла ныряльщик имеет площадь поперечного сечения 0,70 м20,70 м2.

  Стратегия

  При конечной скорости Fnet=0.Fnet=0. Таким образом, сила сопротивления парашютиста должна равняться силе тяжести (весу человека). Используя уравнение силы сопротивления, находим mg=12ρCAv2.mg=12ρCAv2.

  Решение

  Конечная скорость vTvT может быть записана как

  vT=2мгρCA=2(85кг)(9,80м/с2)(1,21кг/м3)(1,0)(0,70м2)=44м/с.vT=2мгρCA=2(85кг)(9,80м/с2)(1,21 кг/м3)(1,0)(0,70м2)=44м/с.

  Значение

  Этот результат согласуется со значением для vTvT, упомянутым ранее. Парашютист весом 75 кг, идущий вперед ногами, имел конечную скорость vT=98 м/с. vT=98 м/с. Он весил меньше, но имел меньшую лобовую площадь и, следовательно, меньшее сопротивление воздуха.

  Проверьте свое понимание 6.10

  Найдите предельную скорость 50-килограммового парашютиста, падающего распростертым орлом.

  Размер объекта, падающего в воздухе, представляет собой еще одно интересное применение сопротивления воздуха. Если вы упадете с 5-метровой ветки дерева, вы, скорее всего, поранитесь — возможно, сломаете кость. Однако маленькая белка делает это все время, не причиняя себе вреда. Вы не достигаете конечной скорости на таком коротком расстоянии, а белка достигает.

  Следующая интересная цитата о размерах животных и конечной скорости взята из эссе 1928 года британского биолога Дж. Б. С. Холдейна, озаглавленного «О правильном размере».

  «Для мышей и любых мелких животных [гравитация] практически не представляет опасности. Вы можете бросить мышь в шахту длиной в тысячу ярдов; и, достигнув дна, он получает легкий толчок и уходит, при условии, что земля достаточно мягкая. Крыса убита, человек разбит, а лошадь забрызгана. Ибо сопротивление воздуха движению пропорционально поверхности движущегося объекта. Разделите длину, ширину и высоту животного на десять; его вес уменьшен в тысячную, а поверхность только в сотые. Таким образом, сопротивление падению маленького животного относительно в десять раз больше, чем движущая сила».

  Приведенная выше квадратичная зависимость сопротивления воздуха от скорости не выполняется, если объект очень мал, движется очень медленно или находится в более плотной среде, чем воздух. Тогда мы находим, что сила сопротивления прямо пропорциональна скорости. Эта зависимость определяется законом Стокса.

  Закон Стокса

  Для сферического объекта, падающего в среду, сила сопротивления равна

  Fs=6πrηv,Fs=6πrηv,

  6,6

  где r — радиус объекта, ηη — вязкость жидкости, а v — скорость объекта.

  Хорошими примерами закона Стокса являются микроорганизмы, пыльца и частицы пыли. Поскольку каждый из этих объектов очень мал, мы обнаруживаем, что многие из этих объектов движутся без посторонней помощи только с постоянной (конечной) скоростью. Конечная скорость для бактерий (размером около 1 мкм) (1 мкм) может составлять около 2 мкм/с. 2 мкм/с. Чтобы двигаться с большей скоростью, многие бактерии плавают с помощью жгутиков (органелл в форме маленьких хвостов), которые приводятся в действие небольшими двигателями, встроенными в клетку.

  Осадок в озере может двигаться с большей конечной скоростью (около 5 мкм/с), 5 мкм/с, поэтому может пройти несколько дней, прежде чем он достигнет дна озера после отложения на поверхности.

  Если мы сравним животных, живущих на суше, с животными, живущими в воде, то увидим, как сопротивление повлияло на эволюцию. Рыбы, дельфины и даже массивные киты имеют обтекаемую форму, чтобы уменьшить силы сопротивления. Птицы имеют обтекаемую форму, а мигрирующие виды, которые летают на большие расстояния, часто имеют особые черты, такие как длинная шея. Стаи птиц летят в форме наконечника копья, образуя обтекаемую форму (рис. 6.32). У людей одним из важных примеров упорядочения является форма сперматозоидов, которые должны эффективно использовать энергию.

  Рисунок 6.32 Гуси летят V-образным строем во время своих длительных миграционных путешествий. Эта форма снижает сопротивление и потребление энергии для отдельных птиц, а также позволяет им лучше общаться. (кредит: модификация работы «Julo»/Wikimedia Commons)

  Интерактивный

  На демонстрациях лекций мы проводим измерения силы сопротивления различных объектов. Объекты помещаются в однородный воздушный поток, создаваемый вентилятором. Вычислите коэффициент сопротивления.

  Расчет сил трения, зависящих от скорости

  Когда тело скользит по поверхности, сила трения на нем приблизительно постоянна и определяется выражением µkN.µkN. К сожалению, сила трения на тело, движущееся через жидкость или газ, не ведет себя так просто. Эта сила сопротивления обычно является сложной функцией скорости тела. Однако для тела, движущегося по прямой с умеренной скоростью через жидкость, например воду, сила трения часто может быть приблизительно равна

  fR=-bv,fR=-bv,

  , где b — постоянная, значение которой зависит от размеров и формы тела и свойств жидкости, а v — скорость тела. Две ситуации, для которых сила трения может быть представлена ​​этим уравнением, — это моторная лодка, движущаяся по воде, и небольшой объект, медленно падающий через жидкость.

  Рассмотрим объект, падающий через жидкость. Диаграмма свободного тела этого объекта с положительным направлением вниз показана на рис. 6.33. Второй закон Ньютона в вертикальном направлении дает дифференциальное уравнение

  мг-бв=мдвдт, мг-бв=мдвдт,

  , где мы записали ускорение как dv/dt.dv/dt. По мере увеличения против сила трения – bv увеличивается до тех пор, пока не совпадет с мг . В этот момент ускорение отсутствует, и скорость остается постоянной на уровне конечной скорости vT.vT. Из предыдущего уравнения

  мг-бвТ=0,мг-бвТ=0,

  так

  vT=mgb.vT=mgb.

  Рисунок 6.33 Схема свободного тела объекта, падающего через резистивную среду.

  Мы можем найти скорость объекта, интегрируя дифференциальное уравнение для v . Во-первых, мы переставляем члены в этом уравнении, чтобы получить

  dvg-(b/m)v=dt.dvg-(b/m)v=dt.

  Предполагая, что v=0att=0,v=0att=0, интегрирование этого уравнения дает

  ∫0vdv′g−(b/m)v′=∫0tdt′,∫0vdv′g−(b/m)v′=∫0tdt′,

  или

  −mbln(g−bmv′)|0v=t′|0t,−mbln(g−bmv′)|0v=t′|0t,

  , где v’andt’v’andt’ — фиктивные переменные интегрирования. В заданных пределах находим

  -mb[ln(g-bmv)-lng]=t.-mb[ln(g-bmv)-lng]=t.

  Поскольку lnA−lnB=ln(A/B),lnA−lnB=ln(A/B) и ln(A/B)=ximpliesex=A/B, ln(A/B)=ximpliesex=A/B , получаем

  g-(bv/m)g=e-bt/m,g-(bv/m)g=e-bt/m,

  и

  v=mgb(1-e-bt/м). v=mgb(1-e-bt/м).

  Обратите внимание, что при t→∞,v→mg/b=vT,t→∞,v→mg/b=vT, что является конечной скоростью.

  Позиция в любое время может быть найдена путем интегрирования уравнения для v . С v=dy/dt, v=dy/dt,

  dy=mgb(1−e−bt/m)dt.dy=mgb(1−e−bt/m)dt.

  Предполагая, что y=0, когда=0, y=0, когда=0,

  ∫0ydy’=mgb∫0t(1-e-bt’/m)dt’, ∫0ydy’=mgb∫0t(1-e-bt’/m)dt’,

  , который интегрируется в

  y=mgbt+m2gb2(e−bt/m−1).y=mgbt+m2gb2(e−bt/m−1).

  Пример 6.18

  Воздействие силы сопротивления на моторную лодку

  Моторная лодка движется по озеру со скоростью v0v0, когда ее мотор внезапно замерзает и останавливается. Затем лодка замедляется под действием силы трения fR=−bv.fR=−bv. а) Каковы скорость и положение лодки как функции времени? б) Если за 10 с скорость лодки уменьшается с 4,0 до 1,0 м/с, какой путь она пройдет до остановки?

  Решение

  1. При остановленном двигателе единственная горизонтальная сила, действующая на лодку, равна fR=−bv,fR=−bv, поэтому, согласно второму закону Ньютона,

     мдвдт=-бв, мдвдт=-бв,

     который мы можем записать как

     dvv=-bmdt. dvv=-bmdt.

     Интегрируя это уравнение между нулевым моментом времени, когда скорость равна v0v0, и временем t , когда скорость равна vv, мы имеем

     ∫0vdv′v′=−bm∫0tdt′.∫0vdv′v′=−bm∫0tdt′.

     Таким образом,

     lnvv0=-bmt,lnvv0=-bmt,

     что, поскольку lnA=ximpliesex=A,lnA=ximpliesex=A, мы можем записать это как

     v=v0e-bt/m.v=v0e-bt/m.

     Теперь из определения скорости

     dxdt=v0e-bt/м, dxdt=v0e-bt/м,

     так что у нас есть

     dx=v0e-bt/mdt.dx=v0e-bt/mdt.

     С начальным положением ноль имеем

     ∫0xdx’=v0∫0te-bt’/mdt’, ∫0xdx’=v0∫0te-bt’/mdt’,

     и

     x=-mv0be-bt’/m|0t=mv0b(1-e-bt/m).x=-mv0be-bt’/m|0t=mv0b(1-e-bt/m).

     С увеличением времени e−bt/m→0,e−bt/m→0, и положение лодки приближается к предельному значению

     хмакс=mv0b.xмакс=mv0b.

     Хотя это говорит нам о том, что лодке требуется бесконечное количество времени, чтобы достичь xmax,xmax, лодка эффективно останавливается через разумное время. Например, при t=10м/б, t=10м/б имеем

     v=v0e-10≃4,5×10-5v0,v=v0e-10≃4,5×10-5v0,

     тогда как у нас также есть

     x=xmax(1−e−10)≃0,99995xmax. x=xmax(1−e−10)≃0,99995xmax.

     Таким образом, скорость и положение лодки практически достигли своих конечных значений.
  2. При v0=4,0 м/sv0=4,0 м/с и v=1,0 м/с, v=1,0 м/с получаем 1,0 м/с=(4,0 м/с)e−(b/м)(10 с ), 1,0 м/с = (4,0 м/с) e−(b/m)(10 с), поэтому

     ln0.25=-ln4.0=-bm(10s),ln0.25=-ln4.0=-bm(10s),

     и

     bm=110ln4.0s-1=0.14s-1.bm=110ln4.0s-1=0.14s-1.

     Теперь предельное положение лодки

     xmax=mv0b=4,0 м/с0,14с-1=29м.xmax=mv0b=4,0м/с0,14с-1=29м.

  Значение

  В обоих предыдущих примерах мы нашли «предельные» значения. Конечная скорость такая же, как и предельная скорость, то есть скорость падающего объекта по прошествии (относительно) длительного времени. Точно так же предельное расстояние лодки — это расстояние, которое лодка пройдет по прошествии большого количества времени. Из-за свойств экспоненциального затухания время, необходимое для достижения любого из этих значений, на самом деле не слишком велико (конечно, не бесконечное количество времени!), но они быстро находятся, если довести предел до бесконечности.