Средняя скорость машины: Средняя скорость — онлайн калькулятор

Содержание

Как определить среднюю скорость. Как найти среднюю скорость

Средняя скорость — машина

Средняя скорость машин ЕС-1030 по Гибсону составляет 100 тыс. операций в секунду.
 

Под средней скоростью машины понимают среднюю линейную скорость одной из точек ведущего вала машины во время ее установившегося движения.
 

Для того чтобы средняя скорость машины могла оставаться постоянной, необходимо, чтобы при этой скорости имело место равновесие между работой движущих сил и работой сопротивлений. Но это равновесие может нарушаться по различным причинам.
 

Для установления козфициента нагрузки двигателя определим среднюю скорость машины v — кгк, момент трения по формуле ( 55), угловую скорость машины ( см. фиг.
 

Очевидно, что такая система позволяет на уровне программирования заботиться о том, чтобы информация была заранее считана в быстрые регистры операндов и арифметическое устройство не ожидало ее поступления из памяти. Средняя скорость машины CDC-6600

оценивается в 3 5 млн. операций в секунду, однако, как утверждают разработчики, при оптимальном программировании она может быть значительно повышена.
 

Сравнение формул ( 52) и ( 58) дает следующий вывод: коэфициент нагрузки двигателя на повороте при бортовых фрикционах в два раза меньше, чем при простом дифе-ренциале. Это снижение нагрузки достигается за счет снижения потери в тормозе, а также вследствие понижения средней скорости машины на повороте. Зависимость между коэ-фициентами нагрузки двигателя и параметром поворота показана на диаграмме фиг.
 

Регуляторы являются приборами, предназначенными для того, чтобы удерживать в возможно близких друг к другу пределах изменения средней скорости машины, вызванные изменениями движущих сил или сил сопротивлений.
 

Если бы движение машины было равномерно, если бы она шла всегда одинаково быстро, то оценка 40 км в час полностью характеризовала бы ее скорость — одну и ту же в любой момент движения. Но машина движется неравномерно; за час скорость ее много раз резко меняется, и когда нам говорят, что машина прошла в час 40 км, то это дает нам представление лишь о некоторой

средней скорости машины за этот час и ничего не говорит о скорости ее в тот или другой определенный момент, в том или другом определенном месте ее пути. Час — это слишком большой промежуток времени, за который скорость движения машины может меняться много раз.
 

Средняя скорость машины при выполнении арифметики тем самым приблизительно равна 10000 операций в секунду. При выполнении логических программ быстродействие резко возрастает. В минимальном комплекте в состав процессора входит оперативная память объемом 8192 байта. Правда, объем памяти при необходимости может быть расширен до 64 Кбайт.
 

На маршруте ABCDE длиной 147 км Турист может сам выбирать способ передвижения. На обратном пути из пункта Е в пункт А он поступил по-другому: до пункта D дошел пешком, преодолев расстояние в 24 км, в пункте D пересел на лошадь и добрался до пункта В за 3 ч 20 мин, а от пункта Л до пункта А доехал на машине за 1 ч 12 мин. Определите скорость передвижения туриста на машине и на лошади, если

средние скорости машины и лошади были постоянными при движении от А к S и обратно.
 

Находим среднюю скорость и средний расход поездки по факту

Если замеры средней скорости поездки важны для вас в коммерческих целях или в качестве отчетности для фирмы, в которой вы работаете, то проще всего купить GPS-навигатор, который обладает функцией учета скорости и времени, проведенного в дороге. Этот прибор полностью заменит бортовой компьютер и сможет без применения различных формул показать вам среднюю скорость поездки.

В иных случаях можно пользоваться более грубыми методами определения. Для замеров вам потребуется секундомер, который будет определять рабочее время поездки. То есть, для нас важна каждая секунда, которую автомобиль проводит в дороге. Время, проведенное на заправках или в придорожных кафе зачастую в расчет не входит. Задачи для точного замера следующие:

  • перед поездкой сбросьте суточный счетчик километров на нуль, начните новый отчет пробега;
  • установите на приборной панели автомобиля секундомер и не забывайте включать его каждый раз, когда трогаетесь;
  • как только вы остановились не по причине дорожной обстановки, а по собственному желанию, выключайте секундомер;
  • после прибытия в пункт назначения выпишите данные суточного счетчика с точностью до одного километра;
  • также выпишите данные секундомера с точностью до минуты — это даст вам возможность развязать уравнение;
  • подставьте полученные данные в формулу Vсредняя = S / t, где V — это средняя скорость, S — пройденное расстояние, а t — затраченное на поездку время.

Предположим, на поездку у вас ушло ровно 5 часов, а пройденное по спидометру расстояние оказалось 300 километров. Это значит, что средняя скорость вашего автомобиля во время движения составила 60 км/ч. Если вы будете практиковать определение средней скорости для каждой дальней поездки, то будете удивлены низкими показателями.

Часто создается впечатление, что средняя скорость должна быть около 120 километров в час, но на деле оказывается меньше 60. Подобным образом вы сможете просчитать средний расход топлива. Нужно затраченные литры поделить на сотни километров пройденного расстояния. К примеру, если вы проехали 300 километров, то делать сумму литров нужно на 3.

Для чего это нужно

Такие расчеты полезны всем. Мы все время планируем свой день и перемещения. Имея дачу за городом, есть смысл узнать среднюю путевую скорость при поездках туда.

Это упростит планирование проведения выходных. Научившись находить эту величину, мы сможем быть более пунктуальными, перестанем опаздывать.

Вернемся к примеру, предложенному в самом начале, когда часть пути автомобиль проехал с одной скоростью, а другую — с иной. Такой вид задач очень часто используется в школьной программе. Поэтому, когда ваш ребенок попросит вас помочь ему с решением подобного вопроса, вам будет просто это сделать.

Сложив длины участков пути, вы получите общее расстояние. Поделив же их значения на указанные в исходных данных скорости, можно определить время, потраченное на каждый из участков. Сложив их, получим время, потраченное на весь путь.

Часто водителю необходимо отыскать такой важный показатель, как средняя скорость автомобиля после той или иной поездки. Иногда эта цифра будет важным фактом для водителя транспорта компании, а в иных случаях — просто интересное число для владельца транспортного средства. В любом случае, расчет средней скорости важен для многих водителей. В современных автомобилях, оснащенных эффективными компьютерными системами управления, достаточно просто выбрать нужный режим отображения информации на экране компьютера, чтобы узнать среднюю скорость за определенный промежуток времени или пробег.

Для вычисления средней скорости поездки на современной машине достаточно подготовиться заранее, сбросив показатели суточного пробега на нуль, а также обнулив средние данные расхода и скорости. После этого вы сможете не засекать никакого времени, а также не продумывать формулы по расчету средней скорости поездки. Тем не менее, такой вариант не всегда подходит, да и не все автомобили оснащены хорошим бортовым компьютером. Потому следует разобраться с тем, как определять среднюю скорость и прочие параметры.

Средняя скорость — движение — автомобиль

Средняя скорость движения автомобиля зависит от максимальной скорости, которую он может развить на дорогах различного качества, и от интенсивности разгона. Кроме того, на среднюю скорость автомобиля существенное влияние оказывают его тормозные свойства.

 

Средние скорости движения автомобилей приведены для дорог с усовершенствованным типом покрытия в хорошем состоянии.
 

Средняя скорость движения автомобиля составляет v км / час.
 

Средняя скорость движения автомобиля зависит от многих факторов: на нее влияют, с одной стороны, конструктивные особенности автомобиля, а с другой — дорожные условия. При испытаниях ее стремятся поддерживать максимально возможной. Чтобы полнее выяснить причины, вызывающие ограничение скорости, принято определять среднюю скорость чистого движения и среднюю техническую скорость.
 

Стремление повысить среднюю скорость движения автомобилей ( автопоездов) при одновременном увеличении их полной массы приводит к повышению мощности двигателя, что, в свою очередь, вызывает повышенные требования к трансмиссии автомобиля. Это непосредственно относится и к ведущему мосту, назначение которого состоит в изменении крутящего момента двигателя при передаче его к ведущим колесам таким образом, чтобы вместе с коробкой передач обеспечить согласование скоростной характеристики двигателя с динамической характеристикой автомобиля.

 

График, для определения нагрузочного режима трансмиссии автомобиля ( по нормали.
 

Угловую скорость рассчитываемых подшипников определяют по средней скорости движения автомобиля аа ср — с учетом соответствующего передаточного числа между валами коробки передач.
 

Эффективность действия тормозов оказывает влияние на среднюю скорость движения автомобиля, особенно в условиях городского движения.
 

Именно эта скорость имеется в виду, когда, например, говорят о средней скорости движения автомобиля

или средней скорости поезда.
 

За эквивалентное число оборотов пэкв принимается число оборотов подшипника ( вала), соответствующее средней скорости движения автомобиля на основной ( прямой) передаче.
 

Установка на шасси автомобиля двигателя повышенной мощности, ранее практиковавшаяся в Америке, повышала среднюю скорость движения автомобиля, уменьшала его износы и шумность работы, но ухудшала топливную экономичность. Последнее объясняется тем, что в двигателях большей мощности и большого рабочего объема при работе на малых нагрузках возрастает относительная величина тепловых, насосных и механических потерь.
 

Расстояние между площадками для кратковременных остановок и стоянок автомобилей зависит от интенсивности движения на дороге, средней скорости движения автомобилей, вместимости стоянки и средней продолжительности пребывания автомобиля на стоянке.
 

Зависимость коэффициента сцепления от различных факторов.
 

В практике управления автомобилем важно знать н только максимальную скорость движения автомобиля на отдельных участках маршрута, но и среднюю скорость на всем маршруте. Возможность определения средней скорости движения автомобиля имеет практическое значение для осуществления планирования перевозок грузов и пассажиров на автомобильном транспорте.
 . Из выражения ( 34) следует, что чем выше удельная мощность, тем больше ускорение разгона и меньше продолжительность этапа разгона до установившейся скорости

В итоге следует ожидать повышения средней скорости движения автомобиля. Для того чтобы оценить степень влияния удельной мощности на среднюю скорость вследствие сокращения именно этого этапа цикла, рассмотрим процесс разгона автомобиля с учетом переключения передач.
 

Из выражения ( 34) следует, что чем выше удельная мощность, тем больше ускорение разгона и меньше продолжительность этапа разгона до установившейся скорости. В итоге следует ожидать повышения средней скорости движения автомобиля. Для того чтобы оценить степень влияния удельной мощности на среднюю скорость вследствие сокращения именно этого этапа цикла, рассмотрим процесс разгона автомобиля с учетом переключения передач.
 

Постоянная скорость

Описание формулы.

Самый простой случай в физике — равномерное движение. Скорость постоянна, не меняется на протяжении всего пути. Есть даже скоростные константы, сведенные в таблицы, — неизменные величины. К примеру, звук распространяется в воздухе со скоростью 340,3 м/с.

А свет — абсолютный чемпион в этом плане, он обладает самой большой в нашей Вселенной скоростью — 300 000 км/с. Эти величины не меняются от начальной точки движения до конечной. Они зависят только от среды, в которой движутся (воздух, вакуум, вода и пр.).

Равномерное движение часто встречается нам и в повседневной жизни. Так работает конвейер на заводе или фабрике, фуникулер на горных трассах, лифт (за исключением очень коротких периодов пуска и остановки).

График такого движения очень прост и представляет собой прямую линию. 1 секунда — 1 м, 2 секунды — 2 м, 100 секунд — 100 м. Все точки находятся на одной прямой.

Частные случаи нахождения средней скорости

1. Два одинаковых участка пути.
 Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

2. Два одинаковых интервала движения.
 Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения.

Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила: м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Сергей Валерьевич

Главная&nbsp>&nbsp Wiki-учебник&nbsp>&nbsp Физика&nbsp>&nbsp7 класс&nbsp>

Как же рассчитать скорость

  • через формулу нахождения мощности;
  • через дифференциальные исчисления;
  • по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

  • v — скорость объекта,
  • S — расстояние, которое пройдено или должно быть пройдено объектом,
  • t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы
, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать
, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

  • vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
  • S1, S2, Sn — отдельные неравномерные участки всего пути,
  • t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

  • vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
  • t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей
.

Не упустите

Советую вам не упускать очень важные моменты. Когда вам дается задача, смотрите внимательно, в каких единицах измерения даны параметры. Автор задачи может схитрить. Напишет в дано:

Человек проехал по тротуару на велосипеде 2 километра за 15 минут. Не спешите сразу решать задачу по формуле, иначе у вас получится ерунда, а учитель ее вам не засчитает. Помните, что ни в коем случае нельзя делать так: 2 км/15 мин. У вас единица измерения получится км/мин, а не км/ч. Вам нужно добиться последнего. Переведите минуты в часы. Как это сделать? 15 минут — это 1/4 часа или 0,25 ч. Теперь можете смело 2км/0,25ч=8 км/ч. Теперь задача решена верно.

Вот так легко запоминается формула «скорость, время, расстояние»

Только соблюдайте все правила математики, обращайте внимание на единицы измерения в задаче. Если есть нюансы, как в рассмотренном чуть выше примере, сразу же переводите в систему единиц СИ, как положено

Уровень B

1. О какой скорости – средней или мгновенной – идет речь в следующих случаях:

а) пуля вылетает из винтовки со скоростью 800 м/с;

б) скорость движения Земли вокруг Солнца 30 км/с;

в) на участке дороги установлен ограничитель максимальной скорости – 60 км/ч;

г) мимо вас проехал автомобиль со скоростью 72 км/ч;

д) автобус преодолел расстояние между Могилевом и Минском со скоростью 50 км/ч?

2. Путь в 63 км от одной станции до другой электропоезд проходит за 1 ч 10 мин со средней скоростью 70 км/ч. Какое время занимают остановки?

3. Самоходная косилка имеет ширину захвата 10 м. Определите площадь поля, скошенного за 10 мин, если средняя скорость косилки 0,1 м/с.

4. На горизонтальном участке пути автомобиль ехал со скоростью 72 км/ч в течение 10 мин, а затем проехал подъем со скоростью 36 км/ч за 20 мин. Чему равна средняя скорость на всем пути?

5. Велосипедист первую половину времени при переезде из одного пункта в другой ехал со скоростью 12 км/ч, а вторую половину времени (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость движения велосипедиста.

6. Школьник проехал 1/3 всего времени на автобусе со скоростью 60 км/ч, еще 1/3 всего времени на велосипеде со скоростью 20 км/ч, остальное время прошел со скоростью 7 км/ч. Определите среднюю скорость движения школьника.

7. Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью 12 км/ч, а вторую половину (из-за прокола шины) шел пешком со скоростью 4 км/ч. Определите среднюю скорость его движения.

8. Из одного пункта в другой мотоциклист двигался со скоростью 60 км/ч, обратный путь им был пройден со скоростью 10 м/с. Определите среднюю скорость мотоциклиста за все время движения.

9. Школьник проехал 1/3 пути на автобусе со скоростью 40 км/ч, еще 1/3 пути на велосипеде со скоростью 20 км/ч, последнюю треть пути прошел со скоростью 10 км/ч. Определите среднюю скорость движения школьника.

10. Пешеход часть пути прошел со скоростью 3 км/ч, затратив на это 2/3 времени своего движения. Оставшееся время он прошел со скоростью 6 км/ч. Определите среднюю скорость.

11. Скорость поезда на подъеме 30 км/ч, а на спуске – 90 км/ч. Определите среднюю скорость на вcем участке пути, если спуск в два раза длиннее подъема.

12. Половину времени при переезде из одного пункта в другой автомобиль двигался с постоянной скоростью 60 км/ч. С какой постоянной скоростью он должен двигаться оставшееся время, если средняя скорость движения равна 65 км/ч?

Аналог средней температуры в механике

В каких случаях каверзно сформулированные условия задачи подталкивают нас к поспешному необдуманному ответу? Если говорится о «частях» пути, но не указывается их протяжённость, это настораживает даже мало искушённого в решении подобных примеров человека. А вот если в задаче прямо указывается на равные промежутки, например, «первую половину пути поезд следовал со скоростью…», или «первую треть пути пешеход прошагал соскоростью…», и далее подробно расписывается, как объёкт передвигался на оставшихся равных участках, то есть известно соотношение S 1 = S 2 = … = S n
 и точные значения скоростей v 1, v 2, … v
 n
, наше мышление нередко даёт непростительную осечку. Считается среднее арифметическое скоростей, то есть все известные значения v
 складываются и делятся на n
. В итоге ответ получается неверный.

Формула скорости математика 4 класс

С какой скоростью черепах ползла после камня, если она проползла 33 см?

3. Поезд шёл до станции 7 ч со скоростью 63 км/ч, а после станции поезд проехал ещё 4 ч. С какой скоростью поезд проедет путь от станции, если всего он прошёл 741 км?

Составные задачи на расстояние.

Образец:

Травоядный динозавр сначала бежал 3 ч со скоростью 6 км/ч, а потом он бежал ещё 4 ч со скоростью 5 км/ч. Какое расстояние пробежал травоядный динозавр?

Рассуждаем так. Это задача в одном направлении.

Составим таблицу.

Слова « скорость », «время», «расстояние» запишем зеленой ручкой.

Скорость (V) Время (t) Расстояние (S)

С. — 6 км/ч Зч? км

П. — 5 км/ч 4ч?км? км

Составим план решения этой задачи. Чтобы узнать какое расстояние пробежал динозавр, надо знать, какое расстояние он пробежал, потом и какое расстояние он пробежал сначала.

S Sп Sс

Чтобы найти расстояние, надо скорость умножить на время.

Sс =Vс t с

6· 3 = 18 (км) — расстояние, которое про­бежал динозавр сначала. Чтобы найти расстояние, надо скорость умножить на время.

Sп = Vп tп

5 4 = 20 (км) — расстояние, которое про­бежал динозавр потом.

18 + 20 = 38 (км)

Составим выражение:6 3 + 5 4 = 38(км)

Ответ: 38 км пробежал травоядный динозавр.

Реши задачу.

1. Ракета сначала летела 28 с со скоростью 15 км/с, а оставшийся путь летела 53 с со скоростью 16 км/с. Какое расстояние проле­тела ракета?

2. Утка сначала плыла 3 ч со, скоростью 19 км/ч, а потом она плыла ещё 2 ч со скоро­стью 17 км/ч. Какое расстояние проплыла утка?

3. Кит полосатик сначала плыл 2 ч со скорос­тью 22 км/ч, а потом он плыл ещё 2 ч со ско­ростью 43 км/ч. Какое расстояние проплыл кит полосатик?

4. Теплоход до пристани шёл 3 ч со скоростью 28 км/ч, а после пристани плыл ещё 2 ч со скоростью 32 км/ч. Какое расстояние про­плыл теплоход?

Задачи на нахождение времени совместной работы.

Образец:

Привезли 240 саженцев елей. Первый лесник может посадить эти ели за 4 дня, а второй за 12 дней. За сколько дней оба лесника могут выполнить задание, рабо­тая вместе?

240: 4 = 60 (саж,) за 1 день сажает пер­вый лесник.

240: 12 — 20 (саж.) за 1 день сажает вто­рой лесник.

60 + 20 = 80 (саж.) за 1 день сажают оба лесника. 240:80 = 3(дн.)

Ответ: за 3 дня лесники посадят сажен­цы, работая вместе.

Реши задачу.

1. В мастерской 140 мониторов. Один мастер отремонтирует их за 70 дней, а другой, за 28 дней. За сколько дней оба мастера отре­монтируют эти мониторы, если будут рабо­тать вместе?

2. Было 600 кг горючего. Один трактор израсходовал его за 6 дней, а другой – за 3 дня. За сколько дней тракторы израсходуют это горючее, работая вместе?

3. Надо перевезти 150 пассажиров. Один катер перевезёт их за 15 рейсов, а другой за 10 рейсов. За сколько рейсов эти катера перевезу всех пассажиров, работая вместе?

4. Один ученик может сделать 120 снежинок 60 мин, а другой — за 30 мин. Сколько потребуется времени ученикам, если они будут работать вместе?

5. Один мастер может изготовить 90 шайбочек за 30 мин, другой—‘за 15 мин. За какое вре­мя они изготовят 90 шайбочек при совмест­ной работе?

⇐ Предыдущая234567891011

Какие машины самые быстрые? — журнал За рулем

Скорость можно наращивать почти бесконечно, но в какой-то момент это теряет практический смысл.

На каждом Гран-при Формулы 1 в Сочи невольно подслушиваю один и тот же вопрос: «Пап, а это самые быстрые машины в мире?». Вариантов ответов два: «Да, сынок, самые быстрые» или «Нет, сынок, есть еще быстрее». И оба папы по-своему правы, но им некогда вступать в длительные объяснения.

Развернутый же ответ не совсем доступен для детского понимания: все гоночные машины быстры ровно настолько, насколько это требуется для выполнения конкретной задачи. С обязательным уточнением: в некоторых гоночных дисциплинах искусственно сдерживают рост скоростей — для безопасности. Иногда этого не требуется, например в ралли-кроссе. С него и начнем краткий обзор самых быстрых гоночных машин.

У ралли-­кроссовых суперкаров фантастическая динамика разгона до сотни, но максимальная скорость ниже, чем у Гранты.

У ралли-­кроссовых суперкаров фантастическая динамика разгона до сотни, но максимальная скорость ниже, чем у Гранты.

Материалы по теме

Ралли-кросс: 150 км/ч

Возьмем топовый класс чемпионата мира World RX — быстрее в ралли-кроссе ничего нет и быть не может по определению. На норвежском этапе прошлого года победитель Андреас Баккеруд преодолел дистанцию финала (шесть кругов по 1019 м) за четыре минуты. Это дает нам среднюю скорость около 90 км/ч — при том что в безостановочном спринте никому не надо экономить резину или топливо. Дубасят во всю дурь!

Технические данные машин представлены скупо. Для чемпионского Audi S1 EKS RX quattro заявлено 560 л.с. и 900 Н·м. Плюс полный привод. Очевидно, что среднестатистический автомобиль с такими параметрами без труда должен набирать 300 км/ч.

Но ралли-кроссовые трассы представляют собой километровое кольцо со множеством поворотов. Самый длинный прямой участок — от силы метров двести. Так что вся мощь болидов уходит в разрыхление утрамбованного гравия и рисование черных полос на асфальтовых участках. Зрелище чумовое, но максималка выше 140–150 км/ч попросту не требуется. С этим расчетом, несомненно, настраивают 6-ступенчатые коробки передач, посему даже на бесконечной прямой машина ощутимо быстрее не поедет. По разгону до сотни — он занимает около двух секунд — ралли-кросс, тем не менее, близок к Формуле 1.

Ралли: 200 км/ч

Гравийное Ралли Финляндии — одно из самых быстрых в чемпионате мира. А в его программе выделяют легендарный скоростной участок «Оунинпохья» длиной 33 км. Лидеры гонки в прошлом году проходили его за 15 минут, со средней скоростью 132 км/ч. Это при езде по лесным дорогам с закрытыми поворотами и десятками трамплинов!

Команды Volkswagen и «КАМАЗ-Мастер» одна­жды провели «совместные учения» на финском скоростном участке «Оунинпохья». Конечно, это была пиар-акция — ни одна марафонская машина не догонит Polo WRC в его родной стихии.

Команды Volkswagen и «КАМАЗ-Мастер» одна­жды провели «совместные учения» на финском скоростном участке «Оунинпохья». Конечно, это была пиар-акция — ни одна марафонская машина не догонит Polo WRC в его родной стихии.

Материалы по теме

Нет нужды гадать относительно максималки, выдаваемой машинами категории WRC (мощность примерно 315 л.с., крутящий момент около 420 Н·м). Производитель чемпионского VW Polo R сообщает, что его скорость не выше 200 км/ч, а на разгон до сотни уходит 3,9 секунды.

Собственно, в формате современного ралли ехать быстрее и не требуется, хотя есть и довольно прямолинейные отрезки, по полкилометра или больше, где обороты мотора упираются в ограничитель.

Новый регламент, принятый в 2017 году, поднял мощность техники WRC до 380 л.с. Но вряд ли дополнительные силы пошли на увеличение максимальной скорости. Поднимешь максималку — потеряешь в динамике разгона, а там, где поворот на повороте, она важнее.

Формула‑1: 350 км/ч

Наивысшую скорость в сезоне‑2016 показал Валттери Боттас (команда Williams) — 378 км/ч. Достигнута в квалификации на бакинской трассе с ее двухкилометровым прямым участком.

В гонках скорости ниже, а официальный рекорд — 372,6 км/ч — установлен в Монце и держится с 2005 года. Но, заметим, пилоты, наиболее быстрые на длинных прямых участках, уже давно не становятся чемпионами. Болиды Mercedes быстрее 362 км/ч в прошлом году не ехали.

Williams на трассе в Баку демонстрировал наивысшую максималку, но за весь сезон у Валттери Боттаса лишь один подиум и восьмое место по сумме очков.

Williams на трассе в Баку демонстрировал наивысшую максималку, но за весь сезон у Валттери Боттаса лишь один подиум и восьмое место по сумме очков.

Материалы по теме

Залог успеха в Формуле 1 — скорость прохождения поворотов. И как раз в этом «зачете» машины Формулы 1 самые быстрые в мире. Способствуют тому передовая аэродинамика, обеспечивающая огромную прижимную силу (до 3000 кгс), и сверхмягкие шины. В Формуле 1 феноменальный разгон до сотни (за 1,9 с), до двухсот (около 4 с) и до трехсот (около 12 с). Но максималка не ее призвание, на некоторых трассах высшая, восьмая передача вообще не задействуется.

Как ни крути, техника Формулы 1 с ее современными 900‑сильными моторами уступает в максималке дорожному купе Bugatti Chiron, коему приписывают 420 км/ч. Хотя разгоняется он не столь шустро да и в поворотах существенно медленнее.

Схожие принципы заложены и в основу конструкции прототипов высшей категории LMP1 в чемпионате мира гонок на выносливость (WEC). Они чуть мощнее, максималка чуть выше, но средние скорости на дистанции сопоставимы с развиваемыми в гонках Формулы 1.

Можно ли машины Формулы 1 разогнать, скажем, до 500 км/ч? Легко! Скорее всего, будет достаточно поменять передаточные отношения. Но — не нужно.

Дрег-рейсинг: 530 км/ч

Так мы добрались до машин, чье предназначение — езда только по прямой, а минимальный радиус разворота может составлять десятки метров. Дрэгстеры приспособлены «выжать из себя всё» на дистанции от ⅛ до ¼ мили при старте с места.

Дрэгстер ­класса Top Fuel проезжает триста метров за 3,7 секунды. При этом расход топлива (смесь нитрометана с метанолом) — около 50 литров в секунду. Полезнейшая в хозяйстве вещь!

Дрэгстер ­класса Top Fuel проезжает триста метров за 3,7 секунды. При этом расход топлива (смесь нитрометана с метанолом) — около 50 литров в секунду. Полезнейшая в хозяйстве вещь!

Материалы по теме

Электрические, реактивные и прочие экзотические вариации оставим в стороне. В более-менее официальных гонках дрэгстеров с ДВС самый быстрый класс — Top Fuel. Здесь динамика ограничена возможностями блока цилиндров, изготовленного из алюминия по чертежам культового мотора семейства Hemi V8 (выпуска 1964–1971 годов). Нагнетатель воздуха и система подачи нитрометана — обязательные элементы. На выходе получают 8000–10 000 л.с.

Разгон до 100 миль в час происходит за секунду (дорожку загодя покрывают клейким составом, чтобы улучшить сцепление мягких шин низкого давления). Чемпионской скоростью на финише считается 530 км/ч, хотя в дрэге скорость не замеряют — только «время в пути». На что способен дрэгстер Top Fuel после финиша, изучено плохо, поскольку запас топлива рассчитан на 1000 футов, то есть 305 метров (ограничение введено в 2008 году из соображений безопасности). И нет коробки передач (момент передает пятидисковое «тракторное» сцепление Caterpillar), а обороты мотора не могут расти бесконечно.

Рекордные заезды: 707 км/ч

Официальные мировые рекорды скорости на суше курирует вовсе не Книга рекордов Гиннесса, а та же организация, что занимается всеми гоночными чемпионатами мира, - FIA. Поэтому установление рекордов причисляют к гонкам, да и занимаются этим чаще всего опытные гонщики. Для фиксации лучших результатов разработана сложная градация — с хода и с места, максимальная или средняя скорость на

Какая скорость автомобиля действительно безопасна для города и для трассы? | Безопасность | Авто

Дороги, по которым приходится ездить автомобилистам, подразделяются на несколько классов. Есть небольшие дворовые проезды, межрайонные внутри мегаполиса, междугородние шоссе и многополосные автомагистрали. Как ездить по ним максимально безопасно? 

Для каждой дороги существует своя приемлемая скорость, обоснованная спецификой езды и окружающей обстановкой. Эти безопасные скорости отличаются от тех, что приходится видеть на знаках, но их нужно знать, так как от правильно выбранного темпа движения зависит жизнь своя и чужая. 

Жилая зона 

При езде внутри жилых зон скорость ограничена 20 км/ч плюс 20 км/ч ненаказуемого порога. В итоге некоторые водители рядом с подъездами разгоняются до 40 км/ч. Между тем из-за припаркованных автомобилей обзор значительно сокращается. Сбоку может выскочить человек или животное и попасть под колеса. Заметить их трудно, и порой человек оказывается прямо перед машиной в 3-5 м. 

При скорости в 40 км/ч это расстояние машина пролетает за секунду. Водитель не успеет среагировать и затормозить. Кроме того, на сухом асфальте тормозной путь составляет 10 м, а в гололед и вовсе растягивается до 15-20 м. Если ударить по педали, сработает АБС, машина начнет скользить и неминуемо врежется в препятствие. 

Какая же скорость может быть безопасной в этом случае? Это та скорость, при которой можно полностью остановиться перед внезапно появившимся человеком или так сбросить скорость, чтобы не причинить ему большого вреда при столкновении. Зимой в гололед тормозной путь машины составляет 3-5 м при скорости в 10 км/ч, а значит, ее и необходимо придерживаться, чтобы вовремя замедлиться. 

Квартальная скорость 

При движении по городскому кварталу рекомендуется ездить не быстрее 40 км/ч. Дороги здесь тоже узкие, заставлены транспортом и плохо просматриваются на расстояние свыше 10 м. Однако это не мешает многим разгоняться до 60 км/ч и более. Между тем спешащие водители забывают, что внутри квартала нет дорожных знаков, отдающих приоритет той или иной дороге, и зачастую внутри квартала действует правило правой руки. Автомобили с правого поворота имеют безусловный приоритет и могут выскакивать наперерез совершенно свободно. 

Если машина движется со скоростью 60 км/ч и больше, то она не успевает остановиться перед таким выруливающим автомобилем, так как ее тормозной путь на сухом асфальте составит 23 м, а в гололед превысит 30 м. 

В таблицах зависимости тормозного пути от скорости четко указано, что тормозной путь на сухом асфальте в 10 м соответствует 40 км/ч. И этой скорости нужно придерживаться, чтобы успеть вовремя среагировать на другие машины. 

Движение в городе 

На городских магистралях ездить можно быстрее. Правила вводят ограничение в 60 км/ч. Но из-за так называемого ненаказуемого порога в 20 км/ч многие разгоняются до 80 км/ч и надеются, что современный автомобиль вполне способен быстро сбросить скорость, если возникнет необходимость. На больших московских проспектах такая возможность есть. А вот на небольших дорожках, петляющих вокруг школ и в исторических районах, лучше придерживаться установленных правилами ограничений. 

Просматриваемое расстояние в таких местах редко превышает 30-40 м. Нужно помнить, что тормозной путь с 80 км/ составляет уже 42 м на сухом асфальте. А с 60 км/ч — только 23 м. Выигрыш расстояния в 19 м может кому-то спасти жизнь. 

Поездки за городом 

На междугородних трассах разрешено ездить со скоростью 90-110 км/ч и особое влияние на безопасность оказывает способность человека быстро реагировать на неожиданные препятствия. Чем дальше видишь, тем больше времени остается на принятие решений. Однако с ростом скорости машины поле зрения человека сужается в результате уменьшения угла бинокулярного зрения. Водитель перестает различать объекты по сторонам. Они сливаются в одну сплошную стену. Водитель борется с этим эффектом, пытается смотреть на обочину, читать знаки, и на скорости свыше 120 км/ч внимание фокусируется на расстоянии около 150 м. Из-за этой борьбы внимания с законами физики время реакции человека увеличивается в 2–3 раза. При этом возрастает тормозной след машины, который со 120 км/ч на автостраде составляет уже более 110 м.

Если происходит нечто неожиданное, то требуется около секунды, чтобы принять решение, еще секунда уходит на реакцию человека, а за это время автомобиль успевает проехать около 45-50 м. Дальше — удар по тормозам, и путь до полной остановки машины при экстренном торможении составляет около 160 м. 

Таким образом, чтобы гарантированно остановиться перед препятствием, увиденным за 150 м, требуется ехать со скоростью не более 110 км/ч. За этим порогом наступает повышенная концентрация внимания и быстрая утомляемость водителя, что сказывается на его работоспособности. 

В общем, лучше ездить медленнее, но безопаснее.

Скорость автомобиля и безопасность. Часть 1: engineering_ru — LiveJournal

Оригинал на сайте Трансспот. Дороги и Транспорт.

Эта первая статья из небольшой серии посвященной положительному и отрицательному влиянию скорости на нашу жизнь. Все статьи для сжатия материала будут представлены в виде тезисов.

В последующих статьях речь пойдет об окружающей среде, о воздействии на общество в долговременной перспективе, а также о преимуществах, которые предоставляет высокая скорость. Также будут приведены примеры ограничения скоростных режимов в городах развитых стран.

Но сначала о самом наболевшем – о безопасности. Как известно в России в год гибнет в ДТП 1 человек из 6 000. Разберемся, как скорость влияет на количество ДТП и вероятность смертельного исхода. Основной упор будет сделан на взаимодействие пешехода и автомобиля, как наиболее сильно конкурирующих объектов дорожного движения.


Скорость и вероятность ДТП

Рассмотрим тормозной путь автомобиля. Длину тормозного пути можно рассчитать, зная время реакции водителя и длину тормозного пути после нажатия на тормоз.

Среднее время реакции составляет 1 секунду. При увеличении скорости движения увеличивается и пройденное за 1 секунду расстояние. Расстояние, пройденное с момента нажатия педали до полной остановки, пропорционально квадрату скорости. При увеличении скорости с 50 км/ч до 80 км/ч тормозной путь увеличивается в 2 раза. Соответственно избежать столкновения намного тяжелее.

Необходимо также учитывать, что на сыром асфальте тормозной путь увеличивается на 25%. То есть тормозной путь автомобиля с 60 км/ч на сыром асфальте будет равен тормозному пути на 70 км/ч на сухом асфальте.

При скорости автомобиля 80 км/ч время реакции в пересчете на дистанцию займет 22 метра. Дополнительно на сухом асфальте водителю потребуется минимум 36 метров для полной остановки.

Если ребенок выбежит на дорогу перед водителем на расстоянии 36 метров, то почти наверняка он умрет при начальной скорости автомобиля 70 км/ч, получит увечья при скорости автомобиля 60 км/ч, а при скорости автомобиля 50 км/ч водитель избежит столкновения.

Но если ребенок выбежит на дорогу за 15 метров перед автомобилем, он, скорее всего, получит смертельные травмы, даже если автомобиль двигается со скоростью 50 км/ч.

Скорость и частота ДТП

Проектные и функциональные характеристики дорог сильно влияют на зависимость между скоростью и частотой аварий. Влияет, например, наличие и вид пересечений, присутствие пешеходов и велосипедистов.

В более сложных ситуациях риски аварий и влияния скорости больше.

Скоростные магистрали, например, это простые случаи с меньшими рисками аварий. Городские дороги, наоборот, более комплексные с более высокими рисками ДТП.

Основными жертвами ДТП в городских условиях являются пешеходы, велосипедисты, мотоциклисты. Основные факторы, способствующие этому – разница в скорости и в весе.

В южной Австралии проводили сравнение между рисками из-за превышения скорости с рисками из-за содержания алкоголя в крови. Было принято, что при 60 км/ч и 0 промилле относительные риски равны единице.

С 70 км/ч относительные риски начинают резко расти. Это превышение всего на 10 км/ч и соответствует 0.8 промилле алкоголя в крови при 60 км/ч.

Влияние неоднородности скорости на ДТП

Неоднородность скорости в транспортном потоке приводит к увеличению количества обгонов и, как следствие, более высокому уровню рисков. Высокий разброс скоростей тесно связан с авариями со смертельным исходом на всех дорогах — городских и загородных.

Чаще всего снижение скорости приводит к снижению неоднородности скоростей в потоке.

Частота аварий вырастает на 10-15% при превышении средней скорости на 1 км/ч. При превышении средней скорости потока на 10 и более км/ч количество аварий начинает резко расти для городских дорог. Для загородных дорог рост количества аварий не настолько критичен.
Из графика также видно, что уменьшение скорости отдельного автомобиля относительно средней скорости потока не приводит к увеличению числа аварий.

Влияние скорости на тяжесть ДТП

Даже если превышение скорости не является основной причиной аварии, от скорости в момент столкновения сильно зависит тяжесть последствий ДТП. Приблизительная зависимость количества тяжелых аварий и аварий со смертельным исходом от изменения скорости движения представлена на графике.

Повышение скорости на 10% приводит к увеличению количества всех аварий на 21%, к увеличению количества тяжелых аварий или аварий со смертельным исходом на 33%, к увеличению количества аварий со смертельным исходом на 46%. Снижение скорости на 10% — к уменьшению этих видов аварий на, соответственно, 19%, 27% и 34%.

Ситуация сильно зависит от типа дороги и допустимой скорости на этих дорогах. На графике ниже представлен прирост ДТП при изменении скорости движения на 1 км/ч для различных скоростей движения.

Наиболее серьезное влияние на тяжесть аварии при изменении скорости, как видно из таблицы, приходится на дороги с низкими допустимыми скоростями. Это городские дороги.

Тяжесть последствий сильно зависит от участников дорожного движения. Пешеходы, велосипедисты и мотоциклисты имеют большой риск получения серьезных травм, так как они не защищены. У них нет металлического каркаса, ремней и подушек безопасности.

Вероятность гибели пешехода в ДТП увеличивается с ростом скорости столкновения. Расследования показали, что при столкновении с пешеходом на скорости 30 км/ч 90% пешеходов выживают, в то время как столкновения на скорости 50 км/ч приводят к гибели 80% пешеходов.

Водитель и пассажиры автомобиля при этом практически не страдают.

Влияние скорости на область обзора

При увеличении скорости движения область обзора существенно уменьшается. Таким образом, высокая скорость в городских условиях не дает водителю возможность правильно спрогнозировать ситуацию, потому что он не видит окружающую обстановку.

На скорости 40 км/ч угол обзора водителя составляет 100 градусов. Это позволяет видеть препятствия на дороге, а также оценивать ситуацию справа и слева от дороги. На скорости 130 км/ч угол обзора составляет 30 градусов и менее, что значительно снижает возможность оценки водителем потенциальной опасности.

Выводы

Высокая скорость является причиной трети всех ДТП. Кроме того, высокая скорость отягчает последствия ДТП, произошедших по другим причинам.

Влияние скорости на несчастные случаи особо серьезно в городах, где имеет место взаимодействие нескольких групп участников дорожного движения: автомобили, пешеходы, велосипедисты.

Существует порог скорости автомобиля, выше которого организм пешехода физически не может выжить. При столкновении на скорости 45 км/ч выживает только 50 % пешеходов.

Для снижения травматизма на дорогах необходимо принять меры для соблюдения обоснованного скоростного режима, а также свести к минимуму разброс скорости в потоке.

Скорость автомобиля и безопасность

Эта первая статья из небольшой серии посвященной положительному и отрицательному влиянию скорости на нашу жизнь. Все статьи для сжатия материала будут представлены в виде тезисов.

В последующих статьях речь пойдет об окружающей среде, о воздействии на общество в долговременной перспективе, а также о преимуществах, которые предоставляет высокая скорость. Также будут приведены примеры ограничения скоростных режимов в городах развитых стран.

Но сначала о самом наболевшем – о безопасности. Как известно в России в год гибнет в ДТП 1 человек из 6 000. Разберемся, как скорость влияет на количество ДТП и вероятность смертельного исхода. Основной упор будет сделан на взаимодействие пешехода и автомобиля, как наиболее сильно конкурирующих объектов дорожного движения.

Социальная реклама

Скорость и вероятность ДТП

Рассмотрим тормозной путь автомобиля. Длину тормозного пути можно рассчитать, зная время реакции водителя и длину тормозного пути после нажатия на тормоз.

Среднее время реакции составляет 1 секунду. При увеличении скорости движения увеличивается и пройденное за 1 секунду расстояние. Расстояние, пройденное с момента нажатия педали до полной остановки, пропорционально квадрату скорости. При увеличении скорости с 50 км/ч до 80 км/ч тормозной путь увеличивается в 2 раза. Соответственно избежать столкновения намного тяжелее.

Необходимо также учитывать, что на сыром асфальте тормозной путь увеличивается на 25%. То есть тормозной путь автомобиля с 60 км/ч на сыром асфальте будет равен тормозному пути на 70 км/ч на сухом асфальте.

Тормозной путь в зависимости от скорости движения

При скорости автомобиля 80 км/ч время реакции в пересчете на дистанцию займет 22 метра. Дополнительно на сухом асфальте водителю потребуется минимум 36 метров для полной остановки.

Если ребенок выбежит на дорогу перед водителем на расстоянии 36 метров, то почти наверняка он умрет при начальной скорости автомобиля 70 км/ч, получит увечья при скорости автомобиля 60 км/ч, а при скорости автомобиля 50 км/ч водитель избежит столкновения.

Но если ребенок выбежит на дорогу за 15 метров перед автомобилем, он, скорее всего, получит смертельные травмы, даже если автомобиль двигается со скоростью 50 км/ч.

Рассчитать длину тормозного пути и время торможения, а также скорость во время торможения на определенном расстоянии после начала торможения при различных условиях (начальная скорость, время реакции, тип покрытия) можно на этом немецком сайте.

Скорость и частота ДТП

Проектные и функциональные характеристики дорог сильно влияют на зависимость между скоростью и частотой аварий. Влияет, например, наличие и вид пересечений, присутствие пешеходов и велосипедистов.

В более сложных ситуациях риски аварий и влияния скорости больше.

Скоростные магистрали, например, это простые случаи с меньшими рисками аварий. Городские дороги, наоборот, более комплексные с более высокими рисками ДТП.

Основными жертвами ДТП в городских условиях являются пешеходы, велосипедисты, мотоциклисты. Основные факторы, способствующие этому – разница в скорости и в весе.

В южной Австралии проводили сравнение между рисками из-за превышения скорости с рисками из-за содержания алкоголя в крови. Было принято, что при 60 км/ч и 0 промилле относительные риски равны единице.

Относительные риски возникновения ДТП в зависимости от скорости и содержания алкоголя в крови

С 70 км/ч относительные риски начинают резко расти. Это превышение всего на 10 км/ч и соответствует 0.8 промилле алкоголя в крови при 60 км/ч.

Влияние неоднородности скорости на ДТП

Неоднородность скорости в транспортном потоке приводит к увеличению количества обгонов и, как следствие, более высокому уровню рисков. Высокий разброс скоростей тесно связан с авариями со смертельным исходом на всех дорогах — городских и загородных.

Чаще всего снижение скорости приводит к снижению неоднородности скоростей в потоке.

Частота аварий в зависимости от отличия скорости отдельного автомобиля от средней скорости потока

Частота аварий вырастает на 10-15% при превышении средней скорости на 1 км/ч. При превышении средней скорости потока на 10 и более км/ч количество аварий начинает резко расти для городских дорог. Для загородных дорог рост количества аварий не настолько критичен.

Из графика также видно, что уменьшение скорости отдельного автомобиля относительно средней скорости потока не приводит к увеличению числа аварий.

Влияние скорости на тяжесть ДТП

Даже если превышение скорости не является основной причиной аварии, от скорости в момент столкновения сильно зависит тяжесть последствий ДТП. Приблизительная зависимость количества тяжелых аварий и аварий со смертельным исходом от изменения скорости движения представлена на графике.

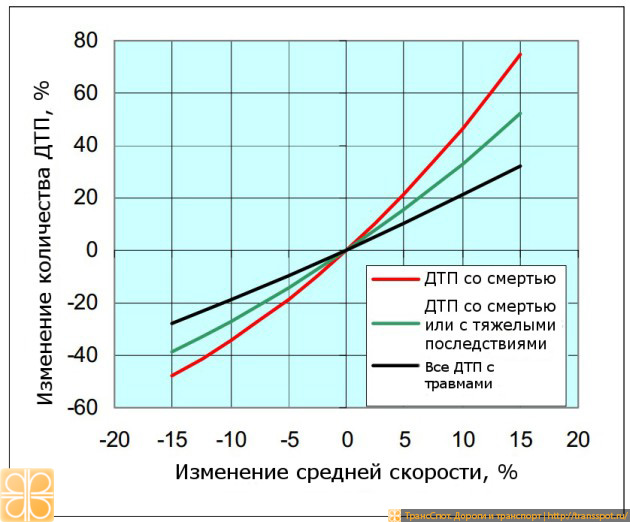
Изменение количества ДТП в зависимости от изменения скорости

Повышение скорости на 10% приводит к увеличению количества всех аварий на 21%, к увеличению количества тяжелых аварий или аварий со смертельным исходом на 33%, к увеличению количества аварий со смертельным исходом на 46%. Снижение скорости на 10% — к уменьшению этих видов аварий на, соответственно, 19%, 27% и 34%.

Ситуация сильно зависит от типа дороги и допустимой скорости на этих дорогах. На графике ниже представлен прирост ДТП при изменении скорости движения на 1 км/ч для различных скоростей движения.

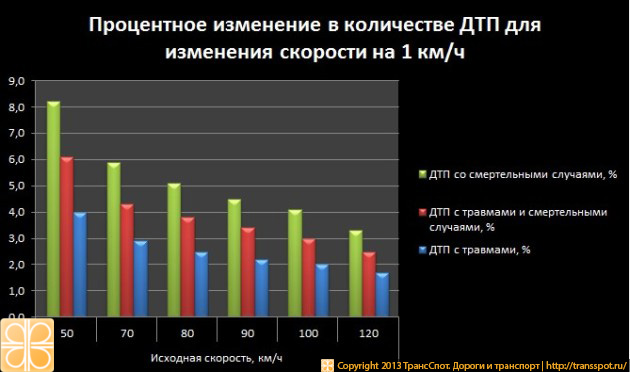
Изменение в количестве ДТП для отдельной скорости при изменении скорости на 1 км/ч

Наиболее серьезное влияние на тяжесть аварии при изменении скорости, как видно из таблицы, приходится на дороги с низкими допустимыми скоростями. Это городские дороги.

Тяжесть последствий сильно зависит от участников дорожного движения. Пешеходы, велосипедисты и мотоциклисты имеют большой риск получения серьезных травм, так как они не защищены. У них нет металлического каркаса, ремней и подушек безопасности.

Вероятность гибели пешехода в ДТП увеличивается с ростом скорости столкновения. Расследования показали, что при столкновении с пешеходом на скорости 30 км/ч 90% пешеходов выживают, в то время как столкновения на скорости 50 км/ч приводят к гибели 80% пешеходов.

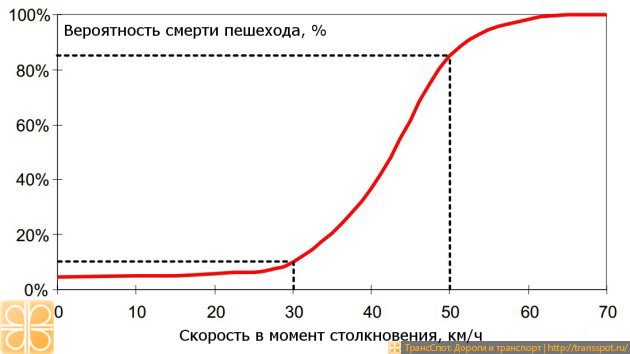
Вероятность смерти пешехода в зависимости от скорости автомобиля

Водитель и пассажиры автомобиля при этом практически не страдают.

Влияние скорости на область обзора

При увеличении скорости движения область обзора существенно уменьшается. Таким образом, высокая скорость в городских условиях не дает водителю возможность правильно спрогнозировать ситуацию, потому что он не видит окружающую обстановку.

На скорости 40 км/ч угол обзора водителя составляет 100 градусов. Это позволяет видеть препятствия на дороге, а также оценивать ситуацию справа и слева от дороги. На скорости 130 км/ч угол обзора составляет 30 градусов и менее, что значительно снижает возможность оценки водителем потенциальной опасности.

Обзор водителя при увеличении скорости движения

Выводы

Высокая скорость является причиной трети всех ДТП. Кроме того, высокая скорость отягчает последствия ДТП, произошедших по другим причинам.

Влияние скорости на несчастные случаи особо серьезно в городах, где имеет место взаимодействие нескольких групп участников дорожного движения: автомобили, пешеходы, велосипедисты.

Существует порог скорости автомобиля, выше которого организм пешехода физически не может выжить. При столкновении на скорости 45 км/ч выживает только 50 % пешеходов.

Для снижения травматизма на дорогах необходимо принять меры для соблюдения обоснованного скоростного режима, а также свести к минимуму разброс скорости в потоке.

Спасибо за статью Сергею Давыдову, материал с сайта http://transspot.ru

Средняя скорость

При решении этих задач обязательно помним, что средняя скорость может быть найдена только делением всего пути на все время движения, даже если какое-то время объект не двигался (делал остановку). Если путь не задан, то необходимо ввести буквенное обозначение длины пути.

Задача 1. Поезд прошел путь 200 км. В течение времени t_1=1 ч он двигался со скоростью \upsilon_1=100 км/ч, затем сделал остановку на время t_2=30 мин. Оставшуюся часть пути он шел со скоростью \upsilon_3=40 км/ч. Какова средняя скорость движения поезда?

Путь в этой задаче известен. Значит, осталось определить время движения поезда. Кроме того, известно и время его движения на первом участке, значит, нам осталось определить время движения поезда на последнем кусочке, где он двигался со скоростью \upsilon_3=40 км/ч. Нетрудно понять, что длина этого отрезка пути равна 100 км, так как поезд уже преодолел 100 км за первый час. Поэтому

    \[S_3=200-\upsilon_1 \cdot t_1=200-100\]

    \[t_3=\frac{S_3}{\upsilon_3}=\frac{100}{40}=2,5\]

Таким образом,

    \[\upsilon_{sr}=\frac{S}{t_1+t_2+t_3}=\frac{200}{1+0,5+2,5}=50\]

Ответ: 50 км/ч

 

Задача 2. Определить среднюю скорость поезда, если первую половину пути он шел со скоростью \upsilon_1=50 км/ч, а вторую половину пути  – со скоростью \upsilon_2=100 км/ч.

В этой задаче путь неизвестен. Обозначим его S. Тогда время движения поезда на первой половине пути

    \[t_1=\frac{\frac{S}{2}}{\upsilon_1}\]

Время движения на второй половине –

    \[t_1=\frac{\frac{S}{2}}{\upsilon_2}\]

Средняя скорость – результат деления всего пути, пройденного поездом, на все время:

    \[\upsilon_{sr}=\frac{S}{t_1+t_2}\]

    \[\upsilon_{sr}=\frac{S}{\frac{S}{2\upsilon_1}+\frac{S}{2\upsilon_2}}\]

    \[\upsilon_{sr}=\frac{2}{\frac{1}{\upsilon_1}+\frac{1}{\upsilon_2}}\]

    \[\upsilon_{sr}=\frac{2 \upsilon_1 \upsilon_2}{\upsilon_1+\upsilon_2}\]

    \[\upsilon_{sr}=\frac{2 \cdot50\cdot100}{150}=\frac{10000}{150}=66,7\]

Ответ: \upsilon_{sr}=66,7 км/ч

 

Задача 3. Два автомобиля одновременно выехали из Москвы в Петербург.  Один автомобиль первую половину пути ехал со скоростью \upsilon_1=120 км/ч, а вторую половину – со скоростью \upsilon_2=80 км/ч. Другой автомобиль первую половину времени ехал со скоростью \upsilon_1=120 км/ч, а вторую – со скоростью \upsilon_2=80 км/ч. Какой автомобиль приедет в Петербург раньше?

Если окажется, что средняя скорость одного из автомобилей больше, чем у другого, то он и должен прибыть раньше. Определим среднюю скорость каждого автомобиля. Первый:

    \[\upsilon_{sr1}=\frac{S}{t_1+t_2}\]

    \[\upsilon_{sr1}=\frac{S}{\frac{S}{2\upsilon_1}+\frac{S}{2\upsilon_2}}\]

    \[\upsilon_{sr1}=\frac{2}{\frac{1}{\upsilon_1}+\frac{1}{\upsilon_2}}\]

    \[\upsilon_{sr1}=\frac{2 \upsilon_1 \upsilon_2}{\upsilon_1+\upsilon_2}\]

    \[\upsilon_{sr1}=\frac{2 \cdot120\cdot80}{200}=\frac{19200}{200}=96\]

Второй за первую половину времени прошел:

    \[S_1=\frac{t}{2}\cdot \upsilon_1\]

За вторую половину времени:

    \[S_2=\frac{t}{2}\cdot \upsilon_2\]

Тогда его средняя скорость:

    \[\upsilon_{sr2}=\frac{S}{t}=\frac{S_1+S_2}{t}=\frac{t\cdot \upsilon_1+t\cdot\upsilon_2}{2t}=\frac{\upsilon_1+\upsilon_2}{2}\]

    \[\upsilon_{sr2}=\frac{120+80}{2}=100\]

Таким образом, второй автомобиль прибудет раньше.

Задача 4. Найти среднюю скорость самолета, если известно, что первую треть пути он летел со скоростью \upsilon_1=700 км/ч, вторую треть – со скоростью \upsilon_2=500 км/ч, а последнюю часть пути – со скоростью, вдвое большей средней скорости  на первых двух участках пути.

Найдем среднюю скорость самолета на двух первых участках пути.

    \[\upsilon_{sr12}=\frac{\frac{2S}{3}}{\frac{S}{3\upsilon_1}+\frac{S}{3\upsilon_2}}\]

    \[\upsilon_{sr12}=\frac{2}{\frac{1}{\upsilon_1}+\frac{1}{\upsilon_2}}\]

    \[\upsilon_{sr12}=\frac{2\upsilon_1 \upsilon_2}{\upsilon_1+\upsilon_2}\]

    \[\upsilon_{sr12}=\frac{2\cdot700 \cdot500}{700+500}=583\]

Тогда \upsilon_3=1166.

Определяем среднюю скорость на всем участке пути:

    \[\upsilon_{sr123}=\frac{S}{\frac{S}{3\upsilon_1}+\frac{S}{3\upsilon_2}+\frac{S}{3\upsilon_3}}\]

    \[\upsilon_{sr123}=\frac{3}{\frac{1}{\upsilon_1}+\frac{1}{\upsilon_2}+\frac{1}{\upsilon_3}}\]

    \[\upsilon_{sr123}=\frac{3\upsilon_1 \upsilon_2 \upsilon_3}{\upsilon_1\upsilon_2+\upsilon_2\upsilon_3+\upsilon_1\upsilon_3}\]

    \[\upsilon_{sr123}=\frac{500\cdot700 \cdot1166}{500\cdot700+700\cdot1166+500\cdot1166}=700\]

Ответ: 700 км/ч

 

Задача 5. Найти среднюю скорость поезда, если известно, что на прохождение отдельных участков дистанции, длины которых относятся как 1: 3: 4: 2, потребовались промежутки времени, находящиеся в отношении 2:4:3:1, и на последнем участке скорость поезда \upsilon=80 км/ч. Считать, что на каждом из участков поезд двигался равномерно.

Определим весь путь по его частям:

    \[S_1:S_2:S_3:S_4=1: 3: 4: 2\]

Если S_1=l, то S_2=3l, S_3=4l, S_4=2l, а весь путь

    \[S_1+S_2+S_3+S_4=l+3l+4l+2l=10l\]

Определим время движения поезда на последнем участке, зная его скорость:

    \[t_4=\frac{2l}{\upsilon }\]

Тогда, так как

    \[t_1:t_2:t_3:t_4=2:4:3:1\]

Отсюда найдем t_1, t_2, t_3:

    \[t_3=3t_4=\frac{6l}{\upsilon }\]

    \[t_2=\frac{4}{3}t_3=\frac{8l}{\upsilon }\]

    \[t_1=\frac{1}{2}t_3=\frac{4l}{\upsilon }\]

Общее время движения:

    \[t_1+t_2+t_3+t_4=\frac{4l}{\upsilon }+\frac{8l}{\upsilon }+\frac{6l}{\upsilon }+\frac{2l}{\upsilon }=\frac{20l}{\upsilon }\]

Наконец, находим среднюю скорость:

    \[\upsilon_{sr}=\frac{S}{t}=\frac{10l}{\frac{20l}{\upsilon }}=\frac{\upsilon }{2}\]

    \[\upsilon_{sr}=\frac{80}{2}=40\]

Ответ: средняя скорость поезда – 40 км/ч.

python — Проверка средней скорости для автомобилей

Переполнение стека
  1. Товары
  2. Клиенты
  3. Случаи использования
  1. Переполнение стека Общественные вопросы и ответы
  2. Команды Частные вопросы и ответы для вашей команды
  3. предприятие Частные вопросы и ответы для вашего предприятия
  4. работы Программирование и связанные с ним возможности технической карьеры
  5. Талант Нанять технических талантов
  6. реклама Обратитесь к разработчикам по всему миру
,

Какой средний вес автомобиля?

Средний вес автомобиля в 2018 году составил более 4000 фунтов, который практически не изменился с 2015 года. График EPA для экономии топлива, веса и мощности с 1975 модельного года по 2017 год показывает, что экономия топлива и мощность в лошадиных силах растут вместе на протяжении большей части лет. при этом вес оставался в основном стабильным.

Повышенная экономия топлива

Вес автомобиля был тесно связан с экономией топлива, и EPA отслеживает оба показателя для автомобилей с 1975 модельного года.Средняя экономия топлива для автомобилей 2016 года составила 24,7 миль на галлон, что немного выше, чем в предыдущем году и является рекордным уровнем. С 2004 года экономия топлива улучшилась за десять из 12 лет, всего за два сокращения.

Еще более обнадеживающим является тот факт, что экономия топлива продолжала улучшаться, в то время как вес и мощность начали выравниваться. В 2005 году технологии позволили увеличить как мощность, так и экономию топлива, при этом вес остался в основном прежним. Как упоминалось ранее, с годами вес в значительной степени увеличивался постепенно, и только за несколько лет наблюдался спад или всплеск.

Как правило, более тяжелые автомобили считаются более безопасными, и на современном рынке больший вес не всегда коррелирует с низкой экономией топлива из-за повышения эффективности двигателя и трансмиссии. Более того, технологии не только повысили эффективность, но и одновременно помогли автопроизводителям улучшить мощность без увеличения веса. Эта тенденция особенно сильна с середины 2000-х годов.

Стабильный след нового транспортного средства

Площадь следа — это размер транспортного средства, оцененный по площади, которую он занимает со всеми четырьмя шинами.Это число можно найти, умножив колесную базу на среднюю ширину колеи (ширина колеи — это ширина между правой и левой шинами). Стандарты экономии топлива основываются на занимаемой площади транспортного средства для определения целей экономии топлива. Агентство по охране окружающей среды начало сбор данных о следах транспортных средств 2008 года. В период с 2008 по 2016 год средний размер занимаемой площади для всех пяти типов транспортных средств оставался довольно стабильным. Площадь грузовых автомобилей увеличилась на 2,4 процента, легковых автомобилей — на 2,1 процента, минивэнов и фургонов — на 1,9 процента, внедорожников на базе грузовиков — на 0.7 процентов, а CUV снизились на 0,4 процента.

Среднее значение этих следов в значительной степени зависит от рыночных тенденций и типов производимых новых автомобилей. С 2008 года рыночные тенденции сильно изменились в сторону грузовиков, внедорожников и внедорожников, в то время как легковые автомобили и фургоны несколько снизились. Из-за этого сдвига общая средняя площадь по отрасли увеличилась на 1,2 процента до среднего размера 49,5 квадратных футов. Показатели за 2017 год не изменились по сравнению с 2016 годом.

Доля рынка внедорожников на рекордно высоком уровне

Кроссоверы (CUV или известные как легковые внедорожники в отчете EPA) занимали долю рынка в течение нескольких лет, но данные также показывают, что грузовые внедорожники также пользуется большей долей.Оба типа также достигли рекордной экономии топлива.

CUV составили 12 процентов от всех серийных автомобилей в 2016 году, что является рекордом. CUV и SUV вместе занимают 41% рынка.

Средний галлон для внедорожников составил 26,2 мили на галлон, что на 1,1 мили на галлон больше. Экономия топлива для внедорожников составила 22,2. Грузовики также продемонстрировали заметный рост экономии топлива, что ставит их на самый высокий средний уровень по сравнению с грузовиками в 1986 году. Это достижение, учитывая, что грузовики тогда были намного меньше и весили на треть меньше, чем грузовики сегодня.

Тот факт, что внедорожники составляют такую ​​большую долю рынка, способствует тому, что средний вес остается неизменным, а не уменьшается, что может произойти с большей долей рынка небольших легковых автомобилей.

Влияние технологий

К 2017 году прогнозировалось, что более половины всех транспортных средств будут использовать непосредственный впрыск бензина (GDI). Это значительное увеличение; Десять лет назад эта технология использовалась только примерно в трех процентах автомобилей. Некоторые автопроизводители внедрили эту технологию во всю линейку автомобилей.

Такие бренды, как Ford, BMW, Mercedes и VW, лидируют в использовании турбокомпрессоров вместе с GDI, что привело к четверти доли рынка. Почти четверть автомобилей также используют бесступенчатые коробки передач, которые увеличивают экономию топлива и уменьшают вес. Японские автопроизводители чаще всего используют вариаторы, в то время как отечественные и европейские бренды перешли на трансмиссии с семью и более скоростями или трансмиссии с двойным сцеплением.

Какие автомобили самые легкие в США.С. рынок?

Несмотря на то, что самый легкий новый автомобиль, проданный в Америке в 2018 году, весил меньше, чем четырехдверный Toyota Tercel 1998 года, в среднем Америка по-прежнему покупает более тяжелые автомобили, чем остальной мир. Например, Honda Fit занимает 10-е место среди самых легких новых автомобилей на рынке США и весит чуть более 2500 фунтов. Сравните это с 1988 годом, когда базовый Civic весил 1933 фунта. Некоторые другие примеры более легких автомобилей на американском рынке включают Nissan Versa за 2400 фунтов, Mazda MX-5 Miata за 2332 фунта, Toyota Yaris за 2315 фунтов и Chevy Spark за 2246 фунтов.

Несмотря на то, что на американском рынке доступно множество легких автомобилей, доминирование на рынке внедорожников и грузовиков привело к увеличению среднего размера рынка.

Какие тяжеловесы представлены на рынке США?

Удивительно, но самые тяжелые автомобили на американском рынке — это не просто внедорожники. Например, седан Mercedes-Maybach S560 4Matic весит чуть более 5000 фунтов. Это всего на 300 фунтов меньше, чем у Mercedes-Benz GLS, который является внедорожником.Этот конкретный внедорожник становится еще тяжелее с дополнительным двигателем на 5 700 фунтов.

Ford Expedition всегда был тяжелым транспортным средством, но недавно Ford удалось уменьшить его вес за счет использования алюминия для панелей кузова и использования двигателя V6 с турбонаддувом вместо более тяжелого V8. Сейчас он весит чуть более 5400 фунтов. Его двоюродный брат класса люкс, Lincoln Navigator, с полным приводом весит до 6000 фунтов.

На американском рынке есть и другие автомобили с ограниченными масштабами, включая роскошный седан Rolls-Royce Phantom (5643 фунта), внедорожник Infiniti QX80 (5676 фунтов), внедорожник Toyota Sequoia (5730 фунтов) и кроссовер Cadillac Escalade ESV (5831 фунт). фунты).Помните также, что в большинстве случаев это фигурки базовой модели. Более крупные двигатели, полный привод и роскошная отделка салона увеличивают вес некоторых автомобилей на 500 или 600 фунтов.

.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *