2.2. Сжимаемость жидкости
Сжимаемостью называют свойство жидкости обратимым образом изменять свой объем при всестороннем сжатии.
Характеризуется сжимаемость коэффициентом объемного сжатия, который представляет собой относительное изменение объема, приходящееся на единицу давления:
 ,
м2/Н
(2.7)
,
м2/Н
(2.7)
Знак минус в формуле имеет символическое значение и обусловлен тем, что положительному приращению давления р соответствует отрицательное приращение (уменьшение) объема W.
Величина, обратная коэффициенту βр, представляет собой объемный модуль упругости К:
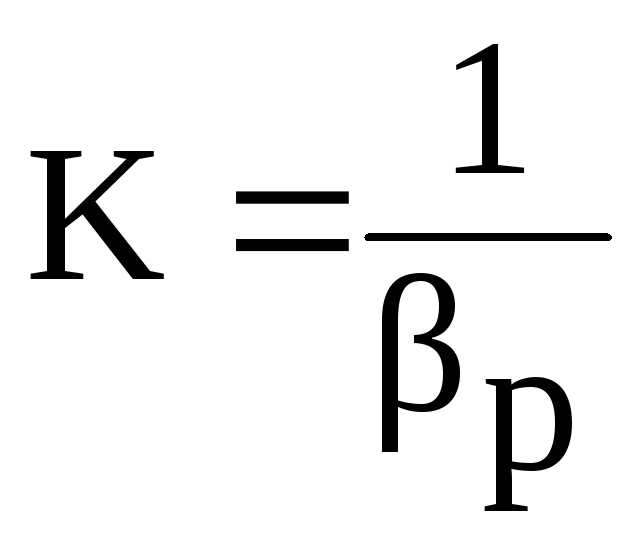
Для жидкостей модуль К несколько уменьшается с увеличением температуры и возрастает с повышением давления. Для воды он составляет при атмосферном давлении приблизительно 2000 МПа. Следовательно, при повышении давления на 0,1 МПа объем воды уменьшается всего на 1/20000 часть. Такого же порядка модуль упругости и для других жидкостей.
В большинстве случаев жидкости можно считать практически несжимаемыми, т.е. принимать их плотность не зависящей от давления. Но при очень высоких давлениях и упругих колебаниях сжимаемость жидкости следует учитывать.
2.3. Температурное расширение жидкости
Повышая температуру жидкости, мы обычно заставляем ее молекулы удаляться друг от друга. Температурное расширение характеризуется коэффициентом температурного расширения βt, который равен относительному изменению объема W при изменении температуры на один градус:
 ,
1/град (2.9)
,
1/град (2.9)
При нагревании жидкости в герметичном объеме в последнем повысится давление на величину Δр:
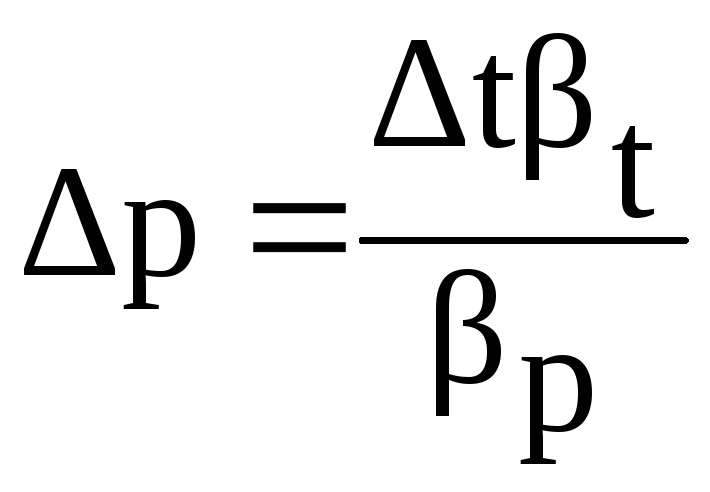 ,
Н/м2 (2.10)
,
Н/м2 (2.10)
Значение коэффициента температурного расширения βt зависит от давления, действующего на рассматриваемый объем жидкости. В частности, у воды он увеличивается с возрастанием давления при повышении ее температуры от 0 до 50оС и уменьшается с возрастанием давления при дальнейшем повышении ее температуры. У большинства других жидкостей коэффициент βt уменьшается с увеличением давления при любой температуре.
При гидравлических расчетах водопроводных сооружений температурным расширением воды можно пренебречь из-за незначительного изменения температуры и давления воды, а при расчете тепловых сетей температурное расширение воды учитывают.
Для воды, например, осредненное ориентировочное значение коэффициента температурного расширения βt равно 14·10-6 1/град.
2.4. Вязкость жидкостей
При движении жидкости в трубах и открытых руслах каждый слой ее частиц скользит по другому, т.е. внутри жидкости происходит процесс, аналогичный трению. Силы, возникающие в результате скольжения слоев жидкости, называют силами внутреннего трения, или силами вязкости.
Свойство жидкости оказывать сопротивление касательным усилиям называют тангенциальной вязкостью.
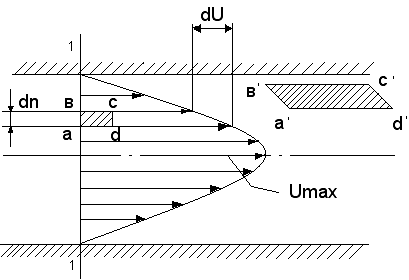
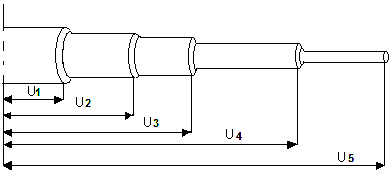
Рассмотрим движение жидкости, при котором скорости отдельных ее частиц параллельны оси трубы. Опыт показывает, что такое движение жидкости существует в природе (оно называется ламинарным и в дальнейшем будет подробно изучено). Скорости частиц, расположенных в некотором поперечном сечении трубы 1-1, отличаются друг от друга (рис. 2.1).
Скорость жидкости у стенки равна нулю, возрастает по направлению к оси трубы, достигая на оси наибольшего значения Umax. Поток жидкости может быть представлен как движение отдельных бесконечно тонких цилиндрических слоев жидкости, перемещающихся с различными скоростями, увеличивающимися к оси трубы.
| |
Рис.2.1
Вследствие
молекулярного движения молекулы жидкости
пересекают слои жидкости, движущиеся
по отношению друг к другу с относительной
скоростью, благодаря чему на поверхности
соприкасающихся слоев жидкости возникают
силы трения. При этом слои жидкости,
движущиеся быстрее, увлекают за собой
слои, движущиеся медленнее, тормозят
движение слоев, движущихся быстрее. В
таком движении частицы жидкости в виде
прямоугольника a,
b,
c,
d
деформируются в параллелограмм a
Исаак Ньютон в 1687 году сумел установить, что силы внутреннего трения, возникающие между соседними движущимися слоями жидкости, прямо пропорциональны скорости относительного движения и площади поверхности соприкосновения, вдоль которых совершается относительное движение, зависят от рода жидкости и не зависят от давления.
Гипотеза Ньютона подвергалась многократной опытной проверке и полностью подтвердилась. Чрезвычайно ценные исследования для доказательства этой гипотезы были выполнены крупнейшим русским ученым, профессором Н.П. Петровым (1836-1920 гг.), создателем гидродинамической теории смазки.
гипотеза Ньютона стала законом жидкостного трения. В математической форме он выражается следующим образом
 ,
(2.11)
,
(2.11)
где
Т – сила внутреннего трения, н;  –
градиент скорости, имеющий положительный
или отрицательный знак в зависимости
от характера изменения скорости по
сечению;dU
– разность скоростей движения соседних
соприкасающихся слоев жидкости в
предположении, что эти слои являются
бесконечно тонкими, м/с; dn
– расстояние между осями соседних
слоев, м; ω – площадь соприкасающихся
слоев, м2;
μ — динамический коэффициент вязкости,
Па·с.
–
градиент скорости, имеющий положительный
или отрицательный знак в зависимости
от характера изменения скорости по
сечению;dU
– разность скоростей движения соседних
соприкасающихся слоев жидкости в
предположении, что эти слои являются
бесконечно тонкими, м/с; dn
– расстояние между осями соседних
слоев, м; ω – площадь соприкасающихся
слоев, м2;
μ — динамический коэффициент вязкости,
Па·с.
Силу трения Т, отнесенную к единице площади ω, называют касательным напряжением:
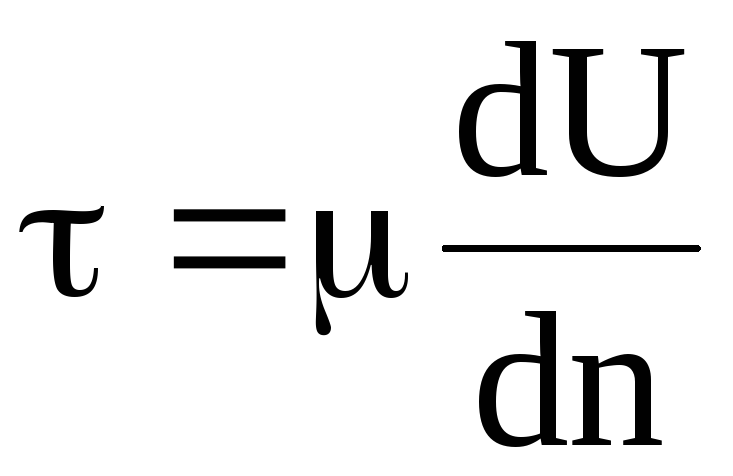 .
(2.12)
.
(2.12)
Жидкости, подчиняющиеся выражениям (2.11) и (2.12), принято называть ньютоновскими.
Наряду с динамической вязкостью μ в гидравлических расчетах применяют кинематическую вязкость:
 ,м2/с
(2.13)
,м2/с
(2.13)
Единицей измерения кинематической вязкости является стокс 1 Ст = 1 см2/с. Сотая часть стокса называется сантистоксом (сСт). Приборы для измерения вязкости называются вискозиметрами. Динамическую вязкость можно определить ротационными вискозиметрами.
На практике часто сравнивают время истечения жидкости со временем истечения воды. Это отношение называют условной вязкостью (ВУ) и измеряют в градусах Энглера:  .
(2.14)
.
(2.14)
Но величина условной вязкости безразмерна и при решении задач неудобна, поэтому существуют эмпирические формулы пересчета. Одна из них
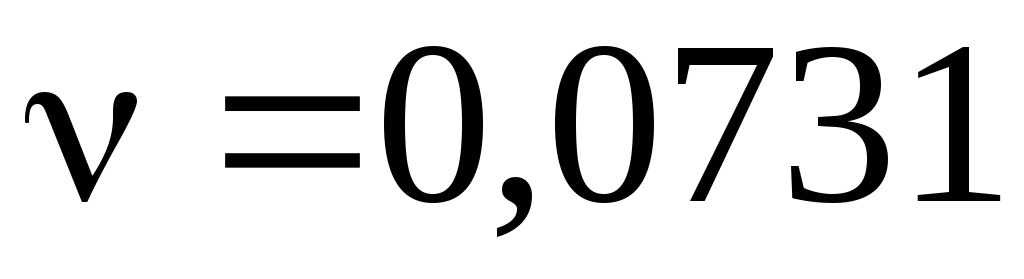 ºЕ
—
ºЕ
— 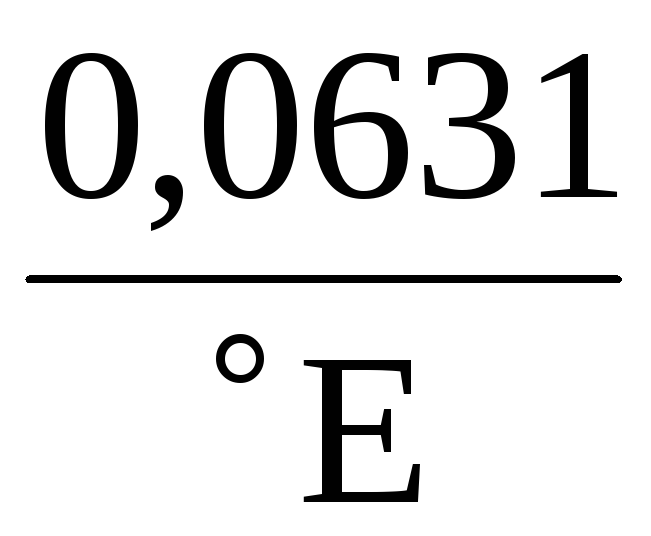 ,
см2/с
(2.15)
,
см2/с
(2.15)
В США и Англии получили распространение единицы измерения вязкости в секундах Редвуда (´´Re) и Сейболта (´´S), во Франции – градусы Барбье (оВ).
Вязкость жидкостей существенным образом зависит от температуры. Она уменьшается с ее ростом. От увеличения давления вязкость также зависит, увеличиваясь с его ростом. Причем эта зависимость для разных температур будет различной.
В пределах относительно небольших давлений (0…40 МПа) вязкость, например, минеральных масел изменяется с изменением давления практически линейно (примерно в три раза). В пределах давления 0…150 МПа вязкость повышается в 17 раз, 0…400 МПа – в сотни раз. При давлениях порядка 150…2000 МПа минеральные масла затвердевают.
Кроме ньютоновских жидкостей, существуют жидкости аномальные (структурные), которые не подчиняются закону Ньютона, и поэтому их называют неньютоновскими. Это осадки сточных вод (гели), цементные, глинистые и меловые растворы, парафинистые нефти вблизи температуры их застывания, разнообразные коллоидные растворы (белок, крахмал, клей), нефтяные эмульсии (смеси с водой), суспензии (шламы, гидроторф, озерный ил, битумы), молочные продукты, кормовые смеси, различного рода пасты.
Перечисленные аномальные жидкости подчиняются закону Шведова – Бингама
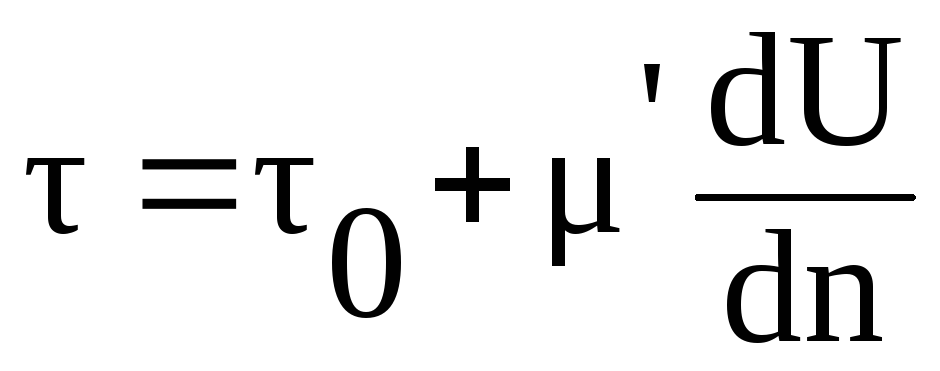 ,
Н/м2 (2.16)
,
Н/м2 (2.16)
где — начальное напряжение сдвига; µ′ — структурная вязкость.
Жидкости,
подчиняющиеся выражению (2.16), называются
еще бингамовскими, или вязко-пластичными.
Для повышения достоверности расчетов
таких жидкостей начальное напряжение
сдвига  ,
как правило, определяют экспериментально.
,
как правило, определяют экспериментально.
studfile.net
2.2. Сжимаемость жидкости
Характеризуется сжимаемость коэффициентом объемного сжатия, который представляет собой относительное изменение объема, приходящееся на единицу давления:
 ,
м2/Н
(2.7)
,
м2/Н
(2.7)
Знак минус в формуле имеет символическое значение и обусловлен тем, что положительному приращению давления р соответствует отрицательное приращение (т.е. уменьшение) объема W.
Величина, обратная коэффициенту βр, представляет собой объемный модуль упругости К:
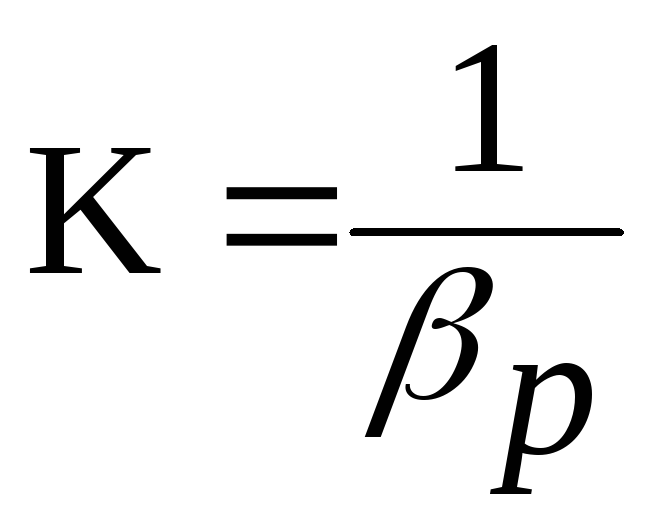 ,
Н/м2 (2.8)
,
Н/м2 (2.8)
Для жидкостей модуль К несколько уменьшается с увеличением температуры и возрастает с повышением давления. Для воды он составляет при атмосферном давлении приблизительно 2000 МПа. Следовательно, при повышении давления на 0,1 МПа объем воды уменьшается всего на 1/20000 часть. Такого же порядка модуль упругости и для других жидкостей.
В большинстве случаев жидкости можно считать практически несжимаемыми, т.е. принимать их плотность не зависящей от давления. Но при очень высоких давлениях и упругих колебаниях сжимаемость жидкости следует учитывать.
2.3. Температурное расширение жидкости
Повышая температуру жидкости, мы обычно заставляем ее молекулы удаляться друг от друга. Температурное расширение характеризуется коэффициентом температурного расширения βt, который равен относительному изменению объема W при изменении температуры на один градус:
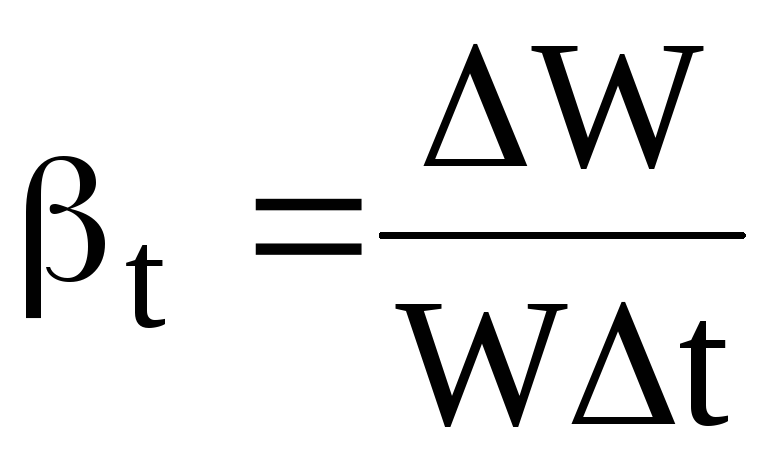 ,
1/град (2.9)
,
1/град (2.9)
При нагревании жидкости в герметичном объеме в последнем повысится давление на величину Δр:
 ,
Н/м2 (2.10)
,
Н/м2 (2.10)
Значение коэффициента температурного расширения βt зависит от давления, действующего на рассматриваемый объем жидкости. В частности, у воды он увеличивается с возрастанием давления при повышении ее температуры от 0 до 50оС и уменьшается с возрастанием давления при дальнейшем повышении ее температуры. У большинства других жидкостей коэффициент βt уменьшается с увеличением давления при любой температуре.
При гидравлических расчетах водопроводных сооружений температурным расширением воды можно пренебречь из-за незначительного изменения температуры и давления воды, а при расчете тепловых сетей температурное расширение воды учитывают.
Для воды, например, осредненное ориентировочное значение коэффициента температурного расширения βt равно 14·10-6 1/град.
2.4. Вязкость жидкостей
При движении жидкости в трубах и открытых руслах каждый слой ее частиц скользит по другому, т.е. внутри жидкости происходит процесс, аналогичный трению. Силы, возникающие в результате скольжения слоев жидкости, называют силами внутреннего трения, или силами вязкости.
Свойство жидкости оказывать сопротивление касательным усилиям называют тангенциальной вязкостью.
Рассмотрим движение жидкости, при котором скорости отдельных ее частиц параллельны оси трубы. Опыт показывает, что такое движение жидкости существует в природе (оно называется ламинарным и в дальнейшем будет подробно изучено). Скорости частиц, расположенных в некотором поперечном сечении трубы 1-1, отличаются друг от друга (рис. 2.1).
Скорость жидкости у стенки равна нулю, возрастает по направлению к оси трубы, достигая на оси наибольшего значения Umax. Поток жидкости может быть представлен как движение отдельных бесконечно тонких цилиндрических слоев жидкости, перемещающихся с различными скоростями, увеличивающимися к оси трубы.
| |
Рис.2.1
Вследствие молекулярного движения молекулы жидкости пересекают слои жидкости, движущиеся по отношению друг к другу с относительной скоростью, благодаря чему на поверхности соприкасающихся слоев жидкости возникают силы трения. При этом слои жидкости, движущиеся быстрее, увлекают за собой слои, движущиеся медленнее, тормозят движение слоев, движущихся быстрее. В таком движении частицы жидкости в виде прямоугольника a, b, c, d деформируются в параллелограмм a,,b,, c,, d,. Деформация объема является обязательным условием возникновения сил трения.
Исаак Ньютон в 1687 году сумел установить, что силы внутреннего трения, возникающие между соседними движущимися слоями жидкости, прямо пропорциональны скорости относительного движения и площади поверхности соприкосновения, вдоль которых совершается относительное движение, зависят от рода жидкости и не зависят от давления.
Гипотеза Ньютона подвергалась многократной опытной проверке и полностью подтвердилась. Чрезвычайно ценные исследования для доказательства этой гипотезы были выполнены крупнейшим русским ученым, профессором Н.П. Петровым (1836-1920 гг.), создателем гидродинамической теории смазки.
гипотеза Ньютона стала законом жидкостного трения. В математической форме он выражается следующим образом
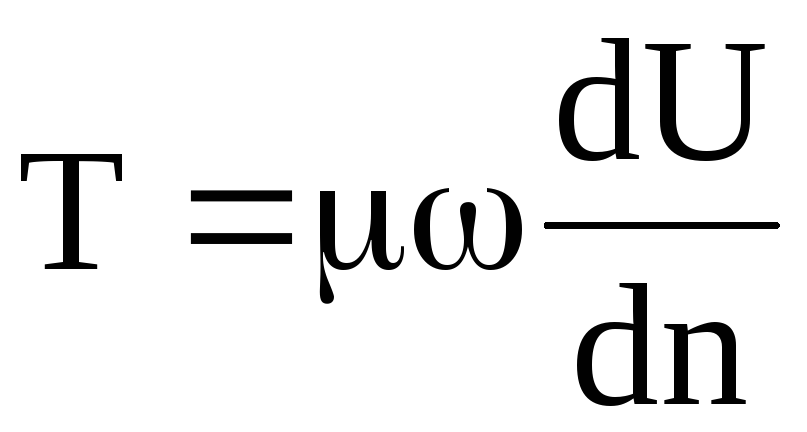 ,
(2.11)
,
(2.11)
где
Т – сила внутреннего трения, н; 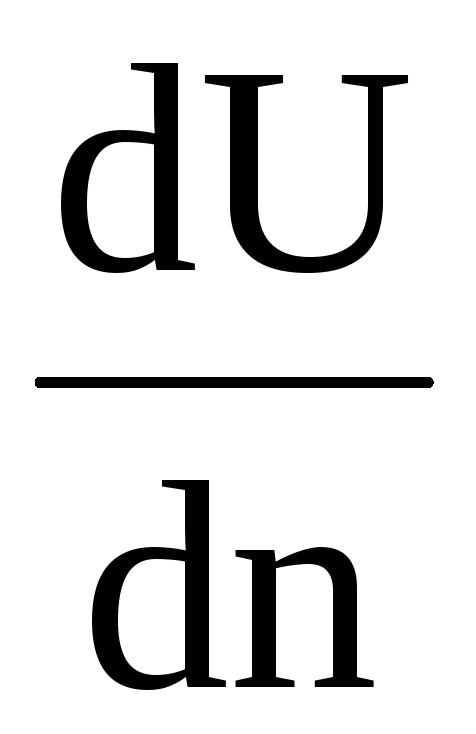 –
градиент скорости, имеющий положительный
или отрицательный знак в зависимости
от характера изменения скорости по
сечению;dU
– разность скоростей движения соседних
соприкасающихся слоев жидкости в
предположении, что эти слои являются
бесконечно тонкими, м/с; dn
– расстояние между осями соседних
слоев, м; ω – площадь соприкасающихся
слоев, м2;
μ — динамический коэффициент вязкости,
Па·с.
–
градиент скорости, имеющий положительный
или отрицательный знак в зависимости
от характера изменения скорости по
сечению;dU
– разность скоростей движения соседних
соприкасающихся слоев жидкости в
предположении, что эти слои являются
бесконечно тонкими, м/с; dn
– расстояние между осями соседних
слоев, м; ω – площадь соприкасающихся
слоев, м2;
μ — динамический коэффициент вязкости,
Па·с.
Силу трения Т, отнесенную к единице площади ω, называют касательным напряжением:
 .
(2.12)
.
(2.12)
Жидкости, подчиняющиеся выражениям (2.11) и (2.12), принято называть ньютоновскими.
Наряду с динамической вязкостью μ в гидравлических расчетах применяют кинематическую вязкость:
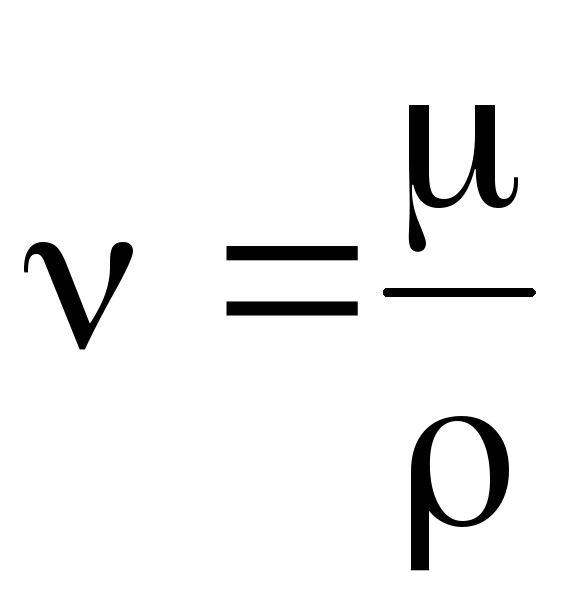 ,м2/с
(2.13)
,м2/с
(2.13)
Единицей измерения кинематической вязкости является стокс 1 Ст = 1 см2/с. Сотая часть стокса называется сантистоксом (сСт). Приборы для измерения вязкости называются вискозиметрами.
Динамическую вязкость можно определить ротационными вискозиметрами.
На практике часто сравнивают время истечения жидкости со временем истечения воды. Это отношение называют условной вязкостью (ВУ) и измеряют в градусах Энглера:
º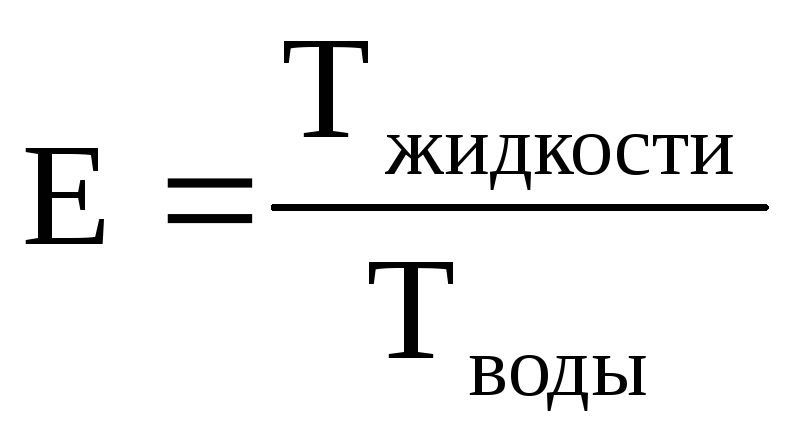 .
(2.14)
.
(2.14)
Но величина условной вязкости безразмерна и при решении задач неудобна, поэтому существуют эмпирические формулы пересчета. Одна из них
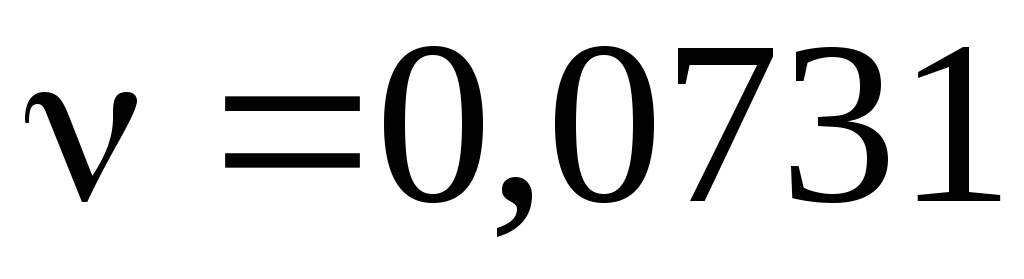 ºЕ
—
ºЕ
—  ,
см2/с
(2.15)
,
см2/с
(2.15)
В США и Англии получили распространение единицы измерения вязкости в секундах Редвуда (´´Re) и Сейболта (´´S), во Франции – градусы Барбье (оВ).
Вязкость жидкостей существенным образом зависит от температуры. Она уменьшается с ее ростом. От увеличения давления вязкость также зависит, увеличиваясь с его ростом. Причем эта зависимость для разных температур будет различной.
В пределах относительно небольших давлений (0…40 МПа) вязкость, например, минеральных масел изменяется с изменением давления практически линейно (примерно в три раза). В пределах давления 0…150 МПа вязкость повышается в 17 раз, 0…400 МПа – в сотни раз. При давлениях порядка 150…2000 МПа минеральные масла затвердевают.
Кроме ньютоновских жидкостей, существуют жидкости аномальные (структурные), которые не подчиняются закону Ньютона, и поэтому их называют неньютоновскими. Это осадки сточных вод (гели), цементные, глинистые и меловые растворы, парафинистые нефти вблизи температуры их застывания, разнообразные коллоидные растворы (белок, крахмал, клей), нефтяные эмульсии (смеси с водой), суспензии (шламы, гидроторф, озерный ил, битумы), молочные продукты, кормовые смеси, различного рода пасты.
Перечисленные аномальные жидкости подчиняются закону Шведова – Бингама
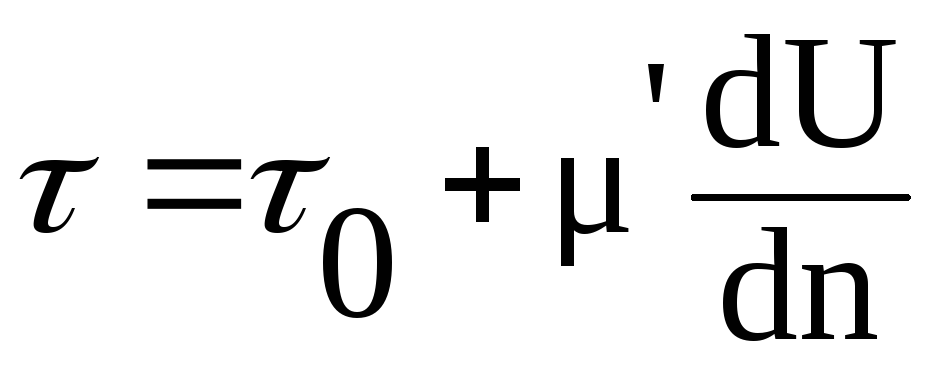 ,
Н/м2 (2.16)
,
Н/м2 (2.16)
где 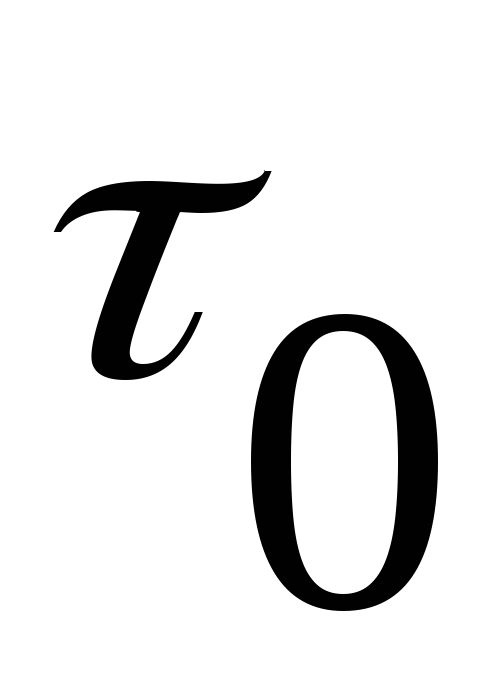 — начальное напряжение сдвига; µ′ — структурная вязкость.
— начальное напряжение сдвига; µ′ — структурная вязкость.
Жидкости,
подчиняющиеся выражению (2.16), называются
еще бингамовскими, или вязко-пластичными.
Для повышения достоверности расчетов
таких жидкостей начальное напряжение
сдвига 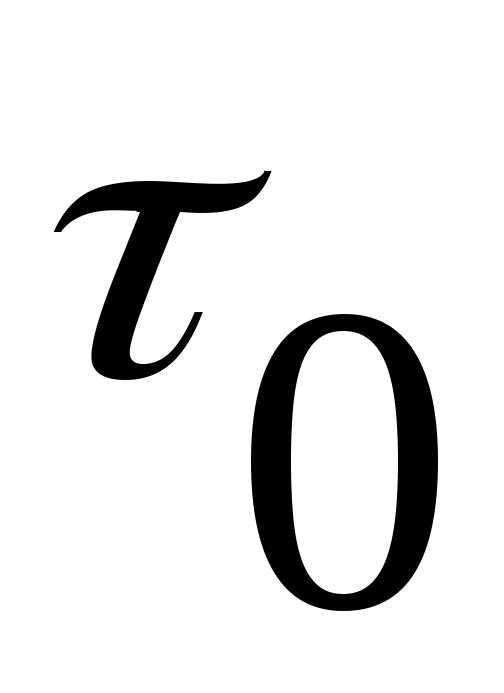 ,
как правило, определяют экспериментально.
,
как правило, определяют экспериментально.
studfile.net
2.2. Сжимаемость жидкости
Сжимаемостью называют свойство жидкости обратимым образом изменять свой объем при всестороннем сжатии.
Характеризуется сжимаемость коэффициентом объемного сжатия, который представляет собой относительное изменение объема, приходящееся на единицу давления:
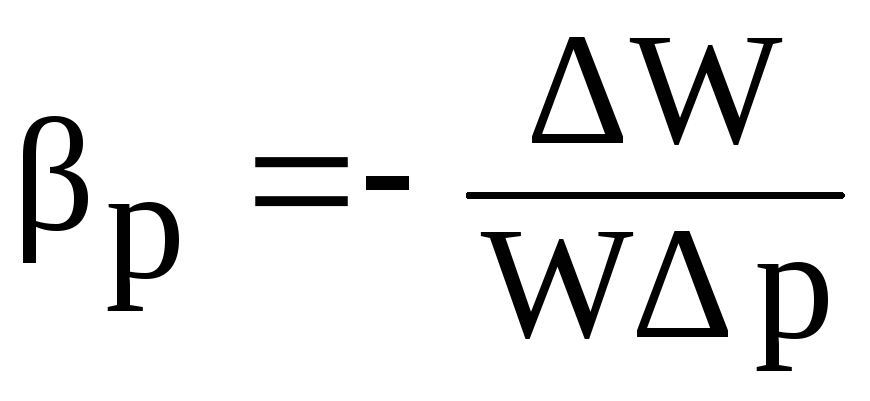 ,
м2/Н
(2.7)
,
м2/Н
(2.7)
Знак минус в формуле имеет символическое значение и обусловлен тем, что положительному приращению давления р соответствует отрицательное приращение (т.е. уменьшение) объема W.
Величина, обратная коэффициенту βр, представляет собой объемный модуль упругости К:
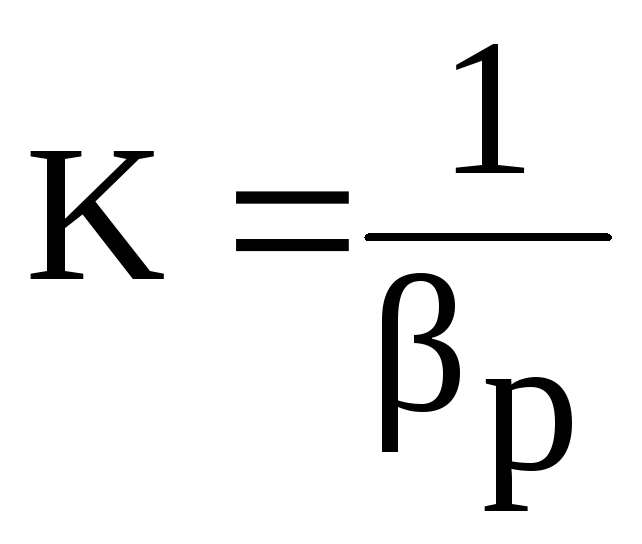 ,
Н/м2 (2.8)
,
Н/м2 (2.8)
Для жидкостей модуль К несколько уменьшается с увеличением температуры и возрастает с повышением давления. Для воды он составляет при атмосферном давлении приблизительно 2000 МПа. Следовательно, при повышении давления на 0,1 МПа объем воды уменьшается всего на 1/20000 часть. Такого же порядка модуль упругости и для других жидкостей.
В большинстве случаев жидкости можно считать практически несжимаемыми, т.е. принимать их плотность не зависящей от давления. Но при очень высоких давлениях и упругих колебаниях сжимаемость жидкости следует учитывать.
2.3. Температурное расширение жидкости
Повышая температуру жидкости, мы обычно заставляем ее молекулы удаляться друг от друга. Температурное расширение характеризуется коэффициентом температурного расширения βt, который равен относительному изменению объема W при изменении температуры на один градус:
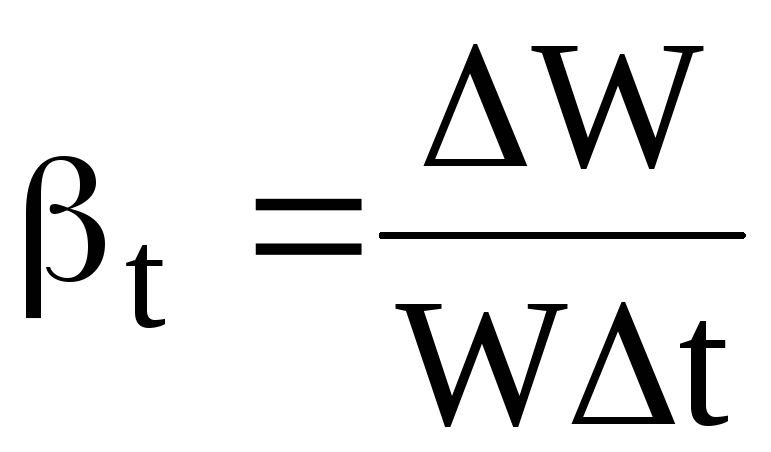 ,
1/град (2.9)
,
1/град (2.9)
При нагревании жидкости в герметичном объеме в последнем повысится давление на величину Δр:
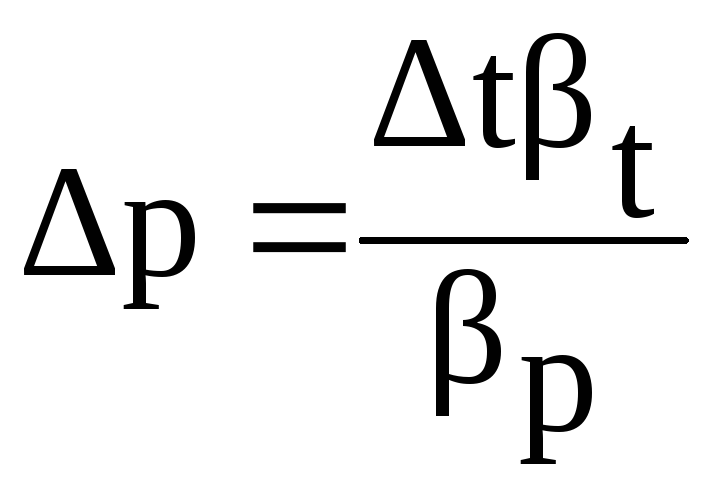 ,
Н/м2 (2.10)
,
Н/м2 (2.10)
Значение коэффициента температурного расширения βt зависит от давления, действующего на рассматриваемый объем жидкости. В частности, у воды он увеличивается с возрастанием давления при повышении ее температуры от 0 до 50оС и уменьшается с возрастанием давления при дальнейшем повышении ее температуры. У большинства других жидкостей коэффициент βt уменьшается с увеличением давления при любой температуре.
При гидравлических расчетах водопроводных сооружений температурным расширением воды можно пренебречь из-за незначительного изменения температуры и давления воды, а при расчете тепловых сетей температурное расширение воды учитывают.
Для воды, например, осредненное ориентировочное значение коэффициента температурного расширения βt равно 14·10-6 1/град.
2.4. Вязкость жидкостей
При движении жидкости в трубах и открытых руслах каждый слой ее частиц скользит по другому, т.е. внутри жидкости происходит процесс, аналогичный трению. Силы, возникающие в результате скольжения слоев жидкости, называют силами внутреннего трения, или силами вязкости.
Свойство жидкости оказывать сопротивление касательным усилиям называют тангенциальной вязкостью.
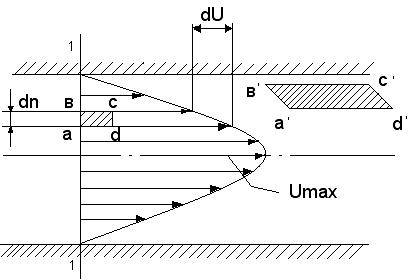
Рассмотрим движение жидкости, при котором скорости отдельных ее частиц параллельны оси трубы. Опыт показывает, что такое движение жидкости существует в природе (оно называется ламинарным и в дальнейшем будет подробно изучено). Скорости частиц, расположенных в некотором поперечном сечении трубы 1-1, отличаются друг от друга (рис. 2.1).
Скорость жидкости у стенки равна нулю, возрастает по направлению к оси трубы, достигая на оси наибольшего значения Umax. Поток жидкости может быть представлен как движение отдельных бесконечно тонких цилиндрических слоев жидкости, перемещающихся с различными скоростями, увеличивающимися к оси трубы.
| |
Рис.2.1
Вследствие молекулярного движения молекулы жидкости пересекают слои жидкости, движущиеся по отношению друг к другу с относительной скоростью, благодаря чему на поверхности соприкасающихся слоев жидкости возникают силы трения. При этом слои жидкости, движущиеся быстрее, увлекают за собой слои, движущиеся медленнее, тормозят движение слоев, движущихся быстрее. В таком движении частицы жидкости в виде прямоугольника a, b, c, d деформируются в параллелограмм a,,b,, c,, d,. Деформация объема является обязательным условием возникновения сил трения.
Исаак Ньютон в 1687 году сумел установить, что силы внутреннего трения, возникающие между соседними движущимися слоями жидкости, прямо пропорциональны скорости относительного движения и площади поверхности соприкосновения, вдоль которых совершается относительное движение, зависят от рода жидкости и не зависят от давления.
Гипотеза Ньютона подвергалась многократной опытной проверке и полностью подтвердилась. Чрезвычайно ценные исследования для доказательства этой гипотезы были выполнены крупнейшим русским ученым, профессором Н.П. Петровым (1836-1920 гг.), создателем гидродинамической теории смазки.
гипотеза Ньютона стала законом жидкостного трения. В математической форме он выражается следующим образом
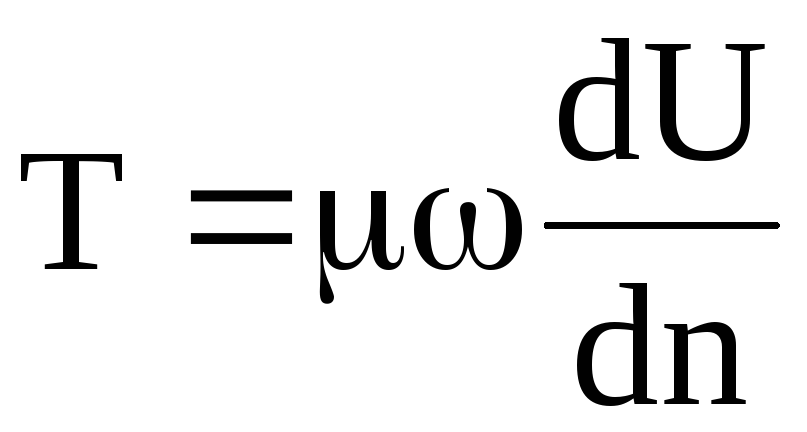 ,
(2.11)
,
(2.11)
где
Т – сила внутреннего трения, н; 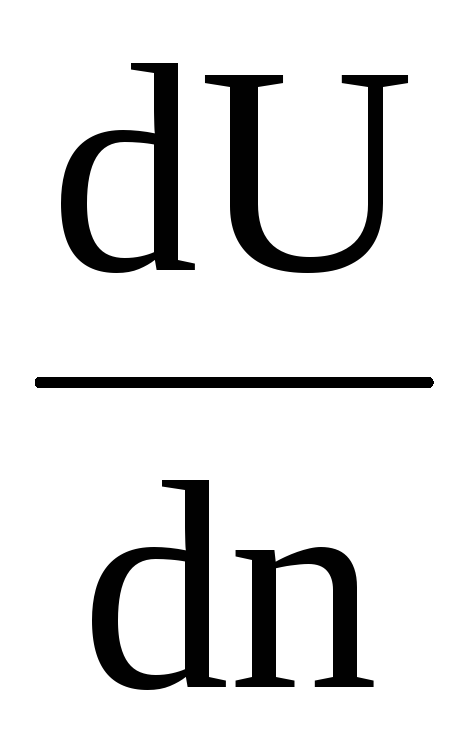 –
градиент скорости, имеющий положительный
или отрицательный знак в зависимости
от характера изменения скорости по
сечению;dU
– разность скоростей движения соседних
соприкасающихся слоев жидкости в
предположении, что эти слои являются
бесконечно тонкими, м/с; dn
– расстояние между осями соседних
слоев, м; ω – площадь соприкасающихся
слоев, м2;
μ — динамический коэффициент вязкости,
Па·с.
–
градиент скорости, имеющий положительный
или отрицательный знак в зависимости
от характера изменения скорости по
сечению;dU
– разность скоростей движения соседних
соприкасающихся слоев жидкости в
предположении, что эти слои являются
бесконечно тонкими, м/с; dn
– расстояние между осями соседних
слоев, м; ω – площадь соприкасающихся
слоев, м2;
μ — динамический коэффициент вязкости,
Па·с.
Силу трения Т, отнесенную к единице площади ω, называют касательным напряжением:
 .
(2.12)
.
(2.12)
Жидкости, подчиняющиеся выражениям (2.11) и (2.12), принято называть ньютоновскими.
Наряду с динамической вязкостью μ в гидравлических расчетах применяют кинематическую вязкость:
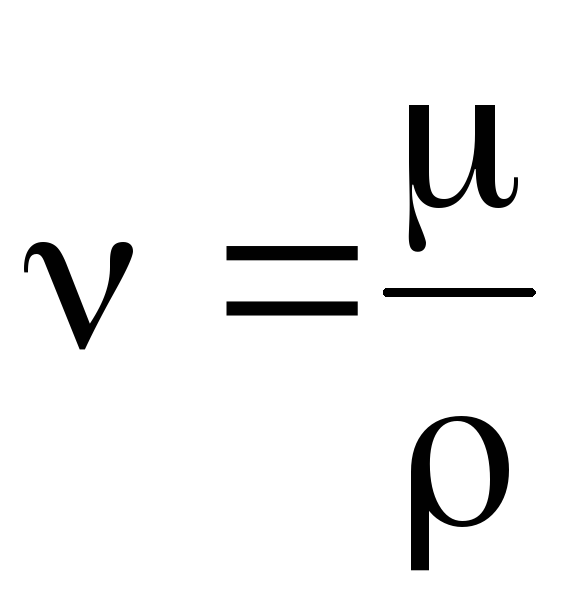 ,м2/с
(2.13)
,м2/с
(2.13)
Единицей измерения кинематической вязкости является стокс 1 Ст = 1 см2/с. Сотая часть стокса называется сантистоксом (сСт). Приборы для измерения вязкости называются вискозиметрами.
Динамическую вязкость можно определить ротационными вискозиметрами.
На практике часто сравнивают время истечения жидкости со временем истечения воды. Это отношение называют условной вязкостью (ВУ) и измеряют в градусах Энглера:
º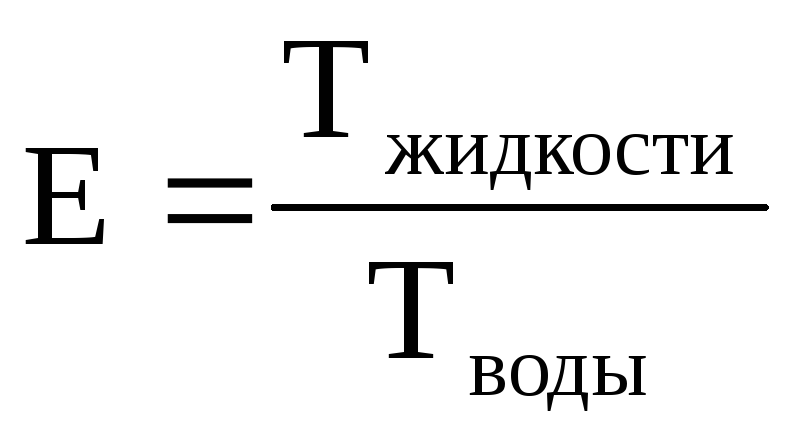 .
(2.14)
.
(2.14)
Но величина условной вязкости безразмерна и при решении задач неудобна, поэтому существуют эмпирические формулы пересчета. Одна из них
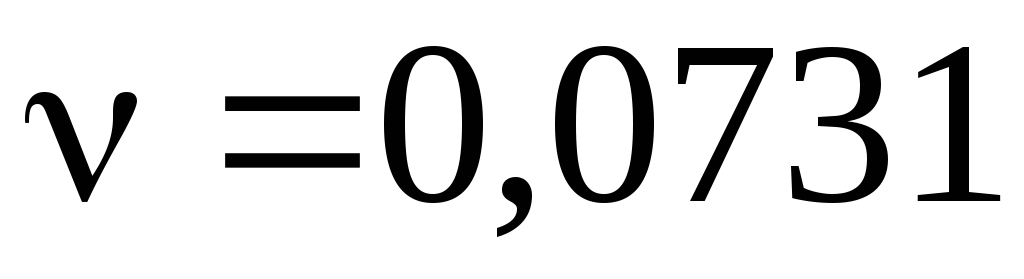 ºЕ
—
ºЕ
—  ,
см2/с
(2.15)
,
см2/с
(2.15)
В США и Англии получили распространение единицы измерения вязкости в секундах Редвуда (´´Re) и Сейболта (´´S), во Франции – градусы Барбье (оВ).
Вязкость жидкостей существенным образом зависит от температуры. Она уменьшается с ее ростом. От увеличения давления вязкость также зависит, увеличиваясь с его ростом. Причем эта зависимость для разных температур будет различной.
В пределах относительно небольших давлений (0…40 МПа) вязкость, например, минеральных масел изменяется с изменением давления практически линейно (примерно в три раза). В пределах давления 0…150 МПа вязкость повышается в 17 раз, 0…400 МПа – в сотни раз. При давлениях порядка 150…2000 МПа минеральные масла затвердевают.
Кроме ньютоновских жидкостей, существуют жидкости аномальные (структурные), которые не подчиняются закону Ньютона, и поэтому их называют неньютоновскими. Это осадки сточных вод (гели), цементные, глинистые и меловые растворы, парафинистые нефти вблизи температуры их застывания, разнообразные коллоидные растворы (белок, крахмал, клей), нефтяные эмульсии (смеси с водой), суспензии (шламы, гидроторф, озерный ил, битумы), молочные продукты, кормовые смеси, различного рода пасты.
Перечисленные аномальные жидкости подчиняются закону Шведова – Бингама
 ,
Н/м2 (2.16)
,
Н/м2 (2.16)
где  — начальное напряжение сдвига; µ′ — структурная вязкость.
— начальное напряжение сдвига; µ′ — структурная вязкость.
Жидкости,
подчиняющиеся выражению (2.16), называются
еще бингамовскими, или вязко-пластичными.
Для повышения достоверности расчетов
таких жидкостей начальное напряжение
сдвига  ,
как правило, определяют экспериментально.
,
как правило, определяют экспериментально.
studfile.net
Сжимаемость и стойкость жидкости
Сжимаемость
жидкости. Капельная жидкость является упругим
телом, которое при давлениях примерно
свыше 60 МПа подчиняется с некоторым
приближением закону Гука.
Жесткость жидкости
можно оценить коэффициентом
относительной объемной сжимаемости  , который характеризует изменение единицы
объема жидкости, приходящееся на единицу
изменения (приращения) давления:
, который характеризует изменение единицы
объема жидкости, приходящееся на единицу
изменения (приращения) давления:
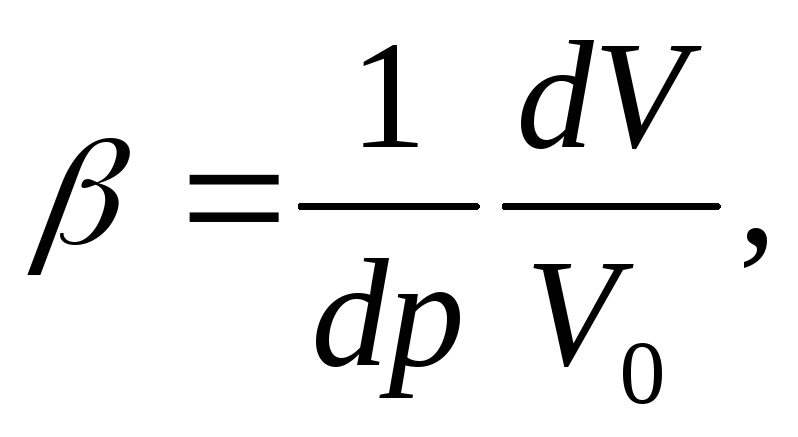
или
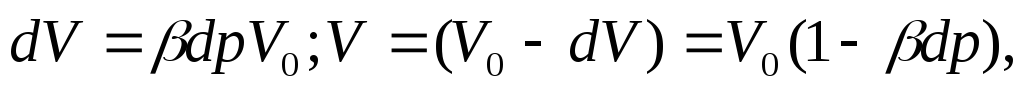
где 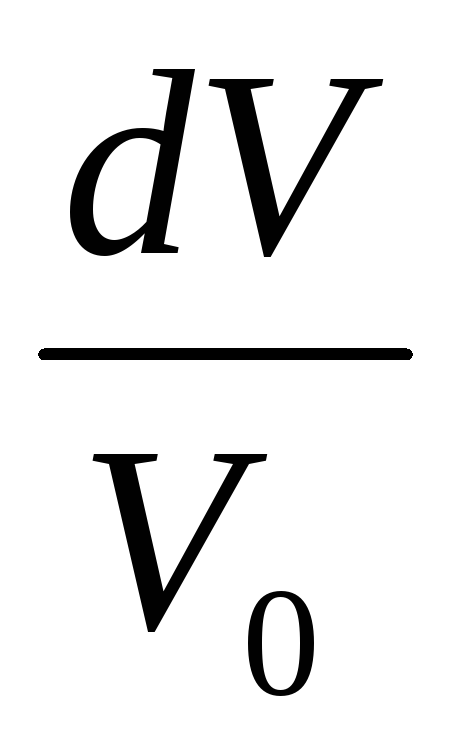 — относительное изменение объема при
изменении давления на;
— относительное изменение объема при
изменении давления на;
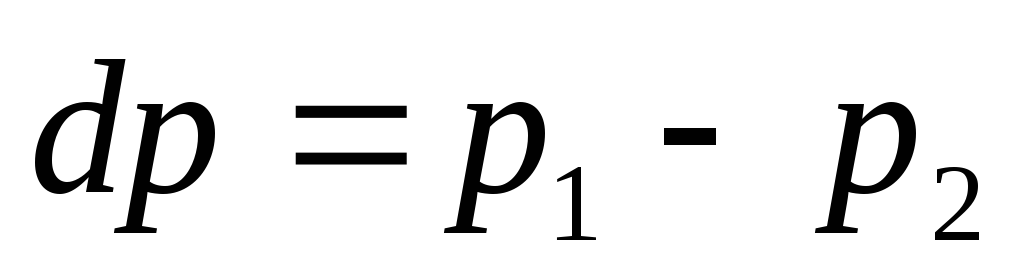 — изменение давления,
действующего на жидкость;
— изменение давления,
действующего на жидкость;
 и
и  — начальный объем жидкости при атмосферном
давлении и объем при изменении давления
на
— начальный объем жидкости при атмосферном
давлении и объем при изменении давления
на ;
;
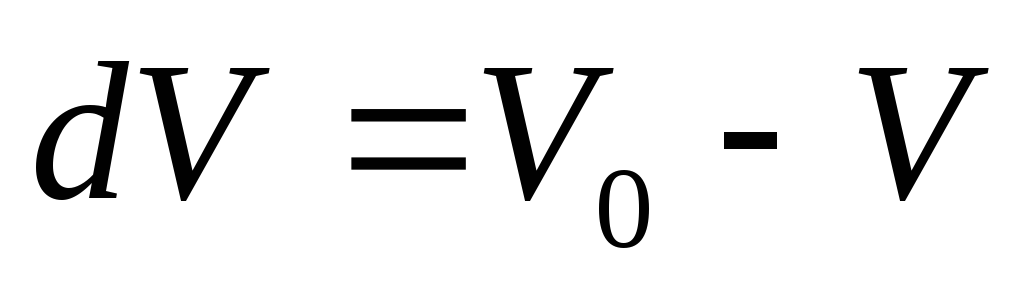 — изменение объема
жидкости при изменении давления на
— изменение объема
жидкости при изменении давления на 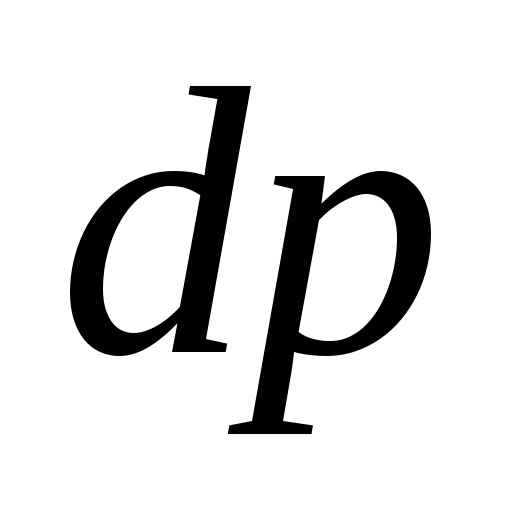 .
.
Величина, обратная  ,
называется объемным модулем упругости
жидкости при всестороннем сжатии:
,
называется объемным модулем упругости
жидкости при всестороннем сжатии:
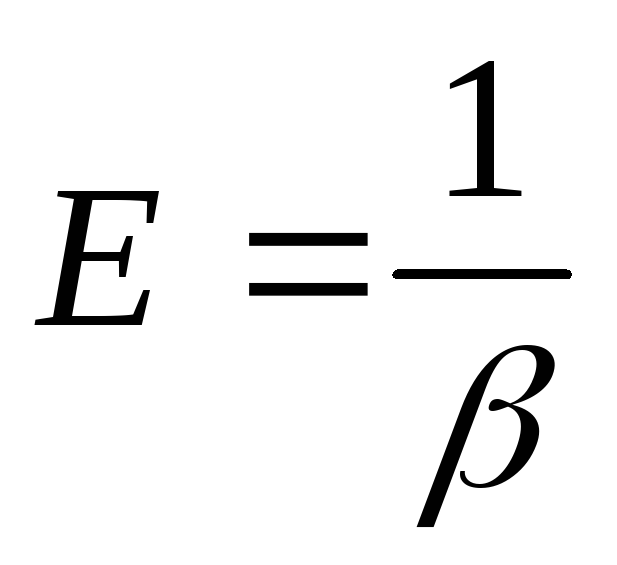 .
.
Объемный модуль
упругости  и соответственно коэффициент сжимаемости
и соответственно коэффициент сжимаемости жидкости изменяется в широких пределах
в зависимости от типа жидкости, давления
и температуры.С
повышением температуры объемный модуль
упругости уменьшается, а коэффициент
сжимаемости повышается.
жидкости изменяется в широких пределах
в зависимости от типа жидкости, давления
и температуры.С
повышением температуры объемный модуль
упругости уменьшается, а коэффициент
сжимаемости повышается.
С повышением
давления коэффициент сжимаемости жидкости уменьшается, особенно при
сравнительно низких давлениях.
жидкости уменьшается, особенно при
сравнительно низких давлениях.
При изменениях
давления жидкости от 0 до 60 МПа изменением
значений  и
и можно пренебречь; при этих условиях
относительное изменение объема
можно пренебречь; при этих условиях
относительное изменение объема в процессе сжатия будет пропорционально
изменению давления
в процессе сжатия будет пропорционально
изменению давления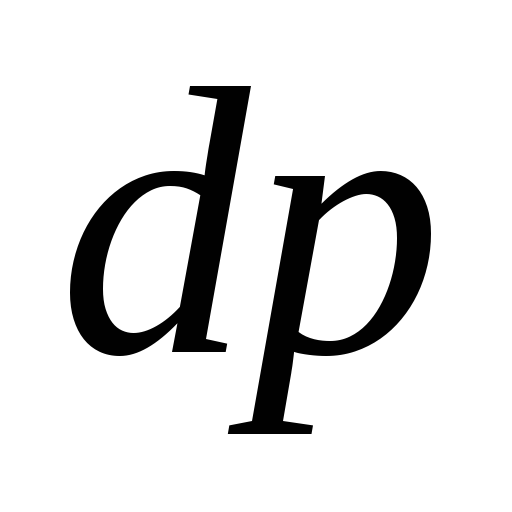 .
.
Значение объемного
модуля упругости  (при температуре 200С
и атмосферном давлении) для легких
минеральных масел, используемых в
гидросистемах, колеблется в пределах
1350-1750 МПа, что соответствует значениям
коэффициента
(при температуре 200С
и атмосферном давлении) для легких
минеральных масел, используемых в
гидросистемах, колеблется в пределах
1350-1750 МПа, что соответствует значениям
коэффициента  от 74.10-11 до 57.10-11 м2/Н.
Для воды и рабочих жидкостей на водной
основе значение модуля упругости при
относительно небольших давлениях (до
20 МПа) можно принять равным 2000 МПа.
от 74.10-11 до 57.10-11 м2/Н.
Для воды и рабочих жидкостей на водной
основе значение модуля упругости при
относительно небольших давлениях (до
20 МПа) можно принять равным 2000 МПа.
Среднее значение
коэффициента сжимаемости  масла АМГ-10 для диапазона давлений 0-20
МПа и температуры 200С
можно принимать
масла АМГ-10 для диапазона давлений 0-20
МПа и температуры 200С
можно принимать  = 7.10-10 м2/Н,
а для более тяжелых масел
= 7.10-10 м2/Н,
а для более тяжелых масел  = 6.10-10 м2/Н.
= 6.10-10 м2/Н.
Ввиду высокого значения объемного модуля упругости жидкости в ряде технических расчетов сжимаемостью при типовых давлениях (до 20 МПа) можно пренебречь, считая жидкость несжимаемой.
Механическая и химическая стойкость жидкостей. Для практических целей важно, чтобы рабочие жидкости в условиях применения и хранения не изменяли своих первоначальных физических и химических свойств, т.е. сохраняли физическую и химическую стабильность.
Основной причиной нарушения физической стабильности жидкости является мятие ее при работе в условиях высоких давлений, в особенности при дросселировании с большим перепадом давления, вызывающим молекулярно-структурные изменения (деструкцию) жидкости. В результате вязкость жидкости может понизиться, а ее смазывающие свойства ухудшиться.
Важным фактором является также химическая стабильность жидкости, или стойкость к окислению, в результате которого происходит выпадение из нее отложений в виде смол, сопровождающееся понижением вязкости и потерей смазывающих качеств.
Воздействие жидкости на резиновые детали. Важным параметром, характеризующим качество рабочих жидкостей для гидросистем, является степень воздействия их на применяемые материалы, в частности – на резиновые детали. Усадка, набухание и размягчение резиновых деталей уплотнительных узлов под воздействием жидкости сопровождается нарушением герметичности и другими дефектами в работе гидроагрегатов. При длительном контакте рабочей жидкости с резиновыми деталями происходит сложный физико-химический процесс вымывания отдельных компонентов резины и замещения их жидкостью. При этом изменяется масса и объем резиновой детали и физико-механических свойств резины.
Обычно требуется,
чтобы твердость испытываемого резинового
образца после воздействия минерального
масла не изменялась больше чем на 4-5 единиц по Шору. Разница между объемами
резинового образца в начале и в конце
испытания не должна превышать3%
первоначального объема. По техническим
условиям набухание синтетической резины
в жидкостях допускается до 5-6%.
4-5 единиц по Шору. Разница между объемами
резинового образца в начале и в конце
испытания не должна превышать3%
первоначального объема. По техническим
условиям набухание синтетической резины
в жидкостях допускается до 5-6%.
Особо следует отметить влияние на резину синтетических жидкостей, одни из которых вызывают либо чрезмерное набухание уплотнительных материалов, либо, наоборот, значительную его усадку.
Растворение в жидкостях газов. Газы, находящиеся в жидкости в растворенном состоянии, не оказывают существенного влияния на ее механические свойства. Однако, если давление в какой-либо точке объема жидкости уменьшается, газы выделяются из раствора в виде пузырьков, которые ухудшают свойства жидкости, уменьшая ее модуль упругости.
Объем газа, который может раствориться в жидкости до ее полного насыщения
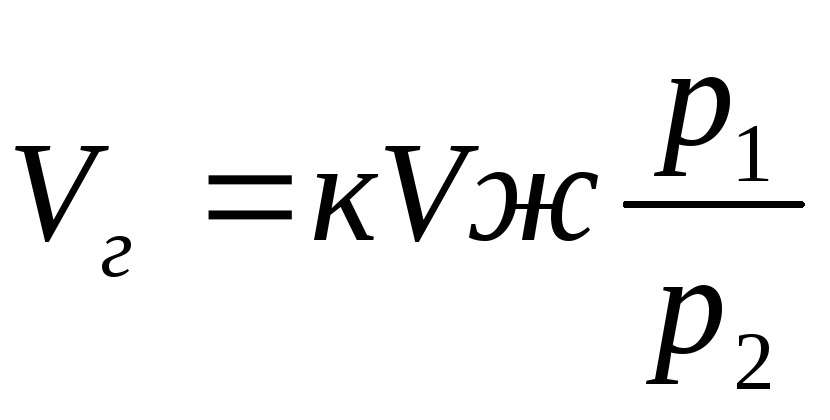 ,
,
где 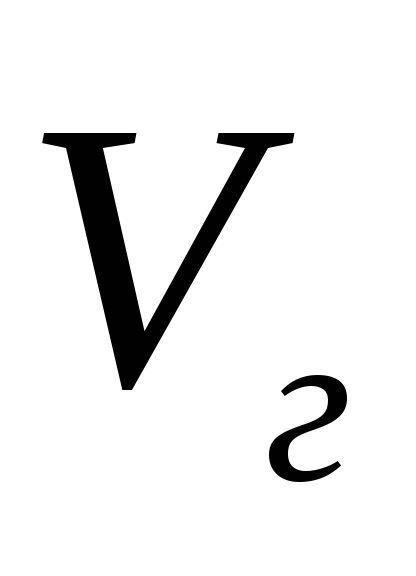 — объем газа при начальном давлении
— объем газа при начальном давлении ;
;
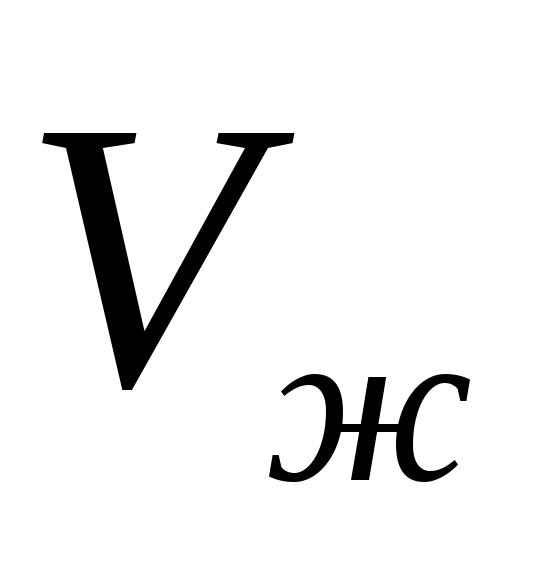 —
объем жидкости при конечном давлении
—
объем жидкости при конечном давлении 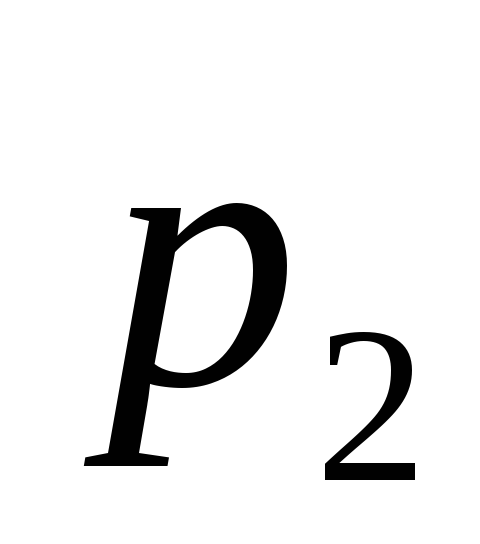 ;
;
 — коэффициент
растворимости ( при 200С
коэффициент растворимости воздуха в
масле равен 0,08-0,1).
— коэффициент
растворимости ( при 200С
коэффициент растворимости воздуха в
масле равен 0,08-0,1).
Присутствие нерастворенного газа ухудшает, а во многих случаях может полностью нарушить работу гидросистемы и ее агрегатов. В частности, при наличии газа ускоряется наступление кавитации. Газ, выделившийся из жидкости в местах пониженного давления, может частично заполнить рабочие полости насоса, уменьшая тем самым его подачу и ухудшая режим работы.
Механическая смесь воздуха с жидкостью. Воздух (газ) может находиться в жидкости в механической смеси, причем в зависимости от размеров пузырьков воздуха (диаметр пузырька равен 0,4 – 0,8 мкм) эта смесь обладает меньшей или большей устойчивостью. При определенных условиях, характеризуемых в основном размерами пузырьков и вязкостью жидкости, скорость вытеснения пузырьков воздуха становится столь малой, что воздух может находиться в смеси с маслом длительное время. Это значительно понижает модуль упругости жидкости и, следовательно, понижается жесткость гидравлического механизма. Так, при давлении 15 МПа модуль упругости гидрогазовой смеси, содержащей 1% газа (приведенного к нормальным техническим условиям), почти в 2 раза меньше модуля упругости однородной жидкости.
При наличии в жидкости нерастворенного воздуха подача насосов понижается, а также сокращается вследствие гидравлических ударов срок их службы.
studfile.net
плотность, сжимаемость, растворимость газов, объёмное расширение, парообразование, кипение, кавитация.
Важнейшим физическим свойством жидкости, определяющим её концентрацию в пространстве, является плотность жидкости. Под плотностью жидкости понимается масса единицы объёма жидкости:
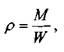
где: М — масса жидкости,
W — объём, занимаемый жидкостью.
В международной системе единиц СИ масса вещества измеряется в кг, объём жидкого тела в м 3 ,тогда размерность плотности жидкости в системе единиц СИ — кг/м 3.
Сжимаемость
жидкости — это ее свойство изменять
объем при изменении давления. Это
свойство характеризуется коэффициентом
объемного сжатия или сжимаемости,
выражающим относительное уменьшение
объема жидкости при увеличении давления
на единицу площади. Для расчетов в
области строительной гидравлики воду
считают несжимаемой. В связи с этим при
решении практических задач сжимаемостью
жидкости обычно пренебрегают. 
начальный
объём жидкости, (при начальном давлении),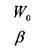
коэффициент объёмного (упругого) сжатия жидкости.
Испарянемость. При повышении температуры жидкости и, в некоторых случаях, при снижении давления часть массы капельной жидкости постепенно переходит в газообразное состояние (пар). Интенсивность процесса парообразования зависит от температуры кипения жидкости при нормальном атмосферном давлении: чем выше температура кипения жидкости, тем меньше её испаряемость. Однако, более полной характеристикой испаряемости следует считать давление (упругость) насыщенных паров, данное в функции температуры. Чем больше насыщенность паров при данной температуре, тем больше испаряемость жидкости.
Температурное расширение. Это свойство жидкостей изменять свой объем характеризуется коэффициентом температурного расширения (t) представляющим собой относительное изменение объема жидкости W при изменении температуры t на 1°С и постоянном давлении:
t=  , оС-1.
(2.8)
, оС-1.
(2.8)
Растворимость газов в жидкостях характеризуется объемом растворенного газа в единице объема жидкости и определяется по закону Генри:
Wг= Wг a Р/ Ратм, где Wг – объем растворенного газа; Wж – объем жидкости; a – коэффициент растворимости; Р — давление; Ратм — атмосферное давление.
Кавитация – это местное нарушение сплошности течения жидкости с образованием паровых и газовых пузырей (каверн), обусловленное местным падением давления в потоке. В движущейся жидкости возможны локальные изменения давления, например при обтекании твердых тел пли вибрации.
Вязкость жидкости. Формула Ньютона. Динамическая и кинематическая вязкость. Единицы и приборы для измерения жидкости.
Вязкость, внутреннее трение, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Вязкость – важная физико-химическая характеристика веществ, которую приходится учитывать при перекачивании жидкостей и газов по трубам (нефтепроводы, газопроводы).
Основной закон вязкого течения был установлен И. Ньютоном:
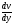 , где τ – касательные напряжения жидкости τ = T/w, T – тангенциальная (касательная) сила,
вызывающая сдвиг слоёв жидкости (газа)
относительно друг друга, w – площадь слоя, по которому происходит
сдвиг;
, где τ – касательные напряжения жидкости τ = T/w, T – тангенциальная (касательная) сила,
вызывающая сдвиг слоёв жидкости (газа)
относительно друг друга, w – площадь слоя, по которому происходит
сдвиг; 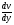 =
=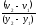 –
градиент скорости течения (быстрота её
изменения от слоя к слою), иначе –
скорость сдвига. Коэффициент
пропорциональности называется коэффициентом
динамической вязкости ().
Он количественно характеризует
сопротивление жидкости (газа) смещению
её слоёв. Знак «плюс» или «минус» в
формулах принимается в зависимости от
знака градиента скорости.
–
градиент скорости течения (быстрота её
изменения от слоя к слою), иначе –
скорость сдвига. Коэффициент
пропорциональности называется коэффициентом
динамической вязкости ().
Он количественно характеризует
сопротивление жидкости (газа) смещению
её слоёв. Знак «плюс» или «минус» в
формулах принимается в зависимости от
знака градиента скорости.
Величина обратная коэффициенту динамической вязкости , называется текучестью
j= . Наряду
с динамической вязкостью ( часто рассматривают кинематическую
вязкость ():
. Наряду
с динамической вязкостью ( часто рассматривают кинематическую
вязкость ():
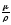 (2.12)
(2.12)
где – плотность жидкости или газа.
Единицами кинематической вязкости служат м2/с и см2/с, ранее использовались стоксы, 1 Стокс=1∙10-4 м2/с. Вязкость жидкостей измеряют с помощью приборов-вискозиметров (от позднелатинского viscosus – вязкий). Наиболее распространены вискозиметры капиллярные, ротационные, с падающим шариком, ультразвуковые.
studfile.net
11. Сжимаемость жидкости
Сжимаемость – это свойство жидкости изменять плотность (объём) при изменении давления и температуры. Для количественной оценки сжимаемости используются изотермический коэффициент сжимаемости βpи коэффициент температурного расширенияβΤ.Причем, первый отражает относительное изменение плотности жидкости при изменении только давления (приT= Const), а второй – то же явление, но при изменении только температуры жидкости (приp= Const).
Для решения вопроса о необходимости учета сжимаемости при исследовании того или иного течения жидкости, т.е. для выбора модели – сжимаемой или несжимаемой жидкости, необходимо знать изменения давления и температуры в рассматриваемой области течения и оценить вызванное ими относительное изменение плотности. Обычно для многих задач прикладной газовой динамики, если они не связаны с исследованием пограничного слоя, учет температурного расширения жидкости не является актуальным; наибольший интерес представляет сжимаемость жидкости, обусловленная изменением давления.
Относительное изменение плотности ∆ρ/ρ при заданном изменении давления∆pпропорционально изотермическому коэффициенту сжимаемостиβpи обратно пропорционально модулю упругости, посколькуβp и по определению являются величинами обратными друг другу:
∆ρ/ρ = βp ∆p = ∆p / –закон Гука для жидкости.
Сжимаемость свойственна всем жидкостям (и капельным и газам), однако её количественное проявление будет различным в зависимости от физических свойств среды. Капельные жидкости малосжимаемы или практически несжимаемы, поскольку их модули упругости достаточно велики (например, для воды = 2∙ 109 Па).
По сравнению с капельными жидкостями сжимаемость газов очень велика:при атмосферном давлении и изотермическом процессесжимаемость воздуха в 20 тысяч раз больше сжимаемости воды.
При изотермическом процессетечения газа:
T= Const ; p/ρ=RT=Const; dp/dρ=p/ρ
= dp / dρ/ρ= p/ρ/ρ= p,
т.е. сжимаемость газов тем больше, чем меньше давление. При атмосферном давлении модуль упругости воздуха = p=B= 105 Па, что в2·104 раза меньше величины модуля упругости воды(см. выше).
При изоэнтропийном процессетечения газа:
p/ρk= Const; dp/dρ=kp/ρ
= dp / dρ/ρ= kp,
т.е. сжимаемость газов определяется не только давлением, но ипоказателем изоэнтропы k, уменьшаясь с его увеличением.
Течение жидкости допустимо рассматривать как несжимаемое до тех пор, пока относительное изменение плотности ∆ρ/ρ остается весьма малым, т.е.∆ρ/ρ<<1.
При энергоизолированномдвижении жидкостиизменение давления∆p,связанное с процессом течения, имеет величину такого же порядка, как идинамическое давлениеρW2/2; поэтому∆ρ/ρ≈ ρW2/2. Таким образом, течение жидкости можно рассматривать как несжимаемое до тех пор,пока динамическое давление остается весьма малым по сравнению с модулем упругости.
Если ввести в рассмотрение скорость звукаa, которая согласноформуле Лапласаопределяется равенствомa2= /ρ, то условие ∆ρ/ρ<<1можно переписать в виде ∆ρ/ρ≈ ρW2/2 ≈ (W/a)2/2<<1. Отношение скорости теченияW к скорости звукаaназываютчислом Маха: М=W/a .Таким образом, течение можно рассматривать приближенно как несжимаемое еслиМ2/2 <<1, т.е. при условии, чточисло Маха мало по сравнению с единицей(обычно принято считать–приМ≤ 0.3 … 0.4), или другими словами, при условии, чтоскорость течения мала по сравнению со скоростью звука.
При М=0.3,например, относительное изменение плотности составит
∆ρ/ρ≈ М2/2=0.32/2≈0.05,
т.е. порядка 5%.
studfile.net
Сжимаемость жидкостей и элементов (Таблица)
Таблица сжимаемость элементов
Коэффициент сжимаемости определяется выражением
k = (1/V)·(δV/δP)
Где δV – изменение объема V при изменении давления на величину δP; температура предполагается постоянной.
Величина k в бар-1 (бар=108 дин/см2) даны в таблице для комнатной температуры. Чтобы выразить сжимаемость в атм-1, надо увеличить kна 1/80 его значения.
Результаты измерений k показывают его периодическую зависимость от атомного веса.
Элемент | Сжимаемость элементов k*108 | Элемент | Сжимаемость элементов k*108 |
Алюминий | 1,37 | Литий | 9,0 |
Бром | 51,8 | Магний | 2,85 |
Висмут | 3,0 | Марганец | 0,85 |
Железо | 0,59 | Медь | 0,73 |
Золото | 0,61 | Молибден | 0,46 |
Йод | 13,0 | Мышьяк | 4,5 |
Кадмий | 2,1 | Натрий | 15,8 |
Калий | 32,0 | Никель | 0,62 |
Кальций | 5,8 | Олово | 1,8 |
Кремний | 0,32 | Палладий | 0,55 |
Платина | 0,38 | Углерод | 0,23 |
Ртуть | 4,0 | Графит | 3,0 |
Рубидий | 40,0 | Фосфор (красный) | 9,2 |
Свинец | 2,2 | Фосфор (белый) | 20,5 |
Селен | 12,0 | Хлор (жидкий) | 95,0 |
Сера | 13,0 | Хром | 0,9 |
Серебро | 1,0 | Цензий | 62,0 |
Сурьма | 2,4 | Цинк | 1,7 |
Талий | 2,3 |
|
|
Таблица сжимаемость жидкостей
k – коэффициент сжимаемости в бар-1 (бар=108 дин/см2). Чтобы выразить сжимаемость в атм-1, надо увеличить k на 1/80 его значения.
С увеличением давления k уменьшается. При повышении температуры сжимаемость жидкостей в общем случае увеличивается, однако вода является исключением: ее сжимаемость обнаруживает минимум около 500 С. Сжимаемость растворов уменьшается с увеличением их концентрации.
Жидкость | Температура, °С | Сжимаемость жидкостей, k*108 |
Бензол, 8 атм | 17,9 | 90,8 |
Вода 1-25 атм | 15 | 48,9 |
900-1000 атм | 15 | 36,3 |
900-1000 | 198 | 35,4 |
2500-3000 атм | 14,2 | 25,8 |
Вода морская | — | 43,1 |
Глицерин | 20,5 | 24,8 |
Керосин | 16,5 | 68,7 |
Кислота уксусная 1-16 атм | 0 | 40,2 |
Масло прованское | 20,5 | 62,5 |
Парафиновое | 14,8 | 61,9 |
Метилацетат | 14,3 | 95,8 |
Пентан | 20 | 314 |
Ртуть 8-37 атм | 20 | 3,82 |
T | 15 | 3,71 |
Сероуглерод 8-37 атм | 15,6 | 85,9 |
Скипидар | 19,7 | 78,14 |
Спирт амиловый, 8 атм | 17,7 | 89,4 |
Спирт бутиловый 8 атм | 17,4 | 88,9 |
Спирт изо | 17,9 | 96,8 |
Спирт метиловый | 14,7 | 102,7 |
Пропиловный | 17,7 | 95,8 |
Спирт изо | 27,8 | 101,7 |
Спирт этиловый 1-500 | 0 | 6 |
Спирт этиловый 150-200 | 310 | 4147 |
Углерод четыреххлористый | 20 | 89,6 |
Хлороморм 100-200 | 20 | 89 |
Этил бромистый 8-37 | 99,3 | 291,3 |
Этил хлористый 8-37 | 15,2 | 151,1 |
Этилацетат 8-37 | 13,3 | 102,7 |
Эфир серный 1-50 | 0 | 145,2 |
Эфир серный 900-100 | 0 | 64,2 |
Эфир серный 900-1000 | 198 | 142,2 |
infotables.ru