Течение реальной жидкости: Течение — реальная жидкость — Большая Энциклопедия Нефти и Газа, статья, страница 1

Течение — реальная жидкость — Большая Энциклопедия Нефти и Газа, статья, страница 1

Течение — реальная жидкость

Cтраница 1

Течение реальных жидкостей происходит в условиях взаимодействия, борьбы сил внутреннего трения, стабилизирующих поток, и сил инерционных, поддерживающих появившееся возмущение.  [1]

Течение реальной жидкости отличается от течения идеальной жидкости наличием вязкости, проявляющейся в виде силы внутреннего трения. Как известно из гидравлики, сила трения, по гипотезе Ньютона, пропорциональна изменению величины скорости, приходящемуся на единицу длины в направлении нормали к поверхности тела.  [2]

Течение реальной жидкости в центробежных форсунках, применяемых на практике, значительно отличается от рассмотренного выше течения в идеальной форсунке.  [3]

Течения реальных жидкостей между твердыми стенками, как правило, являются вихревыми и в других случаях.

 [4]

Течение реальной жидкости характеризуется различными режимами ее движения, которые при определенных условиях могут переходить один в другой. В 1880 г. Д. И. Менделеев впервые высказал суждение о существовании двух режимов движения жидкости, которые в 1883 г. блестяще экспериментально подтвердил и изучил О.  [5]

Рассмотрим течение реальной жидкости в камере закручивания постоянной высоты.  [7]

Рассмотрим течение реальной жидкости в короткой камере закручивания постоянной высоты. Как показывают расчеты и результаты опытов, изменение длины камеры закручивания в пределах dax LK 3dBX практически не влияет на гидравлические характеристики форсунки.  [9]

Скорость течения реальной жидкости может быть определена с помощью уравнения ( 4 — 4г) и диаграммы свойств. Расход жидкости на единицу ллощади находится делением скорости на удельный объем. В Гз-диаграмме ( рис. 18 — 2) показаны — четыре типа обратимого адиабатического процесса расширения: процесс ab происходит полностью в жидкой фазе, cd начинается в жидкой фазе, заканчиваясь в двухфазной области, ef — полностью в паровой фазе и gh начинается в паровой фазе и заканчивается в двухфазной области.  [10]

При течении реальной жидкости в рабочих каналах насоса часть энергии расходуется на преодоление гидравлических сопротивлений.  [12]

При течении реальных жидкостей возникают так называемые силы внутреннего трения.  [13]

При течении реальных жидкостей в них возникают силы внутреннего трения.  [14]

При течении реальной жидкости по каналам реального рабочего колеса с конечным числом лопаток характер потока существенно отличается от струйного — появляются вихри, ускорения, замедления.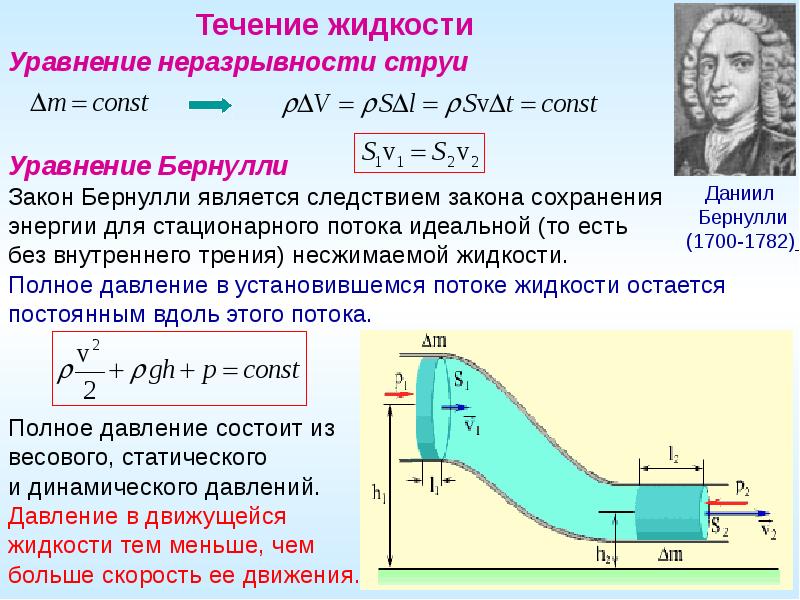 Действительное распределение относительных скоростей в канале рабочего колеса конечных размеров не осесимметрично из-за силового взаимодействия между лопатками и потоком. Таким образом, циркуляция снижает теоретический напор, создаваемы.  [15]

Страницы:      1    2    3    4

6.3. Течение вязкой жидкости

%PDF-1.5 % 2 0 obj > /Metadata 4 0 R /Pages 5 0 R /StructTreeRoot 6 0 R /Type /Catalog >> endobj 4 0 obj > stream

Ivanov V.K.

application/pdf

6.3. Течение вязкой жидкости

2020-03-29T21:28:37+03:00Microsoft® Office Word 20072020-03-30T16:41+03:00Microsoft® Office Word 2007uuid:5eae5449-f2eb-46b4-8bd6-258a6ad8e850uuid:d6b1bf2f-00d5-4fa3-8da0-608efe0f49bb endstream endobj 13 0 obj > stream x]]o^p. \I,fw}q%o?_z=jzW/tYbe30Y83I9{7jP֯ĩO_>Lӫ?

Течение вязкой жидкости в трубе

Течение вязкой жидкости в трубе  [c.376]

ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ В ТРУБЕ  [c.377]

Распределение скоростей течения вязкой жидкости в трубе можно наблюдать по движению границы раздела двух различно окрашенных жидкостей В вертикальной трубке налит окрашенный сахарный сироп (рис 306, о), а сверху нужно аккуратно налить тот же сироп, но без краски.  [c.379]

ТЕЧЕНИИ ВЯЗКОЙ ЖИДКОСТИ В ТРУБЕ 381  [c.381]

Наконец, та же теория может быть применена к решению задачи о медленном течении вязкой жидкости в трубе, радиус сечения которой периодически изменяется [171.  [c.643]

Уравнение Навье — Стокса, описывающее установившееся течение вязкой жидкости в трубе произвольного поперечного сечения, имеет вид  [c. 132]

Интересной особенностью турбулентного режима течения вязкой жидкости в трубе является зависимость величины (йср/мтах) от числа Рейнольдса.  [c.77]

Ламинарное течение жидкости в трубе. При течении вязкой жидкости по трубе постоянного сечения соответствующий данным условиям течения профиль скорости устанавливается не сразу, а на некотором расстоянии от входного сечения трубы. Это объясняется тем, что на входе в трубу скорость жидкости обычно одна и та же во всех точках входного сечения, т. е. более или менее постоянна по сечению. По мере удаления от входного сечения слои жидкости, расположенные ближе к стенкам трубы, будут тормозиться сильнее по сравнению с более удаленными слоями, в результате чего профиль скорости будет изменяться, переходя из плоского в выпуклый, пока не достигнет степени выпуклости, вполне отвечающей условиям рассматриваемого течения. В дальнейшем профиль скорости остается неизменным, так что скорость жидкости в любом сечении изменяется от нуля у стенки трубы до одного и того же наибольшего значения на оси трубы одинаковым образом.  [c.387]

Реальные потоки конечных размеров, строго говоря, не могут быть одномерными, так как в вязких жидкостях ввиду влияния граничных поверхностей всегда наблюдается неравномерное распределение скоростей в живых сечениях. Но некоторые реальные потоки могут быть сведены к одномерной модели. Так, напр,и.мер, при течении вязкой жидкости в круглой цилиндрической трубе или канале между параллельными плоскостями имеет место неравномерное распределение скоростей, но оно иногда бывает несущественным с прикладной точки зрения, так как во многих технических задачах достаточно знать среднюю по сечению скорость и закон изменения давления вдоль трубы (канала). Среднюю скорость V можно определить, усредняя по сечению местные скорости и в соответствии с соотношением  [c.145]

Рассмотрим теперь аналогичную задачу об установившемся движении несжимаемой вязкой жидкости в трубе с произвольным фиксированным поперечным сечением. В этом случае определяющими параметрами течения несжимаемой вязкой жидкости в целом в неподвижной цилиндрической трубе, очевидно, будут  [c.240]

Рассмотрим стационарное ламинарное течение вязкой жидкости в круглой трубе (рис. 6-1). На входе в трубу скорость по сечению однородна. Вследствие того, что скорость жидкости на стенке трубы равна нулю, на поверхности образуется и нарастает пограничный слой приторможенной жидкости.  [c.76]

Слой окружающей тело жидкости, в котором нарастает скорость и в котором влияние вязкости существенно, называется пограничным слоем. В некоторых случаях этот слой очень тонок и влиянием его можно пренебречь течение вязкой жидкости или газа близко к тому течению, которое имело бы место при обтекании этого тела идеальной жидкостью, лишенной вязкости. В других случаях пограничный слой не будет тонким, и тогда уже нельзя пренебрегать вязкостью Так, например, при течении вязкой жидкости в узкой трубе такой слой может заполнить весь объем текущей жидкостью, и при анализе этого течения необходимо учитывать силы вязкости.  [c.376]

Рассмотрим подробнее стационарное течение вязкой жидкости в прямой горизонтальной трубе постоянного сечения. Давление в каждом поперечном сечении можно считать одинаковым. Если этого не было бы, то линии тока изгибались бы или возникали бы течения поперек трубы. Все частицы жидкости, прилегающие к стенке круглой трубы, прилипли к ней и имеют скорость, равную нулю, кольцевой слой, прилегающий к иим, из условия симметрии должен иметь по всей окружности одинаковую скорость. Если представим себе жидкость разделенной на достаточно тонкие концентрические кольцевые слои, то скорость в каждом таком слое одинакова поэтому величину скорости течения можно полагать только функцией расстояния г данной частицы от оси трубы.  [c.377]

Чтобы определить характер течения вязкой жидкости в плоской трубе для весьма далёких расстояний от входа, достаточно найти выражение изображения основной скорости при малых значениях параметра преобразования. Раскладывая каждое слагаемое в числителе и знаменателе (1.19) и ограничиваясь слагаемыми не выше второй степени от аргумента, найдём  [c.354]

На основании результатов своих опытов с окрашенными струйками Рейнольдс показал, что ламинарный режим течения вязкой жидкости в цилиндрической трубе осуществляется только до тех пор, пока безразмерный параметр течения, названный позднее числом Рейнольдса, не будет превышать своего критического значения. Если же этот параметр превысит своё критическое значение, то течение вязкой жидкости из ламинарного режима внезапно, скачком переходит в турбулентный режим при этом скачком меняется и зависимость коэффициента сопротивления от значений числа Рейнольдса.  [c.434]

Для турбулентного режима течения вязкой жидкости в цилиндрической трубе соответственными необходимыми признаками будут 1) извилистый и неупорядоченный характер траекторий отдельных частиц, 2) почти равномерное распределение осредненных скоростей по поперечному сечению, но с резким уменьшением их до нуля в тонком слое вблизи стенки, 3) превышение максимальной скорости над средней имеет порядок 10—20% и 4) график зависимости коэффициента сопротивления от числа Рейнольдса представляется кривой с медленно убывающим наклоном.

Как показано на рис. 31, при переходе через критическое значение числа Рейнольдса коэффициент сопротивления трубы увеличивается скачком, а затем медленно уменьшается с увеличением числа Рейнольдса.  [c.435]

Уравнение (138) есть уравнение параболы. Следовательно, при стационарном течении вязкой жидкости в прямой круглой трубе скорости в любом меридиональном сечении распределены по параболическому закону (138).  [c.327]

Итак, функция (13.15) решает задачу о ламинарном течении вязкой жидкости через трубу эллиптическою сечения. Полагая а — Ь, мы вновь восстановим решение задачи о течении Пуазейля. Простое вычисление даёт для объёма протекающей в единицу времени через трубу жидкости выражение  

[c.437]

Дальнейшее уточнение постановки и решения пространственной задачи идет в направлении уточнения моделей течения с учетом эффектов реального газа, в первую очередь вязкости. Дело в том, что теория вторичных течений в невязкой жидкости качественно правильно описывает явление, однако не объясняет возникновение градиента полного давления в основном потоке и затухание вторичных течений, для чего необходима учитывать влияние вязкости, не малое вблизи ограничивающих поверхностей и в областях с большими градиентами полных давлений. Интересно отметить, что Н. Е. Жуковский в уже упомянутой работе (1914) дал теорию вторичных течений в вязкой жидкости в тонком слое, справедливую с точностью до малых второго порядка. В 1935 г. П. А. Вальтер подробно исследовал развитое вторичное течение вязкой жидкости в изогнутой трубе круглого сечения. Турбулентные течения долгое время  

[c.151]

ЛАМИНАРНОЕ ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ В КРУГЛОЙ ЦИЛИНДРИЧЕСКОЙ ТРУБЕ  [c.220]

Полученные в этой главе общие дифференциальные уравнения движения вязкой несжимаемой жидкости (9.11) интегрируются только в некоторых частных случаях, к числу которых, в частности, принадлежит так называемое ламинарное течение вязкой жидкости в круглой цилиндрической трубе.  [c.220]

Колбрука — Уайта и ВНИИГаза, которые отражают закономерность изменения коэффициента гидравлического сопротивления от числа Re и относительной шероховатости при напорном режиме течения вязкой жидкости в трубах.  [c. 184]

Очень напряженная программа. 19 февраля встречался с сотрудниками Mathemati s Department. Сотрудник этого отделения D. Ri hardson -молодой человек, занимается течением вязких жидкостей в трубах, штампах. В настоящее время — применительно к технологии получения изделий из пластмасс. Последние — вязкая жидкость с особыми реологическими свойствами, зависящими от температуры и скорости деформации. Кажется мне, что у него что-то неладно с проблемой граничных условий (движущиеся границы) в эйлеровой постановке.  

[c.146]

Dr. К. Parker занимается течением вязкой жидкости в трубах с сужениями. Моделирует нестационарное течение крови в сосудах. Эти вопросы нам близки по математической постановке. Вечером prof. Kennaway катал на своей машине. Заходили в какие-то дома, в частности в Королевское общество, школу директоров кампаний. Были в парламенте, послушали выступления (есть балкон для посетителей и журналистов).  [c.147]

Теплообмен и гидравлическое сопротивление при ламинарном течении вязкой жидкости в трубах с искусственной щероховатостью/ Ю.

Г. Назмеев,  [c.610]

Трубопроводы служат каналами, по которым энергия от насосов поступает к гидродвигателям. В зависимости от условий работы применяют жесткие и гибкие трубопроводы. Чаще всего в качестве трубопроводов гидроприводов применяют круглые стальные бесшовные трубы и иногда трубы из алюминиевых сплавов и чугуна. Гидравлический расчет трубопроводов производится по формулам гидравлики применительно к течению вязкой жидкости, Соединения труб и присоединение их к элементам и узлам гидроприводов должны быть прочными и гер-. метичными. При соединении стальных труб применяют сварку, фланцевые соединения. Соединение труб небольшого диаметра производится накидными гайками с развальцовкой соединяемых концов труб для высоких и сверхвысоких давлений используют ниппельное соединение.  [c.364]

Прыжок жидкости наблюдается и при поступательновращательном течении вязкой жидкости по трубе. Участок трубы, на котором достигается критическое значение скорости поступательного течения и в конце которого возникает прыжок , называется предельной длиной трубы на этом участке движение жидкости устойчиво. За этим участком поток становится неустойчивым и в нем возникают сильные пульсации, затем поток успокаивается.  [c.328]

Уравнение энергии (3.17) связывает скорость, плотность и давление и, как было сказано, пригодно для расчета течения вязкой жидкости в теплоизолированной трубе, где процесс не является изоэнтропийным. Если применить уравнение энергии для изоэнтропийного процесса, то можно заменить плотносто через давление по формуле (3.8) и тогда оно совпадает с уравнением Бернулли (3.18).  [c.36]

Подобное обсуждение применительно к жидкости было проведено Вильсоном [31], который решил ряд интересных задач, связанных с установившимися распределениями температур. Следует также указать на некоторые другие работы [32, 33, 34]. Известен целый ряд точных решений для случая ламинарного течения вязких жидкостей, в частности для течения в трубе при пуазейлевском распределении скоростей [35, 36].  [c.21]

Рассмотрим установивщееся течение вязкой жидкости в круглой трубе радиуса R (рис. 54). Труба неподвижна, ось. i совпадает с осью трубы. Для определения поля скоростей надо решить уравнение 0-13) при условии, что в любом поперечном сечении на контуре трубы у — — = скорость равна нулю. Естественно ввести цилиндрические координаты. Переходя от координат у, Z к координатам г, 0, получим у = г os 0, z = = г sin 0,  [c.255]

Турбулентность, а) В 1 мы вывели закон Гагена-Пуа-зейля, согласно которому при течении вязкой жидкости в круглой трубе падение давления пропорционально расходу жидкости [формула (4)]. Там же мы упомянули, что закон Гагена-Пуазейля имеет место для движения в очень узких трубках при любых практически возможных скоростях, а для движения в широких трубах — только при малых  [c.156]

Трежде чем приступить к решению этой задачи, сделаем несколько предварительных замечаний о возможных режимах течения вязкой жидкости (в том числе в круглой цилиндрической трубе).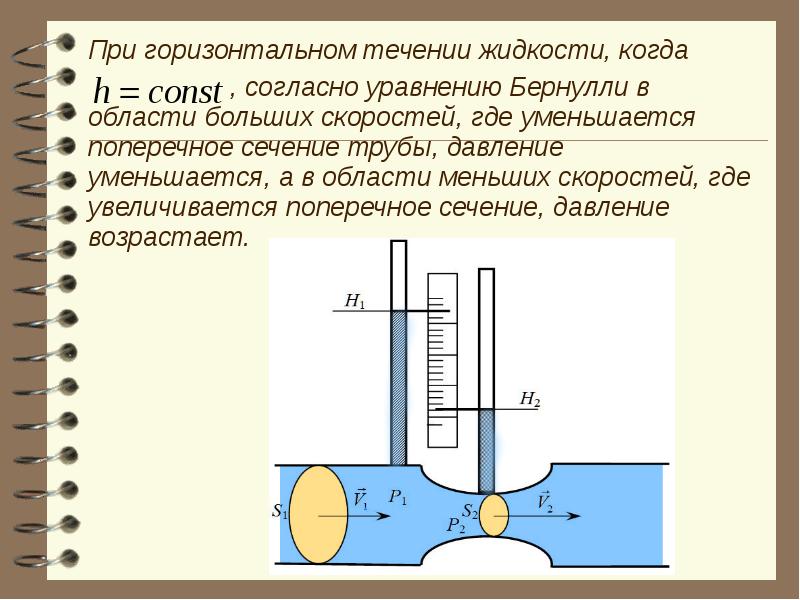 Наблюдения показали, что могут существовать два различных типа течения вязкой жидкости  [c.220]

---

53. Течение вязкой жидкости. Формула Пуазейля.

При течении реальной жидкости отдельные слои ее воздейст­вуют друг на друга с силами, касательными к слоям. Это явление называют внутренним трением или вязкостью.

Для многих жидкостей вязкость не зависит от градиента ско­рости, такие жидкости подчиняются уравнению Ньютона (7.1), и их называют ньютоновскими. Жидкости, не подчиняющиеся уравнению (7.1), относят к неньютоновским. Иногда вязкость ньютоновских жидкостей называют нормальной, а неньютонов­ских — аномальной.

. Кровь является неньютоновской жидкостью

Течение вязкой жидкости по трубам представляет для медици­ны особый интерес, так как кровеносная система состоит в основ­ном из цилиндрических сосудов разного диаметра.

Вследствие симметрии ясно, что в трубе частицы текущей жидкости, равноудаленные от оси, имеют одинаковую скорость. Наибольшей скоростью обладают частицы, движущиеся вдоль оси трубы; примыкающий к трубе слой жидкости неподвижен.

Для определения зависимости ско­рости слоев от их расстояния r от оси выделим мысленно цилиндрический объем жидкости некоторого радиуса r и длины l (рис. 7.3, а). На торцах этого цилиндра поддерживаются давления p_l и р₂ соответственно, что обусловливает результирующую силу

На боковую поверхность цилиндра со стороны окружающего слоя жидкости действует сила внутреннего трения, равная [см. (7.1)]

где S = 2rl—площадь боковой поверхности цилиндра. Так как жидкость движется равномерно, то силы, действующие на выде­ленный цилиндр, уравновешены: F = F_тр . Подставляя в это равен­ство (7.2) и (7.3), получаем

) имеем

Проинтегрируем это уравнение:

(7.5)

здесь нижние пределы соответствуют слою, «прилипшему» к внут­ренней поверхности трубы (= 0 при r = R), а верхние пределы — переменные. После интегрирования (7.5) получаем параболиче­скую зависимость скорости слоев жидкости от расстояния их до оси трубы

Наибольшую скорость имеет слой, текущий вдоль оси трубы (r = 0):

Установим, от каких факторов зависит объем Q жидкости, про­текающей через горизонтальную трубу за 1 с. Для этого выделим цилиндрический слой радиусом r и толщиной dr. Площадь сече­ния этого слоя (рис. 7.3, б) dS = 2rdr. Так как слой тонкий, то можно считать, что он перемещается с одинаковой скоростью 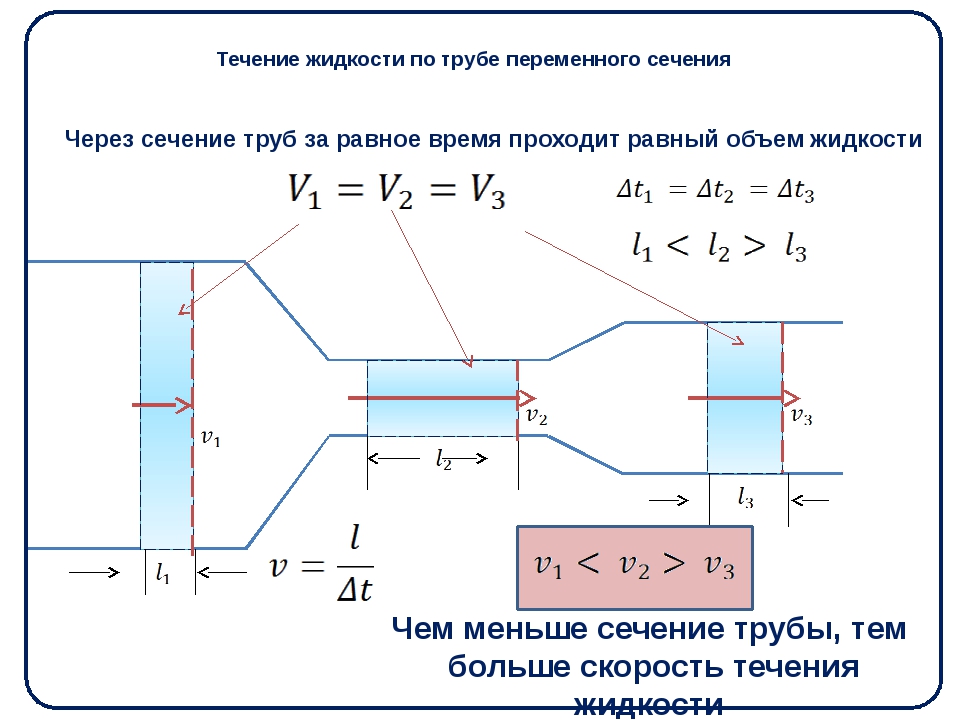. За 1 с слой переносит объем жидкости

dQ = dS =  • 2rdr/. (7.7)

Подставляя (7.6) в (7.7), получаем

откуда интегрированием по всему сечению находим

Зависимость объема жидкости Q, протекающей через горизон­тальную трубу радиуса R за 1 с, определяется формулой Пуазейля (7.8), где  — вязкость жидкости, а р₁ — р₂ — разность давле­ний, поддерживаемая на торцах трубы длиной l.

Как видно из (7.8), при заданных внешних условиях (р₁ и р₂) через трубу протекает тем больший объем жидкости, чем меньше ее вязкость и больше радиус трубы.

Проведем аналогию между формулой Пуазейля (7.8) и законом Ома для участка цепи без источника тока. Разность потенциалов соответствует разности давлений на концах трубы, сила тока — объему жидкости, протекающей через сечение трубы в 1 с, элект­рическое сопротивление — гидравлическому сопротивлению:

Гидравлическое сопротивление тем больше, чем больше вязкость , длина l трубы и меньше площадь поперечного сечения.

Течение вязкой жидкости в трубе

Во многих случаях допустимо пренебречь силами вязкости и приближенно анализировать явление так, как если бы силы вяз­кости отсутствовали. Это желательно делать не только потому, что еще не известны общие методы анализа течения при учете сил вязкости, но главным образом потому, что в ряде практически важных примеров результаты опытов с обычной жидкостью в пределах известной точности согласуются с результатами теоре­тического анализа течения «идеальной» жидкости. Важно только знать, когда пренебрежение вязкостью не ведет кпринципиальным и большим ошибкам.

Как известно, силы вязкости пропорциональны изменению скорости потока в направлении, перпендикулярном к скорости, и, следовательно, они будут сказываться особенно резко там, где эти изменения скорости велики. При обтекании вязкой жид­костью твердых тел частицы жидкости, непосредственно приле­гающие к телу, как бы «прилипают» к нему и имеют нулевую ско­рость относительно тела. Поэтому в непосредственной близости от поверхности твердого тела скорость потока нарастает от нулевого значения до некоторой величины. Дальше от тела изменения ско­рости потока сравнительно малы, и там совершенно ничтожно влияние вязкости.

Слой окружающей тело жидкости, в котором нарастает скорость и в котором влияние вязкости существенно, называется погранич­ным слоем. В некоторых случаях этот слой очень тонок и влиянием его можно пренебречь: течение вязкой жидкости или газа близко к тому течению, которое имело бы место при обтекании этого тела идеальной жидкостью, лишенной вязкости. В других случаях погра­ничный слой не будет тонким, и тогда уже нельзя пренебрегать вяз­костью. Так, например, при течении’ вязкой жидкости в узкой трубе такой слой может заполнить весь объем текущей жидкостью, и при анализе этого течения необходимо учитывать силы вязкости.

Произведем опыты с измерением распределения давления мано­метрическими трубками в жидкости, текущей по горизонтальной трубе постоянного сечения (рис. 303). Если жидкость достаточно вязкая, например глицерин или какой-нибудь сироп, или труба достаточно тонкая, то давление будет падать равномерно вдоль трубы. Это можно видеть по тому, что уровни во всех равноотстоя­щих друг от друга манометрических трубках лежат на наклон­ной прямой (см. рис. 303). Если .бы жидкость была невязкой, то уровни во всех трубках были бы одинаковы, давление вдоль трубки было бы постоянным.

Действительно, жидкость можно считать вполне несжимаемой, поэтому скорость течения в каждом сечении трубки одинакова, — ведь трубка имеет постоянное сечение, а по уравнению Бернулли и давление должно было быть одинаковым. В данном случае в вязкой жидкости на частицу, кроме сил давления, действуют еще и силы вязкости, поэтому при стационарном течении с постоянной скоростью давление падает вдоль трубки тока.

Течение происходит вдоль трубы прямолинейно, скорости всех частиц направлены вдоль оси трубы, следовательно, силы вяз-

Рис. 303.

кости будут действовать только в направлении оси трубы. Падение давления вдоль трубки тока уравновешивается силами вязкости, и поэтому скорость течения жидкости остается постоянной вдоль трубки.

Рассмотрим подробнее стационарное течение вязкой жидкости в прямой горизонтальной трубе постоянного сечения. Давление в каждом поперечном сечении можно считать одинаковым. Если этого не было бы, то линии тока изгибались бы или возникали бы течения поперек трубы. Все частицы жидкости, прилегающие к стенке круглой трубы, прилипли к ней и имеют скорость, равную нулю, кольцевой слой, прилегающий к ним, из условия симметрии должен иметь по всей окружности одинаковую скорость. Если представим себе жидкость разделенной на достаточно тонкие концентрические кольцевые слои, то скорость в каждом таком слое одинакова; поэтому величину скорости течения можно полагать только функцией расстояния r данной частицы от оси трубы.

Выделим из объема текущей жидкости цилиндр радиуса r, длиной dl (рис. 304) и напишем условия движения цилиндра.

 

Жидкость движется равномерно, следовательно, сумма всех сил, приложенных к выделенному цилиндру, равна нулю. Разность сил давлений на концах цилиндра

должна быть уравновешена силами вязкости, приложенными на поверхности цилиндра. Сумма сил вязкости равна площади боковой поверхности цилиндра 2prdl, умноженной на напряжение сил

вязкости t. Равенство нулю всех внешних сил, действую­щих на цилиндр, теперь можно записать так:

или

(111.1)

По закону Ньютона (см. (39.1)) напряжение сил вязкости

пропорционально производной от скорости в перпендикулярном

направлении, в направлении радиуса,

(111.2)

где m — коэффициент вязкости жидкости и знак минус стоит потому, что скорость убывает с увеличением радиуса. Подставляя (111.2) в равенство (111.1), получаем

(111.3)

Величина градиента давления вдоль оси трубы dp/dl не зависит от радиуса, так как давление р в любом поперечном сечении одина­ково. Поэтому из уравнения (111.3) можно найти зависимость ско­рости течения от радиуса, проинтегрировав это уравнение по радиусу, учитывая при этом, что у стенки скорость v(R)=0,

(111.4)

где R — радиус трубы. После вычислений получаем

или

(111.5)

 

Рис. 304.

Давление равномерно падает в направлении скорости, и поэтому величина — dp/dl положительна и постоянна. Скорость будет макси­мальна на оси трубы, и распределение вели­чины скорости по диаметру трубы происхо­дит по параболическому закону (рис. 305). Максимальная скорость равна

Распределение скоростей течения вязкой жид­кости в трубе можно наблюдать по движению границы раздела двух различно окрашенных жидкостей.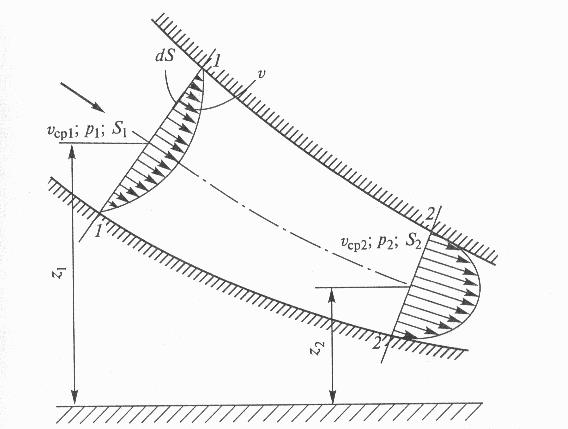 В вертикальной трубке налит окрашен­ный сахарный сироп (рис. 306, а), а сверху нужно аккуратно налить тот же сироп, но без краски. В состоянии покоя граница раздела горизонтальна. После открытия крана внизу трубки начинается медленное движение вязкой жидкости, и граница раздела начинает изменять с течением времени свою форму, все вытягиваясь по оси (см. рис. 306, а).

Зная распределение скорости, можно подсчитать объемный расход жид­кости Q через поперечное сечение трубы. Через кольцо радиуса r и площадью

Рис. 305.

Рис. 306.

2prdr за секунду пройдет объем жидкости dQ=v2prdr (рис. 306, б), а через все сечение

(111.6)

Здесь мы приняли во внимание формулу (111.5).

 

 

Пользуясь этим законом, можно построить простой прибор для измерения коэффициента вязкости mжидкости, схема которого дана на рис. 303. Величину dp/dl можно вычислить на основании результатов измерения давления в раз­личных точках трубы. Так как давление падает пропорционально длине, то

(111.7)

где р_н — давление в начале, а р_к — в конце отрезка трубы длиной l.

Величину расхода Q можно измерить непосредственно, измерив количество жидкости, прошедшей за определенное время через трубу. Зная радиус трубы R, можно на основании этих данных определить коэффициент вязкости mжидкости.

Течение жидкости в цилиндрической трубе, при котором ско­рости частиц всюду направлены вдоль оси, называется ламинар­ным или слоистым. Такое течение наблюдается при небольшом

значении скорости потока вязкой жидкости. С увеличением ско­рости потока, с увеличением перепада давления на концах трубы, течение принципиально изменяет свой характер: вместо спокойного слоистого течения наблюдается турбулентное, или завихренное, течение.

Рис. 307.

Рис. 308.

Возникновение завихренного течения легко наблюдать, если в стеклянную трубочку, по которой протекает вода из сосуда, пустить подкрашенную струйку (рис. 307, а).При небольшой скорости потока течение будет слоистым и подкрашенная струйка в виде почти прямой линии будет идти параллельно оси трубки (рис. 307, б). Затем, при постепенном увеличении скорости потока, внезапно начинается завихренное движение и струйка размывается в широкую ленту с неровными краями, как показано на рис. 307, в.

При стационарном турбулентном движении скорость в данном месте не остается постоянной по величине и направлению, а совер­шает быстрые беспорядочные колебания как по величине, так и по направлению. Но среднее значение скорости будет постоянной определенной величиной, направленной вдоль оси трубки. Поэтому в завихренном потоке чаще всего определяют среднее значение скорости.

Чем определяется возникновение турбулентности, мы скажем ниже, в § 113, а здесь отметим, что распределение средней скорости при турбулентном потоке по диаметру трубы совсем иное (рис. 308), отличное от того, что мы видели при ламинарном движении (см. рис. 305). При завихренном движении средняя скорость почти по всему сечению трубы остается почти постоянной и только вблизи стенок быстро спадает до нуля; пограничный слой вблизи стенок занимает сравнительно небольшую долю потока, а’ в центре поле скоростей почти однородно и более похоже на то, которое должно быть в трубе при отсутствии вязкости жидкости. При слоистом движении (см. рис. 305) нет четкого пограничного слоя, во всех частях трубы поле скоростей изменяется из-за сил вязкости так же, как вблизи стенок; можно даже сказать, что в этом случае погра­ничный слой занимает весь поток жидкости.

 

Узнать еще:

Архив документации

Настоящая книга основана на курсе лекций по физической океанографии, в течение многих лет читаемом одним из авторов книги студентам 3-го курса кафедры термогидромеханики океана Московского физико-технического института (государственного университета).

Задача курса состоит в сообщении студентам основных  сведений об океане, необходимых для более живого вос- приятия последующих теоретических курсов по динамике океана. В связи с этим особенно большое внимание уделяется географическим распределениям океанографических характеристик, следствием чего является обилие в книге иллюстраций, более 80% из которых представляют собой карты, океанские разрезы и вертикальные кривые свойств океана.

В этом отношении предлагаемую книгу с равной степенью обоснованности можно рассматривать и как учебный текст, богато иллюстрированный рисунками, и как атлас с поясняющим текстом. При этом везде, где только это возможно, авторы стараются дать простое, с минимальным употреблением математики, физическое объяснение наблюдаемым в океане географическим распределениям океанографических характеристик.

Следование книги годовому курсу лекций накладывает жесткие ограничения на ее объем и содержание, которое сводится исключительно к проблемам макроокеанографии с упором на крупномасштабную термохалинную структуру океана и океанскую циркуляцию. Ограниченность объема книги определяет и лаконичный стиль изложения материала.

Так как книга предлагаемого типа не должна иметь большого списка литературы, ссылки на оригинальные работы в большинстве случаев даются для указания источника иллюстративного материала или количественной оценки того или иного явления. Авторы оказывают некоторое предпочтение описанию реультатов отечественных исследований, что представляется особенно обоснованным для последней главы книги.

Авторы выражают глубокую благодарность выпускникам кафедры термогидромеханики океана МФТИ: кандидату физико-математических наук Н. А. Максименко (выпуск 1983 г.) за помощь в подборе данных спутниковых наблюдений и численного моделирования океана, кандидату физико-математических наук Е. М. Кошлякову (выпуск 1987 г.) за тщательное прочтение рукописи и ряд важных замечаний и заведующему кафедрой термогидромеханики океана профессору В. В. Жмуру (выпуск 1973 г.) за поддержку работы над книгой и ее издания. Авторы благодарят также доктора географических наук П. Н. Маккавеева за просмотр раздела 1.2 и сделанные замечания.

Физические свойства жидкости, термины, определения и параметры :: HighExpert.RU

Термины, определения и параметры

Жидкость — физическое тело, которое обладает свойством текучести, т. е. не имеющее способности самостоятельно сохранять свою форму.Текучесть жидкости обусловлена подвижностью молекул, составляющих жидкость.

Жидкостью называется агрегатное состояние вещества, промежуточное между твердым и газообразным. Жидкость характеризуется следующими свойствами: 1) сохраняет объем; 2) образует поверхность; 3) обладает прочностью на разрыв; 4) принимает форму сосуда; 5) обладает текучестью. Свойства жидкости с 1) по 3) подобны свойствам твёрдых тел, а свойство 4) — свойству жидкости.

Жидкости, законы движения и равновесия которых изучаются в гидравлике (механике жидкости и жидкости), делятся на два класса: сжимаемые жидкости или газы, почти несжимаемые — капельные жидкости.

В гидравлике рассматриваются как идеальные, так и реальные жидкости.

Идеальная жидкость — жидкость, между частицами которой отсутствуют силы внутреннего трения. Вследствие этого такая жидкость не сопротивляется касательным силам сдвига и силам растяжения. Идеальная жидкость совершенно не сжимается, она оказывает бесконечно большое сопротивление силам сжатия. Такой жидкости в природе не существует — это научная абстракция, необходимая для упрощения анализа общих законов механики применительно к жидким телам.

Реальная жидкость — жидкость, которая не обладает в совершенстве свойствами идеальной жидкости, она в некоторой степени сопротивляется касательным и растягивающим усилиям, а также отчасти сжимается. Для решения многих задач гидравлики этим отличием в свойствах идеальной и реальной жидкостей можно пренебречь. В связи с этим физические законы, выведенные для идеальной жидкости, могут быть применены к жидкостям реальным с соответствующими поправками.

Ниже кратко представлены общие сведения, касающиеся физических свойств жидкостей. Ссылки на страницы с конкретными физическими свойствами разных жидкостей находятся в здесь. Эти разделы будут постепенно пополняться новой информацией, которая, возможно, окажется полезной инженерам и конструкторам при выполнении расчётов.

Идеальная жидкость — WikiLectures

послать

Спасибо за ваши Коментарии.

Спасибо за просмотр этой статьи.

Ваш отзыв не был вставлен (допускается один отзыв на статью в день)!

Проверяемый товар

Требуется проверка этой статьи. Предлагаемый рецензент: Carmeljcaruana

СЛИШКОМ КОРОТКИЙ

Эту статью проверил педагог

Статья была проверена педагогом, но впоследствии изменена.

Жидкость: [править | править источник]

Жидкость — это газ или жидкость, которая, в отличие от твердого тела, течет, принимая форму емкости, в которую она помещена. Это происходит потому, что жидкость реагирует на напряжение сдвига или силу на единицу площади, направленную вдоль грани куба жидкости, течением, а не упругим смещением, как в твердом теле.

СВОЙСТВА ЖИДКОСТИ [править | править источник]

1.ПЛОТНОСТЬ:

Плотность жидкости определяется как отношение массы жидкости к ее объему.

2.УДЕЛЬНЫЙ ОБЪЕМ:

Удельный объем жидкости определяется как объем жидкости, занимаемый единицей массы или объемом на единицу массы жидкости.

3.ВЯЗКОСТЬ ЖИДКОСТИ:

Вязкость определяется как свойство жидкости, которая оказывает сопротивление движению одного слоя жидкости по соседнему слою жидкости.

ВИДЫ ЖИДКОСТЕЙ ПО ВЯЗКОСТИ: [править | править источник]

Жидкости можно разделить на следующие пять типов:

1. Идеальная жидкость
2. Настоящая жидкость
3. Ньютоновская жидкость
4. Неньютоновская жидкость
5. Идеальная пластиковая жидкость

Идеальная жидкость [править | править источник]

Идеальная жидкость — это жидкость, которая обладает несколькими свойствами, включая то, что она:

 • Несжимаемый - плотность постоянная. 
 • Безвихревой - поток плавный, без турбулентности.
 • Невязкая - (Невязкая) жидкость не имеет внутреннего трения (η = 0)
 

мммм

 Идеальной жидкости в природе не существует, но иногда она используется для решения проблем с потоком жидкости.

2. Реальная жидкость: жидкости с вязкостью (μ> 0) и их движение, известное как вязкий поток.

Все жидкости на практике являются настоящими жидкостями.

Гидродинамика:

мы используем идеальную жидкость в 2 уравнениях:

1.Уравнение неразрывности

2 Уравнение Бернулли

3. Ньютоновские жидкости:

Реальная жидкость, в которой напряжение сдвига прямо пропорционально скорости деформации сдвига (или градиенту скорости).

4.Неньютоновская жидкость:

Реальная жидкость, в которой напряжение сдвига не пропорционально скорости деформации сдвига.

5. Идеальная пластиковая жидкость:

Жидкость, в которой напряжение сдвига больше, чем значение текучести, а напряжение сдвига пропорционально скорости деформации сдвига (или градиенту скорости).

Источники [править | править источник]

^{[1] [2]}

Течение реальной жидкости

Abstract

Отличия в поведении реальной жидкости от поведения идеальной жидкости классической гидродинамики возникают в первую очередь из-за наличия в реальной жидкости свойства вязкости.Другие отличительные особенности реальных жидкостей, такие как их поверхностное натяжение и способность к испарению, приводят к заметным отличиям в поведении от поведения идеальной жидкости при определенных обстоятельствах, но влияние вязкости присутствует в большей или меньшей степени во всех случаях. потока жидкости, и именно эти эффекты являются объектами изучения в настоящей главе.

Ключевые слова

Граничный слой Турбулентный пограничный слой Вязкая сила Ламинарный пограничный слой Реальная жидкость

Эти ключевые слова были добавлены машиной, а не авторами.Это экспериментальный процесс, и ключевые слова могут обновляться по мере улучшения алгоритма обучения.

Это предварительный просмотр содержимого подписки,

войдите в

, чтобы проверить доступ.

Предварительный просмотр

Невозможно отобразить предварительный просмотр. Скачать превью PDF.

Список литературы

1. (1).

   Rouse

   ,

   H.

   , «Fundamental Principles of Flow», Chapter 1 of

   Engineering Hydraulics

   , Wiley, 1950.

   Google Scholar

2. (2).

   Schlichting

   ,

   H.

   ,

   Теория пограничного слоя

   , Pergamon, 1955.

   zbMATHGoogle Scholar

3. (3).

   Ричардсон

   ,

   Э. Г.

   ,

   Динамика реальных жидкостей;

   Arnold, 1950.

   zbMATHGoogle Scholar

4. (4).

   Prandtl

   ,

   L.

   ,

   Essentials of Fluid Dynamics

   , Blackie, 1952.

   zbMATHGoogle Scholar

5. (5).

   Гольдштейн

   ,

   С.

   (ред.),

   Современные разработки в динамике жидкостей

   , Оксфорд, 1938.

   zbMATHGoogle Scholar

Информация об авторских правах

© Springer Science + Business Media New York 1967

Авторы и аффилированные лица

1. org/Organization»> 1. Университет of NewcastleAustralia

Real Fluid — обзор

3.2.1 Свободный вихрь

Вихрь безвихревого потока также известен как свободный вихрь, линейный вихрь или потенциальный вихрь.Здесь в основном будет использоваться термин свободный вихрь . Фундаментальные соотношения, управляющие потоком, связанным со свободным вихрем, можно разработать, рассмотрев небольшой элемент жидкости, показанный на рисунке 3.5, где элемент жидкости в плоскости отсчета ограничен двумя линиями тока и двумя радиусами.

Рисунок 3.5. Элемент жидкости.

Радиус r здесь представляет радиус кривизны и используется для обеспечения общности результатов. Циркуляция вокруг элемента равна

(3.20) Γ = (uφ + δuφ) (r + δr) δφ − uφrδφ

Если пренебречь высокими порядками малых величин, уравнение 3.20 принимает вид

(3.21) Γ = (rδuφ + uφδr) δφ

Завихренность соотношение циркуляции и площади

(3,22) ω = площадь циркуляции = (rδuφ + uφδr) δφrδrδφ = uφr + δuφδr

В пределе, как δr → 0

(3,23) ω = uφr + ∂uφ2∂r

Соотношение для завихренности, приведенное в уравнении 3. 23, может быть получено непосредственно из уравнения 3.13, учитывая, что u _r и u _z оба равны нулю, и, следовательно, в цилиндрических полярных координатах

(3.24) ωz = (uφr + ∂uφ∂r)

Для безвихревого потока ω = 0, поэтому из уравнения 3.23,

(3.25) uφr + ∂uφ∂r = 0

Поскольку линии тока представляют собой концентрические круги в круговой вихрь, площадь поперечного сечения струйной трубки будет постоянной по ее длине. Непрерывность материи означает, что скорость будет постоянной вдоль каждой линии тока. Следовательно, скорость изменяется только как функция радиуса, и уравнение 3.25 можно переписать как обыкновенное дифференциальное уравнение.

(3,26) uφr + duφdr = 0

Это может быть указано как

(3,27) duφdr = −uφr

, которое может быть интегрировано, чтобы получить

(3,29) uφr = constant = C

Константа C известен как сила вихря при любом радиусе r , а угловой момент в свободном вихре постоянен.

Уравнение 3.29 утверждает, что при стремлении радиуса к нулю скорость стремится к бесконечности. На практике это, конечно, невозможно. В реальной жидкости эффекты трения становятся значительными, когда радиус стремится к нулю, а в реальной жидкости, ведущей себя как свободный вихрь, центральная область имеет тенденцию вращаться как твердое тело.Анализ, представленный для свободного вихря, обычно используется только для областей, удаленных от центрального ядра.

Циркуляция вокруг контура, соответствующая линии тока свободного вихря, определяется линейным интегралом тангенциальной составляющей скорости, взятой один раз вокруг замкнутого контура в жидкости. Циркуляция на радиусе r , таким образом, задается для вращения против часовой стрелки как

(3.30) Γ = 2πruφ

При вращении по часовой стрелке циркуляция задается как –2 πru _φ .

Поскольку u _φ r = постоянная, циркуляция также постоянна для всего вихря. Теоретически сюда входит центр вихря. Циркуляция вокруг бесконечно малого контура в центре имеет значение той же ненулевой константы и, следовательно, не равна нулю. Свободный вихрь, хотя и вращающийся повсюду, имеет ядро ​​вращения в центре. Центр — это «особая» точка, в которой скорость теоретически бесконечна. Поскольку это практически невозможно, уравнения не обязательно применимы здесь, и результаты, полученные с их помощью для этой области, следует рассматривать с соответствующей осторожностью.

Для вихря с центром в начале координат функция тока, ψ , определяется выражением

(3.31) ψ = ∫∂ψ∂rdr + ∫∂ψ∂φdφ = ∫uφdr + 0 = ∫Γ2πrdr = Γ2πln (rro)

, где r _o — радиус, при котором функция тока равна нулю.

Потенциал скорости, Φ , определяется формулой

(3,32) dΦ = urdr + ruφdφ

(3,33) Φ = ∫Γ2πdφ = Γ2πφ

Из уравнения 2.58 с F r = r , μ = 0 и u _r = 0,

(3. 34) −∂p∂r = −ρuφ2r

Из уравнения 2.60 с u _z = 0 и основной силой F _z = –ρg .

(3,36) −∂p∂z − ρg = 0

Давление, p изменяется как для r, , так и для z , поэтому p = f (r, z) ,

(3,37 ) dpdr = ∂p∂r + ∂p∂zdzdr

(3.38) dp = ∂p∂rdr + ∂p∂zdz

Следовательно, замена ∂p / ∂r и ∂p / ∂z

(3.39 ) dp = ρuφ2rdr − ρgdz

Преобразование и деление на ρg дает

(3.40) dpρg + dz = uφ2rgdr

Для горизонтального потока из уравнения Бернулли с z = 0 и для вихревого потока u = u _φ полный напор, H , равен

(3,41) H = pρg + uφ22g + z

Дифференциация по радиусу дает

(3,42) dHdr = 1ρgdpdr + uφgduφdr + dzdr

или

(3,43) dH = dpρg + uφgdupit 9 + dz для подстановки + Dz в уравнении 3.43 с использованием уравнения 3.40 дает

(3. 44) dH = uφg (duφdr + uφr) dr

В общем случае δψ = u _φ δn , поэтому

(3,45) δψ = uφδr

Завихренность для свободного вихря приведена в 3.24, и сравнение уравнений 3.44 и 3.45 дает соотношение

(3.46) dH = ωδψg

Как полный напор, так и функция тока постоянны вдоль любой линии тока, и в результате пространство между двумя соседними линиями тока соответствует фиксированным значениям. значений δH и δψ.Из уравнения 3.46 завихренность также должна иметь фиксированное значение между двумя линиями тока, а предел постоянен вдоль линии тока. Таким образом, частицы, находящиеся в стационарном движении, имеют постоянную завихренность при движении по линии тока. Если поток является безвихревым, как в свободном вихре, то ω = 0 и, следовательно, δH = 0. Это означает, что общий напор постоянен не только вдоль линии тока, но и во всей области потока.

Подставляем тангенциальную скорость в уравнение 3. 39 с использованием уравнения 3.29 и интегрирования дает

(3.47) p — poρ = −C22r2 + g (zo — z)

Для случая вихря, свободного от жидкости, профиль свободной поверхности жидкости можно получить, задав p = p _o = атмосферное давление на свободной поверхности. Это дает

(3.48) z = zo − C22gr2

Изучение уравнения 3.48 подразумевает, что высота свободной поверхности будет -∞ на оси, r = 0, наряду с бесконечной скоростью.Профиль свободной поверхности между вихрем, не содержащим жидкости, и атмосферой, обозначенный уравнением 3.48, показан на рисунке 3.6.

Рисунок 3.6. Свободная поверхность между вихрем без жидкости и атмосферой.

Анализ и результаты, представленные здесь для свободного вихря, основаны на предположении об идеальной жидкости без вязкости. Обычно течение в свободном вихре характеризуется уменьшением давления и увеличением тангенциальной скорости с уменьшением радиуса.Однако движение многих реальных жидкостей действительно приближается к движению свободного вихря. Примеры включают обтекание изгиба трубы, вихрь, образующийся на выходе из ванны или раковины, водовороты, вихри, излучаемые кончиками крыльев самолета, и торнадо.

В идеальной жидкости свободный вихрь постоянен и неразрушим. После начала движения скорость в ядре бесконечна, и вихрь может быть остановлен только приложением тангенциальной силы, что в идеальной жидкости с нулевой вязкостью невозможно.Однако в реальной жидкости вихри образуются из-за вязкости, и они рассеиваются также в результате вязкости. В идеальной жидкости у вихря не может быть свободного конца, потому что это повлечет за собой скачок давления. Вместо этого он должен заканчиваться твердой границей или свободной поверхностью или образовывать замкнутый контур.

Показатель того, как поведение вихрей в реальной жидкости приближается к поведению идеальной жидкости, дается на примерах вихрей на конце хвостового крыла и вихрей, создаваемых лопастями в воде.Оба они требуют значительного времени для распада по сравнению с масштабом времени их движения. Стандартной эксплуатационной практикой на воздушном транспорте является обеспечение установленных расстояний между воздушными судами, чтобы предотвратить попадание воздушного судна в вихревые структуры потока, возникающие в следе за предшествующим воздушным судном.

Пример 3.1

Для свободного вихря в воздухе вычислите компоненты давления и тангенциальной скорости на радиусе 0,05 м и радиусе 0.03 м, если тангенциальная составляющая скорости и статическое давление на радиусе 0,06 м составляют 15 м / с и 100000 Па соответственно. Плотность можно принять постоянной со значением 1,1 кг / м ³ .

Решение

Местное статическое давление можно определить из уравнения 3.47, пренебрегая разницей в высоте

p — poρ = −C22r2

Из уравнения 3.29 сила вихря определяется как

C = uφr = 15 × 0,06 = 0,9 м2 / с

При радиусе 0.05 м, давление определяется как

p = −ρC22r2 + po = −1.10.922 × 0,052 + 105 = 99820 Па

Тангенциальная скорость определяется как

uφ = Cr = 0,90,05 = 18 м / с

На радиусе 0,03 м давление определяется как

po = −1,10,922 × 0,032 + 105 = 99510 Па

Тангенциальная скорость определяется как

uφ = Cr = 0,90,03 = 30 м / с

As Видно, что статическое давление уменьшается, а тангенциальная составляющая скорости увеличивается с уменьшением радиуса.

Пример 3.2

Свободный вихрь, который имеет тенденцию образовываться над открытым сливом в относительно неглубоком резервуаре, характеризуется тангенциальной скоростью, которая изменяется обратно пропорционально радиальному расстоянию от вертикальной оси через слив. Если тангенциальная скорость равна 0,1 м / с на радиусе 0,3 м, каково уменьшение возвышения поверхности на этом радиусе и каково уменьшение возвышения в радиусе 0,03 м и в радиусе 0,01 м?

Решение

Из уравнения 3.29, сила вихря определяется как

C = uφr = 0,1 × 0,3 = 0,03 м2 / с

Из уравнения 3.48

z — zo = −C22gr2 = −0,0322 × 9,81 × 0,32 = −0,5097 × 10−3 м.

При r = 0,03 м,

z — zo = −0,0322 × 9,81 × 0,032 = −0,05097 м

При r = 0,01 м,

z — zo = −0,0322 × 9,81 × 0,012 = — 0,4587 м

Этот пример иллюстрирует существенное уменьшение высоты поверхности с уменьшением радиуса.

Уравнение энергии для реального потока жидкости — сопротивление трению потоку жидкости

При выводе уравнения энергии для идеального потока жидкости мы сделали некоторые допущения, например, жидкость не является вязкой, а поток жидкости устойчивым.Но эти предположения верны только для очень конкретных случаев. Чтобы иметь дело с реальными потоками жидкости, мы должны учитывать различные потери, называемые потерями напора, вызванные трением и резкими изменениями пути потока жидкости. Более того, в идеальном случае поток жидкости считался ламинарным, но для реальных условий потока потоки жидкости могут быть как ламинарными, так и турбулентными. Потери на трение для турбулентных потоков имеют отношения с параметрами потока, отличными от ламинарного потока.

Модификация уравнения энергии

Для реальных потоков мы можем сохранить то же уравнение энергии, уравнение Бернулли, но с некоторыми изменениями.Новое модифицированное уравнение должно отражать два важных аспекта реальных потоков,

1. Компоненты потерь
2. Распределение реальной скорости

К уравнению добавляется член потерь, а влияние распределения реальной скорости учитывается путем изменения члена скорости в уравнении Бернулли. Уравнение.

Потери в реальном потоке

Потери в реальном потоке, фактически это потеря энергии, связанной с жидкостью, вызваны сопротивлениями, вызываемыми потоком жидкости.Сопротивления вызываются двумя факторами:

1. Трение в потоке
2. Изменение пути потока

Потери из-за трения в потоке

Часть энергии текучей среды при течении теряется на сопротивления из-за трения, вызванного напряжениями сдвига. . Напряжения сдвига различны для ламинарных и турбулентных течений; следовательно, сопротивления трению также различны.

Для ламинарного потока напряжение сдвига прямо пропорционально вязкости и градиенту скорости вдоль участка потока жидкости.Поскольку трение в ламинарном потоке вызывается напряжением сдвига, сопротивление трения или потери напрямую зависят от вязкости, скорости и длины пути потока.

Для турбулентного потока напряжение сдвига не прямо пропорционально скорости. Напряжения сдвига в турбулентных потоках не имеют определенной аналитической зависимости. Для турбулентных потоков связь сопротивлений трения с параметрами потока в основном определяется эмпирическим путем путем анализа размеров экспериментальных результатов.Сопротивление трения в турбулентном потоке напрямую зависит от длины пути потока и квадрата скорости потока.

Сопротивление трения в ламинарных потоках не зависит от поверхности канала, через который проходит поток. Но для турбулентных потоков сопротивление трения также зависит от шероховатости поверхности, контактирующей с потоком.

Потери из-за трения в потоке называются большими потерями, поскольку они ответственны за большую часть потерь энергии.Потери из-за изменения пути потока называются незначительными потерями. В следующей статье мы продолжим вывод уравнения энергии для реальных потоков жидкости с малыми потерями.

Этот пост является частью серии: Уравнение энергии для реального потока жидкости

Для анализа потока жидкости в реальных условиях мы должны учитывать влияние вязкости, потерь на трение и резких изменений геометрии пути потока. В этой серии статей мы выведем уравнение энергии для реальных потоков жидкости, обсуждая различные аспекты реальных потоков жидкости.

1. Сопротивление трения потоку жидкости
2. Потери из-за внезапных изменений пути потока
3. Распределение реальной скорости

Идеальная жидкость — поток жидкости гидравлический и пневматический

Теория идеальной жидкости — Поток жидкости

Расход жидкости Содержание
Гидравлические и пневматические знания
Гидравлическое оборудование

Идеальная жидкость (также называемая Perfect Fluid) — это несжимаемый и не имеющий вязкости.Идеальных жидкостей на самом деле нет. существуют, но иногда полезно рассмотреть, что случится с идеальной жидкостью в конкретной жидкости проблема потока, чтобы упростить проблему.

Настоящие жидкости «липкие» и содержат (и проводят) тепло. Идеальные жидкости — это идеализированные модели, в которых эти возможности не учитываются. В частности, идеальные жидкости не имеют касательных напряжений, вязкости или теплопроводности.

В обозначении пространственно-положительного метрического тензора сигнатуры тензор энергии-импульса идеальной жидкости можно записать в виде:

Где U — векторное поле скорости жидкости, а где:

— метрический тензор пространства-времени Минковского.

В обозначении положительного по времени метрического тензора сигнатуры тензор энергии-импульса идеальной жидкости можно записать в виде:

Где U — векторное поле скорости жидкости, а где:

— метрический тензор пространства-времени Минковского. Он принимает особенно простую форму в системе отсчета покоя:

где:

— это плотность энергии , а p — давление жидкости.

Совершенные жидкости допускают лагранжеву формулировку, которая позволяет применять к жидкостям методы, используемые в теории поля, в частности, квантование. Эта формулировка может быть обобщена, но, к сожалению, теплопроводность и анизотропные напряжения не могут быть учтены в этих обобщенных формулировках.

Совершенные жидкости часто используются в общей теории относительности для моделирования идеализированных распределений материи, например, внутренней части звезды или изотропной Вселенной.В последнем случае уравнение состояния идеальной жидкости может быть использовано в уравнениях Фридмана – Лемэтра – Робертсона – Уокера для описания эволюции Вселенной.

классической механики — поток жидкости и число Рейнольдса

… Я тоже думал, что идеальный поток жидкости — ламинарный … Турбулентный поток не характерен для идеального потока жидкости.

Я предполагаю, что под идеальной жидкостью вы подразумеваете невязкую жидкость.Чтобы поток можно было назвать турбулентным, в отличие от сложного ламинарного потока, он должен обладать несколькими характеристиками (см. Первое направление турбулентности Теннекеса и Ламли, глава 1). Среди прочего, он должен содержать трехмерное распределение завихренности и быть диссипативным. В идеальной жидкости из-за отсутствия вязкости не возникает завихренности на стенках и других границах (поскольку не соблюдается противодействие скольжению). Следовательно, идеальная жидкость с однородной плотностью, которая изначально не содержит завихренности, не будет иметь завихренности все последующие времена.Такое течение, каким бы сложным оно ни стало из-за инерционной неустойчивости, нельзя назвать турбулентным. Если бы идеальная жидкость изначально имела некоторое распределение завихренности, все равно не было бы диссипации механической энергии потока из-за отсутствия вязкости. Опять же, как и прежде, каким бы сложным ни было течение, его нельзя назвать турбулентным.

Завихрение может быть создано в невязкой жидкости другими способами, например, из-за нестабильных перепадов плотности. Я не знаю других диссипативных механизмов, кроме вязкости.Так что, возможно, отсутствие диссипации не позволит назвать идеальный поток жидкости турбулентным. Но идеальный поток жидкости может быть таким же сложным, как турбулентный поток.

Я не уверен в утверждении @ tpg2114 о том, что «… энергетический каскад и скорость диссипации в турбулентных потоках обусловлены вязкостью». Я согласен с диссипацией, но каскад энергии возникает из-за инерционной нестабильности, которая (насколько мне известно) не имеет никакого отношения к вязкости. Вязкость рассеивает механическую энергию потока и устанавливает наименьший масштаб, при котором могут возникать турбулентные колебания.В диссипативной жидкости для поддержания турбулентности требуется постоянный приток энергии извне; в отсутствие вязкости такая непрерывная подача не требуется (кинетическая энергия жидкости сохраняется всегда), но каскад энергии все еще может происходить, и результирующий поток может казаться таким же сложным, как турбулентный поток. Однако нет вязкости для установки наименьшего масштаба, поэтому на профиле скорости могут появиться сингулярности (поскольку идеальных жидкостей не существует, все это в любом случае гипотетически).

…. идеальный поток жидкости аппроксимируется реальным потоком жидкости с высоким числом Рейнольдса … Очень большое число Рейнольдса соответствует пренебрежимо малому напряжению сдвига.

Верно. Вязкими эффектами нельзя пренебречь в определенных частях потока (как указал @ChesterMiller), например, на жестких границах, где реальная жидкость должна подчиняться условию отсутствия проскальзывания. Вдали от таких областей средний поток может быть приближен к потоку идеальной жидкости. Уравнение Бернулли приблизительно справедливо для среднего расхода.(Полагаю, вы знакомы с усреднением по Рейнольдсу турбулентных потоков)

Что такое жидкость? & типы жидкости.

Что такое жидкость?

Жидкость — это вещество, которое непрерывно течет под воздействием внешней силы. Жидкости обычно включают жидкости, газы и плазму. В некоторой степени пластичные твердые тела также считаются жидкостями.

Жидкости можно классифицировать по следующим свойствам:

• Вязкость
• Электропроводность
• плотность
• сжимаемый или нет.

Распространенные типы жидкостей в зависимости от вязкости:

Жидкости разделяются на пять основных типов:

1. Идеальная жидкость
2. Реальная жидкость
3. Ньютоновская жидкость
4. Неньютоновская жидкость
5. Идеальная пластиковая жидкость

1. Идеальная жидкость:

Идеальная жидкость — это жидкость, несжимаемая по своей природе и не имеющая вязкости. На практике никакая жидкость не является идеальной жидкостью, потому что все жидкости имеют некоторую вязкость.Таким образом, это также называется воображаемой жидкостью.

2. Реальная жидкость:

Настоящие жидкости — это жидкости, обладающие некоторой вязкостью и сжимаемые по своей природе. Все жидкости на самом деле являются настоящими жидкостями.

Примеры: керосин, бензин, касторовое масло

3. Ньютоновская жидкость:

Ньютоновские жидкости — это жидкости, подчиняющиеся закону вязкости Ньютона. Другими словами, реальная жидкость, напряжение сдвига которой прямо пропорционально скорости деформации сдвига, называется ньютоновской жидкостью.Для ньютоновской жидкости вязкость полностью зависит от температуры и давления жидкости.

Примеры: вода, воздух, эмульсии, водород

Основные характеристики:

• Ньютоновские жидкости не обладают упругими свойствами.
• Они несжимаемы, изотропны и нереальны.
• Вязкость зависит от температуры,
• Вязкость также зависит от различных давлений, при которых она находится.
• При фиксированной температуре их вязкость остается постоянной.
• С повышением температуры жидкости вязкость уменьшается.
• Вязкость этого типа жидкости обратно пропорциональна повышению ее температуры.
• Ньютоновская жидкость была названа в честь сэра Исаака Ньютона, который определил ее как вязкое течение.
• Они соответствуют закону вязкости Ньютона.

4. Неньютоновская жидкость:

Неньютоновские жидкости — это жидкости, которые не подчиняются закону вязкости Ньютона.Другими словами, реальная жидкость, в которой напряжение сдвига не прямо пропорционально скорости деформации сдвига, называется неньютоновской жидкостью.

Примеры: Flubber, Oobleck

Неньютоновские жидкости можно далее классифицировать как:

1. Жидкости, зависящие от времени: Эти жидкости, для которых напряжение сдвига или вязкость уменьшается со временем из-за изотермических условий и устойчивого сдвига, известны как Тиксотропные , а те, которые со временем увеличиваются при тех же обстоятельствах, известны как Реопектик или Анти-тиксотропный .
2. Жидкости, не зависящие от времени: Для этих жидкостей скорость сдвига в данной точке зависит от мгновенного напряжения сдвига в этой точке. Они также известны как неньютоновские вязкие жидкости или чисто вязкие жидкости.

Эти жидкости бывают двух типов:

• • Жидкости с пределом текучести
  • Жидкости без предела текучести: они также бывают двух видов:
    • Псевдопластические жидкости
    • Дилатантные жидкости

3.Вязкоупругие жидкости

5. Идеальная пластиковая жидкость:

Идеальная пластическая жидкость — это жидкость, напряжение сдвига пропорционально скорости деформации сдвига, и в которой напряжение сдвига больше, чем значение текучести, известна как идеальная пластическая жидкость.

Распространенные типы жидкостей в зависимости от плотности:

1. Газ
2. Жидкость

Существует два подхода к изучению поведения жидкости:

1. Лагранжианский подход: В этом методе берется отдельная частица жидкости и тщательно изучается ее поведение при различных размерах секций.