Задачи по теме «Теплоемкость идеального газа»
Решение задач дело полезное, но не всегда интересное. Чтобы вы справлялись с решением задач по теме «Теплоемкость идеального газа» быстрее, приведем здесь несколько примеров и вопросов с объяснениями.
Подписывайтесь на наш телеграм-канал, чтобы получать полезную и интересную рассылку.
Задачи по теме «Теплоемкость идеального газа» с решениями
Повторение и практика – залог успеха в любом деле. И решение задач не исключение. Поэтому не забываем держать под рукой памятку по задачам и полезные формулы
Задача №1. Определить удельную теплоемкость идеального газа
Условие
Определить молярную массу M двухатомного газа и его удельные теплоемкости, если известно, что разность cр — cv удельных теплоемкостей этого газа равна 260 Дж/(кг*К)
Решение
По определению:
Значит, газ из задачи – кислород. Если кто не понял, как это определяется, учитесь пользоваться таблицей Менделеева.
Считаем удельные теплоемкости:
Ответ: 32 г/моль; 649 Дж/кг*К; 909 Дж/кг*К.
Задача №2. Удельная теплоемкость
Условие
Плотность некоторого газа при нормальных условиях ρ = 1,25 кг/м3. Отношение удельных теплоемкостей γ = 1,4. Определить удельные теплоемкости cv и сp этого газа.
Решение
Исходя из отношения удельных теплоемкостей, можно сделать вывод, что газ – двухатомный, i=5. При постоянном объеме удельная теплоемкость равна:
Молярную массу можно найти из уравнения Клапейрона-Менделеева:
Отсюда:
Ответ: 742 Дж/кг*К; 1039 Дж/кг*К.
Задача №3. Молярная теплоемкость
Условие
Вычислить молярные теплоемкости газа, зная, что его молярная масса М = 4∙10 3 кг/моль и отношение удельных теплоемкостей ср/сv = 1,67.
Решение
Удельные теплоемкости равны:
Можно найти:
Ответ: 12,4 Дж/моль*К; 20,71 Дж/моль*К
Задача №4.
Теплоемкость при изопроцессахУсловие
На рисунке изображен изотермический процесс с газом постоянной массы. Сравните теплоемкость в процессе АВ с теплоемкостью этой же массы газа в изохорном процессе.
Решение
Теплоемкость при изохорном процессе является постоянной величиной. При изотермическом процесса она равна бесконечности. Значит, теплоемкость в процессе АВ больше.
Ответ: Теплоемкость в процессе АВ больше.
Задача №5. Теплоемкость при политропическом процессе
Условие
Найдите молярную теплоемкость идеального газа при политропическом процессе pVn = const, если показатель адиабаты газа равен γ. При каких значениях показателя политропы n теплоемкость газа будет отрицательной?
Решение
Запишем первое начало термодинамики, выражения для работы и изменения внутренней энергии в политропическом процессе соответственно:
Если количество вещества и изменение температуры принять равными единице, это выражение будет равно молярной теплоемкости (по определению теплоемкости):
Ответ: см.
выражение выше.
Вопросы по теме «Теплоемкость идеального газа»
Вопрос 1. Что такое теплоемкость идеального газа?
Ответ. Когда газу сообщается определенное количество теплоты, меняется его температура.
Отношение количества теплоты, сообщенного газу, к изменению его температуры, называется теплоемкостью идеального газа.
Вопрос 2. Что такое молярная и удельная теплоемкость идеального газа?
Ответ.
Удельная теплоемкость – теплоемкость единичной массы вещества.
Вопрос 3. Как определяется теплоемкость газа при изопроцессах?
Ответ.
При изотермическом процессе T=const. Теплоемкость равна плюс/минус бесконечности.
При адиабатном процессе нет теплообмена с окружающей средой, теплоемкость равна нулю.
При изохорном процессе газ не совершает работы, а теплоемкость равна:
Здесь i – количество степеней свободы молекул газа. Для одноатомных газов i=3, для двухатомных i=5.
При изобарном процессе теплоемкость определяется соотношением Мейера:
Вопрос 4. Как еще связаны теплоемкости при постоянном давлении и постоянном объеме?
Ответ. Отношение теплоемкостей при постоянном давлении и постоянном объеме обозначается греческой буквой «гамма» и называется показателем адиабаты.
Вопрос 5. Как называются процессы, в которых теплоемкость газа остается неизменной?
Ответ. Такие процессы называются политропными. Адиабатный процесс – частный случай политропного процесса.
Теплоемкость реального газа не равна теплоемкости идеального газа и может сильно отличаться.
Нужна помощь в решении задач и выполнении других заданий? Специальный студенческий сервис готов оказать ее!
Удельная теплоемкость при постоянном объеме Калькулятор
✖Изменение теплоты определяется как изменение энтальпии реакции. | АттоджоульМиллиарда баррелей нефтяного эквивалентаБританская тепловая единица (IT)Британская тепловая единица (th)Калорийность (ИТ)Калорийность (питательная)Калорийность (тыс.)сантиджоульCHUдекаджоульДециджоульДин СантиметрЭлектрон-вольтЭргЭкзаджоульФемтоджоульфут-фунтГигагерцГигаджоульГигатонна тротилаГигаватт-часГрамм-сила-сантиметрграмм-сила-метрХартри энергия гектоджоульГерцЛошадиная сила (метрическая) ЧассилочасДюйм-фунтДжоульКельвинКилокалория (IT)Килокалория (й)килоэлектрон вольтКилограммКилограмм тротилаКилограмм-сила-сантиметрКилограмм-сила-метркилоджоульKilopond Meterкиловатт-часкиловатт-секундаМБТУ (ИТ)Мега БТЕ (ИТ)Мегаэлектрон-ВольтмегаджоульМегатонна тротиламегаватт-часмикроджоульМиллиджоульММБТУ (ИТ)наноджоульНьютон-метрУнция-сила-дюймПетаджоульПикоджоульПланка Энергияфунт-сила футафунт силы дюймпостоянная РидбергаТерагерцТераджоультермтерм (EC)Therm (США)Тон (взрывчатые вещества)Тон-час (Охлаждение)Тонна нефтяного эквивалентаБлок Единая атомная массаВатт-часДжоуль | +10% -10% | |
✖Количество молей – это количество газа в молях. | +10% -10% | ||
✖Изменение температуры – это процесс, при котором изменяется степень нагретости тела (или среды).ⓘ Изменение температуры [ΔT] | ЦельсияДелильФаренгейтКельвинНьютонРанкинтемпература по реомюруРомерТройной точки воды | +10% -10% |
1 моль газа весит столько же, сколько его молекулярная масса.ⓘ Количество молей [Nmoles]|
✖Молярная удельная теплоемкость при постоянном объеме (газа) – это количество теплоты, необходимое для повышения температуры 1 моль газа на 1 °C при постоянном объеме.ⓘ Удельная теплоемкость при постоянном объеме [C |
Джоуль на градус Цельсия на декамольДжоуль на градус Цельсия на мольДжоуль на градус Фаренгейта на мольДжоуль на кельвин на мольДжоуль на Реомюра на моль |
⎘ копия |
👎
Формула
сбросить
👍
Удельная теплоемкость при постоянном объеме Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Преобразование входов в базовый блок
Изменение тепла: 107 Джоуль —> 107 Джоуль Конверсия не требуется
Количество молей: 2 —> Конверсия не требуется
Изменение температуры: 21 Кельвин —> 21 Кельвин Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
2.54761904761905 Джоуль на кельвин на моль —> Конверсия не требуется
< 14 Тепловые параметры Калькуляторы
Удельная теплоемкость газовой смеси
Идти Удельная теплоемкость газовой смеси = ((Количество молей газа 1*Удельная теплоемкость газа 1 при постоянном объеме)+(Количество молей газа 2*Удельная теплоемкость газа 2 при постоянном объеме))/(Количество молей газа 1+Количество молей газа 2)
Термическое напряжение материала
Идти Тепловая нагрузка = (Модуль для младших*Коэффициент линейного теплового расширения*Изменение температуры)/(Начальная длина)
Изменение потенциальной энергии
Идти Изменение потенциальной энергии = масса*[g]*(Высота объекта в точке 2-Высота объекта в точке 1)
Коэффициент удельной теплоемкости
Идти Коэффициент удельной теплоемкости = Молярная удельная теплоемкость при постоянном давлении/Молярная удельная теплоемкость при постоянном объеме
Удельная теплоемкость при постоянном объеме
Идти Молярная удельная теплоемкость при постоянном объеме = Изменение тепла/(Количество молей*Изменение температуры)
Удельная энтальпия насыщенной смеси
Идти Энтальпия насыщенной смеси = Удельная энтальпия жидкости+(Качество пара*Скрытая теплота парообразования)
Тепловое расширение
Идти Коэффициент линейного теплового расширения = (1*Изменение длины)/(Начальная длина*Изменение температуры)
Изменение кинетической энергии
Идти Изменение кинетической энергии = масса*(Конечная скорость в точке 2^2-Конечная скорость в точке 1^2)/2
Общая энергия системы
Идти Полная энергия системы = (Потенциальная энергия)+(Кинетическая энергия)+(Внутренняя энергия)
Коэффициент удельной теплоемкости
Идти Динамический коэффициент теплоемкости = Теплоемкость при постоянном давлении/Постоянный объем теплоемкости
Удельная теплоемкость
Идти Удельная теплоемкость = Нагревать*(масса*Изменение температуры)
фактор явного тепла
Идти Фактор явного тепла = 1/(1+(Скрытая теплота/Явное тепло))
Теплоемкость
Идти Теплоемкость = (масса)*(Удельная теплоемкость)
Скрытая теплота
Идти Скрытая теплота = Нагревать/масса
Удельная теплоемкость при постоянном объеме формула
Молярная удельная теплоемкость при постоянном объеме = Изменение тепла/(Количество молей*Изменение температуры)
Cv molar = ΔQ/(Nmoles*ΔT)
Определите удельную теплоемкость?
Удельная теплоемкость — это количество тепла на единицу массы, необходимое для повышения температуры на один градус Цельсия.
Связь между теплотой и изменением температуры обычно выражается в виде Q = mcΔt, где c — удельная теплоемкость. Это соотношение не применяется, если происходит фазовый переход, потому что тепло, добавляемое или отводимое во время фазового перехода, не изменяет температуру.
Share
Copied!
определение, C, Cp и Cv
Дата последнего обновления: 23 марта 2023 г. изменение температуры называется теплоемкостью. С точки зрения фактического количества рассматриваемого материала, чаще всего в молях, оно обычно указывается в калориях на градус (молекулярная масса в граммах). Удельная теплоемкость – это теплоемкость в калориях на грамм. Калорийность определяется удельной теплоемкостью воды, которая определяется как одна калория на градус Цельсия.
Теплоемкость – это отношение тепла, поглощаемого материалом, к изменению температуры. Следовательно, изменение температуры тела прямо пропорционально теплоте, переданной данному телу.
Что такое теплоемкость C, C
p и C v ?Определение молярной теплоемкости (C)
Общее количество энергии в виде тепла, необходимое для повышения температуры 1 моля любого вещества на 1 единицу, называется молярной теплоемкостью (C) этого вещества. . Он также существенно зависит от природы, размера и состава вещества в системе.
q = n C ∆T
Где,
q — теплота, подведенная или необходимая для изменения температуры (∆T) на 1 моль любого данного вещества,
n — количество в молях,
Константа C известна как молярная теплоемкость тела данного вещества.
\[C_{p}\]
В системе C p — количество тепловой энергии, выделяемой или поглощаемой единицей массы вещества при изменении температуры при постоянном давлении.
Другими словами, при постоянном давлении это передача тепловой энергии между системой и окружающей средой. Итак, С p представляет собой молярную теплоемкость, C, при постоянном давлении. Изменение температуры всегда вызывает изменение энтальпии системы.
Энтальпия (∆H) – это тепловая энергия, поглощаемая или выделяемая системой. Кроме того, изменение энтальпии происходит при изменении фазы или состояния вещества.
Например, когда твердое тело переходит в жидкую форму (т. е. превращается из льда в воду), изменение энтальпии называется теплотой плавления. Когда жидкость переходит в газообразную форму (то есть из воды в водяной пар), изменение энтальпии называется тепловым испарением.
Система поглощает или выделяет теплоту без изменения давления в этом веществе, тогда ее удельная теплоемкость при постоянном давлении C p может быть записана как:
\[C_{p} = [\frac{dH}{ dT}]_{p}\] — (1)
где Cp представляет удельную теплоемкость при постоянном давлении; dH — изменение энтальпии; dT – изменение температуры.
\[C_{v}\]
При небольшом изменении температуры вещества C v представляет собой количество тепловой энергии, поглощаемой/выделяемой на единицу массы вещества, объем которого не изменяется. Другими словами, С v — это передача тепловой энергии между системой и окружающей средой без изменения объема этой системы. C v представляет собой молярную теплоемкость C при постоянном объеме. При постоянном объеме объем вещества не изменяется, поэтому изменение объема равно нулю.
Поскольку этот термин относится к внутренней энергии системы, которая является суммой потенциальной и кинетической энергии этой системы. Система поглощает или выделяет теплоту без изменения объема этого вещества, тогда его удельная теплоемкость при постоянном объеме C v может быть:
\[C_{v} = [\frac{dU}{dT}]_{v}\] — (2)
Где
C v представляет удельная теплоемкость при постоянном объеме;
dU — малое изменение внутренней энергии системы;
dT — изменение температуры системы.
Связь между C p и C v
Согласно первому закону термодинамики:
\[\Delta Q = \Delta U + \Delta W\], где \[\Delta Q\] — количество теплоты, переданной системе, U — изменение внутренней энергии, а W — работа. сделанный.
Мы можем написать,
\[\Delta Q = \Delta U + P\Delta V as \Delta W = P\Delta V\]
Так как \[\Delta Q = \Delta n C_{p}\ Delta T \, и \, \Delta U = \Delta n_{v}C \Delta T\]
Следовательно,
\[n C_{p} \Delta T = n C_{v} \Delta T + P \Delta V\] —— (3)
Как мы видим, что PV = nRT
При T1 по Кельвину: \[PV_{1} = nRT_{1}\] ———— (a)
При T2 по Кельвину: \[PV_{2} = nRT_{2 }\] ———— (b)
Вычитание уравнения (a) из (b):
\[PV_{2} — PV_{1} = nRT_{2} — nRT_{1}\]
\[P(V_{2} — V_{1}) = nR (T_{2} — T_{1})\]
Где,
\[V_{2} — V_{1} = \Delta V\] и \[T_{2} — T_{1} = \Delta T\]
Следовательно,
\[P \Delta V = nR \Delta T\]
Подстановка значение \[P \Delta V\] в уравнении (3), получаем,
\[n C_{p} \Delta T = n C_{v} \Delta T + nR \Delta T\]
\[n C_{p}\Delta T = n\Delta T (C_{v} + R)\]
\[C_{p} = C_{v} + R\]
Или
\[C_{p} — C_{v} = R\]
Можно дать следующее соотношение рассматривая идеальное газовое поведение газа.
\[C_{p} — C_{v} = R\]
Где R называется универсальной газовой постоянной.
Коэффициент теплоемкости
В термодинамике — коэффициент теплоемкости или коэффициент удельной теплоемкости (C p :C v ) также известен как показатель адиабаты. Это отношение двух удельных теплоемкостей, C p и C v , определяется по формуле:
Теплоемкость при постоянном давлении (C p )/ Теплоемкость при постоянном объеме (C v )
Коэффициент изоэнтропического расширения — это другое название коэффициента теплоемкости, который также обозначается для идеального газа как γ (гамма). Следовательно, соотношение между C p и C v представляет собой коэффициент удельной теплоемкости γ.
Итак,
\[\gamma = \frac{C_{p}}{C_{v}}\]
Необходимо изучить коэффициент теплоемкости для применения в обратимых процессах термодинамики, особенно там, где идеальны участвуют газы.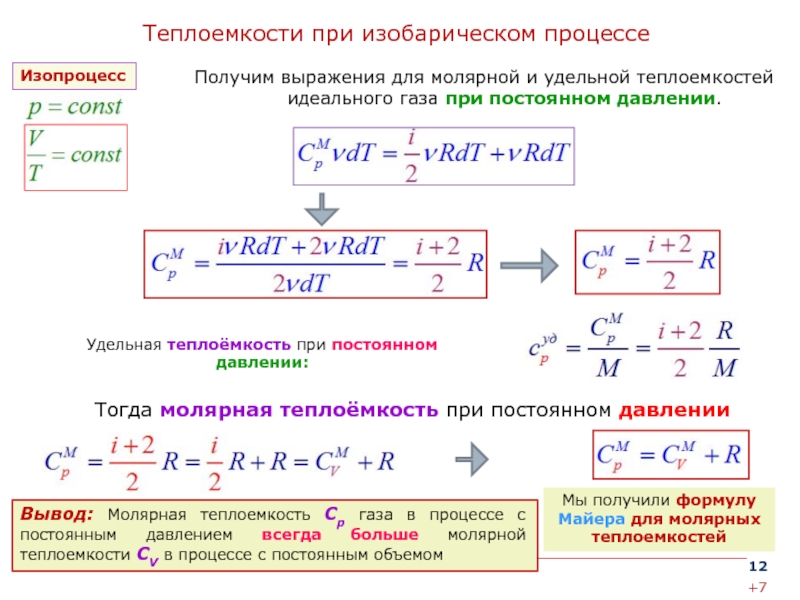
Например, для изучения связи со степенями свободы,
Коэффициент теплоемкости (гамма, γ) идеального газа можно связать со степенями свободы ( f ) молекул газа формулой:
\ [\gamma = 1 + 2f\] или \[f = 2\gamma — 1\]
Удельная теплоемкость газа при постоянном объеме в терминах степени свободы ‘f’ определяется как:
\[C_{v} = (\frac{f}{2})R\]
Кроме того,
\[C_{p} — C_{v} = R\]
Следовательно,
\[C_{p} = (\frac{f}{2})R + R = R(1 + \frac{ f}{2})\]
Теперь отношение удельных теплоемкостей γ задается как:
\[\gamma = \frac{C_{p}}{C_{v}} = \frac{R(1 + \frac{f}{2})}{(\frac{f}{2})R}\]
\[= \frac{(2 + f)}{f}\]
Или \[\ гамма = \frac{C_{p}}{C_{v}}\] 9{2}\]
где m — масса молекулы, v (\[V_{x}\],\[V_{y}\] и \[V_{z}\]) — импульс молекула вместе с осью x, осью y и осью z.
Закон равнораспределения дает,
\[E = \frac{1}{2}k_{B} T + \frac{1}{2}k_{B} T + \frac{1}{2} k_{B} T\]
Здесь \[K_{B}\] — средняя поступательная кинетическая энергия, а T — температура.
Энергия на молекулу газа определяется как,
\[U = \frac{3}{2}k_{B}T\]
\[= \frac{3}{2} RT\]
Таким образом, \[\frac{dU}{dT} = R\]
Но, \[\frac{dU}{dT} = C_{v}\]
Таким образом, \[C_{v} = \frac{3}{2} R\]
Теперь \[C_{p} — C_{v} = R\]
Тогда \[C_{p} = R + C_{v}\]
Это дает \[\gamma = \frac{C_{p}}{C_{v}} = \frac{{\frac{5}{2}R}}{{\frac{3}{2}R }} =\frac{5}{3} = 0,67\]
Для двухатомного газа (например, H 2 , O 2 и N 2 ) он имеет 5 степеней свободы ( 3 как поступательные и 2 как вращательные степени свободы при комнатной температуре, тогда как, за исключением высоких температур, колебательная степень свободы не задействована).
Почему C
p больше, чем C v ?Значения, указанные C p и C v , являются удельной теплоемкостью идеального газа. Они показывают количество теплоты, которое может увеличить температуру единицы массы на 1°C.
Согласно первому закону термодинамики,
\[\Delta Q = \Delta U + \Delta W\]
Где,
\[\Delta Q\] — количество теплоты, переданной системе , \[\Delta U\] — изменение внутренней энергии, а W — проделанная работа.
Итак, при постоянном давлении теплота поглощается не только для увеличения внутренней энергии (функция температуры), но и для совершения работы. Принимая во внимание, что при постоянном объеме тепло поглощается только для повышения внутренней энергии, а не для совершения какой-либо работы над системой, как (для замкнутой системы): \[W = P \Delta V\], где W — работа сделанный. Здесь \[\Delta V = 0\]. (Замкнутая система также является одним из важнейших условий постоянного объема).
Следовательно, удельная теплоемкость при постоянном давлении больше, чем удельная теплоемкость при постоянном объеме, т. е. \[C_{p} > C_{v}\].
Мы можем
умножьте конкретную переменную на количество вещества в любой момент времени
для определения фактического значения переменной потока.
Из наших исследований
теплопередача,
мы знаем, что количество теплоты, переданное между двумя телами, равно
пропорционально
температура
разница между предметами и
теплоемкость объектов. теплоемкость это
постоянная, показывающая, сколько тепла добавляется на единицу повышения температуры.
Значение константы различно для разных материалов и зависит
на процессе. Теплоемкость не является переменной состояния .
Таким образом, «дельта h» означает изменение «h» из состояния 1 в состояние 2 во время процесса.
Затем для процесса постоянного давления уравнение энтальпии принимает следующий вид:
Несмотря на то, что изменение температуры для этого процесса одинаково и постоянная
процесс давления, значение удельной теплоемкости различно.