Тепловой баланс двигателя: Тепловой баланс двигателя

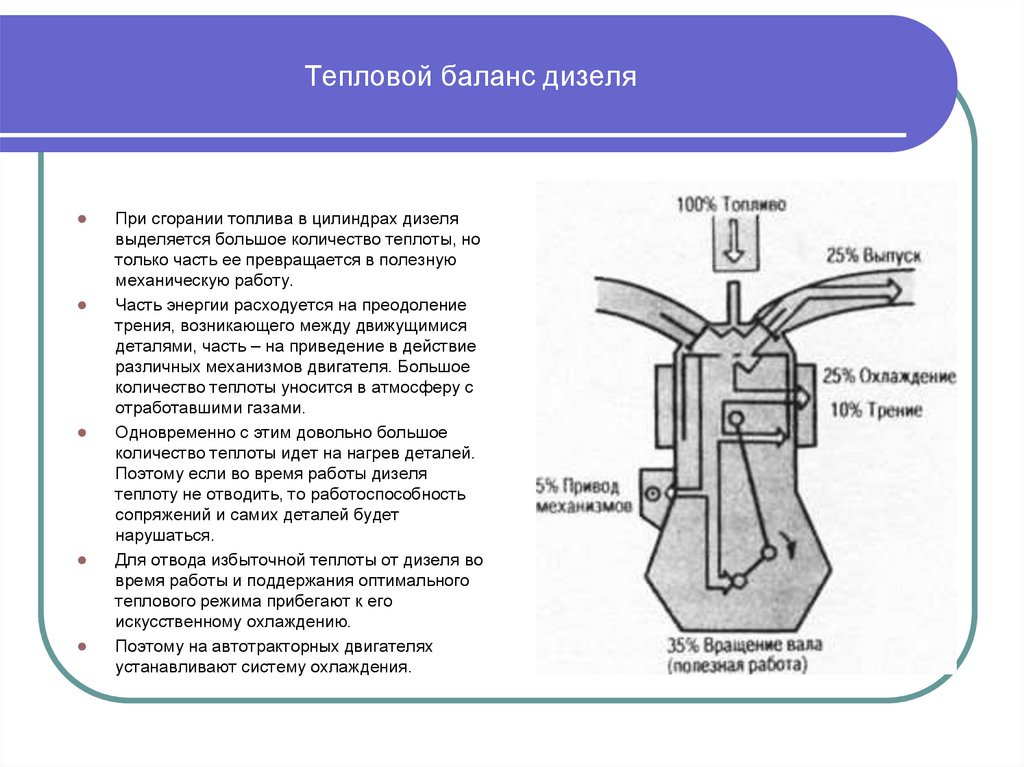
2.2.8. Тепловой Баланс Двигателя Внутреннего Сгорания

Тепловой баланс ДВС характеризует распределение количества теплоты, кДж, выделяющейся при сгорании топлива, на полезную работу и тепловые потери:

Q =Qе+Q_в+Q_г+Q_н.с+Q_м+Q_ост

где Q — общее количество теплоты, введенной в двигатель с топливом (располагаемое количество теплоты), кДж; Q_е — теплота, эквивалентная эффективной работе двигателя (полезно использованная теплота), кДж; Q_в — теплота, отведенная в охлаждающую среду, кДж; Q_г, — потери теплоты с отработавшими газами, кДж; Q_н.с — потери теплоты от неполного сгорания топлива, кДж; Q_м — потери теплоты в масло, кДж; Q_ост — потери теплоты путем теплообмена нагретых деталей с окружающей средой и другие (остальные) потери, кДж.

Тепловой баланс определяется на основе экспериментальных данных и выражается в абсолютных или относительных единицах. Составляющие теплового баланса могут выражаться в процентах к располагаемому количеству теплоты. В этом случае уравнение теплового баланса приобретает вид

q_е+q_в+q_г+q_н.с+q_м+q_{ост = 100%}.

Располагаемое количество теплоты после сгорания, кДж/ч, определяется по низшей теплотворной способности топлива h_u, кДж/кг, и его часовому расходу G_T, кг/ч: Q = h_uG_T.

В табл. 2.5 приведены средние значения доли составляющих теплового баланса четырехтактного ДВС.

Двигатель	Доля, %, составляющей теплового баланса
	qе	q в	qг	qн.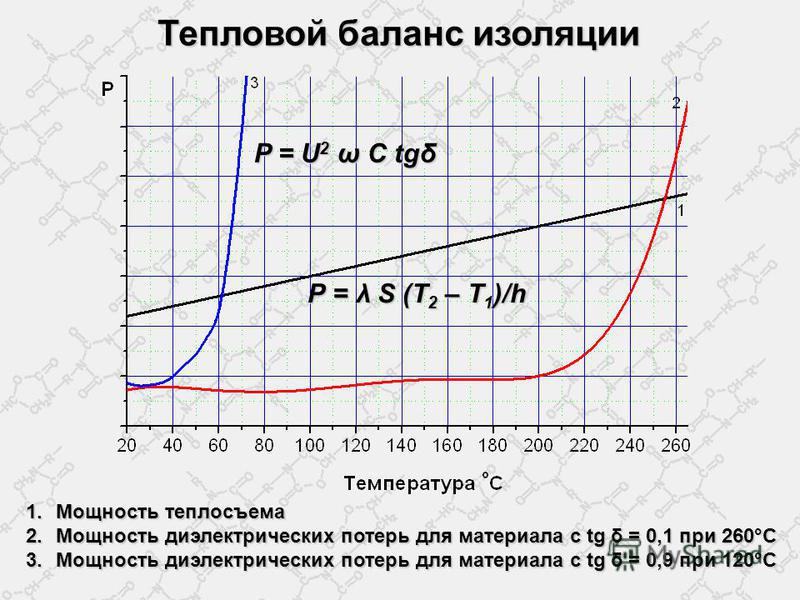 с	qм	qост
Бензиновый	22…28	14…28	30…40	0 …15	2…4	3…8
Дизель	29…42	16…35	25…40	0…5	6…7	2…5

На долю потерь приходится 50… 70% теплоты, выделившейся при сгорании топлива в двигателе, поэтому задача утилизации этих потерь является очень важной. Теплота охлаждающей жидкости используется для отопления кабин машин, обдува стекол теплым воздухом. В дизелях теплота отработавших газов частично используется в газовых турбинах турбокомпрессоров, которые применяются для наддува, благодаря чему удается повысить мощность

и КПД этих двигателей.

Тепловой баланс двигателя улучшается, если повышается температура охлаждающей жидкости, при которой двигатель работает нормально. При повышении рабочей температуры охлаждающей жидкости с 60 до 90 °С мощность двигателя может быть повышена на 2…6%, а удельный эффективный расход топлива снижен на 2…4 г/(кВт • ч).

Тепловой баланс двигателя — что это такое?

Каждому автовладельцу известен такой термин, как тепловой баланс двигателя внутреннего сгорания. Но что конкретно несёт в себе это понятие, как измеряется и на каких принципах основано? Об этом и пойдёт речь сегодня.

Не все до конца понимают, что такое тепловой баланс двигателя

Если бы можно было приостановить действие некоторых законов физики, человечество уже давно достигло пика своего развития. Но к сожалению, это невозможно. Нам остаётся только использовать их, стараясь извлечь при этом максимальную пользу.

С одним из таких «неудобных» законов напрямую связан низкий КПД силовых агрегатов автомобиля. Что же не позволяет нам развивать немыслимую скорость на своих авто? Какие попытки предпринимаются для преодоления этого препятствия? Сейчас мы с вами выясним.

Содержание

• Почему я не сокол, отчего не летаю
• Формулировка понятия тепловой баланс
• Причины утраты
• Как рассчитывают потери
• Извлечение пользы из потери
• Подведение итога

Почему я не сокол, отчего не летаю

Принципы термодинамики — это основа работы всех двигателей внутреннего сгорания. Один из них гласит, что при сгорании топлива часть выделяемого тепла в любом случае поглощается средой происхождения реакции.

Видео о том, как работает ДВС:

В нашем случае средой является сам двигатель и его системы. Лишь от 20 до 40 процентов вырабатываемой здесь тепловой энергии используется для работы мотора. Остальное утрачено безвозвратно. Но куда девается львиная доля энергии? Давайте разбираться по порядку.

Формулировка понятия тепловой баланс

Итак, тепловой баланс двигателя — это разделение расхода полученной энергии на полезную отдачу и растрату впустую.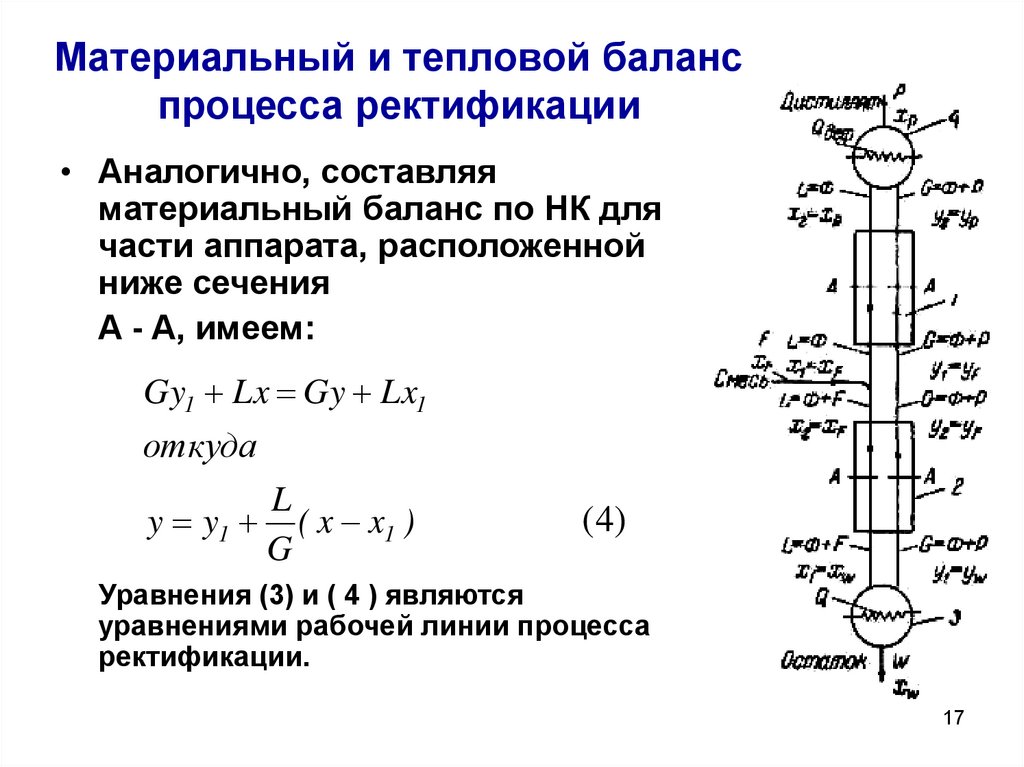 Неизменным здесь является равенство или же баланс между полученной энергией тепла и её расходом.

Что такое полезная отдача, все мы понимаем. Это движение автомобиля. О расходе впустую — читаем дальше.

Причины утраты

Существует несколько причин бесполезной растраты энергии тепла. Вот так мы их сформулируем:

• преодоление энергией сопротивления при сжатии;
• отдача тепла двигателем в окружающую среду, по простому его остывание;
• выход в атмосферу вместе с выхлопными газами;
• расход некоторой доли энергии на работу охлаждающей системы двигателя и других агрегатов.

Количественный показатель этих статей растраты величина непостоянная. А от чего он зависит, мы рассмотрим в следующем разделе.

Как рассчитывают потери

Количество растраты зависит от многих факторов. Вот основные из них:

• нагрузка на силовую установку;
• конструкция двигателя и его систем;
• скорость, развиваемая автомобилем;
• состав смеси горючего;
• температура окружающей среды.

Скорость автомобиля может влиять на растраты энергии

Здесь стоит также отметить, что теплопотеря дизельного агрегата, ниже чем у карбюраторного на 10–12%. Измерения ведутся в абсолютных единицах теплопередачи или в процентном соотношении количества полученного тепла к его бесполезной растрате. Всё это принимается во внимание при расчётах, что позволяет достичь извлечения максимальной пользы от горения топлива.

Извлечение пользы из потери

Конечно, при таком раскладе, потеря энергии всё ещё остаётся огромной. Но в отрасли постоянно ведутся работы по улучшению результата. Внедряются инновационные методы разработки двигателей внутреннего сгорания.

Например, турбонаддувная установка, использующая давление горячих газов из выхлопа. Принцип её работы заключается в том, что выхлопные газы приводят в действие турбину, вращающую лопасти нагнетателя, обогащающего компонента внутрь цилиндров двигателя.

Ещё тепло, поглощённое охлаждающей системой, используется для обогрева салона автомобиля.

Горячая вода из радиатора подаётся по нагревательным элементам печки.

Подведение итога

Мы выяснили, что такое тепловой баланс двигателя и какие есть потери энергии тепла. Вывод отсюда следующий — существующие на сегодняшний день двигатели внутреннего сгорания далеки от совершенства. Но разработчики не сидят сложа руки, ведутся постоянные поиски способа обернуть потерю в пользу. И нам остаётся только пожелать им удачи.

Внизу можно высказываться по теме. Ждём ваших комментариев. До скорых встреч!

Понимание тепловых параметров двигателей постоянного тока

Тепловая модель: Для тепловой системы есть только два основных строительных блока; а именно, тепловое сопротивление и теплоемкость. Простая тепловая модель, описывающая нагрев двигателя постоянного тока без сердечника и ее аналог электрической цепи, показана на рис.2. Модель состоит из двух компонентов, а именно катушки и статора, каждый из которых действует как тепловая емкость (аналог емкости в электрической цепи) и разделен тепловыми сопротивлениями (аналогично сопротивлению в электрической цепи). В самонесущем змеевике двигателя постоянного тока без сердечника выделяется тепло из-за резистивного нагрева (I ² р потерь). Некоторое количество тепла будет отводиться на нагрев самой самонесущей катушки, что называется теплоемкостью катушки Cth(c), а часть тепла будет рассеиваться на статоре через воздушный зазор. Воздушный зазор можно рассматривать как тепловое сопротивление Rth2 между катушкой и статором. Затем статор начнет нагреваться в зависимости от тепловой емкости статора Cth(s) и отдаст некоторое количество тепла в окружающую среду (аналогично заземлению в электрической цепи). Тепловое сопротивление между статором и окружающей средой обозначается как Rth3. Обратите внимание, что в двигателе есть много других мелких компонентов, таких как щетки, магнит, шариковый подшипник и т. д., изготовленных из разных материалов и имеющих разную массу. Но в этой тепловой модели мы рассмотрели только катушку и статор. В расчетах теплоемкости сделаны подходящие допущения относительно материала и массы, чтобы привести тепловую модель к этой упрощенной форме.

Тепловое сопротивление (Rth) — это единый параметр, объединяющий кумулятивные эффекты различных режимов теплопередачи, а именно. проводимость, конвекция и излучение, которые имеют место для двигателя. Чем выше тепловое сопротивление, тем медленнее теплопередача. Обычно оценивается экспериментально. Со ссылкой на приведенную выше тепловую модель полное тепловое сопротивление двигателя Rth = Rth2 + Rth3.

Теплоемкость или теплоемкость (Cth) – это произведение массы на удельную теплоемкость материала. На рис. 2 у нас есть медный материал для катушки и стальной материал для статора. Чем выше значение теплоемкости, тем больше тепла может аккумулировать тело. В приведенной выше модели статор может аккумулировать больше тепла, и, следовательно, потребуется гораздо больше времени, чтобы насытиться или завершить свою способность аккумулировать тепло.

Тепловое равновесие или установившееся состояние : Пока входная электрическая мощность или электрический ток постоянны, после начального переходного периода нагрева двигателя достигается установившееся состояние или тепловое равновесие, при котором части двигателя достижения соответствующих стабильных температур. В этом состоянии отдельные тепловые емкости заполнены, и будет происходить только рассеивание тепла, а не накопление тепла.

Термический дисбаланс или переходное состояние: Указывает период повышения температуры двигателя, когда активны тепловые емкости.

Тепловая постоянная времени: Нагрев и охлаждение имеют экспоненциальный характер. Термическая постоянная времени — это время, за которое тело достигает ~ 63 % своей установившейся температуры. Он рассчитывается путем умножения Cth и Rth. Статору требуется гораздо больше времени для нагрева, чем катушке, из-за его большей теплоемкости Cth(s) и более высокого теплового сопротивления Rth3, и, следовательно, он имеет сравнительно более высокое значение тепловой постоянной времени. Для катушки тепловая постоянная времени находится в диапазоне от секунд до минут в зависимости от размера двигателя, а для статора она находится в диапазоне от нескольких минут до нескольких минут в зависимости от размера двигателя.

Тепловой предел двигателя: Максимальный непрерывный крутящий момент в непрерывном режиме потребляет максимальный непрерывный ток , который ограничен тепловым пределом двигателя. Превышение максимального продолжительного тока, указанного в каталоге для непрерывной работы, приведет к превышению теплового предела катушки. Таким образом, для непрерывного применения выбор двигателя обычно выполняется таким образом, чтобы крутящий момент приложения составлял 70–80 % от максимального продолжительного крутящего момента, чтобы сохранить запас прочности по тепловому пределу катушки. Температурный предел катушки, как указано в каталогах производителей двигателей без сердечника, обычно составляет около 100 ° C или до 125 ° C. Максимальный непрерывный ток может быть превышен в приложениях с кратковременной работой, за которой следует достаточное «время отключения». что позволит змеевику остыть в течение этого периода и предотвратит превышение теплового предела змеевика. При выборе такого двигателя рекомендуется проконсультироваться с производителями двигателей.

Регулирование двигателя (R/k ² ): Параметр регулирования двигателя R/k ² напрямую связан со способностью двигателя преобразовывать электрическую энергию в механическую. Более низкое значение R/k2 означает лучшее преобразование энергии. Значения R/k ² обычно находятся в одном и том же диапазоне для семейства двигателей и являются очень хорошими индикаторами рабочих характеристик двигателей различных типоразмеров. Чтобы учесть тепловые свойства двигателя, можно сравнить значения R/k ² x Rth, которые отражают способность двигателя преобразовывать электрическую энергию в механическую и рассеивать джоулевые потери для данной работы. Чем ниже значение R/k ² x Rth, тем выше КПД двигателя и лучше рассеивается тепло двигателя. Более высокая эффективность является желательным критическим параметром в некоторых приложениях, таких как устройства с батарейным питанием.

 

Рис. 2. Тепловая модель двигателя постоянного тока без сердечника и ее аналогия с электрической схемой

 

Внимательное рассмотрение этих параметров необходимо для выбора правильного решения для движения постоянным током. Позвоните в Portescap сегодня и поговорите с инженером, который поможет вам оптимизировать двигатель и определить его размеры для ваших нужд. Или отправляйтесь прямо в наш интернет-магазин, чтобы приобрести образец.

 

Охлаждение и обогрев электродвигателя | Постоянная времени нагрева

Геометрия системы охлаждения электродвигателя слишком сложна для точного прогнозирования теплового потока и распределения температуры. Это трудная задача. Часть проводников обмотки якоря заделана в пазы, а часть находится вне стального материала в виде выступа. Расчеты нагрева также усложняются загрузкой двигателя. Направление теплового потока не остается одинаковым при всех нагруженных режимах. На холостом ходу или при небольшой нагрузке тепло передается от железных деталей к обмотке из-за температурного градиента. Когда нагрузка увеличивается, градиент изменяется, так как тепло (потери), генерируемое в обмотке, больше, чем тепло (потери), генерируемое в железе, и, следовательно, тепло переходит от обмотки к железному сердечнику. Поэтому необходимо значительное упрощение для расчета повышения температуры двигателя.

Расчет нагрева и охлаждения электродвигателя основан на следующих упрощениях:

1. Машина считается однородным телом, имеющим равномерный температурный градиент. Все точки, в которых выделяется тепло, имеют одинаковую температуру. Все точки, в которых тепло отводится к охлаждающей среде, также имеют одинаковую температуру.

2. Тепловыделение пропорционально разности температур  тела и окружающей среды. Тепло не излучается.

3. Скорость рассеивания тепла постоянна при всех температурах.

При этих предположениях машина вырабатывает тепло внутри с постоянной скоростью и отдает его в окружающую среду пропорционально повышению температуры. Можно показать, что рост температуры тела происходит по экспоненциальному закону. Предполагая, что выделяемое тепло пропорционально потерям, мы получаем уравнение теплового баланса.

где

Вт – мощность потерь двигателя на нагрев, Вт.

G – масса активных частей двигателя, кг

s – удельная теплоемкость материала корпуса, Дж/град/кг

A – поверхность охлаждения, м ²

4

λ – удельная теплоотдача или коэффициент излучения в Дж/с/м ² /градус разницы температур

θ – превышение температуры тела

dθ – повышение температуры на малом интервале dt

Из уравнения (5.2) следует, что общее тепло, выделяемое в теле (W dt), равно сумме теплоты, рассеиваемой в окружающую среду (Aλθ dt) и тепло, накопленное в теле, вызывающее повышение температуры θ по сравнению с окружающей средой (Gs dθ).

Следующие результаты могут быть получены путем тщательного изучения уравнения. 5.2.

Когда повышение температуры достигает постоянного значения, говорят, что тело достигло максимального повышения температуры θ _м . При достижении этого условия dθ = 0. Вырабатываемое в теле тепло полностью рассеивается в окружающую среду. В теле больше не накапливается тепло, и тело достигает теплового равновесия. Следовательно,

и максимальное повышение температуры

Преобразование уравнения. 5.2 у нас есть

Если бы не было охлаждения электродвигателя, машина бы сильно нагревалась и повышение температуры достигло бы очень высоких значений. Но θ должно быть ограничено θ _м . Время, необходимое машине для достижения этого повышения температуры при отсутствии рассеяния, можно определить с помощью

, что дает линейную зависимость между θ и t. Следовательно,

Если r ₁ – это время, необходимое для достижения θ _м (рис. 5.1). У нас есть

Заменив θ _м из уравнения. 5.4 имеем значение r _1,  время, за которое тело достигает максимального повышения температуры

r ₁ называется тепловой постоянной времени (нагрева) . Другими словами, это время, необходимое двигателю для достижения конечного стационарного повышения температуры, если первоначальная скорость повышения температуры сохраняется.

Уравнение теплового баланса (уравнение 5.2) необходимо решить, чтобы получить зависимость между повышением температуры и временем. Преобразование уравнения. 5.2 имеем

из которых

Интегрируя обе стороны имеем

где log C ₁ — константа интегрирования. Его оценивают, используя начальные условия в начале нагрева. Это уравнение можно записать как

Для простоты предполагается, что машина запускается из холодного состояния. Следовательно, θ = 0, при t = 0.

Подставив C ₁ и переставив члены, мы получим

Используя соотношения уравнений 5.8 и 5.9, мы получим

7 кривую роста температуры. .

Однако при рассмотрении нагрева и охлаждения электродвигателя во многих случаях начальный подъем температуры не равен нулю, т.е. при t = 0, θ = θ ₀ .

Подставляя начальные условия в уравнение. 15.12 имеем

Используя значение C ₁ в уравнении. 5.13.

Переставляя слагаемые, получаем

Кривую отопления можно рассматривать (рис. 5.2) как сумму двух кривых:

1. кривая нагрева, когда машина имеет нагрузку, обеспечивающую максимальное повышение температуры θ _м .

2.кривая охлаждения при отключении машины от сети с начальным повышением температуры θ ₀ .

Постоянная времени нагрева r ₁  : r ₁  в уравнениях 5. 16 и 5.21 называется постоянной времени нагрева . Это видно из уравнения 5.5, что это было бы время, которое потребовалось бы неэффективному или если бы начальная скорость повышения температуры сохранялась, т. е.

Но у машины есть охлаждение, машине требуется больше времени для достижения максимального повышения температуры, и это время больше, чем r ₁  Подставляя t = r ₁  в уравнение, мы видим, что повышение температуры тела составляет 63,2% от θ _м . Следовательно, его можно определить как время, необходимое машине для достижения повышения температуры на 63,2% от максимального повышения температуры. Все они изображены на рис. 5.1,

Значение r ₁ дает представление об эффективности охлаждения. Машины с хорошей вентиляцией имеют меньшие постоянные времени. Постоянные времени открытых машин порядка 25 минут. Полностью закрытые машины имеют плохую вентиляцию.

Постоянную времени нагрева можно определить по экспериментальной кривой, используя определение, что это время, необходимое для достижения 63,2% от θ 90 129 м.  Постоянная времени

Кривая охлаждения

При отключении машины от сети или при снижении нагрузки на двигатель машина охлаждается. В первом случае он охлаждается до температуры окружающей среды, а во втором — до температуры, определяемой потерями мощности при пониженной нагрузке. Кривая охлаждения также является экспоненциальной кривой. Когда машина выключена, в двигателе не выделяется тепло, и все тепло, хранящееся в машине, теперь рассеивается в окружающую среду. В этом уравнении 5.2 уменьшается до

Где r ₂ — постоянная времени при охлаждении. На рис. 5.3 изображена кривая.

Иногда машина не выключается, но нагрузка на нее снижается, и в этом случае она охлаждается до температуры

где W ₁ — общие потери при уменьшенной нагрузке. Кривая охлаждения в этом случае определяется как

, что также может быть записано как

Кривая охлаждения показана на рис. 5.4. Это также можно рассматривать как сумму двух кривых

1. кривая нагрева, как если бы машина была нагружена, чтобы обеспечить максимальное повышение температуры θ _f .

2. кривая охлаждения, как если бы машина была отключена от источника питания, когда ее температура повысилась на θ

м .

r ₂ на кривой охлаждения – постоянная времени охлаждения. Постоянная времени нагрева r ₁ и постоянная времени охлаждения r ₂ не равны в машинах с самоохлаждением. r ₂ в два-три раза больше, чем r ₁ . При прочих равных условиях время, необходимое двигателю для охлаждения до температуры окружающей среды, больше, чем время, необходимое двигателю для нагрева. При принудительном охлаждении r ₂ = r _1, В таких случаях кривая нагрева и кривая охлаждения являются зеркальными отражениями друг друга.

Номинальная мощность двигателя для конкретных условий эксплуатации выбирается на основе теплового номинала двигателя таким образом, чтобы он соответствовал техническим условиям в отношении конечного установившегося повышения температуры, т.