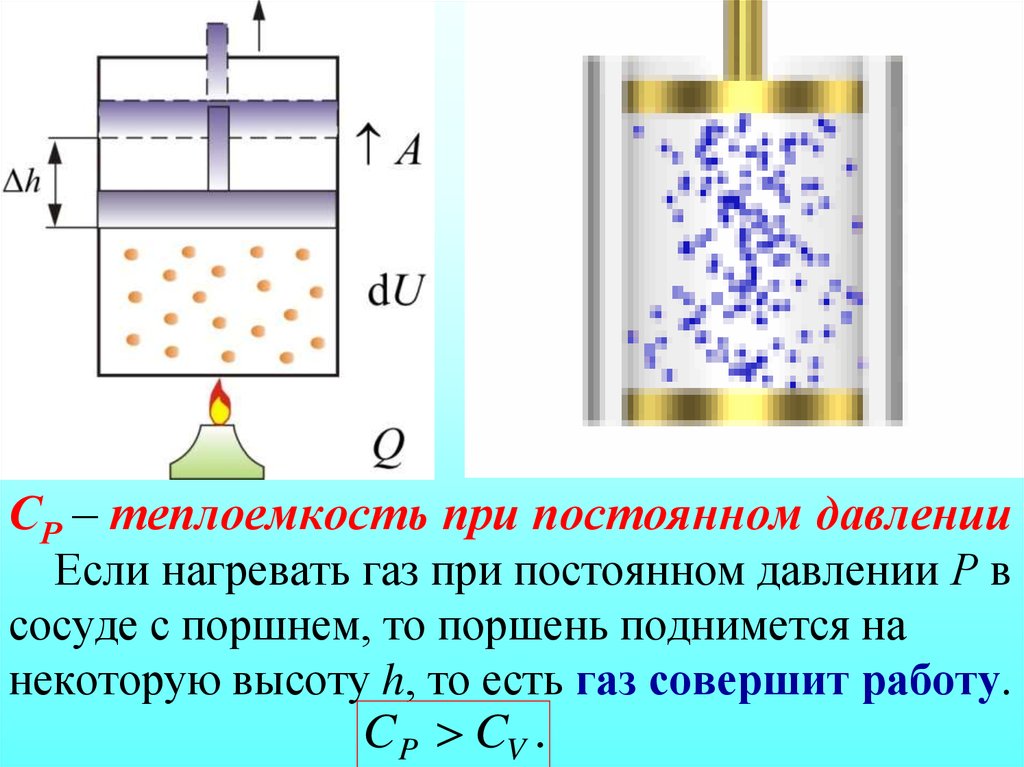
§ 5.6. Теплоемкости газа при постоянном объеме и постоянном давлении
При введении понятия теплоемкости мы не обращали внимание на одно существенное обстоятельство: теплоемкости зависят не только от свойств вещества, но и от процесса, при котором осуществляется теплопередача.
Если нагревать тело при постоянном давлении, то оно будет расширяться и совершать работу. Для нагревания тела на 1 К при постоянном давлении ему нужно передать большее количество теплоты, чем при таком же нагревании при постоянном объеме.
Жидкие и твердые тела расширяются при нагревании незначительно, и их теплоемкости при постоянном объеме и постоянном давлении мало различаются. Но для газов это различие существенно. С помощью первого закона термодинамики можно найти связь между теплоемкостями газа при постоянном объеме и постоянном давлении.
Теплоемкость газа при постоянном объеме Найдем молярную теплоемкость газа при постоянном объеме.
 Согласно определению теплоемкости
Согласно определению теплоемкостигде ΔT — изменение температуры. Если процесс происходит при постоянном объеме, то эту теплоемкость обозначим через
(5.6.1)
При постоянном объеме работа не совершается. Поэтому первый закон термодинамики запишется так:
(5.6.2)
Изменение энергии одного моля достаточно разреженного (идеального) одноатомного газа равно: (см. § 4.8).
Следовательно, молярная теплоемкость при постоянном объеме одноатомного газа равна:
(5.6.3)
Теплоемкость газа при постоянном давлении
Согласно определению теплоемкости при постоянном давлении Ср
(5.6.4)
Работа, которую совершит 1 моль идеального газа, расширяющегося при постоянном давлении, равна:
(5.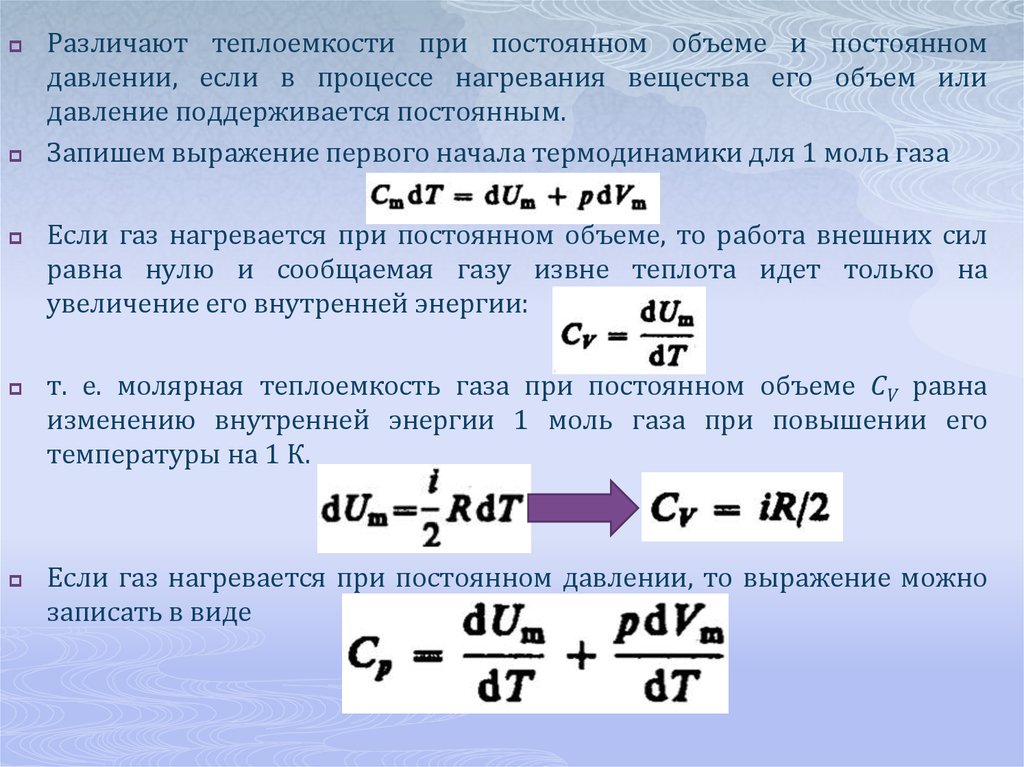 6.5)
6.5)
Это следует из выражения для работы газа при постоянном давлении А’ = pΔV и уравнения состояния (для одного моля) идеального газа pV = RT.
Внутренняя энергия идеального газа от объема не зависит. Поэтому и при постоянном давлении изменение внутренней энергии ΔU = CVΔT, как и при постоянном объеме. Применяя первый закон термодинамики, получим:
(5.6.6)
Следовательно, молярные теплоемкости идеального газа связаны соотношением
(5.6.7)
Впервые эта формула
была получена Р. Майером и носит его
имя.
В случае идеального одноатомного газа
(5.6.8)
Теплоемкость идеального газа при изотермическом процессе
Можно формально ввести понятие теплоемкости и при изотермическом процессе. Так как при этом процессе внутренняя энергия идеального газа не меняется, какое бы количество теплоты ему ни было передано, то теплоемкость бесконечна.
Молярная теплоемкость идеального газа при постоянном давлении больше теплоемкости при постоянном объеме на величину универсальной газовой постоянной R.
§ 5.7. Адиабатный процесс
Мы рассмотрели изотермический, изобарный и изохорный процессы. После ознакомления с первым законом термодинамики появляется возможность изучить еще один процесс, — это процесс, протекающий в системе при отсутствии теплообмена с окружающими телами. (Но работу над окружающими телами система может совершать.)
Процесс в
теплоизолированной системе называют
адиабатным.
При адиабатном процессе Q = 0 и согласно закону (5.5.3) изменение внутренней энергии происходит только за счет совершения работы:
(5.7.1)
Конечно, нельзя окружить систему оболочкой, абсолютно исключающей теплообмен. Но в ряде случаев реальные процессы очень близки к адиабатным. Существуют оболочки, обладающие малой теплопроводностью, например двойные стенки с вакуумом между ними. Так изготовляются термосы.
Процесс можно считать адиабатным даже без теплоизолирующей оболочки, если он происходит достаточно быстро, т. е. так, чтобы за время процесса не происходило заметного теплообмена между системой и окружающими телами.
Согласно выражению (5.7.1) при совершении над системой положительной работы, например при сжатии газа, внутренняя энергия его увеличивается; газ нагревается. Наоборот, при расширении газ сам совершает положительную работу (А’ > 0), но

Зависимость давления газа от его объема при адиабатном процессе изображается кривой, называемой адиабатой (рис. 5.9). Адиабата обязательно идет круче изотермы. Ведь при адиабатном процессе давление газа уменьшается не только за счет увеличения объема, как при изотермическом процессе, но и за счет уменьшения его температуры.
Рис. 5.9
Адиабатные процессы широко используются в технике. Они играют немалую роль в природе.
Нагревание воздуха
при быстром сжатии нашло применение в
двигателях Дизеля. В этих двигателях
отсутствуют системы приготовления и
зажигания горючей смеси, необходимые
для обычных бензиновых двигателей
внутреннего сгорания. В цилиндр
засасывается не горючая смесь, а
атмосферный воздух. К концу такта сжатия
в цилиндр с помощью специальной форсунки
впрыскивается жидкое топливо (рис.
5.10). К этому моменту температура сжатого
воздуха так велика, что горючее
воспламеняется.
Рис. 5.10
Так как в двигателе Дизеля сжимается не горючая смесь, а воздух, то степень сжатия у этого двигателя больше, а значит, коэффициент полезного действия (КПД) двигателей Дизеля выше, чем у обычных двигателей внутреннего сгорания. Кроме того, они могут работать на более дешевом низкосортном топливе. Есть, однако, у двигателя Дизеля и недостатки: необходимость высоких степеней сжатия и большое рабочее давление делают эти двигатели массивными и вследствие этого более инерционными — они медленнее набирают мощность. Двигатели Дизеля более сложны в изготовлении и эксплуатации, тем не менее они постепенно вытесняют обычные бензиновые двигатели, используемые в автомобилях.
Охлаждение газа
при адиабатном расширении происходит
в грандиозных масштабах в атмосфере
Земли. Нагретый воздух поднимается
вверх и расширяется, так как атмосферное
давление падает с высотой. Это расширение
сопровождается значительным охлаждением. В результате водяные пары конденсируются
и образуются облака.
В результате водяные пары конденсируются
и образуются облака.
Задачи по теме «Теплоемкость идеального газа»
Решение задач дело полезное, но не всегда интересное. Чтобы вы справлялись с решением задач по теме «Теплоемкость идеального газа» быстрее, приведем здесь несколько примеров и вопросов с объяснениями.
Подписывайтесь на наш телеграм-канал, чтобы получать полезную и интересную рассылку.
Задачи по теме «Теплоемкость идеального газа» с решениями
Повторение и практика – залог успеха в любом деле. И решение задач не исключение. Поэтому не забываем держать под рукой памятку по задачам и полезные формулы
Задача №1. Определить удельную теплоемкость идеального газа
Условие
Определить молярную массу M двухатомного газа и его удельные теплоемкости, если известно, что разность cр — cv удельных теплоемкостей этого газа равна 260 Дж/(кг*К)
Решение
По определению:
Значит, газ из задачи – кислород.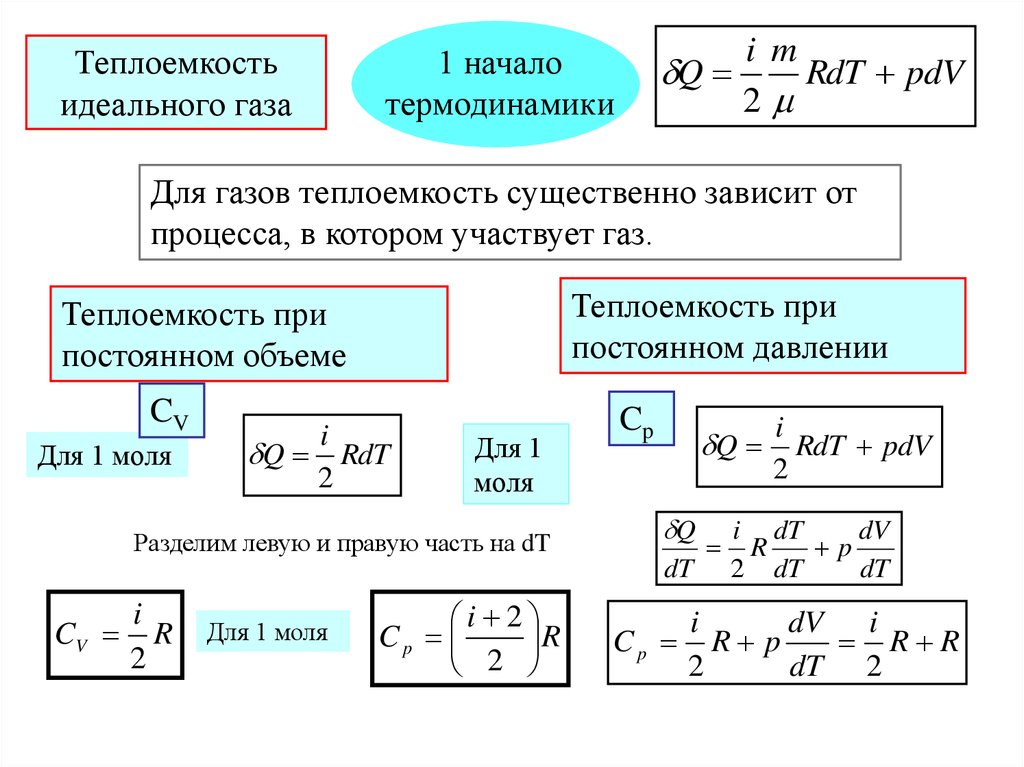
Считаем удельные теплоемкости:
Ответ: 32 г/моль; 649 Дж/кг*К; 909 Дж/кг*К.
Задача №2. Удельная теплоемкость
Условие
Плотность некоторого газа при нормальных условиях ρ = 1,25 кг/м3. Отношение удельных теплоемкостей γ = 1,4. Определить удельные теплоемкости cv и сp этого газа.
Решение
Исходя из отношения удельных теплоемкостей, можно сделать вывод, что газ – двухатомный, i=5. При постоянном объеме удельная теплоемкость равна:
Молярную массу можно найти из уравнения Клапейрона-Менделеева:
Отсюда:
Ответ: 742 Дж/кг*К; 1039 Дж/кг*К.
Задача №3. Молярная теплоемкость
Условие
Вычислить молярные теплоемкости газа, зная, что его молярная масса М = 4∙10 3 кг/моль и отношение удельных теплоемкостей ср/сv = 1,67.
Решение
Удельные теплоемкости равны:
Можно найти:
Ответ: 12,4 Дж/моль*К; 20,71 Дж/моль*К
Задача №4.
 Теплоемкость при изопроцессах
Теплоемкость при изопроцессахУсловие
На рисунке изображен изотермический процесс с газом постоянной массы. Сравните теплоемкость в процессе АВ с теплоемкостью этой же массы газа в изохорном процессе.
Решение
Теплоемкость при изохорном процессе является постоянной величиной. При изотермическом процесса она равна бесконечности. Значит, теплоемкость в процессе АВ больше.
Ответ: Теплоемкость в процессе АВ больше.
Задача №5. Теплоемкость при политропическом процессе
Условие
Найдите молярную теплоемкость идеального газа при политропическом процессе pVn = const, если показатель адиабаты газа равен γ. При каких значениях показателя политропы n теплоемкость газа будет отрицательной?
Решение
Запишем первое начало термодинамики, выражения для работы и изменения внутренней энергии в политропическом процессе соответственно:
Если количество вещества и изменение температуры принять равными единице, это выражение будет равно молярной теплоемкости (по определению теплоемкости):
Ответ: см. выражение выше.
выражение выше.
Вопросы по теме «Теплоемкость идеального газа»
Вопрос 1. Что такое теплоемкость идеального газа?
Ответ. Когда газу сообщается определенное количество теплоты, меняется его температура.
Отношение количества теплоты, сообщенного газу, к изменению его температуры, называется теплоемкостью идеального газа.
Вопрос 2. Что такое молярная и удельная теплоемкость идеального газа?
Ответ. Молярная и удельная теплоемкости активно используются в термодинамике. Молярная теплоемкость – это теплоемкость одного моля вещества.
Удельная теплоемкость – теплоемкость единичной массы вещества.
Вопрос 3. Как определяется теплоемкость газа при изопроцессах?
Ответ.
При изотермическом процессе T=const. Теплоемкость равна плюс/минус бесконечности.
При адиабатном процессе нет теплообмена с окружающей средой, теплоемкость равна нулю.
При изохорном процессе газ не совершает работы, а теплоемкость равна:
Здесь i – количество степеней свободы молекул газа. Для одноатомных газов i=3, для двухатомных i=5.
При изобарном процессе теплоемкость определяется соотношением Мейера:
Вопрос 4. Как еще связаны теплоемкости при постоянном давлении и постоянном объеме?
Ответ. Отношение теплоемкостей при постоянном давлении и постоянном объеме обозначается греческой буквой «гамма» и называется показателем адиабаты.
Вопрос 5. Как называются процессы, в которых теплоемкость газа остается неизменной?
Ответ. Такие процессы называются политропными. Адиабатный процесс – частный случай политропного процесса.
Теплоемкость реального газа не равна теплоемкости идеального газа и может сильно отличаться.
Нужна помощь в решении задач и выполнении других заданий? Специальный студенческий сервис готов оказать ее!
3.
 5 Теплоемкость идеального газа – University Physics Volume 2
5 Теплоемкость идеального газа – University Physics Volume 2Глава 3. Первый закон термодинамики
Цели обучения
К концу этого раздела вы сможете:
- Определить теплоемкость идеального газа для конкретного процесса
- Рассчитайте удельную теплоемкость идеального газа для изобарного или изохорного процесса
- Объясните разницу между теплоемкостью идеального газа и реального газа
- Оценка изменения удельной теплоемкости газа в диапазоне температур
Мы узнали об удельной теплоемкости и молярной теплоемкости в Температуре и Теплоте; однако мы не рассматривали процесс, в котором добавляется тепло. Мы делаем это в этом разделе. Сначала мы исследуем процесс, в котором система имеет постоянный объем, затем сопоставляем его с системой при постоянном давлении и показываем, как связаны их удельные теплоемкости.
Начнем с рисунка 3.12, на котором показаны два судна 9.0023 A и B , каждый из которых содержит 1 моль идеального газа того же типа при температуре T и объеме V . Единственная разница между двумя сосудами заключается в том, что поршень в верхней части A неподвижен, тогда как поршень в верхней части B может свободно двигаться против постоянного внешнего давления p . Теперь рассмотрим, что происходит, когда температура газа в каждом сосуде медленно повышается до [латекс]Т+дТ[/латекс] при добавлении тепла.
Единственная разница между двумя сосудами заключается в том, что поршень в верхней части A неподвижен, тогда как поршень в верхней части B может свободно двигаться против постоянного внешнего давления p . Теперь рассмотрим, что происходит, когда температура газа в каждом сосуде медленно повышается до [латекс]Т+дТ[/латекс] при добавлении тепла.
Поскольку поршень сосуда A зафиксирован, объем заключенного газа не меняется. Следовательно, газ не работает, и мы имеем по первому закону
[латекс] d {E} _ {\ text {int}} = dQ-dW = dQ. [/ латекс]
Тот факт, что теплота обменивается при постоянном объеме, представим, написав
[латекс]dQ={C}_{V}dT,[/латекс]
, где [латекс]{C}_{V}[/латекс] — молярная теплоемкость при постоянном объеме газа. Кроме того, поскольку [latex]d{E}_{\text{int}}=dQ[/latex] для этого конкретного процесса,
Кроме того, поскольку [latex]d{E}_{\text{int}}=dQ[/latex] для этого конкретного процесса,
[латекс] d {E} _ {\ text {int}} = {C} _ {V} dT. [/latex]
Мы получили это уравнение, предполагая, что объем газа фиксирован. Однако внутренняя энергия — это функция состояния, зависящая только от температуры идеального газа. Следовательно, [latex]d{E}_{\text{int}}={C}_{V}dT[/latex] дает изменение внутренней энергии идеального газа для любого процесса, связанного с изменением температуры дТ .
Когда газ в сосуде B нагревается, он расширяется против подвижного поршня и совершает работу [латекс]dW=pdV.[/латекс] В этом случае тепло добавляется при постоянном давлении, и мы пишем
[латекс]dQ={C}_{p}dT,[/латекс]
, где [латекс]{C}_{p}[/латекс] — молярная теплоемкость газа при постоянном давлении . Кроме того, поскольку идеальный газ расширяется против постоянного давления,
[латекс]d\левый(pV\правый)=d\левый(RT\правый)[/латекс]
становится
[латекс]pdV=RdT. [/латекс]
[/латекс]
Наконец, подставляя выражения для dQ и pdV в первый закон, получаем
[латекс]d{E}_{\text{int}}=dQ-pdV=\left({C}_{p}-R\right)dT.[/latex]
Мы нашли [латекс]d{E}_{\text{int}}[/latex] как для изохорного, так и для изобарического процесса. Поскольку внутренняя энергия идеального газа зависит только от температуры, [latex]d{E}_{\text{int}}[/latex] должен быть одинаковым для обоих процессов. Таким образом,
[латекс] {C}_{V}dT=\left({C}_{p}-R\right)dT,[/latex]
и
[латекс]{C}_{p}={C}_{V}+R.[/латекс]
Вывод уравнения 3.10 был основан только на законе идеального газа. Следовательно, это соотношение приблизительно справедливо для всех разбавленных газов, будь то одноатомные, такие как He, двухатомные, такие как [латекс] {\ text {O}} _ {2}, [/ латекс], или многоатомные, такие как [латекс] {\ текст {CO} }_{2}{\phantom{\rule{0.2em}{0ex}}\text{или NH}}_{3}\text{.}[/latex]
В предыдущей главе мы нашли, что молярная теплоемкость идеального газа при постоянном объеме равна
[латекс]{C}_{V}=\frac{d}{2}R,[/латекс]
, где d — число степеней свободы молекулы в системе. В таблице 3.3 показаны молярные теплоемкости некоторых разбавленных идеальных газов при комнатной температуре. Теплоемкости реальных газов несколько выше, чем те, которые предсказываются выражениями [латекс]{C}_{V}[/латекс] и [латекс]{С}_{р}[/латекс], приведенными в уравнении 3.10. Это указывает на то, что колебательное движение в многоатомных молекулах существенно даже при комнатной температуре. Тем не менее разница в молярных теплоемкостях, [латекс]{C}_{p}-{C}_{V},[/latex] очень близка к R даже для многоатомных газов.
В таблице 3.3 показаны молярные теплоемкости некоторых разбавленных идеальных газов при комнатной температуре. Теплоемкости реальных газов несколько выше, чем те, которые предсказываются выражениями [латекс]{C}_{V}[/латекс] и [латекс]{С}_{р}[/латекс], приведенными в уравнении 3.10. Это указывает на то, что колебательное движение в многоатомных молекулах существенно даже при комнатной температуре. Тем не менее разница в молярных теплоемкостях, [латекс]{C}_{p}-{C}_{V},[/latex] очень близка к R даже для многоатомных газов.
| Молярная теплоемкость разбавленных идеальных газов при комнатной температуре | ||||
|---|---|---|---|---|
| Тип молекулы | Газ | [латекс]{C}_{p}[/латекс] (Дж/моль К) | [латекс]{C}_{V}[/латекс] (Дж/моль К) | [латекс]{C}_{p}-{C}_{V}[/латекс] (Дж/моль К) |
| Одноатомный | Идеал | [латекс]\фракция{5}{2}R=20,79[/латекс] | [латекс]\фракция{3}{2}R=12,47[/латекс] | [латекс]R=8,31[/латекс] |
| Двухатомный | Идеал | [латекс]\frac{7}{2}R=29,10[/латекс] | [латекс]\фракция{5}{2}R=20,79[/латекс] | [латекс]R=8,31[/латекс] |
| Многоатомный | Идеал | [латекс]4R=33,26[/латекс] | [латекс]3R=24,94[/латекс] | [латекс]R=8,31[/латекс] |
Резюме
- Для идеального газа молярная емкость при постоянном давлении [латекс]{C}_{p}[/латекс] определяется выражением [латекс]{C}_{p}={C}_{V}+R =dR\text{/}2+R[/latex], где d — количество степеней свободы каждой молекулы/объекта в системе.

- У реального газа удельная теплоемкость близка, но немного выше, чем у соответствующего идеального газа с [латексом]{C}_{p}\simeq {C}_{V}+R.[/latex]
Концептуальные вопросы
Как объект может передавать тепло, если объект не обладает дискретным количеством тепла?
Большинство материалов расширяются при нагревании. Одним заметным исключением является вода между [латексом]0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] и [латексом]4\phantom{\rule{0.2em }{0ex}}\text{°}\text{C,}[/latex], объем которого фактически уменьшается с повышением температуры. Что лучше для воды в этом температурном диапазоне, [латекс]{C}_{p}[/латекс] или [латекс]{C}_{V}[/латекс]?
Показать решение Обычно [латекс]{C}_{p}[/латекс] больше, чем [латекс]{C}_{V}[/латекс], потому что, когда расширение происходит под постоянным давлением, оно работает на окрестности. Следовательно, теплота может переходить во внутреннюю энергию и совершать работу. При постоянном объеме все тепло переходит во внутреннюю энергию. В этом примере вода сжимается при нагревании, поэтому, если мы добавляем тепло при постоянном давлении, работа над водой выполняется окружающей средой, и, следовательно, [латекс]{С}_{р}[/латекс] меньше, чем [латекс]{ C}_{V}[/латекс].
В этом примере вода сжимается при нагревании, поэтому, если мы добавляем тепло при постоянном давлении, работа над водой выполняется окружающей средой, и, следовательно, [латекс]{С}_{р}[/латекс] меньше, чем [латекс]{ C}_{V}[/латекс].
Почему для газов [латекс]{C}_{p}[/латекс] и [латекс]{C}_{V}[/латекс] указаны две удельные теплоемкости, а для твердого тела – только одна?
Задачи
Температура идеального одноатомного газа повышается на 8,0 К. Как изменится внутренняя энергия 1 моль газа при постоянном объеме?
Показать раствор100 Дж
При повышении температуры на [латекс]10\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] при постоянном объеме, какое количество тепла поглощается (a) 3,0 моль разбавленного одноатомного газа; б) 0,50 моль разбавленного двухатомного газа; в) 15 моль разбавленного многоатомного газа?
Если газы из предыдущей задачи изначально имеют температуру 300 К, какова их внутренняя энергия после того, как они поглотят тепло?
Показать решение а. 370 Дж; б. 100 Дж; в. 500 Дж
370 Дж; б. 100 Дж; в. 500 Дж
Рассмотрим 0,40 моль разбавленного углекислого газа при давлении 0,50 атм и объеме 50 л. Какова внутренняя энергия газа?
Когда 400 Дж тепла медленно добавляют к 10 молям идеального одноатомного газа, его температура повышается на [латекс]10\phantom{\rule{0.2em}{0ex}}\text{°}\text{C} [/латекс]. Какую работу совершил газ?
Показать раствор850 Дж
Один моль разбавленного двухатомного газа, занимающий объем 10,00 л, расширяется при постоянном давлении 2000 атм при медленном нагревании. Если температура газа повышается на 10,00 К и при этом выделяется 400,0 Дж теплоты, каков его конечный объем?
Глоссарий
- молярная теплоемкость при постоянном давлении
- количественно определяет отношение количества подведенного тепла к температуре при измерении при постоянном давлении
- молярная теплоемкость при постоянном объеме
- количественно определяет отношение количества подведенного тепла к температуре при измерении при постоянном объеме
Теплоемкость идеального газа. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/3-5-heat-capacities-of-an-ideal-gas. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу https://openstax.org/books/university-physics-volume-2/pages/1-introduction
Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/3-5-heat-capacities-of-an-ideal-gas. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу https://openstax.org/books/university-physics-volume-2/pages/1-introduction

 Для ученого «конкретная» переменная состояния означает значение переменной
разделить на массу вещества. Это позволяет нам установить отношения между
переменных без учета количества вещества, которое у нас есть. Мы можем
умножьте конкретную переменную на количество вещества в любой момент времени
для определения фактического значения переменной потока.
Из наших исследований
теплопередача,
мы знаем, что количество теплоты, переданное между двумя телами, равно
пропорционально
температура
разница между предметами и
теплоемкость объектов. теплоемкость это
постоянная, показывающая, сколько тепла добавляется на единицу повышения температуры.
Значение константы различно для разных материалов и зависит
на процессе. Теплоемкость не является переменной состояния .
Для ученого «конкретная» переменная состояния означает значение переменной
разделить на массу вещества. Это позволяет нам установить отношения между
переменных без учета количества вещества, которое у нас есть. Мы можем
умножьте конкретную переменную на количество вещества в любой момент времени
для определения фактического значения переменной потока.
Из наших исследований
теплопередача,
мы знаем, что количество теплоты, переданное между двумя телами, равно
пропорционально
температура
разница между предметами и
теплоемкость объектов. теплоемкость это
постоянная, показывающая, сколько тепла добавляется на единицу повышения температуры.
Значение константы различно для разных материалов и зависит
на процессе. Теплоемкость не является переменной состояния . В ходе процесса значения этих переменных изменяются. Обозначим
изменение греческой буквы дельта , которая выглядит как треугольник.
Таким образом, «дельта h» означает изменение «h» из состояния 1 в состояние 2 во время процесса.
Затем для процесса постоянного давления уравнение энтальпии становится:
В ходе процесса значения этих переменных изменяются. Обозначим
изменение греческой буквы дельта , которая выглядит как треугольник.
Таким образом, «дельта h» означает изменение «h» из состояния 1 в состояние 2 во время процесса.
Затем для процесса постоянного давления уравнение энтальпии становится: Газовая постоянная, используемая
аэродинамики выводится из универсальной газовой постоянной, но имеет уникальное значение
для каждого газа.
Газовая постоянная, используемая
аэродинамики выводится из универсальной газовой постоянной, но имеет уникальное значение
для каждого газа. Мы добавили индекс «v» к удельной теплоемкости, чтобы напомнить нам, что это значение
относится только к процессу с постоянным объемом.
Несмотря на то, что изменение температуры для этого процесса одинаково и постоянная
процесс давления, значение удельной теплоемкости различно.
Мы добавили индекс «v» к удельной теплоемкости, чтобы напомнить нам, что это значение
относится только к процессу с постоянным объемом.
Несмотря на то, что изменение температуры для этого процесса одинаково и постоянная
процесс давления, значение удельной теплоемкости различно.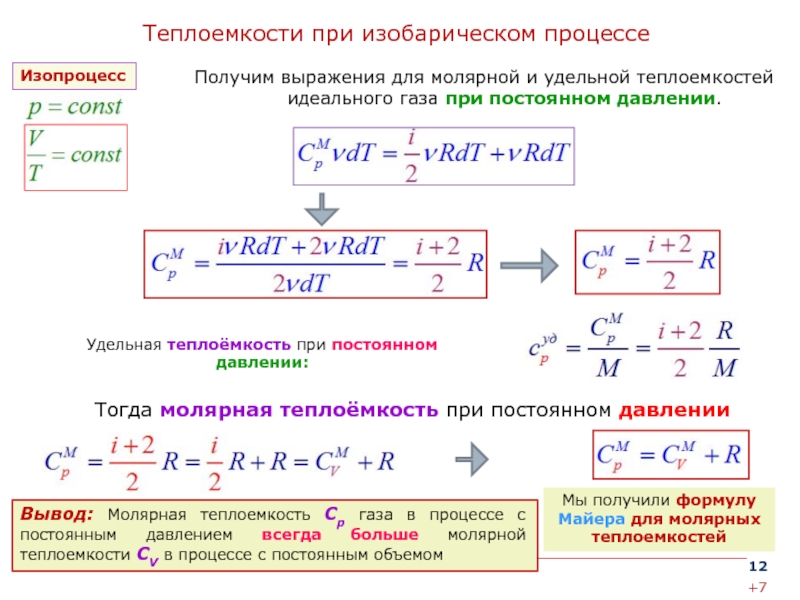 Этот весьма примечательный результат
был получен из термодинамических соотношений, которые основаны на наблюдениях
физических систем и процессов. Используя
кинетическая теория
газов, тот же результат можно получить
из соображений сохранения энергии на молекулярном уровне.
Этот весьма примечательный результат
был получен из термодинамических соотношений, которые основаны на наблюдениях
физических систем и процессов. Используя
кинетическая теория
газов, тот же результат можно получить
из соображений сохранения энергии на молекулярном уровне.