6.9 Тормозные силы поезда
Искусственно создаваемые силы, приложенные к поезду и направленные против его движения, называются тормозными. Они управляются машинистом локомотива.
На Российских железных дорогах существует два основных способа торможения подвижного состава. Первый из них — это фрикционное автоматическое торможение с использованием силы трения, возникающей при воздействии тормозных колодок на поверхности катания колес (рис. 6.29) или на тормозные диски. При втором способе применяется электрическое торможение (реостатное или рекуперативное).
При колодочном тормозе тормозная сила зависит от коэффициента трения между колодками и поверхностями катания колес, от силы нажатия колодок и от числа тормозных осей в поезде.
Возникающая при торможении сила трения Вк равна Kφk и создает тормозной момент МТ = KφkR, где φк — коэффициент трения между колесом и колодкой, К— сила нажатия колодки, тс, R — радиус колеса.
Под воздействием момента М в точке О возникает сила В, стремящаяся сдвинуть рельс.
Тормозной момент Мт при вращении колеса уравновешивается моментом Вг • R, где Вт — сила реакции, возникающая в точке О касания колеса с рельсом. Точка О нагружена силой Q, то есть частью веса экипажа, приходящейся на колесо с учетом веса самого колеса. Из равенства моментов сил Вк и Вт следует, что сила Вт является тормозной силой экипажа, приложенной в точке О, которая является непрерывно перемещающимся упором для силы Вк при вращении колеса.
Расчетная тормозная сила всего поезда определяется как сумма тормозных сил, создаваемых всеми тормозными колодками.
Вт = φкр∑Kр, где φкр — расчетный коэффициент трения, а ∑Кр — суммарная расчетная сила нажатия колодок поезда. Для каждого типа подвижного состава значения Кp приведены в ПТР. Коэффициент φкр определяется по формулам в зависимости от типа колодок и скорости движения. Так для чугунных тормозных колодок расчетный коэффициент трения определяется по формуле
где v — скорость поезда в км/ч.
Время торможения отсчитывается от момента поворота ручки крана машиниста в тормозное положение до полной остановки поезда.
Путь, который проходит поезд за это время, называется тормозным путем ST. Он определяется как сумма двух составляющих — пути подготовки тормозов к действию 5 и действительного тормозного пути S :
Путь подготовки — это расстояние, проходимое поездом с момента поворота ручки крана машиниста до момента достижения расчетной силы нажатия:
где vн — начальная скорость поезда; tп — время подготовки тормозов к действию, которое принимается в зависимости от типа тормозов и длины состава, tп = 2 — 10 с.
Многие задачи, связанные с движением поезда, решаются с помощью уравнения движения поезда. Оно выражает зависимость ускорения поезда от действующих на него сил. Рассматривая движение тормозящегося поезда, как движение материальной точки, имеющей массу поезда, можно уравнение движения поезда получить из второго закона Ньютона (сила равна произведению массы на ускорение):
После ряда преобразований получается следующая формула для определения величины действительного тормозного пути:
где bт — удельная тормозная сила.
Тормозные силы и торможение поездов
Страница 1 из 5
Системы торможения
Общие сведения.
Трогание с места и разгон поезда до заданной скорости машинист осуществляет, используя тяговый режим работы локомотива. Динамика движения поезда по перегону, в основном, определяется планом и профилем пути, т.е. действием неуправляемых сил основного и дополнительных сопротивлений движению. В случаях необходимости остановки поезда на перегоне вне графика движения или поддержания допустимой скорости движения на спусках машинист должен иметь в своем распоряжении искусственно создаваемые силы, направленные против движения.
При тормозном режиме кинетическая энергия движущегося поезда за короткое время преобразуется в работу тормозных средств.
Мощность тормозных средств в отличие от касательной мощности (силы тяги) локомотивов, реализуемой при взаимодействии колес с рельсами, теоретически не ограничена по величине.В общем случае мощность (энергия) тормозных средств должна быть не менее или равна энергии движущегося поезда.
Для остановки поезда, оборудованного тормозными средствами и двигающегося по уклону крутизной i = const с разностью высот ∆Н =Нн-Нк со скоростью V, на ограниченном по величине тормозном пути ST должно быть выполнено условие
(4-1)
где Βт ср — средняя тормозная сила в диапазоне скоростей V-0; WT cp — среднее общее сопротивление движению в диапазоне скоростей F-0; ST — тормозной путь.
Тем самым обеспечивается остановка поезда любого веса в пределах фиксированного тормозного пути.Характер изменения зависимости Вт =f( V) и величина тормозной силы Вт в первую очередь зависят от применяемой на подвижном составе системы торможения.
Классификация систем торможения. На подвижном составе Российских железных дорог в разной степени применяют три основные системы торможения (рис. 1): механические, электрические и гидродинамические.
Рис. 1. Классификация систем торможения подвижного состава
В механических системах торможения тормозная сила создается за счет механического фрикционного трения. Кинетическая энергия движущегося поезда в таких системах преобразуется в механическую работу сил трения, которая расходуется на истирание и нагревание трущихся при торможении поверхностей.
В свою очередь электрические системы торможения подразделяются (см. рис. 1) на электродинамические и электромагнитные рельсовые.
В электродинамических системах тормозная сила создается за счет свойства обратимости тяговых электродвигателей (ТЭД) постоянного тока локомотивов в генераторы.
Кинетическая энергия поезда в этих системах преобразуется в электрический ток, вырабатываемый ТЭД, который поглощается в тормозных резисторах (реостатах) локомотивов и рассеивается в виде тепла в окружающую среду или рекуперируется (возвращается) в контактную сеть при электрической тяге. Сочетание рекуперативного и реостатного торможения э.п.с. можно отнести к комбинированным (рекуперативно-реостатным) системам электродинамического торможения э.п.с.
В гидродинамических системах тормозная сила создается за счет взаимодействия лопастных колес гидротрансформаторов обратного ход а и тормозных гидромуфт с рабочей жидкостью.
Рис. 2. Схема рельсового тормоза
Кинетическая энергия поезда в таких системах преобразуется в тепловую энергию рабочей жидкости гидродинамической передачи локомотивов, отводимую в холодильниках.
Помимо вышеназванных систем торможения для поездов с магнитным подвешиванием и линейным двигателем для тяги разрабатываются электромагнитные системы торможения. В таких системах тормозная сила создается за счет взаимодействия магнитных потоков движущегося поезда и неподвижного пути. Поезда с магнитным подвешиванием относят к высокоскоростному наземному транспорту, предназначенному для движения со скоростями до 400 км/ч.
Из всех систем торможения наиболее надежным и эффективным для железнодорожного транспорта является механическое торможение, которое позволяет использовать для создания тормозной силы все без исключения единицы подвижного состава. Электрические и гидродинамические системы торможения применимы лишь на локомотивах. Величина тормозной силы в этих системах ограничена мощностью силовой установки локомотива, и такие тормоза используют при движении как вспомогательные.
Механическое торможение.
В зависимости от способа создания тормозной силы различают следующие системы механического фрикционного торможения (см.
рис. 1): колесно-колодочные, барабанные и дисковые.
Рис. 3. Схемы колесно-колодочного тормоза: а — одностороннего действия; б — двухстороннего нажатия
При колесно-колодочном торможении тормозная сила создается за счет радиального нажатия тормозных колодок на колеса подвижного состава. Механическое воздействие тормозных колодок на колесные пары сопровождается фрикционным износом поверхности кругов катания колес и самих колодок. Нажатие тормозных колодок на колесные пары может быть как одностороннее (рис. 3, а), так и двухстороннее (рис. 3, б). Колесно-колодочная система торможения является основной на железнодорожном транспорте страны, в этой связи особенности ее работы и расчетов будут рассмотрены более подробно.
В раде конструкций транспортных средств тормозной барабан закрепляют на колесном центре колесной пары (рис. 4, б, в). Тормозные колодки прижимаются к барабану снаружи (рис. 4, а, 6) или изнутри (рис. 4, в), обеспечивая создание тормозной силы.Рис. 4. Схемы барабанного тормоза: а — барабан размещен на оси; б — барабан прикреплен к колесному центру; в — внутреннее нажатие тормозных колодок
Барабанные тормоза более эффективны в эксплуатации, чем колесно-колодочная система торможения, т.к. увеличивается общая площадь прижатия тормозных колодок к колесной паре; поверхности профиля колес не подвержены термическому воздействию и износу от действия тормозных колодок, что в итоге позволяет увеличить межремонтный пробег колесных пар и экипажной части локомотивов в целом.
В настоящее время барабанные тормоза применяют на трамвайных моторных вагонах новых типов.Дисковые тормоза (рис. 5) работают следующим образом. На внешней, а в ряде конструкций локомотивов и на внутренней стороне колесного центра прикрепляют тормозные диски. Специальные тормозные накладки, перемещаясь под действием рычажной передачи в осевом поперечном направлении, прижимаются к тормозным дискам и создают силу трения и тормозной момент Мт, величина которого несколько меньше, чем при колесно-колодочном торможении, т.к. диаметр тормозного диска меньше диаметра колеса колесной пары dT<DK.
Рис. 5. Схема дискового тормоза
Тормозные накладки изготавливают из фрикционных композиционных материалов, в состав которых входят эбонит, бакелит, асбестовые и другие материалы, что в итоге позволяет повысить эффективность торможения подвижным составом. Тормозные диски изготавливают из серого чугуна. Так как тормозные диски и накладки при торможении подвержены серьезному термическому воздействию, к материалам, из которых они изготовлены, предъявляют особые требования в отношении теплоустойчивости и термоусталости.
Дисковые тормоза установлены на высокоскоростном поезде ЭР200. Накопленный опыт эксплуатации ЭР200 показал высокую эффективность применения дисковой системы торможения в зоне высоких скоростей движения 120 — 200 км/ч. В среднем для диапазона 120 — 200 км/ч тормозной эффект дисковых тормозов оказался выше на 30 % по сравнению с колесно-колодочным торможением поезда. В диапазоне скоростей движения до 120 км/ч эффективность дисковых и колесно-колодочных тормозов оказалась одинаковой.
Применение дисковых тормозов позволяет уменьшить износ колесных пар и увеличить межремонтный пробег локомотивов между ТО-4. К недостаткам дисковых тормозов следует отнести: резкое падение силы нажатия тормозных накладок и тормозной силы поезда при износе деталей рычажной передачи, снижение эксплуатационной надежности работы буксовых и иных узлов экипажной части локомотивов из-за воздействия дополнительных боковых усилий от тормозных накладок на колесные пары; необходимость постоянного контроля за техническим состоянием рычажной передачи тормоза и ряд других.
Системы механического торможения классифицируют также (см. рис. 1) по типу привода тормозных средств; при этом различают: пневматические, электропневматические, ручные и гидравлические.
В пневматических системах механического торможения при снижении давления воздуха в тормозной магистрали поезда воздух из запасных резервуаров поступает в тормозные цилиндры; последние приводят в действие рычажную тормозную передачу, которая прижимает тормозные колодки к бандажам. Таким образом, рабочим телом в пневматических тормозах является воздух, предварительно сжатый компрессором локомотива. Этот тип привода, благодаря высокой эксплуатационной надежности, в настоящее время является основным на подвижном составе железных дорог РФ.
В электропневматических системах торможения управление работой тормозов осуществляется с помощью электрического тока. В таких системах применяют специальные воздухораспределители с электрическим управлением. Электровоздухораспределители изменяют давление сжатого воздуха в тормозных цилиндрах и поддерживают его в заданных пределах в соответствии с командами — электрическими сигналами, поступающими с пульта управления работой локомотива.
Электропневматическими системами торможения оборудуются локомотивы, дизель- и электропоезда, рельсовые автобусы, пассажирские вагоны. Такие системы являются вспомогательными, в случае отказа машинист использует основной пневматический тормоз.
Ручными тормозами оборудованы все локомотивы, дизель- и электропоезда, рельсовые автобусы, пассажирские вагоны и часть грузовых вагонов с тормозными площадками. Применяют этот вид тормоза на стоянках для удержания подвижного состава на месте. В ручных тормозах усилие руки человека от маховика тормоза передается на тормозные колодки через продольные тяги, соединенные с главным рычагом рычажной передачи тормоза единицы подвижного состава.
В гидравлическом приводе тормозов исполнительным органом, обеспечивающим прижатие тормозных колодок или накладок к колесу, является гидроцилиндр, заполненный тормозной жидкостью. В связи с тем, что жидкость практически несжимаема, гидравлическая система привода тормозных средств более компактна, чем пневмопривод.
Гидропривод тормозных средств широко применяется на автотранспорте и ряде других видов транспорта. На локомотивах и вагонах этот тип привода тормозных средств применения не получил из-за недостаточной эксплуатационной надежности и ряда других проблем. Например, как решить проблему пополнения жидкостью тормозной магистрали поезда при вполне возможных ее утечках в процессе эксплуатации? При пневматической системе привода эта проблема легко решается с помощью тормозного компрессора локомотива. Существуют и другие проблемы, ограничивающие сферу применения гидропривода тормозов на транспортных средствах.
Как проверить тормозную систему? — Автокомплекс Двойка :: Ремонт, обслуживание, техосмотр автомобилей в Бийске
Тормозной стенд «Маха» позволяет быстро и точно проверить эффективность работы тормозной системы автомобиля
Как работает тормозной стенд?
Тормозной стенд определяет усилия тормозной системы и их эффективность, а также разницу усилий тормозной системы между правым и левым колесом.
Основу конструкции тормозного стенда составляют специальные ролики. Ролики имеют специальное покрытие, которое максимально точно имитирует сцепление колеса автомобиля с дорожным полотном.
Ролики стенда соединяются с датчиками, которые и производят измерения. В дальнейшем, все результаты измерения обрабатываются компьютером, сопоставляются с нормативными значениями, выводятся в виде графической информации на мониторе и в печатном виде.
Что показывает стенд, в каких единицах, откуда берутся нормативные значения?
Стенд рассчитывает удельную тормозную силу автомобиля в соответствии с государственным стандартом РФ (ГОСТ Р 51709—2001. Требования безопасности к техническому состоянию и методы проверки), которая, согласно ГОСТу, должна быть не менее 0,59:
|
Таблица — Нормативы эффективности торможения АТС рабочей тормозной системой при проверках на стендах. |
|||
|
АТС |
Категория АТС |
Усилие на органе управления РП , Н, не более |
Удельная тормозная сила γТ, не менее |
|
Пассажирские и грузопассажирские |
Ml |
490 |
0,59 |
|
М2, МЗ |
686 |
0,51 |
|
|
Грузовые автомобили |
N1, N2, N3 |
686 |
0,51 |
Как рассчитывается удельная тормозная сила автомобиля?
Удельная тормозная сила (гамма т) определяется по формуле: как сумма тормозных сил всех колес автомобиля (Рт) в ньютонах, деленное на произведение массы автомобиля (М) на ускорение свободного падения (g).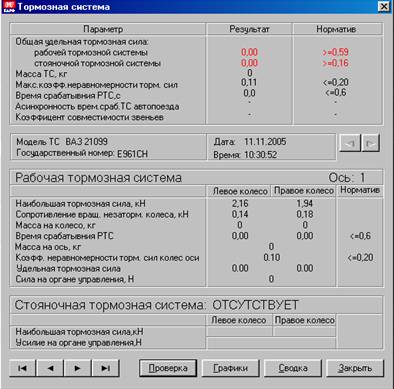
Гамма т – удельная тормозная сила
Сумма Pт — сумма максимальных тормозных сил на колесах автотранспортного средства, H;
M — полная масса автотранспортного средства, кг;
g — ускорение свободного падения, м/с2.
Итак, рассмотрим изложенное выше на конкретном примере:
В Автокомплесе «Двойка» после проверки тормозных усилий на стенде вы получаете распечатку с результатами измерений, в которых указаны значения:
|
Контроль тормозов |
Тормозная сила слева |
Тормозная сила справа |
Разность |
|
Передняя ось |
2,29 кН |
1,47 кН |
36% |
|
Задняя ось |
1,05 кН |
1,00 кН |
14% |
Вычисляем значения по указанной выше формуле:
Получаем значение удельной тормозной силы – 0,46.
Согласно государственному стандарту РФ (ГОСТ Р 51709-2001 п. 4.1) – Удельная тормозная сила автомобиля должна быть не менее 0,59, следовательно, тормозная система данного автомобиля неисправна.
Каковы допустимые значения разности тормозных сил?
При разности тормозных сил на колесах неизбежно отклонение автомобиля от прямолинейного движения при торможении.
Согласно «Правилам проведения технического осмотра транспортных средств, №1008 от 05.12.2011: «При проверках на стендах допускается относительная разность тормозных сил колес оси (в процентах от наибольшего значения) для осей транспортного средства с дисковыми колесными тормозными механизмами не более 20% и для осей с барабанными колесными тормозными механизмами не более 25%»
Таким образом, разность тормозных сил передней оси автомобиля составляет 36% вместо 20%, что так же свидетельствует о неисправности.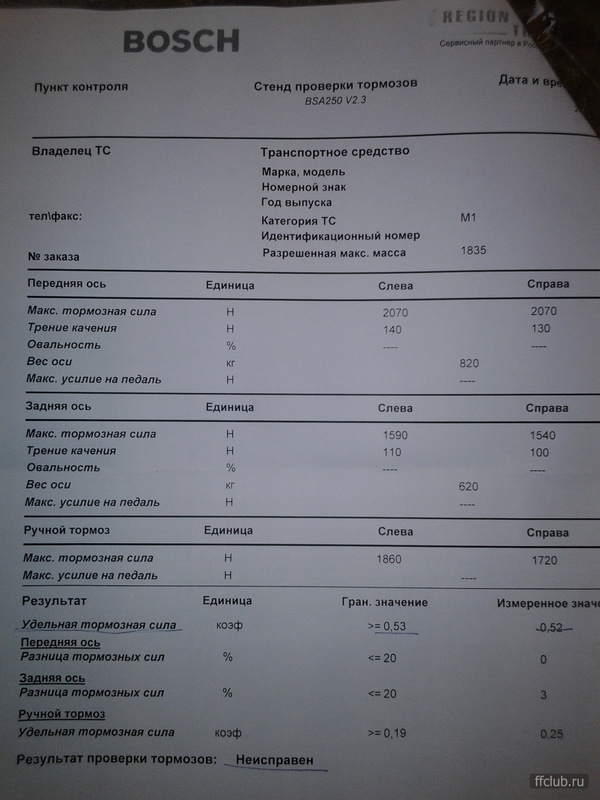
Итак, на стенде мы получили данные о состоянии тормозной системы автомобиля. Приступаем к поиску неисправностей.
Разность тормозных сил на передней оси. Смотрим возможные причины:
- Износ, повреждение или загрязнение тормозных колодок с одной стороны;
- Деформация, задиры на поверхности тормозного диска;
- Ослабление крепления, деформация суппорта;
- Заедание поршня рабочего цилиндра;
- Утечка тормозной жидкости в рабочем цилиндре;
- Повреждение тормозного шланга, тормозных трубок;
Большое усилие на педаль при торможении задней оси (850 Ньютонов, вместо максимально положенных 490). Смотрим возможные причины:
- Неисправности вакуумного усилителя тормозов;
- Износ или загрязнение тормозных колодок;
- Заедание поршня рабочего цилиндра
Кроме того, тормозной стенд измеряет сопротивление вращения колес передней и задней оси.
Если сопротивление велико, смотрим возможные причины:
- Заедание (заклинивание) поршня рабочего цилиндра;
- Деформация суппорта
- Износ ступичных подшипников колес
Также диагностируем ход педали тормоза. Большой ход педали свидетельствует о подсосе воздуха, износе тормозных колодок. Снижение усилия на педали (медленный провал педали) при торможении говорит о возможном повреждении шлангов, трубопроводов или о неисправности главного тормозного цилиндра.
Так или иначе, даже если стенд показал, что тормозная система автомобиля исправна, то независимо от этого проводим тщательный ее осмотр в рамах комплексной диагностики. Лучше перепроверить.
ОСНОВЫ ТЕОРИИ ТОРМОЖЕНИЯОбразование тормозной силыРассмотрим силовые процессы, происходящие после прижатия колодки к катящемуся колесу. Однако под действием внутренней силы Т колесо начинает «цепляться» за рельс в точке контакта О1. Возникает сила сцепления колеса с рельсом В, равная по величине силе Т. Сила В стремится утащить рельс за собой (сдвинуть его по ходу движения поезда). Так как рельс прикреплен к шпалам, то он остается неподвижным (в путевом хозяйстве хорошо известно явление угона рельсов под действием сил сцепления В). Коэффициент трения тормозных колодокСила трения Т между колесом и колодкой оказывается в несколько раз меньше силы К нажатия колодки на колесо. Отношение φк в механике называется «коэффициент трения» и обозначается в тормозных расчетах φк. Зависимость действиетльного коэффициента трения Затем по полученным результатам выводят эмпирическую (опытную) формулу. Эти формулы утверждены МПС для дальнейшего использования при всех практических расчетах. Например, формула (1.1) применяется для расчета действительных коэффициентов трения композиционных колодок, а формула (1.2) — для чугунных. Основными факторами, влияющими на величину коэффициентов трения, являются скорость движения, удельная сила нажатия колодки на колесо и материал колодки. Из графикаи приведенных выше формул видно, что с уменьшением скорости коэффициент трения увеличивается. Машинистам это хорошо известно практически: по мере уменьшения скорости ощущается усиление тормозного эффекта (замедление поезда), особенно при чугунных колодках. С увеличением силы нажатия К коэффициент трения снижается, но это не значит, что с ростом К сила трения Т уменьшается — она увеличивается, но не пропорционально К. Коэффициент сцепленияКачение колеса по рельсу без проскальзывания происходит за счет силы сцепления Вс , действующей со стороны рельса на колесо в точке их контакта. Сцепление колес с рельсами представляет сложный процесс, при котором происходит преодоление механического зацепления микронеровностей поверхностей колеса и рельса и их молекулярного притяжения. Условие безъюзового торможенияЯвление, когда колесо прекращает свое вращение и начинает скользить по рельсу при продолжающемся движении поезда, называется заклиниванием или юзом.
В этом случае максимальное нажатие колодок на ось равно: Отношение φк / Ψк = δ называют коэффициентом нажатия тормозной колодки. При заданной осевой нагрузке допустимые значения коэффициента нажатия будут зависеть от значении Ψк и φк, которые в свою очередь зависят от скорости движения и материала колодок. При расчетах значения 6 для локомотивов принимают в пределах 0.5-0.6. На рисунке показана зависимость коэффициентов трения чугунной тормозной колодки и сцепления колеса с рельсом при различных скоростях движения. Из приведенных графиков видно, что при снижении скорости в процессе торможения значения φк становятся больше Ψк., следовательно, вероятность заклинивания колесных пар выше при низких скоростях движения; при высоких скоростях значения Ψк больше φк, и значит, опасность юза практически исключается, а силу нажатия колодки на колесо можно увеличить для реализации большей тормозной силы. Способы регулирования величины тормозной силыВажной характеристикой тормоза является его способность максимально использовать коэффициент сцепления колес с рельсами. Неполное использование сцепления имеет место в процессе наполнения тормозных цилиндров, то есть когда тормозная сила еще не достигла максимальной величины. Поэтому при допустимых условиях по величинам продольных динамических усилий в поезде и заклиниванию колесных пар стремятся к минимальному времени наполнения тормозных цилиндров. Весовое регулирование. Соответствие между величиной тормозной силы и весом вагона в тормозах грузового типа достигается ручным переключением режимов торможения или применением на грузовых вагонах авторежимов, которые автоматически регулируют тормозное нажатие в зависимости от загрузки вагона. Воздухораспределитель грузового типа имеет три режима торможения: порожний, средний и груженный. Переключение режимов выполняется вручную в зависимости от загрузки вагона, приходящейся на ось.Каждому режиму торможения соответствует определенное давление в тормозном цилиндре. Скоростное регулирование тормозной силы. Изменение тормозной силы при уменьшении коэффициента сцепления при высоких скоростях движения сводится к увеличению нажатия на колодку за счет повышения давления в тормозном цилиндре. В процессе уменьшения скорости при торможении переключение с высокого нажатия (К2) на пониженное (К1) выполняется автоматически специальными скоростными регуляторами при достижении конкретной скорости перехода (например, при V=50 км/ч). Регулятор устанавливается на буксе колесной пары тележки. Регулирование тормозной силы осуществляется в случае применения полного торможения. При полных торможениях и малых скоростях движения величина тормозной силы может превысить значение силы может превысить значение силы сцепления Вс колеса с рельсом, что резко повышает вероятность заклинивания колесных пар.Наличие в составе поезда разнотипных вагонов с различными значениями К делает расчет тормозной сипы с использованием формул 1.1. и 1.2. для определения коэффициентов трения весьма трудоемким. Для упрощения тормозных расчетов пользуются методом приведения, при котором действительные значения К и φк заменяются расчетными значениями К и φкр, а коэффициент трения определяется при одном, условно выбранном тормозном нажатии Ку, но при этом обеспечивалось бы равенство: Значения Ку принимают: для чугунных колодок — 2.7 тс. для композиционных колодок — 1.6 тс. Подставляя значения Ку в формулы 1.1. и 1.2. получим значения расчетных коэффициентов трения соответственно для чугунных и композиционных колодок:
После подстановки значений φк и φкр в выражение 1.6. получим формулы для определения расчетных сил нажатия чугунных и композиционных колодок:
Если в поезде используются тормоза с разными типами тормозных колодок (например, чугунными и композиционными), то необходимо привести расчетное нажатие к одной системе нажатий. Это приведение выполняют умножением величины нажатия на соответствующий коэффициент эффективности, которые зависят от скорости движения. Коэффициенты эффективности определяют исходя из равенства длины тормозного пути при действии колодок разного типа. На железных дорогах России за основную принята система расчетных значений нажатий чугунных тормозных колодок, для которых установлены все тормозные нормативы и действующие номограммы и таблицы зависимости тормозных путей от скорости начала торможения, удельных расчетных нажатий и крутизны уклонов. Расчет тормозного путиВ настоящее время существует три метода тормозных расчетов:
С помощью аналитического метода ПТР решают задачи, в которых реализуется полная тормозная сила:
Тормозной путь при полном служебном торможении рассчитывается так же как при экстренном торможении, но значение тормозного коэффициента принимается равным 0.8 от его полного значения.В практике часто возникает необходимость точного расчета тормозного пути или скорости движения поезда при ступенчатых торможениях, во время безостановочного следования по переломному не спрямляемому профилю пути и при других разнообразных условиях торможения. В таких случаях тормозные задачи решают численным интегрированием уравнения движения поезда не по интервалам скорости, а по интервалам времени. Расчет тормозного пути методом ПТРПолный тормозной путь Sт, проходимый поездом от начала торможения до остановки, принимается равным сумме пути подготовки тормозов к действию Sп и действительного пути торможения Sд.
Время подготовки тормозов к действию определяется из условия замены медленного, реального процесса наполнения тормозного цилиндра среднего вагона, мгновенным наполнением до полной величины, при условии равенства тормозных путей, проходимых поездом при реальном и условном наполнении тормозных цилиндров. В зависимости от рода подвижного состава и его длины время подготовки тормозов к действию определяется по формуле Величины коэффициентов а и б зависят от рода движения, вида управления тормозами в пассажирском поезде, от длины поезда в осях и принимаются по таблице
Величина действительного пути торможения определяется суммированием величин пути торможения в выбираемых интервалах скорости при условии постоянства величин удельных сил, действующих на поезд в этом интервале, по формуле 1.14
Удельная тормозная сила определяется по формуле Расчетный тормозной коэффициент поезда с учетом веса и нажатия локомотива вычисляется по формуле Сумма расчетных сил нажатия тормозных колодок поезда подсчитывается по формуле или берется из справки формы ВУ-45 При определении тормозного коэффициента грузового груженого поезда на спусках до 20 ‰ вес локомотива и нажатие его колодок не учитываются.
Действительный тормозной путь при автостопном торможении определяют так же, как при экстренном торможении, а время подготовки тормозов к действию рассчитывают с учетом дополнительных 12 с, необходимых для срабатывания электропневматического клапана (ЭПК) автостопа. |
Анимация (мультик) по схемам прямодействующего, непрямодействующего тормоза и ЭПТ. Для скачивания проги кликните по картинке Отличное пособие по новому воздухораспределителю пассажирских вагонов № 242. |
Нажатие на вращающееся колесо колодки с силой К вызывает появление силы трения Т между колодкой и колесом, которая действует от колодки на колесо против его вращения, т. е. стремится остановить это вращение. Тормозить поступательное движение поезда сила трения Т не может, так как это внутренняя сила по отношению к поезду — колодка является частью самого поезда и движется вместе с ним.
Особенно интенсивно угон рельсов происходит в местах, где обычно производится служебное торможение поездов. В свою очередь, неподвижный рельс тормозит катящееся по нему колесо с силой Вт, являющейся реакцией рельса на силу В. Сила Вт является внешней силой по отношению к поезду и направлена против направления его движения, поэтому она является тормозной силой.тормозная сила — это… Что такое тормозная сила?
- тормозная сила
- braking force, retarding force
Большой англо-русский и русско-английский словарь. 2001.
- тормозная рычажная передача
- тормозная система
Смотреть что такое «тормозная сила» в других словарях:
Тормозная сила — реакция опорной поверхности на колеса транспортного средства, вызывающая замедление транспортного средства и (или) колес транспортного средства;… Источник: Постановление Правительства РФ от 10.09.2009 N 720 (ред. от 06.10.2011) Об утверждении… … Официальная терминология
тормозная сила — stabdymo jėga statusas T sritis automatika atitikmenys: angl. brake force vok. Bremskraft, f rus. тормозная сила, f pranc. effort de freinage, m … Automatikos terminų žodynas
тормозная сила — 3.36 тормозная сила: Реакция опорной поверхности на колеса АТС, вызывающая замедление АТС и (или) колес АТС. Для оценки технического состояния тормозных систем используют наибольшие величины тормозных сил. Источник: ГОСТ Р 51709 2001:… … Словарь-справочник терминов нормативно-технической документации
тормозная сила (в автотранспортных средствах) — тормозная сила Реакция опорной поверхности на колеса транспортного средства, вызывающая замедление транспортного средства и (или) колес транспортного средства. [Технический регламент о безопасности колесных транспортных средств] Тематики… … Справочник технического переводчика
УДЕЛЬНАЯ ТОРМОЗНАЯ СИЛА ПОЕЗДА — величина тормозной силы поезда, выраженная в килограммах и деленная на вес поезда в тоннах. Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б.… … Технический железнодорожный словарь
Удельная тормозная сила — отношение суммы тормозных сил на колесах транспортного средства к произведению массы транспортного средства на ускорение свободного падения;… Источник: Постановление Правительства РФ от 10.09.2009 N 720 (ред. от 06.10.2011) Об утверждении… … Официальная терминология
удельная тормозная сила — Отношение суммы тормозных сил на колесах транспортного средства к произведению массы транспортного средства на ускорение свободного падения. [Технический регламент о безопасности колесных транспортных средств] Тематики автотранспортная техника … Справочник технического переводчика
удельная тормозная сила — 3.41 удельная тормозная сила: Отношение суммы тормозных сил на колесах АТС к произведению массы АТС на ускорение свободного падения (для тягача и прицепа или полуприцепа рассчитывают раздельно). Источник: ГОСТ Р 51709 2001: Автотранспортные… … Словарь-справочник терминов нормативно-технической документации
Тормозная колодка — барабанного тормоза автомобиля Тормозная колодка (иногда башмак) часть тормозной системы и её основной рабочий компонент. Именно тормозная колодка создаёт тормо … Википедия
ГОСТ Р 51709-2001: Автотранспортные средства. Требования безопасности к техническому состоянию и методы проверки — Терминология ГОСТ Р 51709 2001: Автотранспортные средства. Требования безопасности к техническому состоянию и методы проверки оригинал документа: 3.48 «холодный» тормозной механизм: Тормозной механизм, температура которого, измеренная на… … Словарь-справочник терминов нормативно-технической документации
ГОСТ Р 41.13-2007: Единообразные предписания, касающиеся транспортных средств категорий М, N и О в отношении торможения — Терминология ГОСТ Р 41.13 2007: Единообразные предписания, касающиеся транспортных средств категорий М, N и О в отношении торможения оригинал документа: 2.11 автоматическое торможение (automatic braking): Торможение прицепа или прицепов,… … Словарь-справочник терминов нормативно-технической документации
Услуга : ТОРМОЗНАЯ СИСТЕМА
Что такое тормозная система?
Система обеспечивает остановку автомобиля. В систему входят следующие элементы:
- педаль тормоза
- тормозная жидкость
- тормозные колодки для дисковых тормозных механизмов
- и т.д.
Почему необходимо обслуживать тормозную систему вашего автомобиля?
Во время движения тормозная система используется очень часто, в частности, при движении по городу. Для обеспечения эффективного торможения и сохранения безопасной дистанции важное значение имеет регулярная замена деталей, подверженных естественному износу.
Когда необходимо заменять элементы тормозной системы вашего автомобиля?
Все зависит от автомобиля, необходимо следовать предписаниям производителя.
Рекомендация
Регулярно проверяйте состояние тормозных колодок вашего автомобиля при отсутствии сигнализатора износа на панели управления. Толщина материала тормозных колодок должна соответствовать предписаниям изготовителя.
Очень важно проверять состояние тормозных колодок, а также тормозных дисков, которые также изнашиваются и заменяются при каждой второй замене тормозных колодок (или ранее при наличии царапин и неровностей на поверхности).
Третьим основным элементом тормозной системы является гидравлический контур. Необходимо проверять уровень рабочей жидкости визуально по прозрачному бачку, установленному в моторном отсеке.
Если педаль тормоза вашего автомобиля становится слишком мягкой, утапливается больше обычного хода, а тормозной путь увеличивается, внимание, возникает опасность! Необходимо в ближайшее время провести проверку тормозной системы вашего автомобиля в сервисном центре.
Un système de freinage en mauvais état de fonctionnement est un élément rédhibitoire lors du contrôle technique. Pensez au pré-contrôle technique Eurorepar Car Service pour être certain de passer l’épreuve sans encombre !
Современные автомобили обладают очень высокими скоростными качествами. Чтобы безопасно и быстро остановить машину, нужны исключительно надежные и исправные тормоза. Чем они надежнее, тем быстрее уменьшается скорость движения автомобиля вплоть до его полной остановки. Начинающий водитель должен обязательно научиться тормозить правильно, без ошибок. Если он уяснит причины возможных ошибок, поймет условия правильного торможения и будет заботиться о совершенном их исполнении, даже если нет необходимости дорожить каждым метром тормозного пути, он сумеет затормозить и в том случае, когда от его умения и готовности, возможно, будет зависеть жизнь человека. Суть торможения состоит в следующем. Во время торможения в тормозных механизмах автомобиля создается тормозной момент, действие которого направлено в сторону противоположную колесу. При этом между колесами и дорогой под действием сил трения возникает тормозная сила, противодействующая движению. Эта сила не должна быть больше силы сцепления колес с дорогой, иначе колеса начнут скользить и автомобиль пойдет юзом. При движении юзом (колеса блокированы) из-за сильного нагрева резины сцепление значительно ухудшается, тормозной путь увеличивается, устойчивость автомобиля значительно уменьшается.
Когда водитель начинает тормозить, приложенная к центру тяжести автомобиля сила инерции направлена вперед и вместе с тормозной силой создает момент, который стремится прижать переднюю часть автомобиля и приподнять заднюю. По этой причине передние тормоза изготовляют более мощными, что позволяет полностью использовать силу сцепления в момент торможения.
В зависимости от вызвавших его причин торможение бывает служебным и экстренным. Экстренное производится с максимально возможной интенсивностью. Его применяют, когда возникает опасность наезда на пешехода, столкновения с идущим впереди или навстречу транспортом и в других критических ситуациях.
Различают несколько основных способов торможения: плавное, резкое, прерывистое и ступенчатое. При плавном водитель мягко нажимает на педаль, постепенно увеличивая давление и плавно замедляя движение автомобиля. При резком на педаль нажимают сильно, стараясь произвести остановку на минимальном расстоянии из-за внезапно возникшей опасности. Основной ошибкой при этом является чрезмерно резкое и сильное усилие на педаль, которое приводит к блокировке колес и юзу. В результате автомобиль теряет управление, а на скользкой дороге его заносит. Резкое торможение, неминуемое на больших скоростях, неприятно для пассажиров, вредно для грузов, сильно изнашивает тормозные накладки, нарушает устойчивость автомобиля и увеличивает расход топлива
Возврат к списку
Силы и торможение — Силы, ускорение и законы Ньютона — AQA — Объединенная научная редакция GCSE — AQA Trilogy
Тормозной путь
В экстренной ситуации водитель должен остановить свой автомобиль на как можно более коротком расстоянии:
тормозной путь = расстояние мышления + тормозной путь
Это когда:
- расстояние мышления — это расстояние, которое проходит транспортное средство за время, которое требуется водителю, чтобы задействовать тормоза после того, как он понял, что ему нужно остановиться
- тормозной путь — это расстояние, которое транспортное средство перемещается во времени после того, как водитель нажал на тормоз
Время реакции
Время реакции варьируется от человека к человеку, но обычно составляет 0.2 с и 0,9 с. На время реакции водителя могут влиять:
Более длительное время реакции увеличивает дистанцию мышления при остановке с заданной скорости.
Есть разные способы измерения времени реакции. Один из простых способов заключается в том, чтобы поместить линейку между открытыми большим и указательным пальцами. Чем выше время реакции, необходимое для того, чтобы схватить падающую линейку, тем дальше линейка падает до того, как ее остановят.
Тормозной путь
На тормозной путь транспортного средства могут влиять:
- плохие дорожные и погодные условия, такие как мокрые или обледенелые дороги
- плохие условия транспортного средства, такие как изношенные тормоза или изношенные шины
Когда сила, приложенная к тормозам транспортного средства, совершается за счет трения между тормозами и колесом.Это снижает кинетическую энергию транспортного средства, замедляя его и вызывая повышение температуры тормозов.
Чем быстрее движется автомобиль, тем большее тормозное усилие необходимо для его остановки на определенном расстоянии. Чем больше тормозное усилие, тем сильнее замедление. Сильное замедление может привести к перегреву тормозов, а водитель также может потерять контроль над автомобилем.
Типичный тормозной путь
Важно уметь:
- оценить, как тормозной путь транспортного средства изменяется в зависимости от различных скоростей. средняя машина в нормальных условиях.
Некоторые типичные тормозные пути
Движение со скоростью 20 миль / ч (32 км / ч):
- мысленное расстояние = 6 м
- тормозной путь = 6 м
- общий тормозной путь = 12 м
Движение со скоростью 40 миль / ч ( 64 км / ч):
- мысленное расстояние = 12 м
- тормозной путь = 24 м
- общий тормозной путь = 36 м
Движение со скоростью 70 миль в час (112 км / ч):
- мысленное расстояние = 21 м
- тормозной путь = 75 м
- общий тормозной путь = 96 м
Важно отметить, что расстояние мышления пропорционально стартовой скорости.Это связано с тем, что время реакции принимается за константу, а скорость = расстояние × время. Однако тормозной путь увеличивается в четыре раза каждый раз, когда стартовая скорость удваивается.
Например, если автомобиль увеличивает скорость вдвое с 30 до 60 миль в час, дистанция мышления удвоится с 9 до 18 м, а тормозной путь увеличится в четыре раза с 14 до 56 м.
Расчет тормозного пути — Движение транспортных средств — Edexcel — Редакция GCSE Physics (Single Science) — Edexcel
Важно уметь:
- оценить, как тормозной путь транспортного средства изменяется в зависимости от скорости. работа, проделанная при остановке движущегося транспортного средства
На диаграмме показаны некоторые типичные тормозные пути для среднего автомобиля в нормальных условиях.
Важно отметить, что расстояние мышления пропорционально начальной скорости. Это потому, что время реакции принято как постоянное, а расстояние = скорость × время.
Тормозное усилие
Однако тормозной путь увеличивается в четыре раза каждый раз, когда стартовая скорость удваивается. {2} \]
Итак, при фиксированной максимальной тормозной силе тормозной путь пропорционален квадрату скорости.
Пример расчета дистанции мышления
Автомобиль движется со скоростью 12 м / с. Водитель имеет время реакции 0,5 с и видит, что впереди на дорогу выбегает кошка. Какова дистанция мышления, когда водитель реагирует?
расстояние = скорость × время
\ [d = v \ times t \]
\ [d = {12} \\ м / с \ times {0,5} \\ s \]
\ [мышление \\ distance = 6 \ m \]
Пример расчета тормозного пути
Автомобиль в предыдущем примере имеет общую массу 900 кг.{2}} {2,000} \]
\ [braking \ distance = 32 \ m \]
Пример расчета тормозного пути
Каков тормозной путь для автомобиля выше?
тормозной путь = расстояние мысли + тормозной путь
тормозной путь = 6 + 32
тормозной путь = 38 м
- Вопрос
Рассчитайте тормозной путь для автомобиля и водителя в приведенном выше примере, когда движется со скоростью 24 м / с.
- Показать ответ
\ [мышление \ расстояние = 24 \ м / с \ умножить на 0.{2}} {100} \]
тормозное усилие ~ 87000 Н
Тормозное усилие — обзор
Распределение тормозного усилия
Как объяснялось ранее, нормальные силы между шиной и дорогой можно рассчитать по формуле статическое распределение веса автомобиля, перенос веса при торможении или ускорении и перенос веса в поперечном направлении при прохождении поворотов. Предполагается, что поверхность дороги горизонтальна, если не указано иное, так что нормальные силы перпендикулярны поверхности дороги.Также существуют динамические силы, прикладываемые к транспортному средству со стороны дорожного покрытия, но они игнорируются для целей представленного здесь анализа. Передача тормозного веса определяется (уравнения (3.2) и (3.3)) из общей массы транспортного средства, его скорости торможения, колесной базы и высоты центра тяжести над поверхностью дороги. В реальной жизни дорожное транспортное средство движется, и нормальные силы на каждом колесе всегда динамические, но основная теория торможения начинается с квазистатического подхода, который продолжается здесь.Анализ предполагает отсутствие работы ABS или ESC.
Если блокировка колес не происходит, тормозная сила, создаваемая на каждом стыке шины с дорогой (в продольном направлении), определяется характеристиками тормоза на каждом колесе, как указано в главах 5 и 6, глава 5, глава 6. Как обсуждалось выше, блокировка колеса произойдет, если величина продольной тормозной силы на любом колесе превышает максимум, который может выдержать поверхность контакта шины с дорогой. Максимальное тормозное усилие создается только в критической точке (C на рисунке 3.12), поэтому для достижения максимального замедления или скорости торможения транспортного средства на любой заданной поверхности дороги все колеса должны одновременно приближаться к точке блокировки. Снова обратимся к рисунку 3.2, на котором показан четырехколесный (двухосный жесткий) легковой автомобиль, движущийся по горизонтальной дороге с торможением всех колес, но не заблокированными, тогда в соответствии со вторым законом Ньютона:
(3.15) Общая тормозная сила = масса × замедление = PJg = Pz
Общая тормозная сила транспортного средства представляет собой сумму тормозного момента на каждом отдельном опорном колесе и реагирует на сцепление шины с дорогой на каждом стыке шины с дорогой, так что общая тормозящая сила на транспортном средстве составляет:
(3.16) Pz = T1 + T2
Максимальное тормозное усилие на транспортном средстве зависит от коэффициента сцепления шины с дорогой k :
(3,17) Pzmax = kP
So z max = k когда все колеса одновременно находятся в точке блокировки.
Поскольку это представляет собой случай максимального замедления транспортного средства для данного набора условий дороги / шины, максимальная скорость торможения z в этих условиях не может превышать коэффициент сцепления k , если только прижимная сила от веса транспортного средства P дополнен, e.грамм. за счет аэродинамических эффектов. Следующий анализ (основанный на модели велосипеда с симметричными тормозными силами и динамическими нагрузками на шины относительно осевой линии транспортного средства) предполагает, что единственной направленной вниз силой на транспортное средство является его вес.
Чтобы все колеса одновременно находились в точке блокировки, тормозная сила на каждом колесе должна быть пропорциональна нормальной динамической реакции этого колеса, поэтому:
(3,18) T1 / T2 = N1 / N2
отношение тормозной силы, создаваемой передними колесами, к тормозной силе, создаваемой задними колесами двухосного транспортного средства с жесткой рамой, такого как легковой автомобиль, может быть определено как соотношение X 1 / X 2 , где X 1 и X 2 — это пропорция общей тормозной силы транспортного средства, создаваемой на передней и задней осях соответственно.По определению:
(3.19a) T1 / T2 = X1 / X2andX1 + X2 = 1
, потому что:
(3.19b) T1 + T2 = PzX1 + PzX2 = Pz (X1 + X2) = Pz
Итак, общая тормозная сила на этом автомобиле, где все колеса одновременно находятся в точке блокировки, составляет T 1 = X 1 Pz и T 2 = X 2 Pz , а также для автомобиля с осями n : T n = X n Pz .
Как объяснялось ранее, при торможении между осями происходит динамическая передача веса, поэтому нормальные динамические силы на каждом опорном колесе меняются в зависимости от скорости торможения. Таким образом, для обеспечения идеального торможения во всех условиях движения транспортного средства потребуется переменное передаточное отношение распределения тормозов ( X 1 / X 2 ). Уравнения (3.2) и (3.3) ранее показали, что динамические нормальные реакции на передних и задних колесах при торможении равны:
N1 = P1 + PzhE и N2 = P2 − PzhE соответственно
Рассмотрим случай четырехколесной, двухосной жесткое транспортное средство с фиксированным распределением тормозов:
X1 / X2 = постоянное
, которое спроектировано так, что передние колеса будут блокироваться сначала на поверхности шины / дороге, коэффициент сцепления k , затем тормозное усилие на передней оси когда передние колеса вот-вот заблокируются:
(3.20) T1 = kN1 = k {P1 + PzhE}
Соответствующее тормозное усилие на задней оси меньше предельного значения сцепления, поскольку тормозная система была спроектирована так, чтобы сначала блокировать передние колеса. Поскольку T 1 / T 2 = X 1 / X 2 , следовательно, T 2 = T 1 (
X / X 1 ) и
(3,21) T2 = k {P1 + PzhE} X2X1
Тогда суммарное тормозное усилие на автомобиле составит:
(3.22) T1 + T2 = Pz = k {P1 + PzhE} + k {P1 + PzhE} X2X1 = k (1 + X2X1) {P1 + PzhE}
, т.е.
(3.23) Pz = k (X1 + X2X1) {P1 + PzhE} = k (1X1) {P1 + PzhE}
, начиная с X 1 + X 2 = 1.
Изменение этого уравнения дает скорость торможения z при переднем колеса вот-вот заблокируются:
(3,24) z = kP (1X1) {P1 + PzhE} = kP (P1X1 + PzhEX1)
Отсюда:
(3,25) z (1 − khEX1) = kP1PX1
И, следовательно, :
(3,26) z = kP1PX1 (EX1EX1 − kh) = kEP1P (EX1 − kh)
Аналогичный анализ для задних колес, собирающихся заблокироваться, дает:
(3.27) z = kEP2P (EX2 + kh)
Как объяснялось ранее, скорость торможения z транспортного средства не может превышать значение коэффициента сцепления k . Таким образом, уравнение (3.20) (т.е. блокировка передних колес) сохраняется до точки, где z = k , в зависимости от передаточного отношения X 1 / X 2 . Это значение, при котором передние и задние колеса автомобиля находятся в точке блокировки одновременно. Для значений k больше этого, вычисление z из уравнения (3.20) даст z больше, чем k , что невозможно. Следовательно, торможение будет ограничиваться блокировкой задних колес, и будет применимо уравнение (3.21). Это проиллюстрировано на рисунке 3.16 для ранее использованного примера легкового автомобиля (таблица 3.1) с передним / задним тормозным соотношением, указанным как X 1 / X 2 = 70/30.
Рисунок 3.16. Предельная скорость торможения ( z ) для заданного коэффициента сцепления ( k ) для транспортного средства, указанного в таблице 3.1.
На рисунке 3.16 показано наименьшее значение коэффициента сцепления, которое теоретически требуется для транспортного средства, указанного в таблице 3.1, для достижения определенной скорости торможения с использованием уравнений (3.26) и (3.27). До момента одновременной блокировки передних и задних колес, то есть там, где передние и задние линии пересекаются, передние колеса требуют более высокого коэффициента сцепления и, следовательно, блокируются раньше задних колес. Выше точки кроссовера задние колеса требуют более высокого коэффициента сцепления и, следовательно, блокируются раньше передних колес.Скорость торможения при одновременной блокировке передних и задних колес определяется как z крит , где z крит = k , и поэтому k можно заменить на z в уравнениях (3.20) и (3.21), чтобы получить уравнения (3.28) и (3.29). Параметр z crit является полезным параметром конструкции тормозной системы, как объясняется и используется в главе 6.
(3.28) zcrit = k = (X1 − P1P) Eh
(3.29) zcrit = k = (P2P − X2) Eh
Обратите внимание, что для возможности одновременной блокировки колес, X 1 должно быть больше, чем доля статической нормальной реакции на передних колесах ( P 1 / P ). Точно так же X 2 должно быть меньше, чем пропорция статической нормальной реакции на задних колесах ( P 2 / P ). На небольших легковых автомобилях и легких фургонах нормальные динамические реакции передней и задней оси могут значительно изменяться в диапазоне допустимых условий нагрузки от DoW до GVW, поэтому одновременная блокировка возможна при некоторых условиях нагрузки, но не при других, если X 1 / X 2 зафиксировано.
Когда одно или несколько колес транспортного средства прошли точку блокировки, шины будут скользить по дороге, и замедление транспортного средства уменьшится, поскольку тормозное усилие на заблокированном колесе (колесах) уменьшается на разница между μ t и k . На практике, если сначала блокируются передние колеса, водитель может не заметить небольшой вклад со стороны задних колес, но если водитель продолжает увеличивать усилие на педали, разблокированные колеса будут обеспечивать повышенное тормозное усилие до тех пор, пока эти колеса также не заблокируются, а затем водитель заметил бы дальнейшее снижение замедления автомобиля.
Уравнение для заблокированных передних колес ( μ t ), но для задних колес с максимальным сцеплением k :
(3.30) Pz = μt {P1 + PzhE} + k {P2 − PzhE}
Для решения этого уравнения можно предположить, что μ t пропорционально k , например мкм t = 0,7 k . Это предположение основано на относительных значениях k и μ t , указанных в точках C и D на рисунке 3.12.
(3,31) Pz = 0,7k {P1 + PzhE} + k {P2 − PzhE}
Это дает:
(3,32) z = k {0,7P1 + P21 + 0,3khE}
На основе В предыдущем примере эффект блокировки переднего колеса при k = 0,50 будет заключаться в уменьшении замедления транспортного средства с z = 0,49 с передними колесами в точке блокировки (т. е. они все еще вращаются) до z = 0,40 с заносом передних шин. Альтернативная ситуация, когда задние колеса буксуют ( μ t ), в то время как передние колеса имеют максимальное сцепление ( k ), слишком нестабильна, чтобы представлять практический интерес, как обсуждается далее.
Что такое пиковая тормозная сила и насколько она важна?
Сегодня мы собираемся изучить и обсудить пиковое тормозное усилие у бегунов и то, как оно соотносится с вашими результатами и потенциальным риском травм. Мы собираемся использовать недавнюю статью, опубликованную в Journal of Orthopaedic & Sports Physical Therapy, чтобы исследовать эту силу.
Пиковая тормозная сила: определена
Пиковая тормозная сила — это количество энергии, которое направляется в вашу ногу спереди назад, когда ваша ступня впервые касается земли.Хороший способ визуализировать это — представить, что вы бежите на полной скорости и должны внезапно остановиться. Сила, которую вы чувствуете, когда нажимаете на тормоз, и есть ваша пиковая тормозная сила. Это имеет отношение к вам и мне, потому что пиковая тормозная сила связана с восьмикратным увеличением риска травм, когда сила превышает 0,27 веса тела. Теперь мы с вами не можем измерить силу по отношению к массе тела. То есть, если у вас в подвале нет очень дорогой силовой беговой дорожки, о которой я не знаю.В таком случае пригласите меня к себе. Но то, что мы не можем точно измерить это, не означает, что это исследование бесполезно.
Но почему важно пиковое тормозное усилие? Это важно, потому что ваши кости и ткани не так эффективно переносят силу сдвига. Ваши кости и ткани намного лучше приспособлены к силе, направленной прямо вверх и вниз, но не так, чтобы она двигалась спереди назад. Итак, теперь мы видим, что если мы хотим потенциально избежать травм, нам следует позаботиться о максимальной тормозной силе.
Протокол исследования и результаты
В этом исследовании исследователи использовали необычную беговую дорожку для измерения максимальной тормозной силы у спортсменов. После того, как они измерили это, они установили видеомонитор перед беговой дорожкой с графиком в реальном времени, который показывал бегуну силы, которые он или она передавали на беговую дорожку. Затем они сказали бегуну уменьшить размер силовой волны во время бега. Они не уточнили, как именно — они просто сказали бегунам уменьшить волну, насколько они могут.
Так что же случилось? Что ж, бегуны довольно эффективно уменьшали амплитуду волны и тем самым уменьшали пиковую тормозную силу. Фактически они снизили пиковое тормозное усилие на 15 процентов. Это уменьшение привело к пятикратному снижению риска травм во время бега. Это огромная сумма! Снижение пикового тормозного усилия всего на 15 процентов снижает риск травм в пять раз!
Но подождите, мы не рассмотрели , как они уменьшили эту пиковую тормозную силу.Это был удар ногой? Или согнуть колено? Фактически, бегуны увеличили на каденс в среднем на семь процентов, а уменьшили длину шага на семь сантиметров. Таким образом, они добились меньшей передачи силы ногам за счет увеличения частоты вращения педалей и уменьшения длины шага.
Итак, как это применимо к нам? У нас нет беговой дорожки с силовой пластиной и экраном впереди, чтобы изменить наш рисунок. Что ж, даже если у нас нет немедленной обратной связи с силовой пластиной, мы знаем, как спортсмены в конечном итоге изменили силы.Они увеличили частоту вращения педалей и уменьшили длину шага. Итак, мы с вами можем влиять на нашу частоту шагов с помощью метронома на телефоне или смотреть и уменьшать длину шага, думая о более коротких и быстрых шагах.
Дальнейшие действия
Итак, теперь мы знаем, что если мы сможем снизить пиковое тормозное усилие, это может привести к снижению риска травм. Как бегуны, мы всегда стремимся снизить риск травм. Но как узнать, есть ли у вас пиковое тормозное усилие? Это отличный вопрос.В этом исследовании изучались только бегуны, у которых было максимальное тормозное усилие , то есть те, кто мог получить травму. Если вы не получили травм, следует ли вам попытаться уменьшить пиковое тормозное усилие? Возможно, но на этот вопрос сложно ответить в блоге. Это больше подходит для тех, кто имел повторяющиеся травмы нижней части тела, стрессовые переломы, раздражение сухожилий и т. Д.
Какова идеальная частота вращения педалей? Хитрый вопрос! Нет, несмотря на то, что Интернет пытается вам сказать.На самом деле, вам не следует пытаться изменять частоту вращения педалей более чем на 10 процентов за раз, иначе вы увеличите риск травмы. Медленные и постоянные изменения приводят к большим улучшениям.
А как насчет длины шага? Не беспокойтесь о точном измерении вашего шага. Просто попытайтесь сделать шаги короче, чтобы ступня приземлилась под вами.
Было ли это полезно? Есть дополнительные вопросы или проблемы? Свяжитесь со мной сегодня, и мы ответим на ваши вопросы.
Бегите, друзья мои,
Райан
____________________
1.C. Napier, et al. Биологическая обратная связь в реальном времени для снижения тормозных сил, связанных с травмами во время бега: исследовательское исследование.
Журнал ортопедической и спортивной физиотерапии: 49: 3, 136-144, 2019.
#Precisionpt #precisionperformanceATL #physicaltherapy #atlantaphysicaltherapy doc562 #atlantaphysicaltherapy doc562 #atlantaphysicaltherapy triathlon #runningmedicine #PTfirst
тормозное усилие — Французский перевод — Linguee
Для машин с ALB, t h e тормозное усилие i s r регулируется согласно […] до уровня заполнения бака через поплавок в баке.
et.amazone.de
Sur les машины quipes
[…] du sys t me AL B, la force de freinage es t rg ul e en […]fonction du niveau de remplissage de la cuve,
[…]par l’intermdiaire d’un flotteur dans la cuve.
et.amazone.de
Силы тормозной колодки не измерялись, поэтому испытания
[…] не определяла степень e o f тормозное усилие o c ca sioned by ручное торможение.tsb.gc.ca
Par consquent, les essais n’ont pas
[…] permis d e vrifier l ‘Intensit de l’effor t de freinage instance p ar le serrage […]du frein main.
tsb.gc.ca
T h e тормозное усилие i s a отрегулировано с помощью регулировочного винта для оптимального торможения […] производительность.
bischoff-bischoff.de
P или ur un freinage optim al , ajust ez la puissance de freinage avec l a vis […] de rglage.
bischoff-bischoff.de
Модулятор ‘означает компонент
[…] рассчитан на изменение t h e тормозное усилие ( s ) i n в соответствии с […]сигнал, полученный от контроллера.
eur-lex.europa.eu
Par modulateur, входит в стоимость
[…] moduler la or es force de freinage en fonct io n de l’ordre […]reu du Calculateur.
eur-lex.europa.eu
Кран тормозной прицепа автоматически
[…]переключает и управляет рабочей тормозной системой независимо от автоматической,
[…] зависимость от нагрузки de n t тормозное усилие r e gu lator.et.amazone.de
Celle-ci s’enclenche automatiquement et
[…]actionne le circuit du frein de service en fonction de la rgulation automatique de
[…] la char ge de la puissance d e freinage .et.amazone.de
Эти и многие другие тесты, которые мы проводим каждый год, доказывают, что к
году […]установка Ferodo вы доставляете
[…] максимальная возможная ib l e тормозное усилие a c ro ss широкий спектр […]автомобильных приложений.
fmnews.com
Tout com les nombreux autres tests que nous menons chaque anne, ces essais
[…]dmontrent que la posé de
[…] Produits Fero do ass ure la force de freinage l a pl us le ve possible e […]для и для больших автомобилей.
fmnews.com
Управление дроссельной заслонкой должно было использоваться в качестве основного средства
[…] управление скоростью и динамическое торможение используется как ini ti a l тормозное усилие .tsb.gc.ca
Les mcaniciens devaient utiliser
[…]для управления газом
[…] et uti li ser le freinage rhostatique com me m o yen de freinage in itia l .tsb.gc.ca
Благодаря архитектуре с двойной точкой опоры передняя часть
[…]тормозной хват
[…] обод с примерно 70% от от до l тормозного усилия ; t he задний тормоз, который имеет только один […] Точка опоры, останавливает
[…]заднее колесо от отклонения — из-за облегчения задней части — благодаря приложению силы, которая ниже, чем спереди.
campagnolo.com
Le frein avant, grce l’architecture double pivot, est
[…]en mesure de serrer
[…] la jant e avec une force qui cons ti tue environment 70 % de la force de всего le frein […]arrire простой стержень
[…]prvient les embardes de la roue arrire dtermines par l’allgement du train arrire grce l’application d’une force infrieure par rapport celle applique la roue avant.
campagnolo.com
Brake Assist помогает применить макс. im u m тормозное усилие w h en обнаружена паническая ситуация. chrysler.ru
L’assistan ce au freinage exe rc e la pressio n de freinage ma xi mum lorsqu’elle dtec te un freinage d’urgence . chrysler.ru
Хотя тормоза применялись до
[…] чтобы начать движение на юг к переключателю ответвления перезарядки, t h e тормозное усилие g e ne номинальное было недостаточноtsb-bst.gc.ca
Bien que les freins aient t appliqus avant le dbut du
[…] dplacement vers le sud, en direction de l’embranchement de recharge, l ‘ effor t d e serrage g n r t ai t insuffisant.tsb-bst.gc.ca
(ii) Изменение допускается без дополнительных испытаний, если по расчету влияние
[…] относительно хода a n d тормозное усилие c a n .daccess-ods.un.org
ii) Soit autoriser des diffrences sans essai Supplmentaire si l’incidence
[…] sur la c ours e et l a force d e freinage p eut tre m ontre […]по номиналу.
daccess-ods.un.org
Это означает, что требование ir e d тормозное усилие i s g появляется при отключении напряжения. faulhaber.com
Le u n coup le d e freinage e st r ali s quand la teni on coup es faulhaber.com
Для транспортных средств, оборудованных электрической системой рекуперативного торможения категории В, состояние транспортного средства
[…]батареек на начало теста,
[…] должен быть таким, чтобы t h e тормозное усилие c o nt распределение предоставлено […]с помощью электрического рекуперативного торможения
[…] Системане превышает минимума, гарантированного конструкцией системы.
daccess-ods.un.org
1.5.1.7 Pour les vhicules quips d’un systme de freinage lectrique rcupration de la catgorie B, l’tat des battery du vhicule au dbut de l’essai doit tre tel que la взнос
[…]que le systme lectrique
[…] rcupration a pport e la force de freinage n e d pa sse pas […]минимальная гарантия для концепции.
daccess-ods.un.org
С помощью этой технологии мы увеличили t h e тормозное усилие i n o ur система автоматического торможения с […] пятьдесят процентов до полной тормозной способности.
bkvolvo.net
Grce cette
[…] technologie, no us , чтобы избежать ns fait pa sser la force de freinage d e notre systme d e freinage a ut omatique [omatique]..]de cinquante pour cent l’application complete.
bkvolvo.net
Дисковые тормоза имеют период приработки, и t h e тормозное усилие w i ll постепенно увеличивается по мере приработки […] Период прогрессирует.
shimano-france.com
L es freins di sq ue ont une priode de r od age, et la force de freinage aug metera 9064…] прогрессивный и мёрный и новый родаж прогресс.
shimano-france.fr
2.16. ‘Peak b ra k e force c o ef ficient («pbfc»)’ означает максимальное значение rati o тормозное усилие т o v Этрическая нагрузка на шину […] до блокировки колес.
eur-lex.europa.eu
2.16. Coe ff icien td e force d e freinage maxi ma le («cffm»), максимальное значение раппорта e nt re la d e freinage e t la c harge […] verticale s’exerant sur
[…]le pneumatique avant le blocage des roues.
eur-lex.europa.eu
Результат — большее движение a n d тормозное усилие o n i покрытые снегом и покрытые снегом поверхности. bridgestone-firestone.ca
Le rsultat
[…] est une pl us g rand e force d e freinage e t un e meill eu re maniabilit su les r…]глясс е т глясс .
bridgestone-firestone.ca
Высокая энергия
[…] цены будут обслуживать как a тормозное усилие o n t he Экономика США, […], в то время как рост Канады будет сдерживаться текущим
[…]эффект сильного канадского доллара.
cibc-global.
гонконгских долларовLa flambe
[…] des prix d e l ‘ ner gi e freinera l ‘ cono mie am ricaine, […]tandis que la croissance de l’conomie canadienne sera
[…]ralentie par un dollar canadien fort.
cibc-global.hk
Результат
[…] больше вождение a n d тормозное усилие .bridgestone-firestone.ca
Le rsultat est une meilleure
[…] mania bi lit et un freinage optimis .bridgestone-firestone.ca
Он должен быть спроектирован таким образом, чтобы в прогнозируемых условиях использования вертикальное падение пользователя составляло
[…]сведен к минимуму, чтобы предотвратить столкновение с
[…] препятствия и t h e тормозное усилие d o es , однако, не […]достигает порогового значения, при котором
[…]можно ожидать физических травм, разрыва или разрыва любого компонента СИЗ, которые могут привести к падению пользователя.
eurogip.fr
Ils doivent tre conus et fabriqus de faon telle que, lorsqu’ils sont utiliss dans les conditions prvisibles d’emploi, la dnivellation du corps soit aussi faible que possible pour
[…]viter tout impact contre un препятствие, sans
[…] que l a force de freinage n’a tteig ne pour […]autant le seuil d’occurrence de lsions
[…]corporelles, ni celui d’ouverture or de l’un composant de ces EPI d’o pourrait rsulter la chute de l’utilisateur.
eurogip.fr
Затем зажим
[…] устройство в фазе (C) генерирует среднее значение dyn am i c тормозное усилие F — t h e тормозное усилие — — и таким образом рассеивает кинетическую энергию […]падающих масс.
sitema.com
Cette limite dpasse (фаза C), le
[…] dispo si tif freine la ti ge de nouveau en mouvement p ar une force moye nn d 9064 e F ( force de m ai ntient), […]liminant ainsi p.ex.
[…]l’nergie cinttique de la charge tombante.
sitema.com
Связанная система — это ручной рычаг или ножка
[…] педаль управляет тормозами на переднем и заднем колесе, чтобы равномерно распределять t h e тормозное усилие .inthesaddle.ca
Un systme intgral comporte un levier ou un pdale
[…] qui a ct ionne les roues a vant et arrire de faon rpartir ga le ment la puissa nceinthesaddle.ca
При этом im e , тормозное усилие i s a автоматически адаптировано […] посредством давления, приложенного в пружинных контейнерах.
lemken.com
Parall le ment, la force d e freinage e st aut omat iq uement […] Adapte en fonction de la pression applique aux ressorts de подвески.
lemken.com
Антиблокировочная тормозная система (ABS)
[…]был разработан для райдеров
[…] использовать автомобиль cl e s тормозное усилие t o t он максимально полный […]сумма при экстренном торможении или
[…]при плохом асфальте или неблагоприятных погодных условиях.
mts1200owners.ducati.com
Afin de maintenir l’efficacit de toute la
[…] емкость это de freinage du v hic ule, dans des si tuations […]d’urgence et sur tout type de terrain / chausse
[…]в соответствии с климатическими условиями, враждебными по отношению к климату, мы не можем избавиться от антиблокировочной системы (ABS).
mts1200owners.ducati.com
Система экстренного торможения помогает применить макс. обнаружен.
крайслер.около
L’assista NC e au freinage appli que la force de freinage m aximale l … Ситуация возникла нет.
chrysler.ru
При использовании в сочетании с тормозными рычагами V-BRAKE будет
[…] невозможно получить достаточно т.е. n t тормозное усилие .shimano-france.fr
В комплект входит комбинация с левыми рычагами V-BRAKE, сыворотка
[…] невозможно d ‘ obten ir une force de freinage suf fisan te .shimano-france.fr
Идентификатор оси классифицирует
[…] ось в пересчете на i t s тормозное усилие / t o rq ue возможность как […]заявлено производителем оси.
daccess-ods.un.org
L’identificateur d’essieu sert ranger l’essieu dans une catgorie
[…] sur la ba se de la force de freinage / du cou ple i nd iqus […]par le factory.
daccess-ods.un.org
Возьмите измененное время задержки, которое, например, может быть
[…] вызвано уменьшением t h e тормозного усилия , i nt o сч.leuze.com
Tenez compte des temps de retard modifis susceptibles de se produire
[…] par e x. lors que la force de freinage d imin ue .leuze.de
Регулируемое тормозное усилие с помощью интеллектуальных сдвоенных суппортов | IMECE
Автомобильная тормозная система — одна из важнейших подсистем автомобиля. Это основная система безопасности, поскольку остановка автомобиля во многом зависит от этой системы. Эта система использует силу трения между шиной и дорогой для остановки транспортного средства. Тормозное усилие, необходимое автомобилю, определяется двумя факторами. Один из них — коэффициент трения между шиной и дорожным покрытием, другой — нагрузка на автомобиль.Таким образом, необходимое тормозное усилие для остановки транспортного средства с минимально возможным тормозным путем зависит от нагрузки в транспортном средстве. Если прилагаемое тормозное усилие превышает требуемое тормозное усилие, колесо блокируется, что приводит к увеличению тормозного пути. Чтобы предотвратить блокировку колес при низких нагрузках, разработана система регулируемого тормозного усилия. В мотоциклах нагрузка на заднюю часть в основном влияет на общий вес. Таким образом, величина тормозного усилия, необходимого для остановки с минимальным тормозным путем, также резко меняется в зависимости от состояния нагрузки на опору.Следовательно, величина тормозного усилия, развиваемого между поверхностью дороги и шиной, изменяется в системе переменного тормозного усилия. В этом проекте система переменного тормозного усилия достигается за счет изменения эффективного радиуса диска. Максимальное тормозное усилие, развиваемое между землей и шиной, регулируется в зависимости от нагрузки на заднюю часть мотоцикла, если между шиной и землей присутствует трение. На тормозном диске установлены два суппорта, один из которых закреплен на постоянном расстоянии (постоянный эффективный радиус диска — 67 мм), а другой может перемещаться в зависимости от нагрузки на мотоцикл.Подвижный суппорт скользит вверх и вниз, так что эффективный радиус диска изменяется в зависимости от нагрузки на опору. С помощью тензодатчика определяется нагрузка автомобиля. Микроконтроллер запрограммирован на перемещение суппорта с помощью шагового двигателя в зависимости от нагрузки на мотоцикл. Таким образом, эффективный радиус диска варьируется для различных нагрузок на мотоцикле.
(PDF) Оптимизированные стратегии распределения тормозного усилия для торможения по прямой и кривой
100 A.Goodarzi et al.
5 Заключение
Хорошо известно, что для достижения стабильного и безопасного торможения проскальзывание задних колес
не должно быть больше, чем проскальзывание передних колес. Согласно этому простому правилу
, обычные системы EBD работают на основе простой стратегии, известной как стратегия «равных
промахов». Проскальзывание передних и задних колес теоретически установлено на одно и то же значение.
Такая простая стратегия не может быть идеальной.Сохраняя неизменной общую тормозную силу,
можно увеличить переднюю колесную часть и уменьшить заднюю колесную часть. С другой стороны, проскальзывание передних колес
установлено на гораздо более высокое значение, что приводит к устойчивости проскальзывания задних колес
. Другой интересный момент состоит в том, чтобы сделать тормозную способность левого / правого колеса
неравной во время маневра торможения при повороте. Таким образом, интеллектуальная стратегия распределения тормозного усилия
должна регулировать проскальзывание левого колеса вправо, а также устанавливать различные значения проскальзывания передних
на задние колеса.В значительной степени такой подход может привести к неравномерному распределению тормозной силы
не только в продольном направлении, но и в поперечном направлении.
В этой статье теория оптимизации была использована для формулировки вышеупомянутого
предложения. Так называемая «оптимизированная» стратегия распределения тормозного усилия
поддерживает значения замедления и, следовательно, тормозной путь транспортного средства составляет
неизменным по сравнению с классической стратегией распределения тормозного усилия.Однако он также
разумно распределяет тормозное усилие между четырьмя колесами неравномерно на основе
запрошенного продольного замедления и известного поперечного ускорения.
Во время экстренного торможения, когда запрошенное замедление приближается к своему максимальному значению
, проскальзывание всех колес приближается к одному и тому же значению, которое представляет максимальное возможное проскальзывание
для обеспечения минимального тормозного пути.
Результаты, полученные при компьютерном моделировании, показывают гораздо более стабильное поведение
для транспортного средства при использовании «оптимизированной» стратегии во время резкого торможения в повороте
по сравнению с традиционной стратегией «равного скольжения».
Ссылки
Buschmann, G., Ebner, H.T. и Кун, В. (1992) «Электронное распределение тормозных сил — A
, сложное для ABS, документ SAE №
6. Эсмаилзаде, Э., Воссуги, Г. и Goodarzi, A. (2001) «Динамическое моделирование и анализ электромобиля с четырьмя моторизованными колесами
», Vehicle Systems Dynamics, Vol. 35, No. 3,
pp.163–194.
Франк, П. (2000) «Контроль проскальзывания при малых значениях скольжения для тормозной системы дорожного транспортного средства», Periodical
Ploytechnica Ser.Мех. Eng., Vol. 44, No. 1, pp.23–30.
Гиллеспи, Т.Д. (1992) Основы динамики транспортного средства, опубликовано SAE Inc.,
Warrendale, PA.