Удельная теплоемкость газа формула: Теплоёмкость идеального газа

Содержание

Теплоёмкость идеального газа

В случае, если результатом теплообмена становится передача телу некоего количества теплоты Q, то его температура и внутренняя энергия претерпевают изменения.

Определение 1

Необходимое для нагревания 1 кг вещества на 1 К количество теплоты Q носит название удельной теплоемкости вещества c, а ее формула выглядит следующим образом:

c=Qm∆T.

В большом количестве ситуаций удобной для использования является молярная теплоемкость C:

C=M·c, где M представляет собой молярную массу вещества.

Теплоемкость, полученная таким способом, не является однозначной характеристикой вещества. Исходя из первого закона термодинамики, можно сказать, что изменение внутренней энергии тела зависимо не только от количества полученной теплоты, но и от величины совершенной телом работы. В разных условиях осуществления процесса теплопередачи тело может совершать различную работу.

Таким образом, переданное телу одинаковое количество теплоты способно провоцировать изменения его внутренней энергии и, соответственно, температуры.

Подобной неоднозначностью при определении теплоемкости характеризуются только газообразные вещества. Объем в процессе нагрева практически не меняет своей величины, что сводит работу расширения к нулю. По этой причине вся полученная телом теплота уходит на изменение его внутренней энергии. Газ в процессе теплопередачи может значительно менять свой объем и совершать работу, чем отличается от твердых тел и жидкостей. Таким образом, теплоемкость газообразного вещества имеет зависимость от характера термодинамического процесса.

Изопроцессы в газах

Определение 2

Чаще всего рассматриваются два значения теплоемкости газов:

CV являющаяся молярной теплоемкостью в изохорном процессе (V=const);
Cp представляющая собой молярную теплоемкость в изобарном процессе (p=const).

При условии постоянного объема газ не совершает работы: A=0. Исходя из первого закона термодинамики для 1 моля газа, можно сказать, что справедливым является следующее выражение:

QV=CV∆T=∆U.

Изменение величины ΔU внутренней энергии газа прямо пропорционально изменению значения ΔT его температуры.

В условиях процесса при постоянном давлении первый закон термодинамики дает такую формулу:

Qp=∆U+p(V2-V1)=CV∆T+pV.

В котором ΔV является изменением объема 1 моля идеального газа при изменении его температуры на ΔT. Таким образом, можно заявить, что:

Cp=Qp∆T=CV+p∆V∆T.

Из уравнения состояния идеального газа, записанного для 1 моля, может выражаться отношение ΔVΔT:

pV=R.

В котором R представляет собой универсальную газовую постоянную. При условии постоянства давления p=const, можно записать следующее:p∆V=R∆T или ∆V∆T=Rp.

Определение 3

Из этого следует, что выражающее связь между молярными теплоемкостями Cp и CV_{соотношение имеет вид (формула Майера):}

Cp=CV+R.

В процессе с неизменным давлением молярная теплоемкость Cp газа всегда превышает молярную теплоемкость CV в процессе с не подверженным изменениям объемом, что демонстрируется на рисунке 3. 10.1.

Рисунок 3.10.1. Два возможных процесса нагревания газа на ΔT=T2 –T1. При p=const газ совершает работу A=p1(V2 – V1). Поэтому Cp>CV.

Определение 4

Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом занимает важное место в термодинамике и обозначается в виде греческой буквы γ.

γ=CpCV.

Данное отношение включено в формулу для адиабатического процесса.

Между двумя изотермами, обладающими температурами T1 и T2 на диаграмме (p, V) реальны различные варианты перехода. Так как для всех подобных переходов изменение величины температуры ΔT=T2 –T1 является одним и тем же, выходит, что изменение значения
ΔU внутренней энергии тоже одинаково. С другой стороны, совершенные при этом работы A и количества теплоты Q, полученные в результате теплообмена, выйдут разными для различных путей перехода. Из этого следует, что газа имеет относительно приближенное к бесконечности число теплоемкостей. Cp и CV представляют собой частные, однако, очень важные для теории газов, значения теплоемкостей.

Рисунок 3.10.2. Модель теплоемкости идеального газа.

Определение 5

Термодинамические процессы, в которых теплоемкость газа не подвергается изменениям, носят название политропических.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Каждый изопроцесс являются политропическим. В изотермическом процессе ΔT=0, из-за чего CT=∞. В адиабатическом процессе ΔQ=0, выходит, что Cад=0.

Замечание 1

Стоит обратить внимание на то, что «теплоемкость» и «количество теплоты» являются крайне неудачными терминами, доставшимися современной науке в качестве наследства теории теплорода, которая господствовала в XVIII веке.

Данная теория представляла теплоту в виде содержащегося в телах особого невесомого вещества. Считалось, что оно не подвержено уничтожению и не может быть созданным. Явление нагрева объясняли повышением, а охлаждение – понижением содержания в телах теплорода. Однако теория теплорода оказалась несостоятельной, так как не смогла дать ответа на вопрос, почему одинаковое изменение внутренней энергии тела возможно получить, приводя ему разное количество теплоты в зависимости от совершаемой им работы. По этой причине утверждение, что в данном теле содержится некоторый запас теплорода лишено смысла.

Молекулярно-кинетическая теория

В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией E→ поступательного движения молекул и абсолютной температурой T:

E→=32kT.

Внутренняя энергия 1 моля идеального газа эквивалентна произведению E→ на число АвогадроNА:

U=32kNAT=32RT.

При условии изменения температуры на величину ΔT внутренняя энергия изменяется на величину:

U=32R∆T=CV∆T.

Коэффициент пропорциональности между ΔU и ΔT эквивалентен теплоемкости CV в условиях постоянного давления:

CV=32R=12,47 ДЖ/моль·К.

Данное выражение подтверждается экспериментами с газами, которые состоят из одноатомных молекул вроде гелия, неона или аргона.

При этом для двухатомных (водород, азот) и многоатомных (углекислый газ) газов такое соотношение не согласуется с полученными в результате опытов данными. Причина этого расхождения заключается в том, что для двух- и многоатомных молекул средняя кинетическая энергия должна включать энергию как поступательного, так и вращательного их движения.

Рисунок 3.10.3. Модель двухатомной молекулы. Точка O совпадает с центром масс молекулы.

Рисунок 3.10.3 иллюстрирует модель двухатомной молекулы. Молекула имеет возможность производить пять независимых типов движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y.

Опытным путем выяснено, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких значениях температуры. В условиях обычных температур вращение вокруг оси Z не происходит.

Определение 6

Каждое независимое движение в молекуле носит название степени свободы.

Выходит, что одноатомная молекула обладает 3 поступательными степенями свободы, «жесткая» двухатомная молекула 5 степенями, то есть 3 поступательными и 2 вращательными, а многоатомная молекула 6 степенями свободы, из которых 3 приходятся на поступательные и 3 на вращательные.

Теорема 1

В классической статистической физике доказывается теорема о равномерном распределении энергии по степеням свободы:

Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна 12kT.

Из данной теоремы следует, что для молярных теплоемкостей газа Cp и CV и их отношения
γ справедлива запись в следующем виде:

CV=i2R, Cp=Cv+R=i+22R, γ=CpCV=i+2i,

где i представляет собой количество степеней свободы газа.

Для газа, состоящего из одноатомных молекул (i=3)

CV=32R, Cp=Cv+R=52R, γ=CpCV=53=1,66.

Для газа, состоящего из двухатомных молекул (i=5)

CV=52R, Cp=Cv+R=72R, γ=CpCV=75=1,4.

Для газа, состоящего из многоатомных молекул (i=6)

CV=3R, Cp=Cv+R=4R, γ=CpCV=43=1,33.

В обычных условиях экспериментально измеренные теплоемкости многих газов неплохо согласуются с приведенными выражениями, но в целом классическая теория теплоемкости газов вполне удовлетворительной не является. Существует колоссальное число примеров со значительной разницей между результатами эксперимента и теорией. Данный факт объясняется тем, что классическая теория не может полностью учесть, связанную с внутренними движениями в молекуле энергию.

Теорема о равномерном распределении энергии по степеням свободы может быть применена и по отношению к тепловому движению частиц в твердом теле. Входящие в состав кристаллической решетки атомы колеблются около положений равновесия. Энергия данных колебаний представляет собой внутреннюю энергию твердого тела. Каждый конкретный атом может колебаться в кристаллической решетке в трех взаимно перпендикулярных направлениях. Выходит, что каждый атом имеет 3 колебательные степени свободы.

При условии гармонических колебаний средняя кинетическая энергия эквивалентна средней потенциальной энергии. По этой причине в соответствии с теоремой о равномерном распределении на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом – 3kT.

Определение 7

Внутренняя энергия 1 моля твердого вещества равна следующему выражению:

U=3RNAkt=3Rt.

Следовательно, молярная теплоемкость вещества в твердом состоянии равняется:

С=3R=25,12 Дж/моль·К.

Данное выражение носит название закона Дюлонга–Пти. Для твердых тел почти нет различия между Cp и CV по причине пренебрежительно малой работы при сжатии или расширении.

Опыт показывает, что молярная теплоемкость у многих твердых тел (химических элементов) при обычных температурах на самом деле близка к 3R. При этом, в условиях низких температур заметны довольно сильные расхождения между теорией и экспериментом. Таким образом, гипотеза о равномерном распределении энергии по степеням свободы может считаться лишь приближением. Заметная в опыте зависимость теплоемкости от температуры объясняется только при условии использования квантовых представлений.

Теплоемкость газа и газовой смеси.

Теплоемкость газов

Понятие о теплоемкости

Замысловатый термин «теплоемкость» не что иное, как способность тела расходовать внешнюю тепловую энергию для повышения внутренней кинетической энергии собственных молекул, т. е. повышать температуру при подводе тепла извне.
Как мы уже знаем из предыдущих статей, повышение температуры любого вещества сопровождается увеличением кинетической энергии его частиц, скорость которых начинает возрастать. Этот процесс неизбежно сопровождается уменьшением внутренней потенциальной энергии молекул тела, поскольку они слабее взаимодействуют посредством гравитационных и электромагнитных полей (в первую очередь из-за увеличения расстояния между ними).

Различные вещества способны по-разному «впитывать» внешнюю энергию. Чтобы нагреть до определенной температуры, например, 1 кг нержавеющей стали, необходимо затратить значительно больше тепла, чем для нагрева 1 кг чугуна.
Подобный факт наталкивает на мысль о введении понятия некоторой способности материальных тел «захватывать» и «впитывать» поступающее от окружающей среды тепло. Именно этим физическим свойством материальных тел является теплоемкость.

Чтобы повысить температуру единицы количества вещества на dT, необходимо сообщить ему теплоту dq.
Отношение c = dq/dT называют удельной теплоемкостью вещества.
Удельная теплоемкость показывает, какое количество теплоты необходимо подвести к единице вещества, чтобы нагреть его на 1К (один градус Кельвина).

В зависимости от выбранной единице количества вещества различают массовую (отнесенную к 1 кг), киломольную (отнесенную к 1 кмолю) и объемную (отнесенную к 1 м³) удельные теплоемкости.
Удельная теплоемкость газа зависит от способа подвода к нему теплоты. Очевидно, что на основании определения теплоемкости и уравнения первого закона термодинамики можно записать:

c = dq/dT = (du + pdv)/dT = du/dT + pdv/dT.

Величину pdv/dT называют удельной работой. Она показывает, какую работу совершает единица количества газа при повышении его температуры на 1К.
Если при подводе теплоты к газу занимаемый им объем остается постоянным (v = const), то dv = 0 и удельная теплоемкость c_v = du/dT, откуда du = c_vdT.

Если же при подводе к газу теплоты его давление остается неизменным (p = const), то удельная теплоемкость будет равна:

c_p = c_v + pdv/dT. (1)

Следовательно, удельная теплоемкость при постоянном давлении больше удельной теплоемкости при постоянном объеме на удельную работу.

Если продифференцировать уравнение состояния pv = RT при p = const, получим выражение удельной работы для идеальных газов:

dA = pdv/dT = R.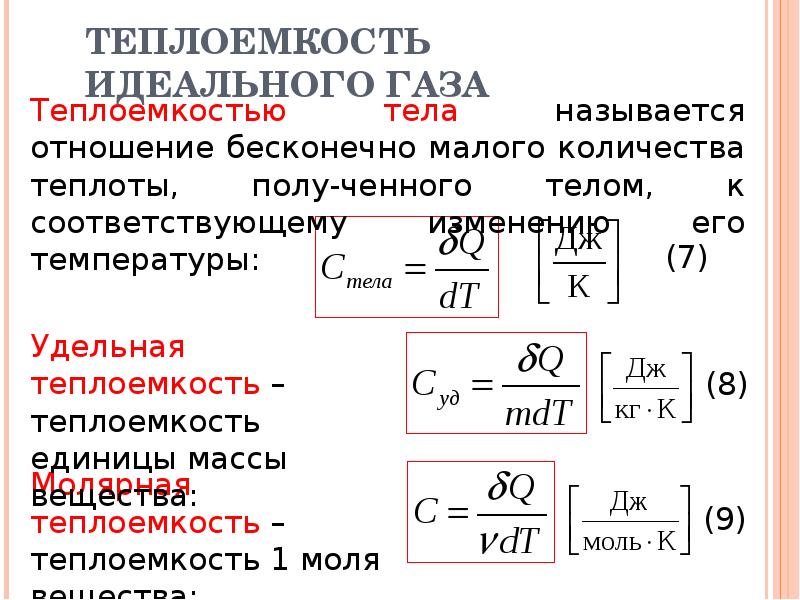 (2)

Эта формула позволяет уяснить физический смысл газовой постоянной. Газовая постоянная R – это работа, совершаемая единицей количества газа при нагревании на 1К, если теплота подводилась при постоянном давлении.
Подставив в уравнение (1) значение удельной газовой постоянной из формулы (2), получим уравнение Майера:

c_v – c_p = R.

Для идеального газа значения cp и cv постоянны, поэтому и отношение c_p/c_v = k тоже является величиной постоянной.
Нагревая идеальный газ от температуры T₁ до T₂ при постоянном объеме, необходимо подвести количество теплоты, равное:

q_v = c_v(T₁ – T₂),

а для нагревания при постоянном давлении:

q_p = c_p(T₁ – T₂).

***

Зависимость теплоемкости от температуры

Удельная теплоемкость реальных газов в отличие от идеальных газов зависит от давления и температуры. Зависимостью удельной теплоемкости от давления в практических расчетах можно пренебречь. Но зависимость удельной теплоемкости от температуры необходимо учитывать, поскольку она очень существенна.
Исследования показывают, что удельная теплоемкость реальных газов является сложной функцией температуры:

c = f(T).

Из этого следует, что в различных температурных интервалах для нагревания единицы количества газа на 1К требуется разное количество теплоты.
Однако, если выбрать достаточно узкий температурный интервал, то для него можно принять удельную теплоемкость постоянной. Очевидно, что если этот температурный интервал стремится к нулю, удельная теплоемкость соответствует истинной удельной теплоемкости при данной температуре:

c = lim Δq/ΔT при Т стремящемся к нулю, или c = dq/dT, откуда

dq = cdT.

Чтобы определить количество теплоты, необходимое для нагревания газа от T₁ до T₂, необходимо проинтегрировать полученную дифференциальную зависимость.

При практическом решении теплотехнических задач пользуются понятием средней удельной теплоемкости в заданном температурном интервале.
Средняя удельная теплоемкость (c_m) газа в некотором интервале температур – это количество теплоты, которое необходимо подвести к газу или отвести от него, чтобы изменить температуру на 1К в данном температурном интервале.

***

Удельная теплоемкость газовой смеси

Под удельной массовой теплоемкостью ссм газовой смеси понимают количество теплоты, необходимое для нагревания 1 кг смеси на 1К. Очевидно, что это количество теплоты можно получить путем суммирования количества теплоты, необходимое для нагревания каждого компонента, входящего в состав смеси:

с_см = Σ c_im_i,

где:
c_i – удельная массовая теплоемкость i-го компонента смеси;
m_i — массовая доля этого компонента в смеси.

Аналогично можно определить удельную объемную теплоемкость газовой смеси – как сумму удельных объемных теплоемкостей ее компонентов. Удельная киломольная теплоемкость смеси газов определяется по формуле:

μ_см с_см = Σ μ_ic_ir_i,

где: μ_i – молекулярная масса компонента смеси; r_i – объемная доля компонента в составе смеси.

***

Термодинамические процессы

Скачать теоретические вопросы к экзаменационным билетам
по учебной дисциплине «Основы гидравлики и теплотехники»
(в формате Word, размер файла 68 кБ)

Скачать рабочую программу
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word):

Скачать календарно-тематический план
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word):

Главная страница

Дистанционное образование

Специальности

Учебные дисциплины

Олимпиады и тесты

28.

Теплоёмкость. Молярная и удельная теплоёмкости. Связь между ними. Формула Майера.

Количество тепла, при получении которого температура тела повышается на один градус, называется теплоемкостью. Согласно этому определению.

Теплоемкость, отнесенная к единице массы, называется удельной теплоемкостью. Теплоемкость, отнесенная к одному молю, называется моляpной теплоемкостью.

Итак, теплоемкость опpеделяется чеpез понятие количества теплоты. Но последнее, как и pабота, зависит от пpоцесса. Значит и теплоемкость зависит от пpоцесса. Сообщать теплоту — нагpевать тело — можно пpи pазличных условиях. Однако пpи pазличных условиях на одно и то же увеличение темпеpатуpы тела потpебуется pазличное количество теплоты. Следовательно, тела можно хаpактеpизовать не одной теплоемкостью, а бесчисленным множеством (столько же, сколько можно пpидумать всевозможных пpоцессов, пpи котоpых пpоисходит теплопеpедача). Однако на пpактике обычно пользуются опpеделением двух теплоемкостей: теплоемкости пpи постоянном объеме и теплоемкости пpи постоянном давлении.

Теплоемкость различается в зависимости от того, при каких условиях происходит нагревание тела — при постоянном объеме или при постоянном давлении.

Если нагревание тела происходит при постоянном объеме, т. е. dV = 0, то работа равна нулю. В этом случае передаваемое телу тепло идет только на изменение его внутренней энергии, dQ = dE, и в этом случае теплоемкость равна изменению внутренней энергии при изменении температуры на 1 К, т. е.

.Поскольку для газа , то.Эта формула определяет теплоемкость 1 моля идеального газа, называемую молярной. При нагревании газа при постоянном давлении его объем меняется, сообщенное телу тепло идет не только на увеличение его внутренней энергии, но и на совершение работы, т.е.dQ = dE + PdV. Теплоемкость при постоянном давлении .

Для идеального газа PV = RT и поэтому PdV = RdT.

Учитывая это, найдем.Отношение представляет собой величину, характерную для каждого газа и определяемую числом степеней свободы молекул газа. Измерение теплоемкости тела есть, таким образом, способ непосредственного измерения микроскопических характеристик составляющих его молекул.

Формулы для теплоемкости идеального газа приблизительно верно описывают эксперимент, причем, в основном, для одноатомных газов. Согласно формулам, полученным выше, теплоемкость не должна зависеть от температуры. На самом деле наблюдается картина, изображенная на рис., полученная опытным путем для двухатомного газа водорода. На участке 1 газ ведет себя как система частиц, обладающих лишь поступательными степенями свободы, на участке 2 возбуждается движение, связанное с вращательными степенями свободы и, наконец, на участке 3 появляются две колебательные степени свободы. Ступеньки на кривой хорошо согласуются с формулой (2.35), однако между ними теплоемкость растет с температурой, что соответствует как бы нецелому переменному числу степеней свободы. Такое поведение теплоемкости указывает на недостаточность используемого нами представления об идеальном газе для описания реальных свойств вещества.

Связь молярной теплоёмкости с удельной теплоёмкостьюС=M•с, где с — удельная теплоёмкость, М — молярная масса.Формула Майера.

Для любого идеального газа справедливо соотношение Майера:

,где R — универсальная газовая постоянная, — молярная теплоемкость при постоянном давлении, — молярная теплоемкость при постоянном объёме.

Задачи по теме «Теплоемкость идеального газа»

Решение задач дело полезное, но не всегда интересное. Чтобы вы справлялись с решением задач по теме «Теплоемкость идеального газа» быстрее, приведем здесь несколько примеров и вопросов с объяснениями.

Подписывайтесь на наш телеграм-канал, чтобы получать полезную и интересную рассылку.

Задачи по теме «Теплоемкость идеального газа» с решениями

Повторение и практика – залог успеха в любом деле. И решение задач не исключение. Поэтому не забываем держать под рукой памятку по задачам и полезные формулы

Задача №1. Определить удельную теплоемкость идеального газа

Условие

Определить молярную массу M двухатомного газа и его удельные теплоемкости, если известно, что разность cр — cv удельных теплоемкостей этого газа равна 260 Дж/(кг*К)

Решение

По определению:

Значит, газ из задачи – кислород. Если кто не понял, как это определяется, учитесь пользоваться таблицей Менделеева.

Считаем удельные теплоемкости:

Ответ: 32 г/моль; 649 Дж/кг*К; 909 Дж/кг*К.

Задача №2. Удельная теплоемкость

Условие

Плотность некоторого газа при нормальных условиях ρ = 1,25 кг/м3. Отношение удельных теплоемкостей γ = 1,4. Определить удельные теплоемкости cv и сp этого газа.

Решение

Исходя из отношения удельных теплоемкостей, можно сделать вывод, что газ – двухатомный, i=5. При постоянном объеме удельная теплоемкость равна:

Молярную массу можно найти из уравнения Клапейрона-Менделеева:

Отсюда:

Ответ: 742 Дж/кг*К; 1039 Дж/кг*К.

Задача №3. Молярная теплоемкость

Условие

Вычислить молярные теплоемкости газа, зная, что его молярная масса М = 4∙10 3 кг/моль и отношение удельных теплоемкостей ср/сv = 1,67.

Решение

Удельные теплоемкости равны:

Можно найти:

Ответ: 12,4 Дж/моль*К; 20,71 Дж/моль*К

Задача №4. Теплоемкость при изопроцессах

Условие

На рисунке изображен изотермический процесс с газом постоянной массы. Сравните теплоемкость в процессе АВ с теплоемкостью этой же массы газа в изохорном процессе.

Решение

Теплоемкость при изохорном процессе является постоянной величиной. При изотермическом процесса она равна бесконечности. Значит, теплоемкость в процессе АВ больше.

Ответ: Теплоемкость в процессе АВ больше.

Задача №5. Теплоемкость при политропическом процессе

Условие

Найдите молярную теплоемкость идеального газа при политропическом процессе pVn = const, если показатель адиабаты газа равен γ. При каких значениях показателя политропы n теплоемкость газа будет отрицательной?

Решение

Запишем первое начало термодинамики, выражения для работы и изменения внутренней энергии в политропическом процессе соответственно:

Если количество вещества и изменение температуры принять равными единице, это выражение будет равно молярной теплоемкости (по определению теплоемкости):

Ответ: см. выражение выше.

Вопросы по теме «Теплоемкость идеального газа»

Вопрос 1. Что такое теплоемкость идеального газа?

Ответ. Когда газу сообщается определенное количество теплоты, меняется его температура.

Отношение количества теплоты, сообщенного газу, к изменению его температуры, называется теплоемкостью идеального газа.

Вопрос 2. Что такое молярная и удельная теплоемкость идеального газа?

Ответ. Молярная и удельная теплоемкости активно используются в термодинамике. Молярная теплоемкость – это теплоемкость одного моля вещества.

Удельная теплоемкость – теплоемкость единичной массы вещества.

Вопрос 3. Как определяется теплоемкость газа при изопроцессах?

Ответ.

При изотермическом процессе T=const. Теплоемкость равна плюс/минус бесконечности.
При адиабатном процессе нет теплообмена с окружающей средой, теплоемкость равна нулю.
При изохорном процессе газ не совершает работы, а теплоемкость равна:

Здесь i – количество степеней свободы молекул газа. Для одноатомных газов i=3, для двухатомных i=5.

При изобарном процессе теплоемкость определяется соотношением Мейера:

Вопрос 4. Как еще связаны теплоемкости при постоянном давлении и постоянном объеме?

Ответ. Отношение теплоемкостей при постоянном давлении и постоянном объеме обозначается греческой буквой «гамма» и называется показателем адиабаты.

Вопрос 5. Как называются процессы, в которых теплоемкость газа остается неизменной?

Ответ. Такие процессы называются политропными. Адиабатный процесс – частный случай политропного процесса.

Теплоемкость реального газа не равна теплоемкости идеального газа и может сильно отличаться.

Нужна помощь в решении задач и выполнении других заданий? Специальный студенческий сервис готов оказать ее!

лабораторная работа 209

Лабораторная работа № 209

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ВОЗДУХА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ И ПОСТОЯННОМ ОБЪЕМЕ

Цель работы: определить методом Клемана-Дезорма отношение теплоемкостей воздуха при постоянном давлении и постоянном объеме.

Приборы и принадлежности:

стеклянный баллон,

насос Камовского,

U–образный водяной манометр,

соединительные шланги.

1. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА

В молекулярной физике термодинамическое состояние газа характеризуется параметрами состояния: давлением Р, объемом V, температурой Т, массой m и т.д. Уравнение, связывающие эти величины называется уравнением состояния вещества. Для случая идеального газа уравнением состояния является уравнение Менделеева-Клапейрона, которое имеет вид:

(1)

где R – молярная газовая постоянная, m — масса одного моля газа.

Теплоемкостью вещества называется величина, равная количеству теплоты, которое нужно сообщить веществу, чтобы изменить его температуру на один градус. Математически это определение записывается следующим образом:

где dQ – бесконечно малое количество теплоты, при сообщении которого изменяется температура вещества на dT. Теплоемкость вещества измеряется в Дж/K.

На практике часто пользуются понятиями удельной и молярной теплоемкостей вещества. Удельная теплоемкость – теплоемкость единицы массы вещества, т.е. она равна количеству теплоты, которое нужно сообщить единице массы вещества, чтобы изменить его температуру на один градус:

Молярная теплоемкость – теплоемкость одного моля вещества, т.е. она равна количеству теплоты, которое нужно сообщить одному молю вещества, чтобы изменить его температуру на один градус:

где — количество молей вещества (понятие идеального газа и моля вещества см. в лаб. раб. № 201).

Удельная и молярная теплоемкости связаны соотношением

Величина теплоемкости газа зависит от условий, при которых он нагревается. Выясним эту зависимость, воспользовавшись уравнением состояния (1) и первым законом термодинамики, который можно сформулировать следующим образом: количество теплоты dQ, сообщаемое термодинамической системе (в нашем случае воздуху), расходуется на увеличение внутренней энергии dU и на совершение системой работы dA против внешних сил. Математическая запись первого закона термодинамики:

(2)

где dU — бесконечно малое изменение внутренней энергии системы; dQ, dA — соответственно, бесконечно малая теплота, подводимая к системе и элементарная работа.

Тогда теплоемкость вещества равна

(3)

Из уравнения (3) видно, что теплоемкость имеет различные значения в зависимости от способа нагревания газа, т.к. одному и тому же значению dT могут соответствовать различные значения dU и dA. Элементарная работа в газовом процессе равна

(4)

Рассмотрим основные процессы, протекающие в идеальном газе при изменении температуры, когда количество вещества остается неизменным.

Если нагревание производится при постоянном объеме, то газ не совершает работы над внешними телами и, следовательно, вся теплота идет на приращение внутренней энергии газа:

при .

Тогда молярная теплоемкость газа при постоянном объеме равна:

(5)

Если нагревание происходит при постоянном давлении, то теплота, сообщаемая газу, идет и на изменение внутренней энергии газа и на совершение газом работы против внешних сил:

при

В этом случае молярная теплоемкость газа при постоянном давлении равна:

(6)

Дифференцируя уравнение (1), получим:

(7)

но если Р = const, тогда

(8)

С учетом (8), (4) и (5) уравнение (6) запишется:

(9)

Из формулы (9) следует, что С_Р > C_V на величину R, которая равна работе, совершаемой молем идеального газа при повышении его температуры на один градус при постоянном давлении.

Необходимо отметить, что соотношение (9) справедливо только для идеального газа. Отношение теплоемкостей

(10)

представляет собой характерную для каждого газа величину, которая называется постоянной адиабаты.

2. УРАВНЕНИЕ АДИАБАТЫ ИДЕАЛЬНОГО ГАЗА

Процесс, протекающий в термодинамической системе без теплообмена с внешней средой, называется адиабатическим. Первый закон термодинамики для идеального газа в этом случае будет иметь вид:

т.к. dQ = 0 или, используя (2) и (5), запишем

(11)

Разделив уравнение (7) на (11) и учитывая формулу (9), получим:

или

(12)

где Интегрируя и потенцируя формулу (12), получим уравнение адиабаты идеального газа в переменных Р и V:

(13)

Полученное выражение есть уравнение газового состояния при адиабатическом процессе, называемое также уравнением Пуассона.

3. ВНУТРЕННЯЯ ЭНЕРГИЯ И ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ

МОЛЕКУЛ ИДЕАЛЬНОГО ГАЗА

Из молекулярно-кинетической теории идеального газа следует, что средняя кинетическая энергия молекулы равна

где k – постоянная Больцмана, Т – термодинамическая температура, i — число степеней свободы молекулы газа.

Числом степеней свободы i называют наименьшее число независимых координат, с помощью которых можно однозначно определить положение тела в пространстве. Силы, ограничивающие движение тела, называются связями. Если тело движется без связей, то такое движение тела называется свободным. Так, свободное положение в пространстве материальной точки полностью определяется заданием значений трех ее координат (например, х, y, z – в декартовой системе координат). В соответствии с этим материальная точка имеет три степени свободы (i = 3). Если эта точка движется по некоторой поверхности, то она обладает двумя степенями свободы.

Абсолютно твердое тело имеет шесть степеней свободы (i = 6). Для определения его положения в пространстве нужно задать три координаты его центра масс (х,y,z), два угла (например, q и j), указывающих направление какой-либо оси, проходящей через центр масс тела и, наконец, угол y, определяющий направление второй, связанной с телом оси, перпендикулярной к первой. Степени свободы х, y, z называются поступательными. Изменение любого из углов q, j, y при неизменном положении центра масс обуславливается вращением тела, в связи с чем, соответствующие степени свободы называются вращательными. Следовательно, из шести степеней свободы абсолютно твердого тела три являются поступательными и три — вращательными.

Молекулу одноатомного газа можно рассматривать как материальную точку, поэтому число степеней свободы одноатомной молекулы равно трем. Молекулы, состоящие из двух, трех и большего числа атомов не могут быть уподоблены материальным точкам. «Жесткая» молекула двухатомного газа в первом приближении представляет собой два жестко связанных атома, находящихся на некотором расстоянии друг от друга (см. рис. 1а).

Такая молекула напоминает гимнастическую гантель с невесомой ручкой, обладающую тремя степенями свободы поступательного движения относительно осей х, y, z, и двумя степенями свободы вращательного движения вокруг осей х и z. Вращение вокруг третьей оси y рассматривать не нужно, т.к. момент инерции атомов относительно этой оси ничтожно мал, а, следовательно, ничтожно мала и кинетическая энергия молекулы, связанная с этим вращением.

Трехатомные и более сложные молекулы подобно абсолютно твердому телу обладают тремя степенями свободы поступательного движения и тремя степенями свободы вращательного движения (рис. 1b).

Если атомы в молекуле совершают еще и колебания, то кроме кинетической энергии необходимо учитывать потенциальную энергию взаимодействия этих атомов, и как показывает опыт, средняя потенциальная энергия атомов равна их средней кинетической энергии. Тогда полную энергию, приходящуюся на одну колебательную степень свободы, можно считать равной удвоенной ее кинетической энергии. Поэтому при учете колебательных степеней свободы необходимо энергию молекулы увеличивать на величину kT, а число i соответственно на два. В случае молекулы, состоящей из N-атомов, число степеней свободы равно

При этом i_пост= 3. Для линейной молекулы i_вращ = 2, i_кол= 3N – 5. Для всех других молекул i_вращ = 3, i_кол= 3N – 6.

Так как молекулы идеального газа не взаимодействуют между собой, то внутреннюю энергию идеального газа массы m можно найти, умножив среднюю кинетическую энергию одной молекулы на число молекул:

т.к. где N_A — число Авогадро, а R = kN_A.

Сравнение этого выражения с формулой (5) дает, что молярная теплоемкость идеального газа при постоянном объеме равна:

Приняв во внимание формулу (9), найдем молярную теплоемкость идеального газа при постоянном давлении:

Т. о., постоянная адиабаты для идеального газа выражается формулой:

(14)

Соотношение (14) позволяет по значению g оценить число степеней свободы молекул газа.

4. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И

МЕТОДА ИЗМЕРЕНИЙ

Величину g, т.е. отношение теплоемкости С_P газа при постоянном давлении к его теплоемкости С_V при постоянном объеме можно определить с помощью прибора Клемана-Дезорма, состоящего из стеклянного баллона 1; крана 2, позволяющего изолировать или сообщать баллон с атмосферой; крана 3, разобщающего баллон и насос; насоса 4, служащего для создания в баллоне избыточного давления; U-образного водяного манометра 5, служащего для регистрации разности между давлением воздуха в баллоне и атмосферным давлением.

Рис. 2.

В роли крана 2 используется пробка, перекрывающая отверстие в крышке баллона.

Закрывают плотно пробку 2 и открывают кран 3. Небольшими порциями с помощью насоса 4 накачивают воздух в баллон до некоторого давления. Затем с помощью крана 3 разобщают баллон с насосом. Если повышение давления было произведено достаточно быстро, манометрический столбик жидкости не сразу займет окончательное положение, т.к. сжатие воздуха было близким к адиабатическому, и, следовательно, температура его повысилась. Окончательная разность уровней в манометре (h) установится только тогда, когда температура воздуха внутри сосуда сравняется благодаря теплопроводности стенок с температурой окружающего воздуха.

Обозначим через Т₁ абсолютную температуру окружающего воздуха и через Р₁ – давление газа внутри сосуда, тогда после накачки воздуха

(15)

где – избыточное давление воздуха в баллоне над внешним — атмосферным Р₀, обусловленное накачкой воздуха.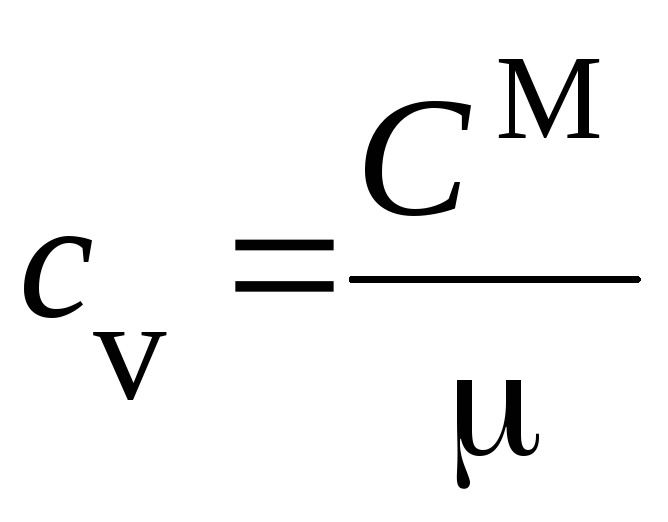

Пусть параметры Т₁, V₁ и Р₁ характеризуют состояние газа, которое будем называть первым состоянием (состояние 1, см. рис. 3). Здесь V₁ – объем той массы m воздуха, которая при любых протекающих в баллоне процессах остается постоянной.

Газовые законы обычно применяются для расчетов изменений, происходящих с газом, масса которого остается постоянной. В нашем же случае часть воздуха выходит из баллона при сообщении его с атмосферой. Поэтому все дальнейшие рассуждения относятся не ко всему воздуху в баллоне, а лишь к той его части, которая все время присутствует в баллоне и остается в нем после его разобщения с атмосферой в точке 3 (рис. 3). Остальная часть воздуха может рассматриваться как поршень, который выдвигается из баллона при расширении.

Если теперь быстро открыть пробку 2, то воздух в сосуде будет расширяться адиабатически, пока давление его не сделается равным атмосферному Р₀; при этом он охладится до температуры Т₂. Это будет второе состояние газа (состояние 2).

Изменение состояния газа графически можно изобразить адиабатой (1 ® 2). Для данной массы газа m согласно уравнению Пуассона (13) можно записать соотношение

(16)

Если сразу после открывания снова закрыть пробку 2, то давление внутри сосуда начнет возрастать от Р₀ до Р₂ вследствие того, что охладившийся при расширении воздух в сосуде станет снова нагреваться. Возрастание давления, которое происходит при постоянном объеме, прекратится, когда температура воздуха в сосуде сравняется с температурой окружающей среды (Т₃ = Т₁). Получим третье состояние газа (состояние 3).

Обозначим давление воздуха в сосуде в этот момент через Р₂ и соответствующее избыточное давление, которое установилось в сосуде при нагревании воздуха от температуры Т₂ до комнатной температуры Т₁ через . Тогда

(17)

Начальное 1 и конечное 3 состояния газа массы m наблюдаются при одинаковой температуре (Т₃ = Т₁), т.е. кривая 1-3 является изотермой. Поэтому на основании закона Бойля-Мариотта можно записать:

(18)

Возведя обе части уравнения (18) в степень g, получим

(19)

После того как уравнение (19) разделим на уравнение (16) и результат прологарифмируем, путем простых преобразований получим:

(20)

Поскольку и малы по сравнению с атмосферным давлением , то

можно разложить в ряд Тейлора по малым параметрам, ограничившись двумя первыми членами:



                                                                                                                  (21)



Подставляя (21) в (20), получим

                                                                                            (22)

Избыточное давление, определяемое по манометру, можно выразить соотношением

где h – разность уровней жидкости в манометре, a — постоянный для данного манометра коэффициент, зависящий от плотности жидкости и от площади сечения трубок манометра. Тогда можно записать, что

                                         а

Подставив значения и в (22), получим формулу, удобную для расчета постоянной адиабаты

                                                                                              (23)

5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКА

РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Перед тем как выполнять работу, проверьте, чтобы уровень воды в трубках U-образного манометра при открытой пробке 2 находился на половине высоты манометра. Если воды мало, долейте, попросив мерный стакан у лаборанта.

1.      Пробкой 2 перекрыть отверстие в крышке баллона и открыть кран 3, соединяющий баллон с насосом 4.

2.       Вращая рукоятку насоса, осторожно накачивают воздух в баллон так, чтобы разность уровней жидкости в трубках U-образного манометра составила 25 – 30 см.

3.      Закрыть кран 3, разобщающий баллон и насос. Подождать 2-3 мин. пока жидкость не перестанет перетекать из одной трубки манометра в другую. При накачивании сжатый воздух в баллоне нагревается, поэтому необходимо выждать некоторое время, пока благодаря теплообмену температура в баллоне не станет равной комнатной. По шкале манометра измерьте установившуюся в конце изохорного охлаждения (состояние 1, см. рис. 3) разность уровней жидкости в обоих коленах манометра h₁.

4.      На 2-3 секунды вынимают пробку 2 в крышке баллона и выпускают из него часть воздуха. В первые доли секунды происходит адиабатическое расширение газа (переход 1®2). Пробку быстро ставят на место, плотно закрывая баллон. Выждав 1-2 мин. пока газ, охлажденный при адиабатическом расширении, нагреется до комнатной температуры, измеряют разность уровней жидкости в коленах манометра h₂ в конце изохорного нагревания (состояние 3, см. рис. 3).

5.      По формуле (23) вычисляют значение g.

6.      Опыт повторяют 8 – 10 раз, причем для каждого опыта рассчитывают свое значение g, затем находят среднее арифметическое значение искомой величины по формуле:



где N – число измерений.

7.   Вычисляют абсолютную Dg и относительную Е погрешности результата, исходя из истинного значения искомой величины:

                        и

Данные результатов измерений и вычислений занесите в таблицу.

Таблица результатов

№

опыта

h₁

h₂

g

g_теор.

Dg

Е

м

м

%

1,4

6. ВОПРОСЫ ДЛЯ ДОПУСКА К РАБОТЕ

Какова цель работы?

Опишите устройство рабочей установки и ход эксперимента.

3.      Какой процесс называется адиабатическим? Какие условия соответствуют осуществлению адиабатического процесса на данной установке?

7. ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ

1.      Что называют удельной теплоемкостью вещества? Молярной теплоемкостью? Какая связь между ними?

2.      Сформулируйте первый закон термодинамики.

3.      Чему равны молярные теплоемкости идеальных газов при изопроцессах?

4.      Докажите, что С_Р > C_V.

5.      Получите уравнение Пуассона для адиабатического процесса.

6.      Что называется числом степеней свободы?

7.      Запишите выражение для внутренней энергии идеального газа и поясните его.

8.      Используя уравнение Пуассона, выведите рабочую формулу для расчета постоянной адиабаты g.

9.      Из каких процессов состоит рабочий цикл, осуществляемый на данной установке при выполнении работы? Начертите график цикла.

Удельная теплоемкость газа — Справочник химика 21

Теплоемкость. Для измерения количества теплоты, подводимой к га у (или отводимой от него), надо знать удельную теплоемкость газа. Удельной теплоемкостью (или просто теплоемкостью) называется количество теплоты, которое необходимо подвести к единице количества вещества (или отвести от него), чтобы повысить (или понизить) его температуру на один градус. [c.25]
Удельная теплоемкость газа [c.20]
Удельные теплоемкости газов при постоянном давлении в калориях на 1 кг газа при нагреве на 1 С при температуре, С [c.99]
Удельная теплоемкость (газ), кал/(моль °С) [c.101]
Здесь t — время x,y,z — составляющие декартовых координат v,,v,w — соответствующие составляющие вектора скорости i — внутренняя энергия п = li m m — плотность I = f — 1 f — отношение удельных теплоемкостей газа. [c.18]
Удельной теплоемкостью газа называется количество теплоты, необходимое для нагрева единицы массы газа на один градус. В дальнейшем мы будем иметь дело только с удельной теплоемкостью и назовем ее для краткости просто теплоемкостью. [c.13]
Ср, с, — удельные теплоемкости газа и частиц, ккал/(м -град) с, У —относительные концентрации реагента Со — исходная концентрация, моль/м [c.63]
При средней удельной теплоемкости газов с = ИЗО дж/кг-град (0,27 ккал, кг град) по формуле (11-4) имеем [c.442]
Ср — средняя удельная теплоемкость газа, ккал/(кг- град), I — длина трубки, м. [c.66]
Ср, Су — удельная теплоемкость газа щ постоянном давлении и при постоянном объеме. [c.26]
Пренебрегая незначительными изменениями теплоемкости газов от температуры (изменение удельной теплоемкости газов в диапазоне температур 500 100° С не превышает 3%) [c.269]
Здесь Ра — парциальное давление после сжатия от объема газа V + АУ с давлением до объема У у = с су — отношение удельной теплоемкости газа при постоянном давлении к его удельной теплоемкости при постоянном объеме. Для воздуха, если пары, например воды, составляют малую долю в нем, у = 1,4 при комнатной температуре и атмосферном давлении. При фор- [c.278]
Такое определение справедливо и для жидкости, если при этом не происходит конвективного теплопереноса. Кинетическая теория дает простое объяснение теплопроводности в газа , связывая ее с удельной теплоемкостью газа с , средней скоростью частицы и и средней длиной свободного пробега [c.190]
Пример 12-15. Определить производительность на 1 м сечения аппарата при нагревании Твердых частиц в кипящем слое в условиях примера 12-14. если начальная температура газов равна Г] = 1050° С начальная температура твердых частиц /i = 10° , конечная температура частиц 2 = 950° С. удельная теплоемкость газов С =1170 дж/кг-град (0,28 ккал/кг-град). удельная теплоемкость частиц с = 1420 дж/кг-град (0.34 ккал/кг град), насыпная масса частиц Рнас. = 850 кг/м . [c.463]
Примем далее, что процесс слабо экзотермичен и тепловой эффект реакции составляет = 6-10 Дж/кг газовой смеси, а удельная теплоемкость газа и катализатора равна 10 Дж/(кг-К). Примем также, что катализатор в процессе работы отравляется контактными ядами (или покрывается сажей, как при каталитическом крекинге) и его нужно регенерировать. Для поддержания нужной его активности среднее время пребывания не должно [c.276]
УДЕЛЬНАЯ ТЕПЛОЕМКОСТЬ ГАЗОВ [c.13]
Полагая, что температура материала дм = 22,2 удельная теплоемкость газа с г = 0,24 ккал/(кг-°С), теплосодержание водяного пара п = 595 + + 0,47-160 = 670 ккал/кг, т], = 0,9, /о = 11.58 ккал/кг, с1о = 10,3 г/кг (при [c.295]
Сд(/р —/ ) — количество тепла, отдаваемого при охлаждении некопден-сируемого газа, вт [ккал/ч] Со — удельная теплоемкость газа, дж1(кг-град) [ккол/(кг гросЗ)] — количество тепла, отдаваемого при охлаждении несконденсированного пара, вт [ккал/ч] Сп=Оо- ———колпче- [c.194]
Средняя удельная 1еплоемкость Ср у идеального газа зависит от температуры, а у реального, кроме того, от давления. В формуле( 1.56) указана средняя удельная теплоемкость газа в процессе охлаждения. Она приближенно равна удельной теплоемкости при средней температуре в холодильнике. [c.28]

Здесь д и да — тепловые эффекты окисления диоксида серы кислородом в расчете на 1 м ЗО2 и на 1 м- обжигового газа, кДж/м р — плотность исходного обжигового газа при нормальных условиях, кг/м С — средняя удельная теплоемкость газа в интервале температур Твх—Твых. кДж/(кг-К) Ар — прирост степени превращения на слое катализатора (ограничивается условиями равновесия). [c.212]
В этом уравнении С, Т » — скорость и температура заторможенного газа Ср — удельная теплоемкость газа при постоянном давлении. [c.69]
Удельная теплоемкость газа (при р=101325 Па и 7 =273 К), кДж/(кг-°С) [c.57]
Коэффициент Сж зависит от соотношения газовой константы, приведенной в стандартах ASME, и коэффициента скорости истечения. Он является функцией соотношения удельных теплоемкостей газа ( j v), которые, в свою очередь, зависят от плотности газа. На рис. 55 представлена зависимость коэффициента Сж от относительной плотности газа для сопла, имеющего коэффициент скорости истечения, равный 97,5%. Если обратное давление составляет менее 20% от прямого давления, то Fr и F можно принять равными единице. На рис. 56 приводятся значения Fp и F>k для аппаратов, рабочее давление в которых превышает 7 кгс/см . С помощью рис. 55, 56, зная другие переменные уравнения (73), (74), легко определить величину S. В зависимости от S подбирается предохранительный клапан. При этом необходимо учитывать давление в аппарате, размеры фланцев, температуру среды, материал, из которого изготовлен клапан, и другие ограничения, например обратное давление и т. д. [c.102]
Недостатками этого способа обогрева являются 1) низкий коэффициент теплоотдачи 2) малая объемная удельная теплоемкость газов ( 1500 дж1м -град), что вызывает необходимость пропускания значительных объемов газа 3) неравномер- [c.416]
Термодинамика — Физика — Теория, тесты, формулы и задачи
Оглавление:

Основные теоретические сведения
Теплоемкость вещества
К оглавлению…
Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c. Тогда количество теплоты (энергии) необходимое для изменения температуры некоторого тела массой m можно рассчитать по формуле:
При этом в этой формуле абсолютно не важно в каких единицах подставлена температура, так как нам важно не ее абсолютное значение, а изменение. Единица измерения удельной теплоемкости вещества: Дж/(кг∙К).
Если t₂ > t₁, то Q > 0 – тело нагревается (получает тепло).

Если t₂ < t₁, то Q < 0 – тело охлаждается (отдает тепло).

Произведение массы тела на удельную теплоемкость вещества, из которого оно изготовлено называется теплоемкостью тела (т.е. просто теплоемкостью без слова «удельная»):
Если в условии задачи сказано про теплоемкость тела, то количество теплоты, отданное или полученное этим телом, можно рассчитать по формуле:
Итак, запомните:
Удельная теплоемкость обозначается маленькой буквой с, и является характеристикой вещества.

(Просто) Теплоемкость обозначается большой буквой С, и является характеристикой данного тела.

Напомним, что количество теплоты Q отданное каким–либо источником (нагревателем) рассчитывается по формуле: Q = Pt, где: P – мощность источника, t – время, в течение которого источник отдавал тепло. При решении задач не путайте время работы источника и температуру.

Фазовые превращения
К оглавлению…
Фазой вещества называется однородная система, например, твердое тело, физические свойства которой во всех точках одинаковые. Между различными фазами вещества при обычных условиях существует четко выраженная граница (поверхность) раздела. При изменении внешних условий (температуры, давления, электрических и магнитных полей) вещество может переходить из одной фазы в другую. Такие процессы называются фазовыми превращениями (переходами).
Процесс фазового перехода из жидкого состояния в газообразное (парообразование) или из твердого в жидкое (плавление) может происходить только при сообщении веществу некоторого количества теплоты. Обратные фазовые переходы (конденсация и кристаллизация, или отвердевание) сопровождаются выделением такого же количества теплоты.
Количество теплоты, поступающее в систему или выделяющееся из нее, изменяет ее внутреннюю энергию. Это означает, что внутренняя энергия пара при 100°С больше, чем жидкости при той же температуре. Указанные фазовые переходы идут при постоянных температурах, которые называются соответственно температурой кипения и температурой плавления. Количество теплоты, необходимое для превращения жидкости в пар или выделяемое паром при конденсации, называется теплотой парообразования:
где: r – удельная теплота парообразования. Единица измерения [r] = 1 Дж/кг. Физический смысл удельной теплоты парообразования: она равна количеству теплоты, необходимому для превращения в пар 1 кг жидкости, находящейся при температуре кипения. Превращение жидкости в пар не требует доведение жидкости до кипения. Вода может превратиться в пар и при комнатной температуре. Такой процесс называется испарением.
Количество теплоты, необходимое для плавления тела или выделяемое при кристаллизации (отвердевании), называется теплотой плавления:
где: λ – удельная теплота плавления. Единица измерения [λ] = 1 Дж/кг. Физический смысл удельной теплоты плавления: теплота, необходимая для плавления 1 кг вещества, находящегося при температуре плавления. Удельные теплоты парообразования и плавления называются также скрытыми теплотами, поскольку при фазовых переходах температура системы не меняется, несмотря на то, что теплота к ней подводится.
Обратите внимание: что во время фазовых переходов температура системы не изменяется. А также на то, что сами фазовые переходы начинаются только после достижения необходимой температуры.
Наиболее распространенным источником энергии для нужд человека является топливо – вещество, при сгорании которого выделяется некоторое количество теплоты. Количество теплоты, выделяемое при сгорании топлива массой m, называется теплотой сгорания топлива:
где: q – удельная теплота сгорания (теплотворная способность, калорийность) топлива. Единица измерения [q] = 1 Дж/кг. Физический смысл удельной теплоты сгорания топлива: величина, показывающая, какое количество теплоты выделяется при полном сгорании 1 кг топлива.

Уравнение теплового баланса
К оглавлению…
В соответствии с законом сохранения энергии для замкнутой системы тел, в которой не происходит никаких превращений энергии, кроме теплообмена, количество теплоты, отдаваемое более нагретыми телами, равно количеству теплоты, получаемому более холодными. Теплообмен прекращается в состоянии термодинамического равновесия, т.е. когда температура всех тел системы становится одинаковой. Сформулируем уравнение теплового баланса: в замкнутой системе тел алгебраическая сумма количеств теплоты, отданных и полученных всеми телами, участвующими в теплообмене, равна нулю:
При использовании такой формы записи уравнения теплового баланса, чтобы не сделать ошибку, запомните: когда Вы будете считать теплоту при нагревании или охлаждении тела, нужно из большей температуры вычитать меньшую, чтобы теплота всегда была положительной. Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то уравнение теплового баланса можно записать в виде:
При использовании такой формы записи, нужно всегда от конечной температуры отнимать начальную. При таком подходе знак их разности сам «покажет» отдаёт тело теплоту или получает.
Запомните, что тело поглощает теплоту если происходит:
Нагревание,

Плавление,

Парообразование.

Тело отдает теплоту если происходит:
Охлаждение,

Кристаллизация,

Конденсация,

Сгорание топлива.

Именно в этой теме, имеет смысл не решать задачи в общем виде, а сразу подставлять числа.
Взаимные превращения механической и внутренней энергии
При неупругих ударах механическая энергия частично или полностью переходит во внутреннюю энергию тел, то есть тела могут нагреваться и плавится. В общем случае изменение механической энергии равно выделяющемуся количеству теплоты.

Работа идеального газа
К оглавлению…
Термодинамика – это наука о тепловых явлениях. В противоположность молекулярно–кинетической теории, которая делает выводы на основе представлений о молекулярном строении вещества, термодинамика исходит из наиболее общих закономерностей тепловых процессов и свойств макроскопических систем. Выводы термодинамики опираются на совокупность опытных фактов и не зависят от наших знаний о внутреннем устройстве вещества, хотя в целом ряде случаев термодинамика использует молекулярно–кинетические модели для иллюстрации своих выводов.
Термодинамика рассматривает изолированные системы тел, находящиеся в состоянии термодинамического равновесия. Это означает, что в таких системах прекратились все наблюдаемые макроскопические процессы. Важным свойством термодинамически равновесной системы является выравнивание температуры всех ее частей.
Если термодинамическая система была подвержена внешнему воздействию, то в конечном итоге она перейдет в другое равновесное состояние. Такой переход называется термодинамическим процессом. Если процесс протекает достаточно медленно (в пределе бесконечно медленно), то система в каждый момент времени оказывается близкой к равновесному состоянию. Процессы, состоящие из последовательности равновесных состояний, называются квазистатическими (или квазистационарными, еще одно название таких процессов — равновесные).
В изобарном процессе работу идеального газа можно рассчитывать по формулам:
Подчеркнем еще раз: работу газа по расширению можно считать по этим формулам только если давление постоянно. Согласно данной формуле, при расширении газ совершает положительную работу, а при сжатии – отрицательную (т.е. газ сопротивляется сжатию и над ним нужно совершать работу чтобы оно состоялось).
Если давление нельзя считать постоянным, то работу газа находят, как площадь фигуры под графиком в координатах (p, V). Очевидно, что в изохорном процессе работа газа равна нулю.
Ввиду того, что работа газа численно равна площади под графиком, становится понятно, что величина работы зависит от того, какой именно процесс происходил, ведь у каждого процесса свой график, а под ним своя площадь. Таким образом, работа зависит не только и не столько от начального и конечного состояний газа, сколько от процесса, с помощью которого конечное состояние было достигнуто.

Внутренняя энергия
К оглавлению…
Одним из важнейших понятий термодинамики является внутренняя энергия тела. Все макроскопические тела обладают энергией, заключенной внутри самих тел. С точки зрения молекулярно–кинетической теории внутренняя энергия вещества складывается из кинетической энергии всех атомов и молекул и потенциальной энергии их взаимодействия друг с другом. В частности, внутренняя энергия идеального газа равна сумме кинетических энергий всех частиц газа, находящихся в непрерывном и беспорядочном тепловом движении. Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема. Внутренняя энергия одноатомного идеального газа рассчитывается по формулам:
Таким образом, внутренняя энергия U тела однозначно определяется макроскопическими параметрами, характеризующими состояние тела. Она не зависит от того, каким путем было реализовано данное состояние. Принято говорить, что внутренняя энергия является функцией состояния. Это значит, что изменение внутренней энергии не зависит от того, как система была переведена из одного состояния в другое (а зависит лишь от характеристик первоначального и конечного состояний) и всегда, в любых процессах для одноатомного идеального газа определяется выражением:
Обратите внимание: эта формула верна только для одноатомного газа, зато она применима ко всем процессам (а не только к изобарному, как формула для работы). Как видно из формулы, если температура не изменялась, то внутренняя энергия остаётся постоянной.

Первый закон термодинамики
К оглавлению…
Если система обменивается теплом с окружающими телами и совершает работу (положительную или отрицательную), то изменяется состояние системы, то есть изменяются ее макроскопические параметры (температура, давление, объем). Так как внутренняя энергия U однозначно определяется макроскопическими параметрами, характеризующими состояние системы, то отсюда следует, что процессы теплообмена и совершения работы сопровождаются изменением ΔU внутренней энергии системы.
Первый закон (начало) термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом: Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами. Однако, соотношение, выражающее первый закон термодинамики, чаще записывают в немного другой форме:
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами (такая формулировка более удобна и понятна, в таком виде совсем очевидно, что это просто закон сохранения энергии).
Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких–либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии.
Адиабатным (адиабатическим) называют процесс, в ходе которого система не обменивается теплотой с окружающей средой. При адиабатном процессе Q = 0. Поэтому: ΔU + A = 0, то есть: A = – ΔU. Газ совершает работу за счет уменьшения собственной внутренней энергии.

Первое начало термодинамики и изопроцессы
К оглавлению…
Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const):
Изобарный процесс (p = const):
Изотермический процесс (T = const):
Адиабатный процесс (Q = 0):
Если в задаче явно не сказано, что газ одноатомный (или не назван один из инертных газов, например, гелий), то применять формулы из этого раздела нельзя.

Циклы. Тепловые машины
К оглавлению…
Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами.
Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т.д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние.
Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q₁ > 0 и отдает холодильнику количество теплоты Q₂ < 0.
КПД тепловой машины может быть рассчитан по формуле:
где: Q₁ – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q₂ – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:
Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть (1 – η) была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (η < 1).
Наибольший КПД при заданных температурах нагревателя T₁ и холодильника T₂, достигается если тепловая машина работает по циклу Карно. Цикл Карно состоит из двух изотерм и двух адиабат. КПД цикла Карно равен:

Второе начало (второй закон) термодинамики
К оглавлению…
Первый закон термодинамики не устанавливает направление протекания тепловых процессов. Однако, как показывает опыт, многие тепловые процессы могут протекать только в одном направлении. Такие процессы называются необратимыми. Например, при тепловом контакте двух тел с разными температурами тепловой поток всегда направлен от более теплого тела к более холодному. Никогда не наблюдается самопроизвольный процесс передачи тепла от тела с низкой температурой к телу с более высокой температурой. Следовательно, процесс теплообмена при конечной разности температур является необратимым.
Обратимыми процессами называют процессы перехода системы из одного равновесного состояния в другое, которые можно провести в обратном направлении через ту же последовательность промежуточных равновесных состояний. При этом сама система и окружающие тела возвращаются к исходному состоянию.
Необратимыми являются процессы превращения механической работы во внутреннюю энергию тела из–за наличия трения, процессы диффузии в газах и жидкостях, процессы перемешивания газа при наличии начальной разности давлений и т.д. Все реальные процессы необратимы, но они могут сколь угодно близко приближаться к обратимым процессам. Обратимые процессы являются идеализацией реальных процессов.
Первый закон термодинамики не может отличить обратимые процессы от необратимых. Он просто требует от термодинамического процесса определенного энергетического баланса и ничего не говорит о том, возможен такой процесс или нет. Направление самопроизвольно протекающих процессов устанавливает второй закон термодинамики. Он может быть сформулирован в виде запрета на определенные виды термодинамических процессов.
Английский физик У.Кельвин дал в 1851 году следующую формулировку второго закона: В циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара.
Гипотетическую тепловую машину, в которой мог бы происходить такой процесс, называют «вечным двигателем второго рода». Как уже должно было стать понятно, второе начало термодинамики запрещает существование такого двигателя.
Немецкий физик Р.Клаузиус дал другую формулировку второго закона термодинамики: Невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от тела с низкой температурой к телу с более высокой температурой. Следует отметить, что обе формулировки второго закона термодинамики эквивалентны.

Сложные задачи по термодинамике
К оглавлению…
При решении различных нестандартных задач по термодинамике необходимо учитывать следующие замечания:
Для нахождения работы идеального газа надо построить график процесса в координатах p(V) и найти площадь фигуры под графиком. Если дан график процесса в координатах p(T) или V(T), то его сначала перестраивают в координаты p(V). Если же в условии задаётся математическая зависимость между параметрами газа, то сначала находят зависимость между давлением и объёмом, а затем строят график p(V).

Для нахождения работы смеси газов используют закон Дальтона.

При объединении теплоизолированных сосудов не должна изменяться внутренняя энергия всей системы, т.е. на сколько джоулей увеличится внутренняя энергия газа в одном сосуде, на столько уменьшится в другом.

Вообще говоря, давление и температуру газа можно измерять только в состоянии термодинамического равновесия, когда давление и температура во всех точках сосуда одинаковы. Но бывают ситуации, когда давление одинаково во всех точках, а температура нет. Это может быть следствием разной концентрации молекул в разных частях сосуда (проанализируйте формулу: p = nkT).

Иногда приходится в задачах по термодинамике использовать знания из механики.

Расчет КПД циклов по графику
К оглавлению…
Задачи данной темы по праву считаются одними из самых сложных задач в термодинамике. Итак, для решения Вам придется, во-первых, перевести график процесса в p(V) – координаты. Во-вторых, надо рассчитать работу газа за цикл. Полезная работа равна площади фигуры внутри графика циклического процесса в координатах p(V). В-третьих, необходимо разобраться, где газ получает, а где отдает теплоту. Для этого вспомните первое начало термодинамики. Внутренняя энергия идеального газа зависит только от его температуры, а работа – от объема. Поэтому, газ получает теплоту, если:
Увеличиваются и его температура, и объем;

Увеличивается объем, а температура постоянна;

Увеличивается температура, а объем постоянен.

Газ отдает теплоту, если:
Уменьшаются и его температура, и объем;

Уменьшается объем, а температура постоянна;

Уменьшается температура, а объем постоянен.

Если один из параметров увеличивается, а другой уменьшается, для того, чтобы понять, отдает газ теплоту или получает ее, необходимо «в лоб» по первому началу термодинамики рассчитать теплоту и посмотреть на ее знак. Положительная теплота – газ ее получает. Отрицательная – отдает.
Первый тип задач. В p(V) – координатах график цикла представляет собой фигуру с легко вычисляемой площадью, и газ получает теплоту в изохорных и изобарных процессах. Применяйте формулу:
Обратите внимание, что в знаменателе стоит только теплота, полученная газом за один цикл, то есть теплота только в тех процессах, в которых газ получал ее.
Второй тип задач. В p(V) – координатах график цикла представляет собой фигуру с легко вычисляемой площадью, и газ отдает теплоту в изохорных и изобарных процессах. Применяйте формулу:
Обратите внимание, что в знаменателе стоит только теплота, отданная газом за один цикл, то есть теплота только в тех процессах, в которых газ отдавал ее.
Третий тип задач. Газ получает теплоту не в удобных для расчета изохорных или изобарных процессах, в цикле есть изотермы или адиабаты, или вообще «никакие» процессы. Применяйте формулу:

Свойства паров. Влажность
К оглавлению…
Любое вещество при определенных условиях может находиться в различных агрегатных состояниях – твердом, жидком и газообразном. Переход из одного состояния в другое называется фазовым переходом. Испарение и конденсация являются примерами фазовых переходов.
Испарением называется фазовый переход из жидкого состояния в газообразное. С точки зрения молекулярно–кинетической теории, испарение – это процесс, при котором с поверхности жидкости вылетают наиболее быстрые молекулы, кинетическая энергия которых превышает энергию их связи с остальными молекулами жидкости. Это приводит к уменьшению средней кинетической энергии оставшихся молекул, то есть к охлаждению жидкости (если нет подвода энергии от окружающих тел).
Конденсация – это процесс, обратный процессу испарения. При конденсации молекулы пара возвращаются в жидкость.
В закрытом сосуде жидкость и ее пар могут находиться в состоянии динамического равновесия, т.е. число молекул, вылетающих из жидкости, равно числу молекул, возвращающихся в жидкость из пара, это значит, что скорости процессов испарения и конденсации одинаковы. Такую систему называют двухфазной. Пар, находящийся в равновесии со своей жидкостью, называют насыщенным.
Насыщенный пар имеет максимальные: давление, концентрацию, плотность при данной температуре. Они зависят только от температуры насыщенного пара, но не от его объема.
Это означает, что если бы мы сосуд закрыли не крышкой, а поршнем, и после того, как пар стал насыщенным, стали бы его сжимать, то давление, плотность и концентрация пара не изменились бы. Если быть более точным, то давление, плотность и концентрация на небольшое время увеличились бы, и пар стал бы перенасыщенным. Но сразу же часть пара превратилась бы в воду, и параметры пара стали бы прежними. Если поднять поршень, то пар перестанет быть насыщенным. Однако за счёт испарения через некоторое время снова станет насыщенным. Здесь следует учесть, что если воды на дне сосуда нет или её немного, то это испарение может оказаться недостаточным, чтобы пар снова стал насыщенным.
Фраза: «В закрытом сосуде с водой…» – означает, что над водой насыщенный пар.

Выпадение росы означает, что пар становится насыщенным.

Абсолютной влажностью ρ называют количество водяного пара, содержащегося в 1 м³ воздуха (т.е. просто плотность водяных паров; из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):
где: р – парциальное давление водяного пара, М – молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура. Единица измерения абсолютной влажности в СИ [ρ] = 1 кг/м³, хотя обычно используют 1 г/м³.
Относительной влажностью φ называется отношение абсолютной влажности ρ к тому количеству водяного пара ρ₀, которое необходимо для насыщения 1 м³ воздуха при данной температуре:
Относительную влажность можно также определить как отношение давления водяного пара р к давлению насыщенного пара р₀ при данной температуре:
Испарение может происходить не только с поверхности, но и в объеме жидкости. В жидкости всегда имеются мельчайшие пузырьки газа. Если давление насыщенного пара жидкости равно внешнему давлению (то есть давлению газа в пузырьках) или превышает его, жидкость будет испаряться внутрь пузырьков. Пузырьки, наполненные паром, расширяются и всплывают на поверхность. Этот процесс называется кипением. Таким образом, кипение жидкости начинается при такой температуре, при которой давление ее насыщенных паров становится равным внешнему давлению.
В частности, при нормальном атмосферном давлении вода кипит при температуре 100°С. Это значит, что при такой температуре давление насыщенных паров воды равно 1 атм. Важно знать, что температура кипения жидкости зависит от давления. В герметически закрытом сосуде жидкость кипеть не может, т.к. при каждом значении температуры устанавливается равновесие между жидкостью и ее насыщенным паром.

Поверхностное натяжение
К оглавлению…
Молекулы вещества в жидком состоянии расположены почти вплотную друг к другу. В отличие от твердых кристаллических тел, в которых молекулы образуют упорядоченные структуры во всем объеме кристалла и могут совершать тепловые колебания около фиксированных центров, молекулы жидкости обладают большей свободой. Каждая молекула жидкости, также как и в твердом теле, «зажата» со всех сторон соседними молекулами и совершает тепловые колебания около некоторого положения равновесия. Однако, время от времени любая молекула может скачком переместиться в соседнее вакантное место. Такие перескоки в жидкостях происходят довольно часто; поэтому молекулы не привязаны к определенным центрам, как в кристаллах, и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей.
Вследствие плотной упаковки молекул сжимаемость жидкостей, то есть изменение объема при изменении давления, очень мала; она в десятки и сотни тысяч раз меньше, чем в газах.
Наиболее интересной особенностью жидкостей является наличие свободной поверхности. Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости. Молекулы в пограничном слое жидкости, в отличие от молекул в ее глубине, окружены другими молекулами той же жидкости не со всех сторон. Силы межмолекулярного взаимодействия, действующие на одну из молекул внутри жидкости со стороны соседних молекул, в среднем взаимно скомпенсированы. Любая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости (силами, действующими на данную молекулу жидкости со стороны молекул газа (или пара) можно пренебречь). В результате появляется некоторая равнодействующая сила, направленная вглубь жидкости. Если молекула переместится с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу. Наоборот, чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность (то есть увеличить площадь поверхности жидкости), надо затратить положительную работу внешних сил ΔA_внеш, пропорциональную изменению ΔS площади поверхности.
Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия E_p поверхности жидкости пропорциональна ее площади:
Коэффициент σ называется коэффициентом поверхностного натяжения (σ > 0). Таким образом, коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости на единицу при постоянной температуре. В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м²) или в ньютонах на метр (1 Н/м = 1 Дж/м²).
Из механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии (любое тело всегда стремится скатиться с горы, а не забраться на нее). Отсюда следует, что свободная поверхность жидкости стремится сократить свою площадь. По этой причине свободная капля жидкости принимает шарообразную форму. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы называются силами поверхностного натяжения. Наличие сил поверхностного натяжения делает поверхность жидкости похожей на упругую растянутую пленку. Сила поверхностного натяжения, действующая на участок границы жидкости длиной L вычисляется по формуле:
Таким образом, коэффициент поверхностного натяжения σ может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.
Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются. При этом высота столба жидкости в капилляре:
где: r – радиус капиляра (т.е. тонкой трубки). При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной:
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Удельная плавка
Термодинамика — это раздел физики который имеет дело с энергией и работой системы. Термодинамика занимается только крупномасштабный ответ системы, которую мы можем наблюдайте и измеряйте в экспериментах. В аэродинамике мы больше всех интересуется термодинамикой из-за той роли, которую она играет в конструкция двигателя а также высокоскоростной полет.
На этом слайде мы выводим некоторые уравнения, которые связывают теплоемкость газа к газовой постоянной, используемой в уравнение состояния.Мы собираемся использовать специальный значения переменных состояния. Для ученого «конкретная» переменная состояния означает значение переменной. делится на массу вещества. Это позволяет установить отношения между переменные без учета количества имеющегося у нас вещества. Мы можем умножьте конкретную переменную на количество вещества в любое время для определения фактического значения переменной расхода. Из наших исследований теплопередача, мы знаем, что количество тепла, передаваемого между двумя объектами, равно пропорционально температура разница между объектами и теплоемкость объектов.Тепловая мощность — это константа, показывающая, сколько тепла добавляется на единицу повышения температуры. Значение константы различно для разных материалов и зависит от о процессе. Теплоемкость не является переменной состояния .
Если мы имеем дело с газом, удобнее всего использовать формы уравнения термодинамики на основе энтальпия газа. Из определения энтальпии:
ч = е + р * v
где удельная энтальпия h , p давление, v — это удельный объем, и e — специфический внутренняя энергия.Во время процесса значения этих переменных изменяются. Обозначим изменение на греческую букву дельта , которая выглядит как треугольник. Таким образом, «дельта h» означает изменение «h» из состояния 1 в состояние 2 во время процесса. Тогда для процесса с постоянным давлением уравнение энтальпии принимает следующий вид:
дельта h = дельта е + р * дельта v
Энтальпия, внутренняя энергия и объем изменяются, но давление остается прежним. Из нашего вывода уравнение энтальпии, изменение удельной энтальпии равно теплоотдаче для процесса постоянного давления:
дельта h = cp * дельта T
где дельта T — изменение температуры газа в процессе, а c — удельная теплоемкость.Мы добавили индекс «p» к удельной теплоемкости, чтобы напомнить нам, что это значение относится только к процессу с постоянным давлением.
Уравнение состояния газа связывает температуру, давление и объем через газовую постоянную R . Газовая постоянная, используемая аэродинамики выводится из универсальной газовой постоянной, но имеет уникальное значение на каждый газ.
р * v = R * T
Если у нас процесс постоянного давления, то:
p * дельта v = R * дельта T
Теперь представим, что у нас есть постоянный объем процесса с нашим газом, который производит точно такое же изменение температуры, что и процесс постоянного давления, который мы обсуждали.Тогда Первый закон термодинамики говорит нам:
дельта е = дельта q — дельта w
где q — удельная теплоотдача, а w — работа, выполняемая газ. Для процесса с постоянным объемом Работа равно нулю. И мы можем выразить теплопередача как постоянная величина, умноженная на изменение температуры. Это дает:
дельта е = cv * дельта T
где дельта T — изменение температуры газа в процессе, а c — удельная теплоемкость.Мы добавили индекс «v» к удельной теплоемкости, чтобы напомнить нам, что это значение применимо только к процессу с постоянным объемом. Несмотря на то, что изменение температуры одинаково для этого процесса и постоянная давления процесса, значение удельной теплоемкости другое.
Поскольку мы выбрали процесс постоянного объема, чтобы получить такое же изменение в температура в качестве нашего процесса постоянного давления, мы можем заменить выражение приведено выше для «дельта е» в уравнении энтальпии. В общем нельзя сделайте эту замену, потому что процесс с постоянным давлением и процесс с постоянным объемом производить различные изменения температуры Если мы подставим выражения для «дельта е», «р * дельта v» и «дельта h» в уравнение энтальпии получим:
cp * дельта T = cv * дельта T + R * дельта T
деление на «дельту Т» дает соотношение:
cp = cv + рэнд
Константы теплоемкости для процессов с постоянным давлением и постоянным объемом связаны с газовой постоянной для данного газа.Этот довольно замечательный результат был получен из термодинамических соотношений, которые основаны на наблюдениях физических систем и процессов. С помощью кинетическая теория газов, тот же результат может быть получен из соображений сохранения энергии на молекулярном уровне.
Мы можем определить дополнительные переменная, называемая удельной теплоемкостью соотношение, что дано греческому символ «гамма», который равен cp, деленному на cv:
гамма = cp / cv
«Гамма» — это просто число, значение которого зависит от состояния газа.Для воздуха, гамма = 1,4 для стандартных дневных условий. «Гамма» появляется во многих уравнениях жидкостей. включая уравнение, связывающее давление, температуру и объем во время простое сжатие или расширение процесса, уравнение для скорость звука, и все уравнения для изэнтропические потоки, а также ударные волны. Потому что ценность «гамма» просто зависит от состояния газа, есть таблицы этих значений для данных газов. Таблицы можно использовать для решения задач газовой динамики.
Действия:
Экскурсии
Навигация..

Руководство для начинающих Домашняя страница
Удельная теплоемкость | Безграничная физика
Тепловая мощность
Теплоемкость измеряет количество тепла, необходимое для повышения температуры объекта или системы на один градус Цельсия.
Цели обучения
Объясните энтальпию в системе с постоянным объемом и давлением
Основные выводы
Ключевые моменты
Теплоемкость — это измеримая физическая величина, которая характеризует количество тепла, необходимое для изменения температуры вещества на заданную величину.Он измеряется в джоулях на Кельвин и выражается в.
Теплоемкость — это обширное свойство, которое зависит от размера системы.
Теплоемкость большинства систем непостоянна (хотя ее часто можно рассматривать как таковую). Это зависит от температуры, давления и объема рассматриваемой системы.
Ключевые термины
теплоемкость : количество тепловой энергии, необходимое для повышения температуры объекта или единицы материи на один градус Цельсия; в джоулях на кельвин (Дж / К).
энтальпия : общее количество энергии в системе, включая внутреннюю энергию и энергию, необходимую для вытеснения окружающей среды
Тепловая мощность
Теплоемкость (обычно обозначается заглавной буквой C, часто с индексами) или теплоемкость — это измеримая физическая величина, которая характеризует количество тепла, необходимое для изменения температуры вещества на заданную величину. В единицах СИ теплоемкость выражается в джоулях на кельвин (Дж / К).
Теплоемкость объекта (обозначение C ) определяется как отношение количества тепловой энергии, переданной объекту, к результирующему увеличению температуры объекта.
[латекс] \ displaystyle {\ text {C} = \ frac {\ text {Q}} {\ Delta \ text {T}}.} [/ Latex]
Теплоемкость — это обширное свойство, поэтому она масштабируется в зависимости от размера системы. Образец, содержащий вдвое больше вещества, чем другой образец, требует передачи вдвое большего количества тепла (Q) для достижения такого же изменения температуры (ΔT).Например, если для нагрева блока железа требуется 1000 Дж, то для нагрева второго блока железа, масса которого в два раза больше массы первого, потребуется 2000 Дж.
Измерение теплоемкости
Тепловая мощность большинства систем непостоянна. Скорее, это зависит от переменных состояния исследуемой термодинамической системы. В частности, это зависит от самой температуры, а также от давления и объема системы, а также от способов изменения давлений и объемов при переходе системы от одной температуры к другой.Причина этого заключается в том, что работа давления-объема, выполняемая в системе, повышает ее температуру за счет механизма, отличного от нагрева, в то время как работа объема-давления, выполняемая системой, поглощает тепло, не повышая температуру системы. (Из-за температурной зависимости калорийность формально определяется как энергия, необходимая для нагрева 1 г воды с 14,5 до 15,5 ° C, а не обычно на 1 ° C.)
Таким образом, можно выполнять различные измерения теплоемкости, чаще всего при постоянном давлении и постоянном объеме.Измеренные таким образом значения обычно имеют нижний индекс (соответственно p и V) для обозначения определения. Газы и жидкости обычно также измеряются при постоянном объеме. Измерения при постоянном давлении дают большие значения, чем при постоянном объеме, потому что значения постоянного давления также включают тепловую энергию, которая используется для выполнения работы по расширению вещества против постоянного давления при повышении его температуры. Эта разница особенно заметна для газов, где значения при постоянном давлении обычно составляют от 30% до 66.На 7% больше, чем при постоянной громкости.
Термодинамические соотношения и определение теплоемкости
Внутренняя энергия замкнутой системы изменяется либо за счет добавления тепла в систему, либо за счет выполнения системой работы. Вспоминая первый закон термодинамики,
[латекс] \ text {dU} = \ delta \ text {Q} — \ delta \ text {W} [/ latex].
За работу в результате увеличения объема системы можем написать:
[латекс] \ text {dU} = \ delta \ text {Q} — \ text {PdV} [/ latex].
Если тепло добавляется при постоянном объеме, то второй член этого соотношения исчезает и легко получается
[латекс] \ displaystyle {\ left (\ frac {\ partial \ text {U}} {\ partial \ text {T}} \ right) _ {\ text {V}} = \ left (\ frac {\ partial \ text {Q}} {\ partial \ text {T}} \ right) _ {\ text {V}} = \ text {C} _ {\ text {V}}} [/ latex].
Это определяет теплоемкость при постоянном объеме , C _V. Еще одна полезная величина — это теплоемкость при постоянном давлении , C, , _P.При энтальпии системы, заданной
[латекс] \ text {H} = \ text {U} + \ text {PV} [/ latex],
наше уравнение для d U меняется на
[латекс] \ text {dH} = \ delta \ text {Q} + \ text {VdP} [/ latex],
и, следовательно, при постоянном давлении имеем
[латекс] (\ frac {\ partial \ text {H}} {\ partial \ text {T}}) _ {\ text {P}} = (\ frac {\ partial \ text {Q}} {\ partial \ text {T}}) _ {\ text {P}} = \ text {C} _ {\ text {P}} [/ latex].
Удельная теплоемкость
Удельная теплоемкость — это интенсивное свойство, которое описывает, сколько тепла необходимо добавить к определенному веществу, чтобы повысить его температуру.
Цели обучения
Обобщите количественную взаимосвязь между теплопередачей и изменением температуры
Основные выводы
Ключевые моменты
В отличие от полной теплоемкости, удельная теплоемкость не зависит от массы или объема. Он описывает, сколько тепла необходимо добавить к единице массы данного вещества, чтобы повысить его температуру на один градус Цельсия. Единицы измерения удельной теплоемкости — Дж / (кг ° C) или эквивалентно Дж / (кг · K).
Теплоемкость и удельная теплоемкость связаны соотношением C = см или c = C / м.
Масса m, удельная теплоемкость c, изменение температуры ΔT и добавленное (или вычитаемое) тепло Q связаны уравнением: Q = mcΔT.
Значения удельной теплоемкости зависят от свойств и фазы данного вещества. Поскольку их нелегко рассчитать, они измеряются эмпирически и доступны для справки в таблицах.
Ключевые термины
удельная теплоемкость : Количество тепла, которое должно быть добавлено (или удалено) из единицы массы вещества, чтобы изменить его температуру на один градус Цельсия.Это интенсивное свойство.
Удельная теплоемкость
Теплоемкость — это обширное свойство, которое описывает, сколько тепловой энергии требуется для повышения температуры данной системы. Однако было бы довольно неудобно измерять теплоемкость каждой единицы вещества. Нам нужно интенсивное свойство, которое зависит только от типа и фазы вещества и может быть применено к системам произвольного размера. Эта величина известна как удельная теплоемкость (или просто удельная теплоемкость), которая представляет собой теплоемкость на единицу массы материала.Эксперименты показывают, что передаваемое тепло зависит от трех факторов: (1) изменения температуры, (2) массы системы и (3) вещества и фазы вещества. Последние два фактора заключены в значении удельной теплоемкости.
Теплопередача и удельная теплоемкость : Тепло Q, передаваемое для изменения температуры, зависит от величины изменения температуры, массы системы, а также от вещества и фазы. (а) Количество переданного тепла прямо пропорционально изменению температуры.Чтобы удвоить изменение температуры массы m, вам нужно добавить в два раза больше тепла. (б) Количество передаваемого тепла также прямо пропорционально массе. Чтобы вызвать эквивалентное изменение температуры в удвоенной массе, вам нужно добавить в два раза больше тепла. (c) Количество передаваемого тепла зависит от вещества и его фазы. Если требуется количество тепла Q, чтобы вызвать изменение температуры ΔT в данной массе меди, потребуется в 10,8 раз больше тепла, чтобы вызвать эквивалентное изменение температуры в той же массе воды, при условии отсутствия фазовых изменений ни в одном из веществ.

Удельная теплоемкость : В этом уроке тепло связано с изменением температуры. Мы обсуждаем, как количество тепла, необходимое для изменения температуры, зависит от массы и вещества, и это соотношение представлено удельной теплоемкостью вещества C.
Зависимость от изменения температуры и массы легко понять. Поскольку (средняя) кинетическая энергия атома или молекулы пропорциональна абсолютной температуре, внутренняя энергия системы пропорциональна абсолютной температуре и количеству атомов или молекул.Поскольку переданное тепло равно изменению внутренней энергии, тепло пропорционально массе вещества и изменению температуры. Передаваемое тепло также зависит от вещества, так что, например, количество тепла, необходимое для повышения температуры, меньше для спирта, чем для воды. Для одного и того же вещества передаваемое тепло также зависит от фазы (газ, жидкость или твердое тело).
Количественная связь между теплопередачей и изменением температуры включает все три фактора:
[латекс] \ text {Q} = \ text {mc} \ Delta \ text {T} [/ latex],
где Q — символ теплопередачи, m — масса вещества, а ΔT — изменение температуры.Символ c обозначает удельную теплоемкость и зависит от материала и фазы.
Удельная теплоемкость — это количество тепла, необходимое для изменения температуры 1,00 кг массы на 1,00 ° C. Удельная теплоемкость c — это свойство вещества; его единица СИ — Дж / (кг⋅К) или Дж / (кг⋅К). Напомним, что изменение температуры (ΔT) одинаково в единицах кельвина и градусов Цельсия. Обратите внимание, что общая теплоемкость C — это просто произведение удельной теплоемкости c и массы вещества m, i.е.,
[латекс] \ text {C} = \ text {mc} [/ latex] или [латекс] \ text {c} = \ frac {\ text {C}} {\ text {m}} = \ frac {\ текст {C}} {\ rho \ text {V}} [/ latex],
где ϱ — плотность вещества, V — его объем.
Значения удельной теплоемкости обычно нужно искать в таблицах, потому что нет простого способа их вычислить. Вместо этого они измеряются эмпирически. Как правило, удельная теплоемкость также зависит от температуры. В таблице ниже приведены типичные значения теплоемкости для различных веществ.За исключением газов, температурная и объемная зависимость удельной теплоемкости большинства веществ слабая. Удельная теплоемкость воды в пять раз больше, чем у стекла, и в десять раз больше, чем у железа, что означает, что требуется в пять раз больше тепла, чтобы поднять температуру воды на такое же количество, что и у стекла, и в десять раз больше тепла, чтобы поднять температуру. воды как для железа. Фактически, вода имеет одну из самых высоких удельной теплоемкости из всех материалов, что важно для поддержания жизни на Земле.
Удельная теплоемкость : Указана удельная теплоемкость различных веществ.Эти значения идентичны в единицах кал / (г⋅C) .3. cv при постоянном объеме и 20,0 ° C, если не указано иное, и среднем давлении 1,00 атм. В скобках указаны значения cp при постоянном давлении 1,00 атм.
Калориметрия
Калориметрия — это измерение теплоты химических реакций или физических изменений.
Цели обучения
Проанализировать взаимосвязь между газовой постоянной для получения идеального выхода газа и объемом
Основные выводы
Ключевые моменты
Калориметр используется для измерения тепла, выделяемого (или поглощаемого) в результате физических изменений или химической реакции.Наука об измерении этих изменений известна как калориметрия.
Для проведения калориметрии очень важно знать удельную теплоемкость измеряемых веществ.
Калориметрия может выполняться при постоянном объеме или постоянном давлении. Тип выполняемого расчета зависит от условий эксперимента.
Ключевые термины
калориметр постоянного давления : прибор, используемый для измерения тепла, выделяемого во время изменений, не связанных с изменениями давления.
калориметр : Устройство для измерения тепла, выделяемого или поглощаемого в результате химической реакции, изменения фазы или какого-либо другого физического изменения.
калориметр постоянного объема : прибор, используемый для измерения тепла, выделяемого во время изменений, не связанных с изменением объема.
Калориметрия
Обзор
Калориметрия — это наука об измерении теплоты химических реакций или физических изменений. Калориметрия выполняется калориметром.Простой калориметр состоит из термометра, прикрепленного к металлическому контейнеру с водой, подвешенному над камерой сгорания. Слово калориметрия происходит от латинского слова calor , что означает тепло. Шотландский врач и ученый Джозеф Блэк, который первым осознал разницу между теплом и температурой, считается основоположником калориметрии.
Калориметрия требует, чтобы нагреваемый материал имел известные тепловые свойства, то есть удельную теплоемкость.Классическое правило, признанное Клаузиусом и Кельвином, состоит в том, что давление, оказываемое калориметрическим материалом, полностью и быстро определяется исключительно его температурой и объемом; это правило применяется для изменений, не связанных с фазовым переходом, таких как таяние льда. Есть много материалов, которые не соответствуют этому правилу, и для них требуются более сложные уравнения, чем приведенные ниже.
Ледяной калориметр : первый в мире ледяной калориметр, использованный зимой 1782-83 гг. Антуаном Лавуазье и Пьером-Симоном Лапласом для определения тепла, выделяющегося при различных химических изменениях; расчеты, основанные на предыдущем открытии скрытой теплоты Джозефом Блэком.Эти эксперименты составляют основу термохимии.
Базовая калориметрия при постоянном значении
Калориметрия постоянного объема — это калориметрия, выполняемая при постоянном объеме. Это предполагает использование калориметра постоянного объема (один из типов называется калориметром бомбы). Для калориметрии постоянного объема:
[латекс] \ delta \ text {Q} = \ text {C} _ {\ text {V}} \ Delta \ text {T} = \ text {mc} _ {\ text {V}} \ Delta \ text {T} [/ латекс]
, где δQ — приращение тепла, полученного образцом, C _V — теплоемкость при постоянном объеме, c _v — удельная теплоемкость при постоянном объеме, а ΔT — изменение температуры.
Измерение изменения энтальпии
Чтобы найти изменение энтальпии на массу (или на моль) вещества A в реакции между двумя веществами A и B, эти вещества добавляют в калориметр и определяют начальную и конечную температуры (до начала реакции и после ее завершения. ) отмечены. Умножение изменения температуры на массу и удельную теплоемкость веществ дает значение энергии, выделяемой или поглощаемой во время реакции:
[латекс] \ delta \ text {Q} = \ Delta \ text {T} (\ text {m} _ {\ text {A}} \ text {c} _ {\ text {A}} + \ text { m} _ {\ text {B}} \ text {c} _ {\ text {B}}) [/ latex]
Разделение изменения энергии на количество присутствующих граммов (или молей) A дает изменение энтальпии реакции.Этот метод используется в основном в академическом обучении, поскольку он описывает теорию калориметрии. Он не учитывает потери тепла через контейнер или теплоемкость термометра и самого контейнера. Кроме того, объект, помещенный внутри калориметра, показывает, что объекты передают свое тепло калориметру и жидкости, а тепло, поглощаемое калориметром и жидкостью, равно теплу, отдаваемому металлами.
Калориметрия постоянного давления
Калориметр постоянного давления измеряет изменение энтальпии реакции, протекающей в растворе, в течение которой атмосферное давление остается постоянным.Примером может служить калориметр кофейной чашки, который состоит из двух вложенных друг в друга чашек из пенополистирола и крышки с двумя отверстиями, в которую можно вставить термометр и стержень для перемешивания. Внутренняя чашка содержит известное количество растворенного вещества, обычно воды, которое поглощает тепло от реакции. Когда происходит реакция, внешняя чашка обеспечивает изоляцию. Тогда
[латекс] \ text {C} _ {\ text {P}} = \ frac {\ text {W} \ Delta \ text {H}} {\ text {M} \ Delta \ text {T}} [/ латекс]
, где C _p — удельная теплоемкость при постоянном давлении, ΔH — энтальпия раствора, ΔT — изменение температуры, W — масса растворенного вещества, а M — молекулярная масса растворенного вещества.Измерение тепла с помощью простого калориметра, такого как калориметр для кофейной чашки, является примером калориметрии постоянного давления, поскольку давление (атмосферное давление) остается постоянным во время процесса. Калориметрия постоянного давления используется для определения изменений энтальпии, происходящих в растворе. В этих условиях изменение энтальпии равно теплоте (Q = ΔH).
Удельная теплоемкость идеального газа при постоянном давлении и объеме
Идеальный газ имеет различную удельную теплоемкость при постоянном объеме или постоянном давлении.
Цели обучения
Объясните, как рассчитать индекс адиабаты
Основные выводы
Ключевые моменты
Удельная теплоемкость газа при постоянном объеме задается как [латекс] (\ frac {\ partial \ text {U}} {\ partial \ text {T}}) _ {\ text {V}} = \ text {c} _ {\ text {v}} [/ latex].
Удельная теплоемкость идеального газа при постоянном давлении определяется как [latex] (\ frac {\ partial \ text {H}} {\ partial \ text {T}}) _ {\ text {V}} = \ text {c} _ {\ text {p}} = \ text {c} _ {\ text {v}} + \ text {R} [/ latex].
Коэффициент теплоемкости (или индекс адиабаты) — это отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.
Ключевые термины
Фундаментальное термодинамическое соотношение : В термодинамике фундаментальное термодинамическое соотношение выражает бесконечно малое изменение внутренней энергии в терминах бесконечно малых изменений энтропии и объема для замкнутой системы, находящейся в тепловом равновесии, следующим образом: dU = TdS-PdV. Здесь U — внутренняя энергия, T — абсолютная температура, S — энтропия, P — давление, V — объем.
индекс адиабаты : Отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.
удельная теплоемкость : Отношение количества тепла, необходимого для повышения температуры единицы массы вещества на единицу градуса, к количеству тепла, необходимому для повышения температуры той же массы воды на такое же количество.
Удельная теплоемкость идеального газа при постоянном давлении и объеме
Теплоемкость при постоянном объеме nR = 1 Дж · К ⁻¹ любого газа, включая идеальный газ, составляет:
[латекс] (\ frac {\ partial \ text {U}} {\ partial \ text {T}}) _ {\ text {V}} = \ text {c} _ {\ text {v}} [/ латекс]
Это безразмерная теплоемкость при постоянном объеме; обычно это функция температуры из-за межмолекулярных сил.Для умеренных температур константа одноатомного газа c _v = 3/2, а для двухатомного газа c _v = 5/2 (см.). Макроскопические измерения теплоемкости дают информацию о микроскопической структуре молекул.
Молекулярные внутренние колебания : Когда газ нагревается, поступательная киентная энергия молекул в газе увеличивается. Кроме того, молекулы газа могут улавливать множество характерных внутренних колебаний. Потенциальная энергия, накопленная в этих внутренних степенях свободы, вносит вклад в удельную теплоемкость газа.
Теплоемкость при постоянном давлении 1 Дж · К ⁻¹ идеального газа составляет:
[латекс] (\ frac {\ partial \ text {H}} {\ partial \ text {T}}) _ {\ text {V}} = \ text {c} _ {\ text {p}} = \ текст {c} _ {\ text {v}} + \ text {R} [/ latex]
где H = U + pV — энтальпия газа.
Измерение теплоемкости при постоянном объеме может быть чрезвычайно трудным для жидкостей и твердых тел. То есть небольшие изменения температуры обычно требуют большого давления для поддержания постоянного объема жидкости или твердого вещества (это означает, что содержащий сосуд должен быть почти жестким или, по крайней мере, очень прочным).Легче измерить теплоемкость при постоянном давлении (позволяющем материалу свободно расширяться или сжиматься) и определить теплоемкость при постоянном объеме, используя математические соотношения, выведенные из основных законов термодинамики.
Используя фундаментальную термодинамическую связь, мы можем показать:
[латекс] \ text {C} _ {\ text {p}} — \ text {C} _ {\ text {V}} = \ text {T} (\ frac {\ partial \ text {P}} { \ partial \ text {T}}) _ {\ text {V}, \ text {N}} (\ frac {\ partial \ text {V}} {\ partial \ text {T}}) _ {\ text { p}, \ text {N}} [/ latex]
, где частные производные взяты при постоянном объеме и постоянном количестве частиц, а также при постоянном давлении и постоянном количестве частиц, соответственно.
Коэффициент теплоемкости или показатель адиабаты — это отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме. {2}} = \ text {R} [/ latex]
Это уравнение сводится просто к тому, что известно как соотношение Майера:
Юлиус Роберт Майер : Юлиус Роберт фон Майер (25 ноября 1814 — 20 марта 1878), немецкий врач и физик, был одним из основоположников термодинамики.Он известен прежде всего тем, что в 1841 году сформулировал одно из первоначальных утверждений о сохранении энергии (или то, что сейчас известно как одна из первых версий первого закона термодинамики): «Энергия не может быть ни создана, ни уничтожена. В 1842 году Майер описал жизненно важный химический процесс, который теперь называют окислением, как основной источник энергии для любого живого существа. Его достижения не были замечены, и заслуга в открытии механического эквивалента тепла была приписана Джеймсу Джоулю в следующем году.фон Майер также предположил, что растения превращают свет в химическую энергию.
[латекс] \ text {C} _ {\ text {P}} — \ text {C} _ {\ text {V}} = \ text {R} [/ latex].
Это простое уравнение, связывающее теплоемкость при постоянной температуре и при постоянном давлении.
Решение задач калориметрии
Калориметрия используется для измерения количества тепла, выделяемого или потребляемого в химической реакции.
Цели обучения
Объясните, что калориметр бомбы используется для измерения тепла, выделяемого в реакции горения
Основные выводы
Ключевые моменты
Калориметрия используется для измерения количества тепла, передаваемого веществу или от него.
Калориметр — это устройство, используемое для измерения количества тепла, участвующего в химическом или физическом процессе.
Это означает, что количество тепла, производимого или потребляемого в реакции, равно количеству тепла, поглощаемого или теряемого раствором.
Ключевые термины
теплота реакции : изменение энтальпии в химической реакции; количество тепла, которое система отдает своему окружению, чтобы она могла вернуться к исходной температуре.
горение : Процесс, в котором два химических вещества объединяются для получения тепла.
Калориметры
предназначены для минимизации обмена энергией между исследуемой системой и ее окружением. Они варьируются от простых калориметров для кофейных чашек, используемых студентами начального курса химии, до сложных калориметров-бомб, используемых для определения энергетической ценности пищи.
Калориметрия используется для измерения количества тепла, передаваемого веществу или от него. Для этого происходит обмен тепла с калиброванным объектом (калориметром).Изменение температуры измерительной части калориметра преобразуется в количество тепла (поскольку предыдущая калибровка использовалась для определения его теплоемкости). Измерение теплопередачи с использованием этого подхода требует определения системы (вещества или веществ, подвергающихся химическому или физическому изменению) и ее окружения (других компонентов измерительного устройства, которые служат для обеспечения теплом системы или поглощения тепла от система). Знание теплоемкости окружающей среды и тщательные измерения масс системы и окружающей среды, а также их температуры до и после процесса позволяют рассчитать передаваемое тепло, как описано в этом разделе.
Калориметр — это устройство, используемое для измерения количества тепла, участвующего в химическом или физическом процессе. Например, когда в растворе в калориметре происходит экзотермическая реакция, тепло, выделяемое в результате реакции, поглощается раствором, что увеличивает его температуру. Когда происходит эндотермическая реакция, необходимое тепло поглощается тепловой энергией раствора, что снижает его температуру. Затем изменение температуры, а также удельная теплоемкость и масса раствора можно использовать для расчета количества тепла, задействованного в любом случае.
Калориметры для кофейных чашек
Студенты-общехимики часто используют простые калориметры, изготовленные из полистирольных стаканчиков. Эти простые в использовании калориметры типа «кофейная чашка» обеспечивают больший теплообмен с окружающей средой и, следовательно, дают менее точные значения энергии.
Устройство калориметра постоянного объема (или «бомбы»)
Калориметр бомбы : Это изображение типичной установки калориметра бомбы.
Калориметр другого типа, который работает с постоянным объемом, в просторечии известен как калориметр-бомба, используется для измерения энергии, производимой в реакциях с выделением большого количества тепла и газообразных продуктов, таких как реакции горения.(Термин «бомба» исходит из наблюдения, что эти реакции могут быть достаточно интенсивными, чтобы напоминать взрывы, которые могут повредить другие калориметры.) Этот тип калориметра состоит из прочного стального контейнера («бомба»), который содержит реагенты и сам является погружен в воду. Образец помещается в бомбу, которая затем заполняется кислородом под высоким давлением. Для воспламенения образца используется небольшая электрическая искра. Энергия, произведенная в результате реакции, улавливается стальной бомбой и окружающей водой.Повышение температуры измеряется и, наряду с известной теплоемкостью калориметра, используется для расчета энергии, производимой в результате реакции. Калориметры бомбы требуют калибровки для определения теплоемкости калориметра и обеспечения точных результатов. Калибровка выполняется с использованием реакции с известным q, например измеренного количества бензойной кислоты, воспламененного искрой от никелевой плавкой проволоки, которая взвешивается до и после реакции. Изменение температуры, вызванное известной реакцией, используется для определения теплоемкости калориметра.Калибровка обычно выполняется каждый раз перед использованием калориметра для сбора данных исследования.
Пример: идентификация металла путем измерения удельной теплоемкости
Кусок металла весом 59,7 г, погруженный в кипящую воду, был быстро перенесен в 60,0 мл воды при начальной температуре 22,0 ° C. Конечная температура составляет 28,5 ° C. Используйте эти данные, чтобы определить удельную теплоемкость металла. Используйте этот результат, чтобы идентифицировать металл.
Решение
Предполагая идеальную теплопередачу, тепло, выделяемое металлом, является отрицательной величиной тепла, поглощаемого водой, или:
[латекс] \ text {q} _ {\ text {metal}} = — \ text {q} _ {\ text {water}} [/ latex]
В развернутом виде это:
[латекс] \ text {c} _ {\ text {metal}} \ times \ text {m} _ {\ text {metal}} \ times \ left (\ text {T} _ {\ text {f, металл }} — \ text {T} _ {\ text {i, metal}} \ right) = \ text {c} _ {\ text {water}} \ times \ text {m} _ {\ text {water}} \ times \ left (\ text {T} _ {\ text {f, water}} — \ text {T} _ {\ text {i, water}} \ right) [/ latex]
Отметим, что, поскольку металл был погружен в кипящую воду, его начальная температура составляла 100 ° C.{\ text {o}} \ text {C} [/ latex]
Наша экспериментальная удельная теплоемкость наиболее близка к значению для меди (0,39 Дж / г ° C), поэтому мы идентифицируем металл как медь.
Удельная теплоемкость и отдельные газовые константы газов
Удельная теплоемкость (= удельная теплоемкость) при постоянном давлении и постоянном объеме процессов, а также отношение удельной теплоемкости и индивидуальных газовых постоянных — R — для некоторых обычно используемых «идеальных газы », приведены в таблице ниже (приблизительные значения при 68 ^o F ( 20 ^o C ) и 14.7 фунтов на квадратный дюйм ( 1 атм )).
Для преобразования единиц используйте онлайн-конвертер единиц удельной теплоемкости.
См. Также табличные значения удельной теплоемкости пищевых продуктов, металлов и полуметаллов, обычных жидкостей и жидкостей, обычных твердых веществ и других обычных веществ, а также значения молярной теплоемкости обычных органических и неорганических веществ.
Для полного стола — поворот экрана!
9069 9019 019 019019 H ₁₀844 9069 906924_{2 этилен _{3 _{2 9069}}} 9069 1,304 9069 Тетроксид азота O2 Закись азота88 9069 48,24₆
Газ или пар Формула Удельная теплоемкость Удельная теплоемкость Индивидуальная газовая постоянная
— R —
c _p кг K)) c _v
(кДж / (кг K)) c _p (Btu / (90 фунтов1 _{м) ^o F))} c _v (Btu / (фунт _м ^o F)) κ = c _{p _v} c _p — c _v (кДж / (кг · К)) c _p — c 9007 7 (фут-фунт _f / (фунт _м ^o R))
Ацетон (CH ₃) ₂ CO 1.47 1,32 0,35 0,32 1,11 0,15
Ацетилен C ₂ H ₂ 1,69 9069 59,34
Воздух 1,01 0,718 0,24 0,17 1,40 0,287 53,34 0,287 53,34
9069 C 9069 2 9069 C 9069 2 9069 1.88 1,67 0,45 0,4 1,13 0,22
Спирт (метанол) CH ₃ OH 1,93 1,53 0,43 1,93 1,53 0,46
Аммиак NH ₃ 2,19 1,66 0,52 0,4 1,31 0,53 96.5
Аргон Ar 0,520 0,312 0,12 0,07 1,667 0,208
Бензол
0,26 0,24 1,12 0,1
Доменный газ 1,03 0,73 0,25 0.17 1,41 0,3 55,05
Бром Br ₂ 0,25 0,2 0,06 0,05 1,28 1,67 1,53 0,395 0,356 1,094 0,143 26,5
Углекислый газ CO ₂
0,655 0,21 0,16 1,289 0,189 38,86
Окись углерода CO 1,02 0,72
Дисульфид углерода CS ₂ 0,67 0,55 0,16 0,13 1,21 0.12
Хлор Cl ₂ 0,48 0,36 0,12 0,09 1,34 0,12 1,34 0,12
0,15 0,13 1,15 0,08
Угольный газ 2,14 1,59
Этан C ₂ H ₆ 1,75 1,48 0,39 0,32 1,187 9069 диета (C ₂ H ₅) ₂ O 2,01 1,95 0,48 0,47 1,03 0,06
1.53 1,23 0,4 0,33 1,240 0,296 55,08
Хлордифторметан, R-22 CHClF ₂
Гелий He 5,19 3,12 1,25 0,75 1,667 2,08 386.3
Гексан C ₆ H ₁₄ 1.06
Водород H ₂ 14,32 10,16 3,42 2,43 1,405 4.12 765,9
Хлористый водород HCl 0,8 0,57 0,191 0,135 1,41 0,23 42,4
0,243 0,187 1,32 45,2
Гидроксил OH 1,76 1,27 1.384 0,489
Криптон Kr 0,25 0,151
Метан CH ₄ 0,518 96,4
метилхлорид CH ₃ Cl 0,240 0.200 1,20 30,6
Природный газ 2,34 1,85 0,56 0,44 1,27 0,5 79,1 Neo 1,667 0,412
Оксид азота NO 0,995 0.718 0,23 0,17 1,386 0,277
Азот N ₂ 1,04 0,743 0,25
N ₂ O ₄ 4,69 4,6 1,12 1,1 1,02 0,09
0,69 0,21 0,17 1,27 0,18 35,1
Кислород O ₂ 0,919 0,659 0,919 0,659
Пентан C ₅ H ₁₂ 1,07
9069 Пропан67 1,48 0,39 0,34 1,13 0,189 35,0
Пропен (пропилен) C ₃ H ₆ 1,15 0,18 36,8
Водяной пар
Пар 1 фунт / кв. 120-600 ^o F H ₂ O 1,93 1,46 0.46 0,35 1,32 0,462
Пар 14,7 фунта / кв. 220-600 ^o F H ₂ O 1,97 1,5 0,47 0,36 1,31 0,46
Пар 150 psia. 360-600 ^o F H ₂ O 2,26 1,76 0,54 0,42 1,28 0.5
Двуокись серы (двуокись серы) SO ₂ 0,64 0,51 0,15 0,12 1,29 0,13 9069 X 0,097
Для преобразования единиц используйте онлайн-конвертер единиц удельной теплоемкости.
См. Также табличные значения удельной теплоемкости пищевых продуктов и продуктов питания, металлов и полуметаллов, обычных жидкостей и жидкостей, обычных твердых веществ и других обычных веществ, а также значения молярной теплоемкости обычных органических и неорганических веществ.
Страница не найдена | MIT
Перейти к содержанию ↓
Образование
Исследовать
Инновации
Прием + помощь
Студенческая жизнь
Новости
Выпускников
О MIT
Подробнее ↓
Прием + помощь
Студенческая жизнь
Новости
Выпускников
О MIT
Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
Необходимо определить две удельные теплоемкости
Наука> Физика> Кинетическая теория газов> Удельная теплоемкость газов
В этой статье мы рассмотрим понятие удельной теплоемкости или удельной теплоемкости газов.
Твердые тела и жидкости имеют только одну удельную теплоемкость, а газы — две удельные теплоты:
В случае твердых тел и жидкостей небольшое изменение температуры вызывает незначительное изменение объема и давления, поэтому выполняемая внешняя работа незначительна. В таких случаях все тепло, подводимое к твердому телу или жидкости, используется для повышения температуры. Таким образом, существует только одно значение удельной теплоемкости для твердых тел и жидкостей.
При нагревании газа небольшое изменение температуры вызывает значительное изменение как объема, так и давления.Благодаря этому удельная теплоемкость газа может иметь любое значение от 0 до ∞. Следовательно, чтобы зафиксировать значения удельной теплоемкости газа, его объем или давление поддерживают постоянными. Следовательно, необходимо определить две удельные теплоты газов. а именно Удельная теплоемкость при постоянном давлении и удельная теплоемкость при постоянном объеме.
Молярная удельная теплоемкость газа при постоянном объеме:
Количество тепла, необходимое для повышения температуры одного моля газа на 1 К (или 1 ° C) при постоянном объеме, называется молярной удельной теплотой при постоянном объеме.Обозначается C _V. Единица S.I. — J K ^-1 моль ^-1.
Молярная удельная теплоемкость газа при постоянном давлении:
Количество тепла, необходимое для повышения температуры одного моля газа на 1 К (или 1 ° C) при постоянном давлении, называется молярной удельной теплотой при постоянном давлении. Обозначается C _P. Единица S.I. — J K ^-1 моль ^-1.
Основная удельная теплоемкость газа при постоянном объеме:
Количество тепла, необходимое для повышения температуры единицы массы газа до 1 К (или 1 ° C), когда его объем поддерживается постоянным, называется его основной удельной теплотой при постоянном объеме.Обозначается c _V. Единица S.I. — J K ^-1 кг ^-1.
Основная удельная теплоемкость газа при постоянном давлении:
Количество тепла, необходимое для повышения температуры единицы массы газа на 1 К (или 1 ° C) при постоянном давлении, называется его основной удельной теплотой при постоянном давлении. Обозначается он c _P. Единица S.I. — J K ^-1 кг ^-1.
Связь между удельной молярной теплотой и основной удельной теплоемкостью Нагрев:
молярный удельная теплоемкость при постоянном объеме равна Молекулярной массе, умноженной на основную удельную тепло при постоянном объеме
C _V = M c _V
молярный удельная теплоемкость при постоянном давлении равна молекулярной массе, умноженной на основную удельная теплоемкость при постоянном давлении
C _P = M c _P
Объяснение C _P> C _V:
Когда газ нагревается при постоянном объеме, газ не расширяется, поэтому внешняя работа сделано — ноль.Следовательно, тепло, отдаваемое газу, полностью используется для увеличение внутренней энергии газа.
Тогда как когда газ нагревается при постоянном давлении, тепло, отдаваемое газу, используется в течение двух часть его используется для увеличения внутренней энергии газа и часть его используется для выполнения внешних работ.
Теперь в обоих случаях постоянного объема и постоянного давления увеличение внутренней энергии такое же, как и повышение температуры для одной и той же массы газа.Следовательно, тепло, подаваемое при постоянном давлении, больше, чем тепло, подаваемое при постоянном объеме, за счет количества тепла, которое используется для выполнения внешней работы. Это объясняет, почему удельная теплоемкость газа при постоянном давлении больше, чем удельная теплоемкость при постоянном объеме. то есть C _P> C _{V .}
Далее по соотношению Майера C _P — C _V = R. R — универсальная газовая постоянная, положительная. Следовательно, C _P> C _{V .}
Mayer’s Relay:
Рассмотрим один моль идеального газа, заключенный в цилиндр, снабженный невесомым и герметичным подвижным поршнем без трения. Пусть P, V и T — давление, объем и абсолютная температура газа соответственно. Пусть газ нагревается с постоянным объемом так, чтобы его температура повысилась на dT. Пусть dQ ₁ будет теплотой, отдаваемой газу для этой цели. В этом случае все тепло, подводимое к газу, используется для увеличения внутренней энергии газа.
Теперь, dQ ₁ = 1 × C _V × dT = dE ………… (1)
Где C _V — молярная удельная теплоемкость газа при постоянный объем.
Теперь дайте газу нагреться при постоянном давлении, чтобы его температура повысилась на dT. Пусть dQ2 — тепло, отдаваемое газу для этой цели.
Теперь, dQ ₂ = 1 × C _P × dT = C _P × dT ………… (2)
Где C = 1 × C _P × dT — молярная теплоемкость газа при постоянном давлении.
В этом случае тепло, подводимое к газу, используется для двух целей: часть его используется для увеличения внутренней энергии газа, а часть — для выполнения внешней работы. Таким образом,
dQ ₂ = dE + dW ………… (3)
Из уравнений (1), (2) и (3)
C _P × dT = C _V × dT + DW ………… (4)
Газ нагревается при постоянном давлении, так что он расширяется, и при этом поршень перемещается вверх на расстояние dx.Если A — это площадь поперечного сечения цилиндра (площадь поршня), а dV — увеличение объема газа,
Тогда dV = A dx. ……… (5)
Пусть dW — работа, совершаемая газом при увеличении громкость.
Сейчас, работа = Сила × Водоизмещение
Но, сила = давление × площадь
∴ Работа = Давление × Площадь × Водоизмещение
dW = P × A × dx ……… (6)
Из уравнений (5) и (6) имеем
dW = P dV ……… (7)
Из уравнений (7) и (4)
C _P × dT = C _V × dT + П.dV ………… (8)
За один моль идеального газа
P V = R T
Где, R — универсальная газовая постоянная.
Обе стороны дифференцирования по температуре.
P dV = R dT. ……………. (9)
Из уравнений (8) и (9)
C _P × dT = C _V × dT + R.dT
∴ C _P = C _V + R
∴ C _P — C _V =
R
Это отношение известно как отношение мэра между двумя молярная удельная теплоемкость газа.
Связь между основной удельной теплотой газов:
By Mayer’s отношение
C _P — C _V = Р ……… .. (1)
Пусть c _P и c _V будут основные теплоемкости газа при постоянном давлении и постоянном объем. Пусть M будет молекулярной массой газа.
Тогда C _V = M c _V и C _P = M c _P
Подставляя эти значения в уравнение (1)
M c _P — M c _V = R
∴ M (c _P — c _V) = R
∴ (c _P — c _V) = R / M
∴ (c _P — c _V) = r
Где, r = газовая постоянная рассматриваемого газа.Для разных газов он разный.
Предыдущая тема: Численные задачи кинетической теории
Следующая тема: Степень свободы молекул газа и соотношение теплоемкостей
Наука> Физика> Кинетическая теория газов> Удельная теплоемкость газов
Расчет удельной теплоемкости
Расчет удельной теплоемкости
Следующий: Изотермическое и адиабатическое расширение Up: Классическая термодинамика Предыдущее: Теплоемкость или удельная Теперь, когда мы знаем взаимосвязь между удельной теплоемкостью при постоянном объеме и постоянное давление для идеального газа, было бы хорошо, если бы мы могли вычислить любую из этих величин из первых принципов.Классическая термодинамика здесь нам не поможет. Тем не мение, довольно легко рассчитать удельную теплоемкость при постоянном объеме, используя нашу знание статистической физики. Напомним, что вариация количества доступных состояний идеального газа с энергией и объемом записывается
(301)

Для конкретного случая одноатомного идеального газа мы разработали более точную выражение для в разд. 3.8: i.е. , г.
(302)

где — постоянная, не зависящая от энергии и объема. Следует, что
(303)

Температура определяется как
(304)

так
(305)

Поскольку « и, мы можем переписать приведенное выше выражение как
(306)

где — постоянная идеального газа.Над формула говорит нам, как именно внутренняя энергия одноатомного идеального газа зависит от его температуры.
Молярная теплоемкость одноатомного идеального газа при постоянном объеме равна четко
(307)

Имеет числовое значение
(308)

Кроме того, у нас есть
(309)

а также
(310)

Из предыдущей таблицы видно, что эти прогнозы довольно хорошо подтверждаются. хорошо для одноатомных газов гелия и аргона.Обратите внимание, что удельная теплоемкость многоатомные газы больше, чем одноатомные газы. Это потому что многоатомные молекулы могут вращаться вокруг своих центров масс, а также перемещаться, поэтому многоатомные газы могут накапливать энергию как во вращательном, так и во вращательном переводной, энергетические состояния составляющих их частиц. Мы проанализируем этот эффект в более подробно позже в этом курсе.

Следующий: Изотермическое и адиабатическое расширение Up: Классическая термодинамика Предыдущее: Теплоемкость или удельная
Ричард Фицпатрик 2006-02-02
8.Коэффициенты теплоемкости газов (Cp / Cv)
Введение
Теорема о равнораспределении утверждает, что любой квадратичный член энергии, такой как кинетическая энергия, способствует равенству внутренней энергии системы, находящейся в тепловом равновесии. Это означает, что для газа каждая степень свободы дает ½ RT во внутреннюю энергию на молярной основе (R — постоянная идеального газа)
Атом одноатомного газа может двигаться в трех независимых направлениях, поэтому газ имеет три степени свободы благодаря своему поступательному движению.Следовательно, его внутренняя энергия U подчиняется уравнению U = 3/2 RT. Теплоемкость при постоянном объеме, C _v, является производной внутренней энергии по температуре, поэтому для нашего одноатомного газа C _v = 3/2 R.
Теплоемкость при постоянном давлении может быть оценена, поскольку разность между молярными значениями C _p и C _v составляет R; C _p — C _v = R. Хотя это строго верно для идеального газа, это хорошее приближение для реальных газов.
Вращение молекул газа добавляет дополнительные степени свободы. Линейная молекула вращается по двум независимым осям. Следовательно, линейная молекула имеет две вращательные степени свободы. Общее число степеней свободы линейной молекулы равно 5, поэтому ее внутренняя энергия U = 5/2 RT, ее молярная теплоемкость при постоянном объеме C _v = 5/2 R и ее молярная теплоемкость при постоянном давлении. будет C _p = 7/2 R.
Нелинейная молекула вращается по трем независимым осям.Следовательно, линейная молекула имеет три степени свободы вращения. Общее число степеней свободы линейной молекулы равно 6, поэтому ее внутренняя энергия U = 3 RT, ее молярная теплоемкость при постоянном объеме C _v = 3 R, а ее молярная теплоемкость при постоянном давлении будет C _п = 4 р.
Вибрации могут увеличивать теплоемкость, но только если они термически доступны. Колебательная температура \ (\ Theta _ {vib} \) определяется уравнением:
\ [\ Theta _ {vib} = \ frac {hc \ nu} {k} \]
где h — постоянная Планка, c — скорость света, v — частота, а k — постоянная Больцмана.{2}} \]
где N — число молей, R — постоянная идеального газа, а T — температура. Суммарный вклад в теплоемкость при постоянном объеме от всех колебательных степеней свободы составляет:
\ [C_ {vib, Total} = \ sum \ left (C_ {v} \ right) _ {vib} \]
, где суммирование ведется по всем колебательным степеням свободы, 3N-5 (линейные молекулы) или 3N-6 (нелинейные молекулы)
Экспериментальный
У вас есть большой баллон с впускным отверстием для газа и манометр, прикрепленный к пробке в горлышке баллона, рис. 1.

Рисунок 1. Установка для измерения отношения Cp / Cv для газов.
Теперь вы начинаете с газа при атмосферном давлении (760 Торр), а затем добавляете газ, чтобы немного увеличить давление внутри баллона, скажем, на 1,5% (11,4 Торр).
Теперь очень быстро вытяните стопор из узкого места и очень быстро верните его в исходное положение, Рисунок 2.

Рисунок 2. Очень быстро удалите стопор.
Прежде чем читать дальше, сделайте паузу и подумайте над двумя следующими вопросами.Что происходит с давлением и температурой в бутылке, когда вы снимаете пробку? Как изменится давление и температура в следующие несколько минут? Обратите внимание, что бутылка термически не изолирована от окружающей среды.
Сначала газ возвращается к окружающему атмосферному давлению, когда вы снимаете пробку с баллона и газ выходит. Если вы удалите пробку и быстро вернете ее, этот процесс будет адиабатическим. Адиабатический процесс — это процесс, при котором тепло не передается (dq = 0).Когда газ расширяется, он действует против окружающей среды и немного охлаждается.
Секунда через несколько минут температура газа возвращается к исходной температуре окружающей среды, поскольку баллон не имеет термической изоляции. Что это делает с его давлением? Давление растет из-за закона идеального газа, PV = nRT. После перестановки P = nRT / V. Когда температура газа возвращается к температуре окружающей среды, давление повышается.
Степень увеличения давления связана с отношением теплоемкости газа при постоянном давлении к его теплоемкости при постоянном объеме.Это соотношение определяется следующим образом:
\ [\ frac {C_ {p}} {C_ {v}} = \ frac {\ ln P_ {1} — \ ln P_ {2}} {\ ln P_ {1} — \ ln P_ {3}} \]
, где P ₁ — начальное давление газа, P ₂ — давление окружающей среды в помещении, а P ₃ — конечное давление, достигнутое после открытия пробки.
Процедура
Постройте устройство, как описано выше.