Все о механике: Механика. Раздел кинематика — движение тел

Механика. Конспекты по физике для 10-11 класса. Знаете ли вы? Гравитация :: Класс!ная физика

Для тех, кто хочет хорошо знать физику!
Тесты — задачи по кинематике для 10-11 класса

Здесь представлены конспекты по теме «Механика» для 10-11 классов.
!!! Конспекты с одинаковыми названиями различаются по степени сложности.

1. Гидростатика  ( повторение 7-8 класса)

2. Гидростатика и гидродинамика

3. Законы Ньютона — Механика.

4. Законы сохранения в механике — Механика.

5. Законы сохранения в механике — Механика.

6. Кинематика материальной точки — Механика.

7. Кинематика материальной точки — Механика.

8. Механические колебания 

9. Механические колебания

10. Основные понятия кинематики (повторение 8-9 класса)

11. Основные понятия кинематики

12. Работа и энергия

13.

Работа и энергия

14. Силы в механике

15. Силы в механике

16. Статика

 

Механика, законы, конспекты, конспекты по физике, законы сохранения, работа, энергия, силы.

 

ГРАВИТАЦИЯ. ЗНАЕТЕ ЛИ ВЫ?

Знаете ли Вы, что Кеплер задолго до Ньютона склонялся к мысли о «тяжести», действующей между небесными телами, и именно ею объяснил приливы, приписывая их притяжению вод океана Луной.

… до сих пор существуют сомнения в реальности опытов Галилея по бросанию тел с вершины Пизанской падающей башни. Однако известно, что еще при его жизни эту башню использовал один из сторонников Аристотеля для демонстрации различия в падении тел. Как бы то ни было, Галилею удалось установить независимость ускорения свободного падения от природы падающих тел.

… по Аристотелю, сила тяготения по мере приближения к центру Земли сохраняет численное значение, но при его прохождении скачком изменяет направление на противоположное.

Именно так описывал Данте свое путешествие через самое глубокое место ада (центр Земли). По теории же Ньютона, сила притяжения должна там обратиться в ноль, поскольку им было показано, что помещенное в тонкую сферическую оболочку тело не испытывает на себе действия сил.

… почти 200 лет назад, в 1801 году, немецкий астроном И.Зольднер рассчитал, опираясь на теорию Ньютона, как должны отклоняться световые лучи в поле тяготения Солнца. Более чем через 100 лет английский астроном О.Лодж ввел термин «гравитационная линза», предсказав, что протяженные космические тела, например галактики, отклоняя лучи от далеких объектов, могут создавать несколько их изображений. В 1979 году такая «линза» была впервые обнаружена.

… на поверхности внутренних спутников Юпитера кратеров намного меньше, чем на поверхности внешних. Объясняется это тем, что из-за приливного влияния и магнитного поля гигантской планеты у ближайших спутников выше тектоническая активность, поэтому их поверхность активно «перерабатывается» и старые кратеры исчезают.

… несмотря на то, что на Землю ежесуточно выпадает примерно десять тысяч тонн космического вещества в виде метеоритов и пыли, такой прирост массы за все время эволюции нашей планеты практически не отразился на периоде ее оборота вокруг своей оси.

… под действием приливного «трения» Земля замедляет свое суточное вращение и через миллиарды лет будет смотреть на Луну все время одной стороной, как смотрит Плутон на свой спутник Харон. Луна к тому времени уйдет, по расчетам, на 553 тысячи километров от Земли, а новый месяц станет равным 47,2 суток.

… по теории относительности, переменное движение тел должно приводить к излучению гравитационных волн. Однако из-за слабости гравитационного взаимодействия зарегистрировать эти волны даже от мощных космических источников пока еще не удалось. Кстати, действие их приемников основано на приливном эффекте.

… к черным дырам — объектам, удерживающим своим чудовищным гравитационным полем даже свет, — теория тяготения Ньютона не применима, хотя сама возможность их существования вытекает из этой теории.

… при свободном падении, ногами вниз, на черную дыру гипотетический наблюдатель растягивался бы в длинную тонкую нить, так как его ноги двигались бы несравненно быстрее, чем голова, и в конце концов он был бы разорван приливными силами невероятной мощи.

… разрушающее действие приливных сил было «продемонстрировано» Юпитером, развалившим в июле 1992 года проходившую в опасной для себя близости к нему комету.

… в 1932 году будущий академик Лев Ландау предсказал, что при смерти (гибели) массивной звезды ее центральная часть сжимается в одно гигантское атомное ядро — нейтронную звезду, удерживаемую силами гравитации. Плотность такого образования должна достигать 100 миллионов тонн на кубический сантиметр! 35 лет спустя нейтронные звезды были открыты английскими радиоастрономами.

… долгие годы астрономы безуспешно искали так называемую скрытую массу Вселенной, предотвращающую своим гравитационным полем разлет галактик из их скоплений и тормозящую расширение Вселенной. Однако, по последним данным, никакая сила тяготения не заставит повернуть назад стремительно разбегающиеся галактики. Вселенная ускоренно расширяется, и этот процесс продлится вечно.

Источник: журнал «Квант»

МЕХАНИКА | Энциклопедия Кругосвет

Содержание статьи

МЕХАНИКА, раздел физики, в котором изучается движение тел под действием сил. Механика охватывает очень широкий круг вопросов – в ней рассматриваются объекты от галактик и систем галактик до мельчайших, элементарных частиц вещества. В этих предельных случаях выводы механики представляют, конечно, чисто научный интерес. Но предметом механики является также проектирование строений, мостов и механизмов; этот раздел, обычно называемый прикладной механикой, сам по себе достаточно обширен.

Фундаментальное значение для всей этой тематики имеет механика материальной точки, разделяющаяся на кинематику, предметом которой является математическое описание возможных движений материальной точки, и динамику, которая рассматривает движение материальных точек под действием заданных сил. Основные принципы динамики сведены в законы движения, которые в случае материальных точек имеют самый простой вид. Эти законы были впервые сформулированы в 1687 И.Ньютоном. Если материальные точки движутся с очень большими скоростями, то ньютоновские законы движения следует модифицировать в соответствии с теорией относительности; если же это частицы атомных масштабов, то необходима иная формулировка законов движения – так называемая квантовая механика. Ниже будет изложена ньютоновская механика; ее модификациям посвящены статьи ОТНОСИТЕЛЬНОСТЬ; КВАНТОВАЯ МЕХАНИКА.

Протяженное тело можно формально рассматривать как совокупность идеализированных материальных точек, совершенно не имея в виду атомное строение вещества. Выводы о движении таких тел можно делать, исходя из совокупности движений материальных точек. Здесь тоже проводится различие между кинематикой и динамикой и, кроме того, существует статика, изучающая условия равновесия твердых тел, на которые действуют внешние силы. Эти вопросы обсуждаются ниже.

Механические свойства газов и жидкостей в какой-то мере сходны, и законы, которым подчиняется их движение, тоже можно вывести, рассматривая их как системы материальных точек. Этот раздел, обычно называемый «механикой жидкостей и газов», подразделяется на гидростатику и гидродинамику. Им посвящена статья ГИДРОАЭРОМЕХАНИКА. Специальные вопросы течения газов рассматриваются в статье АЭРОДИНАМИКА, а вопросы движения электропроводящих жидкостей и газов – в статье МАГНИТНАЯ ГИДРОДИНАМИКА. Остаются еще три специальных раздела – аналитическая динамика, небесная механика и статистическая механика. Аналитическая динамика – это математическая дисциплина, в центре внимания которой находятся общие методы составления уравнений движения и их решения, а не анализ конкретных механических систем. В небесной механике методы аналитической динамики применяются при изучении чрезвычайно сложного движения планетных систем. Статистическая механика опирается на теорию газов и рассматривает в общем виде поведение системы, содержащей огромное число молекул или атомов, исходя из свойств таких отдельных частиц и законов, управляющих их поведением.

По этим вопросам имеются отдельные статьи НЕБЕСНАЯ МЕХАНИКА; СТАТИСТИЧЕСКАЯ МЕХАНИКА.

Подобное деление механики отражает историческое развитие физики и, кроме того, соответствует использованию различных математических методов. В конечном итоге механика и физика как наука составляют единое целое, ибо чем больше мы узнаем, например, о таких явлениях, как свет и электричество, которые обычно не рассматриваются в механике, тем яснее становится их фундаментальная связь с атомными явлениями, тесно связанными с механикой.

Исторически развитие статики началось с Архимеда в 3 в. до н.э. До этого периода и много столетий спустя проблемы динамики обсуждались лишь с качественной стороны и соотносились с принципами, которые мы полагаем сегодня ошибочными либо не имеющими отношения к делу. Начало динамике было положено Ньютоном, который сформулировал законы движения и закон всемирного тяготения, опубликованные в первом издании

Математических начал натуральной философии (Philosophiae naturalis principia mathematica, 1687). Ньютону удалось в своей книге заложить основы, а в ряде случаев и далеко продвинуться в изучении динамики, небесной механики, механики твердого тела, гидродинамики и баллистики. Хотя принципы статики к тому времени были хорошо известны, Ньютон впервые рационально обосновал их, показав, как их можно вывести из законов динамики. На протяжении примерно двух столетий после этого механика развивалась путем построения более совершенных математических методов без необходимости внесения каких-либо изменений в основные принципы, и лишь после 1900 развитие теории электромагнетизма и атомной физики потребовало модификации механики для распространения ее принципов на явления, которые она не могла удовлетворительно описывать. Но теория относительности и квантовая механика не отменили ньютоновской теории – она по-прежнему точна, как и раньше, и можно показать, что она строго вытекает из обеих новых теорий в том случае, когда рассматриваемые тела имеют макроскопические размеры и движутся с умеренными скоростями. В остальной части этой статьи мы будем иметь дело только с такими ситуациями.

Механика материальной точки.

Чтобы можно было описывать движение материальной точки, нужно определить ее положение в данный момент. На рис. 1 показана прямоугольная система координат, которая позволяет характеризовать положение материальной точки, находящейся в точке Р, координатами (x, y, z). Поскольку материальная точка не имеет размеров и, следовательно, не может быть ориентирована в том или ином направлении, эти три числа полностью характеризуют ее положение в любой момент. Если раcсматривать их как функции времени t, то функция [x (t), y(t), z (t)] прочерчивает в пространстве траекторию, полностью определяющую движение материальной точки. Основная задача динамики материальной точки – найти зависимость x, y и z от t, если заданы силы, действующие на материальную точку. (Возможна, конечно, задача о нескольких материальных точках, оказывающих силовое воздействие друг на друга; подобные задачи решаются труднее.)

Рассмотрим сначала материальную точку, движущуюся прямолинейно, скажем, вдоль оси x, в отсутствие каких-либо сил. В средневековой механике вслед за Аристотелем утверждалось, что тело движется, пока на него действует сила. Однако Галилей, а за ним и Ньютон установили, что единственное действие силы состоит в изменении движения тела и что в отсутствие силы тело либо остается в покое, либо продолжает двигаться равномерно и прямолинейно. В этом заключается первый закон механики Ньютона. Под равномерным движением подразумевается движение с постоянной скоростью v, при котором путь x, проходимый за время t, равен:

x = vt.

Точнее было бы формулировать это определение, рассматривая короткие интервалы пути и времени: если частица начинает двигаться из точки x₀ в момент времени t₀ и достигает точки х в момент t, то средняя скорость за это время определяется как

Конечно, если материальная точка движется с постоянной скоростью, то нет необходимости говорить о среднем значении. Но если на материальную точку действует сила, то ее движение не является равномерным. В этом случае скорость меняется во времени, и можно говорить о мгновенной скорости v (t) в момент времени t как пределе представленного выше выражения при очень малых интервалах времени и пути. Это записывается следующим образом:

Точно так же можно говорить об изменении скорости во времени, т.е. об ускорении. Если мгновенная скорость изменяется от v₀ в момент t₀ до vв момент t, то среднее ускорение за этот промежуток определяется как

а мгновенное ускорение в момент времени t –

Таким образом, скорость характеризует быстроту изменения положения, а ускорение – быстроту изменения скорости. Рассматривать скорость изменения ускорения и т.д. не имеет особого смысла, поскольку, как это первым понял Ньютон, сила создает лишь ускорение. Действительно, если к небольшому телу приложена сила F, то, как показывает опыт, его ускорение остается постоянным, если сила постоянна, и в любой момент времени ускорение пропорционально этой силе. Данное положение можно записать в виде a ~ F или F ~ a. В этом соотношении коэффициент пропорциональности m есть величина, постоянная для рассматриваемой частицы независимо от того, где и как она движется. Эта величина m называется массой (инертной массой) частицы, и, следовательно, равенство

F = ma

есть установленное опытным путем соотношение между мгновенными значениями величин F и a. В этом суть второго закона Ньютона. Третий закон, который мы приведем в дальнейшем, относится к случаю, когда имеется более одного тела.

Единицы измерения механических величин вводятся следующим образом. На основе эталонов единиц длины и времени – метра и секунды – определяются единицы скорости – метр в секунду (м/с) и ускорения – метр в секунду в квадрате (м/с²). Единица массы килограмм (кг) определяется как масса международного прототипа килограмма, изготовленного из сплава иридия с платиной и хранящегося в Международном бюро мер и весов в Севре под Парижем. Единица силы в системе СИ называется ньютоном (Н) и определяется как сила, сообщающая телу массой 1 кг ускорение 1 м/с². Таким образом, согласно второму закону Ньютона,

1 H = 1 кгЧм/с².

Направление вектора ускорения совпадает с направлением вектора силы.

Тяготение.

Представленное выше определение единицы силы, основанное на незыблемых физических принципах, тем не менее, не удобно для практических измерений. Удобнее исходить из понятия веса, т.е. силы притяжения Земли. Согласно закону всемирного тяготения, сформулированному тоже Ньютоном, между любыми двумя телами во Вселенной действует сила притяжения, пропорциональная произведению масс этих тел и обратно пропорциональная квадрату расстояния между ними. Это положение математически выражается соотношением

где G – универсальная гравитационная постоянная, а m_G и M_G – гравитационные массы тел. Если тела протяженные, то все материальные точки этих тел попарно взаимодействуют друг с другом в соответствии с этой формулой и, чтобы найти полную силу, нужно суммировать все отдельные взаимодействия. В чрезвычайно важном случае тел сферической формы оказывается, что притяжение будет в точности таким, как если бы масса каждого из них находилась в центре сферы.

Предположим теперь, что телу с гравитационной массой m_G и инертной массой m, удерживаемому не очень высоко над поверхностью Земли, предоставляется возможность свободно падать. Сила тяжести ускоряет тело вниз, и мы имеем

где M_G – гравитационная масса Земли, а R – ее радиус. Ускорение падающего тела можно записать в виде

где первый множитель не зависит от свойств тела. Экспериментально установлено, что ускорение несколько изменяется в разных точках на поверхности Земли, поскольку Земля не является идеальной сферой и к тому же вращается. Однако в данном месте оно в точности одно и то же для всех тел. Это означает, что величины m и m_G всегда и всюду пропорциональны, а при надлежащем выборе единиц измерения одинаковы. В таком случае нет необходимости различать гравитационную и инертную массы, и выражение для F_G приобретает вид

где

Аналогично выражению для ускорения a, ускорение силы тяжести g в любой точке дается формулой

Величина g составляет примерно 9,81 м/с² и позволяет определить массу Земли (5,97Ч10²⁴ кг) и ее среднюю плотность, в 5,5 раз превышающую плотность воды. Предположим, теперь, что вес тела равен W. Так как сила веса создает ускорение g, соотношение между массой, весом и ускорением приобретает вид

W = mg.

Между экватором и полюсами на поверхности земли величина g изменяется от 9,78 до 9,83 м/с². Соответственно этому изменяется и вес, но в одной точке вес двух тел с одинаковой массой всегда одинаков, и на этом опытном факте основан гораздо более удобный способ измерения массы и силы, нежели основанный на втором законе Ньютона. Массы двух тел равны, если в одном и том же месте равны их веса.

Импульс и энергия.

Импульс тела р определяется как произведение его массы на скорость:

p = mv.

Эта величина имеет важное значение. В самом деле, предположим, что два тела с массами m и M действуют друг на друга с силой, стремящейся ускорить оба тела. На рис. 2 такую силу создает пружина (происхождение силы может быть любым). Согласно третьему закону Ньютона, в любой момент времени сила, с которой масса m действует на массу M, равна по величине и противоположна по направлению силе, с которой масса M действует на m (действие равно противодействию). Предположим, что в момент времени t₀ скорости масс равны v₀ и V₀. Комбинируя выражение для ускорений со вторым законом Ньютона, мы найдем, что скорости изменяются в соответствии с выражениями

где F_m и F_M – силы, действующие на m и M. Поскольку эти силы равны и противоположно направлены, имеем

откуда, умножая на (t – t₀) получаем

Из этого равенства следует, что хотя отдельные импульсы изменяются, их сумма в момент времени t₀ равна их же сумме в момент t, т.е. в процессе всего движения остается постоянной. Это – так называемый закон сохранения импульса. Он универсален в том смысле, что справедлив независимо от природы сил и длительности их действия между телами.

Работа U, совершаемая силой, приложенной к движущемуся телу, определяется как произведение силы на расстояние:

U = F(x – x₀),

где (как и далее) точки x и x₀ должны выбираться достаточно близко друг к другу, чтобы силу F можно было считать постоянной. Воспользуемся тем, что, как легко доказать, точка, движущаяся с постоянным ускорением, проходит за время (t – t₀) такое же расстояние, как если бы все это время она двигалась со средней скоростью ¹/₂(v + v₀). Таким образом, из выражения для второго закона Ньютона вытекает:

или

Величина ¹/₂mv² называется кинетической энергией. Если обозначить ее через Т, то выражение

U = T – T₀

означает, что работа, совершаемая за любой малый промежуток времени, а следовательно (если просуммировать), и за любой произвольный промежуток времени, равна разности конечной и начальной кинетических энергий. Это положение справедливо независимо от того, какова сила и как она изменяется со временем, а также от того, каково расстояние, на котором она действует.

Путем точно таких же рассуждений можно показать, что тело, обладающее кинетической энергией Т, может совершить работу, равную T – T₀, если его Т уменьшится до величины T₀, или равную Т, если тело в конце останавливается. Таким образом, всю работу, совершенную над телом при его ускорении, можно снова получить, остановив тело. Поэтому движущееся тело можно рассматривать как «носителя» работы. Под энергией понимается способность совершать работу, а запасенная телом кинетическая энергия зависит только от его скорости (и массы) и не зависит от того, как эта скорость была приобретена.

Предположим, что тело массой m поднято на высоту h над поверхностью земли, а затем свободно падает. Если оно падает в течение времени t с постоянным ускорением g, то соотношение между g, h и t можно получить из правила для средних скоростей

где v – скорость, с которой тело ударяется о землю, причем мы положили v₀ = 0, поскольку до начала падения тело покоится. Вновь, поскольку v = gt, можно написать h = v²/2g, а умножив обе части равенства на mg, получим

mgh = ¹/₂mv².

Поскольку mg – вес тела, величина mgh есть работа по подъему тела на высоту h, а ¹/₂mv² – кинетическая энергия тела в момент достижения им земли, равная работе, которую тело может совершить при ударе. Анализируя весь процесс, мы видим, что работа по подъему тела, равная mgh, запасается телом в виде его потенциальной энергии перед тем, как оно начинает падать. По мере падения потенциальная энергия переходит в кинетическую, которая может снова перейти в работу, равную mgh, при ударе тела о землю. Когда тело окончательно приходит в состояние покоя, то на первый взгляд энергия исчезает. Но более тщательный анализ показывает, что она сохранилась в форме усилившегося молекулярного движения в месте падения, т.е. в форме звука и теплоты. В отличие от импульса, энергия принимает разные формы, но при переходе из одной формы в другую полное количество энергии не меняется. Это – так называемый закон сохранения энергии.

В качестве примера применения двух законов сохранения рассмотрим соударение двух шаровых маятников (рис. 3,а). Предположим, что шары маятников имеют одинаковую массу и изготовлены из абсолютно упругого материала. Это означает, что кинетическая энергия при ударе не рассеивается. Пусть V₁ – скорость первого маятника в момент, предшествующий соударению, и нам надо найти v₁ и v₂ – скорости сразу после удара.

При соударении энергия и импульс сохраняются, и мы имеем

Производя сокращения и возводя обе части второго равенства в квадрат, получаем

Эти соотношения могут выполняться одновременно только при v₁v₂ = 0. Таким образом, либо v₁ = 0, либо v₂ = 0, но не то и другое. Поскольку второй шар служит препятствием для первого, в нуль обратится v₁, и в силу закона сохранения импульса системы имеем v₂ = V₁. Первый шар останавливается, а второй движется со скоростью V₁, как показано на рис. 3,б.

Предположим теперь, что на второй шар нанесена мастика, так что при соударении шары прилипают друг к другу и дальше движутся вместе (рис. 3,в). В этом случае v₂ = v₁ и импульс по-прежнему сохраняется, так что

mV₁ = 2mv₁,

откуда v₁ = ¹/₂V₁, т.е. шары будут двигаться со скоростью, которая в два раза меньше начальной скорости первого шара. Начальное значение кинетической энергии равнялось T₁ = ¹/₂mV₁², а конечное значение 2 ґ¹/₂m(¹/₂V₁)² = ¹/₂T₁. Таким образом, кинетическая энергия, равная ¹/₂T₁, рассеивается, причем основная часть этой потери идет на деформацию и нагрев мастики и шаров.

Динамика и статика в трех измерениях.

Чтобы обобщить предыдущие результаты на случай трех измерений, потребуется ввести лишь еще один принцип, который заключается в том, что законы Ньютона справедливы для движения вдоль каждой оси координат независимо от движения по другим осям. Так, если пренебречь сопротивлением воздуха, снаряд вдоль оси z движется с замедлением (рис. 4), а вдоль горизонтальной оси – без внешних сил и без ускорения. Обозначим через t время полета. Половину этого времени снаряд поднимается, а остальное время опускается. Таким образом, его скорость по вертикали изменяется на v_0z за время ¹/₂t, так что

v_0z = ¹/₂gt, t = 2v_0z/g,

и все это время горизонтальное движение происходит со скоростью v_0x и без ускорения. Таким образом, дальность полета равна:

R = v_0xt = 2v_0xv_0z/g.

Если v₀ – начальная скорость, а q – угол возвышения, то легко понять, что v_0x = v₀cosq и v_0x = v₀sinq, так что

и максимальное значение этой величины, равное v₀²/g, достигается при q = 45°.

В приведенном примере начальная скорость v₀ характеризовалась и величиной, и направлением. Такие величины называются векторами, а величины v_0x и v_0z – соcтавляющими или компонентами вектора. (Обычно векторы обозначают полужирными буквами.) Предположим теперь, что в трехмерном пространстве к покоящейся материальной точке приложено несколько сил, под действием которых она остается в покое. О подобной системе сил говорят, что они уравновешены, и законы динамики позволяют определить, каким должно быть соотношение между ними. Если материальная точка покоится и сохраняет это состояние, ее ускорения вдоль осей x, y или z равны нулю, а поскольку ускорения вдоль этих осей не зависят друг от друга, полные силы в каждом из этих трех направлений тоже должны быть равны нулю. (Полная сила, действующая на материальную точку вдоль оси х и стремящаяся привести ее в движение вдоль этой оси, равна сумме x-компонент всех действующих сил; то же самое справедливо и для двух других осей. )

Предположим, что имеются только две силы с компонентами F_1x, F_1y, F_2x и F_2y (для упрощения рисунка ограничимся двумя измерениями). В случае равновесия имеем

F_1x + F_2x = 0 и F_1y + F_2y = 0,

или

F_1x = –F_2x и F_1y = –F_2y.

Так как F_1x и F_1y – компоненты вектора силы F₁, и аналогично F_2x и F_2y – компоненты вектора F₂, то возникает ситуация, показанная на рис. 5, где векторы двух уравновешивающих друг друга сил изображены равными по величине и направленными в противоположные стороны.

Предположим, теперь, что имеются три вектора, причем F₃ уравновешивает F₁ и F₂. В этом случае F_1x + F_2x + F_3x = 0, F_1y + F_2y + F_3y = 0.

Эти соотношения можно переписать в виде

F_1x + F_2x = –F_3x, F_1y + F_2y = –F_3y.

Сравнение с аналогичными соотношениями в случае двух сил показывает, что если мы введем новый вектор R с компонентами

R_x = F_1x + F_2x, R_y = F_1y + F_2y,

который называется равнодействующей сил F₁ и F₂, то R будет в точности уравновешивать F₃. Таким образом, сила R воспроизводит суммарное действие сил F₁ и F₂ в том смысле, что если удалить силы F₁ и F₂, заменив их силой R, то материальная точка по-прежнему останется бы в равновесии. Все сказанное представлено графически на рис. 6,а, где показано сложение компонент. На рис. 6,б вспомогательные линии убраны и оставлены только векторы. Последний рисунок называется параллелограммом сил. Он иллюстрирует один из фундаментальных принципов статики, который, как мы видели, является следствием динамической теории. Этот принцип был установлен С.Стевином (1548–1620), который показал, что если бы это было не так, то имелась бы возможность создать машину, которая производила бы работу, даже если бы к ней не подводилась энергия. Сегодня мы рассматривали бы такую машину как пример нарушения закона сохранения энергии; для Стевина это просто противоречило здравому смыслу, но при этом положения статики тоже обосновывались динамическими соображениями.

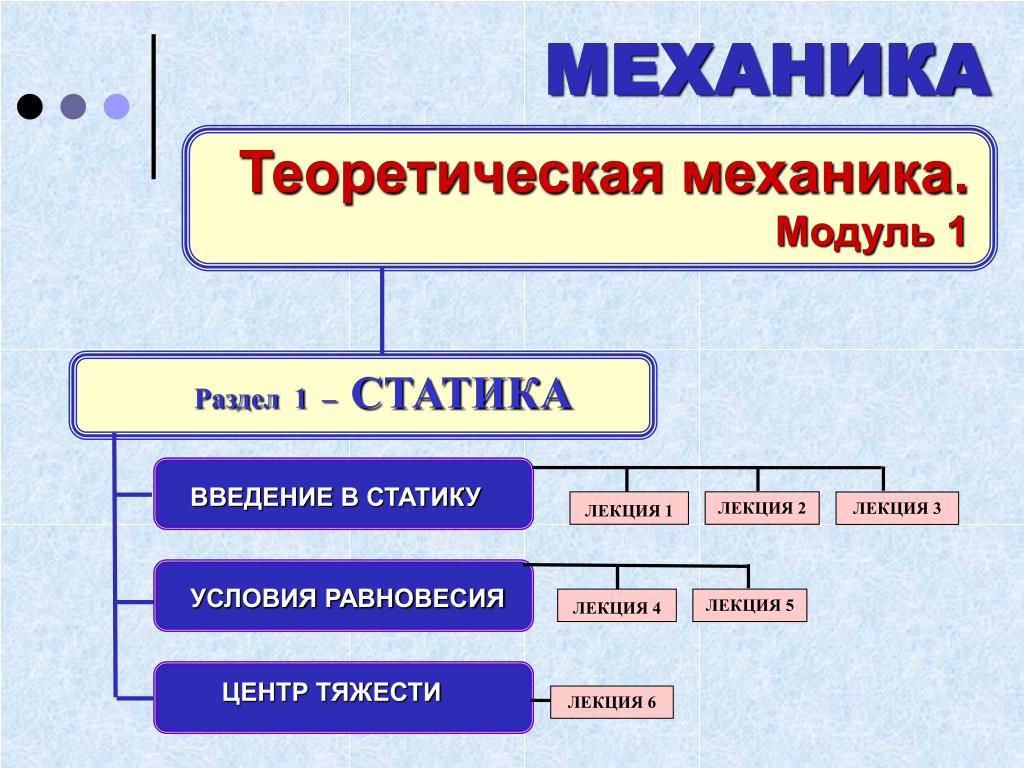
Механика твердого тела.

Твердое тело, которое может принимать различные ориентации в пространстве, можно считать состоящим из материальных точек. (Это просто математический прием, позволяющий расширить применимость законов движения материальных точек, но не имеющий ничего общего с гипотезой атомного строения вещества.) Поскольку материальные точки такого тела будут двигаться в разных направлениях с разными скоростями, приходится прибегать к процедуре суммирования.

Рассмотрим систему, изображенную на рис. 7. Сила F, приложенная к тросу, заставляет массу, имеющую форму цилиндра, изменять свою скорость вращения. Будем характеризовать ориентацию цилиндра углом q между радиусом, проведенным из центра цилиндра в некоторую точку на нем, и произвольно выбранным направлением отсчета. Угол q измеряется в радианах; один радиан (примерно 57°) есть центральный угол, стягивающий дугу длиной r на окружности радиуса r. Таким образом, произвольный угол q стягивает дугу s, равную rq, а вся окружность сoответствует углу 2p радиан. Скорость любой точки на окружности равна

где под q /t понимается скорость, с которой изменяется угол q при вращении. Обозначив эту угловую скорость через w, мы наряду с равенством

s = rq

получим

v = rw.

Нетрудно вычислить кинетическую энергию цилиндра, вращающегося вокруг неподвижной оси с угловой скоростью w. Обозначим через m одну из материальных точек цилиндра, расположенную на расстоянии r_m от оси. Ее кинетическая энергия равна ¹/₂m(r_mw)², а полная кинетическая энергия всех материальных точек может быть представлена в виде суммы

или

T = ¹/₂Iw²,

где . Величина I, называемая моментом инерции, зависит от распределения массы в цилиндре и является его характеристикой. Момент инерции можно вычислить путем интегрирования, и для однородного цилиндра он равен ¹/₂Ma², где M – масса цилиндра, а a – его радиус. Если цилиндр вращается свободно и нет сил, которые совершали бы над ним работу, то из закона сохранения энергии следует, что его кинетическая энергия остается постоянной. В таком случае постоянна и величина w, и мы имеем вращательный аналог первого закона Ньютона.

Предположим теперь, что к тросу, намотанному на цилиндр, на короткое время от t₀ до t прилагается сила F и за это время точка, отмеченная на тросе, проходит расстояние от x₀ до х, а цилиндр поворачивается на угол от q₀ до q, причем

x – x₀ = a(q –q₀).

Работа, совершенная при этом силой, равна:

U = F(x – x₀) = Fa(q – q₀),

и точно так же, как при выводе выражения U = ¹/₂mv² – ¹/₂mv₀², мы можем выразить угловое перемещение через среднюю угловую скорость на этом интервале:

q – q₀ = ¹/₂(w +w₀)(t – t₀),

так что

U = ¹/₂Fa(w +w₀)(t – t₀).

За счет этой работы кинетическая энергия цилиндра изменяется от T₀ до T , так что

U = ¹/₂ I(w²– w₀²).

Приравнивая два последних выражения и производя упрощения, получаем выражение

напоминающее формулу для ускорения частицы. Поэтому мы можем ввести угловое ускорение

и тогда для малого интервала от t₀ до t получим L = Ia, т.е. вращательный аналог второго закона Ньютона, в котором величина Fa, вызывающая вращение, обозначена через L. Она называется вращающим моментом.

Изложенное можно обобщить на случай, когда отсутствуют неподвижные оси и тело свободно вращается в пространстве. В этом случае имеются три момента инерции, относящиеся к «главным осям». Мы не будем углубляться в рассмотрение этих вопросов. Однако можно вывести второй основной принцип статики для случая твердых тел. Пусть силы F₁ и F_2, приложенные к пластине, которая может вращаться, таковы, что вращения нет (рис. 8). Равновесие означает отсутствие углового ускорения, и поэтому полный вращающий момент равен нулю. Моменты сил F₁ и F₂ компенсируют друг друга при условии:

F₁a₁ = F₂a₂,

т.е. получается закон рычага, известный со времен Архимеда. Удалим ось и заменим ее действие третьей силой, как показано на рис. 9, предполагая, что весом пластины можно пренебречь. Для равновесия всех этих сил нужно, во-первых, чтобы пластина не перемещалась и, следовательно, компоненты сил удовлетворяли условию векторного равновесия и, во-вторых, чтобы не было вращения, т.е. выполнялось выведенное только что соотношение. Оба эти принципа составляют основу теории строительной механики и важны при проектировании мостов и зданий.

Проводившиеся выше рассуждения упрощаются, если пользоваться обозначениями математического анализа, в которых подразумевается предельный переход (t → t₀), так что нет необходимости все время говорить о нем. Ньютон первым применил методы дифференциального и интегрального исчисления при решении физических задач, а последующее развитие механики как науки было делом таких математиков, как Л.Эйлер, Ж.Лагранж, П.Лаплас и К.Якоби, каждый из которых находил в ньютоновской механике источник вдохновения для своих математических изысканий.

Изменения в механике расчета рейтинга ALL STARS

В 2021-м году расчет рейтинга ALL STARS будет производиться по новым правилам

• Теперь, рейтинговые баллы, получаемые за каждый старт, определяются дистанцией и временем отставания от лидера гонки в абсолюте. Соответственно: у мужчин отставание считается от лидера-мужчины, у женщин — от лидера-женщины.
• Баллы уменьшаются пропорционально времени отставания от лидера.

Например, вы прошли гонку IRONSTAR SPRINT и финишировали за 1,5 часа (90 минут), а лидер — за 1 час (60 минут). В таком случае лидер получит 750 баллов (максимум для дистанции SPRINT). А вы получите 375 баллов, которые рассчитываются следующим образом: 750 — 750*((90 — 60) / 60) = 375.

• Также с этого года нет минимального количества баллов за пройденную дистанцию. Но баллы участника за гонку не могут упасть ниже нуля. Участник получит за гонку 0 баллов, если его финишное время более чем в два раза превышает время лидера.

В примере выше для гонки IRONSTAR SPRINT, все участники с временем финиша больше 2 часов получат 0 баллов.

• С 2021 года баллы рейтинга присваиваются за участие во всех соревнованиях IRONSTAR (включая заплывы на открытой воде SWIMSTAR, женские забеги IRONLADY, и велогонку BIKESTAR).
• Участники эстафетных команд также получают баллы, соревнуясь друг с другом внутри каждого этапа. Баллы рассчитываются по той же формуле, что и для индивидуальных участников.

Например, эстафетная команда Х заняла 3-е место в абсолюте среди мужских команд. Пловец команды среди всех пловцов-эстафетчиков приплыл 10-ым. Это значит, что он получит баллы за 10-е место (пропорционально отставанию от лидера среди пловцов-эстафетчиков).
Велосипедист команды среди всех велосипедистов-эстафетчиков приехал 1-ый. Это значит, что он получит баллы за 1-е место (максимальный балл за этап для этой дистанции).
Бегун команды среди всех бегунов-эстафетчиков прибежал 2-ой. Это значит, что он получит баллы за 2-е место (пропорционально отставанию от лидера среди бегунов-эстафетчиков).

БОЛЕЕ ПОДРОБНУЮ ИНФОРМАЦИЮ МОЖНО ПРОЧИТАТЬ НА СТРАНИЧКЕ РЕЙТИНГА ALL STARS.

Квантовая механика • Джеймс Трефил, энциклопедия «Двести законов мироздания»

На субатомном уровне частицы описываются волновыми функциями.

Слово «квант» происходит от латинского quantum («сколько, как много») и английского quantum («количество, порция, квант»). «Механикой» издавна принято называть науку о движении материи. Соответственно, термин «квантовая механика» означает науку о движении материи порциями (или, выражаясь современным научным языком науку о движении квантующейся материи). Термин «квант» ввел в обиход немецкий физик Макс Планк (см. Постоянная Планка) для описания взаимодействия света с атомами.

Квантовая механика часто противоречит нашим понятиям о здравом смысле. А всё потому, что здравый смысл подсказывает нам вещи, которые берутся из повседневного опыта, а в своем повседневном опыте нам приходится иметь дело только с крупными объектами и явлениями макромира, а на атомарном и субатомном уровне материальные частицы ведут себя совсем иначе. Принцип неопределенности Гейзенберга как раз и очерчивает смысл этих различий. В макромире мы можем достоверно и однозначно определить местонахождение (пространственные координаты) любого объекта (например, этой книги). Не важно, используем ли мы линейку, радар, сонар, фотометрию или любой другой метод измерения, результаты замеров будут объективными и не зависящими от положения книги (конечно, при условии вашей аккуратности в процессе замера). То есть некоторая неопределенность и неточность возможны — но лишь в силу ограниченных возможностей измерительных приборов и погрешностей наблюдения. Чтобы получить более точные и достоверные результаты, нам достаточно взять более точный измерительный прибор и постараться воспользоваться им без ошибок.

Теперь если вместо координат книги нам нужно измерить координаты микрочастицы, например электрона, то мы уже не можем пренебречь взаимодействиями между измерительным прибором и объектом измерения. Сила воздействия линейки или другого измерительного прибора на книгу пренебрежимо мала и не сказывается на результатах измерений, но чтобы измерить пространственные координаты электрона, нам нужно запустить в его направлении фотон, другой электрон или другую элементарную частицу сопоставимых с измеряемым электроном энергий и замерить ее отклонение. Но при этом сам электрон, являющийся объектом измерения, в результате взаимодействия с этой частицей изменит свое положение в пространстве. Таким образом, сам акт замера приводит к изменению положения измеряемого объекта, и неточность измерения обусловливается самим фактом проведения измерения, а не степенью точности используемого измерительного прибора. Вот с какой ситуацией мы вынуждены мириться в микромире. Измерение невозможно без взаимодействия, а взаимодействие — без воздействия на измеряемый объект и, как следствие, искажения результатов измерения.

О результатах этого взаимодействия можно утверждать лишь одно:

неопределенность пространственных координат × неопределенность скорости частицы > h/m,

или, говоря математическим языком:

Δx × Δv > h/m

где Δx и Δv — неопределенность пространственного положения и скорости частицы соответственно, h — постоянная Планка, а m — масса частицы.

Соответственно, неопределенность возникает при определении пространственных координат не только электрона, но и любой субатомной частицы, да и не только координат, но и других свойств частиц — таких как скорость. Аналогичным образом определяется и погрешность измерения любой такой пары взаимно увязанных характеристик частиц (пример другой пары — энергия, излучаемая электроном, и отрезок времени, за который она испускается). То есть если нам, например, удалось с высокой точностью измерили пространственное положение электрона, значит мы в этот же момент времени имеем лишь самое смутное представление о его скорости, и наоборот. Естественно, при реальных измерениях до этих двух крайностей не доходит, и ситуация всегда находится где-то посередине. То есть если нам удалось, например, измерить положение электрона с точностью до 10^–6 м, значит мы одновременно можем измерить его скорость, в лучшем случае, с точностью до 650 м/с.

Из-за принципа неопределенности описание объектов квантового микромира носит иной характер, нежели привычное описание объектов ньютоновского макромира. Вместо пространственных координат и скорости, которыми мы привыкли описывать механическое движение, например шара по бильярдному столу, в квантовой механике объекты описываются так называемой волновой функцией. Гребень «волны» соответствует максимальной вероятности нахождения частицы в пространстве в момент измерения. Движение такой волны описывается уравнением Шрёдингера, которое и говорит нам о том, как изменяется со временем состояние квантовой системы.

Картина квантовых событий в микромире, рисуемая уравнением Шрёдингера, такова, что частицы уподобляются отдельным приливным волнам, распространяющимся по поверхности океана-пространства. Со временем гребень волны (соответствующий пику вероятности нахождения частицы, например электрона, в пространстве) перемещается в пространстве в соответствии с волновой функцией, являющейся решением этого дифференциального уравнения. Соответственно, то, что нам традиционно представляется частицей, на квантовом уровне проявляет ряд характеристик, свойственных волнам.

Согласование волновых и корпускулярных свойств объектов микромира (см. Соотношение де Бройля) стало возможным после того, как физики условились считать объекты квантового мира не частицами и не волнами, а чем-то промежуточным и обладающим как волновыми, так и корпускулярными свойствами; в ньютоновской механике аналогов таким объектам нет. Хотя и при таком решении парадоксов в квантовой механике всё равно хватает (см. Теорема Белла), лучшей модели для описания процессов, происходящих в микромире, никто до сих пор не предложил.

См. также:

Научные события : Научно-организационный отдел : АлтГТУ

Механико-математический факультет Томского государственного университета проводит Всероссийскую молодежную научную конференцию студентов «Все грани математики и механики», приуроченную к 100-летию со дня рождения академика Н.Н. Яненко. Конференция будет проходить с 27 мая по 1 июня 2021 года.

Программа конференции будет включать следующие научные секции:

• алгебра;
• геометрия и ее приложения;
• задачи механики и экологии: физическое и математическое моделирование;
• математическое моделирование, численные методы и параллельные вычисления;
• теория вероятностей и математическая статистика;
• вещественный, комплексный и функциональный анализ и топология.

Заседания секций будут проводиться в гибридном формате: очное участие при отсутствии ограничительных мер на момент проведения и онлайн-участие через одну из платформ (Adobe Connect, Zoom).

Все доклады, принятые на конференцию, будут представляться в устной форме (пленарный доклад — по согласованию, секционный доклад – 10 минут).

По результатам выступлений будут отобраны лучшие доклады для публикации статей объемом 6−14 страниц в сборнике конференции. Сборник будет зарегистрирован в наукометрической базе РИНЦ  (https://www.elibrary.ru/query_results.asp)  и размещен на сайте электронной библиотеки Elibrary.

Для участия в конференции необходимо зарегистрироваться на сайте конференции http://conf.math.tsu.ru до 20 апреля 2021 года.

 

Контакты: Механико-математический факультет Томского государственного университета
Адрес: 634050 пр. Ленина 36, Второй учебный корпус ТГУ, аудитория 417
Телефон: (3822) 52−97−40
E-mail: conf70@math. tsu.ru

Механико-математический факультет МГУ

Декан — член-корреспондент РАН Шафаревич Андрей Игоревич

Математика во все времена лежала в основе точного естествознания, а вместе с механикой была фундаментом всех технических наук, основным инструментом в познании общих закономерностей мироздания.

Лекции по математике читались в Московском университете со времени его открытия в 1755 г. В Уставе университета, принятом в 1804 г., было впервые закреплено создание отделения физических и математических наук.

К началу XX в. московская математическая школа приобрела мировую известность, ее успехи были связаны с именами Д.Ф. Егорова и его учеников Н.Н. Лузина, И.И. Привалова, В.В. Степанова. Школу механики Московского университета прославили Н.Е. Жуковский, С.А. Чаплыгин.

В 1933 г. реорганизация структуры Московского университета привела к образованию нескольких факультетов, в их числе был и механико-математический факультет. Большую роль в его создании и развитии сыграли член-корресспондент АН СССР В.В. Голубев (первый декан факультета), академики И.Г. Петровский, А.Н. Колмогоров, П.С. Александров.

Своими выпускниками факультет всегда поддерживал академическую науку, и наоборот, многие члены Академии наук и сотрудники академических институтов вели педагогическую работу на факультете. В настоящее время только среди заведующих кафедрами и лабораториями факультета 15 академиков и 9 членов-корреспондентов РАН.

В последние десятилетия значение математики в общей системе человеческих знаний сильно возросло. С помощью математических методов рассчитываются атомные реакторы, изучается строение кристаллов и молекул химических веществ, предсказываются место и глубина залегания полезных ископаемых, прогнозируется погода, анализируются экономические процессы и оптимизируется управление экономическими системами, ставятся диагнозы болезней, расшифровываются неизвестные письмена, обосновываются выводы социологических исследований. Математические методы являются базой и для изменяющих мир информационных технологий.

Наиболее абстрактные направления математической мысли — математическая логика, функциональный анализ, топология, современные алгебраические теории — оказались вовлеченными в вихрь приложений математики к разнообразнейшим практическим потребностям. Радикальное переустройство испытала в последние годы и сама система собственно математических знаний. Возникли новые математические дисциплины, например гомологическая алгебра, дифференциальная топология, компьютерная геометрия, претерпели существенное изменение такие разделы математики, как математическая логика, теория вероятностей, теория оптимального управления.

Ученые МГУ внесли ощутимый вклад в развитие важнейших направлений математики. Университетская математическая школа — одна из наиболее авторитетных в мире. В настоящее время механико-математический факультет — ведущий центр математической науки в нашей стране.

Механика — одна из главных составляющих научного фундамента техники. Ученые-механики исследуют и разрабатывают математические модели движения и взаимодействия тел, частиц, масс, изучают механические свойства различных сред. Не занимаясь деталями расчета конкретных конструкций, механики создают теоретические основы расчетов, применимых в других науках, в различных отраслях техники и промышленности. Достижения механиков МГУ общепризнанны и пользуются мировой известностью, они оказали существенное влияние на развитие современной техники.

Для механики наших дней характерно широкое применение самых разнообразных математических знаний, в том числе новейших разделов теоретической и вычислительной математики. Численный эксперимент на ЭВМ стал одним из самых эффективных рабочих инструментов для механиков. Однако связь между математикой и механикой не является односторонней. Механика также стимулирует развитие многих разделов математики, формулируя часто такие задачи, для решения которых еще не разработаны подходящие математические методы. Именно этим органичным взаимодействием математики и механики объясняется совместное обучение студентов по этим специальностям на механико-математическом факультете.

Факультет имеет два отделения: математики и механики. Отделение математики объединяет кафедры математического анализа, высшей алгебры, высшей геометрии и топологии, теории вероятностей, общих проблем управления, теории чисел, дифференциальных уравнений, теории функций и функционального анализа, математической логики и теории алгоритмов, математической статистики и случайных процессов, дискретной математики, вычислительной математики, общей топологии и геометрии, математической теории интеллектуальных систем, дифференциальной геометрии и приложений, теории динамических систем, математических и компьютерных методов анализа; отделение механики — кафедры теоретической механики и мехатроники, аэромеханики и газовой динамики, теории упругости, гидромеханики, прикладной механики и управления, газовой и волновой динамики, теории пластичности, механики композитов, вычислительной механики.

Учебные планы факультета охватывают все современные направления математики и механики. Такие дисциплины, как математический анализ, алгебра, аналитическая геометрия, дифференциальные уравнения, уравнения математической физики, теория функций и функциональный анализ, теория вероятностей, математическая статистика, методы вычислений, программирование, комплексный анализ, дифференциальная геометрия и топология, теоретическая механика, механика сплошной среды, физика, математические методы в экономике, исследование операций, изучаются на обоих отделениях, хотя и в несколько разных объемах. Кроме того, в план отделения математики входит набор курсов лекций естественнонаучного, прикладного и конкретно-экономического содержания. Значительное место в учебном плане студентов-механиков занимает практикум в лабораториях Института механики МГУ. Студенты факультета изучают также историю и методологию математики и механики, цикл гуманитарных дисциплин, английский язык.

Поступающие на механико-математический факультет смогут получить одну из трех квалификаций: «математик» (специальность «математика»), «механик» (специальность «механика»), «математик» со специализацией в области экономики (специальность «математика»).

Срок обучения на факультете 5  лет (с 2011–2012 учебного года — 6 лет).

На каждом отделении на I и II курсах обучение происходит по общей программе для всех студентов. С III курса студенты разделяются по кафедрам. Каждый студент выбирает преподавателя, который руководит его первыми научными исследованиями. Студенты и аспиранты публикуют результаты своих исследований в ведущих научных журналах, активно участвуют в различных всероссийских и международных олимпиадах и конкурсах по математике, информатике, робототехнике и другим дисциплинам. Так, более десяти лет команды механико-математического факультета принимают участие в Чемпионате мира по программированию среди студенческих команд. Команда мехмата неоднократно выходила в финал чемпионата, при этом трижды (в 2003, 2005 и 2009 гг.) получала золотые медали. Совместно с НИИ механики МГУ на факультете заложена прекрасная традиция проведения соревнований по робототехнике среди студенческих команд. Участники соревнований получают возможность проверить на практике результаты математического моделирования, проходя полный путь от постановки теоретической задачи до практического построения робота.

На факультете имеется отдел прикладных исследований, включающий в себя учебно-научный центр и лаборатории систем искусственного интеллекта, динамики деформируемых сред, навигации и управления космическими системами, математического обеспечения имитационных динамических систем, прикладного математического анализа. При кафедрах работают лаборатории вычислительных методов, математической статистики, теории вероятностей, вычислительных средств вероятностных и статистических исследований, компьютерного моделирования, больших случайных систем, компьютерных методов в естественных и гуманитарных науках, операторных моделей и спектральной теории, а также кабинет истории и методологии математики и механики и кабинет методики преподавания элементарной математики. К научной работе по тематике этих лабораторий привлекаются и аспиранты, и студенты факультета.

Факультет тесно связан в работе с НИИ механики МГУ, экспериментальная база которого используется на отделении механики в учебных и научных целях. Научная тематика института охватывает все основные области механики.

Выпускники факультета работают в научно-исследовательских институтах, на промышленных предприятиях и в банках, в лабораториях и вычислительных центрах, в институтах, высших учебных заведениях, школах. Они с успехом решают как теоретические, так и прикладные задачи, ведут педагогическую работу. Диплом факультета признан во всем мире. Около трети выпускников ежегодно поступают в аспирантуру и продолжают заниматься научной работой, целью которой является подготовка диссертации. После защиты диссертации соискателю присваивается ученая степень кандидата физико-математических наук.

Механико-математический факультет славен своими традициями. На мехмате учат не столько рецептам решения конкретных задач, сколько умению думать самостоятельно, а также извлекать знания из разных источников. Именно это позволяет выпускникам факультета быстро включаться и быть эффективными практически в любой сфере деятельности — от компьютерной или финансовой до управления производством и политики.

Механическое движение — материалы для подготовки к ЕГЭ по Физике

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: механическое движение и его виды, относительность механического движения, скорость, ускорение.

Понятие движения является чрезвычайно общим и охватывает самый широкий круг явлений. В физике изучают различные виды движения. Простейшим из них является механическое движение. Оно изучается в механике.
Механическое движение — это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.

Если тело A меняет своё положение относительно тела B, то и тело B меняет своё положение относительно тела A. Иначе говоря, если тело A движется относительно тела B, то и тело B движется относительно тела A. Механическое движение является относительным — для описания движения необходимо указать, относительно какого тела оно рассматривается.

Так, например, можно говорить о движении поезда относительно земли, пассажира относительно поезда, мухи относительно пассажира и т. д. Понятия абсолютного движения и абсолютного покоя не имеют смысла: пассажир, покоящийся относительно поезда, будет двигаться с ним относительно столба на дороге, совершать вместе с Землёй суточное вращение и двигаться вокруг Солнца.
Тело, относительно которого рассматривается движение, называется телом отсчёта.

Основной задачей механики является определение положения движущегося тела в любой момент времени. Для решения этой задачи удобно представить движение тела как изменение координат его точек с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерять время, нужны часы. Всё это вместе образует систему отсчёта.

Система отсчёта — это тело отсчёта вместе с жёстко связанной с ним («вмороженной»» в него) системой координат и часами.
Система отсчёта показана на рис. 1. Движение точки рассматривается в системе координат . Начало координат является телом отсчёта.

Рисунок 1.

 

Вектор называется радиус-вектором точки . Координаты точки являются в то же время координатами её радиус-вектора .
Решение основной задачи механики для точки состоит в нахождении её координат как функций времени: .
В ряде случаев можно отвлечься от формы и размеров изучаемого объекта и рассматривать его просто как движущуюся точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи.
Так, поезд можно считать материальной точкой при его движении из Москвы в Саратов, но не при посадке в него пассажиров. Землю можно считать материальной точкой при описании её движения вокруг Солнца, но не её суточного вращения вокруг собственной оси.

К характеристикам механического движения относятся траектория, путь, перемещение, скoрость и ускорение.

Траектория, путь, перемещение.

 

В дальнейшем, говоря о движущемся (или покоящемся) теле, мы всегда полагаем, что тело можно принять за материальную точку. Случаи, когда идеализацией материальной точки пользоваться нельзя, будут специально оговариваться.

Траектория — это линия, вдоль которой движется тело. На рис. 1 траекторией точки является синяя дуга, которую описывает в пространстве конец радиус-вектора .
Путь — это длина участка траектории, пройденного телом за данный промежуток времени.
Перемещение — это вектор, соединяющий начальное и конечное положение тела.
Предположим, что тело начало движение в точке и закончило движение в точке (рис. 2). Тогда путь, пройденный телом, это длина траектории . Перемещение тела — это вектор .

Рисунок 2.

 

Скорость и ускорение.

 

Рассмотрим движение тела в прямоугольной системе координат с базисом (рис. 3).

Рисунок 3.

 

Пусть в момент времени тело находилось в точке с радиус-вектором

Спустя малый промежуток времени тело оказалось в точке с
радиус-вектором

Перемещение тела:

(1)

Мгновенная скорость в момент времени — это предел отношения перемещения к интервалу времени , когда величина этого интервала стремится к нулю; иными словами, скорость точки — это производная её радиус-вектора:

(2)

Из (2) и (1) получаем:

Коэффициенты при базисных векторах в пределе дают производные:

(Производная по времени традиционно обозначается точкой над буквой.) Итак,

Мы видим, что проекции вектора скорости на координатные оси являются производными координат точки:

Когда стремится к нулю, точка приближается к точке и вектор перемещения разворачивается в направлении касательной. Оказывается, что в пределе вектор направлен точно по касательной к траектории в точке . Это и показано на рис. 3.

Понятие ускорения вводится похожит образом. Пусть в момент времени скорость тела равна , а спустя малый интервал скорость стала равна .
Ускорение — это предел отношения изменения скорости к интервалу , когда этот интервал стремится к нулю; иначе говоря, ускорение — это производная скорости:

Ускорение, таким образом, есть «cкорость изменения скорости». Имеем:

Следовательно, проекции ускорения являются производными проекций скорости (и, стало быть, вторыми производными координат):

Закон сложения скоростей.

 

Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта . Эту систему отсчёта обозначим и будем называть неподвижной.
Вторая система отсчёта, обозначаемая , связана с телом отсчёта , которое движется относительно тела со скоростью . Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы перемещаются параллельно самим себе (нет вращения системы координат), так что вектор можно считать скоростью движущейся системы относительно неподвижной.

Неподвижная система отсчёта обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью , это система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта .

Заметим, что скорость любой точки вагона (кроме вращающихся колёс!) равна . Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью . Муха переносится вагоном, и потому скорость движущейся системы относительно неподвижной называется переносной скоростью.

Предположим теперь, что муха поползла по вагону. Скорость мухи относительно вагона (то есть в движущейся системе ) обозначается и называется относительной скоростью. Скорость мухи относительно земли (то есть в неподвижной системе ) обозначается и называется абсолютной скоростью.

Выясним, как связаны друг с другом эти три скорости — абсолютная, относительная и переносная.
На рис. 4 муха обозначена точкой .Далее:
— радиус-вектор точки в неподвижной системе ;
— радиус-вектор точки в движущейся системе ;
— радиус-вектор тела отсчёта в неподвижной системе .

Рисунок 4.

 

Как видно из рисунка,

Дифференцируя это равенство, получим:

(3)

(производная суммы равна сумме производных не только для случая скалярных функций, но и для векторов тоже).
Производная есть скорость точки в системе , то есть абсолютная скорость:

.

Аналогично, производная есть скорость точки в системе , то есть относительная скорость:

А что такое ? Это скорость точки в неподвижной системе, то есть — переносная скорость движущейся системы относительно неподвижной:

В результате из (3) получаем:

Закон сложения скоростей. Скорость точки относительно неподвижной системы отсчёта равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы. Иными словами, абсолютная скорость есть сумма переносной и относительной скоростей.

Таким образом, если муха ползёт по движущемуся вагону, то скорость мухи относительно земли равна векторной сумме скорости вагона и скорости мухи относительно вагона. Интуитивно очевидный результат!

Виды механического движения.

 

Простейшими видами механического движения материальной точки являются равномерное и прямолинейное движения.
Движение называется равномерным, если модуль вектора скорости остаётся постоянным (направление скорости при этом может меняться).

Движение называется прямолинейным, если направление вектора скорости остаётся постоянным (а величина скорости при этом может меняться). Траекторией прямолинейного движения служит прямая линия, на которой лежит вектор скорости.
Например, автомобиль, который едет с постоянной скоростью по извилистой дороге, совершает равномерное (но не прямолинейное) движение. Автомобиль, разгоняющийся на прямом участке шоссе, совершает прямолинейное (но не равномерное) движение.

А вот если при движении тела остаются постоянными как модуль скорости, так и его направление, то движение называется равномерным прямолинейным.

В терминах вектора скорости можно дать более короткие определения данным типам движения:

• равномерное движение
• прямолинейное движение
• равномерное прямолинейное движение

Важнейшим частным случаем неравномерного движения является равноускоренное движение, при котором остаются постоянными модуль и направление вектора ускорения:

• равноускоренное движение

Наряду с материальной точкой в механике рассматривается ещё одна идеализация — твёрдое тело.
Твёрдое тело — это система материальных точек, расстояния между которыми не меняются со временем. Модель твёрдого тела применяется в тех случаях, когда мы не можем пренебречь размерами тела, но можем не принимать во внимание изменение размеров и формы тела в процессе движения.

Простейшими видами механического движения твёрдого тела являются поступательное и вращательное движения.
Движение тела называется поступательным, если всякая прямая, соединяющая две какие-либо точки тела, перемещается параллельно своему первоначальному направлению. При поступательном движении траектории всех точек тела идентичны: они получаются друг из друга параллельным сдвигом (рис. 5).

Рисунок 5.

 

Движение тела называется вращательным, если все его точки описывают окружности, лежащие в параллельных плоскостях. При этом центры данных окружностей лежат на одной прямой, которая перпендикулярна всем этим плоскостям и называется осью вращения.

На рис. 6 изображён шар, вращающийся вокруг вертикальной оси. Так обычно рисуют земной шар в соответствующих задачах динамики.

Рисунок 6.

 

механиков | Определение, примеры, законы и факты

Механика , наука, изучающая движение тел под действием сил, включая особый случай, когда тело остается в покое. В первую очередь проблема движения — это силы, которые тела действуют друг на друга. Это приводит к изучению таких тем, как гравитация, электричество и магнетизм, в зависимости от природы задействованных сил. Учитывая силы, можно искать способ, которым тела движутся под действием сил; это предмет собственно механики.

Британская викторина

Викторина «Все о физике»

Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.

Исторически механика была одной из первых возникших точных наук.Его внутренняя красота как математической дисциплины и ранний замечательный успех в количественном учете движений Луны, Земли и других планетных тел оказали огромное влияние на философскую мысль и послужили толчком для систематического развития науки.

Механику можно разделить на три части: статика, которая имеет дело с силами, действующими на покоящееся тело и в нем; кинематика, описывающая возможные движения тела или системы тел; и кинетика, которая пытается объяснить или предсказать движение, которое произойдет в данной ситуации.В качестве альтернативы механику можно разделить по типу изучаемой системы. Простейшей механической системой является частица, определяемая как настолько маленькое тело, что его форма и внутренняя структура не имеют значения в данной задаче. Более сложным является движение системы из двух или более частиц, которые действуют друг на друга и, возможно, испытывают силы, действующие со стороны тел вне системы.

Принципы механики были применены к трем общим областям явлений.Движение таких небесных тел, как звезды, планеты и спутники, можно предсказать с большой точностью за тысячи лет до того, как они произойдут. (Теория относительности предсказывает некоторые отклонения от движения в соответствии с классической или ньютоновской механикой; однако они настолько малы, что их можно наблюдать только с помощью очень точных методов, за исключением задач, затрагивающих всю или большую часть обнаруживаемой Вселенной. ) Как вторая область, обычные объекты на Земле вплоть до микроскопических размеров (движущиеся со скоростью намного ниже скорости света) правильно описываются классической механикой без значительных исправлений.Инженер, проектирующий мосты или самолеты, может с уверенностью использовать ньютоновские законы классической механики, даже если силы могут быть очень сложными, а вычислениям не хватает красивой простоты небесной механики. Третья область явлений включает поведение вещества и электромагнитного излучения в атомном и субатомном масштабах. Хотя вначале были достигнуты ограниченные успехи в описании поведения атомов в терминах классической механики, эти явления должным образом рассматриваются в квантовой механике.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Классическая механика занимается движением тел под действием сил или равновесием тел, когда все силы уравновешены. Этот предмет можно рассматривать как разработку и применение основных постулатов, впервые сформулированных Исааком Ньютоном в его Philosophiae Naturalis Principia Mathematica (1687), широко известном как Principia . Эти постулаты, называемые законами движения Ньютона, изложены ниже.Их можно использовать для предсказания с большой точностью самых разных явлений, от движения отдельных частиц до взаимодействий очень сложных систем. В этой статье обсуждается множество этих приложений.

В рамках современной физики классическую механику можно понять как приближение, вытекающее из более глубоких законов квантовой механики и теории относительности. Однако такой взгляд на место объекта сильно недооценивает его важность в формировании контекста, языка и интуиции современной науки и ученых.Наш современный взгляд на мир и место человека в нем прочно укоренен в классической механике. Более того, многие идеи и результаты классической механики выживают и играют важную роль в новой физике.

Центральными понятиями классической механики являются сила, масса и движение. Ни сила, ни масса не очень четко определены Ньютоном, и оба они были предметом многих философских спекуляций со времен Ньютона. Оба они наиболее известны своими эффектами. Масса — это мера склонности тела сопротивляться изменениям в состоянии движения.С другой стороны, силы ускоряют тела, то есть они изменяют состояние движения тел, к которым они приложены. Взаимодействие этих эффектов — основная тема классической механики.

Хотя законы Ньютона фокусируют внимание на силе и массе, три другие величины приобретают особое значение, потому что их общее количество никогда не меняется. Эти три величины — энергия, (линейный) импульс и угловой момент. Любой из них может быть перемещен из одного тела или системы тел в другое.Кроме того, энергия может менять форму, будучи связанной с единственной системой, проявляясь как кинетическая энергия, энергия движения; потенциальная энергия, энергия позиции; тепло или внутренняя энергия, связанная со случайными движениями атомов или молекул, составляющих любое реальное тело; или любая комбинация из трех. Тем не менее полная энергия, импульс и угловой момент во Вселенной никогда не меняются. Этот факт выражается в физике, говоря, что энергия, импульс и угловой момент сохраняются.Эти три закона сохранения вытекают из законов Ньютона, но сам Ньютон их не выражал. Их нужно было обнаружить позже.

Примечательно то, что, хотя законы Ньютона больше не считаются фундаментальными и даже не совсем правильными, три закона сохранения, вытекающие из законов Ньютона — сохранение энергии, импульса и углового момента — остаются в точности верными даже в квантовая механика и теория относительности. Фактически, в современной физике сила больше не является центральным понятием, а масса — лишь одним из множества атрибутов материи.Однако энергия, импульс и угловой момент по-прежнему прочно занимают центральное место. Сохраняющаяся важность этих идей, унаследованных от классической механики, может помочь объяснить, почему этот предмет сохраняет такое большое значение в современной науке.

Фактов об Auto Diesel Mechanics | Работа

Автор: Chron Contributor Обновлено 17 сентября 2020 г.

Автомобили, работающие на дизельном топливе, всегда превосходили по продажам бензиновые двигатели в Европе. Хотя американцы, кажется, по-прежнему предпочитают бензин в своих автомобилях, все еще существует множество автомобилей, использующих эти двигатели с более высокой степенью сжатия.Фактически, Бюро статистики труда прогнозирует, что количество рабочих мест для дизельных механиков в целом должно увеличиться в период с 2020 по 2029 год, при этом будет почти на 10 000 открытых вакансий.

Механики дизельных двигателей предоставляют различные услуги

Механики дизельных двигателей обычно работают со всеми компонентами автомобиля, включая электрическую систему, трансмиссию и тормозную систему. Они выполняют плановое обслуживание и ремонт, поэтому механики дизельных двигателей могут нести ответственность за замену масла, ротацию шин или проверку аккумулятора.При необходимости ремонта механики восстанавливают или заменяют неисправную деталь.

Автомеханику, работающему с дизельным двигателем, нужны технические знания

Технология интегрирована в большинство авторемонтных мастерских. Автомеханики, работающие с дизельными двигателями, обычно должны знать, как подключить автомобиль к диагностической машине и интерпретировать результаты. Правила во многих штатах требуют, чтобы владельцы транспортных средств прикрепляли контрольные наклейки, подтверждающие, среди прочего, что автомобиль соответствует стандартам по загрязнению воздуха, а механики должны знать, как управлять испытательными машинами. Сами автомобили стали более сложными, включая компьютеры во многие системы, и механики должны обладать знаниями, необходимыми для их обслуживания.

Автомеханики, работающие с дизельными двигателями, становятся более образованными

Когда-то большинство механиков изучало свое дело на рабочем месте. Хотя это все еще возможно, работодатели предпочитают нанимать кандидатов, которые завершили формальную программу. По данным O * Net Online, службы Министерства труда США, более половины всех дизельных механиков имели некоторый уровень послесреднего образования, 40 процентов закончили среднюю школу и только 8 процентов не получили аттестата об окончании средней школы.Многие профессиональные училища и общественные колледжи имеют программы по обучению механиков-дизелей.

Дизель Автомобилистам нужны разные навыки

Хотя механические способности занимают одно из первых мест в списке желаемых навыков для механиков-дизелей, другие способности также могут иметь решающее значение. Многие механики должны объяснять проблемы владельцам транспортных средств, и это иногда включает объяснение, почему часть, которая не перестала работать, все еще нуждается в замене. Это означает, что механику необходимы хорошие навыки межличностного общения и отличные навыки устного общения.Механикам, работающим с дизельными двигателями, требуется ловкость рук, в том числе способность захватывать и манипулировать небольшими предметами, выполнять точную регулировку и держать руки устойчивыми даже при растяжении или работе в неудобном положении.

Заработная плата механика-дизеля

В целом, по данным Бюро статистики труда, в 2019 году средняя заработная плата механиков-дизелей составляла 48 500 долларов США , а 10 процентов заработали не менее 74 090 долларов США . Однако эти данные включали дизельных механиков, которые также работали на автобусах и грузовиках.Дизельные механики, которые работали на оптовых продавцов транспортных средств и запчастей, имели среднюю годовую заработную плату 49 940 долларов, в то время как те, кто работал в автомастерских, получали среднюю заработную плату в размере 46 320 долларов в год. BLS также отмечает, что данные о заработной плате могут включать оплату сверхурочных или комиссионных.

Фактов о механике и 9 специальностях механика

Механику используют в самых разных отраслях, от сельского хозяйства до авиаперевозок. Механики обслуживают и ремонтируют двигатели, используемые в их конкретной отрасли, но есть также механики, которые специализируются на конкретном типе двигателя или оборудования.В этой статье мы обсудим некоторые факты о механике, включая инструменты, используемые в полевых условиях, требования к работе и восемь видов специальной механики.

Зачем нужны специалисты-механики?

Специализированные механики — мастера определенного типа двигателя. Двигатель вашего личного автомобиля отличается от двигателя вашей газонокосилки, а ваша газонокосилка отличается от двигателя лодки. Хотя все двигатели похожи в том, как они могут работать, и даже могут иметь общие характеристики своих частей, не все двигатели одинаковы, и для их обслуживания и ремонта может потребоваться специальная подготовка. Специальные механики учатся ремонтировать двигатели в выбранной ими области.

Связано: Как стать механиком

Какие инструменты используют механики?

Несмотря на большое разнообразие двигателей, большинство механиков используют примерно одни и те же инструменты. Хотя некоторые магазины могут предоставить своим механикам инструменты, которые им понадобятся для работы, многие также покупают инструменты сами. Помимо стандартного списка инструментов для ремонта двигателей, механикам, работающим с различными транспортными средствами, также может потребоваться приобрести инструменты, характерные для каждого производителя транспортного средства.

К стандартным механическим инструментам относятся:

• Запирающийся ящик для хранения инструментов
• Молотки, включая шариковые, ударные и молотковые
• Отвертки различных размеров, Philips и плоские
• Монтировка
• Комбинация Наборы гаечных ключей в английских (дюймах) и метрических (мм) единицах
• Набор разводных гаечных ключей с рукоятками разной длины
• Плоскогубцы, такие как скользящие, фиксирующие, фиксирующие паз и игольчатые
• Наборы трещоток и головок в различных вариантах типоразмеров
• Динамометрический ключ
• Шестигранный ключ
• Ножницы для тяжелых условий эксплуатации или универсальный нож
• Фонари
• Смотровые зеркала
• Приборы и электрические приборы
• Пневматические инструменты и воздушный компрессор

Факты о восьми специальностях механиков

Вот восемь специальностей, которые следует учитывать, если вы хотите работать механиком:

1.

Механик по тяжелому оборудованию

Средняя заработная плата по стране: 40 975 долларов в год

Основные обязанности: Механики по тяжелому оборудованию или автопарку специализируются на обслуживании и ремонте тяжелой техники, используемой в строительстве, сельском хозяйстве, горнодобывающей промышленности и железнодорожном транспорте. Большинство механиков тяжелого оборудования находят работу в пунктах проката оборудования, строительных фирмах, горнодобывающих компаниях и государственных учреждениях. В их типичные рабочие задачи входят:

• Поездки на рабочие места и обратно, где используется тяжелое оборудование
• Использование компьютеризированного оборудования для диагностики механических и электрических проблем
• Ремонт и замена сломанных деталей
• Проведение планового технического обслуживания двигателя
• Очистка и ремонт крупногабаритного навесного оборудования, такого как лопасти, боковые стрелы и лебедки

Средняя заработная плата по стране: 42 693 долл. США в год

Основные обязанности: Механики небольших двигателей, также известные как техники по ремонту оборудования, проверяют, обслуживают и ремонтируют многие типы моторизованная техника.Большинство механиков небольших двигателей специализируются на одном типе двигателей, например, на мотоциклах, скутерах, гольф-карах, вездеходах, снегоходах, газонокосилках или открытом силовом оборудовании. Механики малых двигателей часто находят работу в дилерских центрах по продаже транспортных средств для отдыха, в мастерских по ремонту энергетического оборудования или работают самостоятельно. Общие рабочие задачи могут включать:

• Проверка и диагностика проблем с электрической, механической и топливной системами
• Выполнение планового технического обслуживания, например смазка деталей двигателя, замена ремней или чистка свечей зажигания
• Регулировка компонентов двигателя в соответствии с техническими требованиями производителя
• Замена или ремонт сломанных деталей
• Разборка и повторная сборка двигателей
• Проведение тестовых поездок оборудования после завершения ремонта
• Замена шин

Средняя заработная плата по стране: 44 994 доллара в год

Основные обязанности: Морские механики или морские техники специализируемся на всех видах лодок. Большинство морских механиков работают на причалах, верфях, дилерских центрах и сервисных станциях. В их типичные рабочие обязанности могут входить:

• Проверка и ремонт лодочных двигателей
• Обновление и ремонт навигационного оборудования на лодках
• Установка и обслуживание лодочных электрических систем, систем управления и санитарии
• Ремонт или замена корпусов, такелажа, парусов, мачт и т. Д. гребные винты
• Перемещение лодок с блоков с использованием больших лебедок

Средняя заработная плата по стране: 50 225 долларов в год

Основные обязанности: Дизельные механики проверяют, ремонтируют и обслуживают автомобили с дизельным двигателем.Автобусы, большие буровые установки, пожарные машины и машины скорой помощи — это лишь некоторые из транспортных средств, которым может потребоваться дизель-механик. Дизельные механики находят работу в крупных автотранспортных компаниях, ремонтных мастерских и муниципальных образованиях. Конкретные рабочие обязанности включают:

• Выполнение планового технического обслуживания двигателя
• Замена и ремонт сломанных деталей
• Замена жидкостей и шин
• Выполнение ремонта на рабочем месте или обочине дороги во время чрезвычайной ситуации

Связано: Узнайте о том, как быть Дизельный механик

Средняя заработная плата по стране: 52 594 доллара в год

Основные обязанности: Автомеханики проверяют, обслуживают и ремонтируют повседневные автомобили и легкие грузовики.Некоторые механики специализируются на одной системе транспортного средства (например, специалист по трансмиссии). Автомеханики обычно работают в автосервисе, автосалоне или работают не по найму. Конкретные рабочие задачи могут включать:

• Диагностика проблем двигателя посредством визуального осмотра двигателя или с помощью диагностических инструментов
• Выполнение планового технического обслуживания, такого как замена и вращение шин, замена масла и замена жидкости
• Ремонт изношенных, отозванных или сломанных деталей
• Разборка и сборка двигателей

Связано: Auto Technician vs. Механик: В чем разница?

Средняя заработная плата по стране: 60 401 долл. США в год

Основные обязанности: Техники по кузовным работам ремонтируют и восстанавливают рамы, кузова, окна и лобовые стекла автомобилей. Автомеханики обычно работают в автомастерской или работают не по найму. Помимо обычных инструментов, используемых автомобильными механиками, техники по кузовным работам также используют металлорежущие инструменты, гидравлические домкраты для тяжелых условий эксплуатации, сварочные аппараты и малярные пистолеты. Конкретные рабочие задачи могут включать:

• Проверка повреждений автомобиля и подготовка сметы расходов на ремонт
• Удаление поврежденных деталей, таких как бамперы, капоты, решетки и стекла
• Ремонт структурных повреждений рамы автомобиля
• Вырубка или устранение мелких повреждений кузова
• Приварка запасных частей к кузовам автомобилей
• Шлифовка, шлифовка и грунтовка исправленных поверхностей
• Покраска восстановленных автомобильных деталей

Средняя заработная плата по стране: 69 668 долларов в год

Основные обязанности: Авиамеханики обеспечивают безопасность самолетов, вертолетов и других самолетов и годен для полета. Автомеханики обычно работают на станциях ремонта самолетов, в ангарах или на аэродроме. Конкретные рабочие обязанности могут включать:

• Завершение проверок в соответствии с инструкциями Федерального управления гражданской авиации (FAA)
• Выполнение планового технического обслуживания самолета
• Диагностика механических проблем
• Замена или ремонт крыльев и других частей самолета
• Ведение подробных записей всего технического обслуживания и ремонтные работы

4 мифа о механике | Могучий Авто

Вы, наверное, знакомы со стереотипами о механике.Однако, если вы действительно общались с механиком в автомастерской, они обычно быстро исчезают. Как и многие стереотипы, стереотипы о механике на протяжении многих лет увековечивались их изображениями на телевидении, в фильмах и в массовой культуре. Вот несколько мифов о независимых специалистах по ремонту автомобилей (согласно современной номенклатуре), которые одновременно разрушительны и не соответствуют действительности.

1. Они воспользуются вами

Обман людей на самом деле не является жизнеспособной бизнес-моделью, особенно когда большая часть этого бизнеса ведется лицом к лицу.Большинство механиков гордятся своей работой, и если они что-то рекомендуют, то, вероятно, потому, что думают, что это лучше всего для вашего автомобиля, а не потому, что они пытаются зря тратить ваши деньги.

2. Необразованные

Стереотипы часто пытаются съесть свой пирог. «Механики — мошенники, и они быстро уговорят вас потратить деньги! Но они также исключительно неразумные, бросившие школу! » В любом случае, это довольно нелепо. Современные автомобили — это чрезвычайно сложные машины, которые бывают самых разных конструкций, и для того, чтобы правильно обслуживать автомобили всех этих типов, требуется много специальных знаний.

3. Независимые услуги аннулируют вашу гарантию

Гарантии становятся недействительными только в том случае, если обслуживание, указанное в гарантии, не выполнено своевременно. На самом деле, для производителя крайне незаконно сообщать покупателям, где можно получить техническое обслуживание. Вы имеете право отремонтировать свой автомобиль в любом месте, не опасаясь аннулирования гарантии.

4. У дилера лучше

Многие люди предполагают, что дилерский центр будет предоставлять более качественные услуги, потому что у них будет доступ к лучшему оборудованию и механике.Реальность такова, что все будет по-разному от автосалона к автосалону и от магазина к магазину — не существует могущественного и всемогущего бога ремонта автомобилей, который постановил бы, что все механики и мастерские так или иначе работают. Найдите то, что вам подходит, и не бойтесь искать независимые магазины.

Техники и механики по обслуживанию автомобилей

Обзор специалистов по обслуживанию автомобилей и механиков

Новые методы ремонта и изменяющиеся технологии важны для техников и механиков по обслуживанию автомобилей, имеющих формальное образование. Высшее образование предоставит хорошие возможности для работы, в то время как те, у кого нет такой подготовки, будут конкурировать за рабочие места начального уровня.

Характер работы техников и механиков по обслуживанию автомобилей

Специалисты по обслуживанию автомобилей проверяют и обслуживают легковые и грузовые автомобили, которые работают на бензине, используют электричество или топливо, такое как этанол. В их обязанности входит базовое техническое обслуживание, включая замену шин, замену масла, тестирование и диагностику более сложных проблем, а также выполнение ремонта.Ремонт мотоциклов, скутеров, мопедов и вездеходов выполняется мотористами.

Работа техника по обслуживанию автомобилей изменилась с простого механического ремонта на более сложную работу с новыми электронными системами, которые контролируют и регулируют работу автомобиля в дороге. Техник и механик по обслуживанию автомобилей должны уметь использовать традиционные инструменты, а также использовать компьютеризированное торговое оборудование с электронными компонентами.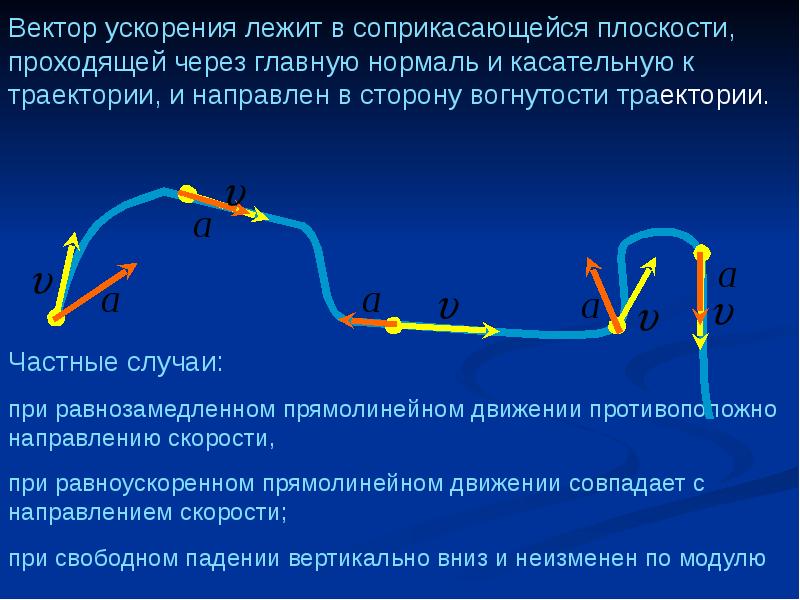

Техник по обслуживанию автомобилей сначала получает описание проблемы от владельца, который пишет смету.Использование диагностического подхода и систем тестирования помогает механику выявить проблему или проблемы в двигателе автомобиля. Технику может потребоваться тест-драйв с использованием различного диагностического оборудования, включая датчики и компьютеры. Важно обеспечить точную и эффективную диагностику и ремонт, чтобы вернуть довольных клиентов.

Регулярные осмотры могут помочь найти и изолировать изношенные детали, которые требуют замены, до того, как они выйдут из строя. Контрольный список используется для того, чтобы обрабатывать список всех элементов, которые необходимо проверить, и чтобы не пропустить проблемные элементы.

Использование различных инструментов очень важно для специалистов по обслуживанию автомобилей. Пневматические ключи могут использоваться для снятия ремней, токарные и шлифовальные станки используются для восстановления тормозов, сварочного оборудования для снятия выхлопных систем и домкратов для подъема автомобиля.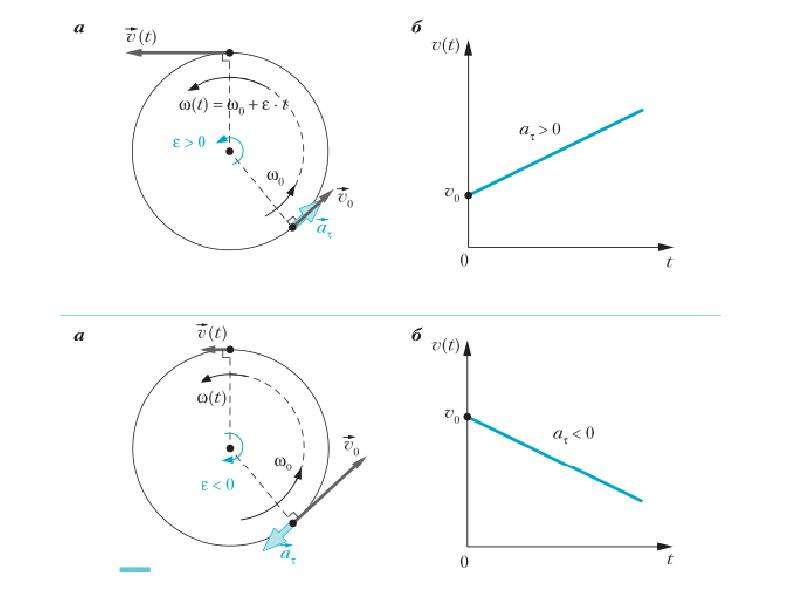 Маленькие инструменты, такие как плоскогубцы, отвертки и гаечные ключи, используются для работы на небольших площадях. Техники часто предоставляют свои собственные ручные инструменты.

Компьютерные распечатки используются техническими специалистами для сравнения руководств и стандартов, рекомендованных производителем.Сервисные бюллетени и автоматические обновления предоставляются из пакетов программного обеспечения и Интернета, что позволяет техническим специалистам оставаться в курсе и получать информацию о новых методах и общих проблемах.

Компьютерное оборудование, которое управляет всем в автомобиле, требует для ремонта высокотехнологичных инструментов. Некоторые роскошные автомобили оснащены системами глобального позиционирования и системами предотвращения аварий. Технику и механику по обслуживанию автомобилей также необходимо будет ознакомиться с транспортными средствами, работающими на альтернативных видах топлива.

В более крупных магазинах, как правило, есть ремонтники, специализирующиеся на определенных видах ремонта. Техники по трансмиссии работают с зубчатыми передачами, насосами, муфтами и другими деталями трансмиссии. Специалисты по настройке регулируют газораспределение и клапаны автомобиля и могут использовать электронные испытательные устройства, чтобы найти проблемы и внести коррективы.

Мастер по ремонту автомобильных кондиционеров занимается установкой и ремонтом кондиционеров и их частей. Эти работники пройдут специальную подготовку по федеральным и государственным правилам обращения с хладагентами и их утилизации.Передний механик выравнивает механизмы рулевого управления колес, мастера по ремонту тормозов регулируют тормоза, накладки и колодки, а также производят другой ремонт тормозной системы.

40-часовая рабочая неделя является стандартной, в то время как около 24% работают сверхурочно и сверхурочно. В выходные и вечерние часы также работают некоторые ремонтники. Работа в хорошо освещенной ремонтной мастерской — обычное дело, хотя в некоторых стандартных мастерских шумно и прохладно.

Обучение, другая квалификация и повышение квалификации для специалистов по обслуживанию автомобилей и механиков

С развитием автомобильных технологий рабочие ищут тех, кто имеет среднее образование.Сертификация Национальным институтом качества автомобильного обслуживания важна для тех, кто ищет работу в больших городах.

Наилучшим вариантом обучения является завершение программы профессионального обучения в области технологий обслуживания автомобилей. Некоторые программы для старших классов участвуют в AYES или Службе автомобильного образования для молодежи, которая сотрудничает с программами ремонта автомобилей, производителями и автомобильными дилерами. Это отличная программа, которая позволяет студентам, завершившим эти программы, начать работу с должностей технического специалиста начального уровня.Курсовая работа по ремонту автомобилей наряду с электроникой, физикой, химией, английским языком и компьютерами обеспечивает хорошее образование и основу для студентов, начинающих работать в этой области.

Программы послесреднего обучения обеспечивают интенсивную профессиональную подготовку с обучением в классе и на практике. Торговые и технические школы часто предлагают программу от 6 месяцев до 1 года, а местные колледжи присуждают степень младшего специалиста или сертификат. Получение степени младшего специалиста займет 2 года и будет включать основные занятия по английскому языку, математике и другим предметам, а также ремонт автомобилей.

Производители автомобилей и представительства также спонсируют двухлетнюю программу получения степени младшего специалиста в средних школах по всей стране. Чередование 6–12-недельных периодов посещения занятий и работы в дилерских центрах позволяет получить практический опыт во время учебы.

Начинающие работники начинают как стажеры, помощники или рабочие, занимающиеся смазкой, и приобретают опыт, отрабатывая свои навыки. Некоторые начинающие работники получат повышение и продвижение по службе, чтобы получить уровень пути через несколько месяцев, но обычно требуется от 2 до 5 лет опыта, чтобы стать полностью квалифицированным техником или механиком по обслуживанию.Для более сложных специальностей, таких как ремонт трансмиссии, может потребоваться еще несколько лет опыта.

Спонсируемое производителем обучение может быть доступно для перспективных новичков или опытных технических специалистов для повышения или поддержания своих навыков. Учебные классы также могут быть предложены представителями завода.

Хорошие рассуждения и способность диагностировать проблемы — важная часть работы техника по обслуживанию автомобилей и механика. Также важна способность идти в ногу с новыми технологиями и изучать новые процедуры обслуживания.

Специалисты по обслуживанию автомобилей также нуждаются в обучении в области электроники из-за важности безопасности электрических компонентов.

Сертификация

не является обязательной для работников автомобильного сервиса, хотя она распространена и доступна в 8 различных областях автомобильного сервиса, от электрических систем до кондиционирования воздуха.

Самые популярные школы автомобилей / автомобильной механики / технических специалистов

1. MMI-Phoenix, Phoenix (Эйвондейл, Аризона)
2.Профессиональные школы WyoTech (несколько кампусов)
3. Технический институт NASCAR, Мурсвилл (Мурсвилл, Северная Каролина)
4. Mech-Tech College, Кагуас (Кагуас, Пуэрто-Рико)
5. Lincoln Tech, Нашвилл (Нашвилл, Теннесси)
6. Lincoln Tech, Филадельфия (Филадельфия, Пенсильвания)
7. Техническая школа Апекс (Нью-Йорк, Нью-Йорк)
8. Jefferson Community & Technical College, Луисвилл (Луисвилл, Кентукки)

См. Все школы автомобилей / автомобильной механики / техников

Онлайн-школа: Ashworth College — Онлайн-школа

Трудоустройство и перспективы трудоустройства техников и механиков автомобильного сервиса

Автомобильные дилеры и мастерские по ремонту и техническому обслуживанию нанимают большинство рабочих, и около 16 процентов работают не по найму.Ожидается, что рост числа рабочих мест для работников автомобильной промышленности будет медленнее, чем в среднем, при этом большинство вакансий будет открываться после выхода на пенсию. Будут востребованы работники с опытом работы в определенных областях. Консолидация в автомобильной промышленности ограничит возможности для новых сотрудников. Помимо роста, многие вакансии будут открыты благодаря выходящим на пенсию техническим специалистам. Те, у кого есть высшее образование и сертификация ASE, будут пользоваться спросом, в то время как вакансии начального уровня будут доступны для работников без какого-либо формального обучения.Большинство вакансий будет в дилерских центрах и независимых магазинах.

Заработная плата техников и механиков по обслуживанию автомобилей

Средняя почасовая оплата техников и механиков по обслуживанию автомобилей, включая комиссионные, составляет 17,03 доллара США. Средние 50 процентов зарабатывают от 12,49 до 22,71 доллара в час. Самые низкие 10 процентов зарабатывают менее 9,54 доллара, а самые высокие 10 процентов зарабатывают более 28,81 доллара в час.

Годовая заработная плата техников и механиков по обслуживанию автомобилей

В среднем специалисты по обслуживанию автомобилей и механики зарабатывают 35 420 долларов в год .

10% 25% 75% 90% 19 840 $ / год 25 970 $ / год 47240 долл. США / год 59 920 долларов США в год

Почасовая оплата техников и механиков по обслуживанию автомобилей

В среднем специалисты по обслуживанию автомобилей и механики зарабатывают 17,03 долларов в час .

10% 25% 75% 90% 9,54 долл. США 12,49 $ 22,71 доллара США 28,81 долл. США

Источник: Справочник прогнозов по профессиональной деятельности Бюро статистики труда

фактов о дизельной механике — Колледж Аламеда

Технические навыки, развитые в рамках программы

• Выявление неисправностей и ремонт дефектных деталей в механических, электрических и электронных системах.
• Используйте компьютеры для диагностики оборудования и поиска информации.
• Выполните профилактическое обслуживание, такое как настройка двигателя, регулировка передней части и регулировка тормозов.
• Эксплуатировать торговую технику и оборудование, включая подъемники, мостовые краны, вилочные погрузчики, гидравлические домкраты, компрессоры, пароочистители, напольные домкраты, демонтажные стенды, шлифовальные машины, сверлильные станки, гидравлические
• прессы, шлифовальные машины для клапанов и седел, а также дробеструйные аппараты.
• Выберите и используйте прецизионные инструменты, такие как динамометрические ключи, микрометры, циферблатные индикаторы, метчики и плашки, а также калибры для измерения внутреннего диаметра.

Профессиональные навыки, развитые в рамках программы

• Применяйте безопасные рабочие привычки и методы.
• Сохранять профессиональный подход в сложных условиях труда.
• Планируйте и реализуйте график работы в сотрудничестве с членами команды и документируйте эффективность.
• Развивайте уверенность в себе и гордость за свое мастерство.
• Мыслить аналитически и принимать профессиональные решения.
• Студентам оказывается помощь в поиске работы в отрасли, пока они завершают программу.Возможна стажировка.

Навыки, опыт и личные качества, необходимые для успеха в программе

• Знание базовой математики и чтения
• Завершение курсов по автомобилестроению, металлургию или механическому цеху и высшей школе науки является полезным.
• Механические способности и способности.
• Самодисциплина для выполнения точной работы в соответствии с отраслевыми стандартами.
• Хорошая физическая форма и координация.
• Стремление к обучению на протяжении всей жизни, чтобы идти в ногу с новыми технологиями.
• Хорошие коммуникативные навыки.
• Опыт работы с оборудованием и инструментами.

Заработная плата, льготы и условия труда

Начальный уровень — примерно от 15 до 18 долларов в час

Опытный — от 18 до 22 долларов в час

Максимальная ставка заработной платы — от 27 до 45 долларов + час

Пособия могут включать медицинские, стоматологические, зрительные, оплачиваемые отпуска и праздничные дни, а также отличные пенсионные планы. Стандартная рабочая неделя составляет 40 часов, и в большинстве магазинов можно приобрести рабочую одежду.

Работа тяжелая. Законы о здоровье и безопасности обеспечивают безопасное рабочее место, и у большинства работодателей есть программы безопасности и оборудование для обучения и использования сотрудников. Механики предоставляют собственный ручной инструмент, а работодатели — специализированное оборудование.

Карьера в области механики дизельных двигателей и грузовиков

Механики по дизельным двигателям и грузовым автомобилям уровня Journey — уважаемые технические специалисты в своей области. Они работают независимо, решая проблемы, используя профессиональное суждение, и берут на себя ответственность за безопасную работу оборудования, которое они ремонтируют и обслуживают.

Diesel and Truck Mechanics также специализируется в определенной области. Сферы специализации включают грузовые автомобили, автобусы, лодки, корабли, локомотивы, строительные машины и все виды вспомогательного оборудования.

На рабочем месте механики по дизельным двигателям и грузовикам выполняют ряд обязанностей, включая следующие:

• Диагностика проблем в механических, электрических и электронных системах, требующих использования сложных компьютеров и другого диагностического тестового оборудования.
• Поиск и устранение неисправностей электронного управления, которое регулирует работу двигателя и мощность в лошадиных силах. Трансмиссии и тормозные системы все чаще контролируются электронными системами, которые взаимодействуют с функциями двигателя.
• Поиск и устранение неисправностей рулевого управления, гидравлических и пневматических систем, а также тормозов, мостов, дифференциалов, электродвигателей и компрессоров.

После приобретения навыков механика-путешественника есть несколько ограничений для карьерных перспектив, связанных с торговлей.Неполный список возможных профессий включает в себя механика-механика, механика шасси, техника выездного обслуживания, механика силового агрегата, инспектора оборудования, специалиста по обслуживанию, мастера, начальника, менеджера, инструктора, сварщика / изготовителя, мастера по кузовному и лакокрасочному ремонту, а также кондиционера / холодильного оборудования. Техник.

Отраслевые партнеры

Cummins West, Inc.

Peterson Tractor & Power Systems *

Комитет по профессиональному обучению специалистов по ремонту автомобилей

Трак-центр Golden Gate

Калифорнийский совет по воздушным ресурсам

Корпорация Eaton

Поощрение за использование альтернативных транспортных технологий

Bendix Air Brake Corporation

Транзит переменного тока

Калифорнийский совет по дизельному образованию и технологиям

Meritor Corporation

Прибрежные округа Грузовик и оборудование

Шеврон

Производитель счетчика ставок

Caltrans

Прямо сейчас Реди Микс

Порт-оф-Окленд

Желтый грузовой

Город Окленд

* Компании Caterpillar и Peterson Tractor & Power Systems предоставили гранты для присуждения стипендий программы «Дизель и механика грузовиков» квалифицированным зачисленным студентам .

Информация об обязательствах по времени программы и расписании

• Вы можете начать как в осеннем, так и в весеннем семестре.
• Сертификат об окончании можно получить за четыре семестра. Многие работодатели считают этот сертификат или его эквивалент минимальной квалификацией для работы на начальном уровне в качестве механика / техника.
• Студенты могут начать с курса «Механика грузовиков и систем шасси» или «Дизельные двигатели».Оба курса включают лекции и лабораторные занятия.
• Предлагаются дневные и вечерние классы.

Стоимость программы

• Стоимость обучения по программе сертификации 46 единиц в настоящее время составляет около 1000 долларов.
• Учебники для программы «Сертификат об окончании» стоят примерно 300 долларов.
• Требуются инструменты и защитное оборудование для двухлетней программы, стоимость которых составляет не менее 350 долларов США. Это будут те же инструменты, которые необходимы для начала вашей карьеры механика / техника.
• Для обеспечения безопасности необходима рабочая одежда и прочная рабочая обувь или обувь.

Финансовая помощь для покрытия этих расходов предоставляется учащимся, отвечающим установленным требованиям.

Степени и сертификаты

Сертификат об окончании курса «Механика дизеля» выдается после успешного завершения основных требований курса.

AS Degree будет присуждаться после завершения основных требований курса и требований общего образования для младшего научного сотрудника.

Подробности см. В Каталоге колледжа в разделе «Механика дизеля».

Все механики мошенники? — Магазин механиков Femme

Люди продолжают обращаться ко мне с одними и теми же вопросами: «Как мне найти хорошего механика? Как выбрать один магазин из другого?

Если вы когда-либо ходили в автомастерскую и уходили с некоторым сомнением, просто ли вас взяли на прогулку, этот курс для вас. Вы уйдете с дорожной картой, которая вам понадобится, чтобы перебрать все варианты, чтобы найти качественного механика, который на долгие годы удовлетворит потребности и вас, и вашего автомобиля.

Воскресенье — 75 мин.

• Где искать механика

• Какие вопросы задавать

• Как сортировать отзывы, которые вы найдете в Интернете

• Различия между франшизами, корпоративными магазинами и независимыми сетями

• Гарантия по ремонту и покрытию

• Этикет механика

Я буду отвечать на вопросы в режиме реального времени и формировать содержание с учетом конкретных потребностей группы, которую я обучаю.У вас будет доступ к моему обширному портфелю информации, чтобы спросить все, что вы хотите, чтобы процесс прошел для вас максимально гладко.