Таблица теплотворности
Мы максимально быстро находим решения для объекта, разрабатываем и согласовываем проект, используем лучшие материалы, комплектующие, оборудование. «Альфа-Инвест» — это компания, которая была создана с целью обеспечения каждого доступным теплом и повышения энергонезависимости Украины. Лидер на рынке модернизации газовых котельных! Сэкономленные деньги — это заработанные деньги!
Обратите внимание на теплотворную способность (удельную теплоту сгорания) различных видов топлива, сравните показатели. Теплотворная способность топлива характеризует количество теплоты, выделяемое при полном сгорании топлива массой 1 кг или объёмом 1 м³ (1 л). Наиболее часто теплотворная способность измеряется в Дж/кг (Дж/м³; Дж/л). Чем выше удельная теплота сгорания топлива, тем меньше его расход.
Удельная теплота сгорания каждого вида топлива зависит:
От его горючих составляющих (углерода, водорода, летучей горючей серы и др.), а также от его влажности и зольности.
| 1,0 | 3,62 | 0,108 | 0,084 | 0,089 | |||
| Дизельное топливо (солярка) | 1 л | 10300 | 11,9 | 43,12 | 1,288 | — | 1,062 |
| Мазут | 1 л | 9700 | 11,2 | 40,61 | 1,213 | 0,942 | — |
| Керосин | 1 л | 10400 | 12,0 | 43,50 | 1,300 | 1,010 | 1,072 |
| Нефть | 1 л | 10500 | 12,2 | 44,00 | 1,313 | 1,019 | 1,082 |
| Бензин | 1 л | 10500 | 12,2 | 44,00 | 1,313 | 1,019 | 1,082 |
| Газ природный | 1 м 3 | 8000 | 9,3 | 33,50 | — | 0,777 | 0,825 |
| Газ сжиженный | 1 кг | 10800 | 12,5 | 45,20 | 1,350 | 1,049 | 1,113 |
| Метан | 1 м 3 | 11950 | 13,8 | 50,03 | 1,494 | 1,160 | 1,232 |
| Пропан | 1 м 3 | 10885 | 12,6 | 45,57 | 1,361 | 1,057 | 1,122 |
| Этилен | 1 м 3 | 11470 | 13,3 | 48,02 | 1,434 | 1,114 | 1,182 |
| Водород | 1 м 3 | 28700 | 33,2 | 120,00 | 3,588 | 2,786 | 2,959 |
| Уголь каменный (W=10%) | 1 кг | 6450 | 7,5 | 27,00 | 0,806 | 0,626 | 0,665 |
| Уголь бурый (W=30…40%) | 1 кг | 3100 | 3,6 | 12,98 | 0,388 | 0,301 | 0,320 |
| Уголь-антрацит | 1 кг | 6700 | 7,8 | 28,05 | 0,838 | 0,650 | 0,691 |
| Уголь древесный | 1 кг | 6510 | 7,5 | 27,26 | 0,814 | 0,632 | 0,671 |
| Торф (W=40%) | 1 кг | 2900 | 3,6 | 12,10 | 0,363 | 0,282 | 0,299 |
| Торф брикеты (W=15%) | 1 кг | 4200 | 4,9 | 17,58 | 0,525 | 0,408 | 0,433 |
| Торф крошка | 1 кг | 2590 | 3,0 | 10,84 | 0,324 | 0,251 | 0,267 |
| Пеллета древесная | 1 кг | 4100 | 4,7 | 17,17 | 0,513 | 0,398 | 0,423 |
| Пеллета из соломы | 1 кг | 3465 | 4,0 | 14,51 | 0,433 | 0,336 | 0,357 |
| Пеллета из лузги подсолнуха | 1 кг | 4320 | 5,0 | 18,09 | 0,540 | 0,419 | 0,445 |
Свежесрубленная древесина (W=50.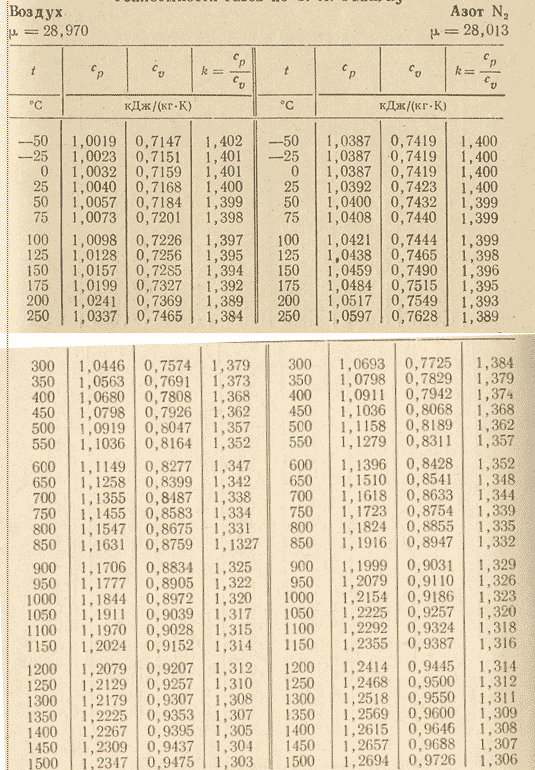 ..60%) ..60%) |
1 кг | 1940 | 2,2 | 8,12 | 0,243 | 0,188 | 0,200 |
| Высушенная древесина (W=20%) | 1 кг | 3400 | 3,9 | 14,24 | 0,425 | 0,330 | 0,351 |
| Щепа | 1 кг | 2610 | 3,0 | 10,93 | 0,326 | 0,253 | 0,269 |
| Опилки | 1 кг | 2000 | 2,3 | 8,37 | 0,250 | 0,194 | 0,206 |
| Бумага | 1 кг | 3970 | 4,6 | 16,62 | 0,496 | 0,385 | 0,409 |
| Лузга подсолнуха, сои | 1 кг | 4060 | 4,7 | 17,00 | 0,508 | 0,394 | 0,419 |
| Лузга рисовая | 1 кг | 3180 | 3,7 | 13,31 | 0,398 | 0,309 | 0,328 |
| Костра льняная | 1 кг | 3805 | 4,4 | 15,93 | 0,477 | 0,369 | 0,392 |
| Кукуруза-початок (W>10%) | 1 кг | 3500 | 4,0 | 14,65 | 0,438 | 0,340 | 0,361 |
| Солома | 1 кг | 3750 | 4,3 | 15,70 | 0,469 | 0,364 | 0,387 |
| Хлопчатник-стебли | 1 кг | 3470 | 4,0 | 14,53 | 0,434 | 0,337 | 0,358 |
| Виноградная лоза (W=20%) | 1 кг | 3345 | 3,9 | 14,00 | 0,418 | 0,325 | 0,345 |
|
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Свойства рабочих сред/ / Метан Ch5 (хладагент R50) / / Метан (Ch5). Удельная теплоемкость cp . Температурный диапазон 200 /1100 °K (-73 /+827 °С ) .
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Теплоемкость газов
При тепловых расчетах газопроводов часто приходится пользоваться понятием удельной теплоемкости газа. Удельной теплоемкостью газа называется количество теплоты, необходимой для нагрева единицы массы вещества (или объема) на один градус в определенном процессе:
, (1.15)
где — количество теплоты, подведенной к единице массы (или объема) газа в процессе его нагрева от температуры до температуры ; и — соответственно начальная и конечная температура газа.
На практике наиболее часто используются
теплоемкости изобарного и изохорного
процессов. Эти теплоемкости называются
изобарной и изохорной и обозначаются
соответственно
и
.
Теплоемкость
— величина переменная, зависящая от
температуры и давления, а для идеальных
газов — только от температуры. Теплоемкость,
определяемую уравнением (1.15), называют
средней теплоемкостью и обозначают
и
в отличие от истинных теплоемкостей
и
,
определяемых для конкретно заданной
температуры.
Эти теплоемкости называются
изобарной и изохорной и обозначаются
соответственно
и
.
Теплоемкость
— величина переменная, зависящая от
температуры и давления, а для идеальных
газов — только от температуры. Теплоемкость,
определяемую уравнением (1.15), называют
средней теплоемкостью и обозначают
и
в отличие от истинных теплоемкостей
и
,
определяемых для конкретно заданной
температуры.
Средняя теплоемкость газа в интервале заданных температур процесса определяется по значению среднеарифметической температуры процесса , т.е. для того чтобы найти среднюю теплоемкость , необходимо знать среднюю температуру процесса . По найденному значению средней температуры определяется с использованием специальных таблиц (табл. 1.1) теплоемкость газов.
В практических расчетах среднюю теплоемкость наиболее просто определять по соотношению:
, (1.16)
где
и
— энтальпии природного газа в начале и
в конце процесса. Значения энтальпий
определяются по соответствующим таблицам
или диаграммам для данного газа или
вещества.
Значения энтальпий
определяются по соответствующим таблицам
или диаграммам для данного газа или
вещества.
Таблица 1.1
#G0Температура °С | Кислород О | Азот N | Водород Н | Углекисл. газ СО | Вода НО | Метан СН | Воздух |
0 | 0,917 | 1,010 | 14,21 | 0,820 | 1,855 | 2,190 | 1,005 |
100 | 0,925 | 1,038 | 14,35 | 0,871 | 1,867 | 2,471 | 1,005 |
200 | 0,938 | 1,047 | 14,43 | 0,913 | 1,888 | 2,800 | 1,013 |
300 | 0,950 | 1,051 | 14,46 | 0,950 | 1,913 | 3,206 | 1,017 |
400 | 0,967 | 1,056 | 14,49 | 0,984 | 1,938 | 3,650 | 1,030 |
500 | 0,980 | 1,060 | 14,52 | 1,013 | 1,968 | 4,104 | 1,038 |
600 | 0,992 | 1,073 | 14,56 | 1,042 | 2,001 | 4,545 | 1,051 |
700 | 1,005 | 1,089 | 14,60 | 1,066 | 2,030 | 4,991 | 1,063 |
800 | 1,017 | 1,101 | 14,66 | 1,088 | 2,064 | — | 1,072 |
900 | 1,026 | 1,109 | 14,72 | 1,109 | 2,097 | — | 1,084 |
1000 | 1,034 | 1,118 | 14,79 | 1,126 | 2,131 | — | 1,093 |
1100 | 1,042 | 1,130 | 14,87 | 1,143 | 2,164 | — | 1,101 |
1200 | 1,051 | 1,139 | 14,95 | 1,160 | 2,194 | — | 1,109 |
1300 | 1,059 | 1,147 | 15,04 | 1,172 | 2,227 | — | 1,118 |
1400 | 1,063 | 1,155 | 15,13 | 1,185 | 2,257 | — | 1,126 |
1500 | 1,072 | 1,164 | 15,22 | 1,197 | 2,286 | — | 1,130 |
Сравнительная таблица теплотворности некоторых видов топлива
- Главная
| Вид топлива | Ед. изм. изм.
|
Удельная теплота сгорания | Эквивалент | ||||
| кКал | кВт | МДж | Природный газ, м3 | Диз. топливо, л | Мазут, л | ||
| Электроэнергия | 1 кВт/ч | 864 | 1,0 | 3,62 | 0,108 | 0,084 | 0,089 |
| Дизельное топливо (солярка) | 1 л | 10300 | 11,9 | 43,12 | 1,288 | - | 1,062 |
| Мазут | 1 л | 9700 | 11,2 | 40,61 | 1,213 | 0,942 | - |
| Керосин | 1 л | 10400 | 12,0 | 43,50 | 1,300 | 1,010 | 1,072 |
| Нефть | 1 л | 10500 | 12,2 | 44,00 | 1,313 | 1,019 | 1,082 |
| Бензин | 1 л | 10500 | 12,2 | 44,00 | 1,313 | 1,019 | 1,082 |
| Газ природный | 1 м 3 | 8000 | 9,3 | 33,50 | - | 0,777 | 0,825 |
| Газ сжиженный | 1 кг | 10800 | 12,5 | 45,20 | 1,350 | 1,049 | 1,113 |
| Метан | 1 м 3 | 11950 | 13,8 | 50,03 | 1,494 | 1,160 | 1,232 |
| Пропан | 1 м 3 | 10885 | 12,6 | 45,57 | 1,361 | 1,057 | 1,122 |
| Этилен | 1 м 3 | 11470 | 13,3 | 48,02 | 1,434 | 1,114 | 1,182 |
| Водород | 1 м 3 | 28700 | 33,2 | 120,00 | 3,588 | 2,786 | 2,959 |
| Уголь каменный (W=10%) | 1 кг | 6450 | 7,5 | 27,00 | 0,806 | 0,626 | 0,665 |
| Уголь бурый (W=30…40%) | 1 кг | 3100 | 3,6 | 12,98 | 0,388 | 0,301 | 0,320 |
| Уголь-антрацит | 1 кг | 6700 | 7,8 | 28,05 | 0,838 | 0,650 | 0,691 |
| Уголь древесный | 1 кг | 6510 | 7,5 | 27,26 | 0,814 | 0,632 | 0,671 |
| Торф (W=40%) | 1 кг | 2900 | 3,6 | 12,10 | 0,363 | 0,282 | 0,299 |
| Торф брикеты (W=15%) | 1 кг | 4200 | 4,9 | 17,58 | 0,525 | 0,408 | 0,433 |
| Торф крошка | 1 кг | 2590 | 3,0 | 10,84 | 0,324 | 0,251 | 0,267 |
| Пеллета древесная | 1 кг | 4100 | 4,7 | 17,17 | 0,513 | 0,398 | 0,423 |
| Пеллета из соломы | 1 кг | 3465 | 4,0 | 14,51 | 0,433 | 0,336 | 0,357 |
| Пеллета из лузги подсолнуха | 1 кг | 4320 | 5,0 | 18,09 | 0,540 | 0,419 | 0,445 |
Свежесрубленная древесина (W=50. ..60%) ..60%)
|
1 кг | 1940 | 2,2 | 8,12 | 0,243 | 0,188 | 0,200 |
| Высушенная древесина (W=20%) | 1 кг | 3400 | 3,9 | 14,24 | 0,425 | 0,330 | 0,351 |
| Щепа | 1 кг | 2610 | 3,0 | 10,93 | 0,326 | 0,253 | 0,269 |
| Опилки | 1 кг | 2000 | 2,3 | 8,37 | 0,250 | 0,194 | 0,206 |
| Бумага | 1 кг | 3970 | 4,6 | 16,62 | 0,496 | 0,385 | 0,409 |
| Лузга подсолнуха, сои | 1 кг | 4060 | 4,7 | 17,00 | 0,508 | 0,394 | 0,419 |
| Лузга рисовая | 1 кг | 3180 | 3,7 | 13,31 | 0,398 | 0,309 | 0,328 |
| Костра льняная | 1 кг | 3805 | 4,4 | 15,93 | 0,477 | 0,369 | 0,392 |
| Кукуруза-початок (W>10%) | 1 кг | 3500 | 4,0 | 14,65 | 0,438 | 0,340 | 0,361 |
| Солома | 1 кг | 3750 | 4,3 | 15,70 | 0,469 | 0,364 | 0,387 |
| Хлопчатник-стебли | 1 кг | 3470 | 4,0 | 14,53 | 0,434 | 0,337 | 0,358 |
| Виноградная лоза (W=20%) | 1 кг | 3345 | 3,9 | 14,00 | 0,418 | 0,325 | 0,345 |
|
⇐ ПредыдущаяСтр 3 из 15Следующая ⇒ Теплоемкость природного газа Удельной теплоемкостью называется количество теплоты, которое необходимо подвести к единице массы вещества, чтобы изменить его температуру на 1 градус. Для газов различают удельные теплоемкости: изобарную ср (р=const) и изохорную сv (v=const) Изобарная молярная теплоемкость природных газов определяется по формуле: ср0=0,523(8,36+0,00892t)Мi3/4, (2.10) где t-температура, С; Мi-молекулярная масса I-го компонента природного газа. Тогда для смеси газов формула (17) преобразуется следующим образом: , (2.11) где yi-молярная доля I-го компонента в смеси, срi-изобарная молярная теплоемкость I-го компонента. Изобарная молярная теплоемкость реальных природных газов зависит от давления и от температуры ср=ср0(t)+cp (P,t), (2.12) где cp (P,t)-изотермическая поправка теплоемкости на давление, ее можно определить по номограмме в зависимости от приведенных параметров. Для приближенных расчетов при 0,02≤Рпр≤4, 1,3≤Тпр≤2,5 c0=32,600Рпр/Тпр4 кДж/(кмоль∙К) (2. Теплоемкость неуглеводородных компонентов (N2, H2S и СО2) примерно равна 0,5 теплоемкости углеводорода с одинаковой молярной массой. Теплотоворная способность или теплота сгорания – количество тепла, выделяемое при сгорании при определенных условиях (чаще всего при Р=0,013 МПа и Т=288К). Единицы измерения — МДж/кг, МДж/м3 (ккал/кг, ккал/м3). Различают высшую и низшую теплоту сгорания. Для получения низшей теплоты сгорания из высшей вычитают тепло, расходуемое на испарение гигроскопической воды. Присутствие в смеси инертных газов понижает теплоту сгорания. При сгорании 1кг каменного угля выделяется 9 ккал, 1кг нефти – 11 ккал, 1м3 газа — 7 ккал. Дросселирование – расширение газа при прохождении через дроссель — местное гидравлическое сопротивление (вентиль, кран, сужение трубопровода и т.д.), сопровождающееся изменением температуры. Изменение температуры газов и жидкостей при изоэнтальпийном расширении называется эффектом Джоуля-Томсона или дроссель-эффектом, а Di часто называют коэффициентом Джоуля-Томсона. Di = (Т/р)i = [T (V/Т)p – V]/сp, или Di = Т/ Р, (2.14) где Т – изменение температуры, а Р- изменение давления. Среднее значение коэффициента Джоуля—Томсона для природного газа изменяется от 2 до 4 К/МПа в зависимости от составагаза,падения давления и начальной температуры газа.
Опасные свойства природного газа Токсичность С увеличением молекулярной массы предельных углеводородов их токсические свойства возрастают. Санитарными нормами проектирования промышленных предприятий предусмотрена в рабочей зоне производственных помещений предельно допустимая концентрация углеводородов (паров бензина), равная 0,3 мг/дм3. Из газовых компонентов природных и нефтяных газов особенно токсичен сероводород. Сероводород — бесцветный газ. Способность к образованию взрывоопасных смесей Природные углеводородные газы образуют взрывоопасные смеси с воздухом. Для каждых данных условий существуют два предела взрываемости газовоздушных смесей: 1) нижний предел соответствует минимальной концентрации горючего газа, при которой горение еще возможно; 2) верхний предел соответствует максимуму этой концентрации. С повышением давления смеси значительно возрастают пределы ее взрываемости. Горение и взрыв — однотипные химические процессы, но резко отличающиеся по интенсивности протекающей реакции. При взрыве реакция происходит очень быстро в замкнутом пространстве без доступа воздуха к очагу воспламенения взрывоопасной газовоздушной смеси. Скорость распространения детонационной волны горения при взрыве (900—3000 м/с) в несколько раз превышает скорость звука в воздухе при комнатной температуре. Сила взрыва максимальна, когда содержание воздуха в смеси становится теоретически необходимым для полного сгорания. ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: |
Удельная теплоемкость и индивидуальные газовые постоянные
Удельная теплоемкость (= удельная теплоемкость) при процессах с постоянным давлением и постоянным объемом, а также отношение удельных теплоемкостей и индивидуальных газовых постоянных — R — для некоторых широко используемых «идеальных газов» , приведены в таблице ниже (приблизительные значения для 68 o F ( 20 o C ) и 14,7 фунтов на кв. дюйм ( 1 атм )).
Для перевода единиц измерения используйте онлайн-конвертер единиц Удельная теплоемкость.
См. также табличные значения удельной теплоемкости пищевых продуктов и пищевых продуктов, металлов и полуметаллов, обычных жидкостей и флюидов, обычных твердых и других обычных веществ, а также значения молярной теплоемкости обычных органических веществ и неорганических веществ.
Для полной таблицы — повернуть экран!
| Газ или пар | Формула | Удельная теплоемкость | Коэффициент удельной теплоемкости | Individual Gas constant — R — | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c p (kJ/(kg K)) | c v (kJ /(kg K)) | c p (Btu/(lb m o F)) | c v (БТЕ/(фунт 9)0054 m o F)) | κ = c p / c v | c p — c v (kJ/( kg K)) | c p — c v (ft lb f /(lb m o R)) | ||||||
| Acetone | (CH 3 ) 2 CO | 1. 47 47 | 1.32 | 0.35 | 0.32 | 1.11 | 0.15 | |||||
| Acetylene | C 2 H 2 | 1.69 | 1.37 | 0.35 | 0.27 | 1,232 | 0,319 | 59,34 | ||||
| воздух | 1,01 | 0,718 | 0,24 | 0,718 | 0,24 | 0,718 | 0,24 | 0,718 | .0162 | 53.34 | ||
| Alcohol (ethanol) | C 2 H 5 OH | 1.88 | 1.67 | 0.45 | 0.4 | 1.13 | 0.22 | |||||
| Alcohol (methanol) | CH 3 OH | 1.93 | 1.53 | 0.46 | 0.37 | 1.26 | 0.39 | |||||
| Ammonia | NH 3 | 2.19 | 1. 66 66 | 0.52 | 0.4 | 1.31 | 0.53 | 96.5 | ||||
| Argon | Ar | 0.520 | 0.312 | 0.12 | 0.07 | 1.667 | 0.208 | |||||
| Бензол | C 6 H 6 | 1,09 | 0,99 | 0,26 | 0,24 | ,112 | 0,24 | ,112 | 0,24 | ,112 | .0162 | |
| Blast furnace gas | 1.03 | 0.73 | 0.25 | 0.17 | 1.41 | 0.3 | 55.05 | |||||
| Bromine | Br 2 | 0.25 | 0.2 | 0.06 | 0.05 | 1.28 | 0.05 | |||||
| Butane | C 4 H 10 | 1.67 | 1.53 | 0.395 | 0. 356 356 | 1.094 | 0.143 | 26.5 | ||||
| Carbon dioxide | CO 2 | 0.844 | 0.655 | 0.21 | 0.16 | 1.289 | 0.189 | 38.86 | ||||
| Carbon monoxide | CO | 1.02 | 0.72 | 0.24 | 0.17 | 1.40 | 0.297 | 55.14 | ||||
| Carbon disulphide | CS 2 | 0.67 | 0.55 | 0.16 | 0.13 | 1.21 | 0.12 | |||||
| Chlorine | Cl 2 | 0.48 | 0.36 | 0.12 | 0.09 | 1.34 | 0.12 | |||||
| Chloroform | CHCl 3 | 0.63 | 0.55 | 0.15 | 0.13 | 1.15 | 0.08 | |||||
| Coal gas | 2. 14 14 | 1.59 | ||||||||||
| Combustion products | 1 | 0.24 | ||||||||||
| Этан | C 2 H 6 | 1,75 | 1,48 | 0,39 | 0,3269 600161 1.1870.276 | 51.5 | ||||||
| Ether (diethyl ether) | (C 2 H 5 ) 2 O | 2.01 | 1.95 | 0.48 | 0.47 | 1.03 | 0.06 | |||||
| Ethylene | C 2 H 4 | 1.53 | 1.23 | 0.4 | 0.33 | 1.240 | 0.296 | 55.08 | ||||
| Chlorodifluoromethane, R-22 | CHClF 2 | 1.18 | ||||||||||
| Helium | He | 5. 19 19 | 3.12 | 1.25 | 0.75 | 1,667 | 2,08 | 386,3 | ||||
| Гексан | C 6 H 6 9 9 10161 9 9 9 0165| | | | 1.06 | | | | |||||
| Hydrochloric acid | 0.795 | 0.567 | ||||||||||
| Hydrogen | H 2 | 14.32 | 10.16 | 3.42 | 2,43 | 1,405 | 4,12 | 765,9 | ||||
| Хлороводород | HCl | 0.8 | 0.57 | 0.191 | 0.135 | 1.41 | 0.23 | 42.4 | ||||
| Hydrogen Sulfide | H 2 S | 0.243 | 0.187 | 1.32 | 45.2 | |||||||
| Hydroxyl | OH | 1. 76 76 | 1.27 | 1.384 | 0.489 | |||||||
| Krypton | Kr | 0.25 | 0.151 | |||||||||
| Methane | CH 4 | 2.22 | 1.70 | 0.59 | 0.45 | 1.304 | 0.518 | 96.4 | ||||
| Метилхлорид | CH 3 Cl | 0,240 | 0,200 | 1,20 | 1,20 | 1,016 | ||||||
| Natural Gas | 2.34 | 1.85 | 0.56 | 0.44 | 1.27 | 0.5 | 79.1 | |||||
| Neon | Ne | 1.03 | 0.618 | 1.667 | 0.412 | |||||||
| Nitric Oxide | NO | 0.995 | 0. 718 718 | 0.23 | 0.17 | 1.386 | 0.277 | |||||
| Nitrogen | N 2 | 1.04 | 0.743 | 0.25 | 0.18 | 1.400 | 0.297 | 54.99 | ||||
| Nitrogen tetroxide | N 2 O 4 | 4,69 | 4,6 | 1,12 | 1,1 | 1,02 | 0,09 | |||||
| 0,09 | ||||||||||||
| 6169 1 | ||||||||||||
| 6169 | 0,09 | |||||||||||
| .0054 2 O | 0.88 | 0.69 | 0.21 | 0.17 | 1.27 | 0.18 | 35.1 | |||||
| Oxygen | O 2 | 0.919 | 0.659 | 0.22 | 0.16 | 1.395 | 0.260 | 48.24 | ||||
| Pentane | C 5 H 12 | 1. 07 07 | ||||||||||
| Propane | C 3 H 8 | 1.67 | 1.48 | 0.39 | 0.34 | 1.13 | 0.189 | 35.0 | ||||
| Propene (propylene ) | C 3 H 6 | 1.5 | 1.31 | 0.36 | 0.31 | 1.15 | 0.18 | 36.8 | ||||
| Водяной пар Пар 1 фунт/кв. дюйм абс. 120 – 600 o F | H 2 O | 1.93 | 1.46 | 0.46 | 0.35 | 1.32 | 0.462 | |||||
| Steam 14.7 psia. 220 – 600 o F | H 2 O | 1.97 | 1.5 | 0.47 | 0.36 | 1.31 | 0.46 | |||||
| Steam 150 psia. 360 – 600 o F | H 2 O | 2. 26 26 | 1.76 | 0.54 | 0.42 | 1.28 | 0.5 | |||||
| Sulfur dioxide (Sulphur dioxide) | SO 2 | 0.64 | 0.51 | 0.15 | 0.12 | 1.29 | 0.13 | 24.1 | ||||
| Xenon | Xe | 0.16 | 0.097 | |||||||||
- κ = C P / C V — Специфический коэффициент тепла
- C 40004 — Специфический коэффициент тепла
- C 4555. c v = удельная теплоемкость в процессе постоянного объема
- R- Индивидуальная газовая постоянная
Для перевода единиц используйте онлайн-конвертер единиц Удельная теплоемкость.
См. также табличные значения удельной теплоемкости пищевых продуктов и пищевых продуктов, металлов и полуметаллов, обычных жидкостей и жидкостей, обычных твердых тел и других обычных веществ, а также значения молярной теплоемкости обычных органических веществ и неорганических веществ.
Свойства различных идеальных газов (при 300 К)
Свойства различных идеальных газов (при 300 К)
| Газ | Формула | Молярная масса | Газовая постоянная | Удельная теплоемкость при пост. Нажимать. | Удельная теплоемкость при пост. Том. | Удельная теплоемкость Отношение |
| Воздух | 28,97 | 0,287 | 1. | 0,718 | 1,4 | |
| Аргон | 39,948 | 0,2081 | 0,5203 | 0,3122 | 1,667 | |
| Бутан | 58.124 | 0,1433 | 1,7164 | 1,5734 | 1.091 | |
| Углекислый газ | 44.01 | 0,1889 | 0,846 | 0,657 | 1,289 | |
| Монооксид углерода | 28. | 0,2968 | 1,04 | 0,744 | 1,4 | |
| Этан | 30.07 | 0,2765 | 1,7662 | 1.4897 | 1,186 | |
| Этилен | 28.054 | 0,2964 | 1,5482 | 1.2518 | 1,237 | |
| Гелий | 4. | 2.0769 | 5.1926 | 3.1156 | 1,667 | |
| Водород | 2.016 | 4.124 | 14.307 | 10.183 | 1.405 | |
| Метан | 16.043 | 0,5182 | 2,2537 | 1,7354 | 1,299 | |
| Неон | 20. | 0,4119 | 1.0299 | 0,6179 | 1,667 | |
| Азот | 28.013 | 0,2968 | 1,039 | 0,743 | 1,4 | |
| Октан | 114.231 | 0,0729 | 1,7113 | 1,6385 | 1.044 | |
| Кислород | 31,999 | 0,2598 | 0,918 | 0,658 | 1,395 | |
| Пропан | 44. | 0,1885 | 1,6794 | 1.4909 | 1.126 | |
| Пар | 18.015 | 0,4615 | 1,8723 | 1.4108 | 1,327 |
Адаптировано из TEST ( T he E xpert S система для T Гермодинамика) < www.thermofluids.net > С. Бхаттачарджи, Государственный университет Сан-Диего
Изменение теплоемкости природного газа в зависимости от температуры, давления и относительной плотности
Изменение энтальпии жидкости, в которой между точками (1) и (2) не происходит фазового перехода, можно выразить следующим образом:
(1)
Второй член в правой части этого уравнения обычно неудобно решать вручную. Однако он тривиален или равен нулю для следующих случаев: (1) идеальные газы, (2) постоянное давление, dP = 0 и (3) для жидкости, считающейся несжимаемой. Во всех трех случаях энтальпия является математической функцией только температуры. Cp обычно выражается уравнениями вида:
Однако он тривиален или равен нулю для следующих случаев: (1) идеальные газы, (2) постоянное давление, dP = 0 и (3) для жидкости, считающейся несжимаемой. Во всех трех случаях энтальпия является математической функцией только температуры. Cp обычно выражается уравнениями вида:
(2)
Где A, B и C — константы, зависящие от состава системы и T — абсолютная температура. В большинстве случаев достаточно точно найти Cp при средней температуре TAvg , где:
(3)
CPAvg затем находится при этой средней температуре и решение первого интеграла, хотя и не точное, но удовлетворительное для большинства приложений. Значения теплоемкости для чистых веществ легко доступны из многих справочников и аналогичных справочных материалов. Как отмечено в главе 7 тома 1 «Подготовка и переработка газа» [1], значения теплоемкости можно найти по наклону 9Графики 0023 h и T при заданном давлении. CP для смесей жидких углеводородов можно оценить по уравнениям, представленным в томе 1 [1].
CP для смесей жидких углеводородов можно оценить по уравнениям, представленным в томе 1 [1].
Для неидеальной сжимаемой жидкости, такой как природный газ, нельзя игнорировать второй член в правой части уравнения (1). Поэтому в программном обеспечении для моделирования процессов для расчета ч используется уравнение состояния, такое как Соав-Редлих-Квонг (SRK) [2] или Пенг-Робинсон (PR) [3]. Для многих расчетов, связанных с теплоемкостью природного газа, подходит рисунок 8.3 в томе 1. Теплоемкость при давлении в системе и средней температуре считывается с графика и умножается на массовый расход газа и T для получения тепловой нагрузки, .
(5)
В этом Совете Месяца (TOTM) будет продемонстрировано изменение теплоемкости природных газов в зависимости от температуры, давления и относительной плотности (состава). Затем будет представлена эмпирическая корреляция для учета этих вариаций. Эта корреляция будет использоваться для оценки теплоемкости природного газа в широком диапазоне значений давления, температуры и относительной плотности. Наконец, будет обсуждаться точность предложенной корреляции.
Наконец, будет обсуждаться точность предложенной корреляции.
Разработка обобщенной корреляции CP:
Как упоминалось ранее, CP можно определить по наклону графиков h и T при постоянном давлении. Математически это выражается как:
(6)
Производная в правой части уравнения (6) может быть получена из уравнения состояния (УС), но это слишком утомительно для ручных вычислений. Поэтому опция PR EOS в ProMax [4] использовалась для генерации CP 9.0024 значений для различных значений давления, температуры и относительной плотности. Общее количество рассчитанных значений CP составило 715. В таблице 1 представлен состав пяти различных смесей природного газа, использованных в этом исследовании.
Таблица 1. Составы газа, использованные для получения значений CP
На рисунках с 1 по 5 представлены варианты CP в зависимости от давления, температуры и относительной плотности газа. Области, выделенные красным цветом на рисунках 3, 4 и 5, обозначают двухфазную область газа и жидкости, где Концепция CP недействительна. Следует отметить, что изобара 20 МПа представляет собой единую фазу даже при низких температурах. Однако при низкой температуре жидкость представляет собой плотную фазу.
Области, выделенные красным цветом на рисунках 3, 4 и 5, обозначают двухфазную область газа и жидкости, где Концепция CP недействительна. Следует отметить, что изобара 20 МПа представляет собой единую фазу даже при низких температурах. Однако при низкой температуре жидкость представляет собой плотную фазу.
Чтобы связать все кривые, показанные на рисунках 1-5, одним уравнением, предлагается следующее выражение.
(7)
Где T — температура, P — давление, а CP — теплоемкость. Алгоритм нелинейной регрессии использовался для определения оптимальных значений параметров от «а» до «f». Во-первых, Значения CP для каждого газа в таблице 1 использовались для определения от «а» до «f». Затем все сгенерированные значения CP использовались для определения набора обобщенных параметров. Эти параметры были настроены и округлены, чтобы наилучшим образом представить все пять газов, охватывающих широкий диапазон относительной плотности от 0,60 до 0,80.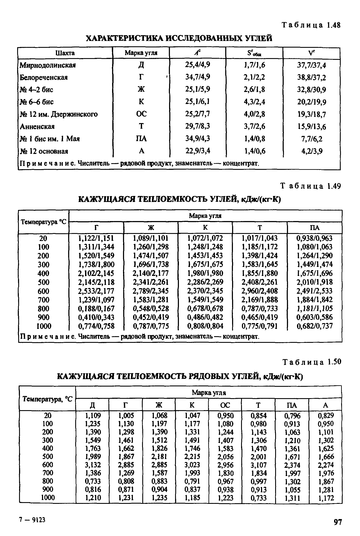 Для каждого случая параметры и сводка статистического анализа ошибок представлены в таблице 2. Обратите внимание, что значения CP двухфазной области не использовались для процесса регрессии. Общий диапазон этой корреляции составляет от 20 до 200 °С (от 68 до 392 °F) и от 0,10 до 20 МПа (от 14,5 до 2900 фунтов на кв. дюйм).
Для каждого случая параметры и сводка статистического анализа ошибок представлены в таблице 2. Обратите внимание, что значения CP двухфазной области не использовались для процесса регрессии. Общий диапазон этой корреляции составляет от 20 до 200 °С (от 68 до 392 °F) и от 0,10 до 20 МПа (от 14,5 до 2900 фунтов на кв. дюйм).
Обсуждение и выводы
Для оценки теплоемкости природных газов в зависимости от давления, температуры и относительной плотности (состава) была разработана единственная и относительно простая зависимость. Эта корреляция охватывает широкий диапазон давления (от 0,10 до 20 МПа, от 14,5 до 2900 фунтов на квадратный дюйм), температуры (от 20 до 200 °C, от 68 до 392 °F) и относительной плотности (от 0,60 до 0,80). Обобщенный набор параметров в дополнение к индивидуальному набору параметров был определен и приведен в Таблице 2. Анализ погрешностей, представленный в Таблице 2, показывает, что точность этого уравнения является достаточно хорошей и может использоваться для расчетов тепловой нагрузки природного газа. Для обобщенного набора параметров средняя абсолютная процентная ошибка (AAPD) и максимальное абсолютное процентное отклонение (MAPD) для суммы 715 баллов составляют 4,34 и 23,61 соответственно. Применимые диапазоны предлагаемой корреляции показаны в таблице 2.
Для обобщенного набора параметров средняя абсолютная процентная ошибка (AAPD) и максимальное абсолютное процентное отклонение (MAPD) для суммы 715 баллов составляют 4,34 и 23,61 соответственно. Применимые диапазоны предлагаемой корреляции показаны в таблице 2.
Таблица 2. Параметры предлагаемой корреляции; уравнение (7) в системе SI и FPS
AAPD= Среднее абсолютное отклонение в процентах и
MAPD= Максимальное абсолютное отклонение в процентах
NPT= Количество точек и
SG = Относительная плотность (удельный вес)
Примечание: Температура ниже указанной выше В диапазонах давлений 2, 5, 7 и 10 МПа (от 14,5 до 1450 фунтов на квадратный дюйм) газовая смесь может находиться в двухфазной (газовой и жидкой) области.
Следует отметить, что понятие теплоемкости справедливо только для однофазной области.
На рисунках с 3 по 5 показано, что при низких температурах наблюдаются жидкие формы и неравномерное поведение CP .
Чтобы узнать больше о подобных случаях и о том, как свести к минимуму эксплуатационные проблемы, мы предлагаем посетить наши курсы G40 (Основы процесса/объекта), G4 (Подготовка и обработка газа) и G5 (Подготовка и обработка газа – специальные).
Автор: Д-р Махмуд Мошфегян
Ссылка:
- Кэмпбелл, Дж. М., «Газовая подготовка и обработка, том. 1, Основные принципы, 8-е изд., Campbell Petroleum Series, Норман, Оклахома, 2001 г.
- G. Soave, Chem. англ. науч. 27 (1972) 1197-1203.
- Д.-Ю. Пэн, Д.Б. Робинсон, штат Индиана, инженер. хим. Фундамент. 15 (1976) 59-64.
- ProMax ® , Bryan Research & Engineering Inc, Версия 2.0, Брайан, Техас, 2007 г.
Газы с теплоемкостью – определение, расчет, единицы измерения, формула
Что такое теплоемкость?
Теплоемкость (Удельная) газов определяется как количество тепла, необходимое для повышения температуры одного грамма газов на единицу градуса, но на моль газа называется молярной теплоемкостью или просто теплоемкостью. Обычно уравнение теплоемкости выражается при постоянном давлении (C p ) и объем (C v ) и единица измерения энергии используются для его вычисления в физике или химии.
Обычно уравнение теплоемкости выражается при постоянном давлении (C p ) и объем (C v ) и единица измерения энергии используются для его вычисления в физике или химии.
Одноатомные молекулы благородных газов, такие как гелий, неон, аргон, при нагревании в постоянном объеме подводимое тепло будет использоваться для увеличения поступательной кинетической энергии, поскольку эти молекулы не имеют колебательного или вращательного момента. Эти одноатомные газы при постоянном объеме без энергии не могут быть использованы для совершения какой-либо механической работы. Но если нагревать при постоянном давлении, газ расширяется против поршня и совершает механическую работу. Для многоатомных газов подведенное тепло использует не только поступательную кинетическую энергию, но также колебательную или вращательную энергию.
Твердые тела также обладают теплоемкостью, измеренной на основании экспериментальных данных Дюлонга Пети о том, что атомная теплота всех кристаллических твердых элементов является постоянной величиной и приблизительно равна 6,4 калории. Атомная теплота является произведением удельной теплоемкости и атомного веса элемента. Этот закон справедлив для многих элементов таблицы Менделеева, таких как серебро, золото, алюминий, свинец, железо и т. д.0009 кг -1 , потому что количество теплоты, необходимое для повышения температуры, зависит от массы веществ. Но молярная теплоемкость является интенсивным свойством в термодинамике и имеет единицу Дж К -1 моль -1 . Мы также используем единицы СГС и калории для определения теплоемкости твердых и газообразных веществ. Но если мы сохранили молярную и удельную теплоемкость, то на моль и на грамм или кг, используемые в этих единицах.
Атомная теплота является произведением удельной теплоемкости и атомного веса элемента. Этот закон справедлив для многих элементов таблицы Менделеева, таких как серебро, золото, алюминий, свинец, железо и т. д.0009 кг -1 , потому что количество теплоты, необходимое для повышения температуры, зависит от массы веществ. Но молярная теплоемкость является интенсивным свойством в термодинамике и имеет единицу Дж К -1 моль -1 . Мы также используем единицы СГС и калории для определения теплоемкости твердых и газообразных веществ. Но если мы сохранили молярную и удельную теплоемкость, то на моль и на грамм или кг, используемые в этих единицах.
Теплоемкость при постоянном давлении
Количество тепла или тепловой энергии, необходимое для повышения температуры одного грамма вещества на 1°К, называется удельной теплоемкостью, а для одного моля называется молярной теплоемкостью. Следовательно, C p = M × c p , где C p измеряется при постоянном давлении, а c p – их удельная теплоемкость. Из этой формулы температура одного гм-моля газа, повышенная на один градус при постоянном давлении, называется теплоемкостью при постоянном давлении или просто С р .
Из этой формулы температура одного гм-моля газа, повышенная на один градус при постоянном давлении, называется теплоемкостью при постоянном давлении или просто С р .
Теплоемкость при постоянном объеме
Опять же из определения, C v = M × c v , где C v измеряется при постоянном объеме, c v — их удельная теплоемкость. Поэтому температуру одного г-моль газа, повышенную на один градус при постоянном объеме, называют теплоемкостью при постоянном объеме или просто С v .
Теплоемкость в термодинамике
Отсюда, подобно внутренней энергии, энтальпии, энтропии и теплоемкости свободной энергии, также и термодинамические свойства. Пусть dq энергия, необходимая для повышения температуры dT одного моля газообразного вещества. Следовательно, термодинамическое определение удельной теплоемкости C = dq/dT, где dq = функция пути. Следовательно, значения изменения теплоты зависят от фактического процесса, который следует за этим измерением.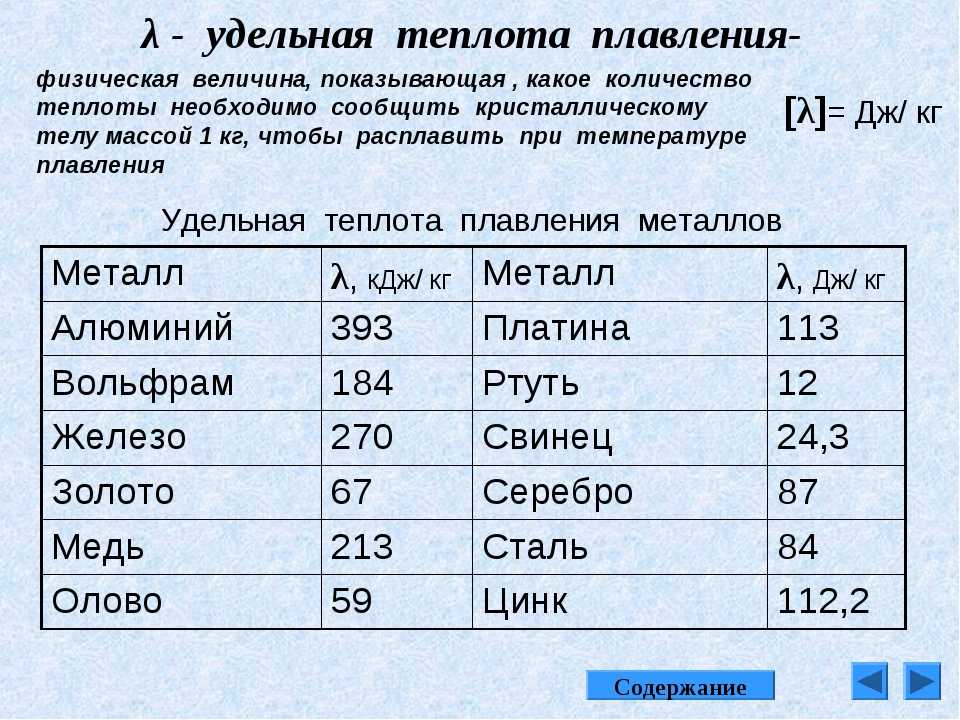 Но мы можем наложить некоторые ограничения, чтобы получить точные значения C p и C v . Обычные ограничения при постоянном давлении и при постоянном объеме.
Но мы можем наложить некоторые ограничения, чтобы получить точные значения C p и C v . Обычные ограничения при постоянном давлении и при постоянном объеме.
Значения Cp и Cv для газов
Расчет C p или C v зависит от давления и объема, особенно в случаях свойств газов. Следовательно, наблюдаемое количество в двух операциях будет разным. Следовательно, для измерения теплоемкости необходимо указать условия давления и объема. При изучении химии и физики С p , C v, и C p /C v или γ некоторых газов при давлении 1 атм и температуре 298 K приведены ниже в таблице,
Газы | Сп | Резюме | γ | |
| Аргон (Ar) | 4,97 | 2,98 | 1,66 |
| Гелий (Не) | 4,97 | 2,98 | 1,66 |
| Ртуть (Hg) | 5,00 | 3,00 | 1,67 |
| Водород (H 2 ) | 6,85 | 4,86 | 1,40 |
| Азот (N 2 ) | 6,96 | 4,97 | 1,40 |
| Кислород (O 2 ) | 7,03 | 5,03 | 1,40 |
| Углекислый газ (CO 2 ) | 8,83 | 6,80 | 1,30 |
| Диоксид серы (SO 2 ) | 9,65 | 7,50 | 1,29 |
| вода (H 2 O) | 8,67 | 6,47 | 1,34 |
| Метан (СН 4 ) | 8,50 | 6,50 | 1,31 |
Проблема: Газы C p и C v имеют 0,125 и 0,075 кал гм -1 K -1 соответственно, как рассчитать молекулярную массу и формулу газа из уравнения удельной теплоемкости. Если можно, назовите газ.
Если можно, назовите газ.
Решение: M = 40 и ⋎ = 1,66 (моноатомный), Ar (аргон).
Формула механической работы
Одноатомный газ можно нагреть при постоянном давлении и постоянном объеме в цилиндре, снабженном поршнем. Когда газ расширяется против поршня, дает механическую энергию. Чтобы добиться повышения температуры на 1°, подведенного тепла должно быть достаточно для увеличения энергии молекул, а также для совершения дополнительной механической работы.
Следовательно, C p равно некоторой механической энергии, необходимой для подъема поршня из объема V 1 в V 2 . C P – C V = механическая работа или энергия = PdV = P(V 2 – V 1 ) = PV 2 – PV 1 . Если газы подчиняются закону идеального газа, PV = RT. Следовательно, C p – C v = R(T + 1) – RT, или C p – C v = R = 2 калории.
Формула теплоемкости
Рассмотрим одноатомные газы, такие как аргон или гелий. Если такие газы нагревают при постоянном объеме, это используется для увеличения кинетической энергии поступательного движения. Так как одноатомные молекулы газа не могут ни поглощаться при колебательном, ни вращательном движении. Если теплота не используется для совершения механической работы расширения, когда объем газа остается постоянным. Следовательно, кинетическая энергия одномолярных идеальных газов при температуре T равна E = 3PV/2 = 3RT/2. Увеличение кинетической энергии при повышении температуры на 1° для одноатомного газа гелия или аргона, ΔE = 3{R(T+1) – RT}/2 = 3R/2 =3 калории.
Теплота, выделяемая при постоянном объеме, равна увеличению кинетической энергии на единицу градуса повышения температуры. Следовательно, C v = ΔE = 3 калории. Для одного моля одноатомного газа отношение C p / C v , универсально выраженное символом γ, вычисляется по следующему уравнению: γ = C p / C v и C p – C v = R.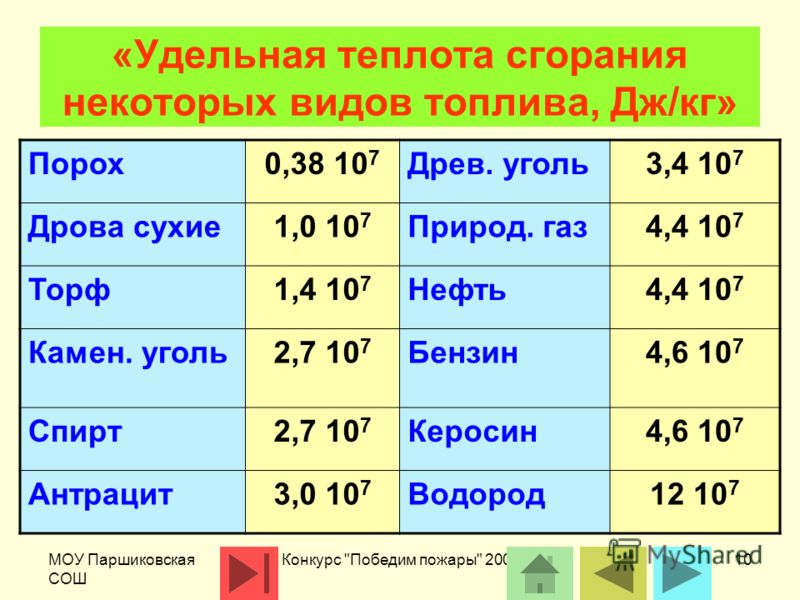 Следовательно, γ = (C v + R)/C v
Следовательно, γ = (C v + R)/C v
= (3 + 2)/3 = 1,66.
Cp и Cv для многоатомного газа
Для многоатомных молекул подведенное тепло расходуется не только на увеличение кинетической энергии, но также на увеличение колебательной или вращательной энергии. Пусть x калорий используется для увеличения вибрационных или вращательных целей.
C p – C v = 2 калории остаются постоянными для этого уравнения энергии, но расчет C p /C v отличается от газа к газу.
Уравнение энергии и удельная теплоемкость
Теплота, подводимая к одному грамм-молю газа при постоянном объеме для повышения температуры на один градус, имеет C v для одноатомных или многоатомных газов. Но одноатомные газы используют эту энергию для увеличения поступательной кинетической энергии, а многоатомные газы используют ее для увеличения поступательной, колебательной и вращательной кинетической энергии.
Расчет теплоемкости
Экспериментальные и расчетные значения C p и C v revels обусловлены следующими фактами. Из-за идеального расположения одноатомных газов C v /R = 1,5. Поэтому значения C p и C v не зависят от температуры в широком диапазоне. Для многоатомных газов были обнаружены две точки неупорядоченности, первая всегда ниже предсказанного значения, а вторая заметна в зависимости от температуры. Наблюдаемые значения теплоемкости многоатомных газов лежат в диапазоне от 2,5 до 3,5.
Классическая механика не описывает изменение этих молекулярных свойств. Поэтому мы используем квантовую механику. Принцип равнораспределения получен из классического рассмотрения непрерывного поглощения энергии атомом, управляемого распределением Максвелла. Колебательная и вращательная энергия имеют место в дискретных единицах, но измеренное значение удельной теплоемкости газа или газов объясняется только на основе квантового уравнения. При высоких температурах энергетические уровни достаточно близки, и наблюдаемый спектр будет непрерывным, и уравнение теплоемкости для молекул газа будет справедливым.
При высоких температурах энергетические уровни достаточно близки, и наблюдаемый спектр будет непрерывным, и уравнение теплоемкости для молекул газа будет справедливым.
Изобарическая удельная теплоемкость природного газа в зависимости от удельного гравитации, давления и температуры
ScienceDirectРегистр. 74-83
https://doi.org/10.1016/j.jngse.2014.04.011Получить права и содержание
Разработка природного газа связана с добычей, переработкой, хранением и транспортировкой природного газа. Правильное обращение с газом требует глубокого понимания того, как его плотность, сжимаемость, псевдодавление и удельная теплоемкость изменяются в зависимости от состояния газа. В журналах по нефти и газу и во множестве учебных материалов были представлены различные методы для оценки других свойств в широком диапазоне температур, однако доступная корреляция для изобарной удельной теплоемкости дается только для 150 °F. Сгенерировано 200 проб газовой смеси с метановой составляющей от 0,74 до 0,9.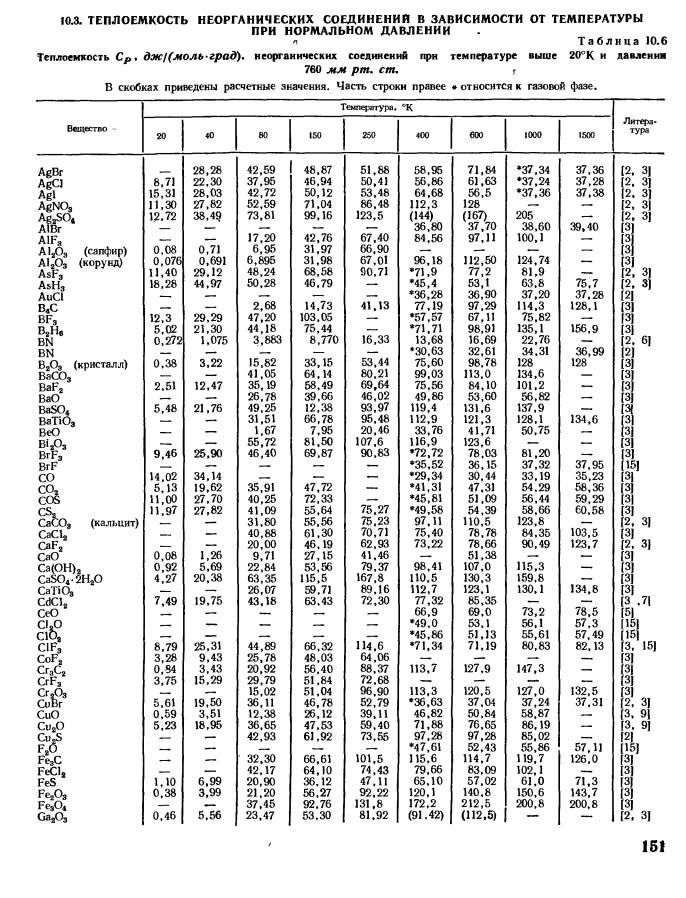 985 с использованием нормально распределенного экспериментального плана. Учитывались вариации соответствующей удельной теплоемкости компонентов и влияние состава на удельный вес и общую удельную теплоемкость газа. Разработанная корреляция учитывает удельный вес и температуру для получения удельной теплоемкости идеального газа образца. Результат дал точность 99,75% при 150 °F по сравнению с экспериментальными данными, в отличие от результата метода изоэнтропического коэффициента, который завышал удельную теплоемкость идеального газа на 25% при той же температуре. Полученная удельная теплоемкость идеального газа по сравнению с 6000 точками данных, полученными по правилу смешивания при различных температурах, привела к коэффициенту корреляционной регрессии 0,9.999. Чтобы учесть отклонение от поведения идеального газа, в этой работе представлено значение 99,7% R в квадрате для безразмерной остаточной удельной теплоемкости как функции пониженной температуры и давления по сравнению с расчетным по уравнению состояния Старлинга-Карнахана.
985 с использованием нормально распределенного экспериментального плана. Учитывались вариации соответствующей удельной теплоемкости компонентов и влияние состава на удельный вес и общую удельную теплоемкость газа. Разработанная корреляция учитывает удельный вес и температуру для получения удельной теплоемкости идеального газа образца. Результат дал точность 99,75% при 150 °F по сравнению с экспериментальными данными, в отличие от результата метода изоэнтропического коэффициента, который завышал удельную теплоемкость идеального газа на 25% при той же температуре. Полученная удельная теплоемкость идеального газа по сравнению с 6000 точками данных, полученными по правилу смешивания при различных температурах, привела к коэффициенту корреляционной регрессии 0,9.999. Чтобы учесть отклонение от поведения идеального газа, в этой работе представлено значение 99,7% R в квадрате для безразмерной остаточной удельной теплоемкости как функции пониженной температуры и давления по сравнению с расчетным по уравнению состояния Старлинга-Карнахана. Эта модель является первой явной корреляцией для определения остаточной удельной теплоемкости природного газа.
Эта модель является первой явной корреляцией для определения остаточной удельной теплоемкости природного газа.
Удельная теплоемкость природного газа – это количество тепла, необходимое для повышения температуры киломоля природного газа на 1 кельвин или градус Фаренгейта (в полевых единицах). Удельная теплоемкость требуется для расчета количества тепловой энергии, поглощаемой или выделяемой при повышении или понижении температуры природного газа. Это требование делает удельную теплоемкость жизненно важной при проектировании промежуточных охладителей, используемых между компрессорами при повышении давления собранного газа для обеспечения необходимой энергии для передачи по трубопроводам.
The heat energy accompanying an isobaric (constant pressure) temperature change (Abou-Kassem and Dranchuk, 1982) is given as:ΔH=nGC¯pΔTorΔH=nG∫T1T2CpⅆTwhere:
n G = Количество киломолей природного газа
C¯p = Изохорная средняя удельная теплоемкость
Δ T = изменение температуры
Если изменение температуры становится изохорным объемом (ΔH): =nGC¯vΔTorΔH=nG∫T1T2CvⅆT
Выражение остается тем же, за исключением изохорной удельной теплоемкости, которая заменяет изобарический аналог. Большинство журналов и учебников по нефти и газу, кажется, пренебрегли необходимостью корреляции для удельной теплоемкости природного газа. Единственная доступная корреляция относится к показателю изоэнтропии k в зависимости от удельного веса γ g при 150 °F, из которого можно рассчитать изобарическую удельную теплоемкость следующим образом: k150°F=2,738-log(γg )2,328,0,55<γg<1
Большинство журналов и учебников по нефти и газу, кажется, пренебрегли необходимостью корреляции для удельной теплоемкости природного газа. Единственная доступная корреляция относится к показателю изоэнтропии k в зависимости от удельного веса γ g при 150 °F, из которого можно рассчитать изобарическую удельную теплоемкость следующим образом: k150°F=2,738-log(γg )2,328,0,55<γg<1
Но,k=CpCvalso,Cp=Cv+R, где R – универсальная газовая постоянная = 8134 Дж/кмоль Kk=CpCp-R1k=1-RCpRCp=k-1k, так что Cp=kR(k-1)
Для того, что уравнение. (8) дает значение изобарной удельной теплоемкости только при температуре 150 °F, его нельзя использовать для оценки параметра при повышенных температурах. Следовательно, для этого необходима корреляция (Trube, 1957).
Фрагменты разделов
Для упрощения предполагается, что природные газы с одинаковым удельным весом имеют одни и те же компоненты в одинаковых пропорциях. Как будет видно позже, это предположение упрощает ситуацию, не влияя на результат.
Например, смесь 80 % метана и 20 % этана имеет точно такой же удельный вес (0,651), что и смесь 90 % метана и 10 % пропана. Можно было ожидать, что удельная теплоемкость будет другой, но удельная теплоемкость оказалась одинаковой при
Некоторые свойства, в том числе псевдокритическая температура и псевдокритическое давление, вычисляются как сумма парциальных псевдокритических давлений и температуры компонентов пробы природного газа (Абу-кассем и Дранчук, 1975, Фарзанех-Горд и др., 2010 г.; Джордж и Браун, 1944). Это поясняется следующими математическими выражениями: Ppc=∑i=1nyiPpciTpc=∑i=1nyiTpci
Кроме того, удельный вес может быть выражен таким же образом. Например, рассмотрим: γg=MWgasMWair=1MWair∑i=1n
Чтобы подтвердить эту корреляцию, график идеальной изобарной удельной теплоемкости, полученный из правила смешивания, показанного на рис. 7, сравнили с графиком, полученным из уравнения. (19) показано на рис. 8. На рис. 9 кросс-график изобарной удельной теплоемкости по смешению и корреляции показывает почти единичную корреляцию коэффициента регрессии. Статистический анализ в таблице 4 показывает, что стандартные отклонения констант составляют 10 2 на порядок меньше значения константы. Узкий
Статистический анализ в таблице 4 показывает, что стандартные отклонения констант составляют 10 2 на порядок меньше значения константы. Узкий
Идеальный газ сохраняет постоянную удельную теплоемкость независимо от его давления, пока температура постоянна. Но природный газ далек от идеала (Абоу-Кассем и Дранчук, 1975, Абу-Кассем и Дранчук, 1982, Дранчук и Куон, 1964, Фарзане-Горд и др., 2010, Джордж и Браун, 1944, Гудвин, 1961, Дранчук et al., 1976; Seifarthi and Joffe, 1952; Weissl and Joffe, 1957; Yorizane et al., 1983). Следовательно, отклонение объясняется остаточной удельной теплоемкостью, равной
Чтобы продемонстрировать, как можно применять модель, приводятся следующие примеры. Обратите внимание, что решения примера 1 приведены после каждой задачи, а решение примера 2 — в подразделе 6.2.1.
Была разработана устойчивая корреляция для изобарной удельной теплоемкости. Эта корреляция состоит из двух частей. Во-первых, это изобарная удельная теплоемкость идеального газа, определяемая уравнениями. (19), (20). Вторая часть является остатком изобарной удельной теплоемкости, заданной уравнением. (27). уравнение (19) имеет корреляцию регрессии 0,9999 и максимальную относительную ошибку 0,04. Он применим к образцам с удельным весом в диапазоне [0,55, 1,0] и температурой в диапазоне [100, 1500] K.
(19), (20). Вторая часть является остатком изобарной удельной теплоемкости, заданной уравнением. (27). уравнение (19) имеет корреляцию регрессии 0,9999 и максимальную относительную ошибку 0,04. Он применим к образцам с удельным весом в диапазоне [0,55, 1,0] и температурой в диапазоне [100, 1500] K.
Авторы выражают благодарность двум анонимным рецензентам за их конструктивную критику, предложения и советы.
Каталожные номера (15)
- J.H. Абу-кассем и др.
Расчет Z-факторов для природных газов с использованием уравнений состояния
Дж. Кан. Домашний питомец. Технол
(1975)
- Дж.Х. Абу-Касем и др.
Изобарная теплоемкость природных газов при повышенных давлениях и температурах
Proc. SPE Анну. Тех. конф. Exhibit
(1982)
- RP Canale et al.
Численные методы для инженеров
(2010)
- Ю.А. Ценгель и др.
Термодинамика: инженерный подход
(2002)
- Б.
 П.М. Дранчук и др.
П.М. Дранчук и др. Общее решение уравнений, описывающих стационарное турбулентное течение сжимаемой жидкости в круглых трубопроводах
(1964)
- P.M. Дранчук и др.
Компьютерный расчет коэффициентов сжимаемости природного газа с использованием корреляций Стэндинга и Каца
Пет. соц. CIM
(1976)
- М. Фарзане-Горд и др.
Расчет тепловых свойств природного газа с использованием уравнения состояния AGA8
Междунар. Дж. Хим. англ. заявл.
(2010)
Дополнительные ссылки доступны в полной текстовой версии этой статьи.
Новая эмпирическая модель и подход на основе нейронных сетей для оценки изобарной теплоемкости природного газа
2022, Journal of Natural Gas Science and Engineering
Изобарная теплоемкость природного газа сама по себе является важным теплофизическим свойством непосредственно связан с термодинамическими энергетическими функциями, поэтому его достоверное предсказание может открыть новое окно для лучшего создания основы для его теоретических и инженерных исследований.
 В настоящем исследовании новая точная и простая эмпирическая корреляция в зависимости от удельного веса (γg), температуры ( T ), а давление ( P ) было разработано для быстрой оценки изобарной удельной теплоемкости ( C p ) природного газа без использования состава газа. Из-за ограничений предложенных экспериментальных моделей и соотношений, полученных из уравнений коэффициента сжимаемости газа (Z-фактора) в литературе, для определенного диапазона температуры, давления и удельного веса, искусственная нейронная сеть (ИНС), основанная на методе обратного распространения, также была применяется для надежного предсказания C p природного газа. 847 наборов данных из различных диапазонов T , P и γg были использованы для разработки архитектуры и топологии нейронной сети. Более того, генетический алгоритм (GA) и оптимизация роя частиц (PS) в качестве алгоритмов стохастического поиска на основе популяции также использовались для оптимизации весов и смещений сетей, чтобы установить наилучшую комбинацию входных переменных, ведущую к минимуму C p.
В настоящем исследовании новая точная и простая эмпирическая корреляция в зависимости от удельного веса (γg), температуры ( T ), а давление ( P ) было разработано для быстрой оценки изобарной удельной теплоемкости ( C p ) природного газа без использования состава газа. Из-за ограничений предложенных экспериментальных моделей и соотношений, полученных из уравнений коэффициента сжимаемости газа (Z-фактора) в литературе, для определенного диапазона температуры, давления и удельного веса, искусственная нейронная сеть (ИНС), основанная на методе обратного распространения, также была применяется для надежного предсказания C p природного газа. 847 наборов данных из различных диапазонов T , P и γg были использованы для разработки архитектуры и топологии нейронной сети. Более того, генетический алгоритм (GA) и оптимизация роя частиц (PS) в качестве алгоритмов стохастического поиска на основе популяции также использовались для оптимизации весов и смещений сетей, чтобы установить наилучшую комбинацию входных переменных, ведущую к минимуму C p. ИНС продемонстрировала точный и многообещающий прогноз с коэффициентом корреляции 0,9.9691 и 0,99518 для общего набора данных и тестовых данных соответственно.
ИНС продемонстрировала точный и многообещающий прогноз с коэффициентом корреляции 0,9.9691 и 0,99518 для общего набора данных и тестовых данных соответственно.Неизотермическая модель ствола скважины для резервуаров с высоким давлением и высокой температурой природного газа и ее применение для уменьшения отложений парафина
2019, Журнал науки и техники о природном газе
проектирование заканчивания, оптимизация добычи и обеспечение притока в нефтяных и газовых скважинах. В местах, где отложения парафина или парафина вдоль ствола скважины вызывают озабоченность, необходима неизотермическая модель ствола скважины для анализа рисков закупорки ствола скважины в различных условиях эксплуатации/коллектора и разработки соответствующих подходов к смягчению последствий. В этом исследовании предлагается неизотермическая модель ствола скважины для коллекторов природного газа с высоким давлением и высокой температурой (HPHT). Математическая основа, изложенная в этой статье, также может быть использована в качестве шаблона для моделирования закачки газа в глубокие скважины. Полевые случаи используются для калибровки и проверки представленной модели, наряду с обсуждением связанных неопределенностей. Поддержание температуры устья скважины выше желаемого уровня имеет решающее значение для смягчения отложений парафина/парафина, и было обнаружено, что наиболее эффективными методами минимизации падения температуры вдоль ствола скважины являются: увеличение производительности за счет гидроразрыва пласта; выбор оптимального размера НКТ и нанесение теплоизоляционного покрытия на НКТ.
Полевые случаи используются для калибровки и проверки представленной модели, наряду с обсуждением связанных неопределенностей. Поддержание температуры устья скважины выше желаемого уровня имеет решающее значение для смягчения отложений парафина/парафина, и было обнаружено, что наиболее эффективными методами минимизации падения температуры вдоль ствола скважины являются: увеличение производительности за счет гидроразрыва пласта; выбор оптимального размера НКТ и нанесение теплоизоляционного покрытия на НКТ.Об изобарной удельной теплоемкости природного газа
2014, Равновесия в жидкой фазе
Колориметр, оснащенный газовым бустером в сочетании с PVT-ячейкой, был использован для измерения теплоемкости природного газа с различным содержанием примесей . На основании новых экспериментальных и литературных данных было проведено общее исследование изобарной удельной теплоемкости с использованием уравнения состояния Джаррахиана–Гейдаряна (J–H-EOS). Получена модель, справедливая в широком диапазоне давлений (0,1–40 МПа) и температур (250–414 К).
 Среднее арифметическое абсолютной погрешности модели приемлемо в инженерных расчетах и имеет преимущество перед другими методами в своем классе.
Среднее арифметическое абсолютной погрешности модели приемлемо в инженерных расчетах и имеет преимущество перед другими методами в своем классе.Тепловое численное моделирование подводных объектов добычи газа на месторождении Амистад
2020, Offshore Technology Conference Brasil 2019, OTCB 2019
Моделирование термодинамических свойств дизельного топлива и бензина в цилиндрах дизельного двигателя Исследование горения
2018, Энергия и топливо
Новый практический метод оценки коэффициента Джоуля–Томсона для природных газов
2018, Journal of Petroleum Exploration and Production Technology
Исследовательская статья
Характеристики, очистка и управление сбросом бытовых сточных вод на газоперерабатывающих заводах Южного Парса
Journal of Natural Gas Science and Engineering, Volume 19, 2014, pp. 91-97
Неправильная или неадекватная очистка, обработка и удаление бытовых сточных вод могут иметь далеко идущие последствия для окружающей среды.
 Эти воздействия являются причинами для управления и регулирования газоперерабатывающих заводов Южного Парса. Вспенивание, высокое содержание взвешенных веществ, высокая биоразлагаемость материала и низкий уровень pH являются основными причинами проблем с загрязнением при очистке бытовых сточных вод (процесс активного ила) на газоперерабатывающем заводе. Недавний осмотр комплекса санитарной обработки показал, что во входном отстойнике и аэротенке установки произошло значительное пенообразование, а также увеличилось БПК (биохимическая потребность в кислороде) сточных вод. Цель настоящего исследования состоит в том, чтобы (а) сосредоточиться на оценке эффективности процесса активного ила и потенциальных причинах загрязнения, которые были получены в результате наблюдений и лабораторных результатов на газоперерабатывающем заводе «Южный Парс» (б) обсудить влияние этих причин. по спецификации сточных вод, (c) для анализа оперативного управления и модификации существующей системы активного ила и (d) по результатам предложить некоторые методы контроля загрязнения на заводе.
Эти воздействия являются причинами для управления и регулирования газоперерабатывающих заводов Южного Парса. Вспенивание, высокое содержание взвешенных веществ, высокая биоразлагаемость материала и низкий уровень pH являются основными причинами проблем с загрязнением при очистке бытовых сточных вод (процесс активного ила) на газоперерабатывающем заводе. Недавний осмотр комплекса санитарной обработки показал, что во входном отстойнике и аэротенке установки произошло значительное пенообразование, а также увеличилось БПК (биохимическая потребность в кислороде) сточных вод. Цель настоящего исследования состоит в том, чтобы (а) сосредоточиться на оценке эффективности процесса активного ила и потенциальных причинах загрязнения, которые были получены в результате наблюдений и лабораторных результатов на газоперерабатывающем заводе «Южный Парс» (б) обсудить влияние этих причин. по спецификации сточных вод, (c) для анализа оперативного управления и модификации существующей системы активного ила и (d) по результатам предложить некоторые методы контроля загрязнения на заводе.
Научная статья
Термодинамическое описание H
2 S–H 2 Растворы O–NaCl при температурах до 573 К и давлениях до 40 МПаХимическая геология, том 424, 2016-1 стр.1
Надежные экспериментальные результаты были отобраны из литературы (с использованием более 700 данных) для разработки термодинамической модели для расчета растворимости сероводорода (H 2 S) в чистой воде и в водных растворах NaCl между 283 и 573 К, 0,1 –40 МПа и м с 0–6 моль·кг − 1 . Термодинамические свойства чистых компонентов рассчитаны с использованием высокоточных многопараметрических уравнений состояния для H 2 S (Lemmon, Span, 2006) и для H 2 O (Wagner, Pruss, 2002). Термодинамические свойства H 2 S(aq) при бесконечном разбавлении были основаны на константах закона Генри, полученных из модели SOCW (Sedlbauer et al., 2000) и представленных Majer et al. (2008). Определены коэффициенты активности H 2 S в чистой воде и в растворах NaCl обрабатывали с использованием модели взаимодействия Питцера.
 Параметры Питцера для H 2 S в бинарных и тройных растворах были определены заново, а параметры для NaCl (водн.) в системе без H 2 S были взяты из обзора Archer (1992). Выбранные для корреляции экспериментальные растворимости воспроизводятся моделью со средними относительными отклонениями 5,2 % и 6,1 % для H 2 S–H 2 O и для H 2 S–H 2 Системы O–NaCl соответственно. Эти значения сравнимы с экспериментальной неопределенностью данных растворимости. Новая модель позволяет термодинамически непротиворечиво описать многие другие свойства жидкой фазы в тройной системе H 2 S–H 2 O–NaCl, в том числе коэффициенты активности H 2 S и NaCl, осмотические коэффициенты , константы Сеченова, молярный объем и плотность объемной жидкости. Эти свойства можно рассчитать для любого H 2 Концентрации S и NaCl до насыщения галита. Модель доступна в виде компьютерного кода, который свободно распространяется.
Параметры Питцера для H 2 S в бинарных и тройных растворах были определены заново, а параметры для NaCl (водн.) в системе без H 2 S были взяты из обзора Archer (1992). Выбранные для корреляции экспериментальные растворимости воспроизводятся моделью со средними относительными отклонениями 5,2 % и 6,1 % для H 2 S–H 2 O и для H 2 S–H 2 Системы O–NaCl соответственно. Эти значения сравнимы с экспериментальной неопределенностью данных растворимости. Новая модель позволяет термодинамически непротиворечиво описать многие другие свойства жидкой фазы в тройной системе H 2 S–H 2 O–NaCl, в том числе коэффициенты активности H 2 S и NaCl, осмотические коэффициенты , константы Сеченова, молярный объем и плотность объемной жидкости. Эти свойства можно рассчитать для любого H 2 Концентрации S и NaCl до насыщения галита. Модель доступна в виде компьютерного кода, который свободно распространяется.
Научная статья
Прогноз изотерм адсорбции смесей н-альдегидов с использованием теории функционала плотности в сочетании с уравнением состояния Пенга-Робинсона
разделение веществ, имеющих очень близкие давления паров, адсорбция является многообещающим методом разделения. Знание изотерм адсорбции, а также явлений капиллярной конденсации необходимо для проектирования и управления процессом. Обычно эти свойства получали опытным путем. Одним из важных технических примеров является очистка н-альдегидов, полученных гидроформилированием олефинов. В случае н-альдегидов экспериментальной информации в литературе найти не удалось. Поэтому теоретический подход к расчету изотерм адсорбции будет очень полезен. Для теоретического моделирования изотерм адсорбции чистых н-альдегидов и смесей н-альдегидов применяется теория функционала плотности (ТФП), в которой термодинамические свойства выражаются как функционалы от пространственно изменяющейся плотности. В этой работе члены свободной энергии большой потенциальной функции рассчитываются по УС Пенга-Робинсона для моделирования реальных молекул, например, н-альдегидов и их смесей. Взаимодействие между жидкостью и стенкой характеризуется внешним потенциалом, и в данной работе предполагается потенциал Стила 10-4-3. На этом фоне приведены расчеты для одномерных щелевых пор в широком диапазоне давлений, начиная от разбавленного газа и заканчивая конденсатной жидкой фазой. Исследовано влияние изменения температуры, потенциалов стенок и длины цепи н-альдегида. Полученные изотермы адсорбции показывают, что адсорбция может быть перспективной технологией для разделения длинноцепочечных н-альдегидов, имеющих очень близкие температуры кипения; однако требуется дальнейшая оптимизация.
Взаимодействие между жидкостью и стенкой характеризуется внешним потенциалом, и в данной работе предполагается потенциал Стила 10-4-3. На этом фоне приведены расчеты для одномерных щелевых пор в широком диапазоне давлений, начиная от разбавленного газа и заканчивая конденсатной жидкой фазой. Исследовано влияние изменения температуры, потенциалов стенок и длины цепи н-альдегида. Полученные изотермы адсорбции показывают, что адсорбция может быть перспективной технологией для разделения длинноцепочечных н-альдегидов, имеющих очень близкие температуры кипения; однако требуется дальнейшая оптимизация.Исследовательская статья
Расширенное кубическое уравнение состояния с новым привлекательным членом (α) существующих в притягивающем члене кубических уравнений состояния (CEOS). Большинство α-функций пытались модифицировать предсказание давления паров полярных компонентов, в то время как другие модификации были сосредоточены как на полярных, так и на неполярных соединениях, а другие соотношения учитывали разложение полиномов в ацентрическом факторе (
ω ) и уменьшенную температуру ( T r ) для более точного прогнозирования давления пара. В большинстве случаев, таких как уравнения состояния Соава и Пенга – Робинсона, предлагаемые α-функции не демонстрируют предельного поведения при бесконечном увеличении температуры. Кроме того, некомпетентность многих α-функций в описании сверхкритического поведения флюидов была изменена путем определения конкретных параметров для некоторых различных компонентов или переключения α-функций. Такие подходы могут создать трудности для расчета свойств, в которых есть уравнения производных состояния. В этой работе была предложена новая α-функция для улучшения привлекательного члена уравнения состояния Пенга-Робинсона. Предложенная модель способна прогнозировать давление насыщенного пара легких газов, полярных, неполярных и тяжелых углеводородных соединений. Нормальная температура кипения ( T b ) используется в качестве дополнительного параметра вместе с ацентрическим фактором ( ω ) и приведенной температурой ( T r ) для повышения способности предложенной α-функции в прогнозировании поведения флюидной фазы особенно для нефтяных фракций и тяжелых фракций, присутствующих в пробах пластовых флюидов.
В большинстве случаев, таких как уравнения состояния Соава и Пенга – Робинсона, предлагаемые α-функции не демонстрируют предельного поведения при бесконечном увеличении температуры. Кроме того, некомпетентность многих α-функций в описании сверхкритического поведения флюидов была изменена путем определения конкретных параметров для некоторых различных компонентов или переключения α-функций. Такие подходы могут создать трудности для расчета свойств, в которых есть уравнения производных состояния. В этой работе была предложена новая α-функция для улучшения привлекательного члена уравнения состояния Пенга-Робинсона. Предложенная модель способна прогнозировать давление насыщенного пара легких газов, полярных, неполярных и тяжелых углеводородных соединений. Нормальная температура кипения ( T b ) используется в качестве дополнительного параметра вместе с ацентрическим фактором ( ω ) и приведенной температурой ( T r ) для повышения способности предложенной α-функции в прогнозировании поведения флюидной фазы особенно для нефтяных фракций и тяжелых фракций, присутствующих в пробах пластовых флюидов. Кроме того, вводятся два дискриминационных индекса ( λ 1 , λ 2 ) для обработки всех чистых веществ и классификации их по отдельным группам для присвоения каждой группе специальных коэффициентов. Было собрано экспериментальное давление паров 31 различных чистых компонентов, 11 бинарных смесей и 12 проб пластовой нефти, чтобы оценить эффективность предложенной модели по сравнению с исходной моделью Пенга-Робинсона. Также было выполнено сравнение между предложенной моделью и другими мощными уравнениями состояния, такими как модифицированная модель PR, PSRK и PC-SAFT, результаты которого показывают, что новая предложенная модель имеет лучшие результаты по сравнению с упомянутыми методами, особенно для сложных смесей. и пластовых флюидов. Кроме того, предложенная α-функция демонстрирует приемлемое предельное поведение при приближении температуры к бесконечности и способна описывать поведение жидкой фазы в сверхкритической области.
Кроме того, вводятся два дискриминационных индекса ( λ 1 , λ 2 ) для обработки всех чистых веществ и классификации их по отдельным группам для присвоения каждой группе специальных коэффициентов. Было собрано экспериментальное давление паров 31 различных чистых компонентов, 11 бинарных смесей и 12 проб пластовой нефти, чтобы оценить эффективность предложенной модели по сравнению с исходной моделью Пенга-Робинсона. Также было выполнено сравнение между предложенной моделью и другими мощными уравнениями состояния, такими как модифицированная модель PR, PSRK и PC-SAFT, результаты которого показывают, что новая предложенная модель имеет лучшие результаты по сравнению с упомянутыми методами, особенно для сложных смесей. и пластовых флюидов. Кроме того, предложенная α-функция демонстрирует приемлемое предельное поведение при приближении температуры к бесконечности и способна описывать поведение жидкой фазы в сверхкритической области.Исследовательская статья
Соответствующий основанный на состояниях метод оценки коэффициентов сжимаемости природного газа
Journal of Molecular Liquids, Volume 216, 2016, pp.
 25-34 предложена модель расчета/оценки коэффициента сжимаемости газа ( z -фактор) природных газов. Метод применяет алгоритм программирования экспрессии генов (GEP). Параметры новой модели включают псевдоприведенное давление и псевдоприведенную температуру. Для оценки производительности и точности разработанной модели одновременно применялись несколько статистических и графических анализов ошибок. Кроме того, были проведены сравнения между этим методом и наиболее широко используемыми корреляциями и уравнениями состояния (EoS), доступными в литературе. Различные статистические параметры также используются для оценки достоверности и прогностической способности недавно разработанного метода. Кроме того, метод кредитного плеча (график Уильямса) используется для определения области возможностей прогнозирования новой модели z-фактора и для обнаружения любых возможных ошибочных точек данных. Полученные результаты демонстрируют, что вновь предложенная модель более надежна и эффективна, чем эмпирические модели и методы EoS для прогнозирования z -факторы природных газов.
25-34 предложена модель расчета/оценки коэффициента сжимаемости газа ( z -фактор) природных газов. Метод применяет алгоритм программирования экспрессии генов (GEP). Параметры новой модели включают псевдоприведенное давление и псевдоприведенную температуру. Для оценки производительности и точности разработанной модели одновременно применялись несколько статистических и графических анализов ошибок. Кроме того, были проведены сравнения между этим методом и наиболее широко используемыми корреляциями и уравнениями состояния (EoS), доступными в литературе. Различные статистические параметры также используются для оценки достоверности и прогностической способности недавно разработанного метода. Кроме того, метод кредитного плеча (график Уильямса) используется для определения области возможностей прогнозирования новой модели z-фактора и для обнаружения любых возможных ошибочных точек данных. Полученные результаты демонстрируют, что вновь предложенная модель более надежна и эффективна, чем эмпирические модели и методы EoS для прогнозирования z -факторы природных газов.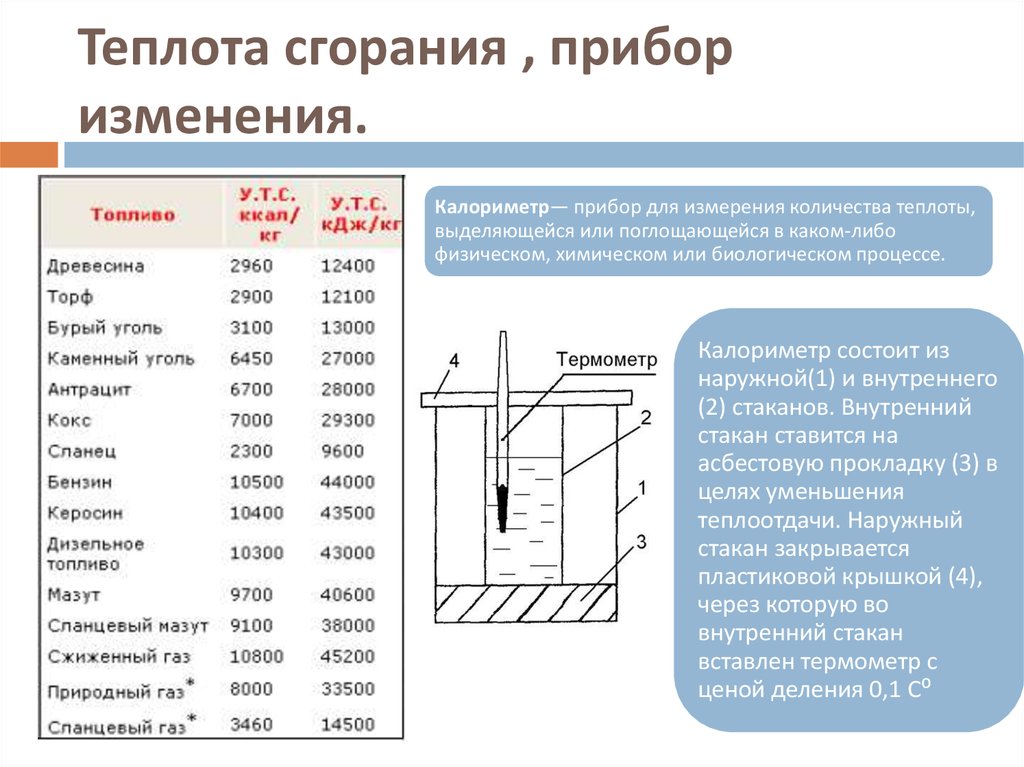
Исследовательская статья
Критерий определения явления пересечения в уравнении состояния с преобразованием объема
) для достижения более точных прогнозов плотности для чистых соединений и смесей. Предыдущие исследования показывают, что зависящее от температуры УС, переведенное по объему, может привести к пересечению изотерм давление-объем для чистого соединения, что приводит к аномальному поведению, заключающемуся в том, что прогнозируемый молярный объем для чистого компонента может быть ниже при более высокой температуре при изобарическое состояние. Такое явление кроссовера не может последовательно предсказать термодинамические свойства чистого соединения, например, дает отрицательное изобарическое тепловое расширение. В этом исследовании мы разрабатываем краткий критерий для оценки того, приведет ли EOS с преобразованием объема к проблемам пересечения, и если да, то в каком диапазоне температур и давлений возникает явление пересечения. Недавно предложенные объемные переводы оцениваются на основе разработанного критерия. Для различных типов температурно-зависимых перемещений объема мы получаем определенные условия температура/давление, при которых, безусловно, не существует явления кроссовера.
Для различных типов температурно-зависимых перемещений объема мы получаем определенные условия температура/давление, при которых, безусловно, не существует явления кроссовера.
- 1
Тел.: +44 7796 722474; Факс: +44 (0) 1223 333450.
- 2
Тел.: +234 803 206 7676.
Теплоемкость | PNG 520: Фазовое поведение природного газа и конденсатных жидкостей
Теплоемкость с постоянным объемом определяется по формуле:
Cv(∂U∂T)VЭто уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.1)
Чтобы увидеть физический смысл теплоемкости постоянного объема, рассмотрим 1 фунт-моль газа в контейнере с жесткими стенками (постоянного объема). Через стенки емкости в систему подводится тепло, и температура газа повышается. Очевидно, что повышение температуры (ΔT) Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
) пропорциональна количеству подведенного тепла,
Очевидно, что повышение температуры (ΔT) Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
) пропорциональна количеству подведенного тепла,
Q∝ΔTЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.2)
Введение константы пропорциональности «cv»,
Q=cvΔTЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.3)
В нашем эксперименте работа не совершалась, так как границы (стенки) системы оставались неизменными. Применяя первый закон термодинамики к этой замкнутой системе, мы имеем:
ΔU=cvΔTЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
в разделе «Технические требования» в руководстве.
(19.4)
Следовательно, для бесконечно малых изменений
Cv=(∂U∂T)VЭто уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19,5)
Как мы видели, постоянной объемной теплоемкостью называется количество теплоты, необходимое для повышения температуры газа на один градус при сохранении своего объема .
Теперь рассмотрим тот же 1 фунт-моль газа, заключенный в поршне-цилиндровом оборудовании (т. е. в системе с нежесткими стенками или границами). Когда в систему добавляется тепло, температура газа повышается, и газ расширяется, так что давление в системе остается неизменным в любое время . Поршень вытесняет объем ΔЭто уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. V и газ увеличивает свою температуру в ΔЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования». Опять же, повышение температуры (ΔЭто уравнение не отображается должным образом из-за несовместимого браузера. См. Технические требования в руководстве для получения списка совместимых браузеров.T) пропорционально количеству добавленного тепла, и новая константа пропорциональности, которую мы используем вот «с p ”,
V и газ увеличивает свою температуру в ΔЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования». Опять же, повышение температуры (ΔЭто уравнение не отображается должным образом из-за несовместимого браузера. См. Технические требования в руководстве для получения списка совместимых браузеров.T) пропорционально количеству добавленного тепла, и новая константа пропорциональности, которую мы используем вот «с p ”,
Q=cPΔTЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.6)
На этот раз некоторая работа была проделана, потому что границы (стенки) системы изменились с их первоначального положения. Применяя первый закон термодинамики к этой закрытой системе, мы получаем:
ΔU=Q−WЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.7)
Если давление оставалось одинаковым как внутри, так и снаружи контейнера, система произвела некоторую работу против окружающей среды в размере W=PΔVЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в Руководстве. Введение (19.7) в (19.6),
ΔU+PΔV=cPΔTЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19,8)
Левая часть этого уравнения представляет собой определение изменения энтальпии (ΔHЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе Технические требования в руководстве. ) для процесса с постоянным давлением. Следовательно:
ΔH=cPΔTЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.9)
Наконец, для бесконечно малых изменений
cP=(∂H∂T)VЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.10)
Функция «c p » называется теплоемкостью при постоянном давлении . Теплоемкостью при постоянном давлении называется количество теплоты, необходимое для повышения температуры газа на один градус 9.0023 при сохранении давления .
Единицами обеих теплоемкостей являются (БТЕ/фунтмоль-°F) и (кал/г-°C). Их значения никогда не равны друг другу даже для идеальных газов. На самом деле, отношение «c p /c v » газа известно как «k» — коэффициент теплоемкости — и оно никогда не равно единице. Это соотношение часто используется в газодинамических исследованиях.
k=cpcvЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.11)
Теплоемкость можно рассчитать с помощью уравнений состояния. Например, Peng and Robinson (1976) представили выражение для энтальпии вылета смеси жидкостей, показанное ниже:
H¨=H−H·=RT(Z−1)+Td(aα)mdT−(aα) m22bmln(Z+(2+1)BZ−(2−1)B) Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.12)
Значение энтальпии жидкости (H) получается путем сложения этой энтальпии вылета (показанной выше) с энтальпией идеального газа (H*). Идеальные энтальпии являются единственными функциями температуры. Для углеводородов Пассют и Даннер (1972) разработал корреляции для свойств идеального газа, таких как энтальпия, теплоемкость и энтропия, в зависимости от температуры. Следовательно, аналитическое соотношение для «c p » может быть получено с помощью производной (19.12), как показано ниже:
Следовательно, аналитическое соотношение для «c p » может быть получено с помощью производной (19.12), как показано ниже:
CP=CP·+R(T(∂Z∂T)P+Z−1)+ Td(aα)mdT−(aα)m22bm[(∂Z∂T)P+2,414(∂B∂T)PZ+2,414B−(∂Z∂T)P−0,414(∂B∂T)PZ−0,414B ]+Td2(aα)mdT222bmln(Z+2.414BZ−414B) Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.13)
где:
CP·=(∂H·∂T)PЭто уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. = идеальный газ C P ,
также найден в работе Passut and Danner (1972).
Вторая производная от (aα)mЭто уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. по температуре можно рассчитать по выражению:
d2dT2(aα)m=−0,45724R22T∑i∑jcicj(1−kij)[f(wj)(αi0,5TciPci0,5)(TcjPcj)0,5ψi+f(wi)(αj0,5TcjPcj0,5) (TciPci)0. 5ψj] Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
5ψj] Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.14a)
где,
ψi=−f(wi)2TciTαi−12TЭто уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.14б)
Для оценки выражения (19.13) требуется также производная коэффициента сжимаемости по температуре. Используя кубическую версию уравнения состояния Пенга-Робинсона, эту производную можно записать как:
(∂Z∂T)P=−((∂Ω2∂T)PZ2+(∂Ω3∂T)PZ+(∂Ω4∂T)P3Z2 +2Ω2Z+Ω3) Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве.
(19.15)
где ∂B∂T)P(∂Ω4∂T)P=−[A(∂B∂T)P+B(∂A∂T)P−2B(∂B∂T)P−3B2(∂B∂T) P](∂A∂T)P=A(aα)md(aα)mdT−2AT(∂B∂T)P=−BTЭто уравнение отображается неправильно из-за несовместимого браузера.




 Удельная теплоемкость cp . Температурный диапазон 200 /1100 °K (-73 /+827 °С ) .
Удельная теплоемкость cp . Температурный диапазон 200 /1100 °K (-73 /+827 °С ) .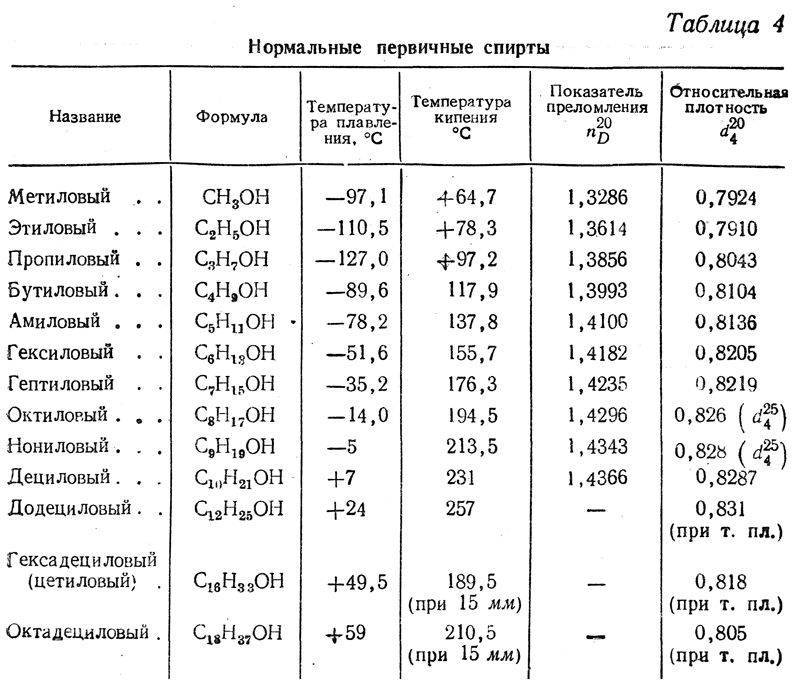 087
087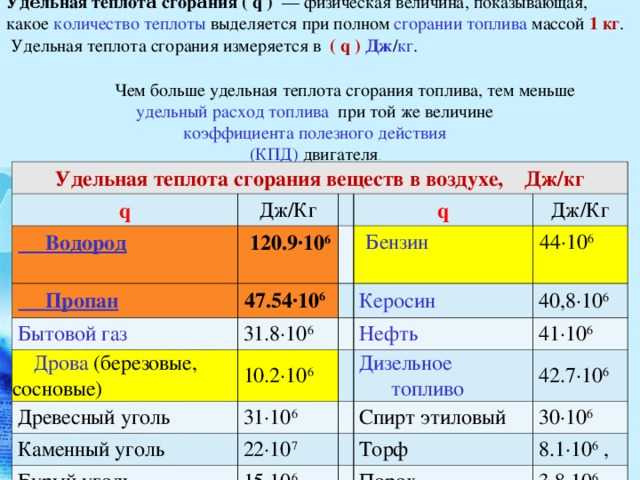 703
703 214
214
 13)
13) Дросселирование – термодинамический процесс, характеризующийся постоянством энтальпии (i = const). В процессе дросселирования реального природного газа при его движении через штуцер, задвижку, регулятор давления, клапан-отсекатель, колонны труб в скважине, неплотности в оборудовании промыслов уменьшается температура газа.
Дросселирование – термодинамический процесс, характеризующийся постоянством энтальпии (i = const). В процессе дросселирования реального природного газа при его движении через штуцер, задвижку, регулятор давления, клапан-отсекатель, колонны труб в скважине, неплотности в оборудовании промыслов уменьшается температура газа.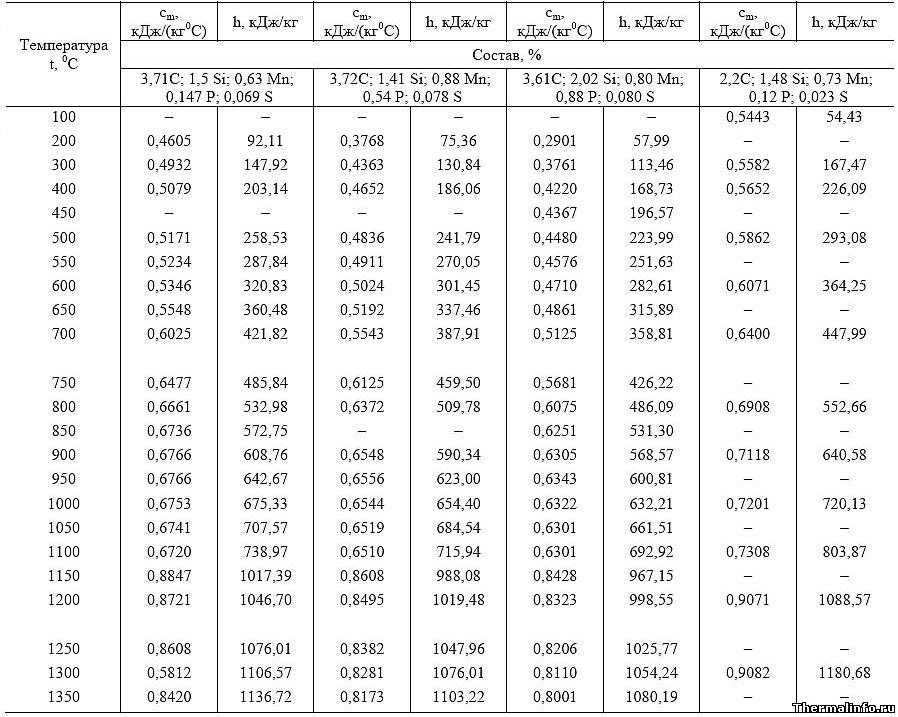 Для приближенных расчетов среднее значение коэффициента Джоуля—Томсона можно принимать равным 3 К/МПа. У жидкостей Di, <;0, поэтому при дросселировании они нагреваются. Для наибольшего снижения температуры газа в штуцере необходимо удалять жидкость из газового потока до его поступления в штуцер.Среднее значение коэффициента Джоуля—Томсона для нефти изменяется от 0,4 до 0,6 К/МПа, для воды оно составляет 0,235 К/МПа.
Для приближенных расчетов среднее значение коэффициента Джоуля—Томсона можно принимать равным 3 К/МПа. У жидкостей Di, <;0, поэтому при дросселировании они нагреваются. Для наибольшего снижения температуры газа в штуцере необходимо удалять жидкость из газового потока до его поступления в штуцер.Среднее значение коэффициента Джоуля—Томсона для нефти изменяется от 0,4 до 0,6 К/МПа, для воды оно составляет 0,235 К/МПа. Относительная плотность его по воздуху 1,19. Человек чувствует сероводород (запах тухлых яиц) даже при содержании его в воздухе 0,0014—0,0023 мг/дм3. Однако даже при непродолжительном пребывании человека в сероводородной среде его обоняние притупляется. Сероводород является ядом, вызывающим паралич органов дыхания и сердца. Предельно допустимая концентрация сероводорода в рабочей зоне производственных помещений —0,01 мг/дм3. Углекислый газ — бесцветный, практически без запаха. Общий характер действия на организм — наркотический и раздражающий кожу и слизистые оболочки. В высоких концентрациях вызывает быстрое удушье вследствие недостатка кислорода. При содержании 4—5% углекислого газа в воздухе у человека раздражается слизистая оболочка дыхательных путей и глаз, появляются кашель, головокружение, повышается кровяное давление. При вдыхании весьма высоких концентраций углекислого газа наступает смерть от остановки дыхания (при 20% газа в воздухе смерть наступает через несколько секунд).
Относительная плотность его по воздуху 1,19. Человек чувствует сероводород (запах тухлых яиц) даже при содержании его в воздухе 0,0014—0,0023 мг/дм3. Однако даже при непродолжительном пребывании человека в сероводородной среде его обоняние притупляется. Сероводород является ядом, вызывающим паралич органов дыхания и сердца. Предельно допустимая концентрация сероводорода в рабочей зоне производственных помещений —0,01 мг/дм3. Углекислый газ — бесцветный, практически без запаха. Общий характер действия на организм — наркотический и раздражающий кожу и слизистые оболочки. В высоких концентрациях вызывает быстрое удушье вследствие недостатка кислорода. При содержании 4—5% углекислого газа в воздухе у человека раздражается слизистая оболочка дыхательных путей и глаз, появляются кашель, головокружение, повышается кровяное давление. При вдыхании весьма высоких концентраций углекислого газа наступает смерть от остановки дыхания (при 20% газа в воздухе смерть наступает через несколько секунд).
 При концентрации газа в воздухе в пределах воспламенения и при наличии источника воспламенения произойдет взрыв; если же содержание газа в воздухе меньше нижнего и больше верхнего пределов воспламенения, то смесь не способна взорваться.
При концентрации газа в воздухе в пределах воспламенения и при наличии источника воспламенения произойдет взрыв; если же содержание газа в воздухе меньше нижнего и больше верхнего пределов воспламенения, то смесь не способна взорваться. 005
005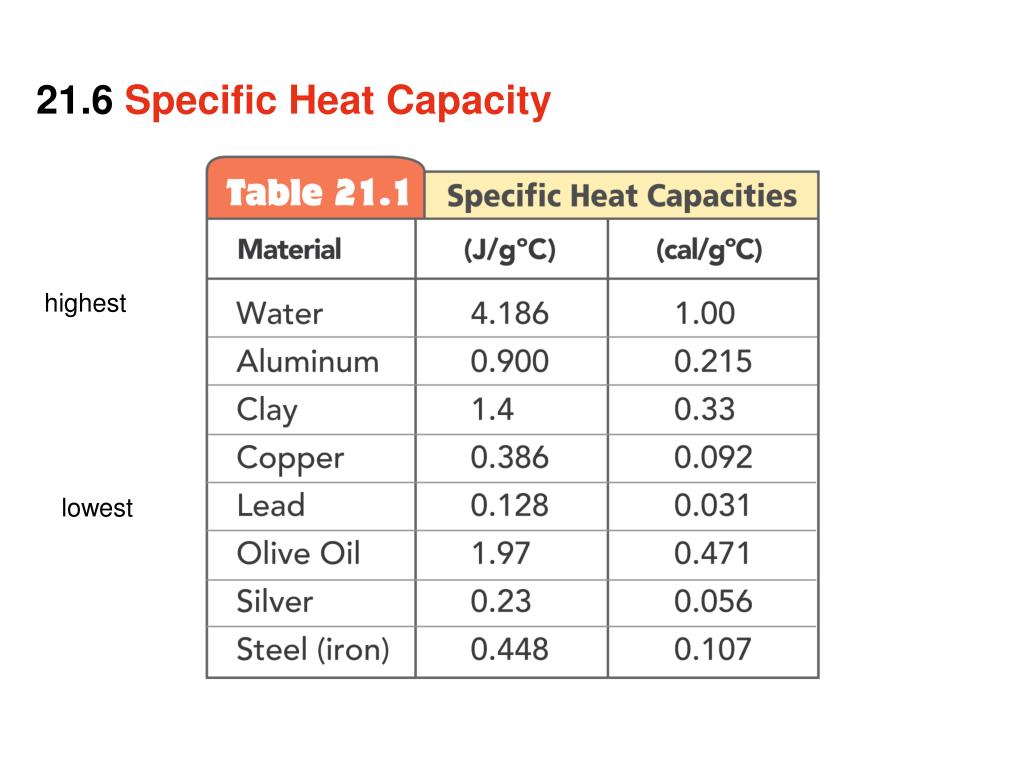 011
011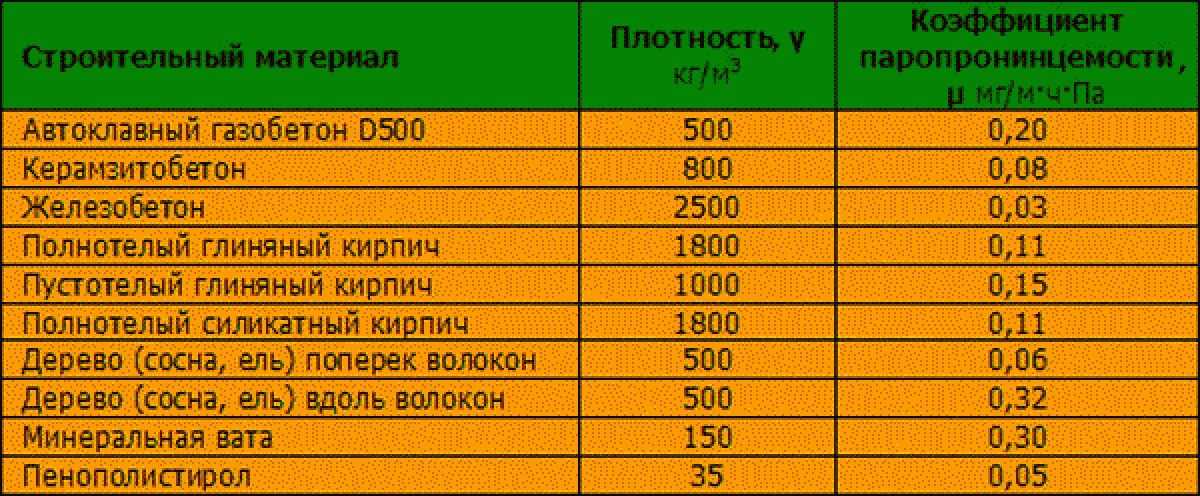 003
003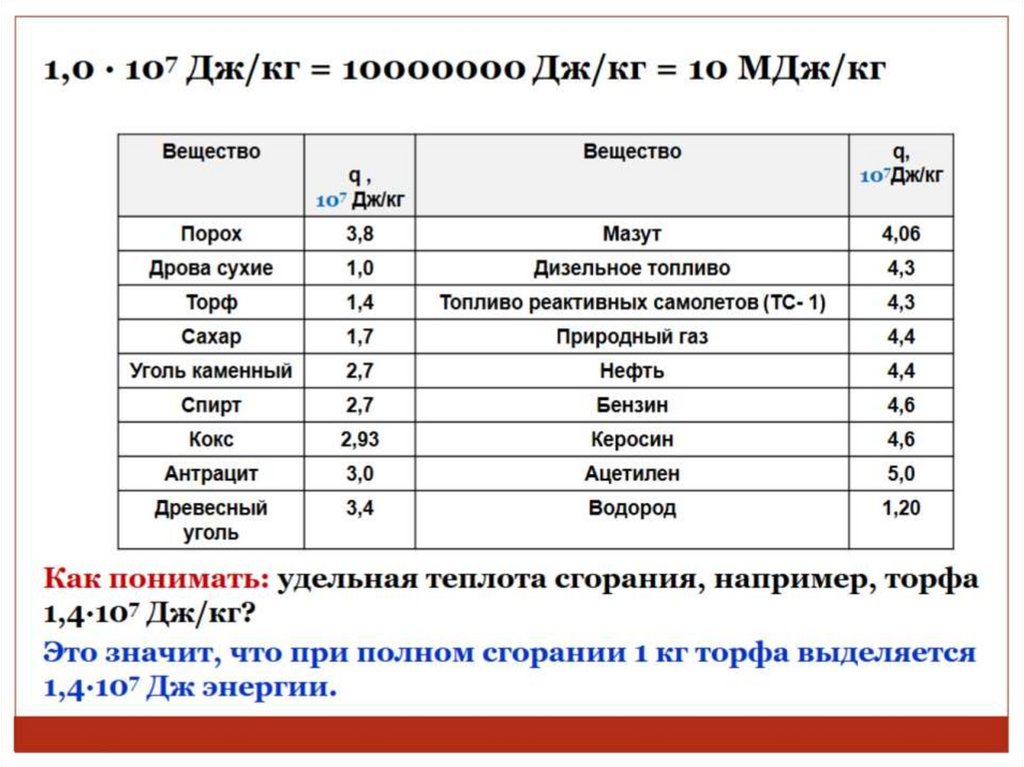 183
183 097
097