Простая физика — EASY-PHYSIC
Предлагаю разбор первой тренировочной работы по физике, Статград, 18 сентября 2018 года. Задачи 25-32.
Задача 25.
Брусок равномерно двигают по горизонтальной поверхности. В процессе движения по этой поверхности он проходит два участка одинаковой длины с различными коэффициентами трения. Известно, что на первом участке модуль работы силы трения 2,5 Дж, а на втором участке модуль работы силы трения 7,5 Дж. При этом на втором участке коэффициент трения на 0,4 больше, чем на первом. Определите, чему равен коэффициент трения на втором участке.
Так как длины участков равны, то очевидно, что величины работ будут относиться так же, как и силы трения. Модули работ равны:
Поделим эти уравнения друг на друга:
Также известно, что
Тогда
Откуда
А
Ответ: 0,6
Задача 26.
Высокий вертикальный цилиндр закрыт тонким поршнем массой 1 кг и площадью 100 см.
Под поршнем находится идеальный газ. Атмосферное давление над поршнем равно 101 кПа, расстояние между дном цилиндра и поршнем 50 см. Цилиндр перевернули так, что поршень оказался снизу, но не выпал из цилиндра. На сколько увеличилось расстояние между дном цилиндра и поршнем в состоянии равновесия? Температура газа в исходном и конечном состоянии одинакова.
Сначала на газ сверху давит атмосфера и вес поршня, распределенный по его площади. Следовательно, давление газа равно
Затем сосуд переворачивают, и сила давления газа складывается с весом поршня, а вверх направлена сила давления атмосферы.
Объем газа в цилиндре изменился при переворачивании, и это произошло изотермически:
Если расписать объемы как произведения площади поршня на его высоту над дном, получим (площади сократим)
Или
Ответ: увеличилось на 1 см.
Задача 27.
Маленький шарик, несущий заряд 2 мкКл, подвешенный в вакууме на нити длиной 50 см, вращается в однородном вертикальном магнитном поле.
При этом шарик движется в горизонтальной плоскости по окружности с постоянной угловой скоростью 20 рад/с, а нить всегда составляет с вертикалью угол . Модуль силы Лоренца, действующей на этот шарик, равен 20 мкН. Определите модуль индукции магнитного поля.
Сила Лоренца равна
Тогда индукция
Где .
Ответ: 2 Тл.
Задача 28.
Бабочки летают, быстро хлопая крыльями. Объясните с точки зрения физических законов и закономерностей, за счёт чего им удаётся удерживаться в воздухе. Оцените, с какой частотой ν бабочке-монарху надо махать крыльями в воздухе плотностью кг/м, чтобы не упасть, если масса бабочки г, площадь крыльев см, максимальная вертикальная скорость концов крыльев в полёте м/c. Считайте, что бабочка опускает крылья вниз плашмя, а поднимает их вверх ребром.
Заметим сразу же, что скорость концов крыльев дана, но скорость любой другой точки крыла (не на конце крыла) – меньше.
Эта скорость по мере приближения к точкам прикрепления крыльев уменьшается вплоть до нуля. Поэтому будем считать, что все крыло двигается вниз со скоростью — это будет средняя скорость. Если крыло двигается вниз плашмя с такой скоростью, то оно «заметает» порцию воздуха объемом . Масса этого воздуха равна
Крыло толкает воздух, сообщает ему импульс, равный
По закону сохранения импульса такой же импульс будет передан и бабочке.
Мы уже учли, что крыльев 2 штуки: дана площадь обоих. Но не учли, что бабочка делает много взмахов. Пусть частота взмахов , то есть
Тогда
Тогда, так как
То можно найти частоту:
Ответ: 4 Гц.
Задача 29.
Гоночный автомобиль едет по треку, имеющему на повороте радиусом м угол наклона полотна дороги к горизонту внутрь поворота. С какой максимальной скоростью может двигаться автомобиль, чтобы не заскользить и не вылететь с трека? Коэффициент трения колёс автомобиля о дорогу .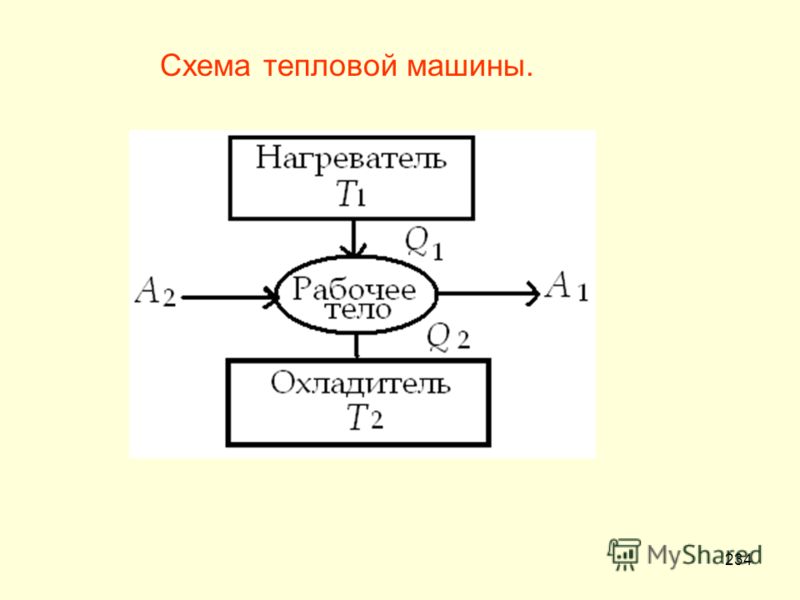
Ответ выразите в км/ч.
Задача 29.
«Честно» расставим силы и запишем уравнение по второму закону Ньютона в проекциях на оси. Оси направим так: Ох вдоль плоскости вниз и Оу перпендикулярно плоскости вверх.
Тогда по оси :
Откуда
Теперь для оси :
Следовательно,
Сократим массу, подставим :
Выразим в км/ч:
Ответ: 129 км/ч.
Задача 30.
В тепловом двигателе в качестве рабочего тела используется идеальный газ, а цикл состоит из двух изохор 1–2 и 3–4 и двух адиабат 2–3 и 4–1 (см. рисунок). Известно, что в адиабатических процессах температура газа изменяется в раза (растёт в процессе 4–1 и падает в процессе 2–3). Найдите КПД цикла.
Задача 30.
Так как в адиабатных процессах газ не обменивается теплотой с внешней средой, то передача тепла газу и обратно происходит только на изохорах. А в изохорном процессе, как известно, работа равна нулю.
Поэтому полученное газом количество теплоты на изохоре 1-2 равно изменению его внутренней энергии:
А отданное количество теплоты равно изменению внутренней энергии газа в процессе 3-4:
Тогда КПД цикла равен
Но по условию и , поэтому
Ответ: 50%
Задача 31.
В электрической цепи, схема которой изображена на рисунке, конденсатор ёмкостью мкФ в начальный момент заряжен до напряжения В, а оба ключа разомкнуты. Замкнув ключ К1, к конденсатору подключили цепочку из двух последовательно соединённых катушек с одинаковой индуктивностью мГн, в результате чего в цепи возникли гармонические колебания. В момент, когда сила тока в цепи при этих колебаниях обратилась в ноль, замкнули ключ К2. Как и на сколько изменилась после этого амплитуда колебаний силы тока в цепи?
Задача 31.
Итак, в конденсаторе сосредоточен заряд
Поэтому при возникновении колебаний заряд будет меняться по закону косинуса:
Где
Здесь при вычислениях мы сложили индуктивности последовательно соединенных катушек.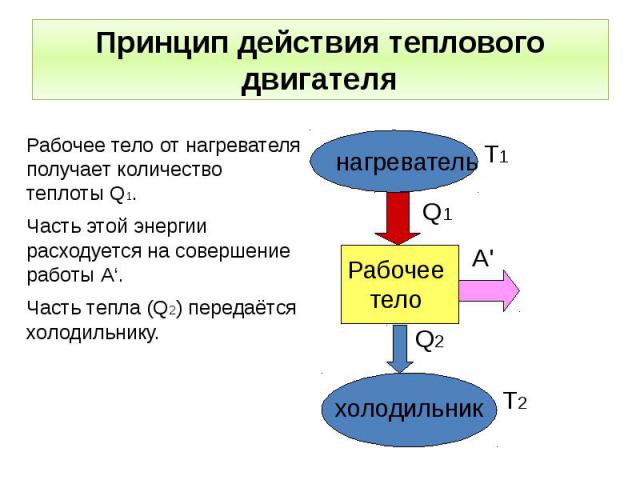
Ток в цепи, как производная заряда, будет меняться по закону синуса:
Максимальное значение тока равно А.
При замыкании ключа 2 в цепи останется только одна катушка, и изменится угловая частота колебаний.
Поэтому изменится и амплитуда тока, которая прямо зависит от угловой частоты:
То есть амплитуда тока возрастет на 0,41 А.
Ответ: 0,41 А.
Задача 32.
Телескопические устройства состоят обычно из двух линз – длиннофокусного объектива и короткофокусного окуляра. В трубе системы Кеплера окуляр – лупа, т. е. собирающая линза, а в трубе системы Галилея окуляр – это рассеивающая линза. В обеих трубах фокальные плоскости объектива и окуляра совпадают, так что параллельный пучок света на входе в систему преобразуется в параллельный же пучок на её выходе. Рассмотрим две такие трубы с одинаковым угловым увеличением , с одинаковыми фокусными расстояниями объективов см и одинаковыми по модулю фокусными расстояниями окуляров.
Какая труба короче и на сколько?
Трубы Кеплера и Галилея отличаются вот чем: для трубы Кеплера
Схема телескопа Кеплера
А для трубы Галилея
Схема телескопа Галилея
Увеличение телескопа определяется выражением:
Тогда
Следовательно, если длины отличаются на , то они отличаются на 5 см. Вот когда на помощь пришла астрономия и задачи на устройство телескопов — кстати, статья на эту тему выйдет 1 ноября.
Ответ: 5 см.
Тепловой двигатель
Термодинамика возникла как наука, основной задачей которой было создание наиболее эффективных тепловых машин.
Обычно в тепловом двигателе механическая работа совершается газом при его расширении. При этом газ в тепловом двигателе называют рабочим телом. Очень часто в качестве рабочего тела выступают воздух или водяные пары. Расширение газа происходит в результате повышения его температуры и давления. Устройство, от которого рабочее тело получает тепло ($Q_n$), называют нагревателем.
Таким образом, рабочее тело сначала расширяется от объема $V_1\ $до объема $V_2$ ${(V}_2>V_1)$, а затем сжимается до первоначального объема. Для того, чтобы работа, которая совершается за цикл, была больше нуля, давление и температура при расширении должны быть больше, чем при сжатии. Следовательно, рабочему телу при расширении теплоту сообщают, а при сжатии забирают. Значит, помимо нагревателя в тепловом двигателе присутствует еще и холодильник, которому рабочее тело тепло отдает. Рабочее тело совершает круговой процесс. Очевидно, что в этом процессе изменение внутренней энергии газа в двигателе равно нулю. Если в ходе расширения от нагревателя к рабочему телу передано $Q_n$- теплоты, при сжатии ${Q’}_{ch}$ теплоты рабочее тело передало холодильнику, исходя из первого начала термодинамики и учитывая, что $\triangle U=0$, получаем, что работа газа в круговом процессе равна:
\[A=Q_n-{Q’}_{ch}\ \left(1\right).\]
Теплота ${Q’}_{ch}\ne 0$. Понятно, что чем лучше тепловой двигатель превращает теплоту, полученную от нагревателя в работу, тем такой двигатель выгоднее.
Эффективность теплового двигателя характеризуют с помощью коэффициента полезного действия (КПД), который определен как:
\[\eta =\frac{A}{Q_n}\left(2\right).\]
Уравнение (2), если учесть (1), можно записать в виде:
\[\eta =\frac{Q_n-{Q’}_{ch}}{Q_n}\left(3\right).\]
КПД всегда $\eta
Машина, которая отбирает от тела с меньшей температурой некоторое количество теплоты $Q_{ch}$ и отдает телу с более высокой температурой количество тепла $Q_n’$, причем $Q_n’>Q_{ch}$, называется холодильной машиной. Над такой машиной должен быть совершена за цикл работа A’. Эффективность холодильной машины характеризуется ее холодильным коэффициентом (a), который вычисляется как:
\[a=\frac{Q_n’}{A’}=\frac{Q_n’}{Q’_n-Q_{ch}}\left(4\right).\]
КПД необратимого теплового двигателя всегда меньше, чем того, который работает по обратимому циклу.
Французский инженер Саади Карно установил важную зависимость КПД теплового двигателя от температуры нагревателя ($T_n$) и холодильника ($T_{ch}$).
\[{\eta }_{max}=\frac{T_n-T_{ch}}{T_n}\left(5\right).\]
Любой реальный тепловой двигатель может иметь КПД $\eta \le {\eta }_{max}$.
Идеальная машина, которую придумал Карно, работает по обратимому циклу, состоящему из двух изотерм (1-2, 4-3) и двух адиабат (2-3, 4-1) (рис.1). Рабочим телом в данном случае является идеальный газ. Мы помним, что адиабатный процесс идет без подвода и отвода тепла.
Рис. 1
На участке 1-2 рабочее тело получает от нагревателя с температурой $T_n$ количество тепла $Q_n$. В случае изотермического процесса мы можем записать, что:
\[Q_n=T_n\left(S_2-S_1\right)\left(6\right),\]
где $S_1,\ S_2$- энтропии в соответствующих точках цикла на рис.1.
На участке 3-4 идеальный газ отдает тепло холодильнику с температурой $T_{ch}$, при этом количество теплоты, что эквивалентно получению газом теплоты ${-Q}_{ch}$, соответственно:
\[{-Q}_{ch}=T_{ch}\left(S_1-S_2\right)\left(7\right).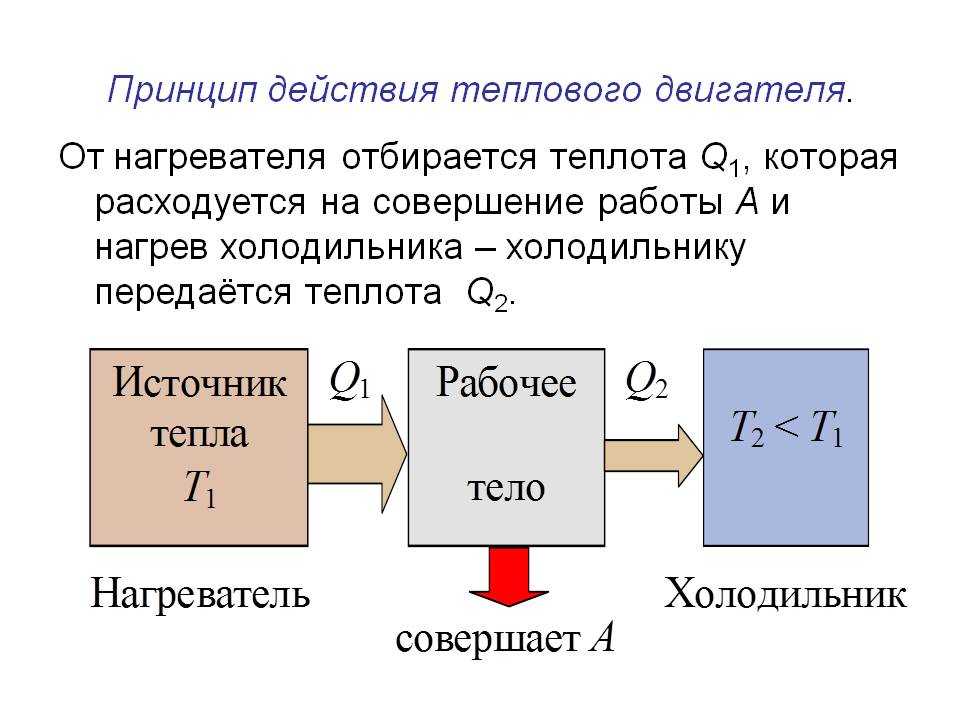
\]
В скобках выражения (7) указано приращение энтропии в процессе 3-4.
Подставим формулы (6), (7) в определение КПД теплового двигателя, получим:
\[\eta =\frac{T_n\left(S_2-S_1\right)+T_{ch}\left(S_1-S_2\right)}{T_n\left(S_2-S_1\right)}=\frac{T_n-T_{ch}}{T_n}\left(8\right).\]
И в нашем выводе уравнения (8) не делалось никаких предположений о свойствах рабочего тела и устройстве теплового двигателя.
Уравнение (8) показывает, что для повышения КПД необходимо повышать $T_n$ и понижать $T_{ch}.$ Но так как абсолютный ноль недостижим, то единственный путь увеличить КПД теплового двигателя, увеличивать $T_n$.
Задача по созданию теплового двигателя, который совершал бы работу без холодильника, кажется весьма интересной. В физике такая машина называется вечным двигателем второго рода. Она в принципе не противоречит первому закону термодинамики. Однако эта проблема также неразрешима, как и создание вечного двигателя первого рода.
Этот опытный факт в термодинамике принят как постулат — второе начало термодинамики.
Пример 2
Задание: Найти КПД цикла, который представлен на рис. 2, если в пределах цикла объем идеального газа изменяется в n раз. Рабочим веществом является газ с показателем адиабаты $\gamma$.
Рис. 2
В качестве основания для расчета КПД используем формулу:
\[\eta =\frac{Q_n-{Q’}_{ch}}{Q_n}\left(2.1\right).\]
Процесс, в котором газ получает тепло — это процесс 1-2 ($Q_{12}=Q_n$):
\[Q_{12}=\triangle U_{12}+A_{12}\left(2.2\right),\]
где $A_{12}=0$ так как это изохорный процесс. Следовательно:
\[Q_{12}=\triangle U_{12}=\frac{i}{2}\nu R\left(T_2-T_1\right)\left(2.3\right).\]
Процесс, в котором газ тепло отдает — это процесс 3-4 изохорный, (${{-Q}}_{34}={Q’}_{ch}$). Следовательно:
\[Q_{34}=\triangle U_{34}=\frac{i}{2}\nu R\left(T_4-T_3\right)\left(2.
{1-г}$.
Тепловые двигатели
Тепловые двигателиТепловой двигатель обычно использует энергию, полученную в виде тепла, для выполнения работы, а затем выбрасывает тепло, которое не может быть использовано для выполнения работы. Термодинамика – это наука о взаимосвязях между теплотой и работой. Первый закон и второй закон термодинамики ограничивают работу тепловой машины. Первый закон представляет собой применение закона сохранения энергии к системе, а второй устанавливает пределы возможного КПД машины и определяет направление потока энергии.
| Индекс Концепции тепловых двигателей | ||||
| Назад |
| Диаграммы давления-объема (PV) являются основным инструментом визуализации для
изучение тепловых двигателей. Поскольку двигатели обычно используют газ в качестве
рабочего вещества, закон идеального газа связывает диаграмму PV с
температуры, так что три существенные переменные состояния газа
можно проследить по циклу двигателя. Так как работа совершается только тогда, когда
объем газа изменяется, диаграмма дает наглядную интерпретацию
работа выполнена. Поскольку внутренняя энергия идеального газа зависит от его
температура, диаграмма PV вместе с температурами, рассчитанными по закону идеального газа, определяют изменения внутренней энергии газа
так что количество подведенного тепла можно оценить из первого закона термодинамики.
| Индекс Концепции фотоэлектрических диаграмм Концепции тепловых двигателей | ||
| Назад |
Термодинамика – это наука о взаимосвязях между теплотой и работой. Первый закон и второй закон термодинамики ограничивают работу тепловой машины. Первый закон представляет собой применение закона сохранения энергии к системе, а второй устанавливает пределы возможного КПД машины и определяет направление потока энергии.
В случае автомобильного двигателя горячим резервуаром является горящее топливо, а холодным резервуаром является среда, в которую выбрасываются продукты сгорания.
Энергетический ресурс. Технол . Декабрь 2007 г., 129(4): 348-354 (7 страниц)
, Линь Б. и Чен Дж. (26 апреля 2007 г.). «Оптимальные критерии важных параметров необратимой тепловой машины Отто с температурно-зависимой теплоемкостью рабочего тела». КАК Я. Дж. Энергетический ресурс. Технол . декабрь 2007 г.; 129(4): 348–354. https://doi.org/10.1115/1.2794770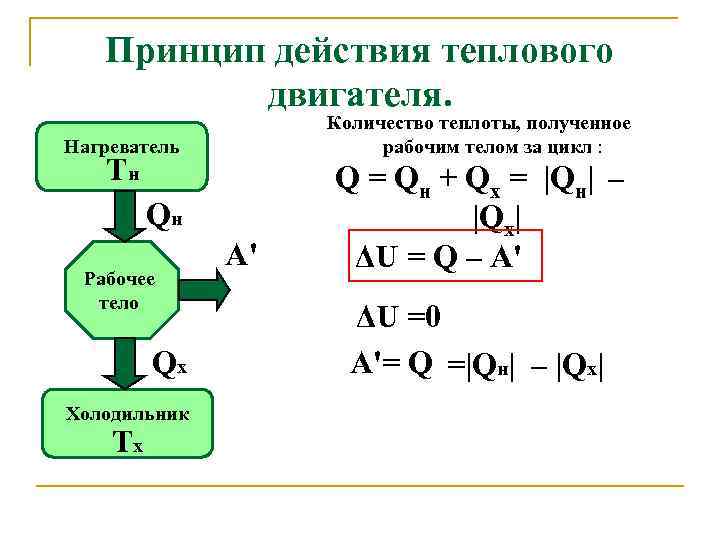
Уравнение адиабаты идеальных газов с зависящей от температуры теплоемкостью выводится строго без использования дополнительных условий аппроксимации в соответствующей литературе и используется для анализа характеристик тепловой машины Отто. Выражения для производительности и эффективности цикла получаются путем введения степени сжатия двух изохорных процессов. Представлены кривые рабочих характеристик тепловой машины Отто для набора заданных параметров. Приведены оптимальные критерии некоторых важных параметров, таких как мощность работы, КПД, степень сжатия и температуры рабочего тела. Кроме того, подробно обсуждается влияние эффективности сжатия и расширения, переменных теплоемкостей, утечки тепла и других параметров на производительность цикла. Полученные результаты являются новыми и общими, из которых могут быть непосредственно получены некоторые соответствующие выводы в литературе. Эта работа может дать важные рекомендации по улучшению характеристик и оптимальной конструкции тепловой машины Отто.
A.
O.
Управлять.
A.
