Внутреннее напряжение физика: Напряжения внутренние

Содержание

Напряжения внутренние — Справочник химика 21

Уравнение (П-12), или (П-12а), выражает закон внутреннего трения Ньютона, согласно которому напряжение внутреннего трения, возникающее между слоями жидкости при ее течении, прямо пропорционально градиенту скорости. [c.26]

Уравнение (3.6) выражает закон внутреннего трения Ньютона. Жидкости, в которых напряжения внутреннего трения подчиняются этому закону, называют ньютоновскими. Жидкости, при течении которых напряжения внутреннего трения не описываются уравнением (3.6), называют неньютоновскими. В технике обычно приходится иметь дело с ньютоновскими жидкостями, поэтому в дальнейшем основное внимание будет уделено именно этим жидкостям. [c.37]

Жидкой фазой суопензии обычно является ньютоновская жидкость, которая соответствует закону внутреннего трения Ньютона, причем напряжение внутреннего трения, возникающее между слоями жидкости при ее течении, пропорционально градиенту скорости по нормали к направлению течения.

На практике встречаются суспензии, жидкая фаза которых отличается аномальными свойствами и относится к неньютоновским жидкостям. Свойства последних разнообразны и характеризуются названиями пластичных, псевдопластичных, дилатантных, тиксотропных, вязкоупругих жидкостей. [c.55]

Величина магнитного момента всех ядер одного изотопа строго одинакова и поэтому на первый взгляд кажется, что в спектре должна присутствовать только одна линия поглощения. На самом деле это не так. Кроме внешнего магнитного поля, в любой молекуле имеются внутренние поля, обусловленные движением электронов. В зависимости от положения, которое занимает данный атом и его ядро в молекуле, оно окажется в определенном внутреннем поле. Поэтому для ядер, находящихся в молекуле в различных положениях, условие резонанса будет наступать при различных значениях внешнего поля в зависимости от того вклада, который вносит в данном месте внутреннее поле. Этот вклад очень мал обычно внутренние поля примерно в миллион раз слабее внешнего.

Однако современные спектрометры ядерного магнитного резонанса имеют очень высокую разрешающую способность и дают отдельные линии поглощения для ядер, которым соответствует разница в напряженности внутренних полей, меньшее одной стомиллионной доли от напряженности внешнего поля. [c.343]

Для пластичных жидкостей зависимость между напряжением внутреннего трения и градиентом скорости по нормали имеет следующий вид [c.127]

Некоторые процессы химической технологии связаны с перемещением жидкостей, которые, в отличие от обычных вязких жидкостей, не следуют закону Ньютона [уравнение (6-8)]. К числу таких жидкостей, называемых пластичными, или неньютоновскими жидкостями, относятся растворы многих полимеров, коллоидные растворы, густые суспензии и др. Эти жидкости при малых напряжениях внутреннего трення х (в н м ) не текут, а лишь изменяют форму. В условиях, когда х становится больше некоторого значения о > о), начинается течение таких жидкостей.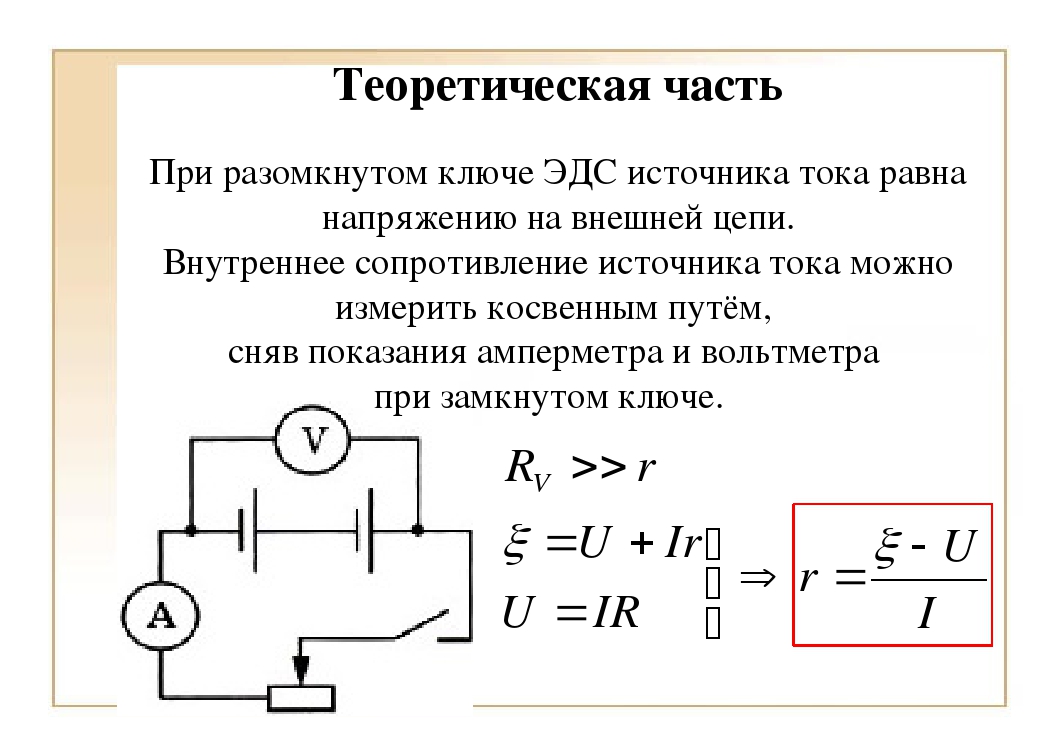

[c.127]

При этом каждая пз горизонтальных поверхностей щели будет заряжена разноименными знаками. Если внещнее поле отсутствует, то напряженность внутреннего поля будет равна нулю. [c.138]

Таким образом, напряженности внутренних полей горизонтально расположенного капилляра и сферической поры больше напряженности поля матрицы пласта. [c.138]

Второй момент (или момент второго порядка) есть среднее значение квадрата напряженности внутреннего поля, действующего на ядра рассматриваемой группы. [c.215]

Ввиду осевой симметрии поля функция U не зависит от ф. Направляющие косинусы явно выражаются через 0, ijj и ф. Функция U может быть выражена через параметры молекулы и напряженность внутреннего поля Fz. [c.241]

Источники внутреннего поля / подразделяются на две группы источники, находящиеся внутри сферы и, и источники, расположенные вне ее, которые соответственно дают вклады /( и/ в напряженность внутреннего поля / [c. 40]

Характерной особенностью кристаллизационных дисперсных структур является развитие в процессе их формирования внутренних напряжений. Внутренние напряжения являются результатом давления, возникающего при направленном росте кристалликов, связанных друг с другом в жесткую пространственную сетку. По данным [c.322]

Охлаждение стекла, а точнее изделия из него проводят медленно, чтобы избежать в нем напряжений. При быстром охлаждении стекла поверхностные слои тела затвердевают и могут иметь температуру, близкую к комнатной, а внутренние части, вследствие низкой теплопроводности, могут иметь температуру до 1000 °С, Поскольку внутренние части при охлаждении сжимаются, а наружные уже не уменьшаются в размере, в них возникают высокие поверхностные сжимающие напряжения, Внутренние слои, наоборот, испытывают высокие растягивающие напряжения. Такое стеклянное тело называют закаленным . Закаленное стекло обладает высокой механической прочностью. Однако у него есть и недостатки.

При нарушении поверхностного слоя (например, нанесение царапины), т, е, при нарушении сжимающих и растягивающих сил, закаленное стекло разлетается вдребезги. [c.47]

Нахождение средней напряженности внутреннего, или локального, электрического поля Ег представляет значительную трудность. Если концентрация полярных молекул мала, можно показать, что Ег = = Е(е+2)/3, где Е, — напряженность внутреннего поля и Е — напряженность приложенного поля. Исключая при помощи этого соот-

[c.450]

Экспериментально установлено, что для многих жидкостей величина касательных напряжений сил трения т в данной точке элемента поверхности, разграничивающего два перемещающихся слоя жидкости, пропорциональна градиенту скорости. В соответствии с этим в случае одномерного течения жидкости (см. рис. 3-1) напряжение внутреннего трения [c.36]

В общем случае, когда поток жидкости не является плоскопараллельным, т. е. когда вектор скорости имеет компоненты w,, и и yv , являющиеся функциями всех трех координат, выражения для напряжения внутреннего трения имеют более сложный вид, отличный от уравнения (3.6).

[c.38]

Проекции напряжений внутреннего трения на ось х имеют вид [c.38]

В напряжении трения [т,,,, (т ) ] первый индекс относится к оси, перпендикулярной плоскости, в которой действует данное напряжение второй индекс указывает ось, на которую оно спроецировано. Например, Тг,-проекция на ось х напряжения, действующего в плоскости 11, перпендикулярной оси г (рис. 3-2). Таким образом, проекции и являются касательными напряжениями, действующими в плоскостях, перпендикулярных осям у и 2. Проекция (т ,) представляет собой нормальное напряжение внутреннего трения, действующее вдоль оси х перпендикулярно плоскости индекс т указывает на то, что это напряжение относится только к трению, в отличие от суммарного нормального напряжения, куда входит также напряжение гидростатического давления.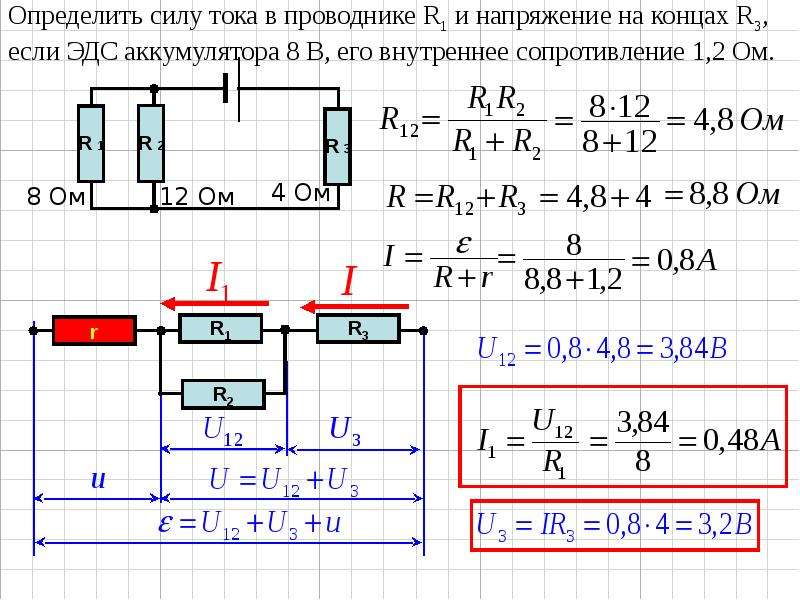 [c.38]

Несмотря на то что система уравнений (3.8) более точно описывает напряжения внутреннего трения, для анализа влияния сил трения при течении жидкостей в процессах химической технологии чаще используют более простое уравнение (3.6). Объяснить это можно тем, что наиболее важные случаи течения (например, различные варианты движения жидкости в тонком слое, граничном с поверхностью твердых стенок) близки к плоскопараллельному течению и поэтому с достаточной точностью описываются уравнением (3.6).

[c.38]

Напряжение внутреннего трения несколько превышает напряжение внешнего трения граничный слой скользит по металлической поверхности оборудования с небольшой скоростью, но при этом не нарушается сплошность, монолитность смеси. Например, поверхность вытекающей из профилирующего отверстия заготовки остается гладкой, ровной. [c.34]

Возникновение указанных аномалий может быть объяснено нарушением оптимальных соотношений напряжений внутреннего и внешнего трения Хц и TJl и сил когезионного ак и адгезионного А взаимодействия смеси с металлическими стенками обрабатывающего оборудования [23].

[c.79]

Рассмотрим движение ламинарного потока неньютоновской жидкости, для которой напряжение внутреннего трения выражается следующим образом [c.48]

Величина второго момента описывает форму резонансной линии поглощения и представляет собой среднее значение квадрата напряженности внутреннего поля, [c.112]

При деформации среды в условиях активного бокового давления характер и интенсивность сдвигов определяются суммарным действием напряжений внутреннего и внешнего полей, относительная роль которых изменяется по мере развития процесса. На первой стадии в большей степени проявляется действие напряжений внешнего поля. Затем пpqи xoдит перестройка полей напряжений, что проявляется в изменении пространственного распреде-144

[c.144]

Уменьшение растягиваюш их напряжений. Внутренние напряжения можно значительно уменьшить или полностью снять отжигом (после пластической обработки или после сварки).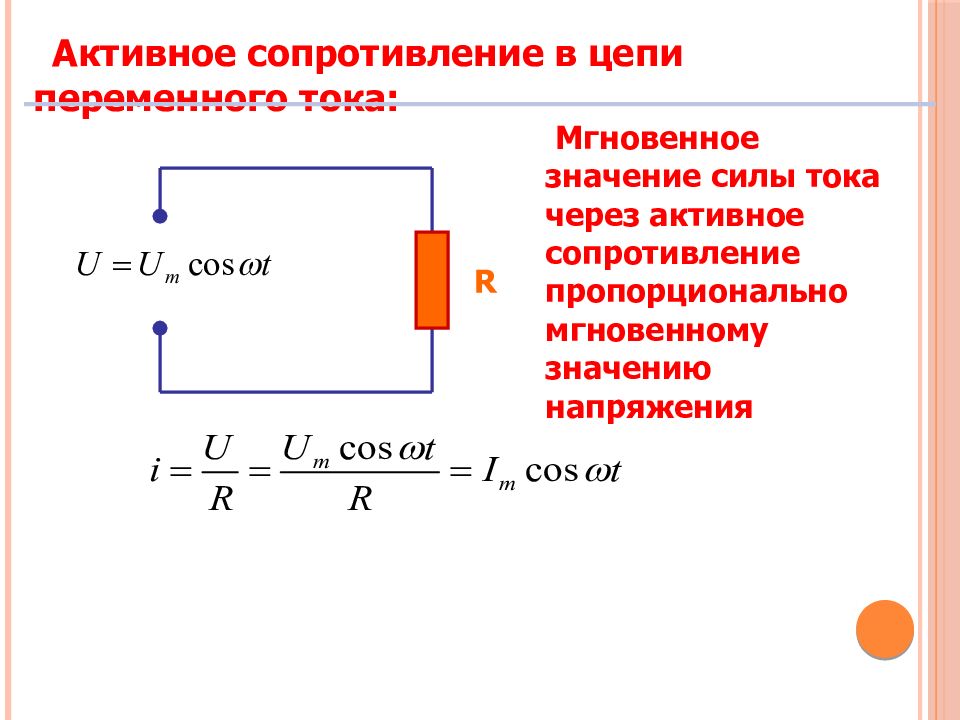 Внешние напряжения иногда можно уменьшить, изменяя конструкцию изделия или условия эксплуатации. [c.453]

Отношение величины [Т] к поверхности соприкосновения слоев обозначают через т и называют напряжением внутреннего трения, а также напряжениемсдвига, или касательным напряжением. Соответственно уравнение (П-11) принимает вид [c.26]

Принциппальная схема четырехплечего уравновешенного моста (рис. 75) в отличие от моста постоянного тока состоит из четырех комплексных сопротивлений 2 , 12, и 1 , указателя равновесия с внутренним сопротивлением 2о и источника переменного напряжения Е с внутренним сопротивлением 2и. Уравнение схемы, связывающее сопротивления плеч моста, э. д. с. источника переменного напряжения, внутренние сопротивления источника и указателя с током в измерительной диагонали, имеет следующий вид

[c.125]

Как осуществляется такое напряжение, в принципе верно объяснил еще в 1912 г. Бернштейн, ученик основоположника электрофизиологии Дюбуа-Реймона. По мнению Бернштейна, клеточная мембрана электрических пластинок, филогенетически происшедших от мышечного волокна, как и клеточные мембраны мышечной ткани, должна обладать избирательной проницаемостью для ионов К+, но не для ионов Ыа+. Между более высокой концентрацией с внутренней стороны и более низкой концентрацией Ыа+ с внешней стороны пластинки возникает потенциал покоя, причем, согласно ряду напряжения, внутренняя сторона становится электроотрицательной. При раздражении, происходящем вследствие нервного нмпульса, изменяется проницаемость мембран и они начинают пропускать ионы, а следовательно, и ток. Как недавно показали измерения Ходчкина с сотрудниками, поляризация при разрядке не только доходит до точки компенсации исходной [c.463]

Типовое обозначение потерпевшего катастрофу самолета— Боинг-747 SR . Последние две буквы — аббревиатура английских слов малая дальность . 27 таких машин компания Боинг построила специально для Японии с ее напряженными внутренними авиатрассами.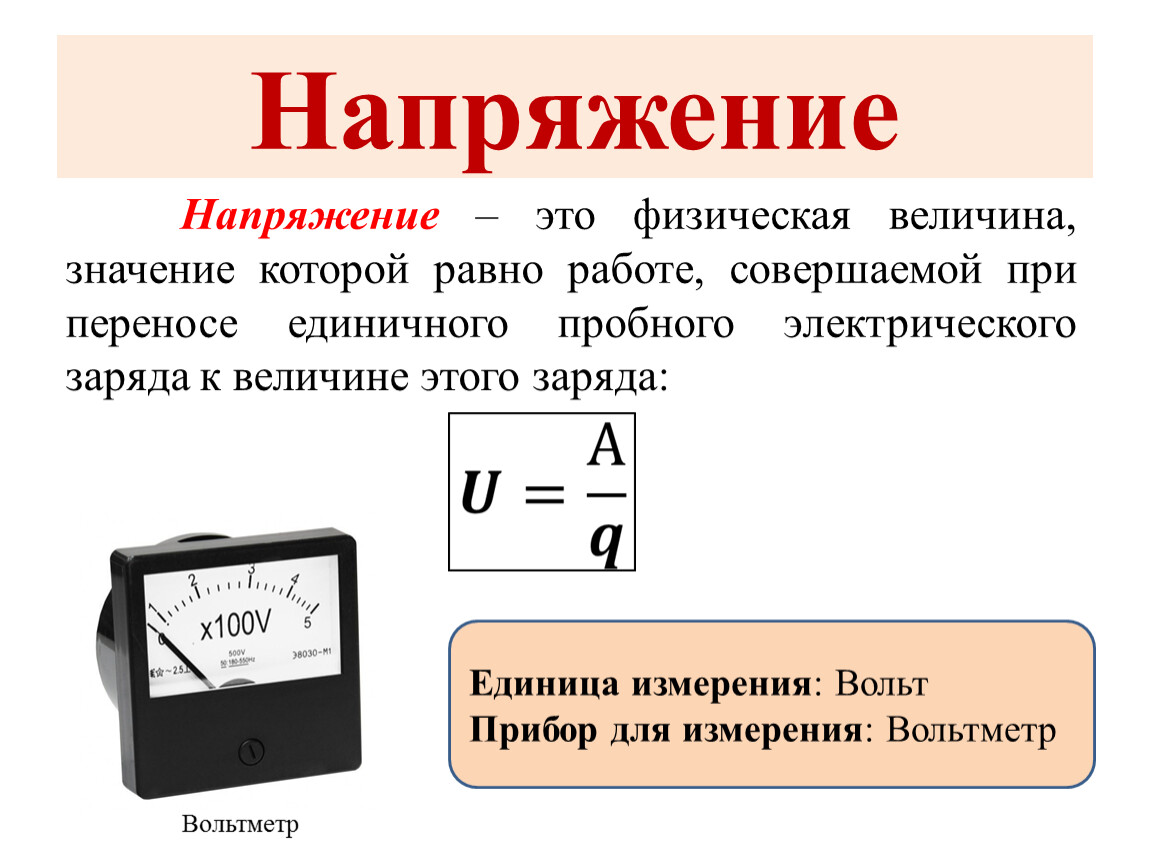 От стандартных магистральных лайнеров эти самолеты отличаются значительно большей пассажировмести-мостью. В 60 рядах — 550 тесно установленных кресел. Учитывая то, что самому большому пассажирскому самолету в мире придется не столько летать, сколько [c.43]

Следует рассмотреть три вклада в поляризацию ориентационную поляризацию, электронную поляризацию и колебательную поляризацию. Ориентационная поляризация обусловлена частичным выравниванием постоянных диполей. Степень, до которой диполи могут быть ориентированы наложенным полем, была рассчитана Дебаем [5] при помощи закона распределения Больцмана. Электрическое поле, действующее на молекулу, обозначается через Е, и называется внутренним полем. Энергия диполя в поле Ei равна—/i-Е ( и—вектор постоянного дипольного момента молекулы), а точка означает скалярное произведение — ii-Ei=—ti i os0, где 0 — угол между двумя векторами. Если энергия диполя в этом поле мала по сравнению с кТ, то можно показать, что в газовой фазе вклад ориентационной поляризуемости на одну молекулу, отнесенный к среднему моменту в направлении поля, дается выражением L Eil3kT, где Е — напряженность внутреннего поля. Когда температура возрастает, тепловое движение становится более интенсивным и в направлении поля ориентируется меньше постоянных диполей. [c.450]

В построении бипротонированного комплекса, по всей вероятности, участвуют депротонированные карбоксильные группы и атомы азота Фенольные гидроксилы при образовании протонированных комплексов не диссоциируют Малая устойчивость нормальных комплексов помимо низкой основности атомов азота может быть вызвана также невозможностью координации всех потенциальных донорных групп лигаида в связи с большим напряжением внутреннего лигандного контура В области существования нормальных комплексов депротонированные фенольные гидроксилы являются претендентами на место во внутренней сфере комплекса, поэтому априори можно предположить, что группами, не участвующими в координации, являются карбоксилы [c.236]

Рис. 1-то. распределение скоростей и напряжений внутреннего трения в сечении ламинарных потоков не-ньютоновскнх жидкостей а — профиль скоростей I — ньютоновская жидкость 2 — псевдо-пластическая 3 — дилатантная 6 — распределение иапряженяй внутреннего трення в — профиль скоростей в сечении потока бин-гамовской жидкости.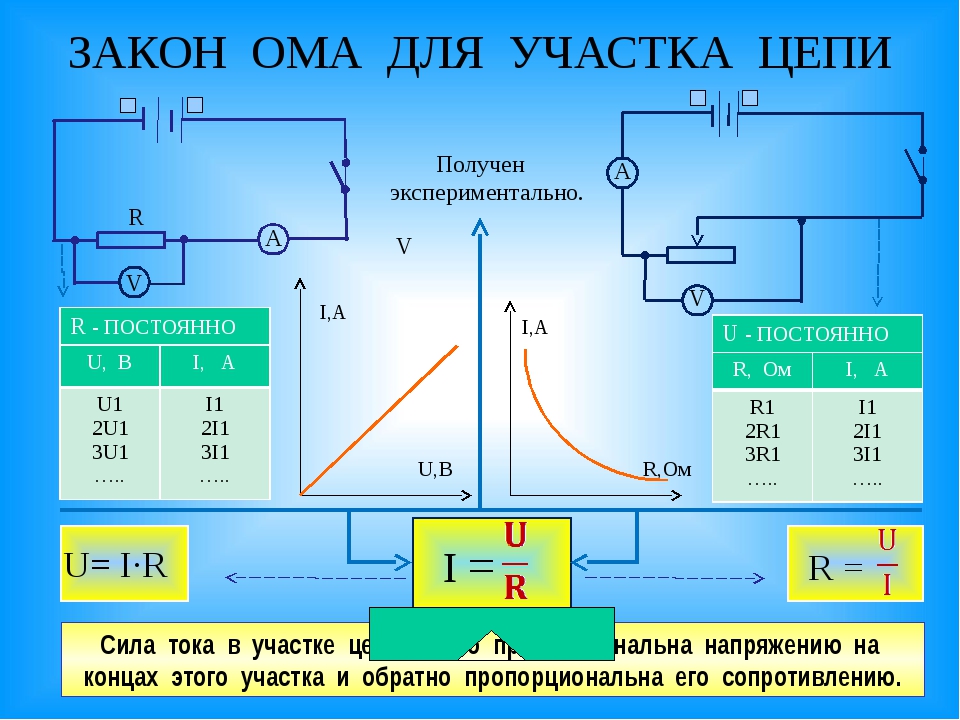 [c.50]

Напряжения — Глоссарий технических терминов

Мерой интенсивности распределения внутренних сил R в окрестности точки в пределах данного сечения площадью A являются напряжения p, измеряемые в единицах силы, отнесенной к единице площади dA
Полные напряжения в точке
Единица измерения напряжений — Паскаль (Н/м²=Па).
Рассмотрим подробнее:

Система приложенных к телу внешних нагрузок, приводит к возникновению в его сечениях внутренней силы R и момента M

Внутренние сила и момент в сечении бруса

При этом надо понимать что внутренняя сила и внутренний момент воздействуют на всё сечение бруса в целом.

Выделим в рассматриваемом сечении элементарную площадку dA бесконечно малой площади.

Элементарная площадка в сечении бруса

Полное напряжение – часть внутренних усилий, приходящаяся на конкретную точку сечения.

Вектор полного напряжения в точке

Обозначение полного напряжения в точке – p.
Единица измерения – Паскаль [Па] (Н/м²).

Ввиду того, что большинство конструкционных материалов обладает высокой прочностью часто напряжения, возникающие в них, измеряются в кратных величинах, например мегапаскаль [МПа].

В общем случае вектор полного напряжения в точке может располагаться под любым углом к сечению. В таких случаях для существенного упрощения расчетов его удобно раскладывать на составляющие (проекции):

Нормальное и касательное напряжения

Проекция вектора полного напряжения p на нормаль к сечению называется нормальным напряжением и обозначается через σ, а проекция вектора полного напряжения на плоскость сечения называется касательным напряжением и обозначается через τ.

Разложение вектора полного напряжения на две указанные составляющие имеет конкретный физический смысл – с нормальным напряжением связано разрушение путем отрыва, а с касательным – разрушение путем сдвига или среза.

В частных случаях (например при растяжении-сжатии и кручении) в поперечных сечениях бруса имеют место только нормальные и только касательные напряжения соответственно.

При решении таких задач, величина нормальных и касательных напряжений сравнивается с соответствующими допустимыми значениями напряжений.

Примеры расчета напряжений >>

Внутреннее сопротивление источника

На внутреннем сопротивлении источника, как и на внешнем, происходит падение напряжения. Поэтому напряжение на зажимах источника меньше ЭДС как раз на эту величину.

Задача 1. Гальванический элемент с ЭДС В и внутренним сопротивлением Ом замкнут накоротко. Определить силу тока короткого замыкания.

При коротком замыкании сопротивляться току будет только внутреннее сопротивление источника:

Ответ: 3 А.

Задача 2. ЭДС элемента В, а внутреннее сопротивление Ом. Какой будет сила тока во внешней цепи, если ее сопротивление равно 0,50; 1; 2 Ом?

К внутреннему сопротивлению здесь добавится еще внешнее сопротивление нагрузки, тогда

Следовательно

Ответ: А, А, А.

Задача 3. Каково внутреннее сопротивление элемента, если его ЭДС В и при внешнем сопротивлении Ом сила тока А?

Следовательно

Таким образом, при .

Ответ: Ом.

Задача 4. ЭДС батарейки от карманного фонаря В, внутреннее сопротивление Ом. Батарейка замкнута на сопротивление Ом. Каково напряжение на зажимах батарейки?

Определим сначала ток:

Следовательно, на внутреннем сопротивлении источника произойдет падение напряжения

На зажимах батарейки будет напряжение

Ответ: В.

Задача 5. ЭДС батареи В, внешнее сопротивление цепи Ом, а внутреннее – Ом. Найти силу тока в цепи, напряжение на зажимах батареи и падение напряжения внутри батареи.

Определим сначала ток:

Следовательно, на внутреннем сопротивлении источника произойдет падение напряжения

На зажимах батарейки будет напряжение

Ответ: В.

Задача 6. Каково напряжение на полюсах источника с ЭДС, равной , когда сопротивление внешней части цепи равно внутреннему сопротивлению источника?
Определим сначала ток:

На внутреннем сопротивлении упадет

Таким же будет напряжение на зажимах источника.

Ответ: .

Внутреннее сопротивление источника-2

Эта статья поможет разобраться с источниками: что такое короткое замыкание, напряжение на зажимах, как найти внутреннее сопротивление источника.

Задача 1. При подключении лампочки к источнику тока с В напряжение на лампочке В, а ток в ней А. Каково внутреннее сопротивление источника?

Падение напряжения на лампочке равно 4 В, следовательно, В падает на внутреннем сопротивлении источника. Тогда, зная ток, можем найти это сопротивление:

Ответ: 2 Ом.

Задача 2. Источник с ЭДС В и внутренним сопротивлением Ом замкнут никелиновой проволокой длиной м и площадью поперечного сечения мм. Каково напряжение на зажимах источника?

Определим сопротивление проволоки:

Таким образом, ток в цепи будет равен:

Тогда на внутреннем сопротивлении при таком токе упадет

И на зажимах источника будет

Можно было найти это напряжение иначе, как напряжение на проволоке:

Ответ: В.

Задача 3. Какого диаметра был выбран железный провод длиной м,
если после замыкания им источника тока с ЭДС В и внутренним сопротивлением Ом сила тока в нем А?

Падение напряжения на внутреннем сопротивлении равно В, на проволоке, следовательно, падает В. При данном токе сопротивление проволоки равно:

Тогда ее сечение равно:

Сечение получено в мм! Поэтому диаметр получится в мм.

Так как , то

Ответ: мм

Задача 4. В проводнике сопротивлением Ом, подключенном к элементу с В, сила тока А. Какова сила тока при коротком замыкании элемента?
Падение напряжения на внешнем сопротивлении равно В. Следовательно, на внутреннем падает В. Значит, его сопротивление в 10 раз меньше и равно Ом. Тогда при коротком замыкании

Ответ: А.
Задача 5. При сопротивлении внешней цепи Ом напряжение на зажимах источника В, а при сопротивлении Ом напряжение В. Найти ЭДС и внутреннее сопротивление источника.

Запишем систему уравнений:

Тогда

Приравнивая, получим:

Откуда

Ответ: Ом.

Задача 6. При подключении к источнику тока сопротивления Ом сила тока в цепи А, а при подключении сопротивления Ом -сила тока А. Найти внутреннее сопротивление и ЭДС батареи.

Ток в цепи:

Тогда запишем:

Разделив уравнения друг на друга, получим:

Ответ: Ом.

Задача 7. В замкнутой цепи при уменьшении внешнего сопротивления на % ток увеличился на % . На сколько процентов увеличился бы ток, если бы внешнее сопротивление уменьшили на % ?

До всевозможных изменений в цепи протекал ток, определяемый выражением:

Затем внешнее сопротивление уменьшили на 20 процентов, и оно стало равно . При этом ток равен :

Теперь запишем, каким будет ток, если внешнее сопротивление уменьшить на 40% ():

Пользуясь первыми двумя уравнениями, определим соотношением между и :

Приравняем правые части:

Или

Теперь разделим друг на друга второе и третье уравнения (третье будем делить на второе):

Подставляя , получим:

Ответ: ток увеличится на 50%.

Урок 31. закон ома для полной цепи — Физика — 10 класс

Физика, 10 класс

Урок 31. Закон Ома для полной цепи

Перечень вопросов, рассматриваемых на уроке:

1) закон Ома для полной цепи;

2) связь ЭДС с внутренним сопротивлением;

3) короткое замыкание;

4) различие между ЭДС, напряжением и разностью потенциалов.

Глоссарий по теме

Электрическая цепь – набор устройств, которые соединены проводниками, предназначенный для протекания тока.

Электродвижущая сила – это отношение работы сторонних сил при перемещении заряда по замкнутому контуру к абсолютной величине этого заряда.

Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению:

Основная и дополнительная литература по теме урока:

1. Мякишев Г. Я., Буховцев Б. Б., Сотский Н.Н. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 348 – 354.

2.Рымкевич А. П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009. С. 106-108.

Теоретический материал для самостоятельного изучения

Любые силы, которые действуют на электрически заряженные частицы, кроме сил электростатического происхождения (т.е. кулоновских), называют сторонними силами. Сторонние силы приводят в движение заряженные частицы внутри всех источников тока.

Действие сторонних сил характеризуется важной физической величиной электродвижущей силой (ЭДС). Электродвижущая сила в замкнутом контуре — отношение работы сторонних сил при перемещении заряда вдоль контура к заряду.

В источнике тока из-за действием сторонних сил происходит разделение зарядов. Так как они движутся, они взаимодействуют с ионами кристаллов и электролитов и отдают им часть своей энергии. Это приводит к уменьшению силы тока, таким образом, источник тока обладает сопротивлением, которое называют внутренним r.

Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление цепи:

Сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению

Короткое замыкание

При коротком замыкании, когда внешнее сопротивление стремится к нулю , сила тока в цепи определяется именно внутренним сопротивлением и может оказаться очень большой . И тогда провода могут расплавиться, что может привести к опасным последствиям.

Примеры и разбор решения заданий:

1. К каждой позиции первого столбца подберите соответствующую позицию второго:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
Электродвижущая сила
Сила тока
Сопротивление
Разность потенциалов

Решение.

Электродвижущая сила гальванического элемента есть величина, численно равная работе сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому.

Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории перемещения зарядов.

ЭДС определяется по формуле:

Сила тока определяется по формуле:

Сопротивление определяется по формуле:

Разность потенциалов определяется по формуле:

Правильный ответ:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
Электродвижущая сила
Сила тока
Сопротивление
Разность потенциалов

2. ЭДС батарейки карманного фонарика — 3,7 В, внутреннее сопротивление 1,5 Ом. Батарейка замкнута на сопротивление 11,7 Ом. Каково напряжение на зажимах батарейки?

Решение:

Напряжение рассчитывается по формуле:

Чтобы найти силу тока применим закон Ома для полной цепи:

Делаем расчёт:

Ответ: U = 3,28 В.

Электрический ток — Физика — Теория, тесты, формулы и задачи

Основные теоретические сведения

Электрический ток. Сила тока. Сопротивление

К оглавлению…

В проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов, хотя в большинстве случае движутся электроны – отрицательно заряженные частицы.

Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда q, переносимого через поперечное сечение проводника за интервал времени t, к этому интервалу времени:

Если ток не постоянный, то для нахождения количества прошедшего через проводник заряда рассчитывают площадь фигуры под графиком зависимости силы тока от времени.

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Сила тока измеряется амперметром, который включается в цепь последовательно. В Международной системе единиц СИ сила тока измеряется в амперах [А]. 1 А = 1 Кл/с.

Средняя сила тока находится как отношение всего заряда ко всему времени (т.е. по тому же принципу, что и средняя скорость или любая другая средняя величина в физике):

Если же ток равномерно меняется с течением времени от значения I₁ до значения I₂, то можно значение среднего тока можно найти как среднеарифметическое крайних значений:

Плотность тока – сила тока, приходящаяся на единицу поперечного сечения проводника, рассчитывается по формуле:

При прохождении тока по проводнику ток испытывает сопротивление со стороны проводника. Причина сопротивления – взаимодействие зарядов с атомами вещества проводника и между собой. Единица измерения сопротивления 1 Ом. Сопротивление проводника R определяется по формуле:

где: l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника (будьте внимательны и не перепутайте последнюю величину с плотностью вещества), которое характеризует способность материала проводника противодействовать прохождению тока. То есть это такая же характеристика вещества, как и многие другие: удельная теплоемкость, плотность, температура плавления и т.д. Единица измерения удельного сопротивления 1 Ом·м. Удельное сопротивление вещества – табличная величина.

Сопротивление проводника зависит и от его температуры:

где: R₀ – сопротивление проводника при 0°С, t – температура, выраженная в градусах Цельсия, α – температурный коэффициент сопротивления. Он равен относительному изменению сопротивления, при увеличении температуры на 1°С. Для металлов он всегда больше нуля, для электролитов наоборот, всегда меньше нуля.

Диод в цепи постоянного тока

Диод – это нелинейный элемент цепи, сопротивление которого зависит от направления протекания тока. Обозначается диод следующим образом:

Стрелка в схематическом обозначении диода показывает, в каком направлении он пропускает ток. В этом случае его сопротивление равно нулю, и диод можно заменить просто на проводник с нулевым сопротивлением. Если ток течет через диод в противоположном направлении, то диод обладает бесконечно большим сопротивлением, то есть не пропускает ток совсем, и является разрывом в цепи. Тогда участок цепи с диодом можно просто вычеркнуть, так как ток по нему не идет.

Закон Ома. Последовательное и параллельное соединение проводников

К оглавлению…

Немецкий физик Г.Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (то есть проводнику, в котором не действуют сторонние силы) сопротивлением R, пропорциональна напряжению U на концах проводника:

Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.

Проводники в электрических цепях можно соединять двумя способами: последовательно и параллельно. У каждого способа есть свои закономерности.

1. Закономерности последовательного соединения:

Формула для общего сопротивления последовательно соединенных резисторов справедлива для любого числа проводников. Если же в цепь последовательно включено n одинаковых сопротивлений R, то общее сопротивление R₀ находится по формуле:

2. Закономерности параллельного соединения:

Формула для общего сопротивления параллельно соединенных резисторов справедлива для любого числа проводников. Если же в цепь параллельно включено n одинаковых сопротивлений R, то общее сопротивление R₀ находится по формуле:

Электроизмерительные приборы

Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры.

Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам.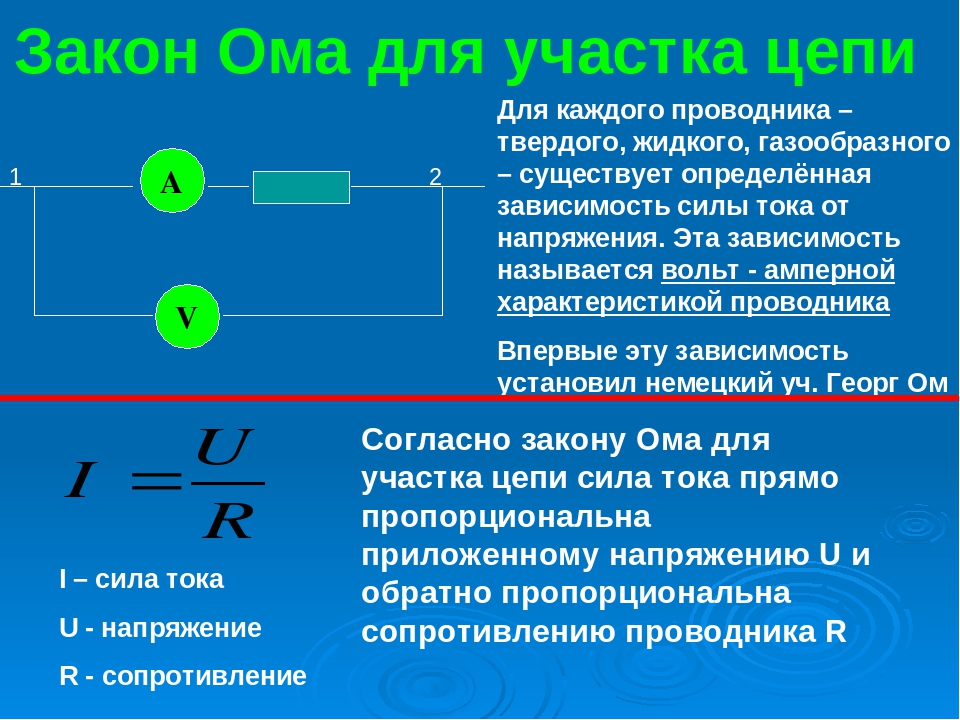 Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением R_B. Для того чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен.

Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением R_A. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи.

ЭДС. Закон Ома для полной цепи

К оглавлению…

Для существования постоянного тока необходимо наличие в электрической замкнутой цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.

Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.

При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу. Физическая величина, равная отношению работы A_ст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):

Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда.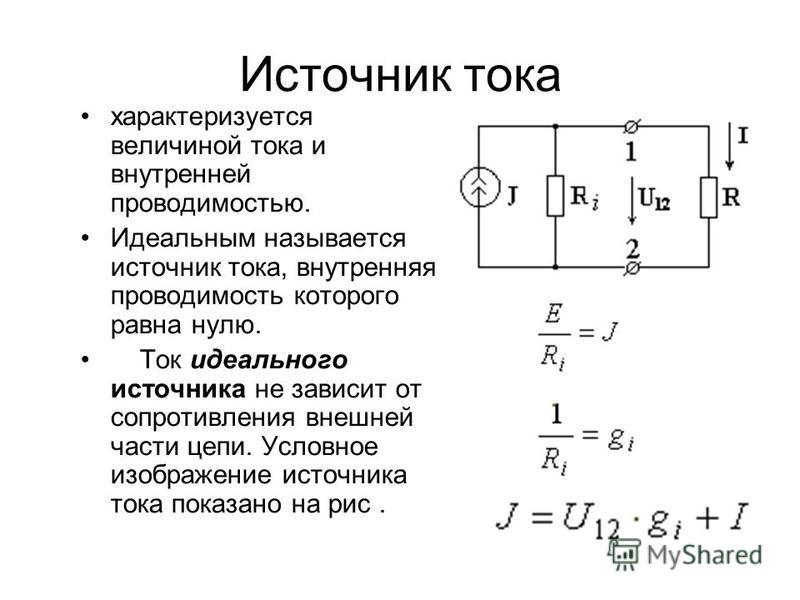 Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).

Закон Ома для полной (замкнутой) цепи: сила тока в замкнутой цепи равна электродвижущей силе источника, деленной на общее (внутреннее + внешнее) сопротивление цепи:

Сопротивление r – внутреннее (собственное) сопротивление источника тока (зависит от внутреннего строения источника). Сопротивление R – сопротивление нагрузки (внешнее сопротивление цепи).

Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):

Важно понять и запомнить: ЭДС и внутреннее сопротивление источника тока не меняются, при подключении разных нагрузок.

Если сопротивление нагрузки равно нулю (источник замыкается сам на себя) или много меньше сопротивления источника, то тогда в цепи потечет ток короткого замыкания:

Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой ε и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик, и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.

Несколько источников ЭДС в цепи

Если в цепи присутствует несколько ЭДС подключенных последовательно, то:

1. При правильном (положительный полюс одного источника присоединяется к отрицательному другого) подключении источников общее ЭДС всех источников и их внутреннее сопротивление может быть найдено по формулам:

Например, такое подключение источников осуществляется в пультах дистанционного управления, фотоаппаратах и других бытовых приборах, работающих от нескольких батареек.

2. При неправильном (источники соединяются одинаковыми полюсами) подключении источников их общее ЭДС и сопротивление рассчитывается по формулам:

В обоих случаях общее сопротивление источников увеличивается.

При параллельном подключении имеет смысл соединять источники только c одинаковой ЭДС, иначе источники будут разряжаться друг на друга. Таким образом суммарное ЭДС будет таким же, как и ЭДС каждого источника, то есть при параллельном соединении мы не получим батарею с большим ЭДС. При этом уменьшается внутреннее сопротивление батареи источников, что позволяет получать большую силу тока и мощность в цепи:

В этом и состоит смысл параллельного соединения источников. В любом случае при решении задач сначала надо найти суммарную ЭДС и полное внутреннее сопротивление получившегося источника, а затем записать закон Ома для полной цепи.

Работа и мощность тока. Закон Джоуля-Ленца

К оглавлению. ..

Работа A электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в теплоту Q, выделяющееся на проводнике. Эту работу можно рассчитать по одной из формул (с учетом закона Ома все они следуют друг из друга):

Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж.Джоулем и Э.Ленцем и носит название закона Джоуля–Ленца. Мощность электрического тока равна отношению работы тока A к интервалу времени Δt, за которое эта работа была совершена, поэтому она может быть рассчитана по следующим формулам:

Работа электрического тока в СИ, как обычно, выражается в джоулях (Дж), мощность – в ваттах (Вт).

Энергобаланс замкнутой цепи

К оглавлению…

Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой ε и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. В этом случае полезная мощность или мощность, выделяемая во внешней цепи:

Максимально возможная полезная мощность источника достигается, если R = r и равна:

Если при подключении к одному и тому же источнику тока разных сопротивлений R₁ и R₂ на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:

Мощность потерь или мощность внутри источника тока:

Полная мощность, развиваемая источником тока:

КПД источника тока:

Электролиз

К оглавлению…

Электролитами принято называть проводящие среды, в которых протекание электрического тока сопровождается переносом вещества. Носителями свободных зарядов в электролитах являются положительно и отрицательно заряженные ионы. К электролитам относятся многие соединения металлов с металлоидами в расплавленном состоянии, а также некоторые твердые вещества. Однако основными представителями электролитов, широко используемыми в технике, являются водные растворы неорганических кислот, солей и оснований.

Прохождение электрического тока через электролит сопровождается выделением вещества на электродах. Это явление получило название электролиза.

Электрический ток в электролитах представляет собой перемещение ионов обоих знаков в противоположных направлениях. Положительные ионы движутся к отрицательному электроду (катоду), отрицательные ионы – к положительному электроду (аноду). Ионы обоих знаков появляются в водных растворах солей, кислот и щелочей в результате расщепления части нейтральных молекул. Это явление называется электролитической диссоциацией.

Закон электролиза был экспериментально установлен английским физиком М.Фарадеем в 1833 году. Закон Фарадея определяет количества первичных продуктов, выделяющихся на электродах при электролизе. Итак, масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:

Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:

где: n – валентность вещества, N_A – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:

Электрический ток в газах и в вакууме

К оглавлению…

Электрический ток в газах

В обычных условиях газы не проводят электрический ток. Это объясняется электрической нейтральностью молекул газов и, следовательно, отсутствием носителей электрических зарядов. Для того чтобы газ стал проводником, от молекул необходимо оторвать один или несколько электронов. Тогда появятся свободные носителя зарядов — электроны и положительные ионы. Этот процесс называется ионизацией газов.

Ионизировать молекулы газа можно внешним воздействием — ионизатором. Ионизаторами может быть: поток света, рентгеновские лучи, поток электронов или α-частиц. Молекулы газа также ионизируются при высокой температуре. Ионизация приводит к возникновению в газах свободных носителей зарядов — электронов, положительных ионов, отрицательных ионов (электрон, объединившийся с нейтральной молекулой).

Если создать в пространстве, занятом ионизированным газом, электрическое поле, то носители электрических зарядов придут в упорядоченное движение – так возникает электрический ток в газах. Если ионизатор перестает действовать, то газ снова становится нейтральным, так как в нем происходит рекомбинация – образование нейтральных атомов ионами и электронами.

Электрический ток в вакууме

Вакуумом называется такая степень разрежения газа, при котором можно пренебречь соударением между его молекулами и считать, что средняя длина свободного пробега превышает линейные размеры сосуда, в котором газ находится.

Электрическим током в вакууме называют проводимость межэлектродного промежутка в состоянии вакуума. Молекул газа при этом столь мало, что процессы их ионизации не могут обеспечить такого числа электронов и ионов, которые необходимы для ионизации. Проводимость межэлектродного промежутка в вакууме может быть обеспечена лишь с помощью заряженных частиц, возникших за счет эмиссионных явлений на электродах.

Напряжение механическое внутреннее — Энциклопедия по машиностроению XXL

Влияние состояния поверхности. В большинстве случаев поверхностные слои элемента конструкции, подверженного действию циклических нагрузок, оказываются более напряженными, чем внутренние (в частности, это имеет место при изгибе и кручении). Кроме того, поверхность детали почти всегда имеет дефекты, связанные с качеством механической обработки, а также с коррозией вследствие воздействия окружающей среды. Поэтому усталостные трещины, как правило, начинаются с поверхности, а плохое качество последней приводит к снижению сопротивления усталости.

[c.671]
Механические напряжения (независимо — внутренние или приложенные извне, лежащие в упругой или упруго-пластической области, растягивающие или сжимающие) могут воздействовать на коррозионное поведение металла вследствие двух факторов сообщения металлу дополнительной энергии и, следовательно, некоторого снижения его термодинамической стабильности нарушения сплошности окисных или пассивных пленок (их защитных свойств). [c.64]

Механический фактор. Под понятием механический фактор подразумевается воздействие па металл механических нагрузок— постоянных или периодических внутренних или внешних напряжений. Механический фактор увеличивает термодинамическую нестабильность металла и может привести к разрушению целостности защитных пленок на его поверхности. [c.27]

Причины нестабильности геометрической формы, размеров и физико-механических свойств металлических деталей. Причинами нестабильности геометрических свойств металлических деталей в основном являются наличие и постепенная релаксация внутренних напряжений и структурная нестабильность. Так, например, непостоянство размеров некоторых деталей машин (специальных осей, подпятников и т. п.), имеющих простую форму и высокую твердость, определяется преимущественно структурным фактором. На стабильность размеров деталей типа корпусов, каркасов, тонкостенных обечаек и т. п., имеющих сложную форму, часто недостаточную жесткость, основное влияние оказывают остаточные внутренние напряжения. Остаточные внутренние напряжения подразделяются (в порядке убывающей значимости) на фазовые или структурные, тепловые (термические), первичные усадочные (в отливках), возникающие в результате механического наклепа и вследствие химического воздействия на поверхность детали. Существенное влияние на стабильность размеров могут оказывать микроскопические напряжения первого рода. Дополнительное влияние на размеры могут оказывать напряжения второго рода, уравновешивающиеся в масштабе отдельных зерен в тех случаях, когда микронапряжения обладают общей ориентировкой (т. е. не погашаются взаимно вследствие противоположной направленности). [c.405]

Механическое воздействие Напряжения от внутреннего давления, соизмеримые с пределом прочности [c.183]

Во время растопки котла в него может длительно не подаваться вода. Если экономайзер не отключен от котла и обогревается дымовыми газами, то вода в нем может полностью испариться, а стенки труб нагреются до температуры омывающих их дымовых газов. При температуре газов до 400—450° С это не представляет непосредственной опасности для стальных и тем более чугунных элементов экономайзеров. Однако подача питательной воды в разогретый экономайзер и резкое его охлаждение крайне опасны, так как при попадании воды в экономайзер она быстро испаряется, поступающая вслед за этим вода конденсирует пар, заполняющий экономайзер, и возможны сильные гидравлические удары неравномерное охлаждение частей экономайзера создает в них большие механические внутренние напряжения и т. п. [c.173]

Методы определения внутренних напряжений.

При механическом методе определения внутренних напряжений первого рода детали разрезают и по деформации после разрезки определяют внутренние напряжения. Механический метод требует уничтожения или порчи исследуемой детали и пригоден лишь для деталей простой формы— прутков, труб с осевой симметрией в распределении напряжений и призматических тел, находящихся в линейном напряженном состоянии. Измерения деформации можно производить различными методами — оптиметром, универсальным измерительным микроскопом, проволочными датчиками, акустическим методом и т. д. [c.78]

Эксплуатационные циклические нагрузки в барабане можно разделить на малоцикловые, возникающие при пусках, остановах, аварийных выводах котла из работы и гидроиспытаниях, и многоцикловые, имеющие место ири длительной работе барабана на номинальных режимах. Механические нагрузки, действующие в зоне кромок отверстий на переходных режимах при аварийных остановах из-за повреждений экранных труб, могут быть значительными. Напряжение при этом составляет 300 МПа. За время эксплуатации барабана может быть до 1500 пусков. Циклические термические напряжения, возникающие при номинальных режимах работы барабана, действуют вместе со статическими растягивающими напряжениями от внутреннего давления, превышающими на кромках отверстий предел текучести. [c.236]

В нашем рассуждении мы предполагали, что деформация образца чисто упругая (как и следует ожидать при малых напряжениях). При больших напряжениях явление внутреннего трения принимает более сложный характер, поскольку нам при этом следует принимать во внимание не только потери механической энергии, являющиеся результатом указанного выше теплообмена, но также и потери, обусловленные пластической деформацией внутри отдельных зерен ). [c.428]

Самым жестким из стандартных статических испытаний гладких (без надрезов) образцов является испытание на растяжение с а=0,5. Для многих пластичных конструкционных материалов та ой жесткости недостаточно для хрупкого разрушения даже при глубоких отрицательных температурах. Однако в реальных условиях эти материалы часто разрушаются хрупко в первую очередь из-за наличия различных концентраторов напряжений — механических надрезов, поверхностных и внутренних трещин, резких переходов от толстого к более тонкому сечению и др. В результате их конструктивная прочность может оказаться значительно ниже, чем определенная методом обычных статических испытаний. Необходима, следовательно, постановка специальных испытаний для оценки чувствительности материала к концентрации напряжений. [c.195]

В местах расположения сварных швов из-за наличия усиления с наружной стороны и механической обработки под стыковку кромок с внутренней стороны имеет место концентрация напряжений. Механические свойства листа, швов и околошовных зон не одинаковы. Поэтому нежелательно располагать отверстия, опоры и другие детали, также вызывающие концентрацию напряжений, рядом со сварными швами. [c.261]

В дальнейшем настает момент, когда влага капилляров перестает достигать поверхности изделия, тогда зона испарения углубляется внутрь сырца. При этом в слоях материала характер напряжений меняется. Внутренние слои более влажные, сокращаясь более интенсивно, начинают испытывать растягивающие усилия, сжимая внешние слои, достигшие уже меньшей влажности и большей прочности. В этот период при возникновении значительных напряжений могут вскрыться дефекты формования в виде разрыва плохо слипшихся слоев (структурные, 5-образные, скобяные и другие трещины, рис. 10). После удаления усадочной влаги напряжения в изделии ослабевают и дальнейший процесс сушки можно резко интенсифицировать. В практике кирпичных заводов известны случаи, когда при очень быстрой сушке сырца в нем оставались настолько значительные напряжения, что при небольшом механическом воздействии он разрушался. При небрежной установке изделий на рамки, последние, углубляясь в тело сырца, вызывают при его усадке так называемые рамочные трещины. [c.57]

Из исследуемых титановых материалов только сплав ВТб способен упрочняться при термической обработке (закалке). Технический титан ВТ1-1 и сплав ВТ5 подвергают термической обработке (отжигу) только для стабилизации свойств и для снятия внутренних напряжений. Механические свойства а-сплавов не изменяются в результате термической обработки [23]. [c.32]

Механическая энергия, рассеянная в микроскопических частицах массы поверхностного слоя, является причиной возникновения упругих колебаний (акустических явлений) и распространения пластических волн напряжений. При распространении в массах трущихся тел упругих и пластических волн напряжений возникает внутреннее трение, вследствие чего рассеянная энергия в микроскопических частицах массы поверхностного слоя с течением времени превращается в тепловую энергию этих частиц. [c.26]

Для увеличения прочности некоторых видов стеклянных изделий применяют закалку стекла созданием в стекле остаточных равномерно распределенных напряжений. Сущность этого процесса состоит в том, что стеклянные изделия, например стекла для автомобилей, нагретые до высшей температуры отжига, подвергают быстрому и равномерному охлаждению. В результате такой обработки в стекле возникают равномерно распределенные напряжения во внутренних слоях — напряжения растяжения, в наружных слоях — напряжения сжатия, которые придают стеклу прочность и термостойкость. Механическая прочность и термостойкость закаленных изделий в 3—5 раз выше, чем у отожженных. [c.484]

Намотанные таким образом сердечники подвергают термической обработке для снятия механических внутренних напряжений, возникших в ленте при намотке. При термической обработке происходит удаление кристаллизационной воды из порошка кремниевой кислоты и последняя переходит в двуокись кремния. [c.73]

НАПРЯЖЕНИЕ МЕХАНИЧЕСКОЕ — мера внутренних сил, возникающих в теле под влиянием внешних воздействий (нагрузок, изменений температуры). [c.234]

НАПРЯЖЕНИЕ МЕХАНИЧЕСКОЕ — мера внутренних сил, возникающих в деформируемом теле нод влиянием внешних воздействий. При изучении Н. м. в любой точке Л/ проводят сечение тела через эту точку (рис.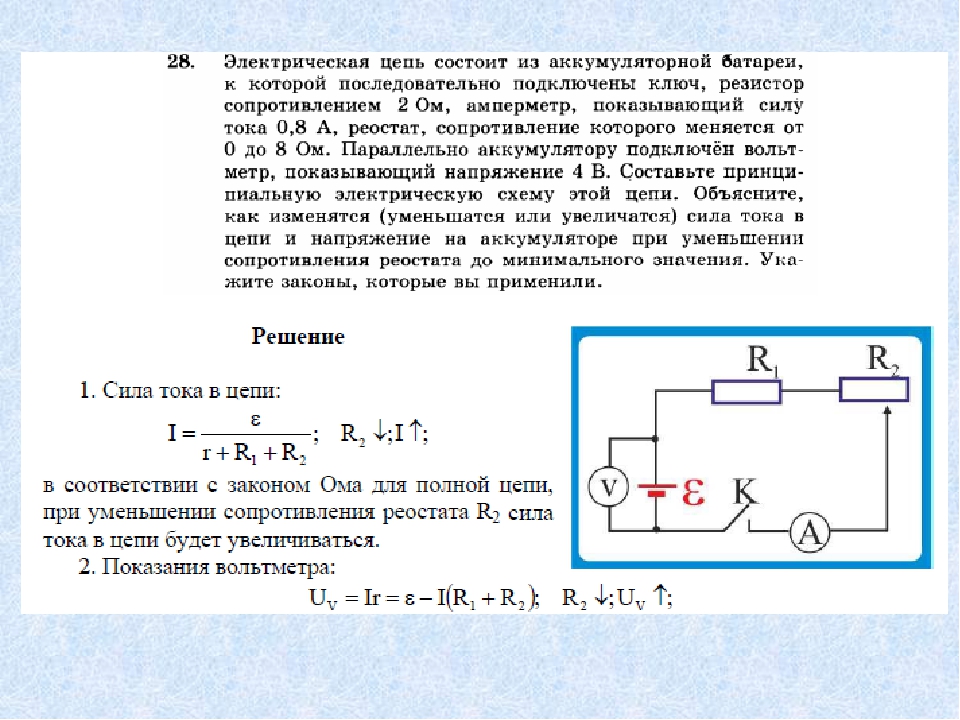 1). Взаимодействие соприкасающихся по сечению частей тела заменяют силами. Если на элементарную площадку dF, окружающую точку Л/, [c.358]

Под действием высокого давления и температуры в металле трубопроводов возникают механические напряжения и происходит его деформация. При расчете напряжений, кроме внутреннего давления протекающей среды, учитывают усилия, обусловливаемые тепловым удлинением трубопровода, иногда и вес металла и протекающей среды. [c.213]

Совместное решение этих трех групп уравнений позволяет определить все реакции связей, т. е. раскрыть статическую неопределимость. Поскольку при установлении реакций связей используются перемещения системы, можно утверждать, что они будут зависимыми от способности к деформированию отдельных частей механической системы. Следовательно, статически неопределимой можно назвать систему, реакции связей которой зависят от деформаций. С примерами таких систем мы уже знакомы. Так, при определении законов распределения напряжений (внутренних сил) по поперечному сечению при растяжении, кручении, чистом изгибе сначала записывали уравнения равновесия (связь напряжений с внутренними силовыми факторами, которые определены через внешние силы), затем — с использованием гипотезы плоских сечений связь между деформациями в различных точках сечения и дополняли полученную систему уравнений физическими законами. [c.508]

Кроме задачи А) рассмотрим еще задачу (В). Пусть внешняя среда Вд не простирается в бесконечность, а имеет внешнюю границу которая также представляет замкнутую поверхность (рис. 2). Пусть на этой поверхности заданы либо а) смещения, либо б) напряжения, либо в) линейная комбинация смещений и напряжений вдоль внутренних границ к=, 2,. .., п) по-прежнему задаются некоторые механически реализуемые условия сопряжения сред. Требуется определить напряженное состояние системы. Эти задачи будут называться соответственно задачами В , В и (В3). [c.79]

Механический фактор. Под механическим фактором понимается воздействие на металл механических усилий в виде постоянных или периодических нагрузок, внешних или внутренних напряжений. Механический фактор увеличивает термодинамическую неравновесность металла, а также может вызвать нарушение сплошности защитных пленок. Все это, естественно, приводит к ускорению коррозионного процесса. [c.70]

Поле напряжений во внутренней зоне определяется так же, как и в 30. Поэтому здесь полностью применимы уравнения (8.07), но они имеют механический смысл лишь при [c.398]

На рис, 10.7 изображено распределение интенсивности механических напряжений по внутренней поверхности втулки в сечении С—С (см. рис. 10.1) для рассматриваемых вариантов расчетной схемы. Характер и значения интенсивности напряжений для всех вариантов очень близки и расхождение не превышает 10 МПа. [c.193]

ЦИйа Протяженностью 120 мм. Паропровод изготовлен из труб диаметром 426X17 мм. Материал — сталь 12Х1МФ. Гиб выполнен в горячем состоянии на ЗиО. Он эксплуатировался при температуре пара 570° С. Трещина начиналась на внутренней поверхности и имела протяженность по этой поверхности около 450 мм. Она была расположена вблизи нейтральной линии гиба около вершины овала с наименьшим радиусом кривизны, т. е. в месте действия наиболее высоких дополнительных растягивающих напряжений на внутренней поверхности от изгиба, возникавшего вследствие того, что под действием внутреннего давления форма сечения гиба стремилась перейти из овальной в круглую. Овальность гиба после обнаружения трещины была в пределах нормы. Рядом со сквозной трещиной имелось много трещин меньших размеров, заполненных окислами. Химический состав и механические свойства трубы и гиба отвечают требованиям ЧМТУ 670-65, по которым была поставлена труба. Структура нерекомендованная — феррит и глобулярные карбиды по границам зерен. Разрушение произошло по границам зерен (рис. 7-8). Гиб разрушился вследствие того, что фактические местные напряжения превышали расчетные, а жаропрочность металла была пониженной. [c.391]

НАПОР [массе жидкости в этом объеме температурный — разность температур двух различных смежных или разделенных стенкой сред, между которыми происходит теплообмен] НАПРЯЖЕНИЕ механическое [служит мерой внутренних сил, возникающих в деформированном теле и определяемой отношением выявленной силы к величине элементарной площадки, выбранной внутри или на поверхности тела в гидроаэростатике определяется как сила, отнесенная к единице площади поверхности, на которую она действует касательное возникает под действием сил, касательных к нормальное возникает под действием сил, нормальных к> поверхности тела трение численно равно силе внутреннего трения в газе, действующей на единицу площади поверхности слоя] электрическое (численно равно суммарной работе, совершаемой кулоновскими и сторонними силами при перемещении по участку цепи единичного положительного заряда анодное прилагается между анодом и катодом электронной лампы или гальванической ванны зажигания обеспечивает переход несамостоятельного газового разряда в самостоятельный переменное, действующее значение которого вычисляют (для периодического напряжения) как среднеквадратичное значение напряжения за период его изменения пробивное вызывает разряд через слой диэлектрика сеточное приложено между сеткой и катодом электронной лампы и служит для запирания лампы при определенном значении его на участке цепи равно произведению его сопротивления на силу тока) НАПРЯЖЕНИЯ механические (контактные возникают на площадках соприкосновения деформируемых тел температурные образуются в теле вследствие различия температур составных его частей и ограничения возможностей теплового расширения со стороны окружающих частей тела или других тел остаточные вызываются крупными дефектами материала, неоднородностью кристаллической структуры и дефектами атомно-кристаллических решеток) [c.253]

Гораздо лучше использовать листы наибольшего размера (массой до 50 т), что позволяет избежать нахлестовых или крестообразных швов. Все листы необходимо контролировать неразрушающими методами, чтобы выявить продольные дефекты и избежать проведения испытаний образцов, вырезаемых из толщи листа. Сварка является наиболее ответственной операцией и выполняется или ручным дуговым способом, или с помощью автоматов с применением соответствующих электродов и основных без-водородистых флюсов. Не рекомендуется делать сразу корневые швы. Например, когда кромки сферической крышки сваривают вручную, может наблюдаться коробление и смещение кромок, в результате чего образуются выступы. В этом случае сварщик вынужден заполнять появившиеся полости серией швов как с одной, так и с другой стороны листа. Поэтому отдельные листы собирают и прихватывают вместе сваркой с использованием специальных прокладок процесс начинают с этих подготовленных участков с наружной стороны, а затем переходят на внутреннюю. Избыточный металл сварного шва позднее удаляют механическим стюсобом. Сложные, на всю толщину корпуса, сварные шйы делают для приварки патрубков, которые изготавливают из отдельных поковок. В настоящее время используют заранее подготовленные секции с вваренными патрубками. В этом случае сварные швы легче подвергнуть термической обработке для снятия внутренних напряжений. Все сварные швы накладывают параллельно кромке, что позволяет обеспечивать достаточное пространство для передвижения электрода. Неразрушающему контролю подвергают все сварные швы (100%) до и посл снятия остаточных напряжений. Вся внутренняя поверхность корпуса реактора PWR и нижние части реактора BWR, которые подвергаются воздействию воды, имеют покрытие из аустенитной стали. Внутренняя поверхность патрубков также имеет аустенитное покрытие, которое выходит на наружную поверхность патрубков, чтобы обеспечить соединение их с трубами из аустенитных сталей. [c.165]

Для того чтобы пойти на снижение общепринятой в настоящее время температуры горячего воздуха при сжигании АШ, нужно иметь подтвержденные длительной эксплуатацией данные о том, что это мероприятие не повлечет за собой ухудшения выжига топлива. Увеличение потери с механическим недожогом хотя бы на полпроцента нельзя окупить уменьшением первоначальных затрат при переходе на одноступенчатую компоновку воздухоподогревателя. Намечается и противоположная тенденция, а именно для интенсификации зажигания и выгорания АШ произвести мобилизацию ряда возможных средств, в первую очередь предварительную подсушку (в разомкнутой схеме) и подогрев топлива и высокий подогрев воздуха. Речь идет о подогреве воздуха до 450—500° С в двух ступенях воздухоподогревателя. Вторая по ходу воздуха ступень в этом случае греет лишь часть воздуха и должна выполняться из недорогих жаростойких сталей, пригодных для работы при температурах 650—700° С, но при низких напряжениях от внутреннего давления. [c.96]

Рас. J.1S9. Фрактограмма поверхности разрушения после 900 ч испытания трубчатого образца Из аустенитной стали ОЗХ17Н15МЗ в воде, содержащей 1 мг/л С1 (с добавкой Fe ls), при 280 С и 10 МПа. Растягивающее напряжение (от внутреннего давления азота) 250 МПа. ТО отжиг при 1050 °С, 15 мин, охлаждение на воздухе. После отжнга — холодная прокатка с обжатием по диаметру 15 %. В верхней части — межкристаллитное КР. начинающееся от внешней поверхности трубки, которая соприкасается с водой. В нижней части г— механическое вязкое разрушение (долом). Сканирующий ЭМ. X 220 [c.328]

Для клепаных барабанов характерны повреждения металла, связанные с щелочной коррозией. Особенности таких повреждений — межкристаллитное расположение начальных трещин, отсутствие деформации металля в зоне образования трещин, сохранение металлом механических свойств даже в непосредственной близости от места разрушения. Такие повреждения являются следствием одновременного воздействия на металл высоких местных механических напряжений (близких или превышающих предел текучести) и щелочно-агрессивной котловой воды. Механические напряжения слагаются из напряжений от внутреннего давления, остаточных напряжений после клепки и развальцовки и дополнительных термических напряжений, которые особенно значительны при резкопеременных условиях работы котла. Воздействие на металл щелочных концентратов щелочно-агрессивной котловой воды становится опасным при Концентрации щелочей, равной 100 г/л. Такие большие концентрации создаются в заклепочных и вальцовочных швах в местах неплотностей вследствие упаривания воды (рис, 8.4). [c.242]

НАПРЯЖЕНИЕ МЕХАНИЧЕСКОЕ— мера внутренних сил, Возникающих в теле под влиянием внещ-нйх воздействий (нагрузок, изменений температуры). - [c.193]

Защитные свойства покрытий определяются поэтому рядом физико-химических свойств (пассивирующая способность грунта, диффузия электролитов, водонабухаемость, паро- и водопроницаемость, адгезия, внутренние напряжения, механические свойства, старение и т. д.). Весь комплекс свойств покрытий может быть изучен путем раздельного определения физико-химических и механических характеристик покрытия. Однако при ускоренных методах испытаний часто достаточно определить лишь защитную способность пленки при воздействии на нее окружающей среды. [c.185]

Установлено, что скорость роста трещин у кромок отверстий с течением времени снижается [52]. Установлено также, что на образование трещин в барабанах отрицательно влияют частые пуски котлов и их остановы, особенно аварийные, связанные с разуплотнением пароводяного тракта и резким снижением давления неудовлетворительная консервация котлов при простоях и стояночная коррозия металла барабанов наличие на поверхности металла местных дополнительных концентраторов напряжений типа рисок, мест подварки, неметаллических включений, непроваров, следов механической обработки частые химические промывки котлов циклические изменения температуры среды, вызывающие переменные напряжения на внутренней поверхности барабана в условиях практически стационарного режима работы когла. Последние составляют 5—20 °С и приводят к дополнительным термическим напряжениям 2—8 кгс/мм при частоте их изменения 1/3—1/50 с. За 100 тыс. ч эксплуатации суммарное число циклов может достигать 5-10 —1-10 . Поскольку [c.112]

Одним из характерных свойств электроосажденных металлов является наличие в них внутренних напряжений. Возникновение внутренних напряжений в процессе электроосаждения оказывает определенное влияние на формирование структуры и определяет некоторые важные физико-механические свойства осадка прочность сцепления с основой, пластичность и др. Под внутренними напряжениями понимают силы, стремящиеся сжать или растянуть осадок металла. При возникновении напряжений сжатия осадок может вспучиваться, отделяясь от основы при напряжениях растяжения, превышающих предел прочности металла, осадок растрескивается и также отслаивается от основы. [c.44]

Величина механических напряжений зависит главным образом от конструкции отливки, а также и от конструкции литейной формы, свойств чугуна и технологии производства. Чем больше в отливке полостей, оформляемых стержнями или болванами, выступов и поднутрений, затрудняющих ее усадку, тем больше напряжения. Механические напряжения. могут возникать и в отливках простой конфигурации, где роль выступающих частей играют литники и выпоры. Напряжги-ность и коробление такой отливки еще более увеличиваются, если литники упираются в крестовины опоки или когда вследствие небрежной заливки сверху образуются натеки металла, удерживающиеся за кромки опоки. В плоскости разъема формы затруднять усадку и создавать механические напряжения способны заливы или разветвленная литниковая система, соединяющая несколько отливок в единый сложный контур, и т. д. Из свойств чугуна на развитие механических напряжений прежде всего влияет его а. Важной особенностью механических напряжений является то, что они не внутренние, поскольку возникают как реакция на действие внешних (по отношению к отливке) сил. При этом первостепенное значение имеет прочность чугуна. Чем она выше, тем легче сокращающаяся отливка преодолевает внешние сопротивления н в ряде случаев вообще их устраняет, сама при этом оставаясь не поврежденной и ие деформированной. Однако [c.661]

Примем термин остаточные напряжения для наименования механических напряжений в литой изоляции. Известна и другая терминология, встречающаяся в литературе и на практике внутренние напряжения , технологические , термоупругие и др. Термин внутренние напряжения малоприемлем, так как все механические напряжения являются внутренними. Термин термоупругие напряжения , или просто температурные напряжения , который используется в механике сплошных сред, является приемлемым, но он имеет более широкий смысл, а именно этим термином называют напряжения, возникающие в твердых телах нри наличии температурных полей — однородных и неоднородных, стационарных и нестационарных. [c.66]

Ответственное назначение и высокие требования к качеству турбинных дисков вызывают необходимость проведения следующих испытаний материала заготовок определение величины внутренних напряжений механических свойств металла отсутствия флокенов, серных и фосфорных включений, внутренних грещин и других дефектов. Все эти испытания проводятся перед окончательной механической обработкой дисков. [c.173]

На практике, однако, минимально допустимый радиус изгиба определяется, исходя из механических свойств волокна, а не потерь на из-1иб. Если волокно изогнуто столь сильно, что поверхностные напряжения превысят 0,2 %, то весьма вероятно, что в процессе эксплуатации в нем возникнут значительные трещины. Чтобы предотвратить это, оптическое волокно помещают в достаточно жесткий кабель. Рассмотрим волокио с радиусом сердцевины а = 30 мкм, диаметром оболочки 2 ) = 125 мкм, которое имеет следующие параметры п 1,5 Ап 0,01 и ЫА 0,17. Пусть это волокно намотано на барабан радиусом Я — Ь) так, что нейтральная ось волокна изогнута по окружности радиуса как это и показано на рис. 3.4. Тогда напряжение сжатия внутренней поверхности волокна и напряжение растяжения его наружной поверхности будут определяться величиной ЬШ. Чтобы эти напряжения не превысили 0,2%, радиус Я должен быть больше >/0,002 = 500 Ь. В данном примере это требование выполняется при > 31 мм. С другой стороны, критический радиус изгиба для рассматриваемого волокна будет равен = а/ 2п-Ап) а/0,03= [c.81]

Напряжение (механика) — Простая английская Википедия, бесплатная энциклопедия

Рис. 1.1 Напряжение в нагруженном деформируемом материальном теле, принимаемое как континуум. Рисунок 1.2 Осевое напряжение в призматическом стержне, нагруженном в осевом направлении. Рис. 1.3 Нормальное напряжение в призматическом (прямолинейном элементе с равномерной площадью поперечного сечения) стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным. Однако можно использовать среднее нормальное напряжение σavg {\ displaystyle \ sigma _ {\ mathrm {avg}} \, \!}.Рисунок 1.4 Напряжение сдвига в призматическом стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным. Тем не менее, среднее напряжение сдвига τavg {\ displaystyle \ tau _ {\ mathrm {avg}} \, \!} Является разумным приближением. ^[1]

Напряжение — это сила, приходящаяся на единицу площади тела, которая вызывает изменение формы. ^[2]

Напряжение — это мера внутренних сил в теле между его частицами. ^[2] Эти внутренние силы являются реакцией на внешние силы, приложенные к телу, которые заставляют его разделяться, сжиматься или скользить.^[2] Внешние силы — это поверхностные или объемные силы. Напряжение — это средняя сила на единицу площади, которую частица тела оказывает на соседнюю частицу через воображаемую поверхность, которая их разделяет.

Формула одноосного нормального напряжения:

σ = FA {\ displaystyle {\ sigma} = {\ frac {F} {A}}}

где σ — напряжение, F — сила, а A — площадь поверхности.

В единицах СИ сила измеряется в ньютонах, а площадь — в квадратных метрах.Это означает, что напряжение составляет ньютоны на квадратный метр или Н / м ². Однако у стресса есть своя собственная единица СИ, называемая паскаль. 1 паскаль (символ Па) равен 1 Н / м ². В британских единицах измерения напряжение измеряется в фунт-силах на квадратный дюйм, что часто сокращается до «psi». Размер напряжения такой же, как и у давления.

В механике сплошных сред нагруженное деформируемое тело ведет себя как сплошная среда. Таким образом, эти внутренние силы непрерывно распределяются в объеме материального тела.(Это означает, что распределение напряжений в теле выражается как кусочно-непрерывная функция пространства и времени.) Силы вызывают деформацию формы тела. Деформация может привести к необратимому изменению формы или разрушению конструкции, если материал недостаточно прочен.

Некоторые модели механики сплошных сред рассматривают силу как нечто, что может изменяться. Другие модели рассматривают деформацию материи и твердых тел, потому что характеристики материи и твердых тел трехмерны.Каждый подход может дать разные результаты. Классические модели механики сплошных сред предполагают среднюю силу и не включают должным образом «геометрические факторы». (Геометрия тела может иметь значение для распределения стресса и накопления энергии во время приложения внешней силы.)

В некоторых ситуациях напряжение внутри объекта можно описать одним числом или одним вектором (числом и направлением). Три таких ситуации простого напряжения : одноосное нормальное напряжение , простое напряжение сдвига и изотропное нормальное напряжение .^[3]

Одноосное нормальное напряжение [изменение | изменить источник]

Напряжение растяжения (или растяжение) — это напряженное состояние, приводящее к расширению; то есть длина материала имеет тенденцию к увеличению в направлении растяжения. Объем материала остается постоянным. Когда к телу прилагаются равные и противоположные силы, то напряжение, создаваемое этой силой, называется растягивающим напряжением.

Следовательно, в одноосном материале длина увеличивается в направлении растягивающего напряжения, а в двух других направлениях уменьшается размер.При одноосном растяжении растягивающее напряжение вызывается растягивающими силами. Напряжение растяжения противоположно напряжению сжатия.

Конструктивные элементы, находящиеся под прямым растяжением, представляют собой канаты, грунтовые анкеры и гвозди, болты и т. Д. Балки, подверженные действию изгибающих моментов, могут включать в себя растягивающее напряжение, а также напряжение сжатия и / или напряжение сдвига.

Растягивающее напряжение может увеличиваться до достижения предела прочности на разрыв , а именно предельного состояния напряжения.

Все реальные объекты занимают трехмерное пространство.Однако, если два измерения очень большие или очень маленькие по сравнению с другими, объект может быть смоделирован как одномерный. Это упрощает математическое моделирование объекта. Одномерные объекты включают кусок проволоки, загруженный на концах и просматриваемый сбоку, и металлический лист, загруженный на лицевую сторону и просматриваемый вблизи и через поперечное сечение.

↑ Уолтер Д. Пилки, Оррин Х. Пилки (1974). Механика твердого тела . п. 292.
↑ ^2.0 ^2,1 ^2,2 Дейнтит, Джон, изд. (2005). Физический словарь (Пятое изд.). Издательство Оксфордского университета. п. 509. ISBN 978-0-19-280628-4 .
↑ Рональд Л. Хьюстон и Гарольд Джозефс (2009), «Практический анализ напряжений в инженерном проектировании». 3-е издание, CRC Press, 634 страницы. ISBN 9781574447132

Амин, Мохаммед (2005). Вычислительная упругость: теория упругости, методы конечных и граничных элементов .Alpha Science Int’l Ltd. стр. 33–66. ISBN 184265201X . CS1 maint: ref = harv (ссылка)
Atanackovic, Teodor M .; Гуран, Ардешир (2000). Теория упругости для ученых и инженеров . Springer. С. 1–46. ISBN 081764072X . CS1 maint: ref = harv (ссылка)
Чедвик, Питер (1999). Механика сплошной среды: краткая теория и проблемы . Дуврские книги по физике (2-е изд.). Dover Publications. С. 90–106. ISBN 0486401804 . CS1 maint: ref = harv (ссылка)
Чакрабарти, Дж. (2006). Теория пластичности (3-е изд.). Баттерворт-Хайнеманн. С. 17–32. ISBN 0750666382 . CS1 maint: ref = harv (ссылка)
Чаттерджи, Рабиндранат (1999). Математическая теория механики сплошной среды . Alpha Science Int’l Ltd. стр. 111–157. ISBN 8173192448 . CS1 maint: ref = harv (ссылка)
Чен, Вай-Фах; Хан, Да-Цзянь (2007). Пластичность для инженеров-строителей .Издательство Дж. Росс. С. 46–71. ISBN 1932159754 . CS1 maint: ref = harv (ссылка)
Fung, Yuan-cheng; Тонг, Пин (2001). Классическая и вычислительная механика твердого тела . Том 1 серии Advanced по техническим наукам. World Scientific. С. 66–96. ISBN 9810241240 . CS1 maint: ref = harv (ссылка)
Хэмрок, Бернард (2005). Основы элементов машин . Макгроу-Хилл. С. 58–59. ISBN 0072976829 . CS1 maint: ref = harv (ссылка)
Хьельмстад, Кейт Д. (2005). Основы строительной механики . Международная серия Prentice-Hall по гражданскому строительству и инженерной механике (2-е изд.). Springer. С. 103–130. ISBN 038723330X . CS1 maint: ref = harv (ссылка)
Иргенс, Фритьов (2008). Механика сплошной среды . Springer. С. 42–81. ISBN 3540742972 . CS1 maint: ref = harv (ссылка)
Джегер, Джон Конрад; Кук, Н.Г.У. и Циммерман Р.В. (2007). Основы механики горных пород (Четвертое изд.). Вили-Блэквелл. С. 9–41. ISBN 0632057599 . CS1 maint: несколько имен: список авторов (ссылка) CS1 maint: ref = harv (ссылка)
Люблинер, Якоб (2008). Теория пластичности (переработанное издание) (PDF). Dover Publications. ISBN 0486462900 . Архивировано из оригинального (PDF) 31 марта 2010 года. Проверено 24 июля 2011. CS1 maint: ref = harv (ссылка)
Мейс, Джордж Э.(1970). Механика сплошной среды . Макгроу-Хилл. С. 44–76. ISBN 0070406634 . CS1 maint: ref = harv (ссылка)
Mase, G. Thomas; Джордж Э. Мейс (1999). Механика сплошной среды для инженеров (Второе изд.). CRC Press. С. 47–102. ISBN 0-8493-1855-6 . CS1 maint: ref = harv (ссылка)
Прагер, Уильям (2004). Введение в механику сплошных сред . Dover Publications. С. 43–61. ISBN 0486438090 . CS1 maint: ref = harv (ссылка)
Смит, Дональд Рэй; Трусделл, Клиффорд (1993). Введение в механику сплошных сред — после Трусделла и Нолла . Springer. ISBN 0792324544 . CS1 maint: ref = harv (ссылка)
Ву, Хан-Чин (2005). Механика сплошной среды и пластичность . CRC Press. С. 45–78. ISBN 1584883634 . CS1 maint: ref = harv (ссылка)

Stress (механика) — Простая английская Википедия, бесплатная энциклопедия

Рисунок 1.1 Напряжение в нагруженном деформируемом материальном теле, принимаемое как сплошная среда. Рисунок 1.2 Осевое напряжение в призматическом стержне, нагруженном в осевом направлении. Рис. 1.3 Нормальное напряжение в призматическом (прямолинейном элементе с равномерной площадью поперечного сечения) стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным. Однако можно использовать среднее нормальное напряжение σavg {\ displaystyle \ sigma _ {\ mathrm {avg}} \, \!}. Рисунок 1.4 Напряжение сдвига в призматическом стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным.Тем не менее, среднее напряжение сдвига τavg {\ displaystyle \ tau _ {\ mathrm {avg}} \, \!} Является разумным приближением. ^[1]

Напряжение — это сила, приходящаяся на единицу площади тела, которая вызывает изменение формы. ^[2]

Напряжение — это мера внутренних сил в теле между его частицами. ^[2] Эти внутренние силы являются реакцией на внешние силы, приложенные к телу, которые заставляют его разделяться, сжиматься или скользить. ^[2] Внешние силы — это поверхностные или объемные силы.Напряжение — это средняя сила на единицу площади, которую частица тела оказывает на соседнюю частицу через воображаемую поверхность, которая их разделяет.

Формула одноосного нормального напряжения:

σ = FA {\ displaystyle {\ sigma} = {\ frac {F} {A}}}

где σ — напряжение, F — сила, а A — площадь поверхности.

В единицах СИ сила измеряется в ньютонах, а площадь — в квадратных метрах. Это означает, что напряжение составляет ньютоны на квадратный метр или Н / м ².Однако у стресса есть своя собственная единица СИ, называемая паскаль. 1 паскаль (символ Па) равен 1 Н / м ². В британских единицах измерения напряжение измеряется в фунт-силах на квадратный дюйм, что часто сокращается до «psi». Размер напряжения такой же, как и у давления.

В механике сплошных сред нагруженное деформируемое тело ведет себя как сплошная среда. Таким образом, эти внутренние силы непрерывно распределяются в объеме материального тела. (Это означает, что распределение напряжений в теле выражается как кусочно-непрерывная функция пространства и времени.) Силы вызывают деформацию формы тела. Деформация может привести к необратимому изменению формы или разрушению конструкции, если материал недостаточно прочен.

Некоторые модели механики сплошных сред рассматривают силу как нечто, что может изменяться. Другие модели рассматривают деформацию материи и твердых тел, потому что характеристики материи и твердых тел трехмерны. Каждый подход может дать разные результаты. Классические модели механики сплошных сред предполагают среднюю силу и не включают должным образом «геометрические факторы».(Геометрия тела может иметь значение для распределения стресса и накопления энергии во время приложения внешней силы.)

Одноосное нормальное напряжение [изменение | изменить источник]

Напряжение растяжения (или растяжение) — это напряженное состояние, приводящее к расширению; то есть длина материала имеет тенденцию к увеличению в направлении растяжения.Объем материала остается постоянным. Когда к телу прилагаются равные и противоположные силы, то напряжение, создаваемое этой силой, называется растягивающим напряжением.

Следовательно, в одноосном материале длина увеличивается в направлении растягивающего напряжения, а в двух других направлениях уменьшается размер. При одноосном растяжении растягивающее напряжение вызывается растягивающими силами. Напряжение растяжения противоположно напряжению сжатия.

Конструктивные элементы, находящиеся на прямом растяжении: канаты, грунтовые анкеры и гвозди, болты и т. Д.Балки, подверженные изгибающим моментам, могут включать в себя напряжение растяжения, а также напряжение сжатия и / или напряжение сдвига.

Все реальные объекты занимают трехмерное пространство. Однако, если два измерения очень большие или очень маленькие по сравнению с другими, объект может быть смоделирован как одномерный. Это упрощает математическое моделирование объекта. Одномерные объекты включают кусок проволоки, загруженный на концах и просматриваемый сбоку, и металлический лист, загруженный на лицевую сторону и просматриваемый вблизи и через поперечное сечение.

↑ Уолтер Д. Пилки, Оррин Х. Пилки (1974). Механика твердого тела . п. 292.
↑ ^2,0 ^2,1 ^2,2 Дейнтит, Джон, изд. (2005). Физический словарь (Пятое изд.). Издательство Оксфордского университета. п. 509. ISBN 978-0-19-280628-4 .
↑ Рональд Л. Хьюстон и Гарольд Джозефс (2009), «Практический анализ напряжений в инженерном проектировании». 3-е издание, CRC Press, 634 страницы.ISBN 9781574447132

Амин, Мохаммед (2005). Вычислительная упругость: теория упругости, методы конечных и граничных элементов . Alpha Science Int’l Ltd. стр. 33–66. ISBN 184265201X . CS1 maint: ref = harv (ссылка)
Atanackovic, Teodor M .; Гуран, Ардешир (2000). Теория упругости для ученых и инженеров . Springer. С. 1–46. ISBN 081764072X . CS1 maint: ref = harv (ссылка)
Чедвик, Питер (1999). Механика сплошной среды: краткая теория и проблемы . Дуврские книги по физике (2-е изд.). Dover Publications. С. 90–106. ISBN 0486401804 . CS1 maint: ref = harv (ссылка)
Чакрабарти, Дж. (2006). Теория пластичности (3-е изд.). Баттерворт-Хайнеманн. С. 17–32. ISBN 0750666382 . CS1 maint: ref = harv (ссылка)
Чаттерджи, Рабиндранат (1999). Математическая теория механики сплошной среды . Alpha Science Int’l Ltd.С. 111–157. ISBN 8173192448 . CS1 maint: ref = harv (ссылка)
Чен, Вай-Фах; Хан, Да-Цзянь (2007). Пластичность для инженеров-строителей . Издательство Дж. Росс. С. 46–71. ISBN 1932159754 . CS1 maint: ref = harv (ссылка)
Fung, Yuan-cheng; Тонг, Пин (2001). Классическая и вычислительная механика твердого тела . Том 1 серии Advanced по техническим наукам. World Scientific. С. 66–96. ISBN 9810241240 . CS1 maint: ref = harv (ссылка)
Хэмрок, Бернард (2005). Основы элементов машин . Макгроу-Хилл. С. 58–59. ISBN 0072976829 . CS1 maint: ref = harv (ссылка)
Хьельмстад, Кейт Д. (2005). Основы строительной механики . Международная серия Prentice-Hall по гражданскому строительству и инженерной механике (2-е изд.). Springer. С. 103–130. ISBN 038723330X . CS1 maint: ref = harv (ссылка)
Иргенс, Фритьов (2008). Механика сплошной среды . Springer. С. 42–81. ISBN 3540742972 . CS1 maint: ref = harv (ссылка)
Джегер, Джон Конрад; Кук, Н. Г. У. и Циммерман, Р. В. (2007). Основы механики горных пород (Четвертое изд.). Вили-Блэквелл. С. 9–41. ISBN 0632057599 . CS1 maint: несколько имен: список авторов (ссылка) CS1 maint: ref = harv (ссылка)
Люблинер, Якоб (2008). Теория пластичности (переработанное издание) (PDF).Dover Publications. ISBN 0486462900 . Архивировано из оригинального (PDF) 31 марта 2010 года. Проверено 24 июля 2011. CS1 maint: ref = harv (ссылка)
Мейс, Джордж Э. (1970). Механика сплошной среды . Макгроу-Хилл. С. 44–76. ISBN 0070406634 . CS1 maint: ref = harv (ссылка)
Mase, G. Thomas; Джордж Э. Мейс (1999). Механика сплошной среды для инженеров (Второе изд.). CRC Press. С. 47–102. ISBN 0-8493-1855-6 . CS1 maint: ref = harv (ссылка)
Прагер, Уильям (2004). Введение в механику сплошных сред . Dover Publications. С. 43–61. ISBN 0486438090 . CS1 maint: ref = harv (ссылка)
Смит, Дональд Рэй; Трусделл, Клиффорд (1993). Введение в механику сплошных сред — после Трусделла и Нолла . Springer. ISBN 0792324544 . CS1 maint: ref = harv (ссылка)
Ву, Хан-Чин (2005). Механика сплошной среды и пластичность .CRC Press. С. 45–78. ISBN 1584883634 . CS1 maint: ref = harv (ссылка)

Напряжение (механика) — Простая английская Википедия, бесплатная энциклопедия

Рис. 1.1 Напряжение в нагруженном деформируемом материальном теле, принимаемое как континуум. Рисунок 1.2 Осевое напряжение в призматическом стержне, нагруженном в осевом направлении. Рис. 1.3 Нормальное напряжение в призматическом (прямолинейном элементе с равномерной площадью поперечного сечения) стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным.Однако можно использовать среднее нормальное напряжение σavg {\ displaystyle \ sigma _ {\ mathrm {avg}} \, \!}. Рисунок 1.4 Напряжение сдвига в призматическом стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным. Тем не менее, среднее напряжение сдвига τavg {\ displaystyle \ tau _ {\ mathrm {avg}} \, \!} Является разумным приближением. ^[1]

Напряжение — это сила, приходящаяся на единицу площади тела, которая вызывает изменение формы. ^[2]

Напряжение — это мера внутренних сил в теле между его частицами.^[2] Эти внутренние силы являются реакцией на внешние силы, приложенные к телу, которые заставляют его разделяться, сжиматься или скользить. ^[2] Внешние силы — это поверхностные или объемные силы. Напряжение — это средняя сила на единицу площади, которую частица тела оказывает на соседнюю частицу через воображаемую поверхность, которая их разделяет.

Формула одноосного нормального напряжения:

σ = FA {\ displaystyle {\ sigma} = {\ frac {F} {A}}}

где σ — напряжение, F — сила, а A — площадь поверхности.

В единицах СИ сила измеряется в ньютонах, а площадь — в квадратных метрах. Это означает, что напряжение составляет ньютоны на квадратный метр или Н / м ². Однако у стресса есть своя собственная единица СИ, называемая паскаль. 1 паскаль (символ Па) равен 1 Н / м ². В британских единицах измерения напряжение измеряется в фунт-силах на квадратный дюйм, что часто сокращается до «psi». Размер напряжения такой же, как и у давления.

В механике сплошных сред нагруженное деформируемое тело ведет себя как сплошная среда.Таким образом, эти внутренние силы непрерывно распределяются в объеме материального тела. (Это означает, что распределение напряжений в теле выражается как кусочно-непрерывная функция пространства и времени.) Силы вызывают деформацию формы тела. Деформация может привести к необратимому изменению формы или разрушению конструкции, если материал недостаточно прочен.

Одноосное нормальное напряжение [изменение | изменить источник]

↑ Уолтер Д. Пилки, Оррин Х. Пилки (1974). Механика твердого тела . п. 292.
↑ ^2.0 ^2,1 ^2,2 Дейнтит, Джон, изд. (2005). Физический словарь (Пятое изд.). Издательство Оксфордского университета. п. 509. ISBN 978-0-19-280628-4 .
↑ Рональд Л. Хьюстон и Гарольд Джозефс (2009), «Практический анализ напряжений в инженерном проектировании». 3-е издание, CRC Press, 634 страницы. ISBN 9781574447132

Амин, Мохаммед (2005). Вычислительная упругость: теория упругости, методы конечных и граничных элементов .Alpha Science Int’l Ltd. стр. 33–66. ISBN 184265201X . CS1 maint: ref = harv (ссылка)
Atanackovic, Teodor M .; Гуран, Ардешир (2000). Теория упругости для ученых и инженеров . Springer. С. 1–46. ISBN 081764072X . CS1 maint: ref = harv (ссылка)
Чедвик, Питер (1999). Механика сплошной среды: краткая теория и проблемы . Дуврские книги по физике (2-е изд.). Dover Publications. С. 90–106. ISBN 0486401804 . CS1 maint: ref = harv (ссылка)
Чакрабарти, Дж. (2006). Теория пластичности (3-е изд.). Баттерворт-Хайнеманн. С. 17–32. ISBN 0750666382 . CS1 maint: ref = harv (ссылка)
Чаттерджи, Рабиндранат (1999). Математическая теория механики сплошной среды . Alpha Science Int’l Ltd. стр. 111–157. ISBN 8173192448 . CS1 maint: ref = harv (ссылка)
Чен, Вай-Фах; Хан, Да-Цзянь (2007). Пластичность для инженеров-строителей .Издательство Дж. Росс. С. 46–71. ISBN 1932159754 . CS1 maint: ref = harv (ссылка)
Fung, Yuan-cheng; Тонг, Пин (2001). Классическая и вычислительная механика твердого тела . Том 1 серии Advanced по техническим наукам. World Scientific. С. 66–96. ISBN 9810241240 . CS1 maint: ref = harv (ссылка)
Хэмрок, Бернард (2005). Основы элементов машин . Макгроу-Хилл. С. 58–59. ISBN 0072976829 . CS1 maint: ref = harv (ссылка)
Хьельмстад, Кейт Д. (2005). Основы строительной механики . Международная серия Prentice-Hall по гражданскому строительству и инженерной механике (2-е изд.). Springer. С. 103–130. ISBN 038723330X . CS1 maint: ref = harv (ссылка)
Иргенс, Фритьов (2008). Механика сплошной среды . Springer. С. 42–81. ISBN 3540742972 . CS1 maint: ref = harv (ссылка)
Джегер, Джон Конрад; Кук, Н.Г.У. и Циммерман Р.В. (2007). Основы механики горных пород (Четвертое изд.). Вили-Блэквелл. С. 9–41. ISBN 0632057599 . CS1 maint: несколько имен: список авторов (ссылка) CS1 maint: ref = harv (ссылка)
Люблинер, Якоб (2008). Теория пластичности (переработанное издание) (PDF). Dover Publications. ISBN 0486462900 . Архивировано из оригинального (PDF) 31 марта 2010 года. Проверено 24 июля 2011. CS1 maint: ref = harv (ссылка)
Мейс, Джордж Э.(1970). Механика сплошной среды . Макгроу-Хилл. С. 44–76. ISBN 0070406634 . CS1 maint: ref = harv (ссылка)
Mase, G. Thomas; Джордж Э. Мейс (1999). Механика сплошной среды для инженеров (Второе изд.). CRC Press. С. 47–102. ISBN 0-8493-1855-6 . CS1 maint: ref = harv (ссылка)
Прагер, Уильям (2004). Введение в механику сплошных сред . Dover Publications. С. 43–61. ISBN 0486438090 . CS1 maint: ref = harv (ссылка)
Смит, Дональд Рэй; Трусделл, Клиффорд (1993). Введение в механику сплошных сред — после Трусделла и Нолла . Springer. ISBN 0792324544 . CS1 maint: ref = harv (ссылка)
Ву, Хан-Чин (2005). Механика сплошной среды и пластичность . CRC Press. С. 45–78. ISBN 1584883634 . CS1 maint: ref = harv (ссылка)

Механика материалов: напряжение »Механика тонких конструкций

Добро пожаловать в Механику материалов.Этот курс основан непосредственно на основах, которые мы изучили в статике, — вычислении статического равновесия различных конструкций при различных нагрузках. В статике мы рассматриваем внешних сил , действующих на твердых тел . В действительности все тела деформируемы , и эти внешние силы создают внутренних напряжений . Ну тогда что за стресс?

Напряжение — это мера внешней силы , действующей на площадь поперечного сечения объекта.Напряжение имеет единицы силы на площадь: Н / м ² (СИ) или фунт / дюйм ² (США). Единицы СИ обычно называют паскалями, сокращенно Па . Поскольку 1 Па является неудобно малым по сравнению с напряжениями, которые испытывает большинство конструкций, мы часто будем сталкиваться с 10 ³ Па = 1 кПа (килопаскаль), 10 ⁶ Па = МПа (мегапаскаль) или 10 ^9. Па = ГПа (гигапаскаль).

Есть два типа стресса, который может испытывать конструкция: 1. Нормальное напряжение и 2. Напряжение сдвига . Когда сила действует перпендикулярно (или «нормально») к поверхности объекта, она вызывает нормальное напряжение. Когда сила действует параллельно поверхности объекта, возникает напряжение сдвига.

Рассмотрим светильник, подвешенный к потолку на веревке. Веревка имеет круглое поперечное сечение, а свет тянет вниз перпендикулярно веревке. Эта сила создает нормальное напряжение внутри каната.

Хорошо, как мы пришли к этому уравнению. За кадром существует множество предположений. На протяжении всего этого курса мы будем предполагать, что все материалы однородны, изотропны и эластичны. Мы также предположим, что объект является «призматическим» — это означает, что поперечные сечения одинаковы по всей его длине (например, огурец является призматическим, а тыквенный орех — нет). Все эти предположения позволяют утверждать, что объект будет деформировать равномерно в каждой точке своего поперечного сечения.Нормальное напряжение в точке поперечного сечения определяется как (с аналогичными уравнениями в направлениях x и y ). :

На каждый небольшой участок поперечного сечения действует одинаковая сила, и сумма всех этих сил должна равняться внутренней равнодействующей силе P . Если мы позволим ΔA перейти к dA, а ΔF перейти к dF, то мы сможем просто проинтегрировать обе части уравнения, и мы придем к нашему соотношению для нормального напряжения.

Это соотношение для нормального напряжения более точно соответствует среднему нормальному напряжению , поскольку мы усреднили внутренние силы по всему поперечному сечению.

Понятие стресса часто бывает трудно понять, потому что его нелегко заметить. Оказывается, размещение прозрачного объекта через кросс-поляризованный свет позволяет непосредственно наблюдать напряжение в материале на основе концепции, называемой фотоупругостью:

Напряжение действительно может существовать в материале при отсутствии приложенной нагрузки. Это называется остаточным напряжением, и его можно использовать как способ упрочнения материалов, например, при изготовлении японского меча катана.И наоборот, нежелательные остаточные напряжения могут стимулировать рост трещин и привести к разрушению, как, например, при обрушении Серебряного моста в Западной Вирджинии в 1967 году. Возможно, самый яркий пример остаточного напряжения связан с быстрым охлаждением расплавленного стекла, известным как « Капля принца Руперта »:

Давайте посмотрим на другой пример. Рассмотрим болт, соединяющий две прямоугольные пластины, и растягивающее усилие, перпендикулярное болту. Из диаграммы свободного тела мы видим, что приложенная извне сила оказывает силу, параллельную круглому поперечному сечению болта.Эта внешняя сила приводит к напряжению сдвига внутри болта.

Теперь формальные определения напряжения сдвига принимают форму, аналогичную описанным выше. Рассмотрим напряжение сдвига, действующее на z -грань элемента:

Напряжение сдвига — это касательное напряжение, действующее по касательной к поперечному сечению, и оно принимает среднее значение:

Важно отметить, что напряжения, которые мы только что описали, составляют средних напряжений .Мы предположили, что вся внешняя сила была равномерно распределена по площади поперечного сечения конструкции — это не всегда так, и мы будем пересматривать это предположение на протяжении всего курса.

Когда вы смотрите на элемент при сдвиге, все кажется немного сложнее. Рассмотрим небольшой кубический элемент внутри конструкции при сдвиге, как показано ниже.

Теперь равновесие требует, чтобы напряжение сдвига, действующее на τ _zy, сопровождалось напряжениями сдвига в других плоскостях.Но давайте рассмотрим равновесие сил в направлении y . Зная, что силу можно записать как напряжение (тау), умноженное на площадь (ΔxΔy), мы можем записать это силовое равновесие как:

Поскольку площади куба по определению одинаковы, это означает, что τ _zy = τ ‘_zy. Подобное силовое равновесие в направлении z приводит к τ _yz = τ ‘_yz. Рассмотрим моментное равновесие относительно оси x . Зная, что мы можем записать силу, как и раньше, и плечо момента будет Δz, этот баланс моментов станет:

Это простое соотношение говорит нам, что τ _zy = τ _yz, и, следовательно, все четыре касательных напряжения имеют равные величины и должны указывать навстречу или от друг друга на противоположных краях элемента.Это соотношение известно как «чистый сдвиг».

1,2 Фактор безопасности

Инженеры используют стресс при проектировании конструкций. Внешняя нагрузка и геометрия конструкции говорят нам, какое напряжение действует в материале, но ничего не говорят нам о самом материале. Каждый материал имеет предельное напряжение — мера того, какое напряжение может выдержать материал перед разрушением. Чтобы правильно спроектировать безопасную конструкцию, нам необходимо убедиться, что приложенное напряжение от внешней нагрузки никогда не превышает предельное напряжение материала. Отчасти сложность этой задачи заключается в том, что мы не всегда точно знаем, какова внешняя нагрузка — она может изменяться непредсказуемо, и конструкции, возможно, придется выдерживать неожиданно высокие нагрузки. Чтобы учесть эту неопределенность, мы включили в нашу конструкцию коэффициент безопасности . Коэффициент безопасности — это просто отношение разрушающей нагрузки или напряжения к допустимой нагрузке или напряжению. Разрушение или предельное значение — это свойство материала , в то время как допустимое значение определяется внешней силой и геометрией конструкции.

Сводка

В этой лекции мы представили понятие стресса. Напряжение — это мера того, что материал ощущает от приложенных извне сил. Это просто отношение внешних сил к площади поперечного сечения материала. Силы, приложенные перпендикулярно поперечному сечению, составляют нормальных напряжений , в то время как силы, приложенные параллельно поперечному сечению, составляют касательных напряжений .Хотя представленные здесь концепции не слишком чужды, большая часть трудностей с этим материалом связана с проблемой правильного расчета статического равновесия . Расчет статического равновесия скажет нам величину и направление приложенных сил, которые мы затем можем использовать для расчета напряжений. Если следующие примеры видео и домашнее задание вызывают у вас трудности, сейчас самое время вернуться и просмотреть некоторые концепции из вашего курса статики.

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта No.1454153. Любые мнения, выводы, выводы или рекомендации, выраженные в этом материале, принадлежат автору (авторам) и не обязательно отражают точку зрения Национального научного фонда.

Контроль постоянного напряжения в стекле

24 мая 2013 г. & bullet; Physics 6, 60

Внутреннее напряжение в стеклянном материале является важным источником прочности. Теория и эксперименты дают новое понимание на молекулярном уровне процесса, посредством которого возникает такой стресс.

Колледж М. Келлера / Оберлина

Никакого снятия стресса. Капли принца Руперта — это стеклянные объекты с высокой прочностью, возникающие в результате «вваренных» внутренних напряжений (которые создают цвета при просмотре между скрещенными поляризаторами). Новая теория, основанная на экспериментах и моделировании, объясняет некоторые аспекты этого так называемого остаточного напряжения на молекулярном уровне. Никакого снятия стресса. Капли принца Руперта — это стеклянные объекты с высокой прочностью, возникающие из-за «запекшихся» внутренних напряжений (которые создают цвета при просмотре между скрещенными поляризаторами).Новая теория, основанная на экспериментах и моделировании, объясняет … Показать больше

M. Keller / Oberlin College

Никакого снятия стресса. Капли принца Руперта — это стеклянные объекты с высокой прочностью, возникающие из-за «запекшихся» внутренних напряжений (которые создают цвета при просмотре между скрещенными поляризаторами). Новая теория, основанная на экспериментах и моделировании, объясняет некоторые аспекты этого так называемого остаточного напряжения на молекулярном уровне. ×
Стекло в таких изделиях, как экраны смартфонов, становится прочнее из-за внутреннего напряжения, которое сохраняется в процессе формирования.В Physical Review Letters исследовательская группа представляет модель этого «остаточного напряжения» в молекулярном масштабе. Они объединили эксперименты, моделирование и теорию для системы микроскопических шариков, имитирующих стекло. Команда обнаружила, что, вопреки некоторым прогнозам, остаточное напряжение может быть постоянным, а не снижаться до нуля со временем, что подтверждает тот факт, что стекла — это не просто высоковязкие жидкости. Кроме того, они точно контролировали величину остаточного напряжения в своем стекле, обеспечивая первую систематическую демонстрацию того, что история напряжений в материале может определять его свойства.
Знаменитым примером остаточного напряжения в стекле является капля принца Руперта (или голландская слеза). При падении расплавленного стекла в холодную воду образуется объект в форме головастика, «голова» которого может выдерживать удары молотка, но все это взрывается, если разрезать тонкий хвост. Когда он впервые попадает в воду, внешняя поверхность быстро охлаждается и затвердевает, предотвращая усадку внутренней части при охлаждении, и возникающее в результате напряжение приводит к высокой прочности головки. Путем проб и ошибок инженеры нашли способы сделать стекло и даже металлические сплавы более прочными, осторожно прикладывая усилия во время изготовления.
Несмотря на свою полезность, мало что известно о микроскопических деталях остаточного напряжения. Одна популярная модель неупорядоченного поведения утверждает, что стекло по сути является очень вязкой жидкостью, поэтому остаточные напряжения должны в конечном итоге «расслабиться» до нуля, когда молекулы движутся в ответ на внутренние силы. Но «эта теоретическая картина неполна», — говорит Томас Фойгтманн из Института физики материалов в космосе Немецкого аэрокосмического центра в Кельне. Он и его коллеги разработали многогранную картину, включающую эксперименты, моделирование и расчеты, сосредоточенные на конкретном случае остаточного напряжения.
В экспериментах использовались пластиковые шарики субмикронного размера, плавающие в жидкости (коллоиде) в качестве заменителя молекул в стакане. Отдельные бусинки по существу попадают в потенциальные ямы или так называемые клетки, определяемые их ближайшими соседями. При низкой концентрации шариков смесь ведет себя как плотная жидкость или гель, но выше определенной плотности шарики могут замерзнуть, оставаясь неупорядоченными, как молекулы в стакане. Изменение концентрации позволило Фойгтманну и его коллегам легко переключаться между жидкоподобным и стеклоподобным состояниями.
Чтобы создать так называемое напряжение сдвига, команда поместила коллоид в стандартный прибор для измерения жидкости с круглым дном и пологим коническим верхом, при этом его острие касалось дна. Пока нижняя пластина оставалась неподвижной, они повернули конус на небольшое расстояние, а затем остановили его. Затем они измерили силу на верхнем конусе, создаваемую напряженным стеклом. В жидком состоянии эта сила исчезла через несколько секунд, так как шарики могли легко перемещаться, чтобы снять напряжение.Однако в стеклоподобном состоянии сила уменьшалась, а затем стабилизировалась до фиксированного значения. Резкий контраст в поведении противоречит представлению о том, что стекла — это просто жидкости с высокой вязкостью.
В различных испытаниях исследователи варьировали скорость вращения конуса («скорость сдвига») и обнаружили, что величина остаточного напряжения уменьшается с увеличением скорости сдвига. Этот результат продемонстрировал, что стекло может существовать в различных состояниях в зависимости от его механической истории. Такие эффекты памяти хорошо известны в отношении тепловой истории — с использованием различных скоростей нагрева и охлаждения — но менее известны в чисто механических ситуациях.
Чтобы лучше понять это поведение, команда выполнила моделирование молекулярной динамики, отслеживающее движение отдельных шариков. На основе моделирования и сложной теории стекла [1] исследователи построили модель, объясняющую, как хранится механическая память. В модели клетки ближайших соседей разрушаются во время сдвига, временно освобождая бусинки для движения к равновесию в ответ на внутренние напряжения. Чем быстрее сдвиг, тем он разрушительнее и, следовательно, тем быстрее могут двигаться высвободившиеся шарики.Но клетки быстро восстанавливаются, удерживая оставшееся напряжение. Величина остаточного напряжения на этом этапе действует как форма памяти, потому что она зависит от скорости сдвига, которую стекло испытывало ранее.
Майк Кейтс из Эдинбургского университета в Великобритании говорит, что понимание остаточных напряжений важно для многих практических применений стекла. «Что оригинально и очень интересно в этой работе, так это то, что они используют чистый экспериментальный протокол», и это, по его словам, позволяет напрямую сравнивать эксперименты, моделирование и расчеты.Его поражает тот факт, что различные конечные состояния могут быть выбраны путем изменения скорости сдвига. По его словам, такой зависимости от скорости не наблюдается в аналогичных материалах, таких как расплавы полимеров.
–Майкл Ширбер
Майкл Ширбер — редактор-корреспондент журнала Physics , базирующийся в Лионе, Франция.
Ссылки
М. Фукс и М. Е. Кейтс, «Теория нелинейной реологии и получение плотных коллоидных суспензий», Phys. Rev. Lett. 89 , 248304 (2002)
Дополнительная информация
Остаточные напряжения в стеклах
М.Ballauff, J. M. Brader, S.U. Egelhaaf, M. Fuchs, J. Horbach, N. Koumakis, M. Krüger, M. Laurati, K. J. Mutch, G. Petekidis, M. Siebenbürger, Th. Voigtmann, J. Zausch
Phys. Rev. Lett. 110 , 215701 (2013)
Опубликовано 24 мая 2013 г.
Тематические области
Наука о мягком веществе
Статьи по теме
Физика конденсированного состояния
Кристаллизация активных частиц
10 мая 2021 г.
Самоходный при правильных условиях Согласно моделированию, частицы коллективно переходят из состояния сосуществования жидкости и газа в состояние, в котором частицы могут кристаллизоваться.Подробнее »
Мягкая материя
Странное шевеление полимеров
4 мая 2021 г.
Согласно результатам новых экспериментов по рассеянию нейтронов, молекулы полимеров в пластмассах движутся способами, которые не улавливаются широко используемыми моделями. Подробнее »
Еще статьи
(PDF) Внутреннее напряжение и его влияние на механическую прочность нанопроволок металлического стекла
дефект, которого невозможно избежать в наномасштабе, даже если
других дефектов отсутствуют. Таким образом, наши результаты предполагают, что
два различных управляющих механизма для деформации MG NW —
: Ниже определенного критического размера dc, скажем, около 10 или 15 нм
поверхность и внутреннее напряжение могут играть более важную роль
.Выше, как полосы сдвига, так и внутренние напряжения
,
вносят вклад в общий механический отклик проволоки MG,
, хотя роль последнего может уменьшаться по мере увеличения размера
. dc определяется поверхностным напряжением материала
через соотношение Юнга – Лапласа.
5. Выводы
Мы подтвердили идею с помощью атомистического моделирования
, что внутреннее напряжение и поверхностное напряжение должны играть ключевую роль, но
разные роли в деформации аморфных нанопроволок
при отсутствии каких-либо явных протяженных структурных дефектов.
Предыдущие работы по механической деформации проволоки MG nano-
были сосредоточены либо на высокотемпературном поведении
[39], либо на процессе внутренних дефектов [40]. Не уделяется внимания внутреннему напряжению
и его систематическим эффектам в зависимости от размеров проволоки
. Как показано здесь, поверхностные и внутренние напряжения играют жизненно важную роль в деформации нанопроволок MG. Основная функция внутреннего остаточного напряжения
— влиять на действующее напряжение и, таким образом, на общее механическое поведение нанопроволок MG
.
Этот эффект становится все более важным, поскольку диаметр проволоки
становится меньше. Переход от механизма
с преобладанием внутренних напряжений к механизму образования полос сдвига составляет
, который определяется поверхностным напряжением и связанным соотношением Лапласа Юнга –
(уравнение 2). Наличие сжимающего остаточного напряжения между
увеличивает прочность, а также стабильность
проволок при растяжении, поэтому проволоки
кажутся более прочными, когда они обладают большей пластичностью.Кроме того,
мы обнаружили, что помимо того, что она является источником внутренних и
поверхностных напряжений, поверхность действует как эффективный дефект при растяжении
. В результате как при растяжении, так и при сжатии аморфный материал
обычно ослабляется, а не упрочняется
, как в кристаллических материалах.
Благодарность
Работа поддержана Китайской национальной программой «Тысячи талантов»
. Мы также хотели бы поблагодарить анонимного рецензента
за предложение, которое побудило нас добавить рис.5c.
Ссылки
[1] M.D. Uchic, D.M. Димидук, Ю. Флорандо, У.Д. Никс,
Размеры образца влияют на прочность и пластичность кристаллов,
Science 305 (2004) 986–989.
[2] Дж. Грир, У. Никс, Наноразмерные золотые столбы, усиленные с помощью дислокационного голодания
, Phys. Ред. B 73 (2006) 245410.
[3] S.M. Han, T. Bozorg-Grayeli, J.R. Groves, W.D. Nix, Size
влияет на прочность и пластичность наностолбиков ванадия,
Scr.Матер. 63 (2010) 1153–1156.
[4] B. Wu, A. Heidelberg, J.J. Боланд, Механические свойства сверхвысокопрочных золотых нанопроволок
, Прим. Матер. 4 (2005) 525–
529.
[5] Р. Доу, Б. Дерби, Универсальный закон масштабирования для прочности металлических микростолбиков и нанопроволок
, Scr. Матер. 61 (2009) 524–
527.
[6] D.M. Норфет, Д. Димидук, С. Polasik, M.D. Uchic,
M.J. Mills, Дислокационные структуры и их связь с прочностью
в деформированных микрокристаллах никеля, Acta Mater.56
(2008) 2988–3001.
[7] A.H.W. Нган, К. Н.Г., Переход от детерминированной к стохастической деформации
, Филос. Mag. 90 (2010) 1937–1954.
[8] A.A. Бенцерга, Анализ твердения при истощении при пластичности
микрон, Междунар. J. Plast. 24 (2008) 1128–1157.
[9] Х. Тан, К. Шварц, Х. Эспиноза, Отключение источника дислокаций
и пластическое поведение монокристаллического микропила
лар, Phys. Rev. Lett.100 (2008) 185503.
[10] Z.W. Шан, Р. Mishra, S.A. Syed, S.A. Syed Asif, O.L.
Уоррен А.М. Незначительный, Механический отжиг и источник —
Ограниченная деформация в кристаллах Ni субмикрометрового диаметра,
Нат. Матер. 7 (2008) 115–119.
[11] К. Чизхолм, Х. Бей, М.Б. Лоури, Дж. О, S.A.S. Асиф, О.
Уоррен, З.У. Шан, Э. Джордж, А. Незначительное, дислокационное
упрочнение голоданием и истощением в нановолокнах сплава Мо,
Acta Mater.60 (2012) 2258–2264.
[12] C.J. Lee, J.C. Huang, T.G. Nieh, Влияние размера образца и микропрессование Mg
65
Cu
25
Gd
10
металлическое стекло, Прил.
Phys. Lett. 91 (2007) 161913.
[13] Y.H. Лай, К.Дж.Ли, Ю.Т. Ченг, Х.С. Чжоу, Х. Чен, X.H.
Du, C.I. Чанг, Дж.К. Хуанг, С.Р. Цзянь, J.S.C. Янг, Т.
Nieh, Объемное и микромасштабное сжатие металлического стекла на основе Zr-
, Scr.Матер. 58 (2008) 890–893.
[14] Д. Джанг, Дж. Р. Грир, Переход от сильного, но хрупкого состояния к более прочному и пластичному состоянию
путем уменьшения размера металлических стекол,
Nat. Матер. 9 (2010) 215–219.
[15] Д. Джанг, С.Т. Гросс, Дж. Р. Грир, Влияние размера на прочность
и механизм деформации металлических стекол на основе Zr, Int.
J. Plast. 27 (2011) 858–867.
[16] C.A. Volkert, A. Donohue, F. Spaepen, Влияние размера образца
на деформацию в аморфных металлах, J.Прил. Phys. 103
(2008) 083539.
[17] К.С. Накаяма, Ю. Йокояма, Т. Оно, М. В. Чен, К.
Акияма, Т. Сакураи, А. Иноуэ, Контролируемое формирование и
механических характеристик металлических стеклянных нанопроволок,
Adv. Матер. 22 (2010) 872–875.
[18] B.E. Шустер, К. Вэй, Т. Hufnagel, K.T. Рамеш, Размер-
независимая прочность и режим деформации при сжатии
металлического стекла на основе Pd, Acta Mater. 56 (2008) 5091–
5100.
[19] C.Q. Чен, Ю. Пей, J.T.M. Де Хоссон, Влияние размера на механический отклик
металлических стекол, исследованное с помощью экспериментов по изгибу и сжатию с помощью ПЭМ
, Acta
Mater. 58 (2010) 189–200.
[20] Янг Й., Й. К. Е, Дж. Лу, Ф. Х. Лю, П. Лиав, Влияние геометрии образца
и основного материала на механическое поведение
изготовленных сфокусированным ионным пучком металлических стеклянных микростолбиков
, Acta Mater.57 (2009) 1613–1623.
[21] D.Z. Чен, Д. Джанг, К.М. Гуан, К. Ан, В. А. Годдард, Дж. Р.
Грир, Нанометаллические стекла: уменьшение размера приводит к пластичности,
Состояние поверхности
определяет ее протяженность, Nano Lett. 13 (2013) 4462–
4468.
[22] D.J. Магагноск, Р. Эрбар, Г. Кумар, М.Р. Хе, Дж.
Шроерс, Д.С. Джанола, Настраиваемая пластичность при растяжении металлических стекол
, Sci. Отчет 3 (2013) 16–18.
[23] Д. Сюй, Б. Лохвонгватана, Г. Дуань, В.L. Johnson, C.
Гарланд, Формирование объемного металлического стекла в бинарных сплавах с высоким содержанием меди
— Cu
100x
Zr
x
(x = 34, 36, 38,2, 40 ат. %) и
механических свойств в массе Cu
64
Zr
36
стекло, Acta Mater. 52
(2004) 2621–2624.
[24] O.J. Квон, Ю. Ким, К. Ким, Ю. Ли, Э. Флери,
Образование аморфной фазы в системе двойного сплава CurZr
, Met.Матер. Int. 12 (2006) 207–212.
[25] Y. Li, Q. Guo, J.A. Kalb, C.V. Thompson, Matching glass-
формирующая способность с плотностью аморфной фазы,
Science 322 (2008) 1816–1819.
[26] Q.-K. Ли, М. Ли, Определение характеристик полос сдвига
в аморфном металле в атомном масштабе, Appl. Phys. Lett. 88 (2006) 241903.
[27] Q.-K. Ли, М. Ли, Эволюция свободного объема в металлических стеклах
, подвергнутых механической деформации, Матер.Пер. 48 (2007)
1816–1821.
Q. Zhang et al. / Acta Materialia 91 (2015) 174–182 181
Инженерное напряжение: определение и уравнение — видео и стенограмма урока
Типы напряжений
Существует шесть основных типов напряжений, вызывающих отказы. Каждое из этих различных стрессов вызвано уникальной ситуацией, и именно способ нагрузки объекта определяет, какой тип стресса испытывает объект.Силы могут быть приложены к объекту двумя основными способами: в осевом или продольном направлении. Когда объект нагружен в осевом направлении, силы прилагаются вдоль главной оси объекта. В продольно нагруженных конструкциях силы прикладываются таким образом, что они перпендикулярны главной оси.
Шесть основных типов напряжения:
Сжатие
Напряжение
Ножницы
Гибка
Торсион
Усталость
Рассмотрим каждый тип подробнее.
Напряжение сжатия и растяжения
Напряжение сжатия является результатом аксиально нагруженных сил, направленных к центру объекта. Есть две основные проблемы, связанные с напряжением сжатия: силы сжатия могут привести к сокращению объекта или к деформации объекта. Когда объект изгибается, он изгибается таким образом, что больше не может удерживать нагрузку, хотя, говоря структурно, объект может выдерживать большее напряжение, чем прикладывается к нему.
Напряжение растяжения возникает, когда аксиально нагруженные силы оттягиваются от центра объекта и перпендикулярны его поверхности.Напряжение растяжения может вызвать удлинение объекта. Есть несколько материалов, например бетон, в которых объект может выдержать лишь небольшую часть нагрузки, когда объект находится в состоянии сжатия.
Напряжение сдвига и изгиба
Напряжение сдвига возникает, когда силы, приложенные к объекту, параллельны его поперечному сечению. Это напряжение может привести к деформации объекта и, в некоторых случаях, к разрыву. По мере того как объект деформируется, он изменяется. Форма объекта может измениться, что может повлиять на то, как объект выдерживает другие силы.
Напряжение изгиба наблюдается в продольно нагруженных объектах. Силы заставляют объект изгибаться, обычно в направлении вниз. Чем дальше от неподвижных опор объекта, тем больше напряжение изгиба, как показано на схеме:
Поскольку напряжение изгиба вызывается изгибом объекта, а не перпендикулярно поверхности объекта, для вычисления напряжения используется другое уравнение.Уравнение для напряжения изгиба:
Нейтральная ось — это ось, на которую не действуют силы и напряжения. Нейтральная ось — это середина площади поперечного сечения для симметричных форм, но для несимметричных форм она отличается.
Момент инерции — это сопротивление объекта изгибу. Это константа, которая зависит от формы объекта.
Напряжение скручивания и усталости
Напряжение скручивания вызывается скручиванием объекта, и используемая сила называется крутящим моментом.Наибольшее скручивание, прикладываемое к объекту, приходится на внешний край объекта. Вот рисунок, показывающий напряжение кручения:
Поскольку напряжение скручивания вызывается скручиванием, а не нормальными силами, оно имеет другое уравнение:
Усталостное напряжение не является уникальным напряжением и не вызвано какой-либо одной ситуацией, как любые другие напряжения, о которых говорилось ранее в этом уроке, а вызвано всеми различными типами стресса.Усталостное напряжение — это результат приложения к объекту различных нагрузок в любой комбинации. Объекты, которые страдают от усталостного напряжения, могут фактически выйти из строя при более низком напряжении, чем объект обычно может выдержать, из-за ослабления материала, вызванного различными напряжениями.

Напряжения внутренние — Справочник химика 21

Напряжения — Глоссарий технических терминов

Внутреннее сопротивление источника

Внутреннее сопротивление источника-2

Урок 31. закон ома для полной цепи — Физика — 10 класс

Электрический ток — Физика — Теория, тесты, формулы и задачи

Оглавление:

Основные теоретические сведения

Электрический ток. Сила тока. Сопротивление

Диод в цепи постоянного тока

Закон Ома. Последовательное и параллельное соединение проводников

Электроизмерительные приборы

ЭДС. Закон Ома для полной цепи

Несколько источников ЭДС в цепи

Работа и мощность тока. Закон Джоуля-Ленца

Энергобаланс замкнутой цепи

Электролиз

Электрический ток в газах и в вакууме

Электрический ток в газах

Электрический ток в вакууме

Напряжение механическое внутреннее — Энциклопедия по машиностроению XXL

Напряжение (механика) — Простая английская Википедия, бесплатная энциклопедия

Одноосное нормальное напряжение [изменение | изменить источник]

Stress (механика) — Простая английская Википедия, бесплатная энциклопедия

Одноосное нормальное напряжение [изменение | изменить источник]

Напряжение (механика) — Простая английская Википедия, бесплатная энциклопедия

Одноосное нормальное напряжение [изменение | изменить источник]

Механика материалов: напряжение »Механика тонких конструкций

Контроль постоянного напряжения в стекле

Ссылки

Дополнительная информация

Остаточные напряжения в стеклах

Тематические области

Статьи по теме

Кристаллизация активных частиц

Странное шевеление полимеров

(PDF) Внутреннее напряжение и его влияние на механическую прочность нанопроволок металлического стекла

Инженерное напряжение: определение и уравнение — видео и стенограмма урока

Типы напряжений

Напряжение сжатия и растяжения

Напряжение сдвига и изгиба

Напряжение скручивания и усталости

Добавить комментарий Отменить ответ