Как диски влияют на разгон и расход топлива
На каждом форуме, посвященном автомобильной тематике, можно найти темы, связанные с экономией топлива. Этот вопрос всегда будет в ТОПе. Несмотря на все рекламные кампании, водителям приходится искать альтернативные пути решения этой задачи. Возможно, если Вы садитесь за руль раз в неделю, то эта тема Вас не волнует. Но для водителей, которые постоянно за рулем, будет интересно узнать, как можно сэкономить. Сегодня чаще интересуются, как диски влияют на разгон и расход топлива? Скептики могут сказать, что никак, но практики постараются доказать обратное.
Влияние веса дисков
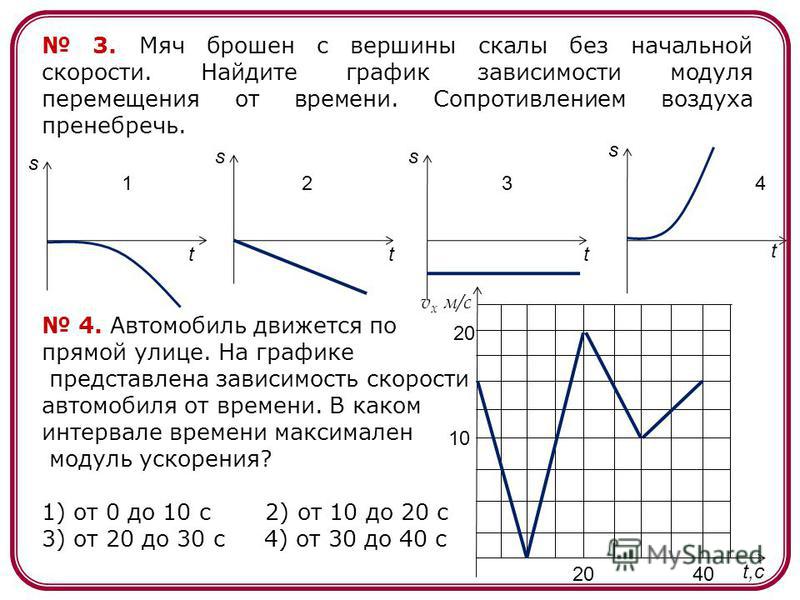
Неоднократно в сети встречались статьи, что тяжелый автомобиль будет расходовать больше топлива, чем аналогичная модель, но с меньшим весом. Водители стараются убрать с автомобиля все лишнее. Некоторые регулярно проводят чистку, чтобы в салоне или багажнике не оставалось ненужных вещей. Практичные задумываются над сменой стальных дисков на литые.
Специалистами был проведен анализ, для которого взяли два авто с разным весом. Результат: каждые 500 кг увеличивают потребление топлива приблизительно на 700 л в год.
Увеличивая размер диска, Вы автоматически увеличиваете размеры покрышек, а значит, вес авто возрастает, что приводит к большему расходу топлива. Лучше устанавливать рекомендуемые производителем диски и шины.
Ширина дисков и покрышек
Гонясь за модными тенденциями, водители пренебрегают советами производителей, устанавливая широкие диски и шины. В качестве маленького эксперимента можно самостоятельно замерить расход. Первое, что будет тормозить – сопротивление воздуху. То есть автомобилю нужно будет больше «энергии», чтобы проехать определенное расстояние. Проведенные наблюдения подтвердили, что автомобили одной марки с разными дисками и покрышками расходуют различное количество литров топлива.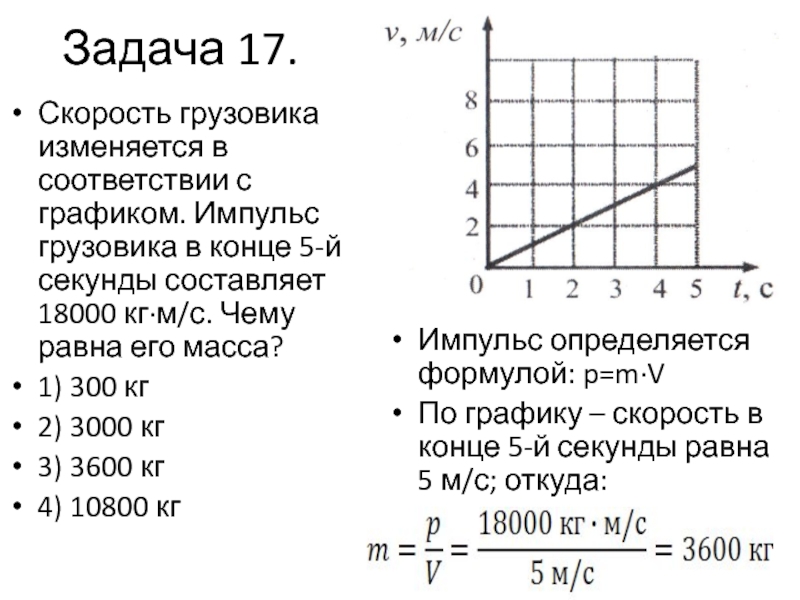
Если установить широкие колеса (в допустимых пределах от заводской комплектации), то разница составит около 0,5 л на 100 км. Для тех водителей, которые всегда за рулем, такая разница может стать ощутимой.
Диаметр диска и разгон авто
Было бы неправильно говорить только о разгоне автомобиля, обязательно нужно обращать внимание и на скорость торможения. В целом можно сделать обобщающий вывод, что на динамику авто влияет диаметр выбранных дисков. Как уже было сказано, увеличиваем диаметр – «растет» масса – снижается управляемость. Учтите, что, меняя колеса даже на 1 размер, можно получить внушительную разницу при разгоне. Шины (резина) по своей плотности будут легче металла, влияет только вес диска? Нет. Дело в том, что многие забывают об инерции, которая будет расти быстрее массы (имеется в виду процентное соотношение меньшего и большего размера). Наибольший вес дискам дает обод. Если взять две одинаковые покрышки и диски меньшего и большего диаметра, то момент инерции меньше будет у колес с меньшим диаметром дисков.
Вывод
Можно выбрать диски меньшего диаметра и подобрать к ним более высокую резину, сохранив внешний диаметр по шине. Автомобиль будет лучше ехать. Почему? У меньшего диаметра диска меньше плечо приложения сил. Считается, что при отличном сцеплении с асфальтированным покрытием и небольшом диаметре колес будет быстрее разгон. Но, к сожалению, не всегда идеальное покрытие, и стопроцентное сцепление невозможно априори. Вся излишне подаваемая мощь уходит в буксировку, разгон на самом деле ограничивается сцеплением.
- проблема в мощности авто — установите немного меньше диски, и сделать передачи более короткими;
- проблема в сцеплении с дорожным покрытием – можно попробовать широкую резину и диски чуть большего размера (в допустимых производителем диапазонах), сделав «длиннее» передачу.
В целом, старайтесь покупать диски, чтобы общий диаметр колес был как можно меньше. Ищите оптимальную середину по качеству, диаметру, весу и дизайну – избегайте крайности.
Выжать максималку можно с большими колесами, быстрее разогнаться и сэкономить на топливе позволят легкие колеса. Если снизить вес каждого колеса на килограмм, то это будет эквивалентно снижению веса в самом салоне авто на 40 кг. Ваш автомобиль поедет плавно и не потеряет своих разгонных характеристик.
Никогда не забывайте о качестве. От фирмы производителя многое зависит. Там и технологии, и «состав», и соблюдение технических параметров, все может отличаться. Идеально – оригинал или рекомендованная производителем реплика.
Там и технологии, и «состав», и соблюдение технических параметров, все может отличаться. Идеально – оригинал или рекомендованная производителем реплика.
Как видно из всего выше описанного, выбор дисков имеет весомое значение для разгона, а вернее, для динамики авто. На длительных дистанциях легкие диски позволят почувствовать экономию на топливе. При этом категорически нельзя выбирать крайности: одинаково плохо слишком большой диаметр колес, и слишком маленький. Безусловно, много зависит от марки авто и производителя дисков и шин, доверяйте проверенным брендам, и тогда не придется платить лишнего.
ГОСТ 22576-90 Автотранспортные средства. Скоростные свойства. Методы испытаний / 22576 90
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
АВТОТРАНСПОРТНЫЕ СРЕДСТВА.
СКОРОСТНЫЕ СВОЙСТВА
МЕТОДЫ ИСПЫТАНИЙ
ГОСТ 22576-90
(СТ СЭВ 6893-89)
ГОСУДАРСТВЕННЫЙ
КОМИТЕТ СССР ПО УПРАВЛЕНИЮ
КАЧЕСТВОМ ПРОДУКЦИИ И СТАНДАРТАМ
Москва
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
|
АВТОТРАНСПОРТНЫЕ СРЕДСТВА. СКОРОСТНЫЕ СВОЙСТВА Методы испытаний Motor vehicles. Speed characteristics. |
ГОСТ (CT СЭВ 6893-89) |
Дата введения 01.01.92
Настоящий стандарт распространяется на автотранспортные средства (АТС) всех типов, кроме внедорожных.
Требования настоящего стандарта являются обязательными, за исключением требований п. 2.5.1.1 и п. 4.3 в части определения поправочного коэффициента.
Устанавливаются следующие показатели и характеристики скоростных свойств АТС:
1.1 — максимальная скорость;
1.2 — время разгона на заданном пути;
1.3 — время разгона до заданной скорости;
1.4 - скоростная характеристика «Разгон-выбег»;
1.5 -
скоростная характеристика «Разгон на передаче, обеспечивающей максимальную
скорость».
Применяемость показателей и характеристик по видам испытаний и типам АТС определяется соответствующими программами.
Пояснения применяемых в настоящем стандарте терминов приведены в приложении 1.
2.1. Требования к объекту испытаний
2.1.1. АТС, предназначенное для испытаний, должно быть исправным, укомплектованным, заправленным ГСМ в соответствии с нормативно-технической документацией. Двигатель, трансмиссия и шины должны пройти надлежащую обкатку в соответствии с инструкцией предприятия-изготовителя и иметь пробег, включая обкатку, не менее 3000 км.
2.1.2. Износ шин на АТС не должен превышать 50 %.
Шины не должны иметь повреждений. Давление в шинах должно отвечать требованиям предприятия-изготовителя.
Давление измеряют и регулируют на «холодных» шинах. В процессе испытаний АТС регулирование давления не допускается.
2.1.3. Окна и вентиляционные люки при проведении
испытаний должны быть закрыты, мягкий откидной верх или тент должен находиться
в рабочем положении.
Агрегаты и механизмы (дополнительный ведущий мост, коробка отбора мощности и др.), не применяемые во время движения по дороге с усовершенствованным покрытием, должны быть выключены; при наличии демультипликатора должна быть включена его повышающая передача.
2.1.4. Устройство для подогрева воздуха системы питания, не имеющее автоматического управления, должно быть установлено в положении «Лето». Системы отопления салона (кабины) и кондиционирования воздуха должны быть выключены. Допускается использование этих систем при сравнительных испытаниях зимой.
2.1.5. Допускается определение показателей скоростных свойств на стенде с беговыми барабанами, обеспечивающем воспроизведение сопротивлений движению АТС на дороге.
2.2. Масса груза
2.2.1. При испытаниях должна применяться:
полная масса груза — для АТС полной массой свыше 3,5 т;
половина массы груза, но не менее 180 кг — для АТС
полной массой до 3,5 т включительно.
2.2.2. В качестве груза применяют негигроскопичные балласт или натуральные грузы для грузовых автомобилей и манекены или балласт (мешки с сыпучим наполнителем) для легковых автомобилей и автобусов.
Допускается применять в качестве балласта гигроскопичные грузы при условии их надежной защиты от атмосферных воздействий.
Балласт (манекены) должен быть надежно закреплен. Массу водителя и контролера, а также массу оборудования и креплений включают в массу груза.
Распределение массы по осям (колесам) должно соответствовать требованиям технической документации.
2.3. Измерительные участки
2.3.1. Измерения проводят на твердом гладком чистом и сухом участке дороги с хорошим сцеплением.
2.3.2. Показатель 1.1 можно измерять на прямом участке дороги или и на горизонтальной кольцевой дороге. Показатели 1.2 — 1.5 измеряют на прямом участке дороги.
2.3.3. Характеристика прямого участка дороги должна быть следующей:
продольный уклон — не более 0,5 % на участке длиной не более 50 м;
поперечный уклон — не более 3 %;
длина измерительного участка не должна быть менее 1000
м для определения показателей 1. 1 и 1.2 и менее 2000 м для
определения показателя 1.3 и характеристик 1.4 и 1.5.
Подъездные дорожные участки должны иметь аналогичное покрытие и длину, достаточную для разгона и стабилизации максимальной скорости АТС.
Прямым участком дороги считают участок кольцевой дороги, если центробежная сила не превышает 20 % первоначальной массы автомобиля и компенсируется поперечным уклоном пути.
2.3.4. Характеристика кольцевой дороги должна быть следующей:
кольцевая дорога должна быть расположена в горизонтальной плоскости и иметь вид выпуклой кривой, включающей криволинейные участки с радиусом кривизны не менее 200 м;
длина измерительного участка пути не должна быть менее 2000 м;
действие центробежной силы должно компенсироваться поперечным профилем поворотов так, чтобы движение АТС на повороте осуществлялось без воздействия на рулевое колесо.
2.4. Средства измерений
2.4.1. Средства измерений должны быть компактными,
простыми в установке и пользовании, вибростойкими и обеспечивать необходимую
точность измерений при температуре воздуха ±40 °С на всех режимах движения АТС, включая максимальную скорость;
установка их на АТС не должна влиять на сопротивление движению.
Средства измерений должны быть компактными,
простыми в установке и пользовании, вибростойкими и обеспечивать необходимую
точность измерений при температуре воздуха ±40 °С на всех режимах движения АТС, включая максимальную скорость;
установка их на АТС не должна влиять на сопротивление движению.
2.4.2. Погрешность средств измерений не должна превышать значений, приведенных в табл. 1.
2.5. Атмосферные условия
2.5.1. При дорожных испытаниях АТС должны соблюдаться следующие требования. Средняя скорость ветра, измеренная на высоте 1 м над поверхностью дороги, не более 3 м/с (при порывах до 5 м/с). Плотность воздуха не должна отличаться более чем на 7,5 % от плотности воздуха, определенной при нормальных атмосферных условиях (атмосферное давление Р0 = 1000 гПа (750 мм рт. ст.). Температура воздуха Т0 = 293 К (20 °С). Плотность воздуха при испытаниях (d1), кг/м3, вычисляют по формуле
(1)
Таблица 1
|
Наименование |
Погрешность, не более |
|
Время |
0,1 с |
|
Путь |
0,5 % |
|
Скорость АТС |
1 % |
|
Скорость ветра |
0,5 м/с |
|
Частота вращения вала двигателя |
1 % |
|
Температура воздуха |
1 °С |
|
Атмосферное давление |
3,0 гПа |
|
Относительная влажность воздуха |
7 % |
|
Масса АТС |
0,3 % |
где d0 - плотность воздуха при нормальных атмосферных условиях, равная 1,189 кг/м3;
H1 — атмосферное давление при проведении испытаний, гПа;
T1 — температура при
проведении испытаний, К.
При этом d1 не должна отличаться более чем на 7,5 % от d0.
Температура воздуха не должна быть ниже 276 К (3 °С), атмосферное давление ниже 910 гПа и относительная влажность воздуха выше 95 %.
2.5.1.1. Допускается проведение испытаний АТС (кроме межведомственных, приемочных и предварительных) при температурах ниже 3 °С с последующей корректировкой результатов согласно рекомендуемому приложению 2.
2.5.1.2. Включение в нормативно-техническую документацию показателя 1.4, полученного при корректировке результатов испытаний при температуре ниже 3 °С (приложение 2), не допускается.
3.1. Общие положения
3.1.1. Перед испытаниями тепловой режим агрегатов и
узлов АТС доводят до нормального установившегося состояния пробегом не менее 50
км при скорости движения не ниже 2/3 максимальной. При вынужденных простоях АТС
в процессе испытаний и снижении температуры агрегатов и узлов необходимо
восстановить их тепловое состояние дополнительным пробегом.
3.1.2. Перед испытаниями должно быть проверено отсутствие повышенных сопротивлений движению измерением пути выбега со скорости 50 км/ч. Результаты оценивают положительно, если приведенный согласно приложению 2 путь выбега не менее заданного в НТД.
3.2. Определение максимальной скорости (показатель 1.1)
3.2.1. Определение максимальной скорости на прямом участке дороги при движении в двух направлениях
Максимальную скорость определяют на передаче, обеспечивающей достижение наибольшей устойчивой скорости движения, которая устанавливается до въезда на измерительный участок.
Педаль управления подачи топлива должна быть нажата до
упора. Число измерений (заездов) — не менее трех в каждом направлении.
Изменение скорости в заезде не должно превышать 2 %. В каждом заезде должно
определяться время прохождения измерительного участка. Разница между крайними
значениями шести измерений не должна превышать 3 %.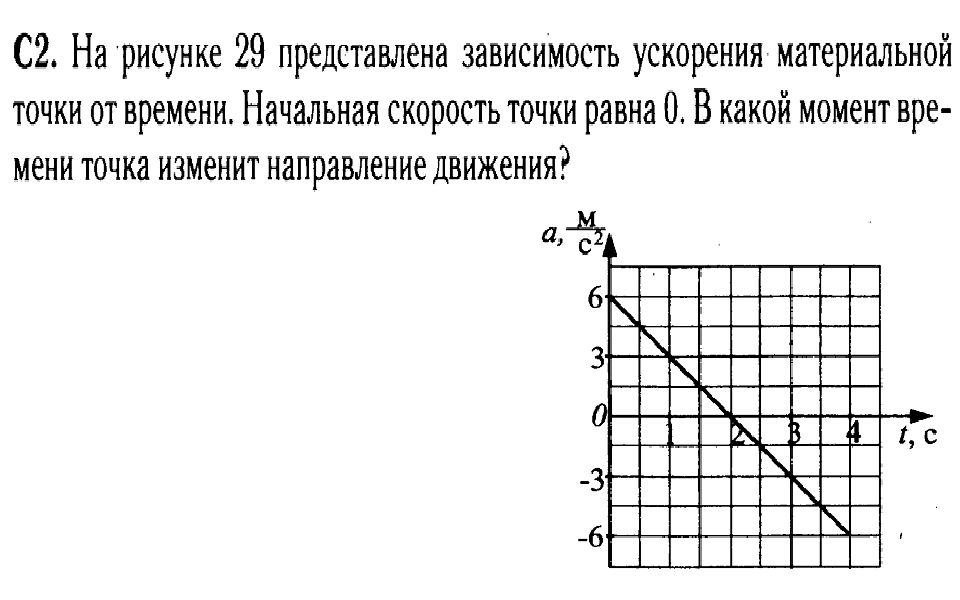
3.2.2. Определение максимальной скорости на прямом участке дороги при движении в одном направлении
Определение максимальной скорости при движении в одном направлении допускается только в том случае, если характеристика дороги не позволяет достичь максимальной скорости в обоих направлениях, при этом должны соблюдаться дополнительные условия:
изменение высоты продольного профиля на всем протяжении горизонтального измерительного участка не должно превышать 1 м;
осевая составляющая скорости ветра не должна превышать 2 м/с.
Измерительный участок проезжают пятикратно; заезды должны следовать непосредственно один за другим, при этом измеряется время каждого заезда.
3.2.3. Определение максимальной скорости на кольцевой дороге
Для определения данной скорости измеряют время,
необходимое для проезда всей кольцевой дороги, проводят не менее трех измерений
для автомобиля, едущего по следу, не нуждающегося в корректировке пути
посредством воздействия на рулевое колесо.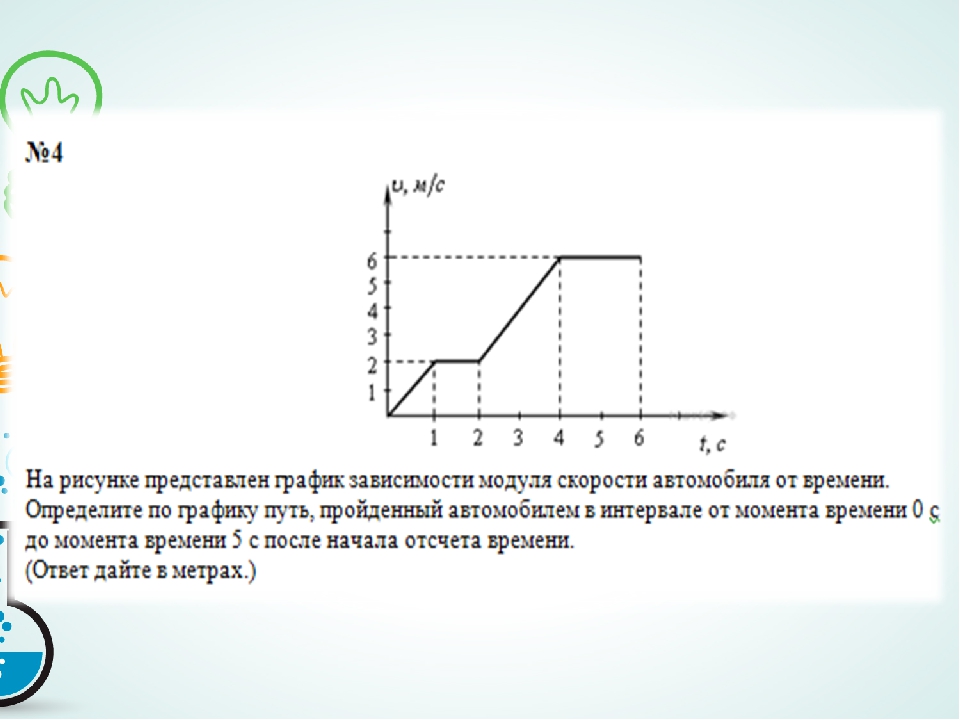 Разница крайних значений не должна
превышать 3 %.
Разница крайних значений не должна
превышать 3 %.
3.3. Определение времени разгона на заданном пути (показатель 1.2)
3.3.1. Время разгона на заданном пути длиной 400 и 1000 м определяют непосредственным его измерением или по результатам записи режима разгона АТС с места. Замеры выполняют в обоих направлениях движения, двукратно, непосредственно один за другим.
Движение начинают с передачи, используемой при
трогании с моста. Разгон выполняют при полной подаче топлива и переключении
передач при номинальной скорости (номинальной частоте вращения коленчатого вала
двигателя) или при скорости (частоте вращения), ограниченной регулятором. При
наличии делителя в коробке передач переключения передач при работе АТС
производят согласно рекомендации предприятия-изготовителя; при отсутствии таких
рекомендаций используют верхний ряд передач. Режимы работы автоматической
трансмиссии должны соответствовать требованиям технической документации.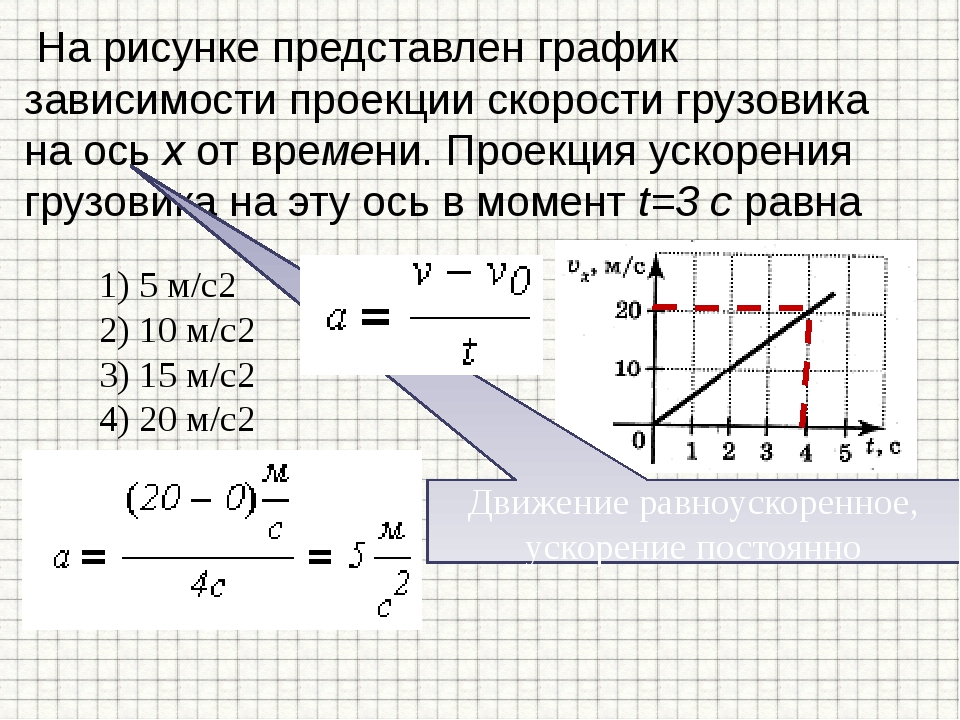
3.4. Определение времени разгона до заданной скорости (показатель 1.3)
3.4.1. Время разгона с места до заданной скорости определяют как среднюю арифметическую величину по результатам заездов, выполненных в соответствии с п. 3.3, или по кривой режима разгона АТС с места.
Устанавливаются следующие значения конечной скорости разгона:
100 км/ч — для АТС всех типов полной массой до 3,5 т;
80 км/ч — для грузовых автомобилей, автобусов (кроме городских) полной массой свыше 3,5 т и автопоездов.
60 км/ч — для городских автобусов.
Для АТС, имеющих максимальную скорость ниже заданной или выше ее не более чем на 5 км/ч, принимается ближайшая меньшая скорость, кратная десяти.
3.5. Определение скоростной характеристики «разгон-выбег» (характеристика 1.4)
3.5.1. Для определения данной характеристики выполняют
разгон с места до наибольшей скорости, достигаемой на пути 2000 м, и выбег с
выключенной передачей до остановки.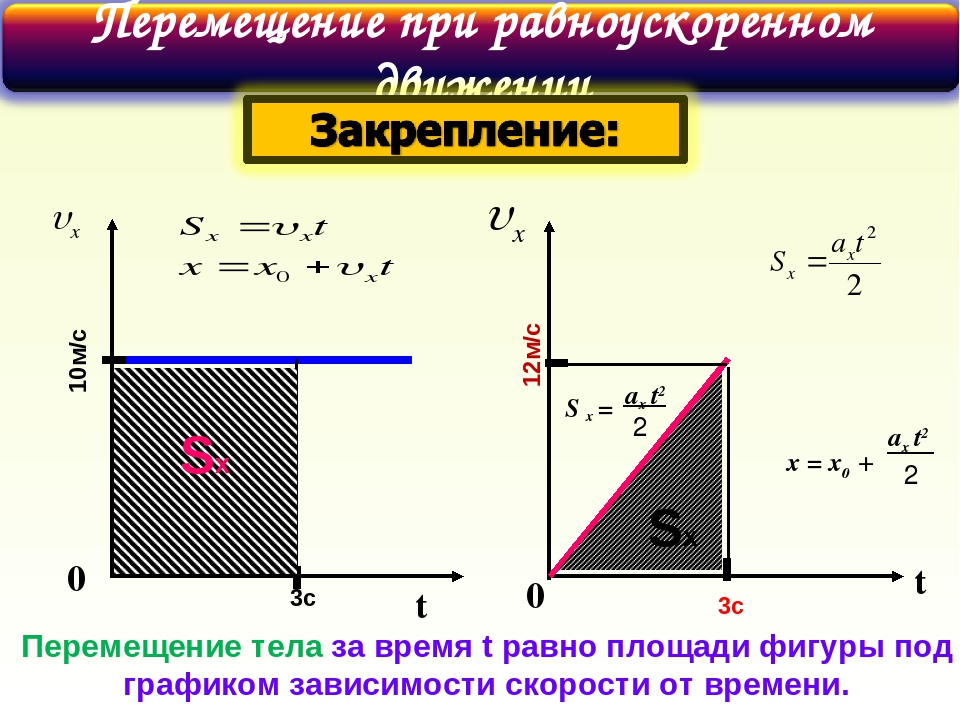 Разгон выполняют в соответствии с п. 3.3.
Разгон выполняют в соответствии с п. 3.3.
Параметры движения (путь, время, скорость) следует регистрировать с помощью измерительной аппаратуры. Допускается параметры разгона и выбега определять раздельно, если длина измерительного участка недостаточна.
3.6. Определение скоростной характеристики «разгон на передаче, обеспечивающей максимальную скорость» (характеристика 1.5)
3.6.1. При определении данной характеристики разгон АТС выполняют на передаче, обеспечивающей достижение максимальной скорости (высшая или предшествующая) с минимальной скорости на этой передаче до скорости 0,9 от максимальной.
Минимальную скорость устанавливают до начала измерительного участка. Применяемая передача должна быть отражена в названии характеристики.
Разгон АТС выполняют при полной подаче топлива.
Замеры, следующие один за другим, необходимо выполнять по одному разу в обоих направлениях движения.
4. 1. Все результаты испытаний и данные
метеорологических измерений должны быть внесены в протокол испытаний.
1. Все результаты испытаний и данные
метеорологических измерений должны быть внесены в протокол испытаний.
4.2. Скорость (vmax) и время () движения АТС, км/ч, вычисляют по формулам:
vmax = 3,6 × s/, (2)
где s — длина измерительного участка, м;
- среднее время проезда измерительного участка, с;
(3)
где п — число измерений;
ti — время прохождения измерительного участка в i-м измерении, с.
4.3. За величину максимальной скорости АТС, полученной на прямом участке дороги при движении в двух направлениях, принимают значение, полученное по формуле (2).
Величину максимальной скорости АТС, полученной на прямом участке дороги при движении в одном направлении (), вычисляют по формуле
(4)
где vmax — скорость автомобиля, вычисленная по формуле (2), км/ч;
vв — осевая составляющая
средней по заездам скорости ветра, км/ч.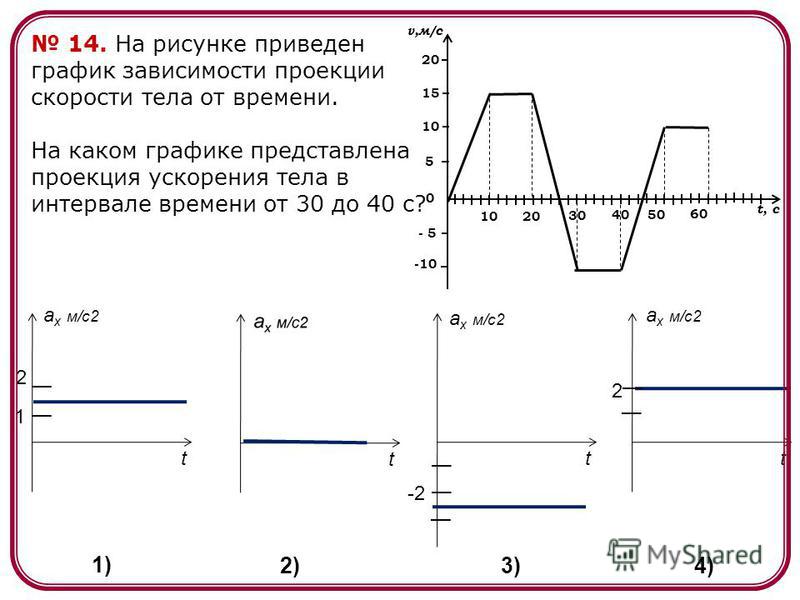
Примечание. Знак (+) применяют, если осевая составляющая ветра противодействует движению АТС, а знак (-) — в противоположном случае.
Величину максимальной скорости АТС, полученной на кольцевой дороге, вычисляют по формуле
(5)
где vк - максимальная скорость, полученная на кольцевой дороге, км/ч;
К - поправочный коэффициент (1 £ К £ 1,05) определяемый согласно приложению 3.
4.4. Номинальную скорость АТС (vN), км/ч, вычисляют по формуле
(6)
где nN — номинальная частота вращения вала двигателя, мин-1;
rк — радиус качения ведущих колес, м;
uтр — передаточное число трансмиссии.
4.5. За результат измерения времени разгона на заданном пути или до заданной скорости принимают среднее время разгона из четырех заездов
(7)
4. 6. За результат измерения скоростных характеристик
принимают определенные зависимости v = f() и v
= f(), для которых
6. За результат измерения скоростных характеристик
принимают определенные зависимости v = f() и v
= f(), для которых
(8)
(9)
где n — число измерений;
tк — время разгона автомобиля до заданной скорости, с;
sк — путь разгона автомобиля до заданной скорости, м.
При обработке скоростной характеристики разгона с переключением передач задают начальную и конечную скорости движения на каждой передаче, а также дополнительно не менее двух значений на каждой передаче, кратных 5 или 10 км/ч.
Скоростная характеристика «Разгон-выбег»
Черт. 1
Скоростная характеристика «Разгон на передаче, обеспечивающей максимальную скорость»
Черт. 2
2
Для характеристики выбега скорости задают кратными десяти с интервалом значений 10 км/ч, если начальная скорость выбега менее 100 км/ч, и 20 км/ч, если начальная скорость выбега равна или больше 100 км/ч.
Для характеристики «разгон на передаче, обеспечивающей максимальную скорость», задают начальную скорость разгона как среднюю величину двух заездов, а также ближайшую к ней, кратную десяти, и последующие значения через 10 км/ч, если конечная скорость разгона меньше 100 км/ч, и через 20 км/ч, если конечная скорость разгона равна или больше 100 км/ч.
Скоростные характеристики 1.4 и 1.5 могут быть представлены в табличной форме или в виде графиков (черт. 1 и 2). При построении графиков одному миллиметру должны соответствовать: скорость 0,5 км/ч, путь 5 м, время 0,5 с.
4.7. Полученные результаты испытаний могут быть скорректированы
согласно приложению 2. По этому же приложению подсчитываются
погрешности измерений.
|
Термин |
Пояснение |
|
Максимальная скорость |
Наибольшая установившаяся скорость (км/ч) движения АТС на прямом горизонтальном измерительном участке дороги |
|
Номинальная скорость |
Скорость движения АТС на данной передаче при номинальной частоте вращения коленчатого вала двигателя (по ГОСТ 14846) |
|
Минимальная скорость |
Наименьшая устойчивая скорость движения на заданной передаче, при которой АТС движется без рывков и стуков в трансмиссии, а при резком увеличении подачи топлива начинает разгоняться |
|
Скоростная характеристика «разгон-выбег» |
Зависимость скорости (км/ч) от пути (м) и времени (с) при разгоне АТС с места на пути 2000 м и выбеге до остановки |
|
Скоростная характеристика «разгон на передаче, обеспечивающей максимальную скорость» |
Зависимость скорости (км/ч) от пути (м) и времени (с) при разгоне АТС на высшей (предшествующей) передаче от минимальной скорости до номинальной |
|
Масса груза |
По ОСТ 37. |
|
Полная масса АТС |
По ОСТ 37.001.408 |
1.1. Путь выбега (sво), м, приводят к нормальным условиям (1000 гПа, 20 °С) по формуле
(10)
где sв — путь выбега, полученный при температуре ниже +3 °С;
К¢ — поправочный коэффициент;
где та — полная масса АТС, т;
t0 — нормальная температура, равная 20 °С;
t — температура воздуха при испытаниях, °С.
1.2. Показатели скоростных свойств, полученные при
температуре ниже +3 °С, допускается корректировать с учетом того, что при
снижении температуры воздуха на каждые 10 °С, показатели
ухудшаются в среднем на 1 %.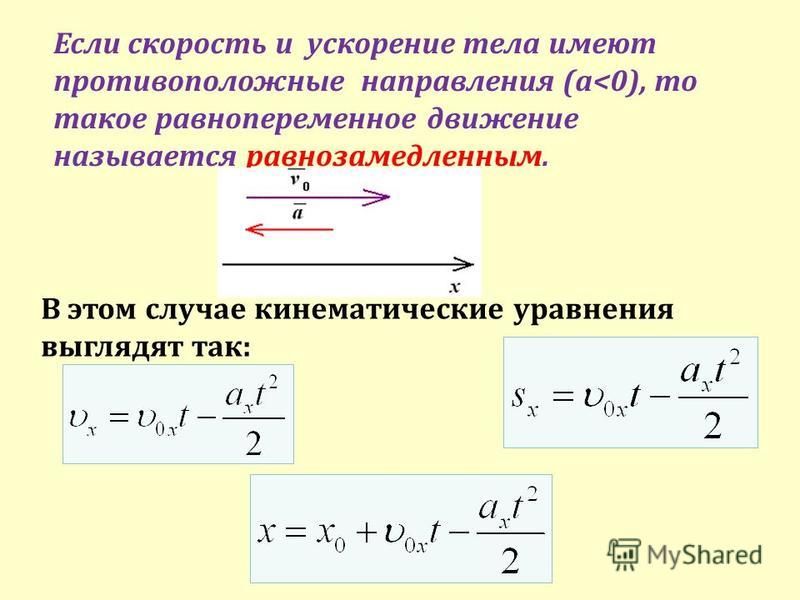
2.1. Относительную погрешность измерений величин (D), %, вычисляют по формуле
(11)
где К — поправочный коэффициент, зависящий от числа измерений п, значения которого приведены в табл. 2.
Таблица 2
|
п |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
К |
1,60 |
1,25 |
1,06 |
0,94 |
0,85 |
0,77 |
0,73 |
s — стандартное отклонение, вычисляемое по формуле
(12)
- среднее арифметическое значение;
qi— значение i-го измерения;
п — число измерений.
2.2. Относительная погрешность измерений не должна превышать 3 %.
Если после 10 измерений погрешность превышает 3 %, то испытание данного образца АТС прекращается.
1. Поправочный коэффициент К равен отношению максимальной скорости vA, измеренной на прямом участке, к максимальной скорости vD, полученной на кольцевой дороге.
2. Данный коэффициент определяют для нескольких скоростей так, чтобы, разница между двумя последующими скоростями не превышала 30 км/ч.
3. По полученным данным строят график vD = f (vA), точки которого соединяют прямыми линиями (черт. 3).
Черт. 3
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАН И ВНЕСЕН Министерством автомобильного и сельскохозяйственного машиностроения СССР
РАЗРАБОТЧИКИ
О.И. Гируцкий, канд. техн. наук; А.А. Токарев, д-р техн. наук; Ю.П. Назаров; Э.И. Наркевич; А.Г. Шмидт, канд. техн. наук; В.И. Чергейко, канд. техн. наук
2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по управлению качеством продукции и стандартам от 20.12.90 № 3204
3. Срок первой проверки — 1995 г., периодичность проверки — 4 года
4. Стандарт содержит все требования СТ СЭВ 6893-89 и соответствует Правилам ЕЭК ООН № 68
5. ВЗАМЕН ГОСТ 22576-77
6. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
|
Обозначение НТД, на который дана ссылка |
Номер приложения |
|
ГОСТ 14846-81 |
Приложение 1 |
|
ОСТ 37.001.408-85 |
Приложение 1 |
СОДЕРЖАНИЕ
Равноускоренное движение, вектор ускорения, направление, перемещение. Формулы, определение, законы
Тестирование онлайн
Равноускоренное движение
В этой теме мы рассмотрим очень особенный вид неравномерного движения. Исходя из противопоставления равномерному движению, неравномерное движение — это движение с неодинаковой скоростью, по любой траектории. В чем особенность равноускоренного движения? Это неравномерное движение, но которое «равно ускоряется». Ускорение у нас ассоциируется с увеличением скорости. Вспомним про слово «равно», получим равное увеличение скорости. А как понимать «равное увеличение скорости», как оценить скорость равно увеличивается или нет? Для этого нам потребуется засечь время, оценить скорость через один и тот же интервал времени. Например, машина начинает двигаться, за первые две секунды она развивает скорость до 10 м/с, за следующие две секунды 20 м/с, еще через две секунды она уже двигается со скоростью 30 м/с. Каждые две секунды скорость увеличивается и каждый раз на 10 м/с. Это и есть равноускоренное движение.
Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.
Можно ли движение велосипедиста считать равноускоренным, если после остановки в первую минуту его скорость 7км/ч, во вторую — 9км/ч, в третью 12км/ч? Нельзя! Велосипедист ускоряется, но не одинаково, сначала ускорился на 7км/ч (7-0), потом на 2 км/ч (9-7), затем на 3 км/ч (12-9).
Обычно движение с возрастающей по модулю скоростью называют ускоренным движением. Движение же с убывающей скоростью — замедленным движением. Но физики любое движение с изменяющейся скоростью называют ускоренным движением. Трогается ли автомобиль с места (скорость растет!), или тормозит (скорость уменьшается!), в любом случае он движется с ускорением.
Равноускоренное движение — это такое движение тела, при котором его скорость за любые равные промежутки времени изменяется (может увеличиваться или уменьшаться) одинаково
Ускорение тела
Ускорение характеризует быстроту изменения скорости. Это число, на которое изменяется скорость за каждую секунду. Если ускорение тела по модулю велико, это значит, что тело быстро набирает скорость (когда оно разгоняется) или быстро теряет ее (при торможении). Ускорение — это физическая векторная величина, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Определим ускорение в следующей задаче. В начальный момент времени скорость теплохода была 3 м/с, в конце первой секунды скорость теплохода стала 5 м/с, в конце второй — 7м/с, в конце третьей 9 м/с и т.д. Очевидно, . Но как мы определили? Мы рассматриваем разницу скоростей за одну секунду. В первую секунду 5-3=2, во вторую секунду 7-5=2, в третью 9-7=2. А как быть, если скорости даны не за каждую секунду? Такая задача: начальная скорость теплохода 3 м/с, в конце второй секунды — 7 м/с, в конце четвертой 11 м/с.В этом случае необходимо 11-7= 4, затем 4/2=2. Разницу скоростей мы делим на промежуток времени.
Эту формулу чаще всего при решении задач применяют в видоизмененном виде:
Формула записана не в векторном виде, поэтому знак «+» пишем, когда тело ускоряется, знак «-» — когда замедляется.
Направление вектора ускорения
Направление вектора ускорения изображено на рисунках
На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо). Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.
При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.
На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.
При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.
Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на «-2м/с». 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.
При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком «минус»!!!
Перемещение при равноускоренном движении
Дополнительная формула, которую называют безвременной
Формула в координатах
Связь со средней скоростью
При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости
Из этого правила следует формула, которую очень удобно использовать при решении многих задач
Соотношение путей
Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.
Главное запомнить
1) Что такое равноускоренное движение;
2) Что характеризует ускорение;
3) Ускорение — вектор. Если тело разгоняется ускорение положительное, если замедляется — ускорение отрицательное;
3) Направление вектора ускорения;
4) Формулы, единицы измерения в СИ
Упражнения
Два поезда идут навстречу друг другу: один — ускоренно на север, другой — замедленно на юг. Как направлены ускорения поездов?
Одинаково на север. Потому что у первого поезда ускорение совпадает по направлению с движением, а у второго — противоположное движению (он замедляется).
Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6м?
Так как поезд движется с ускорением, то скорость его все время возрастает (a>0). Если к концу четвертой секунды скорость равна 6м/с, то в начале четвертой секунды она была меньше 6м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.
Какие из приведенных зависимостей описывают равноускоренное движение?
Уравнение скорости движущегося тела . Каково соответствующее уравнение пути?
*Автомобиль прошел за первую секунду 1м, за вторую секунду 2м, за третью секунду 3м, за четвертую секунду 4м и т.д. Можно ли считать такое движение равноускоренным?
В равноускоренном движении пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Следовательно, описанное движение не равноускоренное.
|
Полезная информация |
|
Обкатка |
|
Для сохранения высоких эксплуатационных характеристик, а также продления срока службы автомобиля, первую 1000 километров соблюдайте следующие рекомендации:
|
|
Тормозная жидкость |
|
Замена каждые 2 года вне зависимости от пробега а/м. Для обеспечения безопасности вождения необходимо регулярно проверять состояние ТЖ. Дело в том, что в тормозной жидкости может накапливаться влага, и именно она способна стать причиной отказа тормозов в самый неподходящий момент.
|
|
Моторное масло |
|
Для обеспечения нормальной работы двигателя необходимо следить за уровнем моторного масла, например, при каждой заправке. Рекомендуемая каждые 10 000 км / 15 000 км в зависимости от модели автомобиля или 1 раз в год что наступит раньше. При каждой замене моторного масла также должна производиться замена фильтра. Масло в двигателе является смазочным и моющим материалом, вследствие силовых и температурных нагрузок в составе масла появляются продукты износа (взвешенные частицы) а также продукты горения (нагар). Ещё используют термин «стареет» когда масло также теряет свои свойства по истечении времени, достаточно 1 года с пробегом менее 10 000 км.
|
|
Масло в автоматической коробке переключения передач |
|
При нормальных условиях эксплуатации трансмиссионное масло рекомендуется менять через 60 тысяч километров пробега автомобиля / каждые 4 года. По мере эксплуатации автомобиля в составе трансмиссионного масла появляются взвешенные частицы, из-за несвоевременной замены масла в АКПП могут быть серьёзные последствия, если продукты износа с трансмиссионной жидкостью попадут, например, в систему управления коробки.
|
|
Жидкость системы охлаждения двигателя |
|
Двигатель внутреннего сгорания необходимо охлаждать для обеспечения нормального теплового режима работы его узлов и деталей. От свойств жидкости во многом зависит эффективность системы охлаждения, надежность и долговечность двигателя. Периодичность замены 1 раз в два года, для Вашего автомобиля указано в сервисной книжке.
|
|
Корректировка плотности антифриза в охлаждающей жидкости |
|
Охлаждающая жидкость должна иметь высокую теплоемкость, теплопроводность, температуру кипения, подвижность, а также низкую температуру кристаллизации и коэффициент объемного расширения. В наших широтах концентрация антифриза должна предотвращать замерзание охлаждающей жидкости по меньшей мере до температуры -30’С. Особенно актуально проверять концентрацию антифриза в охлаждающей жидкости перед наступлением зимы. Температура кристаллизации охлаждающей жидкости определяется с помощью ареометра.
|
|
Фильтр системы кондиционирования воздуха |
|
С помощью фильтра удаляется пыль и другие летучие частицы, проникающие в салон автомобиля через систему отопления и вентиляции. Различают два вида фильтров: обычный и угольный, изготовлены из синтетического материала. Угольный фильтр дополнительно с наполнением из активированного угля, частично улавливает вредные выбросы CO2 и абсорбирует их в активированном угле. Замена при каждом техническом обслуживании — это не только защита испарителя кондиционера, но и Вашего здоровья!
|
|
Фильтр воздушный |
|
Если фильтр забился, то вследствие переобогащения рабочей смеси повышается расход топлива, и ухудшаются динамические свойства двигателя. На каждом ТО фильтр осматривается на пригодность для дальнейшего использования, чистится, продувается сжатым воздухом или плановая замена для Opel каждое второе ТО.
|
|
Топливный фильтр
|
|
Топливные фильтры расположенные снаружи (не интегрированные в топливный бак) меняютя в диапазоне 30 000 — 45 000 км, чтобы защитить дизельные и бензиновые двигатели от преждевременного изнашивания. В дополнение к фильтрации частиц, дизельные фильтры устраняют воду из топлива. Вода тяжелее чем дизельное топливо и собирается в водной камере фильтра, сливается на регламентном ТО.
|
|
Свечи зажигания
|
|
Свеча зажигания — это элемент электрооборудования автомобиля, который преобразует электрическую энергию в искровый разряд, воспламеняющий топливо-воздушную смесь в цилиндрах двигателя. Поводом для замены свечей, обычно являются отклонения в работе двигателя. На замену свечей влияют, как правило, два внешних фактора: качество топлива и частая езда на короткие расстояния. Игнорирование замены свечей может привести к нежелательным последствиям таким как — замена модуля зажигания (не на всех моделях), повышенный расход топлива.
|
|
Ремни привода вспомогательных агрегатов |
|
Своевременная замена позволит избежать многих неприятностей, таких как: езды без ГУР и кондиционера, езды без генератора на аккумуляторе. Регламентные замены и осмотры ремней для каждого двигателя разработаны заводом- изготовителем индивидуально.
|
|
Ремень ГРМ |
|
К ремням ГРМ предъявляются высочайшие требования в плане надёжности и износоустойчивости, ведь обрыв ремня ГРМ приводит к таким серьёзным последствиям, как повреждение клапанов, головки блока цилиндров и поршней. При замене ремня ГРМ всегда осуществляется замена натяжных и направляющих роликов. Регламентная замена ремня для каждого двигателя разработана заводом — изготовителем индивидуально.
|
|
Кондиционер |
|
Автомобильный кондиционер представляет собой фресковую холодильную машину, элементы которой соединены трубками — фреонопроводами. При воздействии вибраций, перепадов температуры и т.п. происходит постепенное изменение свойств уплотнителей, вследствие чего фреон из системы постепенно улетучивается. Из-за этого кондиционер нужно периодически заправлять. Обычно на новом автомобиле фреон требуется дозаправлять один раз в год, через 2-3 года скорость утечки увеличивается и дозаправка необходима, даже при отсутствии явных дефектов. Кстати, все элементы кондиционера смазываются маслом, добавленным в фреон, и именно с этим связана рекомендация включать кондиционер зимой раз в месяц на 10-15 минут. Циркулирующее масло смажет за это время все уплотнители, и они будут дольше служить.
|
|
Сход — развал |
|
Хорошо известная причина снижения первоначальных ездовых качеств автомобиля — эксплуатационные изменения углов установки колес. Они могут вызывать ухудшение его устойчивости и управляемости, а также боковой дрейф. Не стоит забывать и о том, что нарушения геометрии подвески чреваты повышенным износом шин, деталей подвески и рулевого управления. C течением времени заводские регулировки углов сход-развала колес автомобиля нарушаются. Это происходит вследствие естественного износа узлов подвески и деталей рулевого управления, сопровождающегося изменением первоначальных размеров и увеличением люфтов в соединениях. Рекомендуется через каждые 10 000-15 000 км пробега проводить проверку углов установки колёс и при необходимости выполнять их регулировку.
|
Расчет пути, скорости и времени движения: равномерное и неравномерное
Равномерное движение, это вдвижение спостоянной скоростью. То есть другимим словами, тело за одинаковые промежутки времени должно проходить одинаковое расстояние. Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.
Обычно равномерное движение очень редко можно встретить в реальной жизни. За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.
Расчет скорости при равномерном движении
Скорость тела при равномерном движении будет вычисляться по следующей формуле.
- Скорость = путь / время.
Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.
Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.
Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.
Расчет скорости при неравномерном движении
При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.
Средняя скорость неравномерного движения вычисляется по формуле
Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.
Расчет пути при равномерном движении
Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.
То есть, зная скорость и время движения, мы всегда сможем найти путь.
Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.
Расчет времени при равномерном движении
Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.
Полученные выше формулы будут справедливы, если тело совершало равномерное движение.
При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.
Расчет пути при неравномерном движении
Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.
Расчет времени при неравномерном движении
Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.
Графиком равномерного движения, в координатах S(t) будет являться прямая линия.
Нужна помощь в учебе?
Предыдущая тема: Скорость в физике: единицы скорости
Следующая тема:   Явление инерции: в чем заключается и примеры из жизни
При какой максимальной скорости разгона автомобиля с 0-100 км/ч может выжить водитель
Какая скорость разгона с 0 до 100 км/час угрожает жизни человека?
По какой-то особой причине в мире большое внимание уделяется именно скорости разгона автомобиля с 0 до 100 км/час (в США с 0 до 60 миль в час). Эксперты, инженеры, любители спортивных автомобилей а также и простые автолюбители с какой-то одержимостью постоянно следят за технической характеристикой автомобилей, которая как правило раскрывает динамику разгона автомобиля с 0 до 100 км/час. Причем весь этот интерес наблюдается не только к спортивным автомобилям для которых динамика разгона с места является очень важным значением, но и к совсем обычным автомобилям эконом-класса.
В наши дни наибольший интерес к динамике разгона с 0 до 100 км/час направлен на электрические современные автомобили, которые начали потихоньку вытеснять из авто ниши спортивные суперкары с их невероятной скоростью разгона. Вот например, еще несколько лет назад казалось просто фантастикой, что автомобиль может разгоняться до 100 км/час чуть-более чем за 2 секунды. Но сегодня некоторые современные электрокары уже вплотную приблизились к этому показателю.
Это естественно заставляет задуматься: А какая скорость разгона автомобиля с 0 до 100 км/час опасна для здоровья самого человека? Ведь чем быстрее разгоняется автомобиль, тем больше нагрузки испытывает водитель, что находится (сидит) за рулем.
Bugatti Chiron: История создания суперкара мощностью в 1500 л.с.
Согласитесь с нами, что человеческий организм имеет свои определенные пределы и не может выдержать бесконечные нарастающие нагрузки, которые действуют и оказывают на него при быстром разгоне транспортного средства, определенное воздействие. Давайте вместе с нами узнаем, а какой предельный разгон автомобиля может теоретически ну и практически выдержать человек.
Ускорение, как все мы наверно знаем, это простое изменение скорости движения тела за единицу взятого времени. Ускорение любого объекта находящегося на земле зависит, как правило, от силы тяжести. Сила тяжести — это сила, действующая на любое материальное тело, которое находится вблизи к поверхности земли. Сила тяжести на поверхности земли складывается из гравитации и центробежной силы инерции, которая возникает из-за вращения нашей планеты.
Согласно законам физики установлено, что при движении объекта возникает перегрузка (G), которая зависит от ускорения. То есть, чем быстрее происходит ускорение движущего объекта, тем больше возникает перегрузка, образуемая из-за силы тяжести. Например, когда человек стоит неподвижно на месте, то он испытывает перегрузку в 1g, так как по сути, мы движемся в пространстве вместе с нашей планетой и в связи с гравитацией, которая нас и удерживает на поверхности земли.
Такая же перегрузка в 1g действует и на наше тело, когда, мы допустим сидим на стуле. 1g это количество силы, которая оказывается (давит) на нашу поясницу и нижнюю часть спины, все для того, чтобы помешать нам уйти в свободное падение в пространстве. Ведь согласитесь, если бы сила тяжести оказываемая свое давление на нас была бы меньше, то мы просто не смогли бы устоять на поверхности нашей планеты. В этом случае мы бы отправились в свободное падение.
Когда же мы сидим в автомобиле и начинаем ускоряться, то эти G-силы начинают действовать на линейно-горизонтальной оси. Естественно, что перегрузка при разгоне машины будет совершенно иной по сравнению с той, которая воздействует на человека в стоящем автомобиле.
Давайте же выясним, какая перегрузка оказывается на человека при разгоне автомобиля.
Начнем мы с относительно медленной динамики этого ускорения (по современным меркам), с 0 до 100 км/час в периодике 10 секунд.
Для этого можно воспользоваться специальным онлайн-конвектором преобразования величин. Так, с помощью этого калькулятора мы с вами высчитали, что при разгоне автомобиля с 0 до 100 км/час за 10 секунд перегрузка, воздействующая на водителя, составляет 0.28325450 = 0.28. То есть разгон с места с 0 до 100 км/час в течение десяти секунд будет оказывать на человека перегрузку в 0.28g.
Как вы видите, при ускорении за рулем автомобиля линейно горизонтальные G-силы воздействуют на человека гораздо меньше, чем эти силы оказывают воздействие на тело человека в состоянии покоя.
Соответственно, для того, чтобы добиться той же перегрузки в 1g, которая воздействует на человека когда он стоит или сидит неподвижно на стуле необходимо, чтобы автомобиль с 0 до 100 км/час разгонялся за 2,83 секунды. Это можно вычислить и с помощью простого калькулятора.
Если мы хотим быть совсем уж точными, то перегрузка человека в 1g сидящего за рулем автомобиля образуется при ускорении машины с 0 до 100 км/час за 2,83254504 секунды.
И так, мы знаем, что при перегрузке в 1g человек не испытывает на себе ни каких проблем. Например, серийный автомобиль Tesla Model S (дорогая спецверсия) с 0 до 100 км/час может разгоняться за 2,5 секунды (согласно спецификации). Соответственно, водитель находящийся за рулем этого автомобиля при разгоне будет испытывать перегрузку в 1.13g.
Это уже как мы видим, больше чем перегрузка, которая испытывается человеком в обычной жизни и которая возникает из-за гравитации а также из-за движения планеты в пространстве. Но это совсем немного и перегрузка не представляет для человека никакой опасности. Но, если мы сядем за руль мощного драгстера (спортивного автомобиля), то картина здесь уже получается совершенно иная, так как мы с вами наблюдаем уже иные цифры перегрузки.
Например, самый быстрый драгстер может разгоняться с 0 до 100 км/час всего за 0,4 секунды. В итоге получается, что это ускорение вызывает перегрузку внутри машины в 7.08g. Это уже, как вы видите, немало. За рулем такого сумасшедшего транспорта вы будете чувствовать себя не очень-то комфортно, и все из-за того, что ваш вес увеличится по сравнению с прежним почти в семь раз. Но не смотря на такое не очень-то комфортное состояние при такой динамике разгона, эта (данная) перегрузка не способна вас убить.
Так как же тогда автомобиль должен разогнаться, чтобы убить человека (водителя)? На самом деле ответить однозначно на такой вопрос нельзя. Дело тут в следующем. Каждый организм у любого человека сугубо индивидуален и естественно, что последствия воздействия на человека определенных сил будут тоже совершенно разными. Для кого-то перегрузка в 4-6g даже на несколько секунд уже будет (является) критичной. Такая перегрузка может привести к потере сознания и даже к гибели этого человека. Но обычно подобная перегрузка для многих категорий людей не опасна. Известны случаи, когда перегрузка в 100g позволяла человеку выжить. Но правда, это очень большая редкость.
Смотрите также: Сравнение двух американских легенд: 2015 Ford Mustang GT и F-4 Phantom II
Приведем пример, человек на американских горках в парке аттракционов может испытывать перегрузки до 6g, но их длительность настолько мала, что это не опасно для жизни. Летчики пилотируемых истребителей в компрессионных костюмах могут выжить при длительных перегрузках в 8g или 9g. Но это все не те виды перегрузок, которые испытывает человек, находясь за рулем автотранспортного средства с ускорением в пространстве на земле.
Кстате, мы заодно сразу вспомнили, что офицер ВВС США Джон Стапп участвовал в эксперименте по воздействию перегрузки на человека во время ускорения. Джона Стаппа посадили в специальные сани установленные на платформе, которые с помощью тяги ракетных двигателей разогнали до 1017 км/час. Во время этого ускорения Джон выдержал перегрузку в 46.2g.
Таким образом убеждаемся, зная, что человек способен выдержать перегрузку в 46.2g, выяснить с какой скоростью должен разгоняться автомобиль, чтобы перегрузка составляла такое значение, которое выдержал офицер ВВС США Джон Стапп, мы должны снова воспользоваться калькулятором преобразования величин, подставив в соответствующем поле полученное значение в 46.2g.
В итоге, калькулятор помог нам установить следующее, чтобы водитель за рулем автомобиля испытывал перегрузку в 46.2g, необходимо разогнать транспортное средство с места до 100 км/час с ускорением, всего за 0,06131050 = 0,06 секунды.
Хотим вам сказать, что Джон Стапп также участвовал и во многих других подобных экспериментах, где перегрузка во время ускорения составляла тоже до 35g. Во многих этих испытаниях Джон не раз получал травмы. Например, в одном эксперименте у него, от силы тяжести оказываемое на его тело, лопнуло одно ребро. Также, не редко во время проведения экспериментов у офицера вылетали пломбы из зубов.
Таким образом мы с вами убедились, что перегрузка выше 30g все-таки для человека запредельная. Не думаем, что покупатели премиальных дорогих суперкаров были бы довольны такими последствиями разгона своего автомобиля.
И так, на основании выше представленной информации давайте вместе с вами установим, что перегрузка в 30g при ускорении за рулем автомобиля является нашим (человеческим) пределом при котором, ни- каких особых последствий от разгона машины не будет. То есть, не будет травм.
Соответственно от сюда делаем вывод, что максимально безопасная динамика разгона автомобиля с 0 до 100 км/час составляет (составит) 0,09441817 = 0,09 секунды.
Если же мы (Вы) согласны разгоняться на машине с риском получить для себя травмы рёбер или готовы распрощаться с пломбами в зубах, то нам (Вам) нужен автомобиль способный разгоняться с места до 100 км/час за 0,08092986 = 0,08 секунды.
Но, если же мы готовы повторить мировой рекорд по перегрузке организма человека, который был установлен Джоном Стаппом, то ваше транспортное средство должно ускориться с 0 до 100 км/час за 0,06 секунды.
К нашему большому счастью таких автомобилей в мире (на планете) не существует. И что здесь самое главное, что человечеству еще очень далеко до таких динамических характеристик автотранспортных средств. А именно, до таких автомобилей, которые будут способны оказывать на человека невероятную перегрузку, которая будет способна его просто убить. Согласитесь с нами, это очень хорошая новость. Не правда ли друзья?
Исследование точности GPS-приемников «навигаторов»
В Санкт-Петербурге используются интеллектуальные транспортные системы мониторинга и управления городским пассажирским транспортом масштабов федерального округа, республики, края, области и города. Городская Система комплексной автоматизации транспорта (СКАТ) базируется на современных навигационно-коммуникационных технологиях и использует данные глобальных навигационных спутниковых систем ГЛОНАСС и GPS. Кроме того, в современные сотовые радиотелефоны встраиваются GPS-приемники.
В российской системе глобальной радионавигации ГЛОНАСС одной из характеристик точности оценки координат географических объектов является плановая (в горизонтальной плоскости) радиальная среднеквадратическая погрешность местоопределения sr [1]. В аналогичной американской радиосистеме GPS в качестве основной меры точности местоопределения используется величина предвычисленной плановой круговой погрешности местоопределения CEP (Circular Error Probable). Величина CEP, при круговом рассеянии радионавигационных местоположений объекта, связана с величиной σr соотношением [2]:
CEP = 1,2 σr
На фирме GARMIN (а также Magellan) величину предвычисленной плановой круговой погрешности местоопределения (CEP) называют более точно: предвычисленная погрешность местоопределения — EPE (Estimated Positional Error) [2].
В системе GPS предусмотрена возможность искусственного искажения информации о системном времени и эфемеридах, которое не позволяет несанкционированным пользователям получать с помощью сигналов американской спутниковой радионавигационной системы GPS фактическую плановую круговую погрешность местоопределения CEP, меньшую 50 м (режим селективного доступа — Selective Availability, SA). В настоящее время режим селективного доступа в системе GPS не используется, но потенциально, по решению правительства США, он может быть введен в систему [1].
В то же время для надежной проводки по городской автодорожной сети центральных районов мегаполисов требуется точность местоопределения sr порядка 5–10 м [1]. Практика использования GPS-приемников на частном автотранспорте говорит о том, что такая точность в статическом режиме местоопределения в современных GPS-приемниках обеспечивается.
Однако представляется актуальным вопрос о том, каково смещение радионавигационных координат движущегося автомобиля относительно его истинного местоположения (астатизм какого порядка применяется в современных GPS-приемниках), а также какова точность местоопределения автомобиля в зависимости от скорости его движения, то есть какова надежность проводки автотранспорта по городским улицам с помощью GPS-навигатора (сервисная программа Route Guidance [1]).
В статье приводятся соответствующие экспериментальные данные и предварительные выводы по результатам их статистической обработки.
Постановка эксперимента
Экспериментальные исследования проводились с помощью GPS-приемника фирмы GARMIN модели Nuvi 150 LMT (производства 2013 г.) на автомобиле фирмы Renault модели Grand Scenic 3. GPS-приемник устанавливался у ветрового стекла внутри автомобиля.
Для проведения экспериментальных исследований был выбран участок трассы А-128 Санкт-Петербург–Морье («Дорога Жизни») в промежутке от 29 до 39 км. Первый километровый столб находится в поселке Ириновка. Участок трассы проходил в основном с запада на восток, дважды отклоняясь в широтном направлении на ±800 м.
Эксперименты проводились в ноябре 2013 г. в дневных условиях освещенности при температуре воздуха в пределах 0…+5 °С при пасмурной погоде, но без осадков. Хотя максимум 24-го цикла солнечной активности приходится на середину 2013 г. (со среднемесячным максимумом числа Вольфа около 65), во время проведения экспериментов сильных геомагнитных бурь и атмосферных возмущений синоптиками не отмечалось.
Методика проведения экспериментов заключалась в следующем.
На правом краю проезжей части автотрассы намечались контрольные точки, расположенные напротив соответствующих километровых столбов. В этих точках в течение двух минут снимались показания GPS-приемника в формате ХХ°ХХ,ХХХ’ (статический эксперимент). Это соответствовало дискретности отсчетов по широте 1,852 м и по долготе 0,926 м. Кроме того, снимались показания значений EPE в контрольных точках.
Затем проводилось несколько поездок с торможением, остановкой и разгоном до скорости 60 км/час. В этих поездках координаты фиксировались через каждые 2 с.
После этого на скорости 5, 10, 15 и 20 м/c (18, 36, 54 и 72 км/ч) фиксировались показания GPS-приемника в моменты проезда автомобилем контрольных точек (динамический эксперимент). Одиннадцать километровых столбов проходились на скоростях 36 и 72 км/час семь раз, что позволило получить выборку из 77 пар координат (широта и долгота) контрольных точек для каждой скорости.
Кроме того, координаты контрольных точек в системе WGS 84 находились на картах, взятых из интернет-сайтов www.wikimapia.org [3] и www.maps.yandex.ru [4].
Способ обработки экспериментальных данных
Для контрольных точек определялись средние значения их координат и размах выборочных значений.
Для поездок с торможением, остановкой и разгоном строились зависимости изменения координат автомобиля от времени.
Для динамического эксперимента проводилась полная статистическая обработка выборки {(φj1, λj1), (φj2, λj2), …, (φji, λji), …, (φjn, λjn)} из координат контрольных точек, определенных для каждого значения скорости vj, относительно их статических координат (vj= 0). При этом в расчет брались только минуты, десятые, сотые и тысячные минуты широты φji или долготы λji. Значение j= 1 соответствовало скорости v1= 10 м/с, значение j= 2 — скорости v2= 20 м/с.
Эмпирические (выборочные) средние значения вычислялись по формулам [2]:
Эмпирические дисперсии Sjj2 и Slj2 — по формулам:
Оценивался также эмпирический коэффициент корреляции rφλj:
Затем вводилась плановая (в горизонтальной плоскости) топоцентрическая система декартовых координат (x, y): ось Ox направлялась по местной параллели на восток, ось Oy— по местному меридиану на север. В этой системе координат вычислялись оценки средних значений величин отклонения координат автомобиля от его координат в контрольных точках (j= 1, 2), а также оценки эмпирического среднего смещения и радиального среднеквадратического значения погрешностей местоопределения по формулам:
При этом среднеквадратические отклонения σMj величин Mj векторов эмпирического среднего отклонения от их эмпирических средних значений имеют приблизительные оценки: а среднеквадратические отклонения величин от их несмещенных средних значений: σrj/√2(n–1).
Затем по формулам из пособия [1] рассчитывались эмпирические оценки средних по произвольному равновероятному значению дисперсии местоположения , а также эквивалентных радиусов рассеяния .
Наконец, вычислялись оценки полуосей aи bединичных эллипсов рассеяния навигационных местоположений автомобиля и их ориентация (угол Ψ) относительно оси координат Ox:
На графиках эмпирических координат автомобиля строились удвоенные эллипсы рассеяния — для визуального контроля проведенных вычислений.
Результаты обработки экспериментальных данных
Рис. 1. Результаты проведения динамического эксперимента при скоростях автомобиля: а) v = 36 км/ч; б) v = 72 км/ч
В контрольных точках в течение двух минут (120 отсчетов) координаты имели радиальный размах в пределах 8 м, то есть плановая радиальная среднеквадратическая погрешность местоопределения σr была около 2 м. Показания величины EPEGPS-приемника обычно составляло 3–4 м при видимости 9–10 навигационных ИСЗ системы GPS. Эти значения EPE соответствуют величине σr≈2,5–3,3 м.
Различие координат километровых столбов, определенных по GPS-приемнику в системе WGS 84 и согласно Wikimapia- и Yandex-картам, варьировалось (в основном, по долготе) от –5 до +25 и от –36 до +3 м соответственно.
При равномерном торможении и разгоне заметных отклонений радионавигационных координат от маршрута следования автомобиля не наблюдалось.
На рис. 1 показаны результаты динамического эксперимента (при скоростях движения автомобиля v = 10 и 20 м/с), а также показаны удвоенные эмпирические эллипсы рассеяния, содержащие теоретически 86% от общего количества координат радионавигационного местоположения автомобиля.
На рис. 1 видно, что при скорости v = 10 м/с (36 км/час) в экспериментальных данных имеется один промах (в тысячных угловых минут): точка (–35, –35). При скорости v = 20 м/с (72 км/час) — два промаха: точки (–53, 36) и (–166, 27). Эти точки исключены из статистической обработки результатов экспериментов.
Эмпирические коэффициенты корреляции: rφλ1 ≈–0,016 и rφλ2 ≈–0,35. Эллипсы рассеяния радионавигационных местоположений автомобиля имеют большие полуоси a1 ≈11,5 м и a2 ≈24,2 м, малые — b1 ≈10,2 м и b2≈16,3 м, которые повернуты относительно осей координат на углы Ψ1≈–4° (эта величина не значимо отличается от 0) и Ψ2≈–34 ±10°[1].
На рис. 2 приведены величины эмпирического среднего смещения и оценка выборочного радиального среднеквадратического отклонения от среднего σr при величинах скорости движения автомобиля v= 10 и 20 м/с — вместе с 68%-ными доверительными интервалами.
Рис. 2. Зависимости смещения –М(v) (зеленый цвет) и среднеквадратического отклонения σr(v) (красный) от скорости автомобиля v
На рис. 2 приведены также результаты предварительной оценки величин и для скорости движения v= 5 и 15 м/с — вместе с размахом экспериментальных данных. Сплошными линиями на рис. 2 показаны линейные интерполяции эмпирических зависимостей от скорости автомобиля v(м/с). Пунктирные линии показывают 68%-ные доверительные границы этих эмпирических зависимостей (регрессионный анализ в данном исследовании не проводился).
Вариации величины показаны на графике рис. 2 при v = 0 вертикальной черной полосой.
Методические погрешности экспериментальных данных
Прежде чем делать выводы из результатов обработки экспериментальных данных, следует оценить погрешности местоопределения автомобиля, вызванные методикой проведения динамических экспериментов.
При полученных значениях неточностью определения координат контрольных точек, определенных в статическом режиме , можно пренебречь и считать, что координаты этих точек в системе WGS 84 определены точно.
При движении автомобиля мимо километрового столба время реакции оператора, фиксирующего в момент проезда столба показания GPS-приемника, на определении поперечной к трассе движения автомобиля координате практически не сказывается.
Что касается продольной координаты, то необходимо учесть следующее. Оператор заранее видит очередной километровый столб и готовится дотронуться пальцем до сенсорного экрана GPS-приемника — при проезде мимо столба. Поэтому реакция оператора складывается из времени фиксации момента проезда мимо столба (около 0,1 с [5]) и реакции пальца оператора (около 0,1 с [5]). Значит, можно оценить суммарную задержку в фиксации момента проезда очередного километрового столба промежутком времени в 0,2 с.
Далее. После момента активации дисплея GPS-приемник может зафиксировать текущие координаты автомобиля в течение 1 с (дискретность отсчетов GPS-приемника). Следовательно, задержку во времени фиксации продольной координаты автомобиля можно считать распределенной равномерно в промежутке –0,8…+0,2 с со средним значением c и среднеквадратическим отклонением от среднего σt= 1/(2√3) ≈ 0,29 c. Это соответствует смещениям и среднеквадратическим отклонениям продольной координаты автомобиля при скорости v1 = 10 м/с: ΔL1 = –3 м и σL1≈ 3 м; при v2 = 20 м/с: ΔL2 = –6 м и σL2≈ 6 м. Поскольку движение автомобиля происходило в основном в долготном направлении, то на рис. 1 следует ввести смещение начала оси Ox влево на 2,8′ ×10–3 (для v1 = 10 м/с) и на 5,6′ ×10–3 (для v2 = 20 м/с).
Что же касается радиальных среднеквадратических отклонений , то их следует уменьшить — с учетом величин рассмотренных выше методических погрешностей местоопределения — по формуле:
Это дает в результате: .
Предварительные выводы из проведенных экспериментов
В 1990-х годах было выяснено: если для отслеживания динамики морских и речных судов постоянная времени радионавигационных приборов должна быть около 15 с, то для автотранспорта, как более динамичного транспортного средства, — не более 4 с. Исследованный GPS-приемник удовлетворяет последнему требованию. Как показано в статье [6], комплексирование GPS-приемника с автомобильным спидометром позволяет также существенно уменьшить зависимость величины sr от скорости v движения автомобиля.
Заключение
Исследование динамических статистических характеристик автомобильных GPS-приемников вызывает большой практический интерес, так как позволяет понять, почему бортовой комплекс сухопутной навигации (так называемый «навигатор») иногда работает неадекватно: заводит в тупики, неправильно идентифицирует улицы и топографические объекты и т. п.
Однако проведение таких исследований весьма затруднительно, так как для этого нужны приборы, позволяющие при движении автомобиля определять его местоположение с точностью 2–3 м.
В статье предложен метод решения задачи точного местоопределения автомобиля «на ходу» с помощью местных предметов (не обязательно километровых столбов) и проведены предварительные экспериментальные исследования на основе предложенного метода.
Результаты экспериментов показали высокую эффективность предложенной методики и выявили основные статистические характеристики приемников глобальных спутниковых систем радионавигации. Дальнейшие исследования с помощью этой методики должны уточнить полученные данные, привести к усовершенствованию вторичной обработки данных в этих приемниках и к повышению качества работы бортовых комплексов сухопутной навигации.
Авторы благодарят Н. И. Ефремову за помощь в сборе экспериментальных данных.
Литература- Худяков Г. И. Транспортные информационно-управляющие радиоэлектронные системы: Уч. пособие. СПб.: Изд-во СЗТУ. 2003.
- wikipedia.org.
- wikimapia.org.
- maps.yandex.ru.
- google.ru.
- Худяков Г. И., Белова А. А. Эффективность применения датчиков счисления пути для навигационного обеспечения наземного транспорта, использующего спутниковые РНС. Записки Горного института. Т. 205. 2014 (в печати).
3.3 Среднее и мгновенное ускорение — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте среднее ускорение между двумя точками времени.
- Рассчитайте мгновенное ускорение с учетом функциональной формы скорости.
- Объясните векторную природу мгновенного ускорения и скорости.
- Объясните разницу между средним ускорением и мгновенным ускорением.
- Найдите мгновенное ускорение в заданное время на графике зависимости скорости от времени.
Важность понимания ускорения охватывает наш повседневный опыт, а также обширные просторы космического пространства и крошечный мир субатомной физики. В повседневном разговоре до ускоряться, означает ускоряться; нажатие на педаль тормоза приводит к замедлению движения автомобиля. Мы, например, знакомы с ускорением нашей машины. Чем больше ускорение, тем больше изменение скорости за заданный промежуток времени.Ускорение широко наблюдается в экспериментальной физике. Например, в экспериментах с линейным ускорителем частиц субатомные частицы ускоряются до очень высоких скоростей в экспериментах по столкновению, которые сообщают нам информацию о структуре субатомного мира, а также о происхождении Вселенной. В космосе космические лучи — это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывающихся массивных звездах) и активных ядрах галактик. Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат очень проникающее излучение, которое может, например, повредить электронику, установленную на космических кораблях.
Среднее ускорение
Формальное определение ускорения согласуется с этими только что описанными понятиями, но является более всеобъемлющим.
Среднее ускорение
Среднее ускорение — это скорость изменения скорости:
где
— среднее ускорение, v — скорость, t — время. (Полоса над и означает среднее ускорение .)
Поскольку ускорение — это скорость в метрах, разделенная на время в секундах, единицы измерения ускорения в системе СИ часто обозначаются сокращенно: м / с 2 , то есть метры в секунду в квадрате или метры в секунду в секунду. Это буквально означает, на сколько метров в секунду изменяется скорость каждую секунду. Напомним, что скорость — это вектор, он имеет как величину, так и направление, что означает, что изменение скорости может быть изменением величины (или скорости), но это также может быть изменение направления.Например, если бегун, движущийся со скоростью 10 км / ч на восток, замедляется до остановки, меняет направление, продолжает свой бег со скоростью 10 км / ч на запад, его скорость изменилась в результате изменения направления, хотя величина скорости одинаковы в обоих направлениях. Таким образом, ускорение происходит, когда скорость изменяется по величине (увеличение или уменьшение скорости) или по направлению, или по обоим направлениям.
Ускорение как вектор
Ускорение — это вектор в том же направлении, что и , изменение скорости ,
.Поскольку скорость является вектором, она может изменяться по величине или по направлению, или по обоим направлениям. Следовательно, ускорение — это изменение скорости или направления, или и того, и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда в направлении движения. Когда объект замедляется, его ускорение противоположно направлению его движения. Хотя это обычно называется замедлением (рисунок), мы говорим, что поезд ускоряется в направлении, противоположном его направлению движения.
Рисунок 3.10. Поезд метро в Сан-Паулу, Бразилия, замедляет скорость, когда заходит на станцию. Он ускоряется в направлении, противоположном направлению его движения. (Источник: Юсуке Кавасаки)Термин замедление может вызвать путаницу в нашем анализе, потому что он не является вектором и не указывает на конкретное направление относительно системы координат, поэтому мы его не используем. Ускорение — это вектор, поэтому мы должны выбрать для него соответствующий знак в выбранной нами системе координат.В случае поезда на (Рисунок) ускорение составляет в отрицательном направлении в выбранной системе координат , поэтому мы говорим, что поезд испытывает отрицательное ускорение.
Если движущийся объект имеет скорость в положительном направлении по отношению к выбранной исходной точке и приобретает постоянное отрицательное ускорение, объект в конечном итоге останавливается и меняет направление на противоположное. Если мы подождем достаточно долго, объект пройдет через начало координат в противоположном направлении. Это проиллюстрировано на (Рисунок).
Рис. 3.11. Объект, движущийся с вектором скорости на восток при отрицательном ускорении, останавливается и меняет направление на противоположное. Через достаточно долгое время он проходит исходную точку в обратном направлении.Пример
Расчет среднего ускорения: скакун покидает ворота
Скаковая лошадь, выходящая из ворот, ускоряется из состояния покоя до скорости 15,0 м / с на запад за 1,80 с. Какое у него среднее ускорение?
Рисунок 3.12 Скаковые лошади ускоряются из-за ворот. (кредит: Джон Салливан)Стратегия
Сначала мы рисуем эскиз и назначаем систему координат задаче (рисунок). Это простая задача, но всегда помогает ее визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Рисунок 3.13 Определите систему координат, данную информацию и то, что вы хотите определить.Мы можем решить эту проблему, указав
на основе предоставленной информации, а затем вычисление среднего ускорения непосредственно из уравнения
.
Решение
Сначала определите известных:
(знак минус указывает направление на запад), Δ t = 1,80 с.
Во-вторых, найдите изменение скорости. Поскольку лошадь движется с нуля до –15,0 м / с, ее изменение скорости равно ее конечной скорости:
Наконец, подставьте известные значения (
) и найти неизвестное
:
Значение
Отрицательный знак ускорения указывает на то, что ускорение направлено на запад.Ускорение 8,33 м / с 2 на западе означает, что лошадь увеличивает свою скорость на 8,33 м / с на западе каждую секунду; то есть 8,33 метра в секунду в секунду, что мы записываем как 8,33 м / с 2 . Это действительно среднее ускорение, потому что поездка не гладкая. Позже мы увидим, что ускорение такой величины потребовало бы от всадника держаться с силой, почти равной его весу.
Проверьте свое понимание
Протонов в линейном ускорителе ускоряются из состояния покоя до
за 10 –4 с.Какое среднее ускорение протонов?
[показывать-ответ q = ”fs-id1168327875120 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168327875120 ″]
Вставив знания, получим
[/ hidden-answer]
Мгновенное ускорение
Мгновенное ускорение a или ускорение в определенный момент времени получается с использованием того же процесса, который описан для мгновенной скорости.То есть мы вычисляем среднюю скорость между двумя моментами времени, разделенными
и пусть
приближаются к нулю. Результатом является производная функции скорости v ( t ), которая составляет мгновенное ускорение и математически выражается как
.Таким образом, аналогично скорости, являющейся производной функции положения, мгновенное ускорение является производной функции скорости.Мы можем показать это графически так же, как мгновенную скорость. На (Рисунок) мгновенное ускорение в момент времени t 0 — это наклон касательной к графику зависимости скорости от времени в момент времени t 0 . Видим, что среднее ускорение
приближается к мгновенному ускорению как
приближается к нулю. Также в части (а) рисунка мы видим, что скорость имеет максимум, когда ее наклон равен нулю.Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, поскольку наклон кривой там также равен нулю. Таким образом, для заданной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.
Рис. 3.14. На графике зависимости скорости от времени мгновенное ускорение представляет собой наклон касательной. (а) Показано среднее ускорениемежду временами
и
.Когда
, среднее ускорение приближается к мгновенному ускорению в момент времени t0. В виде (а) мгновенное ускорение показано для точки на кривой скорости при максимальной скорости. В этой точке мгновенное ускорение — это наклон касательной, равный нулю. В любое другое время наклон касательной — и, следовательно, мгновенное ускорение — не будет нулевым. (b) То же, что (a), но показано для мгновенного ускорения при минимальной скорости.
Чтобы проиллюстрировать эту концепцию, давайте рассмотрим два примера.Во-первых, простой пример показан с использованием (Рисунок) (b), графика зависимости скорости от времени (Рисунок), для графического определения ускорения. Этот график изображен на (Рисунок) (а), который представляет собой прямую линию. Соответствующий график ускорения в зависимости от времени находится по наклону скорости и показан на (Рисунок) (b). В этом примере функция скорости представляет собой прямую линию с постоянным наклоном, поэтому ускорение является постоянным. В следующем примере функция скорости имеет более сложную функциональную зависимость от времени.
Рис. 3.15. (a, b) График зависимости скорости от времени является линейным и имеет постоянный отрицательный наклон (a), который равен ускорению, показанному на (b).Если мы знаем функциональную форму скорости, v ( t ), мы можем вычислить мгновенное ускорение a ( t ) в любой момент времени в движении, используя (рисунок).
Пример
Расчет мгновенного ускорения
Частица движется и ускоряется.Функциональная форма скорости
.
- Найдите функциональную форму ускорения.
- Найдите мгновенную скорость при t = 1, 2, 3 и 5 с.
- Найдите мгновенное ускорение при t = 1, 2, 3 и 5 с.
- Интерпретируйте результаты (c) в терминах направлений векторов ускорения и скорости.
Стратегия
Мы находим функциональную форму ускорения, взяв производную от функции скорости.Затем мы вычисляем значения мгновенной скорости и ускорения из заданных функций для каждой. Для части (d) нам нужно каждый раз сравнивать направления скорости и ускорения.
Решение
,
,
,
,
,
,
- При т = 1 с, скорость
положительное значение, а ускорение положительное, поэтому скорость и ускорение идут в одном направлении.Частица движется быстрее.
При т = 2 с, скорость увеличилась до
, где он максимальный, что соответствует моменту, когда ускорение равно нулю. Мы видим, что максимальная скорость достигается, когда наклон функции скорости равен нулю, что является просто нулем функции ускорения.
При т = 3 с, скорость
и ускорение отрицательное. Частица уменьшила свою скорость, и вектор ускорения отрицательный.Частица замедляется.
При т = 5 с, скорость
и ускорение становится все более отрицательным. Между моментами времени t = 3 с и t = 5 с частица уменьшила свою скорость до нуля, а затем стала отрицательной, таким образом изменив свое направление. Теперь частица снова ускоряется, но в противоположном направлении.
Мы можем увидеть эти результаты графически на (Рисунок).
Рис. 3.16. (а) Скорость в зависимости от времени.Касательные линии указаны в моменты времени 1, 2 и 3 с. Наклоны касательных — это ускорения. При t = 3 с скорость положительная. При t = 5 с скорость отрицательна, что указывает на то, что частица поменяла направление на противоположное. (б) Ускорение против времени. Сравнивая значения ускорений, представленные черными точками, с соответствующими наклонами касательных линий (наклон линий через черные точки) на (а), мы видим, что они идентичны.Значение
Выполняя численный и графический анализ скорости и ускорения частицы, мы можем многое узнать о ее движении.Численный анализ дополняет графический анализ, давая полное представление о движении. Нуль функции ускорения соответствует максимуму скорости в этом примере. Также в этом примере, когда ускорение положительное и в том же направлении, что и скорость, скорость увеличивается. По мере того, как ускорение стремится к нулю и в конечном итоге становится отрицательным, скорость достигает максимума, после чего начинает уменьшаться. Если мы подождем достаточно долго, скорость также станет отрицательной, что указывает на изменение направления.Реальным примером такого движения является автомобиль, скорость которого увеличивается до максимума, после чего он начинает замедляться, останавливается, а затем меняет направление.
Проверьте свое понимание
Самолет приземляется на взлетно-посадочной полосе, летящей на восток. Опишите его ускорение.
[показывать-ответ q = ”fs-id1168327963777 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168327963777 ″]
Если принять восток за положительное значение, тогда самолет имеет отрицательное ускорение, потому что он ускоряется в сторону запада.Он также замедляется; его ускорение противоположно его скорости.
[/ hidden-answer]
Ощущение ускорения
Вы, вероятно, привыкли испытывать ускорение, когда заходите в лифт или нажимаете на педаль газа в машине. Однако ускорение происходит со многими другими объектами в нашей Вселенной, с которыми у нас нет прямого контакта. (Рисунок) представлено ускорение различных объектов. Мы можем видеть, что величины ускорений простираются на многие порядки.
| Разгон | Значение (м / с 2 ) |
|---|---|
| Скоростной поезд | 0,25 |
| Лифт | 2 |
| Гепард | 5 |
| Объект в свободном падении без сопротивления воздуха у поверхности Земли | 9,8 |
| Максимум космического челнока во время запуска | 29 |
| Пик парашютиста при нормальном раскрытии парашюта | 59 |
| Самолет F16 выходит из пикирования | 79 |
| Взрывное выброс сиденья с самолета | 147 |
| Ракета Sprint | 982 |
| Максимальное пиковое ускорение ракетных салазок | 1540 |
| Прыгающая блоха | 3200 |
| Бейсбольный мяч, пораженный битой | 30 000 |
| Захваты муравья-ловушки | 1 000 000 |
| Протон в большом адронном коллайдере |
В этой таблице мы видим, что типичные ускорения сильно различаются для разных объектов и не имеют никакого отношения к размеру объекта или его массивности.Ускорение также может сильно меняться со временем во время движения объекта. У дрэг-рейсера сразу после старта наблюдается большое ускорение, но затем оно уменьшается, когда транспортное средство достигает постоянной скорости. Его среднее ускорение может сильно отличаться от его мгновенного ускорения в определенный момент времени во время его движения. (Рисунок) графически сравнивает среднее ускорение с мгновенным ускорением для двух очень разных движений.
Рис. 3.17. Графики мгновенного ускорения в зависимости от времени для двух различных одномерных движений.(а) Ускорение меняется незначительно и всегда в одном и том же направлении, поскольку оно положительное. Среднее значение за интервал почти такое же, как и ускорение в любой момент времени. (b) Ускорение сильно различается, возможно, представляя пакет на конвейерной ленте почтового отделения, который ускоряется вперед и назад, когда он натыкается. В такой ситуации необходимо учитывать небольшие интервалы времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.Сводка
- Ускорение — это скорость изменения скорости.Ускорение — это вектор; он имеет как величину, так и направление. Единица измерения ускорения в системе СИ — метр на секунду в квадрате.
- Ускорение может быть вызвано изменением величины или направления скорости, либо и тем, и другим.
- Мгновенное ускорение a ( t ) является непрерывной функцией времени и дает ускорение в любой конкретный момент во время движения. Он рассчитывается по производной функции скорости. Мгновенное ускорение — это наклон графика зависимости скорости от времени.
- Отрицательное ускорение (иногда называемое замедлением) — это ускорение в отрицательном направлении в выбранной системе координат.
Концептуальные вопросы
Возможно ли, чтобы скорость была постоянной, когда ускорение не равно нулю?
[show-answer q = ”fs-id1168328025381 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1168328025381 ″]
Нет, в одном измерении постоянная скорость требует нулевого ускорения.
[/ hidden-answer]
Может ли скорость быть постоянной, если ускорение не равно нулю? Объяснять.
Приведите пример, в котором скорость равна нулю, а ускорение — нет.
[show-answer q = ”fs-id11683282
[скрытый-ответ a = ”fs-id11683282
Мяч подбрасывается в воздух, и его скорость равна нулю на вершине броска, но ускорение не равно нулю.
[/ hidden-answer]
Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, в каком направлении он ускоряется? Ускорение положительное или отрицательное?
Знаки плюс и минус используются в одномерном движении для обозначения направления.Каков знак ускорения, уменьшающего величину отрицательной скорости? Положительной скорости?
[показывать-ответ q = ”fs-id1168328228855 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168328228855 ″]
Плюс, минус
[/ hidden-answer]
Гепард может разогнаться от состояния покоя до скорости 30,0 м / с за 7,00 с. Какое у него ускорение?
[показывать-ответ q = ”fs-id1168328195958 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168328195958 ″]
[/ hidden-answer]
Доктор.Джон Пол Стапп был офицером ВВС США, изучавшим влияние экстремального ускорения на человеческое тело. 10 декабря 1954 года Стапп проехал на ракетных санях, разогнавшись из состояния покоя до максимальной скорости 282 м / с (1015 км / ч) за 5,00 с и резко остановившись всего за 1,40 с. Вычислите его (а) ускорение в направлении его движения и (б) ускорение, противоположное его направлению движения. Выразите каждое значение кратным g (9,80 м / с 2 ), взяв его отношение к ускорению свободного падения.
Нарисуйте график зависимости ускорения от времени из следующего графика зависимости скорости от времени.
[show-answer q = ”1811 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 1811 ″] [/ hidden-answer]
Пассажир выезжает на машине из гаража с ускорением 1,40 м / с. 2 . а) Сколько времени ей нужно, чтобы набрать скорость 2,00 м / с? (b) Если она затем тормозит до остановки за 0,800 с, каково ее ускорение?
Предположим, межконтинентальная баллистическая ракета переходит из состояния покоя в суборбитальную скорость 6.50 км / с за 60,0 с (фактическая скорость и время засекречены). Каково его среднее ускорение в метрах в секунду и кратное g (9,80 м / с 2 )?
[показывать-ответ q = ”fs-id1168325667515 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1168325667515 ″]
[/ hidden-answer]
Самолет, взлетая с места, движется по взлетно-посадочной полосе с постоянным ускорением в течение 18 с, а затем взлетает со скоростью 60 м / с.Какое среднее ускорение самолета?
Глоссарий
- среднее ускорение
- скорость изменения скорости; изменение скорости с течением времени
- мгновенное ускорение
- ускорение в определенный момент времени
3.3 Среднее и мгновенное ускорение
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте среднее ускорение между двумя точками времени.
- Рассчитайте мгновенное ускорение с учетом функциональной формы скорости.
- Объясните векторную природу мгновенного ускорения и скорости.
- Объясните разницу между средним ускорением и мгновенным ускорением.
- Найдите мгновенное ускорение в заданное время на графике зависимости скорости от времени.
Важность понимания ускорения охватывает наш повседневный опыт, а также обширные просторы космического пространства и крошечный мир субатомной физики.В повседневном разговоре до ускоряться, означает ускоряться; нажатие на педаль тормоза приводит к замедлению движения автомобиля. Мы, например, знакомы с ускорением нашей машины. Чем больше ускорение, тем больше изменение скорости за заданный промежуток времени. Ускорение широко наблюдается в экспериментальной физике. Например, в экспериментах с линейным ускорителем частиц субатомные частицы ускоряются до очень высоких скоростей в экспериментах по столкновению, которые сообщают нам информацию о структуре субатомного мира, а также о происхождении Вселенной.В космосе космические лучи — это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывающихся массивных звездах) и активных ядрах галактик. Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат очень проникающее излучение, которое может, например, повредить электронику, установленную на космических кораблях.
Среднее ускорение
Формальное определение ускорения согласуется с этими только что описанными понятиями, но является более всеобъемлющим.
Среднее ускорение
Среднее ускорение — это скорость изменения скорости:
[латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} = \ frac {{v} _ {\ text {f}} — {v} _ {0}} {{t} _ {\ text {f}} — {t} _ {0}}, [/ latex]
, где [latex] \ overset {\ text {-}} {a} [/ latex] — среднее ускорение, v — скорость, а t — время. (Полоса над и означает среднее ускорение .)
Поскольку ускорение — это скорость в метрах, разделенная на время в секундах, единицы измерения ускорения в системе СИ часто обозначаются сокращенно: м / с 2 , то есть метры в секунду в квадрате или метры в секунду в секунду.Это буквально означает, на сколько метров в секунду изменяется скорость каждую секунду. Напомним, что скорость — это вектор, он имеет как величину, так и направление, что означает, что изменение скорости может быть изменением величины (или скорости), но это также может быть изменение направления. Например, если бегун, движущийся со скоростью 10 км / ч на восток, замедляется до остановки, меняет направление, продолжает свой бег со скоростью 10 км / ч на запад, его скорость изменилась в результате изменения направления, хотя величина скорости одинаковы в обоих направлениях.Таким образом, ускорение происходит, когда скорость изменяется по величине (увеличение или уменьшение скорости) или по направлению, или по обоим направлениям.
Ускорение как вектор
Ускорение — это вектор в том же направлении, что и , изменение скорости на , [latex] \ text {Δ} v [/ latex]. Поскольку скорость является вектором, она может изменяться по величине или по направлению, или по обоим направлениям. Следовательно, ускорение — это изменение скорости или направления, или и того, и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда в направлении движения.Когда объект замедляется, его ускорение противоположно направлению его движения. Хотя это обычно называется замедлением (рисунок), мы говорим, что поезд ускоряется в направлении, противоположном его направлению движения.
Рисунок 3.10 Поезд метро в Сан-Паулу, Бразилия, замедляет ход при входе на станцию. Он ускоряется в направлении, противоположном направлению его движения. (кредит: Юсуке Кавасаки)
Термин замедление может вызвать путаницу в нашем анализе, потому что он не является вектором и не указывает на конкретное направление относительно системы координат, поэтому мы его не используем.Ускорение — это вектор, поэтому мы должны выбрать для него соответствующий знак в выбранной нами системе координат. В случае поезда на (Рисунок) ускорение составляет в отрицательном направлении в выбранной системе координат , поэтому мы говорим, что поезд испытывает отрицательное ускорение.
Если движущийся объект имеет скорость в положительном направлении по отношению к выбранной исходной точке и приобретает постоянное отрицательное ускорение, объект в конечном итоге останавливается и меняет направление на противоположное.Если мы подождем достаточно долго, объект пройдет через начало координат в противоположном направлении. Это проиллюстрировано на (Рисунок).
Рисунок 3.11 Объект, движущийся с вектором скорости на восток при отрицательном ускорении, останавливается и меняет направление на противоположное. Через достаточно долгое время он проходит исходную точку в обратном направлении.
Пример
Расчет среднего ускорения: скакун покидает ворота
Скаковая лошадь, выходящая из ворот, набирает скорость до 15.0 м / с на запад за 1.80 с. Какое у него среднее ускорение?
Рисунок 3.12 Скаковые лошади ускоряются из ворот. (кредит: Джон Салливан)
Стратегия
Сначала мы рисуем эскиз и назначаем систему координат задаче (рисунок). Это простая задача, но всегда помогает ее визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Рисунок 3.13 Определите систему координат, данную информацию и то, что вы хотите определить.
Мы можем решить эту проблему, определив [latex] \ text {Δ} v \, \ text {and} \, \ text {Δ} t [/ latex] из заданной информации, а затем вычислив среднее ускорение непосредственно из уравнение [латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} = \ frac {{v} _ {\ text {f}} — {v} _ {0}} {{t} _ {\ text {f}} — {t} _ {0}} [/ latex].
Решение
Сначала определите известные: [latex] {v} _ {0} = 0, {v} _ {\ text {f}} = — 15.0 \, \ text {m / s} [/ latex] (отрицательный указывает направление на запад), Δ t = 1.80 с.
Во-вторых, найдите изменение скорости. Поскольку лошадь движется с нуля до –15,0 м / с, ее изменение скорости равно ее конечной скорости:
[латекс] \ text {Δ} v = {v} _ {\ text {f}} — {v} _ {0} = {v} _ {\ text {f}} = — 15.0 \, \ text { РС}. [/ латекс]
Наконец, подставьте известные значения ([latex] \ text {Δ} v \, \ text {and} \, \ text {Δ} t [/ latex]) и решите для неизвестного [latex] \ overset {\ text {-}} {a} [/ latex]:
[латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} = \ frac {-15.{2}. [/ латекс]
Значение
Отрицательный знак ускорения указывает на то, что ускорение направлено на запад. Ускорение 8,33 м / с 2 на западе означает, что лошадь увеличивает свою скорость на 8,33 м / с на западе каждую секунду; то есть 8,33 метра в секунду в секунду, что мы записываем как 8,33 м / с 2 . Это действительно среднее ускорение, потому что поездка не гладкая. Позже мы увидим, что ускорение такой величины потребовало бы от всадника держаться с силой, почти равной его весу.{2}. [/ латекс]
Мгновенное ускорение
Мгновенное ускорение a или ускорение в определенный момент времени получается с использованием того же процесса, который описан для мгновенной скорости. То есть мы вычисляем среднюю скорость между двумя моментами времени, разделенными [латексом] \ text {Δ} t [/ latex], и позволяем [latex] \ text {Δ} t [/ latex] приближаться к нулю. Результатом является производная функции скорости v ( t ), которая составляет мгновенное ускорение и математически выражается как
.[латекс] a (t) = \ frac {d} {dt} v (t).[/ латекс]
Таким образом, аналогично скорости, являющейся производной функции положения, мгновенное ускорение является производной функции скорости. Мы можем показать это графически так же, как мгновенную скорость. На (Рисунок) мгновенное ускорение в момент времени t 0 — это наклон касательной к графику зависимости скорости от времени в момент времени t 0 . Мы видим, что среднее ускорение [латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} [/ latex] приближается к мгновенному ускорению, как [латекс] \ text {Δ} t [/ latex] стремится к нулю.Также в части (а) рисунка мы видим, что скорость имеет максимум, когда ее наклон равен нулю. Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, поскольку наклон кривой там также равен нулю. Таким образом, для заданной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.
Рис. 3.14 На графике зависимости скорости от времени мгновенное ускорение представляет собой наклон касательной.(a) Показано среднее ускорение [латекс] \ overset {\ text {-}} {a} = \ frac {\ text {Δ} v} {\ text {Δ} t} = \ frac {{v} _ { \ text {f}} — {v} _ {i}} {{t} _ {\ text {f}} — {t} _ {i}} [/ latex] между временами [латекс] \ text {Δ} t = {t} _ {6} — {t} _ {1}, \ text {Δ} t = {t} _ {5} — {t} _ {2} [/ латекс] и [латекс] \ текст {Δ} t = {t} _ {4} — {t} _ {3} [/ latex]. Когда [latex] \ text {Δ} t \ to 0 [/ latex], среднее ускорение приближается к мгновенному ускорению в момент времени t0. В виде (а) мгновенное ускорение показано для точки на кривой скорости при максимальной скорости.В этой точке мгновенное ускорение — это наклон касательной, равный нулю. В любое другое время наклон касательной — и, следовательно, мгновенное ускорение — не будет нулевым. (b) То же, что (a), но показано для мгновенного ускорения при минимальной скорости.
Чтобы проиллюстрировать эту концепцию, давайте рассмотрим два примера. Во-первых, простой пример показан с использованием (Рисунок) (b), графика зависимости скорости от времени (Рисунок), для графического определения ускорения. Этот график изображен на (Рисунок) (а), который представляет собой прямую линию.Соответствующий график ускорения в зависимости от времени находится по наклону скорости и показан на (Рисунок) (b). В этом примере функция скорости представляет собой прямую линию с постоянным наклоном, поэтому ускорение является постоянным. В следующем примере функция скорости имеет более сложную функциональную зависимость от времени.
Рис. 3.15 (a, b) График зависимости скорости от времени является линейным и имеет постоянный отрицательный наклон (a), который равен ускорению, показанному на (b).
Если мы знаем функциональную форму скорости, v ( t ), мы можем вычислить мгновенное ускорение a ( t ) в любой момент времени в движении, используя (рисунок).{2} \, \ text {m / s} [/ латекс].
- Найдите функциональную форму ускорения.
- Найдите мгновенную скорость при t = 1, 2, 3 и 5 с.
- Найдите мгновенное ускорение при t = 1, 2, 3 и 5 с.
- Интерпретируйте результаты (c) в терминах направлений векторов ускорения и скорости.
Стратегия
Мы находим функциональную форму ускорения, взяв производную от функции скорости.{2} [/ латекс]
При t = 2 с, скорость увеличилась до [latex] v (2 \, \ text {s)} = 20 \, \ text {m / s} [/ latex], где она максимальна, что соответствует моменту, когда ускорение равно нулю. Мы видим, что максимальная скорость достигается, когда наклон функции скорости равен нулю, что является просто нулем функции ускорения.
При t = 3 с, скорость равна [latex] v (3 \, \ text {s)} = 15 \, \ text {m / s} [/ latex], а ускорение отрицательное. Частица уменьшила свою скорость, и вектор ускорения отрицательный. Частица замедляется.
При t = 5 с, скорость равна [latex] v (5 \, \ text {s)} = — 25 \, \ text {m / s} [/ latex], а ускорение становится все более отрицательным. Между моментами времени t = 3 с и t = 5 с частица уменьшила свою скорость до нуля, а затем стала отрицательной, таким образом изменив свое направление.Теперь частица снова ускоряется, но в противоположном направлении.
Мы можем увидеть эти результаты графически на (Рисунок).
Рис. 3.16 (а) Скорость в зависимости от времени. Касательные линии указаны в моменты времени 1, 2 и 3 с. Наклоны касательных — это ускорения. При t = 3 с скорость положительная. При t = 5 с скорость отрицательна, что указывает на то, что частица поменяла направление на противоположное. (б) Ускорение против времени. Сравнивая значения ускорений, представленные черными точками, с соответствующими наклонами касательных линий (наклон линий через черные точки) на (а), мы видим, что они идентичны.
Значение
Выполняя численный и графический анализ скорости и ускорения частицы, мы можем многое узнать о ее движении. Численный анализ дополняет графический анализ, давая полное представление о движении. Нуль функции ускорения соответствует максимуму скорости в этом примере. Также в этом примере, когда ускорение положительное и в том же направлении, что и скорость, скорость увеличивается. По мере того, как ускорение стремится к нулю и в конечном итоге становится отрицательным, скорость достигает максимума, после чего начинает уменьшаться.Если мы подождем достаточно долго, скорость также станет отрицательной, что указывает на изменение направления. Реальным примером такого движения является автомобиль, скорость которого увеличивается до максимума, после чего он начинает замедляться, останавливается, а затем меняет направление.
Проверьте свое понимание
Самолет приземляется на взлетно-посадочной полосе, летящей на восток. Опишите его ускорение.
Показать решениеЕсли принять восток за положительное значение, тогда самолет имеет отрицательное ускорение, потому что он ускоряется в сторону запада.Он также замедляется; его ускорение противоположно его скорости.
Ощущение ускорения
Вы, вероятно, привыкли испытывать ускорение, когда заходите в лифт или нажимаете на педаль газа в машине. Однако ускорение происходит со многими другими объектами в нашей Вселенной, с которыми у нас нет прямого контакта. (Рисунок) представлено ускорение различных объектов. Мы можем видеть, что величины ускорений простираются на многие порядки.
| Разгон | Значение (м / с 2 ) |
|---|---|
| Скоростной поезд | 0,25 |
| Лифт | 2 |
| Гепард | 5 |
| Объект в свободном падении без сопротивления воздуха у поверхности Земли | 9,8 |
| Максимум космического челнока во время запуска | 29 |
| Пик парашютиста при нормальном раскрытии парашюта | 59 |
| Самолет F16 выходит из пикирования | 79 |
| Взрывное выброс сиденья с самолета | 147 |
| Ракета Sprint | 982 |
| Максимальное пиковое ускорение ракетных салазок | 1540 |
| Прыгающая блоха | 3200 |
| Бейсбольный мяч, пораженный битой | 30 000 |
| Захваты муравья-ловушки | 1 000 000 |
| Протон в большом адронном коллайдере | [латекс] 1.{9} [/ латекс] |
В этой таблице мы видим, что типичные ускорения сильно различаются для разных объектов и не имеют никакого отношения к размеру объекта или его массивности. Ускорение также может сильно меняться со временем во время движения объекта. У дрэг-рейсера сразу после старта наблюдается большое ускорение, но затем оно уменьшается, когда транспортное средство достигает постоянной скорости. Его среднее ускорение может сильно отличаться от его мгновенного ускорения в определенный момент времени во время его движения.(Рисунок) графически сравнивает среднее ускорение с мгновенным ускорением для двух очень разных движений.
Рис. 3.17 Графики мгновенного ускорения в зависимости от времени для двух различных одномерных движений. (а) Ускорение меняется незначительно и всегда в одном и том же направлении, поскольку оно положительное. Среднее значение за интервал почти такое же, как и ускорение в любой момент времени. (b) Ускорение сильно различается, возможно, представляя пакет на конвейерной ленте почтового отделения, который ускоряется вперед и назад, когда он натыкается.В такой ситуации необходимо учитывать небольшие интервалы времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.
Сводка
- Ускорение — это скорость изменения скорости. Ускорение — это вектор; он имеет как величину, так и направление. Единица измерения ускорения в системе СИ — метр на секунду в квадрате.
- Ускорение может быть вызвано изменением величины или направления скорости, либо и тем, и другим.
- Мгновенное ускорение a ( t ) является непрерывной функцией времени и дает ускорение в любой конкретный момент во время движения.Он рассчитывается по производной функции скорости. Мгновенное ускорение — это наклон графика зависимости скорости от времени.
- Отрицательное ускорение (иногда называемое замедлением) — это ускорение в отрицательном направлении в выбранной системе координат.
Концептуальные вопросы
Возможно ли, чтобы скорость была постоянной, когда ускорение не равно нулю?
Показать решениеНет, в одном измерении постоянная скорость требует нулевого ускорения.
Может ли скорость быть постоянной, если ускорение не равно нулю? Объяснять.
Приведите пример, в котором скорость равна нулю, а ускорение — нет.
Показать решениеМяч подбрасывается в воздух, и его скорость равна нулю на вершине броска, но ускорение не равно нулю.
Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, в каком направлении он ускоряется? Ускорение положительное или отрицательное?
Знаки плюс и минус используются в одномерном движении для обозначения направления.{2} [/ латекс]
Доктор Джон Пол Стапп был офицером ВВС США, изучавшим влияние экстремального ускорения на человеческое тело. 10 декабря 1954 года Стапп проехал на ракетных санях, разогнавшись из состояния покоя до максимальной скорости 282 м / с (1015 км / ч) за 5,00 с и резко остановившись всего за 1,40 с. Вычислите его (а) ускорение в направлении его движения и (б) ускорение, противоположное его направлению движения. Выразите каждое значение кратным g (9,80 м / с 2 ), взяв его отношение к ускорению свободного падения.
Нарисуйте график зависимости ускорения от времени из следующего графика зависимости скорости от времени.
Покажи ответПассажир выезжает на машине из гаража с ускорением 1,40 м / с. 2 . а) Сколько времени ей нужно, чтобы набрать скорость 2,00 м / с? (b) Если она затем тормозит до остановки за 0,800 с, каково ее ускорение?
Предположим, что межконтинентальная баллистическая ракета переходит из состояния покоя в суборбитальную скорость 6,50 км / с за 60,0 с (фактическая скорость и время засекречены).Каково его среднее ускорение в метрах в секунду и кратное g (9,80 м / с 2 )?
Самолет, взлетая с места, движется по взлетно-посадочной полосе с постоянным ускорением в течение 18 с, а затем взлетает со скоростью 60 м / с. Какое среднее ускорение самолета?
Глоссарий
- среднее ускорение
- скорость изменения скорости; изменение скорости с течением времени
- мгновенное ускорение
- ускорение в определенный момент времени
Equations of Motion — The Physics Hypertextbook
Обсуждение
постоянное ускорение
Для большей точности этот раздел следует называть «Одномерные уравнения движения при постоянном ускорении».Учитывая, что такое название было бы стилистическим кошмаром, позвольте мне начать этот раздел со следующей оговорки. Эти уравнения движения действительны только тогда, когда ускорение постоянное и движение ограничено прямой линией.
Учитывая, что мы живем в трехмерной вселенной, в которой единственная константа — это изменение, у вас может возникнуть соблазн сразу отказаться от этого раздела. Было бы правильно сказать, что ни один объект никогда не двигался по прямой с постоянным ускорением в любом месте Вселенной в любое время — ни сегодня, ни вчера, ни завтра, ни пять миллиардов лет назад, ни тридцать миллиардов лет в будущем. , никогда.Об этом я могу сказать с абсолютной метафизической уверенностью.
Так что же тогда хорошего в этом разделе? Что ж, во многих случаях полезно предположить, что объект путешествовал или будет двигаться по прямому пути с почти постоянным ускорением; то есть любое отклонение от идеального движения можно по существу игнорировать. Движение по криволинейной траектории можно считать фактически одномерным, если существует только одна степень свободы для задействованных объектов.Дорога может изгибаться и поворачиваться и исследовать всевозможные направления, но автомобили, движущиеся по ней, имеют только одну степень свободы — свободу двигаться в одном или противоположном направлении. (Вы не можете ездить по дороге по диагонали и надеетесь остаться на ней надолго.) В этом отношении это мало чем отличается от движения, ограниченного прямой линией. Аппроксимация реальных ситуаций моделями, основанными на идеальных ситуациях, не считается обманом. Так поступают в физике. Это настолько полезный метод, что мы будем использовать его снова и снова.
Наша цель в этом разделе состоит в том, чтобы вывести новые уравнения, которые можно использовать для описания движения объекта в терминах его трех кинематических переменных: скорости ( v ), положения ( с ) и времени ( с ). т ). Есть три способа объединить их в пары: скорость-время, положение-время и скорость-положение. В этом порядке их также часто называют первым, вторым и третьим уравнениями движения, но нет веских причин для изучения этих имен.
Поскольку мы имеем дело с движением по прямой линии, направление будет обозначено знаком — положительные величины указывают в одну сторону, а отрицательные величины указывают в противоположную сторону.Определение того, какое направление является положительным, а какое отрицательным, совершенно произвольно. Законы физики изотропны ; то есть они не зависят от ориентации системы координат. Однако некоторые проблемы легче понять и решить, если одно направление предпочтительнее другого. Пока вы последовательны в решении проблемы, это не имеет значения.
скорость-время
Связь между скоростью и временем проста при равномерно ускоренном прямолинейном движении.Чем дольше ускорение, тем больше изменение скорости. Изменение скорости прямо пропорционально времени, когда ускорение постоянно. Если скорость увеличивается на определенную величину за определенное время, она должна увеличиваться вдвое на эту величину в два раза быстрее. Если объект уже стартовал с определенной скоростью, то его новая скорость будет равна старой скорости плюс это изменение. Вы должны быть в состоянии увидеть уравнение уже мысленным взором.
Это самое простое из трех уравнений, которое можно вывести с помощью алгебры.Начнем с определения ускорения.
Расширить ∆ v до v — v 0 и сжать ∆ t до t .
Затем найдите v как функцию от t .
v = v 0 + на [1]
Это первое уравнение движения . Он записывается как полином — постоянный член ( против 0 ), за которым следует член первого порядка ( на ).Поскольку наивысший порядок равен 1, правильнее называть его линейной функцией .
Символ v 0 [vee naught] называется начальной скоростью или скоростью a раз t = 0. Его часто называют «первой скоростью», но это довольно наивный способ Опишите это. Лучшим определением было бы сказать, что начальная скорость — это скорость, которую имеет движущийся объект, когда он впервые становится важным в проблеме. Скажем, метеор был замечен глубоко в космосе, и проблема заключалась в том, чтобы определить его траекторию, тогда начальная скорость, вероятно, будет той скоростью, которую он имел при первом наблюдении.Но если проблема заключалась в том, что тот же самый метеор сгорает при входе в атмосферу, то начальная скорость, вероятно, равна скорости, которую он имел при входе в атмосферу Земли. Ответ на вопрос «Какая начальная скорость?» «Это зависит от обстоятельств». Это оказывается ответом на множество вопросов.
Символ v — это скорость через некоторое время t после начальной скорости. Его часто называют конечной скоростью , но это не делает его «последней скоростью» объекта. Возьмем случай с метеором.Какая скорость обозначена символом v ? Если вы внимательно слушали, значит, вы должны были ожидать ответа. По-разному. Это может быть скорость метеора, когда он проходит мимо Луны, входит в атмосферу Земли или ударяется о поверхность Земли. Это также может быть скорость метеорита, находящегося на дне кратера. (В этом случае v = 0 м / с.) Является ли какое-либо из этих значений конечной скоростью? Кто знает. Кто-то мог извлечь метеорит из дыры в земле и уехать вместе с ним.Это актуально? Наверное, нет, но это зависит от обстоятельств. Для такого рода вещей нет правил. Вы должны проанализировать текст задачи на предмет физических величин, а затем присвоить значение математическим символам.
Последняя часть этого уравнения на — это изменение скорости по сравнению с начальным значением. Напомним, что a — это скорость изменения скорости, а t — это время после некоторого начального события . Ставка раз время меняется. Учитывая, что объект ускоряется со скоростью 10 м / с 2 , через 5 с он будет двигаться на 50 м / с быстрее.Если бы он стартовал со скоростью 15 м / с, то его скорость через 5 с была бы…
15 м / с + 50 м / с = 65 м / с
время позиции
Смещение движущегося объекта прямо пропорционально скорости и времени. Двигайся быстрее. Иди дальше. Двигайтесь дольше (как и дольше). Иди дальше. Ускорение усугубляет эту простую ситуацию, поскольку скорость теперь также прямо пропорциональна времени. Попробуйте сказать это словами, и это прозвучит нелепо. «Смещение прямо пропорционально времени и прямо пропорционально скорости, которая прямо пропорциональна времени.»Время удваивается, поэтому смещение пропорционально квадрату времени. Автомобиль, ускоряющийся в течение двух секунд, преодолеет в четыре раза расстояние, превышающее скорость автомобиля, ускоряющегося всего за одну секунду (2 2 = 4). Автомобиль, ускоряющийся в течение трех секунды покрыли бы расстояние в девять раз больше (3 2 = 9).
Если бы это было так просто. Этот пример работает, только когда начальная скорость равна нулю. Смещение пропорционально квадрату времени, когда ускорение постоянное, а начальная скорость равна нулю.Истинное общее утверждение должно учитывать любую начальную скорость и то, как она менялась. Это приводит к ужасно запутанному утверждению соразмерности. Смещение прямо пропорционально времени и пропорционально квадрату времени, когда ускорение постоянно. Линейная и квадратная функция называется квадратичной , что позволяет нам значительно сжать предыдущее утверждение. Смещение является квадратичной функцией времени при постоянном ускорении
Формулировки пропорциональности полезны, но не столь общие, как уравнения.Мы до сих пор не знаем, каковы константы пропорциональности для этой проблемы. Один из способов понять их — использовать алгебру.
Начнем с определения средней скорости.
Расширить ∆ с до с — с 0 и сжать ∆ t до t .
Определите позицию.
с = с 0 + vt [a]
Чтобы продолжить, нам нужно прибегнуть к небольшому трюку, известному как теорема о средней скорости или правило Мертона .Я предпочитаю второй вариант, поскольку правило может применяться к любой величине, которая изменяется с одинаковой скоростью, а не только к скорости. Правило Мертона было впервые опубликовано в 1335 году в Мертон-колледже, Оксфорд, английским философом, математиком, логиком и калькулятором Уильямом Хейтсбери (1313–1372). Когда скорость изменения величины постоянна, ее среднее значение находится на полпути между ее конечным и начальным значениями.
v = ½ ( v + v 0 ) [4]
Подставьте первое уравнение движения [1] в это уравнение [4] и упростите его, исключив v .
| v = ½ [( v 0 + при ) + v 0 ] v = ½ (2 v 0 + при 000 v = v 0 + ½ at [b] |
Теперь замените [b] на [a], чтобы исключить v [vee bar].
с = с 0 + ( v 0 + ½ на ) t
И, наконец, найдите s как функцию от t .
с = с 0 + v 0 t + ½ при 2 [2]
Это второе уравнение движения . Он записывается как полином — постоянный член ( s 0 ), за которым следует член первого порядка ( v 0 t ), за которым следует член второго порядка (½ at 2 ). ). Поскольку наивысший порядок равен 2, правильнее называть его квадратичным .
Символ s 0 [ess naught] часто рассматривается как начальная позиция . Символ s — это позиция на некоторое время t позже. Если хотите, вы можете назвать ее конечной позицией . Изменение положения (∆ s ) называется смещением или расстоянием (в зависимости от обстоятельств), и некоторые люди предпочитают писать второе уравнение движения таким образом.
∆ s = v 0 t + ½ at 2 [2]
скорость-позиция
Каждое из первых двух уравнений движения описывает одну кинематическую переменную как функцию времени.По сути…
- Скорость прямо пропорциональна времени при постоянном ускорении ( v ∝ t ).
- Смещение пропорционально квадрату времени при постоянном ускорении (∆ с ∝ т 2 ).
Объединение этих двух утверждений приводит к третьему, не зависящему от времени. При замене должно быть очевидно, что…
- Смещение пропорционально квадрату скорости при постоянном ускорении (∆ с ∝ v 2 ).
Это утверждение особенно важно для безопасности вождения. Когда вы вдвое превышаете скорость автомобиля, требуется в четыре раза больше расстояния, чтобы его остановить. Увеличьте скорость втрое, и вам понадобится в девять раз больше расстояния. Это хорошее практическое правило, которое следует запомнить.
Концептуальное введение сделано. Пришло время вывести формальное уравнение.
метод 1
Объедините первые два уравнения таким образом, чтобы исключить время как переменную. Самый простой способ сделать это — начать с первого уравнения движения…
v = v 0 + на [1]
реши на время…
, а затем подставить его во второе уравнение движения…
с = с 0 + v 0 t + ½ при 2 [2]
нравится…
| с = | с 0 + v 0 | ⎛ ⎜ ⎝ | v — v 0 | ⎞ ⎟ ⎠ | + ½ а | ⎛ ⎜ ⎝ | v — v 0 | ⎞ 2 ⎟ ⎠ |
| а | a |
| с — с 0 = | vv 0 — v 0 2 | + | v 2 -2 vv 0 + v 0 2 |
| а | 2 a |
| 2 a ( с — с 0 ) = 2 ( vv 0 — v 0 2 ) + ( 2 ) + ( 2 2 vv 0 + v 0 2 ) | |
| 2 a ( s — s 0 ) = v 2 — v 0 2 | |
Возведите объект в квадрат скорости, и все готово.
v 2 = v 0 2 + 2 a ( с — с 0 ) [3]
Это третье уравнение движения . Еще раз, символ s 0 [ess naught] — это начальная позиция , а s — это позиция через некоторое время t позже. При желании вы можете написать уравнение, используя ∆ s — изменение положения в положении , смещение или расстояние в зависимости от ситуации.
v 2 = v 0 2 + 2 a ∆ s [3]
метод 2
Более сложный способ вывести это уравнение — начать со второго уравнения движения в этой форме…
∆ s = v 0 t + ½ at 2 [2]
и решите ее на время. Это непростая работа, поскольку уравнение квадратично. Переставьте термины так…
½ при 2 + v 0 t — ∆ s = 0
и сравните его с общей формой квадратичной.
топор 2 + bx + c = 0
Решение этого дается известным уравнением…
| x = | — b ± √ ( b 2 — 4 ac ) |
| 2 а |
Замените символы в общем уравнении эквивалентными символами из нашего преобразованного второго уравнения движения…
| т = | — v 0 ± √ [ v 0 2 — 4 (½ a ) (∆ s )] |
| 2 (½ a ) |
почисти немного…
| т = | — v 0 ± √ ( v 0 2 -2 a ∆ s ) |
| а |
, а затем подставьте его обратно в первое уравнение движения.
v = v 0 + на [1]
| v = v 0 + a | ⎛ ⎜ ⎝ | — v 0 ± √ ( v 0 2 -2 a ∆ s ) | ⎞ ⎟ ⎠ |
| а |
Материал отменяется, и мы получаем это…
v = ± √ ( v 0 2 + 2 a ∆ s )
Выровняйте обе стороны, и все готово.
v 2 = v 0 2 + 2 a ∆ s [3]
Это было не так уж плохо, не так ли?
исчисления выводов
Исчисление — это сложная математическая тема, но она значительно упрощает вывод двух из трех уравнений движения. По определению, ускорение — это первая производная скорости по времени. Возьмите операцию в этом определении и отмените ее. Вместо того, чтобы дифференцировать скорость, чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость.Это дает нам уравнение скорость-время. Если предположить, что ускорение постоянное, мы получим так называемое первое уравнение движения [1].
| а | = | ||
| дв | = | и dt | |
| = | |||
| v — v 0 | = | при | |
| v | = | v 0 + at [1] | |
Опять же, по определению, скорость — это первая производная положения по времени.Выполните эту операцию в обратном порядке. Вместо того, чтобы различать положение для определения скорости, интегрируйте скорость, чтобы найти положение. Это дает нам уравнение положения-времени для постоянного ускорения, также известное как второе уравнение движения [2].
| v | = | |||||||||
| DS | = | v dt | ||||||||
| DS | = | ( v 0 + at ) dt | ||||||||
| = |
| |||||||||
| с — с 0 | = | v 0 t + ½ at 2 | ||||||||
| с | = | s 0 + v 0 t + ½ at 2 [2] | ||||||||
В отличие от первого и второго уравнений движения, нет очевидного способа вывести третье уравнение движения (то, которое связывает скорость с положением) с помощью расчетов.Мы не можем просто перепроектировать это по определению. Нам нужно разыграть довольно изощренный трюк.
Первое уравнение движения связывает скорость со временем. По сути, мы вывели его из этой производной…
Второе уравнение движения связывает положение со временем. Это произошло от этой производной…
Третье уравнение движения связывает скорость с положением. По логике, это должно происходить от производной, которая выглядит так…
Но что это значит? Ну, ничего по определению, но, как и все количества, оно равно самому себе.Оно также равно самому себе, умноженному на 1. Мы будем использовать специальную версию 1 ( dt dt ) и специальную версию алгебры (алгебру с бесконечно малыми). Посмотрите, что происходит, когда мы это делаем. Мы получаем одну производную, равную ускорению ( dv dt ), а другую производную, равную обратной скорости ( dt ds ).
| дв | = | дв | 1 | |
| DS | DS | |||
| дв | = | дв | дт | |
| DS | DS | дт | ||
| дв | = | дв | дт | |
| DS | дт | DS | ||
| дв | = | a | 1 | |
| DS | v |
Следующий шаг, разделение переменных.Соберите вместе похожие вещи и интегрируйте их. Вот что мы получаем при постоянном ускорении…
| = | ||||
| в дв | = | a ds | ||
| = | ||||
| ½ ( v 2 — v 0 2 ) | = | a ( с — с 0 ) | ||
| в 2 | = | v 0 2 + 2 a ( с — с 0 ) [3] | ||
Безусловно, умное решение, и оно было не так уж сложно, чем первые два варианта.Однако на самом деле это сработало только потому, что ускорение было постоянным — постоянным во времени и постоянным в пространстве. Если бы ускорение было каким-либо образом, этот метод был бы неудобно трудным. Мы вернемся к алгебре, чтобы спасти наше здравомыслие. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сэкономить.
| v = | v 0 + в | [1] |
| + | ||
| с = | s 0 + v 0 t + ½ at 2 | [2] |
| = | ||
| v 2 = | v 0 2 + 2 a ( с — с 0 ) | [3] |
Объект движется по кругу с постоянной скоростью по часовой стрелке.Показан круг «глазами Бога». Для указанного положения направление вектора скорости показано стрелкой ____; направление вектора ускорения обозначено ____; и направление вектора чистой силы представлено стрелкой ____. | |
На схеме большая точка обозначает определенное место по кругу, по которому движется объект.Вы должны выбрать три стрелки, которые представляют направления векторов скорости, ускорения и результирующей силы в этом месте. Используйте информацию в разделах Physics Rules ниже, чтобы ответить на этот вопрос. | |
Равномерное круговое движение и скорость: Скорость — это вектор, имеющий направление. Направление скорости объекта всегда совпадает с направлением движения объекта.Для объекта, движущегося по кругу с постоянной скоростью, вектор скорости всегда направлен в направлении, касательном к окружности. | |
Равномерное круговое движение и ускорение: Ускоряющиеся объекты меняют свою скорость — либо величину, либо направление скорости. Объекты, движущиеся по кругу с постоянной скоростью, ускоряются из-за изменения направления.Направление ускорения направлено к центру круга, вокруг которого движется объект. Такое направление описывается как центростремительное . | |
Равномерное круговое движение и полезная сила: Объект, который движется по кругу, ускоряется. Ускорения вызваны неуравновешенной или чистой силой.Чистая сила всегда совпадает с направлением ускорения. Для объектов, движущихся по кругу с постоянной скоростью, результирующая сила направлена к центру круга, вокруг которого движется объект. Такое направление описывается как центростремительное . | |
Каково направление вектора скорости при круговом движении? Каково направление вектора ускорения при круговом движении? Каково направление вектора чистой силы для кругового движения? |
Почему мои обороты подскакивают при ускорении?
Когда ваш автомобиль заводится, поршни внутри двигателя начинают двигаться вверх и вниз, заставляя вращаться коленчатый вал.Когда коленчатый вал поворачивается на 360 градусов, это называется оборотом. Число оборотов в минуту или число оборотов в минуту описывает количество раз, когда коленчатый вал завершает свое вращение, и скорость, с которой он это делает.
Автомобили, работающие с более высокими оборотами, часто требуют больше топлива и заставляют двигатель работать с большей нагрузкой. Если ваш двигатель работает на холостом ходу выше из-за внутренней проблемы, частота вращения вашего автомобиля может быть выше. Узнайте, что вызывает высокие обороты автомобиля и почему они скачут при ускорении.
Причины скачкообразного об / мин
Изношенные свечи зажигания или провода свечей зажигания
Изношенные свечи зажигания борются за своевременное воспламенение топлива в поршне. Это может привести к плохому ускорению. Ваш автомобиль может испытывать пропуски зажигания и рывки при ускорении. Аналогичным образом, если срок годности проводов свечей зажигания или катушек зажигания истек, автомобиль может вести себя так же, как неисправные свечи зажигания.
Ослабленный ремень ГРМ или ремень, в котором не все зубья соединены, может помешать работе двигателя или вызвать резкий холостой ход.Когда клапаны не вовремя, впускные и выпускные клапаны остаются открытыми, когда они должны быть закрыты, уменьшая компрессию. Это заставляет дымовые газы идти туда, где они не должны.
Топливные форсунки забиваются грязью и другими загрязнениями в топливе. Когда это происходит, ускорение может стать резким и может привести к потере мощности автомобиля при попытке ускорения с остановки или при движении с постоянной скоростью. Ваш автомобиль может плохо работать на холостом ходу, и экономия топлива значительно снизится.
Вашему двигателю требуется воздух для смешивания с топливом для завершения процесса сгорания.Работа воздушного фильтра заключается в улавливании загрязняющих веществ в воздухе, которые не могут попасть в ваш двигатель и причинить вред. Со временем воздушный фильтр забивается пылью, грязью и другими частицами.
Забитый воздушный фильтр препятствует поступлению постоянного потока воздуха в двигатель. Когда это произойдет, вашему автомобилю будет трудно разогнаться.
Ваш автомобиль оснащен лабиринтом шлангов для подачи топлива и воздуха в камеру сгорания двигателя. Поврежденный, треснувший или ослабленный вакуумный шланг может помешать любому из этих жизненно важных компонентов подать необходимое количество для сгорания.
Ваш автомобиль может работать на слишком богатой смеси, что означает слишком много топлива, или слишком бедная, слишком много воздуха.
Неисправность клапана управления холостым ходом
Этот жизненно важный компонент используется для поддержания надлежащих оборотов на холостом ходу. Клапан управления холостым ходом регулирует количество воздуха, попадающего в корпус дроссельной заслонки, когда дроссельная заслонка закрыта.
Таким образом он регулирует частоту вращения двигателя на холостом ходу и поддерживает скорость, несмотря на активацию зависящих от двигателя изменений, таких как включение кондиционера.Клапан управления холостым ходом имеет решающее значение при попытке перевернуть двигатель с холодного пуска.
В этом случае проблемы с этим компонентом станут более очевидными.
Трансмиссионная жидкость необходима для работы вашей трансмиссии. В автоматической коробке передач трансмиссионная жидкость используется для смазки, действия как охлаждающая жидкость, а также для передачи мощности от двигателя к трансмиссии.
Когда в трансмиссии обнаруживается течь и уровень жидкости падает, автомобиль начинает набирать обороты на более высоких уровнях в результате проскальзывания ленты коробки передач или гидротрансформатора.
Автомобиль также может переключаться нерегулярно или с задержкой. Автомобиль с ручным управлением, испытывающий эту трудность, может быть связан с проскальзыванием сцепления. Хорошим признаком этого является более мягкое сопротивление педали сцепления, а также потеря мощности и трудности с поддержанием скорости.
Любая из вышеперечисленных проблем может привести к увеличению оборотов двигателя или скачку непостоянно. Высокие обороты и возникающие проблемы могут отрицательно сказаться на расходе топлива и увеличить нагрузку на двигатель.Если двигатель вашего автомобиля начинает набирать обороты до более высоких оборотов перед переключением передачи во время ускорения или испытывает ощущение рывков, пора отвезти автомобиль в ремонтный центр для проверки трансмиссии.
ВSun Auto Service работают специалисты , сертифицированные ASE , которые специализируются на ремонте двигателей и трансмиссий. Автомобиль, у которого обороты выше нормы или возникают проблемы с холостым ходом, следует немедленно осмотреть. Вы можете быть уверены в способностях наших технических специалистов.
Будь то мелкий ремонт или капитальный ремонт, наши специалисты обладают опытом, чтобы правильно выполнить обслуживание. Мы гарантируем нашу работу в письменном виде с общенациональной гарантией сроком на 2 года / 24 000 миль и работаем как можно быстрее, чтобы вернуть ваш автомобиль в дорогу.
Для следующего осмотра, обслуживания или ремонта двигателя или трансмиссии посетите ближайший к вам сервисный центр Sun Auto.
6.2 Равномерное круговое движение — Физика
Задачи обучения разделу
К концу этого раздела вы сможете делать следующее:
- Описывать центростремительное ускорение и связывать его с линейным ускорением
- Опишите центростремительную силу и свяжите ее с линейной силой
- Решение проблем, связанных с центростремительным ускорением и центростремительной силой
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и кругов.
- (D) вычислить влияние сил на объекты, включая закон инерции, соотношение между силой и ускорением и характер пар сил между объектами.
Кроме того, в Руководстве по лаборатории физики средней школы рассматривается содержание этого раздела лаборатории под названием «Круговое и вращательное движение», а также следующие стандарты:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и кругов.

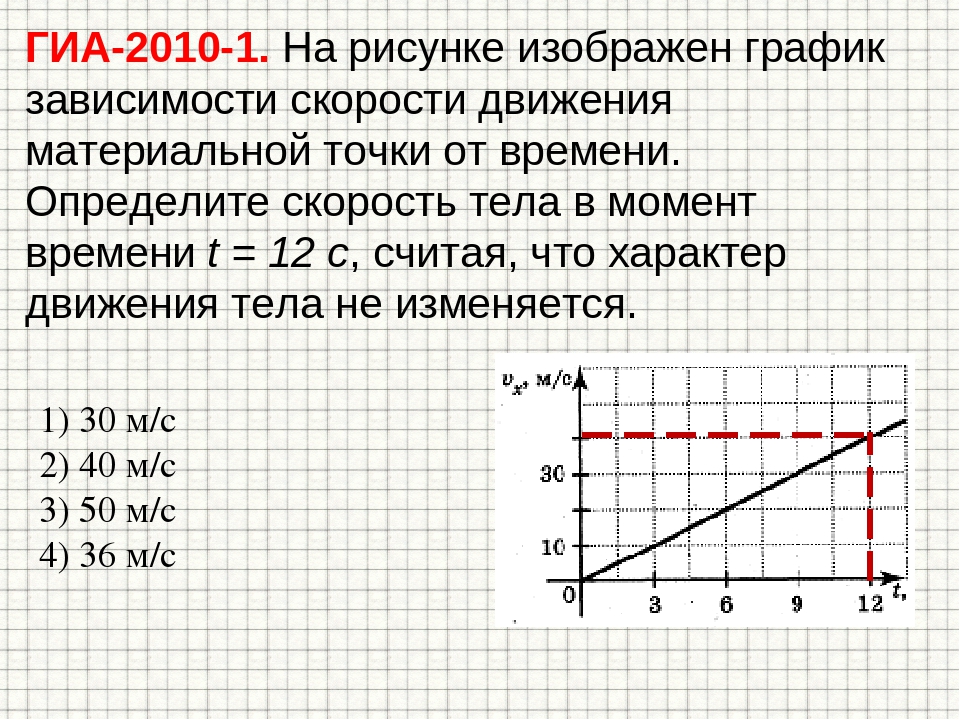 001.408
001.408