Живое сечение потока жидкости это: ЖИВОЕ СЕЧЕНИЕ — это что такое ЖИВОЕ СЕЧЕНИЕ

ЖИВОЕ СЕЧЕНИЕ — это что такое ЖИВОЕ СЕЧЕНИЕ

Значение слова «ЖИВОЕ СЕЧЕНИЕ» найдено в 16 источниках

найдено в «Большой Советской энциклопедии»

        в гидравлике, сечение потока жидкости (в трубопроводе, канале, речном русле и пр.), перпендикулярное направлению скорости её течения. При плавно изменяющемся движении жидкости Ж. с. считается плоским и равным площади поперечного сечения потока.

Найдено 1 изображение:

PreviousNext

Изображения из описаний на этой странице

найдено в «Большой советской энциклопедии»

ЖИВОЕ СЕЧЕНИЕ вгидравлике, сечение потока жидкости (в трубопроводе, канале, речном русле и пр.), перпендикулярное направлению скорости её течения. При плавно изменяющемся движении жидкости Ж. с. считается плоским и равным площади поперечного сечения потока.

найдено в «Техническом железнодорожном словаре»

1) поперечное сечение водного потока (реки, ручья и т. п.), ограниченное сверху поверхностью воды ЛГ, а с боков и снизу — подводным очертанием русла АБВГ. Под мостом Ж. с. потока определяется как сумма живых сечений всех пролетов. Ж. с. определяется непосредственным измерением на месте и служит для вычисления расхода воды, т. е. объема воды, проходящей через Ж. с. водотока в единицу времени; 2) поперечное сечение колосниковой решетки, процентное отношение площади прохода воздуха к общей площади колосниковой решетки; обычно оно составляет около 15%.

Технический железнодорожный словарь. — М.: Государственное транспортное железнодорожное издательство.Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров.1941

найдено в «Энциклопедическом словаре по металлургии»

[cross-section] — площадь сечения образца или изделия за вычетом ее части, занятой трещинами, порами и другого несплошного материала;
Смотри также:
— Сечение
— нейтральное сечение
— контактное сечение
— конечное сечение
— начальное сечение

найдено в «Русско-английском политехническом словаре»

(потока) effective cross-section гидр. , wetted cross-section, cross-section, cross section, hydraulic section, wetted section

* * *

equipotential section

найдено в «Строительном словаре»

вертикальное поперечное сечение водного потока, нормальное к линиям тока.

Источник: Справочник дорожных терминов

найдено в «Русско-чешском словаре»

• profil průtočný

• průtoková plocha průřezu

• průtočný profil

• průtočný průřez

АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
ABCDEFGHIJKLMNOPQRSTUVWXYZ

3.5. Живое сечение. Смоченный периметр. Гидравлический радиус

В гидравлических расчётах для характеристики размеров и формы поперечного сечения потока вводят понятие о

живом сечении и его элементах: смоченном периметре и гидравлическом радиусе.

Живым сечением называется поверхность в пределах потока, проведённая нормально к линиям тока.

Для круглого трубопровода, когда всё поперечное сечение заполнено жидкостью, живым сечение является площадь круга: (рис.3.6).

Рис. 3.6. Элементы потока

Смоченным периметром называют ту часть периметра живого сечения, по которой жидкость соприкасается со стенками трубопровода (рис.3.6). Смоченный периметр обычно обозначают греческой (хи). Для круглой трубы полностью заполненной жидкостью смоченный периметр равен длине окружности:

.

Гидравлическим радиусом называют отношение живого сечения к смоченному периметру, т.е. величину

.

Эта величина характеризует удельную, т.е. приходящуюся на единицу длины смоченного периметра, площадь живого сечения. Легко сделать вывод, что поток с наибольшим гидравлическим радиусом при прочих равных условиях имеет минимальную силу трения, приложенную к смоченной поверхности.

Для круглых труб, полностью заполненных жидкостью, гидравлический радиус равен четверти диаметра:

.

Введение гидравлического радиуса как характерного размера позволяет сравнивать по критерию подобия (Re) потоки с разными формами живого сечения.

Рассмотренные основные понятия позволяют решать самые различные практические задачи гидравлики.

Пример 3.1.

Определить скорость потока в трубопроводе. Диаметр , расход воды (несжимаемой жидкости) -.

Решение. Искомая скорость .

Определим площадь живого сечения:

.

Скорость потока:

.

Гидравлика – это техническая механика жидкости, в которой часто используются упрощённые методы для решения инженерных задач. Во многих случаях при решении практических задач гидравлики удобно применять такие центральные понятия механики, как количество движения (уравнение импульсов) и кинетическая энергия.

В связи с этим необходимо рассмотреть возможность вычисления количества движения и кинетическую энергию потока жидкости по средней скорости, а не по действительным местным скоростям. Это позволит существенно упростить гидравлические расчёты.

Для материального тела массой , движущегося со скоростью, изменение количества движения за времявследствие действия силывыразится векторным уравнением

, (3.7)

где — приращение количества движения, обусловленное импульсом.

Жидкость представляет собой материальную систему, поэтому основной закон механики может быть приложен к любой выделенной из неё массе.

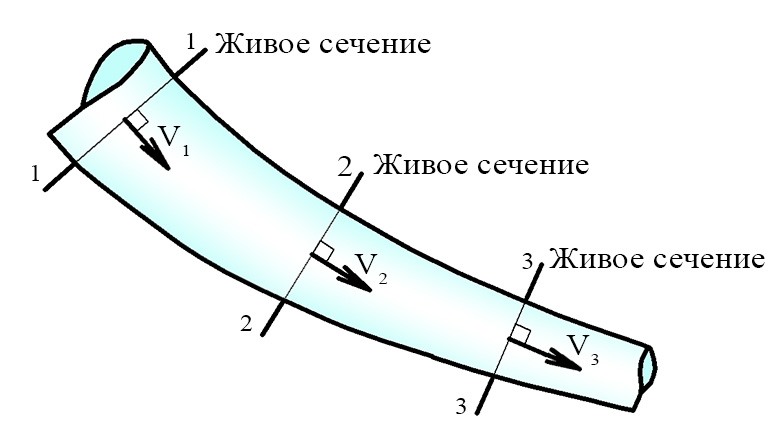
Применим эту теорему механики к участку потока жидкости с расходом между сечениями 1-1 и 2-2 (выделенный участок заштрихован).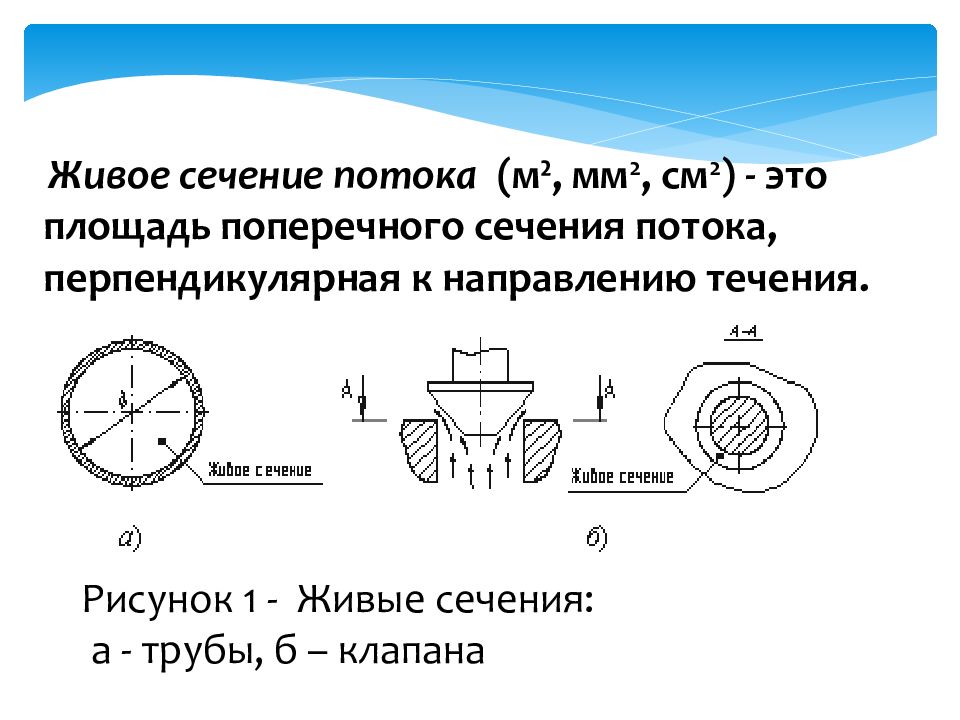 Ограничимся рассмотрением только установившегося движения жидкости (рис. 3.7).

За время этот участок переместится в положение, определяемое сечениямии. Объёмы этих элементов, а, следовательно, и их массыодинаковы, поэтому приращение количества движения будет равно

. (3.8)

Это приращение количества движения обусловлено импульсом всех внешних сил, действующих на объём жидкости между сечениями 1-1 и 2-2. Внешними силами, приложенными к выделенному объёму, являются сила тяжести всего объёма , силы давления в первом и втором сеченияхи(нормальные к этим сечениям и направленные внутрь объёма), а также реакции стенок трубы, которая складывается из сил давления и трения, распределённых по боковой поверхности объёма.

Рис. 3.7. Применение уравнения количества движения

к потоку жидкости

Уравнение импульсов (3.7) для рассматриваемого случая можно записать в виде

.

После сокращения на

. (3.9)

Составив проекции этого векторного уравнения на три координатные оси, получим три алгебраических уравнения с тремя неизвестными — .

Л. Эйлер предложил удобный графический способ нахождения силы . Перенося в формуле (3.?) все слагаемые в одну сторону, можно представить его в виде суммы векторов:

= 0, (3.10)

где вектор взят с обратным знаком (т.е. по направлению обратный действительному). В соответствии с этим выражением (3.10) силуможно найти, построив замкнутый многоугольник сил, как это показано на рис. 3.7,а.

Анализ показывает, что при вычислении количества движения и кинетической энергии по средней скорости допускается ошибка, которую можно учесть с помощью двух коэффициентов:

— коэффициента Буссинеска при вычислении количества движения;

— коэффициента Кориолиса в уравнении Бернулли при вычислении кинетической энергии.

Величина обоих коэффициентов зависит от характера распределения скоростей в поперечном сечении потока жидкости. На практике при турбулентном режиме движения коэффициент Кориолиса , а коэффициент Буссинеска. Поэтому обычно полагают. Однако встречаются отдельные случаи, когдадостигает больших значений, и тогда пренебрежение им может привести к значительным погрешностям.

Пример 3.2. Определить силу воздействия потока жидкости на преграду. Пусть жидкость вытекает в атмосферу и наталкивается на безграничную стенку, установленную нормально к потоку. В результате жидкость растекается по стенке, изменяя направление своего течения на 90⁰ (рис. 3.8). Известны площадь сечения потока , скорость истеченияи плотность жидкости.

Рис. 3.8. Воздействие струи на преграду

Для решения данной задачи берём фиксированный объём, показанный штриховой линией, и применяем теорему Эйлера.

Так как давление внутри струи и по поверхности жидкости равно атмосферному, т.е. избыточное давление равно нулю, уравнение, выражающее теорему Эйлера, для направления, совпадающего с вектором скорости истечения , будет иметь вид

,

или . (3.11)

Это и есть сила воздействия потока жидкости на преграду. При другом угле установке стенки или других её форме и размерах в правую формулы (3.11) вводится безразмерный коэффициент, отличный от единицы, но пропорциональность силы произведениюсохранится.

AP Физика 2 Справка

• Войти
• Биографии репетитора
• Подготовка к тесту

  СРЕДНЯЯ ШКОЛА

  • ACT Репетиторство
  • SAT Репетиторство
  • Репетиторство PSAT
  • ASPIRE Репетиторство
  • ШСАТ Репетиторство
  • Репетиторство STAAR

  ВЫСШАЯ ШКОЛА

  • Репетиторство MCAT
  • Репетиторство GRE
  • Репетиторство по LSAT
  • Репетиторство по GMAT

  К-8

  • Репетиторство AIMS
  • Репетиторство по HSPT
  • Репетиторство ISEE
  • Репетиторство ISAT
  • Репетиторство по SSAT
  • Репетиторство STAAR

  Поиск 50+ тестов

• Академическое обучение

  репетиторство по математике

  • Алгебра
  • Исчисление
  • Элементарная математика
  • Геометрия
  • Предварительный расчет
  • Статистика
  • Тригонометрия

  репетиторство по естественным наукам

  • Анатомия
  • Биология
  • Химия
  • Физика
  • Физиология

  иностранные языки

  • Французский
  • немецкий
  • Латинский
  • Китайский мандарин
  • Испанский

  начальное обучение

  • Чтение
  • Акустика
  • Элементарная математика

  прочее

  • Бухгалтерия
  • Информатика
  • Экономика
  • Английский
  • Финансы
  • История
  • Письмо
  • Лето

  Поиск по 350+ темам

• О
  • Обзор видео
  • Процесс выбора наставника
  • Онлайн-репетиторство
  • Мобильное обучение
  • Мгновенное обучение
  • Как мы работаем
  • Наша гарантия
  • Влияние репетиторства
  • Обзоры и отзывы
  • Освещение в СМИ
  • О преподавателях университета

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Учащиеся, нуждающиеся в помощи по AP Physics 2, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по AP Physics 2. Имея под рукой обязательные концепции обучения и актуальные практические вопросы, AP Physics 2 поможет вам в кратчайшие сроки. Получите помощь сегодня с нашей обширной коллекцией важной информации AP Physics 2.

• AP Физика 2

• Электричество и магнетизм

• Схемы

• Компоненты схемы

• Конденсатор Энергия

• Конденсаторы и емкость

• Конденсаторы и электрические поля

• Свойства конденсаторов и диэлектриков

• Резисторы и сопротивление

• Свойства цепи

• Питание цепи

• Ток и напряжение

• Закон Ома

• Другие принципы схемы

• Удельное сопротивление

• Понимание принципиальных схем постоянного тока

• Принципиальные схемы RC

• Электростатика

• Распределение заряда

• Электрические поля

• Электрическая сила между точечными зарядами

• Электрическая сила в электрическом поле

• Электрическая потенциальная энергия

• Закон Гаусса

• Другие электростатические концепции

• Начисление баллов

• Магнетизм и электромагнетизм

• Электродвижущая сила и магнитный поток

• Индукция

• Магнитные поля

• Магнитная сила

• Другие концепции магнетизма

• Правило правой руки для заряда в магнитном поле

• Правило правой руки для токоведущего провода

• Соленоиды

• Жидкости

• Гидродинамика

• Уравнение Бернулли

• Расход

• Другое гидродинамика

• Поток Пуазейля

• Турбулентность

• Статика жидкости

• Принцип Архимеда

• Выталкивающая сила

• Плотность и удельный вес

• Давление

• Оптика

• Показатель преломления

• Линзы

• Увеличение

• Зеркала

• Другие принципы оптики

• Закон Снелла

• Уравнение тонкой линзы

• Полное внутреннее отражение

• Квантовая и ядерная физика

• Атомная и ядерная физика

• Атомные модели

• Уровни энергии электронов

• Синтез и деление

• Ядерные силы и взаимодействия

• Другие принципы ядерной физики

• Радиоактивный ядерный распад

• Субатомные частицы

• Основы квантовой механики

• Электромагнитный спектр и излучение

• Массово-энергетический эквивалент

• Другие принципы квантовой механики

• Фотоны и фотонная энергия

• Принципы общей теории относительности

• Принципы специальной теории относительности

• Термодинамика

• Теплопередача и тепловое равновесие

• Закон идеального газа

• Кинетическая молекулярная теория

• Законы термодинамики

• Другие концепции термодинамики

• Свойства идеальных газов

• Работа, энтальпия и внутренняя энергия

• Волны

• Эффект Доплера

• Другие концепты Wave

• Представление волн в виде функций синуса и косинуса

• Щелевые эксперименты

• Интерференция волн и дифракция

Создание собственного плана проверки теста AP Physics 2 может занять много времени. Часто время, необходимое для создания учебного пособия, может отнять время, которое можно было бы потратить с большей пользой на изучение материала. Если вы только начинаете подготовку, рассмотрите возможность использования ресурса Varsity Tutors Learning Tools Learn by Concept. Learn by Concept представлен в виде интерактивной программы. Когда вы получите доступ к ресурсу AP Physics Learn by Concept, вы обнаружите, что он выходит далеко за рамки того, что вы ожидаете найти в обычном учебном пособии. Нужен ли вам репетитор по физике в Вирджиния-Бич, репетитор по физике в Индианаполисе или репетитор по физике в Силиконовой долине, работа один на один с экспертом может быть именно тем, что вам нужно для учебы.

Одним из наиболее полезных аспектов Learn by Concept является включение примеров вопросов, ответов и пояснений AP Physics 2. Результатом является упражнение, основанное на вопросах для каждой категории и подкатегории, с которыми вы столкнетесь во время обзора AP Physics. Вы можете просмотреть все темы, затронутые в разделе «Учись по концепции», попытавшись ответить на каждый вопрос, и вы можете сравнить свой ответ с пояснениями, которые сопровождают каждый из примеров вопросов, чтобы еще больше усилить глубину вашей подготовки. Varsity Tutors предлагает ресурсы, такие как бесплатные практические тесты AP Physics 2, которые помогут вам в самостоятельном обучении, или вы можете подумать о репетиторах AP Physics 2 .

Learn by Concept предоставляет вам возможность более глубокого изучения каждой концепции. Например, в категории AP Physics 2 Learn by Concept «Закон Ома» вы найдете вопросы по закону Ома с несколькими вариантами ответов. После того, как вы выберете один из ответов, вам будет показан правильный ответ, сопровождаемый подробным объяснением того, почему этот ответ является правильным. Даже если вы неправильно ответите на первый примерный вопрос AP Physics 2, у вас будет много шансов глубже вникнуть в рассматриваемую концепцию. Интерактивность ресурса Learn by Concept предоставляет вам четкую, краткую и бесплатную практику. В дополнение к справочному разделу AP Physics 2 и репетиторству по AP Physics 2 вы также можете рассмотреть некоторые из наших карточек AP Physics 2 Flashcards.

Еще одним полезным аспектом Learn by Concept является его портативность. Поскольку средство обучения полностью находится в сети, вы сможете использовать ресурс «Учись по концепции» везде, где есть доступ к Интернету. Чтобы сделать обзор еще более удобным, вы можете загрузить приложение Varsity Tutors’ Learning Tools на свое мобильное устройство или планшет. Это дает вам доступ к бесплатной практике AP Physics 2 в любое время, когда вы готовы повторить.

Некоторые из основных понятий, которые вы можете найти в ресурсе Learn by Concept для AP Physics 2, включают:

— Электричество и магнетизм

— Жидкости

— Квантовая и ядерная физика

— Термодинамика

— Волны

— И многие другие.

Когда вы почувствуете, что хорошо разбираетесь в концепциях AP Physics, охватываемых Learn by Concept, вы можете ознакомиться с некоторыми другими бесплатными учебными материалами, доступными через средства обучения Varsity Tutors. Вы найдете карточки, небольшие практические тесты, посвященные конкретному материалу, вопрос дня и даже полноценные практические тесты, предназначенные для имитации реального опыта тестирования. С такими полезными инструментами обучения вы можете создать персонализированный учебный план AP Physics 2, который будет организованным и всеобъемлющим.

Все ресурсы AP Physics 2

6 Диагностические тесты 149 практических тестов Вопрос дня Карточки Learn by Concept

уравнение Бернулли. Равномерны ли давление и скорость в поперечном сечении потока жидкости?

спросил 5 лет, 10 месяцев назад

Изменено 4 года, 11 месяцев назад

Просмотрено 3к раз

$\begingroup$

Течение, изображенное на рисунках, безвихревое, жидкость невязкая, несжимаемая.

Мои вопросы —

1. Является ли давление равномерным и постоянным для всего поперечного сечения (обозначается $A_1$ и $A_2$)?
2. Является ли скорость каждой частицы постоянной для поперечного сечения, перпендикулярного границе трубы, или существует градиент скорости в трубе, перпендикулярной потоку?

Если выше написанное верно, то можно ли применить уравнение неразрывности $A_1 ​​v_1 = A_2 v_2$ к конечным площадям поперечного сечения? Я так не думаю.

Примечание. Сначала я задал этот вопрос, но я чувствую, что он был очень широким, поэтому этот новый вопрос.

• гидродинамика
• уравнение Бернулли

$\endgroup$

$\begingroup$

Учитывая ваши предположения, этот поток удовлетворяет бернуллиевскому закону. Из уравнения неразрывности видно, что скорость будет меняться при изменении площади поперечного сечения. Предполагая, что изменение вертикального расстояния очень незначительно, его можно исключить из уравнения Бернулли. Из уравнения неразрывности v2 меньше v1, так что p2 больше p1. Для данного поперечного сечения, которое перпендикулярно потоку, величина скорости будет такой же, так как на жидкость не действуют силы трения.

$\endgroup$

$\begingroup$

Уравнение неразрывности применимо только к узким трубам бесконечно малой площади поперечного сечения.

Рассмотрим трубку с указанными выше характеристиками. Если жидкость (несжимаемая) не может выйти из боковых стенок трубы, она может втекать и вытекать только через площадь поперечного сечения. В этом предельном случае бесконечно малой площади поперечного сечения мы можем считать, что жидкость имеет постоянную скорость. Таким образом, если мы хотим рассмотреть трубку конечного размера, нам придется написать $$\int \vec{v}_\mathrm{in}\cdot\mathrm{d}\vec{A}_\mathrm{in } = \int \vec{v}_\mathrm{out}\cdot\mathrm{d}\vec{A}_\mathrm{out}$$

Здесь $\vec{v}_\rm{in}$ — скорость элемента жидкости, проходящего внутри трубы и пересекающего малую площадку $\mathrm{d}\vec{A}_\mathrm{in} $. Аналогичные обозначения используются для исходящего потока. Так что в общем случае значение $\vec{v}_\mathrm{out}$ или $\vec{v}_\rm{in}$ может меняться от места к месту и может находиться под любым углом к ​​рассматриваемой область. $\mathrm{d}\vec{A}_\mathrm{in}$ и $\mathrm{d}\vec{A}_\mathrm{out}$ могут быть любыми областями, ограниченными стенками трубы.

Этот результат можно считать подобным закону Гаусса. Если внутри трубы нет источников или стоков, чистый входящий поток жидкости должен быть равен чистому выходящему потоку жидкости.