Поток жидкости и его параметры
Поток жидкости характеризуется такими параметрами как площадь живого сеченияS, расход жидкости Q(G), средняя скорость движения υ.
Живое сечение потока — это сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.
Векторы скорости частиц имеют некоторое расхождение в потоке жидкости.
Живым сечением потока жидкости называется сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости. Поэтому живое сечение потока — криволинейная плоскость (рис. 2, а, линия I—I). В виду незначительного расхождения векторов скорости в гидродинамике за живое сечение принимается плоскость, расположенная перпендикулярно скорости движения жидкости в средней точке потока (рис. 2, б).

Рис. 2. Векторы скорости потока жидкости (
Расход жидкости — это количество жидкости, протекающей через живое сечение потока в единицу времени. Расход может определяться в массовых долях G и объемных Q.
Средняя скорость движения жидкости — это средняя скорость частиц в живом сечении потока.
Если в живом сечении потока, движущегося, например, в трубе, построить векторы скорости частиц и соединить концы этих векторов, то получится график изменения скоростей (эпюра скоростей) (рис. 3).

Рис. 3. Распределение скоростей движения жидкости в живом сечении трубы при течении: а — турбулентном; б — ламинарном
Если площадь такой эпюры разделить на диаметр данной трубы, то получится значение средней скорости движения жидкости в данном сечении:

где Sэ — площадь эпюры местных скоростей;
d — диаметр трубы.
Объемный расход жидкости рассчитывается по формуле
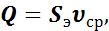
где Q — площадь живого сечения потока.
Параметры потока жидкости определяют характер движения жидкости. При этом оно может быть установившимся и неустановившимся, равномерным и неравномерным, неразрывным и кавитационным, ламинарным и турбулентным.
Похожие статьи:
poznayka.org
3.5. Живое сечение. Смоченный периметр. Гидравлический радиус
В гидравлических расчётах для характеристики размеров и формы поперечного сечения потока вводят понятие о
Живым сечением называется поверхность в пределах потока, проведённая нормально к линиям тока.
Для
круглого трубопровода, когда всё
поперечное сечение заполнено жидкостью,
живым сечение является площадь круга: 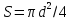 (рис.3.6).
(рис.3.6).

Рис. 3.6. Элементы потока
Смоченным
периметром называют ту часть периметра живого
сечения, по которой жидкость соприкасается
со стенками трубопровода (рис.3.6). Смоченный периметр обычно обозначают
греческой  (хи). Для круглой трубы полностью
заполненной жидкостью смоченный периметр
равен длине окружности:
(хи). Для круглой трубы полностью
заполненной жидкостью смоченный периметр
равен длине окружности:
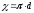 .
.
Гидравлическим радиусом называют отношение живого сечения к смоченному периметру, т.е. величину
 .
.
Эта величина характеризует удельную, т.е. приходящуюся на единицу длины смоченного периметра, площадь живого сечения. Легко сделать вывод, что поток с наибольшим гидравлическим радиусом при прочих равных условиях имеет минимальную силу трения, приложенную к смоченной поверхности.
Для круглых труб, полностью заполненных жидкостью, гидравлический радиус равен четверти диаметра:
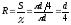 .
.
Введение гидравлического радиуса как характерного размера позволяет сравнивать по критерию подобия (Re) потоки с разными формами живого сечения.
Рассмотренные основные понятия позволяют решать самые различные практические задачи гидравлики.
Пример
3.1. Определить
скорость потока в трубопроводе. Диаметр  ,
расход воды (несжимаемой жидкости) —
,
расход воды (несжимаемой жидкости) —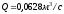 .
.
Решение. Искомая скорость 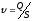 .
.
Определим площадь живого сечения:
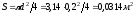 .
.
Скорость потока:

3.6. Уравнение количества движения для потока жидкости
Гидравлика – это техническая механика жидкости, в которой часто используются упрощённые методы для решения инженерных задач. Во многих случаях при решении практических задач гидравлики удобно применять такие центральные понятия механики, как количество движения (уравнение импульсов) и кинетическая энергия.
В связи с этим необходимо рассмотреть возможность вычисления количества движения и кинетическую энергию потока жидкости по средней скорости, а не по действительным местным скоростям. Это позволит существенно упростить гидравлические расчёты.
Для
материального тела массой  ,
движущегося со скоростью
,
движущегося со скоростью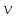 ,
изменение количества движения за время
,
изменение количества движения за время
 выразится векторным уравнением
выразится векторным уравнением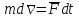 , (3.7)
, (3.7)
где 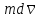 — приращение количества движения,
обусловленное импульсом
— приращение количества движения,
обусловленное импульсом .
.
Жидкость представляет собой материальную систему, поэтому основной закон механики может быть приложен к любой выделенной из неё массе.
Применим
эту теорему механики к участку потока
жидкости с расходом  между сечениями 1-1 и 2-2 (выделенный
участок заштрихован). Ограничимся
рассмотрением только установившегося
движения жидкости (рис. 3.7).
между сечениями 1-1 и 2-2 (выделенный
участок заштрихован). Ограничимся
рассмотрением только установившегося
движения жидкости (рис. 3.7).
За
время  этот участок переместится в положение,
определяемое сечениями
этот участок переместится в положение,
определяемое сечениями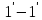 и
и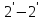 .
Объёмы этих элементов
.
Объёмы этих элементов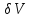 ,
а, следовательно, и их массы
,
а, следовательно, и их массы одинаковы, поэтому приращение количества
движения будет равно
одинаковы, поэтому приращение количества
движения будет равно
 . (3.8)
. (3.8)
Это
приращение количества движения
обусловлено импульсом всех внешних
сил, действующих на объём жидкости между
сечениями 1-1 и 2-2. Внешними силами,
приложенными к выделенному объёму,
являются сила тяжести всего объёма 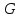
 и
и (нормальные к этим сечениям и направленные
внутрь объёма), а также реакции стенок
трубы
(нормальные к этим сечениям и направленные
внутрь объёма), а также реакции стенок
трубы ,
которая складывается из сил давления
и трения, распределённых по боковой
поверхности объёма.
,
которая складывается из сил давления
и трения, распределённых по боковой
поверхности объёма.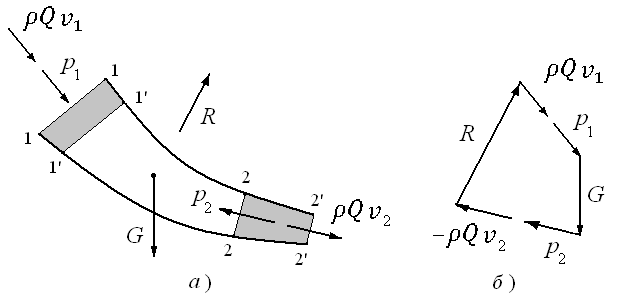
Рис. 3.7. Применение уравнения количества движения
к потоку жидкости
Уравнение импульсов (3.7) для рассматриваемого случая можно записать в виде
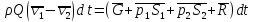 .
.
После
сокращения на 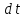
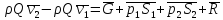 . (3.9)
. (3.9)
Составив
проекции этого векторного уравнения
на три координатные оси, получим три
алгебраических уравнения с тремя
неизвестными —  .
.
Л.
Эйлер предложил удобный графический
способ нахождения силы 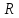 .
Перенося в формуле (3.?) все слагаемые в
одну сторону, можно представить его в
виде суммы векторов:
.
Перенося в формуле (3.?) все слагаемые в
одну сторону, можно представить его в
виде суммы векторов:
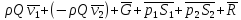 =
0, (3.10)
=
0, (3.10)
где
вектор 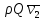 взят с обратным знаком (т.е. по направлению
обратный действительному). В соответствии
с этим выражением (3.10) силу
взят с обратным знаком (т.е. по направлению
обратный действительному). В соответствии
с этим выражением (3.10) силу можно найти, построив замкнутый
многоугольник сил, как это показано на
рис. 3.7,а.
можно найти, построив замкнутый
многоугольник сил, как это показано на
рис. 3.7,а.
Анализ показывает, что при вычислении количества движения и кинетической энергии по средней скорости допускается ошибка, которую можно учесть с помощью двух коэффициентов:
—
коэффициента Буссинеска  при вычислении количества движения
при вычислении количества движения ;
;
—
коэффициента Кориолиса  в уравнении Бернулли при вычислении
кинетической энергии
в уравнении Бернулли при вычислении
кинетической энергии .
.
Величина
обоих коэффициентов зависит от характера
распределения скоростей в поперечном
сечении потока жидкости. На практике
при турбулентном режиме движения
коэффициент Кориолиса 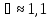 , а коэффициент Буссинеска
, а коэффициент Буссинеска .
Поэтому обычно полагают
.
Поэтому обычно полагают .
Однако встречаются отдельные случаи,
когда
.
Однако встречаются отдельные случаи,
когда достигает больших значений, и тогда
пренебрежение им может привести к
значительным погрешностям.
достигает больших значений, и тогда
пренебрежение им может привести к
значительным погрешностям.
Пример
3.2. Определить
силу воздействия потока жидкости на
преграду. Пусть жидкость вытекает в
атмосферу и наталкивается на безграничную
стенку, установленную нормально к
потоку. В результате жидкость растекается
по стенке, изменяя направление своего
течения на 900 (рис.
3.8). Известны площадь сечения потока  ,
скорость истечения
,
скорость истечения и плотность жидкости
и плотность жидкости .
.
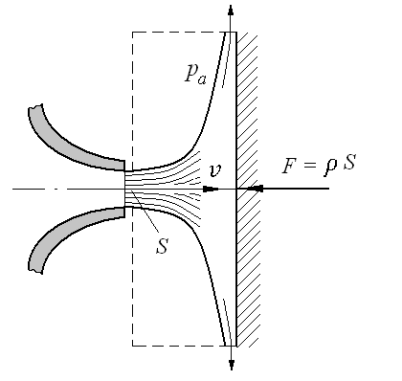
Рис. 3.8. Воздействие струи на преграду
Для
решения данной задачи берём фиксированный
объём, показанный штриховой линией, и
применяем теорему Эйлера. Так как
давление внутри струи и по поверхности
жидкости равно атмосферному, т.е.
избыточное давление равно нулю, уравнение,
выражающее теорему Эйлера, для направления,
совпадающего с вектором скорости
истечения 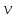 ,
будет иметь вид
,
будет иметь вид
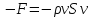 ,
,
или  . (3.11)
. (3.11)
Это
и есть сила воздействия потока жидкости
на преграду. При другом угле установке
стенки или других её форме и размерах
в правую формулы (3.11) вводится безразмерный
коэффициент, отличный от единицы, но
пропорциональность силы 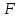 произведению
произведению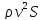 сохранится.
сохранится.
studfile.net
Поток жидкости и его параметры
Поток жидкости — это часть неразрывно движущейся жидкости, ограниченная твердыми деформируемыми или недеформируемыми стенками, образующими русло потока. Потоки, имеющие свободную поверхность, называются безнапорными. Потоки, не имеющие свободной поверхности, называются напорными
Поток жидкости характеризуется такими параметрами как площадь живого сечения S, расход жидкости Q(G), средняя скорость движения v.
Живое сечение потока — это сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.
Векторы скорости частиц имеют некоторое расхождение в потоке жидкости.
Живым сечением потока жидкости называется сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.

Рис. Векторы скорости потока жидкости (а) и живое сечение потока (б)
Поэтому живое сечение потока — криволинейная плоскость (рис. а, линия I—I) В виду незначительного расхождения векторов скорости в гидродинамике за живое сечение принимается плоскость, расположенная перпендикулярно скорости движения жидкости в средней точке потока.
Расход жидкости — это количество жидкости, протекающей через живое сечение потока в единицу времени. Расход может определяться в массовых долях G и объемных Q.
Средняя скорость движения жидкости — это средняя скорость частиц в живом сечении потока.
Если в живом сечении потока, движущегося, например, в трубе, построить векторы скорости частиц и соединить концы этих векторов, то получится график изменения скоростей (эпюра скоростей).

Рис. Распределение скоростей движения жидкости в живом сечении трубы при течении: а — турбулентном; б — ламинарном
Если площадь такой эпюры разделить на диаметр данной трубы, то получится значение средней скорости движения жидкости в данном сечении:
Vcр = Sэ/d,
где Sэ — площадь эпюры местных скоростей; d — диаметр трубы
Объемный расход жидкости рассчитывается по формуле:
Q = Sэ*Мср,
где Q — площадь живого сечения потока.
Параметры потока жидкости определяют характер движения жидкости. При этом оно может быть установившимся и неустановившимся, равномерным и неравномерным, неразрывным и кавитационным, ламинарным и турбулентным.
Если параметры потока жидкости не изменяются во времени, то ее движение называется установившимся.
Равномерным называется движение, при котором параметры потока не изменяются по длине трубопровода или канала. Например, движение жидкости по трубе постоянного диаметра является равномерным.
Неразрывным называется движение жидкости, при котором она перемещается сплошным потоком, заполняющим весь объем трубопровода.
Отрыв потока от стенок трубопровода или от обтекаемого предмета приводит к возникновению кавитации.
Кавитацией называется образование в жидкости пустот, заполненных газом, паром или их смесью.
Кавитация возникает в результате местного уменьшения давления ниже критического значения pкр при данной температуре (для воды ркр= 101,3 кПа при Т= 373 К или ркр= 12,18 кПа при Т= 323 К и т. д.). При попадании таких пузырьков в зону, где давление выше критического, в эти пустоты устремляются частицы жидкости, что приводит к резкому возрастанию давления и температуры. Поэтому кавитация неблагоприятно отражается на работе гидротурбин, жидкостных насосов и других элементов гидравлических устройств.
Ламинарное движение — это упорядоченное движение жидкости без перемешивания между ее соседними слоями. При ламинарном течении скорость и силы инерции, как правило, невелики, а силы трения значительны. При увеличении скорости до некоторого порогового значения ламинарный режим течения переходит в турбулентный.
Турбулентное движение — это течение жидкости, при котором ее частицы совершают неустановившееся беспорядочное движение по сложным траекториям. При турбулентном течении скорость жидкости и ее давление в каждой точке потока хаотически изменяется, при этом происходит интенсивное перемешивание движущейся жидкости.
Для определения режима движения жидкости существуют условия, согласно которым скорость потока может быть больше или меньше той критической скорости, когда ламинарное движение переходит в турбулентное и наоборот.
Однако установлен и более универсальный критерий, который называют критерием или числом Рейнольдса:
Re = vd/V,
где Re — число Рейнольдса; v — средняя скорость потока; d — диаметр трубопровода; V — кинематическая вязкость жидкости.
Опытами было установлено, что в момент перехода ламинарного режима движения жидкости в турбулентный Re = 2320.
Число Рейнольдса, при котором ламинарный режим переходит в турбулентный, называется критическим. Следовательно, при Re < 2320 движение жидкости — ламинарное, а при Re > 2320 — турбулентное. Отсюда критическая скорость для любой жидкости:
vкр = 2320v/d
ustroistvo-avtomobilya.ru
15) Элементарная струйка, поток жидкости, живое сечение. Гидравлический радиус, расход и средняя скорость.
Часть потока, заключенная внутри трубки тока, называется элементарной струйкой. Поток Ж – представляет собой совокупность элементарных струек.
Живым сечением – сечение потока Ж, перпендикулярное направлению скорости ее сечения. При плавно изменяющемся движении Ж сечение считается плоским и равным площади поперечного сечения потока ().
Площадь живого сечения S= dS
Расход
потока Q
— объем жидкости V,
протекающей за единицу времени t
через живое сечение ω. 
Средняя
скорость потока υ
— скорость движения жидкости, определяющаяся
отношением расхода жидкости Q
к площади живого сечения ω 
Гидравлический
радиус потока R
— отношение живого сечения к смоченному
периметру 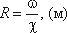 Смоченный
периметр χ
(«хи») — часть периметра живого
сечения, ограниченное твердыми стенками.
Смоченный
периметр χ
(«хи») — часть периметра живого
сечения, ограниченное твердыми стенками.
16) Уравнение неразрывности. Понятие расхода.
Течение жидкости
называют стационарным,
если в каждой точке пространства,
занимаемого жидкостью, ее скорость с
течением времени не изменяется.Жидкости
практически несжимаемы,
т. е. можно считать, что данная масса
жидкости всегда имеет неизменный объем.
Поэтому одинаковость объемов жидкости,
проходящих через разные сечения трубы,
означает, что скорость течения жидкости
зависит от сечения трубы. Пусть скорости
стационарного течения жидкости через
сечения трубы S1 и S2 равны соответственно v1 и v2.
Объем жидкости, протекающей за промежуток
времени t через сечение S1,
равен V1=S1v1t,
а объем жидкости, протекающей за то же
время через сечение S2, равен V2=S2v2t.
Из равенства V1=V2 следует, что  уравнением
неразрывности.
Из него следует, что
уравнением
неразрывности.
Из него следует, что 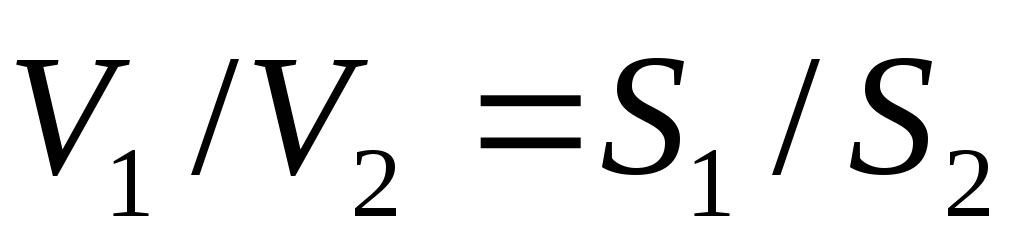 Следовательно, при стационарном течении
жидкости скорости движения ее частиц
через разные поперечные сечения трубы
обратно пропорциональны площадям этих
сечений.
Следовательно, при стационарном течении
жидкости скорости движения ее частиц
через разные поперечные сечения трубы
обратно пропорциональны площадям этих
сечений.
Расходом называется количество жидкости, протекающее через живое течение потока (струйки) в единицу времени. Различают объёмный Q (м3/с), весовой QG(Н/с) и массовый Qm(кг/с) расходы.
 ;
; 

17) Распределение сил в сплошной среде. Объемные и поверхностные силы.
Внешние силы: массовые (объемные) и поверхностные.
Массовые силы в соответствии со вторым законом Ньютона пропорциональны массе жидкости или, для однородной жидкости, — ее объему. К ним относятся сила тяжести и сила инерции переносного движения.
Поверхностные силы непрерывно распределены по поверхности жидкости и при равномерном их распределении пропорциональны площади этой поверхности.
Массовые силы относят к единице массы, а поверхностные к единице площади
Сплошна́я среда́ — механическая система, обладающая бесконечным числом внутренних степеней свободы. Её движение в пространстве, в отличие от других механических систем, описывается не координатами и скоростями отдельных частиц, а скалярным полем плотности и векторным полем скоростей.
Если плотность сплошной среды постулируется равной константе, то такая сплошная среда называется несжимаемой.
18) Уравнение Бернулли для установившегося движения жидкости.
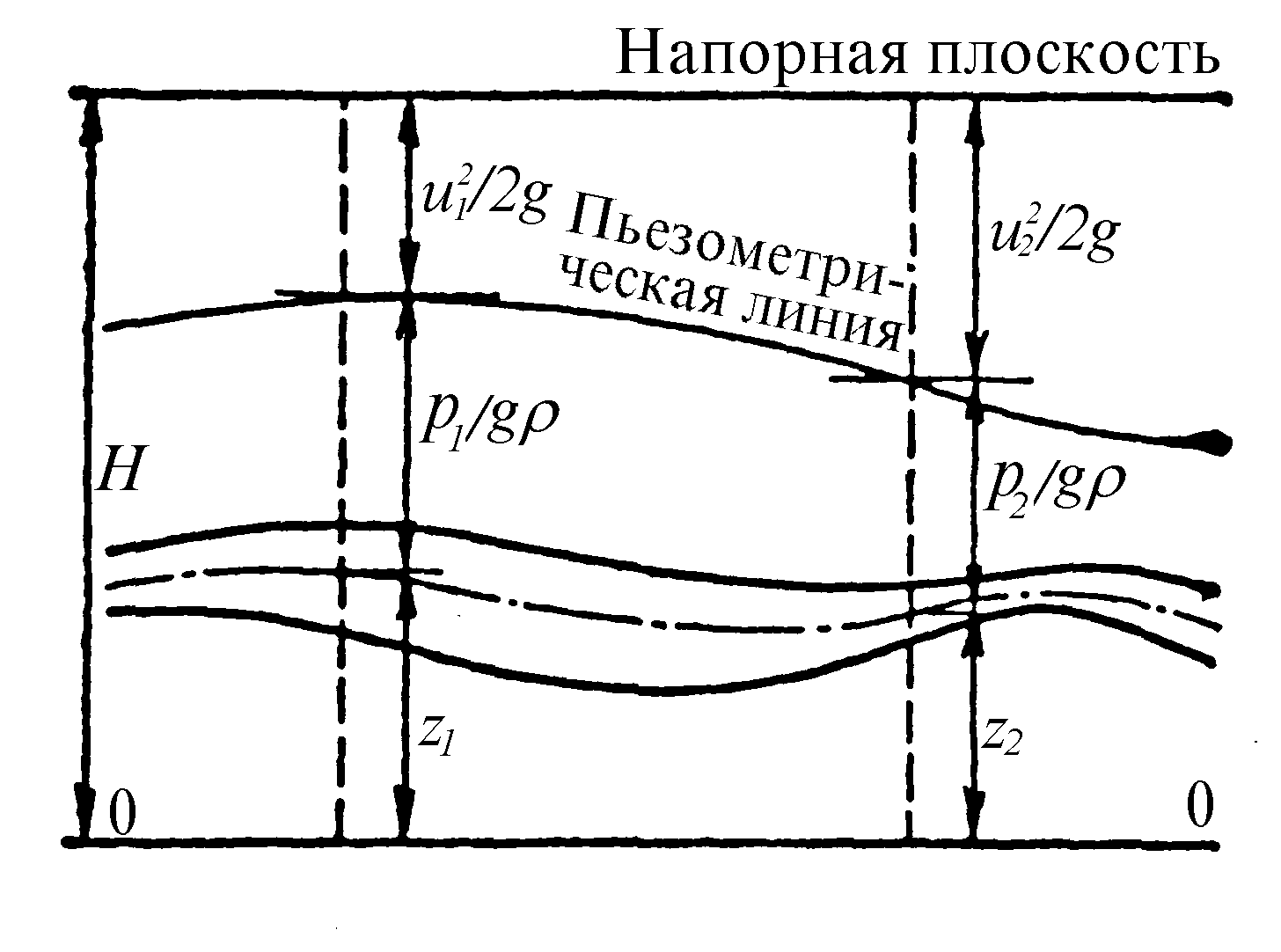
Напорная линия – линия показывающая изменение гидродинамического напора Ж по длине потока
Линия, соединяющая уровни Ж в пьезометрах наз-ся пьезометрической линией
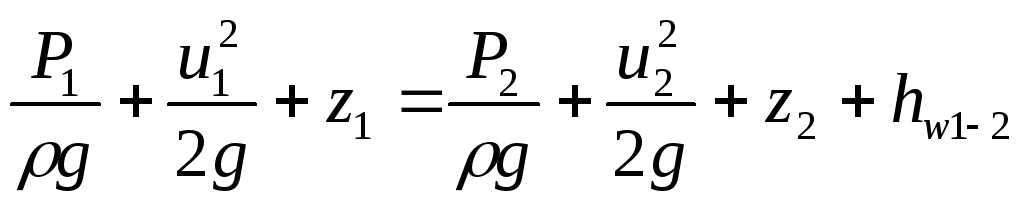
Отметим, что в такой записи члены уравнения выражают удельную энергию, отнесенную к весу (Mg = G).
Как и в гидростатике, величину z называют высотой положения, а величину p/gρ — пьезометрической высотой.
Сумма первых двух членов уравнения z + p/gρ — пьезометрический напор.
Третий член уравнения u2/2g линейная величина. Как известно, начавшаяся двигаться вертикально со скоростью u при отсутствии сопротивления движению, поднялась бы на высоту u2/2g. Этот член уравнения Бернулли называется скоростной высотой или скоростным напором.
studfile.net
Основные параметры потока
Живое сечение потока – поверхность в пределах потока, перпендикулярная к направлению его движения.
Живое сечение потока характеризуется площадью живого сечения ω, смоченным периметром χ, гидравлическим радиусом Rг.
Смоченный периметр χ – часть периметра живого сечения потока, по которому он соприкасается с твердыми стенками.

Рисунок 3.1
Гидравлический радиус R – отношение площади живого сечения потока к смоченному периметру.
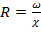 (3.1)
(3.1)
Расход потока (Q) – это количество жидкости, протекающей через живое сечение потока в единицу времени.
Различают расход: объемный Q, весовой G, массовый M.
Объемный расход:
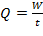 , м3/с (3.2)
, м3/с (3.2)
Весовой расход:
 , Н/с (3.3)
, Н/с (3.3)
Массовый расход:
 , кг/с (3.4)
, кг/с (3.4)
Уравнение расхода. Средняя скорость потока
При установившимся движении несжимаемой жидкости и отсутствии притока и оттока жидкости между рассматриваемыми сечениями 1–1, 2–2 и n–n расход на участке потока между ними является постоянным:
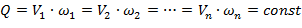 (3.5)
(3.5)

Рисунок 3.2
Выражение (3.5) называется уравнением постоянства объемного или уравнением неразрывности движения для потока.
Из него следует:
 (3.6)
(3.6)
Т.е. средние скорости в живых сечениях потока несжимаемой жидкости обратно пропорциональны их площадям.
Уравнение расхода является законом сохранения вещества для потока (струйки) жидкости, записанное при условии постоянства плотности жидкости в пределах рассматриваемого потока (струйки).
Средней скоростью в живом сечении V называется условная, одинаковая для всех точек сечения скорость, при которой расход потока будет такой же, как и при различных местных скоростях.
Средняя скорость в живом сечении может быть определена из формулы:
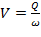 , м/с (3.7)
, м/с (3.7)
Похожие статьи:
poznayka.org
Потоки живое сечение — Справочник химика 21
Живым сечением потока называется сечение в пределах потока, нормальное к направлению движения жидкости. Площадь живого сечения принято измерять в м или см . [c.13]Отношение площади живого сечения потока/к смоченному периметру П называется гидравлическим радиусом г,, и служит одной из важнейших характеристик потока. Учетверенное значение гидравлического радиуса называется эквивалентным диаметром Таким образом, [c.92]
Скорость потока, необходимая для определения величин Ке, St, Ар, рассчитывается по живому сечению, перпендикулярному направлению движения потока. Живое сечение определяется по формуле [c.284]
Задаваясь различными степенями наполнения для данного сечения, можно определить расход воды, соответствующий критической глубине потока. Живое сечение, отвечающее заданному минимальному расходу, будет иметь высоту, равную критической глубине. [c.41]
В гидравлике различают следующие характеристики потока живое сечение, смоченный периметр, гидравлический радиус. [c.52]
Подъемная сила, с которой поток действует на частицы, определяется скоростью потока в живом сечении аппарата, т. е. в пустотах между частицами. Поэтому при заданной линейной скорости потока (отнесенной к полному сечению аппарата) подъемная сила будет тем больше, чем меньше начальная пористость слоя. [c.70]
Уравнение Д. Бернулли справедливо и для потока идеальной жидкости при умеренных скоростях движения жидкости и плавно изменяющемся живом сечении. В этом случае р — среднее гидростатическое давление в данном живом сечении, 2 — геодезическая высота центра тяжести этого сечения, а хз — средняя скорость потока в том же живом сечении. [c.14]
О—поперечное сечение потока (живое сечение) X смоченный периметр — гидравлический ра- [c.21]
Поперечное сечение потока ( живое сечение ), смоченный периметр и гидравлический радиус (фиг. 3-2), [c.42]
Расходом жидкости называется ее количество, протекающее через живое сечение потока в единицу времени. Обычно расход измеряется в единицах объема (м /с, м /ч, л/с), однако может измеряться и в единицах массы (кг/с). В первом случае расход называется объемным, во втором —массовым. [c.13]
Значит, при установившемся движении жидкости средние скорости потока обратно пропорциональны площади живых сечений, т. е. чем меньше сечение, тем больше скорость, и наоборот. [c.13]
Поперечное сечение потока, живое сечение потока— поверхность, нормальная в каждой точке к направлению осредненной скорости в этой точке. [c.8]
О) — поперечное сечение потока (живое сечение) х
www.chem21.info
Основные характеристики движения жидкостей.
Рассмотрим поток жидкости в некоторый момент времени. Для наглядного представления общей картины течения жидкости в каждый данный момент мысленно проведем так называемую линию тока, т.е. линию, в каждой точке которой в данное мгновение вектор скорости жидкости совпадает с на- правлением касательной к этой линии. При установившемся движении линии
 |
тока совпадают с траекториями движущихся частиц. Построим замкнутый контур, образующий малую площадку dS , и через все точки данного контура проведем линии тока. Эти линии образуют поверхность, называемой трубкой тока. Если через все точки площади dS провести линии тока, получим элементарную струйку, т.е. пучок линий тока. Совокупность элементарных струек образует поток.
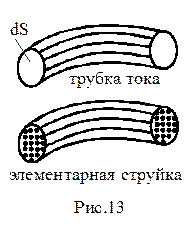 |
При решении многих задач гидродинамики делаются предположения о том, что: а) поток жидкости состоит из отдельных элементарных струек, которые в случае установившегося движения не меняют во времени своей формы; б) поверхность элементарной струйки является как бы непроницаемой для частиц жидкости, движущихся в данной и соседней струйках; в) вследствие малости поперечного сечения элементарной струйки скорости во всех точках ее поперечного сечения можно считать одинаковыми. Такая модель жидкости называется струйной моделью движения жидкости. Данное представление о структуре потока упрощает его теоретическую интерпретацию.
Живое сечение элементарной струйки — элементарно малая площадка, являющаяся площадью поперечного сечения струйки, нормального к линии тока.
Живое сечение потока — площадь поперечного сечения, нормального к вектору средней скорости.
Средней скоростью движения жидкости v в рассматриваемом живом сечении называется скорость, с которой должны были бы двигаться все частицы жидкости через данное живое сечение, чтобы расход всего потока был равен расходу, соответствующему действительным скоростям частиц.
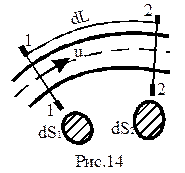 |
Расход элементарной струйки (элементарный расход) dQ- это объем жидкости, проходящий в единицу времени через живое сечение элементарной струйки. Предположим, что в сечении 1-1 скорость движения равна u. Данная скорость одинакова для всех частиц жидкости, движущихся через сечение 1-1 (свойство “в” элементарной струйки). За время dt частицы жидкости, находящиеся в сечении 1-1, двигаясь со скоростью u переместятся в сечение 2-2, совершив путь dL. За время dt через живое сечение элементарной струйки dS пройдет количество жидкости равное объему цилиндра dS•dL. Отнеся расчеты к единице времени, получим dQ=dS•dL=dS•u, т.к. скорость u=dL/dt, то при dt=1 величина u=dL (скорость — путь, совершенный в единицу времени).
Расходом жидкости Q в рассматриваемом сечении называется объем жидкости W проходящей в единицу времени t через живое сечение потока.
Расход равен сумме расходов элементарных струек:
 =
=  (2-17)
(2-17)
Таким образом:
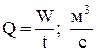 (2-18)
(2-18)
В ряде случаев следует различать объемный расход Q и массовый расход M, который представляет собой массу жидкости m, проходящей в единицу времени:  . Между объемным Q и массовым M расходом существует следующая зависимость: M=rQ. В гидравлике приходиться иметь дело главным образом с объемным расходом. В дальнейшем будем называть его просто расходом.
. Между объемным Q и массовым M расходом существует следующая зависимость: M=rQ. В гидравлике приходиться иметь дело главным образом с объемным расходом. В дальнейшем будем называть его просто расходом.
В соответствии с понятием средней скорости примем, что все частицы движутся с одинаковой средней скоростью v. Тогда в уравнении (2-17) заменим переменную скорость u постоянной средней v:
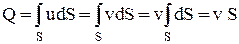 , (2-19)
, (2-19)
т.е. расход потока жидкости равен площади живого сечения потока, умноженной на среднюю скорость.
Гидравлические элементы потока.
Основные гидравлические элементы потока — живое сечение S (см. выше), смоченный периметр P, гидравлический радиус RГ и эквивалентный диаметр dЭ.
Смоченным периметром называется длина контура живого сечения, по которому жидкость соприкасается со стенкой.
Гидравлический радиус равен отношению площади живого сечения потока к смоченному периметру:
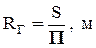 (2-20)
(2-20)
Эквивалентный диаметр — это учетверенный гидравлический радиус
 (2-21)
(2-21)
Иначе говоря, эквивалентный диаметр равен диаметру гипотетического трубопровода круглого сечения, для которого отношение S к P имеет то же значение что и для данного трубопровода некруглого сечения.
Похожие статьи:
poznayka.org
