Кривошипно шатунный механизм схема: ᐉ Схема кривошипно-шатунного механизма

Содержание

Григорьев Е.А. Кинематика и динамика кривошипно-шатунного механизма двигателя

Скачать все файлы (2374.2 kb.)

Доступные файлы (4):

n1.doc	4890kb.	30.01.2012 22:41	скачать
n2.doc	5533kb.	30.01.2012 22:41	скачать
n3.doc	2014kb.	30.01.2012 22:40	скачать
n4.doc	2000kb.	30.01.2012 22:41	скачать

1 2 3 4 5

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Е.А. Григорьев

КИНЕМАТИКА И ДИНАМИКА КРИВОШИПНО-ШАТУННОГО МЕХАНИЗМА ДВИГАТЕЛЯ

Учебное пособие

Волгоград 2004

УДК 621.43

Рецензенты
Кинематика и динамика кривошипно-шатунного механизма двигателя: Учебное пособие / Е. А. Григорьев; Волгорад. гос. техн. ун-т. – Волгоград, 2004. – 105 с.

ISBN
Особенностью настоящей работы является широкое использование обобщенных расчетных схем и формул. Решение рассматриваемых вопросов осуществляется на основе аналитических и численных методов, что позволяет получить более строгие и новые результаты. Кроме того, рассматриваются силы с учетом работы на разных скоростных и нагрузочных режимах, что оказывается возможным на основе теории случайных функций.

Пособие предназначено для студентов специальности 101200 и может быть использовано при изучении курса «Динамика двигателей», а также в процессе курсового и дипломного проектирования.

Ил. . Библиогр.: назв.
Печатается по решению редакционно-издательского совета Волгоградского технического университета
ISBN © Волгоградский
государственный
технический
университет

СОДЕРЖАНИЕ

Предисловие 4

1. Кинематика кривошипно-шатунного механизма 7

1. 1. Общие положения 7

1.2. Кинематика шатуна 8

1.3. Предельный внутренний контур картера двигателя 13

1.4. Кинематика поршня 16

1.5. Кинематика кривошипно-шатунного механизма с прицепным шатуном 30

1.6. Изменение объема надпоршневого пространства 36

2. Динамика кривошипно-шатунного механизма 40

2.1. Приведение масс 40

2.2. Силы, действующие на поршень 44

2.3. Силы, действующие в кривошипно-шатунном механизме 51

2.4. Гармонический анализ сил давления газов 54

2.5. Спектр гармоник тангенциальных сил инерции 58

2.6. Силы, действующие на шатунную шейку и шатунный подшипник 60

2.7. Силы, действующие на коренную шейку и коренной подшипник 66

3. Крутящий момент двигателя 72

3.1. Суммарный момент 72

3.2. Гармоники крутящего момента сил давления газов 76

3.3. Гармоники крутящего момента сил инерции 80

3.4. Неравномерность скорости вращения коленчатого вала 81

4. Оценка сил, действующих на двигатель с учетом работы на разных
скоростных и нагрузочных режимах 88

4.1. Основы теории случайных процессов 88

4.2. Плотность распределения скоростных и нагрузочных режимов работы двигателя 91

4.3. Спектральная плотность гармоник сил давления газов и инерции ………….95

Литература 105

ПРЕДИСЛОВИЕ

Поршневой двигатель внутреннего сгорания (ДВС) является самой распространенной тепловой машиной, в которой теплота, выделяющаяся при сгорании внутри цилиндра топлива, превращается в полезную механическую работу. Это связано, прежде всего, с высоким коэффициентом полезного действия (КПД) и, следовательно, топливной экономичностью. Решающим фактором оказывается возможность реализовать высокую степень сжатия, поскольку рабочие процессы совершаются последовательно (циклически) в замкнутом объеме, ограниченном цилиндром, поршнем и крышкой (головкой).

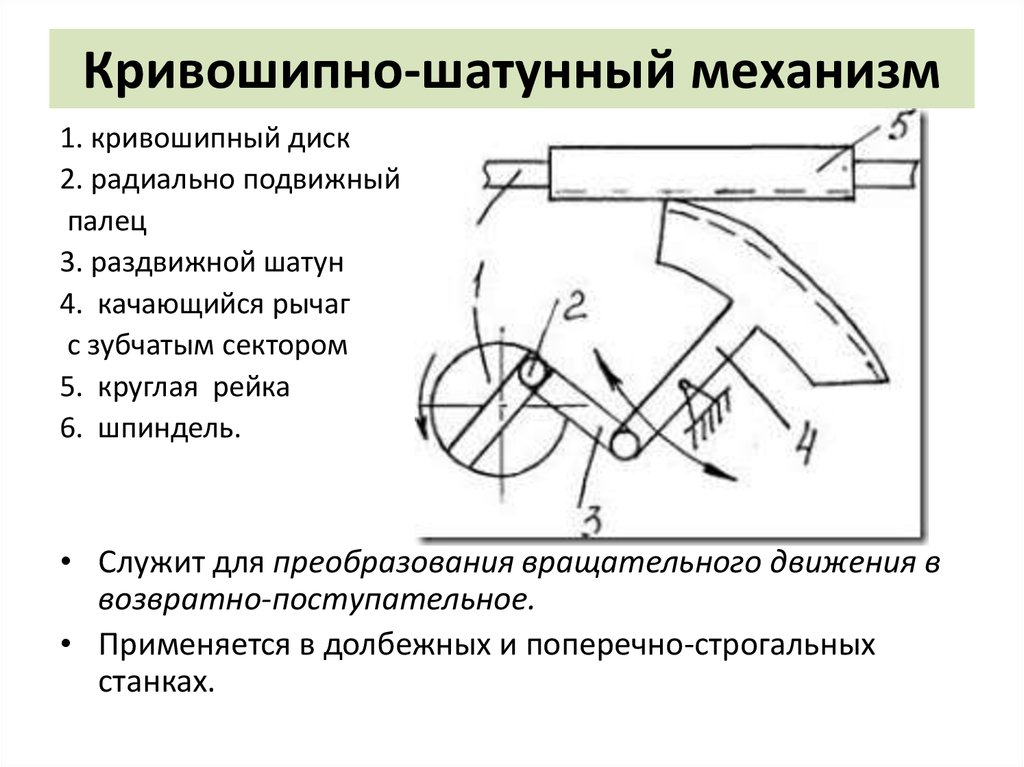
Другой особенностью рассматриваемого типа двигателя является наличие механизма для преобразования возвратно-поступательного движения поршня во вращательное движение вала. Известны различные конструкции такого механизма: механизм с вращающейся шайбой при расположении осей цилиндров параллельной оси вала, механизм С.С. Баландина, симметричный ромбический механизм и др. Однако самое большое распространение имеет кривошипно-шатунный механизм (КШМ). Использование такого механизма порождает, как известно, серьезные проблемы, связанные с кинематикой и динамикой: большие скорости, ускорения и силы инерции возвратно-поступательно движущихся масс, имеющие к тому же ряд частотных составляющих. Сюда следует добавить и силы давления газов, с их сложным периодическим характером, выражающимся спектром гармоник с разной амплитудой и частотой. Что касается роторно-поршневых двигателей, то они несмотря на преимущества, обусловленные отсутствием поступательно движущихся масс и связанных с этим инерционных нагрузок, не получили распространения. Это, однако, определяется недостатками, не связанными с кинематикой и динамикой.

Значительное развитие кинематики и динамики представлено в трудах Российских ученых Л. К. Мартенса (1932 г.), Е.Д. Львова (1936 г.), И.Ш. Нейман (1940 г.), Ф.Ф. Симакова (1954 г.), П.В. Истомина (1964 г.), К.Г. Попык (1970 г.), А.И. Яманина (2004 г.).

Совершенствование поршневых двигателей направлено не только на повышение их КПД, но и непрерывное форсирование их скоростных и нагрузочных режимов. При этом значительно возрастают силы и моменты (инерционные и давления газов), действующие на двигатель и его детали. Связанные с этим повышенные износы и разрушения, усиливаются из-за колебаний двигателя, его частей и машины, на которой он установлен. Кроме того, они оказывают вредное воздействие на человека.

Следует иметь в виду также, что постоянно возрастают требования по повышению надежности и комфортабельности машины при уменьшении материалоемкости и габаритов. Несмотря на большое число исследовательских работ, в свете современного состояния и требований науки и техники эта проблема еще не достаточно изучена.

Первая глава посвящена анализу кинематики КШМ, который строится на основе соотношений для произвольной точки шатуна. Принимая координаты оси поршневого пальца в системе координат, связанной с шатуном, получаем выражение перемещения поршня. Такой подход позволяет получить не только кинематические соотношения для шатуна, но и координаты точек предельного внутреннего контура картера КШМ.

Анализ, основанный на переходе от одной системы прямоугольных координат к другим, позволил получить кинематические соотношения для КШМ с прицепным шатуном, которые являются более простыми и точными.

Во второй главе рассмотрены силы, действующие в КШМ на основе методики, более приспособленной к аналитическому решению и использованию ЭВМ.

В третьей главе дан анализ крутящего момента и неравномерности скорости вращения коленчатого вала.

Четвертая глава посвящена оценке сил и моментов, действующих на двигатель с учетом работы на различных скоростных и нагрузочных режимах. С использованием теории случайных функций получены выражения спектральных плотностей гармоник сил давления газов и инерции.

1 2 3 4 5

Готовые работы

Поиск по сайту

ГОТОВЫЕ РАБОТЫ ПО ТЕМЕ „ТММ“

выберите тип искомой работы

любой • Дипломная работа • Диссертация • Доклад • Контрольная работа • Курсовая работа (с практической частью) • Курсовая (теоретическая) работа • Лабораторная работа • Лекция • Набор текста • Научно-исследовательская работа • Ответы на вопросы • Отчет по практике • Повышения % Авторства работ • Презентация в PowerPoint • Реферат • Рецензия • Статья • Тест • Чертежи • Экзамен (срочная помощь) или тест онлайн на сайте ВУЗа • Эссе

задание 2 вариант 9. 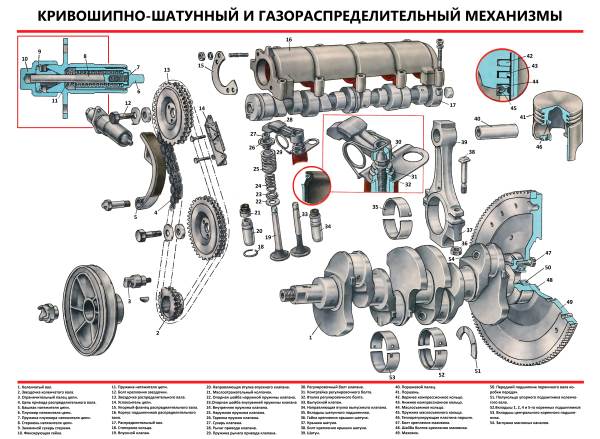Дано: Размеры звеньев, м: lOA = 0,090 lAB = 0,350 lOS1 = 0,040 lOS2 = 0,170 а = 0,0 nОА =2160 об/мин I = 0,12кг•м2 m1 = 3кг m2 = 12кг m3 = 10кг Р = 1,8кН Курсовая работа (с практической частью) 2015
курсовая :Механизм долбежного станка Определение скоростей точек механизма при помощи плана скоростей. Определение ускорений звеньев механизма при помощи плана ускорений. Нахождение уравновешивающей силы и уравновешивающего момента. Находим уравновешивающую силу при помощи групп Ассура. Найдём уравновешивающую силу при помощи рычага Жуковского. Построение графика зависимости приведённого момента, работы и изменения кинетической энергии механизма от угла поворота ведущего звена. Курсовая работа (с практической частью) 2012
курсовая работа задание 3.2 исследование рычажного механизма «проектирование механизма ДВС компрессорной установки» Курсовая работа (с практической частью) 2013
курсовая работа задание 6.2 проектирование механихма блокировки захватного устройства Курсовая работа (с практической частью) 2013
Курсовая работа По «Теории машин и механизмов» Плоский кривошипно-шатунный механизм Вар. 7 схема 10 Курсовая работа (с практической частью) 2016
Курсовая работа По «Теории машин и механизмов» Плоский кривошипно-шатунный механизм Вариант 5. Схема 15 Курсовая работа (с практической частью) 2017
Курсовая работа По «Теории машин и механизмов» Плоский кривошипно-шатунный механизм схема 1 вариант 2 Курсовая работа (с практической частью) 2017
Курсовая работа По «Теории машин и механизмов» Плоский кривошипно-шатунный механизм схема 12 вариант 2. из чертежей делать только кинематическую схему формата А1. Курсовая работа (с практической частью) 2016
Курсовая работа По «Теории машин и механизмов» Плоский кривошипно-шатунный механизм схема 13 вариант 2 Курсовая работа (с практической частью) 2015
Курсовая работа По «Теории машин и механизмов» Плоский кривошипно-шатунный механизм схема 14 вариант 2 Курсовая работа (с практической частью) 2016
Курсовая работа По «Теории машин и механизмов» Плоский кривошипно-шатунный механизм схема 16 вариант 2 Курсовая работа (с практической частью) 2015
Курсовая работа По «Теории машин и механизмов» Плоский кривошипно-шатунный механизм схема 20 вариант 2 Курсовая работа (с практической частью) 2016
Курсовая работа По «Теории машин и механизмов» Плоский кривошипно-шатунный механизм схема 20 вариант 7 Курсовая работа (с практической частью) 2017
Курсовая работа По «Теории машин и механизмов» Плоский кривошипно-шатунный механизм схема 4 вар 6 Курсовая работа (с практической частью) 2017
Курсовая работа По «Теории машин и механизмов» Плоский кривошипно-шатунный механизм Схема 6, вариант 6 Курсовая работа (с практической частью) 2017
Курсовая работа По «Теории машин и механизмов» Плоский кривошипно-шатунный механизм схема 7 вариант 8 Курсовая работа (с практической частью) 2017
Курсовая работа По «Теории машин и механизмов» схема 20, вариант 10 Плоский кривошипно-шатунный механизм Курсовая работа (с практической частью) 2017
курсовая работа по ТММ : Дано: Размеры звеньев, м: lOA = 0,10 lAB = 0,470 lOS1 = 0,050 lOS2 = 0,220 а = 0,2 nОА =300 об/мин I = 0,26кг·м2 m1 = 4кг m2 = 14кг m3 = 12кг Р = 1,0кН Курсовая работа (с практической частью) 2015
Курсовая работа. Теория механизмов и машин Тема 8 ВАР 6. 1. Структурный анализ схем пространственного и сложного плоского рычажных механизмов. 1.1 Вычертить структурную схему сложного плоского рычажного механизма;1.2 Выбрать структурную формулу соответствующую заданной структурной схеме сложного плоского рычажного механизма;1.3 Определить число и кинематического состояние звеньев содержащихся с структуре механизма, результат представить в виде таблицы;1.4 Определить число, название, класс, подвижность, вид контакта и замыкания всех кинематических пар, результат представить в виде таблицы;1.5 Курсовая работа (с практической частью) 2013
курсовая работа: Выполнить кинематический и динамический анализ рычажного механизма. Курсовая работа (с практической частью) 2015
курсовая работа: Задача 1 Для заданной схемы выполнить структурный анализ. Задача 2 По заданным геометрическим параметрам построить кинематическую схему плоского механизма. Считая угловую скорость кривошипа 1 постоянной величиной, выполнить кинематический анализ рычажного механизма графоаналитическим методом. Определить угловые и линейные скорости и ускорения всех звеньев механизма, а также скорость и ускорение точки С для заданного положения механизма. Курсовая работа (с практической частью) 2017
курсовая работа: Исследование кривошипно – ползунного механизма Курсовая работа (с практической частью) 2017
курсовая: Выбор и обоснование метода получения заготовки. Выбор общих припусков и расчет размеров заготовки с допусками Определение коэффициента использования металла Составление плана обработки поверхностей Вычисление припусков на обработку по стадиям Курсовая работа (с практической частью) 2011
курсовая: Дано: Кривошипно – кулисный механизм Число оборотов nОА = 120 об/мин Угол α = 300 Длина кривошипа ОА = 0,05м Длина шатуна АВ = 0,18м Длина АД = 0,06м Длина ДВ = 0,16м Длина СВ = 0,14м Расстояние а = 0,03м, в=0,15м Момент полезных сопротивлений Мп.с. = 55 Н•м Зубчатый механизм Число оборотов n1 = 1600 об/мин Число зубьев шестерни Z4 = 16 Число зубьев колеса Z5 = 29 Модуль зацепления m = 5,0мм Кулачковый механизм Коромысло: угол качения α = 340; длина l = 140 Угол удаления fуд. = 900 Угол верхнего выстоя fВВ = 300 Угол приближ Курсовая работа (с практической частью) 2012
курсовая: Ж Кривошипно-шатунный механизм с качающейся кулисой – вар.5 Курсовая работа (с практической частью) 2012
курсовая:А Механизм дробилки. Определение скоростей точек механизма при помощи плана скоростей. Определение ускорений звеньев механизма при помощи плана ускорений. Нахождение уравновешивающей силы и уравновешивающего момента. Находим уравновешивающую силу при помощи групп Ассура. Найдём уравновешивающую силу при помощи рычага Жуковского. Построение графика Курсовая работа (с практической частью) 2012
курсовая:Б – 1 Механизм продольно строгального станка.Определение скоростей точек механизма при помощи плана скоростей. Определение ускорений звеньев механизма при помощи плана ускорений. Нахождение уравновешивающей силы и уравновешивающего момента. Находим уравновешивающую силу при помощи групп Ассура. Найдём уравновешивающую силу при помощи рычага Жуковского. Построение графика зависимости приведённого момента, работы и изменения кинетической энергии механизма от угла поворота ведущего звена. Курсовая работа (с практической частью) 2012
курсовая:Д – 5 Механизм долбежного станка. Определение скоростей точек механизма при помощи плана скоростей. Определение ускорений звеньев механизма при помощи плана ускорений. Нахождение уравновешивающей силы и уравновешивающего момента. Находим уравновешивающую силу при помощи групп Ассура. Найдём уравновешивающую силу при помощи рычага Жуковского. Построение графика зависимости приведённого момента, работы и изменения кине Курсовая работа (с практической частью) 2012
курсовая:Дано: Кривошипно – кулисный механизм Число оборотов nОА = 120 об/мин Угол α = 600 Длина кривошипа ОА = 0,05м Длина шатуна АВ = 0,20м Длина АД = 0,08м Длина СВ = 0,12м Расстояние ОС = 0,18м Момент полезных сопротивлений Мп.с. = 60 Нм Зубчатый механизм Число оборотов n1 = 1500 об/мин Число зубьев шестерни Z4 = 17 Число зубьев колеса Z5 = 34 Модуль зацепления m = 4,0мм Кулачковый механизм Ход толкателя h = 20 мм Угол удаления fуд. = 900 Угол верхнего выстоя fВВ = 900 Угол приближения fпр. = 900 Угол наклона плоского то Курсовая работа (с практической частью) 2012
курсовая:Дано: Кривошипно – кулисный механизм Число оборотов nОА =100 об/мин Угол α = 600 Длина кривошипа ОА = 0,04м Длина шатуна АВ = 0,12м Длина АД = 0,08м Длина ДВ = 0,10м Длина СВ = 0,10м Момент полезных сопротивлений Мп.с. = 45 Нм Зубчатый механизм Число оборотов n1 = 1600 об/мин Число зубьев шестерни Z4 = 18 Число зубьев колеса Z5 = 33 Модуль зацепления m = 4,0мм Кулачковый механизм Угол качения α = 300 Длина коромысла l = 135vv Угол удаления fуд. = 600 Угол верхнего выстоя fВВ = 900 Угол приближения fпр. = 600 Предел Курсовая работа (с практической частью) 2012
курсовая:Дано: Кривошипно – ползунный механизм Число оборотов nОА =90 об/мин Угол α = 1500 Длина кривошипа ОА = 0,12м Длина шатуна АС = 0,24м Длина АВ = 0,02м Сила полезного сопротивления Рп. с. = 1,2 кН Зубчатый механизм Число оборотов n1 = 1400 об/мин Число зубьев шестерни Z4 = 18 Число зубьев колеса Z5 = 30 Модуль зацепления m = 5,0мм Кулачковый механизм Ход толкателя h = 28 мм Угол удаления fуд. = 300 Угол верхнего выстоя fВВ = 900 Угол приближения fпр. = 300 Предельный угол давления β = 290 Структурный анализ механизма Курсовая работа (с практической частью) 2012
курсовая:Дано: Кривошипно – ползунный механизм Число оборотов nОА =100 об/мин Угол α = 300 Длина кривошипа ОА = 0,07м Длина шатуна АВ = 0,18м Длина DB = 0,03м Длина СВ = 0,22м Момент полезных сопротивлений Мп.с. = 61 Нм Зубчатый механизм Число оборотов n1 = 1450 об/мин Число зубьев шестерни Z4 = 16 Число зубьев колеса Z5 = 33 Модуль зацепления m = 5,0мм Кулачковый механизм Коромысло: угол качения α = 250; длина l = 125 Угол удаления fуд. = 300 Угол верхнего выстоя fВВ = 45 Угол приближения fпр. = 300 Предельный угол давления β = 380Кинем Курсовая работа (с практической частью) 2012
курсовая:Задание на курсовой проект Дано: Кривошипно – ползунный механизм Число оборотов nОА = 120 об/мин Угол α = 300 Длина кривошипа ОА = 0,04м Длина шатуна АВ = 0,20м Длина АС = 0,08м Длина СВ = 0,17м Сила полезного сопротивления Рп. с. = 1350 Н Зубчатый механизм Число оборотов n1 = 1550 об/мин Число зубьев шестерни Z4 = 18 Число зубьев колеса Z5 = 24 Модуль зацепления m = 4,0мм Кулачковый механизм Ход толкателя h = 20 мм Угол удаления fуд. = 900 Угол верхнего выстоя fВВ = 900 Угол приближения fпр. = 900 Предельный угол д Курсовая работа (с практической частью) 2012
курсовая:М – 1 Шарнирно-рычажный механизм . Определение скоростей точек механизма при помощи плана скоростей. Определение ускорений звеньев механизма при помощи плана ускорений. Нахождение уравновешивающей силы и уравновешивающего момента. Находим уравновешивающую силу при помощи групп Ассура. Найдём уравновешивающую силу при помощи рычага Жуковского. Построение графика зависимости приведённого м Курсовая работа (с практической частью) 2012
курсовая:Механизм долбежного станка – вар.3 Определение скоростей точек механизма при помощи плана скоростей. Определение ускорений звеньев механизма при помощи плана ускорений. Нахождение уравновешивающей силы и уравновешивающего момента. Находим уравновешивающую силу при помощи групп Ассура. Найдём уравновешивающую силу при помощи рычага Жуковского. Построение графика зависимости приведённого момента, работы и изменения кинетической энергии механизма от угла поворота ведущего звена. Курсовая работа (с практической частью) 2012
курсовая:Определение скоростей точек механизма при помощи плана скоростей. Определение ускорений звеньев механизма при помощи плана ускорений. Нахождение уравновешивающей силы и уравновешивающего момента. Находим уравновешивающую силу при помощи групп Ассура. Найдём уравновешивающую силу при помощи рычага Жуковского. Построение графика зависимости приведённого момента, работы и изменения кинетической энергии механизма от угла поворота ведущего звена. Курсовая работа (с практической частью) 2012
Курсовой проект Задание на курсовой проект Дано: Кривошипно – кулисный механизм Число оборотов nОА =90 об/мин Угол α = 450 Длина кривошипа ОА = 0,08м Длина шатуна АВ = 0,22м Длина ДB = 0,06м Длина СВ = 0,14м Длина СД = 0,14м Момент полезных сопротивлений Мп. с. = 55 Нм Зубчатый механизм Число оборотов n1 = 1500 об/мин Число зубьев шестерни Z4 = 18 Число зубьев колеса Z5 = 28 Модуль зацепления m = 4,0мм Кулачковый механизм Ход толкателя h = 28 мм Угол удаления fуд. = 900 Угол верхнего выстоя fВВ = 600 Угол приближе Курсовая работа (с практической частью) 2013
Структурный анализ кривошипно-шатунного механизма 1.1 Структурный анализ механизма 1.2 Построение планов положений механизма 1.3 Кинематическое исследование механизма методом диаграмм 2. Кинематический анализ рычажного механизма 2.1 Построение планов скоростей звеньев механизма 2.2 Построение планов ускорений точек и звеньев механизма Курсовая работа (с практической частью) 2016
СТРУКТУРНЫЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА Курсовая работа (с практической частью) 2019
ТММ И.А. Канунник. Курсовая работа: Исследование кривошипно – ползунного механизма Курсовая работа (с практической частью) 2017

Кинематика кривошипно-шатунного механизма — диаграммы скорости и ускорения

В первом уроке этой серии, посвященном ползунковые и кривошипные механизмы мы впервые нашли из геометрии выражение для перемещения x ползунок в зависимости от угла поворота коленчатого вала θ и отношения n (= L / R), а затем дифференцировать по времени, чтобы получить выражения для скорость и линейное ускорение также как функции θ и n.

Этот анализ дал необходимую информацию для ползунка, но не скорость и ускорение шатуна, движение представляет собой комбинацию поступательного и вращательного движения. Этот информацию можно получить из диаграмм скорости и ускорения. Мы рассмотрим эти методы в этом уроке.

В качестве введения рассмотрим некоторые общие принципы и техники.

Диаграммы скоростей и ускорений

Диаграммы скоростей и ускорений вычерчены в масштабе с использованием известных величины и неизвестные значения затем измеряются непосредственно из готовых диаграмм. Также возможно получить неизвестные значения из геометрии диаграмм, и мы принимаем это подход ниже. (В третьем уроке серии мы получаем эквивалентную информацию из векторных уравнений).

Ключевым моментом при построении диаграмм скорости и ускорения является различие между абсолютными и относительное количество. Рассмотреть возможность диаграммы скоростей ниже, которые представляют, скажем, два штифтовых шарнира в механизм, обозначенный a и b . Стрелки v _a и v _b обозначают направление и величина абсолютных скоростей точек и b соответственно относительно o , которые указывает на «наземную точку» в общей системе отсчета.

Для создания диаграмм скоростей v _a и v _b соединены в их общей контрольной точке или и диаграмма закрыта третьей стрелкой. В (i) стрелка направление представляет относительную скорость v _b/a означает скорость точки b относительно точки и . В (ii) стрелка v _a/b представляет собой скорость точки a относительно точка б .

Построение диаграммы скоростей аналогично, но не совсем такие же, как и обычные векторные диаграммы, показанные ниже. В обоих случаях величина и направление результирующих скоростей равны идентичный.

В (i) вектор v _a вычитается из вектор v _b дает результирующий вектор в _б/у которая представляет собой скорость точки

b относительно скорость точки a .

В (ii) вектор v _b вычитается из вектор v _a дает результирующий вектор v _а/б который представляет скорость точки относительно к скорости точки b .

Диаграммы разгона строятся аналогично диаграммы скоростей с учетом того, что направления скорости и ускорения для точки не обязательно одинаковы. Диаграммы ускорения должны также учитывать, что вращательное движение любой точки всегда имеет радиальную составляющую ускорения, направленную центр вращения и тангенциальная составляющая ускорения, когда точка подвергается угловому ускорению. На приведенной ниже диаграмме показан диаграмма ускорения шатунной шейки вращающегося шатуна.

На этой диаграмме точка А вращается вокруг точки О под углом ускорение а. a _Ar радиальный (центростремительный) ускорение точки А относительно точки О с направлением из А в направлении О. а _В тангенциальное ускорение точка А относительно точки О в результате углового ускорения α. a _A — результирующее ускорение точки A относительно точка O. Обратите внимание, что на диаграмме представлен моментальный снимок удельный угол поворота коленчатого вала и угловая скорость ω, которая постоянно изменяется за счет углового ускорения α .

В этом примере диаграмма ускорения совпадает с вектором диаграмме, так как все ускорения относятся к одной точке O. Поскольку мы увидим ниже, что это не относится к полному кривошипу механизм.

Плоское движение твердого тела

Когда мы исследуем движение кривошипа и шатуна в кривошипно-шатунный механизм мы имеем дело с кинематикой твердого тела перемещается в двухмерной плоскости. Подходы классической теории это как комбинация продольного перемещения и вращения представлены в пример ниже.

Диаграмма представляет собой моментальный снимок векторов скорости в один момент времени при нескольких точек вдоль продольной оси жесткого стержня, движущегося в двух направлениях. размерная плоскость. продольная составляющая скорости во всех точках вдоль этой ось должна иметь одинаковую величину, иначе тело было бы расширяется или сужается. Если абсолютные скорости при двух точки на оси известны (в этом примере конечные точки A и B) соответствующие поперечные скорости, перпендикулярные линии в точке точки A и B определяют чисто вращательное движение с центром вращение вокруг продольной оси в точке С*. Этот принцип применим к любому произвольному линия на твердом плоском теле. Выбираем продольную ось здесь просто для удобства.

* Определенную здесь точку C не следует путать с мгновенным центром вращение или полюс скорости , описанный ниже, хотя как мы увидим, что эти две точки связаны. я принимаю описание «центр вращения относительно продольной оси» на на том основании, что для любого практического примера эта ось явно определенный.

Отметим также, что величина скорости вращения для центр вращения на продольной оси, выведенный из этой конструкции, одинаков какую бы произвольную линию ни принять за продольную ось на твердом теле.

Мгновенный центр вращения (полюс скорости)

Вытекает из принципа совмещения поступательного и вращательное движение твердого тела, что будет точка в плоскость движения, где тангенциальная скорость, возникающая при вращении равна и противоположна продольной скорости. Эта точка нулевой скорости, следовательно, должен быть центром вращения для этого мгновенно, когда каждая точка тела находится в чистом вращении вокруг этой точка. Точка называется

мгновенный центр вращения или веха скорости и показана на схеме ниже. Запись что полюс скорости не обязательно лежит на самом теле.

Полюс скорости можно найти двумя способами.

Ось вытянута перпендикулярно продольной оси на тела через центр вращения C. Продольная скорость (синий вектор) является постоянной во всех положениях на этом перпендикулярная ось. Тангенциальная скорость, возникающая из-за вращение тела (красный вектор) также перпендикулярно этому оси, но в противоположном направлении и меняется по величине. Точка на этой перпендикулярной оси, где продольная и тангенциальная скорости равные по величине и, таким образом, отменяют полюс скорости.

Если направления абсолютных скоростей двух точек на тело известно, линии, перпендикулярные этим направлениям, можно быть проведены из соответствующих точек. Точка пересечения этих перпендикулярных прямых полюс скорости. Это простой и полезный конструкции, как мы вскоре увидим. Диаграмма выше ясно показывает, как абсолютная скорость каждой точки на тело (зеленый вектор) касается линии от скорости полюс, указывающий на чистое вращение вокруг полюса скорости при этом мгновенное.

Диаграмма скоростей для ползуна и кривошипно-шатунного механизма

Теперь построим диаграмму скоростей для кривошипно-шатунного механизма ниже, исходя из угла поворота коленчатого вала θ = 50°. Угол между шатуна и горизонтальной оси обозначен φ, который мы использовать в последующих расчетах. Перемещения указаны в метрах.

Диаграмма скоростей состоит из трех компонентов:

скорость точки A относительно O (земли), обозначенная v _A/O
скорость точки B относительно обозначенной точки A v _B/A
скорость точки B относительно обозначенной точки O (земли) v _Б/О

Нам известно следующее:

Линия действия v _A/O перпендикулярна к плечу кривошипа с величиной ω x (OA) = (2 π) x (1) = 2 π. РС. шатун вращается против часовой стрелки, что определяет направление v _A/O
Предполагая, что шатун является жестким, движение точки B относительно точки А должно быть чисто вращательным. Таким образом линия действия v _B/A перпендикулярна AB.
Движение точки ползунка B ограничено по горизонтали плоскость, определяющая линию действия v _B/O

На приведенной ниже диаграмме показаны линии действия этих скоростей.

Теперь построим диаграмму скоростей. Во-первых, рассчитать величина v

A/O и нарисуйте стрелку для масштабирования линия действия. Наконечник стрелки представляет собой точку А относительно точки О на хвосте. Теперь нарисуйте линию действия v _B/A через точку A и линию действия v _B/O через точку O. Точка пересечения этих двух прямых определяет величину и направление v _B/A и v _Б/О

Завершенная диаграмма скорости показана ниже. Обратите внимание, что направления v _B/A и v _B/O разрешаются этой конструкции, наконечник стрелки, обозначающий скорость в этой точке относительно точки на хвосте.

Значения, масштабированные по хорошо нарисованным скоростным диаграммам, достаточно точен для практических целей. В качестве альтернативы скорости могут быть рассчитаны непосредственно по диаграмме.

Во-первых, мы вычисляем угол φ, упомянутый ранее:

Показать угол φ на диаграмме скоростей с горизонтальной осью а ось шатуна продлена до пересечения в точке P .

Теперь довольно просто найти стороны АВ и ВО Дан треугольник ABO, мы знаем, что AO = v _A/O = 2π м/с и угол φ = 14,79°

Из треугольника AOP угол PAO = 180° — (140° + 14,79°) = 25,21°

Таким образом, в треугольнике ABO угол BAO = (90° — 25,21°) = 64,79°

и угол ABO = 180° — (40° + 64,79°) = 75,21°

дает 90 BO = 2 v BO /O = 5,88 м/с

Это идентичное значение скорости ползунка для угла кривошипа θ = 50 °, полученного в предыдущем уроке из дифференцирования по времени, а именно.

Соответственно мы вычисляем v _A/B следующим образом:

дает AB = v _B/A = 4,18 м/с шатуна длиной 3 м в момент, когда угол поворота 50°.

Полюс скорости шатуна

На приведенной ниже схеме показана конструкция мгновенного полюс скорости шатуна в нашем примере механизма, где угол поворота = 50°.

Построение диаграммы полюсов скорости очень простой. Во-первых, стержень AB нарисован в масштабе на правильное угловое положение. В этом случае мы знаем направление скоростей v _A/O и v _B/O, таким образом, скорость полюс P — это пересечение прямых, перпендикулярных этим направлениям простирается от точек A и B.

Принимая во внимание, что полюс скорости представляет собой центр чистое вращательное движение стержня скорость вращения стержня ш _AB определяется путем масштабирования длины AP, т.е. радиус вращения точки A. Мы знаем сверху, что v _A/O = 6,28 м/с. Таким образом, ω _AB = 6,28/AP и соответственно путем масштабирования длины BP из диаграммы скорость v _B/O = ω _AB х АД.

Радиусы от полюса скорости до точек A и B могут быть легко вычислить, учитывая, что мы уже знаем угол φ на диаграмма и AB = 3 м..

Используя тождество триггера:

подтверждение значения ω _AB, полученного из диаграмма скоростей в предыдущем разделе.

подтверждение значения v _B/O, полученного из диаграмма скоростей в предыдущем раздел.

Центр вращения на продольной оси

Выводим центр вращения на продольной оси шатун прямо из диаграммы полюсов скорости. Одинокий нижние индексы указывают абсолютные скорости в точках на стержне.

Линия PD, перпендикулярная AB в точке D, продолжена через полюс скорости P – радиус вращения точки D на продольная ось стержня. Таким образом, направление вектора скорости v _D должны точно совпадать с продольной осью. Точка D – это мгновенный центр вращения на этой оси и является единственной точкой на оси, не имеющей поперечной составляющей скорости.

Рассчитываем v _D со ссылкой на диаграмму как следует.

Из предыдущей диаграммы полюсов скорости: AP = 4,51 м

5,68 м/с — продольная составляющая скорости в каждой точке на оси стержня. Мы можем проверить, так ли это в точке B. где мы знаем v _B = 5,88 м/с по горизонтальной оси.

Диаграмма ускорения ползунково-кривошипного механизма

Диаграмма ускорения для примера механизма имеет компоненты перечислено ниже. Показаны линии действия этих ускорений на схеме выше.

Точка А имеет центростремительное ускорение, обозначенное как _rA/O, действующее радиально вдоль ось кривошипа к его центру вращения в точке О, который также является точкой отсчета для диаграммы. Поскольку кривошип вращается с постоянной угловой скоростью ω. тангенциальная составляющая ускорения в точке А. В нашем пример a _rA/O = ω ² (AO) = (2π) ² (1) = 39,44 м/с ²
Точка B имеет центростремительное ускорение относительно точки A обозначенный как _rB/A, действующий радиально вдоль оси шатуна к точке А, которая является центром вращения в таком случае. В нашем примере механизм a _rB/A = ω ² _AB .(AB) = (1,39) ² (3) = 5,80 м/с ²
Знаем скорость вращения шатуна ω _AB непостоянна и поэтому имеет угловую ускорение α _AB Следовательно, точка B имеет тангенциальное ускорение относительно точки А обозначено как _tB/A с линией действия, перпендикулярной стержню. Величина и направление на линии действия неизвестно.
Точка B имеет ускорение относительно точки O обозначен как _B/O, действующий горизонтально. Величина и направление на линии действия неизвестны.

Теперь построим диаграмму ускорения, начиная с известные количества.

Сначала начертите _A/O из точки O в точку обозначенный A на своей линии действия с направлением от точки A в точку O, показанную на физической схеме для механизма при θ = 50° (см. выше). Важно отметить, что относительно положения А и О на диаграмме ускорения противоположны позиции на физической схеме.

Затем нарисуйте _rB/A на его линии действия из точки A до точки, обозначенной B ^/, отмечая, что это центростремительное ускорение направлено к его центр вращения, который в данном случае находится из точки B в точку A на физическую схему. Зная, что тангенциальное ускорение в точке B относительно точки A также существует, мы обозначаем точку как B ^/, которая может быть считается средней точкой между точкой A и точкой B.

Теперь проведите линию действия _tB/A через точку B ^/ и линия действия _B/O через точку O. пересечение этих линий определяет точку B. a _tB/A проводится из точки B ^/ в точку B, а _B/O из точки O в точку B. Полное ускорение схема показана ниже.

Значения _B/O и _tB/A из масштабной диаграммы удовлетворительны для практических целей. Однако. как мы сделали для диаграммы скорости. мы можем рассчитать значение _Б/О из схемы и сравнить со значением полученное ранее из выражения, полученного из дифференцирования относительно времени в предыдущем руководство.

Расчет немного сложнее, чем для скорости диаграмма. Мы знаем все углы в треугольниках PBO и PB ^/ A и мы знаем длины OA и AB ^/. Затем находим сторону AP в треугольнике PB ^/ A, что дает сторону OP = OA + AP в треугольнике PBO, из которого находим сторону OB. Расчет дает _B/O = 23,4 м/с ² что соответствует ранее полученное значение.

Из этих треугольников мы также вычисляем _tB/A = 29,72 м/с ² . По этому значению определяем угловое ускорение шатуна α _ВА от отношение a _tB/A = AB x α _BA где AB = 3 м, что дает α _BA = 9,91 рад/с ²

Жду отзывов по адресу:

alistair@alistairstutorials.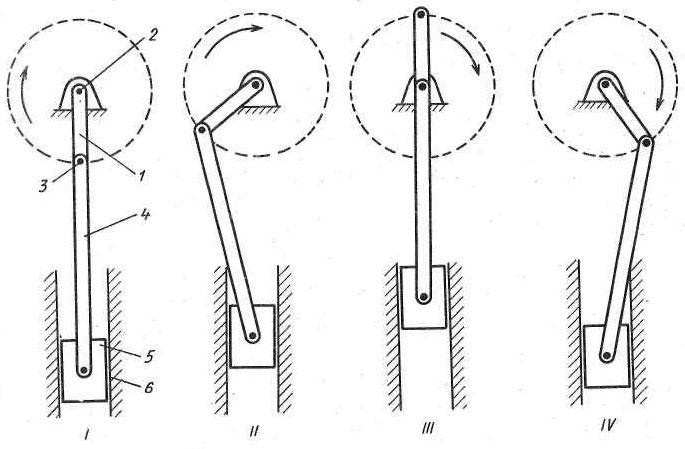 co.uk

[Решено] Кривошипно-кривошипный механизм вращается против часовой стрелки

Кривошипно-кривошипный механизм вращается против часовой стрелки (CCW) с постоянной угловой скоростью ω, как показано. Предположим, что длина кривошипа равна r.

Используя точный анализ, ускорение ползуна в направлении y в показанный момент времени, когда кривошип параллелен оси x, определяется как

Этот вопрос ранее задавался в

PY 4: Gate Me 2019 Официальная статья: Shift 2

Посмотреть все газеты Gate ME>

−ω ² R
2 ООМ 2 ² R
ω ² R
ω ² 2 2 2 2 R
Ω ^{2 ² R}
ω ² R
2 r

Вариант 3 : ω ² r

Бесплатно

CT 1: соотношение и пропорция

10,7 тыс. пользователей

10 вопросов

16 баллов

30 минут

Концепция:

92}\)

Тригонометрические соотношения: у равнобедренного треугольника две стороны равны.

Чтобы найти ускорение кривошипа ползуна с помощью точного анализа.

В _А → скорость А относительно O

V _BA → скорость B w.r.t. A.

Составляющая скорости B вдоль направления x = V _BA cos 45

Также из-за ограничения на ползунок V _BA вдоль x = 0 (т.е. V _BA только вдоль направления y)

⇒ V _BA cos 45 = 0

⇒ V _BA = 0

Also, V _BA = V _B — V _A = 0 ⇒ V _B = V _A (i) Радиальное в сторону 0,

(ii) Тангенциальная a _BA = неизвестно

Кроме того, тангенциальная составляющая скорость A = B и ускорение также будут равны y-компоненте B.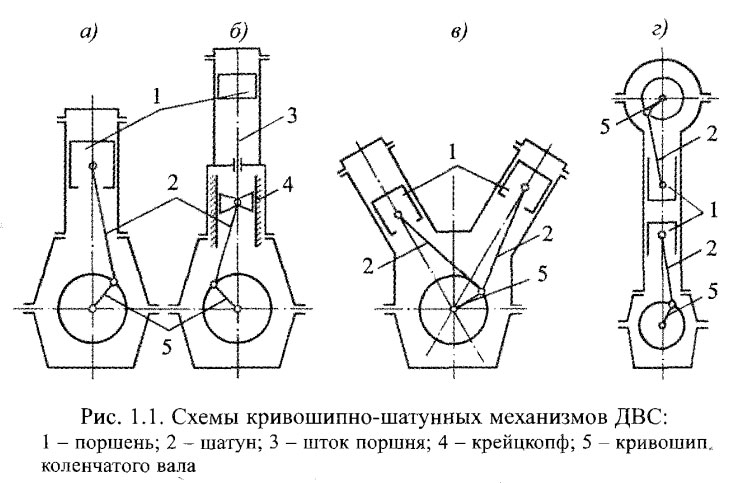 Кроме того, тангенциальное ускорение B будет направлено в направлении, показанном V _BA в схема конфигурации.

⇒ из тригонометрии o’b’ = a’o’

⇒ a _y = rω ² (вверх, значит положительно).

Скачать решение PDF

Поделиться в WhatsApp

Последние обновления GATE ME

Последнее обновление: 15 декабря 2022 г.

HPU, MRPL и NPCIL Опубликовано официальное уведомление! GATE 2023 Официальная ссылка на пробный тест уже активна! Набор ученых ISRO будет осуществляться через GATE 2021 и GATE 2022. Расписание экзаменов GATE ME 2023 опубликовано и будет проводиться 4 февраля 2023 г. во второй половине дня с 14:30 до 17:30. Допуск к экзамену будет доступен с 3 января 2023 года. Индийский технологический институт (IIT) Канпур выпустил официальное уведомление о GATE ME 2023. Результаты GATE ME 2023 будут объявлены 16 марта 2023 года.