Что означают категории в правах нового образца: Категории и подкатегории водительских прав в 2023 году — Оренбург

Содержание

с какого возраста можно их получить — Finance.ua

— Технологии&Авто

Чтобы легально управлять определенным транспортным средством, не обойтись без соответствующей категории вождения. А чтобы не ошибиться с выбором документа, следует знать, какие категории прав в Украине легализованы и какая между ними разница.

Об этом пишет olx.ua.

К примеру, чем отличаются категория С, какие машины предполагает для езды, и категория С1, какие машины можно водить, получив ее.

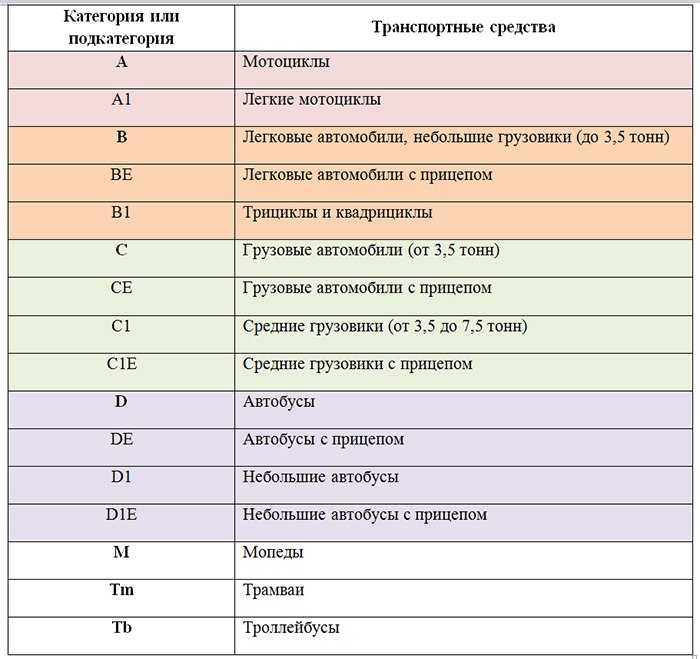
Долгое время в Украине действовали следующие категории водительского удостоверения:

  • А — выдавались мотоциклистам;
  • В — означали право управлять автомобилем массой до 3,5 т, в котором, кроме водителя, может поместиться не более 8 пассажиров;
  • С — разрешали управлять автомобилем массой более 3,5 т;
  • Д — выдавались шоферам автобусов более чем на 8 пассажиров;
  • Е — водительское удостоверение этой категории позволяло ездить с прицепом.

Тем не менее, в 2013 году в украинском законодательстве произошли изменения, и категории прав пополнились подгруппами. Теперь их больше десяти. К слову, аналогичные изменения произошли не только в Украине. Основная причина новаций в системе водительских удостоверений — появление большого количества новых транспортных средств с особыми характеристиками.

Все легализованные в Украине водительские категории можно увидеть на обороте водительского удостоверения государственного образца. На сегодняшний день таких категорий 15.

Первая группа — это водительские права категории А:

  • А — можно управлять мотоциклами, в том числе и моделями с боковым прицепом, другим двухколесным транспортом с двигателем от 50 см3;
  • А1 — выдаются водителям мотороллеров, мопедов и других двухколесных транспортных средств при условии, что объем двигателя не превышает 50 см3.

Категория Б теперь представлена 3 подкатегориями:

  • В — необходимо получить тем, кто планирует управлять автомобилем, в котором количество сидячих мест с сидением водителя — до 9, а масса транспортного средства (ТС) не превышает 3,5 т;
  • В1 — выдается для управления квадро-, трициклами, мотоколясками и другим 3-4-колесным транспортом массой до 400 кг;
  • ВЕ позволяет управлять транспортным средством категории В с прицепом, однако есть условие — общая масса автомобиля и прицепа не может превышать 3,5 т.

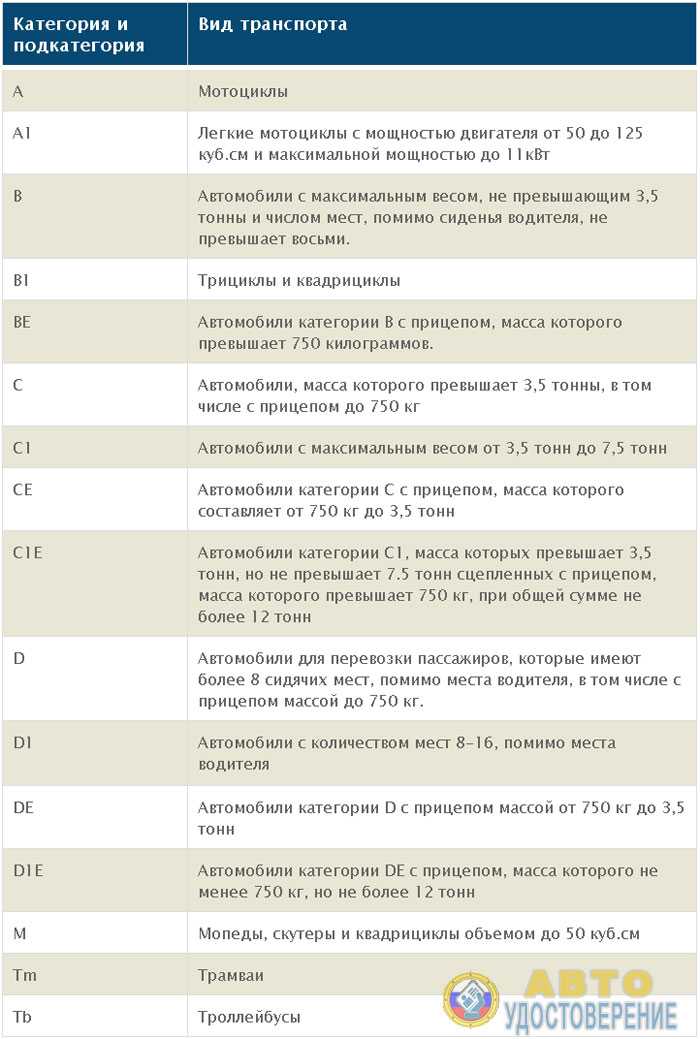
Группа водительских прав с отметкой С:

  • С — выдается водителям грузовиков массой от 7,5 т;
  • С1 — позволяет управлять грузовиками 3,5-7,5 т;
  • СЕ — получают водители фур и дальнобойщики, которые ездят на грузовиках категории С с прицепами весом от 750 кг;
  • С1Е — разрешает управлять транспортным средством С1 с прицепом, при условии, что общая масса обоих не превышает 7,5 т.

В Д категории водительские права могут быть следующие:

  • Д — позволяют быть водителем автобуса с количеством посадочных мест 16 и более;
  • Д1 — понадобятся для вождения автобуса, в котором предусмотрено менее 16 пассажиров;
  • ДЭ — дают разрешение на управление системой автобус Д+ прицеп;
  • Д1Е — допускают управление транспортным средством Д1 с прицепом массой более 750 кг.

Категория Т предназначена для водителей трамваев и троллейбусов. Для буксиров понадобится удостоверение категории Е.

Наиболее популярны в Украине водительские удостоверения категорий В и С.  Категория В позволяет управлять практически любым легковым авто, а С — грузовиками.

Что касается транспортных средств с электродвигателем, то в большинстве случаев водителям также понадобятся специальные права:

  • А1 — для мопедов с двигателем мощностью менее 4 кВт;
  • А — для двухколесных ТС с мощностью двигателя свыше 4 кВт;
  • В — для электромобилей.

Кстати, недавно на автопроме появился электрокар Citroen Ami, у которого скоростные возможности ограничены 45 км/ч. Разработчики планировали, что управлять таким авто можно без прав. В Украине можно купить и такую модель с электродвигателем, и более дешевые автомобили б/у, однако украинцам даже на Citroen Ami нужны права категории В.

Чтобы получить определенную категорию водительского удостоверения, недостаточно изучить правила дорожного движения. Управление транспортными средствами требует от водителя особого внимания, возможности адекватно оценивать ситуацию на дороге и правильно маневрировать. Некоторыми видами транспорта управлять относительно легко. Чтобы покорить другие, понадобятся не только теоретические знания, но и длительная практика.

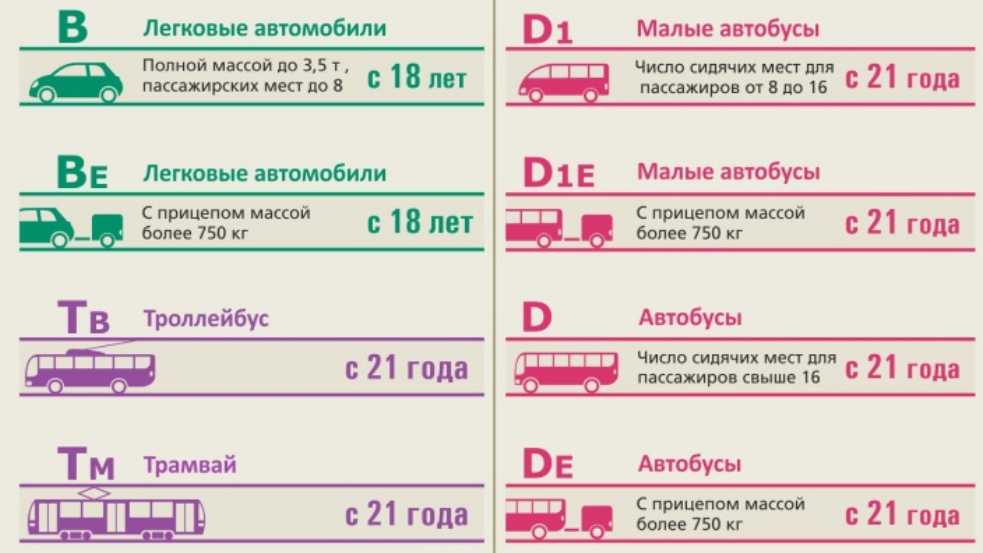
Именно поэтому украинским законодательством предусмотрены возрастные ограничения на получение той или иной категории водительского удостоверения:

  • с 16 лет можно сдавать экзамены на получение удостоверения категорий А, А1;
  • с 18 лет выдают права В, В1, С, С1;
  • по достижении 19-летия можно подавать документы на получение категорий ВЭ, СЭ, С1Э;
  • только с 21 года разрешено сдавать на права категорий Д, ДЭ, Д1, Д1Э, Т.

При наличии прав категорий В, С, Д, С1 и Д1 и практического опыта более 1 года можно получить водительское удостоверение этих же транспортных средств, но уже с прицепом. Если за последние 3 года водитель регулярно управлял ТС категорий В, С, С1 или Т, он может получить права Д1. Удостоверение категории В, С, С1, Д1 или Т дает право на получение документа с маркировкой «Д».

Кстати, на Finance.

ua мы помогаем людям оформлять Зеленую карту быстро и удобно. Все, что вам нужно — доступ к интернету.

По материалам:

Finance.ua

Если Вы заметили ошибку, выделите необходимый текст и нажмите Ctrl+Enter , чтобы сообщить нам об этом.

С 1 апреля ГИБДД начинает выдавать водительские права нового образца

С 1 апреля ГИБДД начинает выдавать водительские права нового образца — Газета.Ru

Помощник канцлера ФРГ Кукис назвал отказ от газа из России огромным стрессом… 08:34

Yomiuri: Китай, Индия и Турция поддерживают российскую экономику на плаву, несмотря… 08:27

Евсеев рассказал, почему игроки РПЛ не потеряли мотивацию без еврокубков 08:25

Жителей Москвы предупредили о низком атмосферном давлении 08:21

Основатель ЧВК «Вагнер» Пригожин: российские силы контролируют восточную часть Артемовска 08:19

Генконсул Захаров: подвижек с выдачей виз сотрудникам генконсульства РФ… 08:18

Глава судей РФС заступился за Мешкова: никто не говорит не ставить Промеса после двух.

.. 08:13

Милош Земан покидает пост президента Чехии 08:12

Аргентина отозвала разрешение на осуществление одного из авиарейсов… 08:12

Густаво Петро: правительство Колумбии не будет вести переговоры с наркокартелями 08:10

Автомобили

close

100%

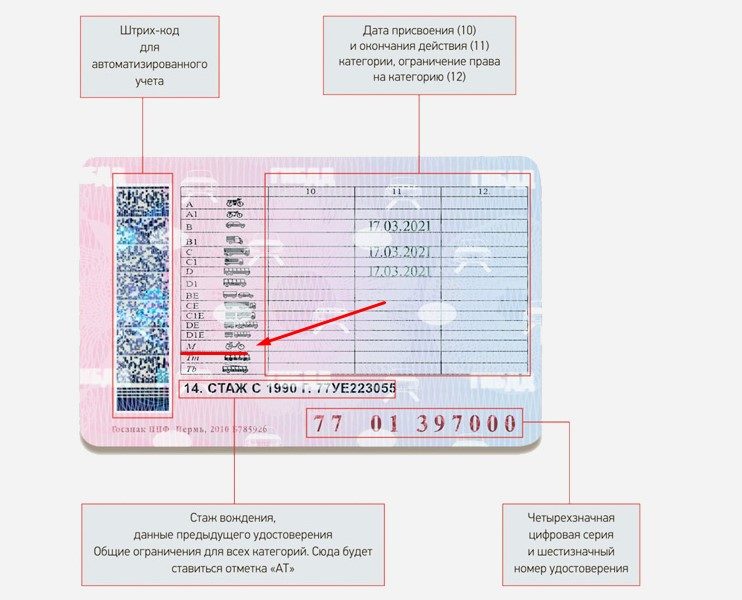
С 1 апреля ГИБДД начинает выдачу водительских прав нового образца. На задней части удостоверения число категорий и подкатегорий увеличится до 16. Кроме того, впервые в правах появится отметка о допуске к управлению транспортным средством только с автоматической трансмиссией. Впрочем, программы обучения на новые категории до сих пор отсутствуют, а значит, для водителей пока все остается по-прежнему.

В России начиная с 1 апреля вводятся водительские удостоверения нового образца. Изменения затронут внешний вид только оборотной части пластиковых прав: там появятся новые категории и подкатегории.

Они были введены 5 ноября 2013 года, когда вступили в силу новые поправки к закону «О безопасности дорожного движения», однако соответствующий приказ об изменении дизайна удостоверения глава МВД Владимир Колокольцев подписал только 19 марта: спустя неделю после официальной публикации он вступает в силу.

В частности, теперь в водительских удостоверениях появится категория «М» — для мопедов. Такие права будут выдавать с 16 лет, но те, у кого уже есть действующие права любой категории, также получат права на управление данным транспортным средством.

Водители-мигранты с «автоматом»

С 5 ноября в России вступают в силу поправки, которые серьезно меняют правила выдачи водительских прав…

08 ноября 14:01

Также появятся категории Tm — трамваи и Tb – троллейбусы, подкатегории А1 — легкие мотоциклы с объемом двигателя до 125 куб. см, В1 — квадроциклы и трициклы, С1 — грузовики массой до 7,5 тонны, D1 — автобусы до 16 мест. Также появляются и такие подкатегории, как С1Е и D1Е. Они дадут право на управление машинами соответствующих подкатегорий с прицепом.

Еще одним важнейшим нововведением с 1 апреля станет появление отметки Automatic Transmission Only: она будет стоять у тех, кто проходил обучение на автомобиле с автоматической трансмиссией. Такие водители не будут иметь права управлять автомобилем с механической коробкой передач.

Те же, кто проходил обучение, которое с недавних пор разрешено только в автошколах, на механике, будут иметь доступ на управление и машиной с автоматом.

Впрочем, пока никаких особенных изменений водителей не ждет: в правительстве никак не разработают программы обучения для новых категорий и подкатегорий, а также методику приема экзамена в ГИБДД. Это значит, что в автошколах пока все останется по-старому. То же касается и приема экзамена на машине с автоматической коробкой передач: как принимать такой экзамен, пока нигде не прописано, а значит, все остается по-прежнему.

Специально приходить в ГИБДД для получения новых прав тоже не нужно: замена будет осуществляться в естественном режиме, при плановой замене действующего удостоверения.

Блондинок научат чинить подвеску

Новые правила обучения водителей в автошколах могут заработать уже в марте. По мнению экспертов, программу…

25 января 14:25

Именно из-за отсутствия программы обучения ГИБДД в преддверии летнего сезона пока не будет выдавать права обладателям скутеров и мопедов. Впрочем, понимая, что вины водителей в задержке нет, в ГИБДД пообещали не штрафовать нарушителей до того, как методика обучения будет принята, а в Госавтоинспекции начнут наконец выдачу прав. А это значит, что из-за волокиты уже с завтрашнего дня тысячи старшеклассников могут совершенно безнаказанно гонять на мопедах, не опасаясь никакого взыскания.

Задержка с введением необходимых подзаконных актов произошла из-за затяжного спора между Минобрнауки и Минтрансом о том, кто именно должен этим заниматься.

В итоге миссию поручили Минобрнауки. Поначалу шла речь о том, что чиновники могут успеть разработать все необходимые методики к новому 2014 году, однако и спустя три месяца после этого срока ни одной программы пока не принято. В середине марта стало известно, что ведомство все же разработало необходимые методики, которые радикально меняют систему обучения водителей в автошколе. В частности, упор будет сделан на психологию будущего водителя, а сам курс обучения станет заметно дольше.

Подписывайтесь на «Газету.Ru» в Новостях, Дзен и Telegram.
Чтобы сообщить об ошибке, выделите текст и нажмите Ctrl+Enter

Новости

Дзен

Telegram

Картина дня

Военная операция на Украине. День 378-й

Онлайн-трансляция военной операции ВС РФ на Украине — 378-й день

«Черный день грузинской демократии»: в Тбилиси начались протесты из-за «закона об иноагентах»

Президент Грузии Зурабишвили поддержала протестующих против законопроекта об иноагентах

«Это были противники Путина». Во взрывах на «Северных потоках» нашли «украинский след»

NYT: проукраинская группировка может стоять за взрывами на «Северных потоках»

Песков назвал новые публикации о терактах на «Северных потоках» скоординированным вбросом

Основатель ЧВК «Вагнер» Пригожин: российские силы контролируют восточную часть Артемовска

Yle: закрытие границы с Россией обернулось проблемами для жителей востока Финляндии

Bloomberg: Казахстан столкнулся с проблемами при поставках нефти в Евросоюз

Новости и материалы

Помощник канцлера ФРГ Кукис назвал отказ от газа из России огромным стрессом для Германии

Yomiuri: Китай, Индия и Турция поддерживают российскую экономику на плаву, несмотря на санкции

Евсеев рассказал, почему игроки РПЛ не потеряли мотивацию без еврокубков

Жителей Москвы предупредили о низком атмосферном давлении

Генконсул Захаров: подвижек с выдачей виз сотрудникам генконсульства РФ в Хьюстоне нет

Глава судей РФС заступился за Мешкова: никто не говорит не ставить Промеса после двух незабитых пенальти

Милош Земан покидает пост президента Чехии

Аргентина отозвала разрешение на осуществление одного из авиарейсов на Мальвинские острова

Густаво Петро: правительство Колумбии не будет вести переговоры с наркокартелями

Генконсул РФ в Хьюстоне Захаров: бизнес США не желает терять российский рынок

Четыре очка Ничушкина помогли «Колорадо» обыграть «Сан-Хосе»

В Тульской области пьяная бабушка чуть не заморозила насмерть восьмимесячного внука

В Минздраве сообщили о быстром распространении ожирения среди мужчин из РФ старше 40 лет

Военная медсестра сообщила об охоте ВСУ на российских медиков в зоне спецоперации

В Петербурге мужчина развращал 15-летнего школьника в сети

Зеленский заявил, что уход ВСУ из Артемовска откроет РФ путь к другим городам Донбасса

Источник: обвиненный в изнасиловании игрок «ПСЖ» Хакими считает, что его подставили

В Пятигорске прооперировали ребенка со сложным переломом

Все новости

Выпить таблетку и забеременеть. Смогут ли женщины продолжать род без мужчин

Генетик Крутовский рассказал о новых технологиях бесполого размножения

Мария Дегтерева

А кто это?

О том, как и почему люди хвастаются незнанием

Тест: что вы знаете об истории 8 Марта

Ответьте на шесть вопросов о Международном женском дне

Солист группы «Динамит», участник «Дома-2», мошенник: как сложилась личная жизнь 40-летней Ксении Бородиной

Два брака и несколько нашумевших романов: все о личной жизни Ксении Бородиной

Кайф, долги, Плутарх и нары: о чем говорил Улюкаев в первом интервью после колонии

Улюкаев рассказал, что получает «удивительный кайф» от жизни среди людей

«Европа собирается с силами». В ЕС придумали, как покупать газ не у России и без переплаты

Зампред ЕК Шефчович: Евросоюз к апрелю 2023 года организует картель для закупок газа

Как в Грузии протестуют против «закона об иноагентах»

«Ночью снял с цепи и увел». У Кадырова похитили задержанного из-за санкций жеребца

Jezdci: в Чехии украли чистокровного английского коня Кадырова стоимостью $18 тысяч

Роботов вывели на подиум, Louis Vuitton обвинили в поддержке СВО: как прошла Неделя моды в Париже

В Париже завершилась Неделя моды

Танки прибыли, ЗРК — нет. Министр обороны Польши запутался в поставках оружия Украине

Минобороны Польши опровергло слова своего руководителя о прибытии ЗРК Patriot на Украину

«Экстраординарная»: хитовый британский сериал, высмеивающий супергероику

Рецензия на комедийный сериал «Экстраординарная»

«Зеленский — просто гнида». Лукашенко дал характеристику диверсантам с Украины

Лукашенко сообщил, что в Белоруссии задержан диверсант, атаковавший самолет А-50 ВКС России

Как в России и мире оценивают потери Украины в ходе СВО

Шойгу заявил, что взятие Артемовска позволит ВС РФ наступать вглубь обороны ВСУ

Мария Дегтерева

А кто это?

О том, как и почему люди хвастаются незнанием

Наталья Тарасова

Страховать нельзя отказывать

Управляющий директор – начальник управления методологии и компетенций СберСтрахования жизни Наталья Тарасова о полисах для людей с инвалидностью

Юлия Меламед

Муж дурак, хоть и помер

О бабификации населения

Георгий Бовт

Сталин жив

К 70-летию временно усопшего

Марина Ярдаева

А кто здесь обезьяна?

О том, сделает ли труд из школьника человека

—>

Читайте также

Как будет меняться Сибирь в новых условиях

Мурманск, Хакасия, Пермский край: где можно отдохнуть в этом году вместо Сочи

Шоколад, секс и холод. Что может вызвать головную боль и как с ней бороться

Тест: узнайте, какой автомобиль вам подходит

Не только Atomic Heart. Семь российских игр, ставших мировыми хитами

Найдена ошибка?

Закрыть

Спасибо за ваше сообщение, мы скоро все поправим.

Продолжить чтение

Двухвыборочный t-критерий | Введение в статистику

Что такое двухвыборочный

t -критерий?

Двухвыборочный t -критерий (также известный как t -критерий независимых выборок) представляет собой метод, используемый для проверки того, равны или нет неизвестные средние значения генеральной совокупности двух групп.

Это то же самое, что и A/B-тест?

Да, двухвыборочный t -тест используется для анализа результатов A/B-тестов.

Когда я могу использовать тест?

Вы можете использовать тест, когда ваши значения данных независимы, случайным образом выбраны из двух нормальных совокупностей и две независимые группы имеют равные отклонения.

Что делать, если у меня более двух групп?

Использовать метод множественного сравнения. Одним из таких методов является дисперсионный анализ (ANOVA). Другие методы множественного сравнения включают тест Тьюки-Крамера для всех попарных различий, анализ средних значений (ANOM) для сравнения групповых средних значений с общим средним значением или критерий Даннета для сравнения каждого среднего значения группы с контрольным средним значением.

Что делать, если дисперсии двух моих групп не равны?

Вы по-прежнему можете использовать двухвыборочный тест t-. Вы используете другую оценку стандартного отклонения.

Что делать, если мои данные не распределены почти нормально?

Если размеры вашей выборки очень малы, вы не сможете проверить нормальность. Возможно, вам придется полагаться на свое понимание данных. Когда вы не можете безопасно предположить нормальность, вы можете выполнить непараметрический тест , который не предполагает нормальность.

Использование двухвыборочного теста

t

В следующих разделах обсуждается, что необходимо для выполнения теста, проверки наших данных, как выполнять тест и статистические данные.

Что нам нужно?

Для двухвыборочного t -теста нам нужны две переменные. Одна переменная определяет две группы. Второй переменной является измерение интереса.

У нас также есть идея или гипотеза о том, что средние значения основных популяций для двух групп различны. Вот пара примеров:

  • У нас есть учащиеся, для которых английский язык является родным, и учащиеся, для которых английский язык не является родным. Все учащиеся проходят тест по чтению. Наши две группы — носители английского языка и не носители английского языка. Наши измерения — это результаты тестов. Наша идея состоит в том, что средние результаты тестов для основной популяции носителей и не носителей английского языка неодинаковы. Мы хотим знать, отличается ли средний балл для населения, для которого английский язык является родным, и для людей, изучающих английский как второй язык.
  • Мы измеряем количество протеина в граммах в энергетических батончиках двух разных марок. Две наши группы — это два бренда. Нашим измерением являются граммы белка для каждого энергетического батончика. Наша идея состоит в том, что средние граммы белка для основных популяций для двух брендов могут быть разными. Мы хотим знать, есть ли у нас доказательства того, что среднее количество белка в граммах для двух марок энергетических батончиков отличается или нет.
Две пробы
t — тестовые допущения

Для проведения действительного теста:

  • Значения данных должны быть независимыми. Измерения для одного наблюдения не влияют на измерения для любого другого наблюдения.
  • Данные в каждой группе должны быть получены путем случайной выборки населения.
  • Данные в каждой группе нормально распределены.
  • Значения данных непрерывны.
  • Дисперсия для двух независимых групп одинакова.

Для очень небольших групп данных может быть сложно протестировать эти требования. Ниже мы обсудим, как проверить требования с помощью программного обеспечения и что делать, если требование не выполняется.

Две пробы

t — тестовый пример

Одним из способов измерения физической подготовки человека является измерение процентного содержания жира в его организме. Средний процент жира в организме зависит от возраста, но, согласно некоторым рекомендациям, нормальный диапазон для мужчин составляет 15–20% жира, а для женщин — 20–25%.

Наши выборочные данные взяты из группы мужчин и женщин, которые занимались в тренажерном зале три раза в неделю в течение года. Затем их тренер измерил жировые отложения. В таблице ниже показаны данные.

Таблица 1. Данные о процентном содержании жира в организме, сгруппированные по полу
13.3 6.0 20.0 8.0 14.0 19.0 18.0 25.0 16.0 24.0 15.0 1.0 15.0    

Женщины

22. 0 16.0 21.7 21.0 30.0 26.0 12.0 23.2 28.0 23.0

You can clearly see some overlap in the body fat measurements for the мужчины и женщины в нашей выборке, но и некоторые различия. Просто взглянув на данные, трудно сделать какие-либо твердые выводы о том, имеют ли основные группы мужчин и женщин в тренажерном зале одинаковый средний процент жира в организме. В этом ценность статистических тестов – они обеспечивают общий, статистически достоверный способ принятия решений, так что все принимают одно и то же решение по одному и тому же набору значений данных.

Проверка данных

Начнем с ответа: Является ли двухвыборочный t -тест подходящим методом для оценки разницы в телесном жире между мужчинами и женщинами?

  • Значения данных независимы. Количество жира в организме одного человека не зависит от количества жира в организме другого человека.
  • Мы предполагаем, что измеренные люди представляют собой простую случайную выборку из популяции членов спортзала.
  • Мы предполагаем, что данные нормально распределены, и мы можем проверить это предположение.
  • Значения данных представляют собой измерения телесного жира. Измерения непрерывны.
  • Мы предполагаем, что дисперсии для мужчин и женщин равны, и мы можем проверить это предположение.

Перед тем, как приступить к анализу, мы всегда должны быстро просмотреть данные. На рисунке ниже показаны гистограммы и сводная статистика для мужчин и женщин.

Рисунок 1: Гистограмма и сводная статистика для данных о телесном жире

Две гистограммы имеют одинаковый масштаб. Бегло взглянув, мы видим, что очень необычных точек нет, или выбросы . Данные выглядят примерно в форме колокола, поэтому наше первоначальное представление о нормальном распределении кажется разумным.

Изучив сводную статистику, мы видим, что стандартные отклонения аналогичны. Это поддерживает идею равных дисперсий. Мы также можем проверить это, используя тест на дисперсию.

Основываясь на этих наблюдениях, двухвыборочный t -критерий представляется подходящим методом для проверки различий в средних значениях.

Как выполнить двухпробный

t -test

Для каждой группы нам нужны среднее значение, стандартное отклонение и размер выборки. Они показаны в таблице ниже.

Table 2: Average, standard deviation and sample size statistics grouped by gender

Group Sample Size (n) Average (X-bar) Standard отклонение (ы)
Женщины 10 22,29 5,32
Мужчины 13 14,95 6,84

без каких -либо испытаний, мы видим, что не являются мужскими, а не на нас. Но насколько они разные? Являются ли средние значения «достаточно близкими», чтобы мы могли сделать вывод, что средний процент жира в организме одинаков для большей части мужчин и женщин, посещающих тренажерный зал? Или средние значения слишком разные, чтобы мы могли сделать такой вывод?

Далее мы объясним принципы, лежащие в основе двух образцов 9.0003 t — тест в разделе статистических данных ниже, но давайте сначала пройдемся по шагам от начала до конца. Начнем с расчета нашей тестовой статистики. Этот расчет начинается с нахождения разницы между двумя средними значениями:

$ 22,29 — 14,95 = 7,34 $

Эта разница в наших выборках оценивает разницу между средними значениями населения для двух групп.

Далее мы вычисляем объединенное стандартное отклонение. Это строит комбинированную оценку общего стандартного отклонения. Оценка корректируется для разных размеров групп. Во-первых, мы вычисляем объединенную дисперсию: 92)}{(10 + 13 — 2)} $

$ = \frac{(9\times28,30) + (12\times46,82)}{21} $

$ = \frac{(254,7 + 561,85)}{21} $

$ =\frac{816,55}{21} = 38,88 $

 

Затем мы извлекаем квадратный корень из объединенной дисперсии, чтобы получить объединенное стандартное отклонение. Это:

$ \sqrt{38,88} = 6,24 $

Теперь у нас есть все части для нашей тестовой статистики. У нас есть разница средних значений, объединенное стандартное отклонение и размеры выборки. Мы рассчитываем нашу тестовую статистику следующим образом:

$ t = \frac{\text{разность средних групп}}{\text{стандартная ошибка разности}} = \frac{7,34}{(6,24\times \sqrt{(1/10 + 1/13) })} = \frac{7,34}{2,62} = 2,80 $

Чтобы оценить разницу между средними значениями и принять решение о наших программах в тренажерном зале, мы сравниваем тестовую статистику с теоретическим значением из t- распределение. Эта деятельность включает четыре шага:

  1. Мы принимаем решение о риске, на который мы готовы пойти, заявляя о существенной разнице. Что касается данных о телесном жире, мы решаем, что готовы пойти на 5%-ный риск, заявив, что неизвестные средние значения населения для мужчин и женщин не равны, когда они действительно равны. На языке статистики уровень значимости, обозначаемый α, устанавливается равным 0,05. Хорошей практикой является принятие этого решения перед сбором данных и расчетом тестовой статистики.
  2. Мы вычисляем тестовую статистику. Наша тестовая статистика 2,80.
  3. Мы находим теоретическое значение из распределения t- на основе нашей нулевой гипотезы, которая утверждает, что средние значения для мужчин и женщин равны. В большинстве статистических книг есть справочные таблицы для распределения t-. Вы также можете найти таблицы в Интернете. Наиболее вероятная ситуация, что вы будете использовать программное обеспечение, а не печатные таблицы.

    Чтобы найти это значение, нам нужен уровень значимости (α = 0,05) и степени свободы . Степени свободы ( df ) основаны на размерах выборки двух групп. Для данных о телесном жире это:

    $ df = n_1 + n_2 — 2 = 10 + 13 — 2 = 21 $

    Значение t с α = 0,05 и 21 степенью свободы равно 2,080.

  4. Мы сравниваем значение нашей статистики (2,80) со значением t . Поскольку 2,80 > 2,080, мы отклоняем нулевую гипотезу о том, что средний процент телесного жира у мужчин и женщин одинаков, и делаем вывод, что у нас есть доказательства того, что жировые отложения в популяции различаются между мужчинами и женщинами.

Статистические данные

Давайте посмотрим на данные о телесном жире и двухвыборочный t -тест с использованием статистических терминов.

Наша нулевая гипотеза состоит в том, что базовые средние значения совокупности одинаковы. Нулевая гипотеза записывается как:

$ H_o:  \mathrm{\mu_1} =\mathrm{\mu_2} $

Альтернативная гипотеза состоит в том, что средние значения не равны. Это записывается как:

$ H_o:  \mathrm{\mu_1} \neq \mathrm{\mu_2} $

Мы вычисляем среднее значение для каждой группы, а затем вычисляем разницу между двумя средними значениями. Записывается так: 92)} {n_1 + n_2 — 2} $

Формула показывает размер выборки для первой группы как n 1 и второй группы как n 2 . Стандартные отклонения для двух групп составляют с 1 и с 2 . Эта оценка позволяет двум группам иметь разное количество наблюдений. Объединенное стандартное отклонение представляет собой квадратный корень из дисперсии и записывается как s p .

92)}{2} $

Статистика теста рассчитывается как:

$ t = \frac{(\overline{x_1} -\overline{x_2})}{s_p\sqrt{1/n_1 + 1/n_2 }} $

Числитель тестовой статистики — это разница между средними значениями двух групп. Он оценивает разницу между двумя неизвестными средними значениями совокупности. Знаменатель представляет собой оценку стандартной ошибки разницы между двумя неизвестными средними значениями генеральной совокупности.

Техническая деталь: Для одного среднего значения стандартная ошибка составляет $ s/\sqrt{n} $ . Приведенная выше формула распространяет эту идею на две группы, которые используют объединенную оценку для s (стандартное отклонение), и которые могут иметь разные размеры групп.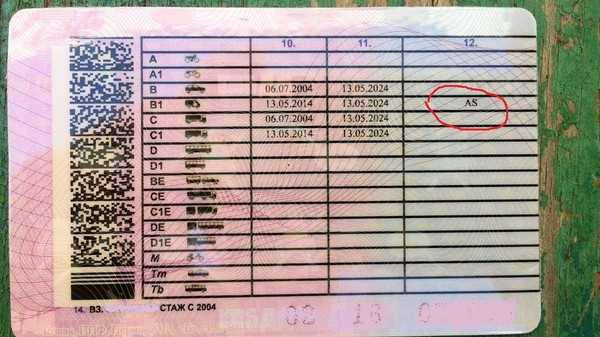

Затем мы сравниваем тестовую статистику со значением t с выбранным нами значением альфа и степенями свободы для наших данных. Используя в качестве примера данные о телесном жире, мы установили α = 0,05. Степени свободы ( df ) основаны на размерах групп и рассчитываются как:

$ df = n_1 + n_2 — 2 = 10 + 13 — 2 = 21 $

Формула показывает размер выборки для первой группы как n 1 и для второй группы как n 2 . Статистики записывают значение t с α = 0,05 и 21 степенью свободы как:

$ t_{0,05,21} $

Значение t с α = 0,05 и 21 степенью свободы равно 2,080. Есть два возможных результата нашего сравнения:

  • Тестовая статистика ниже значения t . Вы не можете отвергнуть гипотезу о равных средствах. Вы заключаете, что данные подтверждают предположение о том, что у мужчин и женщин средний процент жира в организме одинаков.
  • Статистика теста выше значения t . 2/n_2}} $

    Числитель тестовой статистики тот же. Это разница между средними показателями двух групп. Знаменатель представляет собой оценку общей стандартной ошибки разницы между средними значениями. Он основан на отдельной стандартной ошибке для каждой группы.

    Вычисление степеней свободы для значения t является более сложным с неравными дисперсиями, чем с равными дисперсиями, и обычно остается на усмотрение пакетов статистического программного обеспечения. Ключевым моментом, который следует помнить, является то, что если вы не можете использовать объединенную оценку стандартного отклонения, то вы не можете использовать простую формулу для степеней свободы.

    Тестирование на нормальность

    Предположение о нормальности более важно, когда две группы имеют небольшие размеры выборки, чем для больших размеров выборки.

    Нормальные распределения симметричны, что означает, что они «равномерны» по обе стороны от центра. Нормальные распределения не имеют экстремальных значений или выбросов. Вы можете проверить эти две особенности нормального распределения с помощью графиков. Ранее мы решили, что данные о телесном жире «достаточно близки» к норме, чтобы можно было сделать предположение о нормальности. На рисунке ниже показан нормальный квантильный график для мужчин и женщин, что подтверждает наше решение.

    Рисунок 2: Нормальный квантильный график измерений содержания жира в организме мужчин и женщин

    Вы также можете выполнить формальный тест на нормальность с помощью программного обеспечения. На рисунке выше показаны результаты тестирования на нормальность с помощью программного обеспечения JMP. Мы тестируем каждую группу отдельно. И тест для мужчин, и тест для женщин показывают, что мы не можем отвергнуть гипотезу о нормальном распределении. Мы можем предположить, что данные о телесном жире для мужчин и женщин распределены нормально.

    Проверка на неравные дисперсии

    Проверка на неравные дисперсии сложна. Мы не будем подробно показывать расчеты, но покажем результаты из программного обеспечения JMP. На рисунке ниже показаны результаты теста на неравные отклонения для данных о телесном жире.

    Рисунок 3: Тест на неравную дисперсию для данных о телесном жире

    Не вдаваясь в подробности различных типов тестов на неравную дисперсию, мы будем использовать тест F . Перед тестированием мы решаем принять 10%-й риск сделать вывод, что дисперсии равны, когда это не так. Это означает, что мы установили α = 0,10.

    Как и большинство статистических программ, JMP показывает p -значение для теста. Это вероятность найти более экстремальное значение тестовой статистики, чем наблюдаемое. Вручную посчитать сложно. Для приведенного выше рисунка со статистикой теста F , равной 1,654, значение p- равно 0,4561. Это больше, чем наше значение α: 0,4561 > 0,10. Мы не можем отвергнуть гипотезу о равных дисперсиях. С практической точки зрения, мы можем продолжить работу с двумя образцами 9.0003 t — тест с допущением равных дисперсий для двух групп.

    Понимание p-значений

    Используя визуальное представление, вы можете проверить, является ли ваша тестовая статистика более экстремальным значением в распределении. На рисунке ниже показано распределение t- с 21 степенью свободы.

    Рисунок 4: t-распределение с 21 степенью свободы и α = 0,05

    Поскольку наш тест является двусторонним и мы установили α = 0,05, рисунок показывает, что значение 2,080 «отсекает» 2,5 % данных в каждом из двух хвостов. Только 5% данных в целом находятся дальше хвоста, чем 2,080. Поскольку наша тестовая статистика 2,80 выходит за пределы точки отсечения, мы отвергаем нулевую гипотезу о равных средних.

    Соединение всего вместе с программным обеспечением

    На рисунке ниже показаны результаты двухвыборочного теста t для данных о телесном жире из программного обеспечения JMP.

    Рисунок 5: Результаты двухвыборочного t-теста из программного обеспечения JMP

    Результаты двухвыборочного t -критерия, предполагающего равные дисперсии, совпадают с нашими расчетами ранее. Статистика теста составляет 2,79996. Программное обеспечение показывает результаты двустороннего теста и одностороннего теста. Нам нужен двусторонний тест (Prob > |t|). Наша нулевая гипотеза состоит в том, что средний процент жира в организме мужчин и женщин одинаков. Наша альтернативная гипотеза состоит в том, что средний процент жира в организме не равен. Односторонние тесты предназначены для односторонних альтернативных гипотез — например, для нулевой гипотезы о том, что средний процент жира в организме мужчин меньше, чем у женщин.

    Мы можем отвергнуть гипотезу об одинаковом среднем значении жира в организме для двух групп и заключить, что у нас есть доказательства того, что содержание жира в организме у мужчин и женщин различается. Программное обеспечение показывает значение p , равное 0,0107. Мы выбрали 5%-й риск сделать вывод, что средний процент жира в организме мужчин и женщин различен, когда это не так. Важно принять это решение до выполнения статистического теста.

    На рисунке также показаны результаты теста t-, который не предполагает равных дисперсий. Этот тест не использует объединенную оценку стандартного отклонения. Как было сказано выше, этот тест также имеет сложную формулу для степеней свободы. Вы можете видеть, что степени свободы равны 20,9.888. Программное обеспечение показывает значение p-, равное 0,0086. Опять же, приняв решение о риске в 5%, мы можем отвергнуть нулевую гипотезу о равном среднем значении жира в организме мужчин и женщин.

    Другие темы

    Что делать, если у меня более двух групп?

    Если у вас более двух независимых групп, вы не можете использовать двухвыборочный тест t-. Следует использовать метод множественного сравнения. ANOVA, или дисперсионный анализ, является одним из таких методов. Другие методы множественного сравнения включают тест Тьюки-Крамера для всех попарных различий, анализ средних значений (ANOM) для сравнения групповых средних значений с общим средним значением или критерий Даннета для сравнения каждого среднего значения группы с контрольным средним значением.

    Что делать, если мои данные не из нормального распределения?

    Если размер вашей выборки очень мал, проверить нормальность может быть сложно. В этой ситуации вам может понадобиться использовать свое понимание измерений. Например, для данных о телесном жире тренер знает, что лежащее в основе распределение телесного жира является нормальным. Даже для очень маленькой выборки тренер, скорее всего, проведет тест t и предположит, что все нормально.

    Что делать, если вы знаете, что базовые измерения не имеют нормального распределения? Или что, если размер вашей выборки велик, а тест на нормальность отклонен? В этой ситуации можно использовать непараметрический анализ. Эти типы анализа не зависят от предположения, что значения данных взяты из определенного распределения. Для двухвыборочного t -тест, критерий суммы рангов Уилкоксона является непараметрическим критерием, который можно использовать.

    Двухвыборочный критерий средних

    В предыдущем модуле мы обсудили одновыборочный t-критерий, который сравнивает среднее значение одной выборки с заданной константой, и парный t-критерий, который сравнивает среднюю разницу между две переменные в одной выборке. Теперь мы хотим сравнить две независимые группы по среднему значению переменной анализа. В примере с холестерином мы могли бы сравнить средний возраст испытуемых, у которых были коронарные события, с 19 годами.62 к среднему возрасту субъектов, у которых не было коронарного события к 1962 году.

  • Две группы независимы.
  • Каждая из двух совокупностей, из которых взяты данные, имеет нормальное распределение.

 

Гипотеза:

H 0 : µ 1 =µ 2 против H

356 1 : μ 1 ≠ μ 2

 

  Оценка точки:

точка.

Достоверный интервал:

Тестовая статистика:

Как при одном из образцов T-тест, T-статистический расчет, с использованием вышеупомянутой формулы сравнивается с к критической к критической, с критической к критической к критической критической критической цене, по сравнению с вышеуказанной формулой по сравнению с решающей с решающей с образец T-Statistic, расчету выше, по сравнению с критическим с критическим с образец, с использованием вышеупомянутой формулы с критическим с критическим примером. значение t (которое можно найти в таблице t с использованием df и заранее заданного уровня значимости α). Опять же, если абсолютное значение рассчитанной t-статистики больше, чем абсолютное значение критического значения t, нулевая гипотеза отклоняется.

Существуют две формулы, используемые для оценки стандартной ошибки разницы в средних значениях, . Один подходит, если дисперсии совокупности равны, а другой следует использовать, если мы не можем предположить, что они равны.

Тест на равенство дисперсий

Чтобы определить, какую из двух формул использовать, мы сначала проверяем нулевую гипотезу о том, что дисперсии совокупности двух групп равны.

Первое испытание H 0 : σ 1 2 = σ 2 2

Критерий равенства дисперсий основан на распределении отношения дисперсий и использует F-статистику, F = s 1 2 909036 /s 2 2 . Эта статистика имеет распределение в F-семействе распределений и индексируется двумя числами: степенями свободы в знаменателе и степенями свободы в числителе. Степени свободы для вышеуказанного теста равны ( n 1 -1) для числителя и ( n 2 -1) для знаменателя; таким образом, значения тестовой статистики следует сравнивать с критическим значением F-распределения с ( n 1 -1) и ( n 2 -1) степенями свободы.

Обратите внимание, что F-распределение не является симметричным (как нормальное и t-распределение), что затрудняет поиск критических значений. Например, площадь выше z=1,96 равна 0,025, как и площадь ниже z=-1,96. Итак, если α = 0,05, критические значения z составляют ± 1,9.6. Таким образом, таблица должна отображать только одну сторону распределения. Распределение F не так просто. Например, при (12,6) степенях свободы площадь выше 5,37 равна 0,025, а площадь ниже 0,268 равна 0,025. Таким образом, мы бы отклонили тест, если F < 0,268 или > 5,37. Обратите внимание, что если F<1, мы сравниваем F с нижним критическим значением, а если F>1, мы сравниваем F с верхним критическим значением.

Хитрость заключается в том, чтобы заметить, что если мы сравним большую дисперсию с меньшей, так что F = (большая дисперсия)/(меньшая дисперсия), статистика F всегда будет >1. Поскольку F>1, мы будем использовать верхнее критическое значение.

 

  1. Выберите большую оценочную дисперсию в качестве числителя, а меньшую оценочную дисперсию в качестве знаменателя. В этом примере мы предположим, что s 1 больше, чем s 2 , и вычислим F = s 1 2 /s 2 2 .
  2. Сравните F с верхним критическим значением (соответствующим α/2) распределения F. Если F больше критического значения для данного уровня значимости, нулевая гипотеза отклоняется, и мы можем заключить, что существуют существенные доказательства того, что две дисперсии совокупности не равны.

Пример (из Dixon and Massey):

Мы хотели бы сравнить средний возраст субъектов, у которых были коронарные события к 1962 г., со средним возрастом субъектов, у которых не было коронарных событий к 1962 г.

 

Шаг 1 : проверьте предположение о равных дисперсиях генеральной совокупности ( ).

 

Мы используем группу «Нет коронарных событий» в качестве числителя, поскольку она больше. Тогда степени свободы равны (13-1) и (7-1), обычно записываются как (12,6).

 

Критическое значение теста F (если α = 0,05, мы используем верхнее критическое значение с 0,025 выше него) составляет

 

Мы полагаемся на SAS для выполнения этого теста и не ожидаем, до этих критических значений.

Рассчитайте статистику F,

 

F < критического значения, поэтому мы не отвергаем нулевую гипотезу о равенстве дисперсий и, таким образом, можем использовать объединенную стандартную ошибку.

Обратите внимание, что F-критерий чувствителен к отклонениям от нормальности и может иметь низкую мощность для обнаружения различий в отклонениях. Таким образом, его полезность в качестве предварительного теста на равенство дисперсий ограничена. Полезно исследовать изменчивость в двух группах, сравнивая выборочные дисперсии и рассматривая ящичковая диаграмма , чтобы помочь решить, какое предположение о стандартной ошибке является подходящим.

proc boxplot

proc boxplot предоставляет диаграммы для непрерывной переменной var с помощью группирующей переменной group. Примечание: для этого требуется, чтобы данные были отсортированы по группирующей переменной.

 

proc boxplot data=dix;

plot var*group / cboxes=black;

пробег;

 

Давайте проверим диаграммы в каждой из двух групп (cor=1 и cor=2)

 

/* Сортируем данные, чтобы можно было посмотреть на отдельные блок-диаграммы proc */

proc sort data=dixonmassey;

по кор. ;

пробег;

/* Хороший способ обобщить данные и визуально проверить предположение о гомоскедастичности*/

title ‘Графические диаграммы возраста по коронарным событиям’;

proc boxplot data=dix;

график age*cor / cboxes=black;

пробег;

 

 

Думаете, дисперсии равны?

Оценка стандартной ошибки разницы между значением

, предполагая равные различия в популяции (σ 1 2 = σ 2 2 )

IF σ 6 1 )

IF σ 6 1 )

IF σ 6 1 )

. 2 , объединенная дисперсия , S p , может использоваться для оценки общей дисперсии σ 2 .

  

, а стандартная ошибка разности средних оценивается как

 

.

 

Не предполагая равные дисперсии совокупности (не предполагая )

Если мы не можем принять , стандартная ошибка разности средних оценивается как:

Вычисление степеней свободы в этой ситуации сложно (см. «Статистические методы», 8-е издание, GW Snedecor и WG Cochran, стр. 9).7). В наших ручных вычислениях мы будем использовать минимум ( n 1 -1) и ( n 2 -1) для аппроксимации степеней свободы для приведенного выше t-критерия; при использовании SAS будет рассчитано и использовано правильное количество степеней свободы.

В нашем примере мы не отвергли гипотезу о равных дисперсиях, поэтому объединяем дисперсии при вычислении стандартной ошибки.

 

Шаг 2. Рассчитайте стандартную ошибку разницы средних

DF = N 1 + N 2 -2 = 18.

Шаг 3: Рассчитайте статистику T для тестирования

. α=0,05 составляет ± 2,101.

 

Заключение

Средний возраст в группе с коронарными событиями составил 49,29 года (N = 7, SD = 10,19) по сравнению со средним возрастом 42,08 (N = 13, SD = 10,77) в группе без коронарных событий. Поскольку t-статистика с 18 df 1,45 не выходит за пределы критических значений ± 2,101 для α = 0,05, мы не можем отвергнуть нулевую гипотезу о том, что средний возраст одинаков в группе пациентов с коронарными событиями и в группе с субъектов без коронарных событий.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *