Механика | это… Что такое Механика?
Меха́ника (греч. μηχανική — искусство построения машин) — область физики, изучающая движение материальных тел и взаимодействие между ними. Движением в механике называют изменение во времени взаимного положения тел или их частей в пространстве[1]. Важнейшими разделами механики являются классическая механика, релятивистская механика и квантовая механика.
Содержание
|
Механическая система
Механика занимается изучением так называемых механических систем.
Механическая система обладает определённым числом степеней свободы, а её состояние описывается с помощью обобщённых координат и соответствующих им обобщённых импульсов .
Являясь одним из классов физических систем, механические системы по характеру взаимодействия с окружением разделяются на изолированные (замкнутые), закрытые и открытые, по принципу изменения свойств во времени — на статические и динамические.
Наиболее важными механическими системами являются:
- материальная точка
- неголономная система
- гармонический осциллятор
- математический маятник
- физический маятник
- крутильный маятник
- абсолютно твёрдое тело
- деформируемое тело
- абсолютно упругое тело
- сплошная среда
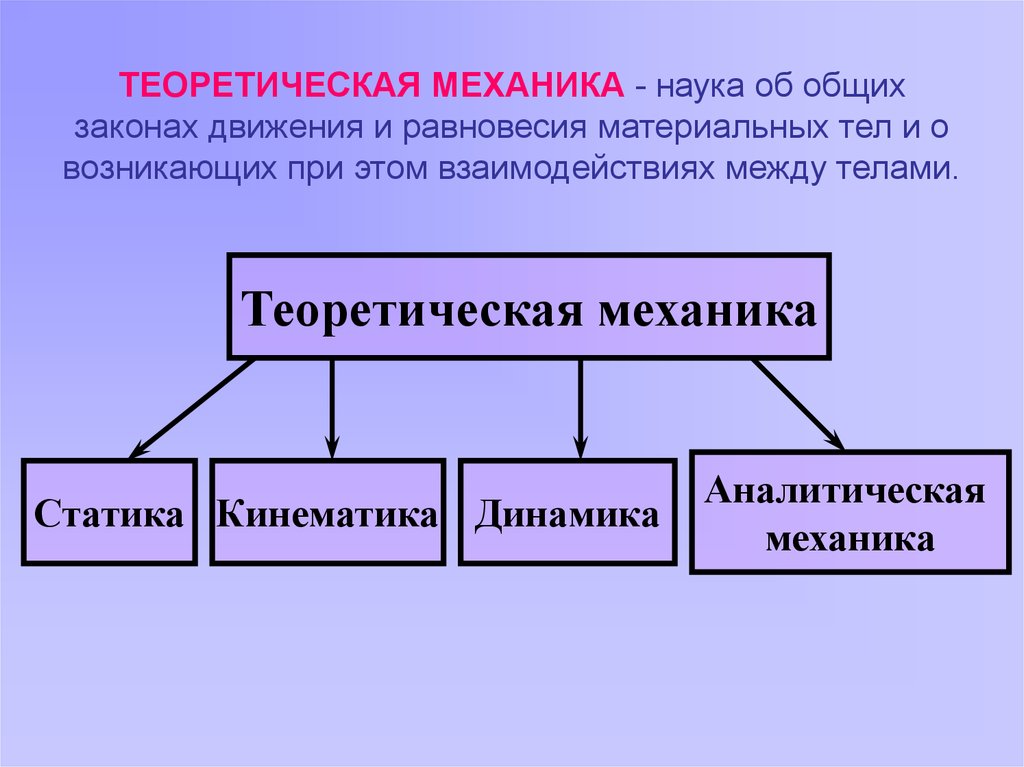
Разделы механики
Стандартные («школьные») разделы механики: кинематика, статика, динамика, законы сохранения. Кроме них, механика включает следующие (во многом перекрывающиеся) разделы:
- классическая механика
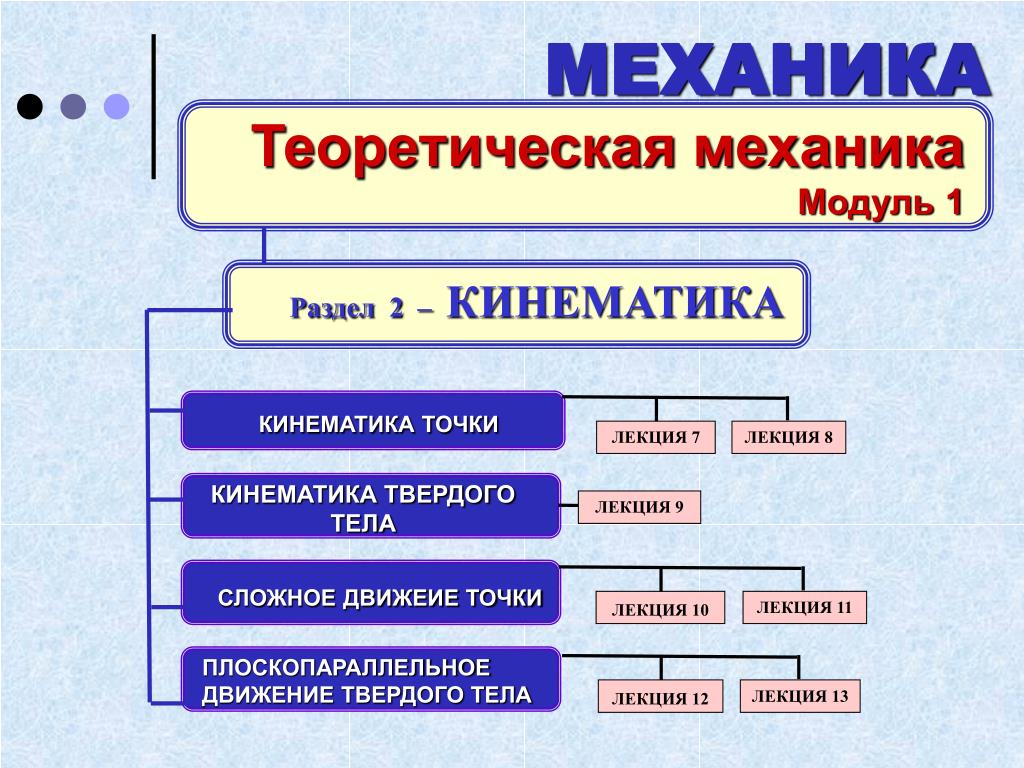
- теоретическая механика
- нелинейная динамика
- релятивистская механика
- квантовая механика
- небесная механика
- неголономная механика
- теория колебаний
- теория устойчивости и катастроф
- механика сплошных сред
- теория упругости
- теория пластичности
- наследственная механика
- механика разрушений
- статистическая механика
- вычислительная механика
- сопротивление материалов
- строительная механика
- механика грунтов
Некоторые курсы механики ограничиваются только твёрдыми телами. Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идёт не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошных сред.
Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идёт не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошных сред.
Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. К современному математическому аппарату классической механики относятся, прежде всего, теория дифференциальных уравнений, дифференциальная геометрия (симплектическая геометрия, контактная геометрия, тензорный анализ, векторные расслоения, теория дифференциальных форм), функциональный анализ и теория операторных алгебр, теория катастроф и бифуркаций. В современной классической механике используются и другие разделы математики. В классической формулировке, механика базируется на трёх законах Ньютона. Решение многих задач механики упрощается, если уравнения движения допускают возможность формулировки законов сохранения (импульса, энергии, момента импульса и других динамических переменных).
В классической формулировке, механика базируется на трёх законах Ньютона. Решение многих задач механики упрощается, если уравнения движения допускают возможность формулировки законов сохранения (импульса, энергии, момента импульса и других динамических переменных).
Различные формулировки механики
Все три закона Ньютона для широкого класса механических систем (консервативных систем, лагранжевых систем, гамильтоновых систем) связаны с различными вариационными принципами. В этой формулировке классическая механика таких систем строится на основе принципа стационарности действия: системы движутся так, чтобы обеспечить стационарность функционала действия. Такая формулировка используется, например, в лагранжевой механике и в гамильтоновой механике. Уравнениями движения в лагранжевой механике являются уравнения Эйлера — Лагранжа, а в гамильтоновой — уравнения Гамильтона.
Независимыми переменными, описывающими состояние системы в гамильтоновой механике, являются обобщённые координаты и импульсы, а в механике Лагранжа — обобщённые координаты и их производные по времени.
Если использовать функционал действия, определённый на реальной траектории системы, соединяющей некую начальную точку с произвольной конечной, то аналогом уравнений движения будут уравнения Гамильтона — Якоби.
Следует отметить, что все формулировки классической механики, основанные на голономных вариационных принципах, являются менее общими, чем формулировка механики, основанная на уравнениях движения. Не все механические системы имеют уравнения движения, представимые в виде уравнения Эйлера — Лагранжа, уравнения Гамильтона или уравнения Гамильтона — Якоби. Тем не менее, все формулировки являются как полезными с практической точки зрения, так и плодотворными с теоретической. Лагранжева формулировка оказалась особенно полезной в теории поля и релятивистской физике, а гамильтонова и Гамильтона — Якоби — в квантовой механике.
Классическая механика
Основная статья: Классическая механика
Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёта.
Границы применимости классической механики
В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.
- Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий (см.Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.)
- При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения. Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду , то придётся вводить тензор масс, компоненты которого растут с ростом скорости.
- Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.
См. также
- Механика (терминология)
- Мехатроника
Примечания
- ↑ Механика – Статья в Физической энциклопедии
Ссылки
- История развития механики до начала XIX века.
| В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Эта отметка установлена 13 мая 2011. |
Механика | это… Что такое Механика?
Меха́ника (греч. μηχανική — искусство построения машин) — область физики, изучающая движение материальных тел и взаимодействие между ними. Движением в механике называют изменение во времени взаимного положения тел или их частей в пространстве[1]. Важнейшими разделами механики являются классическая механика, релятивистская механика и квантовая механика.
μηχανική — искусство построения машин) — область физики, изучающая движение материальных тел и взаимодействие между ними. Движением в механике называют изменение во времени взаимного положения тел или их частей в пространстве[1]. Важнейшими разделами механики являются классическая механика, релятивистская механика и квантовая механика.
Содержание
|
Механическая система
Механика занимается изучением так называемых механических систем.
Механическая система обладает определённым числом степеней свободы, а её состояние описывается с помощью обобщённых координат и соответствующих им обобщённых импульсов . Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени.
Являясь одним из классов физических систем, механические системы по характеру взаимодействия с окружением разделяются на изолированные (замкнутые), закрытые и открытые, по принципу изменения свойств во времени — на статические и динамические.
Наиболее важными механическими системами являются:
- материальная точка
- неголономная система
- гармонический осциллятор
- математический маятник
- физический маятник
- крутильный маятник
- абсолютно твёрдое тело
- деформируемое тело
- абсолютно упругое тело
- сплошная среда
Разделы механики
Стандартные («школьные») разделы механики: кинематика, статика, динамика, законы сохранения. Кроме них, механика включает следующие (во многом перекрывающиеся) разделы:
- классическая механика
- теоретическая механика
- нелинейная динамика
- релятивистская механика
- квантовая механика
- небесная механика
- неголономная механика
- теория колебаний
- теория устойчивости и катастроф
- механика сплошных сред
- теория упругости
- теория пластичности
- наследственная механика
- механика разрушений
- статистическая механика
- вычислительная механика
- сопротивление материалов
- строительная механика
- механика грунтов
Некоторые курсы механики ограничиваются только твёрдыми телами.
Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. К современному математическому аппарату классической механики относятся, прежде всего, теория дифференциальных уравнений, дифференциальная геометрия (симплектическая геометрия, контактная геометрия, тензорный анализ, векторные расслоения, теория дифференциальных форм), функциональный анализ и теория операторных алгебр, теория катастроф и бифуркаций. В современной классической механике используются и другие разделы математики.
Различные формулировки механики
Все три закона Ньютона для широкого класса механических систем (консервативных систем, лагранжевых систем, гамильтоновых систем) связаны с различными вариационными принципами. В этой формулировке классическая механика таких систем строится на основе принципа стационарности действия: системы движутся так, чтобы обеспечить стационарность функционала действия. Такая формулировка используется, например, в лагранжевой механике и в гамильтоновой механике. Уравнениями движения в лагранжевой механике являются уравнения Эйлера — Лагранжа, а в гамильтоновой — уравнения Гамильтона.
Независимыми переменными, описывающими состояние системы в гамильтоновой механике, являются обобщённые координаты и импульсы, а в механике Лагранжа — обобщённые координаты и их производные по времени.
Если использовать функционал действия, определённый на реальной траектории системы, соединяющей некую начальную точку с произвольной конечной, то аналогом уравнений движения будут уравнения Гамильтона — Якоби.
Следует отметить, что все формулировки классической механики, основанные на голономных вариационных принципах, являются менее общими, чем формулировка механики, основанная на уравнениях движения. Не все механические системы имеют уравнения движения, представимые в виде уравнения Эйлера — Лагранжа, уравнения Гамильтона или уравнения Гамильтона — Якоби. Тем не менее, все формулировки являются как полезными с практической точки зрения, так и плодотворными с теоретической. Лагранжева формулировка оказалась особенно полезной в теории поля и релятивистской физике, а гамильтонова и Гамильтона — Якоби — в квантовой механике.
Классическая механика
Основная статья: Классическая механика
Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёта.
Границы применимости классической механики
В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.
- Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий (см.Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.)
- При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения. Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду , то придётся вводить тензор масс, компоненты которого растут с ростом скорости.
 Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.
Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется. - Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.
См. также
- Механика (терминология)
- Мехатроника
Примечания
- ↑ Механика – Статья в Физической энциклопедии
Ссылки
- История развития механики до начала XIX века.
| В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. |
механика | Определение, примеры, законы и факты
векторная математика
Просмотреть все медиа
- Ключевые люди:
- Леонардо да Винчи Галилео Архимед Жан Ле Рон д’Аламбер Анри Пуанкаре
- Похожие темы:
- гидромеханика механика твердого тела квантовая механика небесная механика релятивистская механика
Просмотреть весь соответствующий контент →
Резюме
Прочтите краткий обзор этой темы
механика , наука о движении тел под действием сил, включая частный случай, когда тело остается в покое.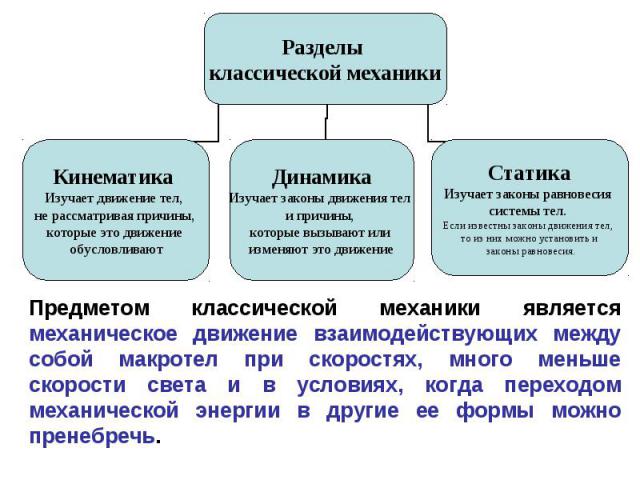 В первую очередь в проблеме движения речь идет о силах, с которыми тела действуют друг на друга. Это приводит к изучению таких тем, как гравитация, электричество и магнетизм, в зависимости от природы задействованных сил. Зная силы, можно искать способ движения тел под действием сил; это предмет собственно механики.
В первую очередь в проблеме движения речь идет о силах, с которыми тела действуют друг на друга. Это приводит к изучению таких тем, как гравитация, электричество и магнетизм, в зависимости от природы задействованных сил. Зная силы, можно искать способ движения тел под действием сил; это предмет собственно механики.
Исторически механика была одной из первых точных наук, получивших развитие. Ее внутренняя красота как математической дисциплины и ее первые замечательные успехи в количественном учете движения Луны, Земли и других планетных тел оказали огромное влияние на философскую мысль и дали толчок систематическому развитию науки.
Механика может быть разделена на три раздела: статика, изучающая силы, действующие на покоящееся тело и в нем; кинематика, описывающая возможные движения тела или системы тел; и кинетика, которая пытается объяснить или предсказать движение, которое произойдет в данной ситуации. В качестве альтернативы механику можно разделить в зависимости от типа изучаемой системы. Простейшей механической системой является частица, определяемая как тело настолько малое, что его форма и внутреннее строение не имеют значения в данной задаче. Более сложным является движение системы из двух или более частиц, которые действуют друг на друга и, возможно, испытывают силы тел вне системы.
Простейшей механической системой является частица, определяемая как тело настолько малое, что его форма и внутреннее строение не имеют значения в данной задаче. Более сложным является движение системы из двух или более частиц, которые действуют друг на друга и, возможно, испытывают силы тел вне системы.
Принципы механики были применены к трем основным сферам явлений. Движения таких небесных тел, как звезды, планеты и спутники, можно предсказать с большой точностью за тысячи лет до того, как они произойдут. (Теория относительности предсказывает некоторые отклонения от движения в соответствии с классической или ньютоновской механикой; однако они настолько малы, что их можно наблюдать только с помощью очень точных методов, за исключением задач, затрагивающих всю или большую часть обнаруживаемой Вселенной. ) Что касается второго царства, то обычные объекты на Земле вплоть до микроскопических размеров (движущиеся со скоростями намного ниже скорости света) должным образом описываются классической механикой без существенных поправок. Инженер, который проектирует мосты или самолеты, может с уверенностью использовать ньютоновские законы классической механики, даже если силы могут быть очень сложными, а расчетам не хватает прекрасной простоты небесной механики. Третья область явлений включает поведение материи и электромагнитного излучения в атомном и субатомном масштабе. Хотя были некоторые ограниченные первые успехи в описании поведения атомов с точки зрения классической механики, эти явления должным образом рассматриваются в квантовой механике.
Инженер, который проектирует мосты или самолеты, может с уверенностью использовать ньютоновские законы классической механики, даже если силы могут быть очень сложными, а расчетам не хватает прекрасной простоты небесной механики. Третья область явлений включает поведение материи и электромагнитного излучения в атомном и субатомном масштабе. Хотя были некоторые ограниченные первые успехи в описании поведения атомов с точки зрения классической механики, эти явления должным образом рассматриваются в квантовой механике.
Тест «Британника»
Физика и законы природы
Какая сила замедляет движение? Каждому действию есть равное и противоположное что? В этом викторине по физике нет ничего, что E = mc было бы квадратным.
Классическая механика имеет дело с движением тел под действием сил или с равновесием тел при уравновешивании всех сил. Субъект можно рассматривать как разработку и применение основных постулатов, впервые сформулированных Исааком Ньютоном в его Philosophiae Naturalis Principia Mathematica (1687), широко известный как Principia .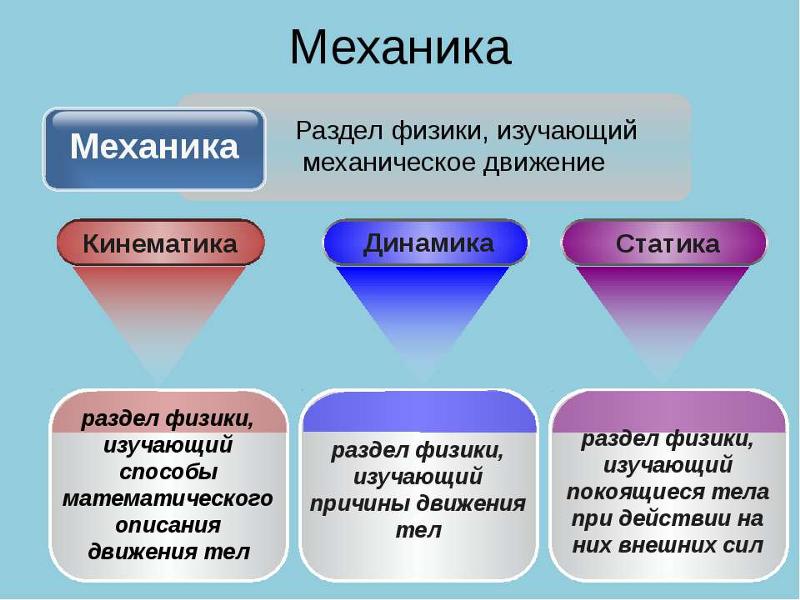 Эти постулаты, называемые законами движения Ньютона, изложены ниже. Их можно использовать для предсказания с большой точностью самых разных явлений, начиная от движения отдельных частиц и заканчивая взаимодействием очень сложных систем. Разнообразие этих приложений обсуждается в этой статье.
Эти постулаты, называемые законами движения Ньютона, изложены ниже. Их можно использовать для предсказания с большой точностью самых разных явлений, начиная от движения отдельных частиц и заканчивая взаимодействием очень сложных систем. Разнообразие этих приложений обсуждается в этой статье.
В рамках современной физики классическую механику можно понимать как приближение, вытекающее из более глубоких законов квантовой механики и теории относительности. Однако такой взгляд на место субъекта сильно недооценивает его важность в формировании контекста, языка и интуиции современной науки и ученых. Наше современное представление о мире и месте человека в нем прочно укоренено в классической механике. Более того, многие идеи и результаты классической механики сохранились и играют важную роль в новой физике.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Центральными понятиями классической механики являются сила, масса и движение. Ни сила, ни масса не определены Ньютоном очень четко, и со времен Ньютона они оба были предметом многочисленных философских рассуждений. Оба они наиболее известны своими эффектами. Масса является мерой тенденции тела сопротивляться изменениям в состоянии его движения. Силы, с другой стороны, ускоряют тела, то есть изменяют состояние движения тел, к которым они приложены. Взаимодействие этих эффектов составляет основную тему классической механики.
Ни сила, ни масса не определены Ньютоном очень четко, и со времен Ньютона они оба были предметом многочисленных философских рассуждений. Оба они наиболее известны своими эффектами. Масса является мерой тенденции тела сопротивляться изменениям в состоянии его движения. Силы, с другой стороны, ускоряют тела, то есть изменяют состояние движения тел, к которым они приложены. Взаимодействие этих эффектов составляет основную тему классической механики.
Хотя законы Ньютона фокусируют внимание на силе и массе, три другие величины приобретают особое значение, поскольку их общая сумма никогда не меняется. Этими тремя величинами являются энергия, (линейный) импульс и угловой момент. Любое из них может быть перенесено из одного тела или системы тел в другое. Кроме того, энергия может изменять форму, будучи связанной с одной системой, выступая в виде кинетической энергии, энергии движения; потенциальная энергия, энергия положения; теплота или внутренняя энергия, связанная со случайным движением атомов или молекул, составляющих любое реальное тело; или любая комбинация из трех. Тем не менее полная энергия, импульс и угловой момент во Вселенной никогда не меняются. Этот факт выражается в физике, говоря, что энергия, импульс и угловой момент сохраняются. Эти три закона сохранения вытекают из законов Ньютона, но сам Ньютон их не формулировал. Их пришлось обнаружить позже.
Тем не менее полная энергия, импульс и угловой момент во Вселенной никогда не меняются. Этот факт выражается в физике, говоря, что энергия, импульс и угловой момент сохраняются. Эти три закона сохранения вытекают из законов Ньютона, но сам Ньютон их не формулировал. Их пришлось обнаружить позже.
Примечателен тот факт, что, хотя законы Ньютона больше не считаются ни фундаментальными, ни даже абсолютно правильными, три закона сохранения, вытекающие из законов Ньютона, — сохранение энергии, импульса и углового момента — остаются в точности верными даже в квантовая механика и теория относительности. Фактически в современной физике сила перестала быть центральным понятием, а масса — лишь одним из ряда атрибутов материи. Однако энергия, импульс и угловой момент по-прежнему прочно занимают центральное место. Сохраняющееся значение этих идей, унаследованных от классической механики, может помочь объяснить, почему этот предмет сохраняет такое большое значение в науке сегодня.
Редакция Британской энциклопедии
квантовая механика | Определение, разработка и уравнения
туннелирование
Посмотреть все СМИ
- Ключевые люди:
- Вернер Гейзенберг
Джон фон Нейман
П.
 А.М. Дирак
Ричард Фейнман
Паскуаль Джордан
А.М. Дирак
Ричард Фейнман
Паскуаль Джордан
- Похожие темы:
- квантовая теория поля квант S-матрица уровень энергии волновая механика
Просмотреть весь соответствующий контент →
Резюме
Прочтите краткий обзор этой темы
квантовая механика , наука о поведении материи и света в атомном и субатомном масштабе. Он пытается описать и объяснить свойства молекул и атомов и их составляющих — электронов, протонов, нейтронов и других более эзотерических частиц, таких как кварки и глюоны. Эти свойства включают взаимодействие частиц друг с другом и с электромагнитным излучением (т. е. со светом, рентгеновскими лучами и гамма-лучами).
Поведение материи и излучения в атомном масштабе часто кажется странным, и, соответственно, трудно понять выводы квантовой теории и поверить в них. Его концепции часто противоречат представлениям здравого смысла, полученным из наблюдений за повседневным миром.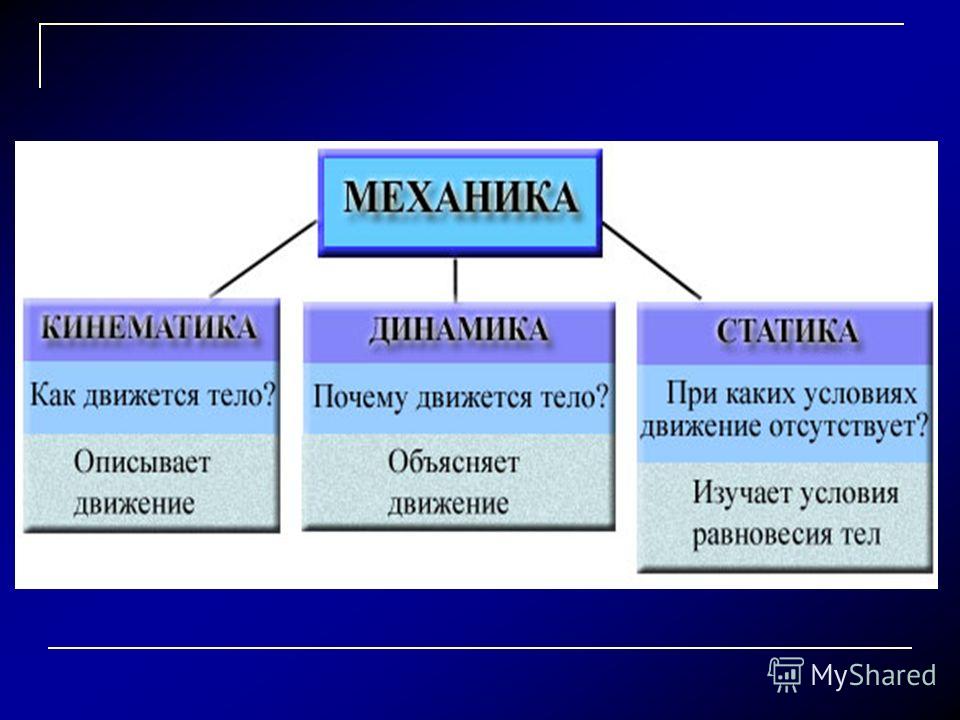 Однако нет причин, по которым поведение атомного мира должно соответствовать поведению знакомого крупномасштабного мира. Важно понимать, что квантовая механика — это раздел физики и что задача физики состоит в том, чтобы описывать и объяснять то, каким мир — как в большом, так и в малом масштабе — является на самом деле, а не так, как его представляют себе или хотели бы. это быть.
Однако нет причин, по которым поведение атомного мира должно соответствовать поведению знакомого крупномасштабного мира. Важно понимать, что квантовая механика — это раздел физики и что задача физики состоит в том, чтобы описывать и объяснять то, каким мир — как в большом, так и в малом масштабе — является на самом деле, а не так, как его представляют себе или хотели бы. это быть.
Изучение квантовой механики полезно по нескольким причинам. Во-первых, он иллюстрирует основную методологию физики. Во-вторых, он чрезвычайно успешно давал правильные результаты практически во всех ситуациях, к которым его применяли. Однако есть интригующий парадокс. Несмотря на ошеломляющие практические успехи квантовой механики, в ее основе лежат нерешенные проблемы, в частности вопросы о природе измерения. Существенной особенностью квантовой механики является то, что вообще невозможно, даже в принципе, измерить систему, не воздействуя на нее; детальная природа этого нарушения и точная точка, в которой оно возникает, неясны и противоречивы.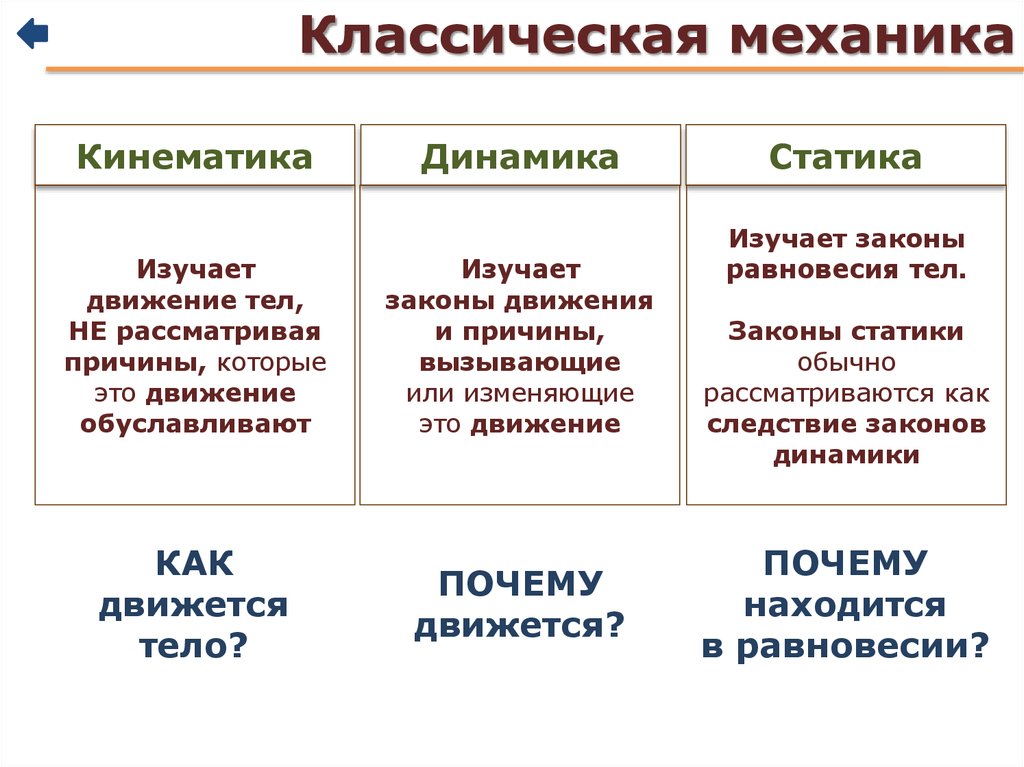 Таким образом, квантовая механика привлекла некоторых из самых способных ученых 20-го века, и они построили, возможно, лучшее интеллектуальное здание того периода.
Таким образом, квантовая механика привлекла некоторых из самых способных ученых 20-го века, и они построили, возможно, лучшее интеллектуальное здание того периода.
Исторические основы квантовой теории
Основные соображения
На фундаментальном уровне и излучение, и материя обладают характеристиками частиц и волн. Постепенное признание учеными того, что излучение обладает корпускулярными свойствами, а материи — волновыми, послужило толчком к развитию квантовой механики. Под влиянием Ньютона большинство физиков 18 века считали, что свет состоит из частиц, которые они называли корпускулами. Примерно с 1800 г. начали накапливаться свидетельства волновой теории света. Примерно в это же время Томас Юнг показал, что если монохроматический свет проходит через пару щелей, два выходящих луча интерферируют, так что на экране появляется бахрома из чередующихся ярких и темных полос. Полосы легко объясняются волновой теорией света. Согласно теории, яркая полоса образуется, когда гребни (и впадины) волн от двух щелей вместе достигают экрана; темная полоса образуется, когда гребень одной волны достигает впадины другой волны одновременно, и эффекты двух световых лучей компенсируются.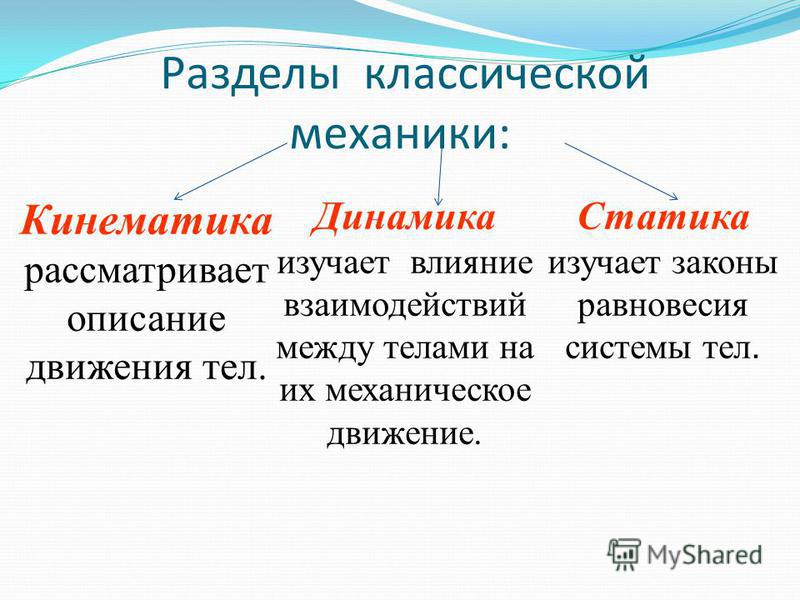 Начиная с 1815 года, серия экспериментов Огюстена-Жана Френеля из Франции и других показала, что, когда параллельный пучок света проходит через единственную щель, выходящий пучок больше не является параллельным, а начинает расходиться; это явление известно как дифракция. Учитывая длину волны света и геометрию устройства (т. Е. Разделение и ширину щелей, а также расстояние от щелей до экрана), можно использовать волновую теорию для расчета ожидаемой картины в каждом случае; теория точно согласуется с экспериментальными данными.
Начиная с 1815 года, серия экспериментов Огюстена-Жана Френеля из Франции и других показала, что, когда параллельный пучок света проходит через единственную щель, выходящий пучок больше не является параллельным, а начинает расходиться; это явление известно как дифракция. Учитывая длину волны света и геометрию устройства (т. Е. Разделение и ширину щелей, а также расстояние от щелей до экрана), можно использовать волновую теорию для расчета ожидаемой картины в каждом случае; теория точно согласуется с экспериментальными данными.
Тест «Британника»
Физика и законы природы
Какая сила замедляет движение? Каждому действию есть равное и противоположное что? В этом викторине по физике нет ничего, что E = mc было бы квадратным.
Ранние разработки
К концу 19 века физики почти повсеместно приняли волновую теорию света. Однако, хотя идеи классической физики объясняют явления интерференции и дифракции, связанные с распространением света, они не учитывают поглощение и испускание света.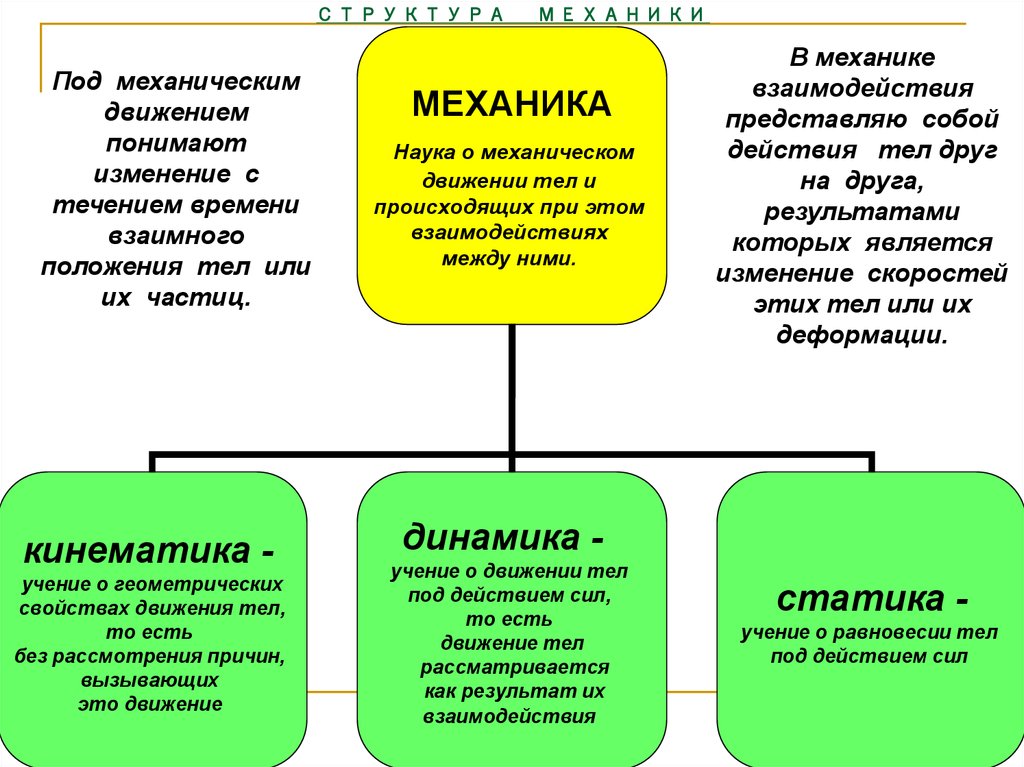 Все тела излучают электромагнитную энергию в виде тепла; на самом деле тело излучает излучение на всех длинах волн. Энергия, излучаемая на разных длинах волн, максимальна на длине волны, зависящей от температуры тела; чем горячее тело, тем короче длина волны для максимального излучения. Попытки рассчитать распределение энергии излучения абсолютно черного тела с использованием классических представлений не увенчались успехом. (Черное тело — это гипотетическое идеальное тело или поверхность, которая поглощает и переизлучает всю падающую на нее лучистую энергию.) Одна формула, предложенная немецким Вильгельмом Вином, не согласовывалась с наблюдениями на длинных волнах, а другая, предложенная лордом Рэлеем (Джон William Strutt) из Англии, не согласен с теми, кто работает на коротких волнах.
Все тела излучают электромагнитную энергию в виде тепла; на самом деле тело излучает излучение на всех длинах волн. Энергия, излучаемая на разных длинах волн, максимальна на длине волны, зависящей от температуры тела; чем горячее тело, тем короче длина волны для максимального излучения. Попытки рассчитать распределение энергии излучения абсолютно черного тела с использованием классических представлений не увенчались успехом. (Черное тело — это гипотетическое идеальное тело или поверхность, которая поглощает и переизлучает всю падающую на нее лучистую энергию.) Одна формула, предложенная немецким Вильгельмом Вином, не согласовывалась с наблюдениями на длинных волнах, а другая, предложенная лордом Рэлеем (Джон William Strutt) из Англии, не согласен с теми, кто работает на коротких волнах.
В 1900 году немецкий физик-теоретик Макс Планк сделал смелое предложение. Он предположил, что энергия излучения излучается не непрерывно, а дискретными порциями, называемыми квантами. Энергия E кванта связана с частотой ν соотношением E = ч ν.