Физика магнетизм: Магнетизм — Физика — Теория, тесты, формулы и задачи

Магнетизм — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Сила Ампера

К оглавлению…

Заряженные тела способны создавать кроме электрического еще один вид поля. Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем. Следовательно, электрический ток, представляющий собой упорядоченное движение зарядов, тоже создает магнитное поле. Как и электрическое поле, магнитное поле не ограничено в пространстве, распространяется очень быстро, но все же с конечной скоростью. Его можно обнаружить только по действию на движущиеся заряженные тела (и, как следствие, токи).

Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E электрического поля. Такой характеристикой является вектор B магнитной индукции. В системе единиц СИ за единицу магнитной индукции принят 1 Тесла (Тл).

 Если в магнитное поле с индукцией B поместить проводник длиной l с током I, то на него будет действовать сила, называемая силой Ампера, которая вычисляется по формуле:

где: В – индукция магнитного поля, I – сила тока в проводнике, l – его длина. Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику. 

Для определения направления силы Ампера обычно используют правило «Левой руки»: если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы Ампера, действующей на проводник (см. рисунок).

Если угол α между направлениями вектора магнитной индукции и тока в проводнике отличен от 90°, то для определения направления силы Ампера надо взять составляющую магнитного поля, которая перпендикулярна направлению тока.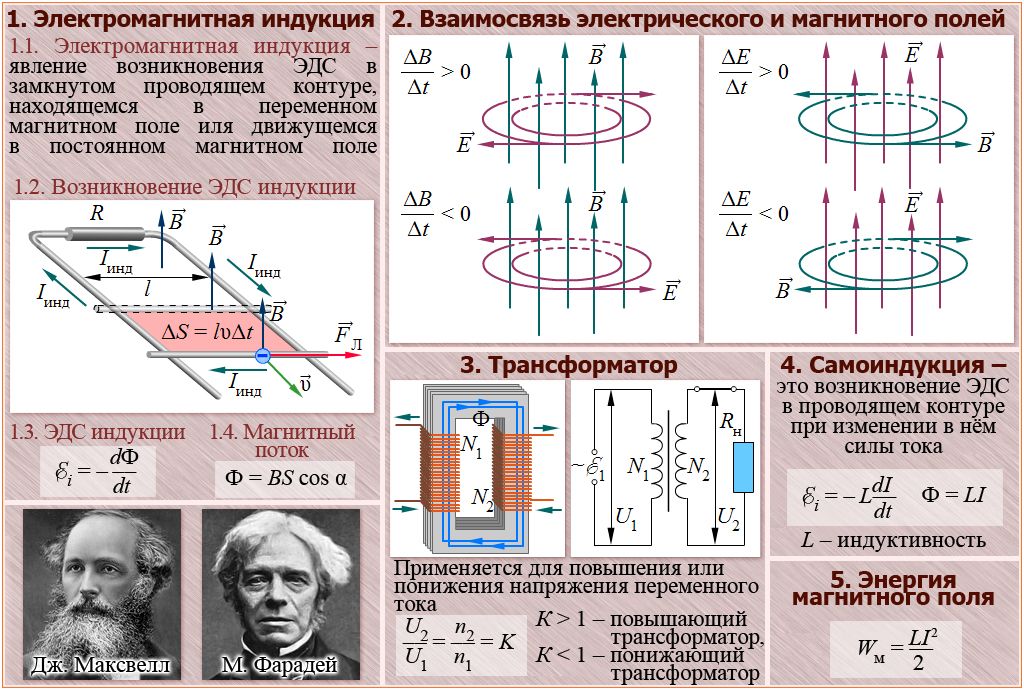

Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.

Момент сил, действующих на рамку с током

Пусть рамка с током находится в магнитном поле, причём плоскость рамки перпендикулярна полю. Силы Ампера будут сжимать рамку, а их равнодействующая будет равна нулю. Если поменять направление тока, то силы Ампера поменяют своё направление, и рамка будет не сжиматься, а растягиваться. Если линии магнитной индукции лежат в плоскости рамки, то возникает вращательный момент сил Ампера. Вращательный момент сил Ампера равен:

где: S — площадь рамки, α — угол между нормалью к рамке и вектором магнитной индукции (нормаль — вектор, перпендикулярный плоскости рамки), N – количество витков, B – индукция магнитного поля, I – сила тока в рамке.

 

Сила Лоренца

К оглавлению…

Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B может быть выражена через силы, действующие на отдельные носители заряда. Эти силы называют силами Лоренца. Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B, двигающуюся со скоростью v, вычисляется по следующей формуле:

Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика (как и сила Ампера). Вектор магнитной индукции нужно мысленно воткнуть в ладонь левой руки, четыре сомкнутых пальца направить по скорости движения заряженной частицы, а отогнутый большой палец покажет направление силы Лоренца. Если частица имеет

отрицательный заряд, то направление силы Лоренца, найденное по правилу левой руки, надо будет заменить на противоположное.

Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:

Сила Лоренца в этом случае играет роль центростремительной силы. Период обращения частицы в однородном магнитном поле равен:

Последнее выражение показывает, что для заряженных частиц заданной массы m период обращения (а значит и частота, и угловая скорость) не зависит от скорости (следовательно, и от кинетической энергии) и радиуса траектории R.

 

Теория о магнитном поле

К оглавлению…

Магнитное взаимодействие токов

Если по двум параллельным проводам идёт ток в одном направлении, то они притягиваются; если в противоположных направлениях, то отталкиваются. Закономерности этого явления были экспериментально установлены Ампером.  Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I₁ и I₂ в проводниках, длине отрезка Δl и обратно пропорционален расстоянию

R между ними:

где: μ₀ – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:

μ₀ = 4π·10^–7 H/A² ≈ 1,26·10^–6 H/A².

Сравнивая приведенное только что выражение для силы взаимодействия двух проводников с током и выражение для силы Ампера нетрудно получить выражение для индукции магнитного поля создаваемого каждым из прямолинейных проводников с током на расстоянии R от него:

где: μ – магнитная проницаемость вещества (об этом чуть ниже). Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:

Силовыми линиями

магнитного поля называют линии, по касательным к которым располагаются магнитные стрелки. Магнитной стрелкой называют длинный и тонкий магнит, его полюса точечны. Подвешенная на нити магнитная стрелка всегда поворачивается в одну сторону. При этом один её конец направлен в сторону севера, второй — на юг. Отсюда название полюсов: северный (N) и южный (S). Магниты всегда имеют два полюса: северный (обозначается синим цветом или буквой N) и южный (красным цветом или буквой S). Магниты взаимодействуют так же, как и заряды: одноименные полюса отталкиваются, а разноименные – притягиваются. Невозможно получить магнит с одним полюсом. Даже если магнит разломать, то у каждой части будет по два разных полюса.

Вектор магнитной индукции

Вектор магнитной индукции — векторная физическая величина, являющаяся характеристикой магнитного поля, численно равная силе, действующей на элемент тока в 1 А и длиной 1 м, если направление силовой линии перпендикулярно проводнику.

Обозначается В, единица измерения — 1 Тесла. 1 Тл — очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.

Вектор магнитной индукции направлен по касательной к силовым линиям, т.е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.

Силовая линия магнитного поля постоянных магнитов направлена по отношению к самим магнитам так, как показано на рисунке:

В случае магнитного поля электрического тока для определения направления силовых линий используют правило «Правой руки»: если взять проводник в правую руку так, чтобы большой палец был направлен по току, то четыре пальца, обхватывающие проводник, показывают направление силовых линий вокруг проводника:

В случае прямого тока линии магнитной индукции — окружности, плоскости которых перпендикулярны току.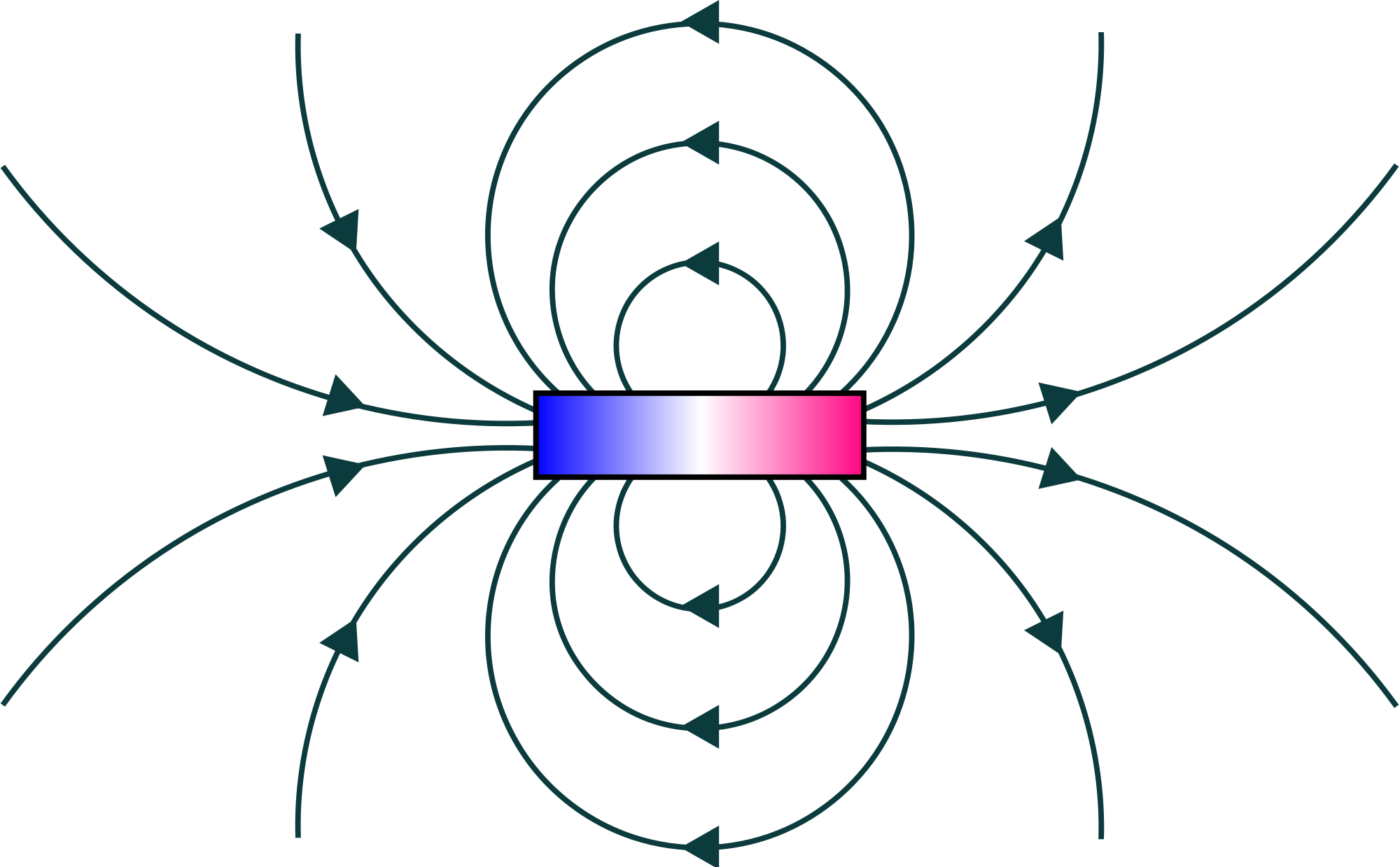 Вектора магнитной индукции направлены по касательной к окружности.

Соленоид — намотанный на цилиндрическую поверхность проводник, по которому течёт электрический ток I. Магнитное поле соленоида подобно полю прямого постоянного магнита. Внутри соленоида длиной l и количеством витков N создается однородное магнитное поле с индукцией (его направление также определяется правилом правой руки):

Линии магнитного поля имеют вид замкнутых линий — это общее свойство всех магнитных линий. Такое поле называют вихревым. В случае постоянных магнитов линии не оканчиваются на поверхности, а проникают внутрь магнита и замыкаются внутри. Это различие электрического и магнитного полей объясняется тем, что, в отличие от электрических, магнитных зарядов не существует.

Магнитные свойства вещества

Все вещества обладают магнитными свойствами. Магнитные свойства вещества характеризуются относительной магнитной проницаемостью μ, для которой верно следующее:

Данная формула выражает соответствие вектора магнитной индукции поля в вакууме и в данной среде. В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле.

Парамагнетики — кислород, платина, магний — несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков — железо, никель, кобальт — μ >> 1. Например, у железа μ ≈ 25000.

 

Магнитный поток. Электромагнитная индукция

К оглавлению…

Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 году. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур. Магнитным потоком Φ через площадь S контура называют величину:

где: B – модуль вектора магнитной индукции, α – угол между вектором магнитной индукции B и нормалью (перпендикуляром) к плоскости контура, S – площадь контура, N – количество витком в контуре. Единица магнитного потока в системе СИ называется Вебером (Вб).

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции ε_инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум возможным причинам.

1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.

При решении задач важно сразу определить за счет чего меняется магнитный поток. Возможно три варианта:

1. Меняется магнитное поле.
2. Меняется площадь контура.
3. Меняется ориентация рамки относительно поля.

При этом при решении задач обычно считают ЭДС по модулю. Обратим внимание также внимание на один частный случай, в котором происходит явление электромагнитной индукции. Итак, максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:

 

Движение проводника в магнитном поле

К оглавлению…

При движении проводника длиной l в магнитном поле B со скоростью v на его концах возникает разность потенциалов, вызванная действием силы Лоренца на свободные электроны в проводнике. Эту разность потенциалов (строго говоря, ЭДС) находят по формуле:

где: α — угол, который измеряется между направлением скорости и вектора магнитной индукции. В неподвижных частях контура ЭДС не возникает.

Если стержень длиной L вращается в магнитном поле В вокруг одного из своих концов с угловой скоростью ω, то на его концах возникнет разность потенциалов (ЭДС), которую можно рассчитать по формуле:

 

Индуктивность. Самоиндукция. Энергия магнитного поля

К оглавлению…

Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:

Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).

Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:

где: n — концентрация витков на единицу длины катушки:

ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:

Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия W_м магнитного поля катушки с индуктивностью L, создаваемого током I, может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI):

Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):

 

Правило Ленца

К оглавлению. ..

Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.

Правило Ленца для определения направления индукционного тока: возникающий в контуре индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывало этот ток.

Физика в опытах. Часть 2. Электричество и магнетизм

Наглядно – интересно – просто – понятно!

Данный курс представляет собой серию физических опытов и экспериментов. Демонстрацию физических явлений проводит незаурядный преподаватель, доцент кафедры общей физики НИЯУ «МИФИ» — Валериан Иванович Гервидс, глубокие знания и огромный преподавательский опыт которого делает курс «Физика в опытах. Электричество и магнетизм» уникальным. Курс состоит из девяти модулей по основным разделам: Электрическое поле, Проводники в электрическом поле, Энергия электрического поля, Постоянный электрический ток, Магнитное поле, Магнитное поле в веществе, Электромагнитная индукция, Квазистационарные токи, Электрический ток в газах. В его основе этого курса лежат 64 опыта, в которых объясняются различные физические явления. Зачем изучать этот курс? • Физика – наука экспериментальная. Лучше один раз увидеть, чем сто раз услышать или прочитать! • Именно эксперименты позволяют продемонстрировать и легко понять и простые, и сложные аспекты, которые традиционно преподаются в виде теоретического материала и математических моделей • Курс поможет Вам научиться использовать: o эксперимент как способ постановки вопроса, o эксперимент как инструмент изучения физического явления o эксперимент как форму ответа на вопрос • Очень часто достаточно «простые» физические вопросы имеют неожиданные ответы, которые зависят от конкретных условий проведения эксперимента. Демонстрация таких опытов и объяснение полученных в них результатов могут оказаться чрезвычайно интересными • Вы сможете увидеть применение изучаемых физических явлений в жизни, в технике и в быту • Изучая этот курс, вы восполните нехватку времени на экспериментальную, «живую» физику, которая ощущается в обычном учебном процесс Чему учит этот курс? • Пониманию широкого круга как простых, так и сложных физических явлений и процессов по тематике соответствующих разделов • Применению физических закономерностей для анализа различных физических явлений и процессов • Навыкам использования эксперимента • Базовым знаниям по физике будущих инженеров и специалистов в различных областях деятельности. Для кого этот курс? • Для тех, кто изучает физику, и хочет прояснить для себя различные вопросы (в школе, в вузе) • Для тех, кто преподает физику (в школе, в вузе) • Для тех, кто использует физику в своем рабочем процессе (инженеры, программисты и т.д.) • Для тех, кому это просто интересно

Физика в опытах.

Часть 2. Электричество и магнетизм

Наглядно – интересно – просто – понятно! Данный курс представляет собой серию физических опытов, наглядно демонстрирующих работу основных законов механики. Демонстрацию физических явлений проводит незаурядный преподаватель, доцент кафедры общей физики НИЯУ «МИФИ» — Валериан Иванович Гервидс, глубокие знания и огромный преподавательский опыт которого делает курс «Физика в опытах. Электричество и магнетизм» уникальным. Курс состоит из девяти модулей по основным разделам: Электрическое поле, Проводники в электрическом поле, Энергия электрического поля, Постоянный электрический ток, Магнитное поле, Магнитное поле в веществе, Электромагнитная индукция, Квазистационарные токи, Электрический ток в газах. В его основе этого курса лежат 64 опыта, в которых объясняются различные физические явления. Зачем изучать этот курс? • Физика – наука экспериментальная. Лучше один раз увидеть, чем сто раз услышать или прочитать! • Именно эксперименты позволяют продемонстрировать и легко понять и простые, и сложные аспекты, которые традиционно преподаются в виде теоретического материала и математических моделей • Курс поможет Вам научиться использовать: o эксперимент как способ постановки вопроса, o эксперимент как инструмент изучения физического явления o эксперимент как форму ответа на вопрос • Очень часто достаточно «простые» физические вопросы имеют неожиданные ответы, которые зависят от конкретных условий проведения эксперимента. Демонстрация таких опытов и объяснение полученных в них результатов могут оказаться чрезвычайно интересными • Вы сможете увидеть применение изучаемых физических явлений в жизни, в технике и в быту • Изучая этот курс, вы восполните нехватку времени на экспериментальную, «живую» физику, которая ощущается в обычном учебном процесс Чему учит этот курс? • Пониманию широкого круга как простых, так и сложных физических явлений и процессов по тематике соответствующих разделов • Применению физических закономерностей для анализа различных физических явлений и процессов • Навыкам использования эксперимента • Базовым знаниям по физике будущих инженеров и специалистов в различных областях деятельности. Для кого этот курс? • Для тех, кто изучает физику, и хочет прояснить для себя различные вопросы (в школе, в вузе) • Для тех, кто преподает физику (в школе, в вузе) • Для тех, кто использует физику в своем рабочем процессе (инженеры, программисты и т.д.) • Для тех, кому это просто интересно

основные формулы, законы и правила

Магнитное поле — это форма материи, окружающей движущиеся электрические заряды. Магнитное поле окружает проводники с током.

Силовой характеристикой магнитного поля является магнитная индукция.

Магнитная индукция — это величина, равная отношению максимального момента силы, вращающей контур с током в магнитном поле, к силе тока в этом контуре и его площади:

Другое определение магнитной индукции: магнитная индукция — это величина, равная отношению максимальной силы, действующей на проводник с током в магнитном поле, к силе тока в нем и длине этого проводника в магнитном поле:

Магнитная индукция — векторная величина. Вектор магнитной индукции совпадает по направлению с положительной нормалью к плоскости контура. За

направление положительной нормали п принято направление поступательного движения правого винта (буравчика), когда его головка вращается по току в контуре (рис. 208).

Правым винтом может служить ваша правая рука. Если свернуть четыре пальца правой руки в направлении тока в контуре, то большой палец, отставленный на 90°, покажет направление положительной нормали и вектора магнитной индукции.

Единица магнитной индукции в СИ — тесла (Тл).

Магнитное поле изображают графически с помощью магнитных силовых линий или линий вектора магнитной индукции.

В природе не существует магнитных зарядов, поэтому линии вектора магнитной индукции всегда замкнуты.

Магнитное поле является вихревым, в отличие от потенциального электростатического поля, линии которого всегда разомкнуты, т. к. начинаются и оканчиваются на электрических зарядах. Линии вектора магнитной индукции охватывают проводники с током. Линии вектора магнитной индукции поля прямого тока представляют собой концентрические окружности с центром на проводнике с током (рис. 209). Их направление можно определить с помощью правого винта (или с помощью вашей правой руки: если большой палец правой руки направить по направлению тока в проводнике, то четыре загнутых пальца покажут направление линии магнитной индукции). По мере удаления от проводника с током индукция магнитного поля этого тока уменьшается.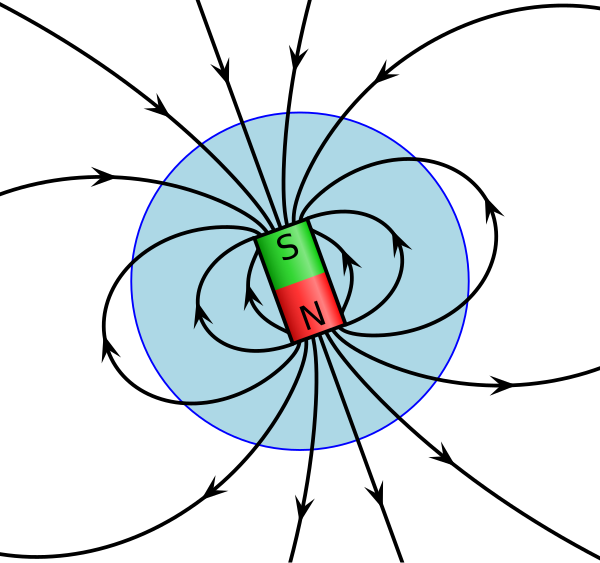

Магнитное поле, в каждой точке которого вектор магнитной индукции одинаков, называется однородным. Линии магнитной индукции однородного поля представляют собой прямые, расположенные на одинаковом расстоянии друг от друга. Чем гуще они располагаются, тем больше магнитная индукция.

Примером однородного магнитного поля является магнитное поле внутри длинного соленоида — катушки с током (рис. 210).

Линии магнитной индукции выходят из северного полюса N и входят в его южный полюс S.

Магнитное поле полосового магнита (рис. 211) наибольшее на его полюсах, а в центре его магнитная индукция равна нулю.

Если в однородное поле внести контур с током, расположив его плоскость параллельно линиям магнитной индукции, то на стороны контура, перпендикулярным линиям магнитной индукции, будет действовать пара сил Ампера, которая создаст максимальный вращающий момент сил , равный произведению индукции магнитного поля, силы тока в ней и ее площади:

Если плоскость контура расположена под углом к линиям вектора индукции однородного магнитного поля, то момент сил определяет формула

Здесь — угол между вектором индукции магнитного поля и нормалью к плоскости рамки.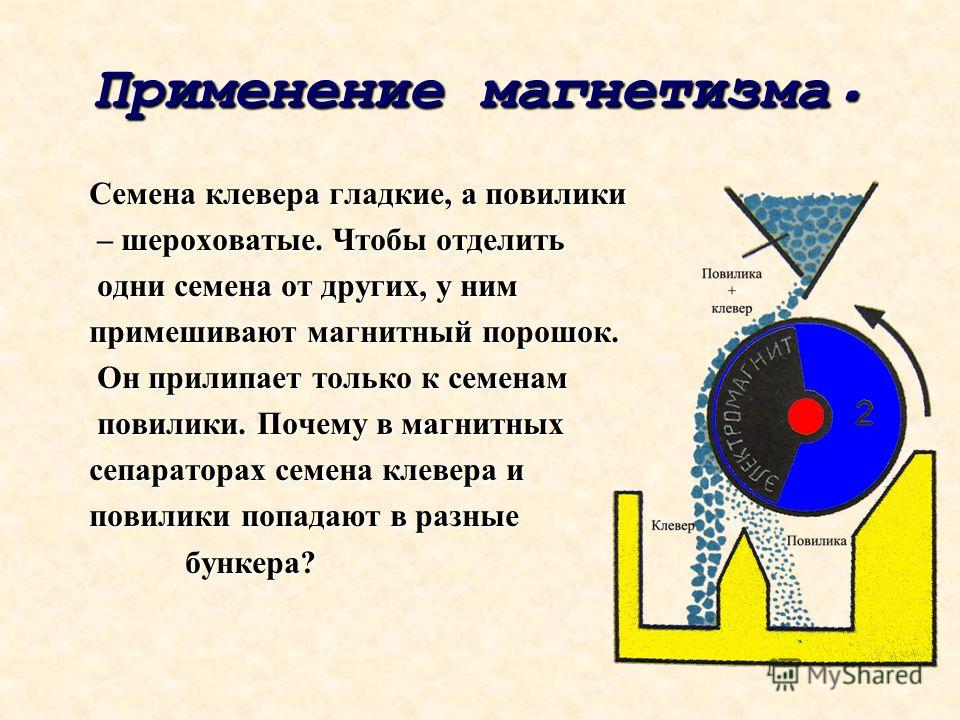

Момент сил, вращающих контур с током в однородном магнитном поле, равен произведению индукции этого поля, силы тока в контуре, площади контура и синуса угла между векторами магнитной индукции и нормали к плоскости контура.

Если плоскость контура перпендикулярна линиям вектора магнитной индукции, то вращающий момент сил равен 0, а силы Ампера действуют в плоскости контура, деформируя его.

Направление силы Ампера можно определить по правилу левой руки: если ладонь левой руки расположить так, чтобы магнитные линии входили в ладонь, а четыре вытянутых пальца направить по току в проводнике, то большой палец, отставленный на 90 , покажет направление силы Ампера, действующей на этот проводник в данном магнитном поле (рис. 212).

Если проводник с током расположить параллельно магнитным линиям, то сила Ампера на него действовать не будет.

Сила Ампера

Величину силы Ампера определяет закон Ампера: сила F, действующая на проводник с током в однородном магнитном поле, равна произведению магнитной индукции этого поля В, силы тока в проводнике I, длины проводника в магнитном поле I и синуса угла а между направлением магнитного поля и направлением тока в проводнике:

Сила, с которой магнитное поле действует на движущийся в нем заряд, называется силой Лоренца.

Сила Лоренца

Сила Лоренца действующая на заряд q, движущийся в однородном магнитном поле, равна произведению индукции этого поля В на заряд, на скорость его движения v и на синус угла между направлением магнитного поля и направлением движения заряда

Определить направление силы Лоренца можно тоже по правилу левой руки: если ладонь левой руки расположить так, чтобы магнитные линии входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления движения отрицательного заряда), то большой палец, отставленный на 90″, покажет направление силы Лоренца.

Заряженная частица, влетевшая в однородное магнитное поле перпендикулярно его магнитным линиям, движется равномерно по окружности, охватывающей магнитные линии.

При этом сила Лоренца направлена по радиусу к центру окружности.

На рис. 213 положительно заряженная частица с зарядом q, влетевшая в направлении, показанном вектором v в однородное магнитное поле индукцией В, направленном за чертеж, движется вокруг магнитных линий против часовой стрелки.

Если заряженная частица влетает в магнитное поле под углом к магнитным линиям, то она станет двигаться по винтовой линии (рис. 214), вращаясь по окружности с линейной скоростью, равной нормальной составляющей вектора скорости usin а, и одновременно перемещаясь

равномерно вдоль линий вектора индукции магнитного поля с тангенциальной составляющей vcos а вектора скорости .

Расстояние х, которое она пролетит вдоль магнитной линии за один оборот, называется шагом винта. Поскольку вдоль магнитной линии частица движется с постоянной скоростью и, то шаг винта равен

Здесь Т — период, т.е. время одного оборота частицы вокруг магнитных линий.

Сила Лоренца всегда перпендикулярна вектору скорости и, следовательно, вектору перемещения заряда, поэтому она работы перемещения заряда в магнитном поле не совершает, вследствие чего кинетическая энергия заряда, движущегося в магнитном поле под действием силы Лоренца, не изменяется.

Если заряженная частица движется одновременно в электрическом и магнитном полях (т. е. в электромагнитном поле), то на нее действует обобщенная сила Лоренца, равная векторной сумме силы Лоренца, действующей на нее со стороны магнитного поля, и силы Кулона, действующей со стороны электрического поля.

Пусть в однородном магнитном поле индукцией находится некоторая площадка S (рис. 215).

Магнитный поток Ф, создаваемый однородным магнитным полем сквозь некоторую площадку, равен произведению индукции этого магнитного поля В на величину площадки S и на косинус угла а между вектором магнитной индукции и нормалью к площадке.

Если площадка S расположена перпендикулярно магнитным линиям однородного поля, то магнитный поток, пересекающий ее, максимален:

Если площадка S расположена параллельно магнитным линиям, то они ее не пересекают, поэтому магнитный поток через площадку в этом случае равен нулю.

Магнитный поток

Магнитный поток — скалярная алгебраическая величина, т. е. он может быть положителен и отрицателен, поскольку косинус угла может быть больше и меньше нуля.

Если магнитный поток пересекает замкнутую поверхность (представьте ее в виде надутого воздушного шарика), то, поскольку все магнитные линии непрерывны и замыкаются сами на себя, число входящих в эту поверхность магнитных линий, создающих отрицательный поток, будет равно числу выходящих магнитных линий, создающих численно такой же по модулю, но положительный поток. Поэтому полный поток вектора магнитной индукции сквозь замкнутую поверхность равен нулю. Это важное свойство магнитного поля свидетельствует об отсутствии в природе магнитных зарядов и вихревом характере магнитного поля.

Единица магнитного потока в СИ — вебер (Вб).

Когда магнитный поток сквозь площадь, ограниченную проводящим контуром, изменяется, в этом контуре возникает индукционный ток.

Правило Ленца: индукционный ток всегда направлен так, что своим магнитным полем он противодействует изменению магнитного потока, вызвавшего этот ток.

Обратимся к рис. 216, а). Когда магнитный поток сквозь контур, создаваемый внешним по отношению к контуру магнитным полем индукцией , нарастает , индукционный ток в контуре направлен так, что его магнитное поле индукцией (на рис. 216, а) оно изображено штриховыми стрелками), антинаправлено внешнему магнитному полю, противодействуя увеличению магнитного потока. Отметим, что направление тока связано с направлением своего магнитного поля правилом правого винта — буравчика. Когда же магнитный поток, создаваемый внешним магнитным полем индукцией убывает (рис. 216, б), индукционный ток в контуре изменяет свое направление на противоположное и при этом его магнитное поле оказывается сонаправленным с внешним полем . Теперь магнитное поле индукционного тока противодействует убыли магнитного потока, создаваемого внешним магнитным полем сквозь контур, поддерживая его.

Явление возникновения индукционного тока в контуре при изменении магнитного потока, пересекающего этот контур, называется электромагнитной индукцией. По закону Ома сила индукционного тока прямо пропорциональна ЭДС индукции и обратно пропорциональна сопротивлению контура В:

Закон Фарадея

Закон Фарадея для электромагнитной индукции: ЭДС электромагнитной индукции, возникающая в контуре при всяком изменении магнитного потока, пересекающего этот контур, равна скорости изменения магнитного потока, взятой со знаком минус,

Здесь — ЭДС индукции в контуре, — скорость изменения магнитного потока, пересекающего контур, N — число витков в контуре (безразмерное).

Эта формула справедлива, когда магнитный поток изменяется монотонно, т.е. когда за равные промежутки времени он изменяется на одинаковую величину и ЭДС индукции постоянна. Если же магнитный поток изменяется произвольно, то увеличиваясь, то уменьшаясь, что бывает при вращении контура в магнитном поле, то пользоваться этой формулой для определения мгновенного значения ЭДС индукции нельзя, по ней можно определить только среднее значение ЭДС индукции.

При произвольном изменении магнитного потока сквозь контур ЭДС индукции равна первой производной магнитного потока по времени, взятой со знаком минус:

Здесь — первая производная магнитного потока по времени.

Знак минус в этих формулах объясняется правилом Ленца.

Если контур, пересекаемый переменным магнитным потоком, содержит не один, а N витков, то ЭДС индукции в нем будет в N раз больше, чем в одном витке. При этом предыдущие формулы примут вид:

ЭДС индукции, возникающая в проводнике, движущемся поступательно в однородном магнитном поле под углом к магнитным линиям, равна произведению индукции этого поля на скорость проводника, на его длину в этом поле и на синус угла между вектором индукции магнитного и вектором скорости проводника:

ЭДС индукции , возникающая в контуре, вращающемся равномерно в однородном магнитном поле, равна произведению угловой скорости контура на индукцию В магнитного поля, на площадь контура S и на синус угла а между вектором магнитной индукции и нормалью к плоскости контура:

В случае, когда плоскость контура параллельна магнитным линиям, угол . Тогда ЭДС индукции в контуре будет максимальна.

Если контур содержит N витков, то ЭДС индукции в нем в N раз больше, чем в одном витке:

Явление возникновения ЭДС индукции и индукционного тока в контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции.

Магнитный поток Ф сквозь катушку (или контур любой иной формы) прямо пропорционален силе тока в ней, т.е. между этими величинами существует прямо пропорциональная зависимость:

Здесь L — коэффициент пропорциональности между током и связанным с ним магнитным потоком. Он называется коэффициентом самоиндукции контура или его индуктивностью. Величина индуктивности зависит от формы и размеров самого контура, а также от магнитных свойств среды, и постоянна для данного контура. Индуктивность контура — скалярная положительная величина. Она не зависит от наличия или отсутствия тока в нем. Индуктивность катушек заводского изготовления указывается в их паспорте.

Единица индуктивности в СИ — генри (Гн).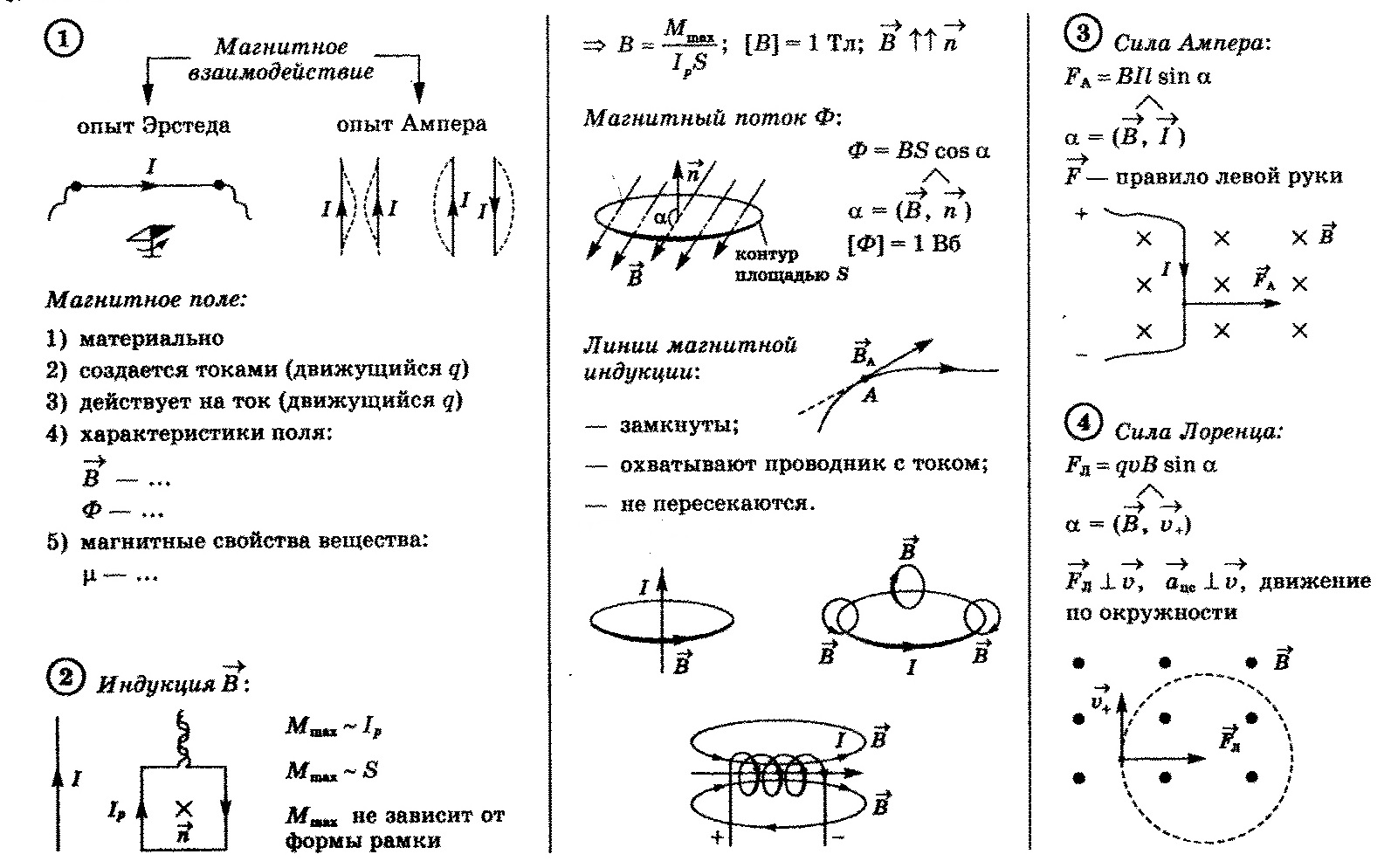

ЭДС самоиндукции , возникающая в контуре при изменении тока в нем, прямо пропорциональна скорости изменения силы тока в контуре, взятой со знаком «минус»:

Здесь —скорость изменения силы тока, т.е. изменение силы тока за единицу времени.

Если ток в контуре изменяется произвольно, то пользоваться этой формулой для определения мгновенной ЭДС самоиндукции нельзя, по ней можно определить лишь среднее значение ЭДС самоиндукции за время . Для определения мгновенного значения ЭДС самоиндукции в этом случае надо пользоваться формулой

Мгновенная ЭДС самоиндукции прямо пропорциональна первой производной силы тока по времени, взятой со знаком «минус».

Магнитное поле, как и всякое силовое поле, обладает энергией.

Энергия магнитного поля катушки с током соленоида равна половине произведения индуктивности этого соленоида на квадрат силы тока в нем:

Поскольку магнитное поле размыто по пространству, то, чтобы охарактеризовать его энергетические свойства, вводят величину, равную энергии магнитного поля в единице объема пространства, занятого этим полем.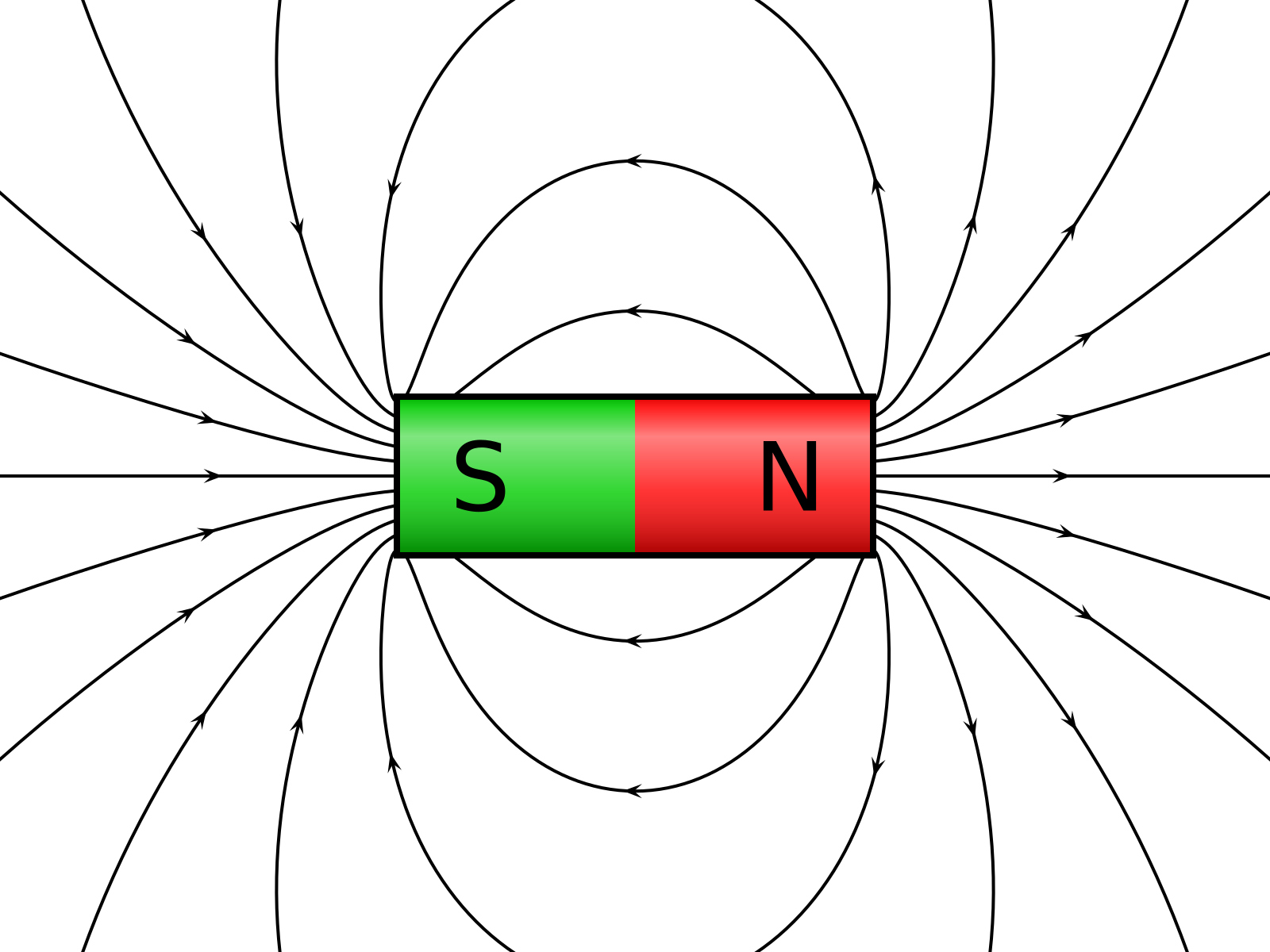 Эта величина называется объемной плотностью энергии магнитного поля .

Объемная плотность энергии магнитного поля равна отношению энергии магнитного поля к объему V пространства, занятого им:

Объемная плотность энергии магнитного поля прямо пропорциональна квадрату магнитной индукции этого поля и обратно пропорциональна относительной магнитной проницаемости окружающей среды:

Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти страницы:

Что такое магнетизм? | Goudsmit Magnetics

Кривая BH позволяет получить представление о следующих магнитных свойствах:

 

Кривая намагничивания (De-) — кривая BH = кривая гистерезиса

При периодически изменяющемся внешнем магнитном поле H намагниченность ферромагнитного материала отражает кривую намагничивания. Начиная с «исходного» материала без чистого намагничивания, синяя кривая появляется при первом приложении поля (см. изображение ниже).

При достижении плотности потока насыщения с напряженностью магнитного поля Hs, намагниченность не увеличивается.

Остаточная напряженность поля BR
Если затем инвертировать поле, намагниченность при напряженности поля H = 0 не уменьшится полностью до нуля. Существует напряженность остаточного поля BRв результате того, что «области Вейса» не вернулись в исходное состояние.

Напряженность коэрцитивного магнитного поля Hc
Только в случае, если внешняя напряженность поля достигла противоположно направленного значения — напряженность коэрцитивного магнитного поля Hc, намагниченность В = 0, и продукт размагничивается. Площадь петли, через которую проходит переменная намагниченность, является мерой потерь. Материалы с низкими значениями Hc и, следовательно, с небольшими гистерезис-петлями называются мягкими магнитными материалами.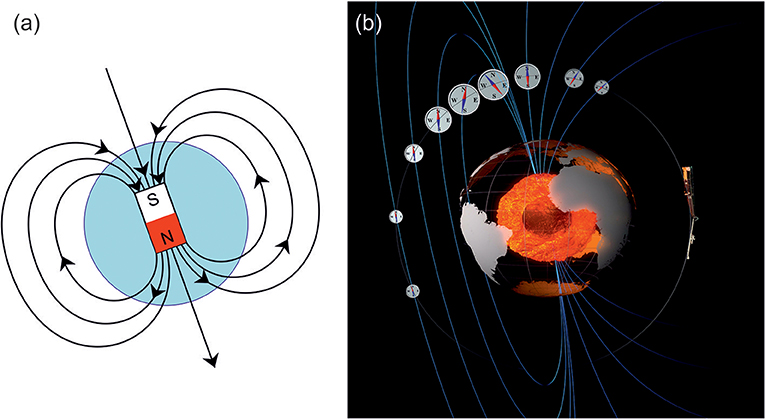 Если Hc очень большой, они называются твердыми магнитными материалами.

 

‘Гистерезис’ присутствует в ферромагнитном материале. Это показано на рисунке ниже. Напряженность магнитного поля H показана вдоль оси x, а степень намагниченности (магнитная индукция) B — вдоль оси у. Если магнитное поле отсутствует, намагниченности в начале нет, и мы снова оказываемся в точке начала координат графика.

 

Если приложить магнитное поле, ферромагнитный материал становится магнитным. Воздействие продолжается до тех пор, пока все «области Вейса» в материале не будут иметь одинаковую ориентацию. Теперь материал имеет максимальную намагниченность, и увеличение магнитного поля не оказывает дальнейшего влияния на степень намагниченности. Если магнитное поле ослабить, области Вейса по большей части сохранят свое положение.

 

Когда поле становится более отрицательным, общая намагниченность также изменяет направление. Это продолжается до тех пор, пока все спины не будут ориентированы в другом направлении и намагниченность не изменится. Теперь продукт размагничен.

 

Назад к содержанию

 

Кривая гистерезиса (кривая BH)

Наглядная физика. Магнетизм

---

Опыт Эрстеда

Модель наглядно демонстрирует известный опыт X. Эрстеда, впервые показавшего действие электрического тока на магнитную стрелку, находящуюся вблизи проводника с током. Можно изменять силу и направление тока, отклоняющего магнитную стрелку.

  

 На рис. 1 показана схема опыта датского ученого X. Эрстеда, впервые обнаружившего в 1820 году действие электрического тока на магнит. В этом опыте магнитная стрелка отклонялась при пропускании тока по прямолинейному проводнику, расположенному над стрелкой. 

Действие проводника с током на магнитную стрелку, находящуюся вблизи этого проводника, определяется не только силой тока (например, как в законе Кулона сила зависит от расстояния), но и от взаимного расположения тока и стрелки.  Будет ли действие обратно пропорционально квадрату расстояния? Как оно зависит от силы тока в проводнике, от взаимной ориентации проводника и стрелки?

Рис 1.  Вблизи провода с током (здесь показан только отрезок провода без остальных, подводящих к нему ток проводов) магнитные стрелки ориентируются перпендикулярно к направлению провода. Показана окружность, лежащая в плоскости, перпендикулярной проводу. Магнитная стрелка над проводом направлена противоположно стрелке под проводом. Для выбора правильного направления стрелок можно указать направление на окружности, которое определяется правилом буравчика: буравчик крутят так, чтобы он вкручивался в направлении тока I, и тогда движение концов ручки буравчика укажет нужное направление на окружностях. 

Чтобы записать закон взаимодействия магнитной стрелки с магнитным полем, аналогичный закону взаимодействия электрического заряда с электрическим полем F=q E, нужно ввести единицу измерения для «силы намагниченности» магнитных стрелок, но сила будет зависеть также и от размеров, и от формы стрелки.  Поэтому в электромагнетизме используют другой элементарный «источник поля»- отрезок провода Δl (векторная величина) и ток I в этом проводе, мысленно пренебрегая силами и полями, связанными с проводами, подводящими ток к нашему элементарному току I Δl.

Магнитное поле в точке пространства M характеризуется вектором B, направленным вдоль магнитной стрелки, (мысленно помещённой в точку M и имеющей возможность свободно поворачиваться вокруг точки M). А длина вектора B характеризует «силу» магнитного поля в точке M: чем сильнее поле, тем длиннее вектор. В некотором смысле вектор B в такой же степени характеризует магнитное поле, в какой вектор напряжённости E характеризует электрическое поле.

Магнитное поле можно наглядно изобразить с помощью линий магнитного поля. (Их называют также линиями индукции магнитного поля, линиями вектора B или силовыми линиями магнитного поля.) Эти линии строятся для B  так же, как и линии электрического поля для E: касательная к линии  магнитного поля в каждой точке совпадает с направлением вектора B, а густота линий пропорциональна модулю B вектора B в данном месте поля. На рис. 1 показана линия магнитного поля прямого провода. Стрелки на ней указывают направление касательных к ней векторов B. Магнитные стрелки ориентируются вдоль линии магнитного поля, но лишь приближённо, из-за своего большого размера относительно неоднородностей поля.

В начале опыта Эрстеда ток равен нулю и магнитная стрелка направлена вдоль линии магнитного поля Земли. Приближённо можно считать, что магнитное поле Земли создаётся постоянным магнитом, помещённым внутри земного шара вдоль оси вращения Земли. Северный полюс этого магнита находится в южном полушарии, а южный — в северном, см. рис. 2. Поскольку одноимённые полюсы магнита отталкиваются, а разноимённые притягиваются, то магнитная стрелка в магнитном поле Земли своим северным (синим) концом направлена на Север, а южным (красным) — на Юг. Маленькая (по сравнению с неоднородностями магнитного поля) магнитная стрелка ориентируется вдоль линии магнитного поля.

 Рис. 2. Схематическое изображение линий магнитного поля Земли и расположение в нём магнитных стрелок. На большей части земной поверхности линии магнитного поля Земли практически горизонтальны, а над полюсами — вертикальны. 

После включения тока магнитное поле в окружающем проводник пространстве является суммой магнитного поля Земли и магнитного поля, создаваемого проводником с током. При сильном токе магнитным полем Земли вблизи проводника можно пренебречь. 

---

Сила Ампера

На проводник с током, находящийся в магнитном поле, действует сила, которая определяется полем в том месте, где расположен проводник, силой тока в проводнике и направлением проводника. Направление силы определяется правилом буравчика. Модель объясняет эту сложную зависимость силы от остальных параметров.

На проводник с током, находящийся в магнитном поле, действует сила, которая определяется только свойствами поля в том месте, где расположен проводник, и не зависит от вида источников этого магнитного поля.

Рассмотрим небольшой элемент проводника с током длины Δl как вектор Δl, направление которого совпадает с направлением тока в проводнике.  Cила F, действующая на такой элемент со стороны магнитного поля, перпендикулярна к плоскости, в которой лежат вектор Δl и вектор магнитной индукции B, причем вращение по кратчайшему расстоянию от Δl к B связано с направлением силы F правилом буравчика (см. рис. 1).  Векторы Δl и B лежат в плоскости рисунка, вектор F направлен от нас перпендикулярно к плоскости  рисунка).

Рис. 1. Сила F, действующая на проводник с током в магнитном поле с индукцией B.

Согласно закону Ампера модуль F магнитной силы F определяется  формулой

где I — сила тока в проводнике, остальные величины те же, что на рис. 1. Из формулы (1) следует, что в случае, когда проводник расположен вдоль линий поля (α = 0),
сила равна нулю.

В простейшем случае, когда проводник с током и поле взаимно перпендикулярны (α =Π/2), для определения направления магнитной силы можно воспользоваться правилом левой руки: если расположить левую руку так, чтобы направление четырех вытянутых пальцев указывало направление тока, а магнитные линии «входили» в ладонь, то отставленный в сторону большой палец укажет направление силы.

Единицей магнитной индукции в системе СИ является тесла (Тл). В однородном магнитном поле с индукцией 1 Тл на 1 м длины перпендикулярного к вектору B прямого провода, по которому течет ток 1 А, действует сила 1 Н:

1Н = 1А·м·1Тл;   отсюда   1Тл = 1Н/(А·м).

Сила тока в металлическом проводнике имеет вид

   I =nevS,

где n — число свободных электронов в единице объема (плотность свободных электронов), e — заряд электрона, v — его скорость, S — площадь поперечного сечения проводника. Подставив это выражение в формулу (1), получим

Произведение nSΔl дает число движущихся зарядов N в элементе Δl проводника. Магнитная сила действует именно на эти заряды, а уже от них передается кристаллической решетке вещества, из которого изготовлен проводник. Поэтому, разделив F на число зарядов N, мы получим магнитную силу, действующую на отдельный заряд e, движущийся со скоростью v

Эта формула справедлива не только для электронов, но и для любого точечного заряда q:

Рис. 2. Сила F, действующая на заряд q, движущийся со скоростью v в магнитном поле с индукцией B.
Направление силы F связано с векторами v и B совершенно аналогично тому, как направление силы F связано с векторами Δl и B на рис. 1. Обратите внимание, что вектор Δl на рис. 1 направлен по току, т. е. в направлении движения положительных зарядов, для отрицательных зарядов направление силы F, определенной по формуле (2), изменится на противоположное.

---

Взаимодействие проводников с током

 Модель наглядно демонстрирует взаимодействие двух параллельных проводников с токам. Показано магнитное поле, создаваемое этими токами, и силы взаимодействия. Величины и направления токов можно изменять.

  

 Покоящиеся заряды взаимодействуют посредством электрического поля. Это взаимодействие сохраняется и при движении зарядов, но в этом случае возникает еще и магнитное взаимодействие, которое осуществляется магнитным полем, создаваемым движущимися зарядами.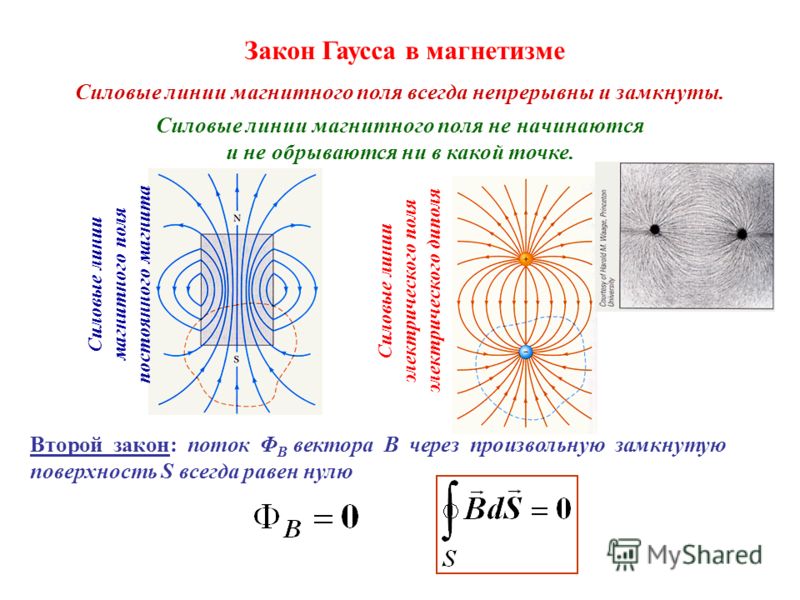  

Магнитное поле порождается движущимися зарядами, т. е. токами. Возникшее поле действует на другие движущиеся заряды и токи. Так возникает взаимодействие токов и движущихся зарядов.  Магнитное поле в данной точке пространства характеризуется векторной величиной B,которую называют магнитной индукцией поля.

Прямой проводник бесконечной длины с током I1 создаёт магнитное поле, модуль индукции которого B на расстоянии r от проводника равна

где  Гн/м -магнитная постоянная, см. рис. 1. Если второй такой же проводник с током I₂ помещён на расстоянии r от первого проводника, то сила F, действующая на отрезок длины Δ l второго проводника равна

где r — расстояние между проводниками. Здесь тонким считается проводник, толщина которого много меньше расстояния r между проводами. В случае проводников конечной длины формула (2) справедлива для участков, удаленных от концов проводников на расстояние, значительно большее r.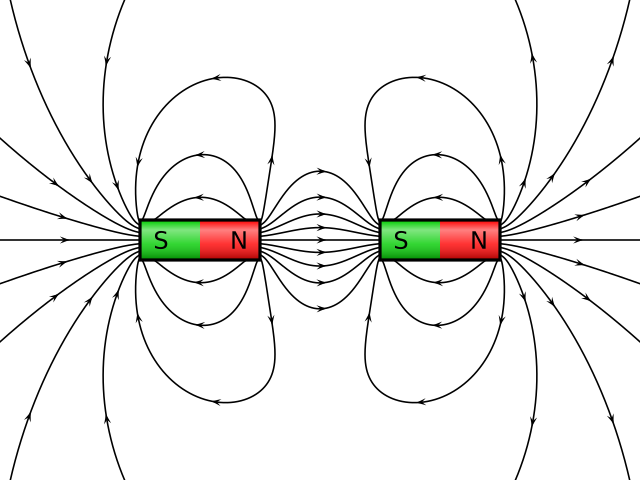

Рис1.График изменения модуля магнитной индукции внутри и вне прямого длинного провода круглого поперечного сечения радиуса a. Внутри проводника B(r) пропорционально r, r< a. Вне проводника индукция определяется формулой (1), r≥a. На графике условно показано поперечное сечение проводника. Для магнитного поля выполняется принцип суперпозиции: поле, созданное несколькими источниками равно сумме полей, созданных каждым источником (без учёта остальных).
На рис. 2 показан график магнитного поля B(x) двух параллельных и очень длинных проводников с током I.

 

Рис 2. Зависимость индукции магнитного поля двух параллельных проводников от положения точки относительно проводников (от координаты x). Здесь положительное значение B(x) означает, что вектор B(x) направлен вверх, а отрицательное — что вектор B(x) направлен вниз. Одинаково направленные токи притягиваются, а встречные — отталкиваются. Обратите внимание, что проводник с током взаимодействует только с магнитным полем, созданным другим проводником, а его взаимодействие с собственным магнитным полем здесь не рассматривается.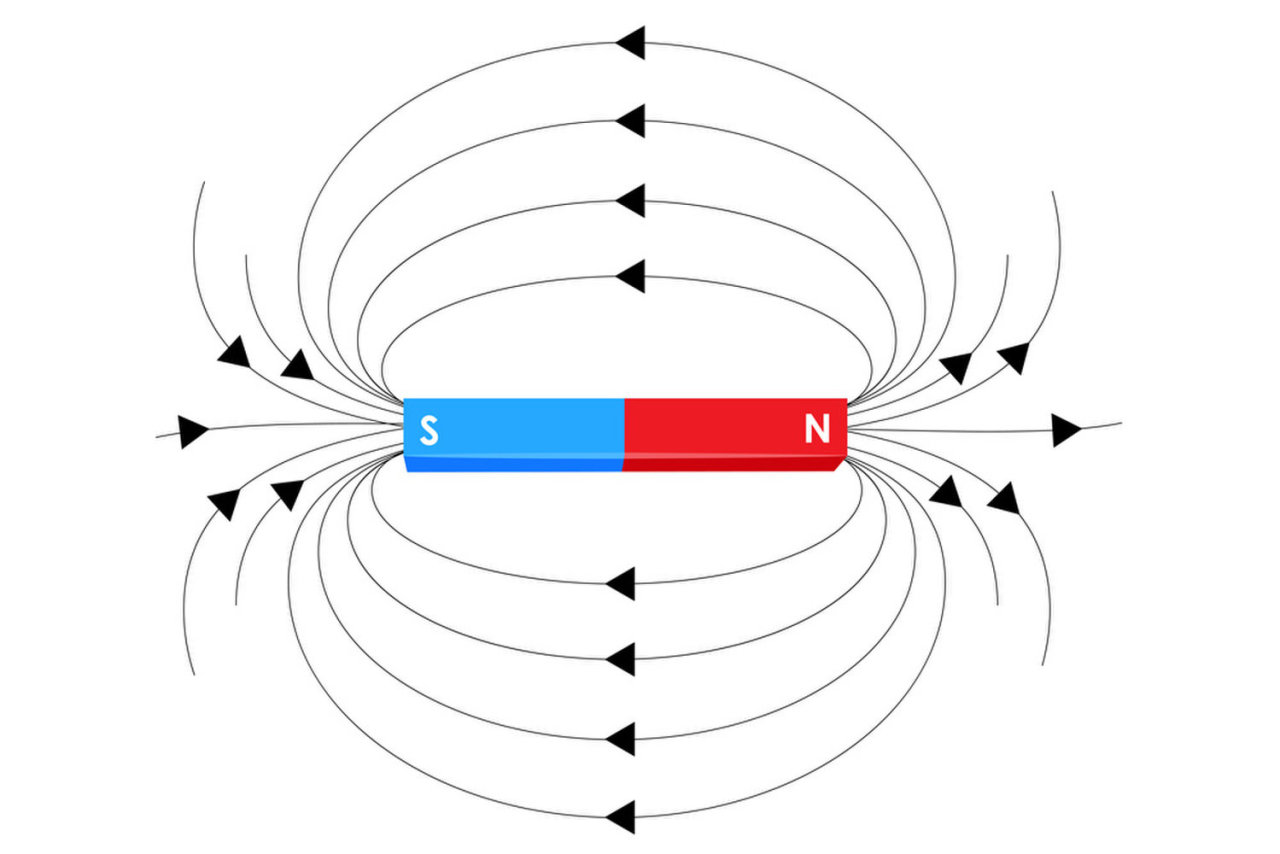  На обоих графиках штриховой линией показано поле, создаваемое только правым проводником, именно оно определяет силу, действующую на левый проводник. а) Токи в одном направлении. Над левым проводником показано, как определяется направление силы F по закону Ампера, все углы между векторами — прямые. б) Токи в противоположных направлениях.

---

Магнитное поле проводников с током

Модель наглядно демонстрирует магнитные поля, создаваемые прямым проводом и витком провода с током.

 

 

Магнитная индукция B поля бесконечного прямого проводника с током I на расстоянии r от проводника равна 

 

(кратко говорят «магнитная индукция B прямого тока»). Эта формула для магнитной индукции поля годится не только для бесконечных проводников. Практически эта формула (1) применима для вычисления B в точках, расположенных в окрестности середины проводника конечной длины l, для которых расстояние r много меньше длины проводника (r<<l).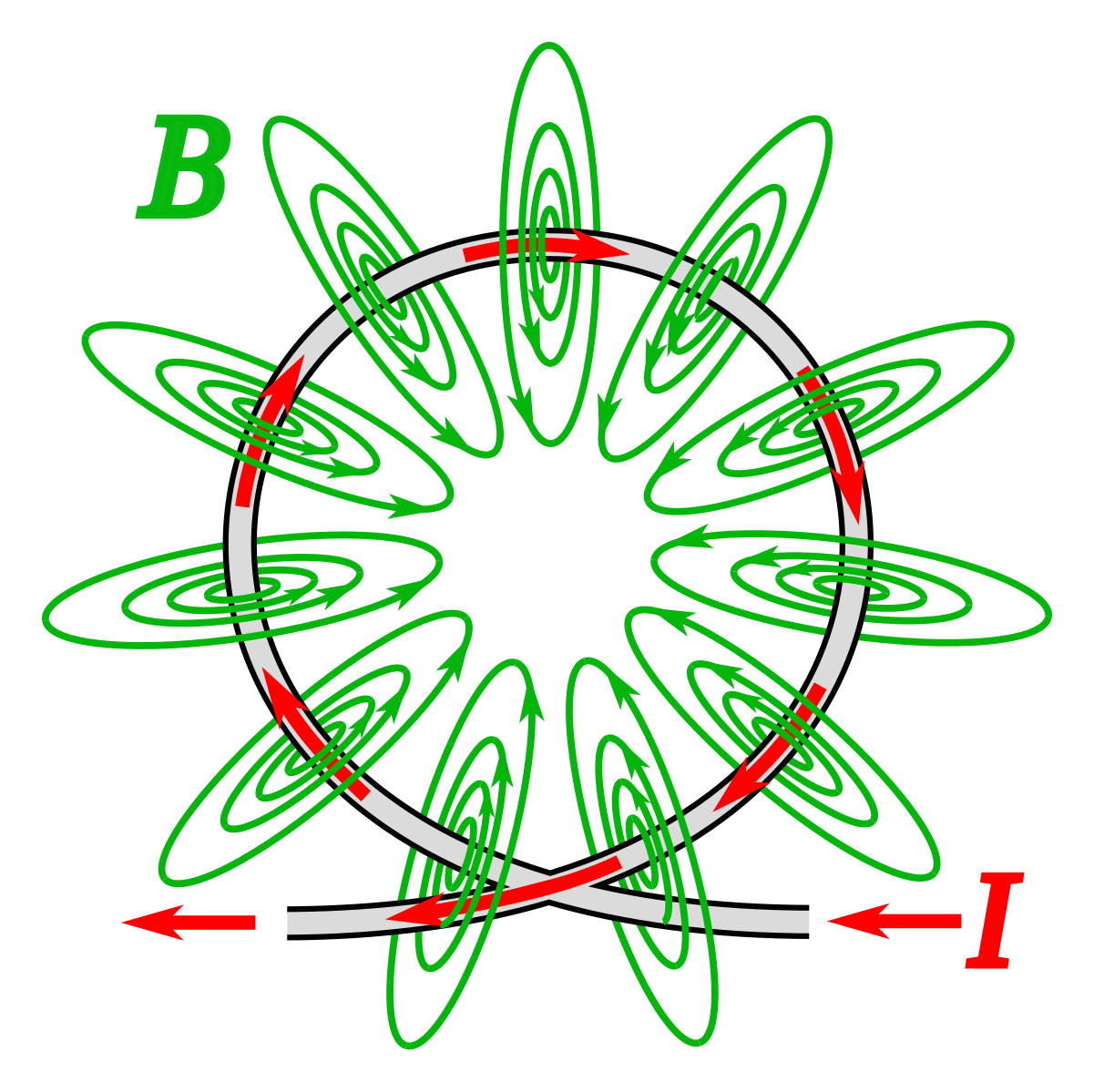

 

 

 

Рис.1. Линии магнитного поля прямолинейного проводника с током изображается окружностями с центрами на оси бесконечного прямого проводника с током I являются окружностями с центрами на оси проводника, лежащими в плоскости, перпендикулярной к его оси. Показан вектор магнитной индукции магнитного поля в точке M, находящейся на расстоянии r от провода.
Вблизи провода линии расположены гуще, т. к. поле с увеличением расстояния r убывает по формуле (1).
Вектор B касателен к окружности, а его направление определяется по правилу буравчика: если ввинчивать буравчик вдоль проводника по направлению тока (синяя стрелка), ось буравчика перемещается по току, то вращение ручки буравчика (красная стрелка) покажет направление магнитного поля.

Разделив соотношение (1) на μ μ0, получим выражение для напряженности H магнитного поля прямого тока. Из этой формулы следует,  что единицей напряженности магнитного поля  является  ампер на метр  (А/м). С формулой (1) связано определение единицы силы тока ампера, являющейся одной из основных в системе СИ. Ампер равен силе не изменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малой площади поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, создаёт на каждом участке проводника длины 1 м силу взаимодействия  Н. Так как проводники бесконечной длины и ничтожно малого сечения практически невыполнимы, то в реальных условиях эталон силы тока воспроизводится по измерению силы взаимодействия катушек с током (на так называемых токовых весах), а затем вводятся поправки, учитывающие размеры и форму проводников. Единицей электрического заряда является кулон (Кл) — производная единица. Кулон — электрический заряд, протекающий через поперечное сечение проводника в течение 1 с при силе постоянного тока 1 А.

 

Рис2. Поперечное сечение  кругового проводника с током I. Крестик и точка на сечениях проводника обозначают направление тока I:  крестик — это вид «хвостового оперения» стрелки, обозначающей ток I, а точка — носик (остриё) этой стрелки. Линии магнитного поля изображается окружностями с центрами на оси бесконечного прямого проводника с током являются замкнутыми линиями, охватывающими провод, и лежат в плоскости, проходящей через ось витка. Ось витка является линией магнитного поля и принято считать, что она замыкается в «бесконечно удалённой точке». Величина вектора магнитной индукции магнитного поля в точке M пропорциональна «густоте» линий поля, находящейся на расстоянии r от провода. Вблизи провода линии расположены гуще, т. к. поле вблизи провода примерно определяется формулой (1). С увеличением расстояния r от провода индукция магнитного поля убывает. Вектор B касателен к линиям поля, а его направление определяется по правилу буравчика: если ввинчивать буравчик вдоль ближайшего участка проводника, то вращение ручки буравчика покажет примерное направлене магнитного поля (см. рис. 1). Зависимость вектора индукции B от точки очень сложно, но величина индукции в центре витка даётся простой формулой:

где r — радиус витка (отличается от (1) лишь отсутствием Π в знаменателе). Вектор B в центре витка показан красным цветом.

---

Магнитное поле катушки с током

 Модель наглядно демонстрирует магнитное поле катушки (соленоида) с током. Поле показано как вне катушки, так и внутри.

 

 

 В катушке витки навиты на цилиндрическую поверхность вплотную друг к другу, причём равномерно, т. е.  число витков на участке катушки длиной l пропорционально l и коэффициент пропорциональности не зависит от выбора участка катушки. Если длина катушки бесконечна (или её длина значительно больше других размеров или расстояний), то магнитное поле внутри катушки можно считать однородным, а полем вне катушки можно пренебречь. Величина индукции магнитного поля B внутри бесконечно длинной катушки определяется формулой

где w -число витков на участке катушки длиной l. Магнитное поле катушки зависит только от произведения Iω и это значит, что одно и то же поле можно получить, либо при большом токе, но малом числе витков, либо при малом токе, но большом числе витков.

Рис. Поперечное сечение  катушки с током I. Крестик и точка на сечениях проводов обозначают направление тока I: крестик -это вид «хвостового оперения» стрелки, обозначающей ток I, а точка -носик (остриё) этой стрелки. Линии магнитного поля изображается окружностями с центрами на оси бесконечного прямого проводника с током являются замкнутыми линиями, охватывающими провод, и лежат в плоскости, проходящей через ось катушки. Ось катушки является линией магнитного поля и принято считать, что она замыкается в «бесконечно удалённой точке». В идеальном случае бесконечно длинной катушки все линии магнитного поля являются прямыми и расположены внутри катушки параллельно её оси. Поле внутри катушки однородно (т. е. одинаково во всех точках внутри катушки). Вектор B в точке внутри катушки показан красным цветом. В катушке конечной длины однородность поля нарушается вблизи концов катушки. На концах катушки линии поля выходят из катушки, сильно расходятся, а затем сходятся и заходят внутрь катушки с другой стороны. Величина вектора магнитной индукции магнитного поля в точке M пропорциональна «густоте» линий поля, находящейся на расстоянии r от провода. Вектор B касателен к линиям поля, а его направление определяется по правилу буравчика: если ввинчивать буравчик вдоль ближайшего участка витка, то вращение ручки буравчика покажет примерное направлене магнитного поля. Условно показана ручка буравчика и красные стрелки, указывающие направление её вращения, при котором буравчик ввинчивается/вывинчивается в направлении тока. Ось буравчика перпендикулярна плоскости рисунка. Видно, что движение концов ручки согласовано с направлением линий магнитного поля, проходящих вблизи буравчика.

---

Электромагнитная индукция

 Модель наглядно демонстрирует явление электромагнитной индукции: при изменении магнитного потока через замкнутый проводник, в проводнике возникает электродвижущая сила индукции. Замыкая и размыкая ключ в цепи первой катушки, мы создаем переменное магнитное поле во второй катушке. Ток индукции вызывает отклонение стрелки гальванометра. Число витков второй катушки можно изменять.

Явление электромагнитной индукции состоит в том, что при изменении магнитного потока через замкнутый контур проводника, в проводнике возникает электродвижущая сила (ЭДС) индукции, вызывающая появление электрического тока, который называется индукционным. ЭДС индукции возникает также и в незамкнутом проводнике при его движении в магнитном поле, если проводник пересекает линии магнитного поля.

Явление электромагнитной индукции было открыто М. Фарадеем в 1831 г. В то время уже существовало мнение, что магнитное поле очень похоже на электрическое. При постановке опытов Фарадей полагал, что если электрический ток создает магнитное поле (опыт Эрстеда), то и обратно, изменяющееся магнитное поле может создавать электрический ток. Опыты Фарадея по электромагнитной индукции показали, что ЭДС индукции возникает в катушке при изменении магнитного потока Φ через катушку, причём независимо от причин, вызывающих это изменение.

а) Изменение магнитного потока в катушке L при перемещении магнита. Катушка L, соединена с  измерительным прибором (миллиамперметром, у которого нейтральное положение стрелки находится в центре шкалы). Если достаточно быстро вдвигать или выдвигать магнит, то стрелка прибора отклоняется. Когда движение магнита прекращается, стрелка прибора не отклоняется (показывает нуль). Тот же результат получается, если надвигать катушку L на неподвижный магнит. б) Изменение магнитного потока в катушке L при включении или выключении тока в близко расположенной катушке L₂. Магнитное поле в катушке можно изменять, изменяя ток в расположенной поблизости другой катушке. На катушку L2, включенную в цепь источника тока GB, надета катушка L, соединённая с измерительным прибором (рис. 1 б).
Катушки L и L₂могут также иметь общий ферромагнитный сердечник, как в трансформаторе. При изменении силы тока в катушке L₂ при замыкании или размыкании выключателя катушка L₂ создаёт изменяющееся магнитное поле и в катушке L возникает индукционный ток, направление которого зависит от того, увеличивается или уменьшается сила тока в катушке L₂, а также от взаимной ориентации катушек. Магнитное поле в катушке можно изменять двигая магнит. То же происходит при замыкании и размыкании цепи катушки 2. Такое замыкание и размыкание цепи изменяет силу тока в катушке 2.

Потоком магнитной индукции или, просто, магнитным потокомчерез поверхность S, расположенную в однородном магнитном поле, называется величина

где B — индукция (однородного) магнитного поля, S —  плоская поверхность S, ориентированная так, что нормаль n к поверхности образует с направлением вектора B угол φ (см. рис. 2).

Рис.2. Поток φ магнитной индукции через поверхность S равен  где B — индукция однородного магнитного поля, S —  площадь плоской поверхности S, α — угол между нормалью n к поверхности и вектором B. Если проводить линии магнитного поля с густотой, численно равной B,  то поток Φ через поверхность S будет численно равен числу линий поля, пронизывающих поверхность S. Единицей магнитного потока является вебер (сокращённо Вб). Из равенства (1) следует, что 1 Вб =1Тл·м².

Если поле неоднородно или поверхность S не плоская, то для вычисления магнитного потока поверхность S разбивают на такие малые элементы ΔSi, что каждый из них можно считать плоским, а поле около каждого из них — однородным. Тогда элементарный поток через элемент поверхности  а полный поток получится суммированием элементарных потоков:


В этой формуле величины Bi и cos(αi) имеют, вообще говоря, различные значения для  различных площадок (т. е. зависят от индексов i), а эта сумма, вообще говоря, зависит от разбиения, но если разбиение очень мелкое, то зависимость Φ от разбиения незначительна. Во многих случаях достататочно вычислить поток приблизительно.

Так, например, вычисляют магнитный поток через катушку равен сумме потоков через каждый виток катушки. Если магнитное поле вдоль катушки не меняется (однородно), то магнитный поток Φ через катушку равен Φ=Φ1w, где Φ1 — магнитный поток через один виток катушки, w — число витков в катушке. ЭДС индукции в катушке возникает при изменении магнитного потока Φ через катушку.

---

ЭДС индукции

Электродвижущая сила (ЭДС) индукции в контуре определяется скоростью изменения магнитного потока через этот контур. Модель демонстрирует возникновение ЭДС индукции в катушке, в которую можно с различными скоростями вдвигать постоянный магнит. Можно изменять число витков в катушке. Отклонение стрелки гальванометра позволяет судить о величине и направлении возникающей ЭДС индукции.

Зависимость ЭДС индукции от скорости изменения магнитного потока Электродвижущая сила (ЭДС) индукции ЭДС индукции в катушке возникает при изменении магнитного потока Φ. через катушку. ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока Φ, пронизывающего этот контур:

Знак минус в этой формуле означает, что если ЭДС индукции вызывает индукционный ток, то создаваемое им магнитное поле противодействует изменению магнитного потока Φ т. е. при  ΔΦ/Δt >0 ЭДС индукции E<0, и наоборот (это правило Ленца).

Если магнитного потока Φ через катушку меняется гармонически:

то ЭДС индукции легко вычислить — это производная синуса по t:
Следовательно,  ЭДС индукции

пропорциональна амплитуде Φ0, частоте ω изменения Φ0, причём ЭДС сдвинута по фазе относительно Φ(t) на полупериод, т. е. на Π.

Индукционные токи возбуждаются также в сплошных проводниках при изменении внутри них магнитного поля, например в сердечниках электромагнитов. В этом случае их называют токами Фуко . В хорошо проводящих телах токи Фуко могут достигать большой силы и при этом выделяется большое количество теплоты. Токи Фуко используются, в металлургии, для прогрева металлических частей внутри вакуумных приборов с целью обезгаживания металла и т. д. В электромагнитах и трансформаторах токи Фуко нежелательны, так как они вызывают потери электроэнергии на нагревание сердечников. Для уменьшения токов Фуко сердечники делаются составными из железных полос, вследствие чего уменьшается проводимость сердечника и, следовательно, токи Фуко в нем.

---

ЭДС самоиндукции

Явление самоиндукции состоит в возникновении ЭДС индукции в проводнике при изменении в нем тока. В модели приводится график силы тока в замкнутой цепи от времени после замыкания цепи. Цепь содержит последовательно соединенные резистор, катушку и батарейку. Параметры цепи (сопротивление резистора, индуктивность катушки м ЭДС батарейки) можно изменять.

Ток I в контуре создаёт магнитное поле, пронизывающее поперечное сечение контура. Поток Φ магнитной индукции B через контур (точнее, его поперечное сечение) Поток Φ магнитного поля, создаваемого током I, пропрционален величине тока I:

      Φ = L I .         (1)

Коэффициент пропорциональности L когда поток Φ вычислен для того же контура, в котором распространяется ток I, называется  индуктивностью контура. Индуктивность зависит от формы контура, его размеров и среды, окружающей контур, в которой находится проводник (точнее, создаваемое им магнитное поле).
Единицей индуктивности в СИ является генри (Гн). Индуктивностью 1 Гн обладает такой проводник, в котором при скорости изменении тока 1 ампер в секунду (А/с) возникает ЭДС самоиндукции 1 В. Из формулы (1) следует, что

1  Гн = 1 В·с/А  .

Индуктивность 1 Гн — это очень большая индуктивность, поэтому обычно используются доли генри: миллигенри (мГн) и микрогенри (мкГн).

   1 Гн = 10³ мГн

Как и ЭДС индукции, ЭДС самоиндукции равна скорости изменения магнитного потока, т. к. ЭДС индукции не зависит от причин изменения потока Φ. Так как по формуле (1) магнитный поток Φ пропорционален силе тока I, Φ = LI, то ЭДС самоиндукции определяется формулой

где L — индуктивность катушки, знак «-» в этой формуле означает, что ЭДС препятствует изменению тока в цепи (правило Ленца). Точнее, при уменьшении тока I, а, следовательно, и создаваемого им потока Φ, ток самоиндукции препятствует уменьшению I. При увеличении тока I, а, следовательно, и создаваемого им потока Φ, ток самоиндукции препятствует увеличению I, т. е. направлен против тока I. 

Индуктивность прямого проводника невелика — создаваемое им поле рассеивается в окружающем пространстве. Индуктивность проводника в форме витка больше — поле концентрируется внутри витка. Индуктивность становится значительно больше, если проводник  состоит из n близко расположенных витков. В этом случае индукция магнитного поля в центре витков будет примерно в n раз больше, чем у одного витка, а поток в катушке с n витками будет ещё в n раз больше (складываются потоки через каждый виток) и, следовательно, индуктивность n таких витков будет в n² раз больше, чем у одного витка.

Так, внутри бесконечно длинной цилиндрической катушки, имеющей w витков на участке длиной l, магнитное поле однородно и величина индукции магнитного поля равна

Поэтому магнитный поток через w витков на участке длиной l равен

где S — площадь поперечного сечения катушки. Поток Ф пропорционален току I, а коэффициент пропорциональности, индуктивность этого участка катушки, равна

Формулу (3) можно использовать для приближённого вычисления индуктивности цилиндрической катушки конечной длины l, если длина катушки значительно больше её диаметра. Для витков в центральной части катушки всё будет почти также, как и в бесконечной катушке, но на краях такой катушки поле, а значит и поток через витки на краях катушки будет меньше, чем в центре. Следовательно, индуктивность конечной катушки будет меньше, чем вычисленная по формуле (3). Чтобы магнитное поле каждого витка пронизывало все остальные витки катушки, используют сердечник с большой магнитной проницаемостью μ, собирающий и направляющий магнитное поле. Формула (3) объясняет, почему для получения большой индуктивности используют катушки с очень большим числом витков (несколько тысяч) на замкнутых ферромагнитных сердечниках (большое μ).

Краткий конспект подготовки к ЗНО по физике №27 «Введение в магнетизм.»

Конспект 27. Введение в магнетизм.
Тема: Магнетизм

1. Введение в магнетизм

Определение. Магнитное поле – вид материи, который создается движущимися зарядами (токами) и проявляется себя действием на движущиеся заряды (токи).
Определение. Магнитная индукция поля  – силовая характеристика точки магнитного поля, показывающая силовое действие поле на заряд, который движется с определенной скоростью.
Силовые линии магнитного поля (линии индукции) – графическая модель магнитного поля, которая позволяет сделать видимым распределение поля в пространстве. Линии индукции – это такие условные линии, касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции поля. Вдоль линий индукции ориентируются оси магнитных стрелок.
Замечание. Для магнитного поля силовые линии выходят из северного полюса магнита (N), а заходят в южный (S), они всегда замкнуты. Линии индукции изображаются так, что плотность их расположения характеризует значение магнитной индукции поля.
Тела, которые проявляют магнитные свойства, в основном делят на постоянные магниты и электромагниты.
Определение. Постоянный магнит – тело (вещество), которое долгое время сохраняет остаточную намагниченность, т.е. само по себе имеет магнитные свойства.

Замечание. Земля по сути является постоянным магнитом.

Основные свойства постоянных магнитов:
1) Одноименные полюса магнитов отталкиваются, а разноименные притягиваются;
2) Сила магнитного взаимодействия больше у краев, т.е. у полюсов магнита. Вблизи середины магнита он, наоборот, практически не взаимодействует;
3) Нельзя создать магнит с одним полюсом. Даже при разделении магнита на две части образуются два полноценных магнита с парой полюсов;
4) При нагревании постоянного магнита до определенной температуры его магнитные свойства исчезают. Такая температура называется точкой Кюри. Для различных веществ она различна, и существуют таблицы, в которых указаны эти температуры для основных веществ.
Определение. Электромагнит – устройство, которое создает магнитное поле при протекании электрического тока.
Замечание. Чем больше сила тока в электромагните, тем он излучает более сильное поле. Наиболее эффективные электромагниты представляют собой катушку с большим количеством витков и ферромагнитным сердечником (соленоид), чем количество витков больше, тем сильнее излучаемое магнитное поле.
В основном графическое изображение поля электромагнитов рассматривают на примере провода и катушки с током:
1) МП прямого проводника с током
Линии МП представляют собой систему концентрических окружностей, опоясывающих провод, причем плотность линий убывает с удалением от проводника.
Правила для определения направления линий индукции:
Правило буравчика (правого винта) – направление вращения буравчика совпадает с направлением линий индукции поля, если он вкручивается по направлению тока.

Правило «правой руки» – мысленно обхватить рукой провод так, чтобы большой палец указывал направление тока в проводнике, тогда четыре согнутых пальца укажут направление линий индукции.

2) МП катушки с током
Направление силовых линий устанавливается правилом «правой руки» (видоизмененным) – руку необходимо мысленно положить на катушку, чтобы четыре согнутых пальца указывали направление тока в витках, тогда отогнутый на 90° большой палец укажет направление выхода линий индукции (северный полюс N катушки).

2. Классификация веществ в магнитном поле

 

Определение. Магнитная проницаемость среды  – величина, характеризующая реакцию вещества на внешнее магнитное поле, т.е. показывающая во сколько раз МП усиливается или ослабляется внутри вещества.  , где  – индукция внешнего МП, B – индукция МП внутри вещества.
В зависимости от μ вещества делятся на:
1) Ферромагнетики (μ≫1) – вещества значительно усиливающие магнитное поле, они сильно втягиваются в МП. При отсутствии внешнего магнитного поля способны продолжительное время сохранять намагниченность.
Примеры: железо, кобальт, никель…
2) Парамагнетики (μ>1) – вещества незначительно усиливающие магнитное поле, они несильно втягиваются в МП. При отсутствии внешнего магнитного поля не способны сохранять намагниченность.
Примеры: алюминий, платина, кислород…
3) Диамагнетики (μ<1) – вещества ослабляющие магнитное поле, они выталкиваются из МП. При отсутствии внешнего магнитного поля не способны сохранять намагниченность.
Примеры: вода, медь, золото, инертные газы…

3. Сила Ампера

Определение. Сила Ампера  – сила, действующая на проводник с током, который находится во внешнем магнитном поле.
 – сила Ампера, Н
Где I – сила тока в проводнике, А
l – длина той части проводника, которая находится в МП, м
α – угол между направлением тока в проводнике и направлением вектора магнитной индукции, рад или град
Определяют направление силы Ампера по правилу «левой руки» – левую руку располагают так, чтобы четыре пальца указывали направление тока в проводнике, а линии магнитной индукции входили в ладонь, тогда отогнутый на 90° большой палец укажет направление силы Ампера.
Замечание. Правило используют в таком виде для случая, когда угол .

Замечание. Опыт Ампера о взаимодействии параллельных проводников с током:
— проводники с сонаправленными токами притягиваются;
— проводники с противонаправленными токами отталкиваются.

4. Сила Лоренца

Определение. Сила Лоренца  – сила, действующая на движущуюся во внешнем МП заряженную частицу.
 – сила Лоренца, Н
Где q – заряд частицы, Кл
v – скорость движения частицы, м/с
α – угол между  и , рад или град
Определяют направление силы Лоренца по правилу «левой руки» с учетом знака частицы:
«+» левую руку располагают так, чтобы четыре пальца указывали направление скорости частицы, …
«-» левую руку располагают так, чтобы четыре пальца были направлены против скорости частицы, …
… а линии магнитной индукции входили в ладонь, тогда отогнутый на 90° большой палец укажет направление силы Лоренца.
Замечание. Правило используют в таком виде для случая, когда угол .

Траектории движения заряженной частицы в однородном МП:
— при влете параллельно линиям индукции () – по прямой линии с постоянной скоростью;
— при влете перпендикулярно линиям индукции () – по окружности с постоянной скоростью;
— при влете под другими углами – по винтовой линии с постоянной скоростью.

магнетизм | Национальное географическое общество

Магнетизм — это сила, проявляемая магнитами, когда они притягиваются или отталкиваются друг от друга. Магнетизм вызывается движением электрических зарядов.

Каждое вещество состоит из крошечных единиц, называемых атомами. В каждом атоме есть электроны, частицы, несущие электрические заряды. Вращаясь, как волчки, электроны вращаются вокруг ядра или остова атома. Их движение генерирует электрический ток и заставляет каждый электрон действовать как микроскопический магнит.

В большинстве веществ одинаковое количество электронов вращается в противоположных направлениях, что нейтрализует их магнетизм. Вот почему такие материалы, как ткань или бумага, считаются слабомагнитными. В таких веществах, как железо, кобальт и никель, большинство электронов вращаются в одном направлении. Это делает атомы в этих веществах сильно магнитными, но они еще не являются магнитами.

Чтобы стать намагниченным, другое сильномагнитное вещество должно войти в магнитное поле существующего магнита.Магнитное поле — это область вокруг магнита, обладающая магнитной силой.

Все магниты имеют северный и южный полюса. Противоположные полюса притягиваются друг к другу, а одни и те же полюса отталкиваются. Когда вы протираете кусок железа по магниту, северные полюса атомов в железе выстраиваются в одном направлении. Сила, создаваемая выровненными атомами, создает магнитное поле. Железка стала магнитом.

Некоторые вещества могут намагничиваться электрическим током.Когда электричество проходит через катушку с проволокой, создается магнитное поле. Однако поле вокруг катушки исчезнет, ​​как только отключится электрический ток.

Геомагнитные полюса

Земля — ​​это магнит. Ученые не до конца понимают, почему, но они думают, что движение расплавленного металла во внешнем ядре Земли порождает электрические токи. Токи создают магнитное поле с невидимыми силовыми линиями, протекающими между магнитными полюсами Земли.

Геомагнитные полюса не совпадают с Северным и Южным полюсами. Магнитные полюса Земли часто перемещаются из-за активности далеко под поверхностью Земли. Смещение геомагнитных полюсов фиксируется в породах, которые образуются, когда расплавленный материал, называемый магмой, проникает сквозь земную кору и изливается в виде лавы. Когда лава охлаждается и превращается в твердую породу, сильно магнитные частицы внутри породы намагничиваются магнитным полем Земли. Частицы выстраиваются вдоль силовых линий в поле Земли.Таким образом, камни фиксируют положение геомагнитных полюсов Земли в то время.

Как ни странно, магнитные записи горных пород, образовавшихся в одно и то же время, похоже, указывают на разные местоположения полюсов. Согласно теории тектоники плит, скальные плиты, составляющие твердую оболочку Земли, постоянно перемещаются. Таким образом, плиты, на которых застывала порода, переместились с тех пор, как породы зафиксировали положение геомагнитных полюсов. Эти магнитные записи также показывают, что геомагнитные полюса менялись на противоположный вид — сотни раз с момента образования Земли.

Магнитное поле Земли не движется быстро и часто не меняется. Следовательно, это может быть полезным инструментом, помогающим людям сориентироваться. Сотни лет люди использовали магнитные компасы для навигации по магнитному полю Земли. Магнитная стрелка компаса совпадает с магнитными полюсами Земли. Северный конец магнита указывает на северный магнитный полюс.

Магнитное поле Земли доминирует в области, называемой магнитосферой, которая охватывает планету и ее атмосферу.Солнечный ветер, заряженные частицы от Солнца, прижимает магнитосферу к Земле со стороны, обращенной к Солнцу, и растягивает ее в форме капли на теневой стороне.

Магнитосфера защищает Землю от большинства частиц, но некоторые из них просачиваются сквозь нее и попадают в ловушку. Когда частицы солнечного ветра сталкиваются с атомами газа в верхних слоях атмосферы вокруг геомагнитных полюсов, они создают световые эффекты, называемые полярными сияниями. Эти полярные сияния появляются над такими местами, как Аляска, Канада и Скандинавия, где их иногда называют «Северным сиянием».«Южное сияние» можно увидеть в Антарктиде и Новой Зеландии.

Магнетизм — гипертекст по физике

Обсуждение

история

Краткое изложение истории, рассказанной исторически. Основные идеи, которые теперь знают даже маленькие дети. Держите все на вводном уровне.

• Есть камни, которые привлекают другие камни, но только если они правильного типа
• Эти камни будут пытаться выровняться с севера на юг (грубо говоря)

Сначала идет Фалес Милетский (635–543 до н.э.) Греция (Иония).Милет сейчас находится на западном побережье Турции, в тогдашнем регионе Греции, известном как Иония (источник химического термина «ион», но это уже другая история).

• Камни Магнезии (μαγνήτης λίθος)
• Μαγνησία сейчас Маниса, Турция
• Магнетит. Кусок магнетита с исключительно сильным магнитным действием иногда называют магнитом.

Здесь было бы неплохо цитата из Фалеса.

Некоторые минералы, такие как магнетит (Fe ₃ O ₄ ), очевидно, обладают магнитными свойствами.

Китайские мореплаватели знали, что магнитные камни выстраиваются в направлении север-юг (ложка, указывающая на юг).

Настоящий компас был создан китайским мастером геомантических предзнаменований в конце династии Тан, который первоначально использовал его для гаданий.

Найдите что-нибудь историческое.

Северный магнитный полюс компаса указывает в общем направлении северного географического полюса Земли. Поскольку противоположные магнитные полюса притягиваются, это означает, что южный магнитный полюс Земли находится где-то рядом с ее северным географическим полюсом .

Затем идет Питер Перегринус (так его называют по-английски), он же Пьер Пелерин де Марикур (предположительно, его настоящее французское имя), он же Петрус Перегринус де Махарнкурия (его латинское название, что означает «Петр, паломник из Марикура»). Петр написал то, что широко известно как Epistole de Magnete или Письмо на магните . Его полное название — Epistola Petri Peregrini de Maricourt ad Sygerum de Foucaucourt, militem, de magnete ( Письмо на магните Петра Перегрина из Марикура к Сигеру из Фукакура, солдату «).Он был написан 8 августа 1269 года во время осады города Лучера — последней уцелевшей крепости ислама на «икроножных мышцах» полуострова в форме сапога, который сейчас называется Италией.

Работа Питера была настолько полной, что никаких дальнейших исследований свойств магнитов не проводилось до монументальной работы Уильяма Гилберта в 1600 — гг. Tractatus sive Physiologia Nova de Magnete, Magneticisque Corporibus, et Magno Magnete Tellure (On the Magnetic, Magnetic Bodies , и Великий Магнит Земли). De Magnete — текст, в котором Гилберт раскрыл результаты своих исследований магнетизма и попытался объяснить природу магнитов и пять движений, связанных с магнитными явлениями. Работа имела большой успех и была переиздана в 1628 и 1633 годах.

Уильям Гилберт (1544–1603) Англия

Найди что-нибудь.

основы

магнитные элементы

Подъемный магнит в действии — Бруклин, Нью-Йорк

• Большая тройка
  • железо (Fe)
  • никель (Ni)
  • кобальт (Co)
• плюс чудаки
  • гадолиний (Gd)
  • диспрозий (Dy)

Подробнее о ферромагнетизме позже

Земля — ​​магнит, геомагнетизм, полюса: север в поисках и юг в поисках

правило действия: противоположные полюса притягиваются, как полюса отталкиваются

типов магнитов

• постоянный
• индуцированный
• электромагнит

магнитное поле

неформальное определение: сравните с другими полями

Сравнение силовых полей

* Совершенно решительно: Нет! Магнитное поле нарушает эту тенденцию.

феномен	происхождение	поле	символ
Плотность	сила из-за массы	силы на массы	г
электричество	усилие за счет заряда	усилие на заряд	E
магнетизм	усилие от полюсов ? *	усилие на полюс ? *	В

настоящее определение появится позже

дилемма: при разрушении магнита магнитный монополь отсутствует, даже в атомных масштабах нет магнитного монополя, силовые линии исцеляются сами собой

Тем не менее, даже несмотря на то, что у нас нет формального определения магнитного поля, нет причин, по которым неформальное определение какое-то время нас не устраивает.

свойства силовых линий магнитного поля

• направление определяется от северного полюса компаса
• напряженность пропорциональна плотности силовых линий
• силовые линии замкнутые
• силовые линии проходят сквозь магнитные материалы (сравните это с силовыми линиями электрического поля, которые заканчиваются на поверхности проводников)
• силовые линии изгибаются на поверхности магнитного материала

Символ магнитного поля: B (жирный шрифт) при описании полной векторной величины и B (курсив) при описании только величины.

Единицей измерения магнитного поля в системе СИ является тесла [Тл], названная в честь сербско-американского инженера-электрика Николы Тесла (1856–1943), родившегося в части Австро-Венгерской или Габсбургской империи, которая в настоящее время является независимым государством. Хорватии. Тесла был пионером в смежных дисциплинах переменного электрического тока и вращающихся магнитных полей. Его основные конструкции электродвигателей, генераторов и трансформаторов в начале 20-го века мало изменились к началу 21-го века.

Другая широко используемая единица — гаусс [G], названная в честь немецкого математика Карла Фридриха Гаусса (1777–1855). Гаусса обычно считают величайшим математиком всех времен. Особый интерес для физиков вызвали работы Гаусса по искривленным поверхностям, которые сыграли важную роль в областях электростатики и общей теории относительности (). Гаусс также является единицей в системе cgs, которая была первоначально разработана Гауссом и иногда также известна как система Гаусса.

Формальное определение каждой из этих единиц будет дано в следующем разделе этой книги. Прямо сейчас я скажу вам, что тесла — это более крупная единица.

На самом деле тесла слишком велика для большинства практических целей. Таким образом, он обычно делится на микротесла [мкТл] или нанотесла [нТл]. Гаусс тоже немного великоват, но не так плох, как тесла, поэтому миллигаусс [мГ] и микрогаусс [мкГ] встречаются чаще.

1 т	=	10 кг
1 мТ	=	10 г
1 мкТл	=	10 мГ
1 нТл	=	10 мкГ

В следующей таблице перечислены напряженности магнитного поля для различных устройств, событий или явлений.По возможности также указывалось местоположение. Подобно гравитационному и электрическому полям, магнитное поле становится меньше с увеличением расстояния от источника.

Выбранные значения магнитного поля (от наибольшего к наименьшему)

B (T)	устройство, событие, явление, процесс
~ 10 13	нейтронная звезда, теоретический верхний предел
10 10 ~ 10 11	нейтронная звезда, магнетар
10 8 ~ 10 9	нейтронная звезда, радиопульсар
1 000	самый сильный лабораторный магнит, эфемерный
100	белый карлик
45	самый сильный лабораторный магнит, устойчивый
16	достаточно сильны, чтобы левитировать лягушек
20	сильнейший сверхпроводящий магнит
2.4	самый сильный постоянный магнит
1–4	МРТ
1	сильный лабораторный магнит
0,45	большое пятно
0,15	магнит железный стержень, на полюсах
0,10	магнит на холодильник
0,001	Солнце на полюсах
400 × 10 −6	Юпитер, средняя поверхность
100 × 10 −6	Солнце, среднее значение поверхности
60 × 10 −6	Земля на полюсах
45 × 10 −6	Земля, среднее значение поверхности
30 × 10 −6	Земля, на экваторе
10 × 10 −6	Радиовещание AM на приемнике
1 × 10 −6	солнечное излучение на поверхности Земли
180 × 10 −9	Лампочка 100 Вт на расстоянии 1 м, пик
150 × 10 −9	Ртуть, среднее значение поверхности
150 × 10 −9	Земля, высота геостационарной орбиты
50 × 10 −9	Земля, нос магнитосферы
35 × 10 −9	Луна, поверхность
5 × 10 −9	межпланетное пространство у Земли
1 × 10 −9	Земля, хвост магнитосферы
500 × 10 −12	межзвездное пространство
100 × 10 −12	межгалактическое пространство
50 × 10 −12	человеческое сердце
100 × 10 −15	человеческий мозг

ферромагнетизм

Этот раздел предназначен для обсуждения магнетизма в мелком масштабе, а не только магнетизма железа, никеля и кобальта (хотя это будет его основным фокусом).Возможно, это стоит назвать «микромагнетизм».

Все из-за спина электрона. Ну почти все.

Типы магнитных свойств (в порядке уменьшения силы)

тип	выравнивание отжима	примеров
ферромагнитный	все вращения параллельны друг другу	железо, кобальт, никель, гадолиний, диспрозий, сплавы Гейслера
ферримагнетик	большинство вращений параллельно друг другу, некоторые вращения антипараллельно	магнетит (Fe 3 O 4 ), железо-иттриевый гранат (ЖИГ)
антиферромагнитный	периодическое параллельно-антипараллельное распределение спинов	хром, FeMn, NiO
парамагнитный	спинов имеют тенденцию выравниваться параллельно внешнему магнитному полю	кислород, натрий, алюминий, кальций, уран
диамагнитный	спинов имеют тенденцию выравниваться антипараллельно внешнему магнитному полю	азот, медь, серебро, золото, вода, органические соединения
супердиамагнитный	все спины выровнены антипараллельно внешнему полю	Эффект Мейснера в сверхпроводниках

сплавы

Сталь…

Основные марки стали (в порядке увеличения содержания углерода)

тип	состав	магнитный?	прочие характеристики
ферритная нержавеющая	Fe, Cr, C	да	умеренная коррозионная стойкость, умеренная стойкость
аустенитная нержавеющая	Fe, Cr, Ni, C	№	высокая коррозионная стойкость, средняя стойкость
мартенситная нержавеющая	Fe, Cr, C	да	умеренная коррозионная стойкость, высокая прочность
нержавеющая (высокоуглеродистая)	Fe, C	да	низкая коррозионная стойкость, высокая прочность

Сплавы, специально предназначенные для постоянных магнитов…

• Алнико
• Сплавы самарий
• Сплавы неодимовые

Ферромагнитные сплавы целиком из цветных металлов…

• Сплав Гейслера: медь, олово, марганец в соотношении 2: 1: 1.Фридрих Гейслер (1866–1947) Германия. Медь можно заменить серебром. Олово можно заменить алюминием, мышьяком, сурьмой, висмутом или бором.
• CrO ₂
• EuO

магнитная запись

основной механизм

Увеличить

медиаформатов

медиа-формы

• провод записи
• катушка
• барабаны
• диски

подложки

• гибкие: лента и гибкие диски, обычно полиэстер
• жесткий: жесткие диски, обычно алюминиевые

ферромагнитный материал

• жесткий vs.мягкий
  • Твердым магнитным материалам требуются относительно сильные магнитные поля для постоянного намагничивания и реверсирования или стирания намагниченности. Они наиболее подходят для хранения цифровых данных
  • Для намагничивания мягких магнитных носителей требуются относительно слабые магнитные поля. Они больше подходят для аналоговой аудио- и видеозаписи.

Обычные материалы, используемые для магнитной ленты

тип	смещение	материал	комментариев
I	нормальный	гамма оксид железа (γ-Fe 2 O 3 )	Впервые серийно произведено в 1937 году
II	высокая	диоксид хрома (CrO 2 )	позже заменен слоями оксида железа (Fe 2 O 3 ) и кобальта (Co) с аналогичными магнитными характеристиками
III		железо хром (FeCr)	быстро устарел
IV	металл	железо металлическое тонкое измельчение	позже заменен на смеси тонкоизмельченного железа и кобальта
н / д		Феррит бария (BaFe 12 O 19 )	магнитные полосы на банковских и кредитных картах, высокая коэрцитивность, меньше подвержены случайному стиранию

температуры перехода

Температура Кюри названа в честь французского физика Пьера Кюри (1859–1906), который открыл законы, связывающие некоторые магнитные свойства с изменением температуры в 1895 году.

Антиферромагнитный эквивалент температуры Кюри назван температурой Нееля в честь французского физика Луи Нееля (1904–2000), который успешно объяснил антиферромагнетизм в 1936 году.

Температуры Кюри выбранных ферромагнитных материалов

элементы	Т С (К)
утюг	1043
кобальт	1404
никель	628
гадолиний	289
эрбий	32
диспрозий	155

соединения железа	Т С (К)
феррит бария	720
феррит стронция	720
Алнико	1160
Алюмель	436
Мутамель	659
Пермаллой	869
Trafoperm	1027
NdFeB	580
SmCo 5	990
Sm 2 Co 17	1070

соединения цветных металлов	Т С (К)
CrO 2	390
CuAlMn 3	?
La x Ca 1 − x B 6	900
MnAs	318
MnBi	633
MnSb	587
полимеризованный C 60	~ 500

Температуры Нееля некоторых антиферромагнитных материалов

материал	Т Н (К)
CoCl 2	25
CoF 2	38
CoO	291
хром	475
Cr 2 O 3	307
эрбий	80
FeCl 2	70
FeF 2	79–90
FeO	198
FeMn	490
α-Fe 2 O 3	953
MnF 2	72–75
MnO	122
MnSe	173
MnTe	310–323
NiCl 2	50
NiF 2	78–83
NiFeO	180
NiO	533–650
TiCl 3	100
UCu 5	15
V 2 O 3	170

животный магнетизм (магнитотаксис?)

• жуткие ползания
  • Магнитотактические бактерии
  • плоских червей ( Platyhelminthes )
  • медоносных пчел?
• рыб
  • чавычи ( Oncorhynchus tshawytscha )
  • желтоперый тунец ( Thunnus albacares )
• земноводных
  • Краснопятнистый тритон ( Notophthalmus viridescens viridescens )
• рептилии
  • головастая морская черепаха ( Caretta caretta )? или это какая-то другая разновидность?
• птиц
  • сизый голубь ( Columba livia )
  • боболинк ( Dolichonyx oryzivorus )
• млекопитающих
  • Голый землекоп ( Heterocephalus glaber )
  • Сибирский хомяк ( Phodopus sungorus )? или это какая-то другая разновидность?
  • коричневая летучая мышь ( Eptesicus fuscus )

здоровье и безопасность

текст

Воздействие магнитного поля при использовании различных устройств

прибор	Б (мкТл)
цветной экран ЭЛТ ТВ / компьютера	500
плита электрическая	1000
фен	1000
поезд на маглеве	100

текст

Среднесуточное воздействие магнитных полей

местонахождение		медиана (мкТл)	диапазон (мкТл)
земная поверхность		45	40–60
рабочее место:	делопроизводитель без компьютера	0.05	0,02–0,20
	делопроизводитель с компьютером	0,12	0,05–0,45
	машинист	0,19	0,06–2,76
	ЛЭП	0,25	0,05–3,48
	электрик	0,54	0,08–3,40
	сварщик	0.82	0,17–9,60
дом:	типичный дом в США	0,09	0,03–0,37

МРТ

Магнитно-резонансная томография (ядерный магнитный резонанс)

• атомы в магнитном поле будут поглощать, а затем выделять энергию в виде радиоволн
• каждый атом, видимый для МРТ, имеет свою собственную радиочастоту (каждый атом — это собственная радиовышка)
• Все ядра, содержащие нечетное число нуклонов, обладают собственным магнитным моментом и угловым моментом
• Какие атомы можно увидеть при МРТ (частоты ЯМР при 1 Тл)?
  • (42.38 МГц) водород 1
  • (40,05 МГц) фтор 19 (в большом количестве лекарств)
  • (16,33 МГц) литий-7 (в нашем организме немного, но содержится в препаратах для лечения биполярного расстройства)
  • натрий 23 (используется нейронами для выработки электрических сигналов)
  • (17,25 МГц) фосфор 31 (участвует в энергосодержащих соединениях)
  • (10,71 МГц) углерод 13
  • калий (используется нейронами для выработки электрических сигналов)
• Одни и те же атомы в разных молекулах поглощают и излучают радиоволны на несколько разных частотах

Магнетизм и электромагнетизм — Высшая школа физики

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы вуза предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

22: Магнетизм — Physics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

1. Авторы и авторства

Магнетизм — это класс физических явлений, которые опосредуются магнитными полями.Электрические токи и магнитные моменты элементарных частиц порождают магнитное поле, которое действует на другие токи и магнитные моменты. На каждый материал в той или иной степени влияет магнитное поле.

• 22.0: Прелюдия к магнетизму

  Магнетизм используется для объяснения уровней энергии атомов, космических лучей и заряженных частиц, захваченных в поясах Ван Аллена. И снова мы обнаружим, что все эти разрозненные явления связаны небольшим количеством основных физических принципов.

• 22.1: Магниты

  Магнетизм — это предмет, который включает в себя свойства магнитов, влияние магнитной силы на движущиеся заряды и токи и создание магнитных полей токами. Есть два типа магнитных полюсов: северный магнитный полюс и южный магнитный полюс. Северные магнитные полюса — это те полюса, которые притягиваются к географическому северному полюсу Земли. Как полюса отталкиваются, а разные полюса притягиваются. Магнитные полюса всегда встречаются парами север и юг.

• 22.2: Ферромагнетики и электромагниты

  Весь магнетизм создается электрическим током. Ферромагнитные материалы, такие как железо, проявляют сильные магнитные эффекты. Атомы в ферромагнитных материалах действуют как маленькие магниты (из-за токов внутри атомов) и могут быть выровнены, обычно в областях миллиметрового размера, называемых доменами. Домены могут расти и выравниваться в большем масштабе, создавая постоянные магниты. Такой материал намагничивается или становится магнитным.

• 22.3: Магнитные поля и линии магнитного поля

  Магнитные поля могут быть графически представлены линиями магнитного поля, свойства которых следующие: Поле касается линии магнитного поля. Напряженность поля пропорциональна плотности линий. Линии поля не могут пересекаться. Линии поля представляют собой непрерывные петли.

• 22.4: Напряженность магнитного поля — сила на движущийся заряд в магнитном поле

  Магнитные поля действуют на движущийся заряд q.Единицей измерения напряженности магнитного поля B в системе СИ является тесла (Тл). Направление силы на движущийся заряд задается правилом правой руки 1: направьте большой палец правой руки в направлении v, пальцы в направлении B, а перпендикуляр к ладони указывает в направлении F. Сила перпендикулярна плоскости, образованной \ (mathbf {v} \) и \ mathbf {B}.

• 22.5: Сила, действующая на движущийся заряд в магнитном поле — примеры и приложения

  Магнитная сила может создавать центростремительную силу и заставлять заряженную частицу двигаться по круговой траектории с радиусом \ [r = \ frac {mv } {qB}, \] где \ (v \) — составляющая скорости, перпендикулярная \ (B \) для заряженной частицы с массой \ (m \) и зарядом \ (q \).

• 22.6: Эффект Холла

  Мы видели влияние магнитного поля на свободно движущиеся заряды. Магнитное поле также влияет на заряды, движущиеся в проводнике. Одним из результатов является эффект Холла, который имеет важные последствия и приложения. Эффект Холла — это создание напряжения εε \ varepsilon, известного как ЭДС Холла, через проводник с током магнитным полем.

• 22.7: Магнитная сила на проводнике с током

  Магнитная сила на проводниках с током определяется выражением \ [F = \ pi B sin \ theta, \], где \ (\) — ток , \ (l \) — длина прямого проводника в однородном магнитном поле \ (B \), а \ (\ theta \) — угол между \ (I \) и \ (B \).Сила следует за RHR-1 большим пальцем в направлении \ (I \). \

• 22.8: Крутящий момент на токовой петле — Двигатели и измерители

  Крутящий момент \ (\ tau \) на токе — петля для переноски любой формы в однородном магнитном поле. это \ [\ tau = NIABsin \ theta, \], где \ (N \) — количество витков, \ (I \) — ток, \ (A \) — площадь петли, \ (B \) — напряженность магнитного поля, а \ (\ theta \) — угол между перпендикуляром к петле и магнитным полем.{-7} T \ cdot m / a \) — проницаемость свободного пространства. Направление магнитного поля, создаваемого длинным прямым проводом, определяется правилом правой руки 2 (RHR-2): направьте большой палец правой руки на d

• 22.10: Магнитная сила между двумя параллельными проводниками

  Сила между двумя параллельными токами \ (I_ {1} \) и \ (I_ {2} \), разделенными расстоянием \ (r \), имеет величину на единицу длины, определяемую как \ [\ frac {F} { l} = \ frac {\ mu_ {0} I_ {1} I_ {2}} {2 \ pi r}. \] Сила притягивает, если токи идут в одном направлении, и отталкивает, если они в противоположных направлениях.

• 22.11: Другие приложения магнетизма

  Перекрещенные (перпендикулярные) электрические и магнитные поля действуют как скоростной фильтр, создавая равные и противоположные силы на любой заряд со скоростью, перпендикулярной полям, и величиной \ [v = \ frac {E} {B}. \]

• 22.E: Магнетизм (упражнения)

Эскиз: магнитное поле идеального цилиндрического магнита с осью симметрии внутри плоскости изображения.Магнитное поле представлено линиями магнитного поля, которые показывают направление поля в разных точках. (CC-SA-BY-3.0; Geek3).

Авторы и авторство

• Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с участвующими авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет). Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (by 4.0).

Магнетизм на равнине | Nature

1

Gong, C. et al. Природа 546 , 265–269 (2017).

ADS CAS Статья Google ученый

2

Huang, B. et al. Природа 546 , 270–273 (2017).

ADS CAS Статья Google ученый

3

Гриффитс, Р.B. Phys. Ред. 136 , A437 – A439 (1964).

ADS Статья Google ученый

4

Mermin, N. D. & Wagner, H. Phys. Rev. Lett. 17 , 1133–1136 (1966).

ADS CAS Статья Google ученый

5

De Jongh, L. J. & Miedema, A. R. Adv. Phys. 50 , 947–1170 (2001).

ADS Статья Google ученый

6

Vaz, C. A. F., Bland, J. A. C. & Lauhoff, G. Rep. Prog. Phys. 71 , 056501 (2008).

ADS Статья Google ученый

7

Новоселов К.С. и др. Наука 306 , 666–669 (2004).

ADS CAS Статья Google ученый

8

Батлер, С.Z. et al. САУ Нано 7 , 2898–2926 (2013).

CAS Статья Google ученый

9

Мак, К. Ф. и Шан, Дж. Nature Photon. 10 , 216–226 (2016).

ADS CAS Статья Google ученый

10

Като Ю. К., Майерс Р. К., Госсард А. К. и Авшалом Д. Д. Science 306 , 1910–1913 (2004).

ADS CAS Статья Google ученый

11

Ся, Дж., Бейерсдорф, П. Т., Фейер, М. М. и Капитульник, А. Прил. Phys. Lett. 89 , 062508 (2006).

ADS Статья Google ученый

12

Макгуайр, М. А., Диксит, Х., Купер, В. Р. и Сейлз, Б. С. Chem. Матер. 27 , 612–620 (2015).

CAS Статья Google ученый

13

Джи, Х.и другие. J. Appl. Phys. 114 , 114907 (2013).

ADS Статья Google ученый

Основы магнетизма Рона Куртуса

SfC Home> Физика> Магнетизм>

Рона Куртуса (от 29 января 2013 г.)

Магнетизм — это сила притяжения или отталкивания, действующая на расстоянии. Это связано с магнитным полем , которое создается движущимися электрически заряженными частицами.Это также присуще магнитным объектам, таким как магнит .

Магнит — это объект, который проявляет сильное магнитное поле и притягивает к себе такие материалы, как железо. Магниты имеют два полюса, которые называются северным (N) и южным (S) полюсами. Два магнита будут притягиваться своими противоположными полюсами, и каждый будет отражать одинаковый полюс другого магнита. Магнетизм имеет множество применений в современной жизни.

Вопросы, которые могут у вас возникнуть:

• Что такое магнитное поле?
• Что такое магнитная сила?
• Какая связь между магнетизмом и электричеством?

Этот урок ответит на эти вопросы.Полезный инструмент: Конвертация единиц

---

---

Магнитное поле

Магнитное поле состоит из воображаемых линий потока, исходящих от движущихся или вращающихся электрически заряженных частиц. Примеры включают спин протона и движение электронов по проводу в электрической цепи.

Из чего на самом деле состоит магнитное поле, остается загадкой, но мы знаем, что это особое свойство пространства.

Магнитное поле или силовые линии движущейся заряженной частицы

Наименования полюсов

Линии магнитного потока текут от одного конца объекта к другому.По соглашению мы называем один конец магнитного объекта северным или северным полюсом, а другой — южным или южным полюсом, что связано с северным и южным магнитными полюсами Земли. Магнитный поток определяется как движущийся от N до S.

Примечание : Земля не соответствует магнитной конфигурации на приведенном выше рисунке. Вместо этого линии потока противоположны движущейся заряженной частице.

( См. Дополнительную информацию в разделе «Заблуждение относительно северного магнитного полюса».)

Магниты

Хотя отдельные частицы, такие как электроны, могут иметь магнитные поля, более крупные объекты, такие как кусок железа, также могут иметь магнитное поле, как сумму полей его частиц. Если более крупный объект демонстрирует достаточно большое магнитное поле, он называется магнитом.

( См. Дополнительную информацию в Магнитах. )

Магнитная сила

Магнитное поле объекта может создавать магнитную силу на других объектах с помощью магнитных полей.Эта сила и есть то, что мы называем магнетизмом.

Когда магнитное поле применяется к движущемуся электрическому заряду, например движущемуся протону или электрическому току в проводе, сила, действующая на заряд, называется силой Лоренца.

(Дополнительную информацию см. В разделе «Магнетизм и сила Лоренца». )

Аттракцион

Когда два магнита или магнитных объекта находятся близко друг к другу, возникает сила, которая притягивает полюса друг к другу.

Сила притягивает N к S

Магниты также сильно притягивают ферромагнитные материалы, такие как железо, никель и кобальт.

( См. Дополнительную информацию о магнитных материалах. )

Отталкивание

Когда два магнитных объекта имеют одинаковые полюса, обращенные друг к другу, магнитная сила раздвигает их.

Сила раздвигает магнитные объекты

Магниты также могут слабо отражать диамагнитные материалы. ( Для получения дополнительной информации см. Магнитные материалы. )

Магнитное и электрическое поля

Магнитное и электрическое поля одинаковы и различны.Они также взаимосвязаны.

Электрические заряды и магнетизм аналогичные

Так же, как положительный (+) и отрицательный (-) электрические заряды притягиваются друг к другу, полюса N и S магнита притягиваются друг к другу.

В электричестве, как заряды, отталкиваются, а в магнетизме, как полюса.

Электрические заряды и магнетизм разные

Магнитное поле — это дипольное поле. Это означает, что у каждого магнита должно быть два полюса.

С другой стороны, положительный (+) или отрицательный (-) электрический заряд может существовать отдельно.Электрические заряды называются монополями, поскольку они могут существовать без противоположного заряда.

Сводка

Магнетизм — это сила, действующая на расстоянии и вызванная магнитным полем. Магнитная сила сильно притягивает противоположный полюс другого магнита и отталкивает такой же полюс. Магнитное поле и похоже, и отличается от электрического поля.

---

Будь ценным для других

---

Ресурсы и ссылки

Полномочия Рона Куртуса

Сайты

Объяснение магнетизма — из НАСА

Как работают магнитные доски

Ресурсы магнетизма

Книги

Книги по магнетизму с самым высоким рейтингом

---

Вопросы и комментарии

Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.Я постараюсь вернуться к вам как можно скорее.

---

Поделиться страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

---

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/
магнетизм.htm

Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.

Авторские права © Ограничения

---

Где ты сейчас?

Школа чемпионов

Магнетизм темы

Основы магнетизма

---

Электричество и магнетизм I: материалы курса | Инициатива естественного образования

Физика 3310, принципы электричества и магнетизма 1, является первым семестром нашей двухсеместровой последовательности классического электромагнетизма младшего уровня.Он использует инструменты векторного исчисления для решения статических и динамических свойств электромагнитных полей. Темы, которые мы рассмотрим, включают особые случаи распределения статического заряда (электростатика), не зависящие от времени распределения тока (магнитостатика), а также электрические и магнитные свойства вещества (диэлектрики и магнитные среды).

О преобразовании:

Мы преобразовали E&M младшего уровня, используя:

• Явные цели обучения
• Интерактивные лекции
• Преобразованные домашние задания (включая «банк» потенциальных проблем с аппаратным обеспечением)
• Общие трудности студентов и групповые занятия в классе
• Концептуальные тесты (вопросы-кликеры)
• Интерактивные учебные листы

Эффективность курса исследовалась с помощью следующих оценок:

• Традиционные экзамены
• Новая основанная на исследованиях концептуальная оценка (Оценка электростатики верхнего отдела Колорадо, или CUE).

Скачать материалы курса

Обращайтесь: Стивен Поллок по тел. [email protected] , если вы хотите получать уведомление об обновлении наших материалов.

Преподаватели и исследователи в области образования могут свободно использовать и адаптировать эти материалы в некоммерческих целях в соответствии с лицензией Creative Commons, приведенной ниже. Мы просим вас сотрудничать и не принимать никаких решений, которые вы можете придумать для домашних заданий (и задач на экзаменах, вопросов для кликеров и т. Д…) доступны в открытом доступе из уважения к преподавателям и студентам других учебных заведений, а также для сохранения целостности наших исследований.

Вы используете эти материалы?

Публикации и плакаты

• См. Все публикации, относящиеся к этой работе.

Прочие ресурсы

Этот материал основан на работе, поддержанной национальным научным фондом в рамках гранта № 0737118.