5.2. Теплоемкости изохорная и изобарная
Общетехнические дисциплины / Теплотехника / 5.2. Теплоемкости изохорная и изобарная
Процесс нагревания или охлаждения может происходить при различных условиях. Рассмотрим процесс нагревания газа одного и того же количества (1 кг) в одинаковых цилиндрах с одинаковыми начальными параметрами (рис. 5.1).
В обоих цилиндрах газ будем нагревать до одинаковой температуры Т2. В первом цилиндре (рис.5.1, а) теплота будет подводиться при постоянном объеме, т.е. процесс будет изохорным. Во втором цилиндре (рис.5.1, б) газ будет расширяться от v1до v2 при постоянном давлении (р), т.е. процесс будет изобарным.
Рис. 5.1. Изохорный (а) и изобарный (б) процессы
Так как в первом случае газ не расширяется, он не совершает работу и поэтому вся подводимая теплота тратится на повышение внутренней энергии и на повышения давления.
.
Во втором цилиндре подведенная к газу теплота расходуется как на повышение температуры, так и на перемещение поршня (т.е. на совершение работы). Удельное количество теплоты в этом случае можно определить по формуле:
. (5.2)
Подогрев газа в обоих цилиндрах идет до одинаковой температуры Т2, но во втором случае теплоты необходимо затратить больше на величину работы l, совершенной для перемещения поршня. Тогда:
или .
Известно, что работа (l) при р = const составляет:
или .
Так как , то .
Следовательно, имеем:
.
откуда
. (5.3)
Полученная связь между изобарной и изохорной теплоемкостями (5.
3) называется уравнением Майера. Зная зависимость между теплоемкостями, можно записать:.
Таким образом, в зависимости от того к какой количественной единице вещества относится теплоемкость, различают следующие виды изобарной и изохорной теплоемкостей:
– массовые изобарная и изохорная теплоемкости;
– объемные изобарная и изохорная теплоемкости;
– мольные изобарная и изохорная теплоемкости.
В термодинамических расчетах часто встречается величина (), называемая показателем адиабаты и равная отношению изобарной теплоемкости к изохорной:
.
Значение показателя адиабаты зависит от температуры, но для газов и паров эта зависимость незначительна, и ею пренебрегают, принимая величиной постоянной. Для идеальных газов значение показателя адиабаты принимают равным:
· одноатомных газов – 1,67;
· двухатомных газов – 1,4;
· трех- и многоатомных газов – 1,29.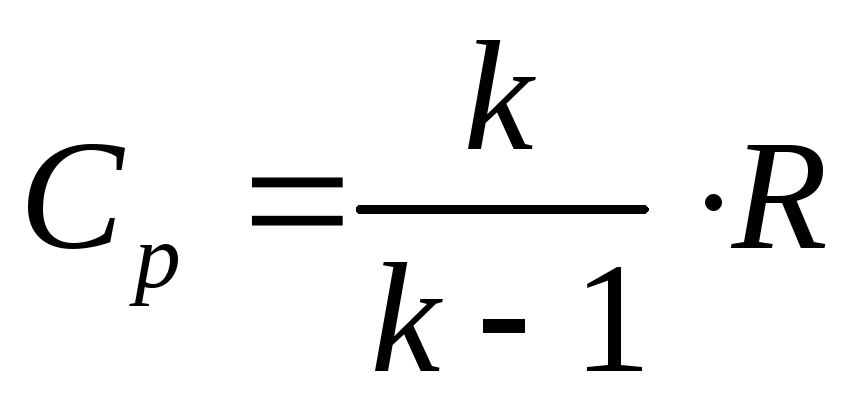
Точные значения для некоторых газов и водяных паров приводятся в справочниках в зависимости от их температур.
Понятие теплоемкости. Виды теплоемкости. Изохорная и изобарная теплоемкость, их связь.
Теплоемкость тела – количество теплоты, необходимой для нагрева тела на один градус (средняя теплоемкость).
Истинная теплоемкость – производная от количества теплоты, подводимой к телу в процессе его нагрева, по температуре этого тела:
.
Виды теплоемкости:
Массовой теплоемкостью (c) называют количество теплоты, необходимой для изменения температуры единицы массы вещества на ;
Мольной теплоемкостью (μc) называют теплоемкость, отнесенную к одному молю вещества;
Объемной теплоемкостью (C) называют теплоемкость, отнесенную к единице объема вещества.
Связь между видами теплоемкостей:
, – плотность вещества,
,
.
В зависимости от вида процесса различают:
Изохорную теплоемкость
,
,
;
Изобарную теплоемкость
,
,
.
Связь между изохорной и изобарной теплоемкостями
Для идеального газа:
,
,
,
,
.
Формула Майера:
,
.
Молекулярно-кинетическая теория теплоемкости идеальных газов (применение для одноатомного и многоатомного газа).
Одноатомный газ
Молекулы одноатомного газа имеют лишь поступательное движение (3 степени свободы):
,
– постоянная Больцмана,
,
,
,
.
Многоатомный газ
.
,
,
Одноатомный: .
Двухатомный: , , .
Трехатомный: , , .
Порядок расчета процесса идеального газа. Расчет теплоты и работы в изобарном, изохорном и изотермическом процессах идеального газа.
Расчет процесса идеального газа:
уравнение процесса;
соотношения термических параметров;
-диаграмма процесса;
изменение внутренней энергии;
изменение энтальпии;
работа расширения процесса;
расчет подводимой/отводимой теплоты.
Изохорный процесс
,
,
,
,
,
,
,
,
,
,
.
Изобарный процесс
,
,
,
,
,
,
,
,
,
,
,
.
Изотермический процесс
,
,
,
,
,
,
,
.
Порядок расчета процесса идеального газа. Адиабатный процесс. Показатель адиабаты, уравнение адиабаты. Построение линии адиабатного процесса в -диаграмме. Расчет работы расширения, совершенной газом в адиабатном процессе.
Расчет процесса идеального газа:
уравнение процесса;
соотношения термических параметров;
-диаграмма процесса;
изменение внутренней энергии;
изменение энтальпии;
работа расширения процесса;
расчет подводимой/отводимой теплоты.
Адиабатный процесс
, – без теплообмена с окружающей средой,
,
,
,
, – показатель адиабаты,
,
,
,
, – уравнение адиабаты (Пуассона).
Расчет работы расширения
,
,
,
,
,
,
,
.
Условие, что является достаточно грубым. В действительности у разреженных газов и возрастают с ростом температуры и показатель адиабаты уменьшается.
,
,
,
,
, , ,
.
Введем функцию:
,
тогда для процесса 1-2:
.
,
,
,
,
,
.
Введем функцию:
,
тогда для процесса 1-2:
.
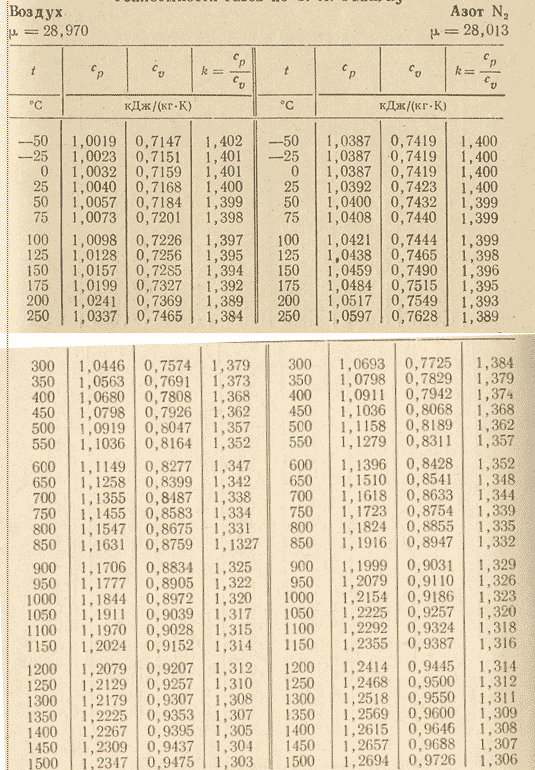
Значения функций и приведены в справочнике, где они рассчитаны с учетом зависимости теплоемкостей от температуры. Используя их, по вычисленным значениям и можно определить температуру газа . Этот метод позволяет произвести точный расчет адиабатного процесса.
Удельная теплоемкость газов (при постоянном объеме или давлении)
Из-за сжимаемости газов необходимо различать изобарную и изохорную удельную теплоемкость.
- 1 Различие изохорной и изобарной теплопередачи
- 2 Экспериментальная установка
- 3 Наблюдение
- 4 Оценка
- 5 Заключение
- 5 Заключение
- 0008
Различие между изохорной и изобарной теплопередачей
В отличие от жидкостей или твердых тел, газы отличаются особой теплоемкостью.
Для этих веществ необходимо учитывать способ передачи тепла. Следует различать два случая, которые будут продемонстрированы следующим экспериментом:
- теплопередача при постоянном объеме (изохорный процесс)
- теплопередача при постоянном давлении (изобарический процесс)
Экспериментальная установка
В первом случае объем замкнутого газа во время нагрева поддерживается постоянным. Это делается путем блокировки поршня в цилиндре. Это приводит к увеличению давления газа в баллоне при нагреве (как, например, в скороварках). Такой термодинамический процесс, при котором объем остается постоянным, называется изохорным процессом .
Рисунок: Нагрев газа при постоянном объеме (слева) и постоянном давлении (справа)Процесс, при котором объем замкнутого газа не изменяется, называется изохорным процессом!
Во втором случае давление газа во время нагрева поддерживается постоянным. Это достигается за счет того, что на этот раз поршни могут свободно перемещаться в цилиндре.
Это позволяет газу «поддаваться» повышающемуся в противном случае давлению за счет увеличения своего объема, так что давление остается постоянным (как это примерно имеет место, например, в дизелях при сгорании топлива). Термодинамический процесс, при котором давление остается постоянным, называется изобарическим процессом!
Процесс, при котором давление замкнутого газа не изменяется, называется изобарическим процессом!
Наблюдение
Причина, по которой необходимо различать эти два процесса в случае газов, можно увидеть, если газ нагревается и в каждом случае наблюдается повышение температуры. Для этого в обоих случаях газ нагревают бунзеновской горелкой в течение одинакового времени. Таким образом, можно предположить, что такое же количество теплоты было поглощено газом.
Анимация: Нагрев газа при постоянном объеме (слева) и постоянном давлении (справа) Однако видно, что повышение температуры значительно больше для изохорного процесса, чем для изобарического.
Еще одно различие в наблюдениях двух экспериментов состоит в том, что в изобарическом процессе объем газа расширяется из-за нагрева и, таким образом, толкает поршень вверх.
Оценка
В чем причина разного изменения температуры в двух случаях?
В то время как при изобарическом процессе работа, очевидно, выполнялась газом для толкания поршня вверх против его веса (и против давления окружающей среды!), в изохорном процессе газ или над ним не совершалась никакой работы. Таким образом, в изобарическом процессе передаваемая тепловая энергия не полностью используется для увеличения кинетической энергии молекул газа (= повышение температуры!). Часть переданной тепловой энергии преобразуется в работу и поэтому не используется для повышения температуры. Та часть тепловой энергии, которая приводит к увеличению кинетической энергии молекул и, таким образом, к повышению температуры, приносит пользу так называемой внутренней энергии ΔU.
Рисунок: Изменение температуры в изохорном процессе (слева) и изобарическом процессе (справа) Таким образом, повышение температуры меньше при изобарическом нагреве, хотя газ поглотил одинаковое количество тепла.
Таким образом, взаимосвязь между переданным теплом и изменением температуры для изохорного и изобарического процессов различна. Это приводит к тому, что удельные теплоемкости газов различны в зависимости от термодинамического процесса (поэтому теплота является так называемой технологической величиной).
Примечание : Поскольку объем газа, очевидно, должен изменяться во время изобарического процесса, чтобы давление оставалось постоянным, работа, совершаемая газом на (или работа, совершаемая газом на в случае сжатия/ охлаждение) также упоминается как работа «давление-объем» . Обратите внимание, что газу пришлось бы совершать работу, даже если бы поршень был невесомым. В этом случае газ должен был бы только расширяться против давления окружающего воздуха (1 бар), но даже это требует работы.
Заключение
Как было показано, при изобарическом нагреве одно и то же количество тепла приводит, таким образом, к меньшему изменению температуры, чем при изохорном нагреве.
И наоборот, это означает: чтобы получить такое же изменение температуры, при изобарическом нагреве необходимо подвести больше тепла, чтобы компенсировать работу, совершаемую в процессе. Следовательно, удельная теплоемкость в изобарическом случае всегда больше, чем в изохорном процессе!
Удельная теплоемкость при постоянном давлении (изобарический процесс) всегда больше по сравнению с удельной теплоемкостью при постоянном объеме (изохорический процесс), потому что необходимо совершить работу!
Поэтому для различения удельная теплоемкость при постоянном давлении обозначается c p , а при постоянном объеме — c v . Для воздуха, например, c p равно 1,005 кДж/(кг⋅K), а c v равно 0,718 кДж/(кг⋅K).
\begin{align}
& \boxed{Q_\text{v} = c_\text{v} \cdot m \cdot \Delta T} ~ \text{изохорный процесс} \\[5px]
& \boxed{Q_\text{p} = c_\text{p} \cdot m \cdot \Delta T} ~ \text{изобарический процесс} \\[5px]
& \boxed{c_\text{p} > c_\text{v}} \\[ 5px]
\end{align}
Более подробные исследования показывают, что удельная изобарная теплоемкость c p больше, чем удельная изохорная теплоемкость c v на величину удельной газовой постоянной R s .
\begin{align}
&\boxed{c_\text{p} = c_\text{v} + R_\text{s}}
\end{align}
Различие для несжимаемых веществ, таких как жидкости и твердые тела
Обратите внимание, что различие между c p и c v относится только к веществам, которые в принципе способны выполнять работу давление-объем. На практике это относится только к сжимаемым веществам, таким как газы, так как они могут очень сильно изменять свой объем под давлением. Для твердых тел и жидкостей такое различие устарело, так как они несжимаемы в отличие от газов. Такие вещества практически не могут изменять своего объема под давлением и, следовательно, не могут совершать никакой работы давление-объем. Низкое тепловое расширение незначительно. Поэтому удельная теплоемкость твердых тел и газов обозначается только символом с (без индекса).
термодинамика. В чем разница между удельной теплоемкостью воды в изобарических и изохорных условиях
спросил
Изменено 13 дней назад
Просмотрено 1к раз
$\begingroup$
Можно ли объяснить разницу удельной теплоемкости воды в изохорных и изобарических условиях с точки зрения внутренней энергии системы? Большинство видеороликов, которые я смотрел, основывают свое объяснение на терминах идеальных газов. Я предполагаю, что это как-то связано с тем фактом, что изохорные условия означают, что вся выделяемая тепловая энергия идет на внутреннюю энергию молекул. У меня также есть графики зависимости удельной теплоемкости от времени.
- термодинамика
- энергия
- вода
$\endgroup$
$\begingroup$
В общем то же самое, что и с идеальными газами. Это здесь не то, что является формальным ответом, потому что удельная теплоемкость обычно определяется энтальпией и внутренней энергией. Это скорее объяснение, почему есть разница.
Чтобы изменить объем $V$ при постоянном давлении, необходимо совершить некоторую работу $A$. В дифференциальном случае (очень маленькое изменение): $dA=pdV$.
Из закона сохранения энергии мы можем определить, что:
$$
dQ=dW+dA
$$
$Q$ — внутренняя энергия системы, dW — добавленная энергия, A — работа, совершаемая системой.
Таким образом, мы можем обозначить удельную теплоемкость как $dQ/dT$:
$$ c_p=\frac{dQ}{dT}=\frac{dW+pdV}{dT} $$ и $$ c_V=\frac{dQ}{dT}=\frac{dW+pdV}{dT}=\frac{dW+p\cdot0}{dT}=\frac{dW}{dT} $$
Отсюда видно, что $c_p$ больше, чем $c_v$. Отношение между этими двумя зависит от уравнения состояния и может быть довольно безобразным для жидкостей. Но в целом, когда у нас есть изобарические условия, некоторая добавленная энергия преобразуется в работу, необходимую для изменения объема системы.
Если вы не знакомы с дифференциалами $d$, то это всего лишь очень маленькие изменения $\Delta$.
$\endgroup$
$\begingroup$
Удельная теплоемкость расходится в основном после 100 C, когда при 1 атмосфере вода меняет фазу и начинает вести себя как газ, поведение которого приближается к идеальному газу.
Основанное на первом законе объяснение внутренней энергии того, что удельная теплоемкость при постоянном давлении (изобарическая) $C_P$ больше, чем удельная теплоемкость при постоянном объеме (изохорическая) $C_V$, заключается в том, что при подводе тепла при постоянном давлении вещество расширяется и работает.