Как определить сопротивление воздуха: Как определить сопротивление воздуха? — Физблог

Коэффициент сопротивления изменяется как квадратное отношение относительной скорости объекта. Рассмотрим метод расчета коэффициента сопротивления воздуха.

Коэффициент сопротивления воздуха рассчитывается по уравнению с = F_воздух /v². В расчете Ф_воздух — силовое сопротивление, а c — силовая постоянная в этом уравнении. Жидкости, обычно вода в спортивной среде, также подвержены силе трения, которая не ограничивается только воздухом.

Сопротивление жидкости, сопротивление воздуха и сопротивление — все это относится к одному и тому же.

Проблема: Если объект движется со скоростью 22 мс^-1 столкнуться с сопротивлением воздуха 50 Н, какова постоянная силы?

Решение: Даны данные,

v = 22 мс^-1

F_воздух = 50 Н

Формула для коэффициента сопротивления воздуха:

с = F_воздух /v²

Замените указанные значения в формуле выше. Затем,

с = 50/(22)²

с = 0.103

Вес пульсирует на шнуре, когда парашют раскрывается. Рассмотрим, как определить аэродинамическое сопротивление парашюта.

• Чтобы определить аэродинамическое сопротивление парашюта. Уравнение для силы сопротивления парашюта, также известной как его сила сопротивления ветру, имеет вид F._D = 1 / 2 ρv²C_DА. Где, Ф_D — сила сопротивления, r — плотность воздуха, C_d — коэффициент лобового сопротивления, A — площадь парашюта, а v — скорость в воздухе.
• Чтобы определить сопротивление воздуха парашюта по квадрату скорости, сопротивление возрастает.
• Чтобы определить сопротивление воздуха парашюта, нет никакой чистой силы, действующей на ракету, когда сопротивление равно весу. F = D – W = 0.
• C_d = 2 Ф_d / ρв²A = W для определения аэродинамического сопротивления парашюта.
• И, наконец, V = sqrt (2W/C_dρ A) используется для определения аэродинамического сопротивления парашюта.

При сравнении двух предметов те, у которых больший вес, меньший коэффициент лобового сопротивления, меньшая плотность газа или меньшая площадь, движутся с большей скоростью.

Единственной силой, воздействующей на людей поначалу, является гравитация, которая толкает их со скоростью -9.8 м/с2. Давайте посмотрим, как можно рассчитать сопротивление воздуха, используя массу и ускорение.

• Чтобы найти сопротивление воздуха с массой и ускорением, мы можем использовать некоторую алгебру, чтобы получить ускорение объекта с точки зрения чистой внешней силы и массы объекта (a = F/m).
• Чистая внешняя сила (F = W – D) равна разнице между силами веса и силы сопротивления. Тогда ускорение объекта определяется выражением a = (W – D) / m.

Задача: Автомобиль массой около 29 кг движется из Калькутты в Раджастхан со скоростью 50 метров в секунду, а гусеница нагружена железом и весит 84 кг. Определить силу сопротивления автомобиля.

Решение: Даны данные,

Ускорение = 50 м/с²

Вес = 84 кг

Масса = 29 кг

Мы знаем, что a = (W – D) / m

50 = (84 – Д)/ 29

1450 = 84 – Д

-Д = 1450 – 84

Д = – 1366 Н

Когда частички воздуха сталкиваются с передней частью объекта, он замедляется. Давайте проверим этот график сопротивления воздуха.

За счет уменьшения угла выпуска можно свести к минимуму влияние сопротивления воздуха на горизонтальную составляющую траектории снаряда. Расстояние и скорость, или скорость, обратно пропорциональны.

Чем больше частиц воздуха воздействует на объект, тем больше его общее сопротивление увеличивается с площадью поверхности.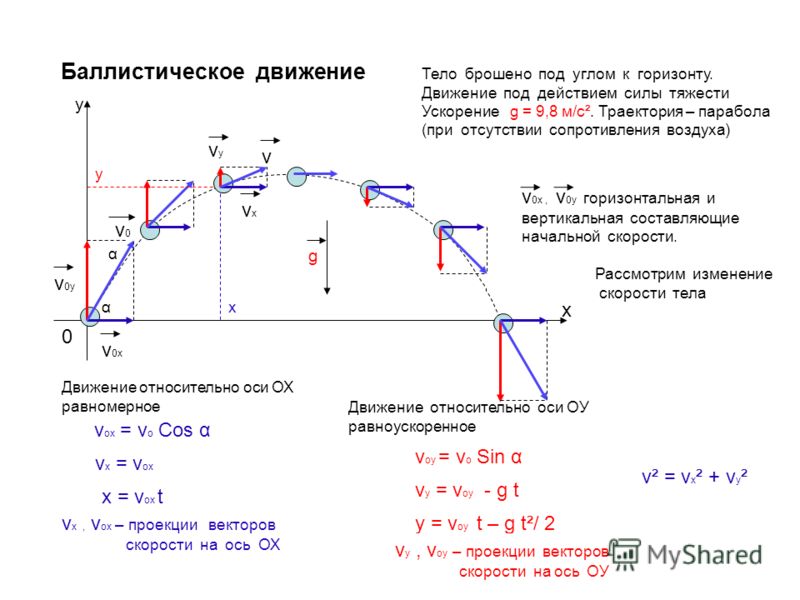 Давайте рассмотрим, как определить сопротивление воздуха на основе скорости.

Формула, используемая для определения сопротивления воздуха по скорости: c = Fv.². Сила сопротивления воздуха представлена ​​в технике буквой F, постоянная силы представлена ​​буквой c, а скорость объекта представлена ​​буквой v. Существует линейная зависимость между сопротивлением воздуха и величиной сопротивления воздуха. плотность.

Между скоростью и сопротивлением воздуха создается квадратичная зависимость. Площадь передней кромки объекта, движущегося по воздуху, определяет, какое сопротивление воздуха он будет испытывать. Сопротивление воздуха увеличивается с увеличением площади.

Задача: Если сопротивление воздуха тела равно 34 Н, а силовая постоянная равна 0.04, какова его скорость?

Данные приведены, F_воздух = 34 Н и с = 0.04

Формула сопротивления воздуха:

F_воздух = резюме²

v² = 34 / 0.04

v² = 850

v = 29. 15 м / с.

Сила сопротивления воздуха измеряется в Ньютонах (Н). Рассмотрим, как определить силу сопротивления воздуха.

F_воздух = — резюме² уравнение, используемое для определения силы сопротивления воздуха. Ф_воздух — силовое сопротивление, а c — силовая постоянная в этом уравнении. Знак минус показывает, что объект движется в направлении, противоположном направлению сопротивления воздуха.

Задача: силовая постоянная для самолета, движущегося со скоростью 50 мс.^-1 составляет 0.05. Определить сопротивление воздуха.

Решение: Даны данные,

Скорость воздуха, v = 50

Силовая постоянная, c = 0.05

Сила воздуха определяется выражением

F = – резюме²

F = (-) 0.05 × 50 × 50

F = – 125 Н.

Зависимость между силой сопротивления, действующей на тело, и сопротивлением воздуха обратная. Давайте посмотрим на формулу сопротивления воздуха шара.

Коэффициент сопротивления воздуха для сферических материалов можно рассчитать по следующей формуле: C_d = 2 Ф_d / ρв²A, где для сферических материалов-

• C_d = коэффициент сопротивления воздуха, 
• F_d сопротивление воздуха по Ньютону, 
• А — площадь формы в плане в квадратных метрах,
• ρ = плотность сферы, выраженная в килограммах на кубический метр,
• А вязкость вещества, выраженная в метрах в секунду, известна как v.

Задача: Плотность воздуха 0.4500 кг/м³, а самолет, летящий на высоте, имеет скорость 250 м/с. 500 м² Крылья самолета открыты ветру. На самолет действует сила сопротивления воздуха 168750 Н. Выполните расчет коэффициента лобового сопротивления.

Решение: Приведенные данные, Сопротивление воздуха для сферических материалов, F_d = 168750 Н

Плотность, ρ = 0. 4500 кг/м³

Площадь поперечного сечения, А = 500 м²

Скорость, v = 250 м/с

Мы знаем, что для сферических материалов

C_d = 2 Ф_d / ρв²A

C_d = 2 × 168750 / (0.4500 × 250² × 500)

C_d = 0.025

Сопротивление воздуха — это разновидность жидкостного трения, которое влияет на падающие в воздухе предметы. Давайте посмотрим, как определить среднее сопротивление воздуха.

Умножив плотность воздуха, коэффициент сопротивления, площадь и скорость на два, можно рассчитать среднее сопротивление воздуха, которое будет испытывать падающий объект. Гравитация заставляет объекты двигаться вниз, в отличие от трения воздуха, которое действует противоположным образом и замедляет скорость.

Сопротивление воздуха возрастает по мере увеличения площади поверхности, на которую падают предметы.

Сопротивление воздуха — это сила, которую испытывает объект при прохождении через воздух, где, если человек движется быстрее, сила сопротивления воздуха возрастает. Безразмерный коэффициент сопротивления C_D, который рассчитывается как C_D = Ф_D/1/2 ρАв² где ρ — плотность жидкости (в данном случае воздуха). Площадь поперечного сечения объекта A = (1/4) ΠD², а его скорость v.

Как определить работу силы сопротивления воздуха. Движение тела в поле тяжести с учётом сопротивления воздуха

Каждый велосипедист, мотоциклист, шофер, машинист, летчик или капитан корабля знает, что у его машины есть предельная скорость; превысить которую не удается никакими усилиями. Можно сколько угодно нажимать на педаль газа, но «выжать» из машины лишний километр в час невозможно. Вся развиваемая скорость идет на преодоление сил сопротивления движению .

Преодоление различного трения

Например, автомобиль имеет двигатель мощностью в пятьдесят лошадиных сил. Когда водитель нажимает газ до отказа, коленчатый вал двигателя начинает делать три тысячи шестьсот оборотов в минуту. Поршни как сумасшедшие мечутся вверх и вниз, подскакивают клапаны, вертятся шестеренки, а автомобиль движется хотя и очень быстро, но совершенно равномерно, и вся сила тяги двигателя уходит на преодоление сил сопротивления движению, в частности преодоление различного трения . Вот, например, как распределяется сила тяги двигателя между его «противниками» — разными видами при скорости автомобиля сто километров в час:

• на преодоление трения в подшипниках и между шестеренками расходуется около шестнадцати процентов силы тяги мотора,
• на преодоление трения качения колес по дороге — примерно двадцать четыре процента,
• на преодоление сопротивления воздуха расходуется шестьдесят процентов силы тяги автомобиля.

Сопротивление воздуха

При рассмотрении сил сопротивления движению, таких как:

• трение скольжения с увеличением скорости немного уменьшается,
• трение качения изменяется очень незначительно,
• сопротивление воздуха , совершенно незаметное при медленном движении, становится грозной тормозящей силой, когда скорость возрастает.

Воздух оказывается главным врагом быстрого движения

Сопротивлением воздуха заинтересовались артиллеристы

Сопротивлением воздуха прежде всего заинтересовались артиллеристы . Они старались понять, почему пушечные снаряды не так далеко летят, как им хотелось бы. Расчеты показали, что, если бы на Земле не было воздуха, снаряд семидесятишестимиллиметровой пушки пролетел бы не менее двадцати трех с половиной километров , а в действительности он падает всего лишь в семи километрах от пушки . Из-за сопротивления воздуха теряется шестнадцать с половиной километров дальности . Обидно, но ничего не поделаешь! Артиллеристы улучшали пушки и снаряды, руководствуясь главным образом догадкой и смекалкой. Что происходит со снарядом в воздухе, сначала было неизвестно. Хотелось бы посмотреть на летящий снаряд и увидеть, как он рассекает воздух, но снаряд летит очень быстро, глаз не может уловить его движения, а воздух и подавно невидим.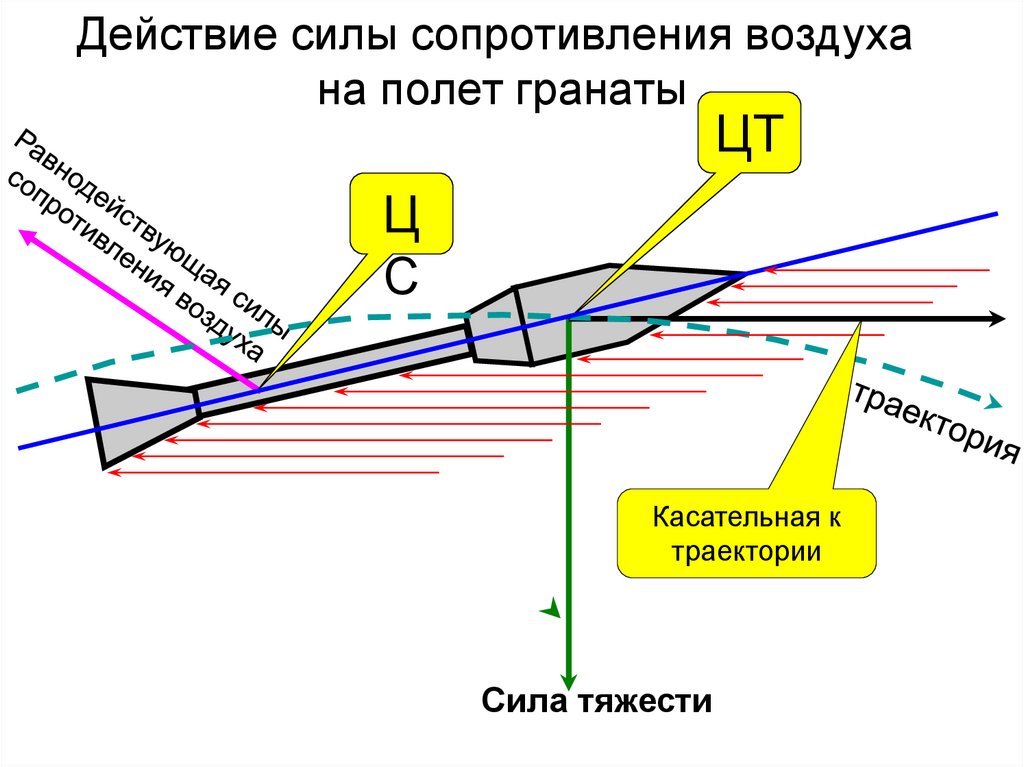

Полоса завихренного воздуха

На фотоснимке летящей пули было видно, что-у нее позади возникает полоса завихренного воздуха . На образование вихрей тоже тратится часть энергии пули или снаряда. Поэтому у снарядов и пуль стали делать донную часть скошенной, это уменьшило силу сопротивления движению в воздухе. Благодаря скошенному дну дальность полета снаряда семидесятишестимиллиметровой пушки достигла одиннадцати — двенадцати километров .

Трение частиц воздуха

При полете в воздухе на скорости движения сказывается также трение частиц воздуха о стенки летящего предмета. Это трение невелико, но оно все же существует и нагревает поверхность. Поэтому приходится красить самолеты глянцевитой краской и покрывать их особым авиационным лаком. Таким образом, силы сопротивления движению в воздухе всем движущимся предметам возникают вследствие трех различных явлений:

• уплотнения воздуха впереди,
• образования завихрений позади,
• небольшого трения воздуха о боковую поверхность предмета.

Сопротивление движению со стороны воды

Предметы, движущиеся в воде — рыбы, подводные лодки, самоходные мины — торпеды и проч.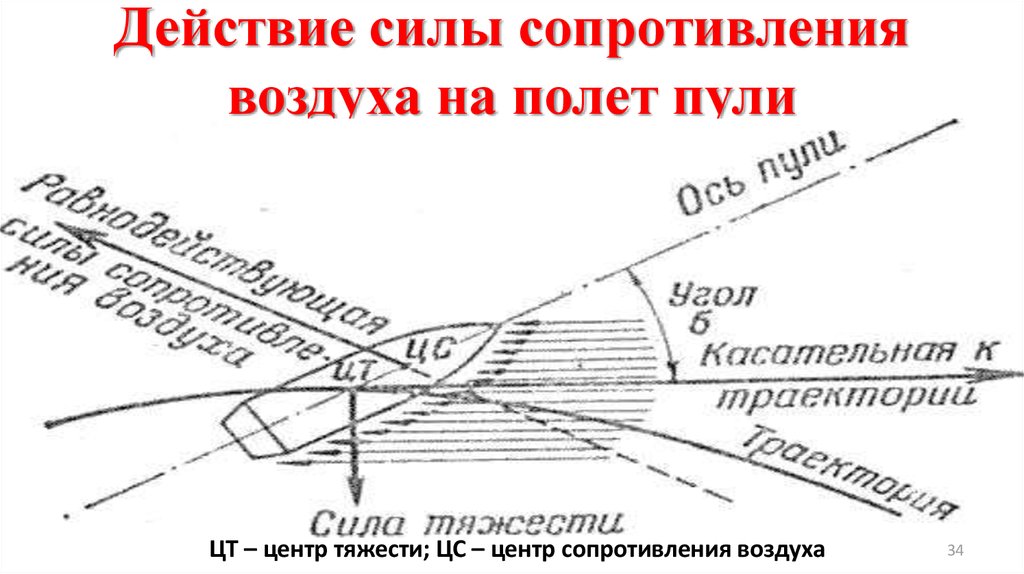 , — встречают большое сопротивление движению со стороны воды . С увеличением скорости силы сопротивления воды растут еще быстрее, чем в воздухе. Поэтому и значение обтекаемой формы возрастает. Достаточно взглянуть на форму тела щуки. Она должна гоняться за мелкими рыбешками, поэтому для нее важно, чтобы вода оказывала минимальное сопротивление ее движению.

Решение.

Для решения задачи рассмотрим физическую систему «тело – гравитационное поле Земли». Тело будем считать материальной точкой, а гравитационное поле Земли — однородным. Выделенная физическая система является незамкнутой, т.к. во время движения тела взаимодействует с воздухом.
Если не учитывать выталкивающую силу, действующую на тело со стороны воздуха, то изменение полной механической энергии системы равняется работе силы сопротивления воздуха, т.

Нулевой уровень потенциальной энергии выберем на поверхности Земли. Единственной внешней силой в отношении системы «тело – Земля» является сила сопротивления воздуха, направленная вертикально вверх. Начальная энергия системы E 1 , конечная E 2 .

Работа силы сопротивления A.

Т.к. угол между силой сопротивления и перемещением равен 180° , то косинус равен -1, поэтому A = — F c h . Приравняем A.

Рассматриваемую незамкнутую физическую систему можно также описать теоремой от изменении кинетической энергии системы взаимодействующих между собой объектов, согласно которой изменение кинетической энергии системы равно работе, совершенной внешними и внутренними силами при ее переходе из начального состояния в конечное. Если не учитывать выталкивающую силу, действующую на тело со стороны воздуха, а внутренней – сила тяжести. Следовательно ∆ E к = A 1 + A 2 , где A 1 = mgh – работа силы тяжести, A 2 = F c hcos 180° = — F c h – работа силы сопротивления; ∆ E = E 2 – E 1 .

Решение.

Для решения задачи рассмотрим физическую систему «тело – гравитационное поле Земли». Тело будем считать материальной точкой, а гравитационное поле Земли — однородным. Выделенная физическая система является незамкнутой, т.к. во время движения тела взаимодействует с воздухом.
Если не учитывать выталкивающую силу, действующую на тело со стороны воздуха, то изменение полной механической энергии системы равняется работе силы сопротивления воздуха, т.е. ∆ E = A c .

Нулевой уровень потенциальной энергии выберем на поверхности Земли. Единственной внешней силой в отношении системы «тело – Земля» является сила сопротивления воздуха, направленная вертикально вверх. Начальная энергия системы E 1 , конечная E 2 .

Работа силы сопротивления A.

Т.к. угол между силой сопротивления и перемещением равен 180° , то косинус равен -1, поэтому A = — F c h . Приравняем A.

Рассматриваемую незамкнутую физическую систему можно также описать теоремой от изменении кинетической энергии системы взаимодействующих между собой объектов, согласно которой изменение кинетической энергии системы равно работе, совершенной внешними и внутренними силами при ее переходе из начального состояния в конечное.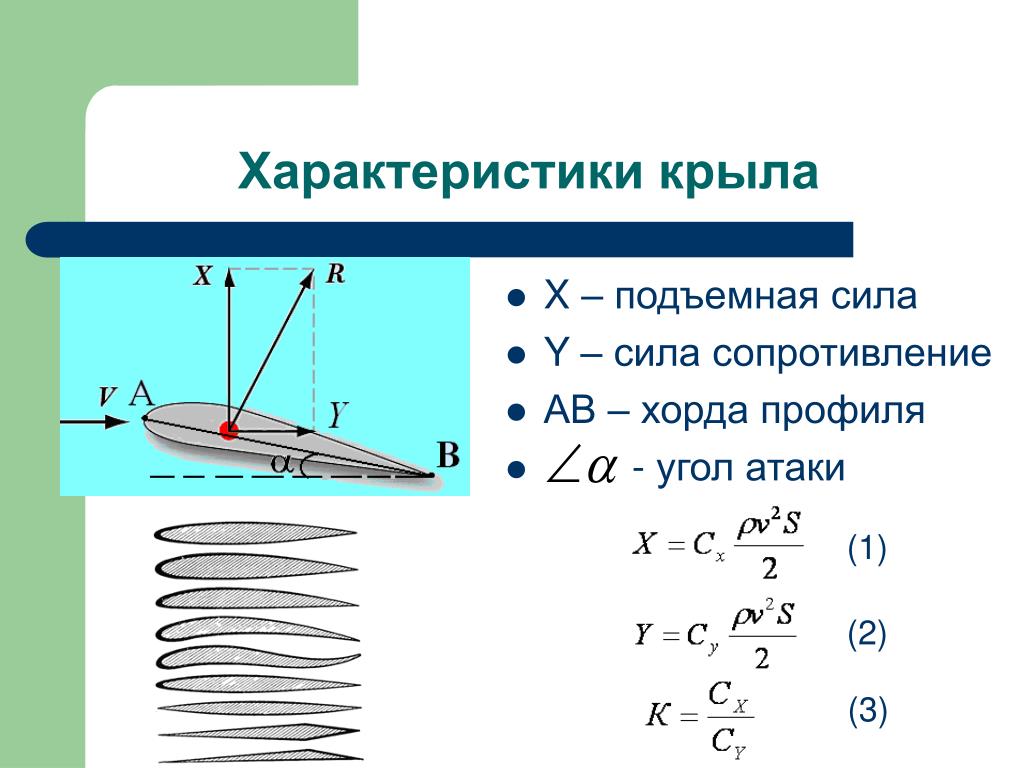 Если не учитывать выталкивающую силу, действующую на тело со стороны воздуха, а внутренней – сила тяжести. Следовательно ∆ E к = A 1 + A 2 , где A 1 = mgh – работа силы тяжести, A 2 = F c hcos 180° = — F c h – работа силы сопротивления; ∆ E = E 2 – E 1 .

Силами сопротивления называются силы, препятствующие движению автомобиля. Эти силы направлены против его движе­ния.

При движении на подъеме, характеризуемом высотой H п, длиной проекции В п на гори­зонтальную плоскость и углом подъема дороги α, на автомобиль действуют следующие силы со­противления (рис. 3.12): сила со­противления качению Р к , равная сумме сил сопротивления каче­нию передних (Р К|) и задних (Р К2) колес, сила сопротивления подъе­му Р п , сила сопротивления воз­духа Д и сила сопротивления раз­гону Р И . Силы сопротивления ка­чению и подъему связаны с особенностями дороги. Сумма этих сил называется силой сопротивления дороги Р Д .

Рис. 3.13. Потери энергии на внутреннее трение в шине:

а — точка, соответствующая мак­симальным значениям нагрузки и прогиба шины

Сила сопротивления качению

Возникновение силы сопротивления качению при движении обусловлено потерями энергии на внутреннее трение в шинах, поверхностное трение шин о дорогу и образование колеи (на деформируемых дорогах).О потерях энергии на внутреннее трение в шине можно судить по рис. 3.13, на котором приведена зависимость между вертикаль­ной нагрузкой на колесо и деформацией шины — ее прогибом f ш .

При движении колеса по неровной поверхности шина, испы­тывая действие переменной нагрузки, деформируется. Линия αО, которая соответствует возрастанию нагрузки, деформирующей шину, не совпадает с линией аО, отвечающей снятию нагрузки. Площадь области, заключенной между указанными кривыми, ха­рактеризует потери энергии на внутреннее трение между отдель­ными частями шины (протектор, каркас, слои корда и др. ).

Потери энергии на трение в шине называются гистерезисом, а линия ОαО — петлей гистерезиса.

Потери на трение в шине необратимы, так как при деформа­ции она нагревается и из нее выделяется теплота, которая рассе­ивается в окружающую среду. Энергия, затрачиваемая на дефор­мацию шины, не возвращается полностью при последующем вос­становлении ее формы.

Сила сопротивления качению Р к достигает наибольшего зна­чения при движении по горизонтальной дороге. В этом случае

где G — вес автомобиля, Н; f — коэффициент сопротивления качению.

При движении на подъеме и спуске сила сопротивления каче­нию уменьшается по сравнению с Р к на горизонтальной дороге, и тем значительнее, чем они круче. Для этого случая движения сила сопротивления качению

где α — угол подъема, °.

Зная силу сопротивления качению, можно определить мощ­ность, кВт,

затрачиваемую на преодоление этого сопротивления:

где v -скорости автомобиля,м/c 2

Для горизонтальной дороги соs0°=1 и

З
ависимости силы сопротивления качениюР к и мощности N К от скорости автомобиля v показаны на рис. 3.14

Коэффициент сопротивления качению

Коэффициент сопротивления качению существенно влияет на потери энергии при движении автомобиля. Он зависит от многих конструктивных и эксплуатационных

Рис 3.15. Зависимости коэффициента сопротивления качению от

Скорости движения (а), давления воздуха в шине (б) и момента, передаваемого через колесо (в)

факторов и определяется экспериментально. Его средние значения для различных дорог при нормальном давлении воздуха в шине составляют 0,01 …0,1.Рассмотрим влияние различных факторов на коэффициент сопротивления качению.

Скорость движения . При изменении скорости движения в ин­тервале 0…50 км/ч коэффициент сопротивления качению изме­няется незначительно и его можно считать постоянным в указан­ном диапазоне скоростей.

При повышении скорости движения за пределами указанного интервала коэффициент сопротивления качению существенно уве­личивается (рис. 3.15, а) вследствие возрастания потерь энергии в шине на трение.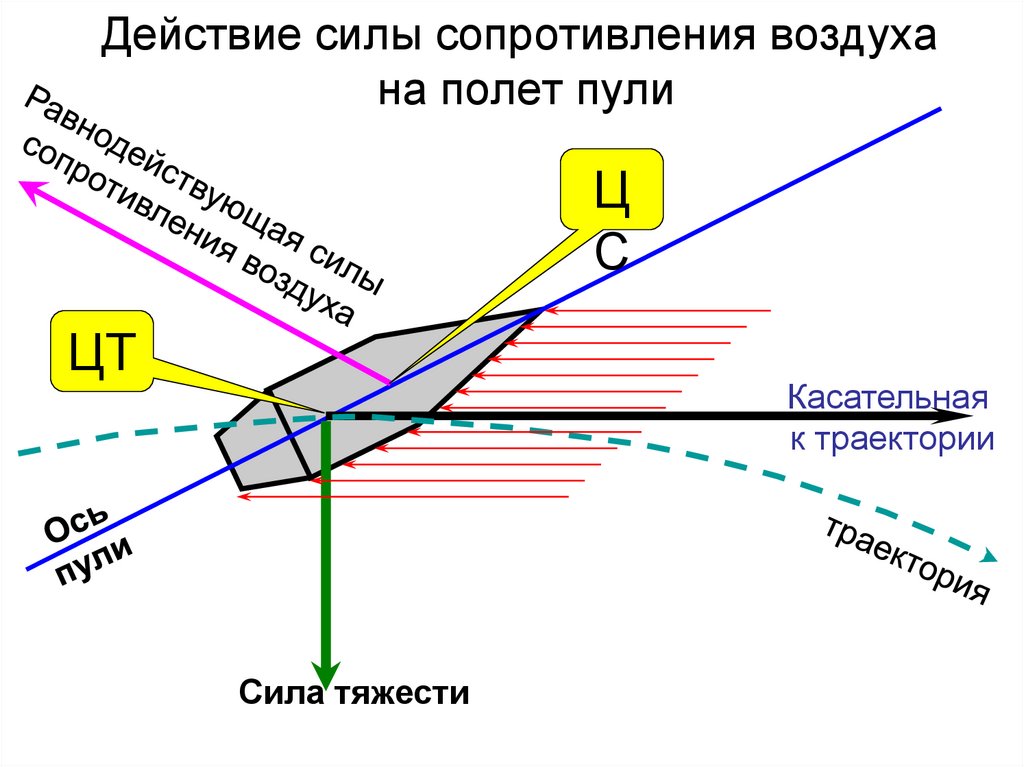

Коэффициент сопротивления качению в зависимости от ско­рости движения можно приближенно рассчитать по формуле

где — скорость автомобиля, км/ч.

Тип и состояние покрытия дороги. На дорогах с твердым по­крытием сопротивление качению обусловлено главным образом деформациями шины.

При увеличении числа дорожных неровностей коэффициент сопротивления качению возрастает.

На деформируемых дорогах коэффициент сопротивления ка­чению определяется деформациями шины и дороги. В этом случае он зависит не только от типа шины, но и от глубины образую­щейся колеи и состояния грунта.

Значения коэффициента сопротивления качению при рекомен­дуемых уровнях давления воздуха и нагрузки на шину и средней скорости движения на различных дорогах приведены ниже:

Асфальто- и цементобетонное шоссе:

в хорошем состоянии………………………………. 0,007…0,015

в удовлетворительном состоянии…………… 0,015…0,02

Гравийная дорога в хорошем состоянии. … 0,02…0,025

Булыжная дорога в хорошем состоянии…… 0,025…0,03

Грунтовая дорога сухая, укатанная………….. 0,025…0,03

Песок………………………………………………………….. 0,1…0,3

Обледенелая дорога, лед…………………………. 0,015…0,03

Укатанная снежная дорога……………………….. 0,03…0,05

Тип шины. Коэффициент сопротивления качению во многом зависит от рисунка протектора, его износа, конструкции каркаса и качества материала шины. Изношенность протектора, уменьше­ние числа слоев корда и улучшение качества материала приводят к падению коэффициента сопротивления качению вследствие снижения потерь энергии в шине.

Давление воздуха в шине . На дорогах с твердым покрытием при уменьшении давления воздуха в шине коэффициент сопро­тивления качению повышается (рис. 3.15, б). На деформируемых дорогах при снижении давления воздуха в шине уменьшается глу­бина колеи, но возрастают потери на внутреннее трение в шине. Поэтому для каждого типа дороги рекомендуется определенное давление воздуха в шине, при котором коэффициент сопротивле­ния качению имеет минимальное значение.

. При увеличении вертикальной нагрузки на колесо коэффициент сопротивления качению существенно возрастает на деформируемых дорогах и незначительно — на до­рогах с твердым покрытием.

Момент, передаваемый через колесо . При передаче момента через колесо коэффициент сопротивления качению возрастает (рис. 3.15, в) вследствие потерь на проскальзывание шины в месте ее контакта с дорогой. Для ведущих колес значение коэффициента сопротивления качению на 10… 15 % больше, чем для ведомых.

Коэффициент сопротивления качению оказывает существен­ное влияние на расход топлива и, следовательно, на топливную экономичность автомобиля. Исследования показали, что даже не­большое уменьшение этого коэффициента обеспечивает ощути­мую экономию топлива. Поэтому неслучайно стремление конст­рукторов и исследователей создать такие шины, при использова­нии которых коэффициент сопротивления качению будет незна­чительным, но это весьма сложная проблема.

Это творческое задание для мастер-класса по информатике для школьников при ДВФУ.
Цель задания — выяснить, как изменится траектория тела, если учитывать сопротивление воздуха. Также необходимо ответить на вопрос, будет ли дальность полёта по-прежнему достигать максимального значения при угле бросания в 45°, если учитывать сопротивление воздуха.

В разделе «Аналитическое исследование» изложена теория. Этот раздел можно пропустить, но он должен быть, в основном, понятным для вас, потому что бо льшую часть из этого вы проходили в школе.
В разделе «Численное исследование» содержится описание алгоритма, который необходимо реализовать на компьютере. Алгоритм простой и краткий, поэтому все должны справиться.

Аналитическое исследование

Введём прямоугольную систему координат так, как показано на рисунке. В начальный момент времени тело массой m находится в начале координат. Вектор ускорения свободного падения направлен вертикально вниз и имеет координаты (0, —g ).
— вектор начальной скорости. Разложим этот вектор по базису: . Здесь , где — модуль вектора скорости, — угол бросания.

Запишем второй закон Ньютона: .
Ускорение в каждый момент времени есть (мгновенная) скорость изменения скорости, то есть производная от скорости по времени: .

Следовательно, 2-й закон Ньютона можно переписать в следующем виде:
, где — это равнодействующая всех сил, действующая на тело.
Так как на тело действуют сила тяжести и сила сопротивления воздуха, то
.

Мы будем рассматривать три случая:
1) Сила сопротивления воздуха равна 0: .
2) Сила сопротивления воздуха противоположно направлена с вектором скорости, и её величина пропорциональна скорости: .
3) Сила сопротивления воздуха противоположно направлена с вектором скорости, и её величина пропорциональна квадрату скорости: .

Вначале рассмотрим 1-й случай.
В этом случае , или .

Из следует, что (равноускоренное движение).
Так как (r — радиус-вектор), то .
Отсюда .
Эта формула есть не что иное, как знакомая вам формула закона движения тела при равноускоренном движении.
Так как , то .
Учитывая, что и , получаем из последнего векторного равенства скалярные равенства:

Проанализируем полученные формулы.
Найдём время полёта тела. Приравняв y к нулю, получим

Дальность полёта равна значению координаты x в момент времени t 0:

Из этой формулы следует, что максимальная дальность полёта достигается при .
Теперь найдём уравнение трактории тела . Для этого выразим t через x

И подставим полученное выражение для t в равенство для y .

Полученная функция y (x ) — квадратичная функция, её графиком является парабола, ветви которой направлены вниз.
Про движение тела, брошенного под углом к горизонту (без учёта сопротивления воздуха), рассказывается в этом видеоролике.

Теперь рассмотрим второй случай: .

Второй закон приобретает вид ,
отсюда .
Запишем это равенство в скалярном виде:

Мы получили два линейных дифференциальных уравнения .
Первое уравнение имеет решение

В чём можно убедиться, подставив данную функцию в уравнение для v x и в начальное условие .
Здесь e = 2,718281828459… — число Эйлера .
Второе уравнение имеет решение

Так как , , то при наличии сопротивления воздуха движение тела стремится к равномерному, в отличие от случая 1, когда скорость неограниченно увеличивается.
В следующем видеоролике говорится, что парашютист сначала движется ускоренно, а потом начинает двигаться равномерно (даже до раскрытия парашюта).

Найдём выражения для x и y .
Так как x (0) = 0, y (0) = 0, то

Нам осталось рассмотреть случай 3, когда .
Второй закон Ньютона имеет вид
, или .
В скалярном виде это уравнение имеет вид:

Это система нелинейных дифференциальных уравнений . Данную систему не удаётся решить в явном виде, поэтому необходимо применять численное моделирование.

Численное исследование

В предыдущем разделе мы увидели, что в первых двух случаях закон движения тела можно получить в явном виде. Однако в третьем случае необходимо решать задачу численно. При помощи численных методов мы получим лишь приближённое решение, но нас вполне устроит и небольшая точность. (Число π или квадратный корень из 2, кстати, нельзя записать абсолютно точно, поэтому при расчётах берут какое-то конечное число цифр, и этого вполне хватает.)

Будем рассматривать второй случай, когда сила сопротивления воздуха определяется формулой. Отметим, что при k = 0 получаем первый случай.

Скорость тела подчиняется следующим уравнениям:

В левых частях этих уравнений записаны компоненты ускорения .
Напомним, что ускорение есть (мгновенная) скорость изменения скорости, то есть производная от скорости по времени.
В правых частях уравнений записаны компоненты скорости. Таким образом, данные уравнения показывают, как скорость изменения скорости связана со скоростью.

Попробуем найти решения этих уравнений при помощи численных методов. Для этого введём на временной оси сетку : выберем число и будем рассматривать моменты времени вида : .

Наша задача — приближённо вычислить значения в узлах сетки.

Заменим в уравнениях ускорение (мгновенную скорость изменения скорости) на среднюю скорость изменения скорости, рассматривая движение тела на промежутке времени :

Теперь подставим полученные аппроксимации в наши уравнения.

Полученные формулы позволяют нам вычислить значения функций в следующем узле сетки, если известны значения этих функций в предыдущем узле сетки.

При помощи описанного метода мы можем получить таблицу приближённых значений компонент скорости.

Как найти закон движения тела, т.е. таблицу приближённых значений координат x (t ), y (t )? Аналогично!
Имеем

Значение vx[j] равняется значению функции , для других массивов аналогично.
Теперь остаётся написать цикл, внутри которого мы будем вычислять vx через уже вычисленное значение vx[j], и с остальными массивами то же самое. Цикл будет по j от 1 до N .
Не забудьте инициализировать начальные значения vx, vy, x, y по формулам , x 0 = 0, y 0 = 0.

В Паскале и Си для вычисления синуса и косинуса имеются функции sin(x) , cos(x) . Обратите внимание, что эти функции принимают аргумент в радианах.

Вам необходимо построить график движения тела при k = 0 и k > 0 и сравнить полученные графики. Графики можно построить в Excel.
Отметим, что расчётные формулы настолько просты, что для вычислений можно использовать один только Excel и даже не использовать язык программирования.
Однако в дальнейшем вам нужно будет решить задачу в CATS, в которой нужно вычислить время и дальность полёта тела, где без языка программирования не обойтись.

Обратите внимание, что вы можете протестировать вашу программу и проверить ваши графики, сравнив результаты вычислений при k = 0 с точными формулами, приведёнными в разделе «Аналитическое исследование».

Поэкспериментируйте со своей программой. Убедитесь в том, что при отсутствии сопротивления воздуха (k = 0) максимальная дальность полёта при фиксированной начальной скорости достигается при угле в 45°.
А с учётом сопротивления воздуха? При каком угле достигается максимальная дальность полёта?

На рисунке представлены траектории тела при v 0 = 10 м/с, α = 45°, g = 9,8 м/с 2 , m = 1 кг, k = 0 и 1, полученные при помощи численного моделирования при Δt = 0,01.

Вы можете ознакомиться с замечательной работой 10-классников из г. Троицка, представленной на конференции «Старт в науку» в 2011 г. Работа посвящена моделированию движения теннисного шарика, брошенного под углом к горизонту (с учетом сопротивления воздуха). Применяется как численное моделирование, так и натурный эксперимент.

Таким образом, данное творческое задание позволяет познакомиться с методами математического и численного моделирования, которые активно используются на практике, но мало изучаются в школе. К примеру, данные методы использовались при реализации атомного и космического проектов в СССР в середине XX века.

Формулы сопротивления воздуха для нескольких сценариев с примером —

Трение между воздухом и другим объектом называется сопротивлением воздуха. Рассмотрим, как определить сопротивление воздуха при падении объекта.

Сопротивление воздуха падающего объекта можно рассчитать, умножив плотность воздуха на коэффициент сопротивления и площадь на два, а затем умножив на скорость.

Гравитация и сопротивление воздуха — две силы естественного поля, которые двигают все на Земле. Формула сопротивления воздуха для сферы, доказательство формулы сопротивления воздуха, формула сопротивления воздуха для свободного падения и то, как получить среднее сопротивление воздуха, будут рассмотрены более подробно.

Скорость, площадь и форма объекта, проходящего через воздух, влияют на сопротивление воздуха. Проверим, как оценить сопротивление воздуха падающего предмета.

Чтобы определить, какое сопротивление воздуха будет испытывать падающий предмет, используйте формулу F _D = 1/2 ρ v ² C _D A. В этом уравнении F _D означает перетаскивание, ρ — плотность жидкости, v — относительная скорость объекта относительно жидкости, C _D — коэффициент сопротивления и A — площадь поперечного сечения.

Задача: Огромный пассажирский самолет летит со скоростью 250 метров в секунду. A = 500 квадратных метров крыльев самолета подвергаются ветру. Коэффициент аэродинамического сопротивления C _D = 0,024. Плотность воздуха ρ = 0,4500 кг на кубический метр на высоте самолета. Какому сопротивлению воздуха подвергается пассажирский самолет?

Решение: Даны следующие данные:

A = 500 квадратных метров

C _D = 0,024

ρ = 0,4500 кг на кубический метр 1/2 ρv ² C _D A

F _D =(0.4500 kg/m ³ × 0.025 × 510.0 m ² )/2 (250.0 m/s) ²

F _D = (0,4500 кг/м ³ × 0,025 × 510,0 м ² )/2 (62500 м ² /с ² )

F _D = 179296 кг·м/с ²

Объект или частица называется снарядом, а его движение называется движением снаряда. Посмотрим, как можно рассчитать сопротивление воздуха при движении снаряда.

Скорость, ускорение и смещение должны быть включены при описании движения снаряда в целом, как описано ниже,

• По осям x и y мы должны расположить их составные части. Предположим, что все силы, кроме силы тяжести, ничтожны.
• Компоненты ускорения тогда чрезвычайно прямолинейны, если положительное направление определено как восходящее, ay = -g = – 0,98 м/с ² (-32 фут/с ² ).
• Поскольку гравитация вертикальна, a _x = 0. a _x = 0 означает, что v _x = v _0x , или что начальная и конечная скорости в направлении x равны.
• При этих ограничениях на ускорение и скорость кинематическое уравнение x (t) = x ₀ + (v _x ) _avg t для движения в однородном гравитационном поле может быть записано через уравнение v ² _y (t) = v ² _oy + 2a _y (y – y ₀ ), куда входят и остальные кинематические уравнения движения с ускорением с постоянным ускорением.
• Кинематические уравнения для движения в однородном гравитационном поле становятся кинематическими уравнениями с х = х ₀ + v _х t.
• Вертикальное движение, y = y ₀ + ½ (v _0y + v _y )t; v _y = v _oy – гт; y = y _o + v _oy t – ½ gt ² , v ² _y = v ² _oy – 2g (y – y _o ).

Задача: Во время фейерверка под углом 75,0 ⁰ над горизонтом с начальной скоростью 70,0 м/с пущен снаряд. Снаряд рассчитан так, что взрыватель сработает именно тогда, когда он будет на максимальной высоте над землей.

• а. Рассчитайте высоту взрыва снаряда.
• б. Через какое время снаряд выстрелит и взорвется?
• г. Что происходит с горизонтальным положением снаряда при его взрыве?
• д. Как далеко в целом продвинулся объект от места запуска до самой высокой точки?

Решение: (a) Под «высотой» мы подразумеваем высоту над начальной точкой или высоту. Когда v _y = 0, достигается высшая точка любой траектории, известная как вершина. Мы используем следующее уравнение, чтобы получить y, потому что мы знаем начальное местоположение, начальную и конечную скорости и начальное положение:

V ² _y = V ² _OY — 2G (Y — Y ₀ )

Уравнение сделано проще из -за того, что Y _O и V _Y — это Zero. .

0 = v ² _oy – 2gy.

Вычислив y, мы получим y = v ² _oy /2g.

Теперь нам нужно выяснить, какова начальная компонента y скорости, или v _0y . Его можно рассчитать по формуле v _0y =v ₀ sin θ, где v ₀ обозначает начальную скорость 70,0 м/с, а θ _o =75° обозначает начальный угол. Таким образом-

v _0y =v ₀ sin θ = (70,0 м/с) sin75 ⁰ = 67,6 м/с и-

y = (67,6 м/с) ^{2 929,28 / м/с 2 )}

y = 233 м.

Начальная вертикальная скорость и максимальная высота положительны, потому что вверх положителен, а ускорение, вызванное силой тяжести, отрицательно. Снаряд с начальной вертикальной составляющей скорости 67,6 м/с достигнет максимальной высоты 233 м. Также имейте в виду, что максимальная высота зависит только от вертикальной составляющей начальной скорости (без учета сопротивления воздуха).

(b) Существуют различные способы определить, когда снаряд достигает высшей точки, как и во многих физических задачах. Самый простой подход в этой ситуации — использовать v _y =v _0y -gt. Это уравнение принимает вид v _y = 0 на вершине

0 = v _0y − gt

или,

t = v _oy /g = (67,6 м/с) / (9,80 м/с 2 )

t = 6,90 с.

Другой способ определения времени — использование y = y _o + ½ (v _0y + v _y ) t.

(c) Сопротивление воздуха мало, следовательно, ax и ay равны нулю. И, как упоминалось ранее, горизонтальная скорость постоянна. Как показывают уравнения x=x ₀ +v _x t, где x ₀ равно нулю, горизонтальное перемещение равно горизонтальной скорости, умноженной на время. Таким образом,

x = v _x t,

.0003

v _x = v ₀ cosθ = (70,0 м/с) cos75°=18,1 м/с.

Поскольку оба движения имеют одинаковое время t, x равно

x = (18,1 м/с) × 6,90 с = 125 м.

Горизонтальное движение без сопротивления воздуха имеет постоянную скорость. Горизонтальное смещение, наблюдаемое здесь, может помочь предотвратить травму зрителей от падающих пиротехнических фрагментов. Немалую роль при взрыве снаряда играет сопротивление воздуха, и многие осколки падают сразу внизу.

(d) Здесь требуется только найти величину и направление смещения в самой высокой точке, так как горизонтальная и вертикальная составляющие смещения уже рассчитаны:

с ^→ = 125 х + 233 х; |ŝ|=√ (125 ² + 233 ² ) = 264 м; Φ = tan ^-1 (233/125) = 61,8°

Сопротивление воздуха эквивалентно по величине весу падающего объекта при конечной скорости. Рассмотрим метод расчета сопротивления воздуха при предельной скорости.

• Используя второй закон Ньютона для падающего объекта в качестве отправной точки, мы можем определить сопротивление воздуха при конечной скорости: F _g + F _ar = ma .
• Для определения сопротивления воздуха при заданной скорости используются следующие два типа сопротивления воздуха: F _ar = – bv альтернативно, F _ar = – bv ² .
• Для расчета сопротивления воздуха при предельной скорости используется закон Ньютона для определения сопротивления воздуха при предельной скорости, поскольку ускорение равно нулю, мг – бв = 0; mg – bv ² = 0.
• Чтобы определить сопротивление воздуха при заданной скорости, ответом на задачу скорости является v _T = mg/b. Альтернативой является то, что v _T = √(мг/б).

Если m представляет массу в килограммах, g — квадрат ускорения свободного падения, а b — произвольная величина.

Проблема: При падении из состояния покоя объект массой 55 кг испытывает силу сопротивления воздуха, определяемую F _ар = -15В ² . Определить конечную скорость объекта.

Решение: Используйте формулу v _T = √ (мг/б) для определения конечной скорости силы сопротивления вида Far = -bv ² . Складывая в уравнение, получаем

v _T = √(55) × (9,81)/15)

v _T = 5,99 м/с