Какие параметры характеризуют состояние газа: Идеальный газ. Параметры состояния газа

Параметры состояния идеального газа

Состояние идеального газа характеризуется тремя параметрами:

1. Давление  скалярная величина, характеризующая отношение силы, действующей по нормали к площадке, к величине этой площадки

, (1)

; .

2. Температура  скалярная величина, характеризующая интенсивность хаотического поступательного движения молекул, и пропорциональная средней кинетической энергии этого движения.

, при(2)

Температурные шкалы

Эмпирическая шкала Цельсия ( t ⁰C): 1⁰C = ⁰C;

Эмпирическая шкала Фаренгейта: .

Пример: t = 36,6⁰C; .

Абсолютная шкала Кельвина:

2. Удельный объем (плотность)

удельный объем это объем вещества массой в 1 кг;

плотность это масса вещества объемом в 1 м³; .

Молекулярно-кинетическая теория газов

1. Все вещества состоят из атомов или молекул, размеры которых порядка 10^-10м.

2.Атомы и молекулы вещества разделены промежутками, свободными от вещества. Косвенным подтверждением этого факта является изменяемость объема тела.

Рис. 2

3.Между молекулами тела одновременно действуют силы взаимного протяжения и силы взаимного отталкивания.

Рис. 3

4.Молекулы всех тел находятся в состоянии беспорядочного непрерывного движения. Хаотическое движение молекул называют также тепловым движением.

Скорость движения молекул связана с температурой тела в целом: чем больше эта скорость, тем выше температура.

Таким образом, скорость движения молекул определяет тепловое состояние тела – его внутреннюю энергию.

16. Основное уравнение молекулярно-кинетической теории газов (уравнение Клаузиуса).

Уравнение состояния идеального газа (Менделеева — Клапейрона) Уравнение Клаузиуса

Вычислим давление, оказываемое молекулами на площадку S.

2-й закон Ньютона:

. (1)

Для одной молекулы:

. (2)

Число молекул в объеме параллелепипеда с основанием S и высотой v_it:

N = n_iV = n_iSv_it (3)

n = N/V – концентрация молекул, равная отношению числа молекул к объему занимаемого ими пространства.

Для молекул, которые передают импульс площадке 

S (в одном из трех взаимно перпендикулярных направлений движется 1/3 молекул, половина из них, т. е. 1/6 – на площадку S)

средняя квадратичная скорость молекул

, (4)

средняя кинетич. энергия поступательного движения молекул

Уравнение Клаузиуса: давление идеального газа численно равно 2/3 средней кинетической энергии поступательного движения молекул, находящихся в единичном объеме.

Уравнение Менделеева — Клапейрона

Это уравнение связывает параметры состояния р, Т, М, V.

,

уравнение Менделеева – Клапейрона (5)

1-й закон Авогадро:

киломоли всех газов при нормальных условиях занимают одинаковый объем, равный 22,4 м³/кмоль. (Если температура газа равна T₀ = 273,15 К (0 °С), а давление p₀ = 1 атм = 1,013·10⁵ Па, то говорят, что газ находится при нормальных условиях. )

Уравнение Менделеева – Клапейрона для 1 моля газа

. (6)

Уравнение Менделеева – Клапейрона для произвольной массы газа

число молей. , (7)

Частные случаи уравнения Менделеева – Клапейрона

1.изотермическое состояние(закон Бойля – Мариотта)

2.изобарное состояние(закон Гей-Люссака)

3.изохорное состояние(закон Шарля)

17. Энергия термодинамической системы. Первый закон термодинамики. Работа, теплота, теплоемкость, ее виды

Энергия – это количественная мера движения материи.

.

Внутренняя энергия системы U равна сумме всех видов энергий движения и взаимодействия частиц, составляющих данную систему.

Работа – это способ передачи энергии, связанный с изменением внешних параметров системы.

Теплота – это способ передачи энергии, связанный с изменением внутренних

параметров системы.

Различия между теплотой и работой:

1. работа может неограниченно превращаться в любой вид энергии, превращение теплоты ограничено рамками 2-го закона термодинамики: она идет только на увеличение внутренней энергии;

2. работа связана с изменением внешних параметров системы, теплота – с изменением внутренних параметров.

Все три величины – энергия, работа и теплота – в системе СИ измеряются в джоулях (Дж).

Квантовые газы при низких температурах

На прошлой неделе у нас вышло сразу три новости [1, 2 и 3], которые так или иначе были связаны с конденсатом Бозе-Эйнштейна — состоянием, в которое переходит газ бозонов при низких температурах. Поскольку формат новости не позволяет подробно объяснять каждое слово, мы рассказали, что это такое, только в общих чертах. На этот раз мы поговорим о конденсате бозонов более подробно, а заодно вспомним про ферми-газ и квазичастицы.

Прежде чем перейти к обсуждению собственно квантовых газов, рассмотрим обычную, классическую систему. Как мы знаем, газ состоит из большого числа хаотически двигающихся по доступному пространству частиц. Температура такой системы — это средняя кинетическая энергия одной частицы (с точностью до множителя, который нас не интересует), давление — средняя сила, с которой частицы давят на стенки, когда ударяются и отскакивают от них. И хотя свойства каждой из частиц постоянно меняются, эти средние величины все время остаются примерно постоянными и характеризуют макроскопическое состояние газа.

Если придерживаться классических законов механики и считать частицы точечными, можно связать между собой известные макроскопические параметры и получить уравнение состояния идеального газа.

Окажется, что температура пропорциональна произведению объема и давления. Эмпирически эту зависимость еще в 1834 году обнаружил Эмиль Клапейрон, теоретически (с использованием молекулярной кинетической теории) ее обосновали Август Крёниг и Рудольф Клаузиус в конце 1850-х.

Однако классические законы работают только при больших температурах. Дело в том, что при таких температурах диапазон энергий, доступных отдельно взятой частице, большой. Грубо говоря, энергия и импульс — а значит, и квантовые состояния разных частиц — хоть чуть-чуть, но отличаются, и из-за этого частицы в принципе можно отличить друг от друга.

Еще можно сказать, что велико число доступных для системы ячеек в фазовом пространстве. Фазовое пространство — это такое пространство, в котором по осям отложены как координаты, так и импульсы всех частиц системы. Поэтому точка, выбранная в нем, однозначно характеризует состояние системы. Правда, из-за принципа неопределенности Гейзенберга одновременно зафиксировать и координату, и импульс нельзя — произведение их неопределенностей не может быть меньше ħ/2.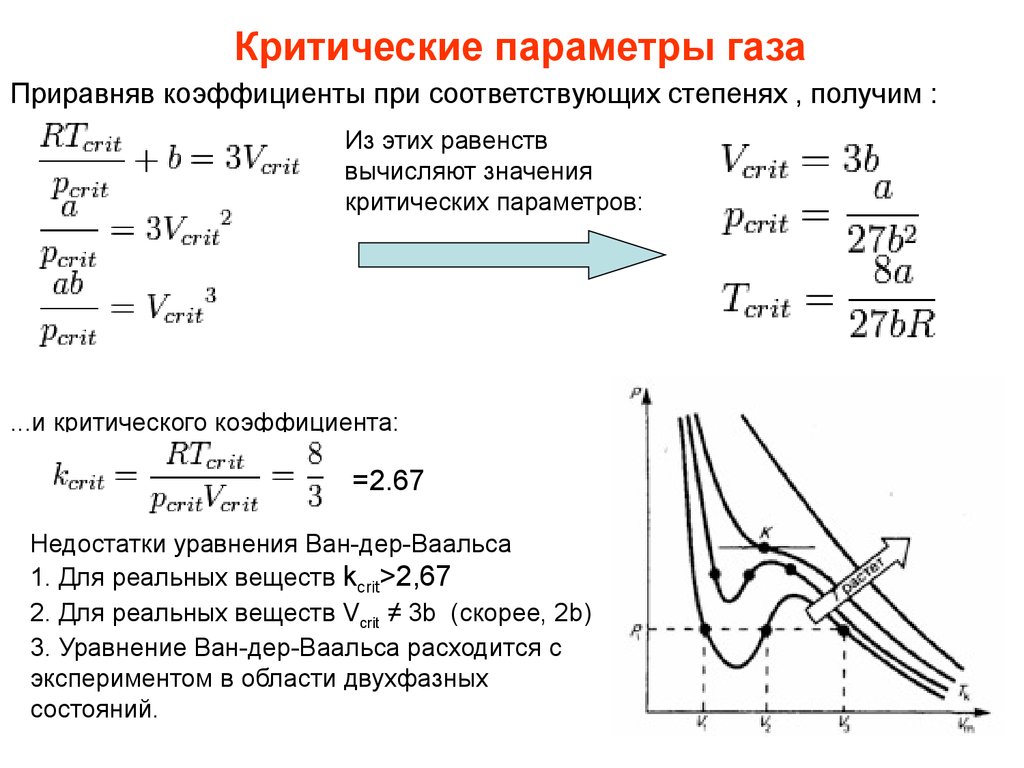

Поэтому фазовое пространство разбивается на ячейки объемом (2πħ)^N, где N — число частиц системы.

При понижении температуры все больше частиц переходят в состояния с одинаковыми энергиями, отличить их друг от друга становится сложнее, и из-за этого начинают сказываться квантовые свойства системы. Как известно, все частицы подчиняются либо статистике Бозе-Эйнштейна (тогда частицы называют бозонами), либо статистике Ферми-Дирака (фермионы). В первом случае волновая функция системы, состоящей из одинаковых бозонов, не будет меняться при перестановке двух частиц. Во втором случае при перестановке она будет менять знак. Проще говоря, два фермиона не могут одновременно находиться в одном квантовом состоянии (принцип запрета Паули), а бозоны могут.

Из-за этого в газе фермионов появляется эффективное отталкивание — частицы вынуждены иметь разные импульсы. При нулевой температуре все частицы располагаются внутри так называемой ферми-сферы, то есть их импульсы лежат в диапазоне от нуля до некоторого определенного значения. При отличной от нуля температуре это распределение немного «размывается». В идеальном газе, на минутку, при нулевой температуре импульсы всех частиц равнялись бы просто нулю. Поэтому при равных объемах и температуре давление в ферми-газе будет больше, чем в аналогичном классическом газе — уравнение состояния меняется.

В газе бозонов, наоборот, наблюдаются обратные эффекты. В нем частицам ничто не мешает собраться всем вместе в самом низком энергетическом состоянии, и они с радостью это делают — можно сказать, что возникает эффективное притягивание. Собственно, это квантовое состояние, в котором одновременно находится большое (как говорят, макроскопическое) число частиц, и называется конденсатом Бозе-Эйнштейна. Чем меньше температура, тем больше бозонов переходит в конденсат, при нулевой температуре в нем находятся все частицы системы.

Конечно, в жизни все немного интереснее — между частицами в квантовых газах есть взаимодействие. И чем меньше температура, тем большую роль оно играет. Вообще говоря, если сила взаимодействия каким-то хитрым образом зависит от расстояния между частицами и от их числа, учесть ее сложно. Однако в некоторых случаях это можно сделать с помощью квазичастиц — возбуждений, распространяющихся в газе реальных частиц.

Для того чтобы описывать взаимодействие было удобнее, вводят операторы рождения и уничтожения частиц с заданным импульсом, то есть переходят к представлению вторичного квантования. Оператор уничтожения устроен таким образом, что при действии на состояние системы, в котором находится n частиц, он возвращает состояние, в котором находится n-1 частица, умноженное дополнительно на √n. Оператор рождения действует в обратную сторону.

Коммутатор операторов рождения и уничтожения бозонов равен нулю, если импульсы частиц отличаются, и единице, если они совпадают. Другими словами, эти операторы можно переставлять, но только в том случае, если их импульсы отличаются. У фермионов при перестановке операторов необходимо менять знак выражения, то есть теми же свойствами обладает антикоммутатор. Собственно, этот факт отражает отличия в симметрии волновых функций систем бозонов и фермионов.

Из-за того, что мы добавили в систему взаимодействие, ее гамильтониан становится недиагональным. Гамильтониан — это оператор, который описывает энергию системы в различных квантовых состояниях. Чтобы привести его снова к диагональному виду, делают поворот — заменяют операторы рождения и уничтожения частиц на сумму новых операторов с некоторыми коэффициентами. При этом также надо следить за тем, чтобы выполнялись коммутационные соотношения операторов.

Эти новые операторы рождения-уничтожения как раз и описывают квазичастицы. С их помощью можно объяснить такие явления, как сверхтекучесть и сверхпроводимость, если посмотреть, как они ведут себя во внешнем поле и при понижении температуры. Например, в бозе-газе при низких температурах энергия квазичастиц будет пропорциональна их импульсу, то есть это звуковые колебания — фононы. Наоборот, при сравнительно больших температурах квазичастицы приобретают массу. В ферми-газе энергетический спектр квазичастиц еще сложнее.

Впрочем, неидеальные бозе- и ферми-газы — это отдельная большая история. Наверное, про них как-нибудь в другой раз.

Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

Газовые законы: Обзор — Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1517

Созданные в начале 17 века газовые законы помогали ученым определять объемы, количество, давление и температуру при работе с газами. Газовые законы состоят из трех основных законов: закона Чарльза, закона Бойля и закона Авогадро (все они позже будут объединены в общее газовое уравнение и закон идеального газа).

Введение

Три фундаментальных газовых закона раскрывают взаимосвязь между давлением, температурой, объемом и количеством газа. Закон Бойля говорит нам, что объем газа увеличивается с уменьшением давления. Закон Чарльза говорит нам, что объем газа увеличивается с повышением температуры. А закон Авогадро говорит нам, что объем газа увеличивается по мере увеличения количества газа. Закон идеального газа представляет собой комбинацию трех простых газовых законов.

Идеальные газы

Идеальный газ, или совершенный газ, является теоретической субстанцией, которая помогает установить взаимосвязь между четырьмя газовыми переменными: давлением (P), объемом (V) , количеством газа (n) и температурой (T) . Его символы описываются следующим образом:

1. Частицы в газе чрезвычайно малы, поэтому газ не занимает места.
2. Идеальный газ имеет постоянное, хаотическое и прямолинейное движение.
3. Нет сил между частицами газа. Частицы только упруго сталкиваются друг с другом и со стенками сосуда.

Реальные газы

Реальный газ, напротив, имеет реальный объем и столкновение частиц не является упругим, поскольку между частицами существуют силы притяжения. В результате объем реального газа намного больше, чем у идеального газа, а давление реального газа ниже, чем у идеального газа. Все реальные газы ведут себя как идеальные газы при низком давлении и относительно высокой температуре.

Коэффициент сжимаемости (Z) (Z) говорит нам, насколько реальные газы отличаются от поведения идеальных газов.

\[ Z = \dfrac{PV}{nRT} \]

Для идеальных газов \( Z = 1 \). Для реальных газов \( Z\neq 1 \).

Закон Бойля

В 1662 году Роберт Бойль обнаружил корреляцию между Давлением (P) и Объемом (V) (при условии, что Температура (T) и 90 032 Количество газа(n) осталось константа):

\[ P\propto \dfrac{1}{V} \rightarrow PV=x \]

где x — константа, зависящая от количества газа при данной температуре.

• Давление обратно пропорционально объему

Другая форма уравнения (при наличии двух наборов условий и сопоставлении обеих констант друг с другом), которая может помочь в решении задач:

Образец газа объемом 17,50 мл находится под давлением 4500 атм. Какой будет объем, если давление станет 1500 атм при фиксированном количестве газа и температуре?

Раствор

\[ V_2= \dfrac {P_1 \centerdot V_1}{P_2} \] \[ =\dfrac{4,500 атм \centerdot 17,50 мл}{1,500 атм} \] \[ = 52,50 мл \]

Закон Шарля

В 1787 году французские физики Жак Шарль обнаружили корреляцию между Температура (T) и Объем (V) (при условии, что Давление (P) и Количество Газ(н) остаются постоянными):

\[ V \propto T \rightarrow V=yT \]

где y — константа, зависящая от количества газа и давления. Объем прямо пропорционален температуре

Другая форма уравнения (при условии, что есть 2 набора условий и привязка обеих констант друг к другу), которая может помочь решить проблемы:

\[ \dfrac{V_1}{T_1} = y = \dfrac{V_2}{T_2} \]

Пример 1.2
Образец углекислого газа в насосе имеет объем 20,5 мл и температуру 40,0 o C. Если количество газа и давление остаются постоянными, найдите новый объем углекислого газа в насосе при повышении температуры до 65,0 o C. СУТИОН \[ V_2=\dfrac{V_1 \centerdot T_2}{T_1}\] \[ =\dfrac{20,5 мл \centerdot (60+273,15K)}{40+273,15K}\] \[ = 22,1 мл \]

Закон Авогадро. остаются постоянными):

\[ V \propto n \rightarrow V = zn\]

где z — константа, зависящая от давления и температуры.

• Объем (V) прямо пропорционален количеству газа (n)

Другая форма уравнения (при условии, что есть 2 набора условий и привязка обеих констант друг к другу), которая может помочь решить проблемы:

\[ \dfrac{P_1}{n_1} = z= \dfrac{P_2}{n_2}\]

Пример 1.3
3,80 г газообразного кислорода в насосе имеет объем 150 мл. постоянная температура и давление. Если в насос добавлено 1,20 г газообразного кислорода. Каким будет новый объем газообразного кислорода в насосе, если температура и давление останутся постоянными? Раствор V 1 =150 мл \[ n_1= \dfrac{m_1}{M_кислород} \] 9-1} \] \[ = 197мл\]

Закон идеального газа представляет собой комбинацию трех законов простого газа. Установив все три закона прямо или обратно пропорционально Volume, вы получите:

\[ V \propto \dfrac{nT}{P}\]

Далее, заменив знак прямо пропорционально на константу (R), вы получите:

\[ V = \dfrac{RnT}{P}\]

И, наконец, получим уравнение:

\[ PV = nRT \]

где P= абсолютное давление идеального газа

• V= объем идеального газа
• n = количество газа
• T = абсолютная температура
• R = газовая постоянная

Здесь R называется газовой постоянной. Значение R определяется по результатам экспериментов. Его числовое значение изменяется с единицами измерения.

R = газовая постоянная = 8,3145 Дж · моль ^-1 · K ^-1 (единица СИ)
= 0,082057 л · атм·K ^{— 1} · моль ^{— 1}

Пример 1.4
При 655 мм рт. ст. и 25,0 o C образец газообразного хлора имеет объем 750 мл. Сколько молей газообразного хлора при этих условиях? P=655 мм рт.ст. Т=25+273.15К V=750 мл=0,75 л н=? Решение \[ n=\frac{PV}{RT} \] 9-1 \centerdot (25+273,15K) }\] \[ =0,026 моль\]

Расчет газовой постоянной, R

Числовое значение газовой постоянной, R, можно получить из уравнения идеального газа PV=nRT. При стандартной температуре и давлении, где температура 0 ^o С, или 273,15 К, давление при 1 атм, а при объеме 22,4140 л,

\[ R= \frac{PV}{RT} \]

\[ \frac{1 атм \centerdot 22,4140L}{1 моль \centerdot 273,15K} \] 9{-1} \]

Общее уравнение газа

В ситуации с идеальным газом \( \frac{PV}{nRT} = 1 \) (при условии, что все газы «идеальны» или совершенны). В случаях, когда \( \frac{PV}{nRT} \neq 1 \) или при наличии нескольких наборов условий (давление (P), объем (V), количество газа (n) и температура (T)) , используйте общее газовое уравнение:

Предполагая 2 набора условий:

Начальный случай: Окончательный случай:

\[ P_iV_i = n_iRT_i \; \; \; \; \; \; P_fV_f = n_fRT_f \]

Присвоив обеим сторонам значение R (которое является константой с одинаковым значением в каждом случае), можно получить:

\[ R= \dfrac{P_iV_i}{n_iT_i} \; \; \; \; \; \; R= \dfrac{P_fV_f}{n_fT_f} \]

Если заменить одно R на другое, то получится итоговое уравнение и общее уравнение газа:

\[ \dfrac{P_iV_i}{n_iT_i} = \dfrac {P_fV_f}{n_fT_f} \]

Стандартные условия

Если в каком-либо из законов переменная не указана, считать, что она задана. Для постоянной температуры, давления и количества:

1. Абсолютный ноль (Кельвин): 0 K = — 273,15 ^или С

T(K) = T( ^o C) + 273,15 (единица измерения температуры должна быть в Кельвинах)

2. Давление: 1 атмосфера (760 мм рт.ст.)

3. Количество: 1 моль = 22,4 л газа

4. В законе идеального газа газовая постоянная R = 8,3145 Дж · моль ^-1 · К ^-1
= 0,082057 л · атм·К ^{— 1} · моль ^{— 1}

Уравнение Ван-дер-Ваальса для реальных газов 92} \) корректирует давление реального газа на действие сил притяжения между молекулами газа.

Точно так же, поскольку молекулы газа имеют объем, объем реального газа намного больше, чем у идеального газа, поправочный член \(1 -nb \) используется для корректировки объема, заполненного молекулами газа.

Практические задачи

1. Если 4 л газа H ₂ при 1,43 атм имеют стандартную температуру, а давление увеличилось в 2/3 раза, каков конечный объем H ₂ газ? (Подсказка: закон Бойля)
2. Если 1,25 л газа существует при температуре 35 ^o C и постоянном давлении 0,70 атм в цилиндрическом блоке, а объем необходимо умножить на коэффициент 3/5, какова новая температура газа? (Подсказка: закон Чарльза)
3. Баллон с 4,00 г газообразного гелия имеет объем 500 мл. Когда температура и давление остаются постоянными. Каков будет новый объем гелия в баллоне, если добавить в баллон еще 4,00 г гелия? (Подсказка: Закон Авогадро)

Решения

1. 2.40L

Для решения этого вопроса необходимо использовать закон Бойля: температура и количество газа постоянны и поэтому можно отложить в сторону, необходимы только:

1. Начальное давление: 1,43 атм
2. Начальный объем: 4 л
3. Конечное давление: 1,43×1,67 = 2,39
4. Последний том (неизвестно): V ₂

Подставив эти значения в уравнение, вы получите:

В ₂ = (1,43 атм x 4 л)/(2,39 атм) = 2,38 л

2, 184,89 К

90 023 Чтобы решить этот вопрос, вам нужно используйте закон Чарльза:

Еще раз помните о ключевых переменных. Давление оставалось постоянным, и, поскольку количество газа не упоминается, мы предполагаем, что оно остается постоянным. В противном случае ключевые переменные:

1. Начальный объем: 1,25 л
2. Начальная температура: 35 ^o C + 273,15 = 308,15K
3. Конечный объем: 1,25 л*3/5 = 0,75 л
4. Конечная температура: T ₂

Поскольку нам нужно решить для конечной температуры, вы можете изменить порядок Чарльза:

После подстановки чисел вы получите: T ₂ = (308,15 K x 0,75 л) / (1,25 л) = 184,89 K

3. 1000 мл или 1 л

Используя закон Авогадро для решения этой задачи, вы можете преобразовать уравнение в \( V_2=\frac{n_1\centerdot V_2}{n_2} \). Однако вам нужно преобразовать граммы газообразного гелия в моли.

\[ n_1 = \frac{4,00г}{4,00г/моль} = \text{1 моль} \]

Аналогично, n ₂ =2 моль

\[ V_2=\frac{n_2 \centerdot V_2}{n_1}\]

\[ =\frac{2 моль \centerdot 500 мл}{1 моль}\]

\[ = \text{1000 мл или 1 л } \]

Ссылки

1. Petrucci, Ральф Х. Общая химия: принципы и современные приложения . 9-е изд. Река Аппер-Сэдл, Нью-Джерси: Pearson Prentice Hall, 2007.
.
2. Стейли, Деннис. Прентис Холл Химия . Бостон, Массачусетс: Пирсон Прентис Холл, 2007.
.

3. Оландер, Дональд Р. «Глава 2 Уравнение состояния». Общая термодинамика . Бока-Ратон, Северо-Запад: CRC, 2008. Печать

   .

4. О’Коннелл, Джон П. и Дж. М. Хейл. «Свойства относительно идеальных газов». Термодинамика: основы приложений . Кембридж: Cambridge UP, 2005. Печать.

5. Гаре, Шакунтала. «Законы идеального газа для одного компонента». Закон идеального газа, энтальпия, теплоемкость, теплота растворения и смешения . Том. 4. Нью-Йорк, 1984. Печать. Ф.

Внешние ссылки

• http://en.Wikipedia.org/wiki/Gas_laws
• www.chem.queensu.ca/people/faculty/mombourquette/firstyrchem/GasLaws/index. htm
• vimeo.com/10588774

---

Законы о газе: обзор распространяется под лицензией CC BY-NC-SA 4.0 и был создан, изменен и/или курирован LibreTexts.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   № на стр.

2. Теги

   На этой странице нет тегов.

Определение уравнения состояния (EOS)

Печать

В предположении состояния равновесия три свойства, необходимые для полного определения состояния системы, — это давление (P), объем (V) и температура (T). Следовательно, мы должны быть в состоянии сформулировать уравнение, связывающее эти 3 переменные, в форме f(P,T,V)=0.

Уравнение состояния (EOS) представляет собой функциональную связь между переменными состояния — обычно полным набором таких переменных. Большинство УС написано, чтобы выразить функциональные отношения между P, T и V. Верно также и то, что большинство УС по-прежнему являются эмпирическими или полуэмпирическими. Отсюда определение:

Уравнение состояния (УС) представляет собой полуэмпирическую функциональную зависимость между давлением, объемом и температурой чистого вещества. Мы также можем применить EOS к смеси, вызвав соответствующие правила смешивания.

Было предпринято несколько попыток вывести теоретически обоснованное EOS; но, вообще говоря, больших успехов на этом пути достигнуто не было. В результате мы используем то, что известно как полуэмпирический EOS. Большинство используемых сегодня уравнений состояния носят полуэмпирический характер, потому что они подгоняются под доступные данные. Кроме того, уравнения состояния обычно разрабатывают для чистых веществ. Их применение к смесям требует дополнительной переменной (состава) и, следовательно, соответствующего правила смешивания.

Функциональная форма EOS может быть выражена следующим образом:

f(P,V,T,ak=1,np)=0Это уравнение отображается неправильно из-за несовместимого браузера. Список совместимых браузеров см. в разделе «Технические требования» в руководстве. (7.4)

, где a _k = параметры EOS.

Как мы уже говорили ранее, большинство применяемых УС сегодня являются полуэмпирическими в том смысле, что они имеют некоторую теоретическую основу, но их параметры (a _k ) должны быть скорректированы. Количество параметров (n _p ) определяет категорию/сложность EOS. Например, 1-параметрические УС — это те, для которых n _p = 1, а 2-параметрические УС — те, для которых n _p = 2. Чем выше «n _p », тем сложнее УС. . Кроме того, в общих чертах, чем сложнее EOS, тем она точнее. Тем не менее, это не всегда так; в некоторых случаях довольно простой EOS может сделать очень хорошую работу.

Со времен закона идеального газа (EOS идеального газа) было предложено большое количество уравнений состояния для описания поведения реального газа. Однако многие из них не прошли проверку временем. Лишь немногие сохранились на протяжении многих лет из-за их относительной простоты. В нефтяном бизнесе наиболее распространенными современными EOS являются Peng Robinson EOS (PR EOS) и Soave-Redlich-Kwong EOS (SRK EOS). Оба они являются кубическими уравнениями состояния и, следовательно, производными уравнения состояния Ван-дер-Ваальса, которое мы обсудим далее. Есть и другие, более сложные ЭОС, хотя широкого применения в нашей сфере они пока не нашли:

• Ли Кеслер EOS (LK EOS)
• Бенедикт-Уэбб-Рубин EOS (BWR EOS)
• Бенедикт-Уэбб-Рубин-Старлинг EOS (BWRS EOS)

В сфере природного газа, особенно в сфере транспортировки газа, стандартным EOS является AGA EOS; это сверхточный EOS для расчетов Z-фактора — очень чувствительной переменной для операций коммерческого учета.