Определение коэффициента лобового сопротивления самолета.
Коэффициент лобового сопротивления компоновки самолета, симметричного относительно плоскости X0Z () при углах атакидля самолета с крылом малого удлинения,для самолета с крылом большого удлинения, определяется как сумма коэффициентов лобового сопротивления при нулевой подъемной силе -и индуктивного сопротивления: .
Коэффициент рассчитывается по формуле:
— коэффициенты лобового сопротивления с учетом интерференции фюзеляжа с крылом, горизонтальным и вертикальным оперениями;
-коэффициент, учитывающий дополнительное сопротивление, обусловленное технологическими неровностями поверхности (стыковочные узлы, люки, царапины) , = 0.003 …0.004 ;
К – поправочный коэффициент, уточняющий формулу на неучтенные факторы,
К =1.05 …1.1.
— коэффициент индуктивного сопротивления самолета,
где А – коэффициент отвала поляры,
—
коэффициент подъемной силы самолета.
Определение коэффициента лобового сопротивления фюзеляжа при нулевой подъемной силе.
Коэффициент лобового сопротивления фюзеляжа самолета при нулевой подъемной силе отличается от соответствующего коэффициента изолированного фюзеляжаувеличением донного сопротивления в диапазоне чисел Маха, что учитывается при расчете коэффициента донного сопротивления фюзеляжа
Расчет коэффициента лобового сопротивления изолированного фюзеляжа при нулевой подъемной силе выполняется по соотношению:
где — коэффициент лобового сопротивления трения,
— коэффициент лобового сопротивления давления.
Коэффициент лобового сопротивления трения определяется по формуле:
где — коэффициент сопротивления трения плоской пластины в несжимаемом потоке для полностью турбулентного пограничного слоя,
— число Рейнольдса, рассчитанное по длине фюзеляжа ,
— коэффициент, учитывающий влияние сжимаемости (снимается с графика),
— коэффициент формы, учитывающий отличие фюзеляжа от плоской пластины (снимается с графика),
— площадь омываемой поверхности фюзеляжа (боковой, без площади поверхности донного среза),
—
кинематический коэффициент вязкости,
определяемый по таблице стандартной
атмосферы в зависимости от высоты
полета.
фюз |
|
К | 1,05 |
xt | 0,5 |
Fф | 64,45919807 |
Sбокнос | 9,124755862 |
Sбокцил | 47,10346945 |
Sбоккорм | 8,230972752 |
M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
Reф | 6,93E+07 | 8,08E+07 | 9,24E+07 | 1,85E+08 | 2,08E+08 | 2,31E+08 |
V∞ | 179,7192 | 209,6724 | 239,6256 | 479,2512 | 539,1576 | 599,064 |
2Cf | 0,0025 | 0,0024 | 0,0023 | 0,0022 | 0,0021 | |
ημ | 0,98 | 0,96 | 0,95 | 0,9 | 0,82 | 0,8 |
ηλ | 1,08 |
|
|
|
|
|
Cxa0фтр | 0,052861174 | 0,043152 | 0,04099438 | 0,037218582 | 0,032435904 | 0,030206 |
Коэффициент сопротивления давления определяется по формуле:
где
— соответственно коэффициенты сопротивления
носовой и кормовой частей, донного
сопротивления.
Коэффициент сопротивления носовой частиопределяется по графикам в зависимости от числа Маха и.
Коэффициент сопротивления кормовой части фюзеляжа форма обводов кормовой части), определяется по графику Коэффициент сопротивления донного среза при неработающем двигателе определяется для всех значений числаМ по формуле:
,
где – площадь донного среза,- диаметр донного среза,– коэффициент донного давления.
При М< 0.8 ,
— коэффициент, учитывающий влияние удлинения и сужения кормовой части, — коэффициент трения плоской пластины, определяемый по числу.
При М>0.8 определяется по графикам в зависимости от числа Маха, коэффициенттакже снимается по графикам.
M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
√(M-1)/λнос | 0,428668942 | 0,3826636 | 0,321501706 | 0,669259171 | 0,801966157 | ё |
(Cханос)при ϕ=1 | 0 | 0 | 0 | 0,104798949 | 0,074651306 | 0,068909 |
Cхакорм | 0,045 | 0,045 | 0,06 | 0,075 | 0,065 | 0,051 |
Коэффициент сопротивления донного среза фюзеляжа:
M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
1-ηкорм | 0,21853068 |
|
|
|
|
|
Kη | 0,18 | 0,18 | 0,18 | 0,42 | 0,5 | 0,55 |
Cр дон | -0,3233 | -0,3542 | -0,3615 | -0,28 | -0,27 | -0,2 |
Cxдон | 0,026020793 | 0,0285044 | 0,029092131 | 0,052573439 | 0,060352163 | 0,049176 |
Cxaфдавл | 0,07102079 | 0,073504 | 0,08909213 | 0,23237239 | 0,20000347 | 0,16908 |
Cxa0ф | 0,123881967 | 0,1166563 | 0,13008651 | 0,26959097 | 0,232439373 | 0,199291 |
Расчет
коэффициента лобового сопротивления
несущей поверхности (крыла, ГО, ВО) при
нулевой подъемной силе.
Коэффициент лобового сопротивления изолированной несущей поверхности при нулевой подъемной силе определяется по формуле:
где — коэффициент профильного сопротивления, состоящий из сопротивления трения и сопротивления давления, обусловленного перераспределением давления из-за влияния вязкости;- коэффициент волнового сопротивления, обусловленный потерями полного давления (потерями энергии) в скачках уплотнения и перераспределением давления на сверхзвуковых скоростях.
Коэффициент профильного сопротивления:
(4.13)
где — коэффициент, учитывающий долю несущей поверхности= 2.
— коэффициент, учитывающий влияние на профильное сопротивление толщины профиля снимается с графика ,
— коэффициент, учитывающий влияние числа Маха берется с графика.
Коэффициент
трения плоской пластины
(верхняя
и нижняя поверхность) определяется по
графику .
Число Рейнольдса для рассматриваемой несущей поверхности ,- средняя аэродинамическая хорда консольной части несущей поверхности (крыла, ГО, ВО). Как и в случае расчета коэффициента сопротивления трения фюзеляжа, для несущей поверхности принимаем пограничный слой турбулентным. Некоторое завышение коэффициента сопротивления допускается, что определяет запас тяги двигателя.
Крыло
M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
Reф | 6,93E+07 | 8,08E+07 | 9,24E+07 | 1,85E+08 | 2,08E+08 | 2,31E+08 |
V∞ | 179,7192 | 209,6724 | 239,6256 | 479,2512 | 539,1576 | 599,064 |
Cf | 0,0015 | 0,00125 | 0,0012 | 0,00115 | 0,0011 | 0,00105 |
Cхар | 0,00304584 | 0,0025382 | 0,002436672 | 0,002335144 | 0,002233616 | 0,002132 |
Вертикальное оперение
M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
Reф | 6,93E+07 | 8,08E+07 | 9,24E+07 | 1,85E+08 | 2,08E+08 | 2,31E+08 |
V∞ | 179,7192 | 209,6724 | 239,6256 | 479,2512 | 539,1576 | 599,064 |
Cf | 0,0015 | 0,0015 | 0,0015 | 0,0011 | 0,001 | 0,001 |
Cхар | 0,003046 | 0,00304584 | 0,00304584 | 0,002233616 | 0,002031 | 0,002031 |
Горизонтальное оперение
M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
Reф | 6,93E+07 | 8,08E+07 | 9,24E+07 | 1,85E+08 | 2,08E+08 | 2,31E+08 |
V∞ | 179,7192 | 209,6724 | 239,6256 | 479,2512 | 539,1576 | 599,064 |
Cf | 0,0015 | 0,0015 | 0,0015 | 0,0011 | 0,001 | 0,001 |
Cхар | 0,003046 | 0,003046 | 0,003046 | 0,002234 | 0,002031 | 0,002031 |
Коэффициент волнового сопротивления несущей поверхности определяется по соотношению
где
— коэффициент волнового сопротивления
несущей поверхности с ромбовидным
профилем.
Зависимостипредставлены на графиках и позволяют
определить коэффициент.
Коэффициенты, учитывающие влияние на волновое сопротивление формы профиля крыла бесконечного размаха –К,(так как форма профиля — синусоидальная), конечного размаха крыла — снимается с графика и зависит от .
Для ориентировочной оценки коэффициента волнового сопротивления крыла сложной формы в плане исходное крыло разбивают на 2 вспомогательных простых крыла с постоянной стреловидностью по передней кромкеи площадью в плане. Коэффициент волнового сопротивления рассчитывается по формуле
где — коэффициент волнового сопротивленияn-го вспомогательного простого крыла,
K -коэффициент, учитывающий влияние интерференции на волновое сопротивление крыла. В приближенных расчетах можно принять K = 1.15…1.2.
Коэффициент волнового сопротивления крыла:
| 1,6 | 1,8 | 2 |
Cxaвлромб | 0,0297216 | 0,02575872 | 0,024343 |
Cxaвл | 0,0297216 | 0,033057024 | 0,025804 |
Коэффициент волнового сопротивления ВО:
| 1,6 | 1,8 | 2 |
Cxaвлромб | 0,022722812 | 0,016896 | 0,013983 |
Cxaвл | 0,022874297 | 0,021402 | 0,018644 |
Коэффициент волнового сопротивления ГО:
| 1,6 | 1,8 | 2 |
Cxaвлромб | 0,022723 | 0,016896 | 0,013983 |
Cxaвл | 0,022874 | 0,021402 | 0,018644 |
Сха0 | 0,01704802 | 0,01583 | 0,01726748 | 0,03278182 | 0,02846074 | 0,02463 |
Определение коэффициента индуктивного сопротивления самолета
Коэффициент индуктивного сопротивления самолета определяется соотношением
где А — коэффициент отвала поляры первого рода,
—
коэффициент подъемной силы самолета.
В пределах линейной зависимости коэффициент,
где — производная коэффициента подъемной силы по углу атаки.
Тогда ,
где при заданном значении произведение.
Отвал поляры при отсутствии подсасывающей силы для всех чисел Маха определяется:
, где
| 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
А | 0,39808507 | 0,3763637 | 0,362863317 | 0,469079925 | 0,435848765 | 0,487484 |
Kmax | 6,069390174 | 6,4776973 | 6,316608962 | 4,032088346 | 4,489303768 | 4,562783 |
| M∞ | 0,6 | 0,7 | 0,8 | 1,6 | 1,8 | 2 |
α | Сxai |
|
|
|
|
|
|
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
2 |
| 0,003060827 | 0,00323748 | 0,00335793 | 0,002598 | 0,002796 | 0,0025 |
4 |
| 0,012243309 | 0,012949918 | 0,013431721 | 0,01039 | 0,011182 | 0,009998 |
6 |
| 0,027547446 | 0,029137316 | 0,030221371 | 0,023378 | 0,025161 | 0,022496 |
8 |
| 0,048973238 | 0,051799673 | 0,053726883 | 0,041561 | 0,04473 | 0,039992 |
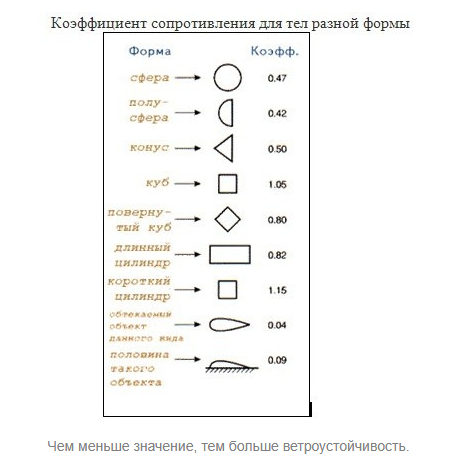
Аэродинамическое сопротивление тел — эффекты отрыва потока.
Сопротивления трения и давленияНесмотря на то что прилегающий к поверхности пограничный слой имеет толщину несколько миллиметров, характер потока в этом пограничном слое, где проявляются силы вязкого трения жидкости, в значительной мере влияет на режим всего потока. Возникновение сопротивления в двухмерном несжимаемом потоке можно объяснить только с помощью трения жидкости.
Образование пограничного слоя (переход от ламинарного состояния потока к турбулентному)
Эпюра распределения скорости потока в пограничном слое для простого случая продольного обтекания пластины показана на рисунке 1.Рисунок 1 — Схематичное изображение пограничного слоя при обтекании пластины в продольном направлении (размеры по оси y сильно увеличены)
В этом случае скорость во внешнем потоке V∞ а значит, и давление p∞ постоянны. Обладающий вязким трением поток прилипает к поверхности стенки. Первоначально вектор скорости потока параллелен стенке, и поток находится в стационарном состоянии.
Такой режим течения потока называется ламинарным. Толщина пограничного слоя, т.е. той области, в которой наблюдается влияние вязкого трения, увеличивается в направлении перемещения потока по закону:
(1)
То есть толщина пограничного слоя δ увеличивается от переднего края обтекаемой поверхности к заднему, и это увеличение тем больше, чем меньше скорость набегающего потока V∞ и больше коэффициент кинематической вязкости ν.
Стабильность ламинарного режима течения потока в пограничном слое достигается только при определенных условиях в отношении шероховатости поверхности. По мере увеличения длины обтекаемой поверхности по ходу потока x > xu наблюдается переход режима течения в пограничном слое в так называемое турбулентное состояние. Большое значение для такого перехода имеет число Рейнольдса. Для рассмотренного случая обтекания пластины, расположенной вдоль потока переход ламинарного режима течения в пограничном слое в турбулентный происходит при числе Рейнольдса
Rexu = V∞xu/ν = 5·105,
зависящем от длины обтекаемой поверхности по ходу потока.
Это относится только к случаю, когда отсутствует градиент давления вдоль пластины. При наличии градиента давления в направлении распространения потока уменьшение давления вызывает стабилизацию ламинарного пограничного слоя, в то время как увеличение давления ведет к очень быстрому переходу его в турбулентное состояние. Помехи ламинарному потоку, например, шероховатость стенок, ускоряют процесс перехода. В общем случае можно констатировать, что переход от ламинарного режима течения потока к турбулентному происходит в зоне минимального давления, если число Рейнольдса при этом имеет не слишком малое значение.
После перехода поток в принципе имеет нестационарное состояние. В нестационарной зоне поток хотя еще прилегает к стенке и параллелен ей, но к средней скорости u прибавляются скорости пульсаций u′, V′, w′ во всех трех направлениях осей координат. Для параллельной стенке компоненты скорости (см. рисунок 1) имеет силу следующее выражение:
(2)
где
(3)
Такой режим течения потока называется турбулентным.
Вследствие пульсаций в пограничном слое происходит интенсивная диффузия. В результате этого дополнительного к касательному напряжению, возникающему из-за молекулярного трения (см. Свойства несжимаемых жидкостей, уравнение 1), добавляется касательное напряжение вследствие турбулентных взаимодействий:
(4)
В этом уравнении u′ и v′ — скорости пульсаций соответственно в направлении осей координат х и у. Поперечная черта означает, что речь идет о средних за бесконечно малый промежуток времени значениях скоростей (пульсаций в соответствии с уравнением 3). τturb всегда имеет положительное значение. Следовательно, турбулентные пульсации действуют так же, как заметное повышение вязкости обтекающей среды. А значит, толщина пограничного слоя для показанной на рисунке 1 пластины в направлении распространения потока после точки перехода увеличивается быстрее, чем до нее. Закон изменения толщины пограничного слоя после перехода его в турбулентное состояние имеет вид:
(5)
Из-за диффузии эпюра скоростей при турбулентном потоке в пограничном слое более выпуклая, чем при ламинарном потоке (см.
рисунок 1).
Отрыв потока
Ламинарный и турбулентный режимы течения в пограничном слое сильно зависят от изменения давления во внешнем потоке. При возрастании давления в направлении движения потока, особенно вблизи стенки, может иметь место его значительное замедление и в связи с этим появление обратных потоков. Схематично это представлено на рисунке 2, из которого видно, что линия тока отрывается от стенки. Этот процесс называется отрывом. Для точки отрыва А имеет силу выражение(du/dy)w = 0 (6)
Рисунок 2 — Схема отрыва потока от стенки в пограничном слое
По сравнению с ламинарным пограничным слоем турбулентный выдерживает более сильные повышения давления, не приводящие к его отрыву. Это объясняется тем, что благодаря присущей турбулентному состоянию потока диффузии близким к стенкам слоям подводится усиленный извне импульс. При понижении давления опасность отрыва потока отсутствует.
Сопротивление трения
При наличии градиента скорости вблизи стенки в любом месте обтекаемого тела (рисунок 3) вследствие молекулярной вязкости тангенциальное напряжение τw, определяемое уравнением 1 (см.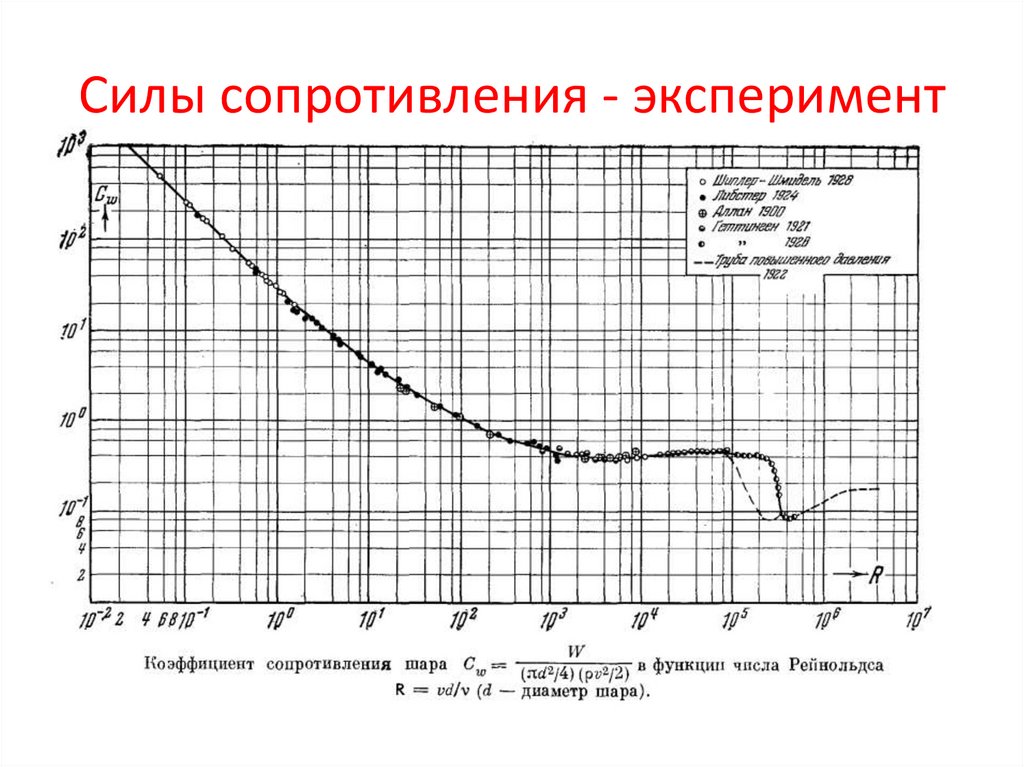
статью Свойства несжимаемых жидкостей), передается от обтекающей среды на стенку.Рисунок 3 — Схема для определения силы сопротивления трения (на примере двухмерного потока)
Если суммировать компоненты элементарных сил в направлении потока
(7)
то получится так называемое сопротивление трения. До тех пор, пока не возникли отрывы потока, эта сила является одной из самых весомых составляющих общего аэродинамического сопротивления тела при двухмерном потоке, это хорошо поясняют два приведенных ниже примера.
Рисунок 4 дает представление об изменении аэродинамического сопротивления плоской пластины, установленной вдоль потока (см. рисунок 1).
Рисунок 4 — Полученная экспериментальным путем зависимость коэффициента сопротивления плоских пластин и крыловидных профилей от числа Рейнольдса:
1 — ламинарное состояние потока, обтекающего плоскую пластину; 2 — турбулентное состояние потока, обтекающего плоскую гладкую пластину
Чтобы характеристика носила более общий характер и не зависела от размеров пластины (ширины b и длины L) и условий обтекания (давление q∞ = ρV∞2/2), можно использовать безразмерный коэффициент сопротивления
cW = W/[(ρV∞2/2)bL] (8)
В рассматриваемом случае обтекания пластины сопротивление трения относится к обеим сторонам пластины (W = WR).
Базовой площадью в данном случае является площадь пластины в плане (bL). Коэффициент сопротивления пластины (см. рисунок 4) представлен функцией от числа Рейнольдса, зависящего от длины пластины (ReL = V∞L/ν).
В случае, если в пограничном слое на поверхности пластины имеет место ламинарный режим течения, зависимость cW = f(Re) имеет вид:
для ReL5 (9)
при переходном от ламинарного к турбулентному режиму течения в пограничном слое:
для 5·105L 7 (10)
При больших значения числа Рейнольдса
cW = 0,91/(log ReL)2,58 при ReL > 107 (11)
в этом случае коэффициент аэродинамического сопротивления изменяется по асимптотическому закону.
Следует отметить, что если в передней части пластины имеет место ламинарный пограничный слой, а в задней части — турбулентный, то получается показанная на рисунке кривая перехода.
Оказывается, что при турбулентном режиме течения в пограничном слое сопротивление трения гораздо больше, чем при ламинарном. Это объясняется тем, что более выпуклые эпюры скоростей в пограничном слое при турбулентном режиме течения проявляются в увеличении градиента скорости вдоль стенки по сравнению с ламинарным. На рисунке 4 показано, что шероховатость стенки существенно увеличивает сопротивление трения. Коэффициент сопротивления сильно увеличивается с возрастанием относительной шероховатости k/L и при этом почти не зависит от числа Рейнольдса. Обтекание пластины, имеющей значительную шероховатость, можно рассматривать как обтекание комбинации из угловатых плохо обтекаемых тел.
Тела с конечной толщиной также обладают сопротивлением трения. Их аэродинамическое сопротивление может иметь малое значение, если удается избежать срывов потока. Этого добиваются за счет пологих форм задней части автомобиля, которые имеют весьма незначительный градиент давления в направлении потока.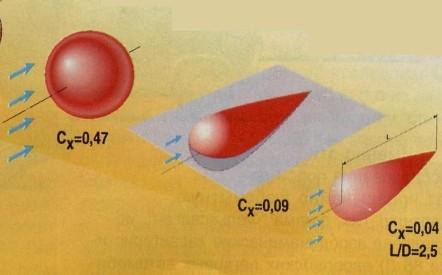
Это же относится к крыловидным профилям и обтекаемым телам, обладающим малым аэродинамическим сопротивлением. На рисунке 4 показаны коэффициенты сопротивления для некоторых крыловидных профилей. Профили NACA 0012, 4412, 23012 имеют в основном турбулентные пограничные слои и ведут себя аналогично пластине, в передней части которой существует турбулентный пограничный слой. Профиль NACA 6 имеет на больших участках ламинарные пограничные слои и в отношении аэродинамического сопротивления существенно лучше.
Сопротивление давления
Плохо обтекаемые тела, такие, как круглый цилиндр, шар или установленная поперек потока пластина, имеют совершенно иной механизм возникновения аэродинамического сопротивления. При обтекании потоком с обратной стороны таких тел во внешнем потоке возникает столь существенное повышение давления, что это приводит к отрыву потока (см. статью Основы аэродинамики автомобиля, рисунок 2). В результате эпюра распределения давления по поверхности тела по сравнению с теоретическим случаем обтекания потоком, не обладающим вязким трением, очень существенно изменяется.
В качестве примера на рисунке 5 представлено распределение давления по поверхности круглого цилиндра.
Рисунок 5 — Распределение давления и характер линий тока для круглого цилиндра при различных числах Рейнольдса:
а — идеальный, не обладающий вязкостью поток, ReD → ∞; б — ламинарный пограничный слой в предкритическом состоянии, ReD = 1,9·105; в — турбулентный пограничный слой в послекритическом состоянии, ReD = 6,7·105
На передней, обращенной к потоку стороне распределение давления в основном соответствует теоретическому распределению давления при обтекании потоком невязкой жидкости, в то время как на обратной стороне вызванное отрывом изменение структуры потока приводит к значительному снижению давления. Эпюра распределения давления относительно оси y становится несимметричной. Суммируя составляющие элементарных сил давления в направлении потока, можно записать (см. рисунок 3):
WD = ∫p sinα dF (12)
Определяемая по формуле 12 величина WD называется сопротивлением давления.
Хотя тангенциальные напряжения, действующие на стенку, вызывают появление сопротивления трения WR, однако для плохообтекаемых тел сопротивление давления является преобладающим. Полное аэродинамическое сопротивление движению тела складывается из сумму указанных составляющих:
W = WD + WR (13)
Коэффициент сопротивления определяют как отношение силы W к скоростному напору ρV∞2/2 и площади лобового сопротивления Fst:
cWst = W/[(ρV∞2/2)Fst] (14)
На рисунке 6 показана зависимость коэффициента аэродинамического сопротивления от числа Рейнольдса ReD = V∞ D/ν для круглого цилиндра и для установленной поперек потока пластины.
Рисунок 6 — Коэффициенты аэродинамического сопротивления тел в зависимости от числа Рейнольдса (для случаев б и в, показанных на рисунке 5, поток двухмерный)
За исключением области очень малых чисел Рейнольдса отрыв потока, обтекающего пластину, всегда происходит одинаково, и коэффициент cW не зависит от числа Рейнольдса.
В отличие от тел, имеющих острые кромки, отрыв потока от поверхностей тел, имеющих скругления, не зафиксирован.
Положение места срыва потока определяется состоянием пограничного слоя. При малых значениях числа Рейнольдса пограничный слой ламинарный (сравните случай «б» на рисунке 5 и 6). Отрыв происходит очень близко к максимальному сечению тела. Возникающая зона вихревого следа широкая, и коэффициент аэродинамического сопротивления имеет большое значение. При критическом значении числа Рейнольдса ReD, krit = 5·105 происходит внезапное преобразование потока. Турбулентный пограничный слой дольше прилегает к поверхности обтекаемого тела (сравните случай «в» на на рисунке 5 и 6). Возникающая зона вихревого следа узкая, и коэффициент аэродинамического сопротивления резко уменьшается.
За исключением особых случаев при проектировании автомобиля стремятся предотвратить внезапное изменение коэффициента cW в зависимости от числа Рейнольдса.
Поэтому для отрыва потока предусматривают определенные места, например, в начале скоса контура задней части автомобиля. Формообразование до места срыва потока направлено на то, чтобы при любых условиях осуществить по возможности продолжающееся повышение давления. Чтобы аэродинамическое сопротивление оставалось небольшим, образующаяся зона вихревого следа должна быть по возможности меньше. С учетом площади лобового сопротивления коэффициенты аэродинамического сопротивления современных европейских автомобилей (исключая спортивные автомобили), по данным Гухо, находятся в пределах 0,37 W числа Рейнольдса и не имеют резких колебаний при его изменении. Это значит, что преобладающей частью полного аэродинамического сопротивления этих автомобилей является сопротивление давления. Для некоторых обтекаемых форм согласно данным Гухо коэффициенты аэродинамического сопротивления имеют значения 0,15 W . Для таких автомобилей относительная часть сопротивления давления существенно меньше, поэтому в общем аэродинамическом сопротивлении такого автомобиля увеличивается доля сопротивления трения и, как следствие, коэффициенты аэродинамического сопротивления сильно зависят от числа Рейнольдса.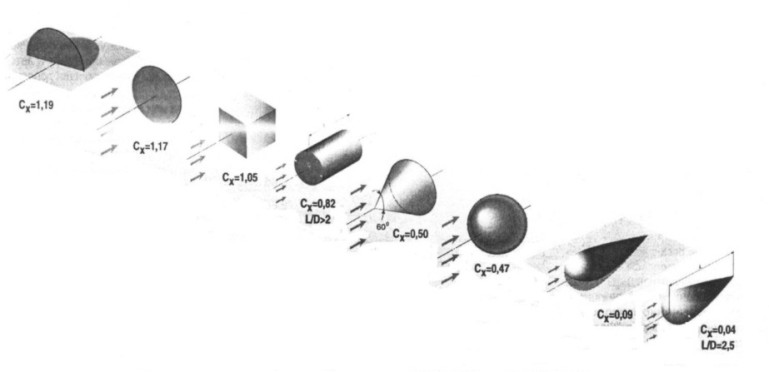
Рассматривая срывное обтекание, можно выделить два различных типа отрывов, приводящих к появлению сопротивления давления. Если кромка отрыва расположена поперечно к направлению потока, то согласно рисунку 7 сначала позади тела возникают вихри, оси которых, в основном перпендикулярны к внешнему потоку.
Рисунок 7 — Отрыв потока от тела с задней частью, оканчивающейся вертикальной стенкой (кромка отрыва перпендикулярна к потоку)
Компоненты скорости в направлении осей вихрей очень малы. Представленное на рисунке 7 симметричное поле потока в области отрыва имеет место только при очень малых значениях числа Рейнольдса (для круглого цилиндра при ReD). При больших числах Рейнольдса происходит периодический отрыв вихрей. Поток в области срыва становится нестационарным. Имеющаяся в начальный момент кинетическая энергия поля завихрения за счет сильной диффузии очень быстро рассеивается и необратимо преобразуется в теплоту. Это проявляется в сильной потере давления позади тела, а потеря энергии соответствует мощности, необходимой для преодоления сопротивления давления.
За телом образуется вихревой след, внутри которого в определенный момент времени существуют довольно равномерно распределенное пониженное давление и очень малые скорости потока.
Другой тип отрыва потока имеет место, если кромка отрыва (рисунок 8) наклонена относительно направления потока.
Рисунок 8 — Отрыв потока от тела со скошенной формой задней части (кромка отрыва расположена под углом к потоку)
В этом случае также образуются вихри, но их оси имеют направление, примерно совпадающее с направлением кромки отрыва. В вихревом поле оторвавшегося потока имеет место значительная по значению составляющая скорости в направлении кромки отрыва, т.е. в направлении оси вихря. За счет этого получается упорядоченный стационарный объемный отрыв. Он также вызывает появление с обратной стороны тела пониженного давления, а значит, ведет к возникновению сопротивления давления. На наклонной поверхности образуется также упорядоченный прилегающий поток. Распределение давления на такой поверхности в области завихрения имеет значительные минимумы пониженного давления.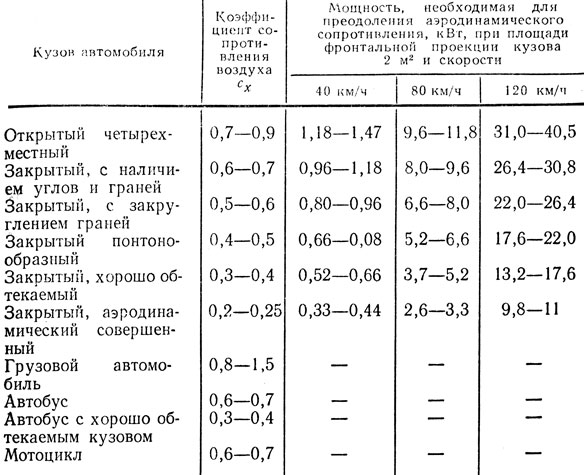
Этот тип отрыва потока очень хорошо известен в авиации в связи с обтеканием треугольных крыльев. В поле потока сзади тела потери полного давления относительно малы. Поле завихрения обладает достаточно большой кинетической энергией, которая соответствует мощности, необходимой для преодоления сопротивления давления.
Между двумя описанными типами отрыва потока позади плохообтекаемого тела существует тесная взаимосвязь, которая в авиации уже хорошо изучена. С увеличением угла установки треугольного крыла (что соответствует уменьшению скоса задней части автомобиля, см. рисунок 8) наблюдается изменение структуры в вихрях, которое называется срывом вихря. Процесс во всех его подробностях до сих пор еще не познан до конца. Но он ведет к разрушению упорядоченного объемного вихревого потока изнутри вихря, что в итоге приводит к образованию беспорядочного вихревого следа. Систематические исследования для автомобилей со скошенной формой задка проведены Янссеном, Гухо и Морелем.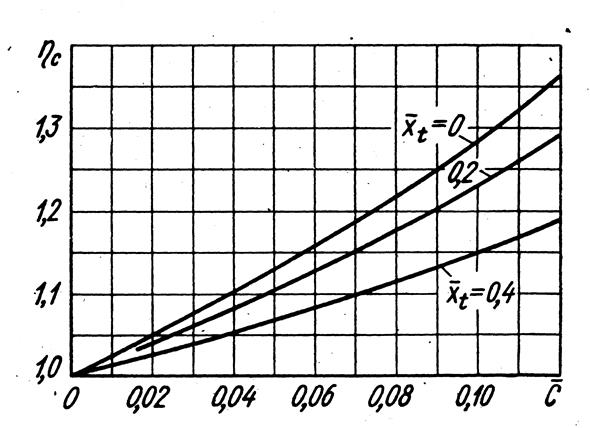
При этом рассмотрены оба типа отрывов. При переходе одной формы потока в другую получаются характерные изменения сопротивления давления, известные из рассмотрения треугольного крыла.
В заключение рассмотрения вопроса об аэродинамическом сопротивлении тела следует отметить, что формообразование тела до его максимального поперечного сечения оказывает лишь относительно малое влияние на полное аэродинамическое сопротивление. Более существенное значение для силы сопротивления воздуха имеет оформление части тела, следующей за максимальным сечением. Ее формообразование в большей степени определяет силу аэродинамического сопротивления.
Вопрос не столько в том, чтобы хорошо распределить набегающий поток, гораздо большее значение имеет то, каким образом разделенный телом поток сольется вместе позади него.
Наилучшим решением являются обтекаемые тела с очень вытянутой задней частью.
О законах и особенностях внешнего обтекания автомобилей читайте также
- Свойства несжимаемых жидкостей
- Вопросы механики обтекания автомобилей
- Основные уравнения потока
Между 1900 и 1905 годами братья Райт спроектировали и построили три
планеры без двигателя и три самолета с двигателем. Братья Райт были велосипедными механиками и дизайнерами. и у них было хорошее практическое знание математики и естественных наук. Они знали о законы Ньютона движения и о силы а также крутящие моменты. Они написали Смитсоновскому институту, когда начинали свое предприятие в 1899 году. и получил технические документы, описывающие авиационную теории дня. Имелись математические уравнения, которые могли использовать для прогнозирования количества поднимать и перетащите который будет генерировать объект. уравнение сопротивления показано на этом слайде. Величина сопротивления, создаваемого объектом, зависит от ряда факторов,
включая
характеристики
воздуха,
скорость между объектом и
воздух, поверхность
над которым циркулирует воздух,
форма
тела, и склонность тела к потоку, называемая также
угол атаки. К тому времени, когда Райты начали свои исследования, было установлено, что сопротивление зависит от квадрат скорости и варьируется линейно с площадью поверхности объекта. Ранние аэродинамики характеризовали зависимость от свойств воздуха коэффициентом давления, называемым коэффициент Смитона, представляющий сила давления (сопротивления) на плоскую пластину площадью один фут, движущуюся со скоростью одна миля в час через воздух. Они считали, что любой объект, движущийся по воздуху, преобразует некоторые часть силы давления в сопротивление, и они представляли эту часть коэффициент сопротивления. Полученное уравнение имеет вид: 92 * А * кд где D — сопротивление, k — коэффициент Смитона, V — скорость, A — площадь крыла, cd — коэффициент лобового сопротивления.
Это уравнение несколько отличается от современного
уравнение сопротивления
используется сегодня. Современное уравнение использует
динамическое давление
движущегося воздуха для зависимости от давления, в то время как это уравнение использует
коэффициент Смитона. Уравнение 1900-х годов предполагает, что вы знаете перпендикулярную силу давления на
подвижная плоская пластина (коэффициент Смитона). Потому что
погрешностей измерения в то время, было много цитируемых значений для
коэффициент в диапазоне от 0,0027 до 0,005. Лилиенталь использовал значение 0,005.
в проектировании и испытании его крыльев.
Когда Райты начали проектировать 1900 самолетов,
они использовали значения коэффициента лобового сопротивления, основанные на работе Лилиенталя. Братья также начали сомневаться в точности подъемной силы Лилиенталя.
коэффициенты.
Так что осенью 1901 года они решили определить собственные ценности
для коэффициента лобового сопротивления с помощью
аэродинамическая труба.
Братья построили умный
остаток средств
непосредственно измерить отношение лобового сопротивления своих моделей к
подъем модели. Вы можете просмотреть короткий кино из «Орвилла и Уилбура Райт», обсуждающих силу сопротивления и как это повлияло на полет их самолетов. Файл фильма может сохранять на свой компьютер и просматривать как подкаст на проигрывателе подкастов. Навигация..
|
При проектировании каждого самолета братья старались
максимизировать
отношение подъемной силы к лобовому сопротивлению, потому что
высокая
поднимать
и низкий
тяга
дает лучший самолет
производительность.
Как они предсказали подъемную силу и сопротивление своей конструкции?
Современные коэффициенты сопротивления связывают силу сопротивления, действующую на объект, с
сила, создаваемая динамическим давлением, умножается на площадь, а 1900-е
коэффициенты сопротивления связывают силу сопротивления с сопротивлением плоской пластины равной площади.
Для современного уравнения сопротивления коэффициент сопротивления плоской пластины
при движении перпендикулярно потоку 1,28; для уравнения сопротивления 1900-х годов,
коэффициент сопротивления для этой задачи
равно 1,0.
поэтому они тоже использовали значение 0,005.
Во время кайта и планера
экспериментах 1900 и 1901 годов братья измерили производительность
своего самолета. Ни один из самолетов не показал себя так, как предполагалось.
уравнениями подъемной силы и сопротивления. Самолет 1901 года
был разработан, чтобы поднимать себя (100 фунтов) и пилота (150 фунтов).
при запуске воздушного змея при скорости ветра 15 миль в час и угле атаки 5 градусов.
Но в полете он едва мог подняться при скорости ветра 15 миль в час.
гораздо больший угол атаки.
Поэтому братья начали сомневаться в значении коэффициента Смитона 0,005 и
они определили, что значение 0,0033 более точно соответствует их данным.
Современное принятое значение составляет 0,00326.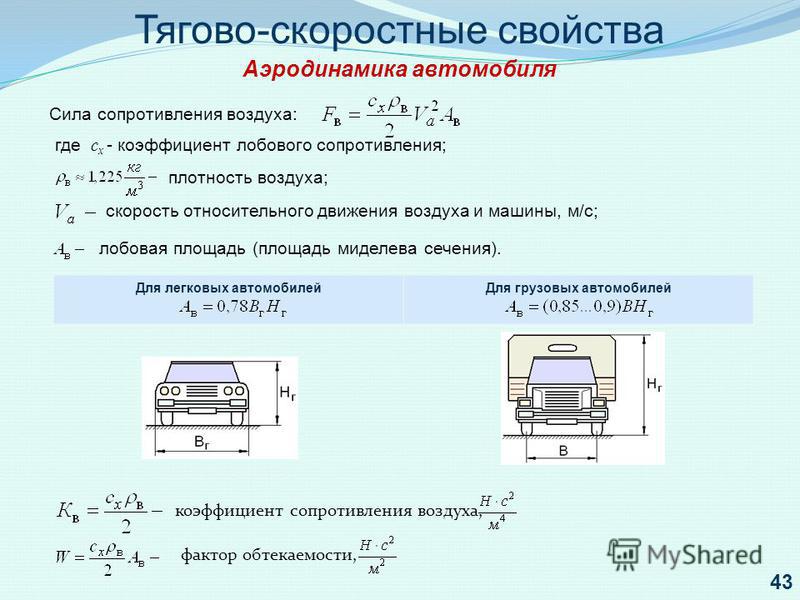
Они построили еще один
остаток средств
для определения подъема.
Мы разработали
интерактивный симулятор туннеля
так что вы можете дублировать их результаты в аэродинамической трубе.
в
процесс
испытав множество моделей аэродинамических профилей, братья обнаружили важность
крыла
форма
на коэффициент лобового сопротивления.
Они определили, что данные Лилиенталя были правильными для геометрии крыла.
которые он использовал, но данные не могли быть применены к крылу с очень
разная геометрия. Крылья Лилиенталя имели довольно короткий размах и эллиптическую форму.
форма в плане, в то время как братья использовали длинную, тонкую, прямоугольную форму в плане.
Братья протестировали более пятидесяти различных
модели
определить
как подъемная сила и лобовое сопротивление зависят от различных параметров конструкции
и они использовали эти данные для разработки своих 1902 самолета
используя уравнение сопротивления, показанное на слайде, со своими собственными коэффициентами сопротивления.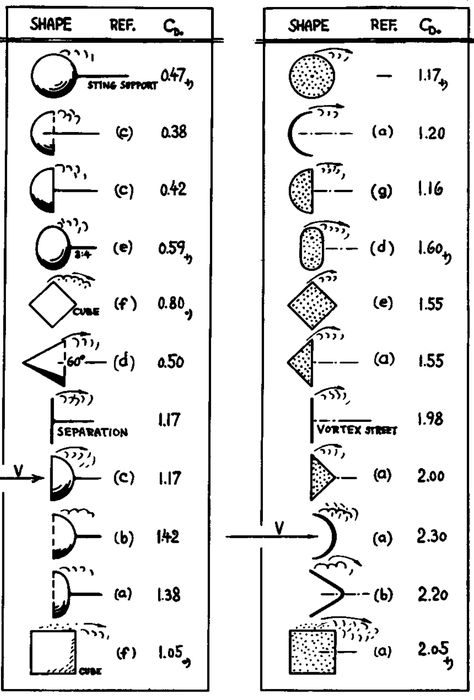
Братья определили требования к мощности для самолета 1903 года.
на основе их данных о перетаскивании.
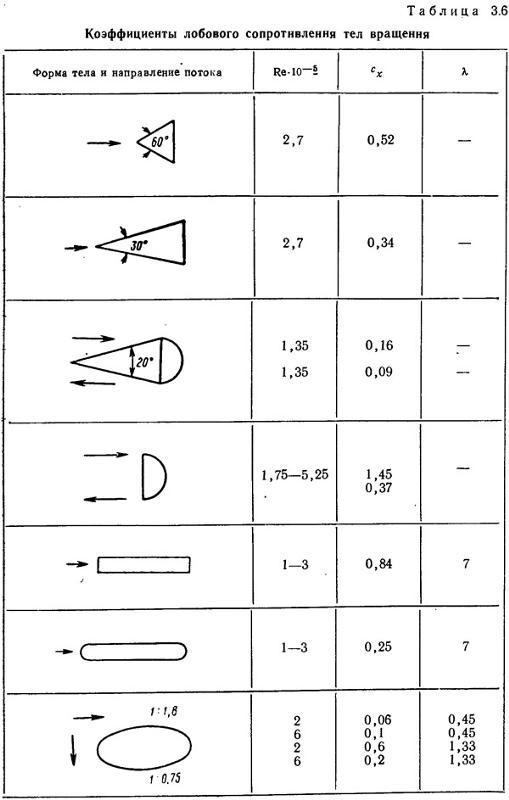в зависимости от числа Рейнольдса. Сила сопротивления, F D = C D A( r U 2 /2) , зависит напрямую
на это количество.