Простая физика — EASY-PHYSIC
Задача 1. За промежуток времени с тело прошло половину окружности радиусом 100 см. Найти среднюю путевую скорость и модуль средней скорости .
Решение: средней путевой скоростью называется средняя скорость прохождения пути, которую мы с вами вычисляем, деля весь путь (длину траектории) на все время. Модуль средней скорости еще называют средней скоростью по перемещению. Ее можно определить, разделив перемещение на время. Тогда длина пути – это длина половины окружности, а перемещение – длина диаметра.
Ответ: средняя путевая скорость – 0,314 м/с, средняя скорость по перемещению – 0,2 м/с
Задача 2. Однородный диск радиусом 0,5 м катится без проскальзывания со скоростью 2 м/с. Найти скорость точек диска . Найти геометрическое место всех точек диска, скорость которых 2 м/с. Угол .
Скорость точек окружности
Решение:
Точка A – центр вращения. Поэтому ее скорость относительно поверхности, по которой катится диск, равна 0. Поскольку в условии сказано, что диск катится со скоростью 2 м/с, то это означает, что с такой скоростью относительно поверхности будет передвигаться его центр: м/с. Поэтому точка А относительно центра будет передвигаться с точно такой же скоростью – со скоростью 2 м/с, и это и будет линейная скорость вращения диска, то есть скорость всех точек, лежащих на его краю, относительно центра м/с. Линейные скорости показаны для точек оранжевыми стрелками. Эти стрелки показывают, какой была бы скорость данной точки, если бы диск не катился, а вращался бы, например, на оси, проходящей через его центр. Но наш диск катится. Поэтому к линейной скорости вращения каждой точки необходимо еще прибавить скорость движения диска относительно опоры. То есть к каждой рыжей стрелке прибавим (векторно) скорость точки О – центра диска – черную стрелку. Тогда-то и становится понятным, почему у точки скорость равна 0 – линейная скорость вращения направлена влево, а скорость качения – вправо, и поскольку они равны, то гасят друг друга: .
Поскольку в условии сказано, что диск катится со скоростью 2 м/с, то это означает, что с такой скоростью относительно поверхности будет передвигаться его центр: м/с. Поэтому точка А относительно центра будет передвигаться с точно такой же скоростью – со скоростью 2 м/с, и это и будет линейная скорость вращения диска, то есть скорость всех точек, лежащих на его краю, относительно центра м/с. Линейные скорости показаны для точек оранжевыми стрелками. Эти стрелки показывают, какой была бы скорость данной точки, если бы диск не катился, а вращался бы, например, на оси, проходящей через его центр. Но наш диск катится. Поэтому к линейной скорости вращения каждой точки необходимо еще прибавить скорость движения диска относительно опоры. То есть к каждой рыжей стрелке прибавим (векторно) скорость точки О – центра диска – черную стрелку. Тогда-то и становится понятным, почему у точки скорость равна 0 – линейная скорость вращения направлена влево, а скорость качения – вправо, и поскольку они равны, то гасят друг друга: . В точке C скорости, напротив, сложатся, поскольку они сонаправлены: м/с.
В точке C скорости, напротив, сложатся, поскольку они сонаправлены: м/с.
Определим теперь скорости точек и . Понятно, что они будут равны численно, но направлены в разные стороны.
Осталось разобраться с точкой . Сделаем еще один рисунок. Линейная скорость вращения всегда направлена по касательной, то есть перпендикулярно радиусу . Углы, которые образуются между векторами, показаны на рисунке, в том числе угол . Тогда в параллелограмме угол , а так как
, то все углы в треугольнике равны и он равносторонний, то есть м/с. Также можно было найти длину этого вектора скорости по теореме косинусов или складывая проекции векторов. Можно догадаться, что точка, симметричная точке E относительно A также имеет скорость, равную 2 м/с. Вообще точки, лежащие на одном и том же расстоянии от центра вращения A будут иметь равные скорости, линии равных скоростей (геометрические места точек с равными скоростями) показаны на рисунке различного цвета дугами: единственная точка (точка C) будет иметь скорость 4 м/с, точки, лежащие на рыжей дуне, будут иметь скорости, равные , точки, лежащие на синей дуге, будут иметь скорости, равные 2 м/с, как у точки E.
Пробуксовывание
Задача 3. Колесо, пробуксовывая, катится по ровной, горизонтальной дороге. Найти скорость центра колеса , если известно, что скорость нижней точки м/c, а верхней — м/c.
Решение:
Если колесо пробуксовывает, то это означает, что скорость его нижней точки не равна нулю, то есть его центр вращения – не точка касания поверхности, центр вращения будет расположен выше. Но центр вращения находится и не в центре колеса. Найти его можно, если провести вертикальный диаметр, построить вектора скоростей в масштабе, а затем, соединив концы векторов скоростей прямой линией, отметить точку пересечения этой линии с диаметром. У нас на рисунке это точка О. Точка К – центр колеса, его скорость нам и нужно найти. Из подобия треугольников и запишем отношения сходственных сторон:
Тогда
Тогда
Теперь обратимся к подобным треугольникам и . Для них отношение сходственных сторон равно:
Откуда м/с.
Ну а более простым решение было бы, если бы мы просто нашли среднее арифметическое скоростей, ведь точка, про которую нас спрашивают, лежит по центру между точками приложения векторов скоростей и , при этом не забываем о векторном сложении скоростей, берем скорость со знаком «минус»:
м/с.
Ответ: 4 м/с.
Проскальзывание
Задача 4. Обруч, проскальзывая, катится по горизонтальной ровной поверхности. В некоторый момент скорость верхней точки А м/с, а нижней точки B м/с. Определить скорость концов диаметра , перпендикулярного к , для того же момента времени. Под какими углами они направлены к горизонту?
Решение:
Проскальзывание – это ситуация, когда скорость нижней точки (точки касания обручем земли) не нулевая, но направлена она в сторону качения. В этом случае центр вращения, так же, как и в случае пробуксовки, не совпадает с центром колеса. Более того, центр вращения даже не внутри колеса – он снаружи (точка О). Как и в предыдущей задаче, можно найти его таким же способом – проведя линию через концы скоростей и найдя ее пересечение с продолжением вертикального диаметра. И, точно так же, как в предыдущей задаче, можно определить скорость центра колеса как среднее арифметическое, только обе скорости направлены у нас теперь в одну сторону, поэтому ставим знак «плюс» перед обеими:
Как и в предыдущей задаче, можно найти его таким же способом – проведя линию через концы скоростей и найдя ее пересечение с продолжением вертикального диаметра. И, точно так же, как в предыдущей задаче, можно определить скорость центра колеса как среднее арифметическое, только обе скорости направлены у нас теперь в одну сторону, поэтому ставим знак «плюс» перед обеими:
м/с.
Так как скорость точки есть результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра колеса , то можем из этого сделать вывод, что линейная скорость вращения равна 2 м/с – ровно на столько скорость центра колеса, найденная нами, отличается от скорости точки , данной в условии задачи. Линейную скорость на рисунке не показывала, или показывала не везде. Скорости точек и равны численно, но направлены по-разному. Их скорости – также результат векторного сложения линейной скорости вращения колеса и скорости поступательного движения центра, а, так как эти две скорости перпендикулярны друг другу, то результат их сложения может быть найден по Пифагору:
Понятно, что раз скорости перпендикулярны друг другу, то являются катетами некоторого прямоугольного треугольника, и связывает их между собой функция тангенса, поэтому угол наклона к горизонту скорости точки можно найти как
Ответ: ,
Шарик катится по двум линейкам
Задача 5. Шарик радиусом см катится равномерно и без проскальзывания по двум параллельным линейкам, расстояние между которыми равно см, и за время с проходит см. С какими скоростями движутся верхняя и нижняя точки шарика?
Шарик радиусом см катится равномерно и без проскальзывания по двум параллельным линейкам, расстояние между которыми равно см, и за время с проходит см. С какими скоростями движутся верхняя и нижняя точки шарика?
На рисунке изображено, как двигается шарик, при этом для удобства показан как вид спереди, так и вид сбоку. Поскольку скорость шарика равна м/с, то эта скорость – скорость поступательного движения его центра масс – точки А. Центр вращения шарика находится в точке О – на уровне края линеек. Определим положение точки О – определим длину отрезка . Это легко сделать, зная радиус шарика и рассмотрев рисунок, из треугольника . Центр вращения в данный момент неподвижен, а точка А двигается относительно него со скоростью 0,6 м/с. Поэтому скорость нижней точки будет
Таким же способом определяем скорость верхней точки :
Ответ: скорость нижней точки 0,15 м/c, скорость верхней 1,35 м/c.
Задача 6. Автомобиль движется по закругленному шоссе, имеющему радиус кривизны м. Закон движения автомобиля имеет вид: , где м, м/с, м/с. Найти скорость автомобиля , его тангенциальное , нормальное и полное ускорения в момент времени с.
Закон движения автомобиля имеет вид: , где м, м/с, м/с. Найти скорость автомобиля , его тангенциальное , нормальное и полное ускорения в момент времени с.
Решение.
Путь:
Производная пути – линейная скорость:
Вторая производная – тангенциальное ускорение:
Нормальное ускорение:
Полное ускорение:
Задача7. Угол поворота диска радиусом см изменяется со временем по закону . Определить зависимости от времени угловой скорости, углового ускорения и линейной скорости точек диска.
Решение: угловая скорость – производная угла:
Угловое ускорение – производная угловой скорости:
Линейная скорость:
Задача 8. Точка движется по окружности с постоянным угловым ускорением рад/. Найти угол между скоростью и ускорением через 1 с после начала движения. Начальная скорость точки равна 0.
Решение: так как тангенциальное ускорение и линейная скорость совпадают по направлению, то определим обе составляющие ускорения: как нормальную, так и тангенциальную. Угол между полным ускорением и его тангенциальной составляющей можно тогда будет найти через функцию тангенса.
Угол между полным ускорением и его тангенциальной составляющей можно тогда будет найти через функцию тангенса.
Известно, что нормальное ускорение , тангенциальное ускорение . При этом , или . Тогда
Искомый угол:
Ответ:
Два концентрических колеса
Задача 9. Два концентрических колеса радиусами см и см вращаются с угловыми скоростями рад/c и рад/с соответственно. Между ними зажато третье колесо так, как показано на рисунке. Какова угловая скорость этого колеса вокруг собственной оси? Проскальзывания нет.
Решение: определим радиус маленького (третьего) колеса, м:
Определим линейную скорость точек первого колеса:
Определим линейную скорость точек второго колеса:
Найдем угловую скорость маленького колеса, зная, что линейная скорость его точек равна линейной скорости больших колес, так как проскальзывания нет:
Ответ: 20 рад/с
Задача 10. Гайку закручивают на болт за время . Длина болта , резьба составляет угол с плоскостью гайки. Найдите угловую скорость гайки, если радиус болта равен .
Длина болта , резьба составляет угол с плоскостью гайки. Найдите угловую скорость гайки, если радиус болта равен .
Скорость вращения гайки по ходу завинчивания на болт
Решение: при закручивании гайка не только вращается, но и движется вдоль болта поступательно, например, спускается вниз. Поэтому точка, взятая на ребре гайки, будет обладать двумя составляющими скорости: скорость, с которой она будет двигаться вниз вдоль болта (назовем ее ) и скорость, с которой эта точка вращается – это уже знакомая нам линейная скорость (). Тогда .
Из рисунка видно, что
С другой стороны, так как длина болта , а гайка спускается по нему за время , то
Тогда
И можно определить :
Тогда
Ответ:
§7. Движение по окружности. Плоское движение
7.1. За
промежуток времени t
= 10 с материальная точка прошла одну
треть окружности радиуса R
= 1 м. Определить среднюю путевую скорость
и модуль средней скорости.
7.2. Две точки равномерно движутся по окружности, причем первая точка движется по часовой стрелке, вторая — против часовой стрелки. Период обращения первой точки Т1 = 5 с, период второй точки Т2 = 2 с. Найти время между двумя последовательными встречами точек.
7.3. Определить линейную скорость Земли v при ее орбитальном движении. Средний радиус земной орбиты R = 1,5108 км.
7.4. Пропеллер самолета радиусом R = 1,5 м вращается при посадке с частотой n = 2000 мин–1, посадочная скорость самолета относительно Земли v = 162 км/ч. Определить скорость точки на конце пропеллера u относительно Земли. Какова траектория движения этой точки?
7.5.Две точки
М и К движутся равномерно по окружности
(см. рисунок) с угловыми скоростями
м = 0,2
рад/с и к = 0,3 рад/с. В начальный момент времени
угол между радиусами этих точек 0 = /3. В какой момент времени эти точки
встретятся?
В какой момент времени эти точки
встретятся?
7.6. Механические часы показывают время t = 4 ч. Через какой промежуток времени t1 минутная стрелка догонит часовую?
7.7. Сколько разNв сутки встречаются часовая и секундная стрелки часов?
7.8. Тяжелый шарик на нити вращается в горизонтальной плоскости так, что нить описывает коническую поверхность. Определить длину нити L, если частота вращения шарика n = 0,5 с–1, его центростремительное ускорение a ц = 8 м/с2 и угол отклонения нити от вертикали = 45.
7.9. Мальчик вращает камень, привязанный к веревке длинной L = 0,8 м, в вертикальной плоскости с частотой n = 4 с–1. В тот момент, когда веревка была расположена горизонтально, она оборвалась. На какую высоту h взлетит камень?
7.10. Пуля, летевшая
горизонтально, пробила один за другим
два диска, насаженных на один вал и
вращающихся с частотой n = 10 с–1. Расстояние между дисками S
= 30 см.
Найти скорость пули v
между дисками, если угловое смещение
пробоин φ = 9
и пробоины оказались расположенными
на одинаковом расстоянии от оси вращения.
Расстояние между дисками S
= 30 см.
Найти скорость пули v
между дисками, если угловое смещение
пробоин φ = 9
и пробоины оказались расположенными
на одинаковом расстоянии от оси вращения.
7.11. Стержень
вращается вокруг оси, походящей
перпендикулярно стержню через некоторую
его точку. Скорости концов стрежня при
этом равны v
7.12. Найти радиус вращающегося колеса, если известно, что линейная скорость точек обода колеса в n = 2,5 раза больше линейной скорости точки, лежащей на расстоянии d = 5 см ближе к оси колеса.
7.13.Диск радиуса R катится без проскальзывания с постоянной скоростью v по горизонтальной дороге (см. рисунок). Найти ускорения точек A и B и скорости точек С и D относительно дороги.
7.14. Катушка
с нитью катится по горизонтальному
столу без проскальзывания. Внутренний
радиус катушки r,
внешний R.
С
какой скоростью vО перемещается
ось катушки O
относительно стола, если конец нити
тянут в горизонтальном
направлении со скоростью v?
Рассмотреть
два случая (см. на рисунке
пункты а и б).
Внутренний
радиус катушки r,
внешний R.
С
какой скоростью vО перемещается
ось катушки O
относительно стола, если конец нити
тянут в горизонтальном
направлении со скоростью v?
Рассмотреть
два случая (см. на рисунке
пункты а и б).
7.15.Цилиндрический каток радиусом R помещен между двумя параллельными рейками. Рейки движутся в одну сторону со скоростями v1 и v2 (см. рисунок). Определить угловую скорость вращения катка и скорость его центра, если проскальзывание отсутствует.
7.16. Диск, радиус которого R, катится без скольжения с постоянной скоростью v. Найти геометрическое место точек на диске, которые в данный момент имеют скорости относительно Земли, модуль которых равен 1,5v.
7.17. Колесо,
пробуксовывая, катится по ровной,
горизонтальной дороге. Найти скорость
центра колеса vО,
если модуль скорости его нижней точки
v1 = 2 м/с, а верхней — v2 = 10 м/с, причем скорости этих точек
направлены в противоположные стороны.
7.18. Шарик, радиус которого R = 5 см, катится равномерно и без проскальзывания по двум параллельным брускам квадратного сечения. Расстояние между брусками d = 6 см. За время t = 2 с шарик проходит путь S = 1,2 м. С какими скоростями движутся верхняя и нижняя точки шарика?
7.19. По горизонтальной плоскости катится без скольжения с постоянной скоростью v обруч радиусом R. Выразить модуль скорости различных точек обруча относительно плоскости как функцию угла между вертикалью и прямой, проведенной между точкой прикосновения обруча с плоскостью и данной точкой обруча. Определить скорость vР точки Р обруча при = 30.
7.20.Автомобиль
движется со скоростью v
= 60 км/ч. С какой частотой n
вращаются его колеса, если они катятся
по шоссе без скольжения, а внешний
диаметр покрышек колес равен d
= 60 см? Найти центростремительное
ускорение а цс внешнего слоя резины на покрышках его
колес.
7.21. Два одинаковых диска расположены так, как показано на рисунке. Диск 1 неподвижен. На какой угол повернется диск 2, обойдя без проскальзывания один раз диск 1?
7.22.У диска 1 радиус R, у диска 2 радиус в два раза больше (см. рисунок). Диск 2 неподвижен. Сколько оборотов N сделает диск 1, обойдя без проскальзывания один раз диск 2?
7.23.Стержень шарнирно соединен с муфтами А и В, которые перемещаются по двум взаимно перпендикулярным рейкам (см. рисунок). Муфта А движется с постоянной скоростью vA = 30 см/с. Найти скорость vB муфты В в момент, когда угол ОАВ = 60.
7.24. Стержень АС движется так, что в данный
момент времени скорость т.А направлена
под углом к АС, а скорость т.В, лежащей
между точками А и С, направлена вдоль
стержня. Определить скорость точки С,
если v
11.
 1 Перекатывание | University Physics Volume 1
1 Перекатывание | University Physics Volume 1Цели обучения
К концу этого раздела вы сможете:
- Описывать физику качения без проскальзывания
- Объясните, как линейные переменные связаны с угловыми переменными для случая качения без проскальзывания
- Найти линейное и угловое ускорения при качении с проскальзыванием и без него
- Расчет статической силы трения, связанной с качением без проскальзывания
- Использование энергосбережения для анализа качения
Вращательное движение — это обычное сочетание вращательного и поступательного движения, которое мы видим повсюду, каждый день. Подумайте о различных ситуациях, когда колеса движутся по шоссе, или колеса самолета приземляются на взлетно-посадочную полосу, или колеса робота-исследователя на другой планете. Понимание сил и крутящих моментов, участвующих в качении , является решающим фактором во многих различных ситуациях.
Для анализа качения в этой главе обратитесь к (Рисунок) в разделе Вращение с фиксированной осью, чтобы найти моменты инерции некоторых общих геометрических объектов. Вы также можете найти его полезным в других расчетах, связанных с вращением.
Вы также можете найти его полезным в других расчетах, связанных с вращением.
Перекатывание без проскальзывания
Люди наблюдали перекатывание без проскальзывания с момента изобретения колеса. Например, мы можем посмотреть на взаимодействие шин автомобиля и поверхности дороги. Если водитель нажимает педаль акселератора в пол так, что шины крутятся, а автомобиль не движется вперед, между колесами и поверхностью дороги должно быть кинетическое трение. Если водитель медленно нажимает на педаль акселератора, заставляя автомобиль двигаться вперед, то шины катятся без проскальзывания. Для большинства людей удивительно, что на самом деле нижняя часть колеса находится в покое по отношению к земле, что указывает на наличие статического трения между шинами и поверхностью дороги. На (рисунке) велосипед движется, а всадник остается в вертикальном положении. Шины соприкасаются с дорожным покрытием, и, несмотря на то, что они катятся, нижняя часть шин слегка деформируется, не скользит и находится в состоянии покоя относительно дорожного покрытия в течение измеримого промежутка времени. Для этого между шиной и поверхностью дороги должно быть статическое трение.
Для этого между шиной и поверхностью дороги должно быть статическое трение.
Рисунок 11.2 (а) Велосипед движется вперед, и его шины не скользят. Нижняя часть слегка деформированной шины находится в покое относительно поверхности дороги в течение измеримого периода времени. (b) На этом изображении видно, что верхняя часть катящегося колеса кажется размытой из-за его движения, но нижняя часть колеса мгновенно остается в покое. (кредит a: модификация работы Нельсона Лоуренсо; кредит b: модификация работы Колина Роуза)
Чтобы проанализировать качение без проскальзывания, мы сначала выводим линейные переменные скорости и ускорения центра масс колеса через угловые переменные, описывающие движение колеса. Ситуация показана на (рис.).
Рисунок 11.3 (a) Колесо тянется по горизонтальной поверхности под действием силы [латекс] \overset{\to }{F} [/латекс]. Сила статического трения [латекс] {\overset{\to }{f}}_{\text{S}},|{\overset{\to }{f}}_{\text{S}}|\ le {\mu }_{\text{S}}N [/latex] достаточно большой, чтобы не скользить. (b) Векторы линейной скорости и ускорения центра масс и соответствующие выражения для [латекс] \omega \,\text{и}\,\alpha [/латекс]. Точка P покоится относительно поверхности. (c) Относительно системы центра масс (ЦМ) точка P имеет линейную скорость [латекс] \текст{−}R\omega \hat{i} [/латекс].
(b) Векторы линейной скорости и ускорения центра масс и соответствующие выражения для [латекс] \omega \,\text{и}\,\alpha [/латекс]. Точка P покоится относительно поверхности. (c) Относительно системы центра масс (ЦМ) точка P имеет линейную скорость [латекс] \текст{−}R\omega \hat{i} [/латекс].
Из (Рисунок)(а) мы видим векторы сил, участвующих в предотвращении проскальзывания колеса. На (b) точка P , которая касается поверхности, покоится относительно поверхности. Относительно центра масс точка P имеет скорость [латекс] \text{−}R\omega \hat{i} [/latex], где R — радиус колеса, а [латекс] \omega [/latex] — угловая скорость колеса относительно своей оси. Поскольку колесо катится, скорость P относительно поверхности равна его скорости относительно центра масс плюс скорость центра масс относительно поверхности:
[латекс] {\ overset {\ to} {v}} _ {P} = \ text {−} R \ omega \ hat {i} + {v} _ {\ text {CM}} \ hat {i }. [/latex]
Поскольку скорость P относительно поверхности равна нулю, [латекс] {v}_{P}=0 [/латекс], это говорит о том, что
[латекс] {v}_{ \text{CM}}=R\omega . [/latex]
[/latex]
Таким образом, скорость центра масс колеса равна его радиусу, умноженному на угловую скорость относительно его оси. Покажем соответствие линейной переменной в левой части уравнения угловой переменной в правой части уравнения. Это сделано ниже для линейного ускорения.
Если продифференцировать (рисунок) в левой части уравнения, то получим выражение для линейного ускорения центра масс. В правой части уравнения R является константой, и поскольку [латекс] \альфа =\фрак{д\омега} {dt}, [/латекс] мы имеем
[латекс] {а}_{\ текст{CM}}=R\alpha . [/latex]
Кроме того, мы можем найти расстояние, которое проходит колесо, в терминах угловых переменных, обратившись к (Рисунок). Когда колесо катится от точки A до точки B , его внешняя поверхность отображается на землю ровно на пройденное расстояние, которое составляет [латекс] {d} _ {\ text {CM}}. [/latex] Мы видим из (Рисунок), что длина внешней поверхности, которая отображается на землю, равна длине дуги [латекс] R\theta \text{} [/латекс]. Приравнивая два расстояния, получаем
Приравнивая два расстояния, получаем
[латекс] {d}_{\text{CM}}=R\theta . [/latex]
Рисунок 11.4 Когда колесо катится по поверхности, длина дуги [латекс] R\theta [/латекс] от А до В отображается на поверхность, что соответствует расстоянию [латекс] {d} _{\text{CM}} [/latex], что центр масс сместился.
Пример
Катится по наклонной плоскости
Твердый цилиндр катится по наклонной плоскости без проскальзывания, начиная с состояния покоя. Он имеет массу m и радиус r . а) Чему равно его ускорение? б) Какому условию должен удовлетворять коэффициент трения покоя [латекс] {\му }_{\текст{S}} [/латекс], чтобы цилиндр не скользил?
Стратегия
Нарисуйте эскиз и диаграмму свободного тела и выберите систему координат. Ставим x в направлении вниз по плоскости и y вверх перпендикулярно плоскости. Определить задействованные силы. Это нормальная сила, сила тяжести и сила трения. Запишите законы Ньютона в направлениях x и y и закон Ньютона для вращения, а затем определите ускорение и силу трения.
Запишите законы Ньютона в направлениях x и y и закон Ньютона для вращения, а затем определите ускорение и силу трения.
Решение
- Диаграмма свободного тела и эскиз показаны на (Рисунок), включая нормальную силу, компоненты веса и силу трения покоя. Трения едва хватает, чтобы цилиндр вращался без проскальзывания. Поскольку проскальзывание отсутствует, величина силы трения меньше или равна [латекс] {\ mu }_{S}N [/латекс]. Запись законов Ньютона в x – и y — направления, имеем
[латекс] \сумма {F}_{x}=m{a}_{x};\enspace\sum {F}_{y}=m{a}_{y}. [/латекс]
Рисунок 11.5 Твердый цилиндр катится по наклонной плоскости, не соскальзывая с места. Система координат имеет x в направлении вниз по наклонной плоскости и y перпендикулярно плоскости. Диаграмма свободного тела показана с нормальной силой, статической силой трения и компонентами веса [латекс] m\overset{\to }{g} [/latex]. Трение заставляет цилиндр катиться по плоскости, а не скользить.

Замена из диаграммы свободного тела,
[латекс] \begin{array}{ccc}\hfill mg\,\text{sin}\,\theta -{f}_{\text{S}}& =\hfill & m{({a}_ {\ text {CM}})} _ {x}, \ hfill \\ \ hfill N-mg \, \ text {cos} \, \ theta & = \ hfill & 0, \ hfill \\ \ hfill {f} _{\text{S}}& \le \hfill & {\mu }_{\text{S}}N,\hfill \end{массив} [/latex]
мы можем тогда найти линейное ускорение центра масс из этих уравнений:
[латекс] {({a} _ {\ text {CM}})} _ {x} = g (\ text {sin} \, \ theta — {\ mu } _ {S} \ text {cos} \ ,\тета). [/латекс]
Однако полезно выразить линейное ускорение через момент инерции. Для этого запишем второй закон Ньютона для вращения
[латекс] \sum {\tau}_{\text{CM}}={I}_{\text{CM}}\alpha . [/латекс]
Крутящие моменты рассчитываются относительно оси, проходящей через центр масс цилиндра. Единственный ненулевой крутящий момент обеспечивается силой трения. У нас есть
[латекс] {f}_{\text{S}}r={I}_{\text{CM}}\alpha . [/латекс]
Наконец, линейное ускорение связано с угловым ускорением на
[латекс] {({a}_{\text{CM}})}_{x}=r\alpha .
 [/латекс]
[/латекс]Эти уравнения можно использовать для решения для [латекса] {a}_{\text{CM}},\alpha ,\,\text{and}\,{f}_{\text{S}} [/latex ] с точки зрения момента инерции, где мы опустили индекс x -. Запишем [латекс] {а}_{\текст{СМ}} [/латекс] через вертикальную составляющую силы тяжести и силы трения и сделаем следующие замены.
[латекс] {a}_{\text{CM}}=g\text{sin}\,\theta -\frac{{f}_{\text{S}}}{m} [/latex] 9{2})}=\frac{1}{3}\text{tan}\,\theta . [/латекс]
Значение
- Линейное ускорение линейно пропорционально [латекс] \text{sin}\,\theta . [/latex] Таким образом, чем больше угол наклона, тем больше линейное ускорение, как и следовало ожидать. Угловое ускорение, однако, линейно пропорционально [латекс] \текст{sin}\,\тета [/латекс] и обратно пропорционально радиусу цилиндра. Таким образом, чем больше радиус, тем меньше угловое ускорение.
- Чтобы не происходило скольжения, коэффициент статического трения должен быть больше или равен [латекс] (1\текст{/}3)\текст{тан}\,\тета [/латекс].
 Таким образом, чем больше угол наклона, тем больше должен быть коэффициент трения покоя, чтобы цилиндр не проскальзывал.
Таким образом, чем больше угол наклона, тем больше должен быть коэффициент трения покоя, чтобы цилиндр не проскальзывал.
Проверьте свое понимание
Полый цилиндр находится на наклонной поверхности под углом [латекс] 60\text{°}. [/latex] Коэффициент статического трения на поверхности [латекс] {\mu }_{S}=0,6 [/латекс]. а) Катится ли цилиндр без проскальзывания? (b) Будет ли сплошной цилиндр катиться без проскальзывания 9{2})}. [/latex]
Это очень полезное уравнение для решения задач, связанных с качением без проскальзывания. Обратите внимание, что ускорение меньше, чем у объекта, скользящего по плоскости без трения без вращения. Ускорение также будет разным для двух вращающихся цилиндров с разной инерцией вращения.
Качение с проскальзыванием
В случае качения с проскальзыванием мы должны использовать коэффициент кинетического трения, который приводит к кинетической силе трения, поскольку статического трения нет. Ситуация показана на (рис. ). В случае проскальзывания [латекс] {v}_{\text{CM}}-R\omega \ne 0 [/латекс], поскольку точка P на колесе не покоится на поверхности, а [латекс] {v}_{P}\ne 0 [/латекс]. Таким образом, [латекс] \omega \ne \frac{{v}_{\text{CM}}}{R},\alpha \ne \frac{{a}_{\text{CM}}}{R} [/латекс].
). В случае проскальзывания [латекс] {v}_{\text{CM}}-R\omega \ne 0 [/латекс], поскольку точка P на колесе не покоится на поверхности, а [латекс] {v}_{P}\ne 0 [/латекс]. Таким образом, [латекс] \omega \ne \frac{{v}_{\text{CM}}}{R},\alpha \ne \frac{{a}_{\text{CM}}}{R} [/латекс].
Рисунок 11.6 (a) Между колесом и поверхностью возникает кинетическое трение, потому что колесо проскальзывает. (b) Простые отношения между линейными и угловыми переменными больше не действуют.
Пример
Скатывание по наклонной плоскости с проскальзыванием
Твердый цилиндр скатывается по наклонной плоскости из состояния покоя и испытывает скольжение ((Рисунок)). Он имеет массу m и радиус r . а) Чему равно его линейное ускорение? б) Чему равно его угловое ускорение относительно оси, проходящей через центр масс?
Стратегия
Нарисуйте эскиз и диаграмму свободного тела, показывающие задействованные силы. Диаграмма свободного тела аналогична случаю отсутствия проскальзывания, за исключением того, что сила трения является кинетической, а не статической.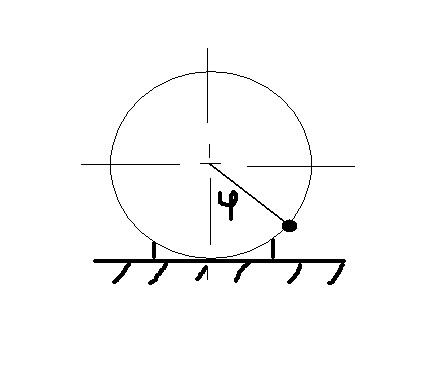 Используя второй закон Ньютона, найдите ускорение в x — направление. Используйте второй закон вращения Ньютона, чтобы найти угловое ускорение.
Используя второй закон Ньютона, найдите ускорение в x — направление. Используйте второй закон вращения Ньютона, чтобы найти угловое ускорение.
Решение
Рис. 11.7 Твердый цилиндр скатывается по наклонной плоскости из состояния покоя и испытывает скольжение. Система координат имеет x в направлении вниз по наклонной плоскости и y вверх перпендикулярно плоскости. Диаграмма свободного тела показывает нормальную силу, кинетическую силу трения и компоненты веса [латекс] m\overset{\to}g}. [/latex]
Сумма сил в y -направление равно нулю, поэтому сила трения теперь равна [латекс] {f} _ {\ text {k}} = {\ mu } _ {\ text {k}} N = {\ mu } _ {\ текст{k}}мг\текст{cos}\,\тета . [/latex]
Второй закон Ньютона в направлении x становится
[латекс] \sum {F}_{x}=m{a}_{x}, [/latex]
[латекс] мг \, \ текст {грех} \, \ тета — {\ му} _ {\ текст {к}} мг \, \ текст {соз} \, \ тета = м {({а} _ {\ текст {CM }})}_{x}, [/latex]
или
[латекс] {({a}_{\text{CM}})}_{x}=g(\text{sin}\, \ тета — {\ му } _ {\ текст {K}} \, \ текст {cos} \, \ тета). [/латекс] 9{2}\альфа . [/latex]
[/латекс] 9{2}\альфа . [/latex]
Решая для [латекс] \альфа [/латекс], мы имеем
[латекс] \альфа =\фрак{2{е}_{\текст{к}}}{мр}=\фракция {2{\mu} _{\text{k}}g\,\text{cos}\,\theta}{r}. [/latex]
Значение
Запишем линейное и угловое ускорения через коэффициент кинетического трения. Линейное ускорение такое же, как у тела, скользящего по наклонной плоскости с кинетическим трением. Угловое ускорение относительно оси вращения линейно пропорционально нормальной силе, зависящей от косинуса угла наклона. Как [латекс]\тета\до 90\text{°} [/latex], эта сила стремится к нулю, и, таким образом, к нулю обращается угловое ускорение.
Сохранение механической энергии при вращении
В предыдущей главе мы ввели кинетическую энергию вращения. Любой катящийся объект несет вращательную кинетическую энергию, а также поступательную кинетическую энергию и потенциальную энергию, если этого требует система. Включая гравитационную потенциальную энергию, полная механическая энергия качения объекта составляет
[латекс] {E} _ {\ text {T}} = \ frac {1} {2} m {v} _ {\ text {CM }}^{2}+\frac{1}{2}{I}_{\text{CM}}{\omega}^{2}+mgh. [/латекс]
[/латекс]
В отсутствие каких-либо неконсервативных сил, которые отбирали бы энергию из системы в виде тепла, полная энергия катящегося объекта без проскальзывания сохраняется и постоянна на протяжении всего движения. Примерами, когда энергия не сохраняется, являются катящийся объект, который скользит, выделение тепла в результате кинетического трения и катящийся объект, встречающий сопротивление воздуха.
Вы можете спросить, почему катящийся объект, который не скользит, сохраняет энергию, ведь сила трения покоя не является консервативной. Ответ можно найти, вернувшись к (Рисунок). Пункт P при контакте с поверхностью находится в состоянии покоя относительно поверхности. Следовательно, его бесконечно малое смещение [латекс] d\overset{\to }{r} [/латекс] относительно поверхности равно нулю, а дополнительная работа силы трения покоя равна нулю. Мы можем применить закон сохранения энергии к нашему изучению качения, чтобы получить некоторые интересные результаты.
Пример
Марсоход Curiosity
Марсоход Curiosity , показанный на (Рисунок), был отправлен на Марс 6 августа 2012 года. Колеса марсохода имеют радиус 25 см. Предположим, астронавты прибывают на Марс в 2050 году и обнаруживают ныне недействующий Curiosity на краю бассейна. Пока разбирают марсоход, космонавт случайно теряет сцепление с одним из колес, которое катится, не соскальзывая, на дно котловины на 25 метров ниже. Если колесо имеет массу 5 кг, какова его скорость на дне чаши?
Колеса марсохода имеют радиус 25 см. Предположим, астронавты прибывают на Марс в 2050 году и обнаруживают ныне недействующий Curiosity на краю бассейна. Пока разбирают марсоход, космонавт случайно теряет сцепление с одним из колес, которое катится, не соскальзывая, на дно котловины на 25 метров ниже. Если колесо имеет массу 5 кг, какова его скорость на дне чаши?
Рис. 11.8 Марсоход НАСА «Кьюриосити» во время испытаний 3 июня 2011 года. Местонахождение находится внутри Цеха сборки космических кораблей в Лаборатории реактивного движения НАСА в Пасадене, Калифорния. (кредит: NASA/JPL-Caltech)
Стратегия
Мы используем сохранение механической энергии для анализа проблемы. На вершине холма колесо покоится и обладает только потенциальной энергией. На дне бассейна колесо имеет вращательную и поступательную кинетическую энергию, которая должна быть равна начальной потенциальной энергии по закону сохранения энергии. Поскольку колесо катится без проскальзывания, мы используем соотношение [латекс] {v}_{\text{CM}}=r\omega [/латекс], чтобы связать поступательные переменные с вращательными переменными в уравнении сохранения энергии. Затем находим скорость. Из (рис.) видно, что полый цилиндр является хорошим приближением для колеса, поэтому мы можем использовать этот момент инерции для упрощения расчета. 9{2})25,0\,\text{m}}=9,63\,\text{m}\text{/}\text{s}\text{.} [/latex]
Затем находим скорость. Из (рис.) видно, что полый цилиндр является хорошим приближением для колеса, поэтому мы можем использовать этот момент инерции для упрощения расчета. 9{2})25,0\,\text{m}}=9,63\,\text{m}\text{/}\text{s}\text{.} [/latex]
Значение
Это довольно точный результат, учитывая, что на Марсе очень мало атмосферы, и потери энергии из-за сопротивления воздуха будут минимальными. Результат также предполагает, что местность гладкая, так что колесо не будет натыкаться на камни и неровности на своем пути.
Кроме того, в этом примере кинетическая энергия или энергия движения поровну распределяется между линейным и вращательным движением. Если мы посмотрим на моменты инерции на (рисунок), то увидим, что полый цилиндр имеет наибольший момент инерции для данного радиуса и массы. Если бы колеса вездехода были твердыми и аппроксимировались твердыми цилиндрами, например, кинетическая энергия была бы больше при прямолинейном движении, чем при вращательном. Это дало бы колесу большую линейную скорость, чем приближение полого цилиндра. Таким образом, сплошной цилиндр достигнет дна бассейна быстрее, чем полый цилиндр.
Таким образом, сплошной цилиндр достигнет дна бассейна быстрее, чем полый цилиндр.
Резюме
- При качении без проскальзывания между катящимся объектом и поверхностью возникает сила трения покоя. Соотношения [латекс] {v}_{\text{CM}}=R\omega ,{a}_{\text{CM}}=R\alpha ,\,\text{and}\,{d}_ Применяются все {\text{CM}}=R\theta [/latex], так что линейная скорость, ускорение и расстояние до центра масс представляют собой угловые переменные, умноженные на радиус объекта.
- При качении с проскальзыванием между катящимся объектом и поверхностью возникает кинетическая сила трения. В этом случае [латекс] {v}_{\text{CM}}\ne R\omega ,{a}_{\text{CM}}\ne R\alpha ,\,\text{and}\, {d}_{\text{CM}}\ne R\theta[/latex].
- Энергосбережение можно использовать для анализа движения качения. Энергия сохраняется при качении без проскальзывания. Энергия не сохраняется при качении с проскальзыванием из-за тепла, выделяемого кинетическим трением.
Концептуальные вопросы
Может ли круглый объект, выведенный из состояния покоя на вершине склона без трения, совершить качение?
Показать раствор
Цилиндрическая банка радиусом R катится по горизонтальной поверхности без проскальзывания. а) На какое расстояние переместится его центр масс после одного полного оборота банки? б) Будет ли это расстояние больше или меньше, если произойдет скольжение?
а) На какое расстояние переместится его центр масс после одного полного оборота банки? б) Будет ли это расстояние больше или меньше, если произойдет скольжение?
Колесо высвобождается сверху на уклоне. Колесо, скорее всего, будет скользить, если уклон будет крутым или пологим?
Показать раствор
Что быстрее катится по наклонной плоскости, полый цилиндр или сплошной шар? Оба имеют одинаковую массу и радиус.
Полая сфера и полый цилиндр одинакового радиуса и массы катятся по склону без проскальзывания и имеют одинаковую начальную скорость центра масс. Какой объект достигает большей высоты, прежде чем остановиться?
Показать раствор
Задачи
Какова угловая скорость шины диаметром 75,0 см на автомобиле, движущемся со скоростью 90,0 км/ч?
Показать ответ
Мальчик проехал на велосипеде 2,00 км. Колеса имеют радиус 30,0 см. На какой общий угол поворачиваются шины во время его поездки?
Если мальчик на велосипеде в предыдущей задаче разгоняется из состояния покоя до скорости 10,0 м/с за 10,0 с, каково угловое ускорение шин?
Показать решение
Гоночные автомобили Формулы-1 имеют шины диаметром 66 см. Если Формула-1 развивает среднюю скорость 300 км/ч во время гонки, каково угловое смещение в оборотах колес, если гоночная машина поддерживает эту скорость в течение 1,5 часов?
Если Формула-1 развивает среднюю скорость 300 км/ч во время гонки, каково угловое смещение в оборотах колес, если гоночная машина поддерживает эту скорость в течение 1,5 часов?
Шарик скатывается по склону на [latex] 30\text{°} [/latex] из состояния покоя. а) Чему равно его ускорение? б) Какой путь он пройдет за 3,0 с?
Показать раствор
Повторите предыдущую задачу, заменив шарик цельным цилиндром. Объясните новый результат.
Твердое тело с цилиндрическим поперечным сечением высвобождается из верхней части склона [латекс] 30\text{°} [/латекс]. Он опускается на 10,0 м за 2,60 с. Найти момент инерции тела через его массу м и радиус р.
Показать решение
Йо-йо можно представить в виде сплошного цилиндра массой m и радиусом r , по окружности которого намотана легкая нить (см. ниже). Один конец нити зафиксирован в пространстве. Если цилиндр падает при разматывании струны без проскальзывания, каково ускорение цилиндра?
Сплошной цилиндр радиусом 10,0 см катится по склону с проскальзыванием. Угол наклона [латекс] 30\text{°}. [/latex] Коэффициент кинетического трения о поверхность 0,400. Чему равно угловое ускорение твердого цилиндра? Чему равно линейное ускорение?
Угол наклона [латекс] 30\text{°}. [/latex] Коэффициент кинетического трения о поверхность 0,400. Чему равно угловое ускорение твердого цилиндра? Чему равно линейное ускорение?
Показать раствор
Шар для боулинга катится по пандусу высотой 0,5 м, не соскальзывая при этом на хранение. Его начальная скорость центра масс равна 3,0 м/с. а) Какова его скорость на вершине рампы? б) Если пандус имеет высоту 1 м, дойдет ли он до вершины?
Сплошной цилиндр массой 40,0 кг катится по горизонтальной поверхности со скоростью 6,0 м/с. Какая работа требуется, чтобы остановить его?
Показать раствор
Твердый шар массой 40,0 кг катится по горизонтальной поверхности со скоростью 6,0 м/с. Какая работа требуется, чтобы остановить его? Сравните результаты с предыдущей задачей.
Сплошной цилиндр катится по склону под углом [латекс] 20\text{°}. [/latex] Если он стартует снизу со скоростью 10 м/с, как далеко он продвинется по склону?
Показать раствор
Сплошное цилиндрическое колесо массой M и радиусом R притягивается силой [латекс] \overset{\to} {F} [/латекс], приложенной к центру колеса в точке [латекс] 37\ text{°} [/latex] по горизонтали (см. следующий рисунок). Если колесо должно катиться без проскальзывания, каково максимальное значение [латекс] |\overset{\to }{F}|? [/latex] Коэффициенты статического и кинетического трения равны [латекс] {\mu }_{\text{S}}=0,40\,\text{and}\,{\mu}_{\text{k}} =0,30. [/латекс]
следующий рисунок). Если колесо должно катиться без проскальзывания, каково максимальное значение [латекс] |\overset{\to }{F}|? [/latex] Коэффициенты статического и кинетического трения равны [латекс] {\mu }_{\text{S}}=0,40\,\text{and}\,{\mu}_{\text{k}} =0,30. [/латекс]
Полому цилиндру придана скорость 5,0 м/с, и он катится по склону на высоту 1,0 м. Если полому шару той же массы и радиуса придать ту же начальную скорость, как высоко он поднимется по склону?
Показать раствор
Глоссарий
- перекатывание
- сочетание вращательного и поступательного движения с проскальзыванием или без него
Катится без проскальзывания
Катание без проскальзывания обычно происходит, когда такой объект, как колесо, цилиндр или шар, катится по поверхности без проскальзывания.
Чтобы определить такое движение, мы должны связать перемещение объекта с его вращением.
Например, рассмотрим колесо (или цилиндр), катящееся по плоской горизонтальной поверхности, как показано ниже.
Где:
α — угловое ускорение колеса (в радианах/с 2 ) относительно земли
w — угловая скорость колеса (в радианах/с) относительно земли.
r радиус колеса
V o — горизонтальная скорость геометрического центра O колеса относительно земли
a o — горизонтальное ускорение геометрического центра O колеса относительно земли
P — место контакта колеса с поверхностью.
Колесо катится без проскальзывания только при отсутствии горизонтального перемещения колеса в точке контакта P (относительно поверхности/грунта). Таким образом, точка контакта P также должна иметь нулевое горизонтальное перемещение (относительно поверхности/земли). Это аналогично ящику, стоящему неподвижно на полу (то есть не скользящему). Ящик имеет нулевое горизонтальное перемещение относительно пола, поэтому площадь контакта ящика (с полом) также имеет нулевое горизонтальное перемещение (относительно пола). В случае колеса это аналогично точке контакта 9.0429 P с нулевым горизонтальным перемещением относительно поверхности.
Ящик имеет нулевое горизонтальное перемещение относительно пола, поэтому площадь контакта ящика (с полом) также имеет нулевое горизонтальное перемещение (относительно пола). В случае колеса это аналогично точке контакта 9.0429 P с нулевым горизонтальным перемещением относительно поверхности.
Теперь, если бы колесо (показанное выше) двигалось вправо или влево, но без вращения, оно скользило бы по поверхности. И в результате точка контакта P тоже будет двигаться либо вправо, либо влево.
Следовательно, делаем вывод, что колесо должно вращаться (с определенной скоростью), чтобы не было буксования на поверхности.
Чтобы начать анализ, создайте схему, как показано ниже, со знаками.
Если вводятся следующие дополнительные переменные:
V rel — горизонтальная скорость точки P (на колесе) относительно точки O
a rel — горизонтальное ускорение точки P (на колесе) относительно точки O
Следовательно, путем сложения векторов скорость точки P относительно поверхности/земли равна:
Теперь для вращательного движения:
Для отсутствия буксования V p = 0. Следовательно,
Следовательно,
В результате
Для случая качения без проскальзывания это уравнение, связывающее скорость геометрического центра колеса O с угловой скоростью w колеса.
Если мы продифференцируем приведенное выше уравнение по времени, мы получим:
Для случая качения без проскальзывания это уравнение, связывающее ускорение геометрического центра колеса O с угловым ускорением α колеса.
Уравнения (1) и (2) также применимы для искривленных поверхностей. Другими словами, даже если бы поверхность качения была искривлена, скорость точки контакта P все равно была бы нулевой при отсутствии проскальзывания, и уравнения (1) и (2) по-прежнему применялись бы. Однако для искривленной поверхности скорость V o параллельно касательной к поверхности в точке контакта P , а ускорение a o параллельно касательной к поверхности в точке контакта P .
