Параметры состояния газа — Справочник химика 21
Основными параметрами состояния газа являются давление, температура и удельный объем. Эти параметры связаны между собой определенной аналитической зависимостью, которая называется уравнением состояния газа. [c.20]Уравнение состояния идеального газа. В общем случае переход газа из одного состояния в другое сопровождается изменением 1 сех трех параметров состояния. Пользуясь законами Бойля — Мариотта и Гей-Люссака, можно вывести уравнение, связывающее параметры состояния газа в этом случае. [c.22]
Параметром состояния газа является его абсолютная температура по термодинамической шкале в кельвинах. [c.21]
Параметры состояния газа [c.20]
Параметром состояния газа является его абсолютное давление. [c.20]
Таким образом, метод Льюиса по существу представляет математический прием, который состоит во введении новой функции /, промежуточной между параметрами состояния газа р и 7″, с одной стороны, и изобарным потенциалом, с другой стороны.
При начальных параметрах состояния газа имеем [c.152]
Основные параметры состояния газа связаны зависимостью [c.9]
Центробежные Нагнетатели на компрессорных станциях магистральных газопроводов эксплуатируются при различных параметрах состояния газа. Поэтому использование характеристик, построенных для определенных значений газовой постоянной Д, коэффициента сжимаемости Z и начальной температуры газа Т , приводит к существенным погрешностям. [c.41]
Используя выражение (34), связывающее скорость звука с параметрами состояния газа, [c.31]
Во многих случаях расчетные формулы упрощаются, если параметры состояния газа определяются в функции не от числа М, а от приведенной скорости. Удобство оперирования приведенной скоростью связано с тем, что ее знаменатель (критическая скорость) зависит только от температуры торможения, которая постоянна для любого участка потока с изолированным процессом.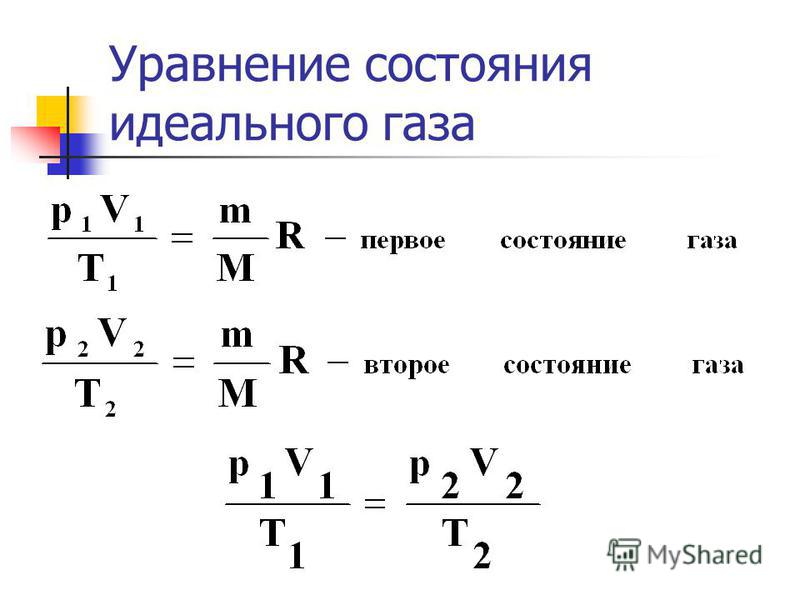
Решая совместно систему из пяти уравнений (155) — (159), можно по заданным значениям скорости распространения прямой магнитогазодинамической волны (wt =—Ua) и параметров состояния газа и магнитного поля перед фронтом волны (рн, Ри, Та, Ва) найти значения относительной скорости газа (lii) и параметров газа и поля (pi, pi, Tu В ) за фронтом волны. [c.231]
Уравнение (1.26) является эмпирическим и справедливо только в достаточно узкой области изменения давления, температуры и удельного (молярного) объема исследуемого газа. Связано это с тем, что фактор сжимаемости существенно зависит от параметров состояния газа. К сожалению, математической формы этой зависимости нет, так что проследить и, тем более, предсказать изменение фактора сжимаемости практически невозможно. Поэтому были созданы таблицы зависимостей значений его от температуры и давления.
Если компрессорные машины работают при давлениях, не превышающих примерно 10 МПа, то можно пренебречь межмолекулярными силами и размерами молекул. И все параметры состояния газа связаны между собой уравнением состояния идеального газа [c.7]
Определить начальные и конечные основные параметры состояния газа, изменение внутренней энергии Ли, энтальпии АЛ, энтропии Aj, внешнюю работу / и теплоту q в процессах. [c.288]
ВЗАИМОЗАВИСИМЫЕ ПАРАМЕТРЫ СОСТОЯНИЯ ГАЗОВ [c.25]
Параметрами называются физические величины, характеризующие состояние газа, жидкости или твердого тела. Основными параметрами состояния газов и паров являются давление, удельный объем и температура. [c.33]
Найдем соотношения, позволяющие рассчитать параметры состояния газа в точке А по их значениям в набегающем потоке, не искаженном присутствием обтекаемого тела. Из уравнений (47,6) для прямой ударной волны при помощи выражения (33,4) для скорости звука и уравнения состояния легко найдем [c.214]
Из уравнений (47,6) для прямой ударной волны при помощи выражения (33,4) для скорости звука и уравнения состояния легко найдем [c.214]
Полученные соотношения показывают, что в непосредственной близости к обтекаемому телу в точке А (рис. 19) параметры состояния газа, вообще говоря, могут значительно отличаться от их значений в набегающем потоке. Это обстоятельство весьма важно с точки зрения выбора разумной методики измерения температуры, давлений и скоростей в сверхзвуковом потоке газа, так как всякий измерительный прибор будет посторонним телом, сильно возмущающим движение газа и его параметры состояния. В связи с этим полезно отметить, что изложенная здесь теория тупого тела имеет значение для приборов по измерению скорости в газодинамических потоках. Действительно, если точку А обтекаемого тела соединить узкой полостью внутри его с трубкой манометра, то последний покажет давление Рд, по которому можно по формуле (48,10) рассчитать если известно давление набегающего потока Р,.
На практике известными величинами обычно являются половина угла раствора обтекаемого конуса 8- (рис. 23), скорость VI и параметры состояния газа Р , рх, в набегающем потоке. Формулы (46,1)—(46,12) показывают, что эти величины однозначно определяют те же параметры газового потока = и, Р > Р2 и за фронтом ударной волны и угол между векторами и сли изве- [c.225]
Все рассмотренные выше параметры р, р, Т, е, / являются параметрами состояния газа. Кроме них, в термодинамике используется понятие функции состояния 5, называемой энтропией, дифференциал которой вводится соотношением [c.23]
ПАРАМЕТРЫ состояния ГАЗА [c.9]
Приводимые в расчетах объемы газов отнесены к нормальным условиям (273 К, 1,013 10 Па), если не сообщаются параметры состояния газа. Это замечание касается всех величин, в которые входит объем газа — объемной теплоемкости, объемной скорости и др. Там, где нет специальной оговорки, состав газов приведен в объемных, а твердых и жидких веществ — в массовых процентах.
За начальные параметры состояния газа принимаются его параметры вблизи входа во всасывающий патрубок машины. Они характеризуются аб- [c.174]
Удельный вес и критические параметры состояния газов [c.345]
Приведенными параметрами называют безразмерные величины, показывающие, во сколько раз действительные параметры состояния газа (давление, температура, объем, плотность, коэф- [c.153]
Это выражение определяет дифференциальный эффект Джоуля — Томсона через абсолютные параметры состояния газа. [c.185]
Если адиабатное расширение или сжатие протекало равновесно, то согласно уравнениям Пуассона, которые были пояснены выше, должно иметь место следующее соотношение между параметрами состояния газа в начале и в конце процесса [c.31]
Графическое построение процессов с отображением внешнего теплообмена газа удобно производить в координатах Т—5.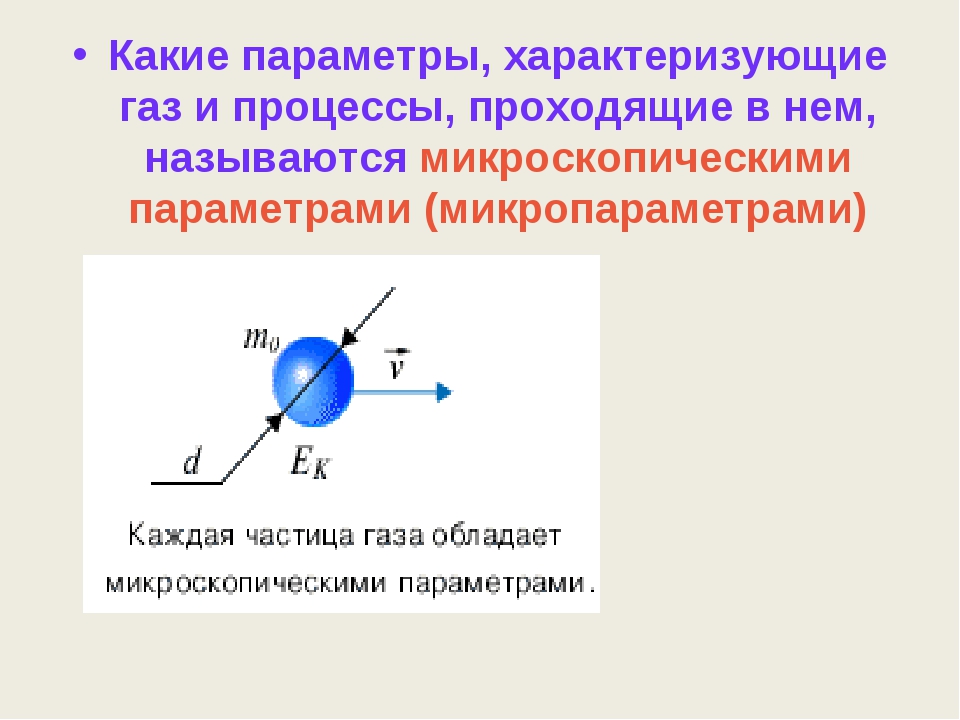
Величина Р измеряется прибором вакуумметром. Параметром состояния газа служит только абсолютное давление. [c.12]
ПАРАМЕТРЫ СОСТОЯНИЯ ГАЗА [c.9]
Сжатый от давления удельного объема и температуры до давления р., удельного объема и температуры Т , газ при постоянном давлении р-2 охлаждается в холодильнике I ступени до температуры и объема после чего производится сжатие во Ii ступени. Параметры состояния газа в начале сжатия во II ступени — р-, -nj и 7 2= Г , конечные—р2> [c.39]
Политропные процессы характеризуются тем, что они протекают с изменением всех параметров состояния газа при наличии теплообмена с окружарощен средой. Уравнение этих процессов имеет вид
Для определения одних параметров состояния газа по другим, а также для их нахождения в термодинамических процессах применяются s, Т и S, -диаграммы, на горизонтальной оси когорых отложена удельная энтропия S, а на вертикальной — абсолютная температура Т или удельная чнтальпия Особенно нужны s, Г и s, i-диаграммы для расчетов при реальных газах. [c.29]
[c.29]
Прежде чем перейти к рассмотрению физико-химических свойств природного газа, необходимо остановиться на законак, связывающих между сабой основные параметры состояния газа так как при добыче, транспортировке и храпении его могут меняться как давление и температура, так и объем, занимаемый им. [c.9]
Основные параметры состояния газа — Энциклопедия по машиностроению XXL
КОЛИЧЕСТВО ВЕЩЕСТВА. ОСНОВНЫЕ ПАРАМЕТРЫ СОСТОЯНИЯ ГАЗА И ЕДИНИЦЫ ИЗМЕРЕНИЯ ИХ [c.19]ОСНОВНЫЕ ПАРАМЕТРЫ СОСТОЯНИЯ ГАЗОВ И ЕДИНИЦЫ ИХ ИЗМЕРЕНИЯ [c.7]
Назовите основные параметры состояния газов и их размерности. [c.13]
Учитывая, что энтропия является функцией состояния, можно выявить следующие функциональные зависимости изменения энтропии от основных параметров состояния газа [c.96]
К основным параметрам состояния газа относятся объем V, давление р, температура Т и масса т. [c.11]
[c.11]
Основные параметры состояния газов. Некоторые, 1 ругие величины, встречающиеся при газодинамических расчетах. [c.456]
В общем случае при изменении состояния газу сообщается теплота и изменяются все параметры его состояния. В отдельных же частных случаях может оставаться неизменным какой-либо из основных параметров состояния газа (объем, давление или температура) или же будет отсутствовать теплообмен газа с внешней средой.
В общем случае политропный процесс протекает с изменением всех основных параметров состояния газа, причем эти параметры связаны между собой определенной зависимостью, вид которой может быть установлен следующим образом. [c.57]
ОСНОВНЫЕ ПАРАМЕТРЫ СОСТОЯНИЯ ГАЗА И ИХ ИЗМЕРЕНИЕ [c.16]
Основные параметры состояния газа — давление, объем и температура — определяют из уравнений состояния (характеристических уравнений)
[c.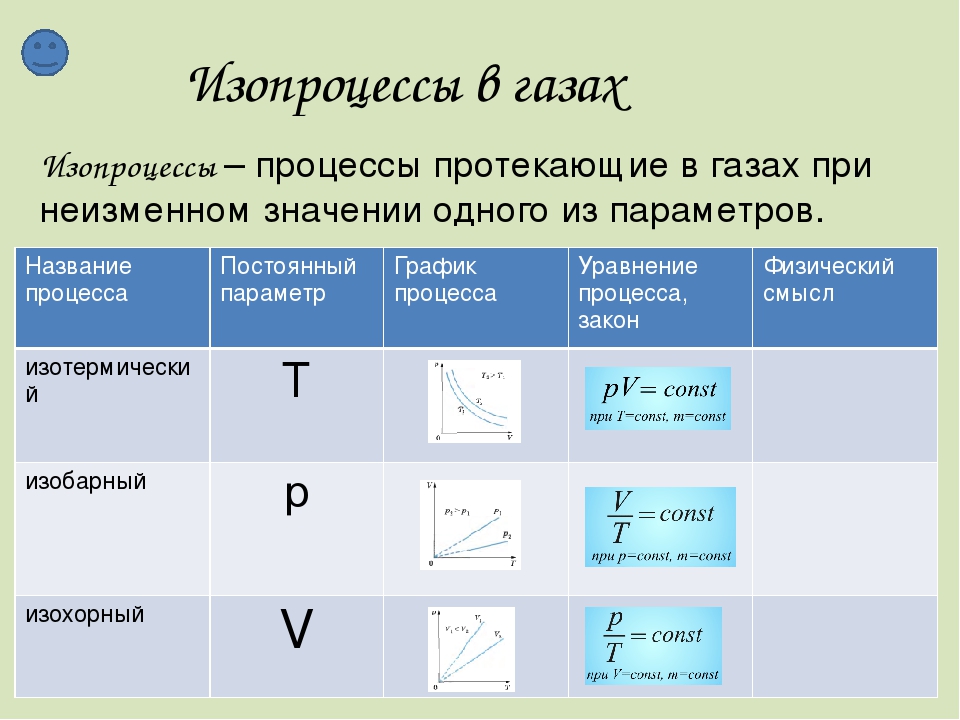 3]
3]
Термическое уравнение состояния. Это уравнение связывает основные параметры состояния газа давление р, температуру Г и удельный объем у. Для идеального газа [c.24]
Основные параметры состояния газов [c.6]
Состояние газа отражают средние величины, характеризующие результат действия молекул, образующих газ. Этим величинам присуще определенное значение для каждого отдельного состояния газа, и они носят название параметров состояния газа. В первую очередь рассмо- -трим основные параметры состояния газов температуру, удельный объем и давление. [c.7]
Из уравнений (2.13)—(2.15) и (2.13 )—(2.15 ) следует, что изменение энтропии газа в процессе Ах и сама энтропия 5 не зависят от характера процесса изменения состояния газа, а определяются только начальным и конечным состояниями рабочего тела, т. е. энтропия 5 действительно является функцией состояния и в соответствии с указан-лыми уравнениями может быть выражена как функция любой пары из трех основных параметров состояния газа
[c. 31]
31]
Основные параметры состояния газов………. 6 [c.434]
Основные термодинамические параметры состояния газа [c.12]
Поскольку энтальпия является функцией основных параметров состояния, то di есть полный дифференциал этой функции при любых независимых переменных, характеризующих состояние газа [c.65]
Определить приращение энтропии идеального газа в зависимости от основных параметров состояния. [c.85]
При исследовании идеальных термодинамических циклов поршневых двигателей внутреннего сгорания обычно определяют количество подведенной и отведенной теплоты, основные параметры состояния рабочего тела в типичных точках цикла, причем температуры в промежуточных точках вычисляют как функции начальной температуры газа вычисляют термический к. п. д, цикла по основным характеристикам и производят анализ термического к. п. д. [c.260]
Характеристическое уравнение идеального газа или уравнение состояния связывает между собой основные параметры состояния — давление, объем и температуру — и может быть представлено следующими уравнениями [c.
 18]
18]При высоких давлениях или температурах, близких к критическим, газы не подчиняются уравнению Менделеева — Клапейрона внутренняя энергия и энтальпия, а следовательно, и теплоемкость зависят не только от температуры, но и от давления. Для реальных газов связь между основными параметрами состояния устанавливается уравнением Ван дер Ваальса, если можно пренебречь энергией ассоциации молекул. В тех случаях, когда энергией ассоциации молекул пренебречь нельзя, связь между р, v и Т можно найти из уравнения (1.19). Однако это уравнение пока не нашло практического применения из-за сложности вычисления вириальных коэффициентов. Поэтому связь между р, v ч Т находят либо из соответствующих таблиц для данного газа, приведенных в теплотехнических справочниках, либо из эмпирических уравнений. [c.30]
Для составления эмпирического уравнения состояния какого-либо газа используют опытные данные, полученные по зависимости между р, V н Т, или по зависимости теплоемкости этого газа от основных параметров состояния, или по температурному эффекту дросселирования. [c.30]
[c.30]
Поскольку внутренняя энергия идеального газа зависит лишь от его температуры, а внутренняя энергия реального газа — от температуры и удельного объема (или давления), т. е. от основных параметров состояния, значения которых не зависят от того, каким путем газ пришел в данное состояние, можно заключить, что и внутренняя энергия газа не зависит от этого пути, т. е. что внутренняя энергия газа также является параметром его состояния. [c.19]
Параметрами называются физические величины, характеризующие состояние газа. Основные параметры состояния для газов и паров — давление, удельный объем и температура. [c.7]
Газовую среду с большой точностью можно рассматривать как смесь идеальных газов. Основные термодинамические параметры состояния газа в каждой точке пространства связаны между собой уравнением Клапейрона. [c.6]
В качестве основных параметров состояния однородного тела, например газа, в термодинамике приняты
[c. 18]
18]
В тепловых машинах применяется рабочее тело — газ, который при любом взаимодействии с внешней окружающей средой изменяет свое состояние. Физические макроскопические величины, характеризующие состояние рабочего тела, называются термодинамическими параметрами состояния или просто параметрами состоя йия. Основными параметрами состояния являются давление, температура и удельный объем. Эти параметры определяют состояние газа в том случае, когда в любой момент давление и температура, а следовательно, и удельный объем по всей массе будут иметь одно и то же значение. Такое состояние газа называется равновесным. [c.9]
Величины, характеризующие физическое состояние тела, называются термодинамическими параметрами состояния. Основными параметрами состояния рабочего тела являются удельный объем V, давление р и температура Т. Удельный объем V представляет собой объем единицы массы вещества, обычно 1 кг. Второй термодинамический параметр —давление/ — это сила, приходящаяся на единицу окружающей газ поверхности.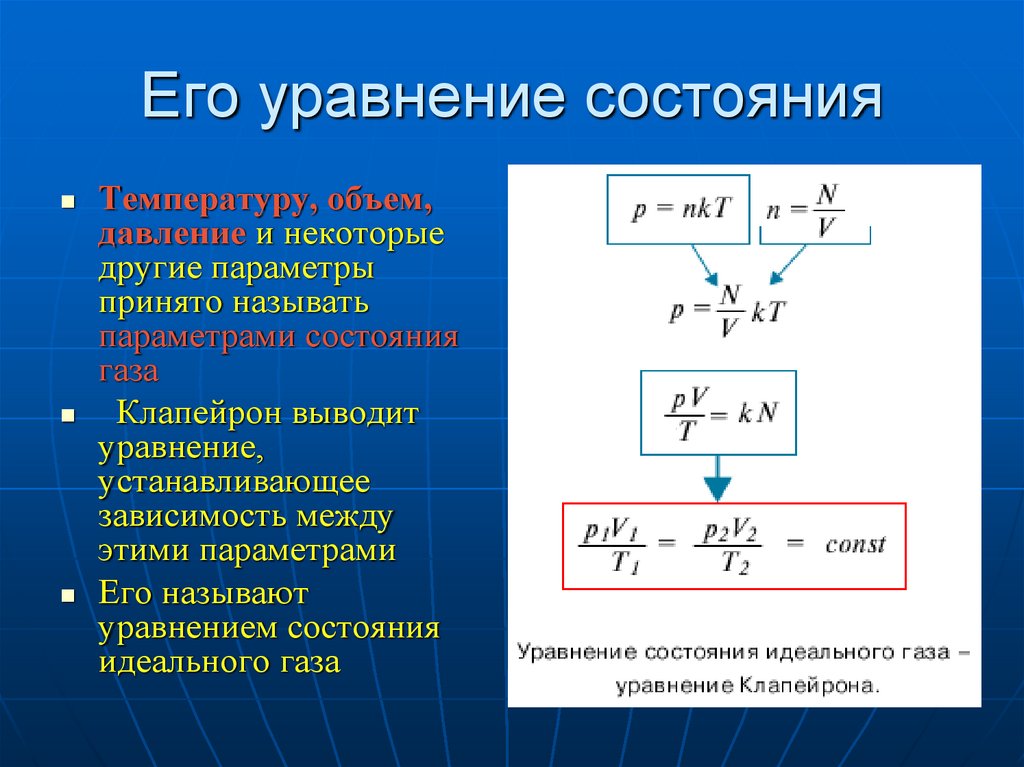 [c.54]
[c.54]
При термодинамическом рассмотрении статистически равновесных процессов в газах, наряду с введенными выше параметрами состояния р. р, г, используются еще два основных параметра состояния абсолютная температура Т и удельная (отнесенная к единице массы) энтропия 8. В дальнейшем предполагается, что газ как термодинамическая система является двухпараметрической С р цон. Это означает, что его состояние вполне определяется заданием каких-либо двух параметров. Следовательно, упомянутые пять параметров должны быть связаны тремя соотношениями. [c.21]
Поскольку из основных параметров р, V я Т только два являются независимыми, то любая пара из них (у и Г, / и Г, р и о) определяет все остальные параметры состояния газов, т. е. [c.63]
Основные зависимости, характеризующие соотношение между параметрами идеального газа при некоторых вполне определенных условиях изменения его состояния, легко получаются из основного уравнения кинетической теории газов. До этого они были получены экспериментальным путем.
[c.17]
До этого они были получены экспериментальным путем.
[c.17]
Как уже было сказано, состояние тела характеризуется тремя основными параметрами давлением р, удельным объемом v и температурой Т. Основные параметры определяются путем непосредственного измерения. Целесообразно найти связь между основными параметрами, т. е. функцию вида F [р, v, Т)=0, которую называют уравнением состояния. Относительно просто найти такую функцию для идеального газа. [c.9]
Теплопроводность является одним из теплофизических параметров вещества. Значения теплопроводности находятся в пределах от нескольких сотых долей (для газов) до нескольких сотен единиц (для металлов) ватт на метр-кельвин. Для простых веществ теплопроводность является, вообще говоря, функцией параметров состояния (давления и температуры). Теплопроводность многокомпонентных веществ зависит от концентрации компонентов, а для пористых материалов — от структуры, плотности и влажности. Основным источником данных по теплопроводности различных материалов является эксперимент. [c.125]
[c.125]
Внутренняя энергия тела U представляет собой энергию, обусловленную движением и силами взаимодействия частиц рабочего тела (молекул, атомов, электронов, атомных ядер), и, следовательно, равна сумме кинетической и потенциальной энергий этих частиц. Отсюда следует, что для реальных рабочих тел внутренняя энергия является функцией основных термодинамических параметров состояния т. е. и = f (р, v), и = (р(р, Т) и и = v /(ii, Г). Для идеальных газов потенциальная энергия мельчайших частиц рабочего тела равна нулю и, следовательно, внутренняя энергия их равна кинетической энергии, которая, в свою очередь, является функцией только температуры. Отсюда следует, что внутренняя энергия идеального газа есть функция температуры, т. е. и = j (Т). Молекулярно-кинетическая теория вещества дает для идеального газа следующую конкретную зависимость внутренней энергии одного киломоля от температуры [c.12]
При изучении равновесных и обратимых термодинамических процессов идеальных газов должны быть выявлены во-первых, закономерность изменения основных параметров, характеризующих состояние рабочего тела во-вторых, особенности реализации условий первого закона термодинамики. [c.20]
[c.20]
Внутренней э-нергией называется совокупность всех видов энергии, которыми обладает любое тело или система тел в данном состоянии, не связанных сдвижением системы как целого или с наличием внешнего силового поля (гравитационного, электрического, магнитного). Поскольку в технической термодинамике изучаются лишь физические процессы, происходящие в тепловых и холодильных установках, будем рассматривать только те виды внутренней энергии, которые возникают при различных термодинамических процессах изменения состояния газов в зависимости от их основных параметров р, и, Т. Внутренняя энергия обозначается буквой и и является функцией этих параметров. Так как основные параметры состояния газа связаны между собой характеристическим уравнением, то внутреннюю энергик> можно представить как функцию только двух основных параметров состояния газа, т. е. V = Д р, Т), или V = ь, Т), или / = /з р, и). [c.21]
Приран1,ение dii, как и любого параметра, является полным дифференциалом. Поскольку состояние газа вполне определяется основными параметрами состояния внутреннюю энергию можно представить как функцию любых двух параметров состояния
[c.55]
Поскольку состояние газа вполне определяется основными параметрами состояния внутреннюю энергию можно представить как функцию любых двух параметров состояния
[c.55]
Для одноатомных газов / = 3, и поэтому для них цс = 4]55-3 = = 12465 и дСр = + 8314 = 20 779 ДжДкмоль К). Соответственно для двухатомных газов ( = 5) дс = 4155-5 = 20 775 и цс, = 20775 4-8314 = = 29 089 ДжДкмоль К). Наконец, для трехатомных газов и более (i = 7) цс = 4155. 7 = 29085 и цСр = 29 085 + 8314 = 3,74 10 ДжДкмоль К). Найденные опытным путем мольные теплоемкости для реальных одно- и двухатомных газов при температурах 15…20°С удовлетворительно согласуются с вычисленными по формуле (1.62) величинами. Однако для трехатомных газов получаются большие расхождения вычисленных значений мольных теплоемкостей с экспериментально найденными. Опытами установлено, что для двух- и многоатомных газов теплоемкость зависит от основных параметров состояния и в первую очередь от температуры. Для реальных газов, практически подчиняющихся уравнению состояния Менделеева — Клапейрона, теплоемкость можно принять не зависящей от давления. Однако для сжатых газов и ларов влияние давления на теплоемкость весьма значительно.
[c.18]
Однако для сжатых газов и ларов влияние давления на теплоемкость весьма значительно.
[c.18]
Это уравнение выражает зависимость между основными параметрами состояния идеального газа и называется его уравнением состояния, или характеристическим, Белйчина 1 в уравнении (2-1) имеет строго определенное значение для каждого газа и называется характеристической газовой постоянной. [c.21]
Для оценки циклов тепловых двигателей применяют еще один параметр состояния газа — энтропию . Основное свойство энтропии состоит в том, что ее величина увеличивается, если к телу тепло подводится, и уменьшается, если тепло отводится. Следовательно, в обратимых адиабатных процессах изжнения состояния газа, т. е. в таких, в которых теплообмен между газом и окружающей средой отсутствует, энтропия газа остается постоянной. Величину энтропии рабочих тел подсчитывают [c.37]
Газовая ди.
 намика — изучает движение газов при су-щесгвенно м изменении их плотности. Основная особенность газодинамического процесса — неразрывная связь одновременно проте-каюш,их механического процесса движения газа (главным образом его ускорения или торможения) и термодинамического процесса его расширения или сжатия. Поэтому для анализа и расчета газодинамических процессов используются законы механики и термодинамики и изменение параметров состояния газа может изображаться в pv, Тз, 8 координатах. Последнее помогает глубже усво ить их физическую сущность и упрощает расчеты. Несмотря нр общ.но ть основных физических законов, которым подчиняется движение любых жидкостей, процессы движения сжимаемой жидкости сложнее процессов движения несжимаемой и отличаются от них не только качественно, но часто и количественно. Например, при течении несжимаемой жидкости по расширяющемуся каналу скорость ее движения всегда уменьшается. При течении газа по расширяющемуся каналу, в зависимости от условий, скорость может и уменьшаться и увеличиваться и не изменяться.
намика — изучает движение газов при су-щесгвенно м изменении их плотности. Основная особенность газодинамического процесса — неразрывная связь одновременно проте-каюш,их механического процесса движения газа (главным образом его ускорения или торможения) и термодинамического процесса его расширения или сжатия. Поэтому для анализа и расчета газодинамических процессов используются законы механики и термодинамики и изменение параметров состояния газа может изображаться в pv, Тз, 8 координатах. Последнее помогает глубже усво ить их физическую сущность и упрощает расчеты. Несмотря нр общ.но ть основных физических законов, которым подчиняется движение любых жидкостей, процессы движения сжимаемой жидкости сложнее процессов движения несжимаемой и отличаются от них не только качественно, но часто и количественно. Например, при течении несжимаемой жидкости по расширяющемуся каналу скорость ее движения всегда уменьшается. При течении газа по расширяющемуся каналу, в зависимости от условий, скорость может и уменьшаться и увеличиваться и не изменяться. Как показывают теория и опыт, плотность существенно изменяется при движении газа С большими скоростями — большими 30. ..40% от скорости распространения звука в этом газе а также при подводе к газу или отводе от него тепла и механической работы.
[c.5]
Как показывают теория и опыт, плотность существенно изменяется при движении газа С большими скоростями — большими 30. ..40% от скорости распространения звука в этом газе а также при подводе к газу или отводе от него тепла и механической работы.
[c.5]5.2. ОСНОВНЫЕ ПАРАМЕТРЫ СОСТОЯНИЯ ГАЗА И ИХ ЕДИНИЦЫ
Введение в строительное дело — И. И. Капцов
5.2.
ОСНОВНЫЕ ПАРАМЕТРЫ
СОСТОЯНИЯ ГАЗА И ИХ ЕДИНИЦЫ
name=bookmark89>ИЗМЕРЕНИЯ
К
основным параметрам состояния газов относятся: давление, абсолютная
температура и удельный объем.
Давление.
Давлением вообще называется сила, действующая на единицу площади поверхности
тела перпендикулярно последней. Давление газа есть средний результат силового
воздействия громадного числа молекул газа на внутреннюю поверхность сосуда, в
котором заключен газ. Молекулы газа, находясь все время в движении, ударяются о
поверхность сосуда и тем самым «давят» на его стенки.
В
технике различают абсолютное давление Рабс,
избыточное давление Ризб и разрежение (вакуум) Рв.
Под
абсолютным давлением подразумевается полное давление, под которым находится
газ. Под избыточным давлением понимают разность между абсолютным давлением,
большим, чем атмосферное, и атмосферным давлением. Разрежение (вакуум)
характеризуется разностью между атмосферным давлением и абсолютным давлением,
меньшим, чем атмосферное.
Температура
— параметр, характеризующий тепловое состояние тела. Температура тела определяет
направление возможного самопроизвольного перехода тепла от тела с большей
температурой к телу с меньшей температурой.
Для
измерения температур принята стоградусная шкала. (ГОСТ 8550—61) и абсолютная термодинамическая
шкала Кельвина. В стоградусной шкале при рб=
101,325 кПа (760 мм рт. ст.) за 0° принимается
температура таяния льда, а за 100° С — температура кипения воды. Градус этой
шкалы обозначается через °С.
В
абсолютной термодинамической шкале Кельвина за нуль принято состояние тела,
при котором тепловое движение молекул теоретически отсутствует. Из физики
известно, что такое состояние наступает при температуре на 273,16° (273° С)
ниже 0°С.
17.Основные термодинамические параметры состояния газа. Теплотехника
17.Основные термодинамические параметры состояния газа
Давление
Р – мера силы, которая действует на единицу поверхности:
Р = lim ?Fn / ?S = dFn/ dS,
где DS ? 0; ?Fn – сила, направленная перпендикулярно участку поверхности.
Удельный объем
V – величина, обратная плотности rвещества:
v = 1 / r= dV/ dm,
где dV– бесконечно малый элемент объема;
dm– масса вещества.
Моль
Количество вещества, которое содержит число молекул, равное числу атомов, содержащихся в 12 г изотопа углерода 12С, называется молем.
Число Авогадро
NA= 6,02 ч 1023 моль-1. Величина, необходимая при расчетах. Показывает, сколько молекул содержится в одном моле любого вещества.
Молярная масса
М – масса одного моля:
М = NAm ? 1а. е. м,
где NA– число Авогадро;
m– молекулярная масса.
Молярная масса [M] = кг/моль и молярный объем [VM] = м3/моль.
Объем одного моля – молярный объем:
VM = M / r
где M– молярная масса;
r– плотность вещества.
Формулы для определения числа молей вещества и числа молекул вещества имеют следующий вид:
u= m /M= V/ VM,
N = uNA= (m / M)NA = (V/ VM)NA.
Температура
За меру температуры принято брать среднюю кинетическую энергию поступательного движения молекул. Если два тела при соприкосновении не обмениваются энергией путем теплообмена, можно говорить, что эти тела имеют одинаковую температуру и в системе существует тепловое равновесие.
Если два тела при соприкосновении не обмениваются энергией путем теплообмена, можно говорить, что эти тела имеют одинаковую температуру и в системе существует тепловое равновесие.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРесУрок-открытие с элементами исследования. Уравнение состояния идеального газа.
Урок проводится в 10 классе, после изучения темы основное уравнение МКТ. (рассчитан на профильный уровень, слайд 0)
Цели урока:
- Образовательные. Показать математическую зависимость между тремя макроскопическими параметрами p,V,T. Научить применять физические законы при решении задач. Научить применять полученные знания как язык науки, имеющий огромные возможности.

- Воспитательные. Дать возможность почувствовать свой потенциал каждому учащемуся, чтобы показать значимость полученных знаний. Побудить к активной работе мысли. Развивать кругозор учащихся и патриотические чувства, гордости за свою страну, которая играла и играет в прогрессе человечества большую роль.
- Развивающие. Формировать умение вести рассказ с помощью опорного конспекта, выражать свои мысли правильным «физическим» языком. Формировать умение выделять главное, обобщать и связывать имеющиеся знания со знаниями из других областей. Формировать умение наблюдать и анализировать явления, кратко и лаконично отвечать на вопросы.
Тип урока: изучение нового материала, с использованием элементов беседы.
Эпиграф к уроку:
«Посев научный взойдет для жатвы народной!»
(Дмитрий Иванович Менделеев) (слайд 1)
Демонстрации: зависимость между объемом, давлением и температурой.
Оборудование: мульдимедийный проектор, компьютер, экран, презентация PowerPoint.
Ход урока
I. Проверка домашнего задания. Повторение ранее изученного. (фронтальный опрос)
Учитель. Здравствуйте ребята. Добрый день. Выполним с вами экспериментальную задачу. Определим атмосферное давление в нашем кабинете. Оборудование: термометр, линейка (рассуждения учащихся).
Ученик. Термометром можно измерить температуру, линейкой измерить размеры комнаты и вычислить объем. А как установить зависимость между давлением, объемом и температурой?
Учитель. И это будет целью нашего урока, вывели физический закон, устанавливающий зависимость между тремя макроскопическими параметрами — p, V, T; научиться использовать закон при решении задач.
Учитель. Что такое идеальный газ? (слайд 2)
Ученик. Идеальным газом называется модель реального газа. Молекулярно-кинетическая теория рассматривает идеальный газ как множество частиц (молекул), расстояние между которыми намного превышает размеры самих частиц, находящихся в состоянии непрерывного хаотичного движения.
Молекулярно-кинетическая теория рассматривает идеальный газ как множество частиц (молекул), расстояние между которыми намного превышает размеры самих частиц, находящихся в состоянии непрерывного хаотичного движения.
Учитель. Назовите условия, при которых газ можно считать идеальным?
Ученик. Газ, удовлетворяющий следующим условиям:
- Межмолекулярные взаимодействия отсутствуют.
- Взаимодействия молекул газа происходит только при соударениях, и являются упругими.
- Молекулы газа не имеют объема – материальные точки.
Учитель. Что называется концентрацией?
Ученик. Концентрация – это число молекул в единице объема.
Учитель. Запишите и объясните физический смысл основного уравнения молекулярно-кинетической теории.
Ученик. Давление идеального газа обусловлено ударами молекул о стенку сосуда, поэтому с помощью молекулярно-кинетической теории его можно выразить через концентрацию молекул, средние скорости молекул и массу одной молекулы.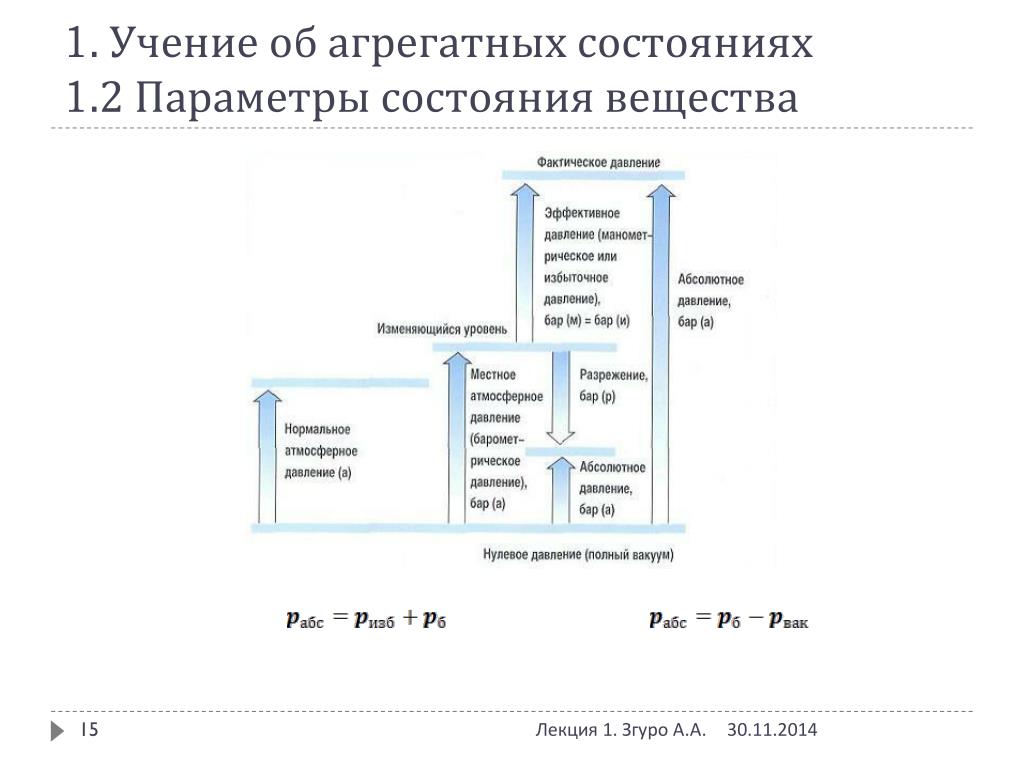 p=⅓nmoυ2 — основное уравнение МКТ (уравнение Клаузиуса), устанавливает связь между микро- и макромиром. (слайд 3)
p=⅓nmoυ2 — основное уравнение МКТ (уравнение Клаузиуса), устанавливает связь между микро- и макромиром. (слайд 3)
II. Постановка проблемного вопроса и решение его
Учитель. Какие параметры, характеризующие газ и процессы, проходящие в нем, называются микроскопическими параметрами (микропараметрами).
Ученик. Состояние идеального газа и процессы, проходящие в нем, будут определяться количеством частиц (молекул), из которых состоит газ, и их параметрами, такими как масса, диаметр, скорость, энергия и пр. (слайд 4) Такие параметры называются микроскопическими или микропараметрами.
Учитель. Какие параметры, характеризующие газ, и процессы, проходящие в нем, называются макроскопическими параметрами (макропараметрами)? (слайд 5)
Ученик. Параметры, характеризующие свойства газа как целого называются макроскопическими или макропараметрами.
Учитель. Если состояние газа не меняется, то не меняются и эти параметры. Назовите макропараметры, характеризующие газ?
Если состояние газа не меняется, то не меняются и эти параметры. Назовите макропараметры, характеризующие газ?
Ученик. p – давление, V – объем, T – температура.
Учитель. Температуру, объем, давление и некоторые другие параметры принято называть параметрами состояния газа. Выведем уравнение, устанавливающее зависимость между этими параметрами. (слайд 6)
III. Изучение нового материала
1. Постоянная Лошмидта. Из основного уравнения МКТ идеального газа можно получить уравнение состояния идеального газа, связывающее между собой параметры состояния p, V и Т.
Если исключим из основного уравнения МКТ микроскопические параметры, заменяя их на макроскопические параметры используя известные соотношения , получаем:
p=nkT (1)
Это соотношение позволяет по двум известным макроскопическим параметрам (давлению и температуре газа) оценить микроскопический параметр (концентрацию).
Найдем концентрацию молекул любого идеального газа при нормальных условиях (н.у.):
Нормальные условия:
атмосферное давление p=1,013·105 Па,
температура 0°С, или Т=273,15К:
n=p/kT=1,01·105/(1,38·10-23·273)м-3≈2,7·1025м-3.
Это значение концентрации молекул идеального газа при нормальных условиях называется постоянной Лошмидта.
2. Уравнение Клапейрона.
Получим теперь с помощью равенства (1) новое уравнение. Если известно полное число частиц газа N, занимающего объем V, то число частиц в единице объема
n=N/V,
N=const
С учетом этого выражение (1) приводится к виду
P=NkT/V
pV=NkT (2)
pV/T=NkT
p1V1/T1=p2V2/T2= const
Так как Nk=const.
Для постоянной массы идеального газа отношение произведения давления на объем к данной температуре есть величина постоянная.
Выведенное нами уравнение связывает давление, объем и температуру, которые определяют состояние идеального газа, называется уравнением состояния идеального газа. – уравнение Клапейрона (слайд 7)
Историческая справка. (сообщение ученика, Приложение 1) В 1834 г. Французский физик Б. Клапейрон, работавший длительное время в России (Петербурге), вывел уравнение состояние идеального газа при постоянной массе газа (m=const).(слайд 8)
3. Уравнение Менделеева – Клапейрона.
Рассмотрим случай для произвольной массы газа
где NA = 6,02·1023моль-1 — число Авогадро,
k=1,38·10-23 Дж/К — постоянная Больцмана
R=kNA = 8,31Дж/( моль·К) — универсальная газовая постоянная.
pV=m/M R T — уравнение Менделеева – Клапейрона- уравнение состояния идеального газа, связывающее три макроскопических параметра (давление, объем и температуру) газа данной массы. (слайд 9)
Историческая справка. (сообщение ученика, Приложение 2) Обобщив уравнение Клапейрона и введя понятие универсальной газовой постоянной, русский ученый Д. И. Менделеев в 1874 г.вывел общее уравнение для состояния идеального газа. (уравнение Менделеева – Клапейрона) (слайд 10)
С помощью данного уравнения можно описывать процессы сжатия и расширения, нагревания и охлаждения идеального газа.
IV.Закрепление изученного материала
1. Беседа с учащимися по вопросам. (слайд 11)
Учитель. Каковы нормальные условия для идеального газа?
Ученик. Нормальные условия для идеального газа: атмосферное давление p=1,013·105 Па, температура t=0°С, или Т=273,15К:
Учитель: Какова концентрация молекул идеального газа при нормальных условиях?
Ученик: n=p/kT=1,01·105/(1,38·10-23·273)м-3≈2,7·1025м-3 , это значение концентрации – число Лошмидта.
Учитель: Какие величины характеризуют состояние газа?
Ученик: Макропараметры p, V, T.
Учитель: Чем отличается уравнение состояния газа от уравнения Менделеева — Клапейрона? Какое из них полнее по содержанию? Почему?
Ученик: Уравнение состояния идеального газа для постоянной массы газа. Уравнение Менделеева – Клапейрона для переменной массы газа
Учитель. Чему равна универсальная газовая постоянная в СИ?
Ученик. R=NAk= 8,31Дж/ моль·К – универсальная газовая постоянная
2. Решение задач у доски с помощью учителя. (слайд 12)
Задачи 1, 3, 4 к § 53 (Приложение 3).
Дополнительная задача. Для постоянной массы идеального газа отношение произведения давления на объем к данной температуре есть величина постоянная.
Вычислите отношение произведения давления на объем к данной температуре, если газ находиться при нормальных условиях
Полагая что моль газа находиться при нормальных условиях: атмосферное давление p0=1,013·105 Па, температура t= 0°С, или Т0=273,15К, молярный объем V0= 22,41·10-3м3/моль): Подставим и получим
p0V0/T0=8,31 Дж/(моль·К)
R=8,31 Дж/(моль·К) –универсальная газовая постоянная.
V. Итоги урока
Ученик. Поставленной цели мы достигли: вывели физический закон, устанавливающий зависимость между тремя макроскопическими параметрами — p, V, T; и использовали его при решении задач.
Учитель. Уравнение состояния — первое из замечательных обобщений в физике, с помощью которых свойства разных веществ выражаются через одни и те же основные величины. Именно к этому стремиться физика — к нахождению общих законов, не зависящих от тех или иных веществ. Газы, существенно простые по своей природе, дали первый пример такого обобщения. (слайд 13)
А завершить урок хотелось словами Д.И. Менделеева, обращенными к нам, его потомкам: «Посев научный взойдет для жатвы народной!». И этот год юбилейный, 175-лет со дня рождения великого русского ученого-естествоиспытателя Д.И. Менделеева (слайд 14).
VI. Домашнее задание
§ 53, задачи 2, 5 к § 53.
Литература: Касьянов В. А.. Физика. 10 кл. Профильный уровень/ Из-во — Москва: Дрофа, 2007.
А.. Физика. 10 кл. Профильный уровень/ Из-во — Москва: Дрофа, 2007.
Презентация — Приложение 4, сообщение ученика о Клапейроне — Приложение 1, сообщение ученика о Менделееве — Приложение 2, задачи для закрепления пройденной темы — Приложение 3.
Лекции о теплотехнике
ЧАСТЬ 1. ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА
Тема 1. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ И ЗАКОНЫ
1.1.Предмет и метод технической термодинамики
Исторически термодинамика возникла как наука, изучающая переход теплоты в механическую работу, что диктовалось необходимостью дать теоретические основы работы тепловых машин.
Принцип построения термодинамики довольно прост. В ее основу положены три экспериментальных закона и уравнение состояния: первый закон (первое начало термодинамики) — закон сохранения и превращения энергии; второй закон (второе начало термодинамики) указывает направление, по которому протекают естественные явления в природе; третий закон (третье начало термодинамики) утверждает, что абсолютный нуль температуры недостижим.
1.2.Термодинамическая система
Термодинамическая система — тело (совокупность тел), способное (способных) обмениваться с другими телами (между собой) энергией и веществом.
Термодинамическая система имеет границы, отделяющие ее от окружающей среды. Границы термодинамической системы могут быть как реальными (газ в резервуаре, граница раздела фаз), так и чисто условными в виде контрольной поверхности.
Термодинамическая система может энергетически взаимодействовать с окружающей средой и с другими системами, а также обмениваться с ними веществом. В зависимости от условий взаимодействия с другими системами различают изолированную, замкнутую, открытую и адиабатно изолированную термодинамические системы.
Термодинамическая система, которая не может обмениваться энергией и веществом с другими системами, называется изолированной. В такой системе отдельные части (подсистемы) могут взаимодействовать между собой. Термодинамическая система называется закрытой, если она не может обмениваться веществом с другими системами. Термодинамические системы, которые могут обмениваться веществом с другими системами, называются открытыми.
Термодинамическая система, которая не может обмениваться теплотой с другими системами (окружающей средой), называется теплоизолированной или адиабатно изолированной.
С окружающей средой термодинамическая система может энергетически взаимодействовать посредством передачи теплоты и производства работы.
По роли отдельных тел, входящих в термодинамическую систему, их делят на рабочие тела (РТ), источники теплоты (ИТ) и объекты работы (ОР).
Рабочими телами являются, как правило, газообразные вещества — газы и пары, которые способны значительно изменять свой объём при изменении внешних условий.
В тех состояниях, когда можно пренебречь влиянием сил взаимодействия между молекулами и объёмом самих молекул (сильно нагретый газ при небольших давлениях), газ называют идеальным. В противном случае газ называется реальным.
Рабочее тело в тепловой машине получает или отдаёт теплоту, взаимодействуя с более нагретыми или более холодными внешними телами. Такие тела носят название источников теплоты.
Тело, которое отдаёт теплоту рабочему телу и не изменяет свою температуру, называется верхним источником теплоты (ВИТ) или теплоотдатчиком. Тело, которое получает теплоту от рабочего тела и не изменяет свою температуру, называется нижним источником теплоты (НИТ) или теплоприёмником.
1.3.Термодинамическое состояние и термодинамический процесс
Совокупность физических свойств системы в рассматриваемых условиях называют термодинамическим состоянием системы.
Различают равновесное (стационарное) и неравновесное (нестационарное) состояния термодинамической системы.
Макроскопические величины (т. е. величины, которые характеризуют тело в целом), характеризующие физические свойства тела в данный момент, называются термодинамическими параметрами состояния. Последние разделяются на интенсивные (не зависящие от массы тела) и на экстенсивные (пропорциональные массе тела).
К основным параметрам состояния, поддающимся непосредственному измерению простыми техническими средствами, относятся абсолютное давление , удельный объём и абсолютная температура . Эти три параметра носят название термических параметров состояния.
К параметрам состояния относятся также внутренняя энергия , энтальпия и энтропия , которые носят название калорических параметров состояния.
Равновесным состоянием термодинамической системы называется такое состояние, которое характеризуется при постоянных внешних условиях неизменностью параметров во времени и отсутствием в системе потоков. Состояние термодинамической системы, при котором во всех ее частях температура одинакова, называют термическим равновесным состоянием.
Изолированная термодинамическая система независимо от своего начального состояния с течением времени всегда приходит в состояние равновесия. Необходимо отметить, что никогда самопроизвольно выйти из него система не может (основной постулат термодинамики — нулевое начало).
Состояние термодинамической системы, при котором значения параметров во всех частях ее остаются неизменными во времени благодаря внешнему воздействию потоков вещества, энергии, импульса, заряда и т. п., называется стационарным. Если значения параметров изменяются во времени, то состояние термодинамической системы называется нестационарным.
Любое изменение в термодинамической системе, связанное с изменением хотя бы одного из ее параметров, называется термодинамическим процессом. Если одна система совершает работу над другой системой с помощью механических и электрических сил, то взаимодействие называется механическим. Взаимодействие, которое приводит к изменению энергии и совершается в форме передачи теплоты посредством теплопроводности или тепловой радиации, называется тепловым. Взаимодействие, приводящее к изменению энергии и совершаемое в форме передачи массы, называется массообменным.
Различают равновесные и неравновесные процессы.
Равновесным процессом называется термодинамический процесс, представляющий собой непрерывную последовательность равновесных состояний. В таком процессе физические параметры изменяются бесконечно медленно, так что система все время находится в равновесном состоянии. Кроме того, все части системы имеют одинаковые температуру и давление.
Неравновесным процессом называется термодинамический процесс, представляющий собой последовательность состояний, среди которых не все являются равновесными. В неравновесном процессе различные части системы имеют разные температуры, давления, плотности, концентрации.
Если термодинамическая система выведена из состояния равновесия и предоставлена сама себе, то через некоторый промежуток времени она снова придет в состояние равновесия. Процесс перехода системы из неравновесного состояния в равновесное называется релаксацией, а время перехода в состояние равновесия — временем релаксации.
1.4.Термические и калорические параметры состояния
К термическим параметрам состояния относятся давление , объем , температура .
К калорическим параметрам состояния относятся следующие основные термодинамические величины: энтропия , внутренняя энергия и энтальпия .
1.4.1.Термические параметры состояния
Давление — физическая величина, численно равная отношению нормальной составляющей силы к площади, на которую действует эта сила.
Единицей давления в СИ является паскаль — давление, вызываемое силой в 1 Н, равномерно распределенной по поверхности площадью 1 м2 (1Па=1 Н/м2). Часто приходится измерять давление высотой столба какой-либо жидкости (воды, ртути и др.).
В табл. 1.1 приведены соотношения между ранее применявшимися единицами измерения давления и единицами давления в СИ.
Таблица 1.1 | ||||||
Единица | Па | бар | кгс/см2 | мм рт.ст. | мм вод.ст. | |
1 Па | 1 | 10-5 | 1,02·10-5 | 7,5024·10-3 | 1,02·10-1 | |
1 бар | 105 | 1 | 1,02 | 7,5024·102 | 1,02·104 | |
1 кгс/см2 | 9,8067·104 | 0,98067 | 1 | 735 | 104 | |
1 мм рт.ст. | 133 | 1,33·10-3 | 1,36·10-3 | 1 | 13,6 | |
1 мм вод.ст. | 9,8067 | 9,8067·10-5 | 10-4 | 7,35·10-2 | 1 | |
Различают атмосферное, или барометрическое, давление , абсолютное давление , манометрическое, или избыточное, разрежение, или вакуум.
Давление, создаваемое атмосферным воздухом, называется барометрическим, или атмосферным.
Абсолютным давлением называется давление, отсчитываемое от нуля (абсолютного вакуума).
Избыточным, или манометрическим, давлением называется давление сверх атмосферного, то есть избыточное давление — это разность между абсолютным и барометрическим давлениями: .
Разрежением, или вакуумом, называется разность между атмосферным давлением и абсолютным давлением той среды, где измеряется давление. Если абсолютное давление газа или пара в сосуде ниже барометрического, то есть , то разность называется разрежением, или вакуумом.
Вакуум показывает, насколько давление газа (пара) меньше давления окружающей среды. Давление атмосферного воздуха измеряется барометрами, избыточное давление — манометрами, а давление разрежения — вакуумметрами.
В термодинамических уравнениях всегда используют значения абсолютного давления ввиду того, что оно является параметром, характеризующим состояние термодинамической системы.
Атмосферное давление — величина переменная, поэтому в технике применяется нормальное атмосферное давление, (760 мм рт. ст.).
Температура тела есть мера его нагретости. Температура определяет направление передачи теплоты. Если два тела А и В имеют соответственно температуру Т1 и Т2 и Т1>Т2, то теплота переходит от тела А к телу В. При этом температура тела А уменьшается, а тела В — увеличивается.
С точки зрения молекулярно-кинетической теории температура есть мера интенсивности теплового движения молекул.
В термодинамике рассматривают температуру как среднестатистическую величину, которая характеризует систему, состоящую из очень большого числа молекул (частиц), находящихся в хаотическом (тепловом) движении. Поэтому к единичным молекулам понятие температуры не применимо. При температуре абсолютного нуля тепловое движение молекул отсутствует. Эта предельная минимальная температура называется абсолютным нулем и является началом для отсчета температур. Понятно, что не может быть , то есть абсолютная температура всегда положительна.
Температура, отсчитываемая от абсолютного нуля, называется абсолютной, а шкала температур называется шкалой Кельвина.
Практически измерять кинетическую энергию молекул газа непосредственно невозможно. Поэтому для измерения температуры используют различные косвенные методы. Температура измеряется при помощи различных термодинамических устройств — термометров).
Использование термометров основано на том факте, что два соприкасающихся тела с разными температурами через некоторое время приходят к состоянию теплового равновесия и принимают одинаковую температуру.
Численный отсчет температуры производится по шкале температур. За основную единицу измерения температуры принимают градус, имеющий разную величину в различных температурных шкалах. Шкала температур устанавливается путем деления разности показаний термометра в двух произвольно выбранных постоянных температурных точках, называемых реперными или опорными, на некоторое число равных частей — градусов.
Ввиду того, что выбор постоянных температурных точек и цены деления шкалы является произвольным, имеется ряд различных шкал температуры.
В настоящее время применяются различные температурные шкалы: Цельсия, Фаренгейта, Реомюра, Ранкина.
По шкале Цельсия () приняты следующие постоянные температурные точки: О°C — температура таяния льда, 100°C — температура кипения воды при нормальном атмосферном давлении.
В 1724 г. Фаренгейт предложил термометр, в качестве реперных точек которого приняты: +212°F — температура кипения воды при нормальном атмосферном давлении; +32°F — температура таяния льда. Разность температур кипения воды и таяния льда по шкале Фаренгейта равна 212°— 32° = 180 °F, а по шкале Цельсия — 100°C. Следовательно, 1°F соответствует 5/9 °C, а 1°C — 1,8°F.
Шкала Реомюра () имеет следующие реперные точки: О°R — температура таяния льда, 80°R — температура кипения воды при нормальном атмосферном давлении.
Шкала Ранкина () — это шкала Фаренгейта, отсчитанная от абсолютного нуля. В этой шкале температура таяния льда (T0=273,15 К) соответствует 491,67°Ra, а температура кипения воды при нормальном атмосферном давлении (T0=373,15 К) соответствует 671,67°Ra.
Решением Международного комитета мер и весов приняты две шкалы: термодинамическая температурная шкала, которая принята основной, и Международная практическая температурная шкала (МПТШ-68), выбранная таким образом, чтобы температура, измеренная по этой шкале, была близка к термодинамической. В основу построения термодинамической шкалы положен тот факт, что в циклах Карно, располагающихся между двумя адиабатами, разность температур изотерм считается постоянной, если в механическую работу превращаются одинаковые количества теплоты. Наиболее универсальной шкалой температур является абсолютная термодинамическая шкала температур — шкала Кельвина.
В шкале Кельвина используется единственная экспериментальная реперная точка — тройная точка химически чистой воды (в термодинамическом равновесии находятся три агрегатных состояния; лед, жидкая вода и пар). Этому состоянию соответствует температура 273,15К (0,01°С). Второй постоянной точкой является абсолютный нуль температур (0К). Кельвин — единица измерения температуры по термодинамической температурной шкале, равная 1/273,15 части интервала от абсолютного нуля температуры до температуры тройной точки воды.
Практическим осуществлением термодинамической шкалы температур является Международная практическая температурная шкала. В этой шкале используется одиннадцать реперных точек. В табл. 1.2 приведены значения основных реперных точек.
Таблица 1.2 | ||
Равновесное состояние | МПШТ-68 | |
T68 | t68 | |
Точка кипения кислорода | 90,188 К | -182,962 0C |
Тройная точка воды | 273,16 К | +0,01 0C |
Точка кипения воды | 373,15 К | +100,0 0C |
Точка плавления цинка | 692,73 К | +419,58 0C |
Точка плавления серебра | 1235,08 К | +961,93 0C |
Точка плавления золота | 1337,58 К | +1064,43 0C |
Температуры кипения и плавления даны при давлении 101325 Па | ||
Удельный объем вещества — это объем, занимаемый единицей массы данного вещества.
Плотность вещества — величина, обратная удельному объему и определяющая количество вещества, заключенное в единице объема.
Единица плотности в СИ — кг/м3, в системе СГС — г/см3. Плотность и удельный объем зависят от температуры и давления, то есть от термодинамического состояния вещества. Обычно в справочниках приводятся их значения при нормальных физических условиях. За нормальные физические условия принимают давление, равное 101,325 кПа (760 мм рт. ст.), и температуру, равную О °С.
Количество вещества. Единицей количества вещества в СИ является моль. Кроме моля применяют кратные и дольные части от моля (кмоль, Ммоль и др.). Количество вещества — это физическая величина, определяемая числом структурных элементов (атомов, молекул, ионов, электронов). Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг.
Молярной массой вещества называют отношение массы вещества к его количеству:
где μ — молярная масса. Если выразить в кг, — в молях, μ — выразится в кг/моль.
1.4.2.Калорические параметры состояния
К калорическим параметрам состояния относятся, как уже отмечалось, внутренняя энергия , энтальпия и энтропия . Своим названием эти параметры обязаны тому, что ранее измерялись в калориях.
Внутренняя энергия. Любая термодинамическая система в каждом состоянии обладает запасом полной энергии , которая состоит из внутренней энергии , зависящей от внутреннего состояния тела, и внешней энергии , связанной с движением тела как целого и положением его в каком-либо внешнем поле сил (например в поле сил тяжести), т. е.
Страница не найдена |
Страница не найдена |404. Страница не найдена
Архив за месяц
ПнВтСрЧтПтСбВс
25262728293031
12
12
1
3031
12
15161718192021
25262728293031
123
45678910
12
17181920212223
31
2728293031
1
1234
567891011
12
891011121314
11121314151617
28293031
1234
12
12345
6789101112
567891011
12131415161718
19202122232425
3456789
17181920212223
24252627282930
12345
13141516171819
20212223242526
2728293031
15161718192021
22232425262728
2930
Архивы
Метки
Настройки
для слабовидящих
законов о газе
законов о газеГазовые законы
Нижеследующее содержание является сутью лекции 18. В этой лекции мы рассматриваем законы газа: законы Шарля, Бойля, Авагадро и Гей-Люссака, а также законы идеального и комбинированного газа.
Законы о свойствах газа
Есть 4 общих закона, которые связывают 4 основных характерных свойства газов друг с другом. Каждый закон назван его первооткрывателем. Хотя важно понимать отношения, охватываемые каждым законом, знание отправителя не так важно и будет лишним после введения закона о комбинированном газе.Поэтому сосредоточьтесь на понимании отношений, а не на запоминании имен.
Закон Чарльза — дает соотношение между объемом и температурой , если давление и количество газа поддерживаются постоянными :
1) Если температура газа по Кельвину увеличивается, объем газа увеличивается. (Постоянная P, n)
2) Если температура газа по Кельвину понижается, объем газа уменьшается. (Постоянная P, n)
Это означает, что объем газа прямо пропорционален его температуре Кельвина.Подумайте об этом так: если вы увеличиваете объем газа и должны поддерживать постоянное давление, единственный способ добиться этого — это также повысить температуру газа.
Расчеты с использованием закона Чарльза включают изменение температуры (T 2 ) или объема (V 2 ) от известного начального количества каждого из них (V 1 и T 1 ):
Закон Бойля — гласит, что объем заданного количества газа, удерживаемого при постоянной температуре, изменяется обратно пропорционально приложенному давлению, когда температура и масса постоянны.
Уменьшение объема газа означает, что молекулы ударяются о стенки чаще, увеличивая давление, и, наоборот, если объем увеличивается, расстояние, которое молекулы должны пройти, чтобы столкнуться со стенками, увеличивается, и они реже ударяются о стенки, тем самым уменьшая давление.
Как и закон Чарльза, закон Бойля можно использовать для определения текущего давления или объема газа, если известны начальные состояния и одно из изменений:
Закон Авагадро — Дает соотношение между объемом и количеством газа в молях, когда давление и температура поддерживаются постоянными.
Если количество газа в баллоне увеличивается, объем увеличивается. Если количество газа в баллоне уменьшается, объем уменьшается. Это, конечно, при условии, что контейнер имеет расширяемые стенки.
Отношение снова прямо пропорционально, поэтому уравнение для вычислений равно
.Закон Гей-Люссака — гласит, что давление заданного количества газа, удерживаемого в постоянном объеме, прямо пропорционально температуре Кельвина.
Если вы нагреете газ, вы дадите молекулам больше энергии, и они будут двигаться быстрее. Это означает большее воздействие на стенки контейнера и увеличение давления. И наоборот, если вы охладите молекулы, они замедлятся, и давление снизится.
Для расчета изменения давления или температуры с использованием закона Гей-Люссака уравнение выглядит следующим образом:
Чтобы немного поиграть с отношениями, попробуйте эту симуляцию.
Закон об идеальном газе:
Комбинация представленных выше законов порождает Закон об идеальном газе:
Добавление константы пропорциональности, называемой идеальной или универсальной газовой постоянной (R), завершает уравнение.
Как видите, для константы возможно множество единиц. Единственная постоянная константы — это то, что шкала температуры во всем — KELVIN.
При использовании закона идеального газа для расчета любого свойства газа вы должны согласовать единицы с газовой постоянной, которую вы выбираете для использования, и вы всегда должны указывать температуру в градусах Кельвина.
Чтобы использовать уравнение, вам просто нужно уметь определить, чего не хватает в вопросе, и изменить уравнение, чтобы решить его.
Типичный вопрос: 6,2 литра идеального газа содержится при 3,0 атм и температуре 37 ° C. Сколько молей этого газа присутствует?
Поскольку единицы газовой постоянной задаются в атмосфере, молях и градусах Кельвина, важно убедиться, что вы конвертируете значения, указанные в других шкалах температуры или давления.Для этой задачи преобразуйте температуру ° C в K с помощью уравнения:
Т = ° С + 273
Т = 37 ° С + 273
Т = 310 К
Теперь вы можете вставить значения. Решите относительно количества родинок
n = PV / RT
n = (3,0 атм x 6,2 л) / (0,08206 л атм / моль K x 310 K)
n = 0,75 моль
Вот некоторые практические проблемы с использованием Закона об идеальном газе: Практика
Закон о комбинированном газе
Я сказал выше, что запоминание всех уравнений для каждого из отдельных законов газа станет неактуальным после введения последующих законов.Закон, о котором я говорил, — это Закон о комбинированном газе:
.Закон комбинированного газа позволяет вывести любое из необходимых соотношений путем объединения всех изменяемых частей в законе идеального газа: а именно давления, температуры и объема. R и количество молей не фигурируют в уравнении, поскольку они обычно постоянны и поэтому сокращаются, поскольку они появляются в равных количествах с обеих сторон уравнения.
Как вы можете видеть выше, уравнение может быть решено для любого из входящих в него параметров.Но что еще более важно, вы можете исключить из уравнения все, что останется постоянным.
Например, если в вопросе говорится, что система с давлением 1 атм и объемом 2 литра претерпела изменение до 3,5 литров, вычислите новое давление, вы можете просто исключить температуру из уравнения и получить:
P 2 = P 1 V 1 / V 2 = (1 атм) (2 л) / 3,5 л) = 0,6 атм
Поскольку в вопросе никогда не упоминается температура, мы можем предположить, что она остается постоянной и поэтому будет отменена при вычислении.Вы также должны подумать над ответом, который вы получите с точки зрения того, что вы знаете о газах и о том, как они действуют. Мы увеличили объем, поэтому давление должно снизиться. Проверив наш ответ, он кажется правильным, поскольку давление упало с 1 атм до 0,6 атм.
Итак, единственное уравнение, которое вам действительно нужно знать, — это закон комбинированного газа для расчета изменений свойств газа.
Вот некоторые практические проблемы с решениями: Практика
Вот некоторые проблемы для других газовых законов, которые вы можете вывести из закона о комбинированном газе: Практика и ПОЗ.
Ideal Gas — обзор
1.5.4.2 Теория идеального газа
Теория идеального газа очень важна для анализа процессов, потому что в большинстве ситуаций влагосодержание извлекается в виде водяного пара, который ведет себя как идеальный газ. Идеальный газ можно описать тремя параметрами: объемом, который он занимает, давлением, которое он оказывает, и его температурой. Согласно определению, идеальный газ представляет собой особое состояние вещества, которое может быть ограничено границей системы. Предполагается, что:
- •
Все частицы имеют массу покоя ( m > 0; частицы не являются фотонами).
- •
Количество частиц по отношению к объему системы невелико.
- •
Общий объем частиц незначителен по сравнению с объемом системы.
- •
Столкновения частиц друг с другом гораздо менее вероятны, чем столкновения с границей системы.
Практическим преимуществом рассмотрения реальных газов как идеальных (в определенных условиях) является простое уравнение состояния с одной константой.Уравнение состояния идеального газа можно записать в следующем виде:
(77) PV = mRTorPv = RTorPv = RT
, где P — давление в Па, V — объем газа в м 3 , m — масса газа в кг, T — температура газа в K, R известна как газовая постоянная и выражается в Дж / кг · K, v — удельный объем массы в м 3 / кг, υ — молярный удельный объем в м 3 / кмоль, а ℛ — универсальная газовая постоянная из 8.134 Дж / моль К.
Обратите внимание на то, что газовая постоянная специфична для каждого конкретного газа и зависит от универсальной газовой постоянной и молекулярной массы ( M ) газа согласно
(78) R = M
Уравнение Уравнение (76) известно как «тепловое уравнение состояния» идеального газа, потому что оно выражает взаимосвязь между давлением, удельным объемом и температурой. Уравнение идеального газа можно выразить через внутреннюю энергию, удельный объем и температуру.В этом случае уравнение состояния называется калорическим уравнением состояния. В частности, только для идеального газа внутренняя энергия зависит только от температуры. Калорическое уравнение состояния одноатомного идеального газа имеет следующий вид:
(79) u = 1,5ℛT
, где u — молярная удельная внутренняя энергия.
Поскольку h = u + P v , получается, что энтальпия одноатомного идеального газа равна
(80) h = 2,5ℛT
Объединяя два калорических уравнения состояния из Ур.(79) и (80) известное уравнение Роберта Мейера для идеального газа может быть получено следующим образом:
(81) Cp = Cv + R
Можно заметить, что для идеального газа внутренняя энергия является функцией температуры Только. Следовательно, удельная теплоемкость идеального газа составляет C v = 1,5 R и C P = 2,5 R . Отношение удельной теплоемкости при постоянном давлении и постоянном объеме известно как показатель адиабаты , а именно
(82) γ = CPCv
Показатель адиабаты для идеального газа имеет следующие значения: одноатомный газ 1.4 и 5/3 = 1,67 для двухатомного газа. Существуют некоторые особые случаи, когда одно из значений P , v или T является постоянным. При фиксированной температуре объем данного количества идеального газа изменяется обратно пропорционально давлению, оказываемому на него (в некоторых книгах это называется законом Бойля), описывая изменение объема следующим образом:
(83) P1V1 = P2V2
где нижние индексы относятся к начальному и конечному состояниям.
Ур. (83) используется аналитиками в различных ситуациях: при выборе воздушного компрессора, для расчета потребления сжатого воздуха в поршневых воздушных цилиндрах и для определения продолжительности времени, необходимого для хранения воздуха.Если процесс происходит при постоянном давлении или постоянном объеме, то применяется закон Чарльза:
(84) V1T1 = V2T2 и P1T1 = P2T2
Если количество молей идеального газа не изменяется в замкнутом объеме, тогда объединенное идеальное уравнение состояния задается следующим образом:
(85) P1V1T1 = P2V2T2
Основные процессы с идеальным газом известны следующим образом: изотермический, изохорный, изобарический, изоэнтропический и политропный. Таблица 4 дает описание и соответствующее уравнение для каждого процесса.Изэнтропический процесс аналогичен политропному, но с показателем n , равным показателю адиабаты. Изохорный, изобарический, изотермический и изоэнтропический (т. Е. Политропный с n = γ = 1,4) процессы идеального газа на воздухе показаны на рис. 26.
Таблица 4. Простые термодинамические процессы и соответствующие уравнения для модели идеального газа
| Процесс | Определение | Уравнение | Рабочее выражение |
|---|---|---|---|
| Изотермический | T = const. | P1v1 = P2v2 | w1−2 = P1v2ln (v2 / v1) |
| Изохорический | v = const. | P1T1 = P2T2 | w1−2 = 0 |
| Изобарический | P = const. | v1T1 = v2T2 | w1−2 = P (v2 − v1) |
| Polytropic | Pv n = const. | P2P1 = (V1V2) n = (T2T1) n / (n − 1) | w1−2 = 1n − 1 (P2v2 − P1v1) |
| Общий | P , v , T изменение постоянной массы | P1v1T1 = P2v2T2 | w1−2 = ∫12Pdv |
Рис.26. Процессы идеального газа, представленные на диаграмме P — v .
Удельное изменение энтропии идеального газа с постоянной удельной теплоемкостью определяется следующими уравнениями в зависимости от типа процесса (при постоянном давлении или постоянном объеме):
(86) s2 − s1 = Cv0ln (T2T1) + Rln (v2v1) и s2 − s1 = Cv0ln (T2T1) + Rln (P2P1)
Предположим, что термодинамическая система произвольной формы содержит идеальный газ. Для простоты пусть эта форма представляет собой куб, как показано на рис. 27.Основываясь на законе сохранения импульса, сила, действующая на стенку одной частицей во время столкновения, определяется следующим образом:
Рис. 27. Кубовидная термодинамическая система, охватывающая идеальный газ во внутреннем термодинамическом равновесии при температуре T и давлении С .
(87) F = mυ − m (−υ) Δt = mυ2l
Также предполагается, что существует равномерное распределение столкновений частиц для трех декартовых направлений; таким образом, только 1/3 частиц оказывает силу на стену.Следовательно, выражение давления определяется делением силы на площадь стенки A следующим образом:
(88) P = 13Nmυ2lA = Nm3V = 13ρυ2
, где N — количество частиц, каждая из которых имеет массу м. , плотность обозначается как ρ = нм / V, а V = мкА — это объем термодинамической системы.
Кинетическая энергия отдельной частицы газа может быть выражена на основе средней скорости частицы; в этом отношении уравнение.(88) решается для v 2 и получается
(89) KE = 12mυ2 = 32PVN
степень свободы одноатомных молекул газа составляет DOF = 3, потому что существует только три возможных трансляционных движения. по декартовой оси. Согласно термодинамическому определению, температура ( T ) является мерой средней кинетической энергии молекул на степень свободы. Количественное соотношение между температурой и кинетической энергией одной отдельной молекулы соответствует
(90) KEDOF≡12kBT
, где k B — постоянная Больцмана, определенная в таблице 3.Решение уравнения. (90) для T приводит к термодинамическому выражению для температуры следующим образом:
(91) T≡2KEkBDOF
Из уравнений. (89) и (91) для температуры получено следующее выражение:
(92) T = PVkBN = PVkB (N / NA) NA = PVkBnNA = PvkBNA
, где v — молярный удельный объем и n — количество вещества (число молей).
Далее получается следующее термодинамическое определение температуры:
(93) T≡PvkBNA≡Pvℛ
, где ℛ — универсальная газовая постоянная , задается следующим образом:
(94) ℛ = kBNA
Во многих практических ситуации смеси реальных газов можно аппроксимировать как смеси идеальных газов.Существуют две модели идеального газа для газовых смесей: модель Дальтона и модель Амагат. Для обеих моделей предполагается, что на каждый газ не влияет присутствие других газов. Модель Дальтона предполагает, что смесь находится при постоянной температуре и объеме, тогда как объем Амагат рассматривает случай, когда температура и давление постоянны. В таблице 5 представлено сравнение моделей Dalton и Amagat для идеальных газовых смесей. Уравнения, связывающие термодинамические параметры составляющих газов с параметрами смеси, приведены в таблице 6.
Таблица 5. Модели Dalton и Amagat для идеальных газовых смесей
| Определение | Модель Dalton | Модель Amagat | ||
|---|---|---|---|---|
| Допущения | T и V являются постоянными постоянны | |||
| Ptot = P1 + P2 + ⋯ + PN | Vtot = V1 + V2 + ⋯ + VN | |||
| Уравнения для компонентов | PiV = niℛT | PVi = niℛT | для смесиPtotV = (∑n) ℛT | PVtot = (∑n) ℛT |
Таблица 6.Соответствующие параметры идеальных газовых смесей
| Параметр | Уравнение |
|---|---|
| Общая масса смеси N компонентов | mtot = ∑mi |
| Общее количество молей смеси N компоненты | ntot = ∑ni |
| Массовая доля для каждого компонента | ci = mi / mtot |
| Мольная доля для каждого компонента | yi = nintot = (PiPtot) Daltonmodel = (ViVtotmodel) |
| Молекулярная масса смеси | Mmix = mtotntot = ∑ (niMi) ntot = ∑ (yiMi) |
| Внутренняя энергия смеси | Umix = ∑ (niUi) | Hmix = ∑ (niHi) |
| Энтропия смеси | Smix = ∑ (niSi) |
| Разность энтропии для смеси | S2 − S1 = −ℛ∑ (nilnyi) |
Химия: состояния материи: твердые тела, жидкости, газы и плазма
Введение
На Земле существует три общих состояния материи: твердое, жидкое и газообразное.Состояние определяет физическое свойство материи. Определяющие характеристики, которые определяют состояние, включают количество и химический состав молекул, а также то, как конкретная их совокупность представлена такими физическими свойствами, как их общий объем и форма, их реакция на температуру и их реакцию на давление.
Твердое состояние вещества характеризуется фиксированной формой, которая зависит от количества и характеристик конкретных атомов и молекул, составляющих твердое тело.Твердое тело сопротивляется изменению формы из-за внешнего давления. В очень небольшой степени по сравнению с другими состояниями плотность (масса / объем) твердых тел зависит от температуры. Твердые вещества могут быть кристаллическими, что означает, что они имеют очень упорядоченную структуру по отношению к частицам, составляющим твердое тело, или твердое вещество может быть аморфным и не иметь симметрии в расположении частиц, составляющих твердое тело.
В жидком состоянии материя будет течь, принимая форму любого сосуда. Плотность жидкостей в значительной степени зависит от температуры, но замкнутые жидкости сопротивляются изменениям из-за давления.Газообразное состояние также будет иметь форму контейнера, но отличается от жидкостей тем, что оно будет расширяться, чтобы заполнить любой контейнер, так что, если размер контейнера увеличивается, газ расширяется, чтобы заполнить его. Температура, давление и количество молекул — все это важные параметры при определении объема газа. Различные газы всегда полностью смешиваются (смешиваются), но разные жидкости не всегда смешиваются.
Термин фаза используется в определенных контекстах, а не состояние, для описания физических свойств материи.Фаза — это более ограничивающий термин, который обычно используется в научных исследованиях, но не часто используется в общей беседе. Если фаза отличается от состояния, это лучше всего понять при описании жидких смесей, таких как масло и вода. Каждая физически и химически отличная и разделяемая жидкость представляет собой отдельную фазу. Отдельные объекты, как и смесь, находятся в жидком состоянии.
Плазма называется четвертым состоянием материи. Это не обычное явление на поверхности Земли, но 90% вещества в космосе находится в плазменном состоянии.Естественная плазма действительно составляет ионосферу, слой заряженных частиц с низкой плотностью в верхних слоях атмосферы Земли. Состояние плазмы похоже на состояние газа, за исключением того, что оно не содержит атомов и молекул. Вместо этого плазма состоит из субатомных частиц, таких как отрицательно заряженные электроны и положительные ионы.
Историческая справка и научное обоснование
Термины «твердый» и «жидкий» являются английскими версиями латинских слов, обозначающих эти термины. У термина «газ» есть история.Его можно проследить до периода Возрождения (1400–1650 гг.), Когда Ян Баптист ван Гельмонт (1579–1644 гг.) Дал название газу тому, что сейчас известно как углекислый газ. До этого времени газы назывались воздухом, духами или парами. Исследования газов стали важной частью эволюции современной химии. Законы идеального газа, которые сегодня используют химики, возникли в результате серии исследований, последовавших за знаменитой работой ван Гельмонта.
Британский ученый Роберт Бойль (1627–1691) экспериментировал с газами и опубликовал свои наблюдения в 1660 году в трактате, который он назвал «Весна воздуха». Бойль заметил, что произведение давления газа на его объем остается постоянным при постоянной температуре для любого захваченного газа. Этот факт теперь называется законом Бойля.
Увлечение газами в целом и недавно обнаруженным газообразным водородом легче воздуха, в частности, привело французского химика Жака Шарля (1746–1823) к признанию в 1787 году, что объем фиксированного веса газа прямо пропорционален до его температуры при постоянном давлении. Этот закон, известный сегодня как закон Чарльза, является вторым из законов о газе.
Другой французский ученый, Жозеф Луи Гей-Люссак (1778–1850), экспериментировал с реакциями определенных газов и обнаружил, что они всегда реагируют в объемных соотношениях малых целых чисел. Он объявил о своей находке в 1808 году. Открытие Гей-Люссака теперь известно как закон объединения объемов.
Открытие Гей-Люссака не является одним из законов идеального газа, но оно было частью фона, который побудил итальянского физика Амадео Авагадро (1776–1856) в 1811 году предположить, что объемы газов определяются количеством молекул присутствует газ.Гипотеза Авогадро также была вдохновлена идеями, продвигающими теорию атомов и молекул британского ученого Джона Далтона (1766–1844), которые были опубликованы в 1808 году. Главный вклад Авогадро заключался в признании того, что количество молекул, а не атомов, определяет объем газа при данной температуре и давлении.
Молекулы состоят из атомов. Число атомов в молекуле зависит от природы конкретной молекулы. Кислород состоит из двух атомов в молекуле.У водяного пара их три, а у метана, обычно обнаруживаемого в разлагающемся материале, — четыре.
Объединяя все индивидуальные составляющие, Законы идеального газа утверждают, что давление, умноженное на объем газа, будет равно количеству молекул, умноженному на температуру, с константой, умноженной для соотношения различных единиц, используемых в измерениях. Математически это выражается как: PV = nRT, , где n — количество молекул, а R — константа.
Твердые тела и жидкости — это конденсированные состояния вещества. Физики проводят исследования конденсированных сред, особенно на атомном и молекулярном уровне. Физика конденсированного состояния также известна как физика твердого тела. Жидкости включены в исследование по физике твердого тела под заголовком «Мягкие конденсированные вещества». Интерес к кристаллическим твердым телам был задокументирован с доисторических времен в коллекциях местных кристаллов, в которых есть отверстия и гравюры. Древние греки также изучали кристаллы.
Структура кристаллов была открыта случайно французским монахом Рене-Жюстом Гёи (1743–1822), когда он уронил прекрасный кристалл кальцита из коллекции кристаллов Казначея Франции. При осмотре произведений Хауи отметил неизменные правильные и повторяющиеся формы всех предметов. В 1817 году он опубликовал рассказ об этом открытии и свою более позднюю работу с кристаллами в ряде книг, в том числе Traité de Cristallographie (Трактат по кристаллографии).Работа Хауи считается началом важной науки кристаллографии, которая привела к значительным успехам в понимании химической структуры кристаллических твердых тел.
Когда были открыты рентгеновские лучи, изучение кристаллов расширилось. Немецкий физик Макс фон Лауэ (1879–1960) получил Нобелевскую премию в 1914 году, а отцовская группа британских физиков сэра Уильяма Генри Брэгга (1862–1942) и Уильяма Лоуренса Брэгга (1890–1971) получила Нобелевскую премию в 1915 году за свои вклад в рентгеновскую кристаллографию.Благодаря успехам в этих ранних исследованиях изучение кристаллических молекул предоставило структурную информацию о большом количестве соединений, которые включают белки и полимеры.
Нет похожего «Эврика!» момент, связанный с историей жидкого состояния вещества. Однако текучесть и растворяющие свойства жидкостей сыграли важную роль в развитии всех наук, таких как науки о жизни, физика и химия.
The Science
Примерно в то же время, когда Авогадро выдвигал свою гипотезу, а Джон Дальтон продвигал теорию атомов и молекул, британский ботаник Роберт Браун (1773–1858) наблюдал в свой микроскоп случайные и непрерывные движения взвешенные в воде пыльцевые зерна.Это наблюдение 1827 года получило название броуновского движения. Браун не пытался объяснить движение, но в 1905 году американский физик немецкого происхождения Альберт Эйнштейн (1879–1955) предположил, что движение было результатом случайных тепловых движений молекул жидкости. Работа Эйнштейна и исследования, в результате которых были сформулированы законы идеального газа, привели к кинетической молекулярной теории, которая объясняет состояния материи и изменения состояния.
Газы описываются как состоящие из беспорядочно движущихся молекул с совершенно упругими столкновениями, когда они отрываются от стенок ограничивающего их контейнера.В жидкостях молекулы движутся одинаково беспорядочно, но молекулы переворачиваются и взаимодействуют в непосредственной близости друг от друга, поэтому они текут, чтобы заполнить контейнер. Вязкость жидкости зависит от типа молекул и их взаимодействия, а также от температуры жидкости. Твердые тела имеют случайные тепловые колебания, степень которых зависит от природы молекул и температуры твердого тела. Молекулы твердых тел колеблются на месте. Они не движутся в пространстве, как молекулы жидкости; поэтому твердое тело имеет фиксированную форму.
Изменение состояния включает добавление (или вычитание) тепла для изменения степени движения молекул, то есть для изменения температуры. Начиная с твердого тела, которое является чистым веществом, добавление тепла увеличивает молекулярные колебания. При температуре плавления добавление тепла больше не нагревает твердое тело, а вместо этого вызывает разрыв связей между молекулами. Когда было добавлено достаточно тепла, чтобы разорвать все межмолекулярные связи, твердое вещество плавится и становится жидкостью.Количество тепла, необходимое для плавления чистого твердого вещества, называется теплотой плавления этого твердого вещества.
Аналогичное увеличение движения и температуры происходит, когда жидкость нагревается до тех пор, пока молекулы жидкости не достигнут температуры, при которой энергия, поглощенная молекулами, увеличивает их скорость до такой степени, что молекулы могут покинуть слабую связь, которая удерживала их близко друг к другу. жидкость. В точке испарения температура снова не повышается, потому что вся добавленная энергия используется, чтобы заставить молекулы улетать с поверхности жидкости до тех пор, пока жидкость полностью не превратится в газ.Как только газ, добавление тепла снова увеличивает температуру. Тепло, необходимое для преобразования чистой жидкости в газ, называется теплотой испарения.
При очень высоких температурах, например, при молнии или на солнце, молекулы газа превращаются в атомы, а атомы превращаются в субатомные частицы, которые заряжены положительно и отрицательно. В этот момент газ превратился в плазму.
Влияние на науку и общество
Газообразное, жидкое и твердое состояния вещества сыграли важную роль в развитии современной химии и физики.Начиная с экспериментов Роберта Бойля с газами, которые привели к публикации им трактата The Spring of the Air в 1660 году, исследования газов значительно повлияли на развитие современных теорий химических элементов, атомов и молекул.
Британский ученый Джозеф Пристли (1733–1804) сделал ключевое открытие, выделив кислород, газ, который он назвал дефлогистированным воздухом, в соответствии с теорией того времени о том, что загадочное вещество под названием флогистон присутствует во всех веществах.Неуверенность в том, что именно открыл Пристли, была разрешена французским химиком Антуаном Лораном Лавуазье (1743–1794), который назвал газ кислородом и назвал его элементом, который по его определению является уникальным химическим веществом. Пристли не соглашался с Лавуазье. Существовавшая концепция элементов была очень ограниченной, но Лавуазье приобрел популярность среди ученых, и открытие большего количества элементов ускорилось.
Газы также участвовали в развитии теории, согласно которой материя состоит из атомов и молекул.Хотя эта теория не была широко принята в то время, когда Далтон и Авогадро продвигали свои идеи, она набрала силу с ростом популярности идей Лавуазье. К сожалению, его карьера лидера в развитии современной химии резко оборвалась. Лавуазье был не только химиком, но и богатым. Аристократический статус его семьи стал причиной его смерти на гильотине во время Французской революции (1789–1799).
Жидкости сыграли роль в продвижении концепции, согласно которой материя состоит из атомов, благодаря наблюдению Робертом Брауном в 1827 году пыльцевых зерен, движущихся в жидкости, хотя влияние этого проявлялось медленно.Несмотря на то, что собирались доказательства в поддержку существования атомов и молекул, эти концепции не были общепринятыми до тех пор, пока Эйнштейн не предположил, что движение молекул жидкости вызывает броуновское движение. Когда Эйнштейн представил свои идеи в 1905 году, теоретическая физика не была хорошо организованной наукой. Исследования Эйнштейна привлекли других ключевых ученых к развитию теории атомов и молекул, а также науки физики.
Твердое состояние оказало особое влияние в результате вклада Эйнштейна и достижений физики, которые привели к развитию атомной энергии.Разработка атомной бомбы и применение ядерной энергии — все это входит в научную дисциплину, которая теперь называется физикой твердого тела.
Современные культурные связи
Австрийский ботаник Фридрих Рейнитцер (1857–1927) обнаружил твердое кристаллическое вещество на основе холестерина, которое не плавится сразу, поскольку предполагается, что чистое твердое вещество плавится. Оказалось, что вещество имеет две точки плавления. При 229 ° F (145 ° C) кристаллы плавились в мутную жидкость. При дальнейшем нагревании до 288 ° F (178 ° C) вещество превратилось в прозрачную жидкость.Рейнитцер спросил немецкого физика Отто Лемана (1855–1922), специалиста по кристаллооптике, может ли он помочь объяснить необычное плавление кристаллов на основе холестерина. Леманн определил, что мутная фаза представляет собой новое состояние вещества, которое он назвал жидкими кристаллами. Исследователи после открытия жидких кристаллов на основе холестерина обнаружили, что другие вещества, часто в форме стержней, также образуют жидкие кристаллы.
Любопытное новое состояние вещества было исследовано в 1960-х годах французским физиком Пьером-Жилем де Женном (1932–2007).В 1991 году он получил Нобелевскую премию за вклад в науку о жидких кристаллах. Сегодня жидкие кристаллы используются в электронных информационных дисплеях для всего, от сотовых телефонов до плоских дисплеев для компьютеров и телевизоров. Эти жидкокристаллические дисплеи обычно называют ЖК-дисплеями. Разработка этих приложений для жидких кристаллов стала возможной благодаря работе де Жена.
Конкурируют с жидкокристаллическими дисплеями для телевизоров плазменные дисплеи, в которых используется газ ксенон и газ неон, заключенные в крошечные ячейки, в которых газы превращаются в плазму под действием высокого напряжения, подаваемого на электроды, прикрепленные к ячейкам.Плазменные дисплеи имеют преимущество более широкого угла обзора, чем у жидкокристаллических дисплеев.
Искусственная плазма также используется в люминесцентном освещении и в неоновых вывесках. Ученые работают над плазменными реакторами, которые когда-нибудь смогут производить энергию в очень больших масштабах, используя тот же процесс термоядерного синтеза, который используется на Солнце.
См. Также Химия: химические связи; Химия: химические реакции и сохранение массы и энергии; Физика: основные силы и синтез теории; Физика: уравнения Максвелла, свет и электромагнитный спектр; Физика: Ньютоновская физика.
библиография
Книги
Мур, Ф.Дж. История химии. Нью-Йорк: McGraw-Hill Book Company, Inc., 1939.
Мур, Уолтер Дж. Physical Chemistry. Энглвуд Клиффс, Нью-Джерси: Прентис Холл, 1979.
Моррис, Ричард. Последние колдуны: путь от алхимии к таблице Менделеева. Вашингтон, округ Колумбия: Джозеф Генри Пресс, 2003.
Табор, Д. Газы, жидкости и твердые вещества. Балтимор, Мэриленд: Penguin Books, Inc.1969.
Веб-сайты
Химический факультет Пердью. «Справка по общей химии: состояния вещества». http://www.chem.purdue.edu/gchelp/atoms/states.html (по состоянию на 18 августа 2007 г.).
Фонд химического наследия. http://www.chemheritage.org/ (по состоянию на 18 августа 2007 г.).
Физический факультет Университета Брауна. http: // www. Physics.brown.edu (дата обращения 18 августа 2007 г.).
Организация, получившая Нобелевскую премию, Информация о премии по физике. http: // nobelprize.org / nobel_prizes / Physics / (по состоянию на 18 августа 2007 г.).
Принстонская лаборатория физики плазмы: Образовательный веб-сайт по термоядерной энергии. http://fusedweb.pppl.gov/FusEdWeb-home.html (по состоянию на 18 августа 2007 г.).
Неделя науки: История физики: Эйнштейн и броуновское движение. http://scienceweek.com/2005/sw050318-1.htm (по состоянию на 18 августа 2007 г.).
Мириам К. Нагель
Уравнение состояния и термодинамических свойств для смесей [… формулы …], [… формула …], [… формула …] и [… формула …] от температуры окружающей среды до 1000 K и 280 МПа
Графическая аннотация
Ключевые слова: Уравнение состояния, термодинамика Свойства, Сверхкритический, Смесь, Объемный перевод
Реферат
Сверхкритическое водное окисление (SCWO) — эффективный метод обработки влажных органических отходов. Его моделирование требует точного расчета термодинамических свойств. В этой работе предлагается уравнение состояния (EOS), которое точно предсказывает термодинамическое состояние смесей воды, кислорода, азота и углекислого газа для широкого диапазона составов, температур и давлений, включая сверхкритические условия.EOS включает в себя преобразование объема, усовершенствованную α-функцию и неквадратичные правила микширования. Введенные параметры приведены к экспериментальным данным. Из явного EOS для давления выводятся и рассчитываются энтальпия, удельная теплоемкость при постоянном объеме и постоянном давлении, а также коэффициенты летучести. Бинарные смеси h3O / O2, h3O / N2, h3O / CO2, N2 / CO2, а также тройная смесь h3O / O2 / N2 хорошо предсказываются предложенным уравнением состояния с относительными ошибками ниже 10% и 15% соответственно. Область низких температур и высокого давления наиболее сложно предсказать с относительной погрешностью до 20%.
1. Введение
Сверхкритическое водное окисление (SCWO), также называемое гидротермальным окислением (HTO), происходит при условиях, превышающих критическую точку воды (Tc = 647,14 K, pc = 22,064 МПа) [1]. Обычно температура и давление находятся в пределах 673–923 К и 22–35 МПа соответственно. SCWO представляет особый интерес для сырья с высоким содержанием воды ( например, осадок сточных вод, бумажный осадок, и т. Д. ), поскольку нет необходимости в энергоемкой сушке перед процессом [2].В течение времени пребывания до нескольких минут исходный материал полностью разлагается, главным образом, на диоксид углерода, воду, азот / аммиак и минералы [3]. По сравнению с горением скорость реакции между азотом и кислородом низкая, поэтому оксид азота не образуется [3]. Сверхкритическая вода представляет собой интересную реакционную среду из-за ее смешиваемости с газами, такими как кислород, азот и диоксид углерода, что обеспечивает гомогенную реакцию и высокие скорости реакции [4].
Моделирование процесса SCWO требует точного расчета термодинамических свойств, таких как температура, давление, молярный объем, энтальпия, теплоемкость и летучесть [4].В широком диапазоне температур и давлений от окружающих условий до 923 К и 35 МПа процесса SCWO смесь, включающая четыре основных вещества — воду, кислород, азот и углекислый газ, ведет себя неидеально. Моделирование SCWO включает в себя задачу прогнозирования состояния вокруг критической точки, а также описание воды в ее жидкой форме. Таким образом, подразумевается необходимость точного прогнозирования плотности в широком диапазоне. Кроме того, вода меняет свой сильный полярный характер на умеренный в сверхкритическом состоянии [4], [5].Эти характеристики процесса SCWO предъявляют сложные требования, которые должны быть удовлетворены для надлежащего моделирования термодинамических свойств [4].
Уравнения состояния (EOS) представляют собой подход к описанию состояний неидеальных газов и их термодинамических свойств [4]. Ван-дер-Ваальс разработал первое уравнение состояния, описывающее плотность жидкости и пара, а также явления критической точки кубическим уравнением [6]. EOS учитывает притяжение между молекулами и совместным объемом из-за пространственного расширения молекул.Он позволяет прогнозировать равновесие жидкость-пар для чистых соединений и сводится к уравнению для идеального газа для высоких температур и низких плотностей. Прогноз состояния pvT становится менее точным, чем выше плотность жидкости. Редлих и Квонг улучшили это уравнение состояния, расширив член притяжения с помощью температурной зависимости (α (T)) [7]. Соаве ввел другую температурную зависимость, включая ацентрический фактор (ω) в качестве третьего параметра по отношению к критической температуре и критическому давлению, что привело к уравнению состояния Редлиха – Квонга – Соаве (RKS) [8].Точность для неполярных веществ с высокими ацентрическими факторами улучшается, в то время как плотности жидкостей все еще трудно предсказать. Дальнейшая модификация члена притяжения Пенга и Робинсона (PR) обеспечивает более точное предсказание плотности жидкости [9]. Упомянутые УС имеют ту же обобщенную кубическую структуру:
p = RTv − b − a (T) v2 + ubv − wb2
(1)
с параметрами a (T) = acα (T), ac = ΩaR2Tc2pc и b = bc = ΩbRTcpc. Зависящие от уравнения параметры α (T), u и w, а также безразмерные константы Ωa и Ωb приведены в.RKS и PR EOS широко используются, особенно для углеводородных систем [10], [11]. Мартин ввел объемный перенос c, который увеличивает точность предсказания плотности в широком диапазоне температур и давлений, включая жидкую и газовую фазы [12]. Разделяя суб- и сверхкритическую область, Бостон и Матиас расширили область применения α (T) [13]. Матиас улучшил эти отношения, изменив высокополярные вещества, такие как вода, введя полярный параметр в α (T) [14].Дальнейшее улучшение было достигнуто Шварцентрубером и Реноном путем введения трех полярных параметров [15]. Перемещение объема в зависимости от температуры может привести к изотермическому пересечению, и . наблюдается при отрицательной теплоемкости [16], [17], [18], [19], [20]. Le Guennec et al. предложены транслируемые согласованные уравнения состояния с согласованными α-функциями и независимым от температуры объемным переносом для точного предсказания термодинамических свойств путем устранения изотермических пересечений и разрывов в α и его производных [21].
Таблица 1
Параметры и α-функции различных кубических УС. Сокращения EOS: Van der Waals (VdW), Redlich – Kwong (RK), Redlich – Kwong – Soave (RKS), Peng – Robinson (PR), Boston – Mathias (BM), Volume-Translation-Boston-Mathias-Schwartzentruber -Ренон (ВТБМСР).
| EOS | Каталожный номер | u | w | α (T) | Ωa | Ωb | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VdW | 0303 [1 | ], [], [] | 1 | 0.421875 | 0,125 | ||||||||
| RK | [1], [11] | 1 | 0 | 1 / Tr | 0,4275 | 0,08664 | |||||||
| 11 RKS | [1]1 | 0 | 1 + m (1-Tr) 2 | 0,42748 | 0,08664 | ||||||||
| m = 0,48 + 1,574ω − 0,176ω6 | PR | [1], [9] | 2 | 1 | 1 + m (1-Tr) 2 | 0.45724 | 0,07780 | ||||||
| m = 0,37464 + 1,54226ω − 0,26772ω2 | |||||||||||||
| i) Tr≤1 | 0,45724 | 0,07780 | |||||||||||
| 1 + m (1-Tr) 2 | 9077 | ||||||||||||
| Tr> 1 | |||||||||||||
| exp {cd (1 − Trd)} | |||||||||||||
| 37464 + 1,54226ω − 0,26992ω2 | |||||||||||||
| d = 1 + m / 2 | 9030 9030 d | ||||||||||||
| Mathias | [14] | 1 | 0 | i) Tr≤1 | 0,42727 | 0,08864 | |||||||
| 1 − Tr) −pi (1 − Tr) (0.7 − Tr) 2 | |||||||||||||
| ii) Tr> 1 | |||||||||||||
| 7 } 2 | |||||||||||||
| m = 0,48508 + 1,55191ω − 0,15613ω2 | 9077 | ||||||||||||
| 9077 | |||||||||||||
| 9077 +0.3pi | |||||||||||||
| d = (cd − 1) / cd | |||||||||||||
| VTBMSR-I | 9077 0 i) Tr≤10,42748 | 0,08664 | |||||||||||
| exp {cd (1-Trd)} 2 | 906 | 906 | 9077 ) Tr> 1 | ||||||||||
| 1 + m (1 − Tr) −p0 (1 − Tr) (1 + p1Tr + p2Tr2) 2 | m = 0.48508 + 1,55191ω − 0,15613ω2 | ||||||||||||
| cd = 1−1 / d | 906 | 9030 1 0,5 м − p0 (1 + p1 + p2) | |||||||||||
| VTBMSR-II | [11] | 1 | 0 | i) Tr≤1 | 0,42748 | 906 0,06 0,06exp {cd (1 − Tr)} 2 | |||||||
| ii) Tr> 1 | 1 + m (1 − Tr) −p0 (1 − Tr) (1 + p1Tr + p2Tr2) 2 | ||||||||||||
| m =.48508 + 1,55191ω − 0,15613ω2 | |||||||||||||
| cd = 1−1 / d | 906 | 9030 1 0,5 м − p0 (1 + p1 + p2) | |||||||||||
| VTBMSR-III | эта работа | 1 | 0 | i) Tr≤1 | 0,42748 | 0,08664 | 0,06 | 1 + m (1 − Tr) −p0 (1 − Tr) (1 + p1Tr + p2Tr2) 2 | |||||
| 9030 ii> 1 | |||||||||||||
| exp {cd (1-Trd)} 2 | 48508 + 1,55191ω − 0,15613ω2 | ||||||||||||
| cd = 1−1 / d | 906 | 9030 1 0,5m − p0 (1 + p1 + p2) |
Уравнение состояния чистого соединения расширено за счет концепции одножидкостной смеси. Для фиксированного состава предполагается, что свойства смеси и их изменения в зависимости от температуры и давления могут быть описаны как чистое соединение с регулируемыми параметрами в зависимости от состава смеси [1].Основным подходом к определению параметров смеси amix и bmix являются обычные правила смешивания, в которых параметры смешивания имеют квадратичную зависимость от состава (правило квадратичного смешивания) [20], [22], [23].
amix = ∑i = 1N∑j = 1Nxixjaij
(2)
bmix = ∑i = 1N∑j = 1Nxixjbij
(3)
cmix = ∑i = 1N∑j = 1Nxix5 9000jcij (9000 )
Состав описывается мольными долями соединений xi и xj соответственно. Перекрестные параметры aij, bij и cij закрываются правилом комбинирования, которое может различаться по сложности.Самая простая форма — среднее арифметическое или геометрическое [1]. В этих случаях правила смешивания сводятся к линейной зависимости. Для перекрестных параметров aij и bij обычно применяются невзвешенные правила комбинирования Лоренца – Бертело [18]. Privat et al. заявил, что только правило комбинирования со средним арифметическим удовлетворяет ограничениям для перевода смешанного объема (cij) [20].
Эти простые правила не могут адекватно описать большинство смесей, особенно смесей, включающих жидкости [1]. Чтобы улучшить aij и bij, вводятся параметры бинарного взаимодействия ka, ij и kb, ij для описания отклонения от среднего геометрического и характеристики взаимодействия i-j [24], [25].
bij = 12 (bi + bj) (1 − kb, ij)
(9)
Параметры взаимодействия могут быть определены путем подгонки к экспериментальным данным. Помимо постоянных параметров взаимодействия они могут быть сформулированы как температурно-зависимые (kij = f (T)) [14]. Шварцентрубер и Ренон дополнительно расширили взаимодействие с помощью третьего параметра взаимодействия lij и зависимости от мольной доли соединений, что привело к неквадратичному правилу смешивания [15].
aij = aiaj1 − ka, ij− (xi − xj) lij
(10)
bij = 12 (bi + bj) (1 − kb, ij)
(11)
Для параметров взаимодействия ka , ij, kb, ij и lij предполагается следующая температурная зависимость.
kij = kij (0) + kij (1) T + kij (2) / T
(12)
lij = lij (0) + lij (1) T + lij (2) / T
( 13)
Параметры взаимодействия kij (z) и lij (z) определяются путем подгонки к экспериментальным данным.
На основе этих разработок соответствующий EOS для моделирования процесса SCWO разработан и подтвержден с доступными экспериментальными данными.
2. Разработка EOS
Характеристики процессов SCWO предполагают следующие требования к EOS, описывающим термодинамическое поведение процесса [11]:
- • Точное предсказание плотности, энтальпии и теплоемкости чистых веществ в широком диапазоне температур и давлений, особенно для воды
- • Распространение на смеси воды, углеводородов и газов без снижения точности
- • Простая математическая формулировка для обеспечения числовой стабильности
- • Явная формулировка давления или объема, позволяющая получить дополнительные термодинамические свойства
- • Минимальное количество настраиваемых параметров, обеспечивающих стабильные и быстрые вычисления
Пока ни один из УРС в литературе не удовлетворяет всем этим требованиям [4], [21].
2.1. Разработанное уравнение состояния
EOS, представленное в этой работе, спроектировано таким образом, чтобы наилучшим образом удовлетворять вышеупомянутым требованиям. Это достигается путем добавления следующих модификаций в кубический RKS EOS [7], [8]:
- • Введение температурно-зависимого преобразования объема для точного предсказания плотности (жидкости) [12]
- • Представление полярной характер воды путем введения полярных параметров в α [13], [14], [15]
- • Применение неквадратичных правил смешивания [15]
Полученный в результате явный EOS по давлению называется VTBMSR EOS, как представлено Пильца [11], [26].Однако параметры VTBMSR EOS еще не опубликованы.
p = RTv + c − b − acα (v + c) (v + c + b)
(14)
Константы ac и b равны
ac = 19 (21 / 3−1) R2Tc2pc
(15)
Объемный перенос c зависит от (приведенной) температуры Tr и параметров объемного переноса ci [11], [26].
- • Tr≤1
- • Tr≤1, c2 = Tr − 1
- • Tr> 1, c1 = 0
- • Tr> 1, c1 ≠ 0
c = b + (c0 − b) c2c1 + 12c11 + c2 (c0 − b) c2c1 + 1 − Tr
(20)
- • Tr> 1, c1 ≠ 0, c2 (c0 − b) c2c1 + 1 = Tr − 1
Ур.(18) и (21) добавляются к определению Пильца [11], [26]. Улучшенный прогноз плотности в жидкой фазе по сравнению с другими EOS показан во вспомогательной информации S3.1.
α-функция представляет собой обобщенный температурно-зависимый подход Матиаса, данный у Шварцентрубера и Ренона, с полярными параметрами pi, приведенной температурой Tr = T / Tc и ацентрическим фактором ω (см.) [14], [ 15].
α = 1 + m1 − Tr0.5 − p01 − Tr1 + p1Tr + p2Tr2Tr≤1
(22a)
d = 1 + 0.5m − p01 + p1 + p2
(22d)
m = 0,48508 + 1,55191ω − 0,15613ω2
(22e)
Предлагаемый VTBMSR-III отличается в двух аспектах от VTBMSR, опубликованного Pilz [11] (см. как ВТБМСР-II). Экспоненциальный член α (уравнение (22b)) расширяется на показатель степени d на основе VTBMSR, опубликованного Pilz [26] (называемого VTBMSR-I). Кроме того, критерий, основанный на пониженной температуре для выбора α-функции, заменен местами по сравнению с VTBMSR-II, взяв за основу Матиаса [14], который ввел расширение для Tr> 1.
Таблица 2
Критические температуры Tc, критические давления pc и ацентрические коэффициенты ω для воды, кислорода, азота и углекислого газа, [1], [27].
| Вода | Кислород | Азот | Углерод | |||||
|---|---|---|---|---|---|---|---|---|
| 154,58 | 126.20 | 304.12 | ||||||
| шт. | [МПа] | 22,064 | 5,043 | 3,398 | 7,374 | |||
| ω | [-] | 9158 0,344 | [-] | 9309 0,029 |
Улучшенные прогнозы энтальпии и теплоемкости, особенно в жидкой фазе, по сравнению с другими EOS показаны во вспомогательной информации S3.2-S3.4.
Параметры смеси для EOS смеси с N соединениями получены с помощью неквадратичных правил смешения, данных Шварцентрубером и Реноном [15].
amix = ∑i = 1N∑j = 1Nxixjaiaj1 − ka, ij− (xi − xj) lij
(23)
bmix = ∑i = 1N∑j = 1N12xixj (bi + bj) 1 − kb, ij
(24)
Температурно-зависимые параметры бинарного взаимодействия ka, ij, kb, ij и lij равны
ka, ij = ka, ij (0) + ka, ij (1) T + ka, ij (2) / T
(25)
кб, ij = kb, ij (0) + kb, ij (1) T + kb, ij (2) / T
(26)
lij = lij (0) + lij (1) T + lij (2) / T
(27)
с ka, ij = ka, ji, kb, ij = kb, ji, lij = lji, ka, ii = 0, kb, ii = 0 и lii = 0.
Для преобразования объема требуется правило сложения среднего арифметического, чтобы сохранить фазовые равновесия и свойства перемешивания [20]. Квадратичные правила смешивания в сочетании с правилом объединения среднего арифметического приводят к линейному правилу смешивания.
Поскольку эти правила смешивания зависят от композиции, они страдают синдромом Микельсена – Кистенмахера [28]. Синдром Микельсена-Кистенмахера описывает эффект отклонений, возникающих в результате применения правил смешивания, зависящих от состава.Эти правила не являются неизменными, когда соединение делится на несколько идентичных субсоединений. Поскольку такие проблемы возникают, когда смеси содержат аналогичные соединения, это не только теоретическая проблема. Другой эффект, называемый «эффектом разбавления», возникает из-за двойного суммирования для вычисления члена lij, в результате чего получается произведение трех мольных долей. Воздействие синдрома уменьшается с увеличением количества соединений. EOS, представленный в этой работе, избегает этого эффекта, исключая параметр взаимодействия lij, подробности показаны во вспомогательной информации S1.4.
Еще одна проблема — изотермическое пересечение, вызванное применением зависящего от температуры преобразования объема. Либол [17] и Privat et al. В [20] упоминаются наблюдения отрицательной теплоемкости при высоких температурах и пересечения изотерм в плоскости давление – объем, когда объемный перенос зависит от температуры. В наших расчетах отрицательных теплоемкостей не наблюдалось. Поведение в плоскости давление – объем не изучалось.
Объемный перевод, параметры полярного и бинарного взаимодействия ci, pi, ka, ij (z) и kb, ij (z) получаются путем регрессии к экспериментальным данным, как описано в разделах 2.3 и 2.4.
2.2. Справочные данные / валидация
Было опубликовано лишь несколько экспериментальных данных для смесей воды, кислорода, азота и двуокиси углерода бинарного или более высокого порядка в сверхкритических условиях. Джапас и Франк опубликовали данные pvT для систем h3O / N2 и h3O / O2 с различными температурой, давлением и концентрацией [29], [30]. Они измерили молярный объем при трехмерном (pTx) фазовом равновесии. Охватываемый диапазон температуры и давления составляет 500–673 К (докритический) и 20–270 МПа.Мольная доля воды изменяется от 0,134 до 0,9 в системе h3O / N2 и от 0,058 до 0,9 в системе h3O / O2. Кроме того, они опубликовали некоторые данные для системы вода – воздух [30].
Gallagher et al. опубликованные экспериментальные данные для системы h3O / N2, а также для системы h3O / CO2 в диапазоне 400–1000 K, до 100 МПа и мольных долях до xN2 = 0,8 и xCO2 = 0,3 соответственно [31], [ 32]. Johns et al. измерили теплопроводность бинарной смеси азота и углекислого газа [33].Полученный диапазон экспериментальных данных охватывает температуры от 302 до 470 К, мольные доли азота от 0,160 до 1 и давления до 26 МПа. Для чистых веществ вода, кислород, азот и углекислый газ справочные данные NIST (Национальный институт стандартов и технологий) с использованием их программного обеспечения Refprop 9.1 используются для проверки улучшенного EOS [27]. Обзор справочных данных показан на.
Таблица 3
Обзор справочных данных для чистых веществ и смесей.
| Ссылка | Вещество (а) | Молярная доля | Температура | Давление | Свойства | |
|---|---|---|---|---|---|---|
| 9029 MP | ||||||
| Refprop [27] | h3O | 292,15–882,15 | 0,1–35,1 | T, p, ρ, v, h, cv, cp | ||
| O2 .15–878,15 | 0,1–35,1 | T, p, ρ, v, h, cv, cp | ||||
| N2 | 298,15–878,15 | 0,1–35,1 | T, p, p, p, v, h, cv, cp | |||
| CO2 | 298,15–878,15 | 0,1–35,1 | T, p, ρ, v, h, cv, cp | |||
| Япония и Франк [ ] | h3O / N2 | 0,14–0,9 | 480–660 | 11,5–270.5 | T, p, v | |
| Джапас и Франк [30] | h3O / O2 | 0,08–0,9 | 470–660 | 19,5–280,0 | T, p, v | Johns | N2 / CO2 | 0,16–0,708 | 320–470 | 9,0–30,8 | T, p, ρ |
| Gallagher et al. [32] | h3O / CO2 | 0,7–0,95 | 400–1000 | 0,05–100,0 | T, p, v, h | |
| Gallagher et al.[31] | h3O / N2 | 0,2–0,95 | 440–700 | 0,05–100,0 | T, p, v, h | |
| Джапас и Франк [30] | h3O / воздух | 03 –0,798620,5–673 | 27,0–279,5 | T, p, v |
2.3. Регрессия
Регрессия различных параметров ci, pi и kb, ij по имеющимся экспериментальным данным была проведена с использованием программного обеспечения Aspen Plus TM , версия 9.x и 10.1 от Aspen Technology Inc. и применяя метод максимального правдоподобия [11], [34]. Благодаря исследовательскому проекту Pilz [11] по моделированию процессов, Aspen считается подходящим инструментом для определения параметров. Регрессия была проведена с помощью Aspen, несмотря на его ограниченную применимость для соответствующих параметров, как указано ниже. Таким образом, текущая работа проводилась с Matlab 2017b (расчеты) и R 3.4 (графики). Используемые справочные данные перечислены в Pilz [11] и во вспомогательной информации S4.1.
Поскольку и температура, и давление менялись одновременно, регрессия была нестабильной и могла прерваться до завершения. Следовательно, стратегия заключалась в том, чтобы сначала регрессировать все три параметра ci с использованием данных pvT. После этого три полярных параметра pi были определены с использованием данных о давлении насыщения и калориях. Однако Aspen Plus TM не различает сверхкритические области или фазы, а рассматривает их как часть паровой фазы. Для регрессии плотности все ее состояния, жидкость и пар / сверхкритическая фаза, а также состояние насыщенной жидкости и пара должны быть приняты во внимание в единой регрессии, поскольку летучесть зависит от этого результата регрессии.Отсюда следует, что хорошее представление плотности, в основном с помощью параметров ci, является решающим для расчета фазовых равновесий и фазового состава. Что касается параметров pi, данные должны быть разделены, поскольку две зависимые от температуры α-функции действительны либо ниже, либо выше критической температуры. Итак, для параметров pi извлекаются два набора данных. Регрессия к кислороду всех трех параметров объемной трансляции CI постоянно терпела неудачу. Вместо этого в процедуре регрессии использовался только один параметр c0.Тем не менее расчет дает разумные результаты. Реализация полярных параметров пи сработала правильно. То же самое и с углекислым газом. Регрессия бинарных параметров основана на результатах регрессии чистого вещества. Однако регрессировать все параметры бинарного взаимодействия не удалось из-за проблем сходимости. Следовательно, основное внимание уделяется определению параметров kb, ij, поскольку они включены как в отталкивающий, так и в притягивающий члены.
Результирующие наборы регрессионных параметров перечислены во вспомогательной информации S1.1.1 – S1.1.3.
2.4. Параметры
Для каждого чистого соединения и бинарной смеси предлагаются разные наборы параметров. Таким образом, наиболее подходящий набор для каждой конкретной системы необходимо определять отдельно. Поэтому справочные данные пересчитываются с каждым набором параметров. На основе усредненных абсолютных относительных ошибок расчетных данных (см.) Выбирается наиболее подходящий набор параметров, как указано в.Из-за минимальных различий в ошибках далее считается, что выбираются наборы параметров, которые регрессируют до данных одного и того же свойства (, например, энтальпии или плотности). Для воды это означает, что для жидкой и паровой фазы выбираются наборы параметров, полученные на основе справочных данных одного и того же свойства (, например, энтальпии). Что касается смесей, наборы параметров, определенные путем регрессии к данным плотности, выбираются для всех бинарных смесей.
Таблица 4
Усредненные абсолютные относительные ошибки и стандартные отклонения [%] между расчетными и справочными данными чистых соединений для различных наборов параметров, полученные на основе разных справочных данных, используемых для регрессии (более подробно в вспомогательной информации S1.1).
| Вещество | Набор | vm | h | cv | cp | ||||
|---|---|---|---|---|---|---|---|---|---|
| h3O (l) | 1 | 1,7 ± 0,1 | |||||||
| 2 | 6,3 ± 0,1 | 94 ± 3 | 11,9 ± 0,3 | 1,8 ± 0,1 | |||||
| h3O (v / sc) | 1 | 2,0 | 0.82 ± 0,02 | 8,7 ± 0,3 | 6,3 ± 0,3 | ||||
| 2 | 2,3 ± 0,1 | 0,87 ± 0,03 | 10,7 ± 0,3 | 6,7 ± 0,3 | |||||
| 9030 ± 0,1 | 0,85 ± 0,03 | 10,4 ± 0,3 | 6,7 ± 0,3 | ||||||
| O2 | 11 | 1,15 ± 0,02 | 0,37 ± 0,01 | 1,69 ± 0,02 | 12 | 0.463 ± 0,008 | 0,584 ± 0,008 | 2,78 ± 0,05 | 1,10 ± 0,03 |
| 13 | 0,78 ± 0,01 | 0,353 ± 0,009 | 2,05 ± 0,03 | 0,0830914 | 0,543 ± 0,009 | 0,668 ± 0,009 | 2,92 ± 0,05 | 1,16 ± 0,03 | |
| 15 | 0,487 ± 0,009 | 0,611 ± 0,008 01598 2,9051,12 ± 0,03 | |||||||
| 21 | 0,418 ± 0,008 | 0,376 ± 0,006 | 1,69 ± 0,02 | 0,83 ± 0,02 | |||||
| 0,02 | |||||||||
| 0,03 9776 220303 9159 0,03 9158 0,03 | |||||||||
| 2,78 ± 0,05 | 1,10 ± 0,03 | ||||||||
| 23 | 0,78 ± 0,01 | 0,517 ± 0,007 | 2,05 ± 0,03 | ||||||
| 1,10 ± 0,02 | 2,92 ± 0,05 | 1,16 ± 0,03 | |||||||
| 25 | 1,55 ± 0,03 | 1,03 ± 0,01 | 2,83 ± 0,05 0,03 9028 1 | 1 | 0,326 ± 0,005 | 0,446 ± 0,006 | 1,97 ± 0,04 | 0,84 ± 0,02 | |
| 2 | 1,95 ± 0,03 | 15 0,97 ± 0,03 0,458 ± 0,03 | 0,97 ± 0,03 | 0,97 ± 0,03 | 9552 ± 0,007|||||
| CO2 | 1 | 3,07 ± 0,05 | 0,69 ± 0,01 | 4,9 ± 0,2 | 2,60 ± 0,08 | ||||
| 2 | 0,48 ± 0,015 3,48 ± 0,072,11 ± 0,04 |
Таблица 5
Оптимальный объемный перенос и полярные параметры чистых соединений. Нижние индексы (l) и (v / sc) указывают жидкую или паровую / сверхкритическую фазу воды.Чтобы избежать ошибок округления, значения перечислены с полными цифрами, несмотря на ограниченную значимость.
| Параметр | Единицы | h3O (л) | h3O (v / sc) | O2 | N2 | CO2 |
|---|---|---|---|---|---|---|
| Набор | 2 1 | 2 | ||||
| Рег. на | h | h | cp | h | cp | |
| c0 | m 3 / моль | 2.8126 × 10 −7 | 2,8126 × 10 −7 | 4.366 × 10 −6 | 0 | 5,47 × 10 −6 |
| c1 | 5,25308 × 10 −6 | 5,25308 × 10 −6 | 0 | 0 | 0 | |
| c2 | — | 0,4059842 | 0,4059842 | 0,4059842 | ||
| п0 | — | 0.20 | 8-1, | |||
| p1 — | -0,01398072 -1,13 | -0,10036104 -0,015334 | ||||
| p2 — | 0,07999497 | 0,22028766 | −0,10036213 | −0,015334 | −0,51240405 |
Для определения наиболее подходящих параметров двоичного взаимодействия (набор параметров двоичного взаимодействия) ) конкретных чистых соединений ().Полученные усредненные абсолютные относительные погрешности бинарных смесей перечислены в, а выбранные наборы параметров и их параметры приведены в. Поскольку диапазон данных Джапаса и Франка в основном превышает рабочий диапазон процесса SCWO, для бинарной смеси h3O / N2 справочные данные Gallagher et al. имеет больший вес из-за лучшего представления диапазона процесса [29], [30], [31]. Помимо относительной ошибки, распределение ошибок рассматривается графически, e.грамм. для h3O / N2, где усредненные относительные ошибки различаются лишь незначительно для наборов параметров 2 и 4. a и b показывают, что набор параметров 2 имеет более низкую максимальную ошибку и более равномерное распределение в пределах наблюдаемого диапазона. Кроме того, считается, что регрессия выполняется на тех же данных свойства (, например, плотность).
Таблица 6
Усредненные абсолютные относительные ошибки и стандартные отклонения [%] между расчетными и эталонными данными бинарных смесей для различных наборов параметров взаимодействия, полученные в результате различных эталонных данных, используемых для регрессии (более подробно в Вспомогательной информации S1.1).
